The Multiple Unmanned Air Vehicle Persistent Surveillance Problem: A Review

Abstract

Control of autonomous vehicles for applications such as surveillance, search, and exploration has been a topic of great interest over the past two decades. In particular, there has been a rising interest in control of multiple vehicles for reasons such as increase in system reliability, robustness, and efficiency, with a possible reduction in cost. The exploration problem is NP hard even for a single vehicle/agent, and the use of multiple vehicles brings forth a whole new suite of problems associated with communication and cooperation between vehicles. The persistent surveillance problem differs from exploration since it involves continuous/repeated coverage of the target space, minimizing time between re-visits. The use of aerial vehicles demands consideration of vehicle dynamic and endurance constraints as well. Another aspect of the problem that has been investigated to a lesser extent is the design of the vehicles for particular missions. The intent of this paper is to thoroughly review the persistent surveillance problem, with particular focus on multiple Unmanned Air Vehicles (UAVs), and present some of our own work in this area. We investigate the different aspects of the problem and slightly digress into techniques that have been applied to exploration and coverage, but a comprehensive survey of all the work in multiple vehicle control for search, exploration, and coverage is beyond the scope of this paper.

1. Introduction

There has been growing interest in control and coordination of autonomous vehicles in the fields of Artificial Intelligence (AI) and controls. Both fields have studied similar problems from different viewpoints, but many recent techniques borrow from both fields. Barto, Bradtke, and Singh [1] describe how these fields fit together for online control and learning and detail several methods for illustration. Cao, Fukunaga, and Kahng [2] provide a broad survey of mobile robotics with emphasis on the mechanism of cooperation. They also give a taxonomical organization of literature based on problems and solutions, while identifying five research axes: group architecture, resource conflict, origin of cooperation, learning, and geometric problems. Jennings, Sycara, and Woolridge [3] look at the problems, application domains, and future research directions for autonomous agents and multi-agent systems. Parker [4] provides a slightly more recent overview of distributed autonomous mobile robotics with particular emphasis on physical implementations. She has identified the following areas of research interest in mobile robotics: biological inspirations, communication architectures, localization/mapping/exploration, object transport and manipulation, motion coordination, reconfigurable robots, and learning. Ref. [5] defines, characterizes, and cites advantages of Multi-Agent Systems (MASs), while analyzing approaches to deal with them. Chandler and Pachter [6] discuss research issues, particularly pertaining to autonomous control of tactical UAVs.

The task of search/exploration/coverage has received particular attention in the past two decades. Hougen et al. [7] categorize exploration missions and detail techniques used to deal with them. They also list the robot capabilities required to deal with each type of mission. Saptharishi et al. [8] describe recent advances in areas of efficient perception (detection, classification, and correspondence) and mission planning (task decomposition, path planning, plan merging, and mission coordination) for surveillance. In their work, the emphasis is on perception and map building for CMU’s Cyberscout project. Choset [9] provides a succint survey of work done on coverage tasks in particular. He classifies coverage algorithms and gives a brief analysis of each, though sufficient attention is not given to cooperative robotics. Polycarpou, Yang, and Passino [10] study several search techniques and divide search problems into 4 types depending upon target dynamics. Ref. [11,12,13,14] give brief surveys of exploration and coverage techniques as well. Enright, Frazzoli, Savla, and Bullo [15] look at the Traveling Salesman Problem (TSP) and related problems, which is one way to pose an exploration problem. In their work, dynamic constraints are imposed on vehicles, resulting in the Dynamic Traveling Repairperson Problem (DTRP). Arkin and Hassin [16] study the geometric covering salesman problem, that is a generalization of TSP, and discuss related problems (for instance sweeping and milling). In this problem, the salesman has to visit neighborhoods around target points, and it becomes the same as a coverage problem if all the neighborhoods are translates of each other. They further point out that the TSP and related problems are NP hard, and this claim is supported by [17]. Yuan, Chen, and Xi [18] review Mobile Sensor Networks (MSNs) (emphasizing the importance of mobility), with particular attention to topology control, coverage control and localization. Cui, Hardin, Ragade, and Elmaghraby [19] survey exploration techniques for detection of hazardous material.

Though the surveys mentioned above are great in their own respect, none of them seem to focus on persistent surveillance. This problem is different from exploration since the target space needs to be continuously surveyed, minimizing the time between visitations to the oldest explored region. It is one of the most common information collection tasks, usually defined as a problem of maintaining an up-to-date picture of the situation in a given area [20]. It also differs from coverage problems which involve determination of the optimum locations of sensors such that a target space is completely covered at all times. Thus, even though some techniques from exploration and dynamic coverage may be modified to apply to persistent surveillance, it is desirable to think of new ideas for more efficient techniques. The existing surveys also tend to focus on robotics, not particularly looking at aerial vehicles and sometimes do not explore the aspect of coordination between multiple vehicles. The issues of vehicle dyanmics and endurance also become particularly important in case of aircraft. In this paper, we try to review several aspects of the “persistent surveillance problem”, focusing on techniques for multiple Unmanned Air Vehicles (UAVs). Though we will digress from this specific objective time and again to provide context for this problem with regards to other work in Multi-Agent Systems (MASs), a comprehensive survey of control and coordination or multiple autonomous vehicles is beyond the scope of this paper. It is also our intent to place some of our own work in context of this review and other research in this area.

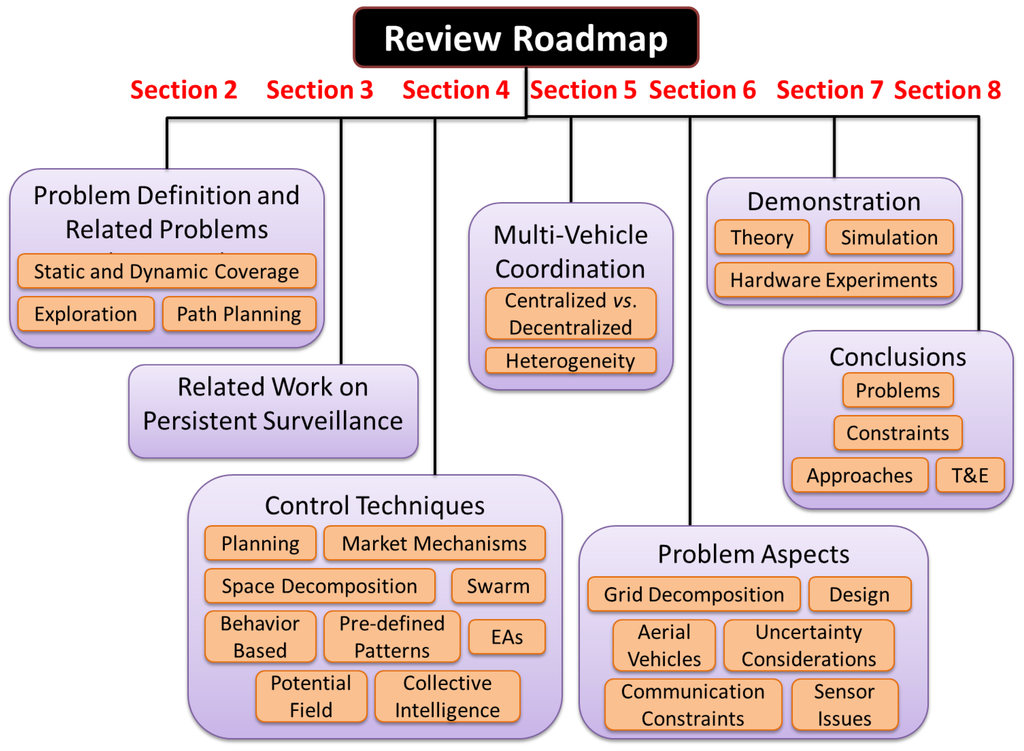
Figure 1. Schematic of the roadmap describing the organization of this paper.

Figure 1. Schematic of the roadmap describing the organization of this paper.

Figure 1 shows the roadmap for this paper. We begin with a discussion of the problem definition and other problems that are related to persistent surveillance, in Section 2. We then look at papers that have looked specifically at variants of this problem in Section 3. Section 4 provides a rough categorization of approaches for single and multi-vehicle control, citing particular work in each of those categories. Note that these categories are not mutually exclusive, and certain work lies in more than one of them. Section 5 briefly discusses ideas for multi-agent coordination used for this problem, along with centralized vs. decentralized techniques and studies with heterogeneous platforms. In Section 6 we looks at certain aspects/extensions of the problem, including grid decompositions, communication architectures, sensor issues, and concerns for aerial vehicles. The section ends with a brief discussion of approaches to deal with uncertainties and a novel aspect coupling control system and vehicle design problems. This provides a quick access to the relevant work associated with particular aspects of interest, while emphasizing on the amount of work done in each domain. The methods proposed in existing literature have used different approaches for verification, ranging from theoretical proofs of soundness and completeness, to hardware demonstrations. These are identified in Section 7 and finally we end with a dicussion of future directions of research in Section 8.

2. Problem Definition

One of the pressing problems in the field of autonomous system control is the lack of standard definitions for problems, due to the variety of research pursued worldwide. This is exemplified by some of the previous work that has tried to categorize problems and provide a taxonomy for them [2,21,22]. Here, we do not attempt to devise a generic definition of persistent surveillance that encompasses all such problems encountered in literature. Instead, we present a particular definition of the problem that will be used to guide the discussion in the remainder of the paper. This definition is close to the ones used by others [20,23,24], and has also been used in our prior work. The idea of “persistence” naturally induces the notion of continuous in time or repetition. This becomes the motivation behind our definition, which is outlined below [25].

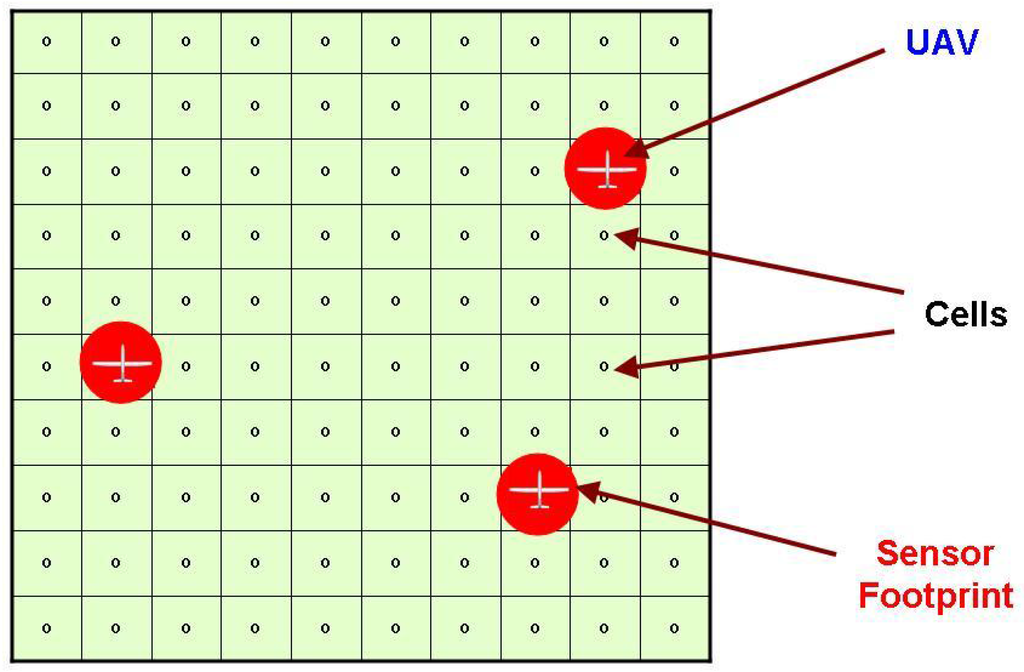
Figure 2. Illustration showing the target space gridded using cells. Each UAV has a circular sensor footprint that equals the grid cell size.

Figure 2. Illustration showing the target space gridded using cells. Each UAV has a circular sensor footprint that equals the grid cell size.

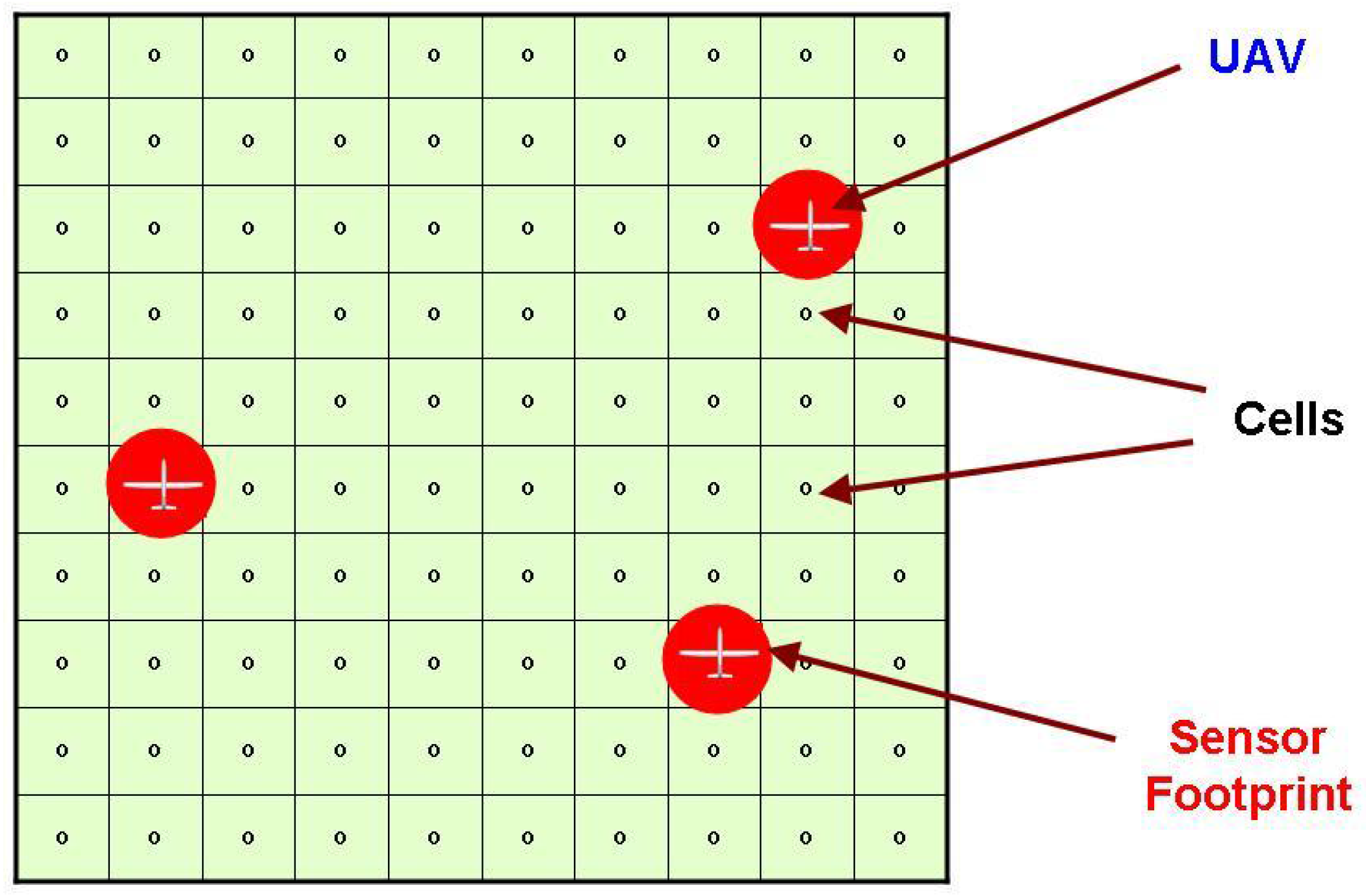
Consider a 2-D target space as shown in Figure 2, which is gridded using an approximate cellular decomposition—this means that the sensor footprint equals the cell size [9]. It is also assumed that the cells exhaustively cover the target space. Each cell has an associated age, which is the time elapsed since it was last observed. The goal of persistent surveillance is to minimize the maximum age over all cells that is observed over a “long” period of time. This is equivalent to leaving no area of the target space unexplored for a long duration. This formulation is useful for several applications. For instance, if we want to constantly monitor a particular area as in a patrolling problem, tactical surveillance, or atmospheric monitoring. Similarly, if a region is expected to have “pop-up” targets, then such a problem needs to be solved in searching for the target. A variant of this problem has been proven to be NP-hard in [26] and APX-hard in [27].

This definition can also be extended to three dimensions in several ways. A straightforward extension is obtained by gridding the space using volume elements. This may be useful in certain applications such as toxic plume detection [28] or urban structure coverage [29]. However, for many applications, the “target space” of interest is 2-D in nature (typically the surface is being observed) and the 3-D extension only involves 3-D dynamics of the vehicles and sometimes 3D occlusions [30]. Moreover, this becomes important when the sensing (either the sensor footprint or the quality) or risk of threat depends on the altitude of the UAV [31]. In this paper, we discuss most of the techniques in context of the 2-D problem, though we make a special note of 3-D applications in Section 6.4.1.

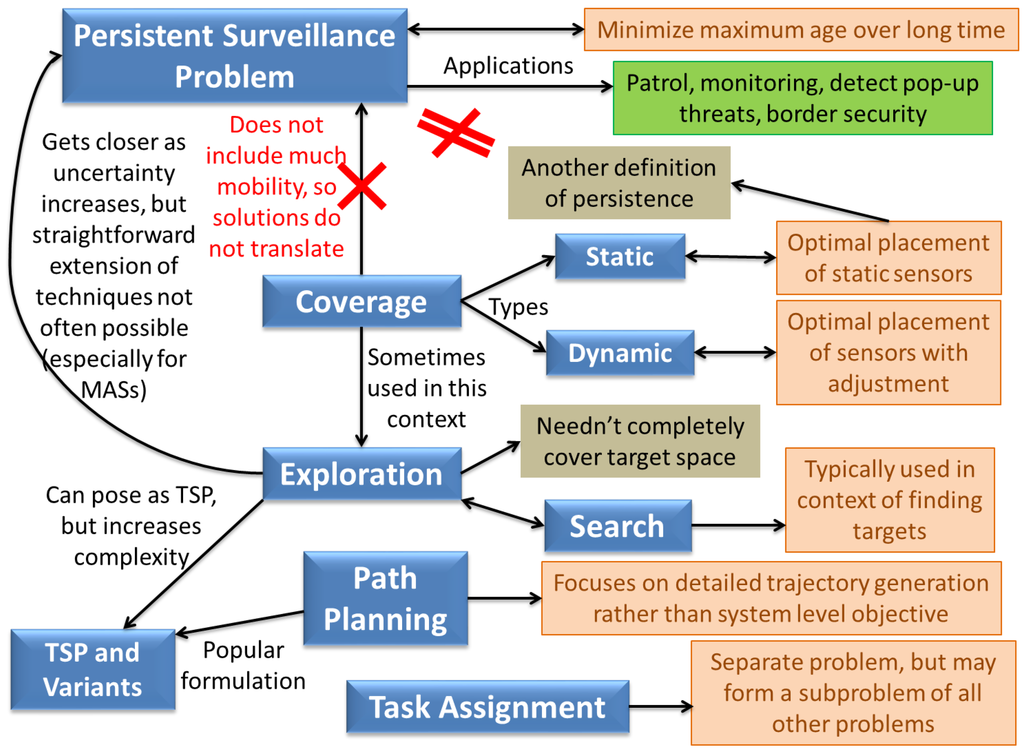
Figure 3. Persistent Surveillance and its relation to other commonly studied problems.

Figure 3. Persistent Surveillance and its relation to other commonly studied problems.

Figure 3 illustrates the relation of persistent surveillance to other related problems. It is different from the coverage problem as defined by Cassandras and Li [32] and Choset [9], which is basically a sensor deployment problem. The latter can be further divided into static coverage, similar to a facility location problem [33], and dynamic coverage which involves environment dynamics [18]. Static coverage tries to find a static configuration of sensors to observe the target space continuously (note that this is another interpretation of persistent surveillance, [34] but we do not include it in our definition). Similarly, dynamic coverage is an extension of the static analog where there can be uncertainties or dynamism in the environment, leading to “adjustment” of optimal static sensor locations. Both these problems do not particularly require mobile nodes or vehicles (except for the initial deployment and occasional adjustment), so the solutions tend to be very different in nature. For instance, in coverage, once the optimal configuration is found, there is no incentive for the agents to move, unless the environment changes [35]. Hence deployment is often more important than control law design [36,37]. The coverage problem has a most direct application in sensor networks [38] that are not the focus of this paper.

Another commonly used definition for coverage [39,41,42,43,44] is in the sense of exploration [45,46,47,48,49]. The former typically involves a complete coverage/exploration of the domain, while the exploration problem is more generic and need not result in completely covering the domain, depending on the objective. The exploration problem is closely related to persistent surveillance, and many problems have a persistence flavor if the sensors are faulty or there are dynamics in the environment (for instance, if the uncertainty grows over time). So the control techniques developed for the former may be extended to the latter. However, there are several differences which do not allow a straightforward application of exploration techniques to the persistent case. A simple example is when the methods developed for one-time coverage are repeatedly applied—this can be done for instance by marking all the cells in the domain as unexplored once exploration is complete. But this may result in inefficiency since the transient information is lost and even if the algorithm is optimal for one time coverage [39], it is not guaranteed to be optimal with respect to the objective defined above (minimizing maximum age over all cells). Certain work in patrolling literature [40] has claimed that the optimal strategy for a single cycle can be repeated to find the optimal strategy for persistent surveillance, but this holds true only if the start and end locations are the same (which is true for a cycle) and there are no dynamics/uncertainties in the environment. Furthermore, when we address multi-agent scenarios, the optimality of single agent coverage algorithms is lost [50,51], not to mention a higher possibility of inefficiency since the actions of other agents often increase the “noise” for each UAV and create different initial conditions each time the search is restarted. Often, exploration problems are posed as maximal information gain or uncertainty minimization problems as well [52,53,54], in which case, the objective is to minimize the cumulative uncertainty over the domain rather than maximum/peak uncertainty. So there are no guarantees that such methods will retain their efficiency with respect to the persistence objective—in fact, they may not even guarantee complete coverage. Hence there is a need for methods that explicitly address the problem posed above [55].

All the above problems in a generic sense incorporate the problem of path planning [56,57,58], which can be described as one of generating trajectories for vehicles to particular goals (either predetermined or decided as part of the problem). Task assignment/allocation is often an important component of the problem as well [59,60], which is often solved separately for tractability [61,62]. The TSP [16] (and its generalization to multiple robots, the Multiple Traveling Saleman Problem (MTSP) [63,64]) can also be considered a path planning problem, where the waypoints are fixed, but their order is not (the minimum length solution is also called the minimum Hamiltonian cycle [26]). Note that the TSP solution is for one agent, but it can be used as a basis for multiple agents by either spacing agents evenly along the solution path [65], or partitioning the graph and solving multiple TSPs [66]. In general, path planning tends to focus on the detailed paths/trajectories being planned and often not on system level objectives of minimizing uncertainty or exploration time—hence resulting in slightly different kinds of solution techniques. All the same, these problems can borrow heavily from one another. For further information on this subject, the reader is encouraged read Ref. [67,68,69,70].

Some other problems that have been extensively studied in multi-agent systems and can give ideas for different aspects of persistent surveillance include mapping [67,71,72,73,74], and search/classify/attack [75,76,77,78,79], cooperative imaging [13,80,81], guard and escort [22,82,83], herding [84], and towing [85].

3. Related Work

Persistent surveillance has been studied under different names, including persistent monitoring [26] and area surveillance [30]. In this section we list some of the work that is most directly related to persistent surveillance. Persistent surveillance can be thought of as a generalization of the patrolling problem which has received much more attention by researchers [86,87]. Patrolling is basically defined as surveillance around an area to protect or supervise it [86]. It often uses concepts such as idleness, refresh time, blanket time, or latency which are similar to “age” defined in the previous section [27]. Often the objective is to minimize the maximum age—same as our definition above. However, the problem often ends up being single dimensional in nature [88] and many of the techniques are based on simple “back and forth” motions which are not easy to extend to generic scenarios [89]. The problem is also often posed as an intruder protection problem, where the time the intruder takes to cross the guarded perimeter is known and the goal is to not let any region unvisited for more than that time [86] — ref. [88] defines a variation to the problem, where the goal is to design a stochastic control scheme which cannot be easily estimated by an adversary. Hence interpreted as an optimization problem, it becomes more of a Constraint Satisfaction Problem (CSP) [90], rather than an objective minimization as posed described in the previous section (according to Smith and Rus [26], this is the distinguishing characteristic between dynamic coverage and persistent monitoring, though we have used a slightly different definition for dynamic coverage). However, depending on the technique used, this difference may become insignificant. Some of the work that has looked at multi-dimensional patrolling, includes that by Guo, Parker, and Madhavan [74]. In previous work, Guo and Qu [91] had devised feasible trajectories and real-time steering control for coverage of space containing moving obstacles in an uncertain environment. Ref. [74] extends this work to a multi-robot patrolling and threat response problem in Global Positioning System (GPS) denied areas, with emphasis on distributed sensing and multi-agent planning. Another generalization of patrolling is the task of guard and escort [22], particularly in context of escorting mobile vehicles. This problem however, tends to emphasize on tracking and formation flying aspects [83]. Certain other work by Soltero et al. [92] has focused on persistent monitoring where robots have intersecting trajectories—so the collision and deadlock avoidance problems become critical. They use an “accumulation function” similar to the age defined above, and design speed controllers, assuming paths are already given—hence the work is similar to 1-D patrolling, though they have planned paths in other work. In [93], they claim that speed control and path planning can be decoupled for efficiency of computation, with paths being determined offline. We do not completely support the idea of offline path planning, but the idea of using speed control along trajectories has not been used much in literature and seems to be interesting, especially from a obstacle avoidance point of view. A very similar idea (though different control approach) has been used in [94] for underwater glider coordinated control system—the objective function (objective analysis mapping error) is related to, but a much more complicated version of the maximum age metric. Similarly, Cassandras, Lin, and Ding [24] present an optimal control framework for persistent monitoring (where the concept of cumulative uncertainty instead of maximum age is used in the objective) in 1-D, and present ideas for extending the work to 2-D. Girard et al. [87] present a hierarchical control architecture for border patrol, assuming the border to be composed of long and thin regions—essentially leading to 1-D nature of the problem. Sauter et al. [95] develop a class of algorithms to enable robust/adaptive, complex, and intelligent behavior for multiple unmanned vehicles for protecting borders and critical infrastructure. Their approach does not seem to be limited to 1-D, though the demonstration example is perimeter protection. For a succint overview of patrolling techniques (heuristic, negotiation mechanisms, learning, graph theory etc.), performance metrics and simulation-based comparisons (using a graph patrol problem), the reader should refer [40]. We have tried to group some of the commonly used metrics for persistent surveillance, in Figure 4, but this is by no means an exhaustive list.

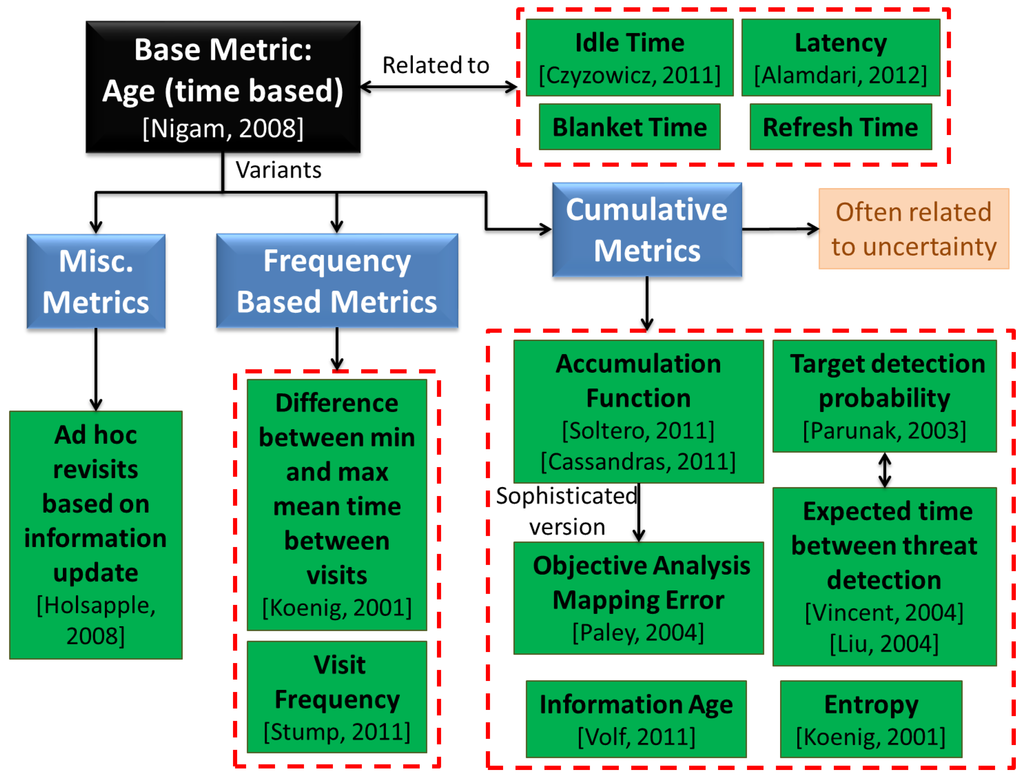
Figure 4. Commonly used performance metrics in context of persistent surveillance.

Figure 4. Commonly used performance metrics in context of persistent surveillance.

On a related note, Hussein and Stipanovic [96] survey previous work on coverage problems, and nicely formulate different types of coverage problems. They address a problem of achieving a preset level of coverage at each point in the domain [97]. Hence the problem has a persistence flavor to it, but the mobile sensors can potentially stay at a location increasing the coverage level—so frequent revisits are not required. Erignac has basically solved a coverage problem as well [98], but also suggests two ways to address the persistence problem of revisiting regions as frequently as possible. Parunak, Brueckner, and Odell [13] solve a type of persistent surveillance problem, among other example applications—they try to revisit areas to maximize detection probability of targets without displaying particular search patterns that can exploited by evading targets. Batalin and Sukhatme [37] solve a combined deployment, exploration, and persistent surveillance problem. Persistent surveillance in general encompasses the exploration aspect as well, but they treat the first exploration/coverage task to be different since the environment is unknown. Ref. [99] enforces persistence by requiring each area in a polygonal space to be re-covered every T* time steps (recall the discussion on CSP in context of patrolling above). Koenig, Szymanski, and Liu [100] address a continuous vacuum cleaning problem and study several kinds of persistence objectives (such as entropy to measure uniformity of persistence and difference between smallest and largest mean times between visits). Vincent and Rubin [101] search for mobile (possibly evasive) targets in a hazardous environment, outlining five main objectives of their work: (1) achieve configurations to maximize probability of target detection; (2) minimize expected time to find target; (3) minimize number of UAVs; (4) robustness; and (5) minimum control information in case of reconfiguration. They further point out the inadequacies of prior research: (1) not revisiting explored regions; (2) stationary targets; (3) excessive information exchange; and (4) often impractical search paths (requiring lots of turns etc.). Holsapple and Chandler [102] use a team of UAVs and MAVs with human-in-the-loop interaction, for surveillance and reconnaissance. The stochastic controller onboard the MAVs, for decision making, is the focus of that paper. The problem has certain aspects of persistent surveillance as well, since the vehicles might decide to revisit targets based on expected information gain and updates from human operator. Gaudiano, Shargel, Bonabeau, and Clough [75,103] survey swarm-based approaches applied to search and attack tasks. For the case of mobile targets, the UAVs revisit locations giving the techniques a persistent quality [104]. In the same vein, Liu, Cruz, and Sparks [105] solve a persistent area denial mission that includes persistent surveillance, tracking, and attack. The persistent aspect of the problem arises from the fact that the targets/threats are pop-up (based on first order Markov-chain model) and not observable at all times—the performance is measured by the expected time to respond to such threats. Ref. [23] designs time-independent memoryless control policies for robots in 2D, performing persistent surveillance of an area with forbidden zones. Volf et al. [20] try to minimize the “information age” of the environment, which is cumulative measure of age, rather than the maximum over all regions. They also couple the collision avoidance problem to the main surveillance problem. Jakob et al. [30,65] have looked at multi-agent persistent area surveillance of urban areas using fixed wing vehicles. This is one of the few 3-D implementations in this area (refer Figure 5). Stump and Michael [66] have addressed a problem of continuously revisiting a discrete set of pre-defined sites periodically with varying priority or hard visitation frequency. This is extended to consider the MAV deployment problem as well in [106]. This is similar to our definition, except for the restriction to discrete Points of Interest (POIs)—we believe that to be a special case of the problem. Also, the varying priorities is an enhancement to the basic problem, but an interesting area of research that has not been sufficiently explored. A similar extension has been studied by Smith and Rus [26], who have different rates of change associated with each POI. The authors of this paper have tried to address the persistent surveillance problem as defined in the previous section under dynamic and endurance constraints and also explored the conceptual design of such vehicles [107].

An inevitable part of persistent surveillance is the ability to support persistent operations in real life—in presence of uncertainties and failures. Another way to look at this problem is, as the case where the task timeline is longer than the lifetime of vehicle [93]. Valenti et al. [108,109] claim that the most important problem in persistent operations is coordination of resources, and advocate the use of a health monitoring system for this purpose. They demonstrate a mission health management system for 24/7 persistent surveillance trying to keep at least one UAV airborne in a target area. The authors of this survey have looked at the other aspect—maintainance of good mission performance in such a scenario [110]. Bethke, Bertuccelli, and How [111] also focus on improving efficiency by finding the optimum health monitoring policy (deciding when the UAVs should land and takeoff) online. Kim, Song, and Morrison [112] have also focused on the refueling issue for border patrol and tracking, but presented results only in simulation. Similar work can be found in [113], where the objective is to continuously survey a target space and closely track objects of interest. However, this is a relatively unexplored area of research and has been gaining importance only recently.

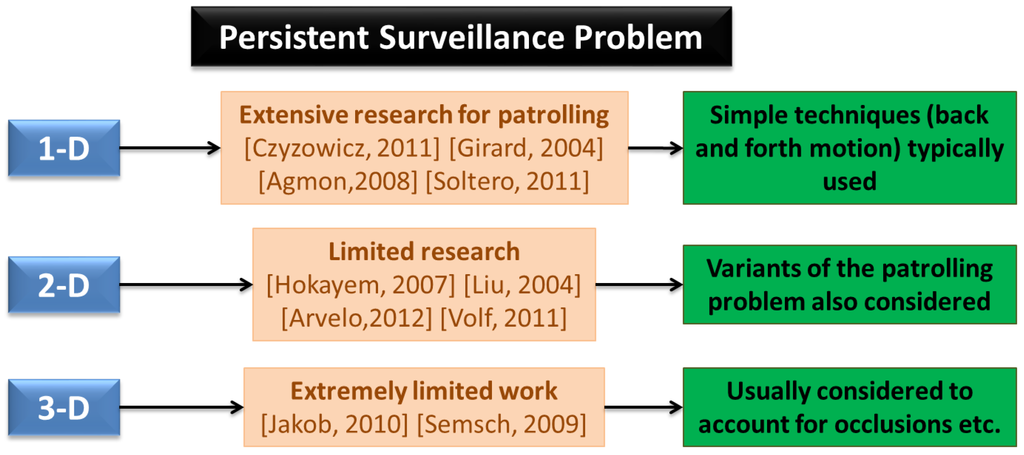
Figure 5. Amount of research effort on increasing dimensionality of the problem.

Figure 5. Amount of research effort on increasing dimensionality of the problem.

4. Techniques for Vehicle Control and Coordination

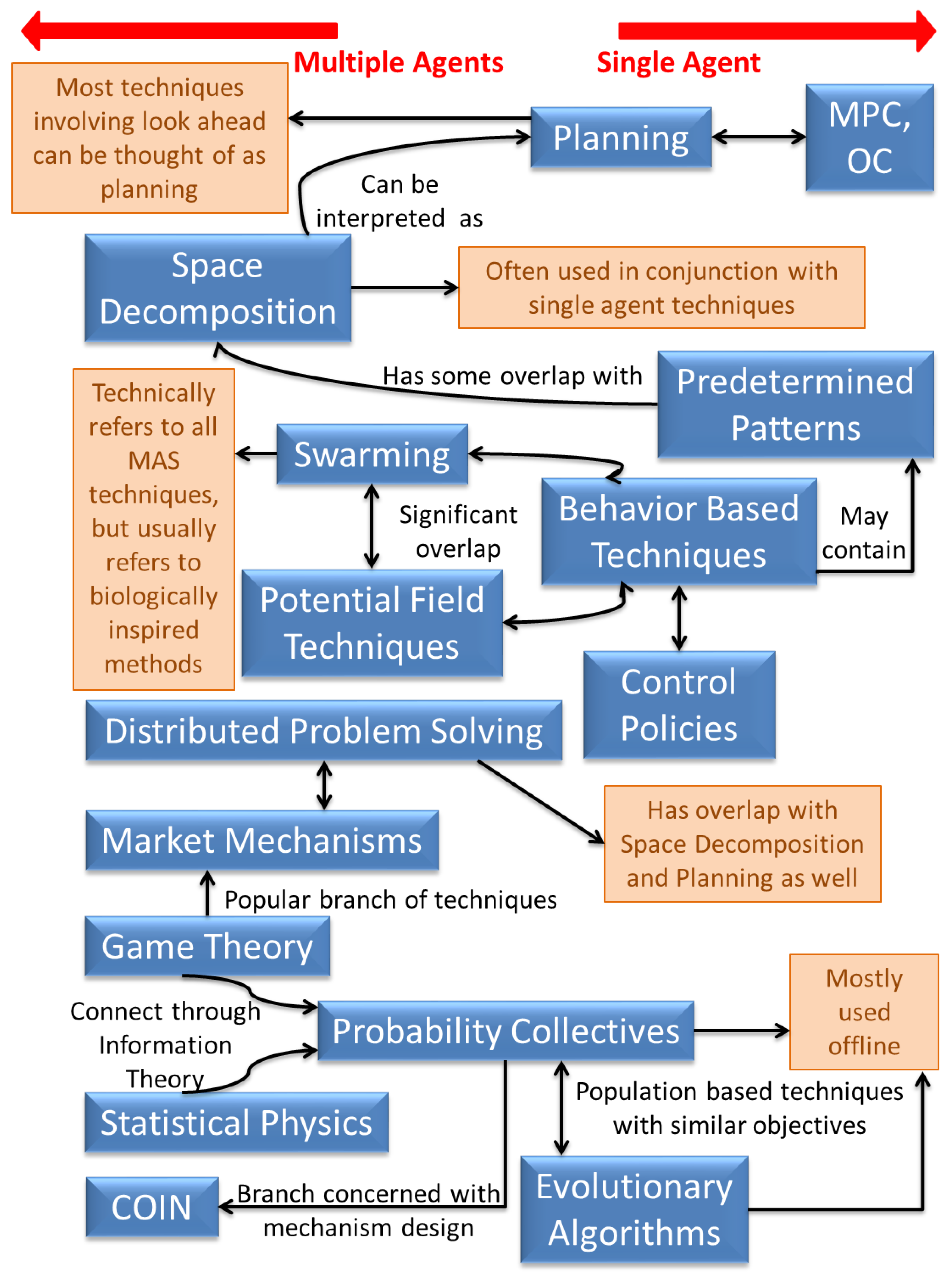
Thrun and Moller [114] claim that random actions for exploration are inefficient (especially if there is a cost for negative experiences) and are unable to adapt to time-varying environments. So there is a need to study techniques that make use of information about the target space and areas already explored—hence the extensive amount of research in autonomous vehicle control. Several techniques already exist for extremely efficient single agent problems (though we are not aware of any optimal technique for the persistent surveillance problem), but the optimality often does not extend to MASs. To deal with multiple robots, a lot of research still leverages on extensions of single robot techniques [4], but this need not be inefficient depending on how the extension is made. As a result of this however, there is considerable overlap between single and multi-agent techniques, and both are discussed in this section. The area of persistent surveillance being relatively new, does not offer a rich variety of techniques (compared to the MAS field in general)—a thorough survey of techniques applied to all related problems is outside the scope of this review. Figure 6 provides an overview of the techniques discussed in this paper and a sense of relationships between them. For a survey of techniques for multi-agent patrolling in particular, refer to [40] which categorizes the techniques as: operations research methods, non-learning MAS methods, and multi-agent learning techniques. The categorization provided herein is a little different and motivated by the broader literature on MASs in general.

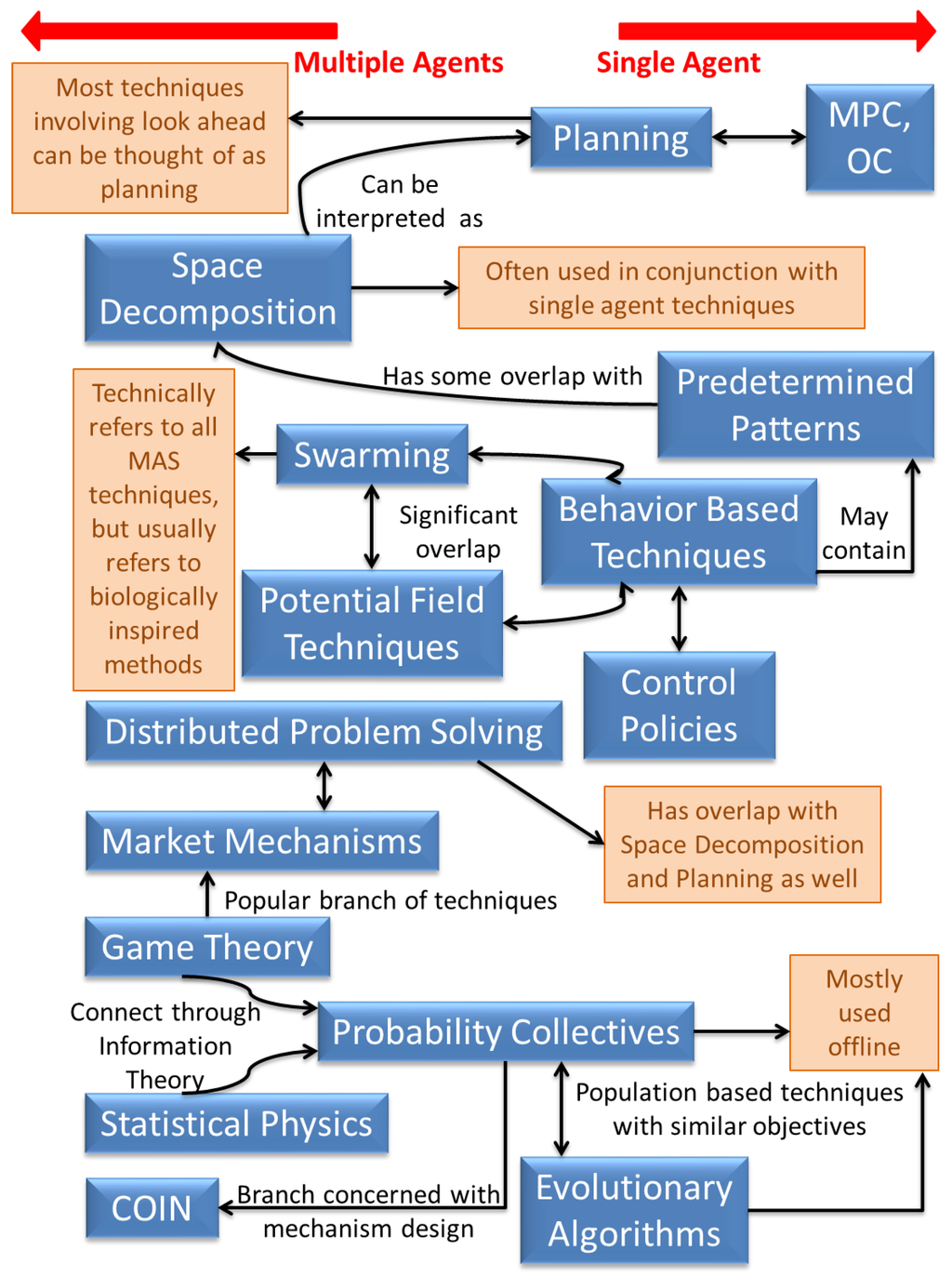
Figure 6. Schematic of the techniques for vehicle control and coordination discussed in this paper.

Figure 6. Schematic of the techniques for vehicle control and coordination discussed in this paper.

4.1. Planning

Planning is one of the most widely used techniques for autonomous control applications. Durfee et al. [115] give an overview of implementation of plans and why they result in better performance. In a very generic sense, any technique that uses look ahead or prediction is using planning. However, planning is often used to refer to a particular set of techniques as identified in literature [59,116] (see Figure 7). Reactive techniques are sometimes favored for their simplicity, online resolutions of issues, lower communication requirements, and ability to deal with uncertainties [14,61]. But planning based methods have a strong support from the AI community who claim that reactive control strategies can lead to inefficiency and instability [59]—it is not clear what “instability” refers to in this case since such instability was not observed by the authors of this paper in their review of reactive techniques. Redding et al. [113] claim that persistent mission scenarios require robustness and initially reactive and ultimately pro-active qualities of planning. They define reactive planning as constructing plans based on deterministic models, with replanning when necessary; and proactive planning as constructing plans based on stochastic models which directly capture possibility of failures and learn to improve models online. The latter are more complex, but expected to have better performance.

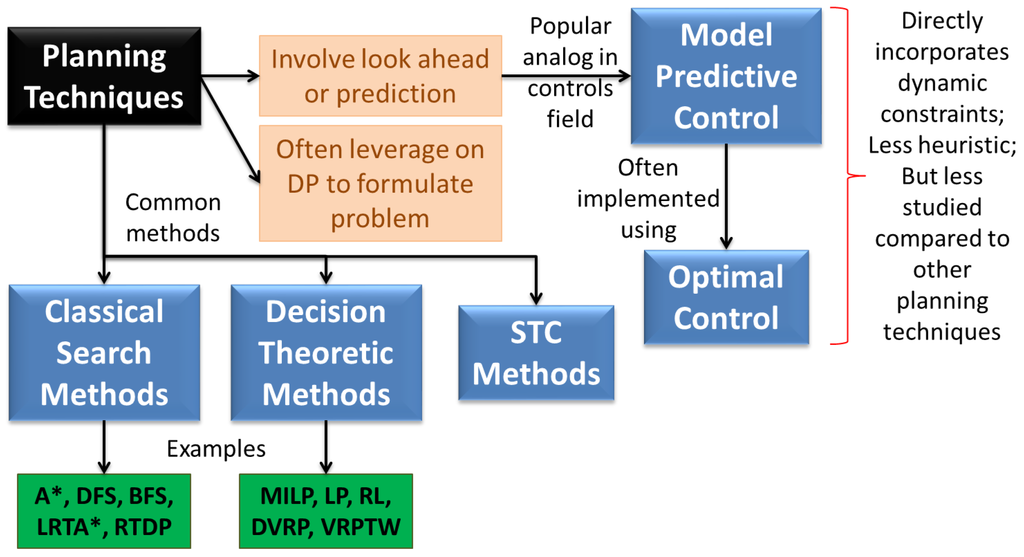
Figure 7. An overview of typical methods used for planning.

Figure 7. An overview of typical methods used for planning.

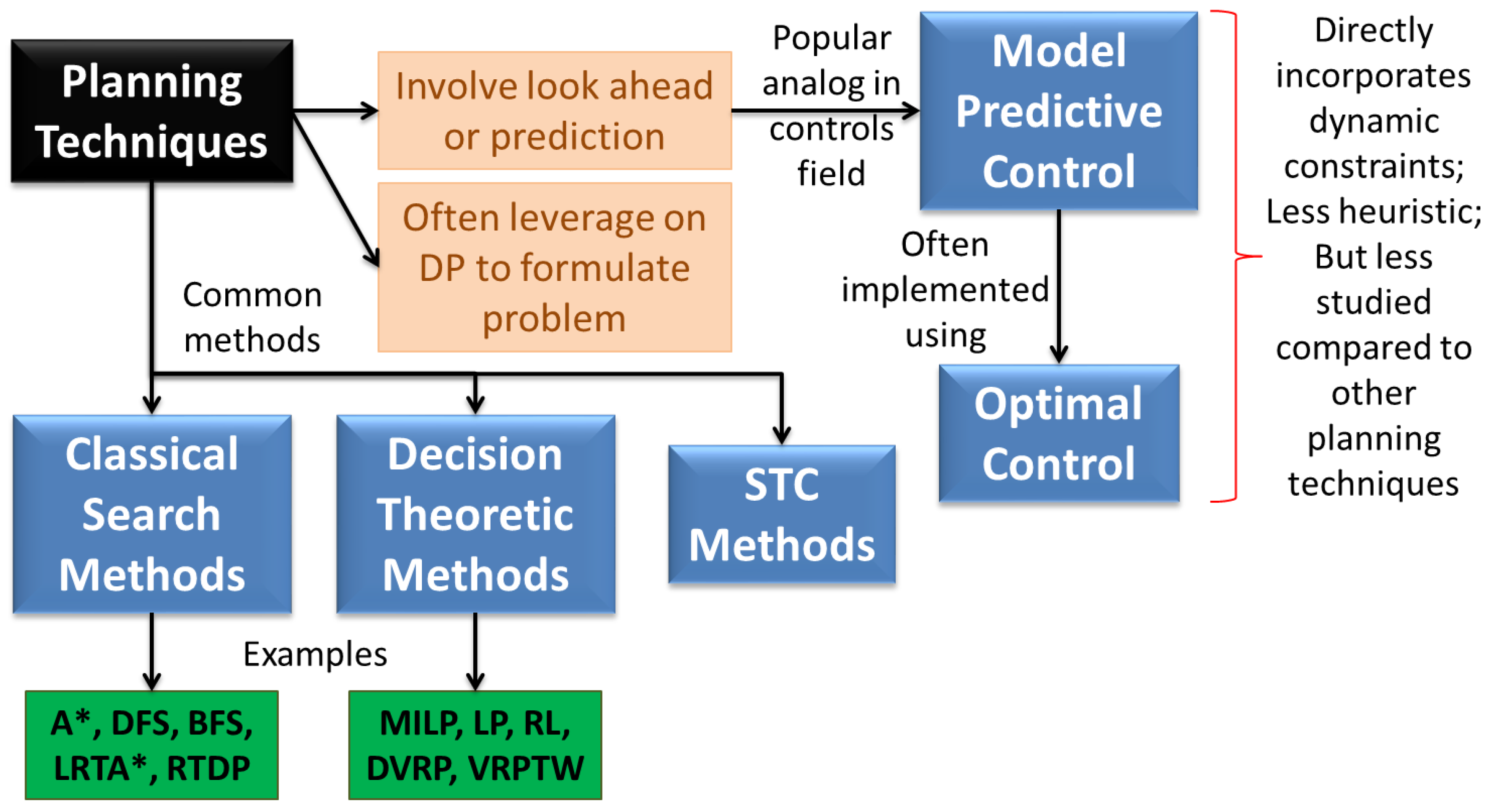
Ideally speaking, planning should perform better than or at least as good as reactive control. However, if planning is used to supplement reactive control, then problems can arise due to inability of the system to react to changes in the environment. To circumvent this problem, the idea of receding horizon control has been used [10,32], but that only partially alleviates the problem unless the time steps are as small as would be used for a completely reactive policy. A rigorous approach to combining planning and reactive control is Optimal Control [117,118]—a kind of Model Predictive Control (MPC) [119]. This typically incorporates the vehicle dynamics in the planning problem and solves it using optimization techniques in general. However, such techniques have received considerably lesser attention for surveillance problems, perhaps due to a neglect of vehicle dynamic constraints. The only work we came across is that by Cassandras et al. [24,120], where the solution is reduced to a simpler parametric optimization problem (based on the fact that the optimal policy in 2-D is a simple back and forth motion)—hence infinitesimal perturbation analysis can be used with online gradient-based optimization. Solving an optimization problem does not necessarily mean that it cannot be used in online settings. Gradient-based methods for optimization tend to be extremely efficient and have been used in conjunction with techniques such as collocation based methods for optimal control. However, the problem is in guaranteeing convergence to a “good” optimum, which oftent gets us into the realm of convex optimization [90]. Another way that planning techniques may suffer in actual applications is due to the finite horizon, which arises due to computational limitations. Often, the finite horizon limits the look-ahead ability of the planner, while a suitably engineered reactive control “policy” might be able to achieve longer look-ahead. This was illustrated by some of our work, where the reactive policy roughly converts a time extended problem into a single time step problem and outperforms a relatively naive implementation of a planning based method [110].

4.1.1. Classical Search Techniques

Among classical search techniques, A* search is a popular method for various applications [30,116]. Foo et al. [121] claim that A* relies on a heuristic to find the best path between two points and is not a good choice for dynamically rich problems, but variations of A* have been used extensively in literature [100]. Batalin and Sukhatme [37] use the least recently visited algorithm for solving the dynamic coverage problem, that is akin to Learning Real-Time A* (LRTA*) [122]—at each node, the robot basically chooses the least visited direction as its next search direction. Some other classical search techniques include Depth First Search (DFS) [123], Breadth First Search (BFS) [124], and shortest path planning [53], but the authors are not aware of their application to persistent surveillance.

4.1.2. Spanning Tree Coverage

An interesting class of algorithms is Spanning Tree Coverage (STC), introduced by Gabriely and Rimon [39]. The algorithms are optimal for single robot coverage of a known static environment and have been extended to stochastic multi-agent problems in several ways [50,125]. These algorithms have not been applied to persistent surveillance per se, though it would be interesting to see extension of such optimality to the persistent case. One of the ways is to repeatedly use the algorithm assuming repeated one time coverage problems. However, that ignores the dynamics in the environment and the transients that may arise in between two repeated coverages.

4.1.3. Dynamic Programming and Decision Theoretic Techniques

While, not a planning method in itself, Dynamic Programming (DP) has been extensively used for formulating cost functions for plan-based approaches and decision theoretic techniques in general [66,102,113,126]. Barto, Bradtke, and Singh [1] give an extensive description of such methods with particular emphasis on discrete time problems. They claim that DP provides a basis for compiling planning results into reactive strategies for real-time control and learning. They also point out that Real-Time Dynamic Programming (RTDP) is a generalization of LRTA* (a variant of which has been applied to persistent surveillance [37]). DP provides a rich set of techniques that are directly relevant to planning problems [127], and though not applied extensively to continuous monitoring problems, it may provide an interesting avenue of future research.

Decision theory is a broad field of research encompassing several disciplines, but only techniques that are directly relevant to surveillance and have little overlap with other categories in this section are discussed here. Valenti et al. [108] set up their task allocation and scheduling problem as a Markov Decision Process (MDP), but instead of using DP to solve it, convert it to an approximate Linear Program (LP) and solve it using a basis function generation approach [109]. Smith et al. [93] have used a similar approach for designing speed controllers for persistent monitoring. The MIT group, in other work has used value iteration and approximate DP techniques for such problems [113]. They have included online Reinforcement Learning (RL) for proactive planning [40], which relaxes assumptions made by most cooperative planners, and produces global policies executable from any part of state space. They also mention three challenges associated with use of online RL: (1) scalability issues; (2) large computation requirements; and (3) possibility of leading to fatal states. In some of our own investigation of RL, we also realized that such techniques should be used with care and a lot of effort should be spent on proper problem formulation to keep solutions tractable. In [111], an optimum policy for coordinating landing and takeoff of UAVs is found by posing the problem as an adaptive stochastic MDP and solving it using a two step procedure. At the top level, the MDP is solved using value iteration, and at the lower level, bayesian estimation is used to find values of uncertain parameters.

MDPs are natural formulations for MASs, since they easily model uncertainties and agent interdependencies [111]. However, discretizing the problem to formulate an MDP, often increases the complexity and solution time tremendously. To address this issue, Bererton et al. [85] combined two lines of research for multi-robot coordination: market mechanisms and large weakly coupled MDPs. Market mechanisms convert the problem of cooperation to one of resource allocation, thus transforming the large MDP into a set of loosely coupled MDPs that interact through resource production and consumption constraints. The planning problem is posed as an LP and solved in a decentralized fashion using the Dantzig-Wolfe decomposition and auction-based algorithms are then used to coordinate between the MDP problems. Another similar approach for task assignment problems is Mixed Integer Linear Programming (MILP) which can easily incorporate both logical and continuous constraints [56,128]. Often, solving the exact problem using MILP can become intractable for a moderate number of vehicles, so typically approximate solutions are used instead, such as heuristic tabu search [57,66,129]. Ref. [112] address a scheduling problem (for refueling) using MILP—combining the use of CPLEX and GAs to solve the problem. A related line of work involves posing the persistent surveillance problem as a Dynamic Vehicle Routing Problem (DVRP), where we seek to task agents to optimally clear task requests that are added to the geometric space stochastically [66]. Compared to TSP solution techniques, DVRP techniques are more amenable to persistent surveillance, but still need to be modified for repeated coverage [106]. The period routing problem is an example, where the POIs must be visited a pre-specified number of times per week—though this is still more of a CSP-like problem. The Vehicle Routing Problem with Time Windows (VRPTW) is addressed by Stump and Michael [66] that seeks to design routes for multiple vehicles to visit all nodes in a graph with time window constraints. The MILP formulation is similar to VRPTW, except that time constraints are encoded as penalties. The authors of this paper however envision a problem with the determination of such time windows that would help minimize the objective of maximum age. In their work, Stump and Michael have used the stabilized cutting-plane algorithm which adapts the trust region approach to solving the problem (the constraints are incorporated via Lagrangian approximation). In general, the problem is strongly NP-hard, but by allowing cyclic paths, the problem can be solved in psedo-polynomial time using DP. Also, receding horizon control is used for tractability. Along similar lines, Ref. [27] has developed two polynomial time algorithms for addressing patrolling using a graph theoretic approach. Inspite of the large amount of work in this area, there is still a need to make such methods more efficient for application to large scale persistent surveillance problems.

4.2. Space Decomposition

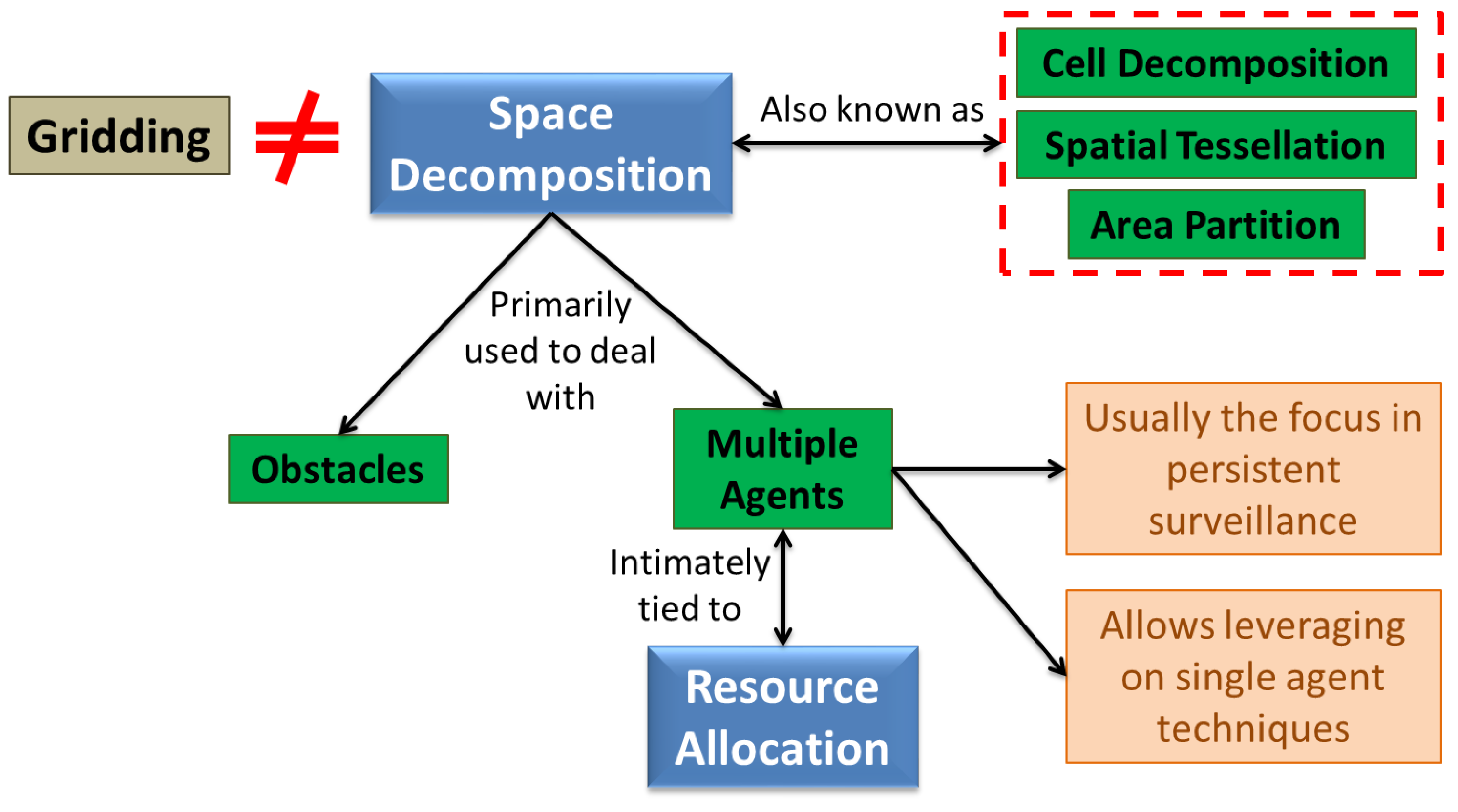
Dividing/partitioning the target space into subspaces has been used in autonomous control literature primarily for two reasons: (1) to find subspaces that are free of untraversable regions; and (2) to divide work among multiple agents [9,70]. Both cases usually fall in the category of exact cellular decomposition that is discussed in Section 6.1. This division of space is known by different names (including cell decomposition, area partition, spatial tessellation etc.), but we call it Space Decomposition in this paper. Also note that this is not the same as “gridding” the space which is typically performed to discretize the problem for book-keeping or approximate quantities of interest (see Figure 8). For persistent surveillance, typically the latter case of dividing work among multiple agents is the main objective. This basically converts the problem into a task assignment problem allowing use of single agent techniques within the assigned domains. Note however, that as opposed to a simple task assignment, the space decomposition problem usually involves determining the size and shape of the partitions as well. Several kinds of decompositions have been used for multi-vehicle control, such as boustrophedon decomposition [123], morse decomposition [130], rectilinear partition [30,131], voronoi decomposition [12] and trapezoidal partitions. For a comprehensive overview of the field of spatial tessellations, refer to Ref. [132].

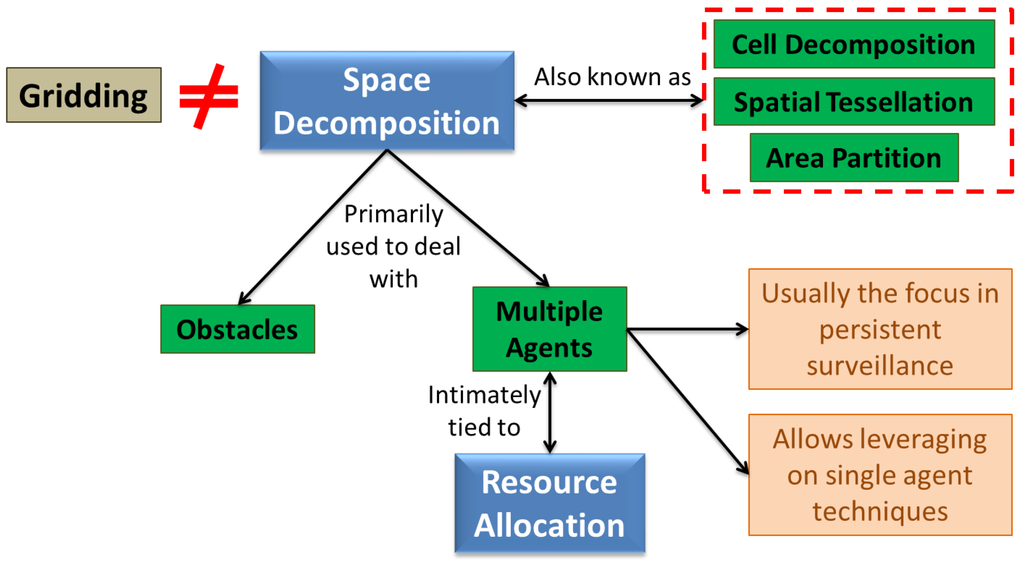
Figure 8. A schematic of the space decomposition methods typically used in literature.

Figure 8. A schematic of the space decomposition methods typically used in literature.

In the patrolling problem, most of the work has focused on the one-dimensional space decomposition problem, which is relatively trivial to solve [88]. Ref. [86] compares the two most common strategies used for patrolling: (1) Cyclic strategy, where agents move in a cycle along the perimeter; and (2) Partition strategy, which is basically space decomposition. It further states that cyclic strategies typically rely on TSP-related solutions or STC approaches. For instance, Ref. [26] uses heuristic solutions to TSP for single agent surveillance, while using space decomposition to deal with multiple robots. Cassandras et al. [24] present an optimal control approach for a 1-D monitoring problem that leverages on queueing theory for assigning sampling points in the target space to agents, which is akin to space decomposition. The approach can also be extended to multiple dimensions, at least in theory. [87] splits the border into roughly similar partitions offline and assigns them to different UAVs, emphasizing on the hierarchical control architecture. Carli et al. [89] focus on the problem of 1-D space decomposition under communication constraints, where an iterative algorithm is used to find nearly non-overlapping regions of surveillance for each agent. On a separate problem (scheduling refueling times of UAVs), we have posed a similar problem as an LP that can be solved online [166], but that assumes complete communication for optimality guarantees.

An extension of using 1-D techniques for a 2-D problem is provided by Hokayem et al. [99], who plan a path for a single robot and divide it among multiple robots. The objective is to minimize the maximum time taken by any robot (minimax problem) and find directions to move the obstacles for relocation. Instead of solving these problems together, they solve the continuous and discrete problems iteratively. [99] uses level sets (polygons inside the main domain such that traversing along the edges of each level set will guarantee coverage), analogous to work in [133], to cover the polygonal space, that are divided and assigned to UAVs based on their capabilities. Ref. [74] uses an asynchronous distributed version of the Lloyd’s algorithm [134] for multi-robot coordination, similar to Ref. [12,135], while addressing a threat response problem. A wide variety of space decomposition techniques that have been developed for coverage problems can be applied to persistent surveillance in a straightforward fashion (replacing coverage algorithms for a single vehicle by a persistent surveillance method for a single vehicle). It is not within the scope of this paper to discuss all such applications, but we would like to point the reader to some work by Hert and Lumelsky [43] on the anchored area partition problem. Variants of this pioneering work have been applied profusely [44]. Though it should be noted that some times the resulting partitions may be oddly shaped, which can be a problem for UAVs operating under vehicle dynamic constraints.

As mentioned before, space decomposition typically involves determining the partitions in addition to the task assignment problem. Different kinds of partitions are determined using different algorithms—for instance voronoi partitions can often be determined by an iterative algorithm that tries to optimize some metric of “equitability” [132]. However, in most such algorithms we do not have explicit control over the metric of interest—we cannot choose an arbitrary metric to optimize the partition shapes and sizes, especially if the metric cannot be formulated mathematically in a closed form. The authors of this paper have addressed this issue by using an optimizer to determine the space decomposition where the metric is the overall system objective (minimizing maximum age) obtained through simulations [55]. This typically tends to be a very expensive procedure, so it may not be tractable for online implementation. However, if suitable approximations to the metric can be made (for instance using response surfaces), then it may be possible to use it for dynamic replanning as well. In fact, space decomposition techniques are often not scalable for real-time implementations and end up being used only initially to divide the domain of interest. However, the ability to deal with uncertainties/dynamics in the environment has been gaining importance, with increasing emphasis on the ability to replan. We have tried to address this issue in some of our recent work in [136].

The formulation of the problem (or the partitioning scheme) is key to efficient space decomposition, especially when using generic optimization. We investigated this issue for rectangular partitions (that offer a nice tradeoff between performance and computational cost), and developed a novel partioning scheme as opposed to choosing the vertices of the rectangle as optimization parameters. The space is divided using horizontal and vertical lines recursively, as illustrated in Figure 9 with three lines resulting in four partitions. The optimizer then decides the orientation and position of each line. A real-encoded Genetic Algorithm (GA), PCGA (refer to [137] for example) finds the optimum decomposition corresponding to minimum mission cost. After finding the optimum partitions, the UAVs are optimally assigned to them using an auctions-based technique. Ideally, the assignment should be coupled with the optimization, but that makes the optimization intractable even for a small number of UAVs. Hence the results of this approach are not necessarily optimal, but are typically close to the optimum—some sample results for this Space Decomposition (SD) approach are shown in Figure 10. Also note that, as the number of UAVs increase, the restriction of using rectilinear partitions may start becoming a problem.

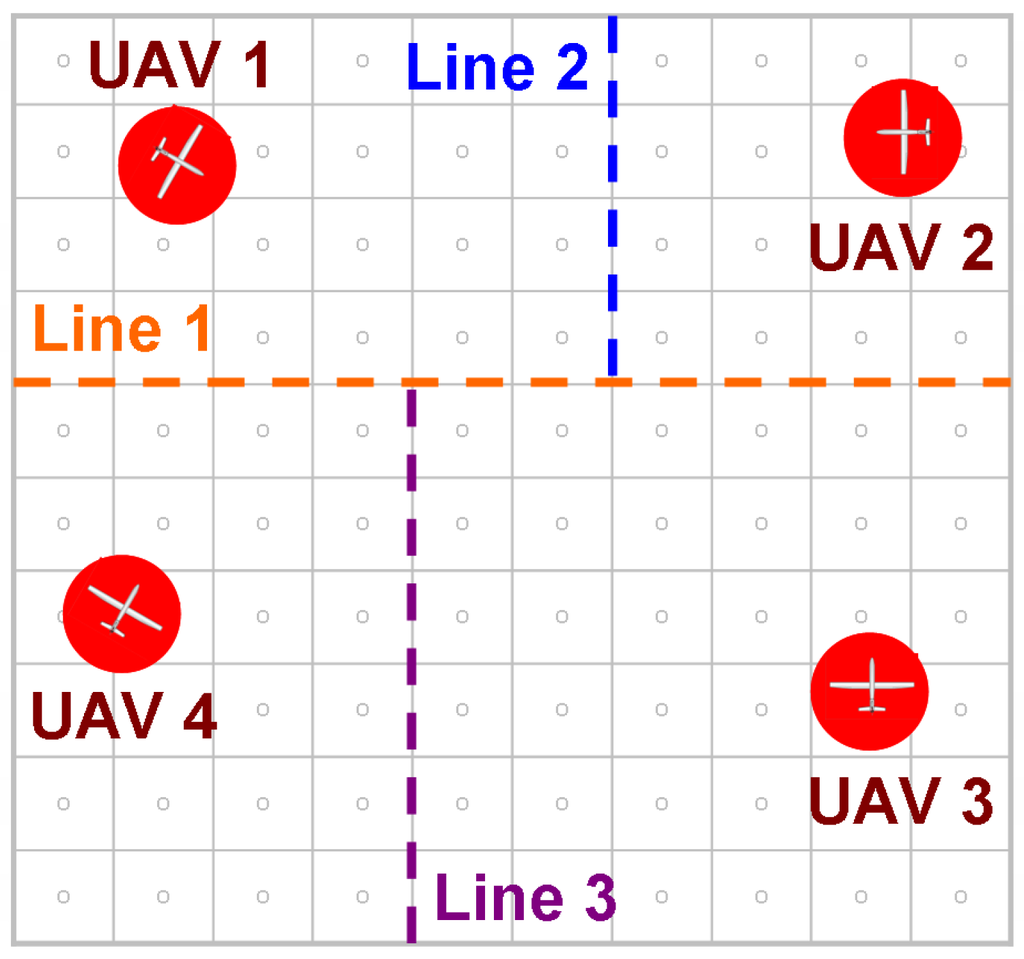
Figure 9. Illustration of recursive partitioning scheme for 4 UAVs. The line numbers indicate the order of the lines.

Figure 9. Illustration of recursive partitioning scheme for 4 UAVs. The line numbers indicate the order of the lines.

4.3. Pre-Determined Search Patterns

Pre-determined patterns for search are often used for exploration and coverage due to their simplicity [36], and completeness, under certain assumptions. This is especially true of patrolling tasks where one might argue that finding the optimal pattern to repeatedly follow is the crux of the problem [89]. In 1-D the pattern basically ends up being a line or a contour that is repeatedly covered either by simple back and forth motion or a continuous cycle (for a closed contour). In case of multiple vehicles, this is typically divided into segments for each agent [87] or spacing the vehicles along the contour and maintaining the spacing [86]. Note that the latter approach may not work in case of heterogenous vehicles (say with different speeds).

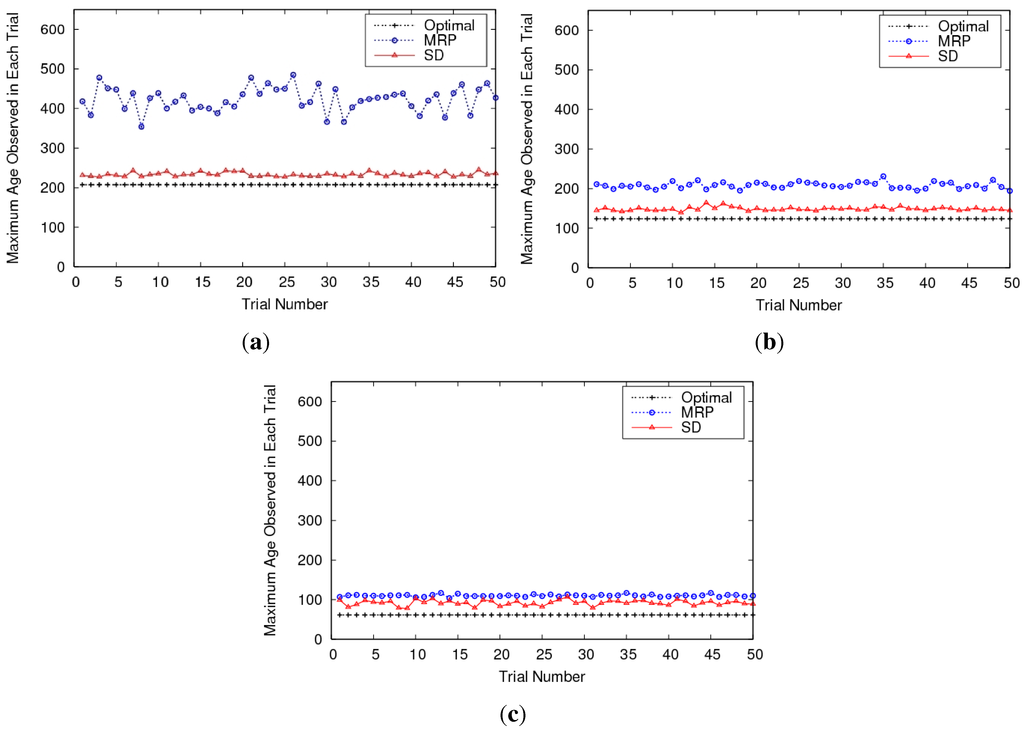
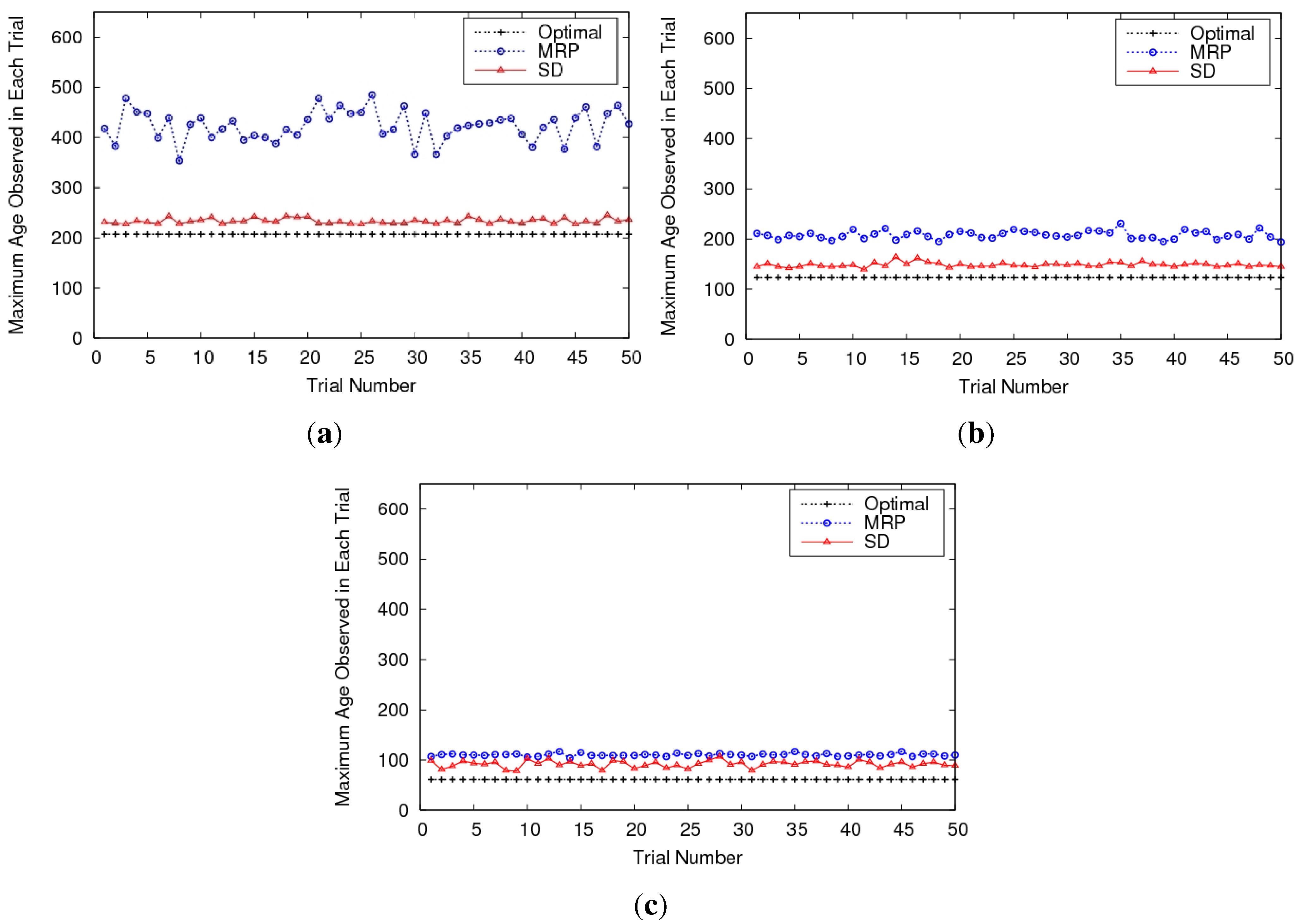
Figure 10. Maximum age observed in each trial over all cells (over entire simulation period). The plots give an idea of the variance in performance using MRP and SD as well. (a) Comparisons for 3 UAVs; (b) Comparisons for 5 UAVs; (c) Comparisons for 10 UAVs.

Figure 10. Maximum age observed in each trial over all cells (over entire simulation period). The plots give an idea of the variance in performance using MRP and SD as well. (a) Comparisons for 3 UAVs; (b) Comparisons for 5 UAVs; (c) Comparisons for 10 UAVs.

2-D target spaces offer a richer variety of patterns—the most common ones being spiral and zigzag patterns (characterized by back and forth motion and is also referred to as zamboni, raster scan, or lawnmower pattern). Different authors have cited pros and cons of each, and do not unanimously agree on one being better than the other [138]. Acar, Choset, and Lee [139] claim that simple zigzag motion is inefficient for narrow alleys, while Maza and Ollero [44] claim that zigzag patterns are faster than spiral search. On the other hand, the STC algorithm that is optimal for a domain without obstacles (refer Section 4.1.2.), results in a spiral search pattern [39]. Chakravorty et al. [140] show that spiral maneuvers form the dominant set of solutions for minimum time coverage solutions. Erignac [98] has also used spiral search patterns (among other behaviors) for their persistent coverage problem. The difference in performance of the two patterns is not significant, especially without dynamic constraints. If dynamic constraints are present however, the spiral pattern results in greater number of turns, and close to the center of the pattern, the turns required could become very tight. The zigzag pattern on the other hand, needs to make 180 degree turns instead of 90 degree ones, and in some cases can result in longer total path lengths. Among other patterns, Ref. [101] uses a line formation (that maximizes sensing while minimizing communication) to search for mobile targets. They also use pre-determined search patterns that push the target to smaller regions in the target space. Similarly, Frew et al. [83] coordinate between UAVs escorting ground vehicles by using simple heuristic rules, predetermined surveillance patterns, and rigid formation control.

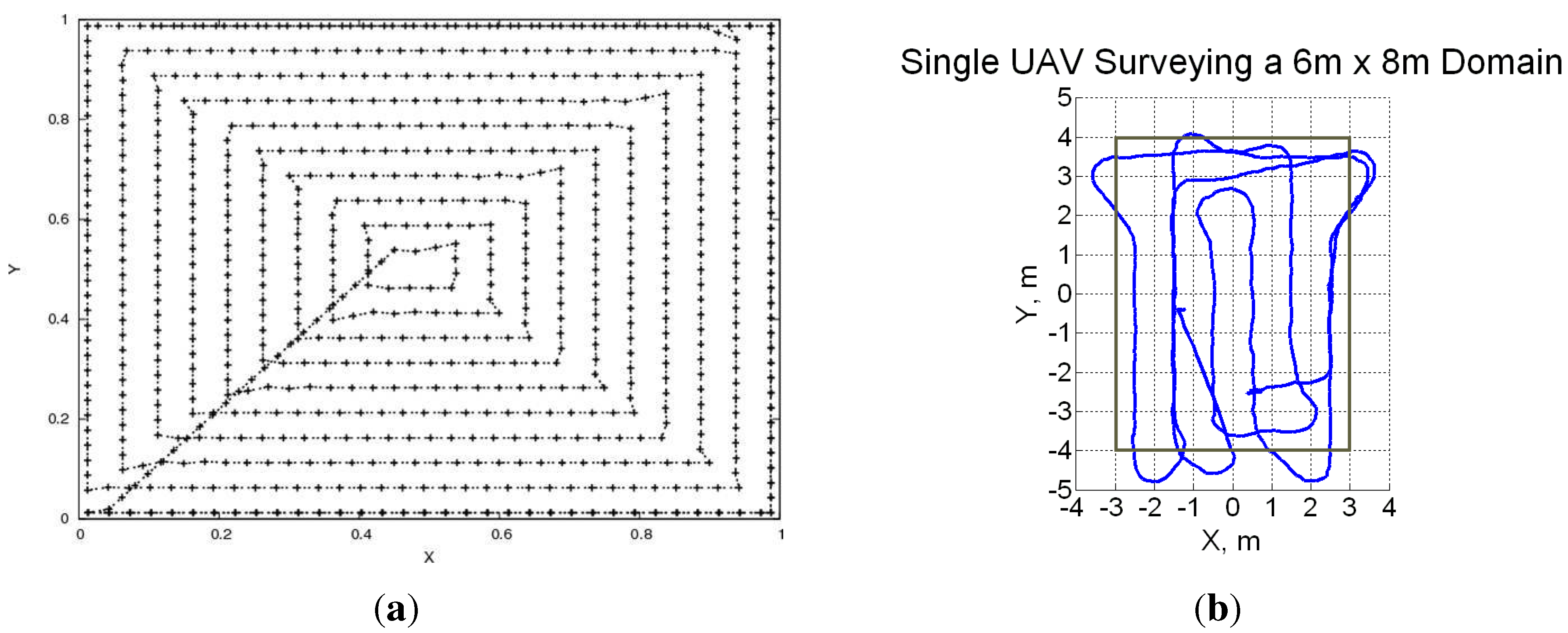
The biggest advantage of pre-determined search patterns is their simplicity, but the ones used in literature typically ignore vehicle dynamic constraints (such as minimum turn radius), though that is not an inherent limitation of pre-determined patterns. For instance, work in [30] compares three methods for single-agent area surveillance: spiral, zig-zag and alternating. The latter approach was introduced specifically for approximately solving the TSP problem with a Dubins dynamics model. They use accelerated A* learning to find shortest paths with dynamic constraints—something that we addressed by finding the analytical solutions [25]. One actual limitation of such methods is the inability to react to changes or dynamism in the environment (for instance in case of vehicle or sensing failure) [119] though there has been some work on heuristic adaptations [141]. In general, the efficiency of these methods is also questionable [142]. To address some of these issues, we have developed reactive control policies for multiple UAVs (MRP policy). The interesting observation with these policies is that a spiral search pattern emerges out of the control policy without any pre-determined pattern being explicitly programmed [25]. Thus the UAVs are able to react to changes in the environment while retaining the advantages of these patterns (such as near-optimality). Furthermore, in presence of vehicle dynamic constraints we observe a lawnmower search pattern (see Figure 11), which is arguably better than spiral search under such constraints.

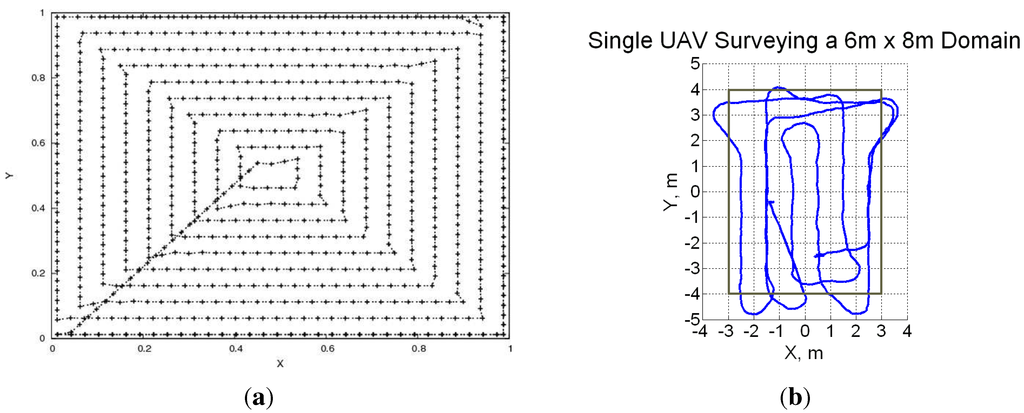
Figure 11. Illustration of the spiral and lawnmower search patterns which emerge out of our reactive control policy [25]. (a) Spiral search pattern (no dynamic constraints); (b) Zigzag search pattern (with turn radius constraints).

Figure 11. Illustration of the spiral and lawnmower search patterns which emerge out of our reactive control policy [25]. (a) Spiral search pattern (no dynamic constraints); (b) Zigzag search pattern (with turn radius constraints).

4.4. Behavior-Based Algorithms

Early work in behavior-based control is described in [143] where the application is a multi-robot clean-up and collection task. Behavior-based control is characterized by a combination of various simple behaviors (either predefined or acquired) describing the actions of an agent [49,98]. Some authors have included swarm behaviors in this category [19], but they are discussed separately in this paper. Erignac [98] combines contour following, avoidance, gradient descent, and random move for covering a domain. The UAVs use a spiral search pattern and share pheromone maps when close. Mataric [168] introduces basis behaviors (such as avoidance, safe wandering, following, aggregation, dispersion, and homing) as building blocks for synthesizing higher level artificial group behavior, and for analyzing natural group behavior. She cites natural examples of these behaviors and the requirements for using such behaviors to solve problems. Mataric further claims that behavior-based methods are usually time-extended compared to reactive techniques, resulting in higher level emergent behaviors [144], but not as expensive as planning methods. The authors of this paper however believe that simple behaviors are akin to control policies, [26] which are basically described as mappings from the state to action space in AI [116] (note that this definition does not preclude pre-determined search patterns from the generic set of mappings—they are basically degenerate cases of the same). Though some of the behavior control theorists may disagree, we think of behavior-based control to be a more generic version of control policies—the former may aggregate several simple control policies to obtain the overall behavior of the system. In some of our prior work [25], we have developed reactive control policies for agents that convert the time-extended planning problem to single-step decisions in a rough sense, and allow us to achieve some of the emergent behaviors that Mataric has referred to.

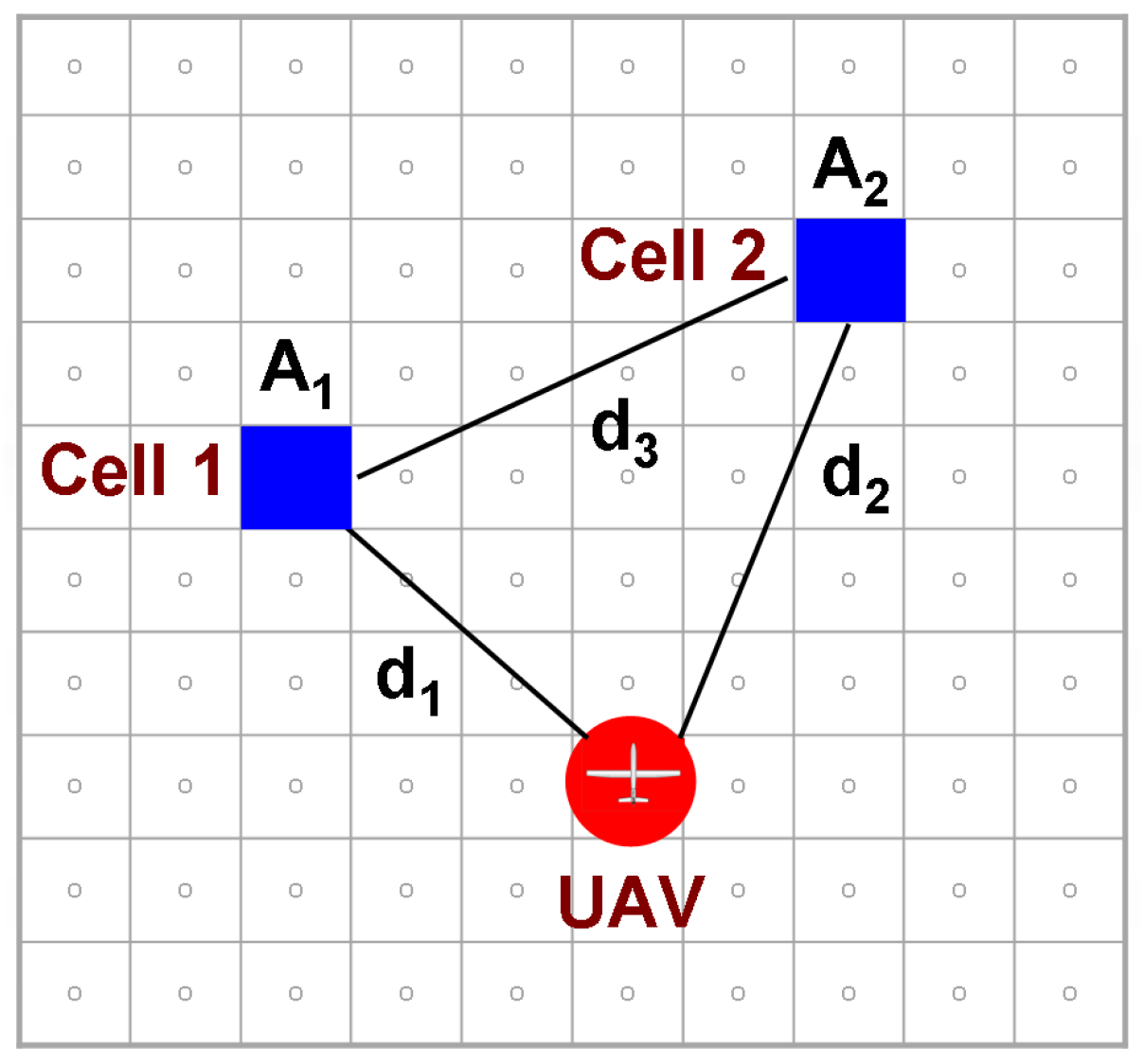
Actually the concept of emergence is not well defined in literature. [165] defines it as the “ability to accomplish complex objectives through synergistic interactions of simple reactionary components” and qualifies it as ability to perform tasks that N agents can do in time T, but single agent cannot do in time $N\ast T$. On the other hand, Erignac [98] has defined it as a combination of simple basic actions. In this paper, emergent behavior is characterized by something that manifests through simpler interactions without being pre-programmed. This does not necessarily mean that it is good—but traditionally the control system engineers have ascribed a positive connotation to it, while the test and evaluation group often refers to it as negative. We developed certain semi-heuristic control policies for multiple UAVs based on the analysis of extremely simple problems, akin to the one shown in Figure 12.

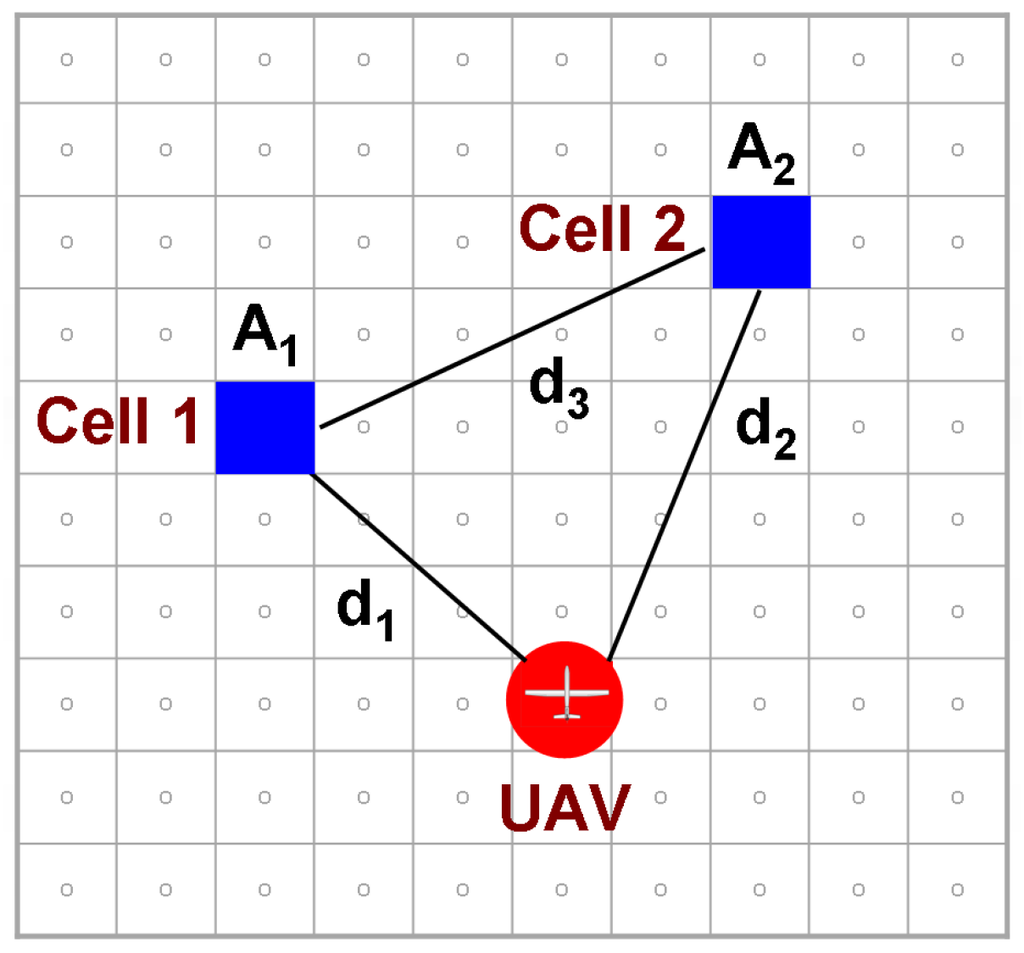
Figure 12. Simple two-cell problem used to derive structure for our control policy.

Figure 12. Simple two-cell problem used to derive structure for our control policy.

These policies were extended to the generic multiple UAV case, resulting in the Multi-agent Reactive Policy (MRP) which was shown to be robust, scalable, simple in concept, and did not require sharing of plans. Details of our simulation and experimental results can be found in [55,166], and we provide a snippet of the comparison between MRP, SD (refer Section 4.2) and a bound on the optimum in Figure 10. Note that since we are plotting the maximum age observed over all cells as a function of time, a lower value indicates better performance. The MRP technique is found to exhibit an interesting “emergent” behavior as the number of UAVs increase—it shows character and performance similar to the SD approach. Some other emergent phenomena of the technique are outlined in the papers.

4.5. Swarming Approaches

Swarm Intelligence is a very broad field and in a sense encompasses techniques applied to MASs in general. In general, swarming approaches overlap with both, behavior-based algorithms discussed above, and potential field methods discussed in the next section. But typically it is used in context of bio-inspired algorithms for groups of agents, such as ants and bees. We think that biological systems have a lot to offer in terms of ideas for algorithms, however the MAS designer should be careful in mimicking biological behaviors, since there is nothing that proves biological techniques to be the “optimum”, especially for arbitrary objectives in robotic applications. Nevertheless there is much to learn from these ideas and they have been successfully implemented in several scenarios. For an in-depth discussion of swarm intelligence, the reader is referred to [145]. Parunak [146] also discusses how to measure and control swarming activity and provides a brief survey of swarming architectures such as centralized command and control, Finite State Machines (FSMs), and stigmergic mechanisms (particle swarms, hybrid co-fields, and digital pheromones). He defines swarming as “useful self-organization of multiple entities through local interactions” and outlines salient characteristics of swarming, claiming that it is useful for diverse, dynamic, distributed and decentralized scenarios. Gaudiano et al. [75] provide a survey of swarming techniques applied for coordination between teams of UAVs. In their work, pheromone markers are used for a search and attack mission [103]. The pheromones are basically used in the search phase, and the UAV enters track mode when a target is detected. Since the targets are mobile, persistent search is achieved by making the pheromones evaporate with time. This work is later combined with an evolutionary approach in [104], where GAs are used to tune the swarm parameters. Parunak, Brueckner, and Odell [13] use pheromone maps to coordinate between UAVs for a dynamic coverage task similar to [100]. Ref. [147] develops two swarming approaches for the multi-agent patrolling problem. Reif and Wang [22] have used social potential fields for controlling a large number of robots. Some of the techniques they use, such as hierarchical control, are similar to weighted combinations of simple behaviors. Similarly, Ref. [95] describes five primary kinds of pheromones for control: (1) uncertainty pheromone (attracts vehicles to areas to be sensed); (2) sensor request pheromone (when a different vehicle is required to address the task); (3) target tracking pheromone (deposited when tracking a target); (4) no-go pheromone (represents no fly zones); and (5) vehicle path pheromone (deposited along planned paths). These kinds of approaches however lie in the gray area between swarming approaches and potential field methods and behavior based control.

4.6. Potential Field Methods

Potential fields are defined based on attraction to certain physical entities (such as goal) and repulsion to others (such as other agents and obstacles). The agent typically tries to find the minima of the potential function, though the multimodal nature of such functions can make it get stuck in undesirable local minima. A majority of effort in this field has hence focused on guaranteeing escape from local minima or fairly efficient behavior [98]. Reif and Wang [22] give a survey of potential field methods (including spring force based control laws). They differentiate between global and local forces—global forces disperse the robots in the environment, while the local forces are used for obstacle avoidance and attraction to goal. Eventually however, these are all combined through weights, making the approach heuristic. Though artificial potential fields are common methods for collision avoidance, Soltero et al. [92] use velocity obstacles approach and develop speed controllers to avoid collisions and deadlock situations. Hussein and Stipanovic [96] use gradient-based kinematic control laws that are similar to potential fields. They use symmetry-breaking control to escape from local minima, and use feedback to guarantee completeness of coverage. Ref. [97] adds flocking behavior to this control strategy.

A big advantage of such methods is their simplicity and ability to combine the treatment of goals, obstacles and inter-vehicle collisions in a common methodology. The local minima problem aside, the efficiency of such methods may be a cause of concern. For instance, we compared a potential field approach to our MRP policy (Section 4.4)—the former approach was similar to work in [148]. A sample result from the comparison is shown in Figure 13, just to give an idea of the efficiency. However, we admit that the efficiency of potential field methods depends strongly on tuning the weights of the potential function, so that could be one of the issues with the performance.

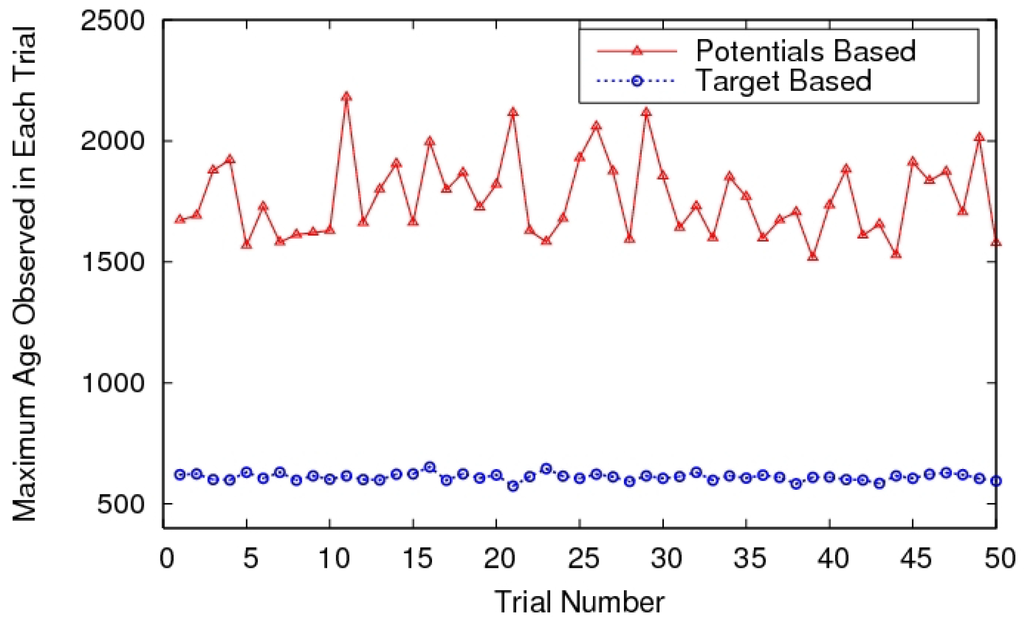
Figure 13. Comparison of a heuristic policy, similar to a potential field method, and the target-based approach.

Figure 13. Comparison of a heuristic policy, similar to a potential field method, and the target-based approach.

4.7. Market Mechanisms

Market mechanisms are a popular choice of methods for cooperative decision making [63], particularly for task assignment [76]. They constitute one branch of game theoretical techniques that have found significant practical application. For instance, Ref. [13] uses bidding for cooperative imaging and task division. Berhault et al. [64] claim that prior work used single-item auctions that fail to identify synergies between targets (i.e., the combined value of a bundle of targets could be different from the sum of values of individual targets, for a single robot). They point out that the issue of different bidding strategies has not been sufficiently addressed, so they use combinatorial auctions with four different bidding strategies. Combinatorial auctions, that deal with multi-agent multi-item assignments, are a field of current research (due to the high computational expense), but are often used with heuristics for practical problems [63]. We have also used auction algorithms in conjunction with our SD approach (Section 4.2), for assigning UAVs to partitions. These algorithms have previously been used for optimal assignment and related problems [149,150]. However, persistent surveillance is a minimax (also called bottleneck) assignment problem, where the goal is to minimize the maximum cost over all assignments, as opposed to minimizing the sum of costs. Garfinkel [151] suggested a threshold algorithm that solves an assignment problem using the Ford Fulkerson method [152] and repeats the process using the Hungarian method. This process however seemed to be an overkill for the problem at hand, so we replaced it by an auction algorithm. There also appears to be a bug in Garfinkel’s algorithm, in the update of a critical parameter, that might result in suboptimal solutions. This was rectified at a minor computational cost.

4.8. Collective Intelligence and Probability Collectives

We are not aware of any direct application of game theoretic techniques to persistent surveillance problems, but two related fields of research have recently emerged, that derive from game theory. COllective INtelligence (COIN) tries to achieve coordination among multiple agents, similar to mechanism design [35,153]. The basic idea is that in an MAS, the private utilities are the objective functions for the agents, and the global utility is the system objective. The trick is to design private utilities such that maximizing them automatically maximizes the global utility. In other words, we aim to find utilities that are factored (such that agents do not work at cross purposes), and learnable (such that agents do not get affected much by actions of other agents). In [48], COIN is combined with offline episodic learning, that helps determine sequence of actions using Q learning. Similar ideas have been used in [40] for the patrolling problem.

Probability Collectives (PC) [153] is a generalization of COIN, that combines game theory and statistical physics, using information theory [154]. The idea behind PC is to find the optimal probability distributions over an agent’s actions instead of the optimal actions. This is analogous to finding the optimal mixed strategies for agents in game theory [155]. The disadvantage is of course the huge computational burden associated with an online implementation, though there may be techniques to circumvent that [156]. It is beyond the scope of this paper to provide a comprehensive overview of PC, but the reader is encouraged to refer to Refs. [153,157,158] for a thorough discussion.

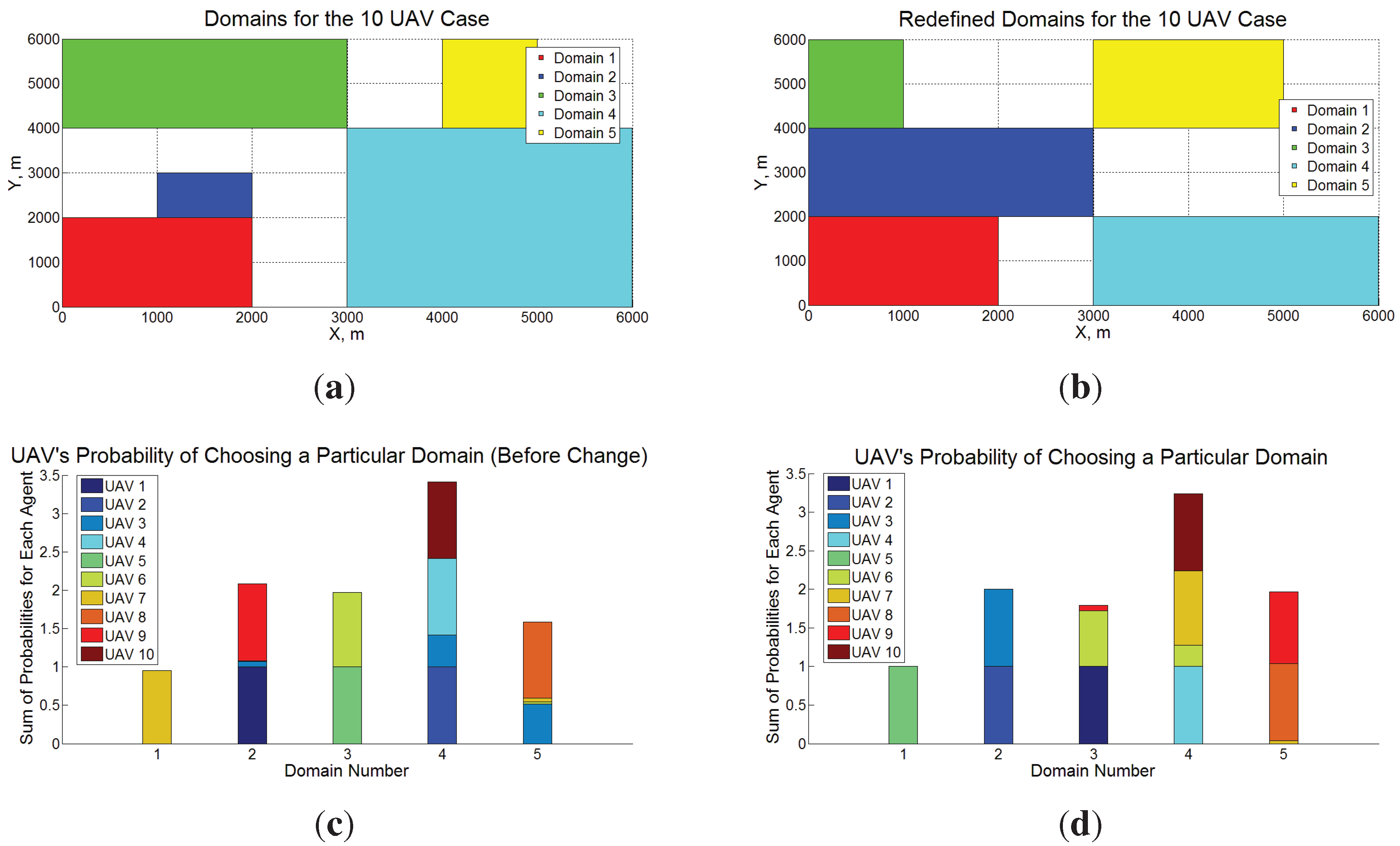
The authors of this paper applied PC for space decomposition, replacing the GA discussed earlier [55] with a decentralized implementation of PC. Figure 14 shows an example of comparison between PCGA and PC for a 36 UAV case. The results show that PC works better than PCGA—the remarkable improvement in efficiency for larger design spaces is a result of using decentralized optimization in PC, which does not exponentially increase in cost with the number of dimensions. Though the results are not conclusive, they are certainly promising from the point of view of PC application. The use of probability distributions also provides an ability to react to uncertainties in environment and “learn” appropriate control policies in dynamic environments. This particular problem has become an interesting avenue of research, especially in the game theoretic learning community [159,160,161,162]. We have also applied PC to a dynamic replanning problem for a persistent surveillance mission—a complete discussion of this application can be found in [136]. Here, we present a snapshot of the results to show the applicability of PC. Figure 15 shows the domains (to which UAVs are assigned for persistent surveillance) and the associated probabilities of UAVs to be assigned to each domain. We observe that the sum of probabilities of UAVs being assigned to a domain are roughly proportional to the domain size and these probabilities are able to adapt to changes in domain sizes.

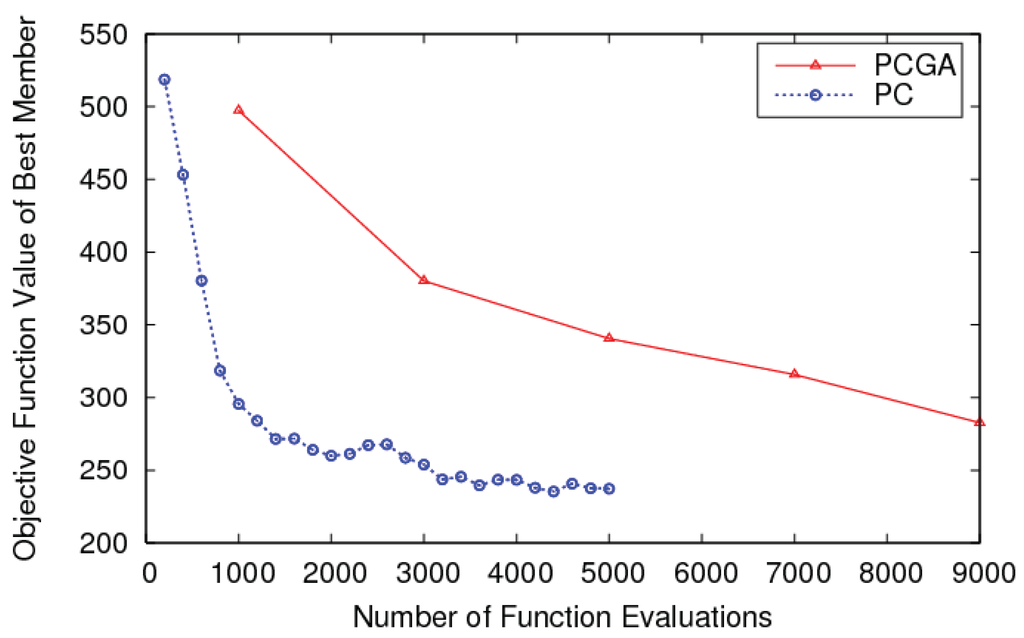
Figure 14. PC vs. PCGA Comparison of Objective Function Value of Best Member vs. Number of Function Evaluations.

Figure 14. PC vs. PCGA Comparison of Objective Function Value of Best Member vs. Number of Function Evaluations.

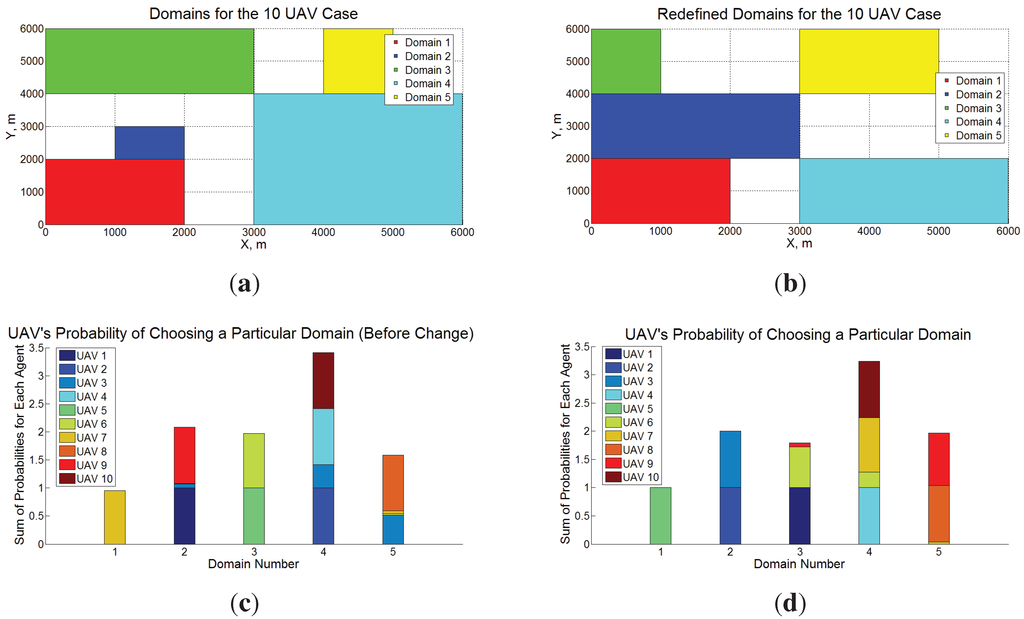
Figure 15. Schematic representation of the initial and redefined target spaces to be surveyed by 10 UAVs and the associated probability distributions before and after the change in domain sizes. (a) Initial Domain Definition; (b) New Domain Definition; (c) Initial Probability Distributions; (d) New Probability Distributions.

Figure 15. Schematic representation of the initial and redefined target spaces to be surveyed by 10 UAVs and the associated probability distributions before and after the change in domain sizes. (a) Initial Domain Definition; (b) New Domain Definition; (c) Initial Probability Distributions; (d) New Probability Distributions.

The only other work we know of, which has used PC for persistent area surveillance, is in [20], where the combined surveillance and collision avoidance (posed as nonlinear constraints) problem is addressed. A related approach that is based on entropy maximization (since the probability mass function that maximizes entropy under convex constraints, has maximal support), designs memoryless control policies using a convex programming approach, which is highly scalable [23]. Another related (though very simplistic) example of design of mixed strategies for agents is presented in [88] for perimeter patrol.

4.9. Evolutionary Algorithms

Evolutionary Algorithms have been used primarily for evolving control policies either online or offline (see [35] for example). They are basically population based optimization methods, akin to GAs, but slightly more generic [163]. For instance, Kim, Song, and Morrison [112] have used GAs for solution of a scheduling (MILP) problem, where CPLEX fails to find a solution. As mentioned earlier, we have also used GAs for the SD approach [25]. Such techniques tend to be expensive for online implementation and have not been used extensively for persistent surveillance per se. The previous section had shown some results comparing PCGA and PC. It is important not to misinterpret these results to mean that the GA does not perform well. In the field of optimization, GAs have proven to be one of the most robust algorithms for extremely complex problems and will continue to be so.

4.10. Distributed Problem Solving

In the above we have tried to categorize the different techniques applied to persistent surveillance, but there may be other techniques that do not fit well in any of these categories (our own work being an example). As the reader may have noticed, there are several approaches that combine methods from different categories as well. As a passing note we would like to mention another set of methods that has been applied to MASs in general. This is the field of distributed problem solving which includes organizational structuring, task passing etc. for achieving coherent cooperation [115,164]. To the best of our understanding, these are basically techniques that have now become popular under different names. For instance, work in [115] uses organizational structuring for achieving cooperation, that is basically space decomposition. They also use a planner at each node, that is the same as planning at the agent level. The task passing used for redistributing loads among the agents, uses an underlying bidding mechanism. Also, the meta-level information used for achieving cooperation, is the same as sharing plans between agents. Though these methods have not been explicitly used for persistent surveillance, the reader is encouraged to review some of this work as well.

5. Multi-Vehicle Coordination

Gaudiano, Shargel, Bonabeau, and Clough [75,103] pointed out that there has been no systematic study of pros and cons of using multiple vehicles for missions, and try to study this through simulations using up to 32 UAVs for a strike task and 110 UAVs for a search task. Ref. [98] also performed some simulations to study the effect of number of UAVs on mission performance. In this section we try to focus on particular mechanisms (whether explicit or implicit) used for coordinating between multiple UAVs. This will help us understand how typical techniques try to extend single agent approaches to multiple agents. Cao et al. [2] define cooperative behavior (that they claim to be a subclass of collective behavior) as “incorporation of certain mechanisms that increase the total utility of the system for accomplishing a particular task”. In this paper, a distinction is made between coordination and cooperation in that cooperation (more specifically active cooperation) necessarily involves sharing of plans between the agents in the system instead of sole information exchange. So cooperation is a means to achieve coordination. Other types of coordination mechanisms can be grouped into what is also called passive cooperation. Anisi and Thunberg [61] also distinguish between them, stating that cooperation arises from the objective of increasing performance, whereas coordination emerges from the constraints of the “optimization problem”. However, since the formulation of the optimization problem depends on the designer, this definition becomes subjective. Below we list some of broad categories of techniques that have been used for coordination among multiple agents.

Among the more explicit schemes for cooperation is space decomposition, which has been extensively used for continuous monitoring tasks [26,55,89]. Typically the 2-D space is divided into regions using voronoi partitions [74] or similar concepts [105]. Ref. [120] takes a slightly different approach, leveraging on queueing theory. Another variation is to divide a path (planned or pre-determined) among multiple vehicles [65,99]. Certain other work has relied on solution of optimization problems, such as solution to MDPs [108,111], PC [136] and MILP [105], though such approaches may have scalability issues. Jakob et al. [30] have used optimization to solve a multi-UAV area allocation problem, but for tractability, the assignment costs are determined somewhat heuristically. Market-based mechanisms have become a popular choice for coordination and have been applied to several problems, such as towing, path-planning, paint ball [85], collecting data about campsites [59], and persistent surveillance [107]. On the less explicit side, inspired by biological agents, pheromones have been used as simple means of coordination for a variety of applications [13,145,147]. Koenig, Szymanski, and Liu [100] characterize “ants” by simple behavior, limited lookahead, reaction to pheromones, and no map of the environment—the last claim is questionable since the use of pheromones can be thought of as sharing a map in some sense. Reif and Wang [22] study social potential field methods and spring-force based methods for control of very large scale robotic systems (upto tens of thousands). Our own work on the MRP doesn’t particularly fall in any of these categories, but provides an implicit mechanism for coordination.

5.1. Centralized vs. Decentralized Techniques

In recent years, there has an emphasis on decentralized approaches, citing advantages such as adaptability [18], simplicity, modularity, low communication bandwidth requirements [1], reliability, diversity, robustness [54], and scalability [166]. There have been similar categorizations in literature which may be a little different from the definitions used here [59,84]. In this work, there are three characteristics used to identify a centralized approach in this work:

• A centralized agent solving the problem, or all agents solving the complete problem (with redundancy) [36,101].
• A high bandwidth of communication that the agents rely on for taking control actions [72].
• Sharing of plans or the sequential decision making [11,17].

Typically, the approaches of multi-agent planning, optimization [105,108], space decomposition [55], market mechanisms [13], and evolutionary algorithms [25] fall in the category of centralized methods, though this is not a strict rule. Decentralized approaches on the other hand, are characterized by agents taking sufficiently high level decisions independently [22,98]. There can be some communication between agents (for instance sharing of maps or position information), but is typically not critical for decision making [110]. Typically the approaches using potential field techniques [22], swarm intelligence [75], behavior-based methods [98], and pre-determined search patterns [101] tend to be decentralized. Note, another commonly used term is “distributed” which is often used to mean the same as decentralized [18]. We however draw a subtle distinction—we believe that decentralized typically has to do with the algorithm, whereas distributed refers to the physical hardware being separated. Hence a centralized technique may still be distributed by applying massively parallel computation (on different platforms for instance), though at the cost of a large communication bandwidth.

5.2. Heterogeneity

Using teams of heterogeneous vehicles for search and exploration has piqued the interest of several researchers in the recent past [99], with some of them emphasizing the need for heterogeneous agents [67,95,167]. Not much work in persistent surveillance has used heterogeneous vehicles, and though some of the techniques seem to be easily extensible to heterogeneous agents [110], particular results with the advantage that heterogeneity offers has not been demonstrated [22]. In fact, some work failed to observe a quantifiable advantage in simulation [168,169]. Potter et al. [84] provide a succint survey of other studies using heterogeneous agents and claim that the need for heterogeneity is not driven by the difficulty of the task, rather by the number of skill sets required to solve the problem. Czyzowicz et al. [86] study a patrolling problem of agents with different maximal speeds, which is probably the first work of its kind. Sauter et al. [95] demonstrate facility protection using a group of UAVs and UGVs with differences in sensors, vehicle dynamics, and communication capabilities. But this is still an open area of research.

6. Particular Aspects of Problem

In this section we look at particular aspects (for lack of a better term) of the problem. These are basically extensions/variants of the basic persistent surveillance problem which basically make it richer, or are sometimes an integral part of the basic problem which may or may not be ignored depending on the application.

6.1. Grid Decomposition

Real UAVs operate in continuous space, and so most surveillance problems are inherently continuous in nature. However, discretization is often required either to obtain tractable approximate solutions or to maintain a “map” of the environment that keeps track of explored regions [20] (refer Figure 16). Some analytical techniques may even obviate this need, but gridding may still be required to keep track of system performance. Note that the discretization discussed here is different from space decomposition in Section 4.2 which is typically a coarser discretization to account for obstacles and to divide work among agents. We have not found any work on persistent surveillance that does not use some sort of gridding. Work on 1-D patrolling [88,89] seems to be an exception, since the vehicles simply go back and forth along a segment, though if one was to try and measure the performance (i.e., keep track of maximum age in the environment), they would need to resort to some discretization. Quijano and Garrido [124] give a brief survey of different grid types and Occupancy Grid Maps (OGMs). They focus on distinction based on shape, claiming that qudrangular grids make it difficult to perform diagonal motions. They further point out that lines and curves can be represented in hexagonal grids more easily and these grids result in shorter distances between points. Thus they are better for exploration of large environments, and also result in lower variance in performance. These claims are however true only when the vehicle is constrained to move from one grid cell center to the next without regard to vehicle dynamics. The authors of this paper have not come across any particular advantage of particular grid shapes [53], and rectangular grids seem to be the norm. Ref. [30] uses two kinds of grids due to their “occlusion-aware” surveillance task—one of the grids (covering vantage set) ensures that all parts of the domain are covered from atleast one point in the grid, and the other grid is the actual target space discretization.

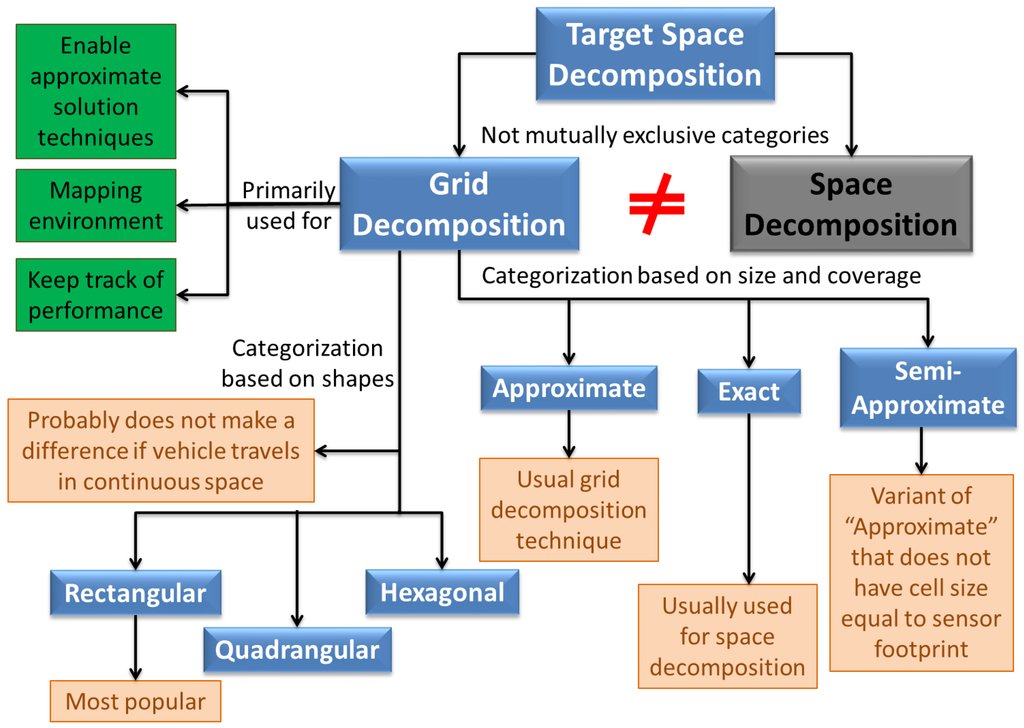
Figure 16. Applications and common types of grid decompositions.

Figure 16. Applications and common types of grid decompositions.

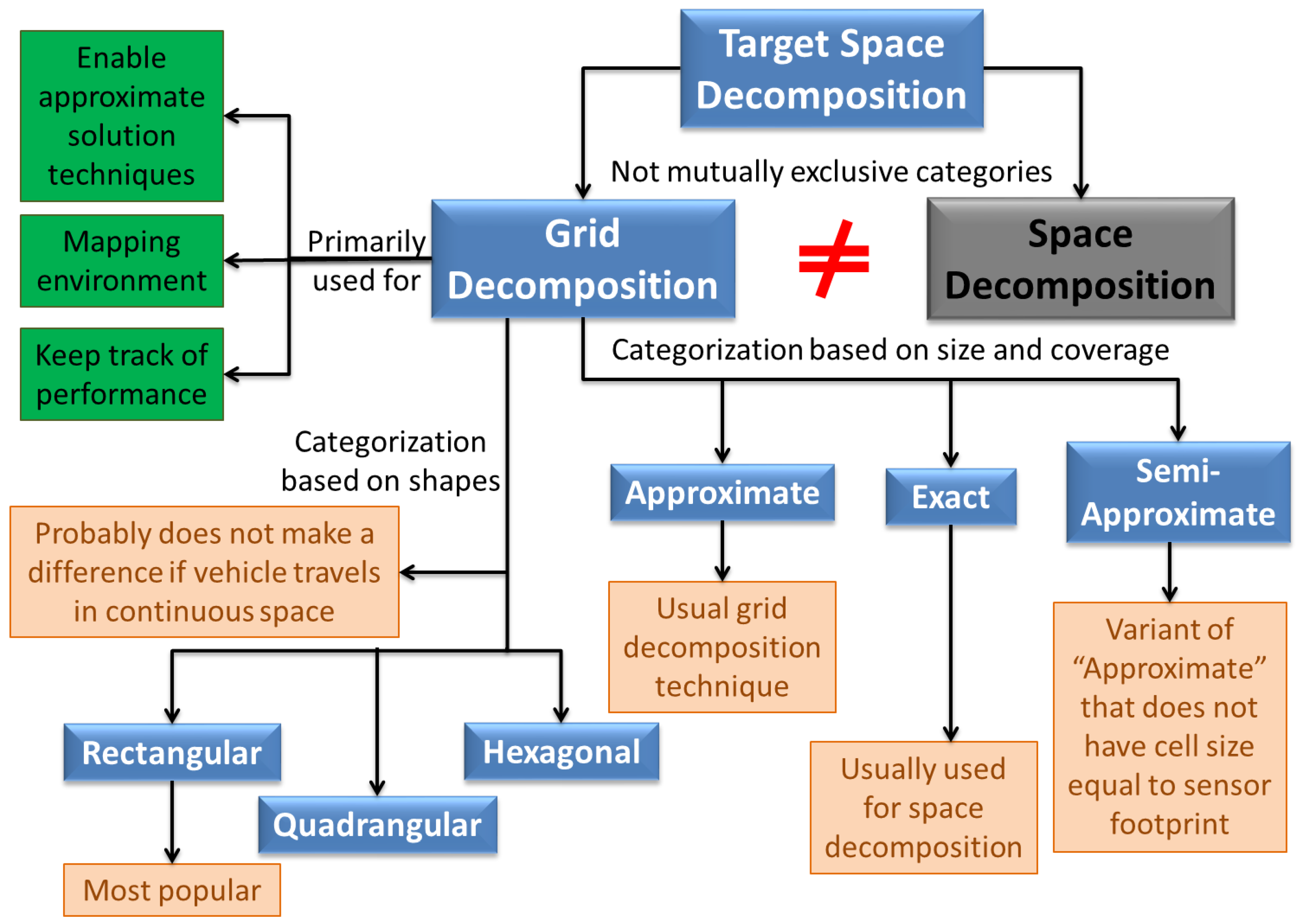
For the sake of completeness, we refer to [9], which classifies cellular decompositions as approximate, semi-approximate, and exact, primarily based on cell-size (not mutually exclusive categories). Approximate cellular decomposition has cells the size of sensor footprint [105], and all the cells cumulatively may not exactly cover the space. Exact cellular decomposition is characterized by bigger cells covering the entire space and the vehicles using simple search patterns within each cell, though strictly speaking they exhaustively cover the space [74]. Note that most grids in literature are both approximate and exact [166]. Semi-approximate decompositions are less clearly defined and rarely used, but the example cited has a pre-specified width of cells. We take the liberty of assuming that it includes cases where the size of the cells does not equal the sensor footprint. Typically, exact decompositions are used in context of space decomposition, while approximate decompositions are used for gridding in the sense used here. A variant of gridding the target space directly, is to represent the space as graphs which need to be traversed repeatedly [40,106]. This generalizes the problem to the case where the Points Of Interest (POIs) are discrete locations in space, not necessarily contiguous in nature [106]. Several techniques, such as TSP-like algorithms and those developed for the DVRP [170] become applicable in that case. However, care should be taken in a direct application of those techniques, since when the POIs are actually located in continuous space, several techniques may be able to take advantage of that fact and reduce computational cost [26].

6.2. Communication Constraints

While many approaches assume complete communication between agents (especially for centralized strategies) [88], there has been a growing emphasis on operation under communication constraints [32,63,171]. Most strategies for persistent surveillance still ignore communication constraints. This does not necessarily entail a high bandwidth of communication, but still requires periodic communication. An example is our own work on the MRP control policy (see Section 4.4) which does not involve centralized planning or decision making per se, but requires to know the positions of other UAVs in the space. This “communication” requirement may be replaced by “observation” of other UAVs (for instance using airborne radars or electro-optical sensors), but for simplicity we treat it as a communication requirement. Our control policies in particular, do not fail under lack of communication, as demonstrated by some flight testing at Boeing [166], but a formal study of effect of limited communication on the system performance has not been conducted by us. Some of the work which has recognized communication constraints is cited below.

Gaudiano et al. [75] compare global and limited communication (along with random to fully cooperative control schemes) for a search and attack task. Erignac [98] gives details of map synchronization and networking, and also demonstrates in simulation that communication requirements grow linearly with the size of the swarm. Hussein and Stipanovic [96] claim that the issue of dynamically changing communication links between agents has not been sufficiently addressed. They introduce flocking behavior in agents to maintain communication [97]. Ad-hoc networks, characterized by dynamically changing networks between communicating agents, are a common form of implementing and dealing with communication constraints [19,130], though applications to persistent surveillance are limited [113]. Other implementations of communication constraints have used less well known architectures, or simply heuristics for communication constraints. For instance, Ref. [99] uses a flooding scheme for limited communication. Similarly, Carli et al. use an iterative scheme based on local communication for partitioning of patrol paths. They study three types of communications: (1) synchronous; (2) asynchronous symmetric gossip; and (3) asynchronous asymmetric gossip.

6.3. Sensor Issues

This section briefly looks at some of the sensor issues considered for surveillance. Sensory perception, and more recently multi-sensor data fusion, have become huge research areas in themselves [74]. Thrun et al. provide a more complete discussion in [172] and emphasize on practical issues in [67], claiming that learning is very important in sensory perception. Most work in persistent surveillance has ignored sensing issues, except for some work on occlusions [20,30]. Part of the reason could be that research on sensor issues in other applications (such as exploration and coverage) may be directly applicable to persistent surveillance, but this is yet to be ascertained.

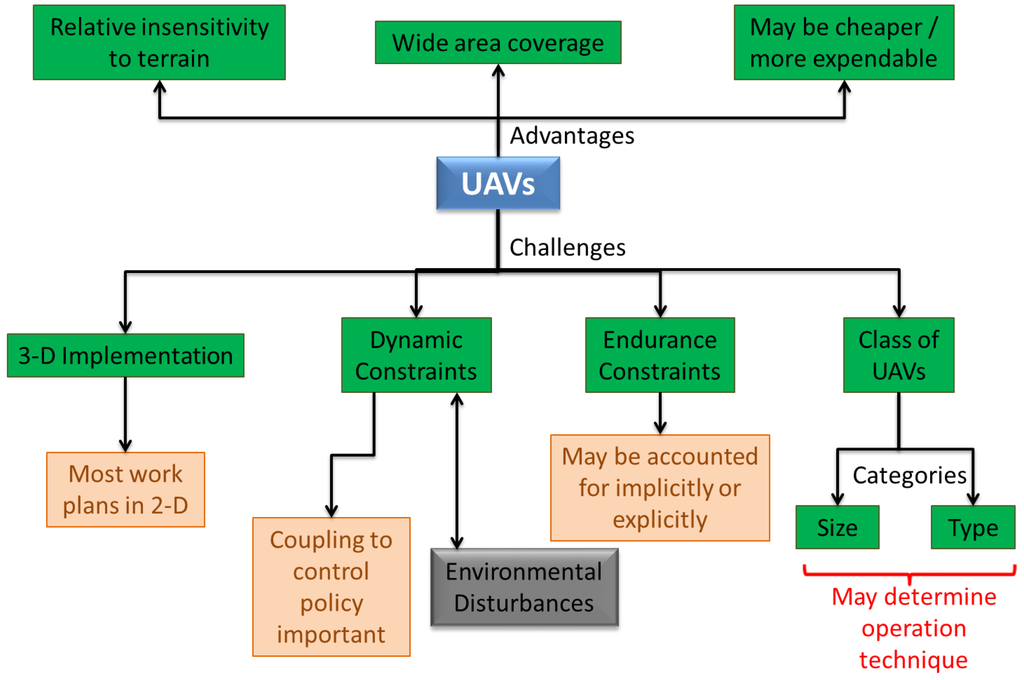
Figure 17. Advantages and issues related to use of aerial vehicles.

Figure 17. Advantages and issues related to use of aerial vehicles.

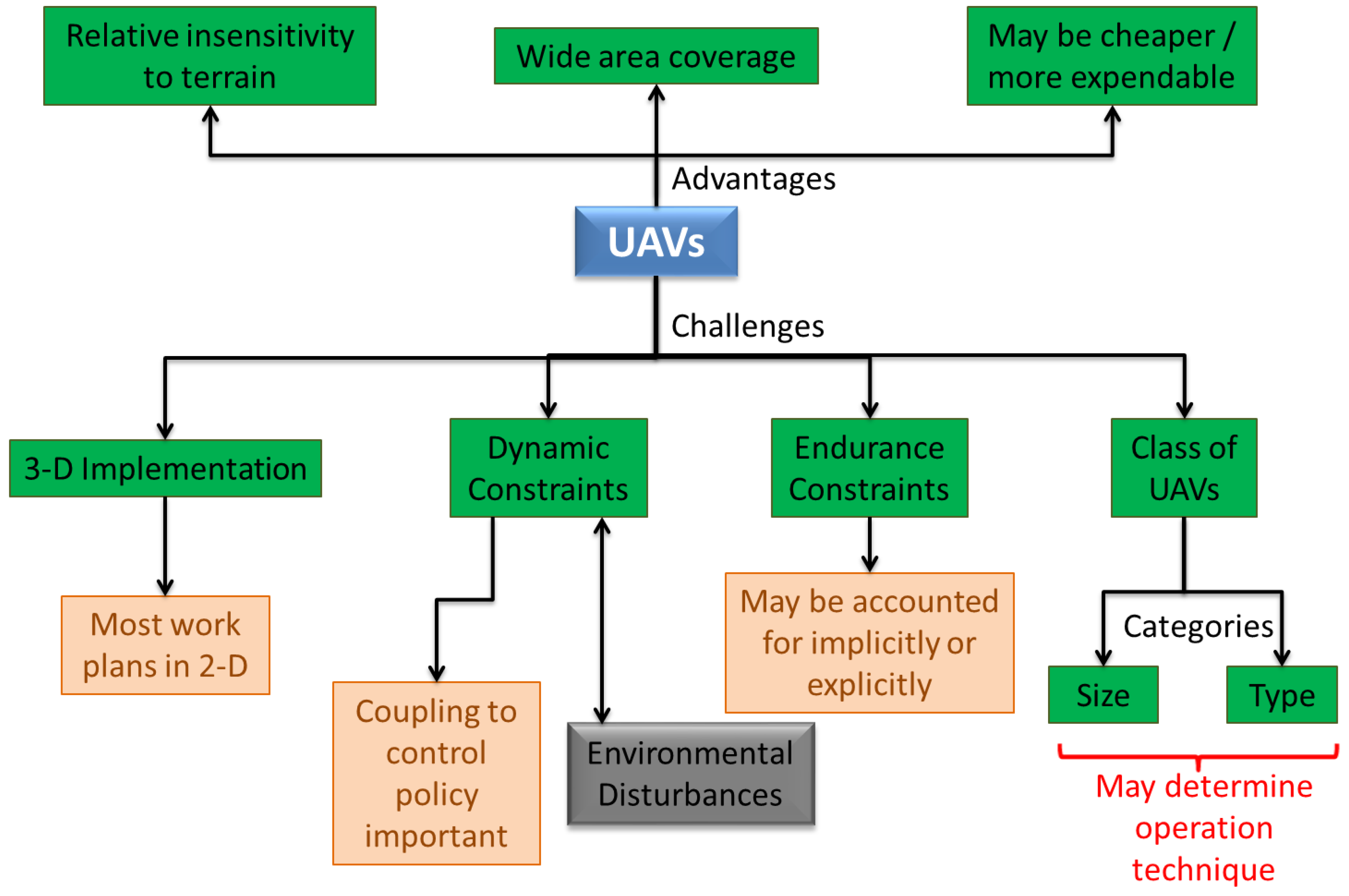
6.4. Use of Aerial Vehicles

Figure 17 shows the advantages and issues associated with using UAVs. For the tasks of surveillance and exploration, aerial vehicles offer the advantage of wider area coverage [77] and essentially being able to ignore terrain [13], though certain applications might require maneuvering through obstacles [29,167]. Agarwal, Hiot, Nghia, and Joo [173] say that low-flying small-endurance UAVs are well suited for region coverage over air-bases or urban zones, since they are cheap, highly maneuverable, and expendable. Hence they have been gaining considerable attention over the past decade [28]. Though the high level control algorithms for ground vehicles can often be adapted for air vehicles, the latter require additional considerations such as more constrained dynamics and endurance, and planning in 3-D space. Aerial vehicles are also limited in their ability to perform detailed surveys of the target space, especially if some interaction with environment is required. Hence, future systems will probably use a combination of airborne and ground vehicles for optimal utilization of resources. Some work that has looked at aerial vehicles, includes that by Erignac [98], Frew et al. [83], Gaudiano et al. [75], Liu et al. [105], and Nigam et al. [107]. In consideration of UAVs, it is important to note if the UAVs are fixed wing [25] or rotorcraft [111] since that directly affects the vehicle dynamics. Also, if MAVs [28] are used in an outdoor environment, they may be particularly susceptible to gusts and disturbances.

6.4.1. 3-D Implementation

Use of aerial vehicles also entails 3-D target space considerations. Whereas most work constrains airborne vehicles to fly in 2-D space [4], there have been some authors who have looked at this aspect, particularly from the point of view of occlusions [30,65]. In that work, occlusions to camera field of view due to buildings are explicitly modeled. In order to ensure covering the space, the covering vantage point set is created, by solving an instance of the 3D Art Gallery Problem. This problem can be defined as finding the minimum number of sensors and their positions in a polygonal area (with or without holes), such that any point inside the area can be seen by at least one sensor.

6.4.2. Vehicle Dynamic Constraints

In case of aerial vehicles, the dynamic constraints on the vehicles (in particular the turn radius constraints for fixed wing aircraft) become important. Most work in MASs has ignored vehicle dynamic constraints by assuming for instance that the cell size is large enough for dynamics not to be an issue [53]. But such an assumption may not be true irrespective of type of decomposition. One may argue that we can always decouple the lower level controls problem (which deals directly with flight dynamics) from the higher level guidance problem. But as shown later in this section, this may induce performance penalties [62]. Moreover, for certain techniques, such as space decomposition, a method that doesn’t consider vehicle dynamics while partitioning the space, may end up with skewed partitions [43]. Certain work dealing with robots has also imposed dynamic models of vehicles in their performance evaluation [12,23,59,88], but this section concentrates on aerial vehicles. There has also been some work on underwater vehicles [94] that is directly related to the UAV problem. In that paper, two glider models have been developed and used, a simple one for path planning and a detailed one (3-D kinematic) for control system design.

We did some preliminary investigation to study the effects of dynamic constraints on the performance of the system [107]. A 3 degree of freedom (DOF) simulation ignoring the turn rates and moments (similar to Ref. [174] was found to be suitable for this purpose (refer to [25] for details). The UAV is assumed to fly at constant altitude. Hence the minimum radius of turn of the UAV, $R_{turn}$, becomes the constraining factor. Assuming the aircraft has sufficient thrust for a sustained turn, $R_{turn}$ is governed by the maximum lift coefficient, $C_{L_{max}}$. Figure 18 shows the mission performance (maximum age as a function of time) for different values of $C_{L_{max}}$. The performance curve with $C_{L_{max}}$ = 1.2 almost coincides with the curve without dynamic constraints, but a moderate change in $C_{L_{max}}$ can cause huge mission performance penalties. Note that increasing the value of $V_{mission}$ would have a similar effect on the performance as well. Therefore, we observe that it is important to consider the coupling between aircraft dynamics and high-level control.

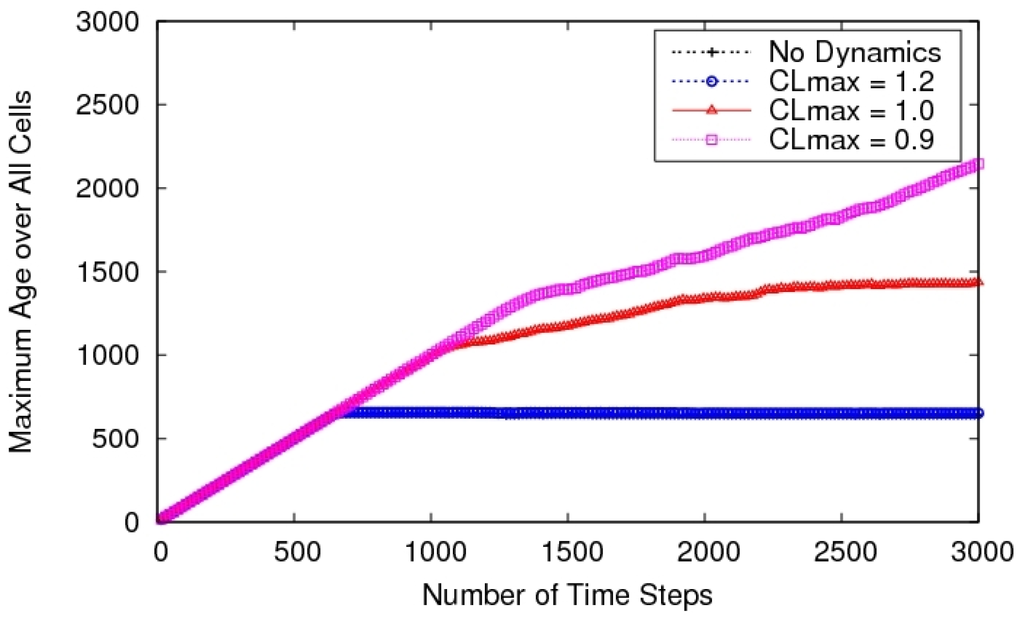
Figure 18. Maximum age as a function of time plotted for the case of a single UAV, with $C_{L_{max}}$ = 0.9, 1.0, 1.2, and compared to the case of no dynamic constraints.

Figure 18. Maximum age as a function of time plotted for the case of a single UAV, with $C_{L_{max}}$ = 0.9, 1.0, 1.2, and compared to the case of no dynamic constraints.

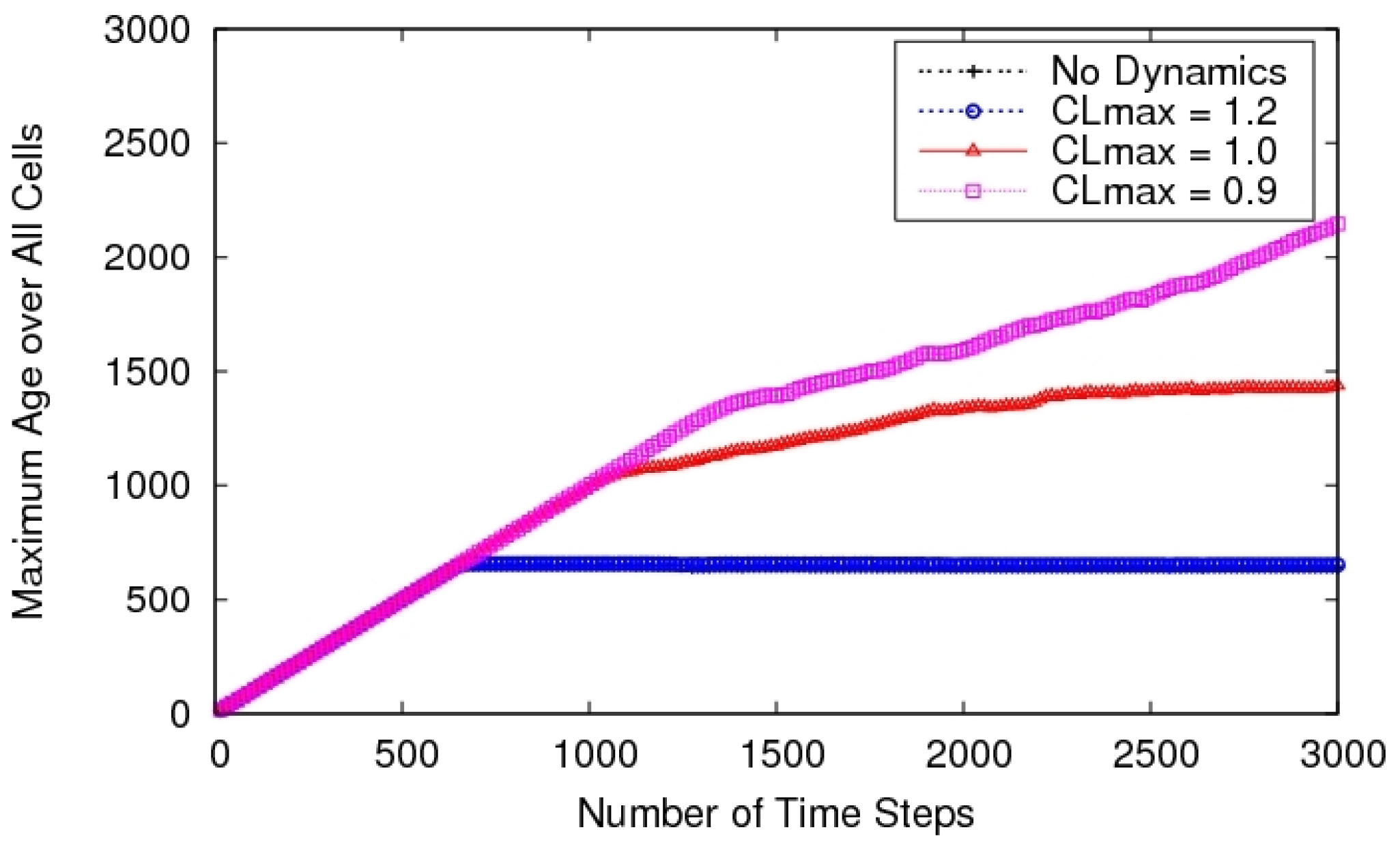
When we introduce the additional nonholonomic constraint of constant velocity, we end up with a simplified dynamics model, akin to the Dubins model [175]. This is one of the most popular dynamic models used in literature, for instance, see [105]. [30] uses an alternating algorithm and accelerated A* algorithm for path planning under dynamic constraints. Girard, Howell, and Hedrick [87] use a similar kinematic model with winds in their work. Ref. [20] uses a 3-D analog of Dubins car with several performance constraints—though it assumes constant altitude and speed. Frew et al. [83] point out the importance of dynamic constraints in a tracking application and use a Picolo autopilot for their UAVs, that reduces the system to a 3-DOF model with nonholonomic constraints. Enright et al. [15] extend the TSP by adding dynamic constraints on the UAVs and introduce the DTRP. In their analysis, they find the performance to be a linear function of the turn radius constraints, though in some of our analysis [55] this was not found to be the case. Certain work has accounted for dynamics heuristically [106]. For instance, Hokayem et al. [99,133] use a simple kinematics model for the UAVs without any turn constraints, claiming that using more complicated dynamics would only add a constant time to their objective. In [96,97], they also guarantee collision avoidance using a technique introduced by Leitmann and Skowronski [177]. Bonabeau, and Clough [103] also use a simple dynamics model with variable speed and maximum turn rates. Along the same lines, Gaudiano et al. [104] use a 3-DOF dynamics model with variable thrust and turn rate.

Dubins proved that the minimum length trajectories between any two points, with initial and target headings, consist only of straight line segments and arcs of minimum turn radius [175]. Erzberger and Lee [176] have described the corresponding trajectories for the shortest paths. Figure 19 shows an example where the UAV has to travel from point A to point B with given initial and desired headings. The circles shown correspond to minimum turn radius and are tangential to the heading direction. The candidate paths for the optimum are numbered 1 through 4 in the figure. To find the shortest trajectory, the lengths of the four paths are found analytically and the optimum is selected. A similar analysis can be done for other cases as well. In spite of its popularity, we were hard pressed to find a detailed algorithm addressing all cases of vehicle position and orientation relative to the target point—several implementations have ignored some of the pathological cases. Hence we had to work out the details on our own, though our detailed implementation has not been published either. Based on the dynamics model, we proposed a simple modification to the MRP (see Section 4.4) that allows accounting for dynamic constraints in calculation of target cells. Detailed results are available in [107] and Table 1 gives a concise list of the results, comparing the original approach (EDP) to the modified approach (ADP).

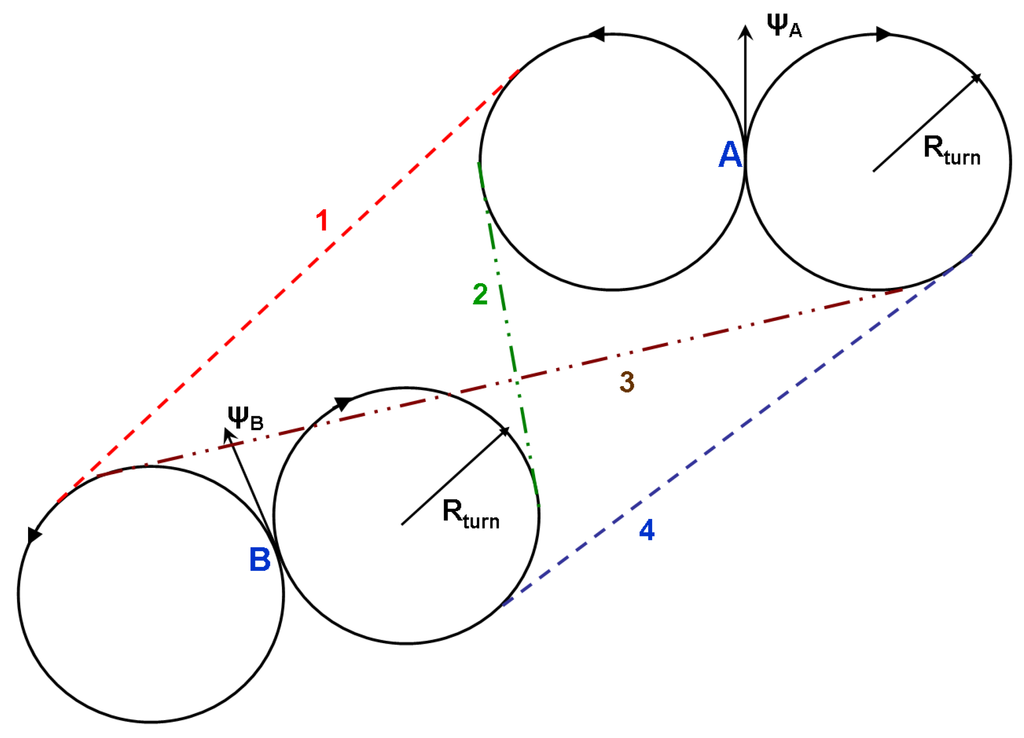
Figure 19. Sample case showing how to find the minimum length trajectory starting from point A (heading, ${\psi }_A$), and reaching B (heading, ${\psi }_B$). There are four candidate paths, numbered 1 to 4, and the shortest path can be found by calculating the lengths for all of them.

Figure 19. Sample case showing how to find the minimum length trajectory starting from point A (heading, ${\psi }_A$), and reaching B (heading, ${\psi }_B$). There are four candidate paths, numbered 1 to 4, and the shortest path can be found by calculating the lengths for all of them.

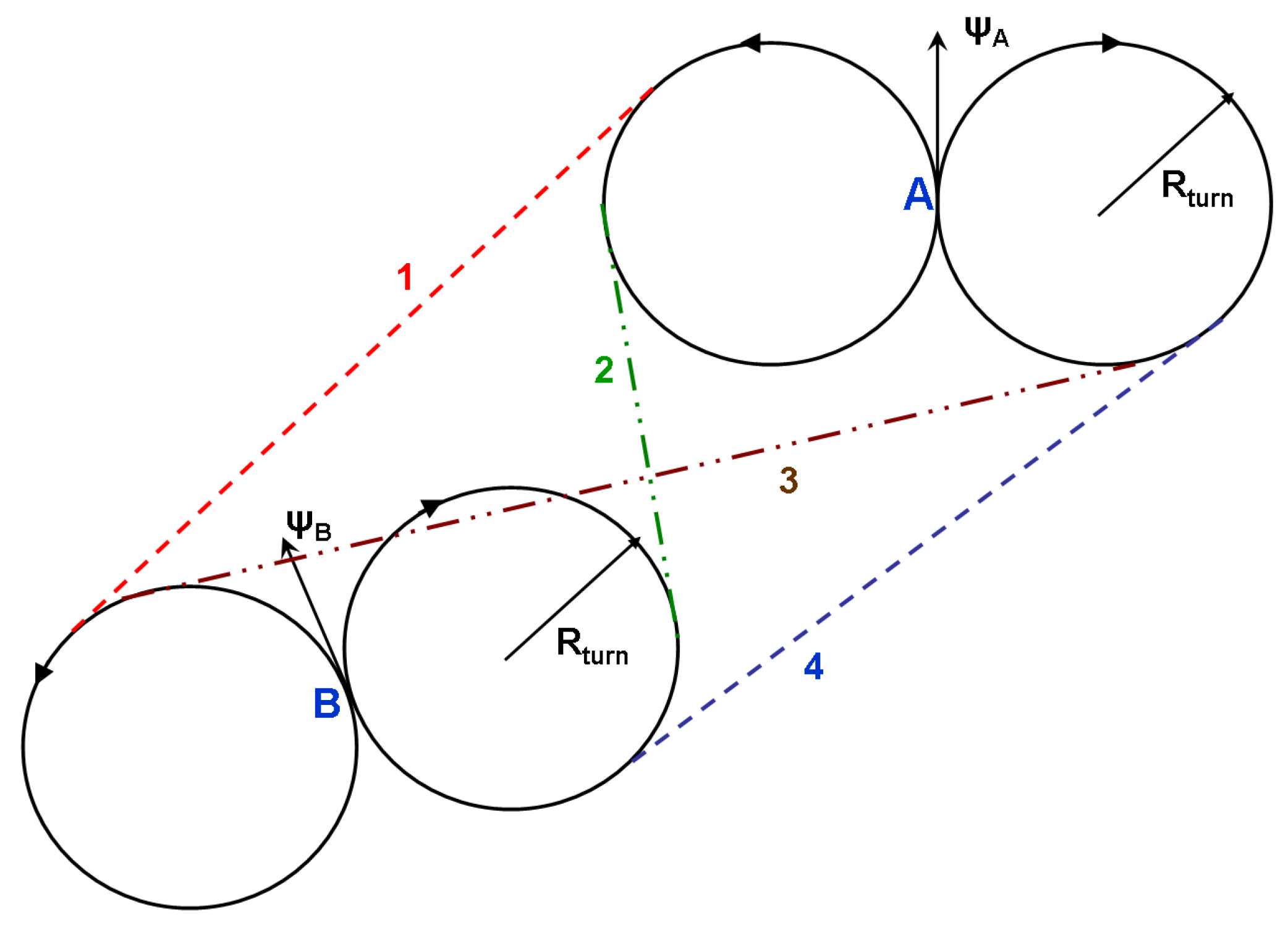
Table 1. Summary of results comparing EDP and ADP for different dynamic constraints.

Case	$C_{L_{max}}$ = 1.03		$C_{L_{max}}$ = 1.18		$C_{L_{max}}$ = 1.67
$N_{UAV}$	EDP	ADP	EDP	ADP	EDP	ADP
1	261.7	255.8	198.5	196.1	108.4	107.1
3	235.9	209.2	194.7	188.2	174.7	144.4
5	226.3	196.9	188.2	174.7	145.7	141.8
10	124.6	106.6	101.3	94.5	80.3	79.0

Table 1. Summary of results comparing EDP and ADP for different dynamic constraints.

Case	$C_{L_{max}}$ = 1.03		$C_{L_{max}}$ = 1.18		$C_{L_{max}}$ = 1.67
$N_{UAV}$	EDP	ADP	EDP	ADP	EDP	ADP
1	261.7	255.8	198.5	196.1	108.4	107.1
3	235.9	209.2	194.7	188.2	174.7	144.4
5	226.3	196.9	188.2	174.7	145.7	141.8
10	124.6	106.6	101.3	94.5	80.3	79.0

6.4.3. Endurance Constraint Considerations

Endurance constraints become important in practical implementations, especially for aerial vehicles. One way to incorporate these (also the most common), is to complete the mission before the vehicle runs out of fuel [10,36,178]. This is not applicable directly to persistent surveillance, but if used in a repeated fashion, could perhaps be applied (in the same way that single-time exploration techniques may be extended to continuous coverage). Certain work has incorporated fuel limitations heuristically as well by dividing work among UAVs according to remaining fuel [79] or simply trying to minimize fuel consumption [121]. A better way to incorporate such constraints, which is directly relevant to our problem, is by addressing periodic refueling/recharging of vehicles [66]. However, work on this problem is limited. Ref. [112] solves a MILP problem to schedule UAVs for border patrol under endurance constraints. The UAVs are assigned parts of a space-time trajectory based on their battery status. Valenti et al. [109] address allocation and scheduling of UAVs for persistent surveillance under limited endurance. The goal is to maintain at least one UAV in the target space at all times in presence of failures and other practical limitations. The focus is on hardware implementation of such techniques, wherein they demonstrate autonomous docking and recharging of the UAVs [108]. Ref. [113] discusses the multi-agent health management problem which can include UAV failures as well. The authors of this paper have also studied this aspect for persistent surveillance, demonstrating autonomous replacement and refueling in hardware [110], and developing a health monitoring policy that coordinates refueling times of UAVs [166]. We present a brief overview of the health monitoring policy below, but the reader is referred to Ref. [25] for further details.

There are two aspects to the refueling problem: one is to decide when each UAV should land, and the other is to modify the control policy to account for the endurance constraints. In general, these problems are coupled, but we do not expect the coupling to be strong. Hence, in our work each problem is analyzed separately. The former problem is posed as an optimization problem which is solved periodically, given the health and refuel times of all UAVs. In general this is a combinatorial optimization problem that can easily become intractable for online implementation. However, we make certain modifications to formulate the problem as a Linear Programming (LP) problem that can be easily solved online using gradient-based optimizer. The latter problem is addressed through a simple modification to our control policy that allows UAVs low on fuel to remain close to the base-station and vice-versa [166]. The resulting LP-based approach is then compared to two benchmark techniques: (1) a pre-determined version of the optimization technique outlined above (does not react to changes in the environment), and (2) a reactive technique that requires half the number of UAVs assigned to the mission to survey the space at a time (the other half is either on standby, getting refueled, or returning to the base-station). Figure 20 illustrates the advantage of online optimization based approach compared to offline and heuristic techniques. Several other results are available in [166].

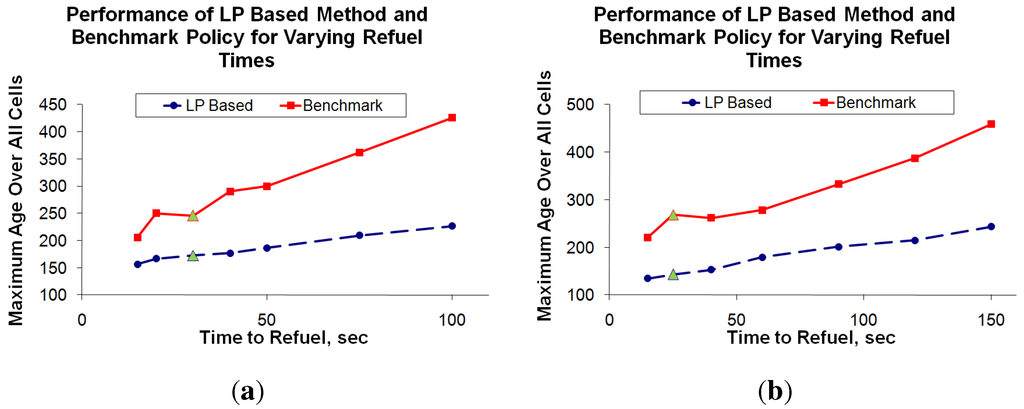
Figure 20. Comparison of LP-based approach to (a) a pre-determined benchmark policy and (b) a heuristic reactive policy, as a function of refueling time. (a) Pre-determined Policy; (b) Heuristic Policy.

Figure 20. Comparison of LP-based approach to (a) a pre-determined benchmark policy and (b) a heuristic reactive policy, as a function of refueling time. (a) Pre-determined Policy; (b) Heuristic Policy.

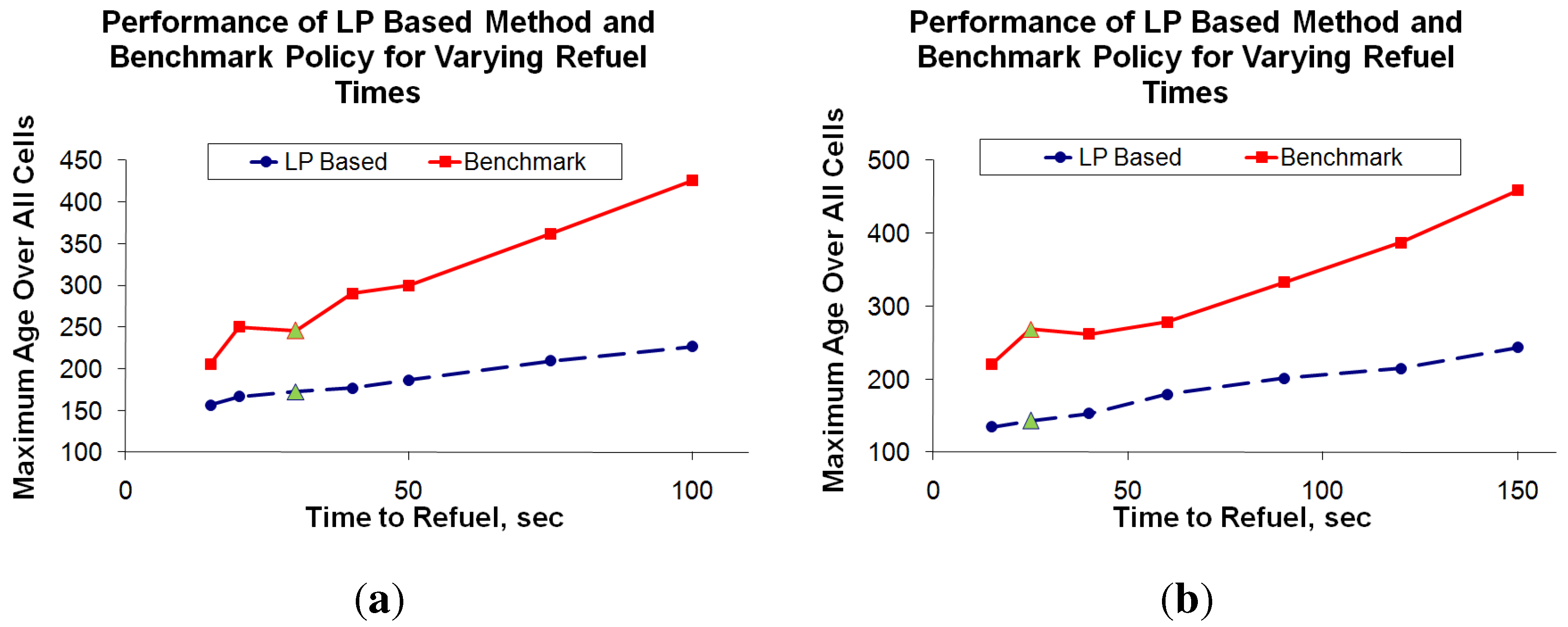
6.5. Explicit Consideration to Uncertainty

Failures, sensing imperfections, and communication losses create uncertainty in the inputs that cannot be ignored in most applications [19,113]. Many of the methods investigated in literature may be inadequate for dealing with autonomous UAVs in changing environments [6]. The others deal with uncertainties in two ways: either by being robust to environment dynamics/failures [24,95,100], or by explicitly considering uncertainties in decision making. The former may include techniques that frequently replan or use real-time control, but we focus on the latter in this section.

Ref. [102] applies controllers based on stochastic DP for Intelligent Surveillance and Reconnaissance (ISR). The need for stochastic controllers in this case is driven by the heterogeneous setting with intermittent inputs by humans. Bethke, Bertuccelli, and How [111] use probability distributions over uncertain parameters (in particular the nominal fuel flow transition probability) and pose the problem as a stochastic MDP, that is solved online. In some other work [113], they adapt the models online using RL as well. Liu, Cruz, and Sparks [105] model the locations of targets using first order Markov-chains. The Markov-chain is homogeneous (i.e., transition probabilities do not evolve with time) but adaptive (i.e., the probabilities are changed based on observations). The authors of this paper are also involved in some ongoing work on using PC for online mission planning [136]. PC is one of the few approaches that directly operate in the space of probability distributions and hence naturally account for uncertainties [153]. However, in general, accounting for uncertainties explicitly can drastically increase the computation requirements and such methods should be used with care for real-time implementations.

6.6. Design

A problem that has been receiving increasing attention, is the task of designing vehicles/sensors for a particular mission (or set of missions). Typically, especially in design of UAVs, the performance requirements are set heuristically and the control strategies are determined independently. However, significant improvements in performance can be obtained, if the vehicles are designed for particular missions [25]. Kovacina et al. [165] discuss effect of aircraft parameters on performance, pointing out how limitations on size, sensor footprint etc. tie in to control policy and emergent behavior. Furthermore, the size of the UAV affects the sensing accuracy and communication capability. We already showed the effect of $C_{L_{max}}$ on the mission performance in Figure 18, which is governed by the vehicle design. Pfister [79] also describes the relation between aircraft design parameters (such as speed, altitude, and sensor footprint) on search characteristics (sensing accuracy and speed). Since operations and design are complex systems, this becomes a System-of-Systems (SoS) problem. Keating et al. [180] develop the foundation and general directions for SoS engineering, and review existing literature. They define it as: “The design, deployment, operation, and transformation of higher level metasystems, that must function as an integrated complex system to produce desirable results. These metasystems are themselves comprised of multiple autonomous embedded complex systems that can be diverse in technology, context, operation, geography, and conceptual frame”. Their definition is extremely broad and hints at physical systems comprised of multiple complex systems. In this survey however, the emphasis is on application of SoS concepts to the design of aircraft systems.

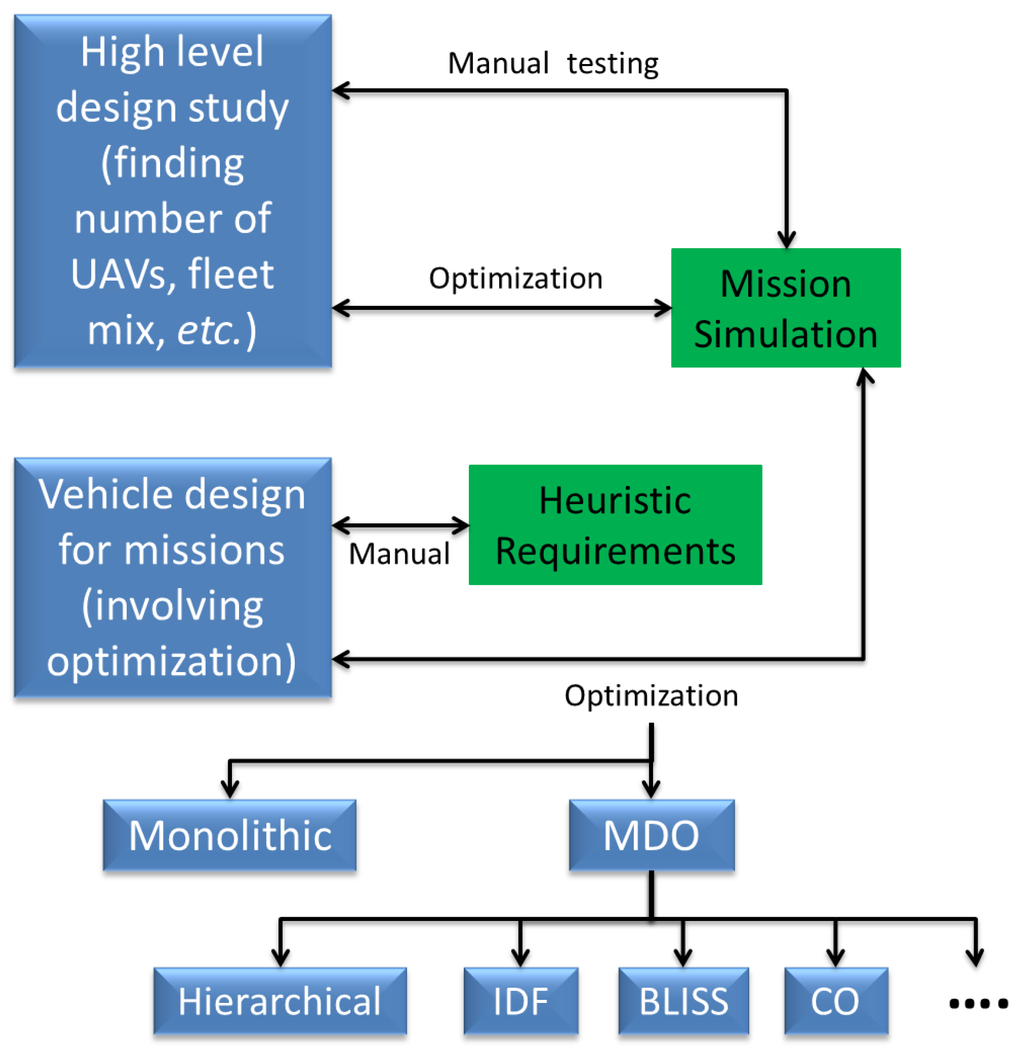
Figure 21. Overview of kind of design studies performed in literature and options for MDO.

Figure 21. Overview of kind of design studies performed in literature and options for MDO.

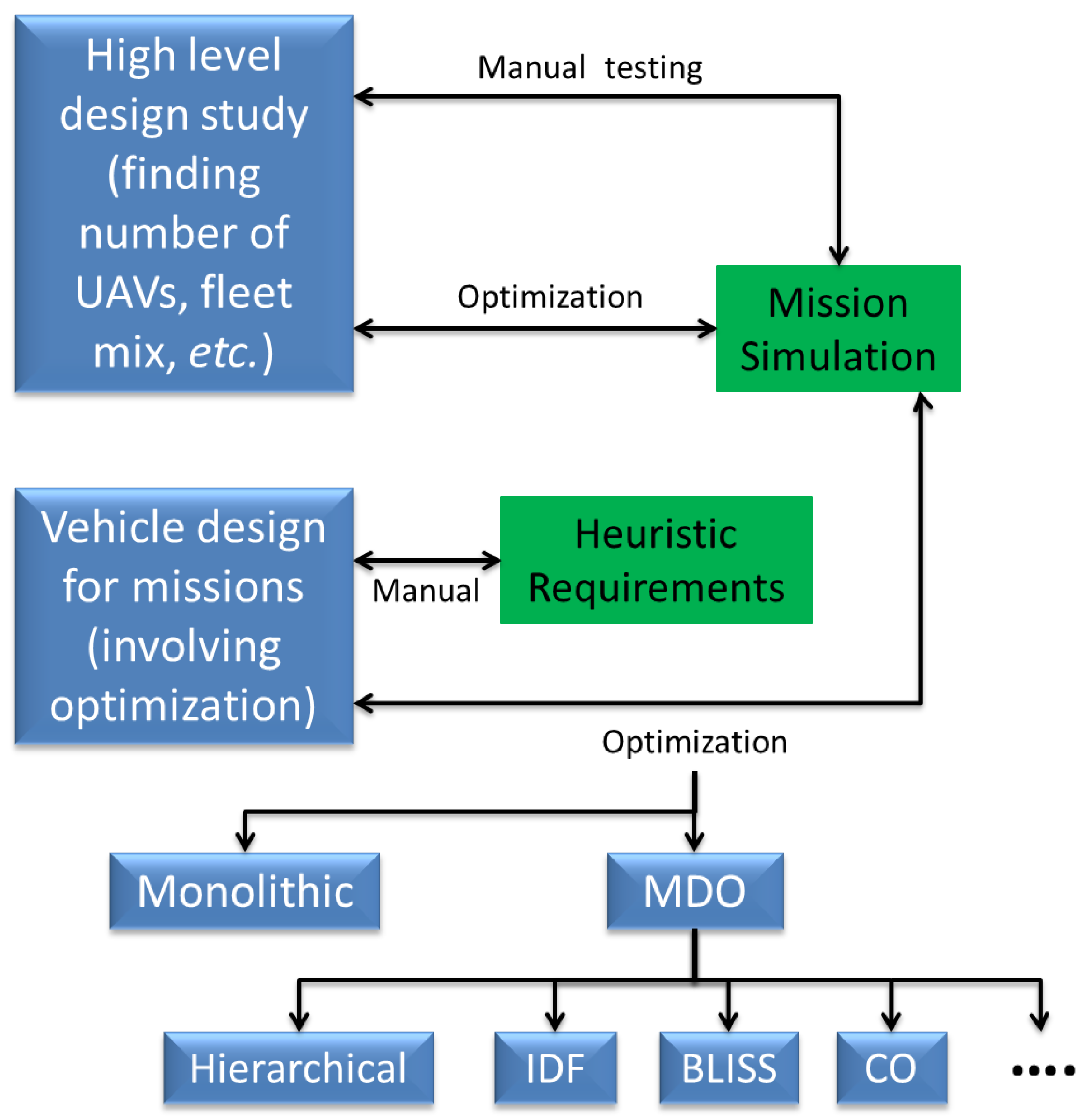
We have addressed a coupled vehicle and control system design problem for persistent surveillance [107]. We don’t know of any other work that has looked specifically at this problem, though some work has introduced certain design aspects in their problem [36], as shown in Figure 21. For instance, Ref. [23] finds the minimum number of robots and associated control policies for surveillance under safety constraints. Ref. [181] describes a methodology for adaptable system studies of future transportation at the conceptual level. It addresses design of Personal Air Vehicles (PAVs) for a search task with emphasis on use of SoS principles—though only a single vehicle is used. Frommer and Crossley [182] develop an SoS design architecture to design a fleet of morphing aircraft for a search mission with a persistence flavor (i.e., the aircraft that run out of fuel are replaced by others). They also use surrogates (approximation surfaces) to reduce the cost of optimization [183]. Underwood and Baldesarra [184] describe MUSE - their software for modeling planetary exploration for design purposes. They emphasize on human-in-the-loop to make certain high-level design decisions and use an iterative procedure for fleet design. Though a human input should be incorporable in the design process, the current research effort is on architectures that do not depend on it.

The system design problem encompasses two disciplines: operations and aircraft design. The two disciplines are typically coupled through the aircraft performance variables (such as UAV speed, minimum turn radius, endurance etc.). Figure 22 illustrates some of the significant design parameters that may affect the UAV performance depending on the underlying analysis. One way to solve the system design problem is to put together all variables from all disciplines in a single monolithic optimization. However, there are several reasons for avoiding such an approach: (1) the mission and design optimizations often use different optimizers and have very different run times, so it is wasteful to include the optimization variables from the less expensive optimization in the other; (2) for multiple aircraft designs, it is much more expensive to solve an optimization problem with all the designs together, since the different designs share very few variables, if at all; (3) decomposition-based design also makes sense from a practical point of view, where the organizational structure often necessitates dealing with operations and design problems in parallel, with minimal interaction. Such multidisciplinary optimization problems have been extensively studied in the field of Multidisciplinary Design Optimization (MDO)—look at [185] for a succint review. Ref. [182] has used a hierarchical design architecture for a similar problem, but there are some limitations of the hierarchical design architecture, so our work has focused on Collaborative Optimization (CO) [107]. CO gives relative independence to each discipline while ensuring conformance across disciplines, and has been extensively used for aircraft design [186]. Figure 23 shows a schematic of a CO-based architecture for this problem. If heterogeneous UAVs are to be designed, we can add additional “disciplinary” subspaces to the architecture. Alternative architectures include Modified Collaborative Optimization (MCO) [187], Enhanced Collaborative Optimization (ECO) [188], or Analytical Target Cascading (ATC) [189], that may be used for this problem, but have not been specifically studied by us.

Figure 22. Some significant geometric parameters that may be used for design parameterization.

Figure 22. Some significant geometric parameters that may be used for design parameterization.

Figure 23. Schematic of an example CO-based design architecture.

Figure 23. Schematic of an example CO-based design architecture.

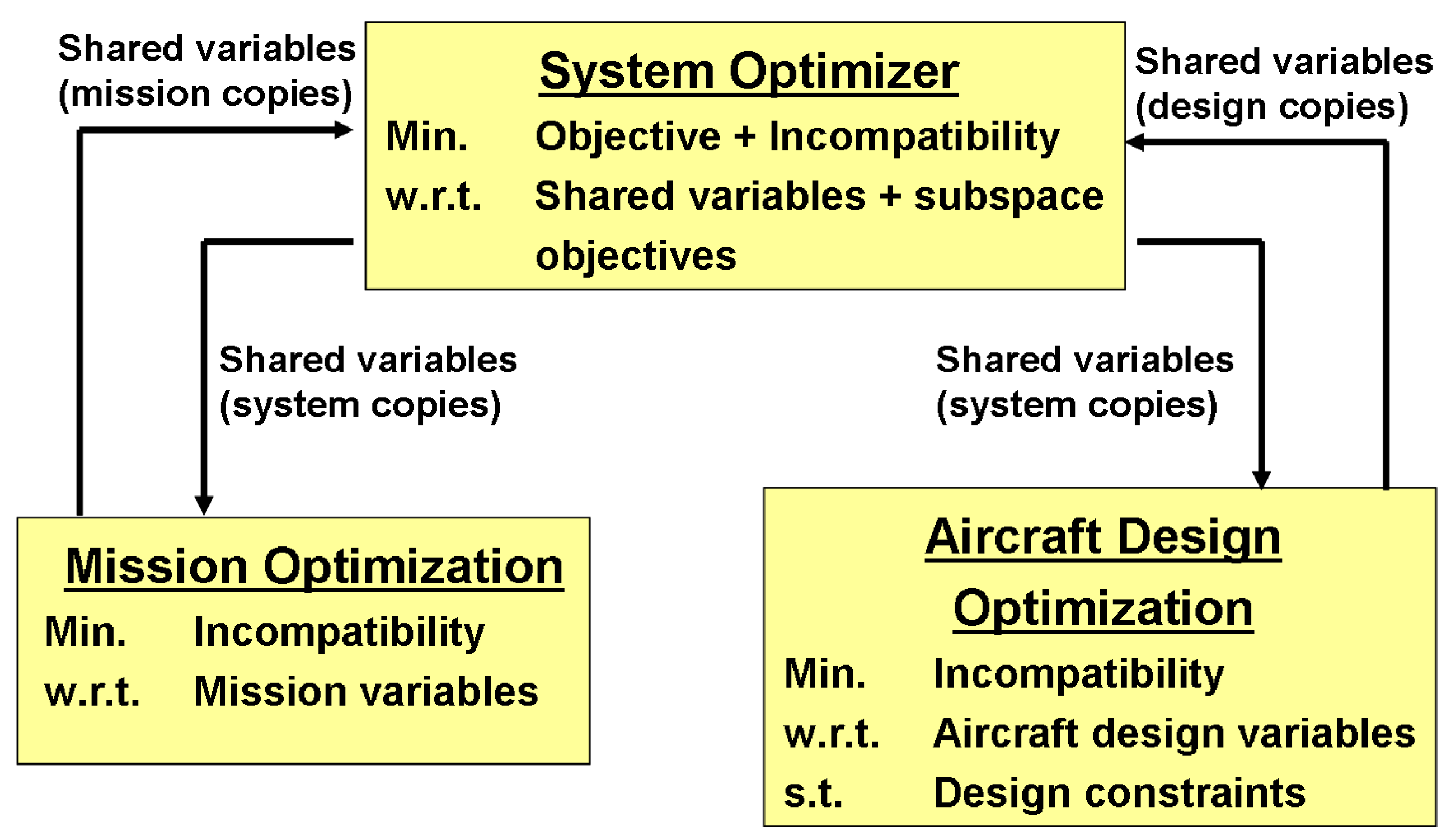
Once the design architecture and parameterization has been chosen, several implementation intricacies may also arise, such as choice of optimizers, the formulation of constraints and objectives etc. This in itself ties into several research areas in the field of optimization and a discussion of these aspects is beyond the scope of this review. But once the details have been worked out, this technique enables us to conduct design studies relating the aircraft design to operational parameters. For instance, Figure 24 shows some sample results we obtained using our CO-based technique—we plot the thrust and aspect ratio requirements as a function of the sensor footprint. For a detailed set of results and discussion, the reader is encouraged to read Ref. [25].

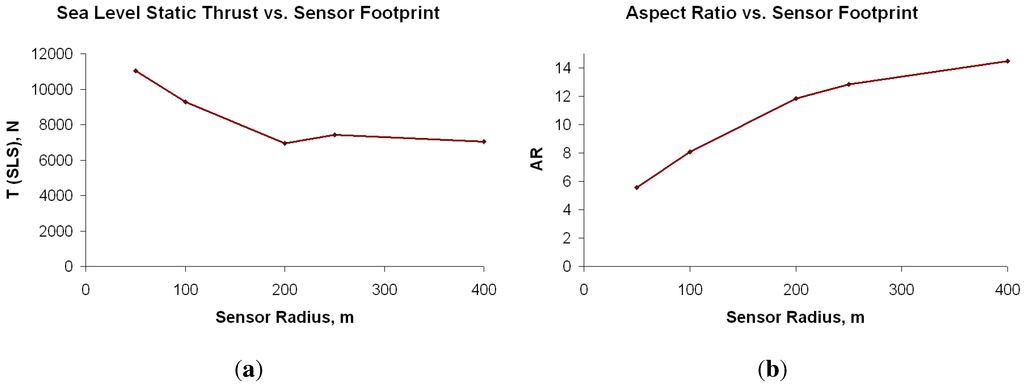
Figure 24. Sample results of design study—the thrust and aspect ratio requirements as function of the sensor footprint. (a) Thrust; (b) Aspect Ratio.

Figure 24. Sample results of design study—the thrust and aspect ratio requirements as function of the sensor footprint. (a) Thrust; (b) Aspect Ratio.

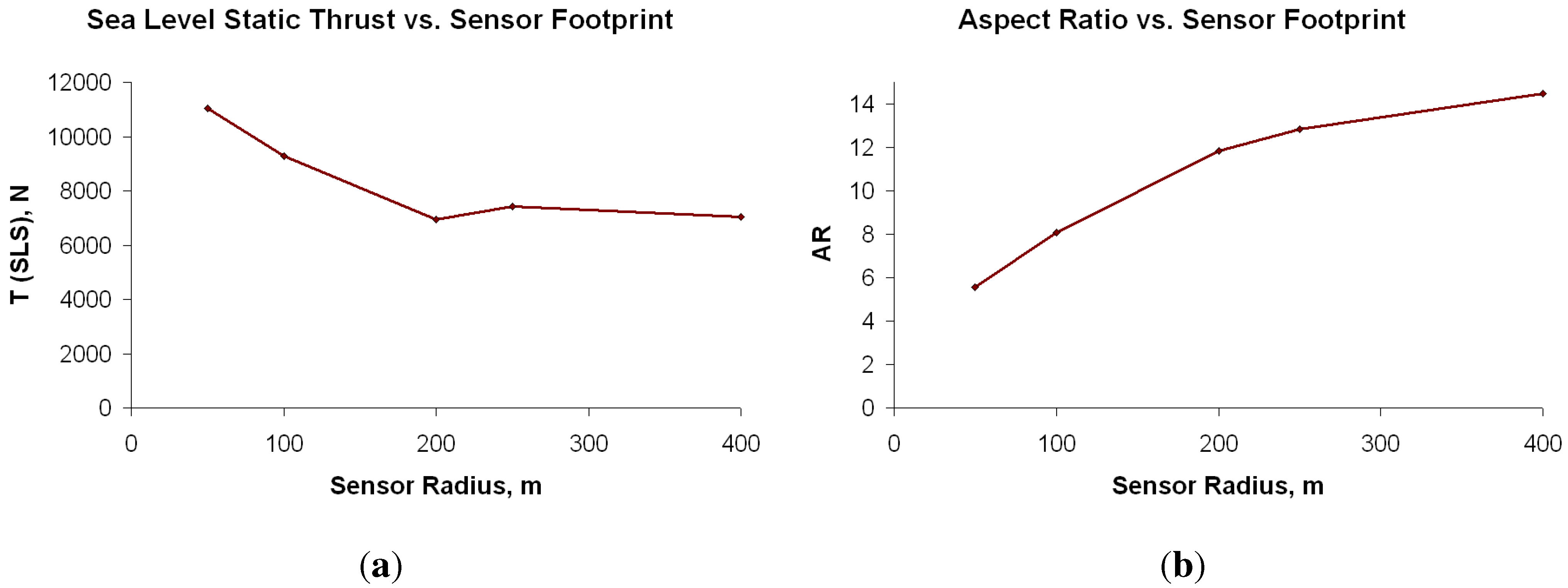
7. Testing/Demonstration of Algorithms

The claims made in literature have been supported in several ways—the methods can be roughly divided into 3 categories: (1) those involving theoretical analysis to prove certain properties of the algorithms; (2) those using simulations to study the algorithm performance; and (3) those demonstrating results in experiment/hardware. Some work has used more than one way for validation. This section lists the important research in each of these categories also noting the size of the problems studied if significant.

7.1. Theoretical Validation

Most of the research involving theoretical validation has proven soundness and completeness [37,96] of algorithms and in some cases also talked about efficiency [88]. For instance, Hokayem et al. [99] show that their techniques lie within a constant factor of the optimal for persistent surveillance. Certain other work has treated miscellaneous aspects of the algorithms depending on the problem at hand. Vincent and Rubin [101] for example, find minimum repeated coverage required to ensure that a target does not escape and the minimum number of UAVs that can complete the search probabilistically within time bounds. Liu, Cruz, and Sparks [105] analyze their approach for persistent area denial, in particular the modeling of pop-up threats, using first order Markov-chains. They also provide a MATLAB simulation for validation and compare different UAV strategies as well as target distributions. The VRPTW approach proposed in [66] ensures bounded sub-optimality with varying priorities for persistent surveillance of discrete locations (assuming dynamic tasks being generated with a uniform distribution over the target space), but makes no guarantees about visit frequency. Arvelo, Kim and Martins [23] prove certain results about their convex programming approach for designing memoryless control policies. Ref. [24] has proven several theorems regarding optimality of their approach for 1-D persistent monitoring—based on queueing theory and infinitesimal perturbation theory. Smith and Rus [26] show that their control policies are within a factor of two of the optimal policy for persistent monitoring, though the proofs seem to be geared towards a single agent and ignore the heuristics used in their approach. Smith et al. [92,93] analytically derive their speed controllers and prove certain properties associated with optimality similar to [94]. Alamdari, Fata, and Smith [27] prove that the patrolling problem (posed as a graph search problem with objective of minimizing weighted latency) can not be optimally solved using a polynomial time algorithm, and present two approximation algorithms to address the same, while proving associated theorems. Of special note is Ref. [89], that analytically discusses communication topologies for a persistent surveillance problem.

7.2. Simulation

Simulations are the most common way of validating the control approaches. Some work has claimed that this is not a good way to compare approaches [100], but we believe that well formulated simulations should give reasonably accurate results. A notable example of a simulation which very accurately represented experiments, was the VSTL simulation (see [110] for details). This is a simulation of the Boeing Vehicle Swarm Technology Laboratory, and in the authors’ experience, accurately represented the aircraft dynamics as well as environment uncertainties, including battery life modeling, failures etc.. Simulations also enable systematic development of control strategies and testing under scenarios that are practically hard to replicate. We however do agree that it is possible to make assumptions or ignore some issues in simulations that may prove disastrous in real life. Hence it is always a good idea to test systems in hardware, whenever feasible.

In existing literature, the simplest results have demonstrated the feasibility of the methods [13,66,74,92,99,112], while others either study effects of changing mission specifications on performance [25,88], or compare their method to certain benchmark techniques [55]. Ref. [93] has in fact tested the robustness properties of their speed controllers by adding noise in the simulations (MATLAB and SeDuMi). Ref. [100] compares LRTA* and node counting analytically as well as in simulation. Erignac [98] has performed various studies to quantify the effect of decentralization, communication constraints, number of UAVs, and swarm parameters on performance. The environment chosen for these studies is a 64 × 64 cell grid with upto 40 UAVs. Gaudiano et al. [75] use an agent-based simulation tool (described further in [103]) to conduct various studies for a search and attack task using a swarm of UAVs. Ref. [37] compares the DFS and 1-LRTA* algorithms with its least-recently-visited algorithm. Some of their previous work has studied the experimental properties of the algorithm, but in this work they characterize the theoretical aspects. Hussein and Stipanovic [96] demonstrate their approach in simulation and demonstrate the flocking behavior introduced for maintaining communication in [97]. Liu, Cruz, and Sparks [105] provide a MATLAB simulation for validating their persistent area denial approach and compare different UAV strategies as well as target distributions for pop-up threats. Jakob [30] describe their AGENT-FLY framework which has been used to simulate multi-vehicle surveillance problems including modeling of occlusions and camera fields of view. They demonstrate their algorithms using 1–12 UAVs in this framework. In our work, we have simulated up to 36 UAVs [136], but mostly worked with about 1–10 for analysis.

7.3. Hardware Implementations

The most rigorous form of validation is of course hardware demonstration, but it tends to be limited in scope and variety. So often simulation results are used to analyze the performance of methods, and experiments are used validate some of those results [110]. A simpler approach however is just to show that the proposed method is sound and does not result in system failure [87]. Koenig, Szymanski, and Liu [100] demonstrate LRTA* in an office environment on a 30 × 40 cell grid, and compare two variants of LRTA* for persistence as well. Ref. [92] shows collision avoidance for a persistent monitoring task using two iRobot Create robots. Paley, Zhang, and Leonard [94] have demonstrated coordinated feedback control of two gliders for continuous ocean sampling. Chandler [102] demonstrate the efficacy of their stochastic DP-based controller in simulation for reconnaissance involving 20 objects of interest and 4 MAVs. They further compare three different reward functions for the DP problem formulation. On the experimental side, they present results examining the cost model, the decision behavior of the controller, and operator model. Frew et al. [83] have built a fleet of Sig Rascal 110 model aircraft to demonstrate road following, obstacle avoidance, tracking and convoy protection. One of the few experimental demonstrations of heterogeneous vehicles is presented in [95] that uses a team of two AAI Aerosonde Mk4.1 UAVs and four Pioneer 3-AT robots for surveillance.

For a survey of physical implementations in autonomous mobile robotics prior to the year 2000, the reader is referred to [4]. For an overview of experiments at MIT’s RAVEN laboratory, refer to [190]. This laboratory has been leading some of the autonomous flight vehicle research, including extensive demonstration of persistence [191]. The testbed has been inspired by the Vehicle Swarm Technology Laboratory (VSTL) testbed at Boeing Research and Technology [110,113], and uses a very similar architecture, including the use of quadrotor vehicles and VICON camera system for positioning, which seems to have become the norm off late (refer Figure 25 and Figure 26). Several other experimental facilities have been inspired by the same ideas, including CDCL at UMD, which includes underwater testing facilities as well [192].

The use of experiments to validate persistence has special merit since that is one of the most challenging problems, and may even include autonomous battery swapping. Valenti, Dale, How, Farias, and Vian [108] discuss issues in management of multiple-UAV systems in a practical setting (lack of coordination and information exchange, failures, delayed information etc.) and the infrastructure requirements for persistent operations. They demonstrate persistent operations (with a UAV airborne most of the time inspite of vehicle failures) using 5 UAVs for upto 6 h [109]. They also successfully show autonomous docking and recharge—which was probably the first such demonstration. The same group has demonstrated hot swap of batteries in [113]. Recently some other authors have also looked at this problem [193]—demonsrating the battery swapping in their indoor Aerospace Robotics and Controls Laboratory using three ESky V4 co-axial helicopters. In later work, Bethke, Bertuccelli, and How [111] have used an online optimum health monitoring policy to demonstrate persistent surveillance on the RAVEN testbed with 3 UAVs.

Figure 25. Pictorial view of Boeing’s Vehicle Swarm Technology Laboratory.

Figure 25. Pictorial view of Boeing’s Vehicle Swarm Technology Laboratory.

Figure 26. The quad-rotor vehicle (a) and its components (b). (a) Quad-rotor vehicle; (b) Vehicle components.

Figure 26. The quad-rotor vehicle (a) and its components (b). (a) Quad-rotor vehicle; (b) Vehicle components.

Persistent surveillance with efficiency, robustness, and cooperation has also been demonstrated on the VSTL testbed by the authors of this paper [166]. Boeing Research and Technology has been developing this facility to provide an environment for testing a variety of vehicles in an indoor, controlled, safe environment[194,195]. This type of facility provides a large number of flight test hours and the payload to fly is significantly reduced through off-board processing. It also offers a tremendous advantage in scalability and risk mitigation. A number of automated safety and health based behaviors have also been implemented to support simple, reliable, safe access to flight testing. An overview of the lab and the quadrotor vehicles used in our study are shown in Figure 25 and Figure 26 respectively.

We have performed several flight test experiments demonstrating the MRP policy (refer Section 4.4) on the VSTL testbed. We present a sample experiment result here. In this case we operated 5 UAVs with 3 on standby, and 2 flying at all times. There was a manual battery replacement on one of the UAVs during the mission as well—demonstrating the ability to handle human interference as well. Figure 27 shows the performance of the system for the complete mission, which was pretty close to an estimate of the optimum. The reader is encouraged to read Ref. [25,166] for a detailed discussion. The increasing research on autonomous vehicles and accruing experience of the community has made experimental testing of small UAV swarms quite feasible nowadays, and some sort of flight testing has almost become necessary for a credible assessment of control techniques.

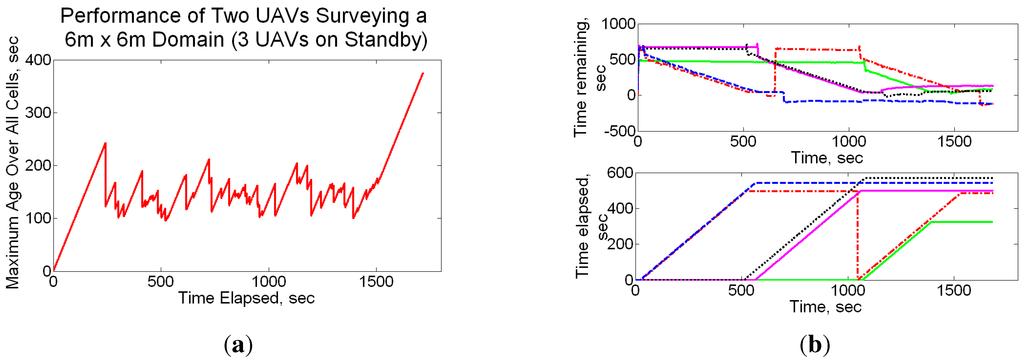
Figure 27. Performance of two UAVs surveying the target space with 3 UAVs on standby. Plot (a) shows the maximum age over all cells as a function of time. Plot (b) shows the health of the UAVs and the time they are active against experiment time. (a) Performance; (b) Health and Active Time of UAVs.

Figure 27. Performance of two UAVs surveying the target space with 3 UAVs on standby. Plot (a) shows the maximum age over all cells as a function of time. Plot (b) shows the health of the UAVs and the time they are active against experiment time. (a) Performance; (b) Health and Active Time of UAVs.

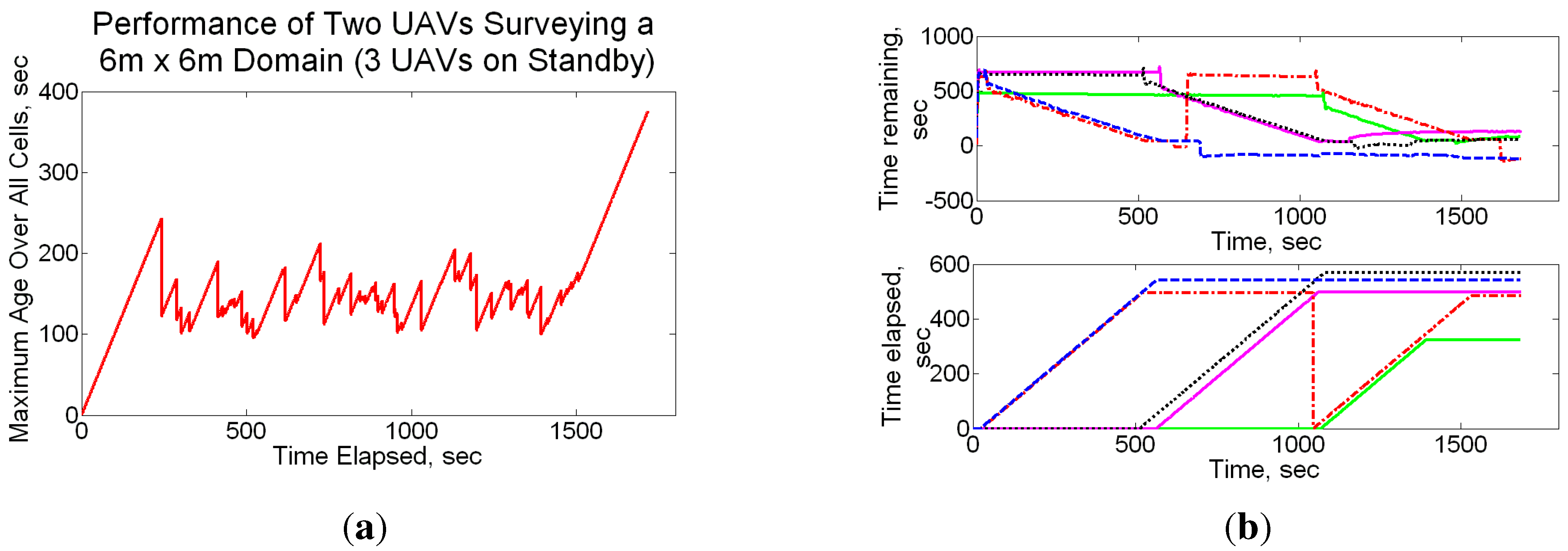
8. Conclusions

This paper has reviewed existing literature on the persistent surveillance problem, and presented some of our work on this problem. We have alluded to literature on other applications as well, when relevant, but a comprehensive survey of all autonomous control literature is beyond the scope of a single review. In this paper, we first define the problem and mention related work, followed by an overview of techniques applied to such problems. We then discuss particular aspects of the problem and the validation methods used, in particular experiments. In this section we briefly point some directions for future research.

Ref. [2] outlines technological constraints facing mobile robotics and future avenues of growth. It claims that Distributed Artificial Intelligence (DAI), biology, and distributed computing are the most critical fields for growth. Reif and Wang [22] identify research directions related to large scale robotic systems, in particular, studies on limited communication, robustness and control law design. Other work identifying research potential includes that by Thrun et al. for indoor mapping and navigation [67], Keating et al. for SoS engineering [180], and Cassandras and Li for sensing applications [32]. None of them however talk about persistent surveillance in particular.

8.1. Problems of Interest

Patrolling has been mostly studied as a 1-D problem, though some 2-D analogs have also been investigated [40]. In the future, it would be useful to study the 2-D and 3-D extensions of the problem in greater detail. The problem of persistence, where different regions have different priorities (or visitation frequency requirements) is also an interesting research area that has not been studied much [20,66]. The health management problem and optimal control approaches to persistence also provide good avenues for future research. Sensing-based exploration is still an active area of research and can be easily extended to continuous coverage applications. The emphasis is on use of passive sensors (that do not deplete the energy resources of the sensing platform as much) and vision-based sensing, particularly in outdoor environments at large distances with mobile platforms [196,197]. The correct identification and following of targets in such environments (especially to the level of gesture recognition) is especially challenging [198]. With aerial vehicles Line-of-Sight (LOS) limitations on vision sensors pose certain constraints, as pointed out by [30]. The cameras onboard the vehicles can be gimballed, but the UAVs might not be free to perform all maneuvers without occluding vision. It may be of interest to see how much effect this has on sensing and if it couples with the control policy of the vehicle as well [199]. Integration of different kinds of sensors onboard airborne platforms has also not been sufficiently addressed either, and multi-sensor fusion is a hot research topic currently.

Some other problems that have been getting more attention, include coordination of multiple kinds of platforms possibly with human-in-the-loop for applications such as battlefield operations and support to ground troops [200,201]. Autonomous airborne and ground-based systems tend to complement each other in terms of wide area coverage and deep penetration respectively, and prove to be a good combination for surveillance and target pursuit [95]. A similar argument holds for using teams of airborne and sea-based platforms as well [202]. A new class of vehicles under experimentation are MAVs - their small size and maneuverability offers tremendous advantage. Of particular note are flapping-wing MAVs that can be extremely agile and robust to environmental disturbances [203]. Currently the biomimetic design of MAVs, sensors as well as controls [204] that leverage on knowledge of unsteady aerodynamics [205,206] are popular research topics. The comparison of homogeneous and heterogeneous groups of vehicles is particularly interesting—there has been work involving heterogeneity, but a proper quantification of performance for homogeneous vs. heterogeneous agents is hard to find. Also, the need for heterogeneity arising from the design of the control policies themselves, instead of being explicitly imposed on the system will be a very interesting result. Design of vehicles for optimum mission performance is also a very rich problem that has not been sufficiently explored. As mentioned in Section 6.6, there has been some work that has looked at design for particular missions, but a lot needs to be done in terms of finding the correct architecture for design. Once the design architecture has been decided, there are several interesting design studies that can be performed on multi-vehicle problems.

8.2. Approaches

Planning-based techniques have been used extensively in literature for robots as well as UAVs. However, the demonstration of these techniques have been limited to small scales and they become intractable for large systems and real-time implementations. Reducing the planning horizon for such techniques to make them tractable can often severely affect their performance, as observed in [55]. Hence there is a need for planning techniques that are tractable and perform well for large scale systems. Distributed control, that has its roots in control systems theory is also an active area of research [94,207,208]. The problems addressed using this are few, centering around formation control [208], target search and detection [209] and wireless networks [210]. Part of the reason is the extensive effort required in posing the scenario of interest as a distributed control problem that can be solved using formal techniques. Hence its application to more generic problems, such as continuous monitoring, is desirable. In general, control and AI have tried to address similar problems using different ideas and a hybrid technique utilizing knowledge from both fields should be helpful [211]. Space decomposition, or spatial tessellations [132] have been extensively studied, as noted in Section 4.2. At present a lot of techniques use space decomposition to divide work among multiple agents, but they do so using standard objective functions or heuristics. There is a need for methods that could handle more generic objectives to come up with optimum partitions [74]. Also, some of the more efficient techniques for space partitioning, result in skewed partitions that might not be good for UAVs operating under dynamic constraints. So there is a need to improve those methods. The application of game theoretic learning for dynamic replanning [136,159,160] in surveillance and other applications is a lucrative area for further research, with several advantages and complexities associated with it.

8.3. Problem Constraints

Several types of constraints have been imposed on vehicles in existing work, but they fall roughly in three main categories: dynamic, endurance, and communication constraints. Previous work has demonstrated approaches on vehicles with dynamic constraints, but there has been little work on studying the coupling between the dynamic constraints and the control policy. For Unmanned Ground Vehicles (UGVs), speed and terrain are typically the constraining factors and for aerial vehicles in level flight, turn radius becomes a constraining factor. As pointed out in some work by the authors of this survey [107], this is a very rich problem, both for ground and air vehicles. There has been some work on vehicles operating under endurance constraints, but only a few feasible solutions to online determination of refuel policy exist. The health monitoring problem in general is an active field of research that is directly relevant to persistent applications. In terms of communication constraints, most methods in literature use heuristics to model them. Moreover, there have only been a few techniques that try to study the relation between communication constraints and the control policy for the agents. In other words, a control policy that tries to account for such constraints and chooses actions also based on ability to communicate, is sought.

8.4. Test and Evaluation

Test and Evaluation (T&E) of the MASs developed is required to assess the performance of the system under consideration [212]. Most of the demonstrations so far have focused on demonstrating feasibility of techniques in simulation or hardware, but as the systems approach deployment stage, a formal analysis of their performance, reliability and robustness is required [213,214]. The testing can be performed at several levels starting from one individual unit to the complete system of systems, and the latter has not been addressed fully. Moreover, expensive hardware testing can be reduced using simulations, but they should be able to capture the realism of the actual scenario. For instance, in case of MASs, characterization of emergent behavior has been gaining attention [215,216]. For hardware tests, a capability to easily plug and play different system components would be very useful to test sets of components, as well as replacement of hardware components with software agents. A formal procedure for balancing workload between simulations and experiments, reducing overall T&E costs should also be desirable.

This is by no means a complete discussion of possible research directions related to this broad area. The attempt in this paper is to familiarize the reader with the plethora of literature and techniques available in the field and present some ideas for initiating new research.