Enhancing Human–Machine Collaboration: A Trust-Aware Trajectory Planning Framework for Assistive Aerial Teleoperation
Abstract
1. Introduction
- We propose an MPD trust model tailored for assistive aerial teleoperation. The model quantifies the UAV’s performance capacity using safety and visibility metrics, which, in contrast to methods relying on abstract or binary scores, enables a more nuanced and dynamic representation of human trust that can inform trajectory planning.
- Building upon this model, we develop a trust-aware trajectory planner that, for the first time, integrates a dynamic trust level directly into the optimization loop. This enables the planner to continuously adapt its assistance strategy, moving beyond simple intent-matching to achieve true human–machine collaboration.
- We validate our approach through extensive simulations in challenging, randomly generated forest environments. The results confirm that our trust-aware method significantly reduces operator workload and enhances trajectory smoothness, achieving superior collaborative performance without compromising task efficiency compared to a trust-unaware baseline.
2. Related Work
2.1. Assistive Aerial Teleoperation
2.2. Trajectory Planning Considering Human Factors
2.3. Trust Models in Human–Machine Interaction
3. Problem Formulation and Preliminaries
3.1. Human–UAV Collaborative Trajectory Planning
3.2. The MPD Human Trust and Its Dynamic Model
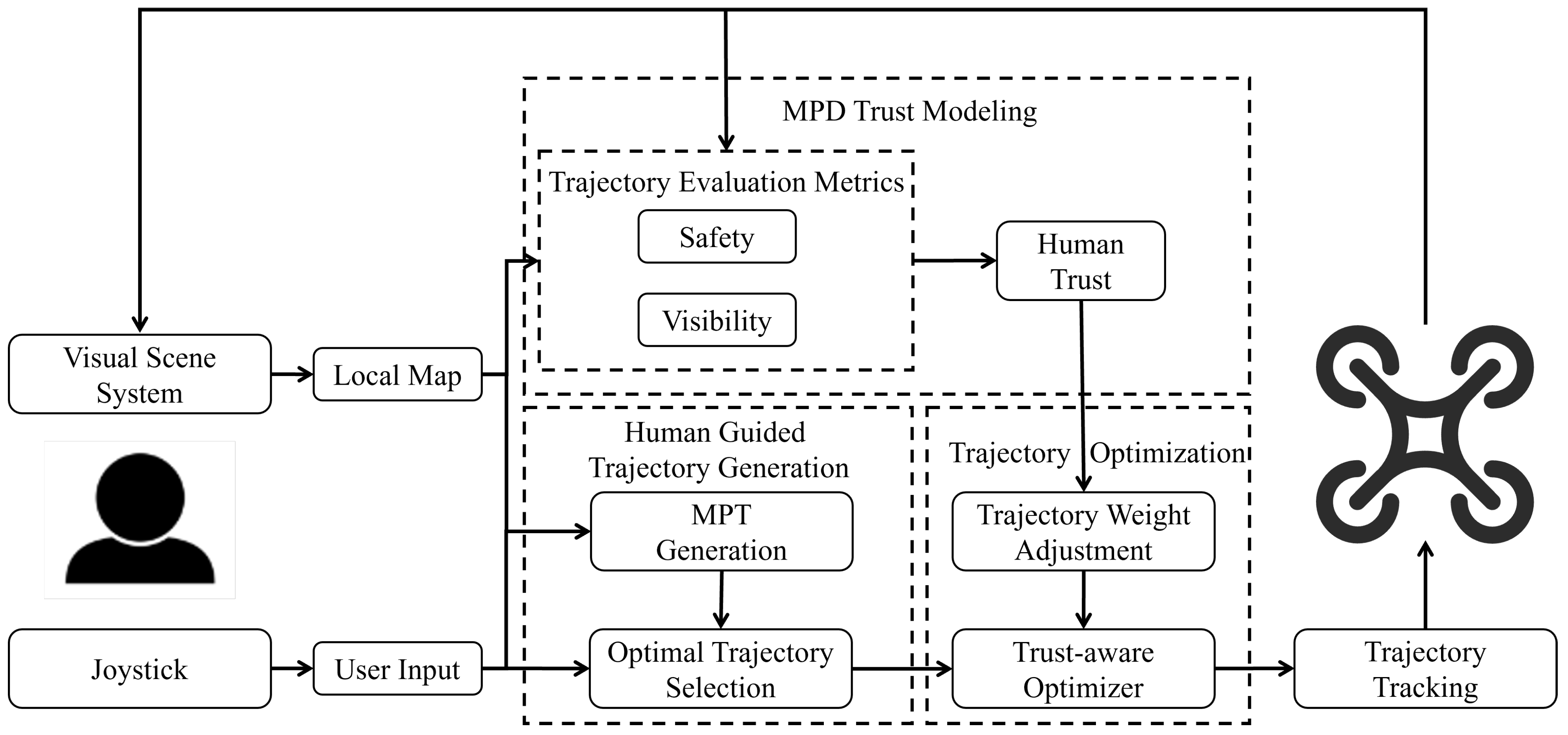
4. MPD Trust Model for Assistive Aerial Teleoperation
4.1. Quantifying Machine Performance and Objective Machine Capability
4.1.1. UAV Trajectory Performance Metrics
- (a)
- SafetySafety is defined as a quantitative index of collision risk. This index reflects the principle that the collision risk increases as the radial distance to obstacles decreases and the velocity component towards them increases. Specifically, suppose that at time k, the position vector from the UAV to the nearest obstacle is . The corresponding minimum radial distance is modeled as the Euclidean norm of this position vector, as given in (10):Meanwhile, the flight velocity vector is . The velocity component in the obstacle direction is calculated by vector projection, as expressed in (11):where denotes the dot product of the velocity vector and the obstacle direction vector. To characterize the relative motion risk, we employ a kinematic risk indicator , which represents the constant deceleration required to avoid a collision [14]. The safety factor is then formulated as given in (12):where is a tunable coefficient that regulates risk sensitivity.
- (b)
- VisibilityVisibility is a metric designed to quantify the level of occlusion within the UAV’s field of view (FOV) [25]. When the occluded area within the FOV exceeds a threshold, the environmental information available to the operator will significantly diminish, thereby affecting decision-making efficiency. As shown in Figure 1, the UAV trajectory point , and the target position . It is assumed that the UAV always faces the target. The blue area in the figure is the UAV’s FOV, and the blue dashed area is defined as the confident FOV, i.e., the core observation area where no occlusion is required in the ideal state. Considering that the computational complexity of the analytical solution for the occluded area of obstacles in the FOV is extremely high, we approximate the visibility by constructing a series of spherical regions , where N is the total number of spherical regions. The center and radius of the spherical regions are defined as given in (13):where , and is a parameter related to the size of the FOV. The visibility of the FOV is measured by comparing the minimum distance from the center point to the nearest obstacle with the radius of the corresponding sphere. The visibility of each area is ensured by the following condition, as given in (14):where denotes the minimum distance from to the nearest obstacle. Accordingly, the visibility factor at time k is defined as given in (15):
4.1.2. Determining Machine Performance
4.1.3. Determining Objective Machine Capacity
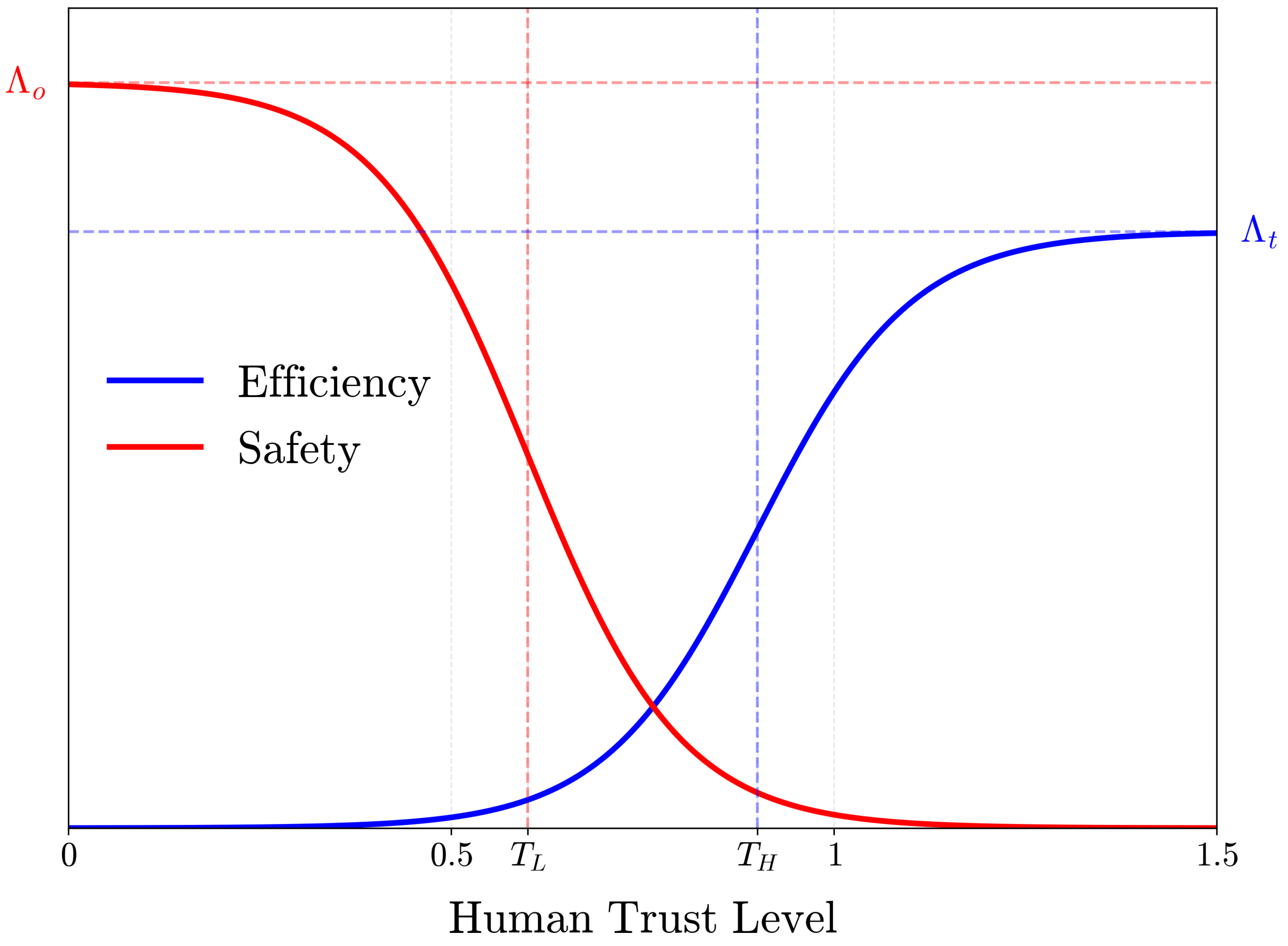
4.2. The MPD Human Trust Model for Assistive Aerial Teleoperation
5. Trust-Aware Human–UAV Collaborative Trajectory Planning
| Algorithm 1 Trust-aware human–UAV collaborative trajectory planning. |
| Require: Initial state , User input , Motion primitive tree , Sample set , Human trust Ensure: Human ideal trajectory
|
5.1. Trajectory Generation Guided by Human Intentions
5.1.1. Motion Primitive Tree Generation
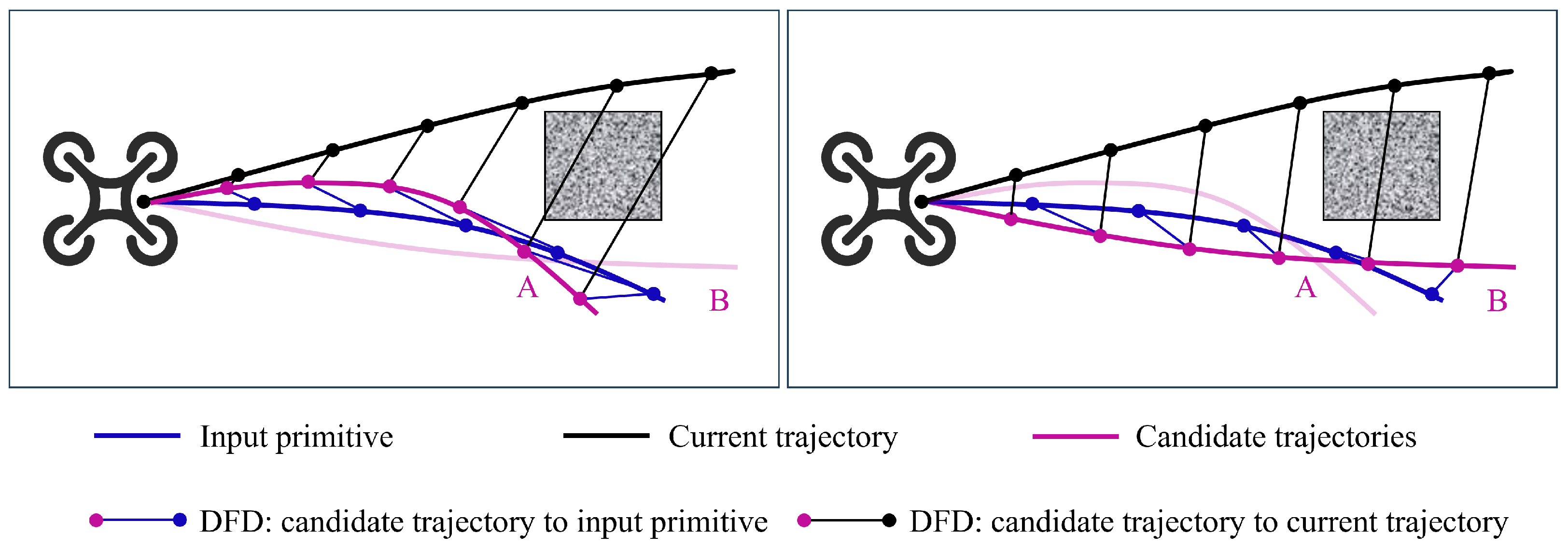
5.1.2. Trajectory Selection
5.2. Optimization Problem Formulation
5.2.1. Execution Time Penalty
5.2.2. Safety Penalty
5.2.3. Control Effort Penalty
5.2.4. Dynamical Feasibility Penalty
5.3. Trajectory Weight Adjustment Based on Human Trust
6. Experiments and Results
6.1. Implementation Details
6.2. Results Analysis
7. Discussion
7.1. Discussion of Findings
7.2. Practical Significance and Scenario-Based Illustration
- Initial trust calibration: As the UAV enters the building, it first navigates through less cluttered corridors. Its smooth, predictable trajectories, reflecting high safety and visibility, rapidly build the operator’s trust in the system’s competence.
- Intent-driven investigation: The operator spots a potential sign of life and issues a command to move closer for a better view. Because the operator’s trust is high, our framework accurately infers a strong, deliberate intent. It then generates a precise trajectory that navigates assertively yet safely around debris, fulfilling the operator’s goal without resistance. This is a stark contrast to a trust-unaware system that might have simply halted.
- Adaptive safety preservation: As the UAV ventures deeper, it enters an area with poor visibility, causing its onboard sensors to become less reliable. Our framework’s machine performance metrics objectively detect this degradation. Consequently, the trust model dynamically lowers its trust value, shifting the system into a more cautious state. If the anxious operator now commands a rapid forward movement, the system will provide stronger assistance, moderating the speed and trajectory to prioritize the UAV’s survival. It intelligently prevents a trust-induced error, safeguarding the mission’s most critical asset.
7.3. Open Issues and Future Work
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MPD | Machine-Performance-Dependent |
| UAV | Unmanned Aerial Vehicle |
| MPT | Motion Primitive Tree |
| DFD | Discrete Fréchet Distance |
| IRL | Inverse Reinforcement Learning |
References
- Perez-Grau, F.; Ragel, R.; Caballero, F.; Viguria, A.; Ollero, A. Semi-autonomous teleoperation of UAVs in search and rescue scenarios. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1066–1074. [Google Scholar] [CrossRef]
- Kanso, A.; Elhajj, I.H.; Shammas, E.; Asmar, D. Enhanced teleoperation of UAVs with haptic feedback. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; pp. 305–310. [Google Scholar] [CrossRef]
- Shi, H.; Luo, L.; Gao, S.; Yu, Q.; Hu, S. Human-guided motion planner with perception awareness for assistive aerial teleoperation. Adv. Robot. 2024, 38, 152–167. [Google Scholar] [CrossRef]
- Boksem, M.A.; Meijman, T.F.; Lorist, M.M. Effects of mental fatigue on attention: An ERP study. Cogn. Brain Res. 2005, 25, 107–116. [Google Scholar] [CrossRef]
- Yang, X.; Cheng, J.; Michael, N. An Intention Guided Hierarchical Framework for Trajectory-based Teleoperation of Mobile Robots. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 482–488. [Google Scholar] [CrossRef]
- Wang, Q.; He, B.; Xun, Z.; Xu, C.; Gao, F. GPA-Teleoperation: Gaze Enhanced Perception-Aware Safe Assistive Aerial Teleoperation. IEEE Robot. Autom. Lett. 2022, 7, 5631–5638. [Google Scholar] [CrossRef]
- Yang, X.; Michael, N. Assisted Mobile Robot Teleoperation with Intent-aligned Trajectories via Biased Incremental Action Sampling. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 10998–11003. [Google Scholar] [CrossRef]
- Gebru, B.; Zeleke, L.; Blankson, D.; Nabil, M.; Nateghi, S.; Homaifar, A.; Tunstel, E. A Review on Human–Machine Trust Evaluation: Human-Centric and Machine-Centric Perspectives. IEEE Trans.-Hum.-Mach. Syst. 2022, 52, 952–962. [Google Scholar] [CrossRef]
- Alhaji, B.; Beecken, J.; Ehlers, R.; Gertheiss, J.; Merz, F.; Müller, J.P.; Prilla, M.; Rausch, A.; Reinhardt, A.; Reinhardt, D.; et al. Engineering Human–Machine Teams for Trusted Collaboration. Big Data Cogn. Comput. 2020, 4, 35. [Google Scholar] [CrossRef]
- Ibrahim, B.; Elhajj, I.H.; Asmar, D. 3D Autocomplete: Enhancing UAV Teleoperation with AI in the Loop. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 17829–17835. [Google Scholar] [CrossRef]
- Steyvers, M.; Tejeda, H.; Kerrigan, G.; Smyth, P. Bayesian modeling of human–AI complementarity. Proc. Natl. Acad. Sci. USA 2022, 119, e2111547119. [Google Scholar] [CrossRef]
- Lyons, J.B.; Stokes, C.K. Human–human reliance in the context of automation. Hum. Factors 2012, 54, 112–121. [Google Scholar] [CrossRef]
- Nam, C.; Walker, P.; Li, H.; Lewis, M.; Sycara, K. Models of Trust in Human Control of Swarms With Varied Levels of Autonomy. IEEE Trans.-Hum.-Mach. Syst. 2020, 50, 194–204. [Google Scholar] [CrossRef]
- Li, Y.; Cui, R.; Yan, W.; Zhang, S.; Yang, C. Reconciling Conflicting Intents: Bidirectional Trust-Based Variable Autonomy for Mobile Robots. IEEE Robot. Autom. Lett. 2024, 9, 5615–5622. [Google Scholar] [CrossRef]
- Saeidi, H.; Wang, Y. Incorporating Trust and Self-Confidence Analysis in the Guidance and Control of (Semi)Autonomous Mobile Robotic Systems. IEEE Robot. Autom. Lett. 2019, 4, 239–246. [Google Scholar] [CrossRef]
- Hu, C.; Shi, Y.; Ge, S.; Hu, H.; Zhao, J.; Zhang, X. Trust-Based Shared Control of Human-Vehicle System Using Model Free Adaptive Dynamic Programming. IEEE Trans. Intell. Veh. 2024, 1–13. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Liang, J.; Yan, Y.; Pi, D.; Zhang, H.; Yin, G. Authority Allocation Strategy for Shared Steering Control Considering Human-Machine Mutual Trust Level. IEEE Trans. Intell. Veh. 2024, 9, 2002–2015. [Google Scholar] [CrossRef]
- Nieuwenhuisen, M.; Droeschel, D.; Schneider, J.; Holz, D.; Läbe, T.; Behnke, S. Multimodal obstacle detection and collision avoidance for micro aerial vehicles. In Proceedings of the 2013 European Conference on Mobile Robots, Barcelona, Spain, 25–27 September 2013; pp. 7–12. [Google Scholar] [CrossRef]
- Odelga, M.; Stegagno, P.; Bülthoff, H.H. Obstacle detection, tracking and avoidance for a teleoperated UAV. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 2984–2990. [Google Scholar] [CrossRef]
- Backman, K.; Kulić, D.; Chung, H. Learning to Assist Drone Landings. IEEE Robot. Autom. Lett. 2021, 6, 3192–3199. [Google Scholar] [CrossRef]
- Zhang, Q.; Xing, Y.; Wang, J.; Fang, Z.; Liu, Y.; Yin, G. Interaction-Aware and Driving Style-Aware Trajectory Prediction for Heterogeneous Vehicles in Mixed Traffic Environment. IEEE Trans. Intell. Transp. Syst. 2025, 26, 10710–10724. [Google Scholar] [CrossRef]
- Igneczi, G.F.; Horvath, E.; Toth, R.; Nyilas, K. Curve Trajectory Model for Human Preferred Path Planning of Automated Vehicles. Automot. Innov. 2024, 7, 59–70. [Google Scholar] [CrossRef]
- Huang, C.; Huang, H.; Hang, P.; Gao, H.; Wu, J.; Huang, Z.; Lv, C. Personalized Trajectory Planning and Control of Lane-Change Maneuvers for Autonomous Driving. IEEE Trans. Veh. Technol. 2021, 70, 5511–5523. [Google Scholar] [CrossRef]
- Yang, X.; Sreenath, K.; Michael, N. A framework for efficient teleoperation via online adaptation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5948–5953. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, Y.; Ji, J.; Xu, C.; Gao, F. Visibility-aware Trajectory Optimization with Application to Aerial Tracking. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 5249–5256. [Google Scholar] [CrossRef]
- Lee, J.D.; See, K.A. Trust in Automation: Designing for Appropriate Reliance. Hum. Factors 2004, 46, 50–80. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar] [CrossRef]
- Falanga, D.; Foehn, P.; Lu, P.; Scaramuzza, D. PAMPC: Perception-Aware Model Predictive Control for Quadrotors. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Eiter, T.; Mannila, H. Computing Discrete Fréchet Distance; Technical Report CD-TR 94/64; Christian Doppler Laboratory: Vienna, Austria, 1994. [Google Scholar]
- Wang, Z.; Zhou, X.; Xu, C.; Gao, F. Geometrically Constrained Trajectory Optimization for Multicopters. IEEE Trans. Robot. 2022, 38, 3259–3278. [Google Scholar] [CrossRef]
- Zhou, B.; Gao, F.; Wang, L.; Liu, C.; Shen, S. Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight. IEEE Robot. Autom. Lett. 2019, 4, 3529–3536. [Google Scholar] [CrossRef]
- Press, W.H.; William, H.; Teukolsky, S.A.; Saul, A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Quan, L.; Yin, L.; Xu, C.; Gao, F. Distributed Swarm Trajectory Optimization for Formation Flight in Dense Environments. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 4979–4985. [Google Scholar] [CrossRef]
- Sanz, D.; Valente, J.; del Cerro, J.; Colorado, J.; Barrientos, A. Safe operation of mini UAVs: A review of regulation and best practices. Adv. Robot. 2015, 29, 1221–1233. [Google Scholar] [CrossRef]
- Broad, A.; Schultz, J.; Derry, M.; Murphey, T.; Argall, B. Trust Adaptation Leads to Lower Control Effort in Shared Control of Crane Automation. IEEE Robot. Autom. Lett. 2017, 2, 239–246. [Google Scholar] [CrossRef]



| Parameter | Min | Max | Num. Discretizations |
|---|---|---|---|
| Duration T | 5 | ||
| Angular vel. | 15 | ||
| Z vel. | 3 |
| Parameter | |||||
|---|---|---|---|---|---|
| Value | 0.5 | 0.92 | 0.09 | 0.42 | 0.85 |
| Approach | Distance (m) | Duration (s) | Avg. Vel. (m/s) | Jerk Integral (m2/s3) | Num. Inputs | Avg. Trust |
|---|---|---|---|---|---|---|
| Sparse (50 trees) | ||||||
| Trust-unaware | 71.15 ± 0.06 | 46.62 ± 1.49 | 1.53 ± 0.05 | 27.49 ± 1.63 | 39 ± 4 | 0.744 ± 0.013 |
| Trust-aware | 70.04 ± 0.63 | 45.53 ± 0.47 | 1.54 ± 0.02 | 21.30 ± 3.39 | 34 ± 3 | 0.813 ± 0.016 |
| Medium (100 trees) | ||||||
| Trust-unaware | 71.33 ± 1.16 | 48.88 ± 1.71 | 1.46 ± 0.06 | 44.88 ± 10.38 | 45 ± 7 | 0.657 ± 0.015 |
| Trust-aware | 70.29 ± 2.44 | 45.84 ± 2.39 | 1.52 ± 0.03 | 31.48 ± 10.60 | 34 ± 5 | 0.750 ± 0.013 |
| Dense (200 trees) | ||||||
| Trust-unaware | 71.73 ± 1.71 | 54.89 ± 5.29 | 1.31 ± 0.14 | 84.69 ± 9.68 | 56 ± 8 | 0.611 ± 0.017 |
| Trust-aware | 71.38 ± 2.00 | 49.86 ± 1.05 | 1.43 ± 0.08 | 48.11 ± 9.44 | 43 ± 5 | 0.693 ± 0.023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Q.; Huang, K.; Jin, X.; Li, P.; Zhao, Y.; Kang, Y. Enhancing Human–Machine Collaboration: A Trust-Aware Trajectory Planning Framework for Assistive Aerial Teleoperation. Machines 2025, 13, 876. https://doi.org/10.3390/machines13090876
Zhuang Q, Huang K, Jin X, Li P, Zhao Y, Kang Y. Enhancing Human–Machine Collaboration: A Trust-Aware Trajectory Planning Framework for Assistive Aerial Teleoperation. Machines. 2025; 13(9):876. https://doi.org/10.3390/machines13090876
Chicago/Turabian StyleZhuang, Qianzheng, Kangjie Huang, Xiaoran Jin, Pengfei Li, Yunbo Zhao, and Yu Kang. 2025. "Enhancing Human–Machine Collaboration: A Trust-Aware Trajectory Planning Framework for Assistive Aerial Teleoperation" Machines 13, no. 9: 876. https://doi.org/10.3390/machines13090876
APA StyleZhuang, Q., Huang, K., Jin, X., Li, P., Zhao, Y., & Kang, Y. (2025). Enhancing Human–Machine Collaboration: A Trust-Aware Trajectory Planning Framework for Assistive Aerial Teleoperation. Machines, 13(9), 876. https://doi.org/10.3390/machines13090876






