Enhancing Human–Machine Collaboration: A Trust-Aware Trajectory Planning Framework for Assistive Aerial Teleoperation

Abstract

Human–machine collaboration in assistive aerial teleoperation is frequently compromised by trust imbalances, which arise from the vehicle’s complex dynamics and the operator’s constrained perceptual feedback. We introduce a novel framework that enhances collaboration by dynamically integrating a model of human trust into the unmanned aerial vehicle’s trajectory planning. We first propose a Machine-Performance-Dependent trust model, specifically tailored for aerial teleoperation, that quantifies trust based on real-time safety and visibility metrics. This model then informs a trust-aware trajectory planning algorithm, which generates smooth and adaptive trajectories that continuously align with the operator’s trust level and intent inferred from control inputs. Extensive simulations conducted in diverse forest environments validate our approach. The results demonstrate that our method achieves task efficiency comparable to that of a trust-unaware baseline while significantly reducing operator workload and improving trajectory smoothness, achieving reductions of up to 23.2% and 43.2%, respectively, in challenging dense environments. By embedding trust dynamics directly into the trajectory optimization loop, this work pioneers a more intuitive, efficient, and resilient paradigm for assistive aerial teleoperation.

1. Introduction

Unmanned aerial vehicle (UAV) teleoperation technology enables UAVs to access hazardous or human-inaccessible environments, performing tasks such as search and rescue [1] and surveillance [2]. It not only ensures the safety of operators but also gives full play to the advantages of human judgment and skills. However, in the traditional direct teleoperation mode, operators are responsible for all control tasks of the UAV, including flight path planning and obstacle avoidance [3], while the UAV itself lacks any high-level decision-making autonomy. This mode not only requires operators to possess extensive professional knowledge and experience but also leads to cognitive fatigue due to frequent manual operations [4]. Therefore, the question of how to reduce operational difficulty and alleviate the operator’s burden, especially when performing tasks in complex and hazardous environments, remains a key challenge in UAV teleoperation technology [3,5].

With the advancement of UAV autonomous technology, the assistive aerial teleoperation mode has been widely recognized as an effective solution to address the aforementioned challenges, for example, by reducing high cognitive load and mitigating the need for extensive operator expertise [3,6]. In this mode, operators provide commands through remote control, while the UAV offers assistance by inferring the operators’ intent [5,6,7] and autonomously plans appropriate action strategies based on mission requirements. By combining human decision-making with machine-assisted execution, this collaborative approach can significantly reduce the operator’s workload while improving task efficiency and safety.

However, while assistive aerial teleoperation technology has made significant progress in reducing operators’ workload and other aspects, it has also triggered the issue of trust imbalance in human–machine collaboration [8,9]. Due to the complex high-dimensional nonlinear dynamic characteristics of a UAV and the limited perceptual capabilities of operators through remote control terminals [10], it is difficult for humans to intuitively understand the UAV’s status and performance. Such information asymmetry [11] can lead to human trust imbalance, resulting in very serious consequences: over-trust may cause operators to fail to intervene in a timely manner in the UAV’s erroneous behaviors [12], thereby leading to mission failure. while a lack of trust may cause operators to frequently conduct unnecessary interventions [13], increasing the operational burden and reducing task execution efficiency.

Addressing this critical issue of trust imbalance reveals a twofold research gap, spanning from theory to application, that has hindered progress in the field. First, in the area of trust modeling, research specific to assistive aerial teleoperation remains limited. Most existing trust models are developed for other scenarios, such as ground mobile robots [14,15] and autonomous vehicles [16,17]. However, as these models do not account for the higher environmental complexity and the operator’s limited perceptual capabilities inherent to UAV teleoperation, they cannot be directly applied. Second, there is a practical gap in trust application. Even with a suitable model, the question of how to operationally use this dynamic trust information to guide the UAV’s behavior remains largely unanswered. Most current assistive planners focus on aligning with operator intent [3,5,7], but they lack a mechanism to modulate their behavior based on the operator’s dynamic trust level. A planning framework that can integrate a real-time trust metric into its decision-making process is a crucial missing piece.

To address this twofold research gap, this paper introduces a novel framework for trust-aware trajectory planning in assistive aerial teleoperation. Our approach is founded upon the Machine-Performance-Dependent (MPD) human trust model framework, which provides a quantitative basis for linking objective system performance to an operator’s trust. We adapt and specialize this general framework for the UAV teleoperation scenario and, crucially, integrate it into a real-time trajectory planner. By tackling both the modeling and application gaps, the key contributions of this work are summarized as follows:

• We propose an MPD trust model tailored for assistive aerial teleoperation. The model quantifies the UAV’s performance capacity using safety and visibility metrics, which, in contrast to methods relying on abstract or binary scores, enables a more nuanced and dynamic representation of human trust that can inform trajectory planning.
• Building upon this model, we develop a trust-aware trajectory planner that, for the first time, integrates a dynamic trust level directly into the optimization loop. This enables the planner to continuously adapt its assistance strategy, moving beyond simple intent-matching to achieve true human–machine collaboration.
• We validate our approach through extensive simulations in challenging, randomly generated forest environments. The results confirm that our trust-aware method significantly reduces operator workload and enhances trajectory smoothness, achieving superior collaborative performance without compromising task efficiency compared to a trust-unaware baseline.

Our approach assumes a stable communication link between the operator and the UAV. The trust model parameters are calibrated using experimental data to estimate human factors. However, the model does not account for real-time adaptation to individual differences. The proposed trust model is validated in simulated forest environments, and its applicability in highly dynamic urban settings remains a subject for future work.

The remainder of this paper is structured as follows. Section 2 surveys the literature on assistive aerial teleoperation, along with related work on human-factor-aware trajectory planning and trust modeling. Section 3 outlines the problem formulation and introduces the foundational MPD trust model. Building on this, Section 4 details the proposed trust model tailored for UAVs, while Section 5 presents our core trust-aware trajectory planning framework. Section 6 describes the experiments and analyzes the results. Section 7 interprets the findings, illustrates the framework’s practical significance through a scenario-based evaluation, and outlines open issues for future work. Finally, Section 8 concludes this paper with a summary of our contributions.

2. Related Work

2.1. Assistive Aerial Teleoperation

Existing research in assistive aerial teleoperation primarily focuses on two levels: operational control and trajectory planning [3]. At the control level, some works model the task as a local safety problem by generating constraints to mitigate collision risks [18,19]. Other works, such as Backman et al. [20], propose a shared autonomy approach that learns a policy module to provide assistive control inputs for safe landing via the reinforcement learning algorithm TD3. At the planning level, other works concentrate on longer-horizon human–machine collaborative planning. For instance, Yang and Michael [7] propose a motion-primitive-based sampling method to generate long-horizon trajectories which align with the human intention while circumventing obstacles. Similarly, Wang et al. [6] present a gaze-enhanced teleoperation framework that generates a safe and perception-aware trajectory by capturing the operator’s exploratory intent from gaze information. However, while these approaches show increasing technical sophistication, their interaction models often lack a deep consideration of human factors, such as operator preferences and trust, which are critical for effective collaboration.

2.2. Trajectory Planning Considering Human Factors

In the field of autonomous driving, significant research has focused on trajectory planning that incorporates human factors to create more intelligent and acceptable vehicle behaviors. Some works focus on understanding the human-like behaviors of surrounding vehicles for better prediction. For instance, Zhang et al. [21] propose an interaction-aware and driving-style-aware model that first uses an unsupervised clustering algorithm to classify the driving styles of other drivers and then employs an encoder–decoder architecture for long-term trajectory prediction. Other works aim to make the autonomous vehicle’s own path feel more natural to the user. Igneczi et al. [22] develop a curve trajectory model based on a linear driver model, which calculates human-preferred node points from road curvature data to design a path that emulates average human driving patterns. Furthermore, to cater to individual user needs, some methods allow for explicit personalization. Huang et al. [23] present a personalized trajectory planning method for lane-change maneuvers, which uses an improved RRT algorithm to generate a cluster of feasible trajectories and then utilizes fuzzy linguistic preference relations and TOPSIS to select the optimal one that matches the user’s subjective preferences for safety and comfort. While these methods effectively integrate human factors like driving style and preference into ground-based trajectory planning, their underlying models and assumptions are tied to the structured nature of road networks and vehicle dynamics, which do not directly apply to the challenges of 3D aerial teleoperation. Among these human factors, the operator’s dynamic trust in the system’s capability is arguably the most critical yet least understood, especially in high-stakes aerial tasks.

2.3. Trust Models in Human–Machine Interaction

In fields beyond UAV teleoperation, particularly in autonomous driving and ground mobile robotics, trust modeling has been explored to facilitate smoother and safer human–machine collaboration. For instance, Li et al. [14] proposed a bidirectional trust-based variable autonomy (BTVA) approach for the field of semi-autonomous mobile robots to balance control between a human and a robot. Similarly, Saeidi and Wang [15] proposed a trust framework for the same field to resolve human–machine intent conflicts by continuously modulating the degree of automation. In the autonomous driving domain, Hu et al. [16] proposed a quantitative trust model to dynamically allocate control authority by measuring the deviation between vehicle performance and driver expectations. Furthermore, Fang et al. [17] proposed a hierarchical framework based on mutual trust evaluation for shared steering control to optimize authority allocation by evaluating driver skill and human–machine conflicts. However, these frameworks’ underlying assumptions do not hold in UAV teleoperation. The key distinction is the shift from navigating on a plane to maneuvering in complex 3D space, a challenge compounded by the operator’s limited situational awareness [10]. A critical consequence is that the machine’s objective capability becomes highly volatile and context-dependent. Existing trust models for more predictable ground systems do not explicitly parameterize this performance volatility. Our work, therefore, builds upon the MPD human trust model, which addresses this gap by modeling the machine’s context-dependent capability to achieve a more accurate and adaptive trust assessment.

3. Problem Formulation and Preliminaries

We formalize assistive aerial teleoperation as a human–UAV collaborative trajectory planning problem and employ the MPD trust model to characterize human trust dynamics. This section provides an overview of human–UAV collaborative trajectory planning and the MPD trust model.

3.1. Human–UAV Collaborative Trajectory Planning

Let the state vector of the UAV be denoted as $\mathbf{x}\left(t\right)\in \mathcal{X}\subset {\mathbb{R}}^n$, where $\mathcal{X}$ represents the state space and n is the dimension of the state vector. Typically, $\mathbf{x}\left(t\right)$ comprises the UAV’s position, velocity, and other variables relevant to its dynamics. The control input is defined as $\mathbf{u}\left(t\right)\in \mathcal{U}\subset {\mathbb{R}}^m$, where $\mathcal{U}$ denotes the admissible set of control inputs and m is the dimension of the control input. The control input $\mathbf{u}\left(t\right)$ governs the state transitions of the UAV.

To ensure both safety and operational feasibility during flight, the UAV’s trajectory must satisfy multiple constraints. These constraints arise from the system’s physical limitations and environmental factors. Specifically, we define $\xi \left(t\right)$ as the position component of the state vector $\mathbf{x}\left(t\right)$, representing the trajectory over a time horizon $t\in [0,T]$. The dynamic feasibility constraints are expressed as shown in (1):

$$\begin{array}{c}\hfill {\xi }^{\left(i\right)}\left(t\right)\le {\mathbf{x}}_{max}^{\left(i\right)},\forall t\in [0,T]\end{array}$$

(1)

where the i-th-order derivative of the trajectory $\xi \left(t\right)$ is upper-bounded by a known limit ${\mathbf{x}}_{max}^{\left(i\right)}$ of the UAV. Additionally, the UAV must avoid obstacles in the environment during flight. To this end, the trajectory should always lie within the safe region, as specified by the constraint in (2):

$$\begin{array}{c}\hfill \xi \left(t\right)\in {\mathcal{X}}_{\mathrm{safe}},\forall t\in [0,T]\end{array}$$

(2)

where ${\mathcal{X}}_{\mathrm{safe}}=\mathcal{X}\setminus \mathcal{O}$, and $\mathcal{O}$ denotes the set of obstacles.

In human–UAV collaborative scenarios without a predefined target, it is more appropriate to model the operator’s intent as directional preferences rather than specific state-space targets [24]. The operator conveys their intent by providing control signals ${\mathbf{u}}_h$ through input devices, such as joysticks. To integrate this intent into trajectory planning, we introduce an intent cost function $C_{{\mathbf{u}}_h}\left(\xi \right)$, which quantifies the alignment between the trajectory $\xi \left(t\right)$ and the operator’s directives. Concurrently, a flight quality cost function $C_q\left(\xi \right)$ is defined to assess metrics such as trajectory smoothness and energy efficiency.

Thus, the human–UAV collaborative trajectory planning problem can be formulated as the following optimization problem: given the operator’s input ${\mathbf{u}}_h$, compute a trajectory $\xi$ within the feasible space to minimize the combined cost, as shown in (3):

$$\begin{array}{c}\hfill \underset{{\xi }^{\left(i\right)}\le {\mathbf{x}}_{max}^{\left(i\right)},\xi \in {\mathcal{X}}_{\mathrm{safe}}}{min}{C}_{{\mathbf{u}}_h}\left(\xi \right)+C_q\left(\xi \right)\end{array}$$

(3)

3.2. The MPD Human Trust and Its Dynamic Model

The MPD trust (denoted by $T_m^h$) is defined as the ratio of subjective machine capability (denoted by $C_m^h$, referring to the machine capability perceived by the human) to objective machine capability (denoted by $C_m^m$, referring to the machine’s actual capability at a given time). This relationship is formally expressed in (4):

$$\begin{array}{cc}\hfill T_m^h\left(k\right)& ={\displaystyle \frac{C_m^h\left(k\right)}{C_m^m\left(k\right)}},k\ge 0\hfill \\ \hfill T_m^h\left(t\right)& =T_m^h\left(k\right),t\in [t_k,t_{k+1}),k\ge 0\hfill \end{array}$$

(4)

where $t_k$ is the time when the human updates their subjective machine capability for the k-th time ($t_0:=0$ is the starting time of the considered human–machine system).

A dynamic model for MPD human trust was built, as detailed in (5):

$$\left\{\begin{array}{cc}{T}_m^h\left(k\right)\hfill & =(1-{\alpha }_h^{*}\left(k\right))T_m^h(k-1)+{\alpha }_h^{*}\left(k\right){\alpha }_h^P\partial P_k,k>0\hfill \\ T_m^h\left(t\right)\hfill & =T_m^h\left(k\right),t\in [t_k,t_{k+1}),k>0\hfill \\ T_m^h\left(0\right)\hfill & ={\alpha }_h^C\hfill \end{array}\right.$$

(5)

where $\partial P_k$ is defined in (6):

$$\partial P_k:={\displaystyle \frac{P_m^m\left(\mathrm{\Delta }k\right)}{C_m^m(k-1)}}$$

(6)

and ${\alpha }_h^{*}\left(k\right)$ is given in (7):

$${\alpha }_h^{*}\left(k\right)=\left\{\begin{array}{cc}{\alpha }_h^{+},\hfill & {\mathrm{\Delta }}^{*}{P}_m^h\left(k\right)>0;\hfill \\ 0,\hfill & {\mathrm{\Delta }}^{*}{P}_m^h\left(k\right)=0;\hfill \\ {\alpha }_h^{-},\hfill & {\mathrm{\Delta }}^{*}{P}_m^h\left(k\right)<0.\hfill \end{array}\right.$$

(7)

with ${\mathrm{\Delta }}^{*}{P}_m^h\left(k\right)$ specified in (8):

$${\mathrm{\Delta }}^{*}{P}_m^h\left(k\right)={\alpha }_h^P{P}_m^m\left(\mathrm{\Delta }k\right)-T_m^h(k-1)C_m^m(k-1)$$

(8)

The four human factors—the static human factor via informed capability ${\alpha }_h^C$, the static human factor via observed performance ${\alpha }_h^P$, conservativeness and risk-awareness human factors ${\alpha }_h^{+}$ and ${\alpha }_h^{-}$, and the actual machine performance $P_m^m\left(\mathrm{\Delta }k\right)$ during time interval $[t_{k-1},t_k)$—can be estimated using experimental data.

4. MPD Trust Model for Assistive Aerial Teleoperation

This section specifies the general MPD trust model, presented in (5), for the context of assistive aerial teleoperation. The initial step is to determine the machine’s performance $P_m^m\left(\mathrm{\Delta }k\right)$ and its objective capability $C_m^m\left(k\right)$. While $C_m^m\left(k\right)$ is often assumed to be a constant value $C_m^m$ for a given task, as expressed in (9),

$$\begin{array}{c}\hfill C_m^m\left(k\right)=C_m^m,\forall k\ge 0\end{array}$$

(9)

this assumption may not hold in practice. Especially for UAVs operating in unknown environments, the machine’s capability can vary due to dynamic environmental factors. Therefore, this work focuses on quantifying both $P_m^m\left(\mathrm{\Delta }k\right)$ and the context-dependent $C_m^m\left(k\right)$ to formulate a specialized trust model for assistive aerial teleoperation.

4.1. Quantifying Machine Performance $P_m^m\left(\mathrm{\Delta }k\right)$ and Objective Machine Capability $C_m^m\left(k\right)$

In practice, the objective machine capability $C_m^m\left(k\right)$ is an idealized benchmark derived from data on actual machine performance collected over an extended period. Consequently, both the machine performance $P_m^m\left(\mathrm{\Delta }k\right)$ and the objective machine capability $C_m^m\left(k\right)$ originate from the same set of evaluation metrics. Their primary distinction lies in the temporal scope of the assessment: $P_m^m\left(\mathrm{\Delta }k\right)$ is evaluated over a discrete time interval $[t_{k-1},t_k)$, whereas $C_m^m\left(k\right)$ reflects the aggregated performance across a long-term horizon.

We first define the evaluation metrics for machine performance and objective machine capability in the context of assistive aerial teleoperation. We then present the specific algorithms used to compute $P_m^m\left(\mathrm{\Delta }k\right)$ and $C_m^m\left(k\right)$.

4.1.1. UAV Trajectory Performance Metrics

To ensure compliance with both flight safety and operator visibility constraints, this work proposes a multi-dimensional metric that incorporates a safety factor and a visibility factor.

(a)

Safety

     Safety is defined as a quantitative index of collision risk. This index reflects the principle that the collision risk increases as the radial distance to obstacles $\mathrm{\Delta }d\left(k\right)$ decreases and the velocity component towards them $v_d\left(k\right)$ increases. Specifically, suppose that at time k, the position vector from the UAV to the nearest obstacle is $\mathit{d}\left(k\right)=[d_x\left(k\right),d_y\left(k\right),d_z\left(k\right)]$. The corresponding minimum radial distance $\mathrm{\Delta }d\left(k\right)$ is modeled as the Euclidean norm of this position vector, as given in (10):

$$\begin{array}{c}\hfill \mathrm{\Delta }d\left(k\right)=\parallel \mathit{d}\left(k\right)\parallel =\sqrt{d_x^2\left(k\right)+d_y^2\left(k\right)+d_z^2\left(k\right)}\end{array}$$

(10)

     Meanwhile, the flight velocity vector is $\mathit{v}\left(k\right)=[v_x\left(k\right),v_y\left(k\right),v_z\left(k\right)]$. The velocity component $v_d\left(k\right)$ in the obstacle direction is calculated by vector projection, as expressed in (11):

$$\begin{array}{c}\hfill v_d\left(k\right)={\displaystyle \frac{\mathit{v}\left(k\right)·\mathit{d}\left(k\right)}{\mathrm{\Delta }d\left(k\right)}}\end{array}$$

(11)

where $\mathit{v}\left(k\right)·\mathit{d}\left(k\right)$ denotes the dot product of the velocity vector and the obstacle direction vector. To characterize the relative motion risk, we employ a kinematic risk indicator ${\displaystyle \frac{v_d^2\left(k\right)}{2\mathrm{\Delta }d\left(k\right)}}$, which represents the constant deceleration required to avoid a collision [14]. The safety factor $S\left(k\right)$ is then formulated as given in (12):

$$\begin{array}{c}\hfill S\left(k\right)=e^{-{\displaystyle \frac{{\gamma }_s{v}_d^2\left(k\right)}{2\mathrm{\Delta }d\left(k\right)}}}\end{array}$$

(12)

where ${\gamma }_s\in {\mathbb{R}}^{+}$ is a tunable coefficient that regulates risk sensitivity.

(b)

Visibility

     Visibility is a metric designed to quantify the level of occlusion within the UAV’s field of view (FOV) [25]. When the occluded area within the FOV exceeds a threshold, the environmental information available to the operator will significantly diminish, thereby affecting decision-making efficiency. As shown in Figure 1, the UAV trajectory point $\mathit{p}\left(k\right)=[p_x\left(k\right),p_y\left(k\right),p_z\left(k\right)]$, and the target position $\mathit{c}\left(k\right)=[c_x\left(k\right),c_y\left(k\right),c_z\left(k\right)]$. It is assumed that the UAV always faces the target. The blue area in the figure is the UAV’s FOV, and the blue dashed area is defined as the confident FOV, i.e., the core observation area where no occlusion is required in the ideal state. Considering that the computational complexity of the analytical solution for the occluded area of obstacles in the FOV is extremely high, we approximate the visibility by constructing a series of spherical regions $\{{\mathcal{B}}_1\left(k\right),{\mathcal{B}}_2\left(k\right),\dots ,{\mathcal{B}}_N\left(k\right)\}$, where N is the total number of spherical regions. The center ${\mathit{c}}_i\left(k\right)$ and radius $r_i\left(k\right)$ of the spherical regions are defined as given in (13):

$$\begin{array}{cc}\hfill {\mathit{c}}_i\left(k\right)& =\mathit{p}\left(k\right)+{\psi }_i(\mathit{c}\left(k\right)-\mathit{p}\left(k\right))\hfill \\ \hfill r_i\left(k\right)& =\rho ·{\psi }_i·\parallel \mathit{c}\left(k\right)-\mathit{p}\left(k\right)\parallel \hfill \end{array}$$

(13)

where ${\psi }_i={\displaystyle \frac{i}{N}},i\in \{1,2,\dots ,N\}$, and $\rho$ is a parameter related to the size of the FOV. The visibility of the FOV is measured by comparing the minimum distance from the center point ${\mathit{c}}_i\left(k\right)$ to the nearest obstacle with the radius $r_i\left(k\right)$ of the corresponding sphere. The visibility of each area ${\mathcal{B}}_i\left(k\right)$ is ensured by the following condition, as given in (14):

$$\begin{array}{c}\hfill \mathrm{\Xi }\left({\mathit{c}}_i\left(k\right)\right)\ge r_i\left(k\right)\end{array}$$

(14)

where $\mathrm{\Xi }\left({\mathit{c}}_i\left(k\right)\right)$ denotes the minimum distance from ${\mathit{c}}_i\left(k\right)$ to the nearest obstacle. Accordingly, the visibility factor $F\left(k\right)$ at time k is defined as given in (15):

$$\begin{array}{c}\hfill F\left(k\right)=1-{\displaystyle \frac{{\sum }_{i=1}^{N}max(0,r_i^2\left(k\right)-{\mathrm{\Xi }}^2\left({\mathit{c}}_i\left(k\right)\right))}{{\sum }_{i=1}^N{r}_i^2\left(k\right)}}\end{array}$$

(15)

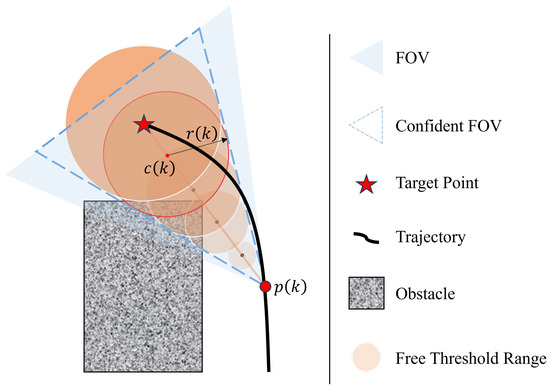Figure 1. Illustration of the visibility metric definition.

4.1.2. Determining Machine Performance $P_m^m\left(\mathrm{\Delta }k\right)$

The machine performance $P_m^m\left(\mathrm{\Delta }k\right)$ is quantified by aggregating trajectory performance metrics within the time interval $[t_{k-1},t_k)$. Research in human–machine interaction suggests that trust formation is subject to two key temporal effects. First, recent performance immediately influences trust, an effect known as immediacy. Second, the cumulative effect of historical performance shapes long-term trust assessment [26]. This dual influence necessitates a modeling approach for machine performance that balances short-term responsiveness with long-term stability.

Specifically, within the interval $[t_{k-1},t_k)$, we define a sampling interval $\mathrm{\Delta }t$, where the interval length is $\mathrm{\Delta }k=t_k-t_{k-1}=N\mathrm{\Delta }t$, comprising N equally spaced sampling points. To incorporate observation data dynamically, we employ a sliding window spanning the most recent N sampling points, covering a duration of $N\mathrm{\Delta }t$. Within this window, the safety indicator $P_S^{\mathrm{\Delta }k}$ and visibility indicator $P_F^{\mathrm{\Delta }k}$ of the UAV trajectory are computed using an Exponentially Weighted Moving Average (EWMA) to emphasize recent performance, as follows in (16):

$$\begin{array}{cc}\hfill P_S^{\mathrm{\Delta }k}& ={\displaystyle \frac{{\sum }_{i=1}^N{\alpha }^{i-1}S(t_k-i\mathrm{\Delta }t)}{{\sum }_{i=1}^N{\alpha }^{i-1}}}\hfill \\ \hfill P_F^{\mathrm{\Delta }k}& ={\displaystyle \frac{{\sum }_{i=1}^N{\alpha }^{i-1}F(t_k-i\mathrm{\Delta }t)}{{\sum }_{i=1}^N{\alpha }^{i-1}}}\hfill \end{array}$$

(16)

where $t_k-i\mathrm{\Delta }t$ represents the i-th sampling point backward from the current time, and $\alpha \in (0,1)$ is a decay factor that adjusts the degree of influence of historical data. A smaller value of $\alpha$ places greater emphasis on more recent data. The machine performance $P_m^m\left(\mathrm{\Delta }k\right)$ is then defined as given in (17):

$$\begin{array}{c}\hfill P_m^m\left(\mathrm{\Delta }k\right)={\omega }_S{P}_S^{\mathrm{\Delta }k}+{\omega }_F{P}_F^{\mathrm{\Delta }k}\end{array}$$

(17)

where ${\omega }_S$ and ${\omega }_F\in [0,1]$ are weighting coefficients for safety and visibility, respectively, satisfying ${\omega }_S+{\omega }_F=1$. The value $P_m^m\left(\mathrm{\Delta }k\right)\in [0,1]$ quantifies the overall trajectory performance within $[t_{k-1},t_k)$.

4.1.3. Determining Objective Machine Capacity $C_m^m\left(k\right)$

Given the dynamic and uncertain environments that UAVs encounter during missions, their objective machine capability $C_m^m\left(k\right)$ may vary due to environmental factors. To calculate $C_m^m\left(k\right)$, we integrate prior knowledge from the system’s predefined capability model with posterior knowledge derived from real-time environmental feedback. The machine capability at time step k is thus expressed as given in (18):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{C}_m^m\left(k\right)=(1-{\alpha }_m)C_m^m(k-1)+{\alpha }_m{P}_m^m\left(\mathrm{\Delta }k\right),k>0\hfill \\ C_m^m\left(0\right)=C_m^m\hfill \end{array}\right.\end{array}$$

(18)

where $P_m^m\left(\mathrm{\Delta }k\right)$ represents the actual machine performance over $[t_{k-1},t_k)$, and ${\alpha }_m\in (0,1)$ is a dynamic factor reflecting the contribution of recent performance to the capability assessment.

4.2. The MPD Human Trust Model for Assistive Aerial Teleoperation

The MPD human trust model for assistive aerial teleoperation can now be formulated as follows in (19):

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{T}_U^h\left(k\right)\hfill & =(1-{\alpha }_h^{*}\left(k\right))T_U^h(k-1)+{\alpha }_h^{*}\left(k\right){\alpha }_h^P\partial P_k,k>0\hfill \\ T_U^h\left(t\right)\hfill & =T_U^h\left(k\right),t\in [t_k,t_{k+1}),k>0\hfill \\ T_U^h\left(0\right)\hfill & ={\alpha }_h^C\hfill \end{array}\right.\end{array}$$

(19)

where $\partial P_k$, ${\alpha }_h^{*}\left(k\right)$, and ${\mathrm{\Delta }}^{*}{P}_m^h\left(k\right)$ can be similarly defined as in (6), (7), and (8), respectively. In particular, $P_m^m\left(\mathrm{\Delta }k\right)$ and $C_m^m\left(k\right)$ can be calculated as in (17) and (18), respectively.

Regarding the human factors from (5), the initial trust value, ${\alpha }_h^C$, must be determined before the system operates. In this work, we initialize this value using a pre-task trust scale. The three human-factor parameters, ${\alpha }_h^P$, ${\alpha }_h^{+}$, and ${\alpha }_h^{-}$, must be estimated from runtime data. Various methods are suitable for this purpose, such as the Least Squares Estimation approach.

5. Trust-Aware Human–UAV Collaborative Trajectory Planning

This section presents a trust-aware method for human–UAV collaborative trajectory planning. First, a trajectory generation method is adopted to generate a candidate trajectory set. Subsequently, the optimal trajectory is selected from the candidate set by minimizing a cost function that incorporates the discrete Fréchet distances to the current trajectory and the human input primitive, as well as the trust value associated with each trajectory. Finally, the selected trajectories are reparameterized and optimized in conjunction with human trust levels using MINCO’s representation. The specific process is detailed in Algorithm 1 and an overview of the entire framework is shown in Figure 2.

Algorithm 1 Trust-aware human–UAV collaborative trajectory planning.

Require: Initial state ${\mathbf{x}}_c$, User input ${\mathbf{u}}_h$, Motion primitive tree $\mathrm{\Gamma }$, Sample set $\mathcal{S}$, Human trust $T_U^h$ Ensure: Human ideal trajectory ${\xi }^{*}$  1: Initialization: $\mathcal{S}\leftarrow \varnothing \cup \left\{{\eta }_c\right\}$, $\mathrm{\Gamma }\leftarrow \varnothing$  2: while terminating condition not met do  3:     for each sampled node ${\eta }_n$ from $\mathcal{S}$ do  4:         Add the sampled node ${\eta }_n$ to the tree $\mathrm{\Gamma }$  5:         Remove the sampled node from $\mathcal{S}$  6:         Generate the primitive ${\gamma }_{{\mathbf{u}}_n}$ and node set ${\mathcal{C}}_n$  7:         if ${\gamma }_{{\mathbf{u}}_n}\in {\mathcal{A}}_{\mathrm{safe}}$ then  8:            Compute cost $f_c^n$ for each node in ${\mathcal{C}}_n$ using Equation (22)  9:            Add the lowest-$f_c^n$ node from ${\mathcal{C}}_n$ to $\mathcal{S}$ 10:         end if 11:     end for 12: end while 13: Convert the tree $\mathrm{\Gamma }$ into a path set ${\left\{{\xi }_i\right\}}_{i=1}^M$ 14: Compute the Discrete Fréchet Distance and average trust for each $\xi$ 15: Select the optimal path ${\xi }^{*}$ from the path set ${\left\{{\xi }_i\right\}}_{i=1}^M$ 16: Adjust the trajectory weights $\mathit{\lambda }$ according to the human trust $T_U^h$ 17: Optimize the trajectory of ${\xi }^{*}$ 18: return ${\xi }^{*}$

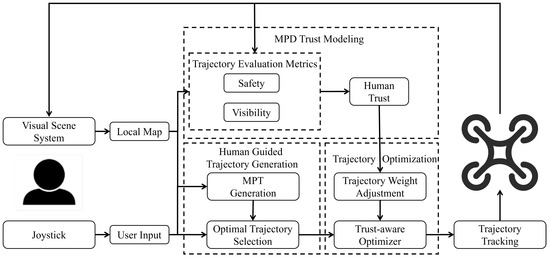
Figure 2. The framework diagram presents a human–UAV system for assistive aerial teleoperation that incorporates human trust into trajectory planning. The system uses human input to guide trajectory planning and generate an initial trajectory while simultaneously modeling human trust via the MPD trust model. Subsequently, the system optimizes the initial trajectory to match the dynamic trust level, ultimately forming an optimized path for UAV trajectory tracking.

5.1. Trajectory Generation Guided by Human Intentions

5.1.1. Motion Primitive Tree Generation

Existing studies have demonstrated that quadrotors are differentially flat systems [27]; thus, we can compute precise inputs to make the vehicle follow a specified trajectory in terms of the flat outputs x, y, z, and yaw angle $\theta$. We define the state as $\mathbf{x}={[x,y,z,\theta ]}^{\top }\in \mathcal{X}$, where the state space $\mathcal{X}\in {\mathbb{R}}^4$. The operator provides inputs ${\mathbf{u}}_h={[v_x,\omega ,v_z]}^{\top }$ with respect to a level frame $\mathcal{C}$, which is a world-z-aligned frame rigidly attached to the vehicle’s origin.

Inspired by [5], we generate motion primitives as polynomial trajectories. This method constrains the trajectory by the vehicle’s current state and a target velocity profile guided by the operator’s input. The state of the motion primitive is set to evolve according to the unicycle model [28], as expressed in (20):

$${\dot{\mathbf{f}}}_{{\mathbf{u}}_h}\left(t\right)={[v_{x}cos\left(\omega t\right),v_{x}sin\left(\omega t\right),v_z,\omega ]}^{\top }$$

(20)

The motion primitive, denoted as ${\gamma }_{{\mathbf{u}}_h}\left(t\right)$, is an eighth-order polynomial trajectory in the world frame $\mathcal{W}$ of the form ${\gamma }_{{\mathbf{u}}_h}\left(t\right)={\sum }_{i=0}^8{\mathbf{c}}_i{t}^i$. Its coefficients are uniquely determined. Given the current state ${\mathbf{x}}_c$ and its higher-order derivatives (up to the fourth order), along with a duration $T_h$, the operator’s input primitive ${\gamma }_{{\mathbf{u}}_h}\left(t\right)$ for $t\in [0,T_h]$ is generated by enforcing the following boundary conditions, as given in (21):

$$\left\{\begin{array}{cc}{\gamma }^{\left(j\right)}\left(0\right)={\mathbf{x}}_c^{\left(j\right)}\hfill & \mathrm{for}j=0,1,2,3,4\hfill \\ \dot{\gamma }\left(T_h\right)={R_t}_{\mathcal{C}}^{\mathcal{W}}{\dot{\mathbf{f}}}_{{\mathbf{u}}_h}\left(T_h\right)\hfill \\ {\gamma }^{\left(j\right)}\left(T_h\right)=0\hfill & \mathrm{for}j=2,3,4\hfill \end{array}\right.$$

(21)

where ${R_t}_{\mathcal{C}}^{\mathcal{W}}$ is the transformation matrix from the level frame $\mathcal{C}$ to the world frame $\mathcal{W}$ at time t. The primary role of this guiding primitive ${\gamma }_{{\mathbf{u}}_h}\left(t\right)$ is to direct the search process, ensuring the generated trajectories align with the user’s desired direction.

For generating the tree, we fix the forward velocity $v_x$ to the value provided by the human operator’s input ${\mathbf{u}}_h$. We then perform discrete sampling on the remaining action parameters: angular velocity $\omega$, vertical velocity $v_z$, and duration T. By iteratively sampling the action space ${\mathcal{A}}_n$, we propagate from node ${\eta }_n$ to its child node set ${\mathcal{C}}_n$. We generate a corresponding candidate primitive ${\gamma }_{{\mathbf{u}}_n}\left(t\right)$ by applying the exact same polynomial generation process defined by Equations (20) and (21). We then check if it lies within the safe space ${\mathcal{X}}_{\mathrm{safe}}$ to ensure all generated primitives are collision-free. This acts as a hard constraint, immediately discarding any inherently unsafe paths and guaranteeing that only collision-free trajectories are considered for the subsequent stages.

To evaluate the directional similarity between a candidate primitive and the human-guided primitive, we compute a cost based on their direction vectors. We define a mapping $p(·)$ that extracts the spatial coordinates from a full state vector. The cost $f_c^n$ is then given by (22):

$$\begin{array}{cc}\hfill f_c^n& =1-{\mathbf{d}}_n·{\mathbf{d}}_h\hfill \\ \hfill {\mathbf{d}}_n& ={\displaystyle \frac{p\left({\gamma }_{{\mathbf{u}}_n}\left(T_n\right)\right)-p\left({\mathbf{x}}_n\right)}{\parallel p\left({\gamma }_{{\mathbf{u}}_n}\left(T_n\right)\right)-p\left({\mathbf{x}}_n\right)\parallel }},{\mathbf{d}}_h={\displaystyle \frac{p\left({\gamma }_{{\mathbf{u}}_h}\left(T_h\right)\right)-p\left({\mathbf{x}}_c\right)}{\parallel p\left({\gamma }_{{\mathbf{u}}_h}\left(T_h\right)\right)-p\left({\mathbf{x}}_c\right)\parallel }}\hfill \end{array}$$

(22)

where $T_n$ is the duration of the motion primitive corresponding to node ${\eta }_n$, ${\mathbf{x}}_n$ is the initial state corresponding to node ${\eta }_n$, and ${\mathbf{x}}_c$ is the current state. We sort the costs $f_c^n$ and select the node with the minimum cost from the candidate node set ${\mathcal{C}}_n$ to add to the sampling set $\mathcal{S}$, which is used for the next round of motion primitive expansion.

When $\parallel {\mathbf{x}}_n-{\mathbf{x}}_c\parallel$ exceeds the range of the local perception, or the number of nodes reaches a preset threshold, the motion primitive tree ceases to expand. By connecting nodes at different depths, a series of trajectories ${\left\{{\xi }_i\right\}}_{i=1}^M$ are obtained.

5.1.2. Trajectory Selection

Given a set of candidate trajectories ${\left\{{\xi }_i\right\}}_{i=1}^M$, we select the human-desired trajectory ${\xi }^{*}$ from them. We need to balance three objectives: minimizing the deviation from the current trajectory to ensure a smooth transition, minimizing the deviation from the human input primitives [3], and maximizing the average trust value associated with each trajectory. To this end, we introduce a selection cost function, which evaluates the proximity of each trajectory to the current trajectory ${\xi }_L$ and the operator input primitive ${\gamma }_{{\mathbf{u}}_h}$ by calculating the discrete Fréchet distance ${\delta }_{dF}$ (see Figure 3) [29] while also considering the trust value $T\left(\xi \right)$ of each trajectory. A brief definition of the discrete Fréchet distance is given as follows.

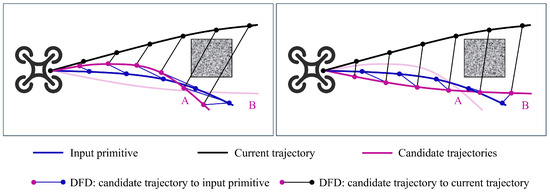
Figure 3. Illustration of the calculation of discrete Fréchet distance (DFD) in trajectory selection. The DFD of each candidate trajectory with respect to the operator input primitives and the current trajectory is calculated.

Consider a discrete sampling of two continuous functions f and g, forming sequences $\mathcal{P}=f_1,f_2,\dots ,f_n$ and $\mathcal{Q}=g_1,g_2,\dots ,g_m$, consisting of n and m discrete points, respectively. An order-preserving complete correspondence between $\mathcal{P}$ and $\mathcal{Q}$ is defined by a pair $(\alpha ,\beta )$ of discrete monotone reparameterizations [5], where $\alpha$ maps $1,\dots ,k$ to $1,\dots ,n$ and $\beta$ maps $1,\dots ,k$ to $1,\dots ,m$. The discrete Fréchet distance of $\mathcal{P}$ and $\mathcal{Q}$ is given by (23):

$${\delta }_{dF}(f,g):=\underset{(\alpha ,\beta )}{min}\underset{i\in [1,k]}{max}d(f_{\alpha \left(i\right)},g_{\beta \left(i\right)})$$

(23)

where $(\alpha ,\beta )$ range over all order-preserving complete correspondences between $\mathcal{P}$ and $\mathcal{Q}$. Thus, for time-parameterized trajectories $\mathrm{\Gamma }$ and $\mathrm{\Phi }$, their Fréchet distance is defined as given in (24):

$${\delta }_{dF}(\mathrm{\Gamma },\mathrm{\Phi }):=\underset{(\alpha ,\beta )}{min}\underset{i\in [1,k]}{max}d({\mathrm{\Gamma }}_{\alpha \left(i\right)},{\mathrm{\Phi }}_{\beta \left(i\right)})$$

(24)

where ${\mathrm{\Gamma }}_i=\mathrm{\Gamma }(i·\mathrm{\Delta }t)$ denotes sampling $\mathrm{\Gamma }$ at a fixed time interval $\mathrm{\Delta }t$.

Based on the above definitions, we derive the trajectory selection mechanism as follows: Given the current trajectory ${\xi }_L$, the operator input primitive ${\gamma }_{\mathbf{u}h}$, and the average trust value $T\left(\xi \right)$ for each candidate trajectory, the desired trajectory is determined by (25):

$${\xi }^{*}=\underset{\xi \in {\left\{{\xi }_i\right\}}_{i=1}^M}{agrmin}{w}_L{\delta }_{dF}(\xi ,{\xi }_L)+w_U{\delta }_{dF}(\xi ,{\gamma }_{{\mathbf{u}}_h})-w_{T}T\left(\xi \right)$$

(25)

where $w_L$ weights the smoothness with the current trajectory, $w_U$ weights the deviation from the human input primitive, and $w_T$ weights the trust value.

5.2. Optimization Problem Formulation

Selected from the motion primitive tree is the desired human trajectory ${\xi }^{*}$. In this section, a trajectory representation method called MINCO [30] is adopted to reparameterize the trajectory. MINCO performs spatiotemporal decoupling transformation on the M-piece trajectory $\xi \left(t\right)$ with flat output through a linear complexity mapping, thereby decoupling the spatial parameters from the temporal parameters. Specifically, the s-order MINCO trajectory is actually a $2s$-order polynomial spline with constant boundary conditions, which is defined as given in (26):

$$\begin{array}{c}\hfill {\mathfrak{T}}_{\mathrm{MINCO}}=\{\xi \left(t\right):[0,T]\mapsto {\mathbb{R}}^m|\mathrm{c}=\mathcal{M}(\mathrm{q},\mathrm{T}),\\ \hfill \mathrm{q}\in {\mathbb{R}}^{m(M-1)},\mathrm{T}\in {\mathbb{R}}_{>0}^M\}\end{array}$$

(26)

where $\xi \left(t\right)$ is an m-dimensional M-piece polynomial trajectory. $\mathbf{c}={({\mathbf{c}}_1^T,\dots ,{\mathbf{c}}_M^T)}^{\mathrm{T}}\in {\mathbb{R}}^{2Ms\times m}$ is the polynomial coefficient, and $\mathcal{M}(\mathbf{q},\mathbf{T})$ is a linear-complexity smooth map from intermediate points $\mathbf{q}$ and a time allocation $\mathbf{T}$ for all pieces to the coefficients of splines. The i-th piece of the trajectory, ${\xi }_i\left(t\right)$, is defined as given in (27):

$$\begin{array}{cc}\hfill \xi \left(t\right)& ={\xi }_i(t-t_{i-1}),\forall t\in [t_{i-1},t_i]\hfill \\ \hfill {\xi }_i\left(t\right)& ={\mathrm{c}}_i^T\beta \left(t\right),\forall t\in [0,T_i]\hfill \end{array}$$

(27)

where $\beta \left(t\right):={[1,t,\dots ,t^N]}^{\mathrm{T}}$ is the natural basis, ${\mathbf{c}}_i$ is the coefficient matrix, $T_i=t_i-t_{i-1}$, and $T={\sum }_{i=1}^M{T}_i$.

Define the constraint points $\mathring{\mathit{\xi }}i,j$. The sampling manner on each piece of the trajectory is given by $\mathring{\mathit{\xi }}i,j={\xi }_i\left({\displaystyle \frac{j}{{\kappa }_i}}{T}_i\right)$, where $j\in 0,1,2,\dots ,{\kappa }_i$ and ${\kappa }_i$ denotes the number of sampling points in the i-th piece. These points serve to convert the time integrals of certain constraint functions into a weighted sum of sampling penalty functions. Considering our requirements, all constraints are converted into penalty terms, and the trajectory optimization problem is formulated as given in (28):

$$\underset{\mathbf{q},\mathbf{T}}{min}\left[J_t,J_o,J_e,J_d\right]·\mathit{\lambda }$$

(28)

where $J_t$ is the execution time penalty, $J_o$ is the safety penalty, $J_e$ is the control effort penalty, and $J_d$ is the dynamic feasibility penalty. $\mathit{\lambda }={\left[{\lambda }_t,{\lambda }_o,{\lambda }_e,{\lambda }_d\right]}^T$ is the weight vector used to balance these respective penalties.

5.2.1. Execution Time Penalty $J_t$

To enhance the flight speed of the UAV, we impose a penalty term on the total execution time $J_t={\sum }_{i=1}^M{T}_i$. Its gradients are given by $\partial J_t/\partial \mathbf{c}=\mathbf{0}$ and $\partial J_t/\partial \mathbf{T}=\mathbf{1}$.

5.2.2. Safety Penalty $J_o$

Inspired by [31], the safety penalty term $J_o$ for obstacle avoidance is computed using the Euclidean Signed Distance Field (ESDF). We penalize sampling points that are too close to obstacles, as expressed in (29):

$$\begin{array}{cc}\hfill {\psi }_o\left({\mathring{\mathit{\xi }}}_{i,j}\right)& ={\mathrm{\Xi }}_{thr}-\mathrm{\Xi }\left({\mathring{\mathit{\xi }}}_{i,j}\right)\hfill \end{array}$$

(29)

where $\mathrm{\Xi }thr$ is the safety distance threshold set according to practical scenarios, and $\mathrm{\Xi }\left(\mathring{\mathit{\xi }}i,j\right)$ represents the distance from $\mathring{\mathit{\xi }}i,j$ to the nearest obstacle. The safety penalty term is then derived by computing the weighted sum of the sampled constraint functions, specifically as given in (30):

$$J_o={\displaystyle \frac{T_i}{{\kappa }_i}}\sum _{j=0}^{{\kappa }_i}{\overline{\omega }}_{j}max{\{{\psi }_o\left({\mathring{\mathit{\xi }}}_{i,j}\right),\mathbf{0}\}}^3$$

(30)

where $(\overline{\omega }0,\overline{\omega }1,\dots ,\overline{\omega }{\kappa }_i-1,\overline{\omega }{\kappa }_i)=(1/2,1,\dots ,1,1/2)$ are the quadrature coefficients following the trapezoidal rule [32]. The detailed derivation of the gradient of $J_o$ is as given in (31):

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial J_o}{\partial {\mathbf{c}}_i}}& ={\displaystyle \frac{\partial J_o}{\partial {\psi }_o}}{\displaystyle \frac{\partial {\psi }_o}{\partial {\mathbf{c}}_i}}\hfill \\ \hfill {\displaystyle \frac{\partial J_o}{\partial T_i}}& ={\displaystyle \frac{J_o}{T_i}}+{\displaystyle \frac{\partial J_o}{\partial {\psi }_o}}{\displaystyle \frac{\partial {\psi }_o}{\partial t}}{\displaystyle \frac{\partial t}{\partial T_i}}\hfill \\ \hfill {\displaystyle \frac{\partial t}{\partial T_i}}& ={\displaystyle \frac{j}{{\kappa }_i}},t={\displaystyle \frac{j}{{\kappa }_i}}{T}_i\hfill \end{array}$$

(31)

where t is the relative time on this piece. For the case where $\mathrm{\Xi }\left({\mathring{\mathit{\xi }}}_{i,j}\right)<{\mathrm{\Xi }}_{thr}$, the gradient is given as expressed in (32):

$${\displaystyle \frac{\partial {\psi }_o}{\partial {\mathbf{c}}_i}}=-\beta \left(t\right)\nabla d^T,{\displaystyle \frac{\partial {\psi }_o}{\partial t}}=-\nabla d^T\dot{\xi }\left(t\right)$$

(32)

where $\nabla d$ is the gradient of the ESDF at ${\mathring{\mathit{\xi }}}_{i,j}$. Otherwise, the gradients become $\partial {\psi }_o/\partial {\mathbf{c}}_i=\mathbf{0}$ and $\partial {\psi }_o/\partial t=0$.

5.2.3. Control Effort Penalty $J_e$

According to [33], the s-order control input and its gradient for the i-th piece of the trajectory can be expressed as given in (33):

$$\begin{array}{cc}\hfill J_e& =\sum _{i=1}^M{\int }_0^{T_i}{\Vert {\xi }_i^{\left(s\right)}\left(t\right)\Vert }^{2}dt\hfill \\ \hfill {\displaystyle \frac{\partial J_e}{\partial {\mathbf{c}}_i}}& =2\left({\int }_0^{T_i}{\beta }^{\left(s\right)}\left(t\right){\beta }^{\left(s\right)}{\left(t\right)}^{T}dt\right){\mathbf{c}}_i\hfill \\ \hfill {\displaystyle \frac{\partial J_e}{\partial T_i}}& ={\mathbf{c}}_i^T{\beta }^{\left(s\right)}\left(T_i\right){\beta }^{\left(s\right)}{\left(T_i\right)}^T{\mathbf{c}}_i\hfill \end{array}$$

(33)

5.2.4. Dynamical Feasibility Penalty $J_d$

When the trajectory of the UAV approaches physical constraints, the dynamic feasibility penalty mechanism is triggered. To ensure that the UAV can execute the trajectory, we impose limits on the maximum values of velocity, acceleration, and jerk, as expressed in (34):

$${\mathcal{G}}_{*}={\xi }_i^{\left(n\right)}{\left(t\right)}^2-ma{x}_{*}^2,\forall t\in [0,T_i]$$

(34)

where $*=\{v,a,j\}$, $n=\{1,2,3\}$, and $t=j{T}_i/{\kappa }_i$ denote velocity, acceleration, jerk, coordinate axis indices, and sampling time, respectively. $V_{max}$, $A_{max}$, and $J_{max}$ are the maximum allowable velocity, acceleration, and jerk. The dynamic feasibility penalty [6] term is obtained by calculating the weighted sum of sampled constraint functions, as given in (35):

$${\left(J_d\right)}_{*}=\sum _{i=1}^M{\displaystyle \frac{T_i}{{\kappa }_i}}\sum _{j=0}^{{\kappa }_i}{\overline{\omega }}_{j}max{\left({\mathcal{G}}_{*}\left({\mathring{\mathit{\xi }}}_{i,j}\right),\mathbf{0}\right)}^3$$

(35)

where $({\overline{\omega }}_0,{\overline{\omega }}_1,\dots ,{\overline{\omega }}_{{\kappa }_i-1},{\overline{\omega }}_{{\kappa }_i})=(1/2,1,\dots ,1,1/2)$. The gradient can be expressed as given in (36):

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\left(J_d\right)}_{*}}{\partial {\mathbf{c}}_i}}& ={\displaystyle \frac{\partial {\left(J_d\right)}_{*}}{\partial \mathcal{G}}}{\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathbf{c}}_i}}\hfill \\ \hfill {\displaystyle \frac{\partial {\left(J_d\right)}_{*}}{\partial T_i}}& ={\displaystyle \frac{\partial {\left(J_d\right)}_{*}}{\partial \mathcal{G}}}{\displaystyle \frac{\partial \mathcal{G}}{\partial t}}{\displaystyle \frac{\partial t}{\partial T_i}}+\sum _{j=0}^{{\kappa }_i}{\displaystyle \frac{{\overline{\omega }}_j}{{\kappa }_i}}max{({\mathcal{G}}_{*}\left({\mathring{\mathit{\xi }}}_{i,j}\right),\mathbf{0})}^3\hfill \\ \hfill {\displaystyle \frac{\partial {\mathcal{G}}_{*}}{\partial {\mathbf{c}}_i}}& =2{\beta }^{\left(n\right)}\left(t\right){\xi }_i^{\left(n\right)}{\left(t\right)}^{\mathrm{T}},{\displaystyle \frac{\partial {\mathcal{G}}_{*}}{\partial t}}=2{\beta }^{(n+1)}{\left(t\right)}^{\mathrm{T}}{\mathbf{c}}_i{\xi }_i^{\left(n\right)}\left(t\right)\hfill \end{array}$$

(36)

In practical implementation, to reserve some power resources and ensure the feasibility of the trajectory, we take 90% of the maximum allowable velocity, acceleration, and jerk as the thresholds.

5.3. Trajectory Weight Adjustment Based on Human Trust

Considering the changes in human trust in the UAV, the optimized trajectory should balance search efficiency and safety, and ${\lambda }_t$ and ${\lambda }_o$ are further optimized as given in (37):

$$\begin{array}{cc}\hfill {\lambda }_t& ={\lambda }_{t,0}+\mathrm{\Delta }{\lambda }_t\hfill \\ \hfill {\lambda }_o& ={\lambda }_{o,0}+\mathrm{\Delta }{\lambda }_o\hfill \end{array}$$

(37)

Based on the historical trajectory of the UAV and the MPD human trust model, we can calculate the human trust level $T_U^h$. We categorize the human trust level $T_U^h$ into three ranges from low to high: $[0,T_L)$, $[T_L,T_H)$, and $[T_H,\infty )$. Here, $T_L$ and $T_H$ represent predefined trust thresholds. When the operator’s trust level in the UAV is low ($T_U^h\in [0,T_L)$), the operator may compete with the UAV for control, posing a significant safety risk. In this scenario, $\mathrm{\Delta }{\lambda }_t$ is assigned a smaller value, while $\mathrm{\Delta }{\lambda }_o$ is assigned a larger value to enhance the safety of the UAV during human intervention. As the operator’s trust level increases ($T_U^h\in [T_L,T_H)$), $\mathrm{\Delta }{\lambda }_t$ is gradually increased, and $\mathrm{\Delta }{\lambda }_o$ is gradually decreased to achieve a balance between trajectory rapidity and safety. Furthermore, when the operator’s trust level is high ($T_U^h\in [T_H,\infty )$), it reflects strong confidence in the UAV’s capabilities. Consequently, $\mathrm{\Delta }{\lambda }_t$ is set to a larger value, and $\mathrm{\Delta }{\lambda }_o$ is set to a smaller value to optimize search efficiency and reduce the operator’s long-term workload. To accommodate the requirements of these distinct trust intervals, the specific expressions for the efficiency weight adjustment $\mathrm{\Delta }{\lambda }_t\left(T\right)$ and the safety weight adjustment $\mathrm{\Delta }{\lambda }_o\left(T\right)$, where T denotes the human trust level $T_U^h$, are given by (38) and illustrated in Figure 4:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{\lambda }_t\left(T\right)& ={\displaystyle \frac{{\mathrm{\Lambda }}_t}{1+e^{-k_1(T-T_H)}}}\hfill \\ \hfill \mathrm{\Delta }{\lambda }_o\left(T\right)& ={\displaystyle \frac{{\mathrm{\Lambda }}_o}{1+e^{k_2(T-T_L)}}}\hfill \end{array}$$

(38)

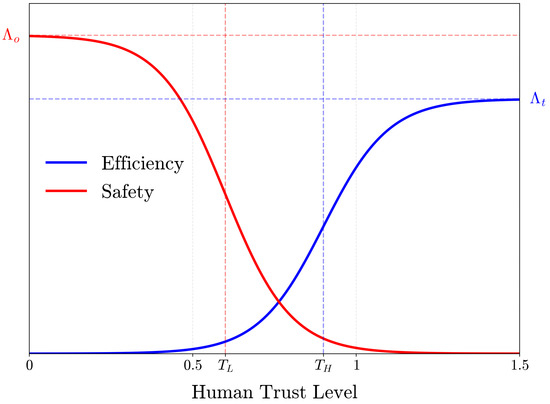
Figure 4. Trust-aware trajectory weight adjustment function.

The key parameters are set based on a combination of pilot studies and design principles. The trust thresholds are set to $T_L=0.6$ and $T_H=0.9$ based on pilot studies. The adjustment bounds follow a safety-first principle where ${\mathrm{\Lambda }}_o>{\mathrm{\Lambda }}_t$, ensuring safety concerns elicit a stronger system response than efficiency gains. Finally, the transition slopes ($k_1,k_2$) were tuned through iterative user feedback to achieve a behavioral transition that operators perceived as smooth and predictable.

6. Experiments and Results

In this section, we design and conduct an experiment on human–UAV collaboration to compare the effectiveness of our proposed method against a baseline approach that does not account for human trust. The experiments are performed on a high-performance desktop equipped with an Intel Core i9-14900KF CPU (32 cores, base frequency 3.2 GHz, maximum turbo frequency 6.0 GHz) and an NVIDIA GeForce RTX 4090 GPU (24 GB VRAM).

6.1. Implementation Details

To evaluate the proposed method, we conducted simulation experiments in three simulated random forest environments with varying tree densities. The simulation area was a rectangular volume measuring 70 m in length, 20 m in width, and 3 m in height, containing 50, 100, or 200 trees to represent sparse, medium, and dense scenarios, respectively. For the experiments, 15 students (ages 22–28) with no prior drone piloting experience were recruited. After a 5 min familiarization session, each operator was tasked with navigating a simulated quadrotor vehicle from one end of the forest to the other end. The experiment followed a within-subjects design, where each participant tested both our proposed method and a baseline approach. The order of the two methods was counterbalanced across participants. For each method, the operator performed the task once in each of the three random forest environments. The task was deemed complete upon reaching the opposite side. Operators were provided with a first-person view of the vehicle and sent commands via a joystick to guide its flight. They were permitted to intervene in the vehicle’s flight at any time.

We evaluate two aspects of the performance of our assistive aerial teleoperation system: (1) navigation efficiency, which mainly includes the distance, duration, and average velocity during the mission; and (2) the cost of human–UAV interaction, for which the core evaluation metrics are the number of operator inputs, jerk integral, and average trust. Specifically, the number of operator inputs indicates the intervention frequency of the assistive system, while the jerk integral reflects the piloting burden and trajectory smoothness. If the former two interaction indicators (operator inputs and jerk integral) are high, it indicates that the path searched by the assistive system does not match the human’s true intention, leading to poor flight quality and requiring more operator interaction to correct, which is often accompanied by lower trust. In contrast, if these indicators are low, it indicates that the operator agrees with the system’s path planning, which implies fluid human–machine collaboration and a smooth flight trajectory, ultimately building and maintaining a higher level of trust.

The motion primitive parameters used in the experiment are shown in Table 1. The maximum linear velocity input by the operator is set to 2 m/s. The parameters of the visibility metric are $N=20$, $\rho =0.8$. The parameters of the safety metric are ${\gamma }_s=2$. The specific parameters for the MPD trust model are detailed in Table 2. In our implementation, these parameters are empirically determined by referencing previous work and our own experiments, and their systematic optimization is beyond the scope of this paper.

Table 1. Motion primitive parameters.

Parameter	Min	Max	Num. Discretizations
Duration T	$0.3\mathrm{s}$	$1.5\mathrm{s}$	5
Angular vel.$\omega$	$-0.75\mathrm{rad}/\mathrm{s}$	$0.75\mathrm{rad}/\mathrm{s}$	15
Z vel.$v_z$	$-0.75\mathrm{m}/\mathrm{s}$	$0.75\mathrm{m}/\mathrm{s}$	3

Table 2. MPD trust model parameters.

Parameter	${\mathit{\alpha }}_{\mathit{h}}^{\mathit{C}}$	${\mathit{\alpha }}_{\mathit{h}}^{\mathit{P}}$	${\mathit{\alpha }}_{\mathit{h}}^{+}$	${\mathit{\alpha }}_{\mathit{h}}^{-}$	${\mathit{C}}_{\mathit{m}}^{\mathit{m}}$
Value	0.5	0.92	0.09	0.42	0.85

6.2. Results Analysis

The quantitative results of our experiments are summarized in Table 3, which compares the performance of our proposed trust-aware approach against the trust-unaware baseline across four key dimensions: task completion efficiency, operator workload, trajectory quality, and human–machine trust. These experiments were conducted in three distinct environments to assess the robustness of both methods under varying levels of complexity. Trajectory comparisons are visually illustrated in Figure 5 (2D) and Figure 6 (3D), offering additional insights into the behavioral differences between the two approaches.

Table 3. Results for the random forest environment.

Approach	Distance (m)	Duration (s)	Avg. Vel. (m/s)	Jerk Integral (m2/s3)	Num. Inputs	Avg. Trust
Sparse (50 trees)
Trust-unaware	71.15 ± 0.06	46.62 ± 1.49	1.53 ± 0.05	27.49 ± 1.63	39 ± 4	0.744 ± 0.013
Trust-aware	70.04 ± 0.63	45.53 ± 0.47	1.54 ± 0.02	21.30 ± 3.39	34 ± 3	0.813 ± 0.016
Medium (100 trees)
Trust-unaware	71.33 ± 1.16	48.88 ± 1.71	1.46 ± 0.06	44.88 ± 10.38	45 ± 7	0.657 ± 0.015
Trust-aware	70.29 ± 2.44	45.84 ± 2.39	1.52 ± 0.03	31.48 ± 10.60	34 ± 5	0.750 ± 0.013
Dense (200 trees)
Trust-unaware	71.73 ± 1.71	54.89 ± 5.29	1.31 ± 0.14	84.69 ± 9.68	56 ± 8	0.611 ± 0.017
Trust-aware	71.38 ± 2.00	49.86 ± 1.05	1.43 ± 0.08	48.11 ± 9.44	43 ± 5	0.693 ± 0.023

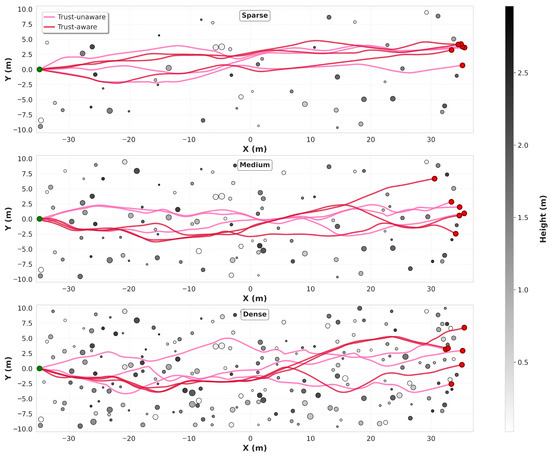
Figure 5. Two-dimensional trajectory comparison between trust-aware and trust-unaware methods under different obstacle densities. The three panels show trajectories in sparse (top, 50 trees), medium (middle, 100 trees), and dense (bottom, 200 trees) environments. The colorbar on the right indicates obstacle heights in meters. Green and red circles represent start and end points, respectively.

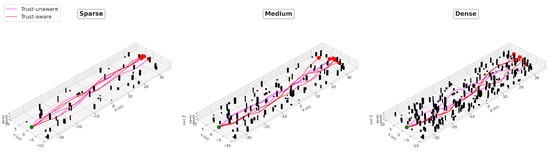
Figure 6. Three-dimensional visualization of trajectory comparison across sparse, medium, and dense obstacle environments.

In terms of fundamental task completion metrics, both methods exhibit comparable performance across all environments. Specifically, flight distance and duration show no significant differences between the trust-aware and trust-unaware approaches. For instance, in the dense environment, the trust-aware method recorded a flight distance of 71.38 m and a duration of 49.86 s, compared to 71.73 m and 54.89 s for the trust-unaware method. Similar trends are observed in the sparse and medium environments, indicating that incorporating the trust model does not compromise basic task execution efficiency. Both methods guide the UAV to plan effective paths of similar lengths, where the paths for both methods closely align in terms of overall distance across sparse, medium, and dense settings. However, the trust-aware method demonstrates a slight advantage in average velocity, particularly in the dense environment. This improvement is primarily attributed to smoother flight trajectories and fewer unnecessary pauses. The trust-aware method produces paths with fewer sharp turns and abrupt changes compared to the trust-unaware baseline, especially in the dense environment, enhancing the overall efficiency of motion.

The number of operator inputs serves as a core metric for evaluating operator intervention frequency and effort, directly reflecting the workload imposed on the operator. As shown in Table 3, the trust-aware method significantly reduces the number of operator inputs compared to the trust-unaware method across all scenarios. In the sparse environment, inputs decreased from 39 to 34 (a reduction of approximately 12.8%), and this gap widened in the dense environment, where inputs dropped from 56 to 43 (a reduction of approximately 23.2%). These results strongly demonstrate that our trust-aware method effectively alleviates the operator’s workload. The trust-aware system’s ability to dynamically adjust its assistance strategy based on real-time trust assessments underlies this improvement. When trust is high, the system operates more autonomously, reducing the need for operator fine-tuning. Conversely, when trust declines, the system adopts conservative behaviors that align better with the operator’s expectations, minimizing interventions caused by mismatches between system decisions and human intent.

The jerk integral metric reflects the smoothness of the UAV’s flight, with lower values indicating smoother trajectories with fewer abrupt changes. The experimental results in Table 3 reveal that the trajectory quality of the trust-aware method consistently surpasses that of the trust-unaware baseline. In the sparse environment, the jerk integral was reduced by approximately 22.5%, and this improvement was even more pronounced in the dense environment, with a reduction of approximately 43.2%. These smoother trajectories imply safer, more energy-efficient flights and provide a more comfortable first-person view experience for the operator. The reduction in the jerk integral is closely tied to the decrease in operator inputs; fewer external interventions prevent frequent, abrupt changes in flight state. Furthermore, the trust-aware model’s ability to predict and align with the operator’s long-term intent results in more proactive and coherent paths, contrasting with the passive, jerky reactions of the trust-unaware baseline, particularly evident in the dense environment.

Finally, the average trust metric directly validates the effectiveness of our trust-aware approach. In all environments, the average trust level of operators was significantly higher with the trust-aware method compared to the trust-unaware baseline. For example, in the medium-density environment, the trust-aware method achieved an average trust of 0.750 compared to 0.657 for the trust-unaware method. Trust levels for both methods decreased as environmental complexity increased, which is expected due to the greater challenges in denser settings. However, the decline was gentler for the trust-aware method (e.g., from 0.813 in the sparse environment to 0.693 in the dense environment compared to a steeper drop from 0.744 to 0.611 for the trust-unaware method). This suggests that by actively modeling and adapting to the operator’s trust state, our system establishes and maintains a more robust and resilient human–machine trust relationship. The higher trust levels both result from and contribute to the benefits observed (fewer inputs, smoother trajectories). As the system’s behavior becomes more reliable and predictable, operators are more willing to reduce interventions, creating a virtuous cycle.

7. Discussion

7.1. Discussion of Findings

The empirical findings provide compelling evidence that our trust-aware framework substantially elevates the quality of human–UAV interactions, as evidenced by reductions in operator workload, smoother trajectories, and more resilient trust dynamics—all without compromising core task metrics such as flight efficiency. This aligns with the framework’s core innovation: integrating an MPD trust model into the real-time planner, which dynamically predicts and adapts to operator intent and trust states. Unlike traditional trust-unaware baselines that react passively to inputs, our approach proactively aligns system behavior with human expectations and fosters more intuitive collaboration. These improvements extend beyond mere performance gains, underscoring the framework’s value in making human–machine systems safer and more user-centric, particularly in variable environments where baseline methods falter.

The core of this success lies in the formation of a virtuous cycle in operator–UAV interaction, a phenomenon observed across different environments. Specifically, this cycle occurs when the system’s trust-aware behavior aligns with operator expectations, which reduces unnecessary interventions and in turn reinforces the operator’s trust, fostering smoother and more effective collaboration. This cycle not only validates the important role of trust in human–machine interaction (e.g., [13]) but also provides a crucial extension to previous studies focused on intent-aligned trajectory generation [3,5]. While these prior works demonstrated that aligning with operator intent improves collaboration, our findings reveal that intent-alignment alone is insufficient under trust-eroding conditions. Specifically, our results in dense environments show that without a trust model, operator interventions remained high despite intent alignment, whereas our trust-aware approach successfully mitigated conflicts by dynamically increasing system caution. Our work thus extends these intent-based models by incorporating a vital second feedback loop, the operator’s dynamic trust state, which proves essential for robust performance in complex scenarios.

Furthermore, our framework makes a tangible contribution to the formal practice of risk analysis in human–UAV interaction. As conceptualized in frameworks like that of Sanz et al. [34], effective risk management for UAVs involves a cycle of hazard identification, assessment, and reduction. Our work provides a concrete, real-time implementation of this cycle. Specifically, the MPD trust model functions as a dynamic risk assessment tool, quantifying the risk of human–machine goal conflicts based on system performance and the operator’s trust level. The adaptive trajectory planner then serves as the risk reduction mechanism, translating this assessed risk into tangible actions by modulating the safety and efficiency weights. By formalizing the link between trust dynamics and system safety behaviors, our approach offers a more structured method for managing risk in collaborative aerial tasks, moving beyond the static safety rules common in prior systems.

However, while these findings affirm the framework’s efficacy in simulated scenarios, they also reveal critical limitations that warrant careful consideration, primarily stemming from the inherent sim-to-real gap. It must be acknowledged that our controlled simulation cannot fully replicate the complex uncertainties of the physical world. These include unmodeled aerodynamics, complex sensor noise profiles, and unpredictable communication latencies. Crucially, such factors could directly corrupt the real-time safety and visibility metrics that are fundamental inputs to our MPD trust model. Furthermore, beyond these physical uncertainties, our study utilized a limited operator cohort, and the framework’s generalizability across operators with varying expertise levels and risk tolerances remains an underexplored but vital area. These limitations, therefore, highlight critical open research issues regarding the framework’s real-world robustness and its capacity for personalization, paving the way for future enhancements.

7.2. Practical Significance and Scenario-Based Illustration

To illuminate the practical significance of our trust-aware framework, we present an illustrative scenario in a high-stakes application: post-disaster search and rescue.

Imagine a rescue mission where an operator must remotely pilot a UAV through a collapsed building to locate survivors. When using a UAV equipped only with basic obstacle avoidance, the operator faces immense cognitive load, simultaneously interpreting video feeds, navigating complex 3D spaces, and fighting against a system that may refuse to approach cluttered areas where a survivor might be. This often leads to human–machine conflict; to complete the mission, the operator might disable the assistance system, risking a catastrophic crash due to a moment of inattention. The loss of an expensive UAV not only incurs a financial cost but, more critically, could prematurely end a life-saving search.

Now, let us envision the same mission executed with our trust-aware framework. Its practical value unfolds in several stages:

• Initial trust calibration: As the UAV enters the building, it first navigates through less cluttered corridors. Its smooth, predictable trajectories, reflecting high safety and visibility, rapidly build the operator’s trust in the system’s competence.
• Intent-driven investigation: The operator spots a potential sign of life and issues a command to move closer for a better view. Because the operator’s trust is high, our framework accurately infers a strong, deliberate intent. It then generates a precise trajectory that navigates assertively yet safely around debris, fulfilling the operator’s goal without resistance. This is a stark contrast to a trust-unaware system that might have simply halted.
• Adaptive safety preservation: As the UAV ventures deeper, it enters an area with poor visibility, causing its onboard sensors to become less reliable. Our framework’s machine performance metrics objectively detect this degradation. Consequently, the trust model dynamically lowers its trust value, shifting the system into a more cautious state. If the anxious operator now commands a rapid forward movement, the system will provide stronger assistance, moderating the speed and trajectory to prioritize the UAV’s survival. It intelligently prevents a trust-induced error, safeguarding the mission’s most critical asset.

In summary, this scenario demonstrates clear practical significance. By fostering a more intuitive human–machine collaboration, our framework simultaneously enhances mission effectiveness and reduces operator cognitive load. Crucially, its ability to dynamically adapt to risk ensures the safety of critical assets, ultimately empowering human–machine teams to confidently undertake complex, high-stakes operations that were previously too hazardous or inefficient, thereby significantly expanding their operational boundaries.

7.3. Open Issues and Future Work

Future work will address several open issues by focusing on three core directions to further enhance the trust-aware framework’s generalization, accuracy, and application scope.

First, in human–machine interaction, a central open issue is how to bridge the sim-to-real gap while enabling genuine user adaptivity. Existing studies have primarily validated trust-aware frameworks in simulation [17,35], and their robustness against real-world uncertainties, such as sensor noise and communication latency, remains insufficiently tested. At the same time, current generic trust models often ignore differences in operator expertise, limiting their ability to meet personalized needs. To address this, our future research will encompass the following: (i) transition the framework from simulated to physical environments to verify robustness in practice; and (ii) develop personalized trust models that identify and adapt to the trust characteristics of operators with varying experience levels, thereby creating a system that is both robust and user-adaptive.

Second, in trust modeling, another open issue is how to reduce the over-reliance on empirical, manually tuned parameters. Existing approaches largely depend on human expertise [14,17] for parameter settings, which restricts scalability and adaptability. To overcome this, we will explore data-driven paradigms such as Inverse Reinforcement Learning (IRL) [13], enabling the model to autonomously learn and optimize intrinsic parameters from interaction data, replacing manual tuning with a more robust self-learning mechanism.

Finally, at the application level, an important open issue is how to scale trust-aware frameworks beyond constrained laboratory tasks into complex, high-stakes real-world scenarios. Prior work has mostly focused on basic navigation [3,5,7] in controlled settings, whereas missions such as large-scale inspection and search and rescue require balancing multiple performance metrics—including speed, safety, and coverage—while maintaining stability in highly dynamic environments that include challenges such as dynamic obstacles. To meet this challenge, we will extend the framework toward these high-stakes missions, using them as testbeds to rigorously evaluate and strengthen the adaptive capabilities of the trust-aware planner under realistic conditions.

8. Conclusions

This work proposes and validates a trust-aware trajectory planning framework to address the critical issue of human–machine trust imbalance in assistive aerial teleoperation. By embedding an MPD trust model into a real-time planner, the approach effectively reduces operator workload, improves flight safety, and establishes a more stable human–machine trust relationship, all while maintaining task efficiency. The results demonstrate that introducing dynamic trust quantification into the control loop of autonomous systems holds significant potential, enabling the creation of a virtuous cycle of reduced human intervention, greater system predictability, and enhanced collaborative performance. Taken together, this work establishes a foundation for developing more intuitive and efficient human–machine collaboration models, making an important contribution to the advancement of intelligent aerial systems. In the future, by addressing the open issues outlined in the Discussion section, this framework holds promise for extension to a broader range of autonomous system applications.