Reliability Assessment for Small-Sample Accelerated Life Tests with Normal Distribution

Abstract

A significant challenge in the accelerated life test (ALT) is the reliance on large sample sizes and multiple stress levels, which results in high costs and long test durations. To address this issue, this paper develops a new reliability assessment method for small-sample ALTs with normal distribution (or lognormal distribution) and censoring. This method enables a high-confidence evaluation of the percentile lifetime (reliable lifetime) under normal operating stress level using censored data from only two accelerated stress levels. Firstly, a relationship is established between the percentile lifetime at normal stress level and the distribution parameters at accelerated stress levels. Subsequently, an initial estimate of the percentile lifetime is obtained from failure data, and its confidence is then refined using a Bayesian update with the nonfailures. Finally, an exact one-sided lower confidence limit (LCL) for the percentile lifetime and reliability is determined. This paper derives an analytical formula for LCLs under Type-II censoring scenarios and further extend the method to accommodate Type-I censored and general incomplete data. The Monte Carlo simulations and case studies show that, the proposed methods significantly reduce the required sample size and testing duration while offering superior theoretical rigor and accuracy than the conventional methods.

1. Introduction

With advancements in reliability engineering and quality technology, modern products are increasingly designed for high reliability and long lifespans. For such products with operating lives often spanning years, or even decades, collecting sufficient failure data under normal operating conditions is incredibly time-consuming and costly. Under these circumstances, the accelerated life test (ALT) has emerged as a crucial method for reliability assessment in practical engineering. In an ALT, the failures are induced more rapidly by applying stresses (involves temperature, humidity, voltage, or mechanical load) that are higher than the normal conditions. The resulting lifetime data, gathered in a compressed period, is then extrapolated to predict the reliability under normal operating conditions [1,2,3].

However, product lifetimes may remain considerable even under acceleration, particularly at low accelerated stress levels. To further reduce the test duration and costs, the life tests are usually terminated before all units have failed. In ALTs, the two most common censoring schemes are Type-I censoring and Type-II censoring [4,5]. The former involves stopping the test when a prefixed time has been reached, while the latter involves stopping the test when a predetermined number of failures has occurred.

In ALT reliability inference, maximum likelihood estimation (MLE) and best linear unbiased estimation (BLUE) are two predominant methods and have been widely adopted in practice [6,7,8,9]. However, neither of them is well-suited for small-sample scenarios. On one hand, MLE exhibits significant errors with small sample sizes, making it unsuitable for practical engineering applications [10,11]. Our simulations in Section 5 further corroborate this problem of MLE. On the other hand, the BLUE method usually requires employing about five accelerated stress levels. This extensive testing, combined with complex assumptions for multiple parameter estimators, increases the difficulty and margin of error. Consequently, BLUE is usually used to provide a point estimate, failing to provide the more crucial lower confidence limits (LCLs) needed for high-reliability assessments. In view of this, there is an urgent need to develop a reliability assessment method suitable for small-sample ALT.

A key challenge in reliability estimation for small-sample ALT is the construction of exact confidence limits for percentile lifetime or reliability function. Balakrishnan et al. [12,13] derived exact confidence intervals for parameters in simple step-stress ALTs for the exponential distribution, covering both Type-II and Type-I scenarios. Based on the generalized fiducial inference, Wang et al. [14] derived confidence intervals for constant-stress ALT (CSALT) with Weibull distribution and progressively Type-II censoring. Their simulation results showed that the coverage probabilities (CPs) are close to the nominal confidence levels. Following this, Chen et al. [15] developed an improved version which is easier to implement and avoids repetitive point estimations. However, the aforementioned research mainly focuses on either the exponential or Weibull distributions. For the widely used normal distribution in engineering, exact inference methods are currently restricted to complete data scenarios [16,17], leaving a conspicuous gap in the literature regarding censored data.

To address the challenges above, this paper proposes an exact method for estimating the one-sided LCLs of percentile lifetime and reliability for CSALT with normal distribution and Type-II censoring. The method first establishes a mathematical expression for the percentile lifetime at the normal operating stress level based on the life–stress relationship. Then, by utilizing the joint confidence distribution of the lifetime distribution parameters and Bayesian updating, an analytical formula for the one-sided LCL of the percentile lifetime is derived. Furthermore, this paper investigates scenarios with Type-I censored data and incomplete data in ALTs.

The major contributions of the proposed methods are summarized as follows:

(1)

A new reliability assessment method is developed for CSALT with normal distribution and Type-II censoring, which can provide exact one-sided LCLs in small-sample scenarios.

(2)

By reducing the requirement from multiple stress levels to just two, the proposed method significantly reduce the experimental time and test samples.

(3)

The proposed method provides an analytical formula for the one-sided LCLs, thereby obviating the need for point estimation or complex sampling. This renders the approach more theoretically rigorous and enhances its accuracy.

The paper is organized as follows. Section 2 presents the small-sample ALT design scheme. Section 3 establishes the mathematical expression for percentile lifetime under normal operating stress level, based on the life–stress relationship. In Section 4, new reliability estimation methods for LCLs are derived for CSALT with Type-II censored, Type-I censored, and general incomplete data. Monte Carlo simulations are conducted in Section 5 to evaluate the performance of the proposed method. Section 6 illustrates a real case study of He-Ne laser. Finally, Section 7 presents the conclusions.

2. Data Description

Generally, when the acceleration factor is unknown, at least two accelerated stress levels are required to enable the extrapolation of lifetime data from accelerated levels to the normal operating stress level. Accordingly, facing the small-sample constraints, this study employs a two-level CSALT with censoring, designed to reduce both the sample size and the test duration. At each accelerated stress level $S_i$, $n_i$ units are tested, $i=1,2$. Let $t_{i1},t_{i2},\cdots ,t_{i{r}_i}$ be the $r_i(r_i\ge 2)$ observed failure times at stress level $S_i$. And the remaining $n_i-r_i$ censored times for the surviving units are denoted by $t_{i\left(r_i+1\right)},t_{i\left(r_i+2\right)},\cdots ,t_{i{n}_i}$. For the subsequent analysis, all collected lifetimes are converted into their corresponding natural logarithms, represented as $x_{i1},x_{i2},\cdots ,x_{i{r}_i}$ and $x_{i\left(r_i+1\right)},x_{i\left(r_i+2\right)},\cdots ,x_{i{n}_i}$.

When selecting the accelerated stress levels, it is required that the failure modes and mechanisms under the accelerated stress levels are same as those under the normal operating stress level $S_0(S_0<S_1<S_2)$. Furthermore, to achieve effective acceleration and robust estimations, $S_2$ should be set as high as possible, with an adequate separation from $S_1$.

3. Statistical Models

Assume that the lifetime $t$ of a test unit at any stress level $S_i$ follows a lognormal distribution with mean ${\mu }_i$ and variance ${\sigma }^2$. Then, the logarithm of the lifetime is normally distributed as $x=\ln t~\mathrm{N}\left({\mu }_i,{\sigma }^2\right)$. The corresponding reliability function is given by

$$\begin{array}{cc}\hfill R\left(x;{\mu }_i,\sigma \right)=\Phi \left({\displaystyle \frac{{\mu }_i-x}{\sigma }}\right),& i=0,1,2\hfill \end{array}$$

(1)

where $\Phi \left(z\right)$ is the standard normal cumulative distribution function (CDF) at $z$.

3.1. Life–Stress Relationship

Under the lognormal distribution, a linear relationship is assumed between the log-percentile lifetime and a function of stress level:

$$x_{Ri}=a+b\phi \left(S_i\right)$$

(2)

In this expression, $x_{Ri}={\mu }_i-u_R\sigma$ represents the log-percentile lifetime with a survival probability of $R$ at stress level $S_i$, where $u_R={\Phi }^{-1}\left(R\right)$ is the standard normal quantile. $a$ and $b$ are unknown model parameters. $\phi \left(S_i\right)$ is a known monotonic function of $S_i$, whose specific form is determined by the type of stress applied. For instance, when dealing with the temperature, the Arrhenius model is typically used, then $\phi \left(S_i\right)=1/S_i$ [18]. For stresses such as voltage, humidity, or mechanical load, the inverse power law model, which defines the function as $\phi \left(S_i\right)=\ln S_i$, is commonly employed [19]. Additionally, the exponential model, where $\phi \left(S_i\right)=S_i$, is applicable for voltage or mechanical load [20].

3.2. Parameter Estimation

As mentioned in Section 2, only two accelerated stress levels are considered in the small-sample ALT. Let $x_{R1}$ and $x_{R2}$ be the log-percentile lifetime with a survival probability of $R$ at accelerated stress level $S_1$ and $S_2$, respectively. Substituting them into Equation (2), the model parameters $a$ and $b$ are estimated by

$$a={\displaystyle \frac{\phi \left(S_2\right)x_{R1}-\phi \left(S_1\right)x_{R2}}{\phi \left(S_2\right)-\phi \left(S_1\right)}}$$

(3)

$$b={\displaystyle \frac{x_{R2}-x_{R1}}{\phi \left(S_2\right)-\phi \left(S_1\right)}}$$

(4)

Then, the log-percentile lifetime $x_{R0}$ with a survival probability of $R$ at the normal operating stress level $S_0$ can be expressed as

$$x_{R0}={\displaystyle \frac{\left[\phi \left(S_2\right)-\phi \left(S_0\right)\right]x_{R1}+\left[\phi \left(S_0\right)-\phi \left(S_1\right)\right]x_{R2}}{\phi \left(S_2\right)-\phi \left(S_1\right)}}$$

(5)

Denote

$$\omega ={\displaystyle \frac{\phi \left(S_2\right)-\phi \left(S_0\right)}{\phi \left(S_2\right)-\phi \left(S_1\right)}}$$

(6)

Therefore, we have

$$x_{R0}=\omega x_{R1}+\left(1-\omega \right)x_{R2}$$

(7)

Since $x_{R1}={\mu }_1-u_R\sigma$ and $x_{R2}={\mu }_2-u_R\sigma$, $x_{R0}$ can be further written as

$$x_{R0}=\omega {\mu }_1+\left(1-\omega \right){\mu }_2-u_R\sigma$$

(8)

From Equation (8), it can be seen that the distribution of $x_{R0}$ is independent of the parameters $a$ and $b$. Therefore, by fusing the confidence distributions of ${\mu }_1$, ${\mu }_2$, and $\sigma$, the confidence distribution of $x_{R0}$ can be derived. This allows the assessment of the confidence limit of the percentile lifetime under the normal operating stress level.

4. Small-Sample Reliability Assessment

In this section, new reliability assessment methods based on the confidence distribution theory and Bayesian updating are presented for CSALT with normal distribution and censoring. The one-sided LCLs for both percentile lifetime and reliability are derived.

4.1. Type-II Censored Data

Theorem 1.

Let $x_{i1}\le x_{i2}\le \cdots \le x_{i{r}_i}$ be the Type-II censored sample of size $n_i$ with $r_i$  failures at accelerated stress level $S_i$, where $i=1,2$ and $2\le r_i\le n_i$ . Then, an exact one-sided LCL for the log-percentile lifetime $x_{R0}$  at the normal operating stress level $S_0$ is given by $x_{R\mathrm{L}0,\gamma }$:

$$x_{R\mathrm{L}0,\gamma }=\omega {\overline{x}}_1+\left(1-\omega \right){\overline{x}}_2-t_{{\gamma }^{**}}\left(\nu ,\delta \right)s/\sqrt{r_e}$$

(9)

which satisfies the condition for a confidence level of $\gamma$ :

$$P\left(x_{R\mathrm{L}0,\gamma }\le x_{R0}\right)=\gamma$$

(10)

In the term $x_{R\mathrm{L}0,\gamma }$, the “$\mathrm{L}$” subscript indicates a lower limit, while $\gamma$ is the nominal confidence level. ${\overline{x}}_i={\displaystyle \frac{1}{r_i}}{\displaystyle \sum _{j=1}^{r_i}{x}_{ij}}$ and $s_i=\sqrt{{\displaystyle \sum _{j=1}^{r_i}{\left(x_{ij}-{\overline{x}}_i\right)}^2}/\left(r_i-1\right)}$ are the sample mean and sample standard deviation of the log-lifetimes, respectively, calculated from the failures at stress level $S_i$, $i=1,2$. And $s=\sqrt{\left[\left(r_1-1\right)s_1^2+\left(r_2-1\right)s_2^2\right]/\left(r_1+r_2-2\right)}$ represents the pooled standard deviation. $\omega$ is given by Equation (6). Furthermore, $t_{\gamma }\left(\nu ,\delta \right)$ is the lower $\gamma$-th percentile of the noncentral t-distribution with $\nu =r_1+r_2-2$ degrees of freedom and non-centrality parameter $\delta =\sqrt{r_e}{u}_R$, where $r_e={\left[{\omega }^2/r_1+{\left(1-\omega \right)}^2/r_2\right]}^{-1}$. ${\gamma }^{**}$ is the solution of the following equation:

$${\displaystyle \sum _{j=1}^M{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{l=q_{jk}+1}^M{w}_{jkl}}}}/{\displaystyle \sum _{j=1}^M{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{l=1}^M{w}_{jkl}}}}=\gamma$$

(11)

where

$$\begin{array}{cc}\hfill w_{jkl}& ={\left\{\Phi \left[\left({\overline{x}}_1-x_{1r_1}\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_l}/\sqrt{r_1}\right]\right\}}^{n_1-r_1}\hfill \\ & \times {\left\{\Phi \left[\left({\overline{x}}_2-x_{2r_2}\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_k}/\sqrt{r_2}\right]\right\}}^{n_2-r_2}\hfill \end{array}$$

(12)

$$q_{jk}=\mathrm{INT}\left\{M-M\Phi \left[{\displaystyle \frac{\sqrt{r_1}{u}_R}{\omega }}+{\displaystyle \frac{\left(1-\omega \right)u_{{\gamma }_k}}{\omega \sqrt{r_2/r_1}}}-{\displaystyle \frac{t_{{\gamma }^{**}}\left(\nu ,\delta \right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}}{\omega \sqrt{\nu r_e/r_1}}}\right]\right\}$$

(13)

$$\begin{array}{ccc}\hfill {\gamma }_d=1-\left(d-0.5\right)/M,& \hfill d\in \left\{j,k,l\right\},\hfill & d=1,2,\cdots ,M\hfill \end{array}$$

(14)

where ${\chi }_{{\gamma }_j}^2\left(\nu \right)$ is the lower ${\gamma }_j$-percentile of the chi-squared distribution with $\nu$ degrees of freedom, while $u_{{\gamma }_k}$ and $u_{{\gamma }_l}$ are the lower ${\gamma }_k$-th and ${\gamma }_l$-th percentiles of the standard normal distribution, respectively. $M$ is the number of discretization subintervals that determines the numerical calculation accuracy (e.g., ${10}^4$, ${10}^5$), and $\mathrm{INT}\left(·\right)$ is the integer-valued function.

Proof of Theorem 1.

Divide the lifetime data into two parts for analysis: failures and non-failures. Firstly, by treating the failure data from two accelerated stress levels as a complete dataset, an initial one-sided LCL for $x_{R0}$ can be derived [21], denoted as $x_{R\mathrm{L}0,\gamma }^{\left(0\right)}$:

$$x_{R\mathrm{L}0,\gamma }^{\left(0\right)}=\omega {\overline{x}}_1+\left(1-\omega \right){\overline{x}}_2-t_{\gamma }\left(\nu ,\delta \right)s/\sqrt{r_e}$$

(15)

Subsequently, the remaining non-failure data are utilized to conduct a Bayesian update on the confidence level of this initial estimate. Define the updated confidence level ${\gamma }^{\ast }$ as

$${\gamma }^{\ast }=P\left(x_{R\mathrm{L}0,\gamma }^{\left(0\right)}\le x_{R0}|A\right)={\displaystyle \frac{P\left(AB\right)}{P\left(AB\right)+P\left(A\overline{B}\right)}}$$

(16)

where event $A$ is the observation that for each stress level $S_i\left(i=1,2\right)$, $n_i-r_i$ units did not fail by the log-lifetime $x_{i{r}_i}$. Event $B=\left\{x_{R\mathrm{L}0,\gamma }^{\left(0\right)}\le x_{R0}\right\}$, and $\overline{B}$ is the opposing event of $B$. Specifically, the probabilities that events $A$ and $B$ occur, and that events $A$ and $\overline{B}$ occur, can be calculated as follows:

$$\begin{array}{cc}P\left(AB\right)\hfill & ={\displaystyle \underset{x_{R\mathrm{L}0,\gamma }^{\left(0\right)}\le x_{R0}}{\iiint }{\displaystyle \prod _{i=1}^2{\left[R_i\left(x_{i{r}_i}\right)\right]}^{n_i-r_i}}g\left({\mu }_1,{\mu }_2,\sigma \right)d{\mu }_{1}d{\mu }_2}d\sigma \hfill \\ & ={\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_{-\infty }^{+\infty }{\displaystyle {\int }_{{\tilde{\mu }}_1}^{+\infty }{\displaystyle \prod _{i=1}^2{\left[R_i\left(x_{i{r}_i}\right)\right]}^{n_i-r_i}}}{g}_1\left({\mu }_1|\sigma \right)g_2\left({\mu }_2|\sigma \right)g_3\left(\sigma \right)}}d{\mu }_{1}d{\mu }_{2}d\sigma \hfill \\ & ={\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{\displaystyle {\int }_{G_1\left({\tilde{\mu }}_1|\sigma \right)}^1{\displaystyle \prod _{i=1}^2{\left\{\Phi \left[\left({\mu }_i-x_{i{r}_i}\right)/\sigma \right]\right\}}^{n_i-r_i}}}}}d{G}_1\left({\mu }_1|\sigma \right)d{G}_2\left({\mu }_2|\sigma \right)d{G}_3\left(\sigma \right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}P\left(A\overline{B}\right)& ={\displaystyle \underset{x_{R\mathrm{L}0,\gamma }^{\left(0\right)}>x_{R0}}{\iiint }{\displaystyle \prod _{i=1}^2{\left[R_i\left(x_{i{r}_i}\right)\right]}^{n_i-r_i}}g\left({\mu }_1,{\mu }_2,\sigma \right)d{\mu }_{1}d{\mu }_2}d\sigma \hfill \\ & ={\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{G_1\left({\tilde{\mu }}_1|\sigma \right)}{\displaystyle \prod _{i=1}^2{\left\{\Phi \left[\left({\mu }_i-x_{i{r}_i}\right)/\sigma \right]\right\}}^{n_i-r_i}}}}}d{G}_1\left({\mu }_1|\sigma \right)d{G}_2\left({\mu }_2|\sigma \right)d{G}_3\left(\sigma \right)\hfill \end{array}$$

(18)

where ${\tilde{\mu }}_1$ is the lower integration bound for ${\mu }_1$, derived from Equation (8) and given by

$${\tilde{\mu }}_1=\left[x_{R\mathrm{L}0,\gamma }^{\left(0\right)}-\left(1-\omega \right){\mu }_2+u_R\sigma \right]/\omega$$

(19)

where $R_i\left(x_{i{r}_i}\right)=\Phi \left[\left({\mu }_i-x_{i{r}_i}\right)/\sigma \right]$ is the reliability at time $x_{i{r}_i}$ under stress level $S_i$, representing the reliability information contained in the non-failures. $g\left({\mu }_1,{\mu }_2,\sigma \right)$ is the probability density function (PDF) of the joint confidence distribution for parameters $\left({\mu }_1,{\mu }_2,\sigma \right)$ that is derived from the failure lifetime data [22,23], with ${\mu }_1$ and ${\mu }_2$ being independent. $g_i\left({\mu }_i|\sigma \right)$ and $G_i\left(\left.{\mu }_i\right|\sigma \right)=\Phi \left[\sqrt{r_i}\left({\mu }_i-{\overline{x}}_i\right)/\sigma \right]$ are the PDF and CDF of the conditional confidence distribution for ${\mu }_i$, respectively [24]. $g_3\left(\sigma \right)$ and $G_3\left(\sigma \right)$ $=1-F_{\nu }\left(\nu s^2/{\sigma }^2\right)$ are the respective confidence PDF and CDF for $\sigma$, where $F_{\nu }\left(·\right)$ represents the CDF of chi-squared distribution with $\nu$ degrees of freedom [24].

Let $y_i=G_i\left(\left.{\mu }_i\right|\sigma \right)$ and $z=G_3\left(\sigma \right)$. Taking inverse of them leads to

$$\sigma =s\sqrt{\nu /{\chi }_{1-z}^2\left(\nu \right)}$$

(20)

$$\begin{array}{cc}\hfill {\mu }_i={\overline{x}}_i+u_{y_i}s\sqrt{\nu /\left(r_i{\chi }_{1-z}^2\left(\nu \right)\right)},& i=1,2\hfill \end{array}$$

(21)

Thus, Equations (17) and (18) can be transformed into

$$P\left(AB\right)={\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{\displaystyle {\int }_{{\tilde{y}}_1}^1{\displaystyle \prod _{i=1}^2{\left\{\Phi \left[\left({\overline{x}}_i-x_{i{r}_i}\right)\sqrt{{\chi }_{1-z}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)+u_{y_i}/\sqrt{r_i}\right]\right\}}^{n_i-r_i}}}}}d{y}_{1}d{y}_{2}dz$$

(22)

$$P\left(A\overline{B}\right)={\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{{\tilde{y}}_1}{\displaystyle \prod _{i=1}^2{\left\{\Phi \left[\left({\overline{x}}_i-x_{i{r}_i}\right)\sqrt{{\chi }_{1-z}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)+u_{y_i}/\sqrt{r_i}\right]\right\}}^{n_i-r_i}}}}}d{y}_{1}d{y}_{2}dz$$

(23)

where

$${\tilde{y}}_1=G_1\left(\left.{\tilde{\mu }}_1\right|\sigma \right)=\Phi \left\{\sqrt{r_1}/\omega \left[u_R+\left(\omega -1\right)u_{y_2}/\sqrt{r_2}-t_{\gamma }\left(\nu ,\delta \right)\sqrt{{\chi }_{1-z}^2\left(\nu \right)}/\sqrt{\nu r_e}\right]\right\}$$

(24)

By substituting Equations (22) and (23) into Equation (16), we have

$${\gamma }^{*}={\displaystyle \frac{{\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{\displaystyle {\int }_{{\tilde{y}}_1}^1{\displaystyle \prod _{i=1}^2{\left\{\Phi \left[\left({\overline{x}}_i-x_{i{r}_i}\right)\sqrt{{\chi }_{1-z}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)+u_{y_i}/\sqrt{r_i}\right]\right\}}^{n_i-r_i}}}}}d{y}_{1}d{y}_{2}dz}{{\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{\displaystyle \prod _{i=1}^2{\left\{\Phi \left[\left({\overline{x}}_i-x_{i{r}_i}\right)\sqrt{{\chi }_{1-z}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)+u_{y_i}/\sqrt{r_i}\right]\right\}}^{n_i-r_i}}}}}d{y}_{1}d{y}_{2}dz}}$$

(25)

Consequently, it is observed that ${\gamma }^{*}$ is a monotonically increasing function of $\gamma$ that ranges from 0 to 1. By adjusting the value of $\gamma$ in Equation (24) to a specific value ${\gamma }^{\ast \ast }$, the resulting ${\gamma }^{*}$ can be set equal to the nominal confidence level $\gamma$$\left(0<\gamma <1\right)$. Therefore, the exact LCL for $x_{R0}$ can be obtained as

$$x_{R\mathrm{L}0,\gamma }=x_{R\mathrm{L}0,{\gamma }^{**}}^{\left(0\right)}=\omega {\overline{x}}_1+\left(1-\omega \right){\overline{x}}_2-t_{{\gamma }^{**}}\left(\nu ,\delta \right)s/\sqrt{r_e}$$

(26)

Due to the complexity of Equation (25), a numerical method based on integral discretization is proposed to compute ${\gamma }^{*}$:

$${\gamma }^{*}={\displaystyle \sum _{j=1}^M{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{l=q_{jk}+1}^M{w}_{jkl}}}}/{\displaystyle \sum _{j=1}^M{\displaystyle \sum _{k=1}^M{\displaystyle \sum _{l=1}^M{w}_{jkl}}}}$$

(27)

where

$$\begin{array}{cc}\hfill w_{jkl}& ={\left\{\Phi \left[\left({\overline{x}}_1-x_{1r_1}\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_l}/\sqrt{r_1}\right]\right\}}^{n_1-r_1}\hfill \\ & \times {\left\{\Phi \left[\left({\overline{x}}_2-x_{2r_2}\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_k}/\sqrt{r_2}\right]\right\}}^{n_2-r_2}\hfill \end{array}$$

(28)

$$q_{jk}=\mathrm{INT}\left\{M-M\Phi \left[{\displaystyle \frac{\sqrt{r_1}{u}_R}{\omega }}+{\displaystyle \frac{\left(1-\omega \right)u_{{\gamma }_k}}{\omega \sqrt{r_2/r_1}}}-{\displaystyle \frac{t_{\gamma }\left(\nu ,\delta \right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}}{\omega \sqrt{\nu r_e/r_1}}}\right]\right\}$$

(29)

$$\begin{array}{ccc}\hfill {\gamma }_d=1-\left(d-0.5\right)/M,& \hfill d\in \left\{j,k,l\right\},\hfill & d=1,2,\cdots ,M\hfill \end{array}$$

(30)

□

The corresponding procedure for updating the confidence level is detailed in pseudo-code in Algorithm 1.

Algorithm 1. Confidence level update algorithm.

1. Input: Censored data $x_{ij}$, confidence level $\gamma$, and number of subintervals $M$

2. Initialization: denominator = 0, numerator = 0

3. Triple summation loop     For $j$ from 1 to $M$:       For $k$ from 1 to $M$:          For $l$ from 1 to $M$:             (1) generate ${\gamma }_j$, ${\gamma }_k$, ${\gamma }_l$ values from Equation (30)             (2) calculate $w_{jkl}$ and $q_{jk}$ from Equations (28) and (29)             (3) denominator → denominator + $w_{jkl}$             (4) if $l\ge q_{jk}+1$               then numerator → numerator + $w_{jkl}$               End if          End For       End For    End For

4. Output: ${\gamma }^{*}$ = numerator/denominator

Based on Theorem 1, the following corollary can be established according to the equivalence of LCL curves.

Corollary 1.

At the normal operating stress level $S_0$, the exact LCL of reliability $R_0$ at a given time $t$ with $\gamma$ confidence level, denoted as $R_{\mathrm{L}0,\gamma }$, can be obtained through the iterative computation using Equation (26). When $x_{R\mathrm{L}0,\gamma }=\ln t$, the term $R$ in Equation (13) corresponds to $R_{\mathrm{L}0,\gamma }$.

4.2. Type-I Censored Data

Corollary 2.

For Type-I censored data, let $x_{i1}\le x_{i2}\le \cdots \le x_{i{r}_i}<x_i$ be the observed failure lifetime data under the accelerated stress level $S_i$, where $x_i=\ln {\tau }_i$ is the prespecified censoring time. Then based on Theorem 1 and Corollary 1, replace Equation (12) by

$$\begin{array}{cc}\hfill w_{jkl}=& {\left\{\Phi \left[\left({\overline{x}}_1-x_1\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_l}/\sqrt{r_1}\right]\right\}}^{n_1-r_1}\hfill \\ & \times {\left\{\Phi \left[\left({\overline{x}}_2-x_2\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_k}/\sqrt{r_2}\right]\right\}}^{n_2-r_2}\hfill \end{array}$$

(31)

to perform approximate assessment of the LCLs for the log-percentile lifetime $x_{R0}$ and reliability $R_0$ at the normal operating stress level $S_0$.

4.3. Incomplete Data

Corollary 3.

For incomplete data, let $x_{i1}\le x_{i2}\le \cdots \le x_{i{r}_i}$ represent the observed failure lifetime data under the accelerated stress level $S_i$, with $x_{i\left(r_i+1\right)},x_{i\left(r_i+2\right)},\cdots ,x_{i{n}_i}$ being the remaining censored data. Then based on Theorem 1 and Corollary 1, replace Equation (12) by

$$\begin{array}{cc}\hfill w_{jkl}=& \left\{{\displaystyle \prod _{m=r_1+1}^{n_1}\Phi \left[\left({\overline{x}}_1-x_{1m}\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_l}/\sqrt{r_1}\right]}\right\}\hfill \\ & \times \left\{{\displaystyle \prod _{m=r_2+1}^{n_2}\Phi \left[\left({\overline{x}}_2-x_{2m}\right)\sqrt{{\chi }_{{\gamma }_j}^2\left(\nu \right)}/\left(s\sqrt{\nu }\right)-u_{{\gamma }_k}/\sqrt{r_2}\right]}\right\}\hfill \end{array}$$

(32)

to perform approximate assessment of the LCLs for the log-percentile lifetime $x_{R0}$ and reliability $R_0$ at the normal operating stress level $S_0$.

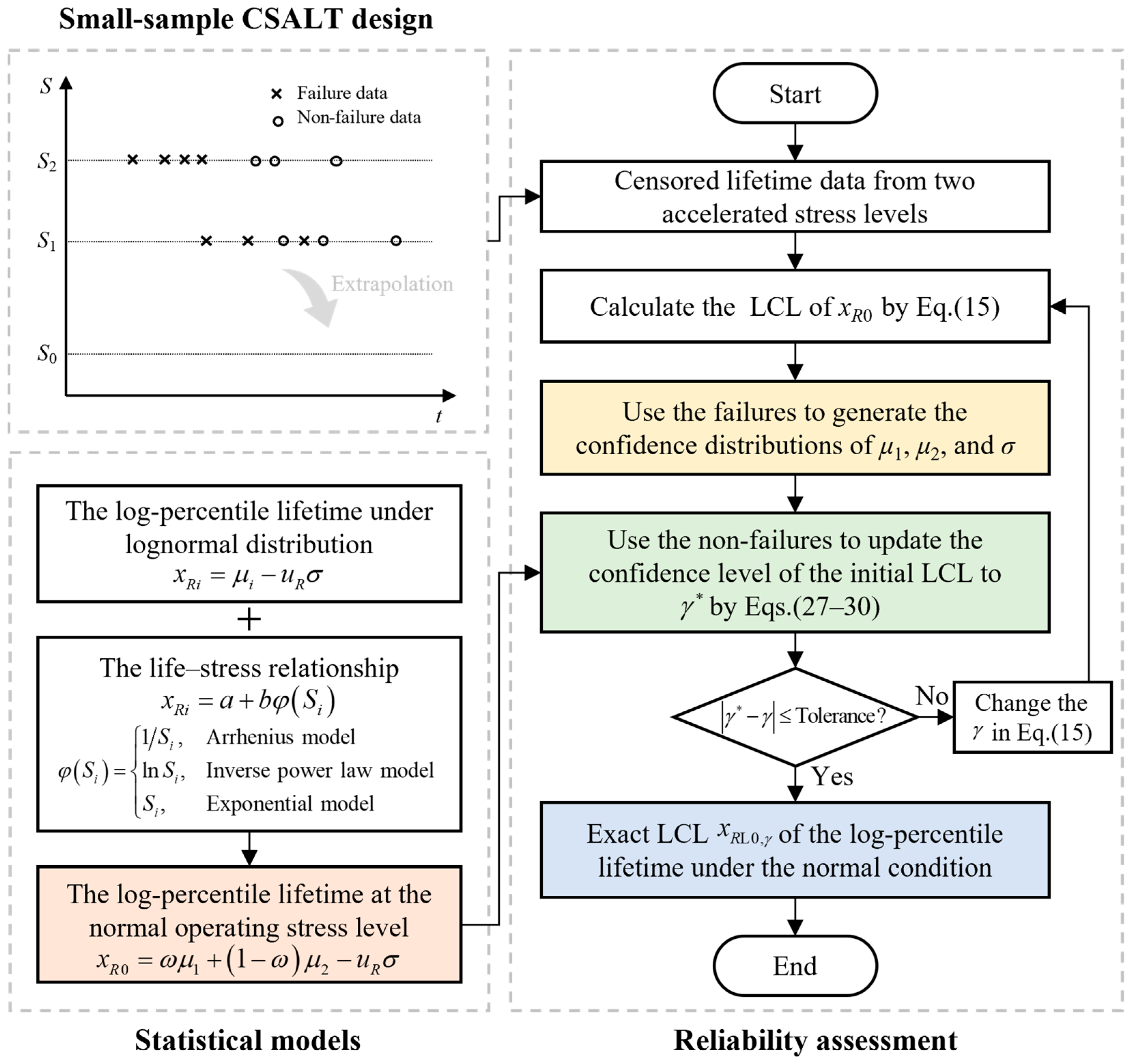
To clearly illustrate the proposed reliability assessment method for small-sample ALTs, a comprehensive overview of the entire process is given below. Figure 1 outlines the complete implementation framework, including test scheme design, statistical model establishment, and the reliability assessment procedure.

Step 1: Establish the life–stress relationship according to the accelerated stress type, and build the mathematical expression of log-percentile lifetime $x_{R0}$ at the normal operating stress level $S_0$ by Equation (8).

Step 2: Calculate an initial LCL for $x_{R0}$ using the failure lifetime data by Equation (15).

Step 3: Establish the confidence distribution of $\left({\mu }_1,{\mu }_2,\sigma \right)$ using the failures, and update the confidence level of the initial LCL using the non-failures by Equations (27)–(30).

Step 4: Adjust the value of $\gamma$ in Equation (15) or (29) to a new value, ${\gamma }^{**}$, to align the updated confidence level with the nominal level, and calculate the exact LCL for $x_{R0}$ by Equation (26).

5. Simulation Study

5.1. Monte Carlo Simulations

To evaluate the performance of the proposed method under small-sample conditions, this section presents a Monte Carlo simulation study. For comparison, the MLE-based inference method is also conducted. In the MLE method, the point estimations are obtained by solving the likelihood equations, while the asymptotic confidence limits are constructed using the Fisher information matrix [25].

The simulation settings are detailed as follows. A two-level CSALT with Type-II censoring is evaluated across five different censoring schemes. For each scheme, 100,000 replicates of ALT samples are generated from the lognormal distribution with parameters ${\mu }_i=-13.2+6600/S_i$ and $\sigma =0.2$. The accelerated stress levels are set as $S_2=393\mathrm{K}$ and $S_1=353\mathrm{K}$, with the normal operating stress level at $S_0=313\mathrm{K}$. For simplicity, both accelerated stress levels are assigned the same sample size $n$ and the same failure number $r$. The objective is to assess the LCL for the percentile lifetime with 99.9% survival probability under the normal conditions.

The validity of the method is assessed at three nominal confidence levels: 0.90, 0.95, and 0.99. For each level, the CP is calculated as the proportion of the estimated LCLs below the true percentile lifetime. This CP is then compared to its nominal target to quantify the method’s accuracy.

Table 1. The CPs for CSALT with Type-II censoring based on 100,000 replications.

(n, r)	Method	Coverage Probability
		γ = $0.90$	γ = $0.95$	γ = $0.99$
$\left(3,2\right)$	Proposed method	0.900	0.950	0.990
	MLE method	0.540	0.594	0.682
$\left(5,3\right)$	Proposed method	0.902	0.951	0.990
	MLE method	0.642	0.708	0.800
$\left(8,5\right)$	Proposed method	0.900	0.950	0.990
	MLE method	0.730	0.799	0.885
$\left(10,6\right)$	Proposed method	0.901	0.950	0.991
	MLE method	0.751	0.819	0.904
$\left(20,12\right)$	Proposed method	0.902	0.952	0.990
	MLE method	0.807	0.872	0.946

summarizes the CPs of the proposed method and the MLE method.

From Table 1, it can be observed that the CPs of the proposed method closely match the nominal confidence levels even in small-sample conditions. This implies that the LCLs are exact in terms of frequentist properties. In contrast, the CPs of the MLE method are consistently below the nominal confidence level, demonstrating that the MLE estimator tends to overestimate. However, its performance improves as the sample size increases, with the CPs gradually converging toward the nominal level. This suggests that the MLE method is more suitable for large-sample applications.

Furthermore, extensive simulation studies were carried out for scenarios involving Type-I censored and incomplete data. The results show that the CPs, derived from Corollary 2 and Corollary 3, are both larger than the nominal confidence level, and approach the nominal level as the sample size increases.

5.2. A Simulation Example

To provide a more intuitive comparison between the proposed method and the MLE method, a specific simulation example is presented below.

Table 2. Simulation dataset for CSALT with Type-II censoring.

Stress Level (Mpa)	Lifetime (Cycles)
600	654, 672, 903, >903, >903
400	4546, 5132, 6253, >6253, >6253

lists a simulation dataset from a CSALT, which was generated from the lognormal distribution with parameters ${\mu }_i=16.5-4.8\ln S_i$ and $\sigma =0.3$. The proposed method and the MLE method are used to estimate the 90% LCL for the percentile lifetime with 99% reliability at 150 MPa.

As shown in

Table 3. Comparison between the proposed method and the MLE method.

$\mathbf{True} \mathbf{Value} {\mathit{t}}_{\mathit{R}0}$ (Cycles)	$\mathbf{LCL} {\mathit{t}}_{\mathit{R}\mathbf{L}0,\mathit{\gamma }}$ (Cycles)
	Proposed Method	MLE Method
137,800	117,800	235,972

, the LCL of the MLE method is non-conservative, overestimating the true percentile lifetime value by 71%. Conversely, the proposed method provides an appropriately conservative estimate, with its LCL falling slightly below the true value. This outcome, which aligns with the Monte Carlo simulation results, reaffirms the superior accuracy and credibility of the proposed method for small-sample analysis.

5.3. Discussions

This study develops a new method for calculating exact LCLs for small-sample CSALT, which demonstrates superior performance over the conventional MLE method. The simulation results reveal that under small-sample conditions, the MLE method tends to overestimate the LCLs, causing the CPs being lower than the corresponding nominal confidence levels. This outcome is consistent with observations by Wang et al. [14] and Chen et al. [15] in their ALT studies of the Weibull distribution. The primary reason for this is that MLE estimators are often unstable in small samples, and the asymptotic normality assumption substantially deviates from the actual in such scenarios.

In contrast, the proposed method exhibits great advantages. Under Type-II censoring, its CPs are consistent with the nominal levels, indicating that the obtained LCLs are exact in terms of frequentist properties. The method constructs the parameter confidence distributions from the failure data, and subsequently performs a Bayesian update using the non-failures. It directly assesses the LCLs without introducing extraneous assumptions.

Compared with the Fiducial inference method, which seeks to establish a global joint confidence distribution for the model parameters $(a,b,\sigma )$, the proposed method constructs local, decoupled confidence distributions for the distribution parameters $({\mu }_1,{\mu }_2,\sigma )$ using only failures. Furthermore, an analytical formula for calculating the LCLs is provided. This avoids the computationally intensive sampling processes commonly required in Fiducial inference, such as Monte Carlo simulation or Gibbs sampling [26], thereby enhancing both computational efficiency and precision.

Although the proposed method performs well under Type-II censoring, simulations indicate that it exhibits conservatism when applying to Type-I censored and general incomplete data. While this conservatism ensures a safe margin for engineering practice, it compromises accuracy. A preliminary investigation into mitigating this conservatism showed promising results. In the Type-I censoring case, by treating one censored observation at each accelerated stress level as a failure when constructing the confidence distributions of ${\mu }_1$ and ${\mu }_2$, a notable improvement in LCL accuracy is observed. The generalizability of this adjustment is yet to be validated. An important direction for future research, therefore, is to extend this framework to other censoring schemes and to investigate methods to improve this conservatism.

In conclusion, this study presents an effective solution to the challenge of small-sample reliability assessment in normally distributed ALT data. It not only establishes a novel computational framework for combining confidence distribution and Bayesian update but also provides a precise and efficient analytical tool for the rapid reliability evaluation of high-reliability, long-lifespan products.

6. Case Study

To illustrate the proposed method, a real CSALT of ring He-Ne laser from [27] is studied in this section. As the core component of laser gyroscopes, its reliability is critical to the performance of avionics measurement and control systems. However, the laser’s extensive operational lifetime, often exceeding tens of thousands of hours, makes conventional reliability assessment impractical. In this case, ALT is necessary to evaluate its reliability within a limited time. The primary failure mechanism is an increase in intracavity optical loss, induced by mirror contamination and particulate deposition from the inherent gas discharge [28]. Since electric current directly governs this discharge process, it was logically chosen as the accelerated stress.

As shown in

Table 4. Small-sample ALT data of the ring He-Ne laser from [27].

Current Level (mA)	Lifetime (h)
10	80, 80, 97, 115, >115
5	420, 459, 580, >580, >580

, two accelerated current levels were applied in the CSALT, and five lasers were tested under each current level. Type-II censoring scheme was adopted for the ALT, whereby the 10 mA test was terminated upon the fourth failure, and the 5 mA test upon the third. Failure is defined as the output power decreasing to 50% of its initial value or the ignition voltage increasing to 120% of the normal value. The main purpose is to evaluate the laser’s reliability at the normal operating current level of $S_0=0.6 \mathrm{mA}$.

Since electric current acts as the accelerated stress, the inverse power law model is used to describe the life–stress relationship:

$$x_{Ri}=a+b\ln S_i$$

(33)

According to Section 3.2, the log-percentile lifetime $x_{R0}$ at the normal operating current level $S_0$ can be expressed as

$$x_{R0}=\omega {\mu }_1+\left(1-\omega \right){\mu }_2-u_R\sigma$$

(34)

where $\omega =\left(\ln S_2-\ln S_0\right)/\left(\ln S_2-\ln S_1\right)=4.059$.

Then, based on Theorem 1, the 90% LCL for the percentile lifetime with 99% survival probability can be obtained as follows:

(1)

Use the failures to calculate an initial 90% LCL for $x_{R0}$ with 99% reliability:

$$x_{R\mathrm{L}0,\gamma }^{\left(0\right)}=\omega {\overline{x}}_1+\left(1-\omega \right){\overline{x}}_2-t_{\gamma }\left(\nu ,\delta \right)s/\sqrt{r_e}=10.0053$$

(35)

(2)

By incorporating the reliability information from the non-failures, update the confidence level of $x_{R\mathrm{L}0,\gamma }^{\left(0\right)}$ to

$${\gamma }^{*}=0.9098>\gamma$$

(36)

(3)

Adjust the value of $\gamma$ in Equation (35) to ${\gamma }^{**}=0.8868$ so as to achieve the nominal confidence level, and the exact 90% LCL for $x_{R0}$ can be determined by

$$x_{R\mathrm{L}0,\gamma }=\omega {\overline{x}}_1+\left(1-\omega \right){\overline{x}}_2-t_{{\gamma }^{**}}\left(\nu ,\delta \right)s/\sqrt{r_e}=10.0633$$

(37)

(4)

The exact 90% LCL for the percentile lifetime under the normal condition is

$$t_{R\mathrm{L}0,\gamma }=\exp \left(x_{R\mathrm{L}0,\gamma }\right)=\mathrm{23,465}\left(\mathrm{h}\right)$$

(38)

This LCL indicates that with 90% confidence, the lifetime at which 1% of the He-Ne lasers are expected to fail is 23,465 h.

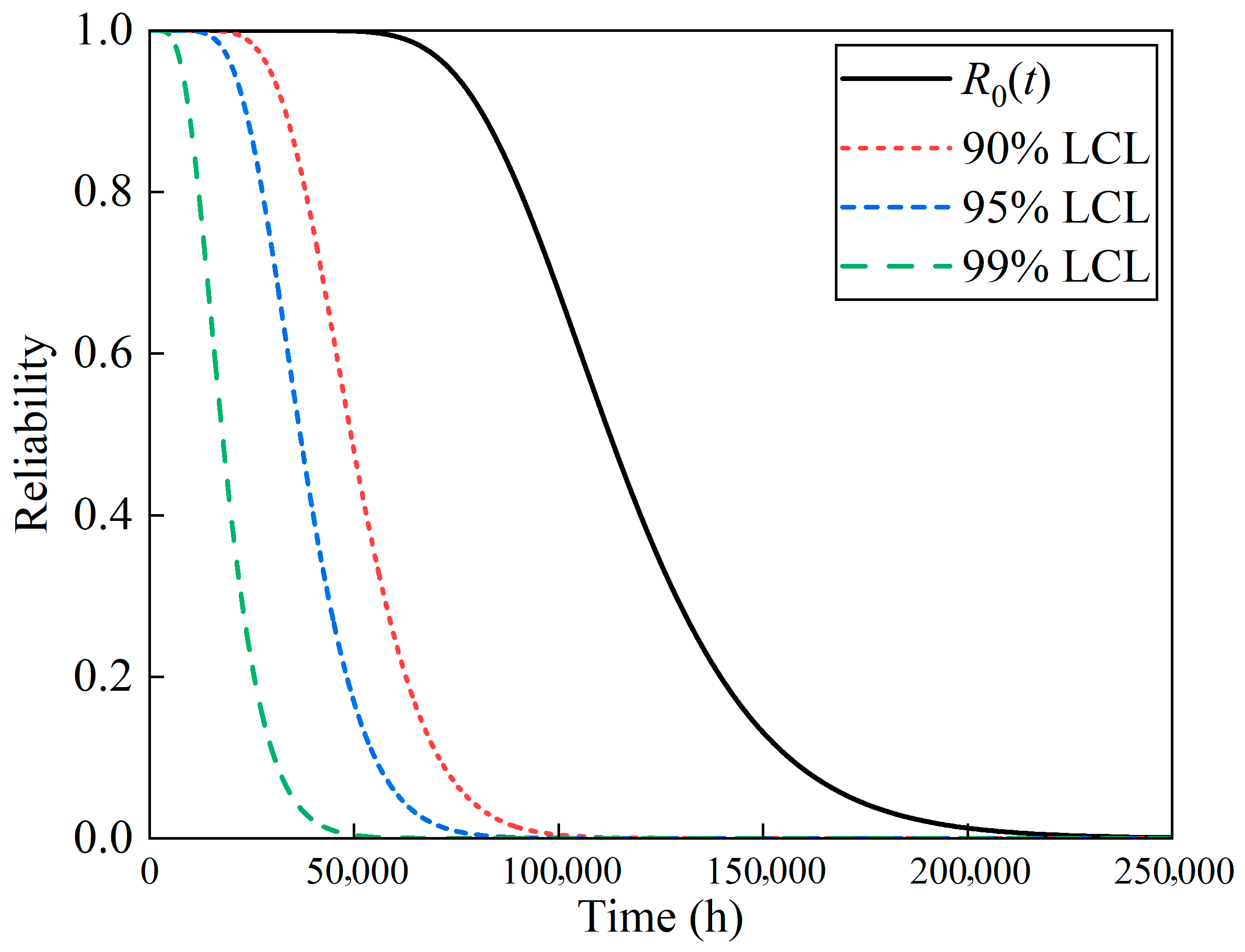
In addition, based on Corollary 1, the corresponding reliability curves are presented in Figure 2. The solid black line, representing the point estimation of reliability over time, shows that the laser maintains high reliability (above 99%) for the first 60,000 h, indicating a low initial failure rate. By quantifying the uncertainty in the sample data, the LCLs of the reliability are also plotted as dashed lines. For example, the 90% LCL (red dashed line) offers a more conservative assessment, signifying with 90% confidence that the laser’s true reliability will not fall below this curve at any time. As the required confidence level increases, the LCL curve shifts to the left, resulting in a more conservative estimate. To illustrate, ensuring a 99% reliability with 99% confidence corresponds to a lifetime of only 5468 h, whereas achieving the same reliability with 90% confidence extends the lifetime to 23,465 h.

In summary, the proposed method provides a new reliability assessment without additional assumptions and quantifies the sample uncertainty via exact LCLs. This analysis deepens the understanding of the laser’s reliability level and provides a scientific basis for developing more reasonable maintenance strategies.

7. Conclusions

This paper develops a new reliability assessment method for ALTs with normal distribution and small sample size. The proposed method enables a high-confidence estimation for percentile lifetime under the normal operating stress level using censored data from only two accelerated stress levels. This approach effectively addresses the critical challenge in current ALT practices of prohibitive costs and extended durations.

Methodologically, a mathematical relationship is first established between the log-percentile lifetime at the normal operating stress level and life distribution parameters at the accelerated stress levels. Then, by using the joint confidence distribution of the lifetime distribution parameters and Bayesian updating, an analytical formula is derived for the one-sided LCL of the percentile lifetime. The study is further extended to address scenarios involving Type-I censored and general incomplete data in ALTs.

Extensive Monte Carlo simulations demonstrate that the CPs of the proposed method closely match the nominal confidence level. In contrast, the CPs from the MLE method fall significantly below the nominal level, rendering it unreliable under small-sample conditions. These results further illustrate the advantage of the proposed method, especially when dealing with limited sample sizes.