Design and Flow Characteristics of a Gravity-Driven Flow Control Valve
Abstract
1. Introduction
2. Key Structural Design and Analytical Modeling
2.1. Composition of Gravity-Driven Flow Control Valve
2.2. Numerical Simulation Methods
3. Results and Discussion
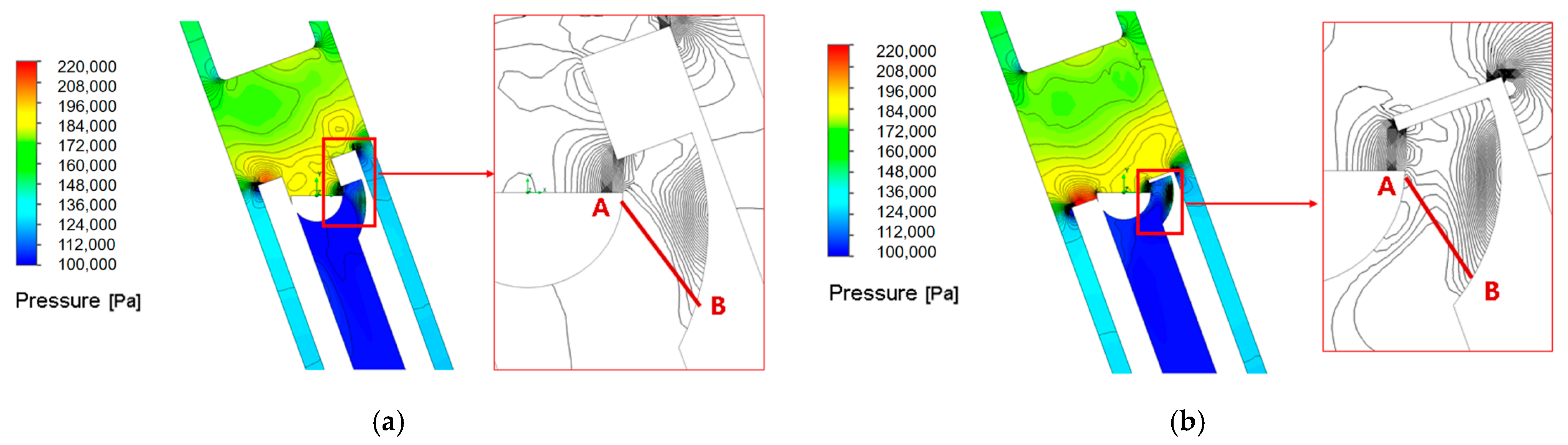
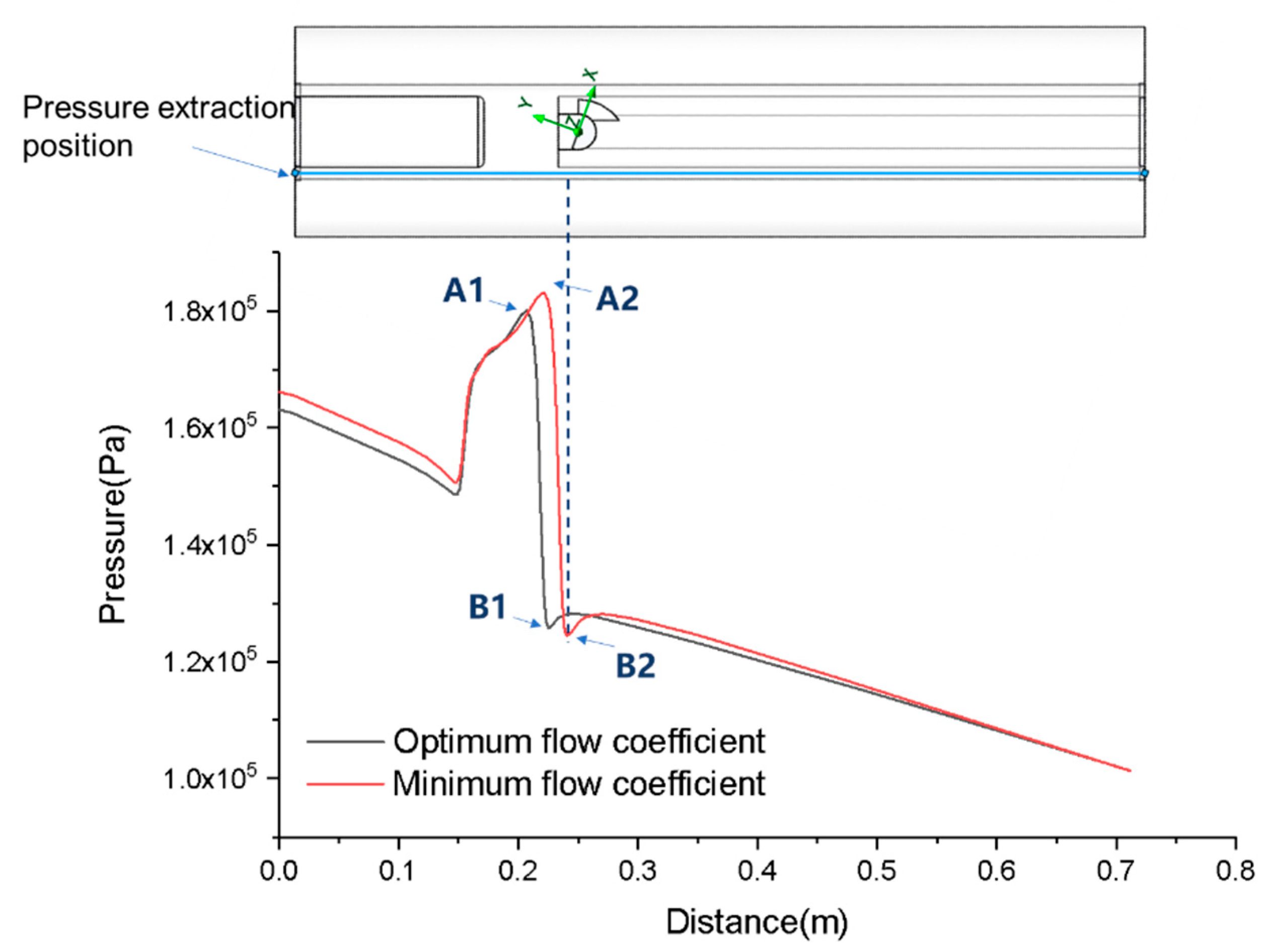
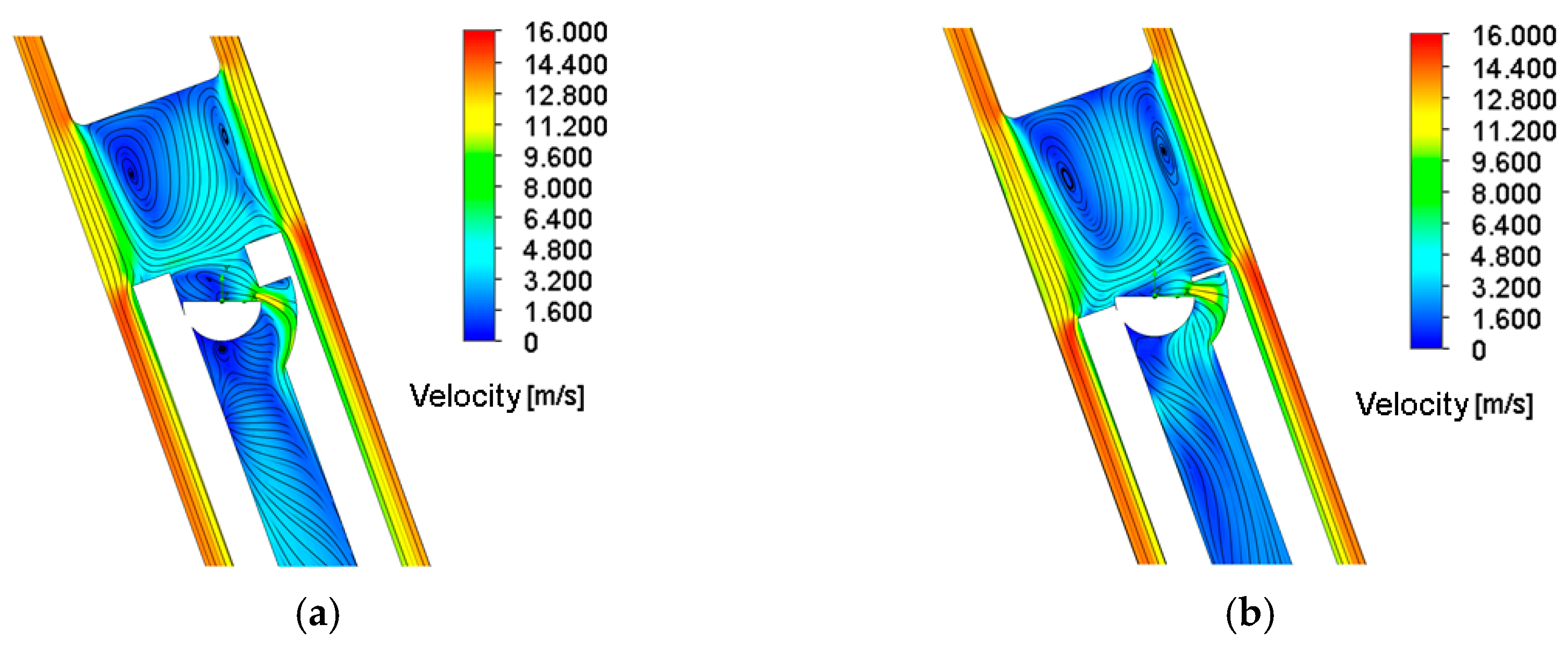
3.1. Valve Port Shunt Characterization
3.2. Valve Flow Characterization
4. Conclusions
- (1)
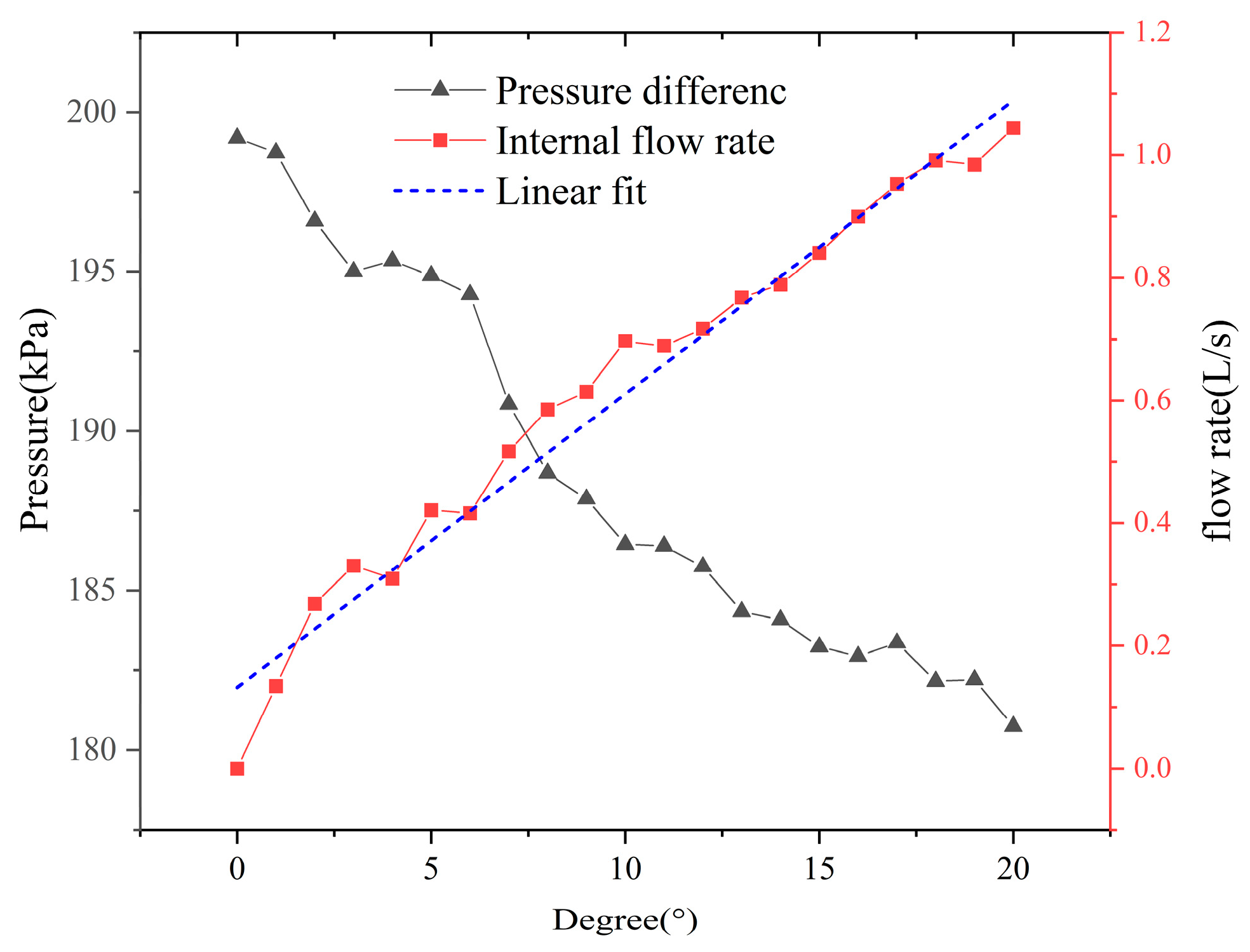
- Numerical simulation analysis reveals the significant effect of the valve body tilt angle on the flow distribution characteristics of the shunt regulator valve. As the tilt angle of the valve body increases, the valve opening gradually enlarges, and the flow rate distributed in the internal flow channel increases approximately linearly, whereas the flow rate in the external flow channel decreases correspondingly. The influence of different fluid viscosities on flow characteristics was discussed. The effect is more pronounced when the fluid viscosity is below 0.05.
- (2)
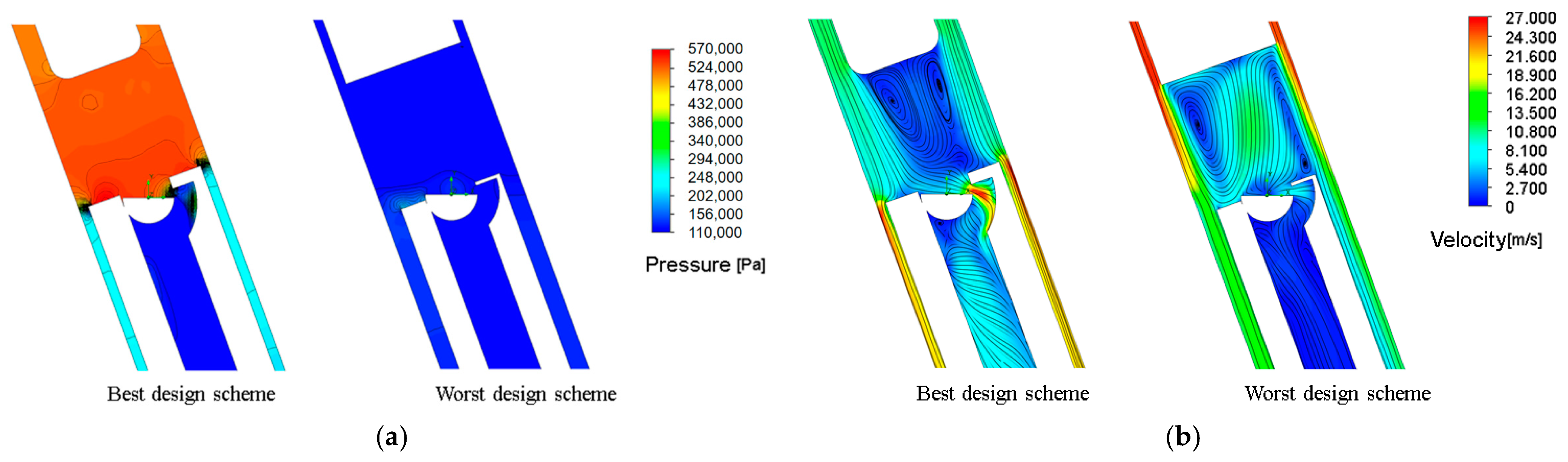
- Through an orthogonal experimental design, it was found that increasing the diameter of the throttle groove and the inlet length of the valve, as well as reducing the outer diameter of the valve body, all contribute to increasing the flow rate in the internal channel and improving the overall flow coefficient. After optimization, the optimal solution was obtained, with an internal flow rate of 2.59 L/s, which is 149% higher than the original solution. The optimal structural scheme not only significantly increases the internal flow path flow rate, but also improves the overall flow capacity by optimizing the design of the throttle groove.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Ar | Minimum flow area between valve spool and valve body |
| ζ | Resistance coefficient |
| Δpr | Pressure loss |
| xi and xj | Coordinate component |
| ui and uj | Velocity components |
| v | Kinematic viscosity |
| vt | Vortex viscosity coefficient |
| ρ | Liquid density |
| P | Pressure |
| k | Turbulent pulsation kinetic energy |
| C | Flow coefficient of a control valve |
| qV | Fluid flow through the regulating valve |
| γ | Density of the fluid medium |
| Δp | Pressure loss generated by the regulating valve |
References
- Yang, C.; Han, L.; Bu, H.; Zhao, J. New Development and Future Direction of Modern Vertical Drilling Technology. Pet. Drill. Tech. 2007, 1, 16–19. [Google Scholar]
- Zhang, D.; Wu, M.; Lu, C.; Chen, L.; Cao, W.; Wang, Y. Tube-Based Adaptive Model Predictive Control for Deviation Correction in Vertical Drilling Process. IEEE Trans. Ind. Electron. 2022, 69, 9419–9428. [Google Scholar] [CrossRef]
- Matheus, J.; Ignova, M.; Hornblower, P. A Hybrid Approach to Closed-loop Directional Drilling Control using Rotary Steerable Systems. IFAC Proc. Vol. 2012, 45, 84–89. [Google Scholar] [CrossRef]
- Chai, L.; Zhang, K.; Yang, D.; Liu, B.; Zhang, D. Integral Modeling for Deviation Correction Trajectory of the Mechanical Vertical Drilling System. Machines 2021, 9, 161. [Google Scholar] [CrossRef]
- Cai, W.; Wang, P.; Zhu, Y.; Chen, G. Design scheme and key techniques for mechanical wireless inclinometer. Acta Pet. Sin. 2006, 2, 103–106. [Google Scholar]
- Li, L.; Xue, Q.; Liu, B.; Li, X.; Wang, J. Straightening Behavior Analysis and Research Progress of Mechanical Automatic Vertical Drilling Tools. J. Xi’an Shiyou Univ. (Nat. Sci. Ed.) 2018, 33, 90–97. [Google Scholar]
- Chen, Z. Self-Adjusting Mechanical Inclinometer While Drilling. China Patent CN86207607, 5 December 1987. [Google Scholar]
- Li, L.; Xue, Q.; Liu, B.; Zhao, L.; Li, X. A static mechanical automatic vertical drilling tool with double-layer positive pushing pistons for slim well drilling. J. China Univ. Pet. (Ed. Nat. Sci.) 2017, 41, 91–98. [Google Scholar]
- Li, L.; Xue, Q.; Liu, B.; Wang, J.; Li, X. Analysis and Optimal Design of Control Performance in Automatic Mechanical Vertical Drilling Tool. Bull. Geol. Sci. Technol. 2018, 37, 268–274. [Google Scholar]
- Wang, J. Research on Work Characteristics of the Eccentric Stable Platform in Mechanical Automatic Vertical Drilling Tool. Doctoral Thesis, China University of Geosciences, Beijing, China, 2020. [Google Scholar]
- Li, P.; Wang, L.; Liu, B. Angular position measurement method for the eccentric mechanism of the automatic vertical drilling tool. Drill. Eng. 2021, 48, 9–13. [Google Scholar]
- Mu, R. Research on the Simple Design of the Control System of Push-Back Rotary Steerable Tool. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2023. [Google Scholar]
- Yin, C.; Bai, J.; Sun, C.; Li, Z.; He, J. Research and application of eccentric assembly. J. Northeast. Pet. Univ. 1999, 3, 58–60+144. [Google Scholar]
- Liu, Z. Application of concentric bias drill collar anti-skew technology in prone formation. Drill. Eng. 2007, 8, 13–14. [Google Scholar]
- Yang, X. Concentric Bias Weighted Drill Collar Deviation Control Effect in Strata Tend to Deflect. Coal Geol. China 2008, 20, 105+117. [Google Scholar]
- Feng, Q.; Dou, Z.; Zhang, Z.; Wang, Z. Study on the eccentric deflection controlling BHA and its application in Jiangsu. Oil Drill. Prod. Technol. 2002, 2, 4–7+82. [Google Scholar]
- Xia, H.; Wang, X.; Dai, J.; Ou, Y.; Tan, J. Establishment of force analysis model of bottom hole assembly for off-axis anti-deviation drill. Drill. Eng. 2004, 10, 39–42. [Google Scholar]
- Tian, H.; Chou, H.; Dong, G. Application of pre-bending pendulum drill tool anti-skew beating technology in Keping high and steep structure formation. West-China Explor. Eng. 2022, 34, 39–43. [Google Scholar]
- Zheng, J. Application of rapid drilling and anti-skew straightening technology of screw pendulum drill. Chem. Eng. Equip. 2019, 2, 58–59+49. [Google Scholar]
- Brackin, V.; Kronman, J.; Lanning, C. Activation of Downhole Mechanical Device with Inclination and/or Change in RPM. United States Patent Application US2023392471, 7 November 2023. [Google Scholar]
- Taylor, R.G., Jr. High or Low Fluid Flow Signalling Apparatus. United States Patent Application US3468035, 23 September 1969. [Google Scholar]
- Meng, Y.; Ren, Q.; Liu, F.; Gao, P.; Wu, X.; Zhao, Y.; Tang, X.; Wang, X.; Chen, J. The Utility Model Relates to a High Temperature and High Pressure Temperature and Inclinometer for Deep Well. China Patent CN110685672A, 14 January 2020. [Google Scholar]
- Liu, Y.; Cai, W.; Wang, P.; Liu, J.; Liu, T. Application of Power V and Mechanical Inclinometer in Heichi l Well. Pet. Drill. Tech. 2006, 1, 71–73. [Google Scholar]
- Liu, J.; Wang, L.; Deng, R.; Liu, M.; Li, X.; Li, P. Numerical Simulation Analysis on Internal Flow Field and Shutdown Characteristics of Anti-Recoil Valve. China Pet. Mach. 2023, 51, 85–91. [Google Scholar]
- Zhang, Z. Valve Design and Application; China Machine Press: Beijing, China, 2015; p. 251. [Google Scholar]
- Zou, Z.; Wang, F.; Wang, L. Study on unsteady flow field of butterfly valve in startup process of pressure-driven water diversion system in pumping station. J. Hydraul. Eng. 2018, 49, 678–686. [Google Scholar]
- Park, J.; Chung, M. Study on hydrodynamic torque of a butterfly valve. J. Fluids Eng.-Trans. ASME 2006, 128, 190–195. [Google Scholar] [CrossRef]
- Guan, Z.; Chen, T. Theory and Technology of Drilling Engineering; Petroleum Industry Press: Beijing, China, 2017; p. 349. [Google Scholar]
- Li, S.; Li, Z.; Zhou, A.; Wang, H. Optimization and test on throttle plate opening profile line of 3-waycontrol ball valve. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2017, 45, 61–66. [Google Scholar]
- Qian, J.; Hou, C.; Mu, J.; Gao, Z.; Jin, Z. Valve core shapes analysis on flux through control valves in nuclear power plants. Nucl. Eng. Technol. 2020, 52, 2173–2182. [Google Scholar] [CrossRef]
- Qu, J.; Ji, G.; Wang, Q.; Wang, J.; Wang, C.; Hu, Y.; Li, Y.; Xue, Q. Analysis of the dynamic characteristics of an eccentric cylinder in axial flow. Geoenergy Sci. Eng. 2024, 236, 212735. [Google Scholar] [CrossRef]
- Qu, J.; Xue, Q.; Wang, J.; Sun, J.; Li, J. Optimization of a Turbine Flow Well Logging Tool Based on the Response Surface Method. Machines 2023, 11, 455. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, Y.; Wen, C.; Tang, J. Study on the design and analysis methods of orthogonal experiment. Exp. Technol. Manag. 2010, 27, 52–55. [Google Scholar]
- Gao, Z.; Yue, Y.; Li, J.; Wu, H.; Jin, Z. Effects of the valve body and the valve seat of regulating valves on thevalve flow characteristics. Fluid Mach. 2021, 49, 43–49. [Google Scholar]
- Wang, C.; Ma, D.; He, T.; Zhou, D.; Hao, F. Analysis Based on Orthogonal Experiment of Lubrication Performance of Micro-exturing Valve Core on Coal Mine Water Hydraulic Relief Valve. Chin. Hydraul. Pneum. 2017, 9, 1–6. [Google Scholar]


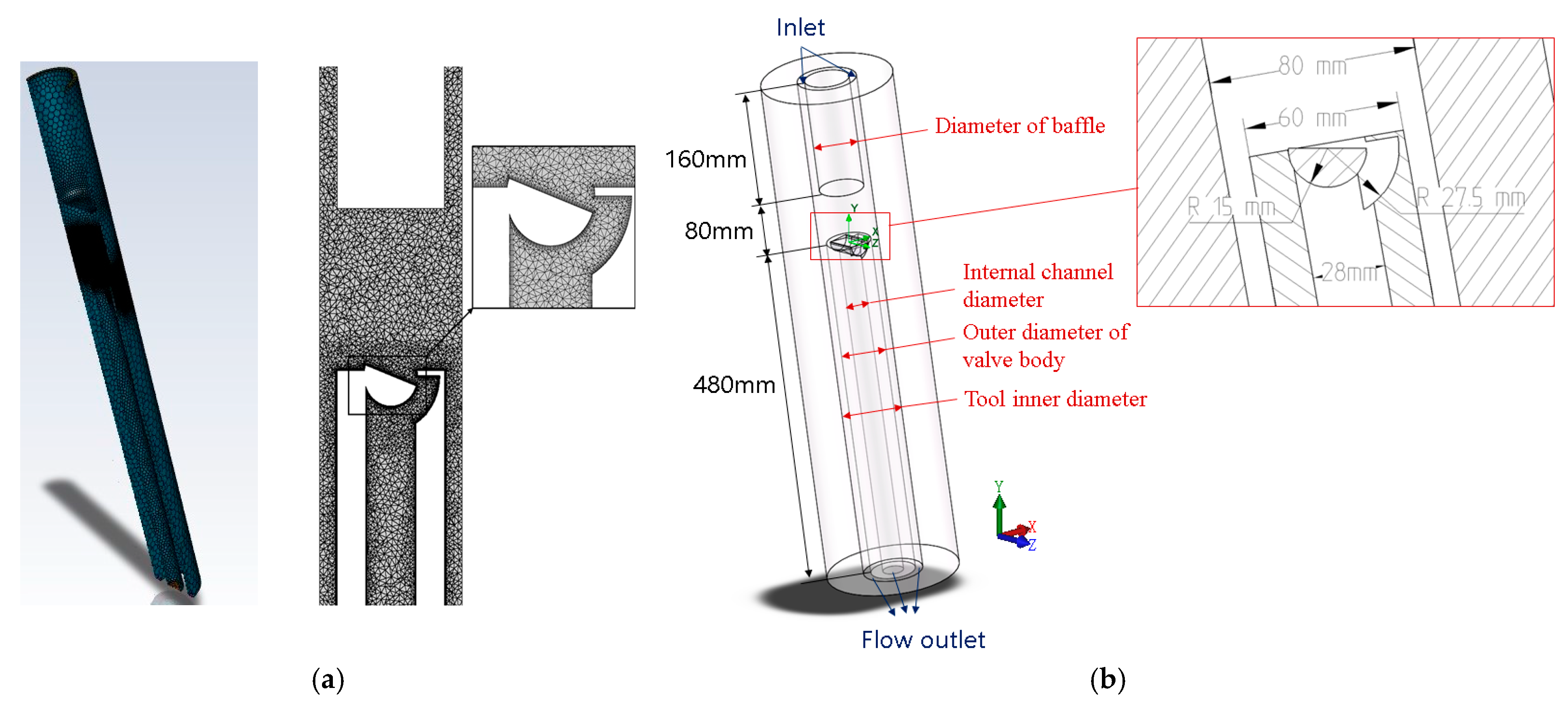
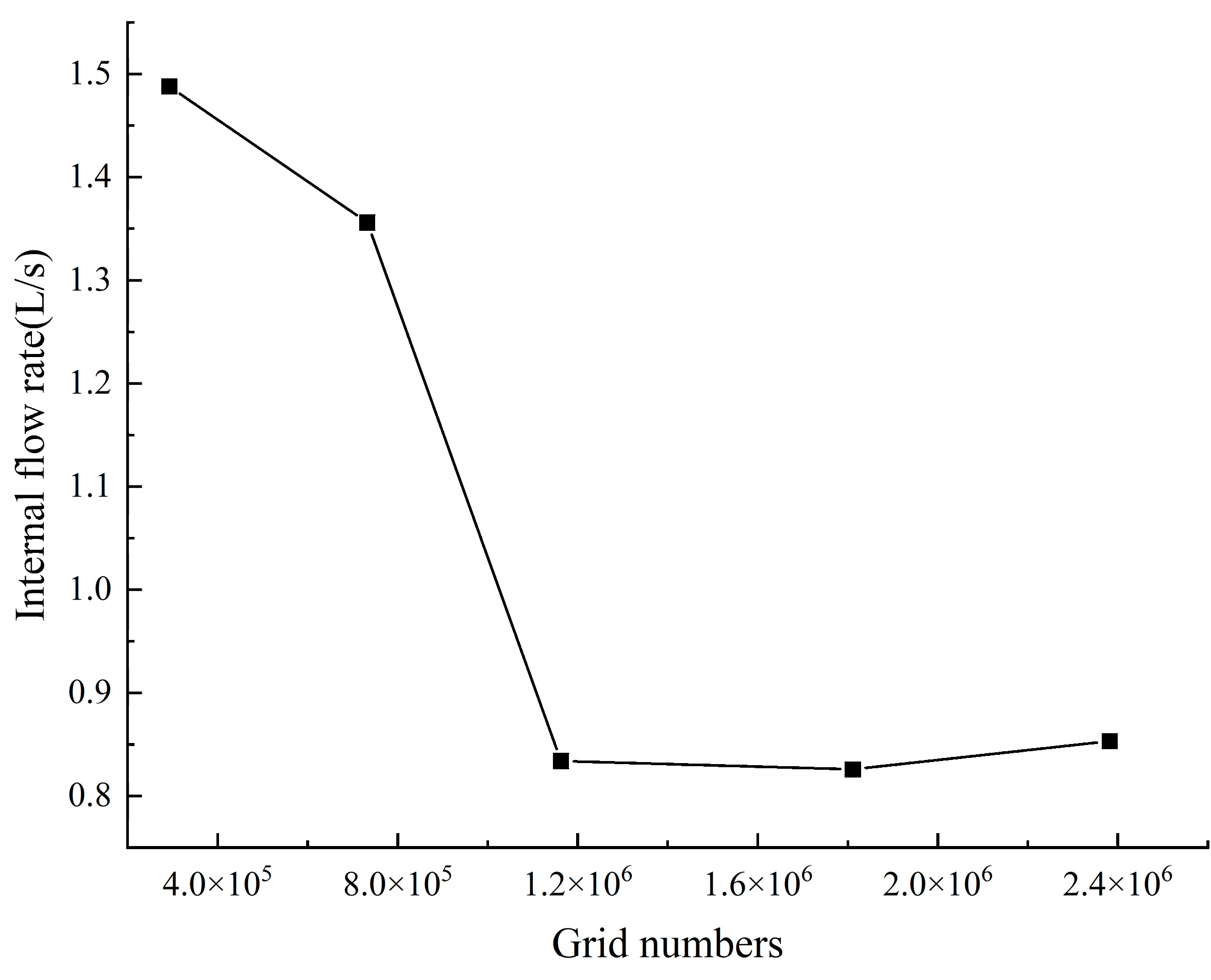

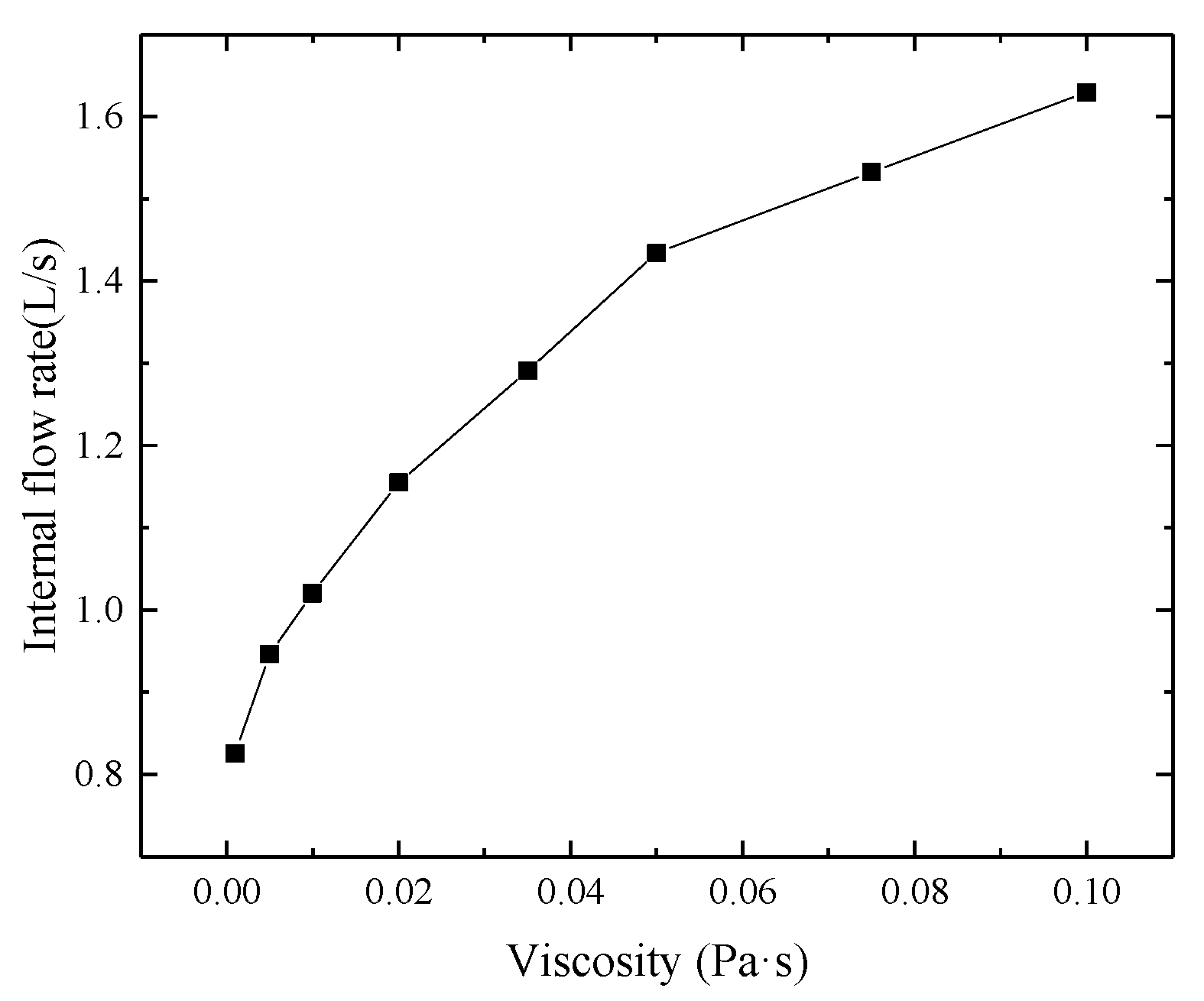



| Baffle (mm) | Internal Channel Diameter (mm) | External Diameter of Valve Body (mm) | Tool Inner Diameter (mm) | Diameter of Eccentric Block (mm) | Diameter of Throttling Groove (mm) |
|---|---|---|---|---|---|
| 60 | 28 | 60 | 80 | 30 | 55 |
| Levels | H1 (mm) | H2 (mm) | H3 (mm) | H4 (mm) | H5 (mm) |
|---|---|---|---|---|---|
| 1 | 55 | 2 | 60 | 55 | 0 |
| 2 | 65 | 7 | 63 | 60 | 5 |
| 3 | 75 | 12 | 66 | 65 | 10 |
| 4 | 85 | 17 | 69 | 70 | 15 |
| Batch Number | Factor 1 | Factor 2 | Factor 3 | Factor 4 | Factor 5 | Flow Rate of Valve (L/s) | Inlet Pressure (MPa) |
|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | H5 | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 1.05 | 0.18 |
| 2 | 1 | 2 | 2 | 2 | 2 | 1.36 | 0.21 |
| 3 | 1 | 3 | 3 | 3 | 3 | 1.69 | 0.27 |
| 4 | 1 | 4 | 4 | 4 | 4 | 2.23 | 0.36 |
| 5 | 2 | 1 | 2 | 3 | 4 | 1.23 | 0.18 |
| 6 | 2 | 2 | 1 | 4 | 3 | 1.16 | 0.50 |
| 7 | 2 | 3 | 4 | 1 | 2 | 2.46 | 0.38 |
| 8 | 2 | 4 | 3 | 2 | 1 | 1.60 | 0.32 |
| 9 | 3 | 1 | 3 | 4 | 2 | 1.64 | 0.20 |
| 10 | 3 | 2 | 4 | 3 | 1 | 2.40 | 0.48 |
| 11 | 3 | 3 | 1 | 2 | 4 | 1.23 | 0.16 |
| 12 | 3 | 4 | 2 | 1 | 3 | 1.55 | 0.23 |
| 13 | 4 | 1 | 4 | 2 | 3 | 2.47 | 0.52 |
| 14 | 4 | 2 | 3 | 1 | 4 | 1.99 | 0.33 |
| 15 | 4 | 3 | 2 | 4 | 1 | 1.07 | 0.19 |
| 16 | 4 | 4 | 1 | 3 | 2 | 1.08 | 0.13 |
| Parameters | Inlet Pressure (MPa) | Internal Flow Rate (L/s) | Hydraulic Torque of Valve Spool (N·mm) |
|---|---|---|---|
| Best design | 0.525 | 2.59 | 467.8 |
| Worst design | 0.158 | 0.37 | 1.863 |
| Parameters | Inlet Pressure (MPa) | Internal Flow Rate (L/s) | Hydraulic Torque of Valve Spool (N·mm) | Flow Coefficient |
|---|---|---|---|---|
| Best design | 0.16 | 1.16 | 83.11 | 0.4338 |
| Worst design | 0.16 | 1.01 | 64.36 | 0.4234 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Qu, J.; Liu, L.; Tan, X.; Guo, J.; Li, Y.; Zhang, J.; Liu, X.; Yu, J.; Ji, G.; et al. Design and Flow Characteristics of a Gravity-Driven Flow Control Valve. Machines 2025, 13, 654. https://doi.org/10.3390/machines13080654
Wang Q, Qu J, Liu L, Tan X, Guo J, Li Y, Zhang J, Liu X, Yu J, Ji G, et al. Design and Flow Characteristics of a Gravity-Driven Flow Control Valve. Machines. 2025; 13(8):654. https://doi.org/10.3390/machines13080654
Chicago/Turabian StyleWang, Qing, Jun Qu, Li Liu, Xingyu Tan, Jianhua Guo, Yingqi Li, Jiawei Zhang, Xiaoao Liu, Jinping Yu, Guodong Ji, and et al. 2025. "Design and Flow Characteristics of a Gravity-Driven Flow Control Valve" Machines 13, no. 8: 654. https://doi.org/10.3390/machines13080654
APA StyleWang, Q., Qu, J., Liu, L., Tan, X., Guo, J., Li, Y., Zhang, J., Liu, X., Yu, J., Ji, G., Zhou, F., & Xue, Q. (2025). Design and Flow Characteristics of a Gravity-Driven Flow Control Valve. Machines, 13(8), 654. https://doi.org/10.3390/machines13080654






