The Reliability Analysis of a Turbine Rotor Structure Based on the Kriging Surrogate Model
Abstract
1. Introduction
2. Hydraulic Turbine Rotor Structure
3. A Method for Reliability Analysis Using a Kriging Surrogate Model
4. Reliability Analysis of a Turbine Rotor Structure Using the Kriging Model
4.1. Determination of Parameters for Rotor Structural Reliability Analysis
4.2. Establishment of Kriging Model for Rotor Structural Reliability
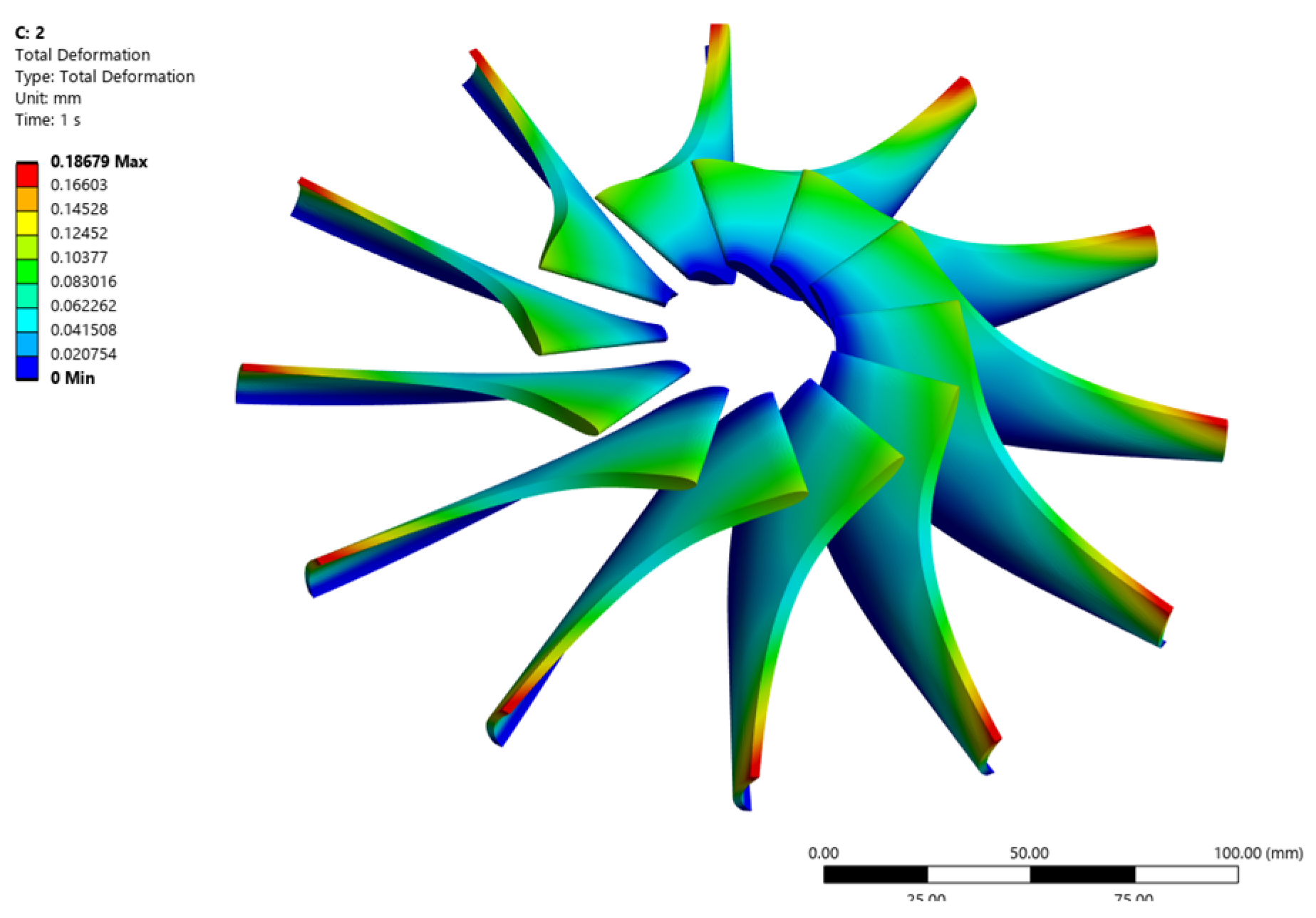
4.3. Reliability and Sensitivity Analyses of a Turbine Rotor
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, Z.; Song, S.; Li, H.; Yuan, X. Reliability and Reliability Sensitivity Analysis of Structure and Mechanisms; Science Press: Beijing, China, 2009. [Google Scholar]
- Miao, S.; Yang, H.; Wang, X.; Li, J.; Li, T. Blade pattern optimization of the hydraulic turbine based on neural network and genetic algorithm. J. Aerosp. Power 2015, 30, 1918–1925. [Google Scholar]
- Yang, S.S.; Zhang, H.; Kong, F.Y.; Xu, R.J. Analysis on Blades Curved Shape of Centrifugal Pump as Turbine. J. Shanghai Jiaotong Univ. 2016, 50, 1467–1472. [Google Scholar]
- Liu, Y.Y.; Yang, S.S.; Kong, F.Y.; Wang, T.; Chen, K. Numerical simulation of hydraulic turbines with forward-curved blades. J. Drain. Irrig. Mach. Eng. 2018, 36, 21–27. [Google Scholar]
- Jiang, B.X. Study on Blade Profile Optimization and Internal Flow Characteristics of PAT. Ph.D. Thesis, Lanzhou University of Technology, Lanzhou, China, 2022. [Google Scholar]
- Miao, S.; Luo, W.; Wang, X.; Yang, H. Impeller internal energy loss mechanism for a double-suction pump as the turbine. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2022, 38, 12–22. [Google Scholar]
- Yu, M.; Liu, Y.; Li, L.; Li, Y.; Yue, Z. Reliability-based multidisciplinary design optimization of centrifugal impeller with double-loop strategy. Acta Aeronaut. Astronaut. Sin. 2012, 33, 650–657. [Google Scholar]
- Qu, X.Z. Time—Varying reliability analysis of discrete methods for random processes of impeller vibration in train traction power. J. Vib. Shock 2024, 43, 50–59. [Google Scholar]
- Li, L.; Li, Y.; Yang, Z.L.; Yuan, T.; Yang, W.; Chen, T. Optimization of life-reliability-based multidisciplinary design of centrifugal impeller. J. Harbin Eng. Univ. 2020, 41, 530–534. [Google Scholar]
- Huang, X.; Wang, P.; Li, H.; Zhang, Z. Fatigue reliability and sensitivity analysis of turbine disk with fuzzy failure status. Xibei Gongye Daxue Xuebao/J. Northwestern Polytech. Univ. 2021, 39, 1312–1319. [Google Scholar] [CrossRef]
- Zhang, W.; Lv, Z. Co-simulation of reliability optimization design for turbine disk’s fatigue with its core optimization strategy. J. Natl. Univ. Def. Technol. 2023, 45, 117–128. [Google Scholar]
- Zheng, H.L.; Wei, R.R.; Nie, Z.H.; Yang, X.; Zhang, L.; Zhang, J. Fluid-solid Coupling Numerical Simulation and Reliability Study of Pipeline Centrifugal Compressor Impeller. Pet. New Energy 2024, 36, 57–67+74. [Google Scholar]
- Wang, Y.; Liu, S.; Liu, C.; Zhang, H. Reliability assessment of centrifugal compressor impeller based on the Monte Carlo method. Int. J. Manuf. Res. 2017, 12, 270–285. [Google Scholar] [CrossRef]
- Dileep, S.; Kumar, S.S.; Thomas, J. Reliability Study and Life Estimation of a Centrifugal Impeller, Under Multiaxial Variable Amplitude Loading. J. Fail. Anal. Prev. 2016, 16, 990–998. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Z.; Xiao, P.; Peng, R.; Liu, X. Uncertainty quantification based optimization of centrifugal compressor impeller for aerodynamic robustness under stochastic operational conditions. Energy 2020, 195, 116930. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, R. Multiobjective Optimization Design of a Pump–Turbine Impeller Based on an Inverse Design Using a Combination Optimization Strategy. J. Fluids Eng. 2014, 136, 014501. [Google Scholar] [CrossRef]
- Yao, Z.; Li, B.; Zhou, X. Simple and Quadratic of the Two Ranks Quadrature of the Structure Reliability. Northwest Hydropower 2005, 3, 20–23. [Google Scholar]
- Shayanfar, M.A.; Barkhordari, M.A.; Roudak, M.A. Locating design point in structural reliability analysis by introduction of a control parameter and moving limited regions. Int. J. Mech. Sci. 2017, 126, 196–202. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The monte carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Pan, B.; Yu, M.; Xiong, W.; Zou, X.; Zhang, L. Research on operational reliability evaluation method based on sequential Monte Carlo simulation of importance sampling. Electr. Power Sci. Eng. 2019, 35, 24. [Google Scholar]
- Melchers, R. Importance sampling in structural systems. Struct. Saf. 1989, 6, 3–10. [Google Scholar] [CrossRef]
- Au, S.-K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probab. Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]
- Koutsourelakis, P.-S.; Pradlwarter, H.; Schuëller, G. Reliability of structures in high dimensions, part I: Algorithms and applications. Probab. Eng. Mech. 2004, 19, 409–417. [Google Scholar] [CrossRef]
- Faravelli, L. Response-surface approach for reliability analysis. J. Eng. Mech. 1989, 115, 2763–2781. [Google Scholar] [CrossRef]
- Meng, G.; Li, G.; Li, F.; Zhou, L. Structural reliability analysis based on polynomial basis function neural network. J. Beijing Univ. Aeronaut. Astronaut. 2013, 39, 1460. [Google Scholar]
- Li, X.K.; Ma, J.; Chen, Z.Z.; Wen, X.Y.; Qiu, H.B. Reliability-based design optimization using inherited Latin hypercube sampling and local Kriging approximation. Comput. Integr. Manuf. Syst. 2018, 24, 3107–3119. [Google Scholar]
- Li, H.; Lü, Z.; Yue, Z. Support vector machine for structural reliability analysis. Appl. Math. Mech. 2006, 27, 1295–1303. [Google Scholar] [CrossRef]
- Hua, Q.; Li, Y. Parametric modeling method for semi-open centrifugal impellers. Neijiang Sci. Technol. 2022, 43, 64+153. [Google Scholar]
- Yang, F.; Wang, Z. Voltage Control Strategy of Microgrid with Unbalanced Load Based on Improved Passive Control. Water Resour. Power 2020, 38, 199–202+168. [Google Scholar]
- Zhang, X.; Jiang, N.Z.; Song, J.; Zhou, G. Reliability Analysis of Charging Wheel for a Micro—Gas Turbine Engine. Mach. Electron. 2014, 7, 31–34. [Google Scholar]
- Meng, D.; Liu, M.; Yang, S.; Zhang, H. A fluid–structure analysis approach and its application in the uncertainty-based multidisciplinary design and optimization for blades. Adv. Mech. Eng. 2018, 10, 168781401878341. [Google Scholar] [CrossRef]
- Helton, J.; Davis, F. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
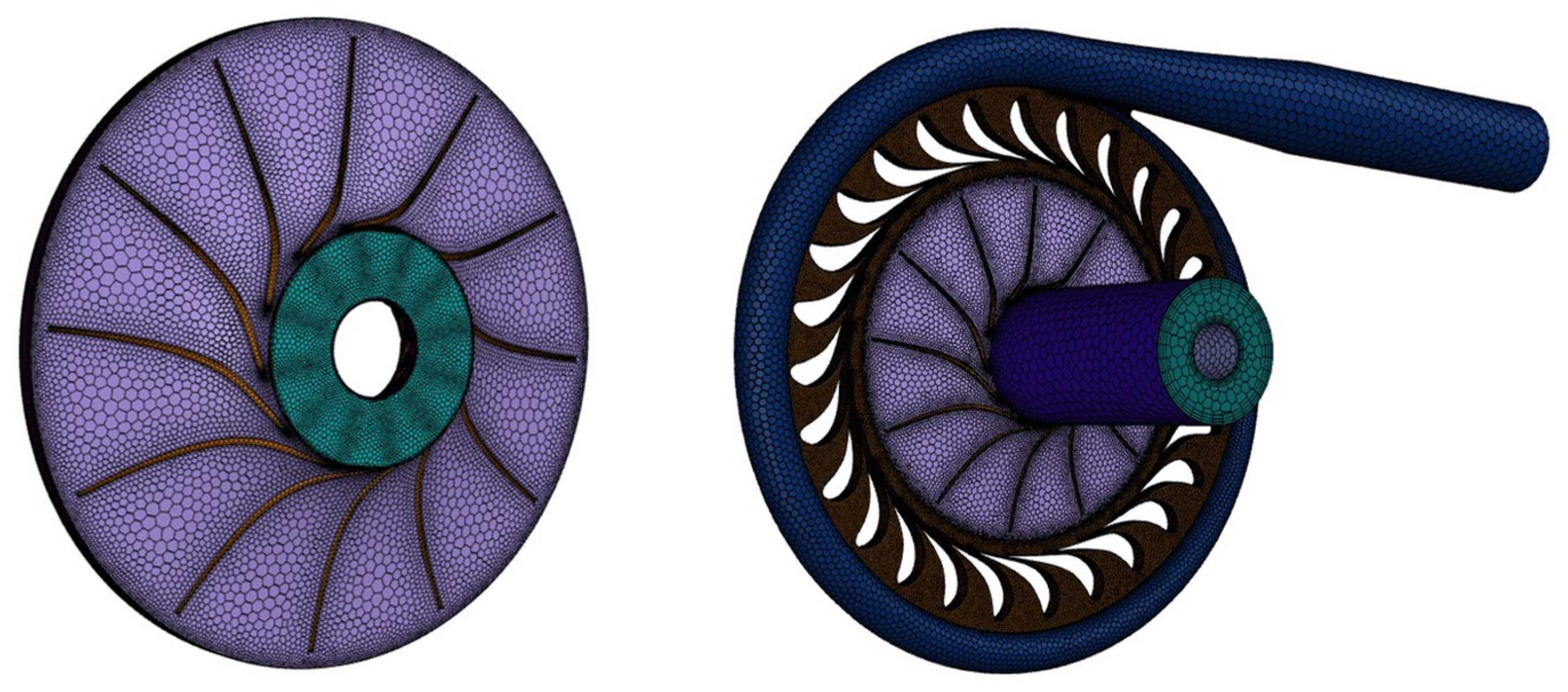




| Variable | Mean Value | Standard Deviation | Distribution |
|---|---|---|---|
| RS (rev/min) | 3000 | 200 | Normal |
| IT (°C) | −160.985 | 10.7317 | Normal |
| OP (MPa) | 0.18 | 0.01333 | Normal |
| IP (MPa) | 4.52 | 0.3 | Normal |
| EM (GPa) | 200 | 13.3333 | Normal |
| BL (mm) | 112 | 3.6667 | Normal |
| BW (mm) | 30 | 1 | Normal |
| Data Set | RS (rev/min) | OT (°C) | OP (MPa) | IT (°C) | IP (MPa) | EM (GPa) | BL (mm) | BW (mm) |
|---|---|---|---|---|---|---|---|---|
| DP 1 | 3249 | 153.87 | 0.146 | 159.87 | 5.245 | 184 | 103.4 | 32.1 |
| DP 2 | 2646 | 176.42 | 0.172 | 182.42 | 3.916 | 214 | 119.1 | 30.4 |
| DP 3 | 3527 | 161.94 | 0.213 | 167.94 | 4.009 | 193 | 101.7 | 27.5 |
| DP 4 | 2575 | 130.62 | 0.164 | 136.62 | 5.064 | 218 | 120.6 | 27.1 |
| DP 5 | 2792 | 124.42 | 0.203 | 130.42 | 4.09 | 190 | 121.3 | 31.3 |
| DP 6 | 2950 | 136.88 | 0.182 | 142.88 | 3.745 | 201 | 111.7 | 29.2 |
| DP 7 | 2912 | 159.75 | 0.193 | 165.75 | 4.615 | 196 | 105.3 | 29.8 |
| DP 8 | 3155 | 143.21 | 0.198 | 149.21 | 5.055 | 174 | 106.4 | 29.4 |
| DP 9 | 3030 | 183.24 | 0.143 | 189.24 | 4.226 | 164 | 114.1 | 27.7 |
| DP 10 | 2872 | 146.56 | 0.154 | 152.56 | 4.881 | 161 | 118.1 | 30 |
| DP 11 | 2632 | 141.18 | 0.186 | 147.18 | 4.811 | 230 | 103.1 | 32.9 |
| DP 12 | 3188 | 150.09 | 0.168 | 156.09 | 4.387 | 176 | 115.9 | 28.8 |
| DP 13 | 2724 | 173.43 | 0.216 | 179.43 | 4.549 | 221 | 122 | 32.7 |
| DP 14 | 3104 | 167.66 | 0.189 | 173.66 | 5.382 | 208 | 109.4 | 31 |
| DP 15 | 3428 | 185.63 | 0.177 | 191.63 | 3.676 | 225 | 113 | 30.8 |
| DP 16 | 2517 | 128.92 | 0.157 | 134.92 | 3.871 | 234 | 110.3 | 28 |
| DP 17 | 3573 | 155.69 | 0.148 | 161.69 | 4.306 | 170 | 106.6 | 28.3 |
| DP 18 | 2417 | 170.67 | 0.212 | 176.67 | 4.787 | 180 | 117.1 | 32.2 |
| DP 19 | 3340 | 132.71 | 0.167 | 138.71 | 5.197 | 240 | 115.3 | 28.9 |
| DP 20 | 3396 | 179.02 | 0.208 | 185.02 | 4.49 | 207 | 108.5 | 31.6 |
| Data Set | Maximum Equivalent Stress (MPa) | Maximum Total Deformation (mm) | Maximum Equivalent Elastic Strain (mm mm−1) |
|---|---|---|---|
| DP 1 | 125.3218 | 0.018499 | 0.000683 |
| DP 2 | 113.2349 | 0.014279 | 0.000531 |
| DP 3 | 99.68007 | 0.014068 | 0.000518 |
| DP 4 | 138.9216 | 0.017197 | 0.000639 |
| DP 5 | 113.1518 | 0.016074 | 0.000597 |
| DP 6 | 104.7671 | 0.014053 | 0.000523 |
| DP 7 | 120.5042 | 0.01662 | 0.000617 |
| DP 8 | 123.2774 | 0.019219 | 0.000711 |
| DP 9 | 112.2253 | 0.018512 | 0.000687 |
| DP 10 | 127.8148 | 0.021477 | 0.000796 |
| DP 11 | 131.7743 | 0.015471 | 0.000575 |
| DP 12 | 111.2072 | 0.017123 | 0.000634 |
| DP 13 | 123.1395 | 0.015038 | 0.000559 |
| DP 14 | 130.3776 | 0.016997 | 0.000629 |
| DP 15 | 96.62382 | 0.011668 | 0.000431 |
| DP 16 | 115.7093 | 0.013341 | 0.000496 |
| DP 17 | 104.6039 | 0.016792 | 0.000617 |
| DP 18 | 136.1921 | 0.020404 | 0.000759 |
| DP 19 | 122.1141 | 0.013835 | 0.00051 |
| DP 20 | 108.6447 | 0.01427 | 0.000527 |
| Method | Failure Probability | Number of Samples |
|---|---|---|
| AFOSM | 2.2807 × 10−5 | —— |
| IS | 3.5000 × 10−5 | 104 |
| SS | 3.3420 × 10−5 | 5 × 103 |
| LS | 1.6430 × 10−5 | 103 |
| MCS | 3.3500 × 10−5 | 107 |
| Method | RS | IT | OP | IP | EM | BL | BW |
|---|---|---|---|---|---|---|---|
| AFOSM | −0.1352 | −4.173 | 343.5 | 46.28 | 4.204 | −0.1345 | 59.34 |
| MCS | 0.1673 | −7.429 | 700.4 | 31.07 | 5.989 | −0.6738 | 49.85 |
| Method | RS | IT | OP | IP | EM | BL | BW |
|---|---|---|---|---|---|---|---|
| AFOSM | 0.1519 | 7.771 | 65.38 | 26.72 | 9.799 | 0.002757 | 146.4 |
| MCS | 0.2357 | 16.09 | −516.1 | 31.41 | 13.03 | −1.567 | 72.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Yang, L.; Bao, H.; Zhang, F.; Zhao, F.; Lu, C. The Reliability Analysis of a Turbine Rotor Structure Based on the Kriging Surrogate Model. Machines 2025, 13, 625. https://doi.org/10.3390/machines13070625
Lin H, Yang L, Bao H, Zhang F, Zhao F, Lu C. The Reliability Analysis of a Turbine Rotor Structure Based on the Kriging Surrogate Model. Machines. 2025; 13(7):625. https://doi.org/10.3390/machines13070625
Chicago/Turabian StyleLin, Haiwei, Liang Yang, Hong Bao, Feng Zhang, Feifei Zhao, and Chaoxin Lu. 2025. "The Reliability Analysis of a Turbine Rotor Structure Based on the Kriging Surrogate Model" Machines 13, no. 7: 625. https://doi.org/10.3390/machines13070625
APA StyleLin, H., Yang, L., Bao, H., Zhang, F., Zhao, F., & Lu, C. (2025). The Reliability Analysis of a Turbine Rotor Structure Based on the Kriging Surrogate Model. Machines, 13(7), 625. https://doi.org/10.3390/machines13070625







