Numerical Study of the Effect of Unsteady Aerodynamic Forces on the Fatigue Load of Yawed Wind Turbines
Abstract
1. Introduction
2. Methodology
2.1. NREL 5 MW Wind Turbine Model
2.2. Wind Field Modeling
2.3. Aerodynamic Force Modeling
2.3.1. Blade Element Momentum (BEM) Theory
2.3.2. Dynamic Blade Element Momentum (DBEM) Theory
2.3.3. Converging Lagrange Filaments (OLAF) Vortex Methods
2.4. Fatigue Load Calculation
3. Numerical Validation
4. Results and Discussion
4.1. Fatigue Loading Comparison
4.2. Power Spectral Analysis of Loading
4.2.1. Blade Root
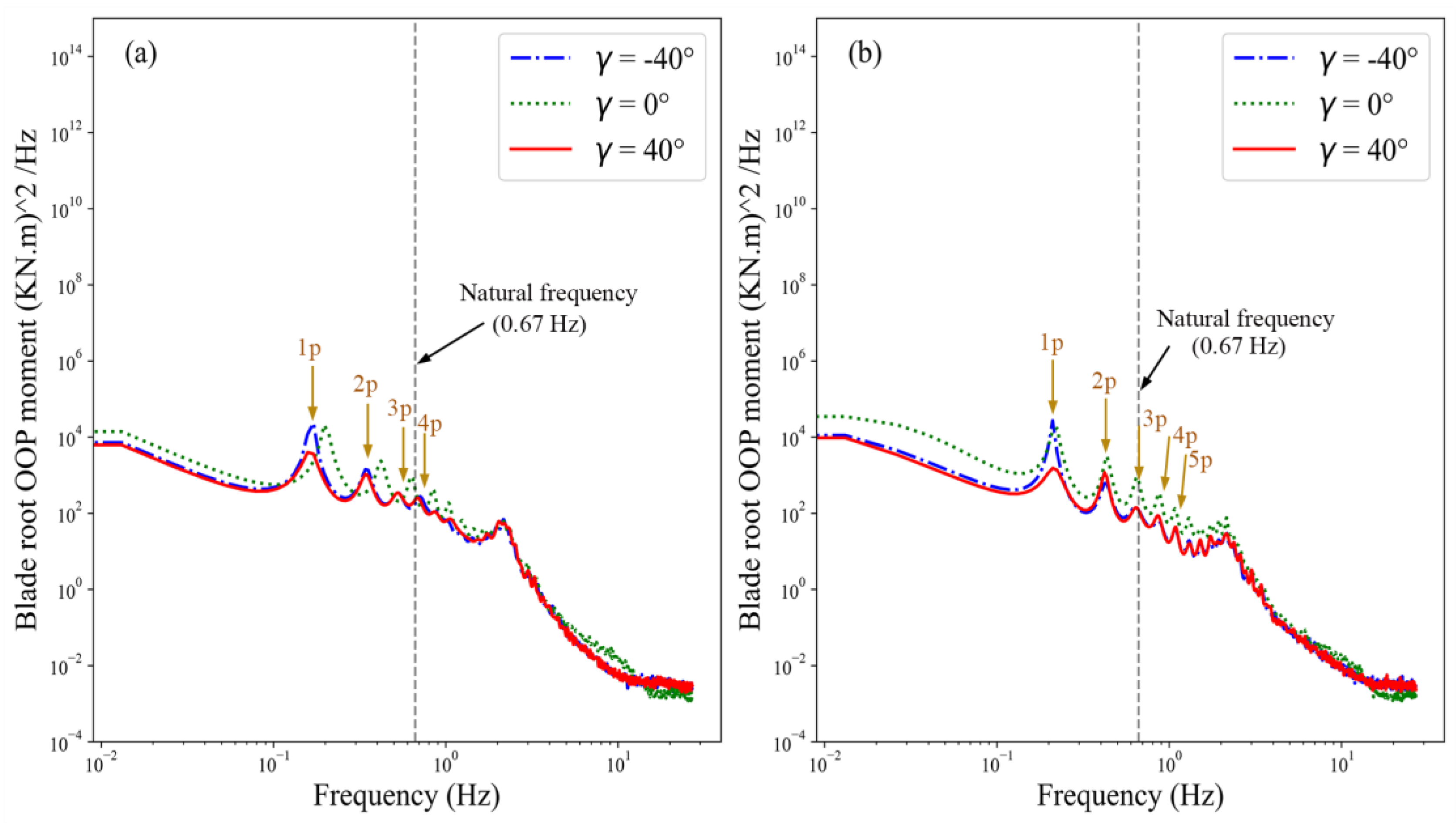
4.2.2. Low-Speed Shaft
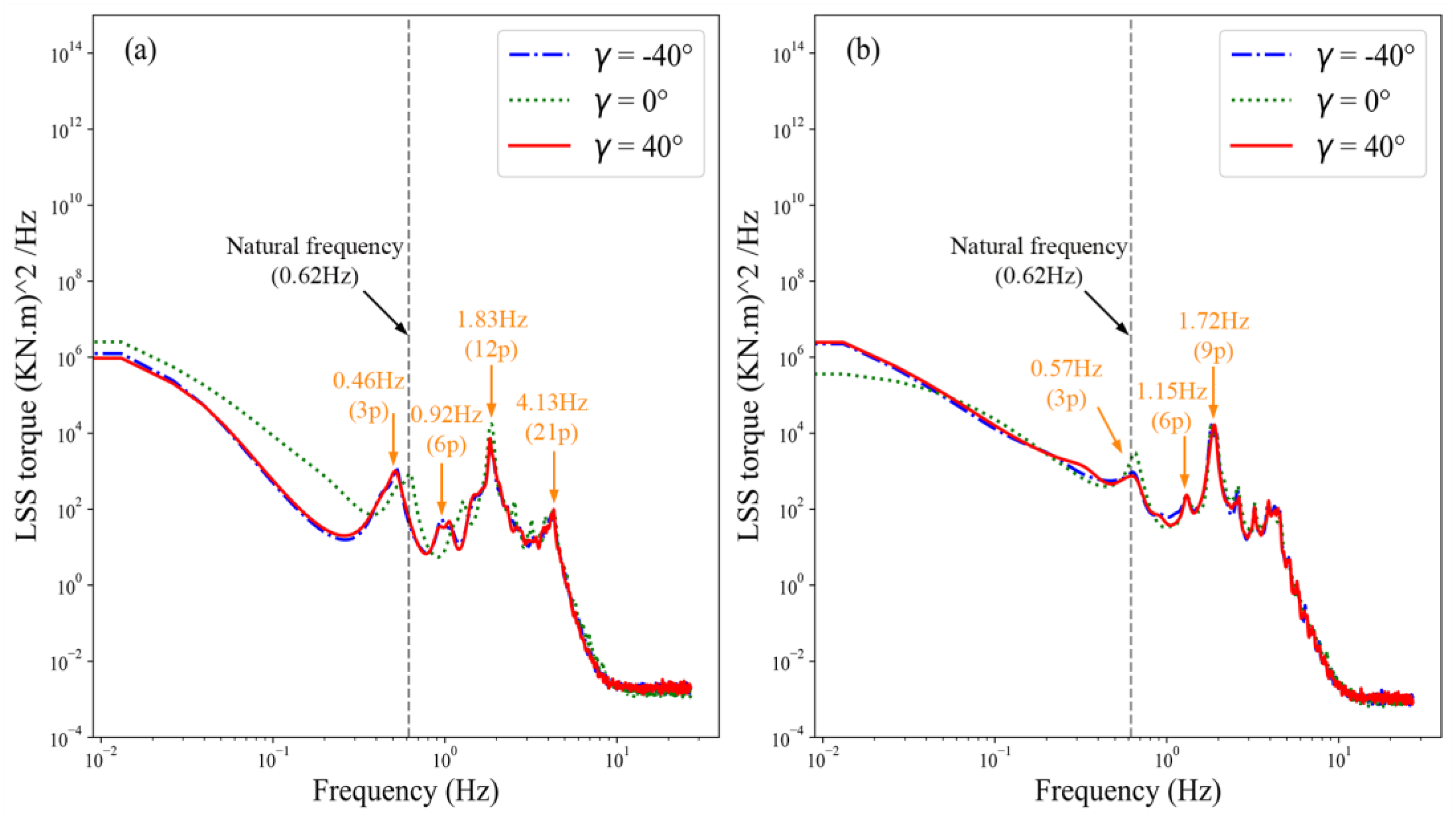
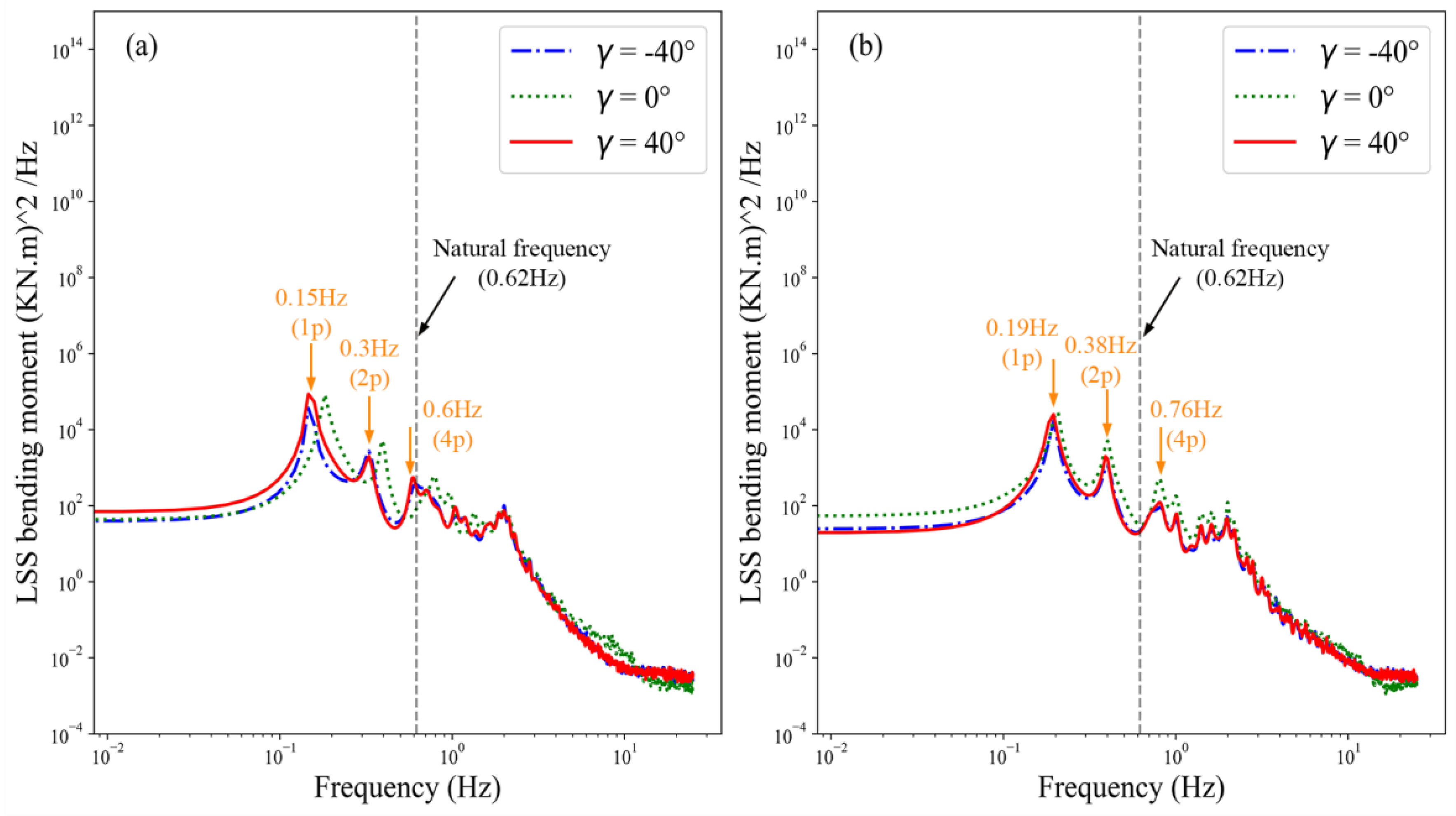
4.2.3. Tower Base

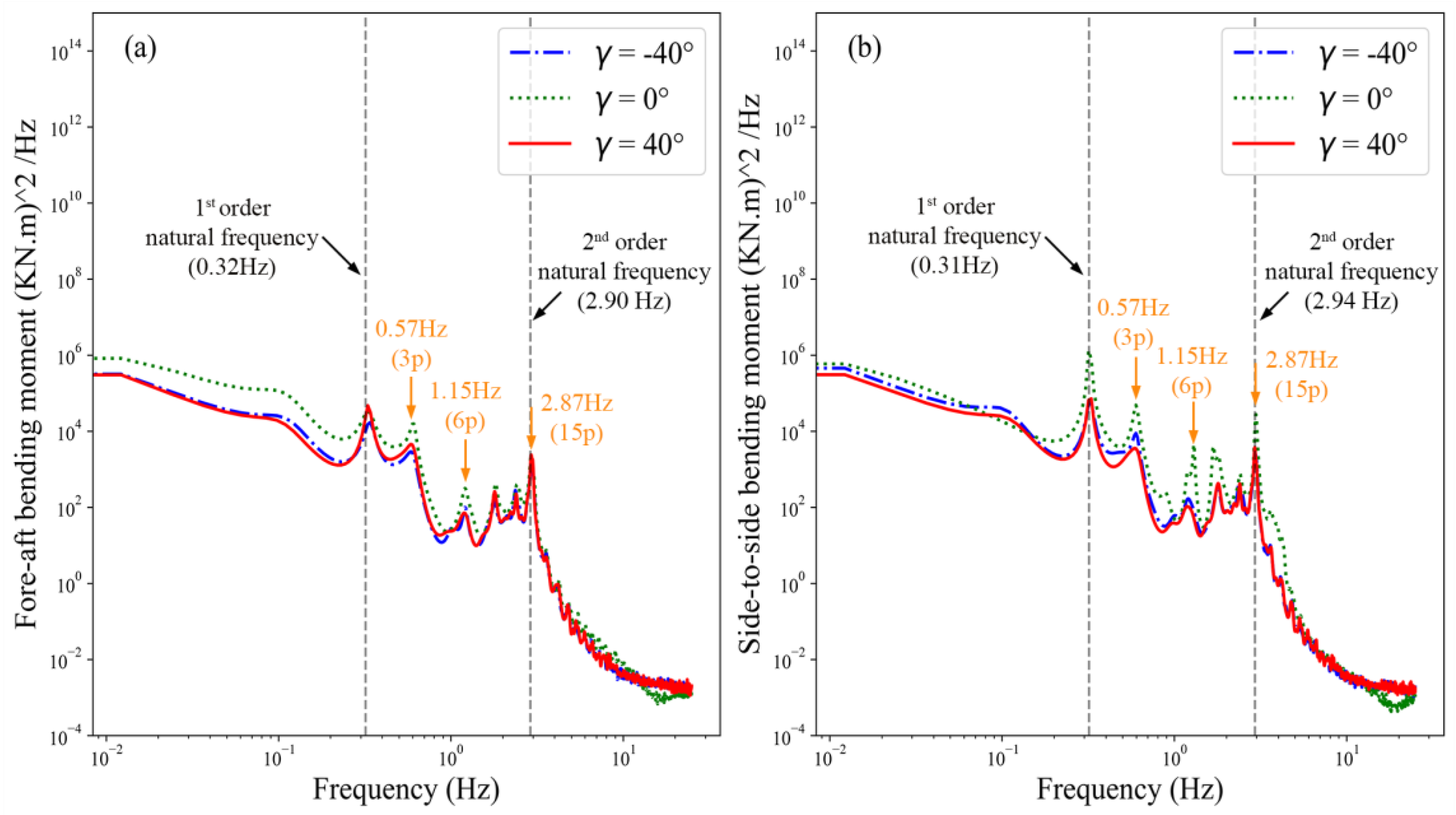
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| α | Shear exponent |
| BEM | Blade element momentum theory |
| BV | Bound vorticity |
| D | Drag force |
| DBEM | Dynamic blade element momentum theory |
| DEL | Damage equivalent load |
| DLC | Design load case |
| Normal force | |
| Tangential force | |
| Γ | Vorticity |
| L | Lift force |
| LE | Leading edge |
| LL | Lifting line |
| LSS | Low-speed shaft |
| LSSBM | Low-speed shaft bending moment |
| MEXICO | Model experiments in controlled conditions |
| NREL | National Renewable Energy Laboratory |
| OLAF | Converging Lagrange filaments |
| OOP | Out of plane |
| Azimuth angle | |
| Torque | |
| TBBM | Tower base bending moment |
| TE | Trailing edge |
| TI | Turbulence intensity |
| Wind speed at arbitrary height | |
| Hub-height wind speed | |
| z | Vertical height |
| Hub height |
References
- Bromm, M.; Rott, A.; Beck, H.; Vollmer, L.; Steinfeld, G.; Kühn, M. Field investigation on the influence of yaw misalignment on the propagation of wind turbine wakes. Wind Energy 2018, 21, 1011–1028. [Google Scholar] [CrossRef]
- Fleming, P.A.; Ning, A.; Gebraad, P.M.; Dykes, K. Wind plant system engineering through optimization of layout and yaw control. Wind Energy 2013, 19, 329–344. [Google Scholar] [CrossRef]
- Zalkind, D.S.; Pao, L.Y. The fatigue loading effects of yaw control for wind plants. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 537–542. [Google Scholar] [CrossRef]
- Han, W.; Kim, H.; Son, E.; Lee, S. Assessment of yaw-control effects on wind turbine-wake interaction: A coupled unsteady vortex lattice method and curled wake model analysis. J. Wind Eng. Ind. Aerodyn. 2023, 242, 105559. [Google Scholar] [CrossRef]
- Ke, S.; Wang, T.; Ge, Y.; Wang, H. Wind-induced fatigue of large HAWT coupled tower–blade structures considering aeroelastic and yaw effects. Struct. Des. Tall Spec. Build. 2018, 27, e1467. [Google Scholar] [CrossRef]
- Fleming, P.; Gebraad, P.M.; Lee, S.; van Wingerden, J.W.; Johnson, K.; Churchfield, M.; Michalakes, J.; Spalart, P.; Moriarty, P. Simulation comparison of wake mitigation control strategies for a two-turbine case. Wind Energy 2015, 18, 2135–2143. [Google Scholar] [CrossRef]
- Kragh, K.A.; Hansen, M.H. Load alleviation of wind turbines by yaw misalignment. Wind Energy 2013, 17, 971–982. [Google Scholar] [CrossRef]
- Gebraad, P.M.; Teeuwisse, F.W.; Van Wingerden, J.W.; Fleming, P.A.; Ruben, S.D.; Marden, J.R.; Pao, L.Y. Wind plant power optimization through yaw controlusing a parametric model for wake effects—A CFD simulation study. Wind Energy 2013, 19, 95–114. [Google Scholar] [CrossRef]
- Branlard, E.; Jonkman, B.; Pirrung, G.R.; Dixon, K.; Jonkman, J. Dynamic inflow and unsteady aerodynamics models for modal and stability analyses in OpenFAST. J. Phys. Conf. Ser. 2022, 2265, 032044. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Z.; Yu, H.; Gao, S.; Wang, B.; Ying, Y.; Sun, Y.; Qian, P.; Zhang, D.; Si, Y. Quantitative evaluation of yaw-misalignment and aerodynamic wake induced fatigue loads of offshore Wind turbines. Renew. Energy 2022, 199, 71–86. [Google Scholar] [CrossRef]
- Zhao, Q.; Sheng, C.; Afjeh, A. Computational Aerodynamic Analysis of Offshore Upwind and Downwind Turbines. J. Aerodyn. 2014, 2014, 860637. [Google Scholar] [CrossRef]
- Lu, F.; Long, K.; Geng, R.; Chen, Y.; Saeed, A.; Zhang, J.; Tao, T. A quantitative approach for evaluating fatigue damage under wake effects and yaw control for offshore wind turbines. Sustain. Energy Technol. Assess. 2024, 66, 103824. [Google Scholar] [CrossRef]
- Zhang, J.; Zuo, H.; Zhu, S.; Yang, J.; Lu, L. Fatigue degradation of wind turbines considering dynamic wake meandering effects. Eng. Struct. 2024, 300, 117132. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. The performance curves. In Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2011; Available online: https://library.uniteddiversity.coop/Energy/Wind/Wind_Energy_Handbook.pdf (accessed on 14 June 2025).
- Mahmuddin, F. Rotor Blade Performance Analysis with Blade Element Momentum Theory. Energy Procedia 2017, 105, 1123–1129. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009; pp. 1–75. [Google Scholar]
- Liu, X.; Lu, C.; Liang, S.; Godbole, A.; Chen, Y. Vibration-induced aerodynamic loads on large horizontal axis wind turbine blades. Appl. Energy 2017, 185, 1109–1119. [Google Scholar] [CrossRef]
- Liu, X.; Lu, C.; Liang, S.; Godbole, A.; Chen, Y. Improved dynamic stall prediction of wind turbine airfoils. Energy Procedia 2019, 158, 1021–1026. [Google Scholar] [CrossRef]
- Moriarty, P.J.; Hansen, A.C. AeroDyn Theory Manual. Annu. Rev. Fluid Mech. 1983, 15, 223–239. Available online: https://docs.nrel.gov/docs/fy05osti/36881.pdf (accessed on 14 June 2025).
- Hansen, M.H.; Gaunaa, M.; Aagaard Madsen, H. A Beddoes-Leishman Type Dynamic Stall Model in State-Space and Indicial Formulations. Denmark. Forskningscenter Risoe. Risoe-R No. 1354(EN). 2004. Available online: https://backend.orbit.dtu.dk/ws/portalfiles/portal/7711084/ris_r_1354.pdf (accessed on 14 June 2025).
- Bangga, G.; Lutz, T.; Arnold, M. An improved second-order dynamic stall model for wind turbine airfoils. Wind Energy Sci. 2020, 5, 1037–1058. [Google Scholar] [CrossRef]
- Qian, G.W.; Ishihara, T. A new analytical wake model for yawed wind turbines. Energies 2018, 11, 665. [Google Scholar] [CrossRef]
- He, R.; Yang, H.; Sun, S.; Lu, L.; Sun, H.; Gao, X. A machine learning-based fatigue loads and power prediction method for wind turbines under yaw control. Appl. Energy 2022, 326, 120013. [Google Scholar] [CrossRef]
- Zhou, L.; Shen, X.; Ma, L.; Chen, J.; Ouyang, H.; Du, Z. Unsteady aerodynamics of the floating offshore wind turbine due to the trailing vortex induction and airfoil dynamic stall. Energy 2024, 304, 19–22. [Google Scholar] [CrossRef]
- Shaler, K.; Branlard, E.; Platt, A. OLAF User’s Guide and Theory Manual; National Renewable Energy Laboratory: Golden, CO, USA, 2020; pp. 1–26. [Google Scholar]
- Jason. Jonkman TurbSim User’s Guide v2. October 2014; pp. 1–28. Available online: https://www.nrel.gov/wind/nwtc/turbsim (accessed on 14 June 2025).
- Commision, I.E. Consolidated Version Version; 2014. Available online: https://webstore.iec.ch/en/publication/3587 (accessed on 13 July 2025).
- Resor, B.R. Definition of a 5 MW/61.5 m Wind Turbine Blade Reference Model; SAND2013-2569; Sandia Report; Sandia National Laboratories: Albuquerque, NM, USA, 2013; Volume 2013, p. 50. [Google Scholar]
- Branlard, E. Wind Turbine Aerodynamics and Vorticity-Based Methods; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’ s Guide; National Renewable Energy Laboratory: Golden, CO, USA, 2005. [Google Scholar]
- TS EN 61400-1; Rüzgar Türbinleri-Bölüm 1: Tasarım Kuralları. No. 112. TSE: Ankara, Turkey, 2006.
- Hayman, G.J. MExtemes Manual Version 1. 00; National Renewable Energy Laboratory: Golden, CO, USA, 2015; p. 7. [Google Scholar]
- Hayman, G.J. MLife Theory Manual; National Renewable Energy Laboratory: Golden, CO, USA, 2012; p. 12. [Google Scholar]
- Schepers, J.G.; Snel, H. Model Experiments in Controlled Conditions—Final Report; ECN Rep. ECN-E-07-042; Energy Research Centre of the Netherlands (ECN): Petten, The Netherlands, 2008; p. 54. [Google Scholar]
- Yang, H.; Shen, W.; Xu, H.; Hong, Z.; Liu, C. Prediction of the wind turbine performance by using BEM with airfoil data extracted from CFD. Renew. Energy 2014, 70, 107–115. [Google Scholar] [CrossRef]
- Boorsma, K. Analysis of Field Measurements and Aerodynamic Predictions. 2012. [Google Scholar]
- Ciri, U.; Rotea, M.A.; Leonardi, S. Effect of the turbine scale on yaw control. Wind Energy 2018, 21, 1395–1405. [Google Scholar] [CrossRef]
- Churchfield, M.J.; Lee, S.; Michalakes, J.; Moriarty, P.J. A numerical study of the effects of atmospheric and wake turbulence on wind turbine dynamics. J. Turbul. 2012, 13, N14. [Google Scholar] [CrossRef]
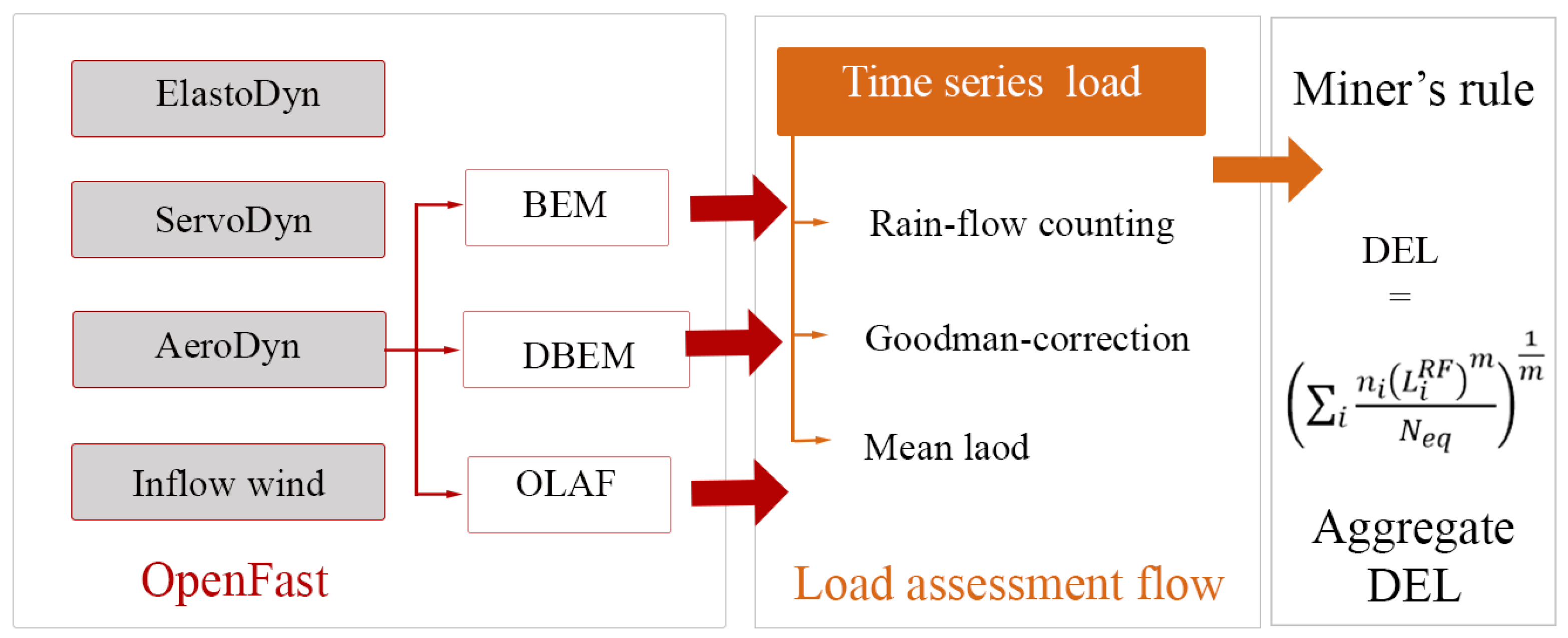
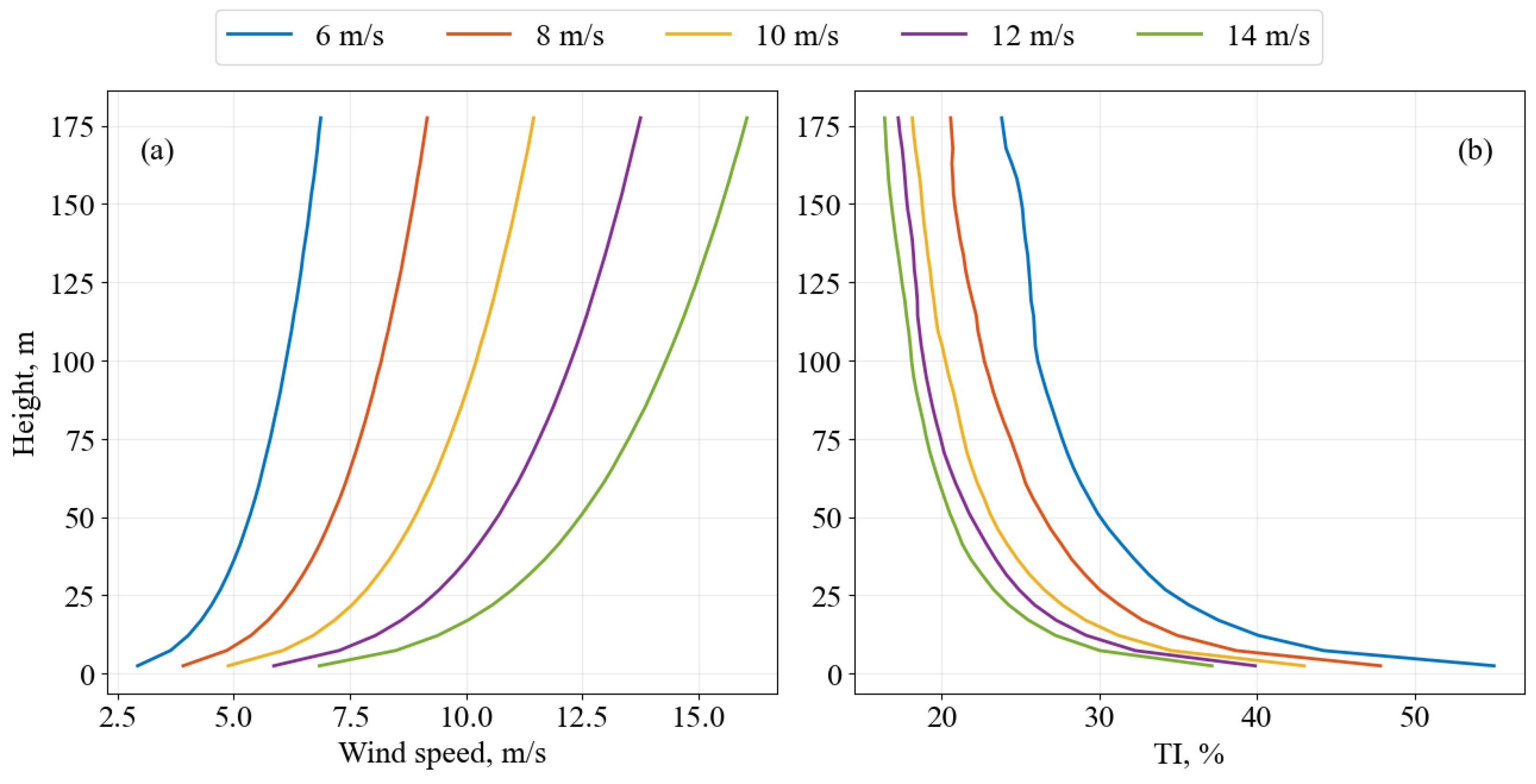
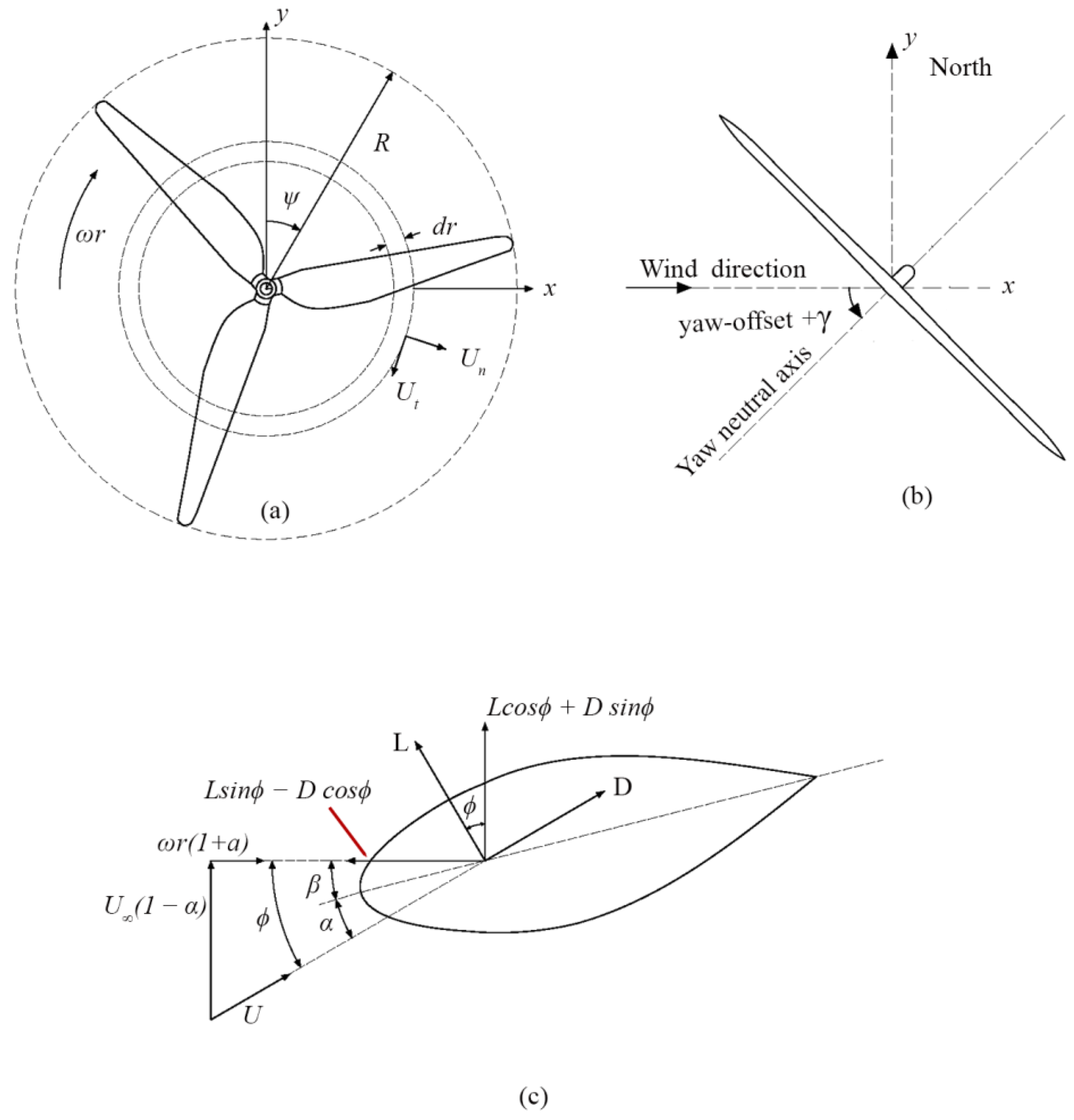


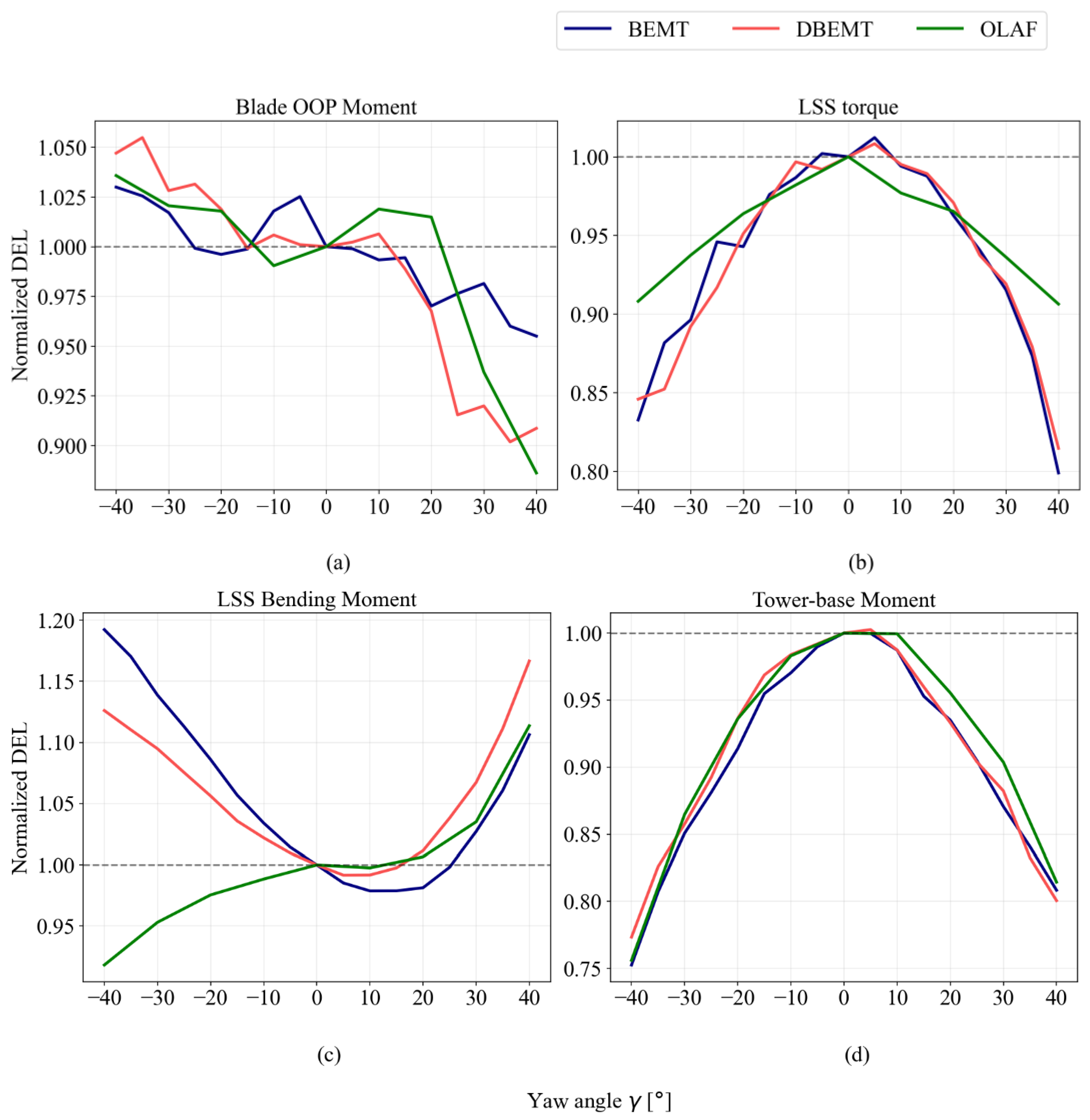
| Components | Material | Outer Diameter (m) | Wall Thickness (m) | Section Area (m2) | Moment of Inertia (m4) | Young’s Modulus −x (Gpa) | Young’s Modulus −y (GPa) | Shear Modulus (GPa) | Ultimate Strength (GPa) |
|---|---|---|---|---|---|---|---|---|---|
| Tower base [16] | Steel S355 | 6.000 | 0.035 | 0.658 | 2.925 | 210 | 210 | 80.8 | 0.56 |
| Blade root [28] | Gelcoat | 3.542 | 0.055 | 0.598 | 0.909 | 3.44 | - | 1.38 | - |
| Triax | 27.7 | 13.65 | 7.20 | 0.70 |
| Name | Value |
|---|---|
| Turbulence model | IECKAI |
| Wind speed | 6 m/s, 8 m/s, 10 m/s 12 m/s, and 14 m/s |
| Turbulence intensity | Category A |
| Wind profile type | Power law |
| Turbulence model | Normal turbulence model |
| Shear exponent | 0.2 |
| Yaw angle |
| Name | Explanation |
|---|---|
| OOP blade moment | Out-of-plane blade moment |
| LSS torque | Low-speed shaft torque |
| LSS bending Moment | Low-speed shaft bending moment |
| Resultant tower moment | The resultant (RTM) of fore–aft and side-to-side tower base bending moment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hirgeto, D.H.; Qian, G.-W.; Zhou, X.-Y.; Wang, W. Numerical Study of the Effect of Unsteady Aerodynamic Forces on the Fatigue Load of Yawed Wind Turbines. Machines 2025, 13, 607. https://doi.org/10.3390/machines13070607
Hirgeto DH, Qian G-W, Zhou X-Y, Wang W. Numerical Study of the Effect of Unsteady Aerodynamic Forces on the Fatigue Load of Yawed Wind Turbines. Machines. 2025; 13(7):607. https://doi.org/10.3390/machines13070607
Chicago/Turabian StyleHirgeto, Dereje Haile, Guo-Wei Qian, Xuan-Yi Zhou, and Wei Wang. 2025. "Numerical Study of the Effect of Unsteady Aerodynamic Forces on the Fatigue Load of Yawed Wind Turbines" Machines 13, no. 7: 607. https://doi.org/10.3390/machines13070607
APA StyleHirgeto, D. H., Qian, G.-W., Zhou, X.-Y., & Wang, W. (2025). Numerical Study of the Effect of Unsteady Aerodynamic Forces on the Fatigue Load of Yawed Wind Turbines. Machines, 13(7), 607. https://doi.org/10.3390/machines13070607








