Research on Path Tracking Technology for Tracked Unmanned Vehicles Based on DDPG-PP
Abstract
1. Introduction
- A DDPG-based upper controller is proposed to dynamically adjust and optimize the look-ahead distance, with the optimization objective of minimizing the path tracking error, which deals with the path tracking problem caused by unreasonable look-ahead distance in the PP algorithm of tracked vehicles.
- A random path generation mechanism is adopted, and the model is trained in a path environment containing various types of random curvature features, which prompts the model to deeply learn the look-ahead distance-adjustment strategies under different complex paths and improves the controller’s generalization ability and adaptability.
- A PP-based lower controller is proposed to accurately calculate the driving moments of the left and right tracks of a tracked vehicle to achieve the stable tracking of a tracked unmanned vehicle against a planned path.
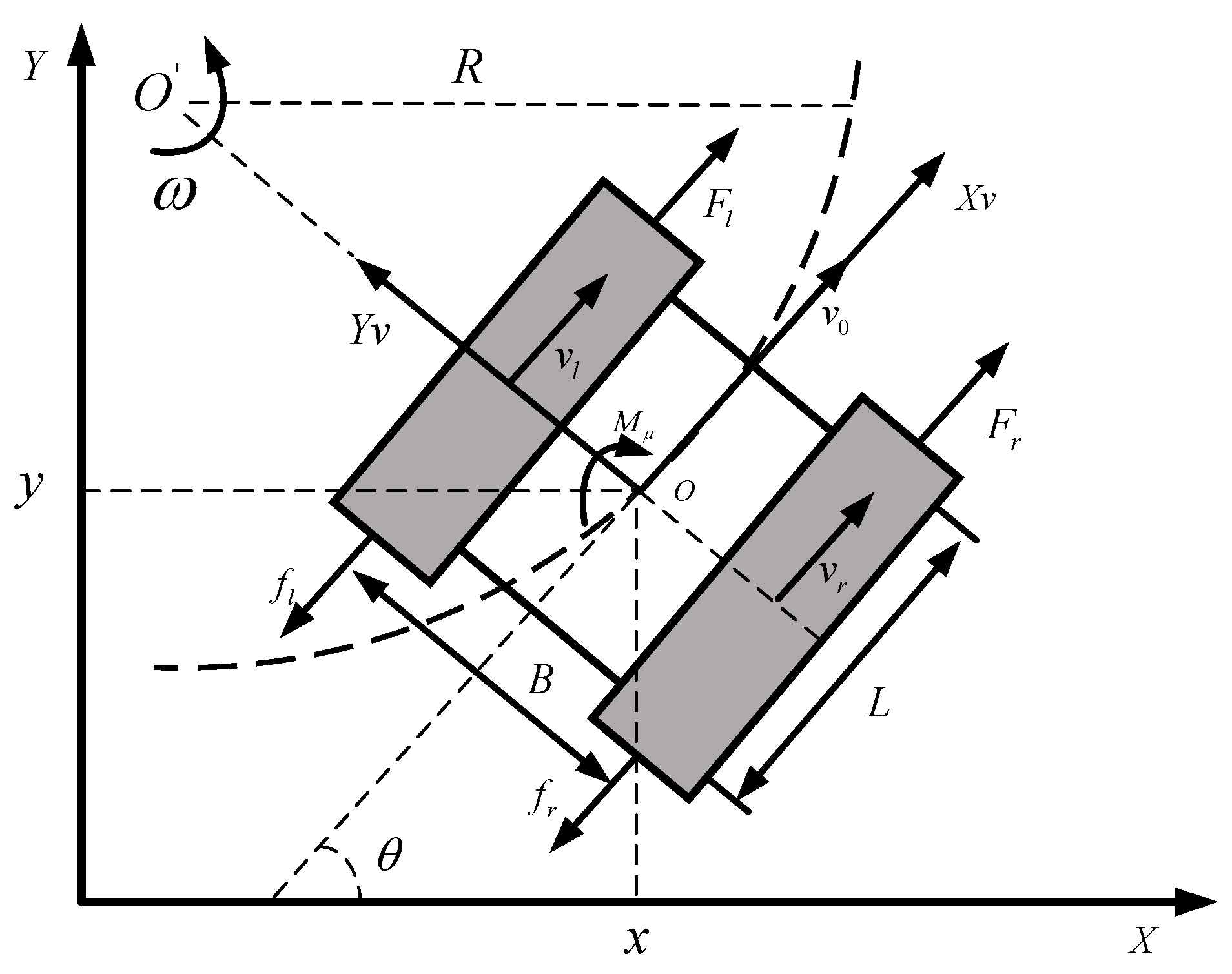
2. Dynamic Model of a Tracked Unmanned Vehicle
3. Path Tracking Control Strategy for Tracked Unmanned Vehicles
3.1. Hierarchical Control Strategy for Path Tracking of a Tracked Unmanned Vehicle
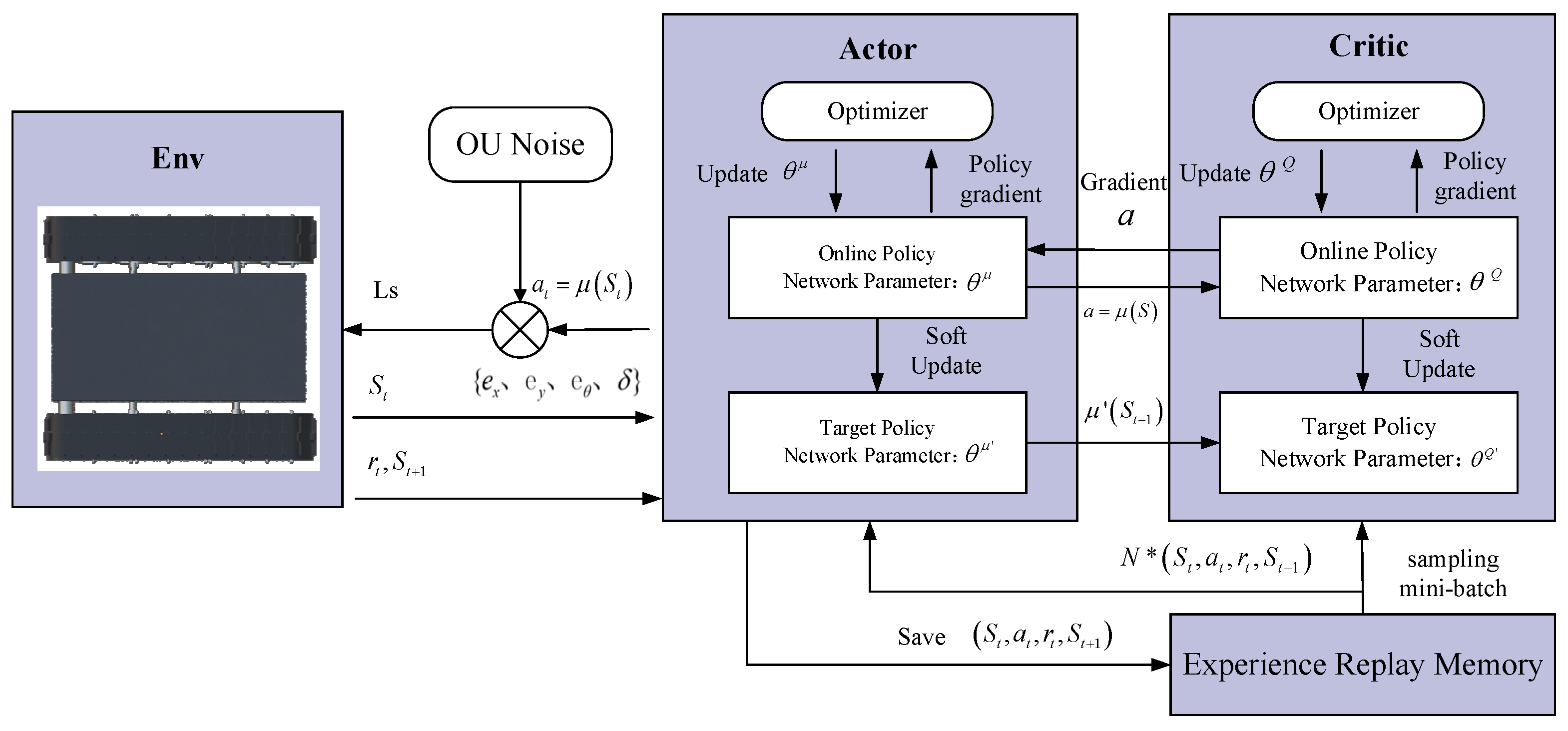
3.2. Tracked Unmanned Vehicle Path Tracking Upper Controller Design
3.2.1. Principle of the DDPG Algorithm
| Algorithm 1 DDPG algorithm |
| and randomly initialize Critic networks and Actor networks initialize target network weights and Initialize the experience playback area R for episode = 1, M do: Action exploration, random noise N initialization Obtaining the initial observation state for t = 1, T do: Execute an action , achieve and environmental state , data save to R. Randomly sample a multidimensional array of batch number values N from R Minimize the loss function L to update the Critic network: The Actor policy network is updated by policy gradient: Update the target network: End For End For |
3.2.2. Upper Controller Design Based on DDPG
| Algorithm 2 Stochastic Path Generate Algorithm |
| Generated waypoint counter n←1, starting waypoint p1←[0,0], Number of path waypoints , Range of length between waypoints While do Sample from Sample from New n←n + 1 End while Create parameterized path using Cubic Spline Interpolator |
3.3. Tracked Unmanned Vehicle Path Tracking Lower Controller Design
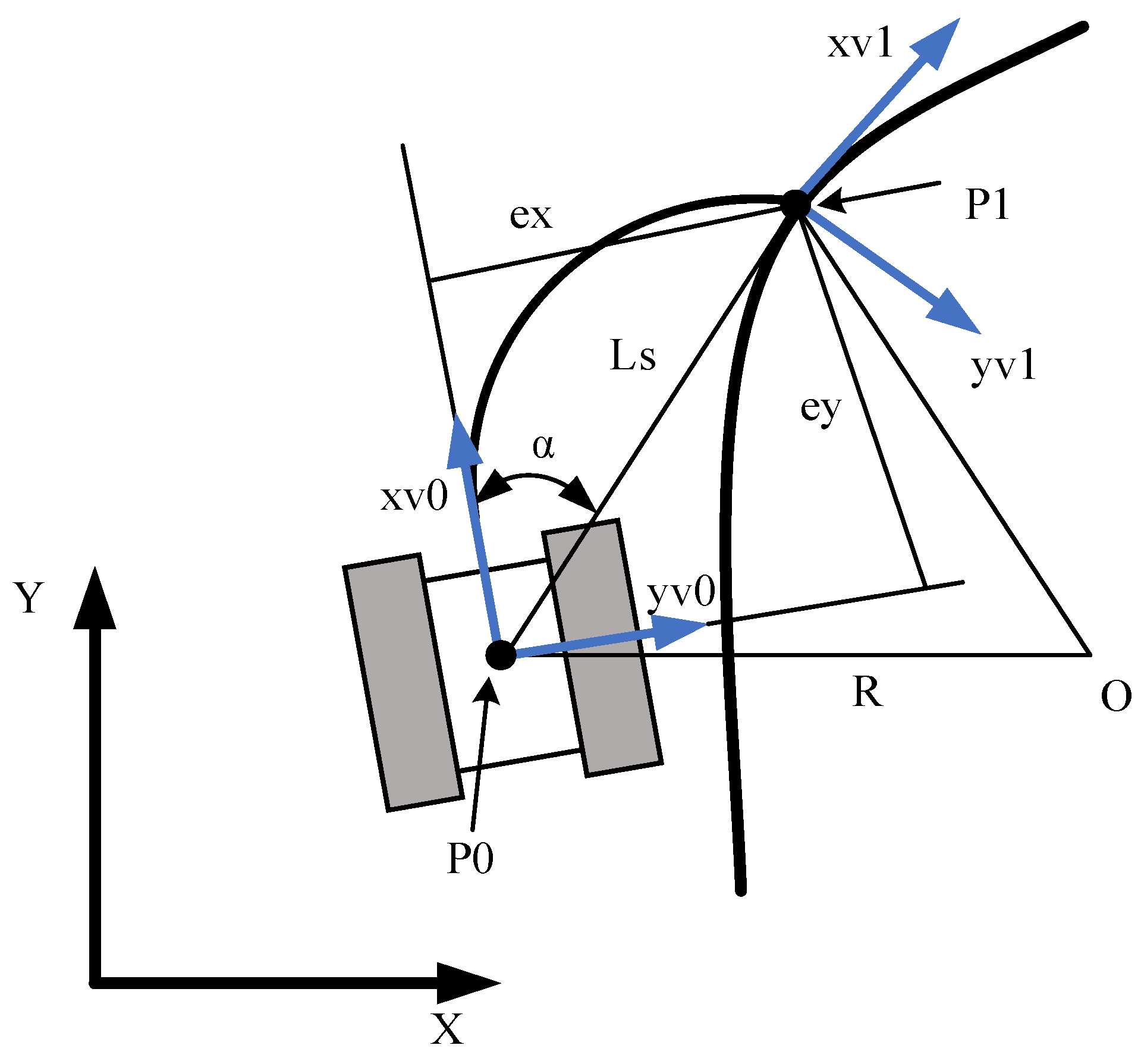
3.3.1. Principles of the PP Algorithm
| Algorithm 3 Look-Ahead Point Generate Algorithm |
| else While Generate Generate End while Generate Generate look-ahead point End if |
3.3.2. PP-Based Lower Controller Design
3.4. LQR Controller Designed for Comparison Experiments
3.4.1. Principle of LQR
3.4.2. Design of LQR Based Path Tracking Controller for Tracked Unmanned Vehicles
4. Simulation and Verification
4.1. Result of Path Tracking Control Strategy Training
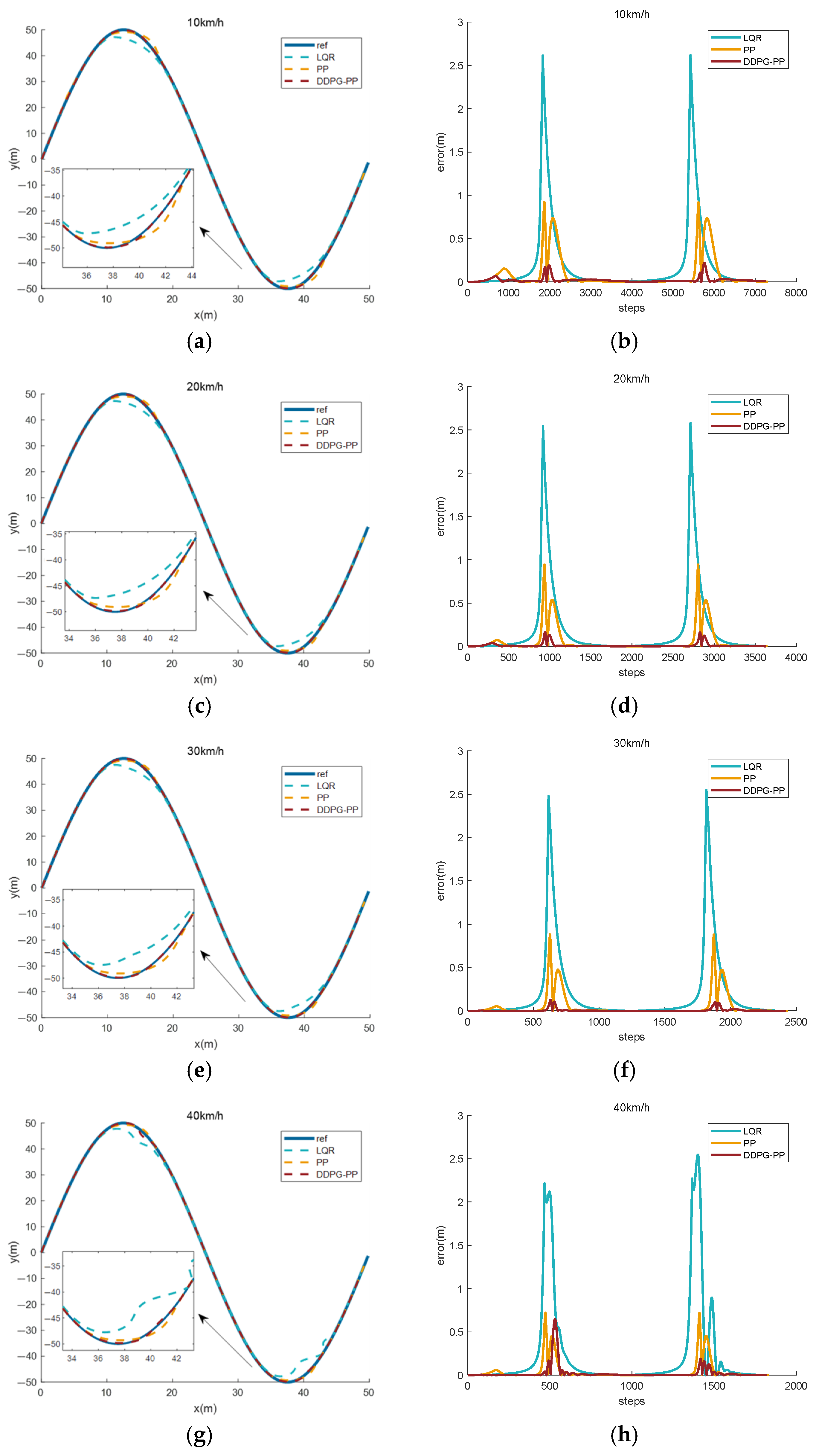
4.2. Effect of Path Tracking at Different Speeds
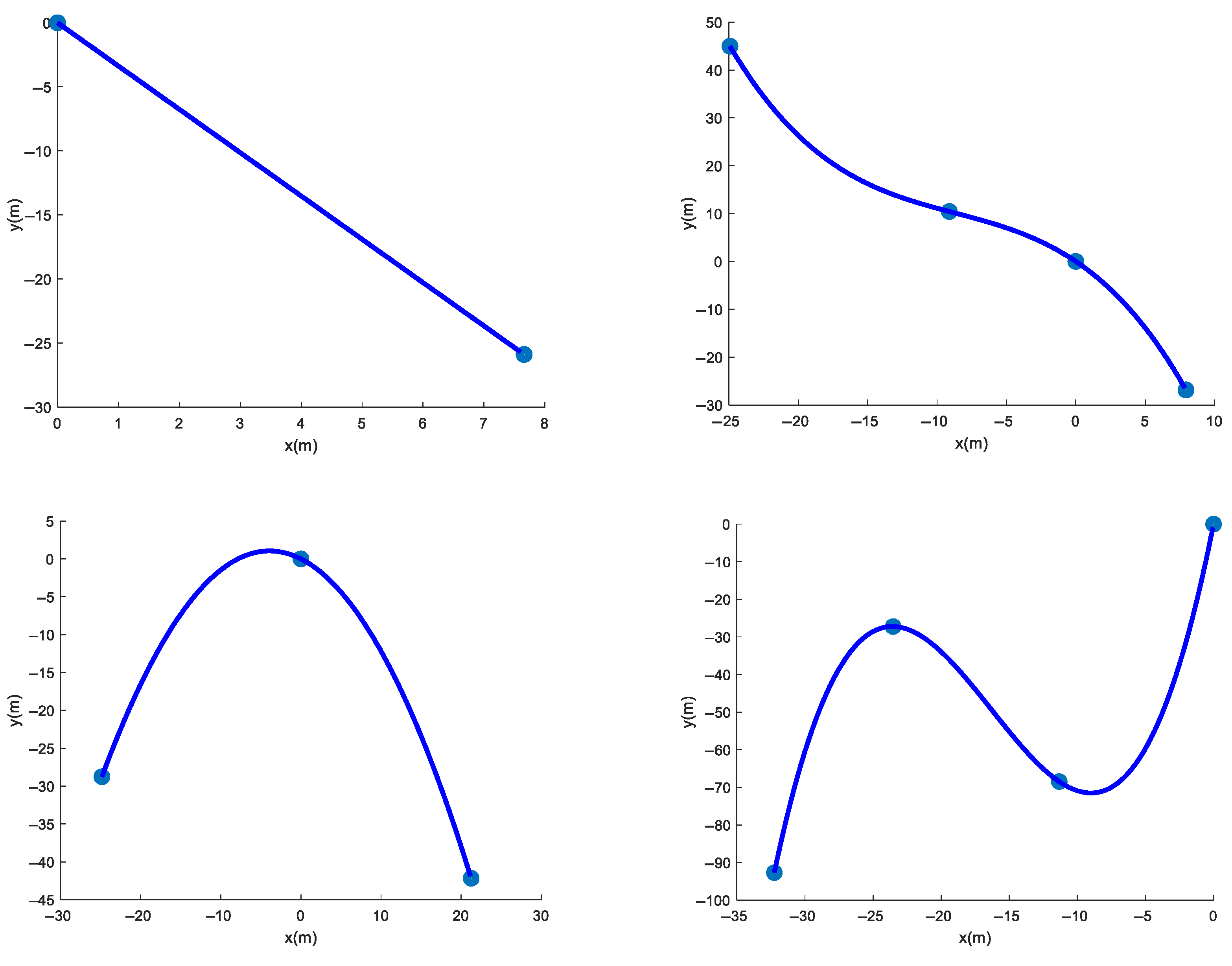
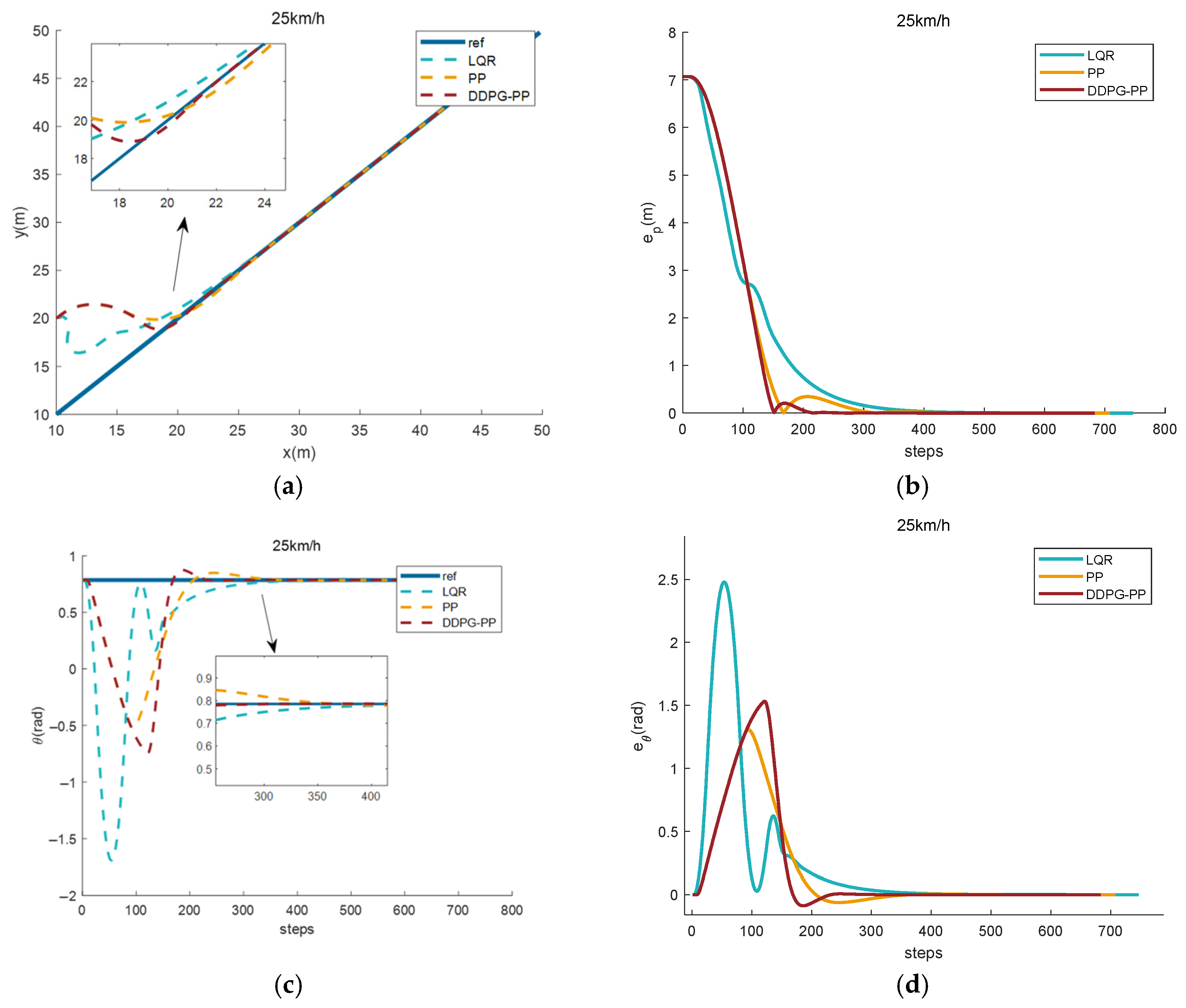
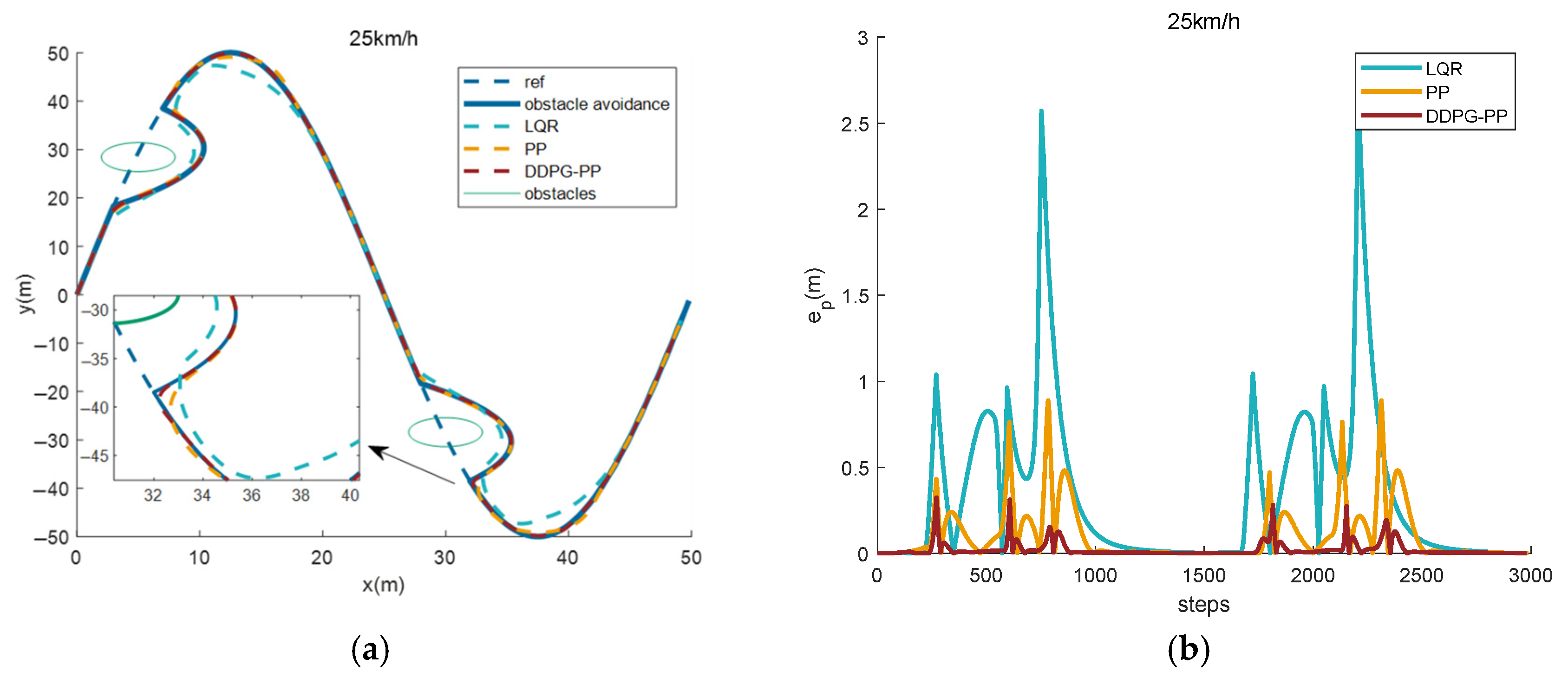
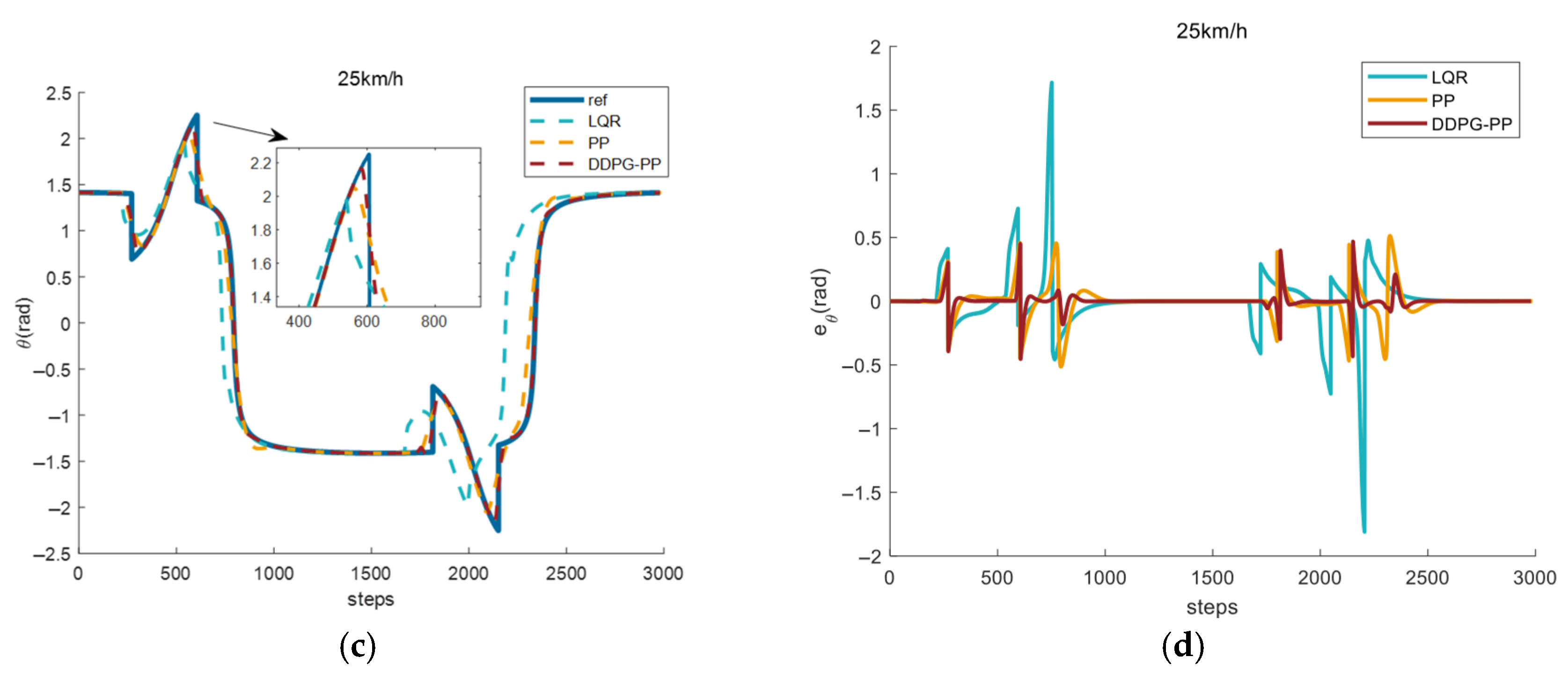
4.3. Effect of Path Tracking at Different Paths
4.3.1. Effect of Path Tracking Under Straight Paths
4.3.2. Effect of Path Tracking Under Sinusoidal Function Paths
4.3.3. Effect of Path Tracking Under Sinusoidal Function Obstacle Avoidance Paths
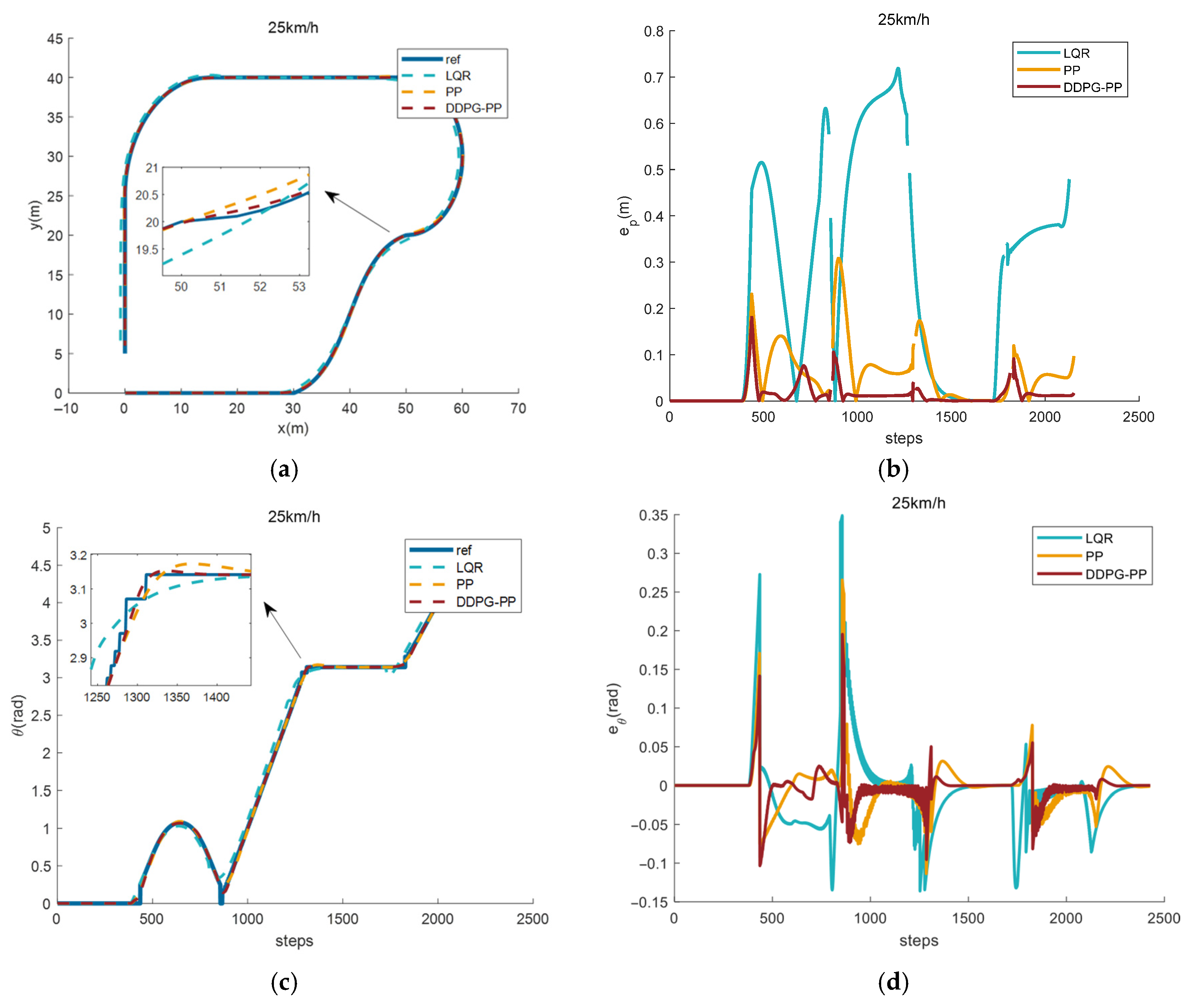
4.3.4. Effect of Path Tracking Under Complex Road Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Wang, Y.; Sun, Q.; Chen, Y.; Al-Zahran, A. Adaptive Robust Control of Unmanned Tracked Vehicles for Trajectory Tracking Based on Constraint Modeling and Analysis. Nonlinear Dyn. 2024, 112, 9117–9135. [Google Scholar] [CrossRef]
- Yao, J.; Li, X.; Zhang, Y.; Chen, K.; Zhang, D.; Ji, J. Autonomous Navigation Control of Tracked Unmanned Vehicle Formation in Communication Restricted Environment. IEEE Trans. Veh. Technol. 2024, 73, 16063–16075. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, T. Research on a Tracked Omnidirectional and Cross-Country Vehicle. Mech. Mach. Theory 2015, 87, 18–44. [Google Scholar] [CrossRef]
- Yue, B.; Zhang, Z.; Zhang, W.; Luo, X.; Zhang, G.; Huang, H.; Wu, X.; Bao, K.; Peng, M. Design of an Automatic Navigation and Operation System for a Crawler-Based Orchard Sprayer Using GNSS Positioning. Agronomy 2024, 14, 271. [Google Scholar] [CrossRef]
- Hu, C.; Ru, Y.; Li, X.; Fang, S.; Zhou, H.; Yan, X.; Liu, M.; Xie, R. Path Tracking Control for Brake-Steering Tracked Vehicles Based on an Improved Pure Pursuit Algorithm. Biosyst. Eng. 2024, 242, 1–15. [Google Scholar] [CrossRef]
- Farag, W. Complex Trajectory Tracking Using PID Control for Autonomous Driving. Int. J. ITS Res. 2020, 18, 356–366. [Google Scholar] [CrossRef]
- Mai, T.A. A Combined Backstepping and Adaptive Fuzzy PID Approach for Trajectory Tracking of Autonomous Mobile Robots. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 156. [Google Scholar] [CrossRef]
- Han, J.; Wang, P.; Yang, X. Tuning of PID Controller Based on Fruit Fly Optimization Algorithm. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 5–8 August 2012; pp. 409–413. [Google Scholar]
- Vo, A.T.; Kang, H.-J. A Chattering-Free, Adaptive, Robust Tracking Control Scheme for Nonlinear Systems with Uncertain Dynamics. IEEE Access 2019, 7, 10457–10466. [Google Scholar] [CrossRef]
- Yang, T.; Bai, Z.; Li, Z.; Feng, N.; Chen, L. Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm. Actuators 2021, 10, 228. [Google Scholar] [CrossRef]
- Fan, Z.; Yan, Y.; Wang, X.; Xu, H. Path Tracking Control of Commercial Vehicle Considering Roll Stability Based on Fuzzy Linear Quadratic Theory. Machines 2023, 11, 382. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. Design of a Path-Tracking Controller with an Adaptive Preview Distance Scheme for Autonomous Vehicles. Machines 2024, 12, 764. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Shu, I.; Yi, K. Time-Varying Parameter Adaptive Vehicle Speed Control. IEEE Trans. Veh. Technol. 2016, 65, 581–588. [Google Scholar] [CrossRef]
- Ding, C.; Ding, S.; Wei, X.; Mei, K. Composite SOSM Controller for Path Tracking Control of Agricultural Tractors Subject to Wheel Slip. ISA Trans. 2022, 130, 389–398. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Receding Horizon Lateral Vehicle Control for Pure Pursuit Path Tracking. J. Vib. Control 2018, 24, 619–642. [Google Scholar] [CrossRef]
- Jiang, X.; Kuroiwa, T.; Cao, Y.; Sun, L.; Zhang, H.; Kawaguchi, T.; Hashimoto, S. Enhanced Pure Pursuit Path Tracking Algorithm for Mobile Robots Optimized by NSGA-II with High-Precision GNSS Navigation. Sensors 2025, 25, 745. [Google Scholar] [CrossRef] [PubMed]
- Qinpeng, S.; Zhonghua, W.; Meng, L.; Bin, L.; Jin, C.; Jiaxiang, T. Path Tracking Control of Wheeled Mobile Robot Based on Improved Pure Pursuit Algorithm. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 4239–4244. [Google Scholar]
- Huang, Y.; Tian, Z.; Jiang, Q.; Xu, J. Path Tracking Based on Improved Pure Pursuit Model and PID. In Proceedings of the 2020 IEEE 2nd International Conference on Civil Aviation Safety and Information Technology (ICCASIT.), Weihai, China, 14 October 2020; pp. 359–364. [Google Scholar]
- Ahn, J.; Shin, S.; Kim, M.; Park, J. Accurate Path Tracking by Adjusting Look-Ahead Point in Pure Pursuit Method. Int. J. Automot. Technol. 2021, 22, 119–129. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Y.; Meng, L.; Yan, J.; Qin, C. Adaptive Critic Design for Safety-Optimal FTC of Unknown Nonlinear Systems with Asymmetric Constrained-Input. ISA Trans. 2024, 155, 309–318. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, Y.; Pan, H.; Yang, M. Path Planning in Complex Environments Using Attention-Based Deep Deterministic Policy Gradient. Electronics 2024, 13, 3746. [Google Scholar] [CrossRef]
- Sun, Y.; Yuan, B.; Zhang, Y.; Zheng, W.; Xia, Q.; Tang, B.; Zhou, X. Research on Action Strategies and Simulations of DRL and MCTS-Based Intelligent Round Game. Int. J. Control Autom. Syst. 2021, 19, 2984–2998. [Google Scholar] [CrossRef]
- Vo, A.K.; Mai, T.L.; Yoon, H.K. Path Planning for Automatic Berthing Using Ship-Maneuvering Simulation-Based Deep Reinforcement Learning. Appl. Sci. 2023, 13, 12731. [Google Scholar] [CrossRef]
- Woo, J. Deep Reinforcement Learning-Based Controller for Path Following of an Unmanned Surface Vehicle. Ocean Eng. 2019, 183, 155–166. [Google Scholar] [CrossRef]
- Yao, J.; Ge, Z. Path-Tracking Control Strategy of Unmanned Vehicle Based on DDPG Algorithm. Sensors 2022, 22, 7881. [Google Scholar] [CrossRef] [PubMed]
- Niu, S.; Pan, X.; Wang, J.; Li, G. Deep Reinforcement Learning from Human Preferences for ROV Path Tracking. Ocean Eng. 2025, 317, 120036. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, R.; Zhang, D.; Yi, T.; Ding, C.; Chen, L. Path Curvature Incorporated Reinforcement Learning Method for Accurate Path Tracking of Agricultural Vehicles. Comput. Electron. Agric. 2025, 234, 110243. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, S.; Cheng, S.; Xia, Q.; Zhang, J. Path-Following and Obstacle Avoidance Control of Nonholonomic Wheeled Mobile Robot Based on Deep Reinforcement Learning. Appl. Sci. 2022, 12, 6874. [Google Scholar] [CrossRef]
- Zheng, Y.; Tao, J.; Hartikainen, J.; Duan, F.; Sun, H.; Sun, M.; Sun, Q.; Zeng, X.; Chen, Z.; Xie, G. DDPG Based LADRC Trajectory Tracking Control for Underactuated Unmanned Ship under Environmental Disturbances. Ocean Eng. 2023, 271, 113667. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, Y.; Tong, L.; Yuan, C.; Shen, B.; Long, T. Energy Management Strategy for Diesel–Electric Hybrid Ship Considering Sailing Route Division Based on DDPG. IEEE Trans. Transp. Electrific. 2024, 10, 187–202. [Google Scholar] [CrossRef]
- Vouros, G.A. Explainable Deep Reinforcement Learning: State of the Art and Challenges. ACM Comput. Surv. 2023, 55, 1–39. [Google Scholar] [CrossRef]
- Liu, J.; Huang, Z.; Xu, X.; Zhang, X.; Sun, S.; Li, D. Multi-Kernel Online Reinforcement Learning for Path Tracking Control of Intelligent Vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6962–6975. [Google Scholar] [CrossRef]
- Qin, C.; Qiao, X.; Wang, J.; Zhang, D.; Hou, Y.; Hu, S. Barrier-Critic Adaptive Robust Control of Nonzero-Sum Differential Games for Uncertain Nonlinear Systems With State Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 50–63. [Google Scholar] [CrossRef]
- Qin, C.; Jiang, K.; Wang, Y.; Zhu, T.; Wu, Y.; Zhang, D. Event-Triggered H∞ Control for Unknown Constrained Nonlinear Systems with Application to Robot Arm. Appl. Math. Model. 2025, 144, 116089. [Google Scholar] [CrossRef]
- Wu, J.; Zou, Y.; Zhang, X.; Du, G.; Du, G.; Zou, R. A Hierarchical Energy Management for Hybrid Electric Tracked Vehicle Considering Velocity Planning With Pseudospectral Method. IEEE Trans. Transp. Electrif. 2020, 6, 703–716. [Google Scholar] [CrossRef]
- Cao, Y.; Ni, K.; Kawaguchi, T.; Hashimoto, S. Path Following for Autonomous Mobile Robots with Deep Reinforcement Learning. Sensors 2024, 24, 561. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Physical Meaning | Value |
|---|---|---|
| m | Curb weigh | 1200 kg |
| g | Gravitational acceleration | 9.8 kg/m2 |
| f | Rolling resistance coefficient | 0.05 |
| r | Driving wheel radius | 0.25 m |
| i0 | Side driving ratio | 8.21 |
| Iz | yaw moment of inertial | 1500 |
| L | Contact length of the track on the ground | 1.6 m |
| Maximum coefficient of lateral resistance | 0.49 | |
| CD | Air resistance coefficient | 0.6 |
| A | Windward area of the vehicle | 1.12 m2 |
| Description | Value |
|---|---|
| Number of hidden layers | 2 |
| Number of neurons per layers | 256 |
| Activation function | ReLU |
| Optimizer | Adam |
| Learning rate | 5 × 10−4 |
| Minibatch size | 256 |
| Method | Velocity (km/h) | |||
|---|---|---|---|---|
| 10 | 20 | 30 | 40 | |
| LQR | 0.2102 | 0.2022 | 0.2011 | 0.2498 |
| PP | 0.0905 | 0.0629 | 0.0547 | 0.0450 |
| DDPG-PP | 0.0215 | 0.0114 | 0.0089 | 0.0236 |
| Method | Evaluation Indicators | ||||
|---|---|---|---|---|---|
| (m) | (m) | (rad) | (rad) | (s) | |
| LQR | 1.0032 | 7.0711 | 0.2277 | 2.4778 | 2.26 |
| PP | 0.9839 | 7.0711 | 0.1852 | 1.3075 | 1.50 |
| DDPG-PP | 0.9663 | 7.0711 | 0.2010 | 1.5323 | 1.40 |
| Method | Evaluation Indicators | |||
|---|---|---|---|---|
| (m) | (m) | (rad) | (rad) | |
| LQR | 0.1998 | 2.6011 | 0.0595 | 1.7352 |
| PP | 0.0588 | 0.9301 | 0.0298 | 0.5418 |
| DDPG -PP | 0.0071 | 0.1742 | 0.0064 | 0.1983 |
| Method | Evaluation Indicators | |||
|---|---|---|---|---|
| (m) | (m) | (rad) | (rad) | |
| LQR | 0.3635 | 2.6414 | 0.1089 | 1.8106 |
| PP | 0.1051 | 0.8882 | 0.0610 | 0.5136 |
| DDPG-PP | 0.0219 | 0.3237 | 0.0214 | 0.4689 |
| Method | Evaluation Indicators | |||
|---|---|---|---|---|
| (m) | (m) | (rad) | ||
| LQR | 0.2530 | 0.7185 | 0.0277 | 0.3489 |
| PP | 0.0526 | 0.3079 | 0.0164 | 0.2657 |
| DDPG-PP | 0.0139 | 0.1832 | 0.0097 | 0.1954 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Guo, C.; Mi, J.; Wang, L.; Wang, H.; Zhang, H. Research on Path Tracking Technology for Tracked Unmanned Vehicles Based on DDPG-PP. Machines 2025, 13, 603. https://doi.org/10.3390/machines13070603
Zhao Y, Guo C, Mi J, Wang L, Wang H, Zhang H. Research on Path Tracking Technology for Tracked Unmanned Vehicles Based on DDPG-PP. Machines. 2025; 13(7):603. https://doi.org/10.3390/machines13070603
Chicago/Turabian StyleZhao, Yongjuan, Chaozhe Guo, Jiangyong Mi, Lijin Wang, Haidi Wang, and Hailong Zhang. 2025. "Research on Path Tracking Technology for Tracked Unmanned Vehicles Based on DDPG-PP" Machines 13, no. 7: 603. https://doi.org/10.3390/machines13070603
APA StyleZhao, Y., Guo, C., Mi, J., Wang, L., Wang, H., & Zhang, H. (2025). Research on Path Tracking Technology for Tracked Unmanned Vehicles Based on DDPG-PP. Machines, 13(7), 603. https://doi.org/10.3390/machines13070603





