Aeroelastic Study of Downwind and Upwind Configurations Under Different Power Levels of Wind Turbines
Abstract
1. Introduction
2. Numerical Method and Wind Turbine Model
2.1. Numerical Method
2.2. Wind Turbine Model
2.3. Validation of Aeroelastic Computations
3. Results and Discussion
3.1. Comparison of Aeroelastic Characteristics of Upwind and Downwind Wind Turbines Under Steady Wind Conditions
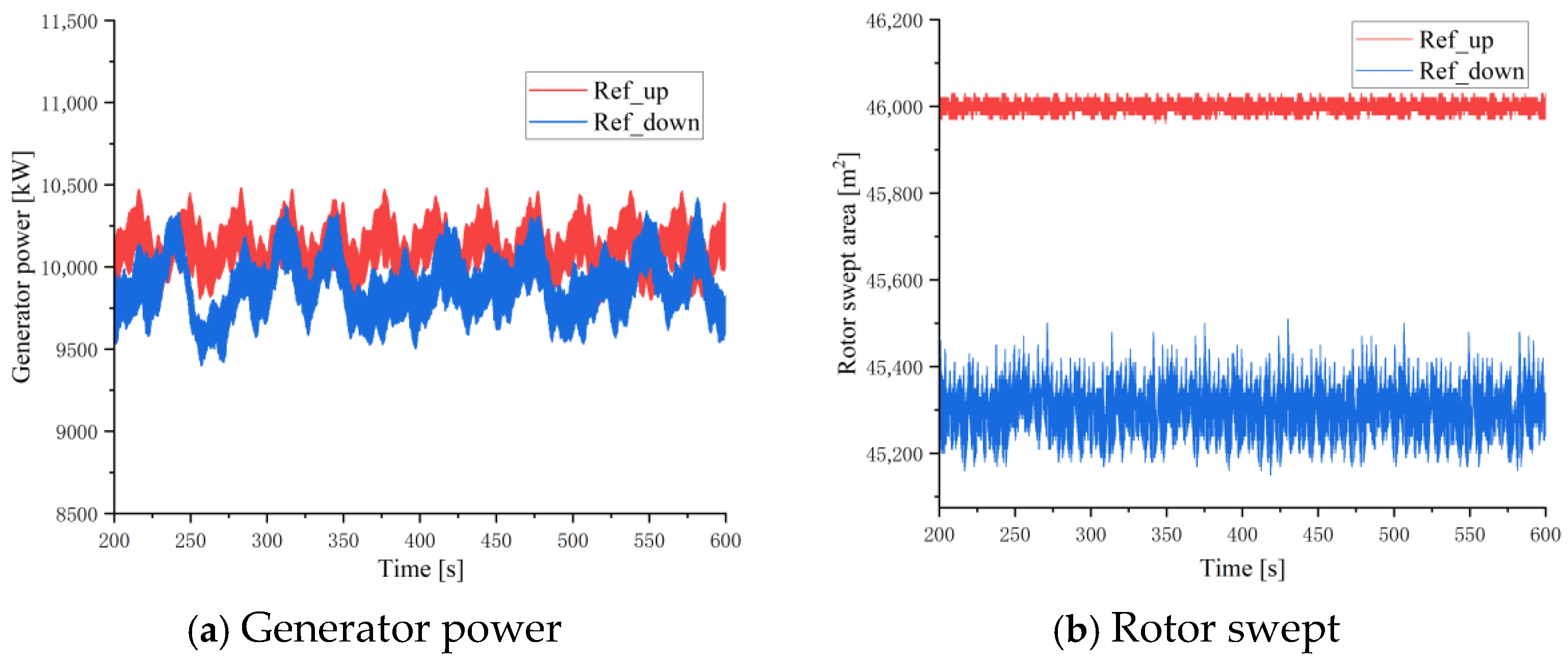
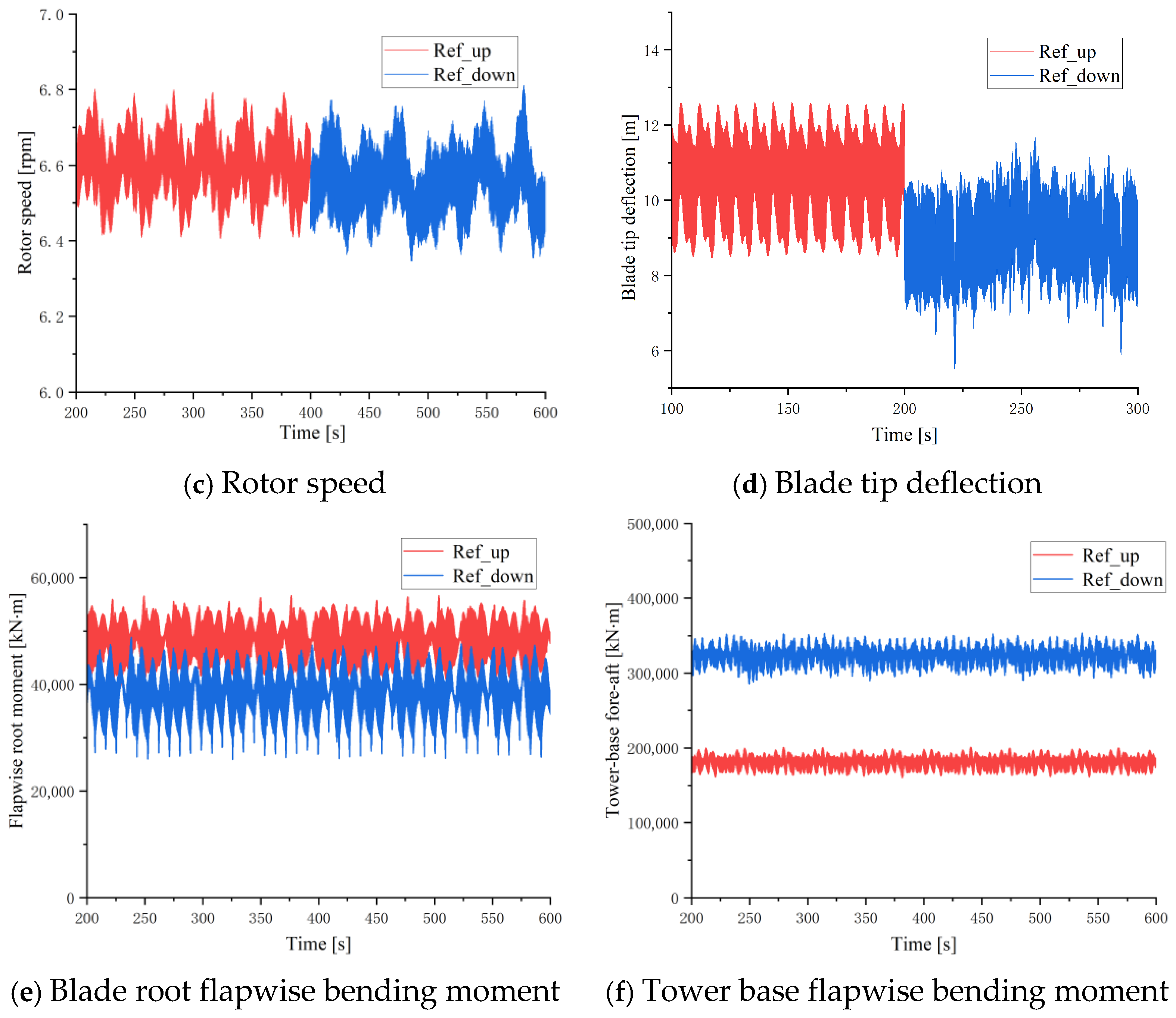
3.1.1. Wind Speed of 10 m/s
3.1.2. Wind Speed of 15 m/s
3.2. Comparison of Ultimate and Fatigue Load Characteristics of the Upwind and Downwind Wind Turbines
3.2.1. Simulation Conditions and Load Analysis Methods
3.2.2. Fatigue Load Analysis
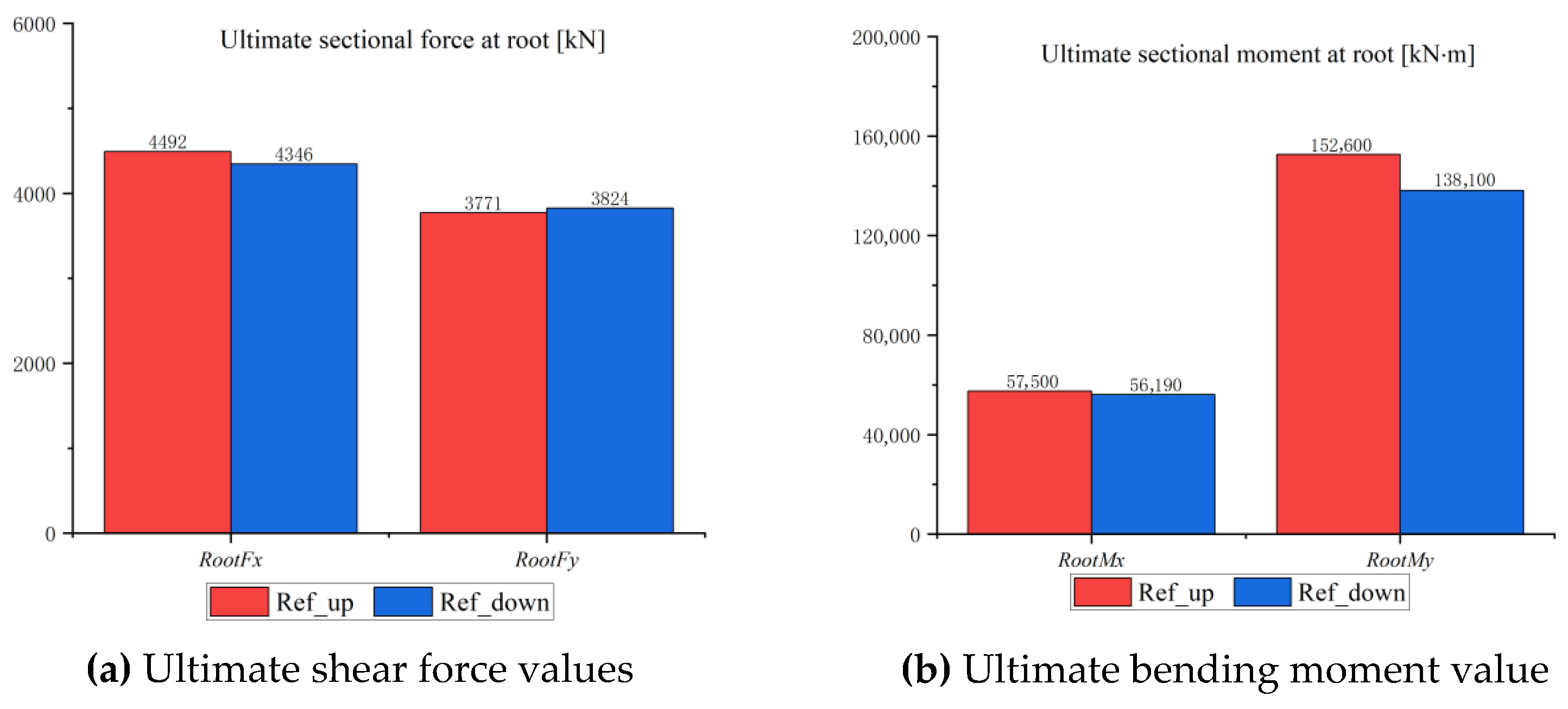
3.2.3. Ultimate Load Analysis
3.3. Comparison of Downwind Versus Upwind for Wind Turbines of Different Sizes
3.3.1. Fatigue Load Analysis
3.3.2. Ultimate Load Analysis
4. Conclusions
- Clear monotonic trend on fatigue bending moments: Downwind turbine’s initial disadvantage (higher fatigue compared with upwind turbine) at 2.1 MW (flapwise increment: +5.00%, edgewise increment: +7.00%) transitions to an advantage at 15 MW (flapwise increment: −2.63%, edgewise increment: −2.41%).
- Clear monotonic trend on extreme edgewise bending moments: Downwind shifts from a disadvantage (+5.00% higher compared with upwind turbine at 2.1 MW) to an advantage (−2.27% at 15 MW).
- Non-monotonic trend on extreme flapwise bending moments: Downwind consistently reduces extreme loads (reduction always surpasses −9.5%), supporting its role in mitigating flapwise extremes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Z.; Zhu, W.J.; Shen, W.Z.; Zhong, W.; Cao, J.; Tao, Q. Aerodynamic Analysis of Coning Effects on the DTU 10 MW Wind Turbine Rotor. Energies 2020, 13, 5753. [Google Scholar] [CrossRef]
- Sun, Z.; Sessarego, M.; Chen, J.; Shen, W.Z. Design of the OffWindChina 5 MW wind turbine rotor. Energies 2017, 10, 777. [Google Scholar] [CrossRef]
- Noyes, C.; Loth, E.; Martin, D.; Johnson, K.; Ananda, G.; Selig, M. Extreme-scale load-aligning rotor: To hinge or not to hinge? Appl. Energy 2020, 257, 113985. [Google Scholar] [CrossRef]
- Noyes, C.; Qin, C.; Loth, E. Analytic analysis of load alignment for coning extreme-scale rotors. Wind Energy 2020, 23, 357–369. [Google Scholar] [CrossRef]
- Noyes, C.; Qin, C.; Loth, E. Pre-aligned downwind rotor for a 13.2 MW wind turbine. Renew. Energy 2018, 116, 749–754. [Google Scholar] [CrossRef]
- Loth, E.; Steele, A.; Qin, C.; Ichter, B.; Selig, M.S.; Moriarty, P. Downwind pre-aligned rotors for extreme-scale wind turbines. Wind Energy 2017, 20, 1241–1259. [Google Scholar] [CrossRef]
- Ichter, B.; Steele, A.; Loth, E.; Moriarty, P.; Selig, M. A morphing downwind-aligned rotor concept based on a 13-MW wind turbine. Wind Energy 2016, 19, 625–637. [Google Scholar] [CrossRef]
- Kaminski, M.; Noyes, C.; Loth, E.; Damiani, R.; Hughes, S.; Bay, C.; Chetan, M.; Griffith, D.T.; Johnson, K.; Martin, D. Gravo-aeroelastic scaling of a 13-MW downwind rotor for 20% scale blades. Wind Energy 2021, 24, 229–245. [Google Scholar] [CrossRef]
- Kaminski, M.; Loth, E.; Fingersh, L.J.; Scholbrock, A.; Selig, M. Parked aeroelastic field rotor response for a 20% scaled demonstrator of a 13-MW downwind turbine. Wind Energy 2023, 26, 182–200. [Google Scholar] [CrossRef]
- Kaminski, M.; Simpson, J.; Loth, E.; Fingersh, L.J.; Scholbrock, A.; Johnson, N.; Johnson, K.; Pao, L.; Griffith, T. Gravo-aeroelastically-scaled demonstrator field tests to represent blade response of a flexible extreme-scale downwind turbine. Renew. Energy 2023, 218, 119217. [Google Scholar] [CrossRef]
- Simpson, J.G.; Kaminski, M.; Loth, E. Influence of tower shadow on downwind flexible rotors: Field tests and simulations. Wind Energy 2022, 25, 881–896. [Google Scholar] [CrossRef]
- Zalkind, D.S.; Ananda, G.K.; Chetan, M.; Martin, D.P.; Bay, C.J.; Johnson, K.E.; Loth, E.; Griffith, D.T.; Selig, M.S.; Pao, L.Y. System-level design studies for large rotors. Wind Energy Sci. 2019, 4, 595–618. [Google Scholar] [CrossRef]
- Phadnis, M.; Escalera Mendoza, A.S.; Jeong, M.; Loth, E.; Todd Griffith, D.; Pusch, M.; Pao, L. Comparison of 25 MW downwind and upwind turbine designs with individual pitch control. In Journal of Physics: Conference Series; Institute of Physics: London, UK, 2024. [Google Scholar]
- OpenFAST Documentation—OpenFAST v4.0.2 Documentation. Available online: https://openfast.readthedocs.io/en/main/ (accessed on 22 March 2025).
- Moriarty, P.J.; Hansen, A.C. AeroDyn Theory Manual; NREL/TP-500-36881; National Renewable Energy Laboratory: Golden, CO, USA, 2005; p. 15014831.
- Wang, Q.; Sprague, M.A.; Jonkman, J.; Johnson, N.; Jonkman, B. BeamDyn: A high-fidelity wind turbine blade solver in the FAST modular framework. Wind Energy 2017, 20, 1439–1462. [Google Scholar] [CrossRef]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. Definition of the IEA 15-Megawatt Offshore Reference Wind; NREL Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2020; p. NREL/TP500075698.
- IEA Task 37 2020 IEA GitHub Repository URL[DB/OL]. Available online: https://github.com/IEAWindTask37/IEA-15-240-RWT (accessed on 26 February 2023).
- Brown, K.; Bortolotti, P.; Branlard, E.; Chetan, M.; Dana, S.; de Velder, N.; Doubrawa, P.; Hamilton, N.; Ivanov, H.; Jonkman, J.; et al. One-to-one aeroservoelastic validation of operational loads and performance of a 2.8MW wind turbine model in OpenFAST. Wind Energy Sci. 2024, 9, 1791–1810. [Google Scholar] [CrossRef]
- Rinker, J.; Gaertner, E.; Zahle, F.; Skrzypiński, W.; Abbas, N.; Bredmose, H.; Barter, G.; Dykes, K. Comparison of loads from HAWC2 and OpenFAST for the IEA Wind 15 MW Reference Wind Turbine. J. Phys. Conf. Ser. 2020, 1618, 052052. [Google Scholar] [CrossRef]
- Das, S.; Karnik, N.; Santoso, S. Time-Domain Modeling of Tower Shadow and Wind Shear in Wind Turbines. Int. Sch. Res. 2011, 2011, 890582. [Google Scholar] [CrossRef]
- IEC 61400-3:2009. Available online: https://webstore.iec.ch/en/publication/5446 (accessed on 26 March 2025).
- TurbSim|Wind Research|NREL. Available online: https://www2.nrel.gov/wind/nwtc/turbsim (accessed on 26 March 2025).
- IECWind|Wind Research|NREL. Available online: https://www2.nrel.gov/wind/nwtc/iecwind (accessed on 26 March 2025).
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009; p. NREL/TP-500-38060. [CrossRef]
- Noyes, C.; Qin, C.; Loth, E. Changes in design driving load cases: Operating an upwind turbine with a downwind rotor configuration. Wind Energy 2019, 23, 1421–1653. [Google Scholar] [CrossRef]
- Bortolotti, P.; Kapila, A.; Bottasso, C.L. Comparison between upwind and downwind designs of a 10 MW wind turbine rotor. Wind Energy Sci. 2019, 4, 115–125. [Google Scholar] [CrossRef]
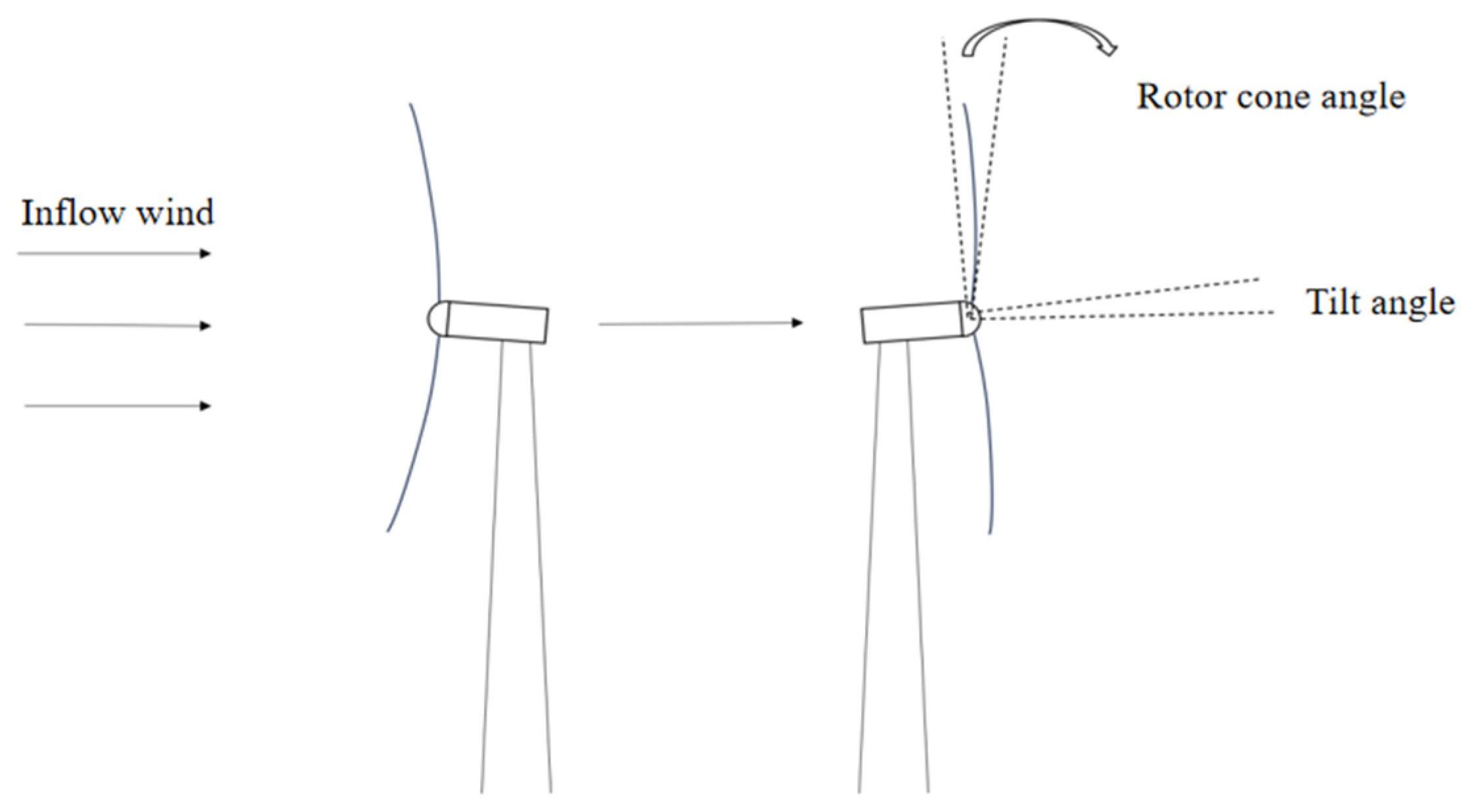
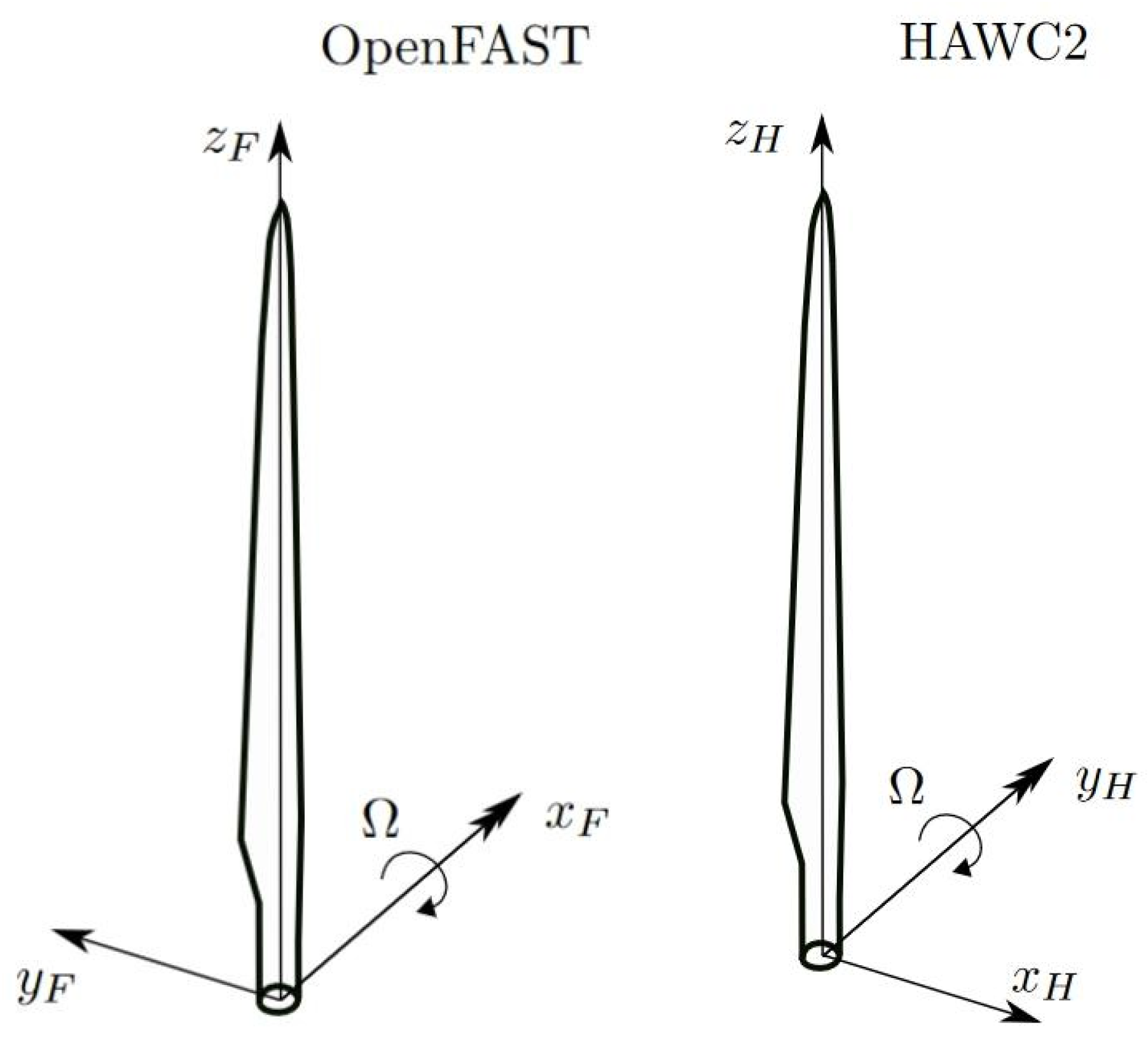
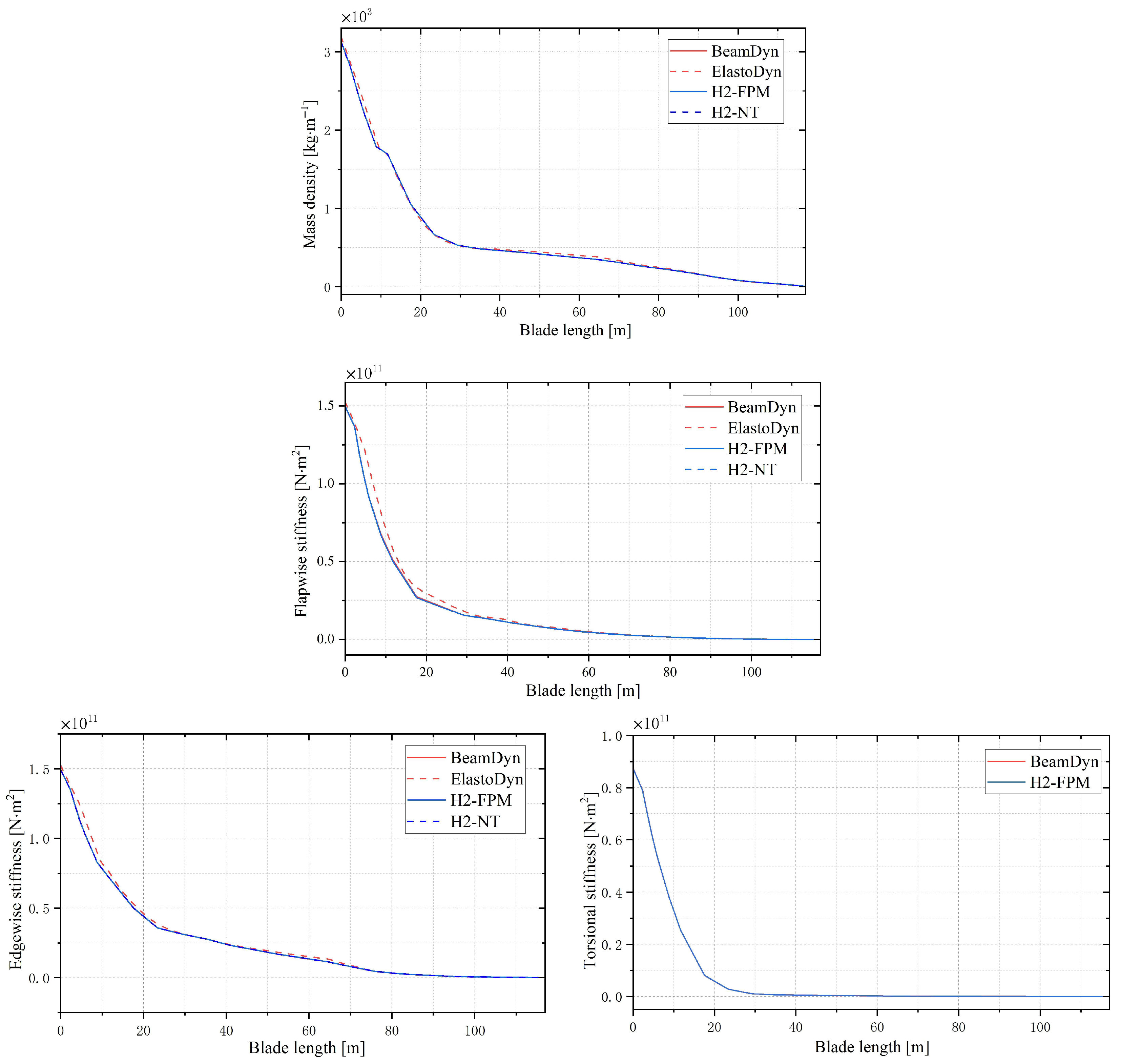
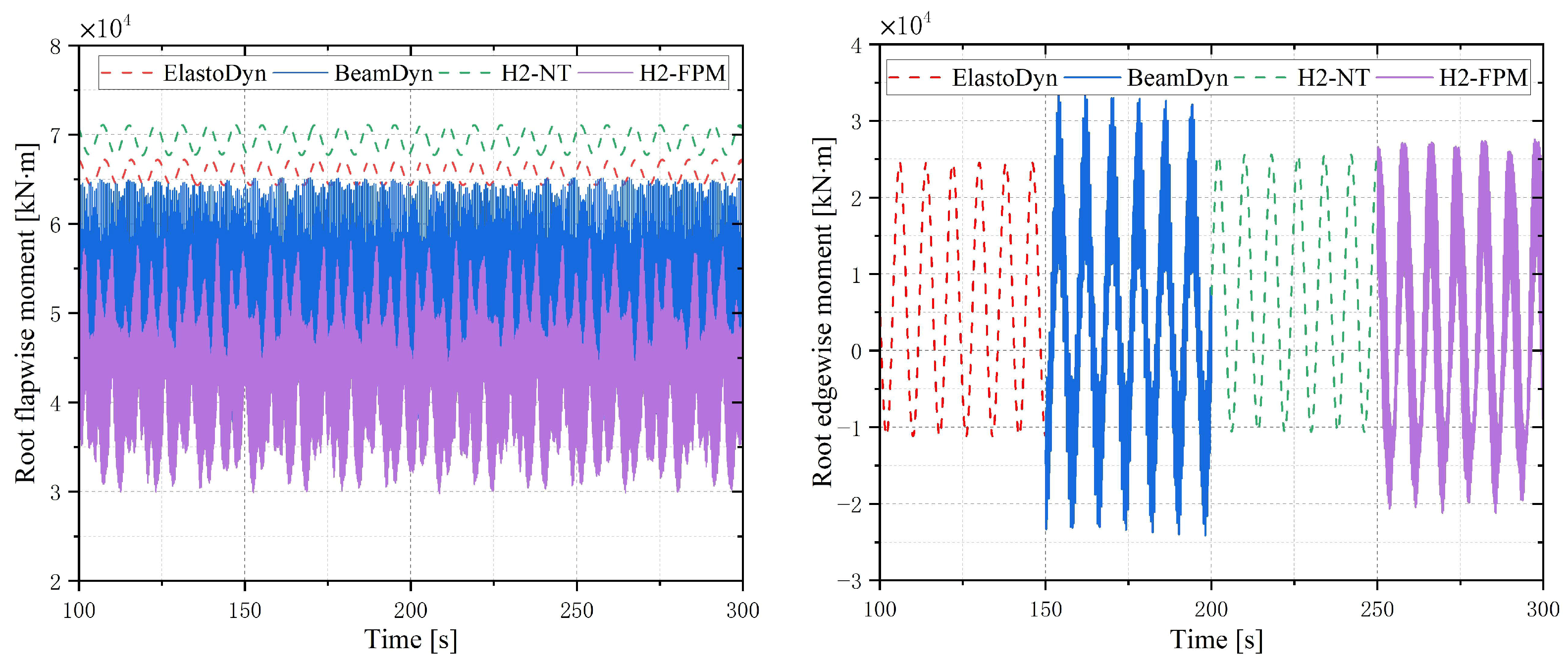





| Parameter | Value |
|---|---|
| Number of rotor blades | 3 |
| Rotor diameter | 242 m |
| Rated aerodynamic power | 15 MW |
| Cut-in speed | 3 m/s |
| Rated wind speed | 10.59 m/s |
| Cut-out speed | 25 m/s |
| Blade cone angle | 4° |
| Blade length | 117 m |
| Wind turbine class | IEC Class 1B |
| Hub height | 150 m |
| Rated rational speed | 7.56 rpm |
| Blade Span [m] | Chord Length [m] | Twist Angle [rad] | Airfoil Selection |
|---|---|---|---|
| 0 | 5.2 | 0.272 | circular |
| 2.34 | 5.208 | 0.272 | circular |
| 17.55 | 5.621 | 0.199 | SNL-FFA-W3-500 |
| 28.68492706 | 5.703 | 0.126 | FFA-W3-360 |
| 38.47474223 | 5.166 | 0.084 | FFA-W3-330blend |
| 51.38398353 | 4.428 | 0.042 | FFA-W3-301 |
| 62.90755463 | 3.998 | 0.023 | FFA-W3-270blend |
| 74.67029586 | 3.525 | 0.004 | FFA-W3-241 |
| 90.29403072 | 2.881 | −0.028 | FFA-W3-211 |
| 117 | 0.5 | −0.021 | FFA-W3-211 |
| Generator Power | Rotor Swept | Rotor Speed | Blade Root Flapwise Bending Moment | Tower Base Flapwise Bending Moment | |
|---|---|---|---|---|---|
| (kW) | (m2) | (rpm) | (kN·m) | (kN·m) | |
| Ref_up | 10,167 | 46,002 | 6.60 | 47,264 | 180,854 |
| Ref_down | 9944 | 45,313 | 6.54 | 37,735 | 322,067 |
| Generator Power | Rotor Swept | Rotor Speed | Blade Root Flapwise Bending Moment | Tower Base Flapwise Bending Moment | |
|---|---|---|---|---|---|
| (kW) | (m2) | (rpm) | (kN·m) | (kN·m) | |
| Ref_up | 14,736 | 46,033 | 7.55 | 47,296 | 204,594 |
| Ref_down | 14,762 | 45,600 | 7.55 | 35,360 | 342,129 |
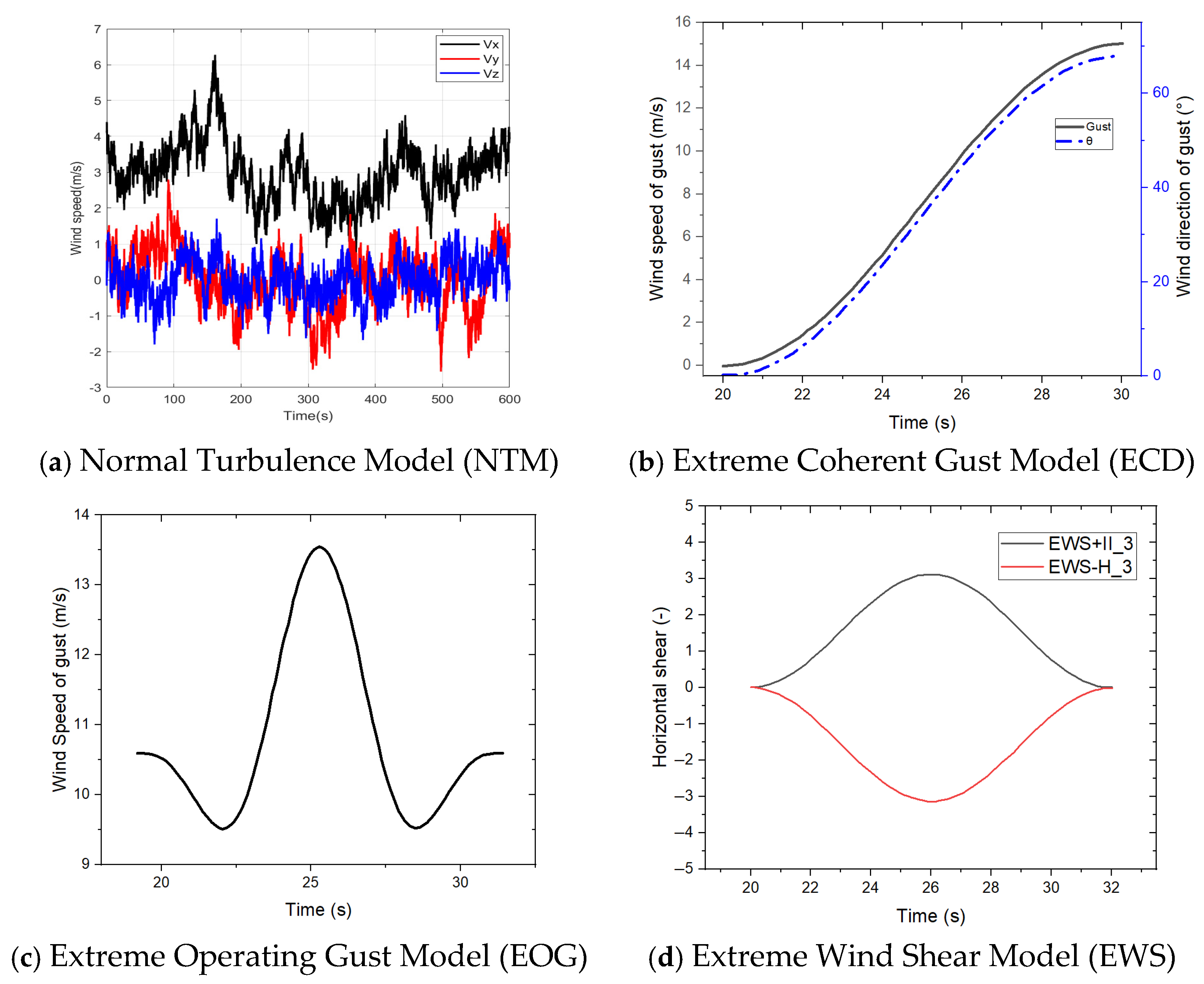
| DLC | Wind Condition | Wind Speeds | Additional Settings | Number of Simulations |
|---|---|---|---|---|
| 1.2 | NTM | 3:2:25 m/s | - | 12 |
| 1.4 | ECD | Vr,Vr ±2 m/s | - | 3 |
| 1.5 | EWS | 3:2:25 m/s | ±Vert/Horz | 48 |
| 2.3 | EOG | Vr,Vr ±2 m/s | - | 3 |
| Fatigue Cycles (20 Years) | RootFx (kN) | RootFy (kN) | RootMx (kN·m) | RootMy (kN·m) | |
|---|---|---|---|---|---|
| m | 3 | 1.1686 × 103 | 1.1632 × 103 | 2.3732 × 104 | 2.5140 × 104 |
| 4 | 1.2354 × 103 | 1.2448 × 103 | 2.7279 × 104 | 2.7490 × 104 | |
| 5 | 1.3006 × 103 | 1.3461 × 103 | 3.0580 × 104 | 3.0086 × 104 | |
| 9 | 1.6249 × 103 | 1.7540 × 103 | 4.0432 × 104 | 4.3249 × 104 | |
| 10 | 1.7539 × 103 | 1.8480 × 103 | 4.2275 × 104 | 4.7584 × 104 | |
| 11 | 1.8993 × 103 | 1.9440 × 103 | 4.3956 × 104 | 5.2348 × 104 | |
| 12 | 2.0506 × 103 | 2.0462 × 103 | 4.5511 × 104 | 5.7345 × 104 | |
| Fatigue Cycles (20 Years) | RootFx (kN) | RootFy (kN) | RootMx (kN·m) | RootMy (kN·m) | |
|---|---|---|---|---|---|
| m | 3 | 1.1366 × 103 | 1.1377 × 103 | 2.3810 × 104 | 2.5467 × 104 |
| 4 | 1.2094 × 103 | 1.2342 × 103 | 2.7085 × 104 | 2.7462 × 104 | |
| 5 | 1.2801 × 103 | 1.3475 × 103 | 3.0221 × 104 | 2.9710 × 104 | |
| 9 | 1.7777 × 103 | 1.8154 × 103 | 3.9465 × 104 | 4.2164 × 104 | |
| 10 | 1.9856 × 103 | 1.9289 × 103 | 4.1162 × 104 | 4.6438 × 104 | |
| 11 | 2.1967 × 103 | 2.0445 × 103 | 4.2714 × 104 | 5.1047 × 104 | |
| 12 | 2.4010 × 103 | 2.1635 × 103 | 4.4166 × 104 | 5.5788 × 104 | |
| Term | Descriptions | Term | Descriptions |
|---|---|---|---|
| RootFx | Flapwise shear force at the blade root | RootFy | Edgewise shear force at the blade root |
| RootMx | Edgewise bending moment at the blade root | RootMy | Flapwise bending moment at the blade root |
| TwrBsMx | Edgewise bending moment at the tower base | TwrBsMy | Flapwise bending moment at the tower base |
| RootFx | RootFy | RootMx | RootMy | ||||
|---|---|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN) | (kN) | (kN·m) | (kN·m) |
| RootFx | Minimum | EWS+H_25.0 | −1668 | −1668 | −861 | 9057 | −31,270 |
| RootFx | Maximum | EWS+H_25.0 | 4492 | 4492 | 1132 | −26,820 | 144,000 |
| RootFy | Minimum | EWS+H_21.0 | −2444 | 249 | −2444 | 34,190 | 17,060 |
| RootFy | Maximum | EWS+H_25.0 | 3771 | 1654 | 3771 | −46,480 | 65,360 |
| RootMx | Minimum | EWS+H_25.0 | −57,500 | 2094 | 3003 | −57,500 | 79,900 |
| RootMx | Maximum | EWS+H_25.0 | 54,730 | 1195 | −1774 | 54,730 | 34,600 |
| RootMy | Minimum | EWS+H_25.0 | −31,270 | −1668 | −861 | 9057 | −31,270 |
| RootMy | Maximum | EWS+H_25.0 | 152,600 | 3754 | 175 | −1910 | 152,600 |
| RootFx | RootFy | RootMx | RootMy | ||||
|---|---|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN) | (kN) | (kN·m) | (kN·m) |
| RootFx | Minimum | EWS+H_25.0 | −2931 | −2931 | 214 | −2834 | −29,050 |
| RootFx | Maximum | EWS+H_25.0 | 4346 | 4346 | 1062 | −18,110 | 127,000 |
| RootFy | Minimum | EWS+H_25.0 | −3824 | −496 | −3824 | 52,010 | −16,310 |
| RootFy | Maximum | EWS+H_25.0 | 2965 | 454 | 2965 | −56,190 | 52,540 |
| RootMx | Minimum | EWS+H_25.0 | 52 | 454 | 2965 | −56,190 | −52,540 |
| RootMx | Maximum | EWS+H_25.0 | 52,690 | 1169 | −2070 | 52,690 | 49,880 |
| RootMy | Minimum | EWS+H_25.0 | −58,430 | −1544 | 592 | −8153 | −58,430 |
| RootMy | Maximum | EWS+H_25.0 | 138,100 | 4214 | 387 | −17,540 | 138,100 |
| TwrBsMx | TwrBsMy | ||||
|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN·m) | (kN·m) |
| TwrBsMx | Minimum | EWS+H_25.0 | −86,840 | −86,840 | 39,580 |
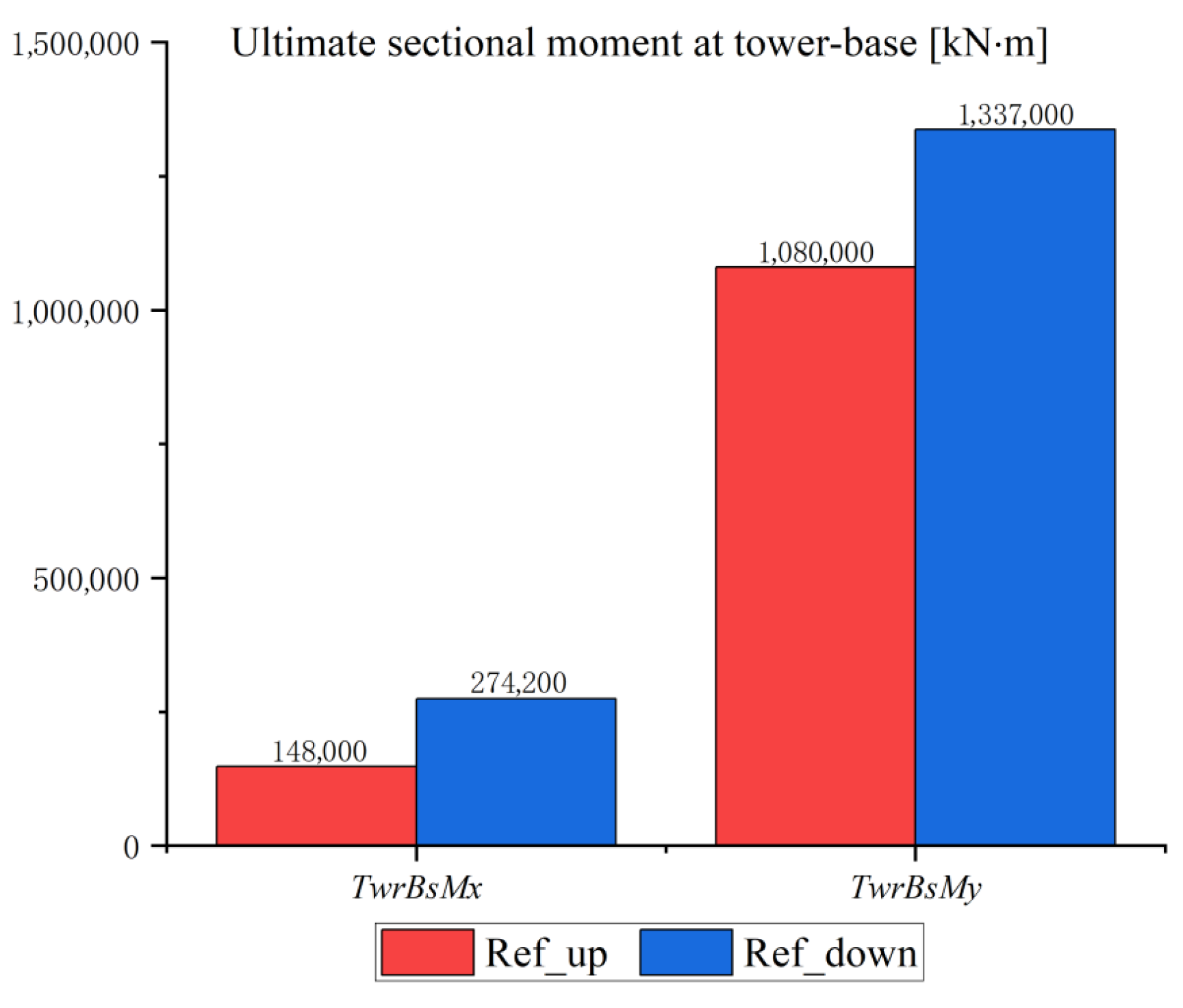
| TwrBsMx | Maximum | EWS+H_25.0 | 148,000 | 148,000 | 147,600 |
| TwrBsMy | Minimum | EWS+H_15.0 | −173,300 | 29,080 | −173,300 |
| TwrBsMy | Maximum | EWS+H_25.0 | 1,080,000 | 66,580 | 1,080,000 |
| TwrBsMx | TwrBsMy | ||||
|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN·m) | (kN·m) |
| TwrBsMx | Minimum | EWS+H_25.0 | −197,300 | −197,300 | 130,600 |
| TwrBsMx | Maximum | EWS+H_25.0 | 274,200 | 274,200 | 64,440 |
| TwrBsMy | Minimum | EWS+H_15.0 | −129,700 | −50,490 | −12,970 |
| TwrBsMy | Maximum | EWS+H_25.0 | 1,337,000 | 61,470 | 1,337,000 |
| RootFx | RootFy | RootMx | RootMy | ||||
|---|---|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN) | (kN) | (kN·m) | (kN·m) |
| RootFx | Minimum | ECDR+2 | −146 | −146 | 106 | −1603 | −5343 |
| RootFx | Maximum | EWSH-21 | 518 | 518 | −143 | 3003 | 16,220 |
| RootFy | Minimum | EWSH-11 | −247 | 345 | −247 | 6148 | 12,550 |
| RootFy | Maximum | EWSH-21 | 205 | 164 | 205 | −5241 | 5033 |
| RootMx | Minimum | EWSH-21 | −5244 | 169 | 203 | −5244 | 5211 |
| RootMx | Maximum | EWSH-11 | 6151 | 346 | −247 | 6151 | 12,560 |
| RootMy | Minimum | ECDR+2 | −5343 | −146 | 106 | −1603 | −5343 |
| RootMy | Maximum | ECDR+2 | 17,800 | 474 | 71 | 318 | 17,800 |
| RootFx | RootFy | RootMx | RootMy | ||||
|---|---|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN) | (kN) | (kN·m) | (kN·m) |
| RootFx | Minimum | DNEWSH-21 | −85 | −85 | −19 | 1242 | −3554 |
| RootFx | Maximum | DNEWSH-21 | 463 | 463 | −154 | 3315 | 14,880 |
| RootFy | Minimum | DNEWSH-11 | −252 | 307 | −252 | 6310 | 11,650 |
| RootFy | Maximum | DNEWSH-21 | 184 | 116 | 184 | −4690 | 3872 |
| RootMx | Minimum | DNEWSH-21 | −4690 | 116 | 184 | −4690 | 3872 |
| RootMx | Maximum | DNEWSH-11 | 6346 | 307 | −251 | 6346 | 11,660 |
| RootMy | Minimum | DNEWSH-21 | −3635 | −83 | −31 | 1330 | −3635 |
| RootMy | Maximum | DNEWSH-21 | −85 | −85 | −19 | 1242 | −3554 |
| TwrBsMx | TwrBsMy | ||||
|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN·m) | (kN·m) |
| TwrBsMx | Minimum | EWSH-21 | −8959 | −8959 | 3414 |
| TwrBsMx | Maximum | ECDR+2 | 20,570 | 20,570 | 2735 |
| TwrBsMy | Minimum | EWSH-21 | −61,380 | 5794 | −61,380 |
| TwrBsMy | Maximum | EWSH-21 | 214,800 | 11,720 | 214,800 |
| TwrBsMx | TwrBsMy | ||||
|---|---|---|---|---|---|
| Variable | Type | Working Conditions | Ultimate Value | (kN·m) | (kN·m) |
| TwrBsMx | Minimum | EWSH-21 | −9003 | −9003 | 2478 |
| TwrBsMx | Maximum | EWSH-21 | 18,250 | 18,250 | 172,000 |
| TwrBsMy | Minimum | EWSH-21 | −64,150 | 4167 | −64,150 |
| TwrBsMy | Maximum | EWSH-21 | 222,700 | 13,890 | 222,700 |
| Topic | Suzlon-Based 2.1 MW | NREL 5 MW | Hitachi-Based 10 MW DW Case | IEA 15 MW |
|---|---|---|---|---|
| Fatigue at blade root: flapwise bending moments | 5.00% | 2.44% | Around 0.00% | −2.63% |
| Fatigue at blade root: edgewise bending moments | 7.00% | 3.32% | Around −1.00% | −2.41% |
| Note: For Hitachi-based 10 MW, the value −1.00% is obtained when the blade mass reduction ratio −6.80% is taken out. This is because the blade of the downwind type is optimized to have less mass. | ||||
| Extreme at blade root: flapwise bending moments | −10.00% | −12.42% | Around −15.50% | −9.50% |
| Extreme at blade root: edgewise bending moments | 5.00% | 3.17% | N/A | −2.27% |
| Extreme at tower base: fore-aft bending moments | 14.00% | 3.68% | Around −9.00% | 19.22% |
| Extreme at tower base: side-to-side bending moments | 10.00% | −11.28% | N/A | 85.27% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Sun, Z.; Xia, Y.; Shen, W.; Zhu, W.; Ferrer, E. Aeroelastic Study of Downwind and Upwind Configurations Under Different Power Levels of Wind Turbines. Machines 2025, 13, 599. https://doi.org/10.3390/machines13070599
Sun Z, Sun Z, Xia Y, Shen W, Zhu W, Ferrer E. Aeroelastic Study of Downwind and Upwind Configurations Under Different Power Levels of Wind Turbines. Machines. 2025; 13(7):599. https://doi.org/10.3390/machines13070599
Chicago/Turabian StyleSun, Zixuan, Zhenye Sun, Yusheng Xia, Wenzhong Shen, Weijun Zhu, and Esteban Ferrer. 2025. "Aeroelastic Study of Downwind and Upwind Configurations Under Different Power Levels of Wind Turbines" Machines 13, no. 7: 599. https://doi.org/10.3390/machines13070599
APA StyleSun, Z., Sun, Z., Xia, Y., Shen, W., Zhu, W., & Ferrer, E. (2025). Aeroelastic Study of Downwind and Upwind Configurations Under Different Power Levels of Wind Turbines. Machines, 13(7), 599. https://doi.org/10.3390/machines13070599










