Energy Efficiency Analysis of Hydraulic Excavators’ Swing Drive Transmission
Abstract
1. Introduction
2. Mathematical Model of the Swing Drive of Excavators
2.1. Synthesis of the Drive System
2.2. Energy Analysis of the Efficiency of the Swing Drive Transmission
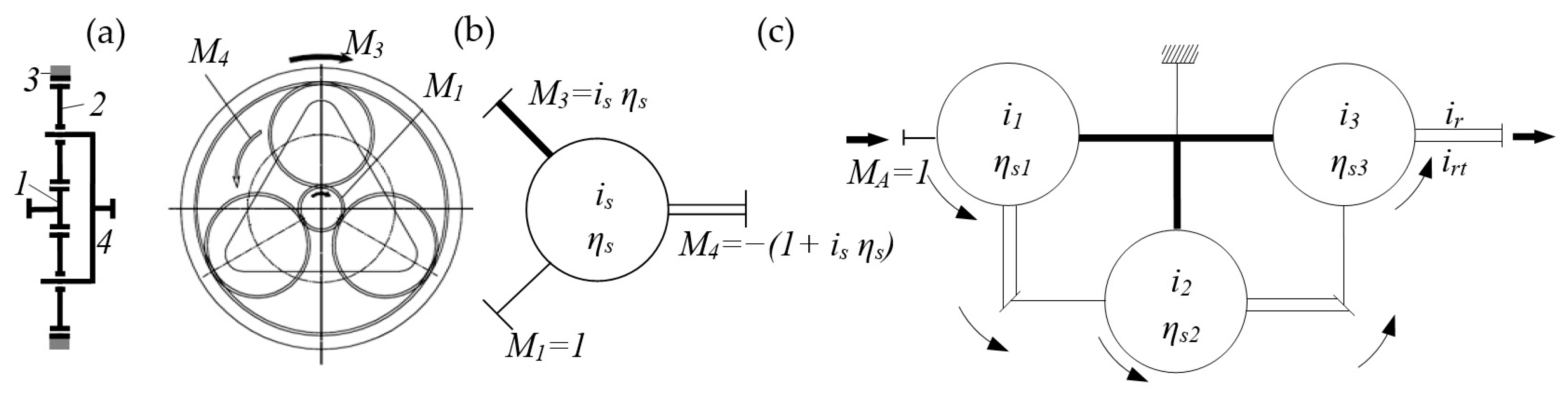
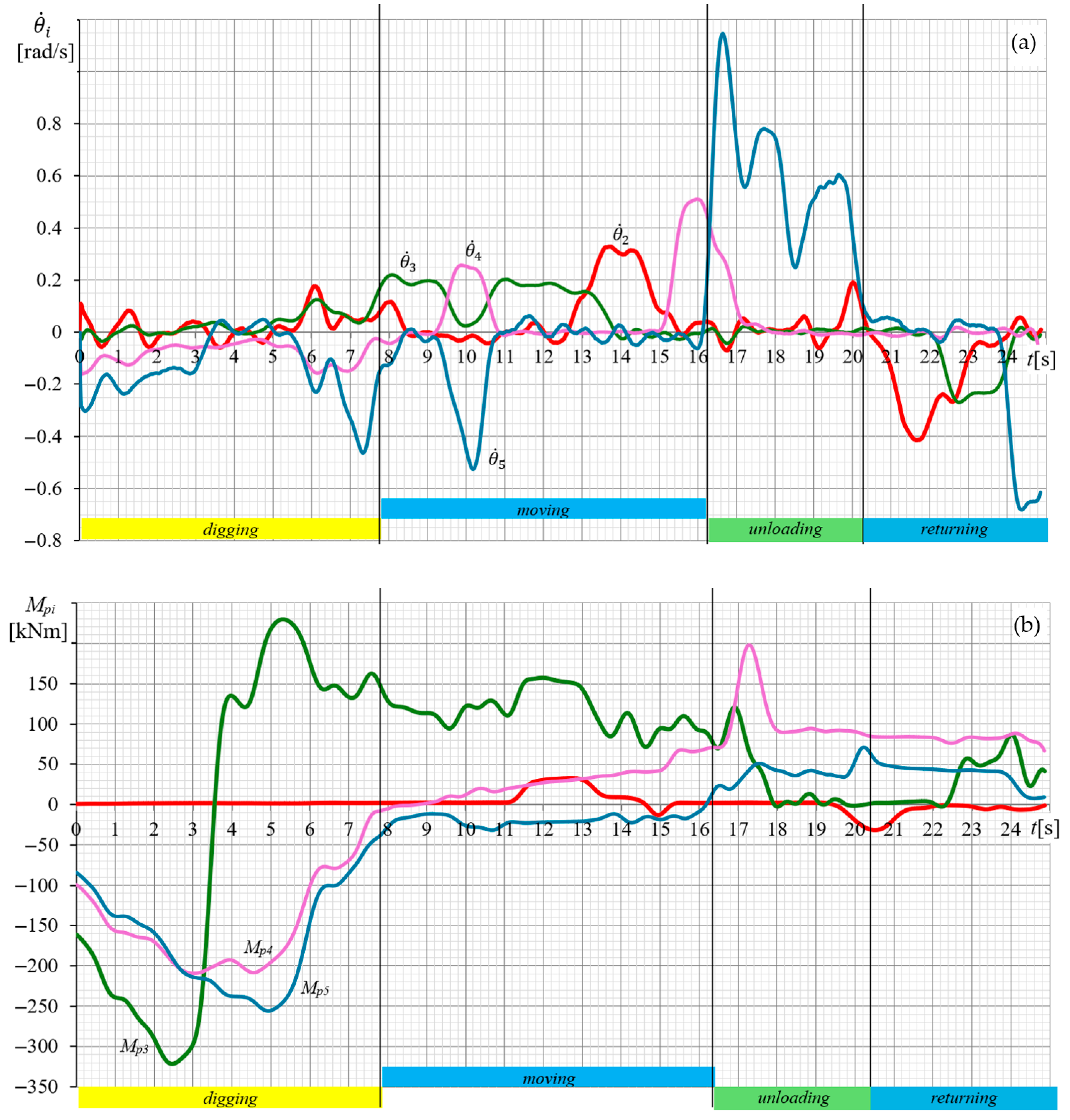
3. Example of Drive Efficiency Analysis
3.1. The First Manipulation Task
3.2. The Second Manipulation Task
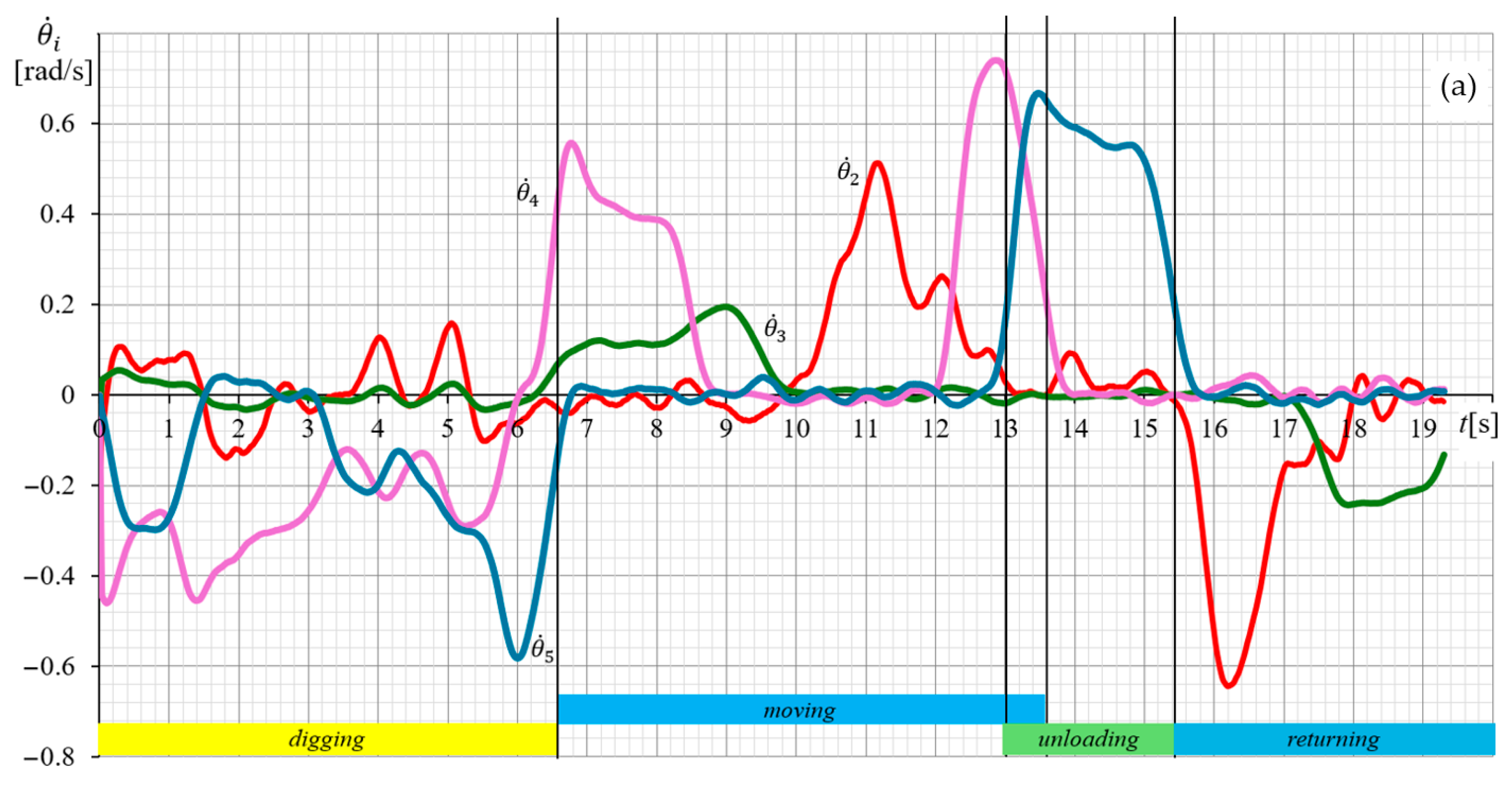
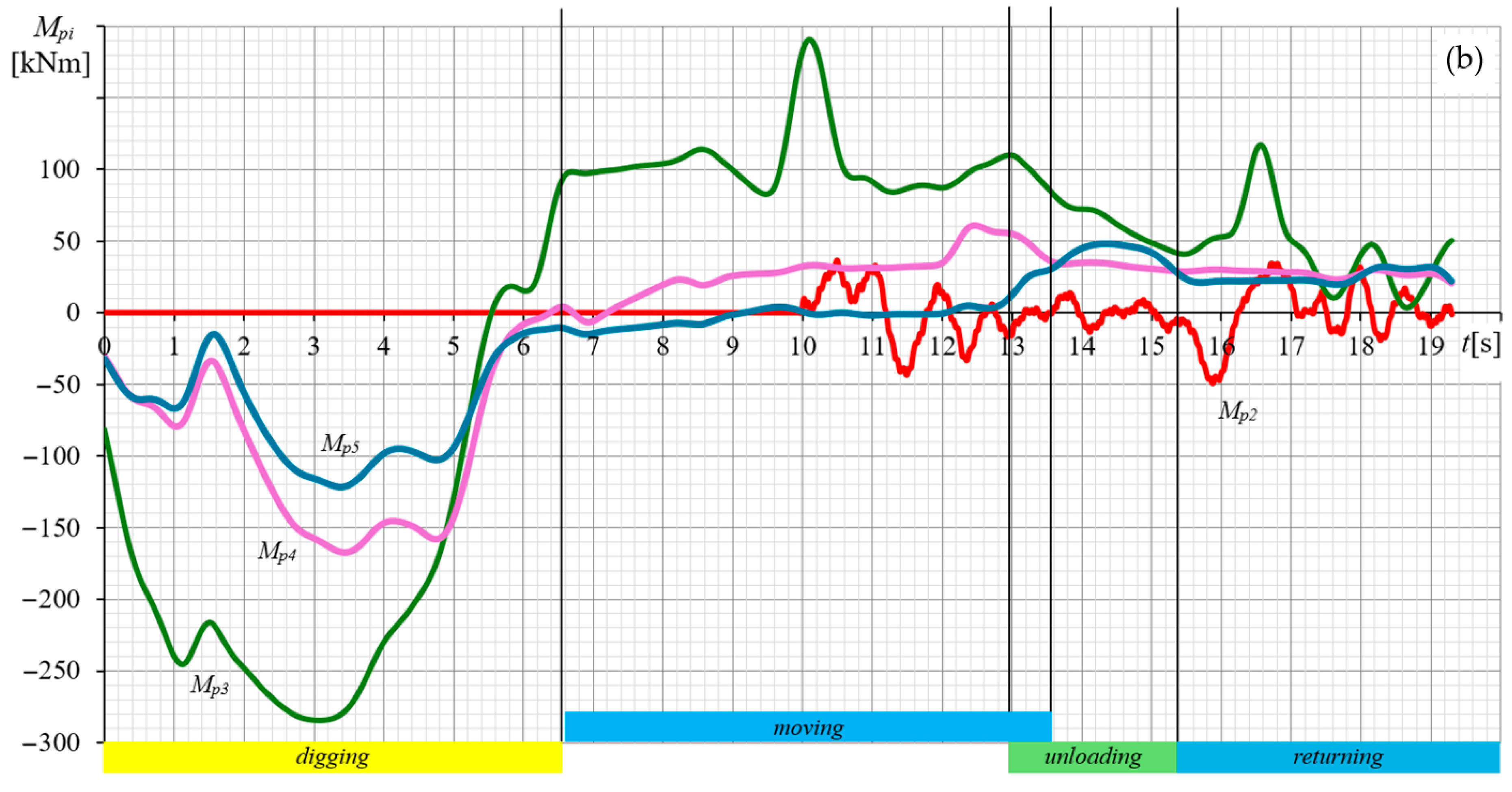
3.3. Comparative Analysis of the Energy Efficiency of the Drive System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Meaning | Units |
| M2 | output torque of the slewing platform | kNm |
| n2 | rotational speed of the slewing platform | min−1 |
| qpmax | maximum displacement of the hydraulic pump | cm3 |
| qmmax | maximum displacement of the hydraulic motor | cm3 |
| p | pressure in the supply lines of the hydraulic motor | MPa |
| po | pressure in the return lines of the hydraulic motor | MPa |
| ir | transmission ratio of the reducer | / |
| ηr | degree of efficiency of the reducer | / |
| ηpv | volumetric degree of efficiency of the hydraulic pump | / |
| ηpm | mechanical degree of efficiency of the hydraulic pump | / |
| ηmv | volumetric degree of efficiency of the hydraulic motor | / |
| ηmm | mechanical degree of efficiency of the hydraulic motor | / |
| εp | hydraulic pump regulation range | / |
| εm | hydraulic motor regulation range | / |
| il | transmission ratio between the reducer and the axial bearing | / |
| ηl | degree of efficiency between the reducer and the axial bearing | / |
| Mrmax | maximum output torque at the gearbox output shaft of the drive mechanism | kNm |
| il | gear ratio between the toothed ring of the bearing and the gear on the output shaft of the gearbox in the drive mechanism | / |
| ηl | efficiency between the toothed ring of the bearing and the gear on the output shaft of the gearbox in the drive mechanism | / |
| nc2 | number of drive mechanisms for the slewing platform | / |
| Mrdmax | maximum allowable torque at the output shaft of the gearbox | kNm |
| kr | deviation coefficient between the required torque and the allowable torque of the gearbox | / |
| kМ | coefficients of the allowable range for the torque of the slewing platform | / |
| kn | coefficients of the allowable range for the rotational speed of the slewing platform | / |
| ηu | overall efficiency of the transmission | / |
| ηmu | efficiency of the hydraulic motor | / |
| ηr | efficiency of the gearbox transmission | / |
| ηmv | volumetric efficiency of the transmission | / |
| ηmm | mechanical efficiency of the transmission | / |
| flow losses of the hydraulic motor | m3/s | |
| torque losses of the hydraulic motor | Nm | |
| h1m, h2m | correlation constants for flow losses | m3/sPa, m3/rad |
| kom, k1m, k2m | correlation constants for torque losses | Nm, Nm/Pa, Nm/(rad/s) |
| irt | torque transmission ratio of the planetary gearbox considering friction losses in gear meshing | / |
| ir | torque transmission ratio of the gearbox without considering friction losses in gear meshing. | / |
| M1 | unit input torque of the sun gear | Nm |
| M3 | output torque on the fixed ring gear | Nm |
| M4 | output torque on the planet carrier | Nm |
| is | gear ratio defined as the number of teeth of the fixed ring gear to the sun gear | / |
| z3 | number of teeth of the fixed ring gear | / |
| z1 | number of teeth of the sun gear | / |
| ηs | efficiency of the elementary planetary gear set accounting for friction in gear meshing | / |
| ns | elementary planetary gear sets | / |
References
- Babaeimorad, S.; Fattahi, P.; Fazlollahtabar, H.; Shafiee, M. An integrated optimization of production and preventive maintenance scheduling in industry 4.0. Facta Univ. Ser. Mech. Eng. 2024, 22, 711–720. [Google Scholar] [CrossRef]
- Lodewyks, J.; Zurbrügg, P. Decentralized energy-saving hydraulic concepts for mobile working machines. In Proceedings of the 10th International Fluid Power Conference, Dresden, German, 8–10 March 2016; pp. 79–87. [Google Scholar]
- Su, D.; Hou, L.; Wang, S.; Bu, X.; Xia, X. Energy Flow Analysis of Excavator System Based on Typical Working Condition Load. Electronics 2022, 11, 1987. [Google Scholar] [CrossRef]
- Do, T.C.; Dang, T.D.; Dinh, T.Q.; Ahn, K.K. Developments in energy regeneration technologies for hydraulic excavators: A review. Renew. Sustain. Energy Rev. 2021, 145, 111076. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Do, T.C.; Dang, T.D.; Ahn, K.K. Improving the efficiency of hybrid hydraulic excavators with a novel powertrain and energy management system. Energy 2025, 323, 135766. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, A.; Thakur, S. Sustainable energy solutions for hydraulic excavators: A comprehensive review and novel energy regeneration approach. Proc. Inst. Mech. Eng. Part E 2025. [Google Scholar] [CrossRef]
- Ge, L.; Quan, L.; Zhang, X.; Zhao, B.; Yang, J. Efficiency improvement and evaluation of electric hydraulic excavator with speed and displacement variable pump. Energy Convers. Manag. 2017, 150, 62–71. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Quan, L.; Hao, Y.; Ge, L.; Xia, L. Study on energy efficiency characteristics of the heavy-duty manipulator driven by electro-hydraulic hybrid active-passive system. Autom. Constr. 2021, 125, 103646. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, X.; Ge, L.; Quan, L. Dual Source Integrated Driving for Hydraulic Excavator Swing System. IEEE Access 2021, 9, 120755–120764. [Google Scholar] [CrossRef]
- Huang, W.; Quan, L.; Ge, L.; Xia, L. Combined velocity and position control of large inertial hydraulic swing mechanism considering energy balance of supply and demand. Autom. Constr. 2019, 106, 102899. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Do, T.C.; Ahn, K.K. Hybrid powertrain with dual energy regeneration for boom cylinder movement in a hydraulic excavator. Autom. Constr. 2025, 171, 105974. [Google Scholar] [CrossRef]
- Tong, Z.; Jiang, Y.; Tong, S.; Zhang, Q.; Wu, J. Hybrid drivetrain with dual energy regeneration and collaborative control of driving and lifting for construction machinery. Autom. Constr. 2023, 150, 104806. [Google Scholar] [CrossRef]
- Yu, Y.; Do, T.C.; Yin, B.; Ahn, K.K. Improvement of energy saving for hybrid hydraulic excavator with novel powertrain. Int. J. Precis. Eng. Manuf.-Green Technol. 2023, 10, 521–534. [Google Scholar] [CrossRef]
- Do, T.C.; Nguyen, D.G.; Dang, T.D.; Ahn, K.K. A Boom Energy Regeneration System of Hybrid Hydraulic Excavator Using Energy Conversion Components. Actuators 2021, 10, 1. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Do, T.C.; Ahn, K.K. Investigation and optimization of energy consumption for hybrid hydraulic excavator with an innovative powertrain. Actuators 2023, 12, 382. [Google Scholar] [CrossRef]
- Truong, D.Q.; Marco, J.; Greenwood, D.; Harper, L.; Corrochano, D.G.; Yoon, J.I. Challenges of micro/mild hybridisation for construction machinery and applicability in UK. Renew. Sustain. Energy Rev. 2018, 91, 301–320. [Google Scholar] [CrossRef]
- Ge, L.; Quan, L.; Zhang, X.; Dong, Z.; Yang, J. Power matching and energy efficiency improvement of hydraulic excavator driven with speed and displacement variable power source. Chin. J. Mech. Eng. 2019, 32, 100. [Google Scholar] [CrossRef]
- Song, H.; Li, G.; Xiong, X.; Li, M.; Qin, Q.; Mitrouchev, P. A novel data fusion based intelligent identification approach for working cycle stages of hydraulic excavators. ISA Trans. 2024, 148, 78–91. [Google Scholar] [CrossRef]
- Precup, R.E.; Roman, R.C.; Hedrea, E.L.; Petriu, E.M.; Bojan-Dragos, C.A.; Szedlak-Stinean, A.I. Metaheuristic-based tuning of proportional-derivative learning rules for proportional-integral fuzzy controllers in tower crane system payload position control. Facta Univ. Ser. Mech. Eng. 2024, 22, 567–582. [Google Scholar] [CrossRef]
- Kim, H.; Yoo, S.; Cho, S.; Yi, K. Hybrid control algorithm for fuel consumption of a compound hybrid excavator. Autom. Constr. 2016, 68, 1–10. [Google Scholar] [CrossRef]
- Zhang, S.; Minav, T.; Pietola, M.; Kauranne, H.; Kajaste, J. The effects of control methods on energy efficiency and position tracking of an electro-hydraulic excavator equipped with zonal hydraulics. Autom. Constr. 2019, 100, 129–144. [Google Scholar] [CrossRef]
- Yao, B.; Liu, S. Energy-saving control of hydraulic systems with novel programmable valves. In Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai, China, 10–14 June 2002; Volume 4, pp. 3219–3223. [Google Scholar]
- Popescu, F.D.; Radu, S.M.; Andraş, A.; Brînaş, I.K. A grafo-numeric method of determination of the operation power of the rotor of EsRc-1400 bucket wheel excavator using computer simulation in SolidWorks. MATEC Web Conf. 2019, 290, 04007. [Google Scholar] [CrossRef]
- Kim, H.; Choi, J.; Yi, K. Development of supervisory control strategy for optimized fuel consumption of the compound hybrid excavator. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2012, 226, 1652–1666. [Google Scholar] [CrossRef]
- Jovanović, V.; Janošević, D.; Marinković, D.; Petrović, N.; Djokić, R. Analysis of Influential Parameters in the Dynamic Loading and Stability of the Swing Drive in Hydraulic Excavators. Machines 2024, 12, 737. [Google Scholar] [CrossRef]
- Modeling of Hydraulic Systems, Tutorial for the Hydraulics Library, Modelon 2013. Available online: https://uomosul.edu.iq/public/files/datafolder_2927/_20200216_095111_580.pdf (accessed on 19 March 2024).
- Arnaudov, K.; Karaivanov, D. The torque method used for studying coupled two-carrier planetary gear trains. Trans. Famena 2013, 37, 49–61. [Google Scholar]
- Vrcan, Ž.; Troha, S.; Marković, K.; Marinković, D. Analysis of complex planetary gearboxes. Spectr. Mech. Eng. Oper. Res. 2024, 1, 227–249. [Google Scholar] [CrossRef]
- Tica, M.; Vrcan, Ž.; Troha, S.; Marinković, D. Reversible planetary gearsets controlled by two brakes, for internal combustion railway vehicle transmission applications. Acta Polytec. Hung. 2023, 20, 95–108. [Google Scholar] [CrossRef]
- Faydor, L.L.; Alfonso, F. Gear Geometry and Applied Theory; Cambridge University Press: New York, NY, USA, 2004; ISBN 9780521815178. [Google Scholar]
- Vrcan, Ž.; Ivanov, V.; Alexandrov, A.; Isametova, M. Size and Efficiency Based Comparison of Kinematically Equivalent Two-Carrier Planetary Gear Trains. Eng. Rev. 2022, 42, 17–31. [Google Scholar] [CrossRef]
- Jodder, C.; Saha, J. Structural analysis of three stage coupled planetary gear train and determination of efficiency. Int. J. Eng. Res. 2016, 5, 746–748. [Google Scholar]
- Bosch Rexroth. Available online: https://store.boschrexroth.com/Hidraulika?cclcl=en_HU (accessed on 9 January 2024).
- Jovanović, V.; Marinković, D.; Janošević, D.; Petrović, N. Influential Factors in the Loading of the Axial Bearing of the Slewing Platform Drive in Hydraulic Excavators. Teh. Vjesn. Teh. Gaz. 2023, 30, 158–168. [Google Scholar]
- Jovanović, V.; Marinković, D.; Petrović, N.; Stojanović, D. The Load Spectrum of Axial Bearing of Hydraulics Excavator with Shovel Attachment. J. Eng. Manag. Syst. Eng. 2024, 3, 175–182. [Google Scholar] [CrossRef]
- Rothe Erde. Available online: https://www.thyssenkrupp-rotheerde.com/en/products/slewing-bearings (accessed on 9 January 2024).
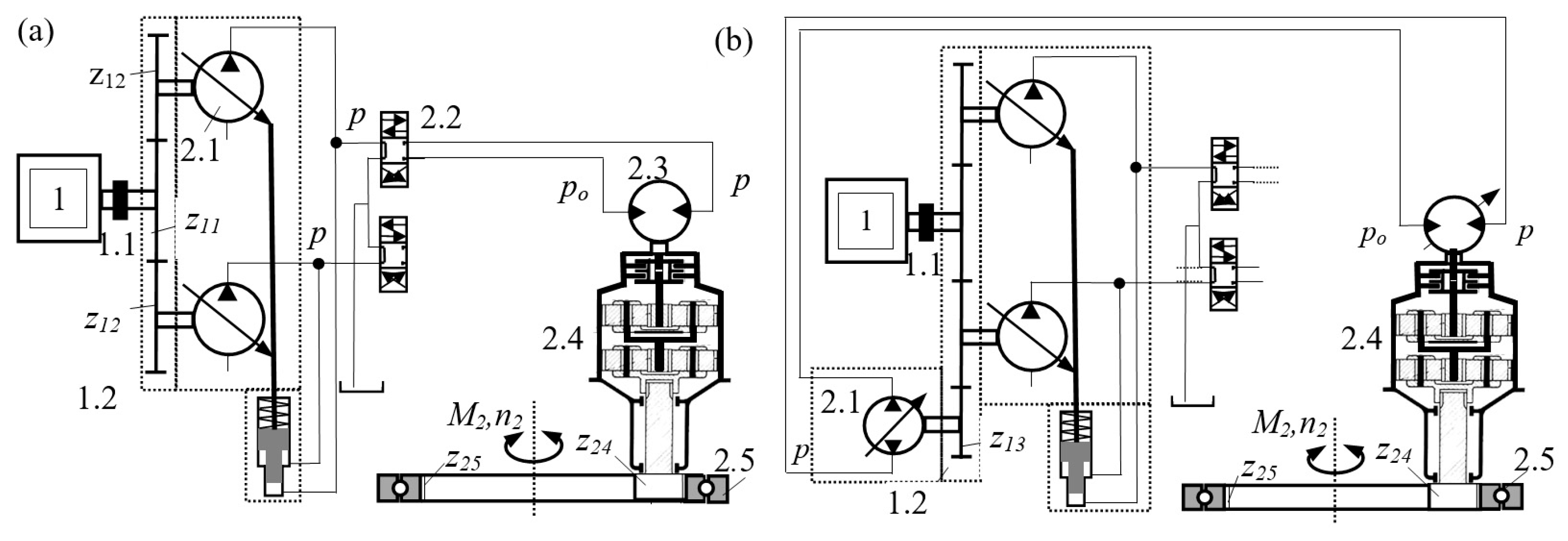

| Parameters | Symbol | Unit | Value |
|---|---|---|---|
| Maximum torque of the slewing platform | M2max | (kNm) | 50 |
| Maximum rotational speed of the slewing platform | n2max/(θ2max) | (min−1/(rad/s)) | 12/(1.25) |
| Number of swing drive mechanisms | nc2 | - | 1 |
| Number of teeth on the ring gear of the axial bearing | z26 | - | 93 |
| Efficiency between the gearbox and the axial bearing | ηl | - | 0.96 |
| Diesel engine max speed range at rated power | nenp, nenk | (min−1) | 2000–2100 |
| Transmission ratio range of the power splitter | iep, iek | - | 0.50–1.20 |
| Pressure range of the hydraulic pump | pmin, pmax | (MPa) | 20–45 |
| Variant/Number of Drives | Hydraulic Pump | Hydraulic Motor | Gearbox | Slewing Platform | |||
|---|---|---|---|---|---|---|---|
| Specific Displacement qp (cm3) | Pressure p (MPa) | Rotational Speed np (min−1) | Specific Displacement qm (cm3) | Transmission Ratio ir | Rotational Speed n2 (min−1) | Torque M2 (kNm) | |
| VE10/1 | 80.00 | 23.00 | 2433.09 | 32.00 | 91.13 | 12.06 | 50.02 |
| VE12/1 | 80.00 | 26.00 | 2141.33 | 80.40 | 31.36 | 12.07 | 50.45 |
| Specific Displacement of the Hydraulic Motor | Flow Loss Constants | Torque Loss Constants | |||
|---|---|---|---|---|---|
| qm cm3 | h1m (m3/sPa) | h2m (m3/rad) | kom (Nm) | k1m (Nm/Pa) | k2m (Nm/(rad/s)) |
| 35 | 1.0565 × 10−12 | 3.0393 × 10−8 | −2.8465 × 10−1 | 3.7989 × 10−7 | 2.1217 × 10−2 |
| 75 | 1.8576 × 10−12 | 5.1773 × 10−8 | 3.4105 | 4.7974 × 10−7 | 6.9763 × 10−2 |
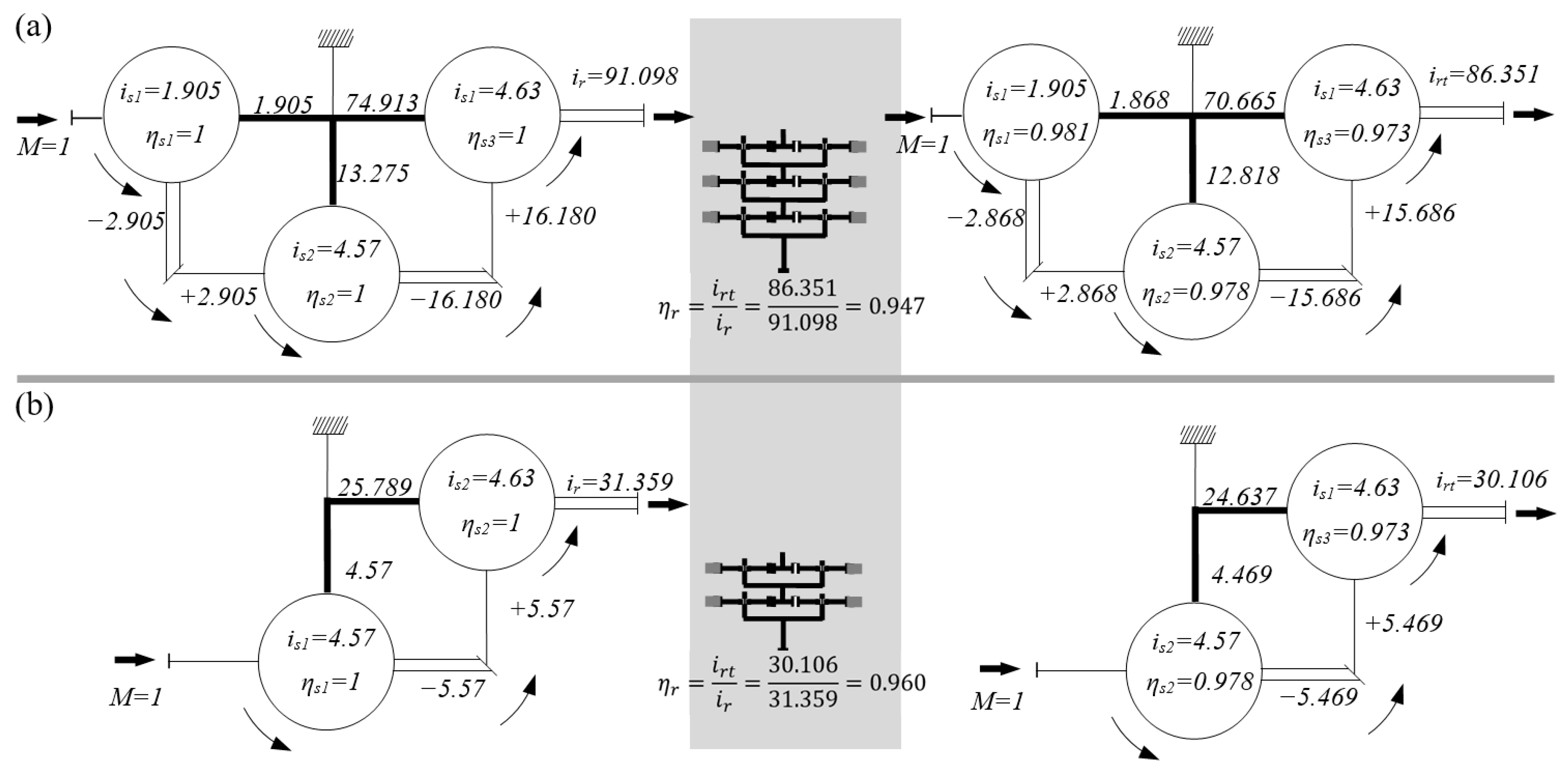
| Name | Symbol | Three-Stage Gearbox | Two-Stage Gearbox | |||
|---|---|---|---|---|---|---|
| First Set | Second Set | Third Set | First Set | Second Set | ||
| Number of teeth on the sun gear | zi1 | 42 | 14 | 11 | 14 | 11 |
| Number of teeth on the planetary gear | zi2 | 19 | 25 | 20 | 25 | 20 |
| Number of teeth on the ring gear | zi3 | 80 | 64 | 51 | 64 | 51 |
| Transmission ratio | isi | 2.905 | 5.57 | 5.63 | 5.57 | 5.63 |
| Efficiency | ηr | 0.947 | 0.960 | |||
| Number of teeth on the output shaft | z24 | 15 | 15 | |||
| Kinematic diagrams of the gearbox |  | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jovanović, V.; Janošević, D.; Marinković, D.; Petrović, N.; Nikolić, B. Energy Efficiency Analysis of Hydraulic Excavators’ Swing Drive Transmission. Machines 2025, 13, 596. https://doi.org/10.3390/machines13070596
Jovanović V, Janošević D, Marinković D, Petrović N, Nikolić B. Energy Efficiency Analysis of Hydraulic Excavators’ Swing Drive Transmission. Machines. 2025; 13(7):596. https://doi.org/10.3390/machines13070596
Chicago/Turabian StyleJovanović, Vesna, Dragoslav Janošević, Dragan Marinković, Nikola Petrović, and Boban Nikolić. 2025. "Energy Efficiency Analysis of Hydraulic Excavators’ Swing Drive Transmission" Machines 13, no. 7: 596. https://doi.org/10.3390/machines13070596
APA StyleJovanović, V., Janošević, D., Marinković, D., Petrović, N., & Nikolić, B. (2025). Energy Efficiency Analysis of Hydraulic Excavators’ Swing Drive Transmission. Machines, 13(7), 596. https://doi.org/10.3390/machines13070596









