Study on Angular Velocity Measurement for Characterizing Viscous Resistance in a Ball Bearing
Abstract
1. Introduction
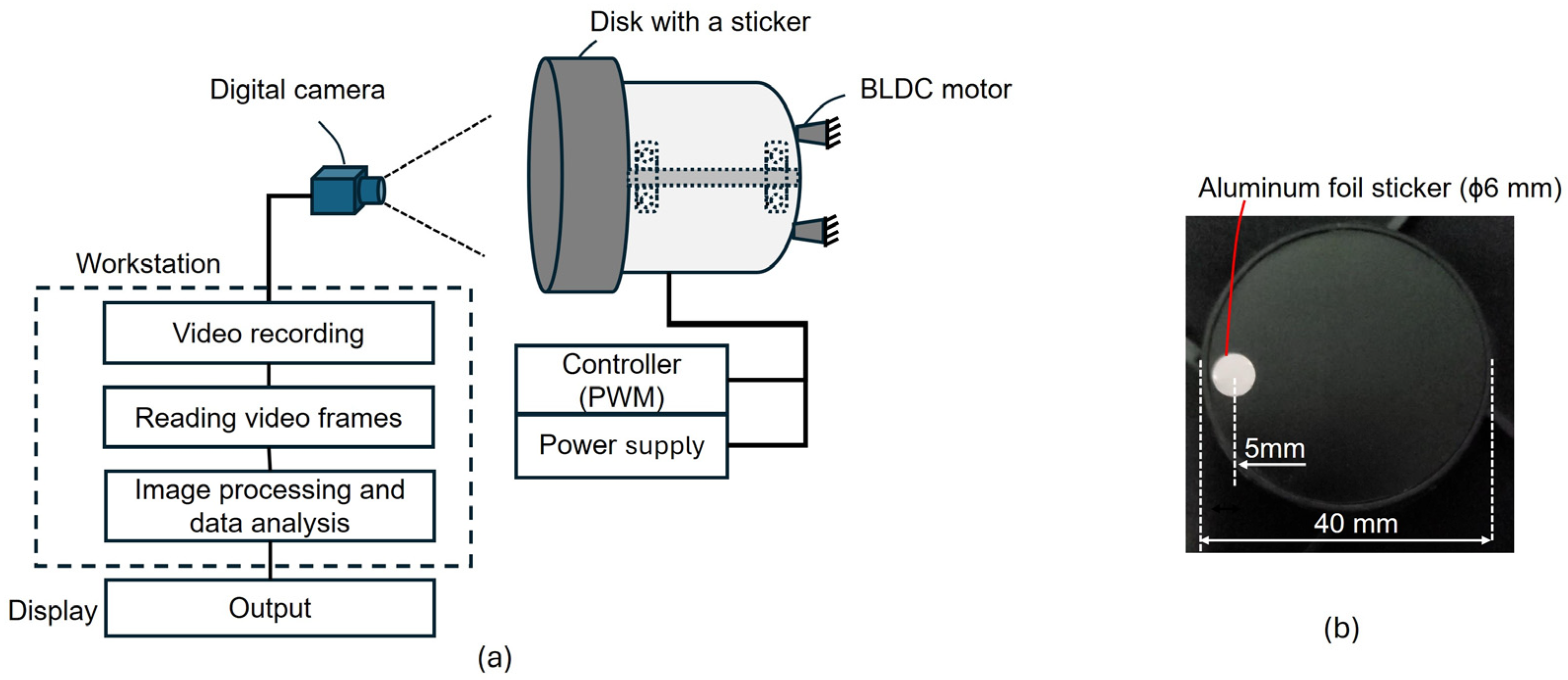
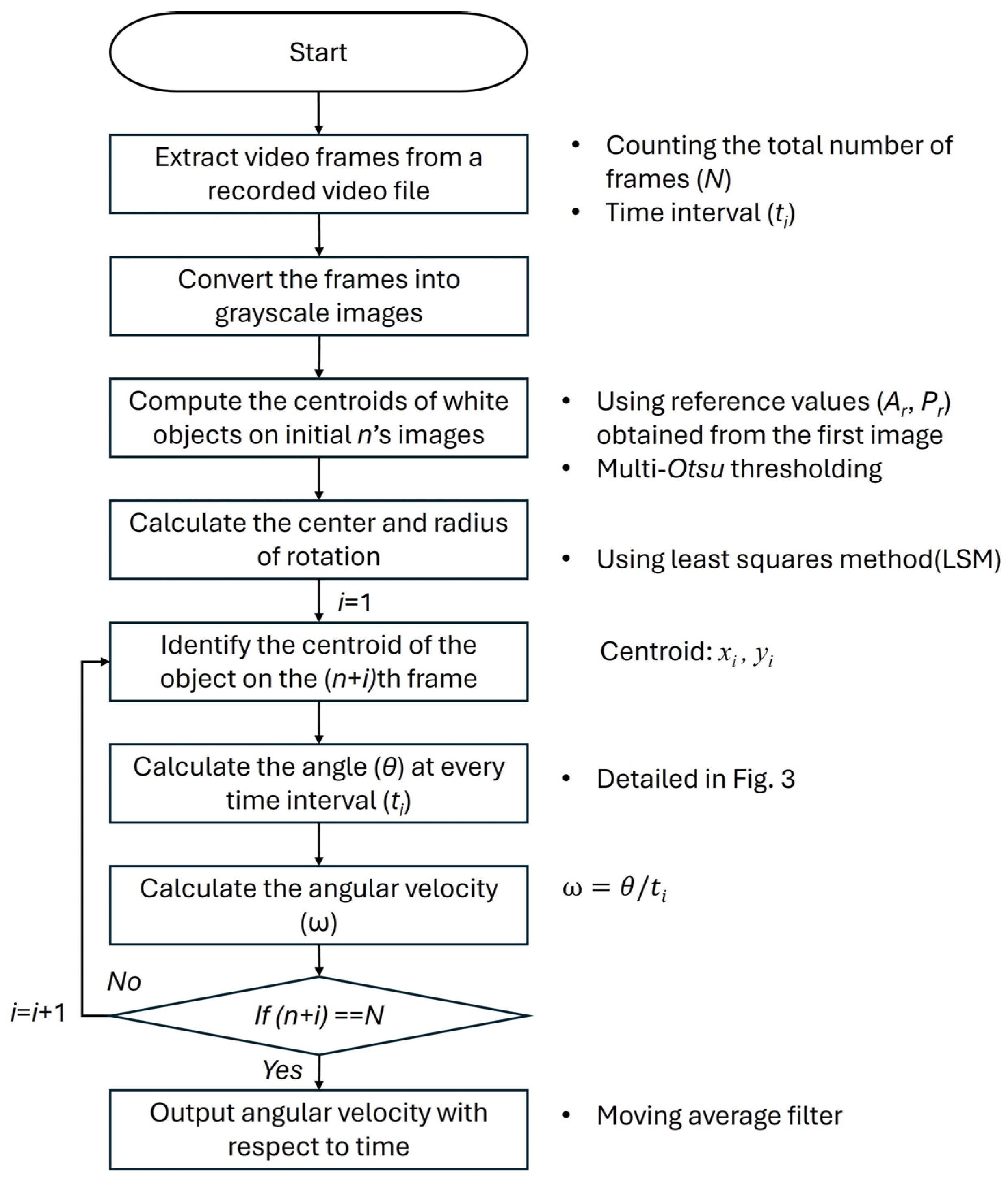
2. Materials and Methods
A Proposed Angular Velocity Measuring System
- Condition 1: and ;
- Condition 2: Among objects satisfying Condition 1, the nearest object to the predicted position (determined with the angular displacement of the previous frame).
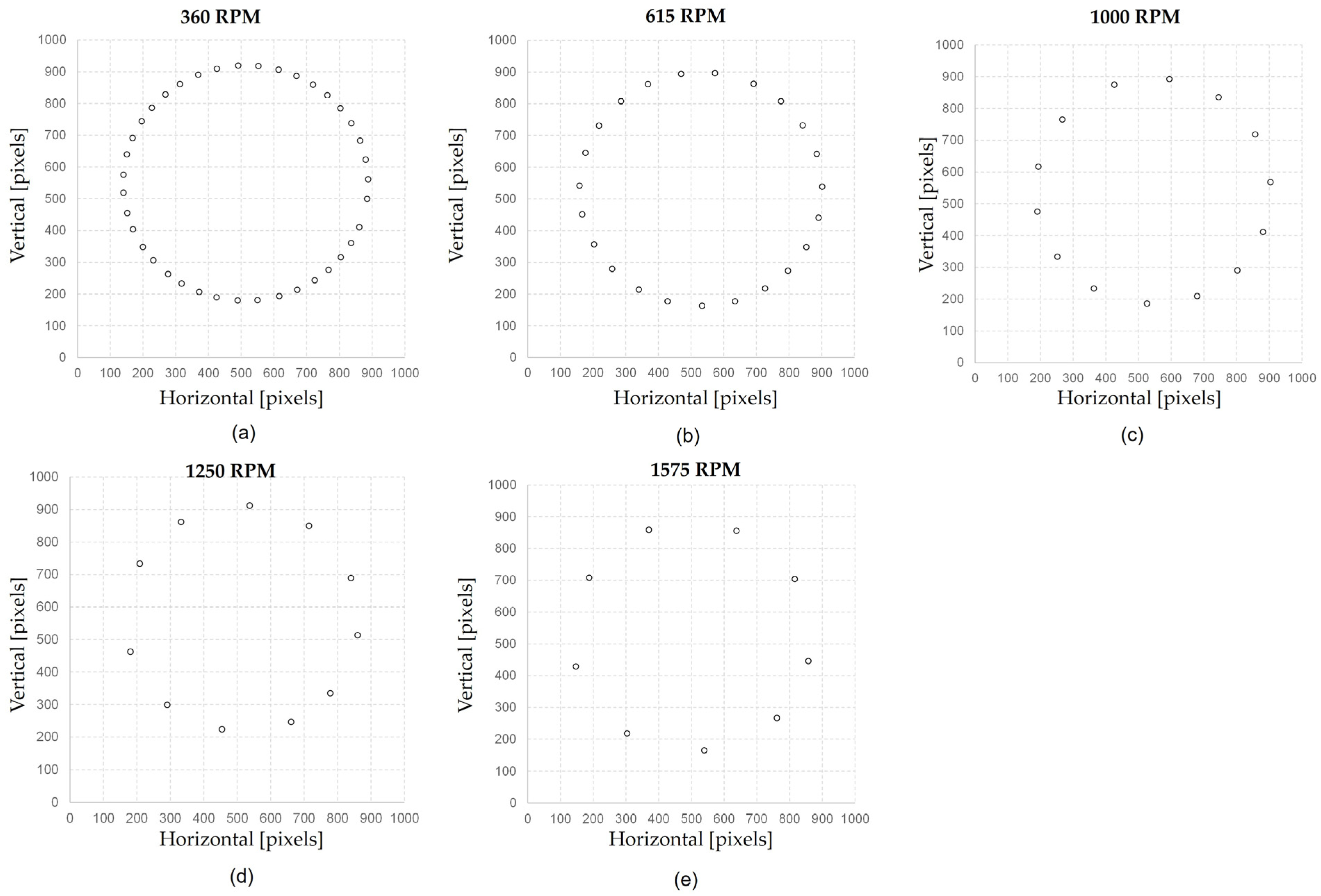
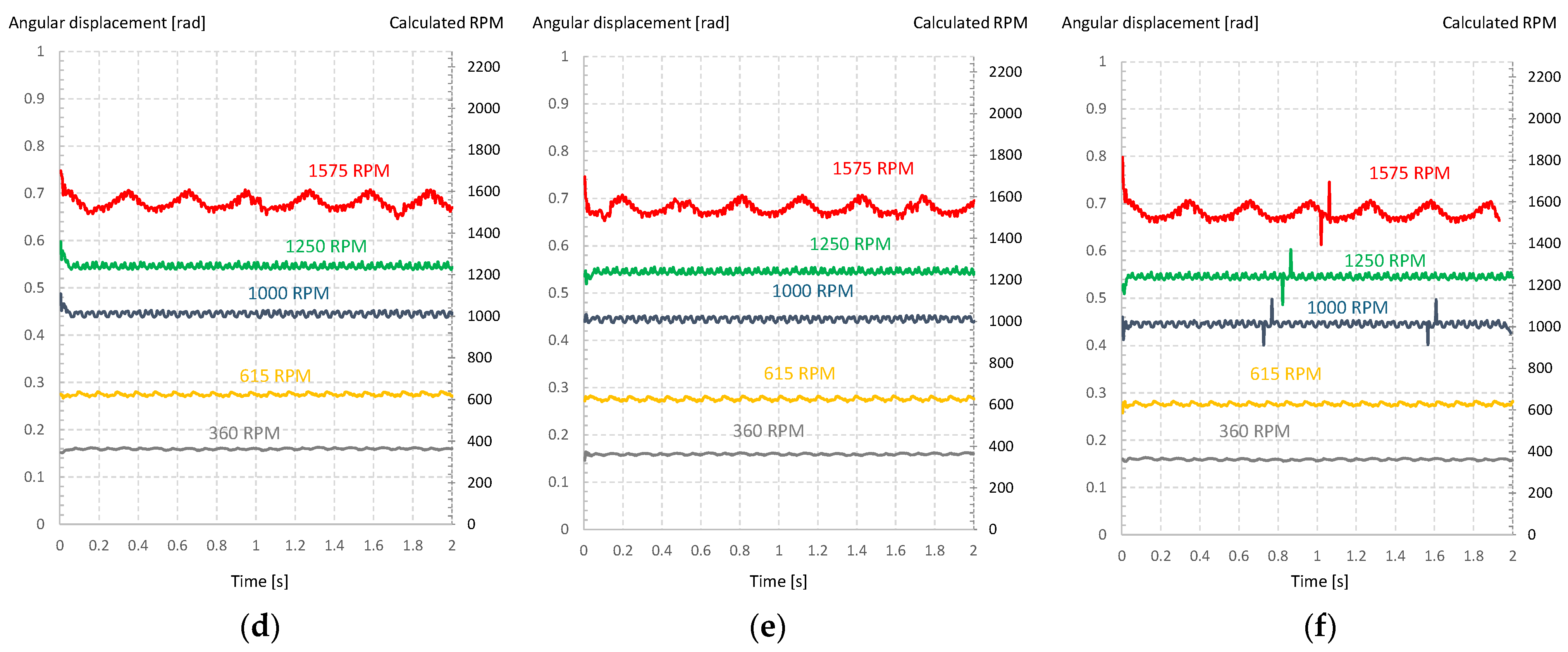
3. Results
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Area of a white region |
| Ar | Reference area of a white region in the first frame |
| N | Total number of frames |
| P | Perimeter of a white region |
| Pr | Reference perimeter of a white region in the first frame |
| R | Radius of the centroid trajectory |
| t | Time |
| ti | Time interval |
| θ | Angular displacement |
| β | Viscous exponent |
| ω | Angular velocity |
| ω0 | The initial angular velocity at power-off |
Appendix A. Brief Code for Finding Motion Trajectory with Five Positions
| for f = frameNo:1:5 fileName = sprintf('%d.jpg', frameNo); Img = rgb2gray(imread(fileName)); level = multithresh(Img,2); bwImg = imbinarize(double(Img), level(1,2)); bwImg = bwareaopen(bwImg, 50); edges= edge(bwImg, 'canny'); % Detection of Boundary [B, L] = bwboundaries(edges, 'noholes'); for i = 1:(length(B)) boundary = B{i}; reducedBoundary = reducepoly(boundary, 0.001); poly = polyshape(reducedBoundary(:,2), reducedBoundary(:,1)); Area_poly = area(poly); Pr = perimeter(poly); % Ref_area and Ref_Pr were determined on the first frame image. if Area_poly > (0.5*Ref_area) && Area_poly < (1.5*Ref_area) if Pr > (0.5*Ref_Pr) && Pr < (1.5*Ref_Pr) [ccx,ccy] = centroid(poly); cx = ccx; cy = SY-ccy; % SY is the height of the image end end end Cdata(frameNo,1) = cx; Cdata(frameNo,2) = cy; end % Initial values for centers and radius Ini_values = [mean(Cdata(:,1)), mean(Cdata(:,2)), 5]; % Definition of an error function CircleFit = @(params, xy) sqrt((xy(:,1) - params(1)).^2 + (xy(:,2) - params(2)).^2) - params(3); % Non-linear least squares method Op_Para = lsqcurvefit(CircleFit,Ini_values,Cdata,zeros(size(Cdata,1),1)); % Opitmal center(a, b) and radius (R) a = Op_Para(1); b = Op_Para(2); R = abs(Op_Para(3)); end |
Appendix B. Brief Code for Predicting Angular Velocity
| for FrameNo = Ni:Ns % Ni is the 6th frame, Ns is the final frame. fileName = sprintf('%d.jpg', FrameNo); Img = rgb2gray(imread(fileName)); level = multithresh(Img,2); bwImg = imbinarize(double(Img), level(1,2)); bwImg = bwareaopen(bwImg, 50); edges= edge(bwImg, 'canny'); [B, L] = bwboundaries(edges, 'noholes'); Min_L = 500; % initial nominal value for i = 1:(length(B)) boundary = B{i}; reducedBoundary = reducepoly(boundary, 0.001); poly = polyshape(reducedBoundary(:,2), reducedBoundary(:,1)); Area_poly = area(poly); Pr = perimeter(poly); if Area_poly > (0.5*Ref_area) && Area_poly < (1.5*Ref_area) if Pr > (0.5*Ref_Pr) && Pr < (1.5*Ref_Pr) [ccx,ccy] = centroid(poly); ccy = SY-ccy; %Prediction of centroid x and y px = a+(Cdata(FrameNo,1)-a)*cos(degree)-(Cdata(FrameNo,2)-b)*sin(degree); % predicted x py = b+(Cdata(FrameNo,1)-a)*sin(degree) + (Cdata(FrameNo,2)-b)*cos(degree); %predicted y L = sqrt((px-ccx)^2 +(py-ccy)^2); if L < Min_L % For detecting the nearest object Min_L = L; cx = ccx; cy = ccy; end end end end Cdata(FrameNo,1) = cx; Cdata(FrameNo,2) = cy; x1= Cdata(FrameNo-1,1); x2= Cdata(FrameNo,1); y1= Cdata(FrameNo-1,2); y2= Cdata(FrameNo,2); %%%%%% Calculation of angular velocity%%%%%%%% chord_length = sqrt(((x2-x1)^2) + ((y2-y1)^2)); degree = 2*asin(chord_length/(2*r)); time_interval = 1/240; % pre-defined value Angular_velocity = degree/time_interval; end |
References
- Huang, G.; Lei, W.; Dong, X.; Zou, D.; Chen, S.; Dong, X. Stage-Based Remaining Useful Life Prediction for Bearings Using GNN and Correlation-Driven Feature Extraction. Machines 2025, 13, 43. [Google Scholar] [CrossRef]
- Doğan, B.K.; Karaçay, T. Temperature and vibration condition monitoring of a polymer hybrid ball bearing. J. Vib. Eng. Technol. 2022, 10, 2385–2390. [Google Scholar] [CrossRef]
- Mokhtari, N.; Pelham, J.G.; Nowoisky, S. Friction and wear monitoring methods for journal bearings of geared turbofans based on acoustic emission signals and machine learning. Lubricants 2020, 8, 29. [Google Scholar] [CrossRef]
- Azevedo, G.O.D.A.; Fernandes, B.J.T.; Silva, L.H.D.S.; Freire, A.; de Araújo, R.P.; Cruz, F. Event-based angular speed measurement and movement monitoring. Sensors 2022, 22, 7963. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Wang, L.; Zhang, J. A visual-based angle measurement method using the rotating spot images: Mathematic modeling and experiment validation. IEEE Sens. J. 2021, 21, 16576–16583. [Google Scholar] [CrossRef]
- Yang, M.; An, H.; Mo, S.; Gong, H.; Dong, B.; Chen, G. Efficient monocular vision method used for measuring the angular rate and acceleration in rotation motion. Opt. Express 2022, 30, 45436–45446. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Yamakawa, Y.; Senoo, T.; Ishikawa, M. Visual encoder: Robust and precise measurement method of rotation angle via high-speed RGB vision. Opt. Express 2016, 24, 13375–13386. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Zhong, S.; Zhang, Q.; Peng, Z.; Liu, S.; Yu, Y. Vision-based measurement system for instantaneous rotational speed monitoring using linearly varying-density fringe pattern. IEEE Trans. Instrum. Meas. 2018, 67, 1434–1445. [Google Scholar] [CrossRef]
- Wang, T.; Wang, L.; Yan, Y.; Zhang, S. Rotational speed Measurement using a low-cost imaging device and image processing algorithms. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Hayakawa, T.; Watanabe, T.; Ishikawa, M. Real-time high-speed motion blur compensation system based on back-and-forth motion control of galvanometer mirror. Opt. Express 2015, 23, 31648–31661. [Google Scholar] [CrossRef] [PubMed]
- Altmann, B.; Pape, C.; Reithmeier, E. Determining angular velocities of fast rotating objects based on motion blur to control an optomechanical derotator. Proc. Appl. Math. Mech. 2018, 18, e201800092. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Guo, S.; Li, T. Measuring the angular velocity of a propeller with a video camera using electronic rolling shutter. J. Sens. 2018, 2018, 1037083. [Google Scholar] [CrossRef]
- Quan, S.; Chen, L.; Wu, S.; Zhang, B. Vectorial doppler complex spectrum and its application to the rotational detection. Appl. Phys. Express 2023, 16, 042002. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Kim, K. Development of a machine vision system for the average roughness measurement of shot- and sand-blasted surfaces. Lubricants 2024, 12, 339. [Google Scholar] [CrossRef]
- Islam, M.S.; Mir, S.; Sebastian, T. Issues in reducing the cogging torque of mass-produced permanent-magnet brushless DC motor. IEEE Trans. Ind. Appl. 2004, 40, 813–820. [Google Scholar] [CrossRef]



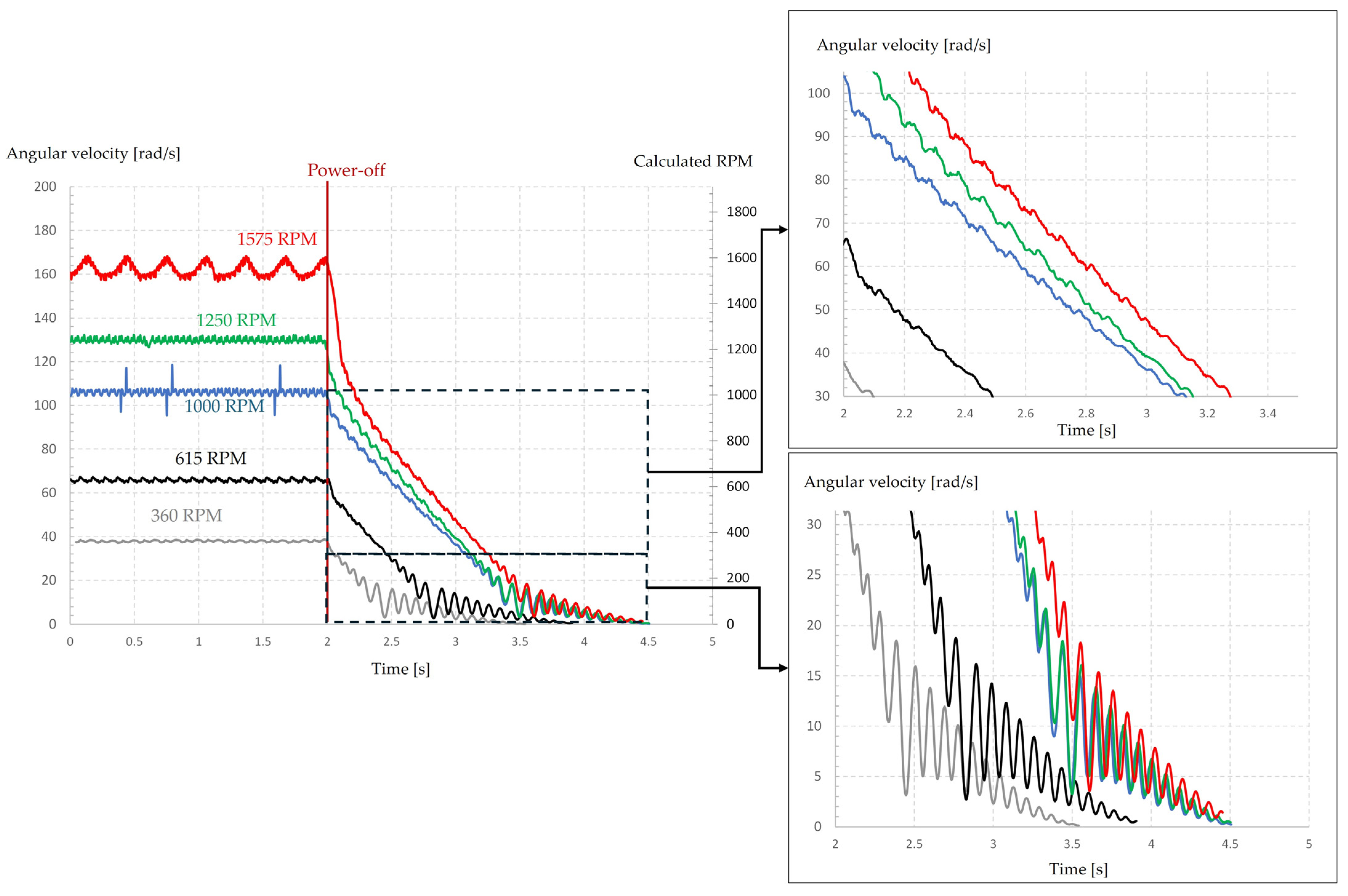
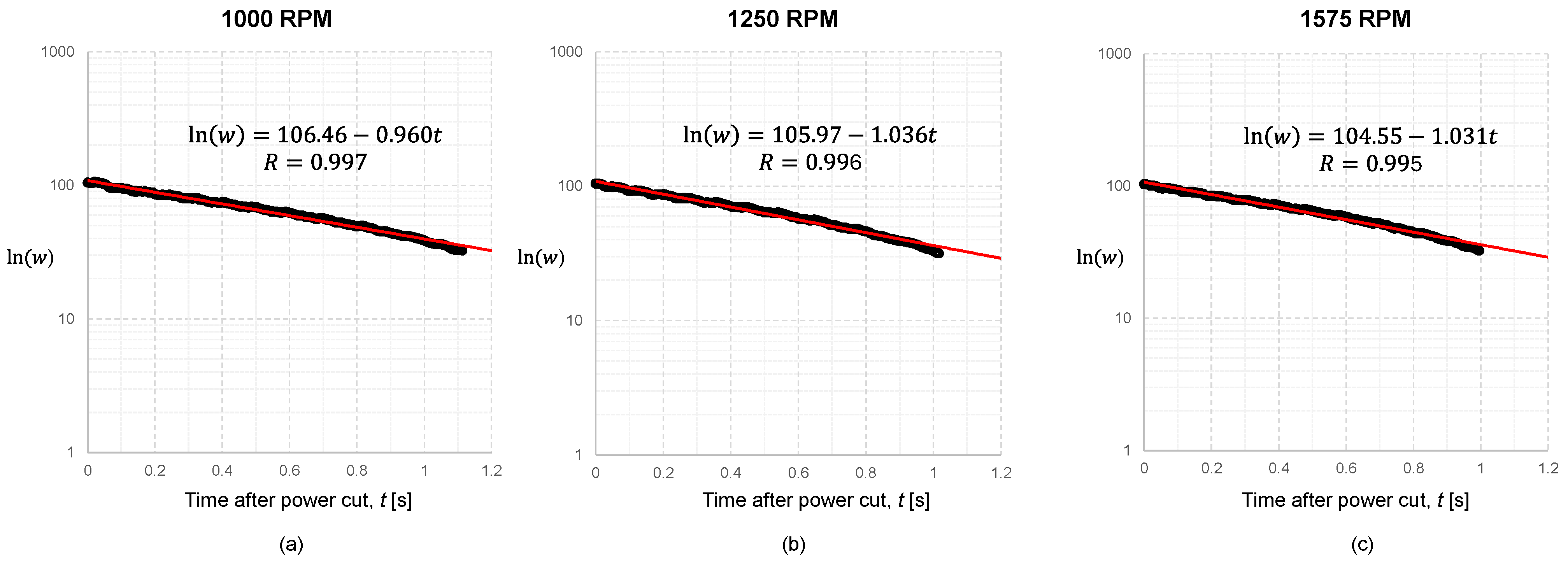
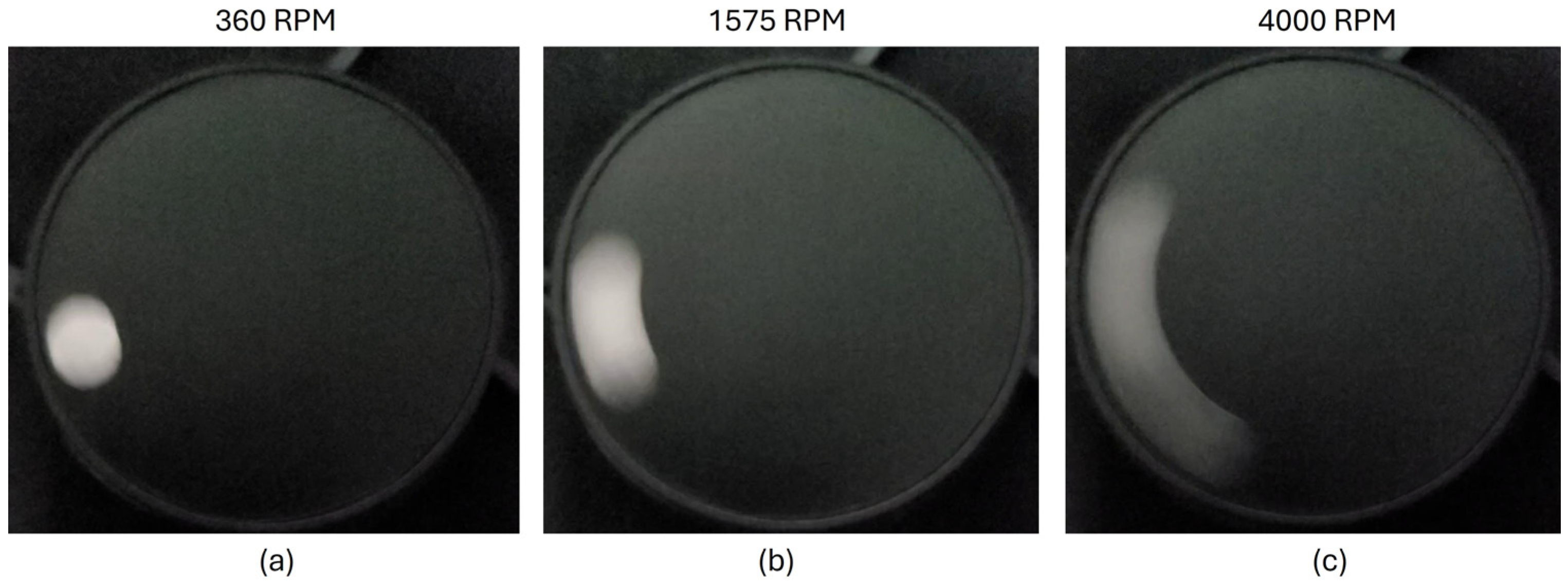
| Index | Tachometer * [RPM] | Measurement, Average for Two Seconds, RPM | Average | Standard Error | |||||
|---|---|---|---|---|---|---|---|---|---|
| No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | No. 6 | ||||
| 1 | 360 | 364 | 363 | 364 | 363 | 362 | 362 | 362.9 | 0.38 |
| 2 | 615 | 619 | 619 | 621 | 624 | 627 | 628 | 623.0 | 1.64 |
| 3 | 1000 | 1021 | 1023 | 1023 | 1013 | 1013 | 1012 | 1017.5 | 2.21 |
| 4 | 1250 | 1248 | 1249 | 1242 | 1241 | 1239 | 1239 | 1242.9 | 1.74 |
| 5 | 1575 | 1567 | 1571 | 1567 | 1549 | 1546 | 1544 | 1557.4 | 4.99 |
| Index | Tachometer [RPM] | Predicted RPM, Average | Percentage Error [%] |
|---|---|---|---|
| 1 | 360 | 362.9 | 0.81 |
| 2 | 615 | 623.0 | 1.30 |
| 3 | 1000 | 1017.5 | 1.75 |
| 4 | 1250 | 1242.9 | 0.57 |
| 5 | 1575 | 1557.4 | 1.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K. Study on Angular Velocity Measurement for Characterizing Viscous Resistance in a Ball Bearing. Machines 2025, 13, 578. https://doi.org/10.3390/machines13070578
Kim K. Study on Angular Velocity Measurement for Characterizing Viscous Resistance in a Ball Bearing. Machines. 2025; 13(7):578. https://doi.org/10.3390/machines13070578
Chicago/Turabian StyleKim, Kyungmok. 2025. "Study on Angular Velocity Measurement for Characterizing Viscous Resistance in a Ball Bearing" Machines 13, no. 7: 578. https://doi.org/10.3390/machines13070578
APA StyleKim, K. (2025). Study on Angular Velocity Measurement for Characterizing Viscous Resistance in a Ball Bearing. Machines, 13(7), 578. https://doi.org/10.3390/machines13070578







