Research on Bearing Fault Diagnosis Method Based on MESO-TCN
Abstract
1. Introduction
- (1)
- A unified diagnostic architecture (MESO-TCN) is proposed, which integrates multi-entropy-based signal preprocessing, kernel-extended temporal convolution, and adaptive parameter optimization. This end-to-end framework enhances the interpretability and adaptability of fault diagnosis under complex conditions.
- (2)
- A hybrid entropy screening mechanism is developed by combining information entropy, relative entropy, and cross-entropy to evaluate intrinsic mode components derived from EEMD. This enables effective selection of high-value signal components while suppressing redundant or noisy features.
- (3)
- A kernel-extended TCN structure with multi-scale dilated convolutions is constructed to capture diverse temporal fault patterns. In addition, an improved whale optimization algorithm incorporating a firefly-inspired attraction mechanism is introduced to jointly optimize key hyperparameters, thereby improving model convergence and robustness.
2. Materials and Methods
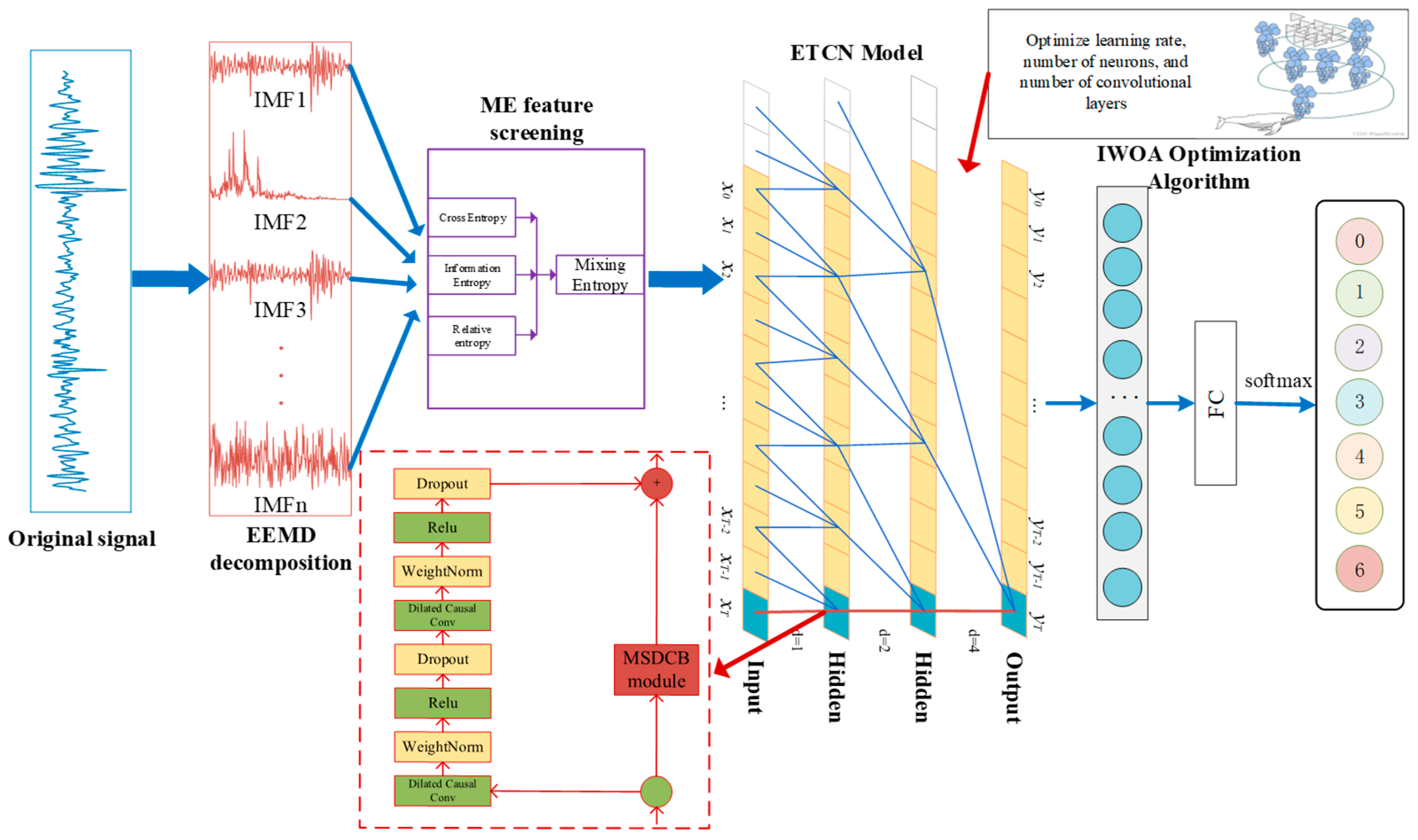
2.1. Signal Preprocessing and Feature Selection
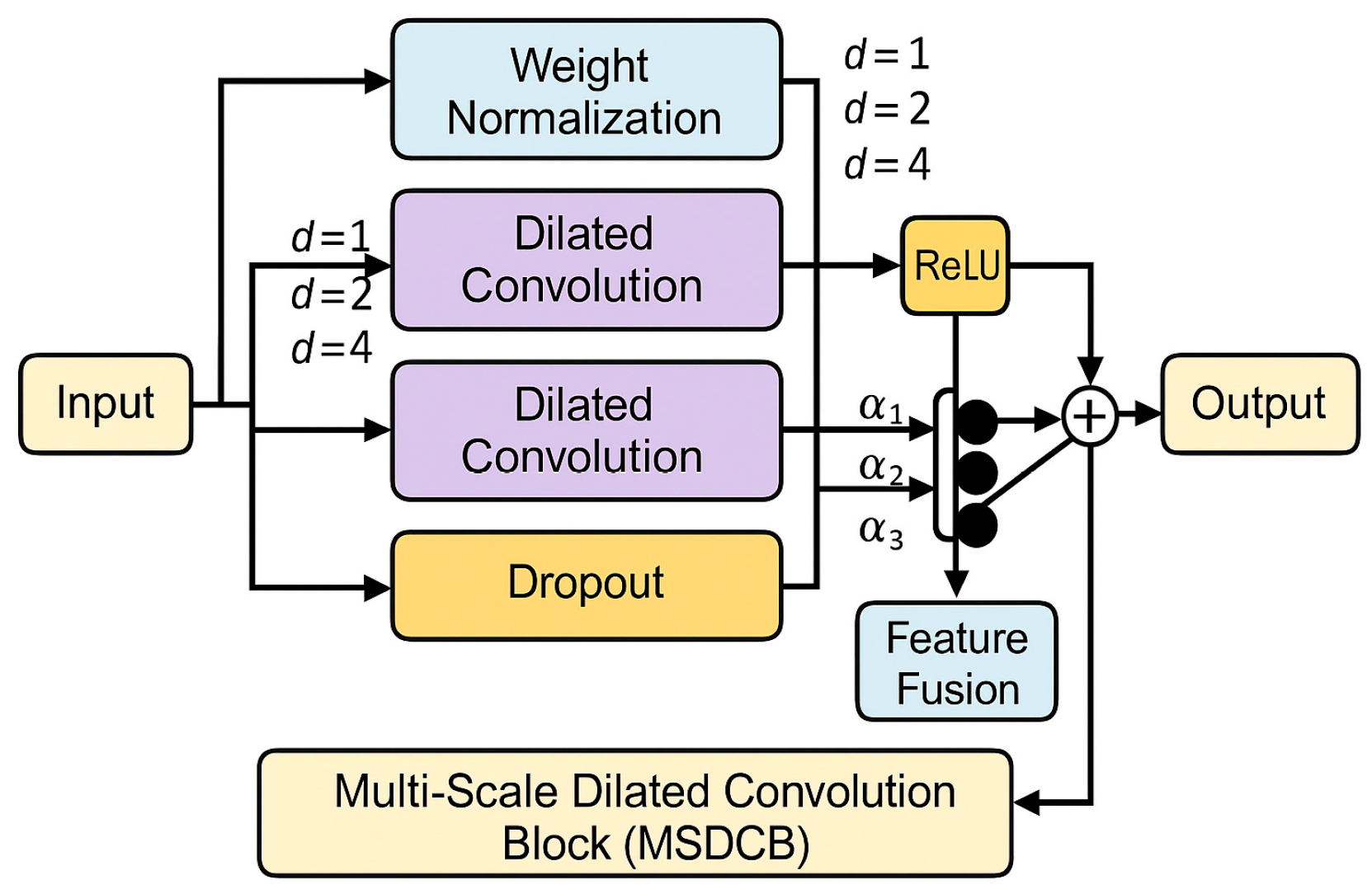
2.2. ETCN Network
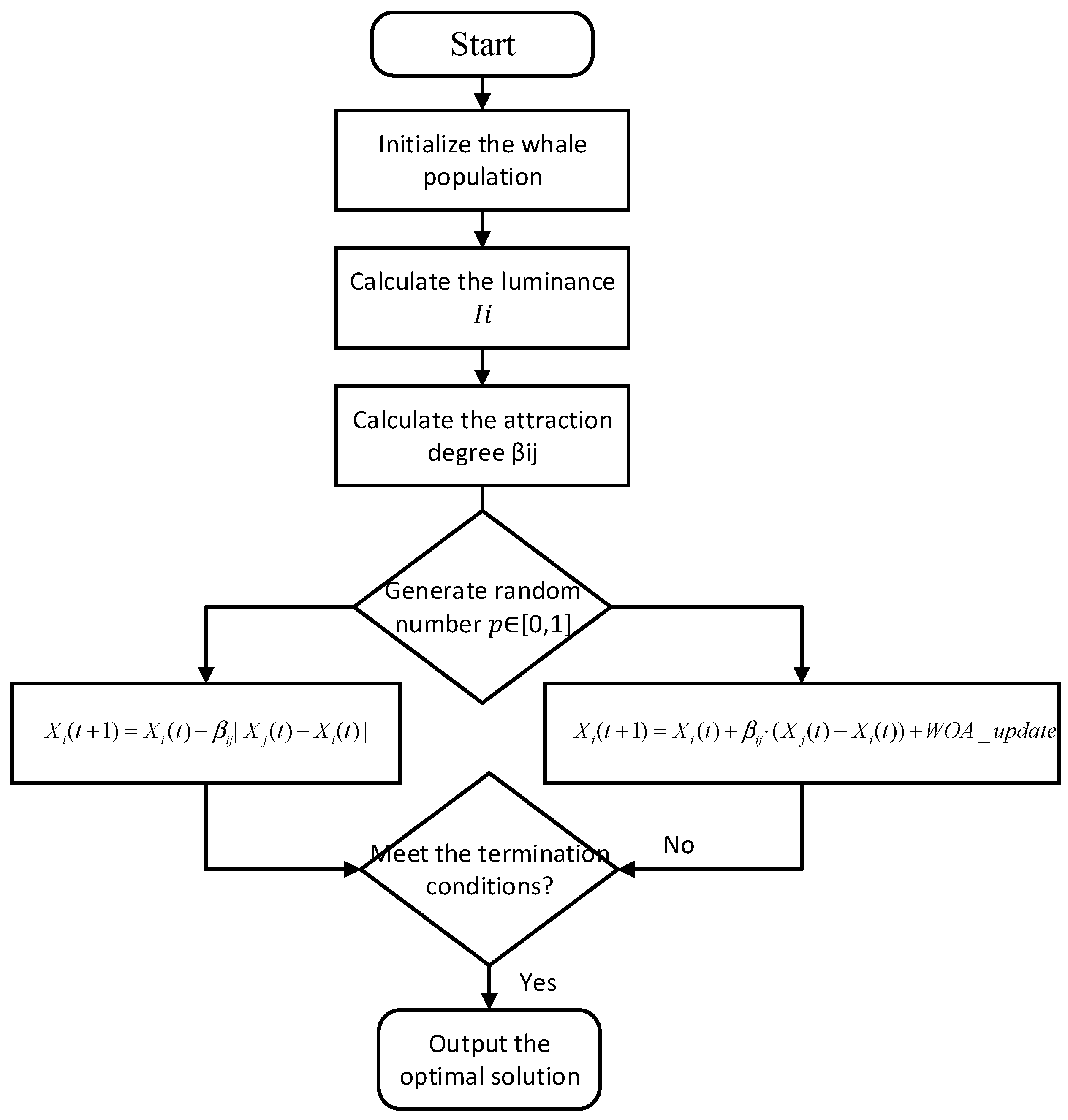
2.3. IWOA Algorithm
2.4. Based on the MESO-TCN Intelligent Diagnosis Process
- (1)
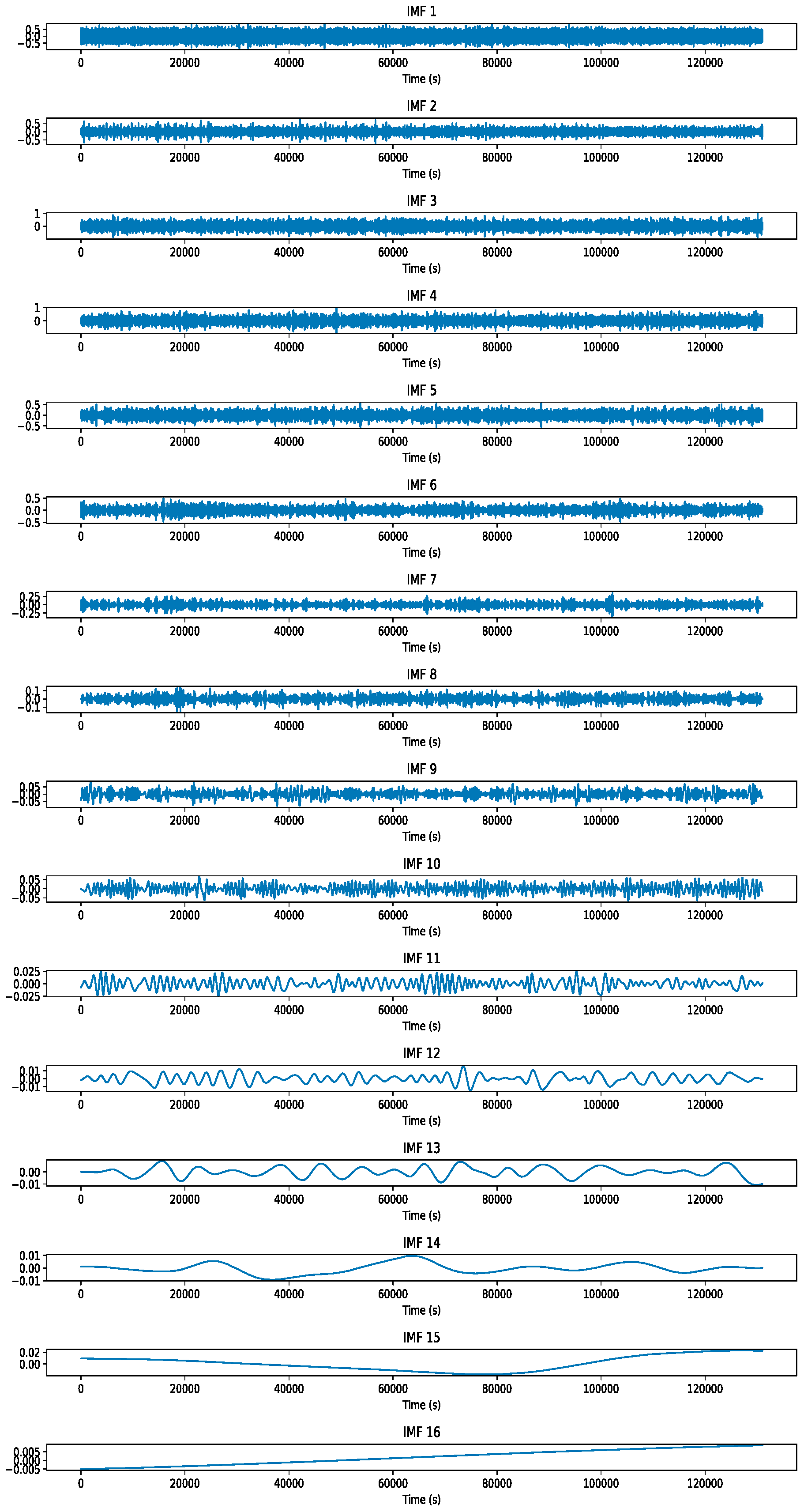
- Signal decomposition and feature enhancement: The original vibration signal is decomposed using Ensemble Empirical Mode Decomposition (EEMD) to extract intrinsic mode functions (IMFs) at multiple frequency scales, which form the temporal basis for representing fault-related information.
- (2)
- Feature screening and signal reconstruction: To suppress redundant and noisy components, a hybrid entropy index (ME), integrating information entropy, relative entropy, and cross-entropy, is employed to comprehensively evaluate each IMF. The most diagnostically relevant components are then selected and reconstructed to form a more targeted and discriminative input signal.
- (3)
- Deep modeling and multi-scale feature extraction: The reconstructed signal is fed into the kernel-extended temporal convolutional network (ETCN), where various fault features—such as local impulses, periodic fluctuations, and long-term dependencies—are extracted in parallel using convolutional paths with diverse receptive fields. A residual fusion strategy is applied to achieve unified modeling across multiple temporal scales.
- (4)
- Model tuning and parameter optimization: An improved whale optimization algorithm (IWOA), enhanced with a firefly-inspired brightness mechanism, is introduced to perform global search and automated tuning of key ETCN parameters, including learning rate, number of convolution kernels, and network depth. This enhances model adaptability and robustness under varying data distributions and operating conditions.
3. Results
3.1. Data Analysis of Rolling Bearings in Xi’an Jiaotong University
3.2. Data Preprocessing
3.3. Ablation Test
3.4. Analysis of AE Signal Data of Rolling Bearings in Southeast University
3.5. PRONOSTIA Bearing Failure Dataset
3.6. Result Summary
4. Conclusions
- (1)
- On the accelerated life test dataset from Xi’an Jiaotong University, the MESO-TCN model achieved an average diagnostic accuracy of 99.78%, with the loss value stably converging to 0.0124. Compared with baseline models such as TCN, ETCN, EMD-TCN, EMD-ME-TCN, and EMD-ME-CNN, the proposed model improved accuracy by 38.94%, 46.88%, 32.83%, 38.42%, and 0.38%, respectively, demonstrating superior diagnostic performance. On the acoustic emission (AE) signal dataset from Southeast University, the model also achieved an average accuracy of 95.82%, validating its robustness and generalization capability under heterogeneous signal conditions.
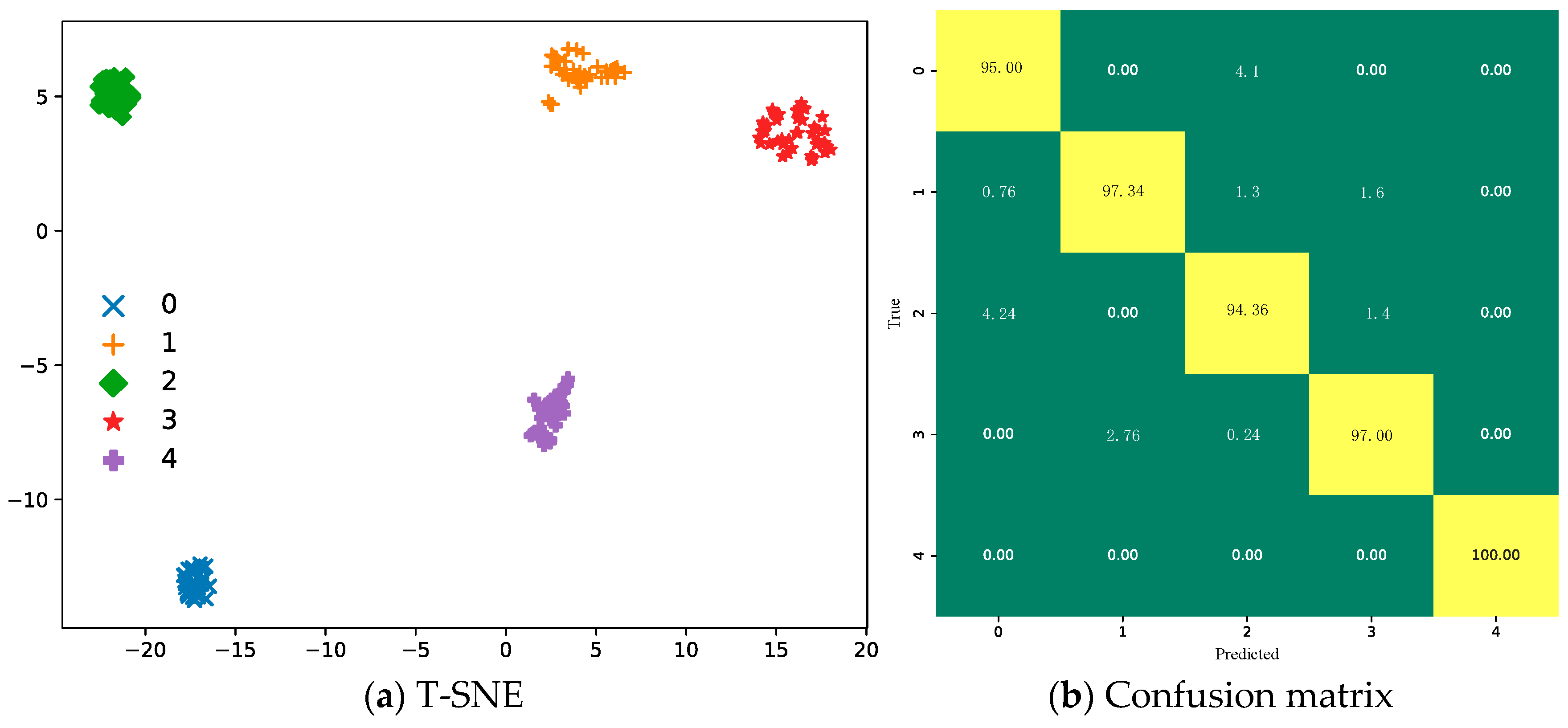
- (2)
- Feature visualization results based on t-SNE indicate that the features extracted by MESO-TCN exhibit clear inter-class separation and tight intra-class clustering, reflecting strong discriminative power and interpretability. The confusion matrix further confirms that the model can accurately and consistently identify all fault categories with extremely low misclassification rates, highlighting its expressive strength and reliability in both feature extraction and fault classification.
- (3)
- The results of comparative experiments confirm the effectiveness of the multi-strategy fusion framework proposed in this study. The hybrid entropy-based feature screening significantly enhances the discriminability of input signals; the extended-kernel TCN improves the model’s capacity to capture multi-scale dynamic features; and the IWOA optimization mechanism ensures efficient and stable parameter tuning. Overall, MESO-TCN achieves high accuracy, rapid convergence, and strong generalization in multi-class fault diagnosis tasks, showing promising potential for engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, Z.; Li, L.; Zhang, C.; Zhao, S.; Gong, L. Fault Feature Extraction Based on Variational Modal Decomposition and Lifting Wavelet Transform: Application in Gear of Mine Scraper Conveyor Gearbox. Machines 2024, 12, 871. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.X. A Bearing Fault Diagnosis Model Based on Synchronous Squeeze Wavelet Transform and Transformer. Electromech. Eng. 2024, 3, 1–10. [Google Scholar]
- Dong, S.; Zhang, Y.; Wang, S. Multisensor Fault Diagnosis of Rolling Bearing with Noisy Unbalanced Data via Intuitionistic Fuzzy Weighted Least Squares Twin Support Higher-Order Tensor Machine. Machines 2025, 13, 445. [Google Scholar] [CrossRef]
- Zeng, M.; Li, S.; Li, R.; Zhang, Y.; Wang, Q.; Liu, H.; Chen, X.; Zhao, L.; Huang, J.; Xu, F. Intelligent Fault Diagnosis Method for Rolling Bearings Based on Stacked Sparse Discriminant Autocoding. Bearing 2024, 3, 77–83, 98. [Google Scholar]
- Fu, W.; Jiang, X.; Li, B.; Tan, C.; Chen, B.; Chen, X. Rolling Bearing Fault Diagnosis Based on 2D Time-Frequency Images and Data Augmentation Technique. Meas. Sci. Technol. 2023, 34, 045005. [Google Scholar] [CrossRef]
- Gu, Y.K.; Shi, C.W.; Chen, J.F. Fault Diagnosis of Planetary Gearbox Based on Gram Angle Field and Deep Convolution Generative Adversarial Network. Noise Vib. Control. 2024, 44, 111–118. [Google Scholar]
- Wang, L.; Wang, Y.; Guo, F.; Yan, H.; Zhao, F. Lower Limb Joint Angle Prediction Based on Multistream Signaling and Quantile Regression, Temporal Convolution Network–Bidirectional Long Short-Term Memory Network Neural Network. Machines 2024, 12, 901. [Google Scholar] [CrossRef]
- Xiaojing, U.; Xue, R.M. Short Term Electricity Price Prediction of Bi-LSTM-TCN Based on Wavelet Transform. Adv. Technol. Electr. Eng. Energy 2020, 24, 16453–16482. [Google Scholar]
- Wang, X.-B.; Zhang, X.; Li, Z.; Wu, J. Ensemble Extreme Learning Machines for Compound-Fault Diagnosis of Rotating Machinery. Knowl.-Based Syst. 2020, 188, 105012. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, K.; Huang, Y.; Zhu, Y.; Chen, B. Parallel Spatio-Temporal Attention-Based TCN for Multivariate Time Series Prediction. Neural Comput. Appl. 2023, 35, 13109–13118. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, S.; Deng, L.; Jia, M.; Xu, J. Ship Motion Attitude Prediction Model Based on IWOA-TCN-Attention. Ocean. Eng. 2023, 272, 113911. [Google Scholar] [CrossRef]
- Gao, Z.W. Units Collaborative Diagnosis with Label Heterogeneity and Communication Redundancy. Eng. Appl. Artif. Intell. 2025, 152, 110724. [Google Scholar] [CrossRef]
- Swain, S.; Khilar, P.M.; Swain, R.R.; Senapati, B.R. A Federated Learning Based Fault Diagnosis in UAV-Reliable Sensor Network. In Proceedings of the 2023 IEEE 20th India Council International Conference (INDICON), Hyderabad, India, 14–17 December 2023; IEEE: Piscataway, NJ, USA, 2024; pp. 1386–1391. [Google Scholar]
- Pan, X.J.; Dong, S.J.; Zhu, P.; Zhou, C.; Song, K. Prediction of Remaining Life Migration of Rolling Bearings under Variable Operating Conditions Based on TCN and Residual Self Attention. Vib. Shock. 2024, 43, 238–259. [Google Scholar]
- Ding, L.; Li, Q. Fault Diagnosis of Rotating Machinery Using Novel Self-Attention Mechanism TCN with Soft Thresholding Method. Meas. Sci. Technol. 2024, 35, 047001. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, Q.; Xia, Y.; Li, C. Fault Diagnosis of Chiller Based on the Combination of Multiple Blocks and Self-Attention TCN. J. Process Eng. 2024, 24, 162–171. [Google Scholar]
- Hu, C.; Li, G.; Ma, L.; Yan, X.; Wei, H. Improve the Fault Diagnosis Method of TCPN Variable Working Condition Bearings. Noise Vib. Control. 2022, 42, 134–141. [Google Scholar]
- Li, S.; Yang, Y.; Li, C.; He, H.; Zhang, Q.; Zhao, S. Research on Signal Processing Technology of Ultrasonic Non-Destructive Testing Based on EEMD Combined with Wavelet Packet. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 686–700. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Varzaneh, Z.A.; Mirjalili, S. A Systematic Review of the Whale Optimization Algorithm: Theoretical Foundation, Improvements, and Hybridizations. Arch. Comput. Methods Eng. 2023, 30, 4113–4159. [Google Scholar] [CrossRef]
- Liu, W.; Liu, S.; He, Y.; Wang, J.; Gu, Y. Rolling Bearing Fault Diagnosis Based on MTF Encoding and CBAM-LCNN Mechanism. Comput. Mater. Contin. 2025, 82, 4863. [Google Scholar] [CrossRef]
- Yao, X.; Zhu, J.; Jiang, Q.; Yao, Q.; Shen, Y.; Zhu, Q. RUL Prediction Method for Rolling Bearing Using Convolutional Denoising Autoencoder and Bidirectional LSTM. Meas. Sci. Technol. 2023, 35, 035111. [Google Scholar] [CrossRef]
- Li, A.; Yao, D.; Yang, J.; Chang, M.; Zhou, T. Bearing Diagnosis Using an Anti-Noise Neural Network Based on Selectable Branch Multiscale Modules and Attention Mechanisms. IEEE Sens. J. 2023, 24, 5830–5840. [Google Scholar] [CrossRef]


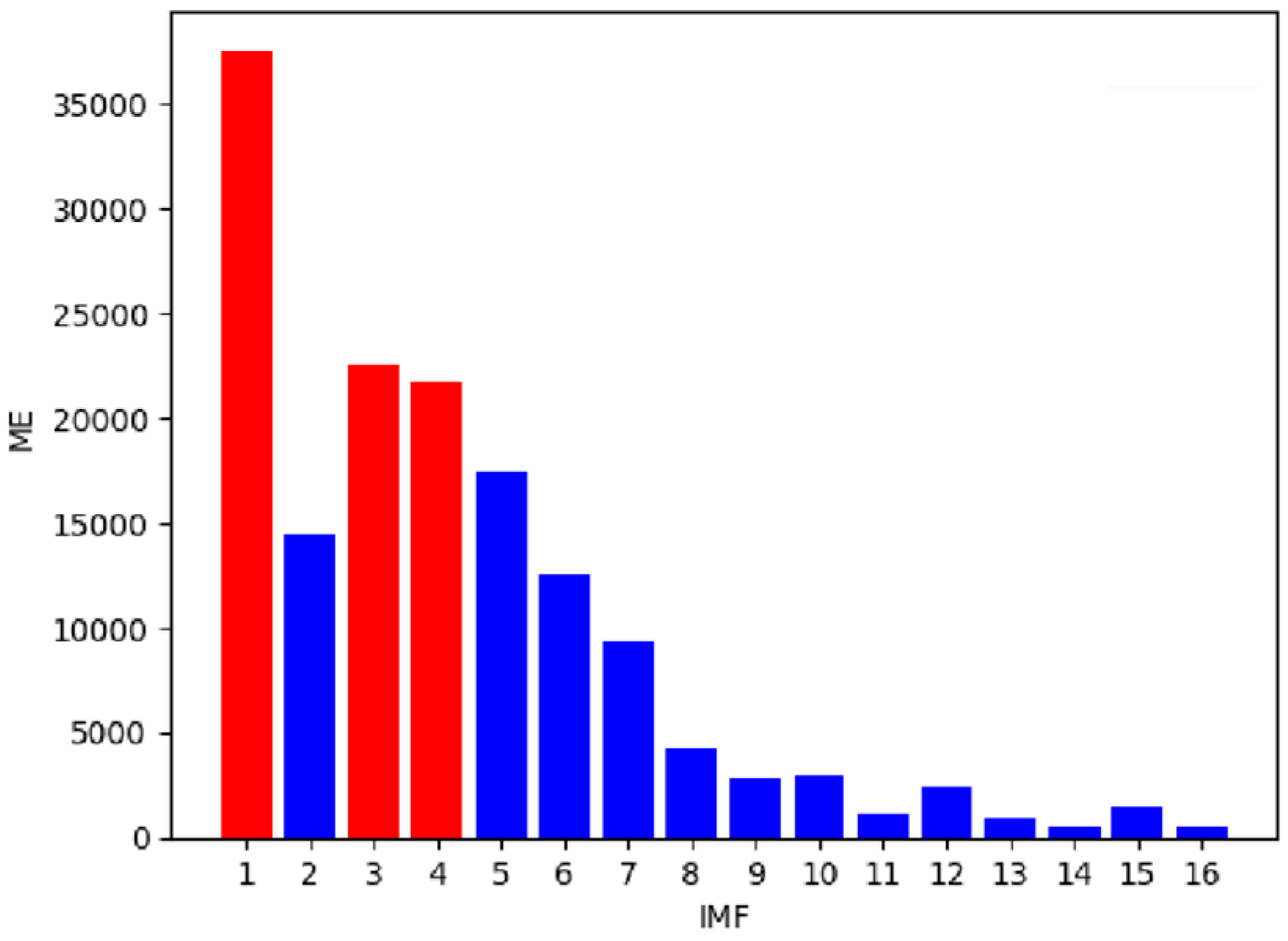


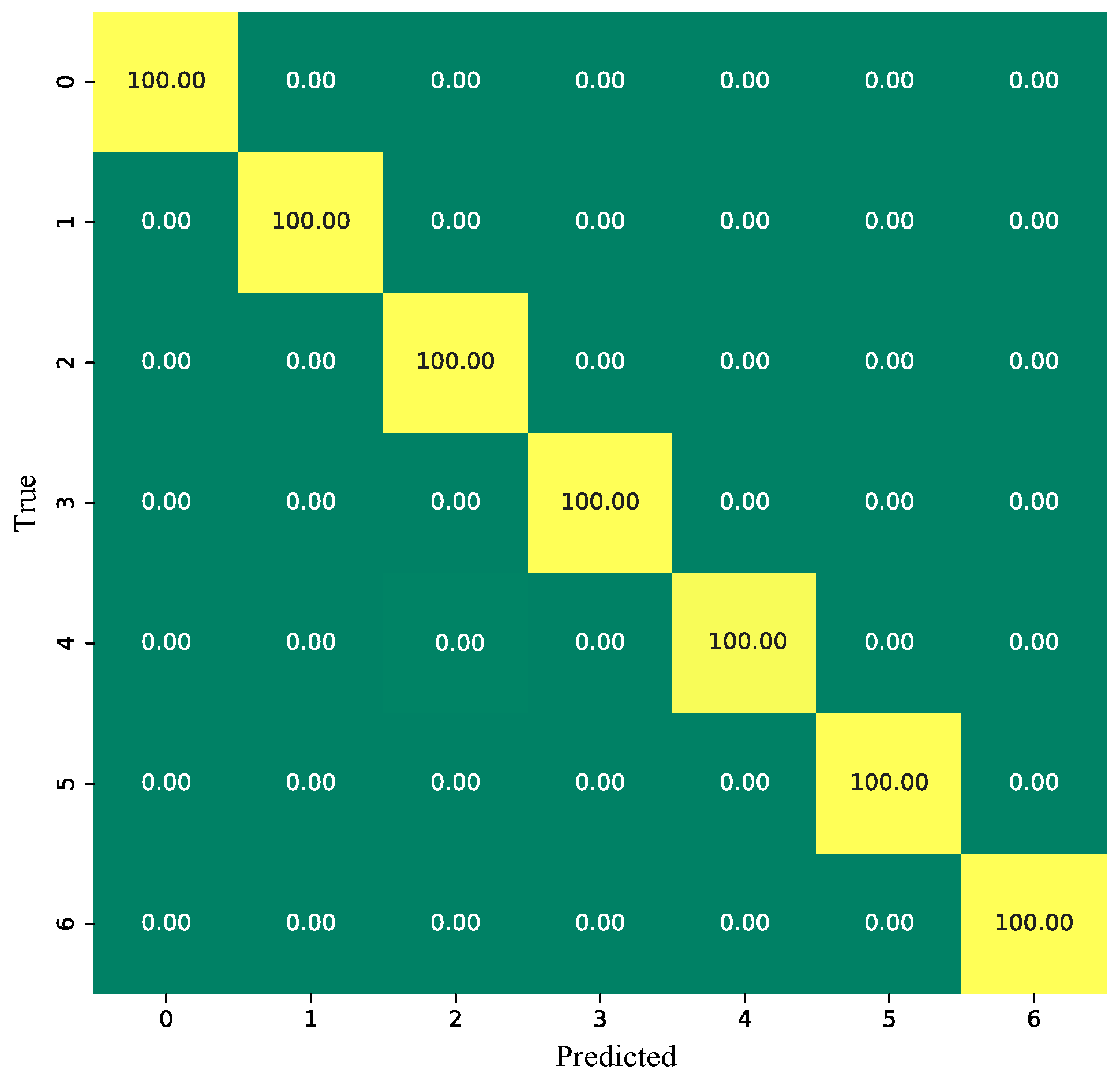
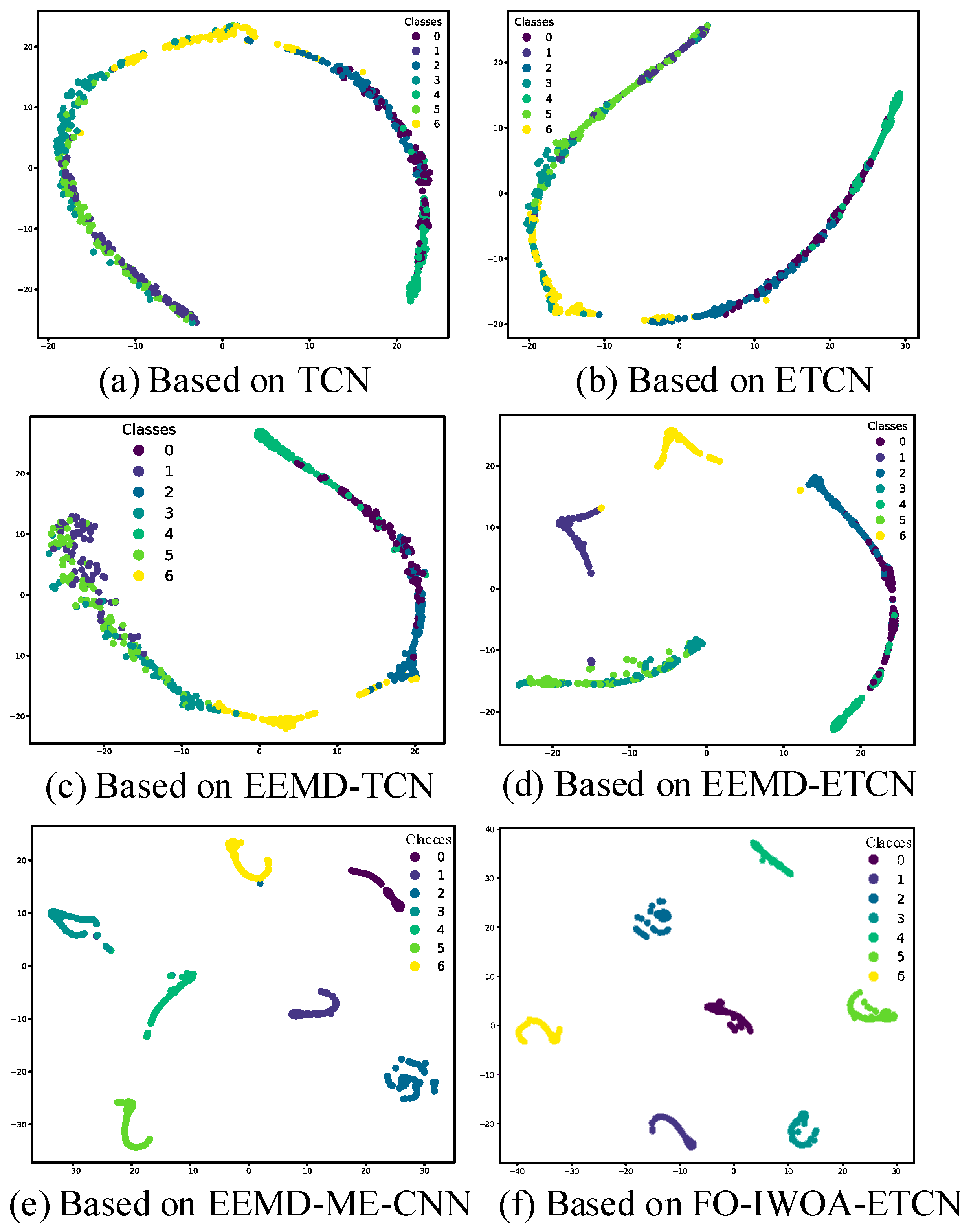
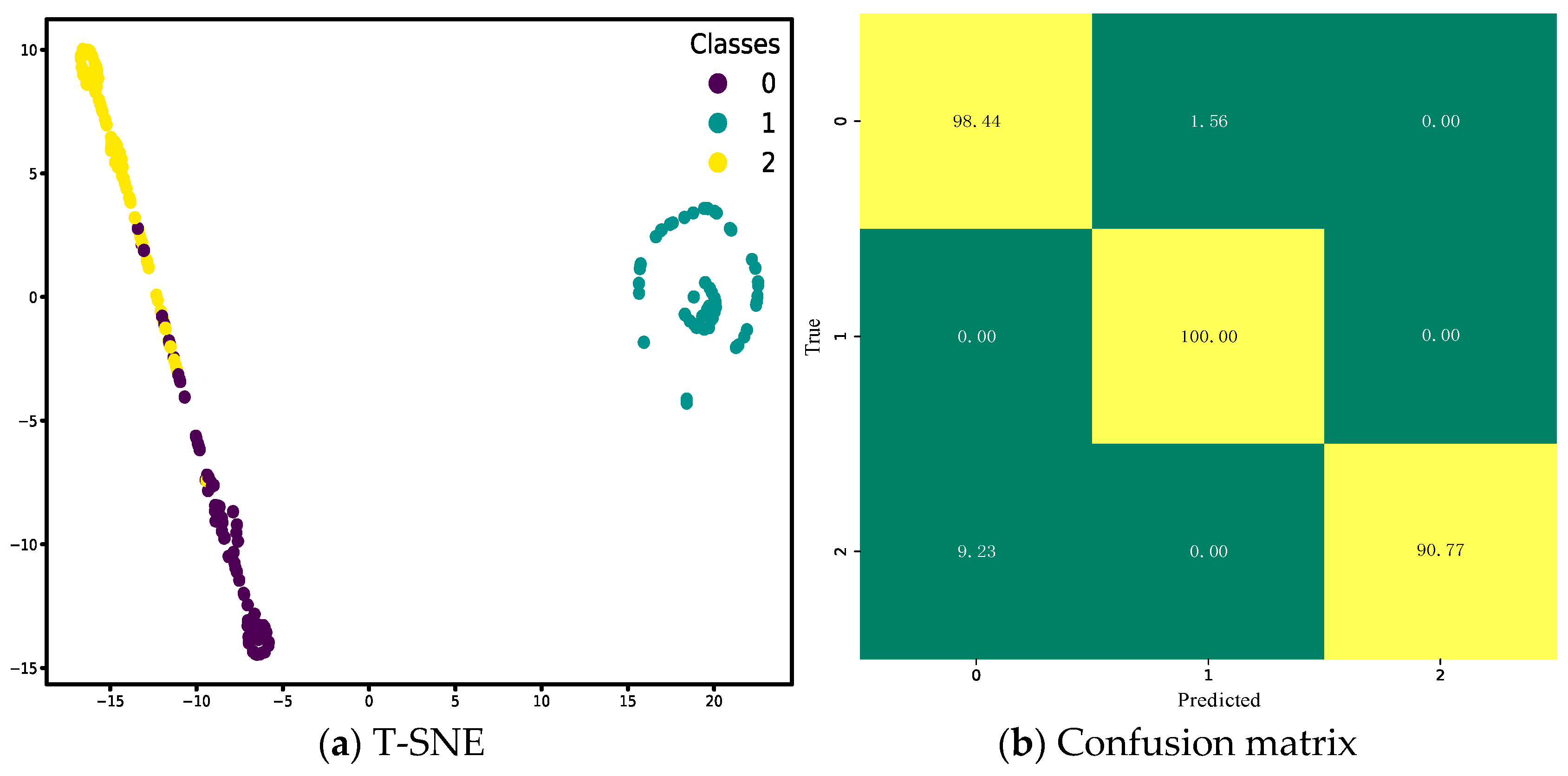
| Working Condition | Label | Data Set | Failure Position |
|---|---|---|---|
| 1 | 0 | Bearing 1_1 | Outer circle |
| 1 | Bearing 1_4 | Cage | |
| 2 | 2 | Bearing 2_1 | Inner circle |
| 3 | Bearing 2_2 | Outer circle | |
| 4 | Bearing 2_3 | Cage | |
| 3 | 5 | Bearing 3_1 | Outer circle |
| 6 | Bearing 3_3 | Inner circle |
| Method | Accuracy Rate/% | Loss Rate | F1 Score/% | Precision/% | Recall/% |
|---|---|---|---|---|---|
| TCN | 60.85 | 0.8370 | 68.16 | 65.90 | 60.72 |
| ETCN | 52.91 | 0.9980 | 60.05 | 69.84 | 63.50 |
| EMD-TCN | 66.95 | 0.6830 | 68.32 | 66.88 | 69.85 |
| EMD-ETCN | 61.36 | 0.8210 | 61.07 | 63.68 | 79.03 |
| EMD-ME-TCN | 99.40 | 0.0193 | 94.66 | 83.53 | 85.94 |
| EMD-ME-CNN | 99.47 | 0.0176 | 91.92 | 89.84 | 90.72 |
| MES-TCN | 98.45 | 0.0183 | 91.45 | 90.85 | 87.45 |
| MESO-TCN | 99.78 | 0.0124 | 98.47 | 97.45 | 94.78 |
| Method | Accuracy Rate/% | Loss Rate | F1 Score/% | Precision/% | Recall/% |
|---|---|---|---|---|---|
| TCN | 60.89 | 0.7370 | 57.45 | 65.90 | 64.77 |
| ETCN | 59.35 | 0.8280 | 64.12 | 45.75 | 45.12 |
| EMD-TCN | 62.77 | 0.6385 | 65.45 | 54.41 | 75.45 |
| EMD-ETCN | 59.63 | 0.6690 | 62.33 | 66.11 | 67.41 |
| EMD-ME-TCN | 94.87 | 0.1270 | 86.45 | 85.44 | 89.44 |
| EMD-ME-CNN | 94.87 | 0.1370 | 90.85 | 86.45 | 87.41 |
| MES-TCN | 93.45 | 0.0173 | 90.31 | 91.85 | 86.45 |
| MESO-TCN | 95.82 | 0.1770 | 97.45 | 98.91 | 96.11 |
| Method | Accuracy Rate/% | Loss Rate | Time/% | Precision/% | Recall/% | Method |
|---|---|---|---|---|---|---|
| TCN | 57.46 | 0.7841 | 45 | 45.12 | 56.41 | 75.45 |
| ETCN | 65.45 | 0.9516 | 67 | 75.45 | 45.12 | 72.42 |
| EMD-TCN | 67.12 | 0.8644 | 135 | 71.64 | 85.75 | 76.34 |
| EMD-ETCN | 57.66 | 0.7341 | 168 | 63.44 | 56.34 | 73.45 |
| EMD-ME-TCN | 93.85 | 0.2270 | 149 | 61.23 | 56.41 | 75.99 |
| EMD-ME-CNN | 94.75 | 0.3451 | 167 | 67.89 | 75.94 | 78.41 |
| MES-TCN | 93.45 | 0.2574 | 150 | 78.45 | 71.94 | 75.41 |
| MESO-TCN | 96.73 | 0.1341 | 231 | 90.54 | 98.15 | 95.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, R.; Zhu, J.; Wu, Y.; Xiao, K.; Shen, Y. Research on Bearing Fault Diagnosis Method Based on MESO-TCN. Machines 2025, 13, 558. https://doi.org/10.3390/machines13070558
Gao R, Zhu J, Wu Y, Xiao K, Shen Y. Research on Bearing Fault Diagnosis Method Based on MESO-TCN. Machines. 2025; 13(7):558. https://doi.org/10.3390/machines13070558
Chicago/Turabian StyleGao, Ruibin, Jing Zhu, Yifan Wu, Kaiwen Xiao, and Yang Shen. 2025. "Research on Bearing Fault Diagnosis Method Based on MESO-TCN" Machines 13, no. 7: 558. https://doi.org/10.3390/machines13070558
APA StyleGao, R., Zhu, J., Wu, Y., Xiao, K., & Shen, Y. (2025). Research on Bearing Fault Diagnosis Method Based on MESO-TCN. Machines, 13(7), 558. https://doi.org/10.3390/machines13070558





