Coordinated Scheduling for Zero-Wait RGV/ASR Warehousing Systems with Finite Buffers

Abstract

Efficient material handling is crucial in the logistics operations of modern salt warehouses, where Rail Guided Vehicles (RGVs) and Air Sorting Robots (ASRs) are often deployed to manage inbound and outbound tasks. However, as the number of tasks increases within a given period, conflicts and deadlocks between simultaneously operating RGVs and ASRs become more frequent, reducing efficiency and increasing energy consumption during transportation. To address this, the research frames the inbound and outbound problem as a task allocation issue for the RGV/ASR system with a finite buffer, and proposes a collision avoidance strategy and a zero-wait strategy for loaded machines to reallocate tasks. To improve computational efficiency, we introduce an adaptive multi-neighborhood hybrid search (AMHS) algorithm, which integrates a dual-sequence coding scheme and an elite solution initialization strategy. A dedicated global search operator is designed to expand the search landscape, while an adaptive local search operator, inspired by biological hormone regulation mechanisms, along with a perturbation strategy, is used to refine the local search. In a case study on packaged salt storage, the proposed AMHS algorithm reduced the total makespan by 30.1% compared to the original task queue. Additionally, in 15 randomized test scenarios, AMHS demonstrated superior performance over three benchmark algorithms—Genetic Algorithm (GA), Discrete Imperialist Competitive Algorithm (DICA), and Improved Whale Optimization Algorithm (IWOA)—achieving an average makespan reduction of 12.6% relative to GA.

1. Introduction

In the era of intelligent logistics, salt warehouses face increasing challenges in operational efficiency, adaptability, and coordination. Bagged salt, characterized by its large volume and heavy weight, is difficult to handle and stack through traditional manual operations [1]. Furthermore, as customer demand shifts from low-frequency, large-batch orders to high-frequency, small-batch, and fragmented orders, the conventional warehouse operation model is becoming increasingly unsustainable [2,3]. Modern automated storage and retrieval systems (AS/RS) achieve full-process automation of goods reception, sorting, inventory management, and transportation by integrating warehouse management systems (WMS) with logistics robot technologies—including Rail Guided Vehicles (RGV), Air Sorting Robots (ASR), and Automated Guided Vehicles (AGV) [4,5]. However, the surge in multi-category, small-batch orders places higher demands on the warehouse system: breakthroughs are urgently needed in efficient task coordination and multi-machine collaborative operations under high-density scheduling environments [6].

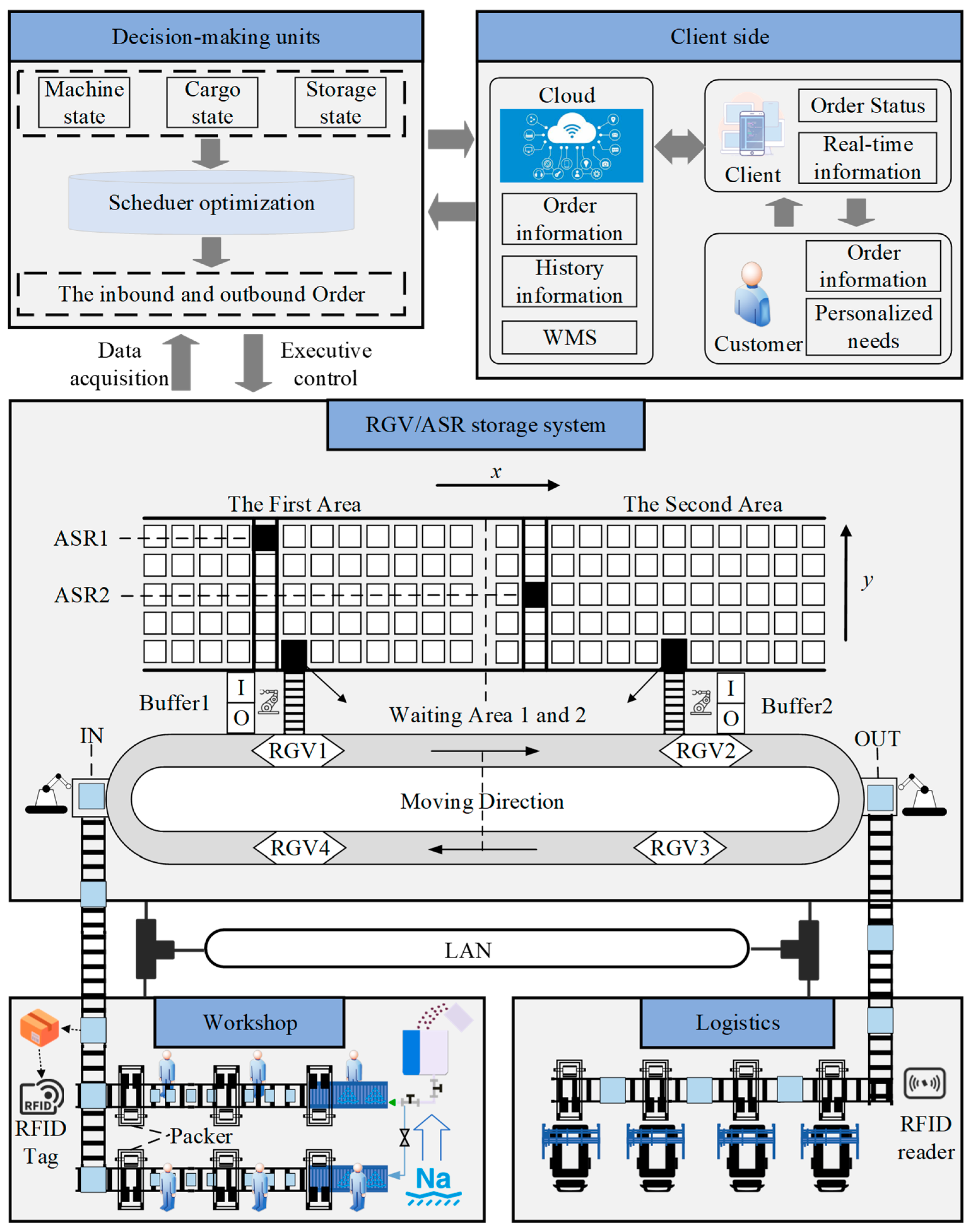
To address this transformation, a salt distribution center in China deployed an intelligent WMS integrated with an AS/RS, aiming to reduce labor costs and improve throughput. A critical issue in this intelligent system is the coordination of Rail Guided Vehicles (RGVs) and Air Sorting Robots (ASRs), two types of heterogeneous handling equipment responsible for executing inbound and outbound logistics tasks.

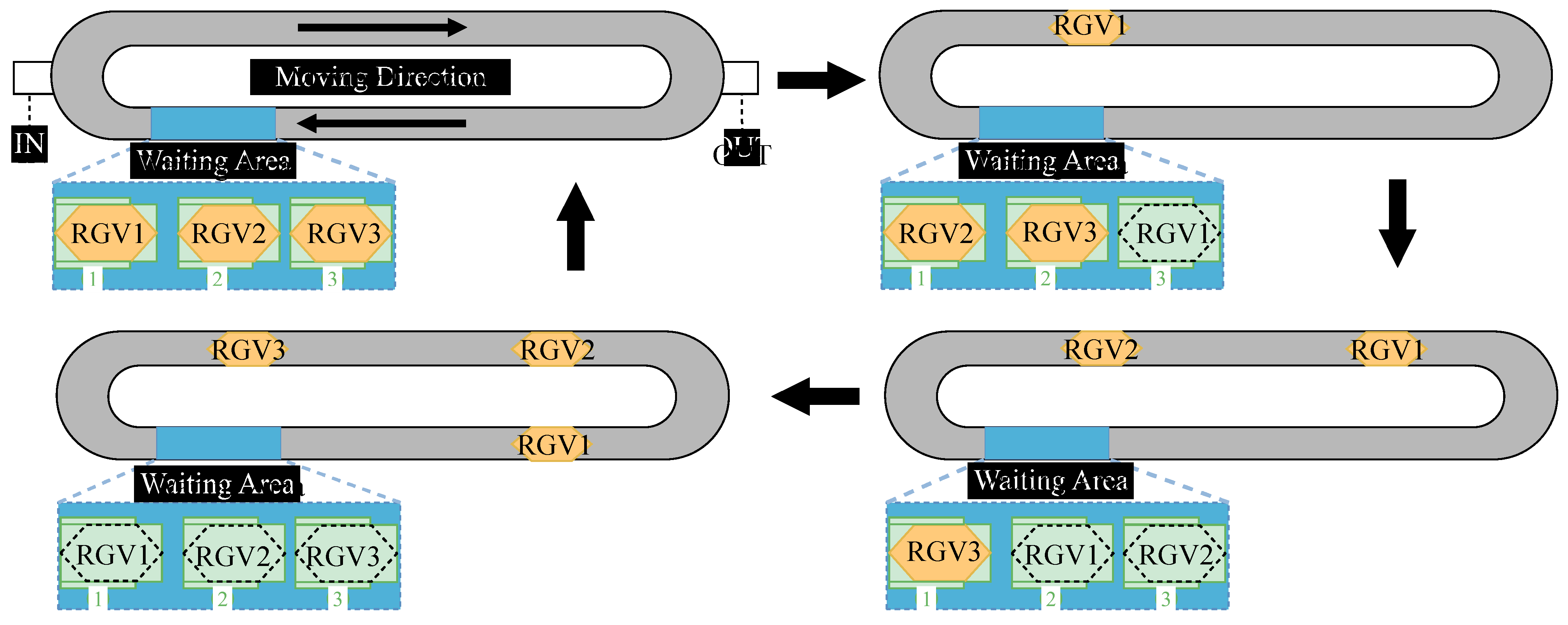
The inbound stage involves RGVs transporting bagged salt to inbound buffer zones, from where ASRs assign goods to designated storage locations. In the outbound stage, online customer orders trigger ASRs to retrieve goods, which are then transferred by RGVs to the outbound area for packaging. The layout of this RGV/ASR collaborative storage system is illustrated in Figure 1. However, the high concurrency of orders in this environment can lead to RGV collisions and prolonged waiting times, significantly degrading system efficiency. Therefore, it is crucial to develop intelligent scheduling methods to achieve efficient, zero-wait, and collision-free coordination among devices.

Recent studies have explored various models and algorithms for warehouse scheduling, including multi-agent frameworks for coordinating AGVs and shuttle robots [7,8], and mixed-integer programming (MIP) models for optimizing task sequencing [9]. Heuristic approaches such as rule-based logic and graph-based planning have been applied for collision avoidance, while capacity constraints have been tackled through discrete optimization techniques [10]. Despite these efforts, existing research often focuses on homogeneous systems or specific sub-problems, with limited attention to the joint scheduling of RGVs and ASRs in zero-wait environments with tight buffer constraints.

Cloud-based WMS have gained increasing attention in recent years as an essential component of smart logistics. By leveraging cloud computing technologies, cloud-based WMS platforms offer scalable, centralized, and real-time capabilities for managing warehouse operations such as inventory control, order tracking, and task dispatching. These systems allow seamless integration across supply chains and provide flexible data access for various stakeholders [11]. Recent studies have demonstrated the effectiveness of cloud-based WMS in enhancing system responsiveness and reducing operational latency, especially in e-commerce-driven logistics environments [12,13]. However, the integration of such platforms with adaptive scheduling algorithms for coordinating heterogeneous robotic fleets remains an open challenge, particularly in environments with high-density traffic and tight buffer constraints.

In parallel, the use of bio-inspired metaheuristic algorithms—such as population-based search [14] and adaptive neighborhood mechanisms [15]—has gained attention for solving complex logistics problems. However, their application to multi-robot coordination in warehouse systems, particularly under high-density scheduling and physical layout limitations, remains insufficient. Additionally, while cloud-based WMS solutions have enhanced responsiveness in logistics systems [16], integrating them with adaptive scheduling algorithms for heterogeneous fleets is still underexplored.

To address the aforementioned gaps, this paper investigates the scheduling problem of zero-wait RGV/ASR storage systems considering finite buffer capacity and proposes a novel Adaptive Multi-neighborhood Hybrid Search (AMHS) algorithm. The approach integrates a mixed-integer linear programming (MILP) model with biologically inspired search operators and elite solution initialization. Performance is evaluated using a case study based on historical order data from a real salt warehouse.

The main contributions are given as follows:

(1)

A MILP model for packaged salt warehouse logistics is developed to solve the task scheduling problem of multiple RGVs and ASRs, considering constraints such as zero-wait strategy, collision avoidance, and resource limitations.

(2)

A rule-based multi-RGV collision avoidance strategy and a zero-wait strategy for loaded machines are proposed, effectively preventing RGV collisions and machine load waiting, offering a greener warehouse logistics solution.

(3)

An improved Adaptive Multi-neighborhood Hybrid Search (AMHS) algorithm is introduced, using a dual-sequence encoding method to optimize the search space, combined with an elite solution initialization strategy. Global and local search operators are designed, with the latter inspired by biological hormone regulation mechanisms, employing a perturbation strategy to enhance local search performance.

(4)

The model is successfully integrated into the WMS of a packaging salt company in China, supporting logistics for RGVs and ASRs, and validating the effectiveness of the proposed algorithm.

The remainder of this paper is organized as follows. Section 2 provides a summary and analysis of the existing research on warehouse scheduling. In Section 3, this article conducts a detailed analysis of the warehouse scheduling problem and establishes the mathematical models. In Section 4, the AMHS algorithm is proposed. In Section 5, a case study on the inbound/outbound scheduling problem of a salt company is simulated. Finally, Section 6 summarizes this study and provides future research prospects.

2. Related Work

This section systematically reviews the research landscape of the AGV and RGV task scheduling and anti-collision, optimization algorithms, and highlights the research gap between existing research.

2.1. Task Scheduling and Coordination in Automated Warehouses

With the rise of automation in modern warehouses, task scheduling has become a central research focus, especially in systems involving multiple types of robots. As operational environments grow in complexity, effective coordination between robots such as RGVs, ASRs, and AGVs is increasingly vital for maintaining system efficiency. Over the years, a rich body of literature has emerged to address various scheduling challenges, ranging from static task assignment to dynamic, multi-robot collaboration.

Xu et al. [17] initiated foundational work by proposing a scheduling framework for container terminals, which provided valuable insights for subsequent warehouse scheduling studies. Building on this, Chen et al. [18] introduced an adaptive task planning algorithm for intelligent warehouses that could dynamically assign tasks from order batches and enhance stacking performance. However, their method processed orders strictly in arrival sequence, limiting scheduling flexibility. Ueno and Hirata [19] focused on minimizing path lengths under dynamic picking orders using the Gurobi solver, but their model did not consider robot load capacities or distinguish between inbound and outbound operations.

To improve scheduling in high-density warehouse systems, Fan et al. [20] developed a lifelong multi-shuttle scheduling framework (LMSSF) that adapts MAPF techniques for dynamic AS/RS environments by incorporating task conflict resolution and real-time re-planning. Similarly, Ren et al. [21] proposed an integrated scheduling method for multi-deep four-way shuttle systems, optimizing request sequencing, equipment assignment, and conflict-free path planning to minimize makespan. Yet both approaches focused solely on outbound logistics, overlooking the interaction with inbound processes. Ho et al. [22] adopted a deep reinforcement learning framework for scheduling heterogeneous robots, but failed to incorporate inbound coordination, which is essential in integrated logistics systems. Xu et al. [23] developed a multi-objective evolutionary algorithm that accounted for both inbound and outbound flows but did not address the risk of robot collisions in narrow aisles. Lu et al. [24] concurrently analyzed inbound and outbound scheduling using rule-based strategies and proposed a Constraint Programming (CP)-based adaptive simulated annealing local search algorithm for optimization, although the algorithm’s performance suffered from instability due to excessive assimilation cycles in its evolutionary process.

Despite notable progress, several gaps remain. Most existing works treat robots as homogeneous units and overlook the scheduling challenges posed by heterogeneous systems like RGV and ASR collaborations. Moreover, few studies explicitly address the combined impact of limited buffer capacities, zero-wait constraints, and real-time responsiveness, factors critical to modern warehouse operations. These limitations highlight the pressing need for integrated scheduling models capable of ensuring efficient, conflict-free coordination among diverse robots in tightly constrained environments.

2.2. Path Planning and Collision Avoidance in High-Density Systems

Path planning and collision avoidance have become crucial aspects of intelligent warehouse operations, especially in high-density and multi-robot environments. Han et al. [25] proposed a novel bubble sort scheduling algorithm for multi-directional RGVs in AS/RS, aiming to reduce queuing times and optimize path planning. Sahu et al. [26] proposed a hybrid metaheuristic combining Modified Cuckoo Search (MCS), Sine Cosine Algorithm (SCA), and Particle Swarm Optimization (PSO) to solve multi-robot cooperation and path planning problems, focusing on collision avoidance and synchronized motion in dynamic environments. Wang et al. [27] examined RGV scheduling on circular tracks, formulating a mixed-integer programming model and solving it with a Hybrid Variable Neighbor Tabu Search (HVNTS) algorithm. These studies laid a solid foundation for path optimization, yet they primarily targeted specific robot types and failed to address coordination across heterogeneous fleets.

Meanwhile, researchers have also explored heuristic and metaheuristic methods to improve task routing efficiency. Jiang et al. [28] applied a two-stage A* algorithm combined with a genetic algorithm to optimize task scheduling in AS/RS systems, while Lu et al. [29] proposed a hybrid GA–MBO algorithm for minimizing operation and completion times in AS/RS hybrid flow shops. Mei et al. [30] proposed an improved NSGA-II algorithm for multi-objective flexible job shop scheduling, integrating adaptive simulated annealing and elite strategies to enhance crossover and mutation, optimizing completion time, production cost, and carbon emissions. Although these methods demonstrate strong performance in small- to mid-scale systems, most assume static task sets and lack adaptability to dynamic task flows typical in real-world warehouses.

Despite significant advancements, existing studies often isolate inbound and outbound task processing, limiting system-wide optimization. Hsu et al. [31] and Yan et al. [32] proposed integrated simulation-optimization frameworks using hybrid algorithms such as WOA, PSO, and NSABC to solve multi-objective AS/RS scheduling problems. However, comprehensive coordination between different robotic agents like RGVs and ASRs remains insufficient. Most current approaches do not address real-time responsiveness, zero-wait constraints, or conflict resolution in shared working zones—key challenges for next-generation warehouse systems.

3. Problem Description and Formulation

3.1. Scheduling Description

A top view of the layout of the RGV/ASR storage system is shown in Figure 1, which consists of a three-dimensional warehouse, RGVs, and ASRs. The three-dimensional warehouse comprises two zones located on the left and right, each containing an inbound buffer and an outbound buffer, respectively. These areas collectively consist of X rows and Y columns, with each grid representing a unique cargo space identified by its (x, y) coordinates. Within each cargo space, multiple layers of goods can be stacked by the ASRs. The position of the goods within the warehouse is specified using three-dimensional coordinates (x, y, z). There are multiple RGVs on the circular RGV track. Each RGV runs in the same direction, and the RGVs cannot cross each other. RGVs collide when the running paths of any two RGVs overlap at the same time. The three-dimensional warehouse consists of two ASRs, each of which works independently and has a workspace that does not coincide with the other, and each of which is responsible for only putting goods in and out of the warehouse in its workspace.

In the logistics system, the inbound and outbound operations are executed as follows: For the inbound process, dispersed finished goods are first delivered to the inbound packing station. Based on order information and product type, these items are packaged into an inbound shipment, forming what is referred to as an inbound task. Upon completion of packaging, the task is transported to the RGV entrance, labeled ‘IN’ in Figure 1, where it awaits further processing. When an RGV becomes available, it conveys the inbound task to the corresponding inbound buffer within the warehouse according to the cargo’s designated location. The ASR responsible for that particular buffer then delivers the cargo to its assigned storage position.

For the outbound process, when a task needs to be removed from the warehouse, its exact coordinates must first be identified. The ASR unit managing the relevant storage area then transfers the task to the waiting outbound buffer. An available RGV subsequently transports the outbound task to the RGV exit, marked ‘OUT’ in Figure 1. From there, the task is conveyed via a conveyor belt to the unpacking station. After unpacking, the goods are ready for loading onto a truck for transportation.

Based on the above description and the actual enterprise site, the packers, unpackers, and conveyors have fixed capacities under certain conditions. Therefore, this paper focuses on the scheduling of the processes between the IN and OUT operations. The zero-waiting RGV/ASR storage scheduling problem, considering a finite buffer, can be described as follows: in an environment where each storage area has only one inbound and one outbound buffer, there are N₁ inbound tasks and N₂ outbound tasks. The storage coordinates (x, y, z) of each task are known, and the system comprises three RGVs and two ASRs. The goal is to schedule the RGV and ASR transportation resources effectively, ensuring that they do not have to wait during the transportation of goods and minimizing the total time for storage operations.

3.2. Modeling of Problem

3.2.1. Inbound/Outbound Model

The symbols representing all variables involved in the mathematical modeling of the scheduling scenario in this paper are presented in

Table 1. Variable symbols and definitions.

Variable Symbol	Meaning
$T_0$	Initial scheduling moment
$N$	The set of tasks to be transported
$n$	Total number of workpieces
$M$	Transport library
$i$	Workpiece index
$O_i$	Number of transportation processes for workpiece i
$j$	Process index
$m$	Machine index
$s$	Machine operation index
$C_{RGV}$	Perimeter of the RGV circular track
$S_m$	Total number of operations on machine m
$O_{i,j}$	jth transportation process for workpiece i
$M_{i,j}$	Transportable machine sets for $O_{i,j}$
$t_{i,j,m}$	Transportation time of $O_{i,j}$ on machine m
$S_{i,j}$	Start transportation time of $O_{i,j}$
$T_{i,j}$	Transportation completion time of $O_{i,j}$
$T_i$	Transportation completion time of Workpiece i
$X_{i,j,m,s}$	Decision variable that is 1 when $O_{i,j}$ is the sth course of transportation by machine m and 0 otherwise
$P_{i,j,m}$	Decision variable that is 1 when $O_{i,j}$ can be transported by machine m and 0 otherwise
$Y_{i,j,m}$	Decision variable that is 1 when $O_{i,j}$ is transported by machine m and 0 otherwise
$T_{\max }$	Maximum completed transportation time of workpieces
$PT{E}_{m,s}$	End transportation time of the sth process transported by machine m

.

To solve the scheduling problem, this paper makes some assumptions.

(1)

One task can be transported per RGV at any given moment.

(2)

RGVs travel in one direction and cannot cross each other.

(3)

Each ASR can transport a maximum of one task at any time and operates within a single depot without crossing depots.

(4)

All RGVs operate at the same speeds and turning speeds, without accounting for speed variations at the start.

(5)

The operating parameters are uniform for all ASRs.

(6)

Battery power of the RGV is not considered.

(7)

Once a task has been initiated, it cannot be interrupted until the current transportation step for that task is completed.

(8)

Unforeseen circumstances, such as equipment damage, are not taken into account.

The system aims to minimize the makespan, defined as the maximum completion time among all tasks:

$$f=\min (\max (T_i)),i\in N$$

(1)

The completion time of task i is calculated as:

$$T_i=T_{i,O_i},\forall i\in N$$

(2)

$$T_{i,j}=S_{i,j}+t_{i,j,m},\forall i\in N,j\in \{2,3,\dots ,O_i\},m\in \{1,2,\dots ,M\}$$

(3)

where Equation (2) states that the task completion time equals the finish time of its final operation. Equation (3) defines operation finish time as the sum of start time and processing duration on machine m.

The start time of operation O_i,j is defined as follows:

$$S_{i,j}=\max (T_{i,j-1},PT{E}_{m,s-1}),\forall i\in N,j\in \{2,3,\dots ,O_i\},m\in \{1,2,\dots ,M\}$$

(4)

where Equation (4) ensures each operation starts after the previous one finishes and the resource is ready.

$$T_{i,j-1}=S_{i,j-1}+{\displaystyle \sum _{m=1}^M{Y}_{i,j-1,m}\ast t_{i,j-1,m}},\forall i\in N,j\in \{2,3,\dots ,O_i\},m\in \{1,2,\dots ,M\}$$

(5)

$$PT{E}_{m,s+1}\ge PT{E}_{m,s}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{O_i}{Y}_{i,j,m}\ast t_{i,j,m}}},\forall m\in \{1,2,\dots ,M\}$$

(6)

where Equation (5) defines the finish time of the previous operation using the selected machine and its processing time; Equation (6) updates the earliest available time of machine m at stage s + 1, based on all tasks assigned at stage s.

Next, the processing time $t_{i,j,m}$ is defined according to the task type.

If the task is inbound:

$$t_{i,1,m}={\displaystyle \frac{w_1{C}_{RGV}}{V_{RGV}}}+{\displaystyle \frac{w_2{C}_{RGV}}{V_{RGV}^{\prime }}},\forall i\in N,m\in M_{RGV}$$

(7)

$$t_{i,2,m}={\displaystyle \frac{l_x\sqrt{{\left(x_i-x_0\right)}^2}}{V_{ASR}^x}}+{\displaystyle \frac{l_y{y}_i}{V_{ASR}^y}}+{\displaystyle \frac{l_y{z}_i}{V_{ASR}^z}}+{\displaystyle \frac{l_x\sqrt{{\left(x_i-x_0\right)}^2}}{V_{ASR}^{x^{\prime }}}}+{\displaystyle \frac{l_y{y}_i}{V_{ASR}^{y^{\prime }}}}+{\displaystyle \frac{l_z{z}_i}{V_{ASR}^{z^{\prime }}}},\forall i\in N,m\in M_{ASR}$$

(8)

If the task is outbound:

$$t_{i,1,m}={\displaystyle \frac{l_x\sqrt{{\left(x_i-x_0\right)}^2}}{V_{ASR}^x}}+{\displaystyle \frac{l_y{y}_i}{V_{ASR}^y}}+{\displaystyle \frac{l_y{z}_i}{V_{ASR}^z}}+{\displaystyle \frac{l_x\sqrt{{\left(x_i-x_0\right)}^2}}{V_{ASR}^{x^{\prime }}}}+{\displaystyle \frac{l_y{y}_i}{V_{ASR}^{y^{\prime }}}}+{\displaystyle \frac{l_z{z}_i}{V_{ASR}^{z^{\prime }}}},\forall i\in N,m\in M_{ASR}$$

(9)

$$t_{i,2,m}={\displaystyle \frac{w_1{C}_{RGV}}{V_{RGV}}}+{\displaystyle \frac{w_2{C}_{RGV}}{V_{RGV}^{\prime }}},\forall i\in N,m\in M_{RGV}$$

(10)

where Equations (7) and (10) denotes the RGV transport time, w₁ and w₂ denote the proportion of no-load and loaded distance travelled by the RGV during operation, $V_{RGV}$ and $V_{RGV}^{\prime }$ denote the no-load and loaded speeds of the RGV, respectively; and Equations (8) and (9) denotes the transport time of the ASR, including the loaded transport time and the no-loaded return time, x_i, y_i, and z_i denote the storage location of task i, x₀ denotes the location of the buffer zone, and $V_{ASR}^x$, $V_{ASR}^y$, and $V_{ASR}^z$ denote the no-load running speed of the ASR in x, y, and z directions, respectively, $V_{ASR}^{x\prime }$, $V_{ASR}^{y\prime }$ and $V_{ASR}^{z\prime }$ denote the loaded running speed of the ASR in the x, y and z directions, respectively, and l_x, l_y and l_z denote the side lengths of a rectangular cargo space in the x, y and z directions.

The constraints are subject as follows:

$$S_{i,j}\ge T_0,\forall i\in N,j\in \{1,2,\dots ,O_i\}$$

(11)

$${\displaystyle \sum _{m=1}^M{\displaystyle \sum _{s=1}^{S_m}{X}_{i,j,m,s}}}=1,\forall i\in N,j\in \{1,2,\dots ,O_i\}$$

(12)

$${\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{O_i}{X}_{i,j,m,s}}}=1,\forall m\in \{1,2,\dots ,M\},s\in \{1,2,\dots ,S_m\}$$

(13)

$${\displaystyle \sum _{m=1}^M{Y}_{i,j,m}=1},\forall i\in N,j\in \{1,2,\dots ,O_i\}$$

(14)

$${\displaystyle \sum _{m=1}^M{Y}_{i,j,m}}\le P_{i,j,m},\forall i\in N,j\in \{1,2,\dots ,O_i\},m\in M_{i,j}$$

(15)

where Equation (11) indicates that the start of transportation of a task must be after the starting moment of scheduling; Equations (12) and (13) indicate that only one robot can be selected for transportation of each process and that only one task can be transported at the same moment by each robot; Equation (14) ensures each operation is executed by one and only one machine. Equation (15) restricts operation assignment to only feasible machines based on processing compatibility matrix $P_{i,j,m}$.

3.2.2. RGV Anti-Collision Strategy

During RGV operation, the operation paths of each RGV cannot overlap with each other, otherwise, a collision will occur. If RGV_i receives a task at a moment earlier than RGV_i−1, path overlap occurs, and in addition, a collision occurs when the moment of the current receiving task of an RGV with a number greater than i is later than the next receiving task of an RGV with a number less than i. Only if RGV_i−1 receives a task earlier than RGV_i in any run cycle, and the moment of the current receiving task of the RGV with the number greater than i is earlier than the next receiving task of the RGV with the number less than i, no collision will occur when multiple RGVs are on the same circular orbit.

Currently, many scholars have established complex mathematical models for scheduling the transportation of RGVs. However, the high complexity of the model brings a lot of difficulties to the overall scheduling optimization for inbound storage, and the algorithms are too slow to solve, on the other hand, the actual scenarios need a fast, lightweight and agile anti-collision strategy to cope with a variety of complex and changing manufacturing environments. To solve the problem, this paper proposes a multi-RGV anti-collision operation rule, and the process is shown in Figure 2.

The multi-RGV anti-collision operation strategy in Figure 2 is expressed as:

All the RGVs are waiting in the RGV waiting area according to the number order. When there is a task to be transported, the task can only be transported by the RGV in the RGV waiting area numbered 1. If there is none, it is necessary to wait. After the departure of the RGV in the RGV waiting area 1, if there is an RGV in the waiting area at its rear, each RGV at its rear travels one waiting area forward. As the tasks continue to be issued, it is sufficient to repeat the above process sequentially, and this process is also the RGV selection mechanism in this paper.

3.2.3. Zero-Wait Strategy for Loaded Machines

In the storage system, the load waiting for transportation machines will bring problems such as increased energy consumption and system blockage to the system. Combined with the above model, this paper proposes a zero-waiting strategy for loaded machines, which mainly realizes uninterrupted operation of RGVs and ASRs under load and waiting in the waiting area under no-load by reasonably planning the devolution time of each task under the load of RGVs and ASRs in the current state.

When inbound, the downtime of task i is calculated as shown below:

$$T{K}_i=\max (T{W}_1,T{B}_{in-i}-t_r)$$

(16)

where TK_i denotes the time when task i is issued; TW_i denotes the earliest available time of the RGV located in the first waiting zone of the idle RGV waiting zone; TB_in-i denotes the earliest available time of the buffer required for task i to be warehoused; and t_r denotes the running time of the RGV from the waiting zone to the buffer.

The ASR arrival buffer pickup time for transportation task i at the time of inbound storage is calculated as:

$$T{A}_i=\max (T{K}_i+t_r,TA{E}_y)$$

(17)

where TA_i denotes the time when the ASR of transportation task i arrives at the buffer to pick up the goods; TK_i denotes the time when task i is issued; assuming that task y is the previous task of ASR transportation task i, TAE_y denotes the time when the transportation of the ASR of transportation task y is completed.

The results of the RGV/ASR warehouse scheduling, with and without the Zero-Wait strategy, are depicted in Figure 3, respectively. As indicated by the solid red lines in the figures, the implementation of zero-wait constraints for load transportation effectively reduces the waiting time of the transport resources. This optimization is achieved without compromising the overall transportation time, thereby leading to energy savings.

4. Improved AMHS Algorithm

The problem involves three subproblems: in/out information classification, task in/out sequencing optimization, and RGV selection. These subproblems are characterized by complexity, a large solution space, and highly coupled constraints. Traditional optimization algorithms face limitations due to fixed search patterns and limited depth, and the coding and decoding dimensions significantly affect the algorithm’s search process [33,34].

To address these challenges, this paper proposes an improved Adaptive Multi-neighborhood Hybrid Search (AMHS) algorithm. The method integrates task type, sequencing, and RGV assignment into a compact chromosome structure by optimizing encoding and decoding schemes, effectively reducing the number of chromosomes and exponentially shrinking the search space. A novel RGV selection mechanism further reduces solution uncertainty. The algorithm incorporates a global search operator and an adaptive local search operator inspired by neuroendocrine coordination mechanisms. The global search serves as the primary exploration method, while the local operator refines each solution through adaptive destruction and reconstruction. AMHS also adopts an elite initialization strategy and employs both point and block exchanges during the global phase, with a hormone-regulation-inspired local search enhancing exploitation. The overall procedure is shown in Figure 4.

4.1. Encoding and Decoding

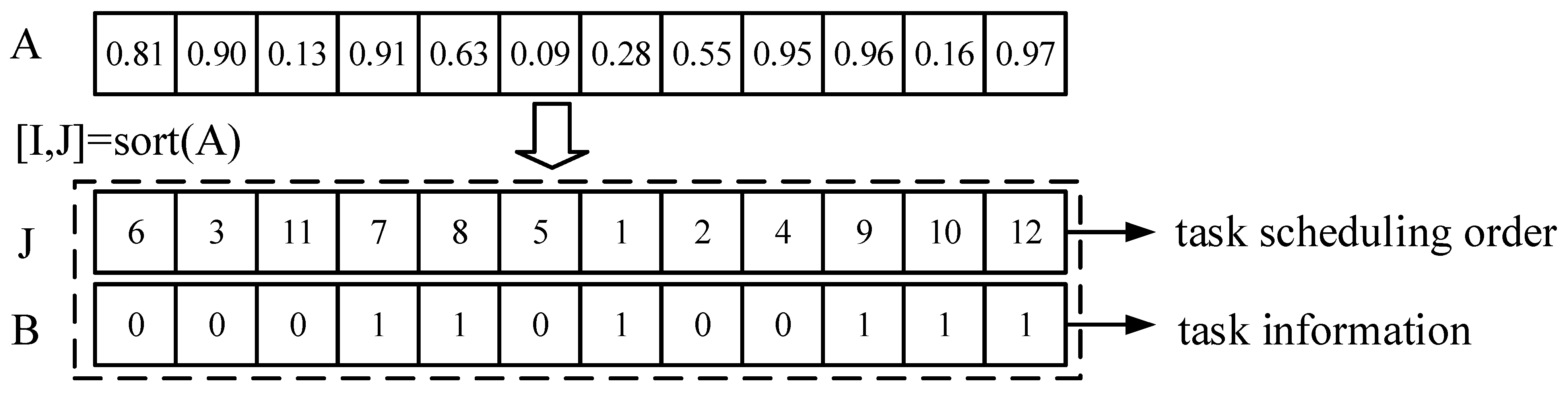
The initial step in solving the problem involves encoding it. Each task includes information such as task number, inbound/outbound details, sequences, and the RGVs assigned for transportation. If all task information is fully represented, four sequences are required, but optimizing all four simultaneously is challenging due to the high degree of coupling among them. To overcome this, a fractional coding approach is proposed, introducing a task scheduling sequence and a task information sequence to represent the encoded data.

This method addresses both the inbound and outbound task operations while considering spatial and scheduling constraints. By transforming the problem into a discrete optimization problem, a dual-sequence-based coding approach is adopted, leading to an adaptive encoding scheme. The process steps are illustrated in Figure 5. This approach aims to enhance warehouse management by optimizing the scheduling of tasks, improving operational efficiency, and maximizing resource utilization.

As illustrated in Figure 5, sequence A represents a series of random numbers, with the number of elements matching the total number of tasks to be scheduled for inbound/outbound operations. Sequence J corresponds to the task scheduling order, while sequence B denotes task information, where “1” indicates an outbound task and “0” indicates an inbound task. For instance, if the second element in J is “3” and the corresponding value in B is “0,” it signifies that task number “3” is an inbound task, scheduled to be processed as the second operation.

The decoding process involves transforming a given solution into a feasible scheduling plan and computing the completion time. In this approach, RGVs are sequentially assigned to the tasks listed in J based on the RGV assignment mechanism, while ASRs are allocated according to the cargo space location. Throughout the process, machine resource utilization is continuously updated to ensure optimal scheduling.

4.2. Population Initialization

To enhance the quality of the initial population, accelerate the convergence speed of the algorithm, and improve the final solution’s quality, this paper introduces an elite solution strategy. The process for initializing the population using this strategy is detailed in Algorithm 1.

Algorithm 1: Initialize population using the elite solution strategy

In this algorithm, the fitness function fit() is defined as the maximum completion time (makespan) across all tasks, i.e.,

$$fit(X)=\max T_i,i\in N$$

(18)

where T_i is the completion time of task i, and N is the task set. This value is used to rank individuals in the population for elite selection.

Through the elite solution initialization strategy, some high-quality solutions are introduced in the initial population, which may be retained and improved in the subsequent optimization process, thus improving the performance and effectiveness of the algorithm. At the same time, the strategy also helps to avoid the algorithm from falling into local optimal solutions and increases the ability of global search.

4.3. Global Search Operator

To enhance the global search capability of the algorithm and expand the search space, the global search operator is designed for task scheduling orders. This operator includes both point exchange and block exchange methods.

4.3.1. Point Exchange

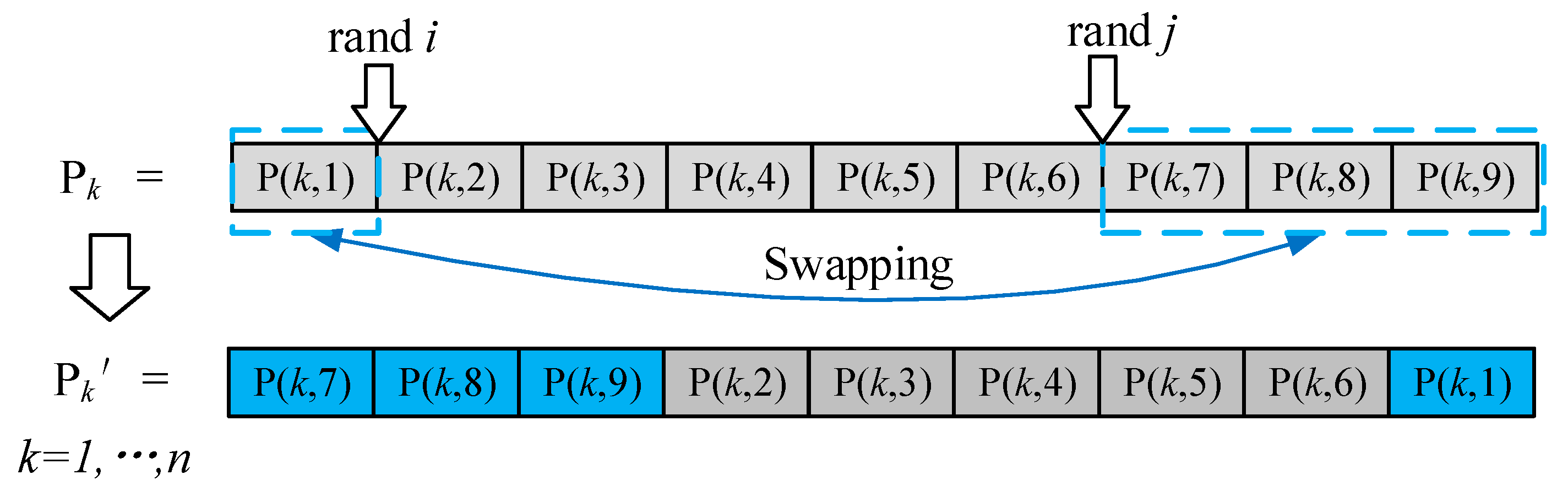
To avoid generating invalid solutions and simplify the process of creating new solutions while preserving some of their original characteristics, a swapping operation is proposed. This involves randomly selecting two positions and then exchanging their elements, resulting in a new population matrix. The process for swapping sequential points in the task scheduling order is illustrated in Figure 6.

4.3.2. Block Exchange

Task Scheduling Sequential Sequence Block Swapping presents a notable feature of having a low search difficulty while concurrently enabling an extensive search range for the solution. Nevertheless, the inherent crossover and its analogous operations may result in genetic drift [35], i.e., a situation where the population undergoes genetic changes without substantial enhancement in individual fitness, potentially leading to a gradual deviation of the population from the optimal solution path. This phenomenon arises from the notion that certain high-quality solutions, once attained, require no obliteration but rather necessitate further local exploration locally [36]. Consequently, the block exchange operator introduced in this study dynamically modulates the crossover probability based on solution quality, with the specific formula for the crossover probability detailed below:

$$p=crossove{r}_{\min }+(crossove{r}_{\max }-crossove{r}_{\min })\times {\displaystyle \frac{quality-qualit{y}_{\min }}{qualit{y}_{\max }-qualit{y}_{\min }}}$$

(19)

where p denotes the crossover probability dynamically adjusted according to the solution quality; crossover_max and crossover_min are the minimum and maximum values of the crossover probability, respectively; quality is the current solution quality; quality_max and quality_min are the minimum and maximum values of the solution quality, respectively.

This equation ensures that the crossover probability is lower when the quality of the solution is higher, and it minimizes when the quality of the solution reaches its highest value, which avoids always destroying high-quality solutions.

In the execution process, a random number is assigned to each solution, and then it is determined whether a block exchange is performed or not. The block exchange process is shown in Figure 7.

As shown above, randomly selected cross positions, cross positions to the nearest end, form a sequence of elements, exchanging the positions of the two sequences.

4.4. Local Search Operator

Although a global search operator is essential, it may be insufficient for ensuring the comprehensiveness and effectiveness of an algorithm in complex optimization problems. The algorithm can still converge to local optima, particularly when the solution space contains numerous local extrema. Additionally, as problem dimensions increase, the distribution of local optima becomes more dispersed and intricate, posing a significant challenge to global search and potentially limiting its effectiveness in high-dimensional scenarios. To address this, we introduce a local search operator inspired by biological hormone regulation mechanisms. This operator aims to enhance the algorithm’s capability for in-depth exploration around known solutions, complementing the global search and collectively improving the overall optimization performance.

Mechanisms of Hormone Regulation in Organisms

In the process of hormone regulation, various glands in the organism (such as thyroid, gonads, etc.) secrete corresponding hormones, which flow throughout the body through the blood circulatory system and act on the cells, tissues and organs of the organism to produce the unique regulation and control of hormones, such as insulin and glucagon secreted by the pancreas to regulate the blood glucose level of the organism. With the characteristics of micro, high efficiency, and specificity of hormone regulation, organisms can rapidly maintain the internal environment homeostasis. The hormone regulation law proposed by Farhy et al. [37] is non-negative and monotonic, and has the characteristics of the ascending function and the descending function, and follows the Hill functional regulation law as shown in Equation (16):

$$F(C)\left\{\begin{array}{c}{F}_{\mathrm{up}}(C)={\displaystyle \frac{C^n}{T^n+C^n}}\\ F_{\mathrm{down}}(C)={\displaystyle \frac{T^n}{T^n+C^n}}\end{array}\right.$$

(20)

where C is the independent variable, T is the threshold, and T > 0; n is the Hill factor $n\ge 1$. The rate of change of the slope of the curve is affected by the values of T and n.

By studying the above, Farhy came up with the mechanism of feedback regulation of hormones and conducted relevant experiments on F(C) in connection with this study. Based on the results of the experiment, the following conclusion was drawn: when hormone 2 regulates the gland that secretes hormone 1, the relationship that exists between the secretion rate of hormone 1 and the concentration of hormone 2 is shown below:

$$V_1=\left\{\begin{array}{c}{V}_{up}^1=V_0^1\times (1+{\displaystyle \frac{C_0}{V_0^1}}\times {\displaystyle \frac{C_2^n}{C_2^n+T^n}})\\ V_{down}^1=V_0^1\times (1-{\displaystyle \frac{C_0}{V_0^1}}\times {\displaystyle \frac{C_2^n}{C_2^n+T^n}})+C_0\end{array}\right.$$

(21)

where C₂ represents the concentration of hormone 2, $V_0^1$ represents the initial secretion rate of hormone 1, and C₀ is a constant.

Linear functions or constants are often used in PSO algorithms to design inertia factors, but due to their linear nature, it is difficult to avoid the search from falling into a locally better neighborhood structure. Given the aforementioned, the bio-hormone feedback regulatory function has monotonicity and nonlinear characteristics, which can better regulate the step size of the local search. Therefore, this paper proposes the following design method of the inertia factor w to improve the performance of the PSO algorithm, and the inertia factor w is designed as follows:

$$w(i)=(w_{\max }-w_{\min })\times {\displaystyle \frac{T^n}{i^n+T^n}}+w_0$$

(22)

where i is the number of iterations, w_max and w_min are the two maximum and minimum extreme values of the inertia factor, and w₀ is the initial value.

According to Ho et al. [38], the self-learning behavior c₁ × r₂ and social learning behavior c₂ × r₂ of bird flocks affect the quality of solutions; however, the regulation of these two learning behaviors is not independent of each other. In other words, the two random weighting parameters (self-learning ability and social learning ability) are not independent of each other. In addition, the random variable r₂ is introduced to control the speed of the local search.

Therefore, based on the hormone regulation mechanism of organisms, combined with the self-learning and social learning behaviors of particles, this paper proposes a deep search operator with the following search process:

$$\begin{array}{c}{V}_i(t+1)=((w_{\max }-w_{\min })\ast {\displaystyle \frac{T^n}{i^n+T^n}}+w_0)\ast V_i(t)+(1-r_2)c_1\ast r_1\ast (P_i(t)-X_i(t))\\ +(1-r_2)c_2\ast (1-r_1)\ast (P_g(t)-X_i(t))\end{array}$$

(23)

$$X_i(t+1)=X_i(t)+V_i(t+1)$$

(24)

where V_i(t) and X_i(t) denote the speed and position of the individual in the t-th iteration, respectively, P_i(t) denotes the optimal position of the individual, and P_g(t) denotes the optimal position of the population. The local search procedure based on hormonal regulation is detailed in Algorithm 2.

Algorithm 2: Local Search

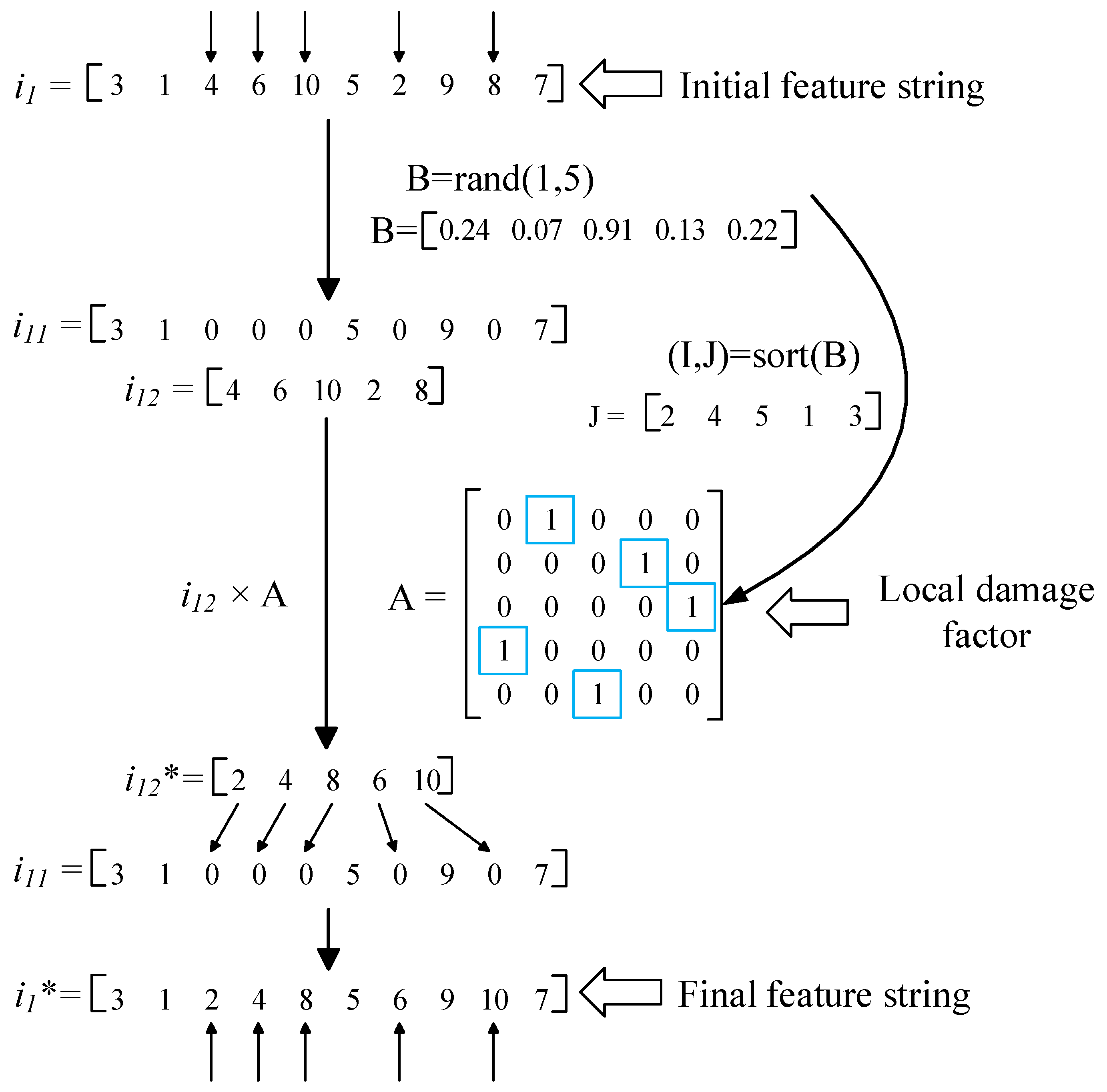
4.5. Localized Destruction and Reconstruction Perturbation Strategies

The Iterated Greedy (IG) algorithm is an efficient method for solving FSPs [39], since its core operations of destruction and reconstruction operators, insertion-based local perturbation operators, can introduce some stochasticity or control parameter variations to explore new solution spaces. This helps the algorithm to adapt to the dynamically changing search process, to avoid falling into local optima during the search process, and to provide more possible solutions for comparison and selection.

In building the zero-wait RGV/ASR warehouse system inbound and outbound scheduling problem considering finite buffers, in this paper, the inbound and outbound tasks are split into two kinds of processes, which are abstracted as extensions of hybrid flow operations. However, in the IG algorithm, the time complexity is O($n^3$) since all n jobs need to be inserted into (n − 1) positions and each insertion will cause n − p + 1 moves (where p is the optimal insertion position). Inspired by the above ideas, a local destruction and reconstruction perturbation strategy with less complexity is proposed to select a random number of jobs for each solution to randomly select a position for insertion, and thus its time complexity is O($n^2$), and its process is shown in Figure 8.

First, the number of random solutions d ($d\in [4,10]$) is randomly selected, a random order is given to each of the selected numbers using the random number matrix and then repopulated according to this order. As shown in the above figure, this approach enables the reordering of some of the sequences in the solution, achieving the goal of introducing randomness in the search process, and the method has a small computational complexity.

5. Numerical Experiments and Result Analysis

The runtime environment is PyCharm with Python version 3.8. The computer configuration is as follows: Windows 11 64-bit operating system; Intel(R) Core(TM) i5-13400F processor (2.50 GHz, Intel Corporation, Santa Clara, CA, USA); 16 GB RAM; and NVIDIA GeForce RTX 4060 Ti GPU (NVIDIA Corporation, Santa Clara, CA, USA).

5.1. Experimental Parameters Setting

To address the zero-wait coordinated scheduling problem of RGVs and ASRs under finite buffer constraints, the motion parameters of RGVs and ASRs were configured based on the actual operational environment of a salt warehouse. The site-specific conditions are summarized as follows: the loop length of the RGV track is 288 m; the average spacing in the x-direction of the cargo area is 1.6 m; the average spacing in the y-direction is 1.1 m. The total no-wait time for one RGV loop is approximately 192 s. For each ASR transportation task, the interaction time is fixed at 30 s. Since this study does not consider space optimization, task coordinates in the y-direction are not specified. Therefore, the RGV’s loaded and unloaded displacements in the y-direction are both approximated as 5 m. Each RGV cycle consists of loading goods, transporting them to storage, and returning empty to the buffer area. The detailed device-related parameters are shown in

Table 2. Equipment-related information.

Device	Quantity	Axis	No-Load Speed (m/s)	Axis	No-Load Speed (m/s)
ASR	2	X-axis	2.4	X-axis	2.0
		Y-axis	1.3	Y-axis	1.0
		Z-axis	0.6	Z-axis	0.5
RGV	1, 2, 3, 4, 5	1.5		1.5

.

To verify the superiority of the proposed algorithm, this paper adopts actual data from the production process of enterprises to verify the search efficiency of the algorithm. The datasets are shown in

Table 3. Cargo-related information.

No.	Out/In	Coordinate	No.	Out/In	Coordinate	No.	Out/In	Coordinate	No.	Out/In	Coordinate
1	1	(16, 5)	26	1	(27, 4)	51	1	(16, 5)	76	1	(13, 11)
2	0	(97, 1)	27	1	(26, 9)	52	0	(83, 3)	77	1	(99, 1)
3	0	(88, 7)	28	1	(68, 7)	53	0	(74, 7)	78	0	(10, 3)
4	1	(49, 7)	29	1	(52, 9)	54	1	(10, 12)	79	1	(69, 10)
5	1	(41, 1)	30	0	(8, 2)	55	0	(83, 3)	80	0	(93, 3)
6	0	(13, 5)	31	0	(6, 4)	56	0	(23, 12)	81	1	(15, 7)
7	1	(93, 7)	32	0	(26, 12)	57	1	(11, 5)	82	1	(89, 4)
8	1	(1, 11)	33	1	(44, 11)	58	1	(67, 4)	83	0	(2, 11)
9	1	(19, 9)	34	0	(29, 8)	59	1	(96, 9)	84	0	(35, 10)
10	0	(33, 9)	35	1	(68, 6)	60	0	(82, 7)	85	0	(24, 12)
11	1	(6, 11)	36	1	(95, 10)	61	1	(63, 5)	86	1	(99, 5)
12	0	(15, 3)	37	1	(78, 10)	62	1	(33, 5)	87	0	(85, 7)
13	0	(73, 5)	38	1	(64, 2)	63	0	(28, 3)	88	0	(80, 9)
14	1	(49, 12)	39	0	(76, 8)	64	1	(44, 11)	89	1	(91, 5)
15	1	(34, 2)	40	0	(75, 10)	65	1	(36, 1)	90	1	(79, 12)
16	1	(24, 2)	41	0	(59, 9)	66	1	(88, 5)	91	0	(84, 6)
17	0	(46,11)	42	0	(78, 1)	67	1	(1, 2)	92	1	(33, 1)
18	1	(19, 2)	43	1	(40, 3)	68	1	(70, 11)	93	0	(75, 2)
19	0	(33, 9)	44	1	(61, 5)	69	0	(34, 1)	94	0	(67, 5)
20	1	(27, 9)	45	1	(25, 6)	70	1	(31, 3)	95	0	(29, 1)
21	0	(84, 2)	46	0	(30, 11)	71	0	(65, 5)	96	0	(34, 11)
22	0	(70, 12)	47	0	(2, 12)	72	0	(93, 11)	97	0	(91, 11)
23	0	(34, 3)	48	0	(35, 8)	73	1	(90, 6)	98	1	(4, 1)
24	0	(59, 3)	49	1	(15, 9)	74	1	(100, 3)	99	1	(70, 3)
25	1	(29, 6)	50	0	(42, 11)	75	0	(8, 4)	100	0	(21, 2)

.

To enhance the optimization performance of the AMHS algorithm, a set of orthogonal experiments was designed to tune its core parameters. Among many influencing factors, population size (PAR), base inertia weight (w₀), and the cognitive and social learning factors (c₁ and c₂) were selected for adjustment. These three parameters directly affect the search ability, convergence behavior, and stability of the algorithm. PAR controls the breadth of the search space. A small population may cause premature convergence, while a large one increases computation. The base inertia weight w₀ is the key parameter in the dynamic inertia strategy. It balances exploration and exploitation by adjusting the influence of current velocity. The cognitive and social factors control learning from individual and global best solutions, respectively. To simplify the design and avoid interaction effects, c₁ and c₂ were set to equal values. The parameter ranges were selected based on existing literature and adjusted to fit the characteristics of this problem. Details are shown in

Table 4. AMHS parameter settings.

Parameters	Value	Parameters	Value
Number of intensive search iterations	100	wmax	0.8
Enhanced search iterations	100	T	12
Population size	[30, 50, 70]	n	2
w0	[0.3, 0.4, 0.5]	c1	[1.5, 1.8, 2.0]
wmin	0.1	c2	[1.5, 1.8, 2.0]

.

To assess performance, each algorithm was run independently 10 times, and the results were compared using the Optimal Average (OA) and Average Relative Percentage Deviation (ARPD), calculated as follows:

$$OA={\displaystyle \frac{{\displaystyle \sum _{i=1}^z{C}_{\min }^i}}{z}}$$

(25)

$$ARPD={\displaystyle \frac{{\displaystyle \sum _{i=1}^z\frac{C_{\min }^i-C^{*}}{C^{*}}}}{z}}\times 100\%$$

(26)

where z is the number of runs, and $C_{\min }^i$ is the result of the i-th run of the algorithm. OA is the average of the results and $C^{*}$ is the optimal solution of the z runs.

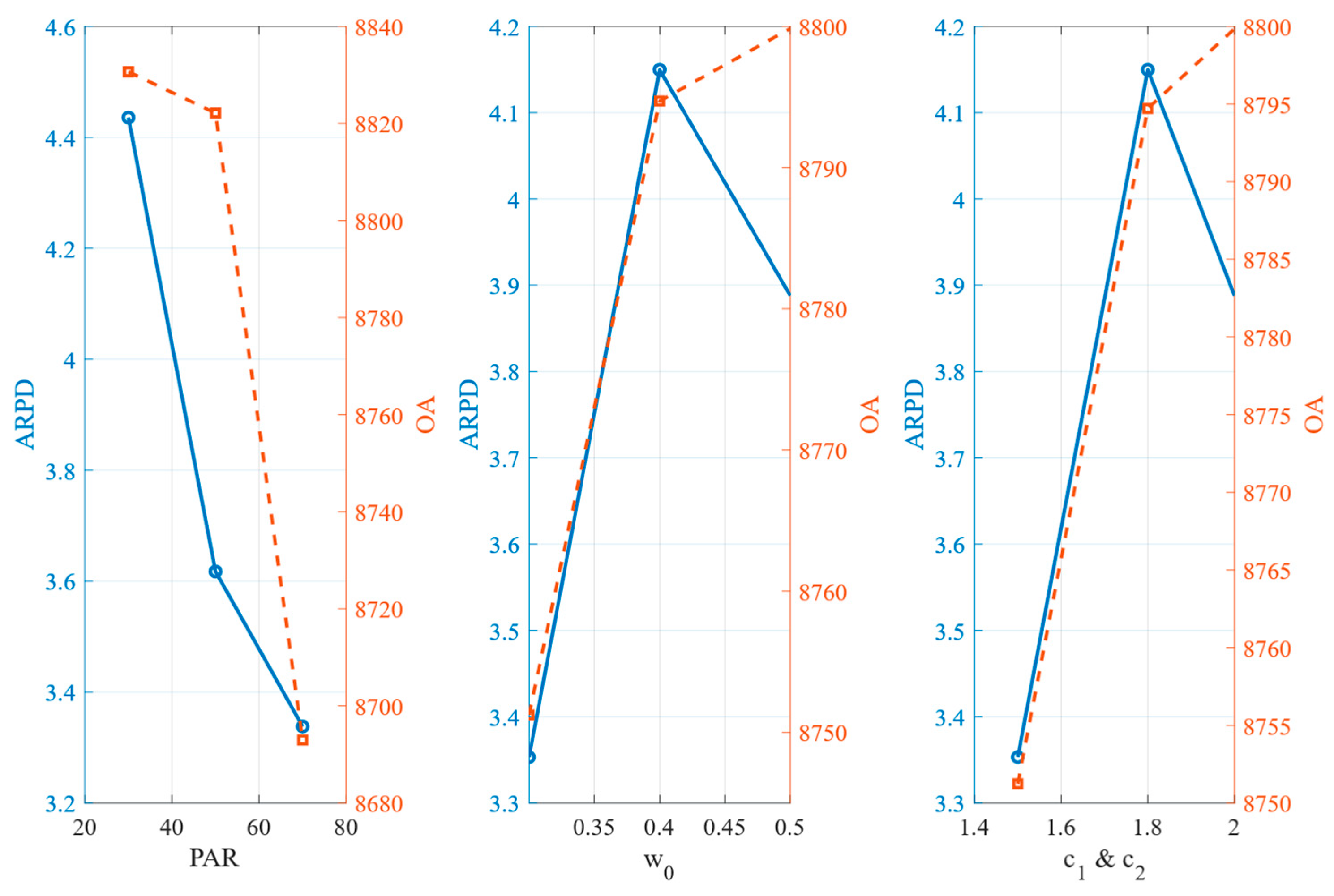
The optimal parameter combination observed from Figure 9 is PAR = 70, w₀ = 0.3, and c₁ = c₂ = 1.5, under which the algorithm achieves superior performance in terms of average ARPD.

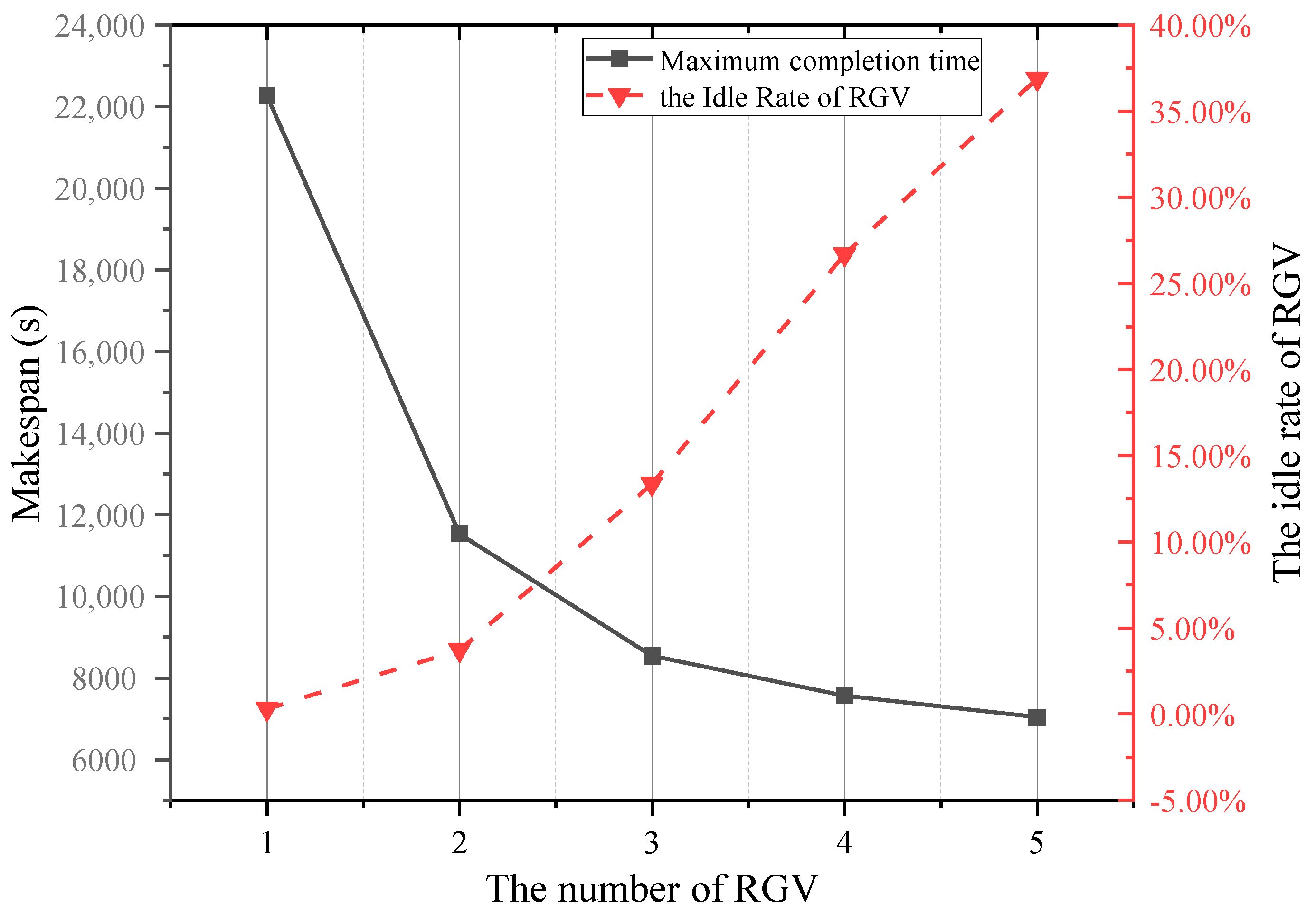
5.2. Effect of RGV Quantity on Warehouse Efficiency

The number of RGVs on the circular track is a critical factor affecting the throughput of the warehouse system per unit time. Therefore, this study investigates the impact of the number of RGVs on the total completion time and RGV idle rate, using the data from Table 3. As shown in Figure 10, the total completion time of the warehouse decreases as the number of RGVs increases, and the reduction becomes more gradual when the number of RGVs reaches 3. Additionally, the RGV idle rate increases with the number of RGVs. To balance the RGV idle rate and the total completion time, it is evident that the optimal number of RGVs in this scenario is 3, providing the best cost-effectiveness. In the following experiments, we set the number of RGVs to 3.

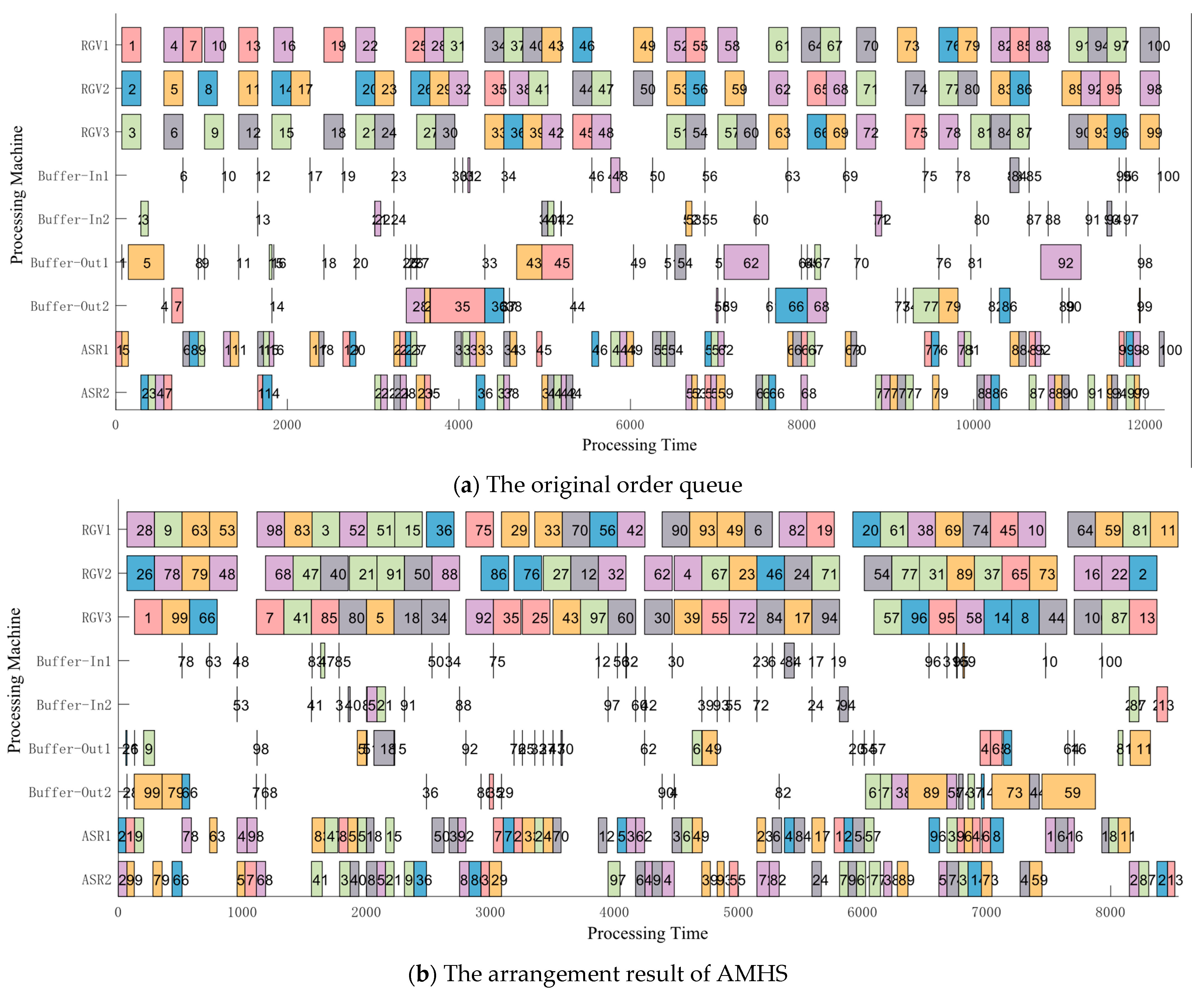
Furthermore, the feasibility of the proposed scheduling model is verified through the case study presented in this section. Specifically, based on the experimental data provided in Table 3, the system successfully schedules 100 inbound and outbound tasks using 3 RGVs and 2 ASRs, without any conflicts, deadlocks, or resource overload. As illustrated in Figure 11, all tasks are processed continuously and efficiently under buffer and collision constraints, demonstrating the model’s applicability and feasibility in practical static warehouse environments.

In the Figure 11b, the horizontal coordinate indicates the time, the vertical coordinate indicates the transportation machine and the buffer zone, the number of each rectangular box in the Figure 11b indicates the number of the goods, the left side of the rectangular box indicates the start time, the right side indicates the end time, if the transportation time or buffer waiting time is 0, then the left side of the rectangular box solid line and the right side of the solid line overlap, for a vertical line. As can be seen from the data in the figure, the scheduling results obtained by the algorithm proposed in this paper are practical and feasible, the goods in and out of the warehouse arrangement are more compact, the load of each device is more balanced, and the utilization rate is high. In addition, through reasonable scheduling, the four buffer zones generally have no large accumulation of goods, and the overall system is not seriously blocked. Compared with the original order queue as Figure 11a, the maximum completion time is reduced by 30.1%.

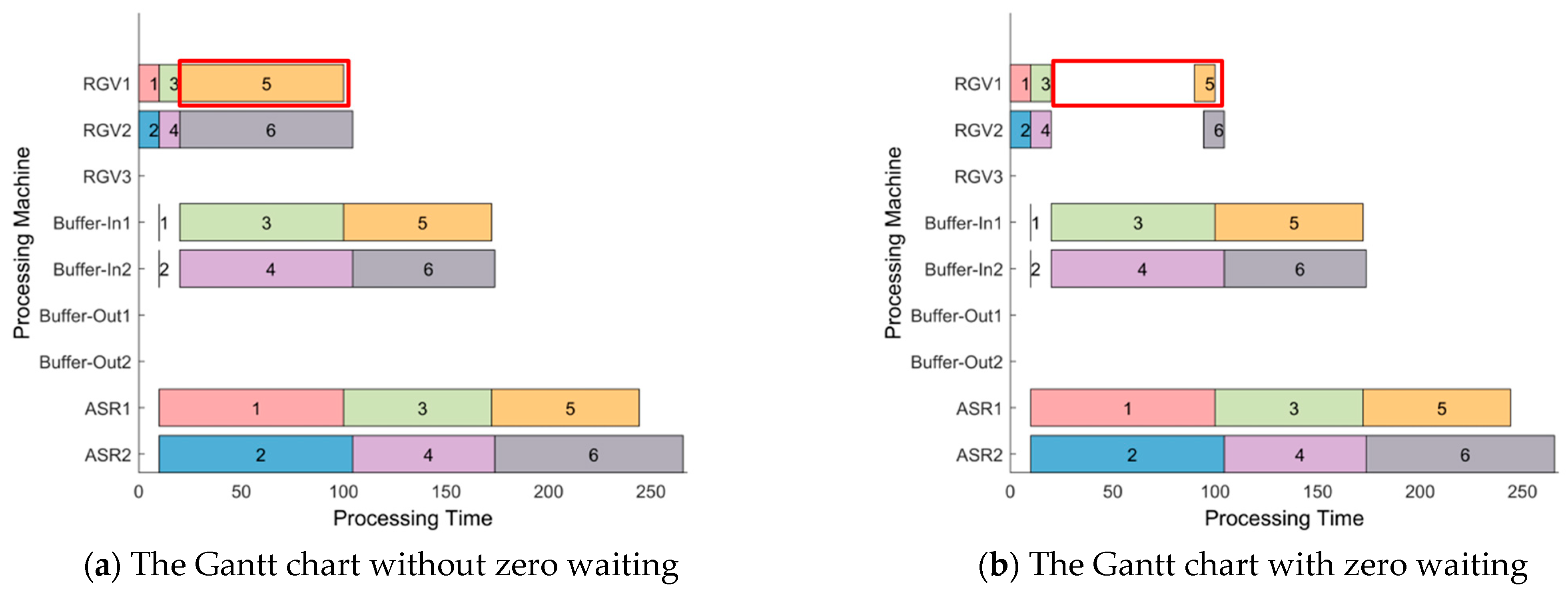
5.3. Validation of Zero-Wait Strategy

To verify the practical value of the zero-waiting RGV/ASR storage system access model proposed in this paper, considering a finite buffer, the time of each transportation process for the first 10 transportation tasks of the above scheduling results is analyzed, and the results are shown in

Table 5. Results of transportation time for each process.

Task No.	I/O	Storage Location	Time of Process 1					Time of Process 2
			Start	End	Actual Transit	Ideal Transit	Load Wait	Start	End	Actual Transit	Ideal Transit	Load Wait
28	1	(68, 7)	0	222	222	222	0	222	290.84	68.84	68.84	0
26	1	(27, 4)	0	222	222	222	0	290.84	345.01	54.17	54.17	0
1	1	(16, 5)	0	84.24	84.24	84.24	0	84.24	306.24	222	222	0
9	1	(19, 9)	222	444	222	222	0	444	527.34	83.34	83.34	0
78	1	(78, 10)	222	444	222	222	0	527.34	608.29	80.94	80.94	0
99	1	(70, 3)	84.24	183.00	98.75	98.75	0	306.24	528.24	222	222	0
63	0	(28, 3)	232.18	306.24	74.06	74.06	0	444	666	222	222	0
79	1	(69, 10)	444	666	222	222	0	666	740.37	74.37	74.37	0
66	1	(88, 5)	740.37	807.41	67.03	67.03	0	807.41	1029.41	222	222	0
53	0	(74, 7)	807.41	881.18	73.77	73.77	0	881.18	1103.18	222	222	0

.

As shown in the table, the difference between the ideal transportation time and the actual transportation time of the scheduling result for each transportation process of each task is always 0. From this, it can be seen that the buffer zone is ready to store the goods before the machine transports the goods to the next destination, and the result of this paper realizes the zero-waiting under the load state of the RGV and the ASR, and the goods can be transported to the target location in a fast and continuous way, which reduces the time of the goods’ stranded. It avoids blockage and congestion in the transportation system and ensures the continuous operation of the means of transportation and the smooth flow of goods. This will improve the fluidity of logistics, reduce the retention and accumulation of goods, reduce the risk of loss and expiration of goods, and greatly improve the stability and reliability of the transportation system, reducing the risk of transportation disruptions and delays.

5.4. Algorithm Comparison

To further validate the optimization performance of the proposed AMHS algorithm in addressing the zero-wait scheduling problem in HRS with finite buffers, a set of random test cases was generated. Specifically, the x-coordinates were randomly selected within the range [1, 196], and the y-coordinates within [1, 12]. This process was repeated 15 times to create 15 unique test cases. In each case, the number of inbound and outbound tasks is equal. Each instance is named using the format “J{task number}”. For example, “J100” refers to an instance with 100 tasks.

To evaluate the effectiveness of the improved search operators in the AMHS algorithm, this section first investigates three basic algorithms: Genetic Algorithm (GA) [40], Discrete Imperialist Competitive Algorithm (DICA) [41], and Improved Whale Optimization Algorithm (IWOA) [42]. The performance of GA, DICA, and IWOA algorithms was optimized through parameter tuning as follows: For GA, the optimal parameters were a population size of 70, crossover rate of 0.8, and mutation rate of 0.1, balancing exploration and exploitation. For DICA, the best performance was achieved with 20 imperialists, a revolution rate of 0.4, and an assimilation rate of 0.2, which effectively balanced global and local search. For IWOA, the optimal parameters were a population size of 60, weight factor of 0.6, and scaling factor of 0.2, which ensured the best convergence speed and solution quality.

Additionally, two variants based on the AMHS algorithm are designed: the first variant, IGPSO, is created by removing the self-learning mechanism and replacing the feedback-based local enhancement operator with standard Particle Swarm Optimization (PSO); the second variant, Standard Local Genetic Algorithm (SLGA), is obtained by removing the feedback-based local enhancement operator. The comparative results are presented in

Table 6. Comparison results of 4 algorithms for multiple experiments.

Instance	AMHS			IGPSO			SLGA			GA			DICA			IWOA
	OA	APRD	CT	OA	APRD	CT	OA	APRD	CT	OA	APRD	CT	OA	APRD	CT	OA	APRD	CT
	(s)	(%)	(s)	(s)	(%)	(s)	(s)	(%)	(s)	(s)	(%)	(s)	(s)	(%)	(s)	(s)	(%)	(s)
J50	3917.06	1.40	0.594	3951.10	1.90	0.516	4239.31	3.00	0.494	4438.43	4.70	0.058	4211.23	2.60	0.118	4146.97	2.10	0.053
J60	4635.83	1.10	0.741	4788.54	2.00	0.553	4952.89	2.20	0.574	5058.19	2.10	0.063	4790.73	2.80	0.13	4825.59	1.90	0.056
J70	5650.64	0.60	0.9	5774.34	0.90	0.689	5862.27	1.00	0.694	6016.40	2.80	0.069	5812.52	2.20	0.146	5978.14	1.80	0.066
J80	6513.88	1.00	1.008	6572.81	1.60	0.805	7027.13	2.00	0.796	7168.51	2.40	0.076	6918.41	2.30	0.156	6710.21	1.70	0.07
J90	7313.02	1.10	1.186	7356.95	1.40	0.948	7709.35	1.60	0.964	7957.78	2.00	0.083	7660.35	1.90	0.168	7574.91	2.00	0.069
J100	8237.24	1.00	1.284	8315.10	1.60	1.075	8512.10	1.60	1.082	8913.45	2.10	0.085	8451.83	2.10	0.186	8491.30	1.50	0.08
J110	9108.56	1.80	1.478	9558.58	2.80	1.199	9713.38	3.60	1.229	9840.05	3.90	0.093	9591.66	6.20	0.202	9496.68	4.10	0.081
J120	9868.72	1.90	1.595	10,200.24	3.90	1.288	10,238.29	1.90	1.309	10,791.64	2.10	0.104	10,233.42	5.90	0.192	10,631.54	5.40	0.095
J130	10,847.60	1.60	1.862	11,062.54	3.10	1.481	11,259.72	2.10	1.44	11,653.69	2.90	0.124	11,187.22	7.20	0.214	11,534.59	8.10	0.094
J150	13,033.77	1.90	2.017	13,436.60	1.30	1.614	13,707.66	1.70	1.658	14,054.53	2.20	0.118	13,458.04	5.20	0.216	13,590.40	4.50	0.104
J160	14,191.60	2.90	2.311	14,519.94	4.10	1.862	14,737.42	3.40	1.692	15,061.74	2.90	0.116	14,319.34	4.20	0.24	14,724.19	4.90	0.111
J170	14,610.91	2.10	2.366	14,790.83	1.20	2.025	15,090.28	2.10	1.892	15,420.85	3.70	0.133	15,082.23	4.30	0.244	15,132.87	3.30	0.127
J180	16,004.61	1.60	2.577	16,274.83	2.70	2.195	16,431.13	1.80	2.01	16,600.16	3.30	0.13	16,416.90	6.30	0.242	16,511.61	3.90	0.124
J190	16,515.58	2.70	2.713	16,740.11	4.30	2.305	17,171.20	3.50	2.204	17,396.60	3.70	0.136	16,944.50	4.70	0.272	17,024.61	5.00	0.13
J200	17,330.44	2.90	2.95	18,270.32	3.50	2.626	18,586.75	3.10	2.572	18,904.97	4.30	0.146	17,967.83	6.20	0.292	18,491.87	6.20	0.144

Note: “CT” stands for Compute Time, measured in seconds. The bold values indicate the best (optimal) results obtained within each set of experiments for comparative purposes.

.

The statistics in the table show that the OA of the proposed AMHS algorithm for multiple solutions outperforms the other five algorithms. The APRE metrics further indicate that, across different experiments, the relative percentage of average deviation generated by the AMHS algorithm is consistently better for most solutions compared to the other algorithms. This demonstrates the superiority and stability of the proposed AMHS in solving these types of problems.

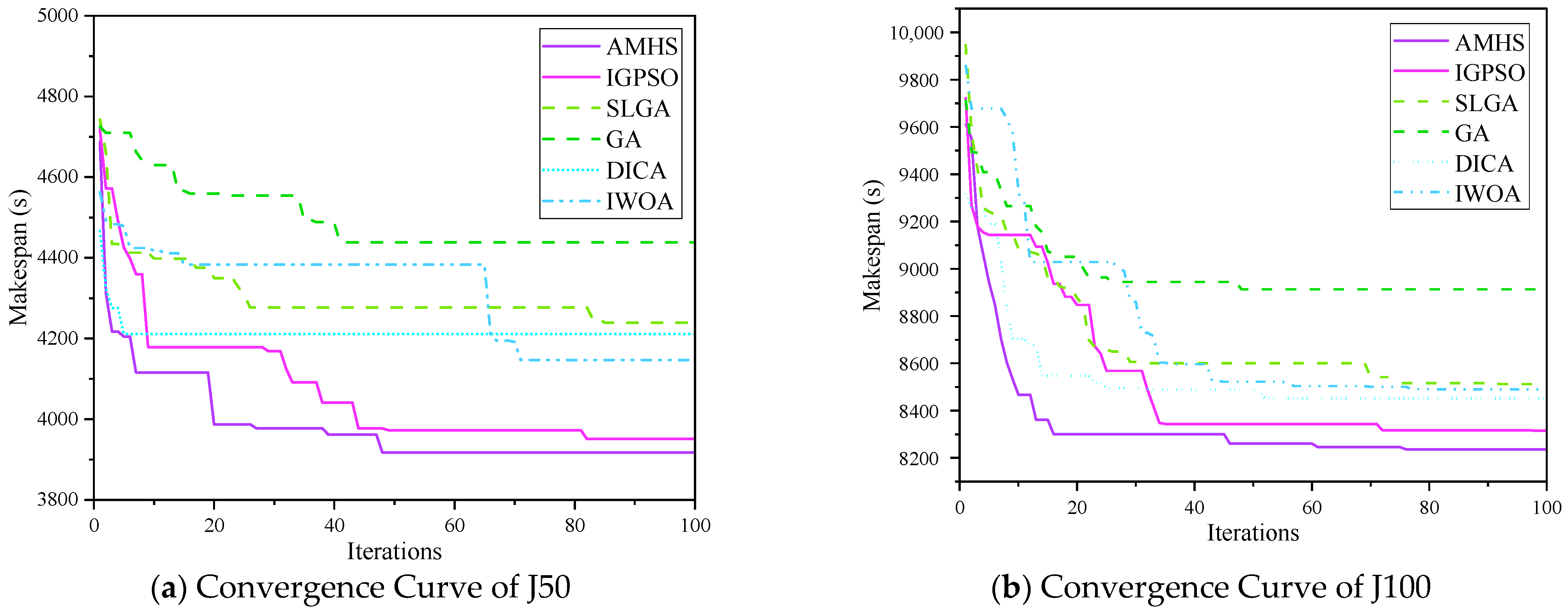
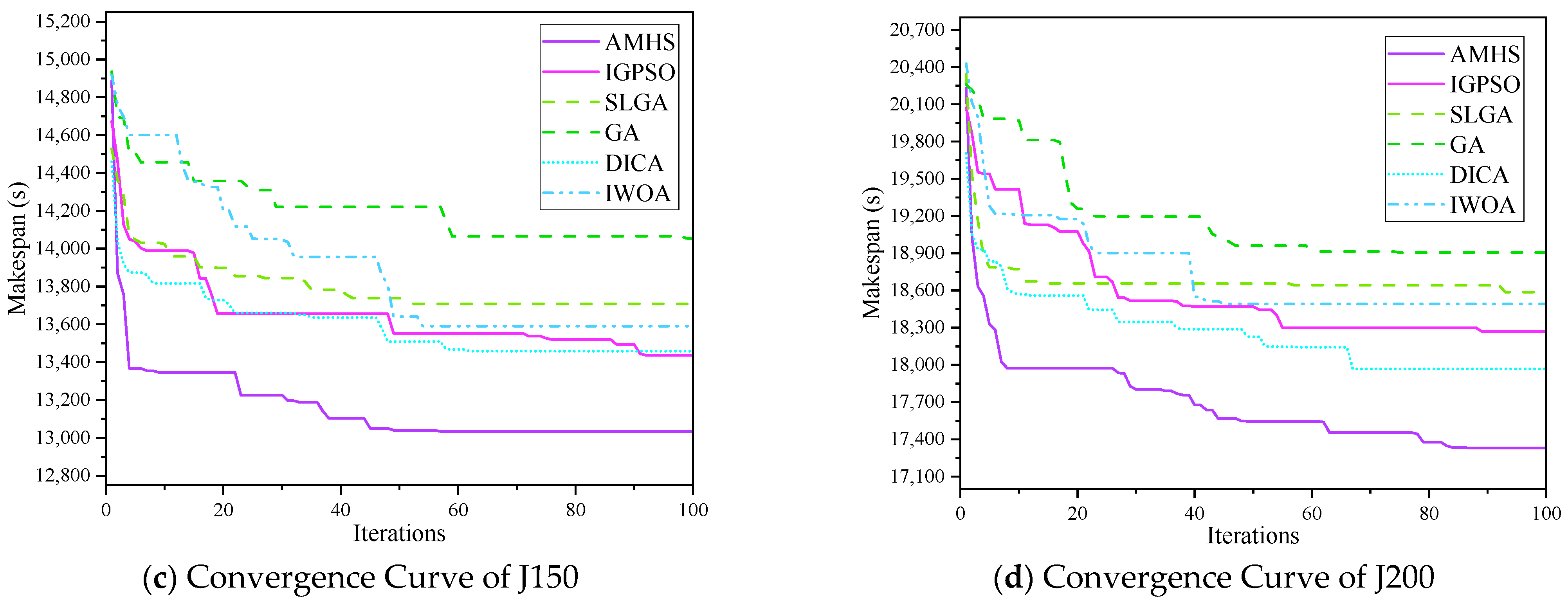
To further validate the efficiency and stability of the proposed algorithm, convergence behaviors were compared. The results are illustrated in Figure 12, which presents the convergence curves of the six algorithms over 100 iterations.

As shown in Figure 12, the proposed AMHS algorithm achieves faster convergence and reaches a lower final objective value compared to DICA, GA, and IWOA. In contrast to the IGPSO, and the SLGA, the AMHS algorithm outperforms these models, achieving lower Makespan values across all task scales (J50, J100, and J200). This further confirms that both the hormonal regulation mechanism and the local enhancement search operators are crucial for enhancing the robustness and stability of the algorithm, reducing variability during optimization, and improving overall task scheduling efficiency. These findings demonstrate that the proposed algorithm not only enhances scheduling efficiency but also improves result stability, reducing the uncertainty of task execution.

In summary, the AMHS algorithm proves effective for solving the zero-wait scheduling problem in RGV/ASR warehousing systems with finite buffers. First, the elite solution initialization strategy introduces high-quality individuals early in the search, providing a strong foundation for subsequent optimization. Second, the global search operator enhances exploration capability by adjusting task scheduling orders and expanding the solution space. Finally, inspired by biological hormone regulation mechanisms, a local search operator and a perturbation-based reconstruction strategy are employed to refine local search and prevent premature convergence. Together, these components ensure that the AMHS algorithm achieves both high efficiency and solution quality in complex scheduling environments.

5.5. Scheduling Application

To demonstrate the real-world applicability of the proposed scheduling model, the AMHS algorithm has been integrated into a customized Warehouse Management System (WMS) developed for a salt production and distribution enterprise.

The graphical user interface (GUI) of the WMS is shown in Figure 13 and Figure 14, which visualize the scheduling results of ASRs and RGVs, respectively. The Gantt chart interface clearly displays the execution timeline and task assignments for each machine. Color-coded bars represent individual tasks, and tooltip overlays provide key metadata such as task ID, start time, and completion time, enabling operators to review task sequences and operational efficiency in detail.

The scheduling module, powered by the AMHS algorithm, has been deployed in the actual warehouse system, where it supports daily operations. While the performance evaluation in this study is simulation-based due to enterprise data confidentiality, the successful integration of the algorithm into an industrial WMS demonstrates its engineering feasibility and practical utility.

6. Conclusions and Future Work

This paper presents the inbound/outbound scheduling problem of a zero-waiting RGV/ASR storage system considering a finite buffer, and a kind of improved Adaptive AMHS algorithm is proposed to solve the problem. The main works are as follows: First, the architecture of the zero-waiting RGV/ASR storage system is designed in detail. And taking a packaged salt storage case as a specific production scenario, construct a mathematical model to describe the entire inbound/outbound process. Secondly, analyzing the multi-RGV same-track problem and establishing a rule-binding-based model of the multi-RGV collision avoidance and zero-waiting. Third, this paper designs the global search operator, the local search operator, and the perturbation operator, which improve the search efficiency of the AMHS algorithm. Specifically, this paper uses a set of inbound/outbound data of a realistic packaged salt storage case. And the superiority of the AMHS algorithm is verified by comparing it against three heuristic and meta-heuristic algorithms in 15 random case sets.

There are some directions for future work. (1) Collecting the historical operation data of RGV/ASR storage system, feature extraction and learning, and constructing a data-driven scheduling model; (2) Integrating the proposed RGV/ASR storage model with location optimization to improve the global efficiency of the warehouse system; (3) Introducing perturbation in the problem for the real-time state of packaged salt transportation factors to realize real-time scheduling of RGV/ASR storage system.