Ultra-Local Model-Based Adaptive Enhanced Model-Free Control for PMSM Speed Regulation

Abstract

Conventional model-free control (MFC) is widely used in motor drives due to its simplicity and model independence, yet its performance suffers from imperfect disturbance estimation and input gain mismatch. To address these issues, this paper proposes an adaptive enhanced model-free speed control (AEMFSC) scheme based on an ultra-local model for permanent magnet synchronous motor (PMSM) drives. First, by integrating a nonlinear disturbance observer (NDOB) and a PD control law into the generalized model-free controller, an enhanced model-free speed controller (EMFSC) was developed to ensure closed-loop stability. Compared with a conventional MFSC, the proposed method eliminated steady-state errors, reduced the speed overshoot, and achieved faster settling with improved disturbance rejection. Second, to address the performance degradation induced by input gain $\alpha$ mismatch during time-varying load conditions, we developed an online parameter identification method for real-time $\alpha$ estimation. This adaptive mechanism enabled automatic controller parameter adjustment, which significantly enhanced the transient tracking performance of the PMSM drive. Furthermore, an algebraic-framework-based high-precision identification technique is proposed to optimize the initial $\alpha$ selection, which effectively reduces the parameter tuning effort. Simulation and experimental results demonstrated that the proposed AEMFSC significantly enhanced the PMSM’s robustness against load torque variations and parameter uncertainties.

1. Introduction

Permanent magnet synchronous motors (PMSMs) offer a high power density and efficiency and low maintenance, making them widely used in applications such as radar and photoelectric detection systems [1]. In PMSM speed control systems, the dual-loop structure serves as the conventional solution, comprising an outer speed loop and an inner current/torque control loop. For the inner-loop implementation, two predominant strategies exist: current regulation via field-oriented control (FOC) [2,3] or direct torque/flux control (DTC) schemes [4,5]. The outer speed controller plays a key role in ensuring precise speed tracking and the effective suppression of load disturbances.

Proportional–integral (PI) control is widely used in PMSM drive systems due to its simplicity, clarity, and effectiveness [6,7]. However, practical challenges such as motor parameter uncertainties and unknown load disturbances limit its speed control performance. To address these issues, advanced control methods, including internal model control [8], sliding mode control [9,10], adaptive control [11], fuzzy control [12], and model predictive control (MPC) [13], have been applied to speed loops.

A key challenge in sliding mode control is the buffeting phenomenon caused by high-frequency switching. High-order sliding mode control techniques have been developed to mitigate this issue [14]. Adaptive sliding modes enhance the robustness of the system in the face of uncertainty and parameter variations but increase the complexity and computational effort of the system [15]. Adaptive control is more complex than traditional methods, and although adaptive controllers can gradually adapt to changes in parameters, they often struggle to respond quickly to sudden changes [16,17].

Disturbance/uncertainty estimation and attenuation (DUEA) [18] control enhances system robustness by estimating and compensating for disturbances and uncertainties in real time. Since the 1960s, various DUEA techniques based on different estimation methods have been developed. Among these, disturbance observer-based control (DOBC) and extended state observer-based control (ESOC, also known as ADRC) are the most widely studied and applied in AC motor drives. As a key component of DOBC, DOB was first proposed by Ohnishi [19] in the 1980s to enhance the disturbance rejection capability and robustness of DC motor drives. In DOBC, the disturbances/uncertainties are estimated by the observer and compensated for by the estimated disturbances/uncertainties [20,21]. ADRC was introduced by Han in the 1990s as a practical control method to replace classical PID controllers [22]. To simplify the ADRC design, a linear extended state observer (LESO) was proposed [23]. An LESO is often combined with other control methods, and the robustness of the PMSM system can be improved by the feedforward compensation of the lumped disturbance estimated by an LESO [24,25].

Recently, the ultra-local model (ULM)-based model-free control (MFC), proposed by Fliess and Join [26], has gained significant attention in areas such as PMSM, autonomous vehicle trajectory, and energy system management. MFC is a control strategy that does not require a precise mathematical model of the system, but uses the input and output data of the system to adjust it in real time. Compared with ADRC, MFC has fewer control parameters and does not need knowledge of the system’s order. In [27], a model-free control strategy based on ultra-local models is proposed for current control in a PMSM and later extended to speed control [28]. However, both methods face issues with complex lumped disturbance estimation and long computation times. To address this, a new observer was designed based on the model-free current control strategy for a PMSM, which significantly reduces the design parameters and computational complexity [29,30,31]. MFC has some limitations, including its reliance on data quality. Since MFC depends on real-time data, it is sensitive to measurement noise and the sensor accuracy. Inaccurate or noisy data can reduce the performance and potentially lead to system instability or a loss of control accuracy.

Model-free control based on the ULM operates without global system models, relying solely on the local dynamics. However, its lack of structural error buffering causes parametric errors to propagate directly into control inputs. The control gain $\alpha$ in a ULM critically determines closed-loop performance as it directly correlates with the plant’s true parameters. Within ULM-based control laws, $\alpha$ appears in the denominator, linearly scaling the control input u and amplifying errors proportionally. Reference signal derivatives introduce additional disturbances under $\alpha$ mismatch conditions, while lumped disturbance estimation errors become magnified. When $\widehat{\alpha }\ne {\alpha }_{true}$, control actions systematically deviate from intended values. An insufficient $\alpha$ reduces the phase margin, potentially inducing tracking error oscillations and control input chattering, whereas an excessive $\alpha$ diminishes the gain margin and degrades the control precision. Consequently, developing effective gain-tuning strategies for ULM-based model-free control remains crucial [32]. To enhance the ULM control performance, several variable-gain model-free approaches have been developed [33,34]. For instance, an online method was proposed to estimate the control gain using previous-step command signals [33]. Alternatively, in [34], the differential Riccati equation used for online gain adaptation was introduced. While these adaptive techniques have improved the overall performance of model-free control, the systematic tuning of gains for optimal performance requires further investigation.

In this study, the nonlinear disturbance observer (NDOB) and PD control law were integrated into a generalized model-free feedback controller to enhance the speed regulation performance of PMSMs. An $\alpha$-adaptive method based on gradient descent was developed to achieve an optimal tracking performance, while a parameter estimation approach was designed to optimize the selection of $\alpha$’s initial value. These methodologies collectively enabled the proposed controller to achieve superior performance through accurate lumped disturbance estimation, input gain adaptation, and rapid response times. The main contributions of this work are summarized as follows:

• Compared with conventional lumped disturbance estimation methods, the incorporation of an NDOB eliminated the steady-state errors caused by load torque variations. The integration of PD control law into the generalized model-free controller effectively reduced the speed overshoot, while the dead-zone method mitigated the control signal oscillations induced by sensor noise.
• The proposed $\alpha$ online adaptive estimation law ensured rapid convergence to the true $\alpha$ value, which significantly improved the speed-tracking accuracy.
• The algebraic-framework-based linear parameter identification method enabled the high-precision estimation of the true $\alpha$ value, eliminating arbitrariness in initial value selection and enhancing transient performance during startup phases.

The remainder of this paper is structured as follows: Section 2 presents the PMSM dynamic model and conventional model-free speed control strategies. Section 3 details the novel enhanced model-free speed control (EMFSC) framework and the proposed input gain identification methodology. A comparative analysis of the simulation and experimental results is provided in Section 4. Finally, the conclusions are presented in Section 5.

2. Conventional Model-Free Speed Control Based on Ultra-Local Model

2.1. Mathematical Model of SMPMSM Direct Drive System

Considering the parametric uncertainties and unknown external disturbance, the electromechanical equation of a PMSM complex direct drive system is given as

$$\left\{\begin{array}{c}{J}_n{\displaystyle \frac{d{\omega }_m}{dt}}=T_e-T_L-B_n{\omega }_m-d_n-f_t,\hfill \\ T_e={\displaystyle \frac{3n_p}{2}}({\phi }_n{i}_q+(L_d-L_q)i_d{i}_q),\hfill \end{array}\right.$$

(1)

where ${\omega }_m$ is the rotor mechanical rotational speed; $J_n$ and $B_n$ express the nominal values of the rotational inertia and the friction coefficient, respectively; $T_e$ stands for the electromagnetic torque; $T_L$ denotes the load torque; $d_n$ is the constant disturbance; $f_t$ expresses the disturbance induced by the parametric uncertainties and other unknown disturbances; $n_p$ is the pole pair number; ${\phi }_n$ express the nominal values of the permanent magnet flux linkage; $i_d$ and $i_q$ represent the d- and q-axis currents, respectively; and $L_d$ and $L_q$ are the stator inductances of the d- and q-axes, respectively.

For the surface-mounted PMSM, the d- and q-axis inductances are equal ($L_d=L_q$). Then, the electromagnetic torque $T_e$ can be represented as follows:

$$T_e={\displaystyle \frac{3n_p{\phi }_n{i}_q}{2}}.$$

(2)

From Equation (1), the motion dynamics can be expressed as

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\omega }_m}{dt}}=& {\displaystyle \frac{1}{J_n}}{T}_e+{\displaystyle \frac{1}{J_n}}\left(-T_L-B_n{\omega }_m-d_n-f_t\right)\hfill \\ \hfill =& {\displaystyle \frac{3n_p{\phi }_n}{2J_n}}{i}_q+{\displaystyle \frac{1}{J_n}}\left(-T_L-B_n{\omega }_m-d_n-f_t\right).\hfill \end{array}$$

(3)

2.2. Principle of Conventional ULM-Based Model-Free Control

The first-order ultra-local model of a single-input single-output (SISO) system is expressed as [26]

$$\dot{y}=F+\alpha u,$$

(4)

where y and u are the output and control variables, respectively; $\alpha$ represents a nonphysical scaling factor selected by the designer; and F represents the known and unknown part of the system. Defining the tracking error $e=y_d-y$, the error dynamic can be gotten using

$$\dot{e}={\dot{y}}_d-F-\alpha u,$$

(5)

where $y_d$ is the desired output. To converge the tracking error e, a generalized model-free feedback controller is proposed as

$$u={\displaystyle \frac{-F+{\dot{y}}_d+C\left(e\right)}{\alpha }},$$

(6)

where $C\left(e\right)$ denotes the error convergence law.

In [28], the principle of model-free control based on an ultra-local model with algebraic parameter identification is applied to the speed control of an SMPMSM drive, and the corresponding controller is called a “conventional MFSC” (MFSC-API). The reference of the torque is calculated using

$$T_e^{\ast }\left(k\right)={\displaystyle \frac{-{\widehat{F}}_{\mathsf{\Omega }}\left(k\right)+{\dot{\omega }}_m^{\ast }\left(k\right)+K_{p}e\left(k\right)}{{\alpha }_{\mathsf{\Omega }}}},$$

(7)

where ${\widehat{F}}_{\mathsf{\Omega }}\left(k\right)$ donates the estimated value of the lumped disturbance $F_{\mathsf{\Omega }}\left(k\right)$, ${\omega }_m^{\ast }\left(k\right)$ is the desired speed, the symbol “(k)” represents value of above variable at the (k)th control period, and $K_P$ represents the parameter of the controller. For the mechatronic system described in (3), in the presence of a mismatch between the controller’s initial parameters and the true machine parameters, the lumped disturbance $F_{\mathsf{\Omega }}$ can be mathematically characterized as

$$F_{\mathsf{\Omega }}=({\displaystyle \frac{1}{J_n}}-{\alpha }_{\mathsf{\Omega }})T_e+{\displaystyle \frac{1}{J_n}}\left(-T_L-B_n{\omega }_m-d_n-f_t\right).$$

(8)

Within a sufficiently “small” time interval, $F_{\mathsf{\Omega }}\left(k\right)$ is treated as a constant parameter and estimated through an algebraic parameter identification technique (API) [35] expressed as

$$\begin{array}{cc}\hfill {\widehat{F}}_{\mathsf{\Omega }}\left(k\right)=& -{\displaystyle \frac{3}{T_F^3}}{\int }_0^{T_F}\left[\left(T_F-2\delta \right){\omega }_m\left(\delta \right)+{\alpha }_{\mathsf{\Omega }}\delta \left(T_F-\delta \right)T_e^{\ast }\left(\delta \right)\right]d\delta \hfill \\ \hfill =& -{\displaystyle \frac{3}{n_F^3}}{T}_s\sum _{m=1}^{n_F}\left[\left(n_F-2\left(m-1\right)\right)\times {\omega }_m\left(m-1\right)\right.\hfill \\ \hfill & +{\alpha }_{\mathsf{\Omega }}\left(m-1\right)T_s\left(n_F-\left(m-1\right)\right)\times T_e^{\ast }\left(m-1\right)\hfill \\ \hfill & \left.+\left(n_F-2m\right)\times {\omega }_m\left(m\right)+{\alpha }_{\mathsf{\Omega }}m{T}_s\left(n_F-m\right)\times T_e^{\ast }\left(m\right)\right],\hfill \end{array}$$

(9)

where $T_F$ is the data window and $T_F=n_F{T}_s$; $n_F$ is the data window length; and $\left[0,T_F\right]$ is a sliding data window.

According to the ultra-local model, $\alpha$ should be designed to keep $\dot{y}$ and $\alpha u$ in the same order of magnitude. The control performance of the system may be adversely affected by the improper selection of the $\alpha$ parameter. Given this, the tuning of the input gain $\alpha$ had a significant impact on the stability and tracking accuracy of the control system.

3. Principle of the Proposed AEMFSC-NDOB

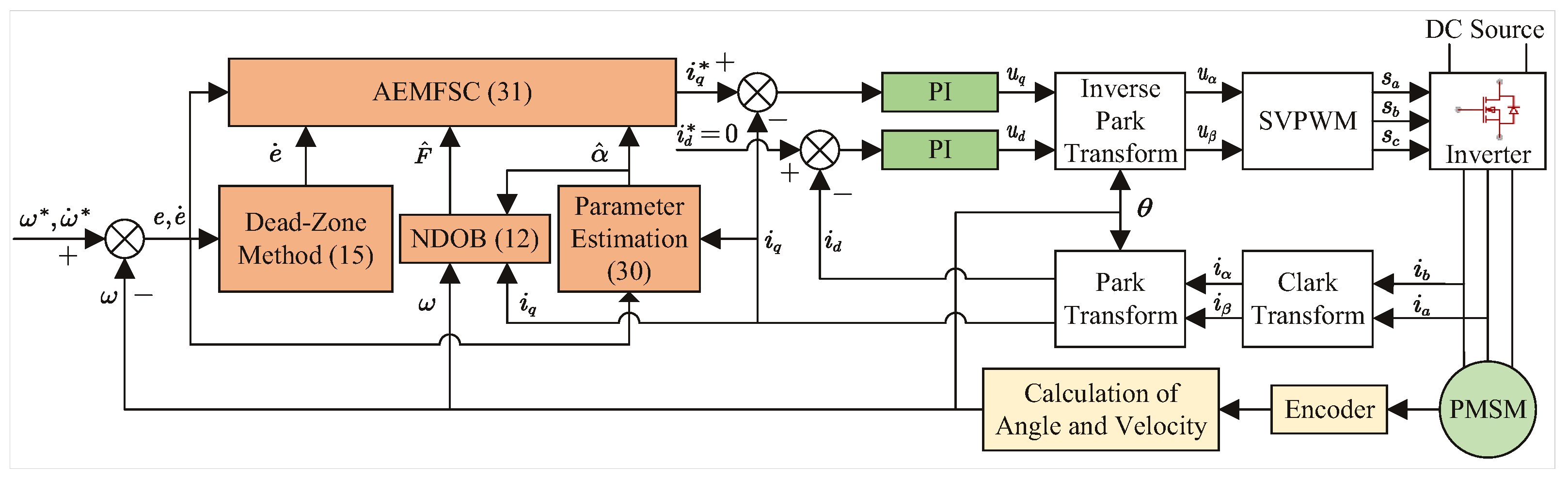
In this section, an adaptive enhanced model-free speed control framework based on the ultra-local model is developed. First, a nonlinear disturbance observer (NDOB)-enhanced model-free controller (EMFSC-NDOB) is developed by integrating a nonlinear disturbance observer with proportional–derivative (PD) control architecture. Subsequently, an adaptive law for the control input gain is derived via the gradient descent method, resulting in an adaptive EMFSC-NDOB method (AEMFSC-NDOB). Finally, an initial value determination method for the control input gain is derived based on algebraic differentiation techniques.

3.1. Enhanced Model-Free Speed Control via Nonlinear Disturbance Observer

In this article, according to (3), considering the SMPMSM q-axis current as the output variable, the ideal ultra-local mathematical model of SMPMSM can be expressed as

$$\dot{y}={\alpha }_{e}u+F_1,$$

(10)

where the output $y={\omega }_m$, the input $u=i_q$, the theoretical control gain ${\alpha }_e=3n_p{\phi }_n/\left(2J_n\right)$, and the lumped disturbance $F_1=\left(-T_L-B_n{\omega }_m-d_n-f_t\right)/J_n$.

The practical difficulty in obtaining accurate machine parameters leads to a parametric mismatch between the designed ultra-local model and the true system dynamics. Therefore, the practically realized ultra-local model takes the following form:

$$\dot{y}=\alpha u+F_2,$$

(11)

where the lumped disturbance $F_2=({\alpha }_e-\alpha )u+F_1$. With model (11) as the basis, the model-free feedback control scheme (6) is subsequently deployed. However, the existence of $F_2$ results in control law (6) not being implemented. To achieve the precise and rapid real-time estimation of $F_2$, the nonlinear disturbance observer (NDOB) was designed as follows [36]:

$$\left\{\begin{array}{c}\dot{Z}=-Lz-L(p+\alpha u)\hfill \\ p=Ly\hfill \\ {\widehat{F}}_2=Z+p.\hfill \end{array}\right.$$

(12)

where Z is an auxiliary variable, L is the positive gain of the nonlinear disturbance observer, and ${\widehat{F}}_2$ is the estimated value of the lumped disturbance.

Taking the derivative of the observer error ${\tilde{F}}_2=F_2-{\widehat{F}}_2$ and using (11) then yields

$$\begin{array}{cc}\hfill {\dot{\tilde{F}}}_2=& \dot{F_2}-{\dot{\widehat{F}}}_2\hfill \\ \hfill =& \dot{F_2}-(\dot{Z}+L\dot{y})\hfill \\ \hfill =& \dot{F_2}-(-L(z+Ly+\alpha u)+L(\alpha u+F_2))\hfill \\ \hfill =& \dot{F_2}-L(-{\widehat{F}}_2+F_2)\hfill \\ \hfill =& \dot{F_2}-L{\tilde{F}}_2.\hfill \end{array}$$

(13)

Considering that the total disturbance $F_2$ and ${\dot{F}}_2$ are bounded, where ${lim}_{t\to \infty }{\dot{F}}_2=0$, according to the principle of Lyapunov function stability, the nonlinear disturbance observer system is progressively stable.

To enhance the transient tracking performance of the speed control system, a PD control law was employed to ensure the convergence of the tracking error. Therefore, the enhanced model-free controller is proposed as

$$u={\displaystyle \frac{-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e}}{\alpha }}.$$

(14)

where $k_p,k_d\in {\mathbb{R}}^{+}$ are the control parameters.

To prevent the amplification of high-frequency noise in the speed-tracking error differentiation, which may cause control signal chattering and potential system instability, a dead-zone method was implemented in the controller. This approach suspends the error derivative calculation when the error magnitude falls below a predefined threshold. Specifically, the dead-zone implementation is as follows:

$$\dot{e}\left(k\right)=\left\{\begin{array}{cc}{\displaystyle \frac{e\left(k\right)-e\left(k-1\right)}{T_s}},\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ 0,\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(15)

where $\delta$ is the error threshold.

Substituting the control law (14) into the tracking error dynamics (5) based on (10), one has the following error equation:

$$\begin{array}{cc}\hfill \dot{e}=& {\dot{y}}_d-{\alpha }_{e}u-F_1\hfill \\ \hfill =& {\dot{y}}_d-F_1-{\displaystyle \frac{{\alpha }_e}{\alpha }}(-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e})\hfill \\ \hfill =& {\dot{y}}_d-F_1-\rho (-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e})\hfill \\ \hfill =& -\rho k_{p}e-\rho k_d\dot{e}+D_r\hfill \end{array}$$

(16)

where $b_e/b=\rho$, $\rho >0$, and the residual disturbance $D_r=-F_1+\rho {\widehat{F}}_2+(1-\rho ){\dot{y}}_d$. Then, rewriting the above equation gives the following:

$$\dot{e}=-Ae+B{D}_r,$$

(17)

where

$$A={\displaystyle \frac{\rho k_p}{1+\rho k_d}}>0,B={\displaystyle \frac{1}{1+\rho k_d}}>0.$$

(18)

The Lyapunov function is defined as $V=P{e}^2$, where $P\in {\mathbb{R}}^{+}$ denotes a positive real number. Taking the derivative of V, it yields

$$\begin{array}{cc}\hfill \dot{V}=2Pe\dot{e}=& -2PA{e}^2+2PB{D}_{r}e\hfill \\ \hfill ⩽& -2PA{e}^2+2PBsup|D_r\left|\right|e|.\hfill \end{array}$$

(19)

where $sup|D_r|$ represents the upper bound of $D_r$. Obviously, when $\left|e\right|⩾A^{-1}Bsup\left|D_r\right|$, $\dot{V}⩽0$ can be guaranteed. Furthermore, one gets

$$\underset{t\to \infty }{lim}\left|e\right|⩽{\displaystyle \frac{Bsup|D_r|}{A}}={\displaystyle \frac{sup|D_r|}{\rho k_p}}.$$

(20)

Thus, the closed-loop system is asymptotically stable, and the tracking error is uniformly ultimately bounded.

3.2. Adaptive Enhanced Model-Free Speed Controller Design

The gain $\alpha$ critically determines both the closed-loop stability and speed regulation quality in PMSM drives. This work proposes a gradient-descent-based online auto-tuning scheme to optimize this essential parameter.

The above (11) can be discretized as follows:

$$\begin{array}{cc}\hfill y\left(k\right)=& y(k-1)+T_s\alpha u(k-1)+T_s{F}_2(k-1),\hfill \\ \hfill y(k-1)=& y(k-2)+T_s\alpha u(k-2)+T_s{F}_2(k-2),\hfill \end{array}$$

(21)

where $T_s$ is the sampling time. Since the change period of the lumped disturbance $F_2$ is much larger than the period of the sampling time $T_s$, it can be considered that the lumped disturbance is unchanged in the adjacent sampling period, namely,

$$F_2(k-1)=F_2(k-2).$$

(22)

On this basis, we have

$$y\left(k\right)=2y(k-1)-y(k-2)+T_s\alpha \mathsf{\Delta }u(k-1),$$

(23)

with $\mathsf{\Delta }u(k-1)=u(k-1)-u(k-2)$.

Then, the output error can be expressed as

$$e\left(k\right)=y_d-y\left(k\right)=y_d-2y(k-1)+y(k-2)-T_s\alpha \mathsf{\Delta }u(k-1).$$

(24)

Define the following cost function:

$$J={\displaystyle \frac{1}{2}}{e}^2\left(k\right).$$

(25)

Therefore, the gradient of the cost function with respect to $\alpha$ is given by

$${\nabla }_{\alpha }J=e\left(k\right){\displaystyle \frac{\partial e\left(k\right)}{\partial \alpha }}=-T_s\mathsf{\Delta }u(k-1)e\left(k\right).$$

(26)

The presence of the measurement noise $n\left(t\right)$ in the error signal $e\left(t\right)$ can corrupt the gradient estimation, causing the parameter $\alpha$ to oscillate randomly around or deviate cumulatively from its true value. To enhance the adaptation law, a dead-zone technique was introduced to suppress noise effects by disabling updates during small-error conditions. The implementation details are as follows:

$${\nabla }_{\alpha }J=\left\{\begin{array}{cc}-T_s\mathsf{\Delta }u(k-1)e\left(k\right),\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ 0,\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(27)

where $\delta$ is the error threshold. Therefore, the update law for $\alpha$ is given as follows:

$$\widehat{\alpha }\left(k\right)=\widehat{\alpha }(k-1)-\eta {\nabla }_{\alpha }J=\left\{\begin{array}{cc}\widehat{\alpha }(k-1)+\eta T_s\mathsf{\Delta }u(k-1)e\left(k\right),\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ \widehat{\alpha }(k-1),\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(28)

where $\eta$ is the learning rate.

To prevent instability in the parameter adaptation caused by excessively large or small control inputs $\mathsf{\Delta }u(k-1)$, a nonlinear modulation scheme was applied to the learning rate. The learning rate $\eta$ is dynamically adjusted based on the input variation $\mathsf{\Delta }u(k-1)$, as specified below:

$$\eta T_s=\mu \to {\displaystyle \frac{\mu }{1+\mu (\mathsf{\Delta }u(k-1){)}^2}}.$$

(29)

By incorporating this nonlinear modulation scheme into the standard gradient update law, the final adaptation rule can be gotten using

$$\widehat{\alpha }\left(k\right)=\left\{\begin{array}{cc}\widehat{\alpha }(k-1)+\mu {\displaystyle \frac{1}{1+\mu (\mathsf{\Delta }u(k-1){)}^2}}\mathsf{\Delta }u(k-1)e\left(k\right),\hfill & \left|e\left(k\right)\right|⩾\delta \hfill \\ \widehat{\alpha }(k-1),\hfill & \left|e\left(k\right)\right|<\delta ,\hfill \end{array}\right.$$

(30)

where $\mu$ is the adaptive coefficient, and ${\alpha }_0$ is the initial value of $\widehat{\alpha }\left(k\right)$.

Combining the nonlinear disturbance observer (12), enhanced model-free speed control law (14), and adaptive gain law (30) based on the gradient descent method, the final adaptive enhanced model-free speed controller (AEMFSC) was designed to be

$$u={\displaystyle \frac{-{\widehat{F}}_2+{\dot{y}}_d+k_{p}e+k_d\dot{e}}{\widehat{\alpha }}}.$$

(31)

The block diagram of the proposed PMSM speed control strategy is shown in Figure 1.

3.3. Initial Value Estimation Method for the Input Gain

In practical motor applications, two major challenges exist: (1) inaccuracies or missing specifications of flux linkage parameters and torque coefficients on nameplates, and (2) considerable difficulties in accurately estimating the moment of inertia under complex loading conditions, resulting in significant deviations between the calculated ${\alpha }_0$ and actual ${\alpha }_e$ values.

For constant-load motor systems, employing a fixed ${\alpha }_0$ value effectively reduces the computational overhead in embedded systems. For variable-load systems, appropriate initial ${\alpha }_0$ values substantially enhance the transient tracking performance during the startup phase. This subsection consequently presents an algebraic-framework-based linear identification method for high-precision ${\alpha }_0$ identification.

The electromechanical Equation (3) of the SMPMSM drive system can be expressed as

$$\ddot{\theta }+a\dot{\theta }=b{i}_q+A_0,$$

(32)

where $\theta$ is the rotor mechanical angle, $\dot{\theta }={\omega }_m$, $a=B_n/J_n$, $b=3n_p{\phi }_n/\left(2J_n\right)$, and $A_0=\left(-T_L-d_n-f_t\right)/J_n$. The constant parameters $a,b\in \mathbb{R}$ are unknown, and the $A_0\in \mathbb{R}$ is considered to be a constant load perturbation [37]. Then (32) in the S-domain is given as

$$(s^2+as)\theta =b{i}_q+s\theta \left(0\right)+{\omega }_m\left(0\right)+a\theta \left(0\right)+A_0/s,$$

(33)

where $\theta \left(0\right)$ is an arbitrary initial angle and ${\omega }_m\left(0\right)$ is an unknown initial velocity.

Introduce a first-order low-pass filter given by

$${\theta }_f={\displaystyle \frac{{\omega }_c}{s+{\omega }_c}}\theta ,$$

(34)

where the known constant parameter ${\omega }_c\in \mathbb{R}$ is strictly positive. Thus

$$(s^2+as)(s+{\omega }_c){\theta }_f={\omega }_c(b{i}_q+s{\theta }_0+{\dot{\theta }}_0+a{\theta }_0+A_0/s)$$

(35)

Multiplying both sides of (35) by s yields

$$s(s^2+as)(s+{\omega }_c){\theta }_f={\omega }_c(bs{i}_q+s^2{\theta }_0+s{\dot{\theta }}_0+as{\theta }_0+A_0)$$

(36)

Deriving both sides three times with respect to s in order to eliminate the unknown parameter $A_0$ and the initial conditions ${\theta }_0$ and ${\dot{\theta }}_0$:

$$\begin{array}{cc}\hfill & 24s{\theta }_f+36s^2{\displaystyle \frac{d{\theta }_f}{ds}}+12s^3{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+s^4{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}+6{\omega }_c{\theta }_f+18{\omega }_{c}s{\displaystyle \frac{d{\theta }_f}{ds}}+9{\omega }_c{s}^2{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+{\omega }_c{s}^3{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\hfill \\ \hfill & +6a{\theta }_f+18as{\displaystyle \frac{d{\theta }_f}{ds}}+9a{s}^2{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+a{s}^3{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}+6a{\omega }_c{\displaystyle \frac{d{\theta }_f}{ds}}+6a{\omega }_{c}s{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+a{\omega }_c{s}^2{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\hfill \\ \hfill & ={\omega }_c\left(3b{\displaystyle \frac{d^2{i}_q}{d{s}^2}}+bs{\displaystyle \frac{d^3{i}_q}{d{s}^3}}\right).\hfill \end{array}$$

(37)

Then multiplying both sides by $s^{-4}$ to avoid derivations with respect to time:

$$\begin{array}{cc}\hfill & a\left(6s^{-4}{\theta }_f+18s^{-3}{\displaystyle \frac{d{\theta }_f}{ds}}+9s^{-2}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+s^{-1}{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}+6{\omega }_c{s}^{-4}{\displaystyle \frac{d{\theta }_f}{ds}}+6{\omega }_c{s}^{-3}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}+{\omega }_c{s}^{-2}{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\right)\hfill \\ \hfill & +b\left(-3s^{-4}{\omega }_c{\displaystyle \frac{d^2{i}_q}{d{s}^2}}-{\omega }_c{s}^{-3}{\displaystyle \frac{d^3{i}_q}{d{s}^3}}\right)=-24s^{-3}{\theta }_f-36s^{-2}{\displaystyle \frac{d{\theta }_f}{ds}}-12s^{-1}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}-{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}\hfill \\ \hfill & -6{\omega }_c{s}^{-4}{\theta }_f-18{\omega }_c{s}^{-3}{\displaystyle \frac{d{\theta }_f}{ds}}-9{\omega }_c{s}^{-2}{\displaystyle \frac{d^2{\theta }_f}{d{s}^2}}-{\omega }_c{s}^{-1}{\displaystyle \frac{d^3{\theta }_f}{d{s}^3}}.\hfill \end{array}$$

(38)

The remaining negative powers of s correspond to iterated time integrals. The corresponding formulae in the time domain are easily deduced thanks to the correspondence between $d^v/d{s}^v,v⩾0$, and the multiplication by ${(-t)}^v$ in the time domain. Equation (38) in time domain can be obtained as

$$a{\pi }_1\left(t\right)+b{\pi }_2\left(t\right)=q\left(t\right)$$

(39)

with

$$\begin{array}{cc}\hfill {\pi }_1\left(t\right)=& -\int t^3{\theta }_{f}dt+{\int }^2\left(9t^2{\theta }_f-{\omega }_c{t}^3{\theta }_f\right)dt+{\int }^3\left(-18t{\theta }_f+6{\omega }_c{t}^2{\theta }_f\right)dt\hfill \\ \hfill & +{\int }^4\left(6{\theta }_f-6{\omega }_{c}t{\theta }_f\right)dt,\hfill \\ \hfill {\pi }_2\left(t\right)=& {\int }^3{\omega }_c{t}^3{i}_{q}dt-{\int }^{4}3{\omega }_c{t}^2{i}_{q}dt,\hfill \\ \hfill q\left(t\right)=& \int \left(-12t^2{\theta }_f+{\omega }_c{t}^3{\theta }_f\right)dt+{\int }^2\left(36t{\theta }_f-9{\omega }_c{t}^2{\theta }_f\right)dt\hfill \\ \hfill & +{\int }^3\left(-24{\theta }_f+18{\omega }_{c}t{\theta }_f\right)dt-{\int }^{4}6{\omega }_c{\theta }_{f}dt+t^3{\theta }_f.\hfill \end{array}$$

(40)

We have denoted by ${\int }^{\left(n\right)}\varphi \left(t\right)$ the quantity ${\int }_0^t{\int }_0^{{\beta }_1}\cdots {\int }_0^{{\beta }_{n-1}}\varphi \left({\beta }_n\right)d{\beta }_n\cdots d{\beta }_{2}d{\beta }_1$. Moreover, $\int \varphi \left(t\right)={\int }_0^t\varphi \left({\beta }_1\right)d{\beta }_1$.

Integrating the expression (40) one time leads to the following system of linear equations for the estimates $a_e$ and $b_e$ of unknown parameters:

$$\left[\begin{array}{cc}{P}_{11}\left(t\right)& P_{12}\left(t\right)\\ P_{21}\left(t\right)& P_{22}\left(t\right)\end{array}\right]\left[\begin{array}{c}a\hfill \\ b\hfill \end{array}\right]=\left[\begin{array}{c}{Q}_1\left(t\right)\hfill \\ Q_2\left(t\right)\hfill \end{array}\right],$$

(41)

with

$$P_{11}={\pi }_1\left(t\right),P_{12}={\pi }_2\left(t\right),Q_1\left(t\right)=q\left(t\right),P_{21}=\int {\pi }_1\left(t\right),P_{22}=\int {\pi }_2\left(t\right),Q_2\left(t\right)=\int q\left(t\right).$$

By applying Fubini’s theorem to reduce the multiple integral to a single integral, and subsequently employing the trapezoidal integration method to discretize (41), we obtain the following discrete equation:

$$\left[\begin{array}{c}\hfill a\\ \hfill b\end{array}\right]={\displaystyle \frac{1}{P_{11}\left(k\right)P_{22}\left(k\right)-P_{12}\left(k\right)P_{21}\left(k\right)}}\left[\begin{array}{cc}{P}_{22}\left(k\right)& -P_{12}\left(k\right)\\ -P_{21}\left(k\right)& P_{11}\left(k\right)\end{array}\right]\left[\begin{array}{c}{Q}_1\left(k\right)\hfill \\ Q_2\left(k\right)\hfill \end{array}\right],$$

(42)

with

$$\begin{array}{cc}\hfill P_{11}\left(k\right)& =k^3{T}_s^4{\chi }_0-\left(12k^2+{\omega }_c{k}^3{T}_s\right)T_s^4{\chi }_1+\left(30k+6{\omega }_c{k}^2{T}_s\right)T_s^4{\chi }_2-\left(20+10{\omega }_{c}k{T}_s\right)T_s^4{\chi }_3+5{\omega }_c{T}_s^5{\chi }_4,\hfill \\ \hfill P_{12}\left(k\right)& =-{\displaystyle \frac{1}{2}}{\omega }_c{k}^3{T}_s^6{\eta }_2+2{\omega }_c{k}^2{T}_s^6{\eta }_3-{\displaystyle \frac{5}{2}}{\omega }_{c}k{T}_s^6{\eta }_4+{\omega }_c{T}_s^6{\eta }_5,\hfill \\ \hfill P_{21}\left(k\right)& ={\displaystyle \frac{1}{4}}{k}^4{T}_s^5{\chi }_0-\left(4k^3+{\displaystyle \frac{1}{4}}{\omega }_c{k}^4{T}_s\right)T_s^5{\chi }_1+\left(15k^2+2{\omega }_c{k}^3{T}_s\right)T_s^5{\chi }_2-\left(20k+5{\omega }_c{k}^2{T}_s\right)T_s^5{\chi }_3\hfill \\ & +\left({\displaystyle \frac{35}{4}}+5{\omega }_{c}k{T}_s\right)T_s^5{\chi }_4-{\displaystyle \frac{7}{4}}{\omega }_c{T}_s^6{\chi }_5,\hfill \\ \hfill P_{22}\left(k\right)& =-{\displaystyle \frac{1}{8}}{\omega }_c{k}^4{T}_s^7{\eta }_2+{\displaystyle \frac{2}{3}}{\omega }_c{k}^3{T}_s^7{\eta }_3-{\displaystyle \frac{5}{4}}{\omega }_c{k}^2{T}_s^7{\eta }_4+{\omega }_{c}k{T}_s^7{\eta }_5-{\displaystyle \frac{7}{24}}{\omega }_c{T}_s^7{\eta }_6,\hfill \\ \hfill Q_{12}\left(k\right)& =-\left(12k^2+{\omega }_c{k}^3{T}_s\right)T_s^3{\chi }_0+\left(60k+12{\omega }_c{k}^2{T}_s\right)T_s^3{\chi }_1-\left(60+30{\omega }_{c}k{T}_s\right)T_s^3{\chi }_2+20{\omega }_c{T}_s^4{\chi }_3+k^3{T}_s^3{\theta }_f\left(k\right),\hfill \\ \hfill Q_{22}\left(k\right)& =-\left(4k^3+{\displaystyle \frac{1}{4}}{\omega }_c{k}^4{T}_s\right)T_s^4{\chi }_0+\left(30k^2+4{\omega }_c{k}^3{T}_s\right)T_s^4{\chi }_1-\left(60k+15{\omega }_c{k}^2{T}_s\right)T_s^4{\chi }_2\hfill \\ & +\left(35+20{\omega }_{c}k{T}_s\right)T_s^4{\chi }_3-{\displaystyle \frac{35}{4}}{\omega }_c{T}_s^5{\chi }_4,\hfill \\ \hfill {\chi }_0& =\sum _{i=1}^k{\displaystyle \frac{{\theta }_f\left(i\right)+{\theta }_f\left(i-1\right)}{2}},{\chi }_1=\sum _{i=1}^k{\displaystyle \frac{i·{\theta }_f\left(i\right)+\left(i-1\right)·{\theta }_f\left(i-1\right)}{2}},{\chi }_2=\sum _{i=1}^k{\displaystyle \frac{i^2·{\theta }_f\left(i\right)+{\left(i-1\right)}^2·{\theta }_f\left(i-1\right)}{2}},\hfill \\ \hfill {\chi }_3& =\sum _{i=1}^k{\displaystyle \frac{i^3·{\theta }_f\left(i\right)+{\left(i-1\right)}^3·{\theta }_f\left(i-1\right)}{2}},{\chi }_4=\sum _{i=1}^k{\displaystyle \frac{i^4·{\theta }_f\left(i\right)+{\left(i-1\right)}^4·{\theta }_f\left(i-1\right)}{2}},{\chi }_5=\sum _{i=1}^k{\displaystyle \frac{i^5·{\theta }_f\left(i\right)+{\left(i-1\right)}^5·{\theta }_f\left(i-1\right)}{2}},\hfill \\ \hfill {\eta }_2& =\sum _{i=1}^k{\displaystyle \frac{i^2·i_q\left(i\right)+{\left(i-1\right)}^2·i_q\left(i-1\right)}{2}},{\eta }_3=\sum _{i=1}^k{\displaystyle \frac{i^3·i_q\left(i\right)+{\left(i-1\right)}^3·i_q\left(i-1\right)}{2}},{\eta }_4=\sum _{i=1}^k{\displaystyle \frac{i^4·i_q\left(i\right)+{\left(i-1\right)}^4·i_q\left(i-1\right)}{2}},\hfill \\ \hfill {\eta }_5& =\sum _{i=1}^k{\displaystyle \frac{i^5·i_q\left(i\right)+{\left(i-1\right)}^5·i_q\left(i-1\right)}{2}},{\eta }_6=\sum _{i=1}^k{\displaystyle \frac{i^6·i_q\left(i\right)+{\left(i-1\right)}^6·i_q\left(i-1\right)}{2}}.\hfill \end{array}$$

After a time interval of the form $\left[0,k{T}_s\right]$, the estimates a and b can be obtained by solving the previous expression. Then the input gain ${\alpha }_0=b$ can be used in the proposed EMFSC (14) or AEMFSC (31).

4. Simulation and Experimental Results

This section conducts a rigorous comparative evaluation of the proposed EMFSC-NDOB (14) and AEMFSC-NDOB (31), comparing them with two control methods: conventional MFSC-API [28] and MFSC-NDOB (7). The assessment examines transient response, steady-state accuracy, and disturbance rejection capabilities under identical operating conditions.

Simulation and experimental studies were conducted on the SMPMSM drive system using a two-level voltage source inverter, with the SVPWM switching frequency, sampling rate, and current-loop control frequency all set to 10 kHz. The dead-time was set as 0.5 µs. The current loop employed a decoupled PI controller with the parameters set to $k_p$ = 3 and $k_i$ = 0.067. The speed loop frequency was 2 kHz.

Table 1. Specification of the SMPMSM.

Parameter Description	Symbol	Value
DC-bus voltage	$U_{dc}$	34 V
Rated voltage	$U_N$	24 V
No-load speed	N	150 rpm
Peak locked torque	$T_p$	10 N·m
Peak locked current	$I_p$	8 A
Pole pairs	$n_p$	20
Stator resistance	$R_s$	1.8 $\mathsf{\Omega }$
Stator inductance	$L_s$	6 mH
Motor inertia	$J_m$	0.00412 kg·m2
Permanent magnet flux	${\phi }_n$	0.05498 Wb

lists the specification of the SMPMSM used in the digital simulation and experimental tests.

The proposed EMFSC-NDOB and AEMFSC-NDOB frameworks exhibit inherent model-free characteristics and nonlinear dynamic coupling, making the analytical determination of optimal parameter combinations currently infeasible. This study adopted a trial-and-error approach coupled with numerical simulations for parameter tuning: Initially, $k_d$ was set to zero while $k_p$ was incrementally increased until critical system oscillations emerged. Subsequently, $k_d$ was introduced to suppress these oscillations, with the final parameter combination determined through a comprehensive evaluation of closed-loop performance metrics, including the overshoot, settling time, and steady-state error.

The proportional gain $k_p$ predominantly governs the system response speed and bandwidth; higher values improve the responsiveness at the cost of an increased overshoot and noise sensitivity. Conversely, the derivative gain kd effectively mitigates high-frequency oscillations and enhances the stability, though potentially introducing high-frequency noise components. To address steady-state noise amplification, a threshold $\delta$ was implemented, which was carefully selected to slightly exceed the observed velocity fluctuation amplitude. The adaptive gain $\mu$ requires careful balancing, as excessive values may induce $\alpha$ oscillations while insufficient values result in sluggish convergence.

Within the NDOB architecture, the observer gain L critically determines the trade-off between the disturbance estimation convergence rate and the high-frequency noise sensitivity. Elevated L values accelerate the disturbance estimation but risk sensor noise amplification and the potential excitation of unmodeled high-frequency dynamics, which manifests as control input chattering. Reduced L values improve the noise robustness and stability, yet incur delayed disturbance estimation that compromises rapid disturbance rejection capability. This fundamental compromise necessitates careful optimization between the convergence speed and noise sensitivity.

4.1. Simulation Results

Numerical simulations of the PMSM speed regulation system were conducted using MATLAB/Simulink (Version R2023b), with the control algorithm executed in the discrete-time domain at a 2 kHz sampling rate. Notably, the simulation model incorporated realistic encoder quantization effects by superimposing discrete position measurement noise.

The parameters of the MFSC-API, MFSC-NDOB, EMFSC-NDOB, and AEMFSC-NDOB controllers were chosen as follows: $k_p$ = 160 and $n_F$ = 10 for the MFSC-API controller; $k_p$ = 400 and L = 50 for the MFSC-NDOB controller; $k_p$ = 400, $k_d$ = 1, L = 50, and $\delta$ = 0.3 rad/s for the EMFSC-NDOB controller; and $k_p$ = 400, $k_d$ = 1, L = 50, $\delta$ = 0.3 rad/s, and $\mu$ = 20 for the AEMFSC-NDOB controller. The reference speed was 90 rpm, and the inertia of the load was chosen as $J_{load}$ = 0.00134 kg·m². Therefore, the theoretical value of the input gain was ${\alpha }_e=1.5n_p{\phi }_n/(J_m+J_{load})=302.07$.

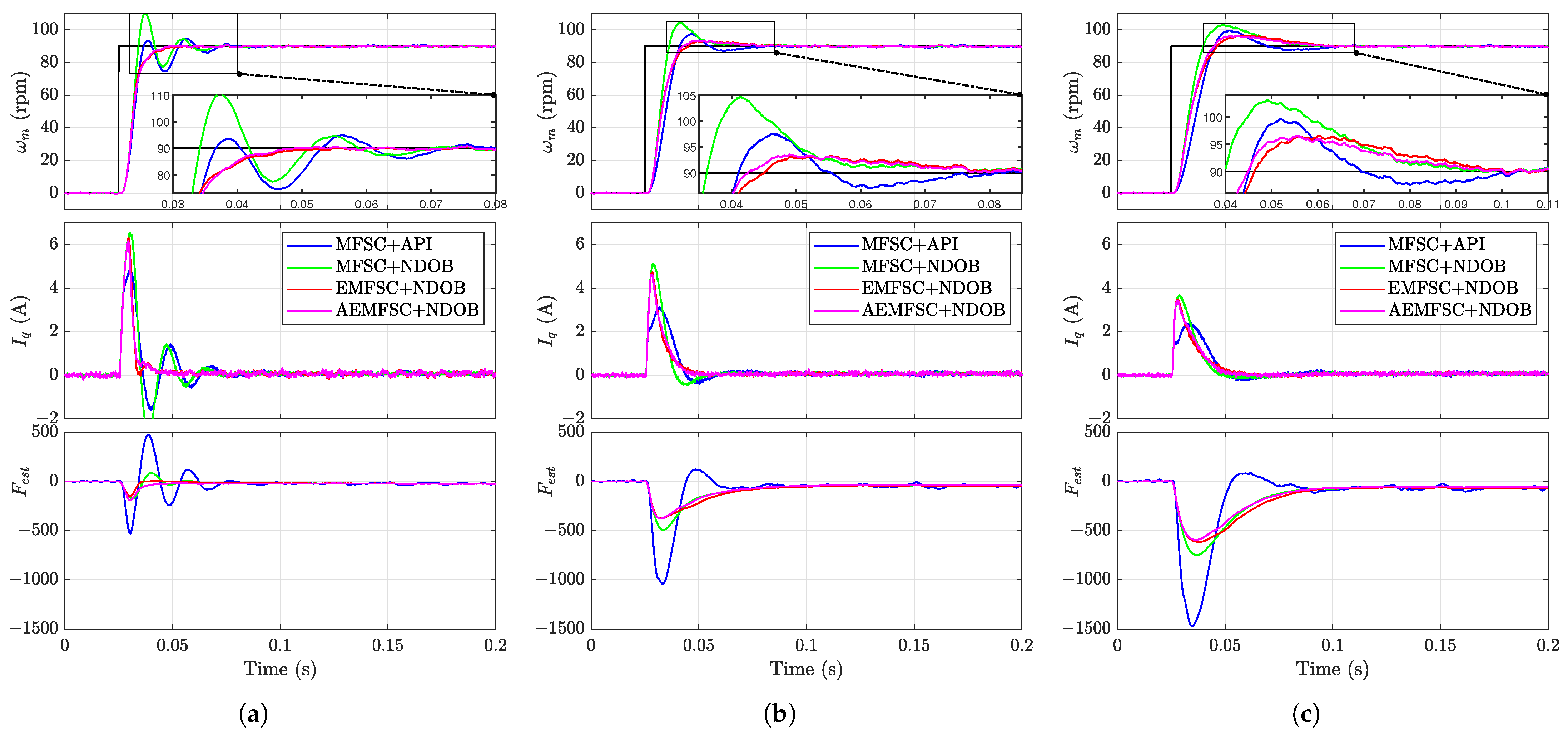
Figure 2 shows the startup responses of the MFSC-API, MFSC-NDOB, EMFSC-NDOB, and AEMFSC-NDOB controllers at the reference speed of 90 rpm. The load torque was initially set to zero, so the PMSM could be assumed to be load-free. Figure 2 clearly demonstrates that both the EMFSC-NDOB and AEMFSC-NDOB controllers exhibited superior dynamic performances, where they achieved minimal overshoots and the fastest settling times among all the compared methods. However, when the selected input gain and the theoretical true input gain was mismatched, the performance of the PMSM system deteriorated.

Figure 3 presents a comparative analysis of the disturbance rejection capabilities among the four control schemes. The results demonstrate that the proposed AEMFSC-NDOB controller exhibited superior load disturbance rejection, with a merely 18.4% speed drop during the sudden load torque application (4.0 N·m step change at t = 0.25s) compared with 25.7% for the MFSC-NDOB method. Furthermore, the parameter mismatch analysis revealed that the input gain variations could degrade the system’s disturbance rejection performance.

Figure 2 and Figure 3 demonstrate that variations in the system input gain $\alpha$ induced corresponding changes in the steady-state value of the observer-estimated lumped disturbance $\widehat{F}$. This phenomenon stems from the composite nature of F, which encompasses unmodeled dynamics, external disturbances, and nonlinearities. Crucially, the disturbance estimation $\widehat{F}$ depends on the input gain $\widehat{\alpha }$ rather than the true value ${\alpha }_{t}rue$. When the observer computes disturbances using an inaccurate $\widehat{\alpha }$, it systematically misattributes the control input effects (resulting from the $\alpha$ mismatch) as part of the disturbance. In the ULM framework, F represents a coupled quantity that combines both the $\alpha$-related terms and true disturbances. Consequently, an $\alpha$ mismatch compromises the decoupling process, causing $\widehat{F}$ to deviate from the actual disturbance characteristics.

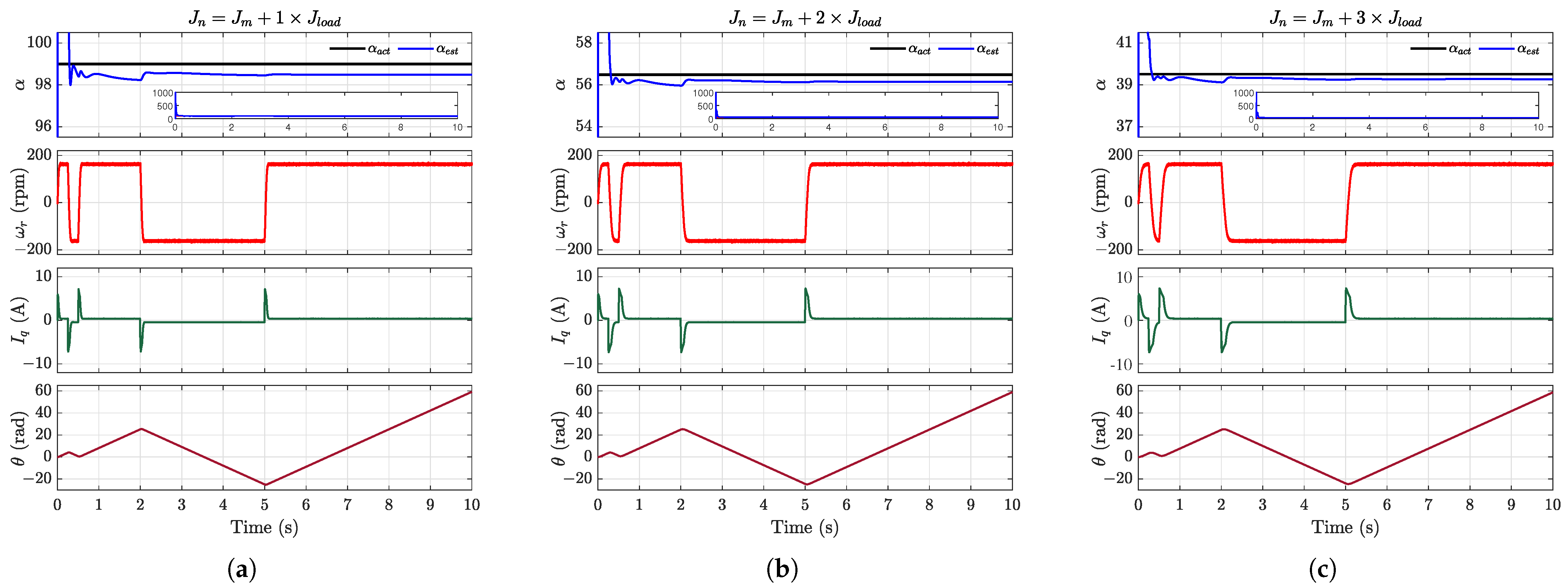
To validate the effectiveness of the $\alpha$ adaptation algorithm, three distinct initial value conditions were experimentally tested. As demonstrated in Figure 4, the results show that (i) the estimated input gain converged to its theoretical actual value within several square-wave cycles, and (ii) the automatic adjustment of the parameter $\alpha$ significantly reduced transient tracking errors.

The preceding analysis reveals that while the proposed AEMFSC-NDOB demonstrates exceptional robustness and rapid tracking performance, inappropriate initial values of $\alpha$ can adversely affect transient tracking during the startup and potentially destabilize the system. To obtain accurate $\alpha$ values, the algebraic-framework-based linear identification method was employed for precise input gain estimation. The estimation procedure, validated under three distinct load inertia conditions ($J_n=J_m+n{J}_{load},n=1,2,3,J_{load}=0.01254$), operated as follows: (a) initialize with an overestimated $\alpha$ value (e.g., $\alpha$ = 1000); (b) execute maximum-speed square-wave rotation; (c) compute $\alpha$ via (41) using the measured position and q-axis current. Figure 5 confirms the high estimation accuracy across all the test cases. Notably, this computationally intensive method may require offline implementation on resource-constrained DSPs after data acquisition.

4.2. Experimental Results

To further verify the effectiveness of the proposed control scheme, some real-time experiments were carried out. Figure 6 depicts the experimental test platform, which was governed by a TMS320F28379D digital signal processor (DSP). The control circuit was composed of a power supply (RU-36-10036), SPMSM (J155LWX001), two-level inverter, and measurement circuit.

A MOSFET module inverter was fed by a programmable DC power supply set at 34 V in the experiments. The rotor position sensor was a 19-bit electromagnetic encoder (EAB42-0M19S-8-B) and the current sensor was a CC6920B-10A current sensor. The nominal parameters of the motor, the sampling time, and all the parameters of the current controller were the same as in the simulation.

To mitigate the sensor noise amplification and prevent motor oscillations, the practical controller implementations employed smaller parameter values compared with the simulation environments. The parameters of the MFSC-API, MFSC-NDOB, EMFSC-NDOB, and AEMFSC-NDOB controllers were chosen as follows: $k_p$ = 80 and $n_F$ = 10 for the MFSC-API controller; $k_p$ = 300 and L = 50 for the MFSC-NDOB controller; $k_p$ = 300, $k_d$ = 1, L = 50, and $\delta$ = 0.3 rad/s for the EMFSC-NDOB controller; and $k_p$ = 300, $k_d$ = 1, L = 50, $\delta$ = 0.3 rad/s, and $\mu$ = 10 for the AEMFSC-NDOB controller.

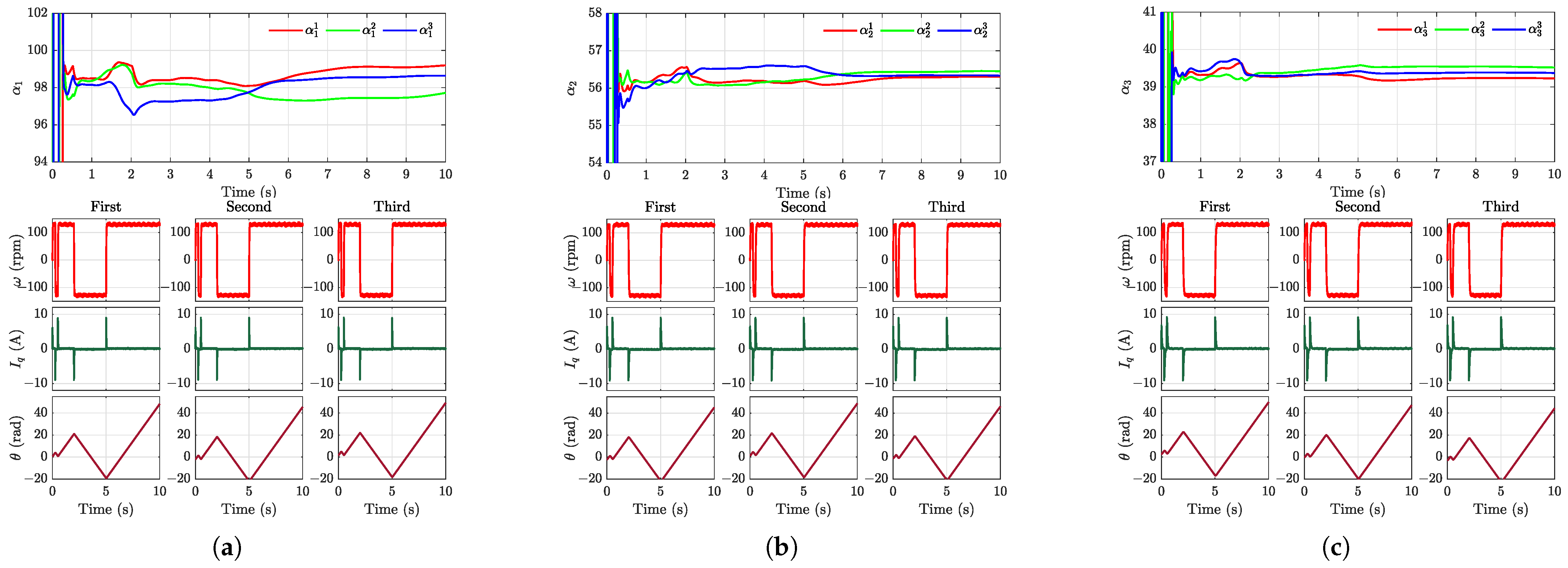
For systems with an uncertain load inertia and motor parameters, an algebraic-framework-based linear identification method can be employed to achieve precise identification of the input gain. Figure 7 displays the estimation results of the parameter $\alpha$ derived from three experimental trials under distinct load conditions. The initial angle position of the motor was different each time. The inertia of each load disk was $J_{load}=0.01254$. The estimated values exhibited remarkable consistency across all the trials, which aligned closely with the simulation outcomes. This agreement further validated the efficacy of the algebraic-framework-based linear estimation method in accurately determining the input gain parameter $\alpha$. The estimated gain value can be directly employed as the fixed parameter $\alpha$ in the EMFSC-NDOB approach or serve as the initial value for $\alpha$ in the adaptive AEMFSC-NDOB scheme.

Applying the aforementioned algebraic-framework-based linear identification method, the input gain was identified as ${\alpha }_e$ = 300 when the load was a magnetic powder brake. Figure 8 compares the startup responses of the MFSC-API, MFSC-NDOB, EMFSC-NDOB, and AEMFSC-NDOB controllers under no-load conditions at a 60 rpm reference speed. As demonstrated in Figure 8a, with accurate input gain, the proposed EMFSC-NDOB and AEMFSC-NDOB controllers exhibited superior transient performances. Although the MFSC-API controller generated lower q-axis current peaks, it had a longer settling time. These results conclusively establish the advantages of the EMFSC-NDOB and AEMFSC-NDOB controllers in PMSM speed transient regulation.

Figure 8b,c reveal significant sensitivity to the input gain variations. When $\alpha =3{\alpha }_e$, both the EMFSC-NDOB and AEMFSC-NDOB exhibited excessive speed overshoots, while the MFSC-NDOB showed a relative improvement. Notably, the elevated gain values universally prolonged the settling time across all four controllers, potentially degrading the system performance during rapid speed transitions.

Table 2. Comparison of performance indices.

Controller	Speed Overshoot (rpm)			Settling Time (s)
	${\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{2}{\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{3}{\mathit{\alpha }}_{\mathit{e}}$	${\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{2}{\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{3}{\mathit{\alpha }}_{\mathit{e}}$
MFSC-API	1.00	1.21	1.63	0.0710	0.0855	0.0895
MFSC-NDOB	18.84	9.17	8.30	0.0485	0.0430	0.0630
EMFSC-NDOB	1.43	3.64	5.72	0.0340	0.0520	0.0765
AEMFSC-NDOB	2.52	5.74	7.62	0.0405	0.0455	0.0585

quantitatively compares the key performance indicators: (i) speed overshoot and (ii) settling time, further validating the proposed controllers’ robustness against parameter mismatches.

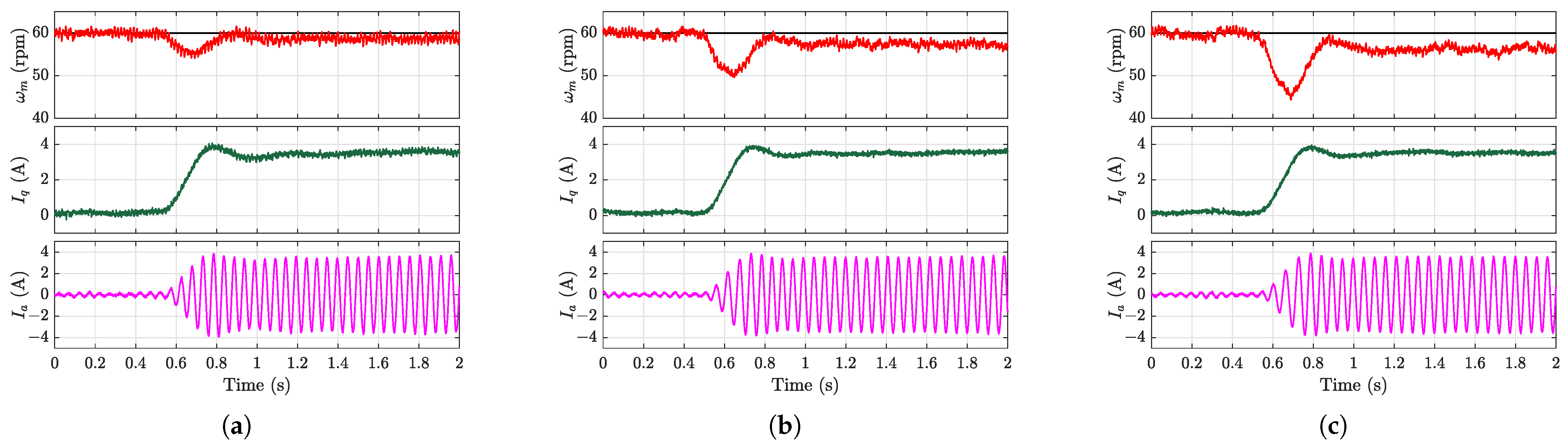
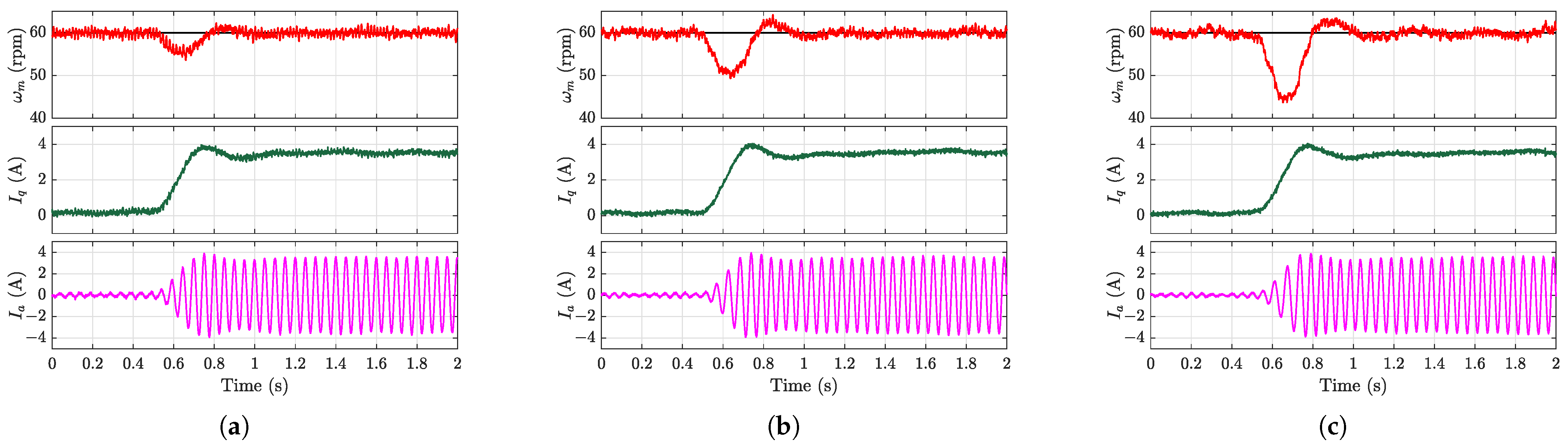
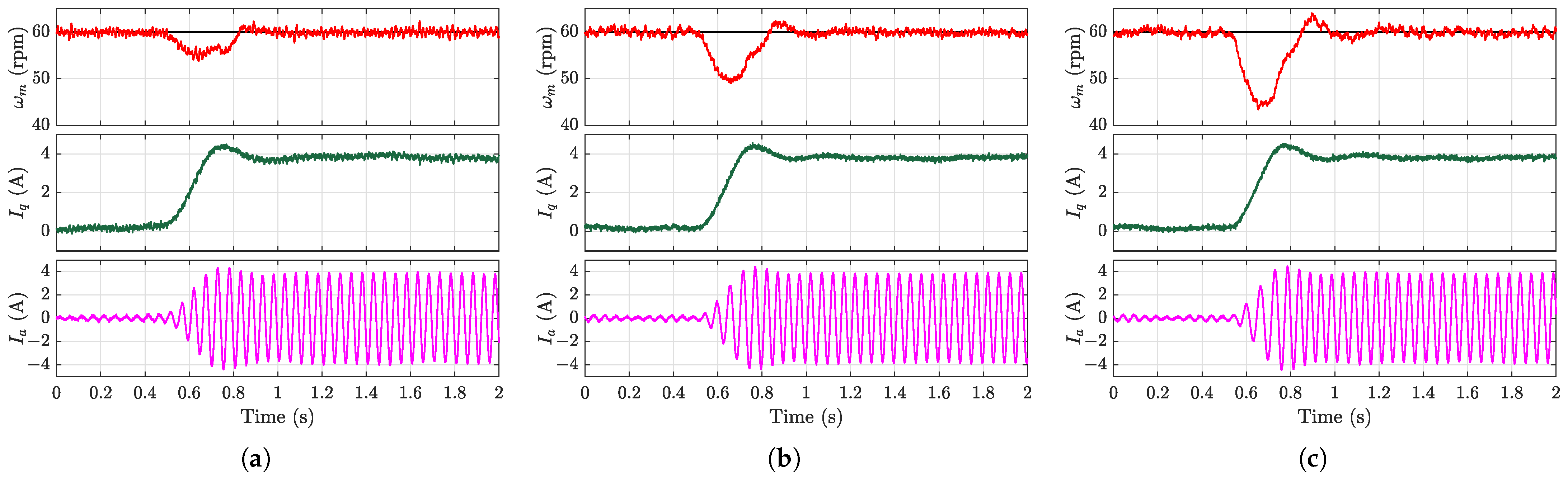
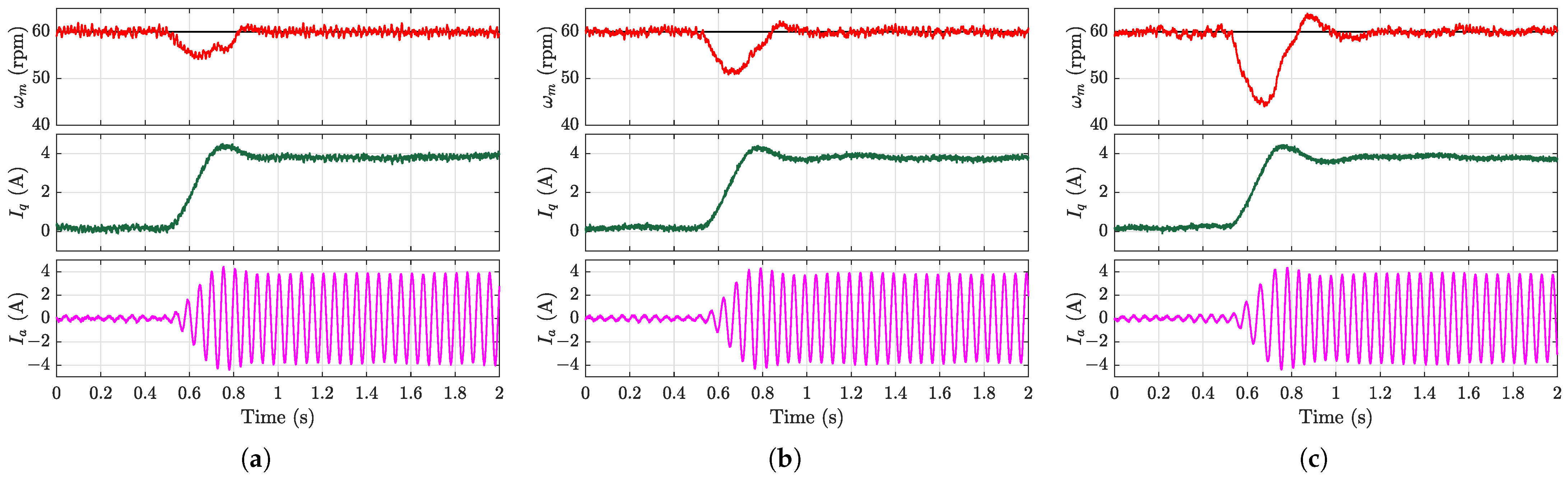
The disturbance rejection capability was evaluated during steady-state operation at 60 rpm by applying an 8 N·m load torque disturbance. Figure 9, Figure 10, Figure 11 and Figure 12 present the experimental results under this loading condition. As revealed in Figure 9a, while the MFSC-API controller exhibited smaller speed drops, it suffered from significant steady-state errors that degraded the control performance. The comparative results in Figure 10a–Figure 12a demonstrate that the proposed EMFSC-NDOB and AEMFSC-NDOB schemes achieved superior disturbance rejection compared with the MFSC-NDOB. The comparison between the MFSC-API and MFSC-NDOB further reveals inherent limitations of the algebraic parameter identification approach in estimating lumped disturbances during abrupt load changes.

The experimental results with different input gain values ($\alpha =2\alpha$ and $\alpha =3\alpha$) show substantially increased speed deviations and prolonged settling times. This confirms that the excessive input gain values severely deteriorated the system’s disturbance rejection capability. In this scenario, the proposed AEMFSC-NDOB control strategy consistently outperformed both the MFSC-NDOB and EMFSC-NDOB approaches. This superiority stemmed from its adaptive $\alpha$ adjustment capability during the load transients, which actively enhanced the disturbance rejection performance. It should be noted that when the controller input satisfied the persistent excitation condition, the AEMFSC-NDOB could recover its nominal anti-disturbance performance through $\alpha$ adaptation, even with an initial parameter mismatch. Quantitative performance metrics under load torque variations are systematically compared in

Table 3. Comparison of performance indices.

Controller	Speed Drop (rpm)			Settling Time (s)
	${\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{2}{\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{3}{\mathit{\alpha }}_{\mathit{e}}$	${\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{2}{\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{3}{\mathit{\alpha }}_{\mathit{e}}$
MFSC-API	5.89	10.41	15.66	–	–	–
MFSC-NDOB	6.42	10.69	16.31	0.372	0.397	0.453
EMFSC-NDOB	6.21	10.92	16.57	0.345	0.379	0.416
AEMFSC-NDOB	5.90	9.20	16.02	0.3355	0.3675	0.4045

.

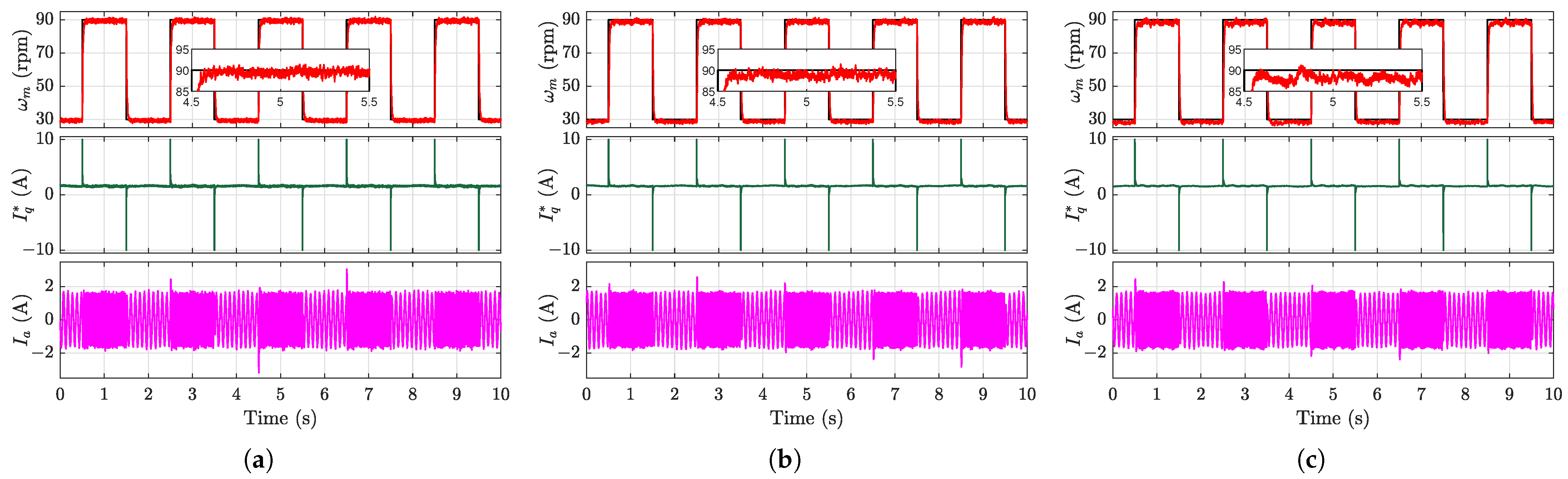
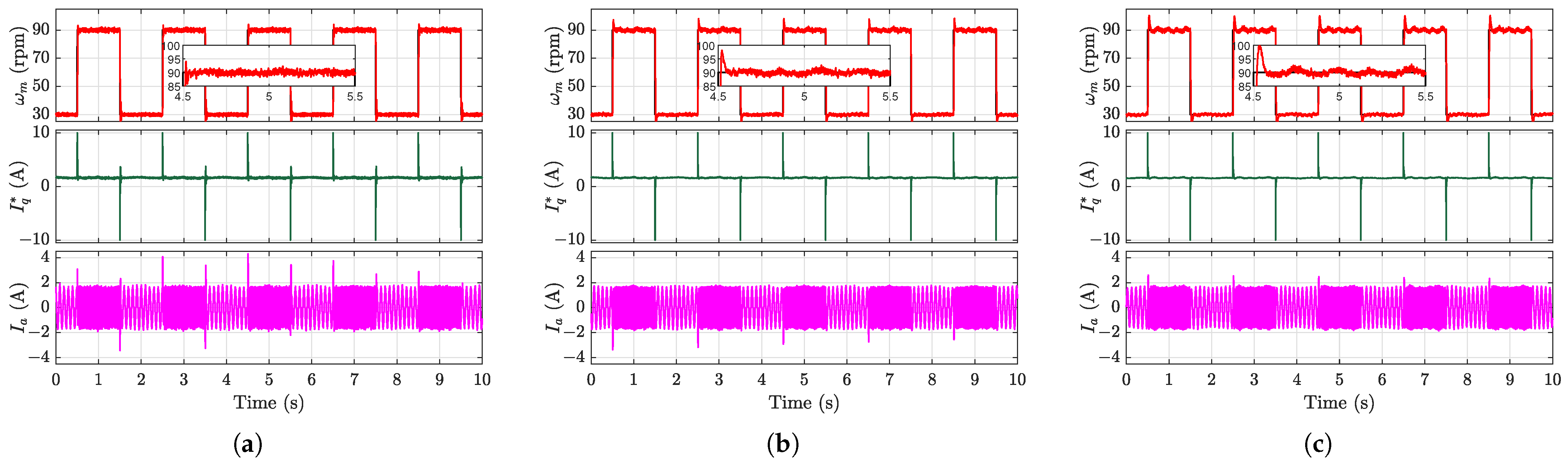
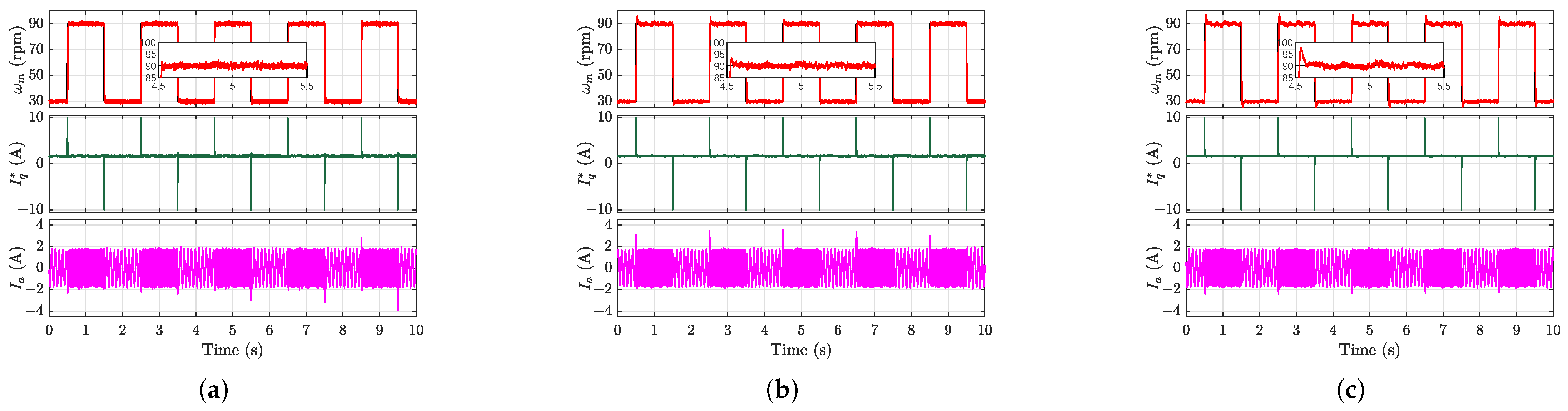
Figure 13, Figure 14, Figure 15 and Figure 16 present the square-wave speed-tracking performance under a 4 N·m load torque, with reference speeds that ranged from 30 to 90 rpm. While the conventional MFSC-API controller exhibited steady-state errors as previously analyzed, the other three controllers achieved rapid and accurate speed tracking. However, elevated input gain values were observed to degrade the tracking performance, particularly during square-wave transitions.

Quantitative evaluations using the Root Mean Square Value (RMSE, entire process) and Integral Absolute Error (IAE, steady-state phase) metrics are summarized in

Table 4. Comparison of performance indices.

Controller	Speed RMSE (rpm)			30 rpm IAE			90 rpm IAE
	${\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{2}{\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{3}{\mathit{\alpha }}_{\mathit{e}}$	${\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{2}{\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{3}{\mathit{\alpha }}_{\mathit{e}}$	${\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{2}{\mathit{\alpha }}_{\mathit{e}}$	$\mathbf{3}{\mathit{\alpha }}_{\mathit{e}}$
MFSC-API	5.773	6.390	6.939	2.640	4.760	6.581	2.962	4.607	6.936
MFSC-NDOB	4.784	5.185	5.548	1.629	1.700	1.795	2.215	2.341	2.881
EMFSC-NDOB	4.772	5.018	5.525	1.608	1.645	1.669	2.203	2.345	2.516
AEMFSC-NDOB	4.786	4.991	5.518	1.679	1.694	1.724	2.224	2.304	2.380

. With matched $\alpha$ values, the EMFSC-NDOB strategy demonstrated a superior tracking accuracy and steady-state performance. Under parameter mismatch conditions, the AEMFSC-NDOB’s adaptive mechanism effectively suppressed the speed overshoot and maintained a better high-speed tracking performance owing to its self-tuning capability.

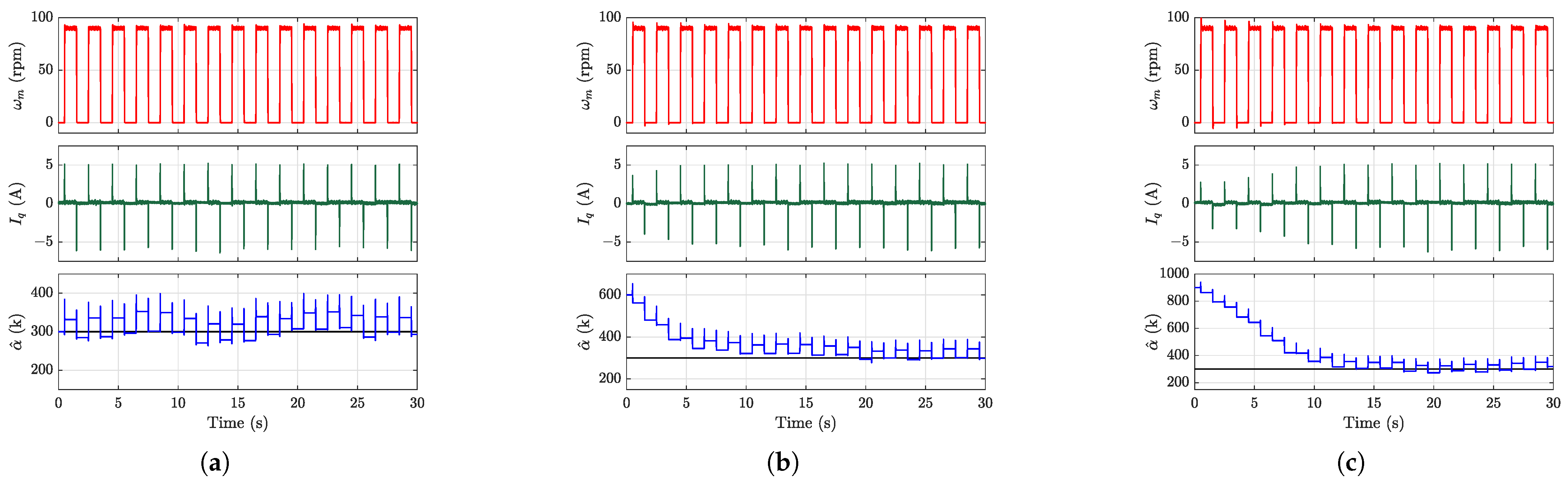
The effectiveness of the proposed $\alpha$-adaptation algorithm was validated through three distinct initial conditions, with the experimental results presented in Figure 17. The data demonstrate that the estimated $\alpha$ converged to the vicinity of its true value within several square-wave cycles. It should be noted that choosing a smaller value of $\mu$ will reduce the oscillation amplitude of the input gain, but this comes at the cost of a longer convergence time.

5. Conclusions

This study developed an NDOB-based EMFSC control algorithm for PMSM systems to achieve a high tracking performance under external disturbances and an unknown load torque. Compared with conventional MFSC-API and MFSC-NDOB methods, the proposed EMFSC-NDOB eliminated steady-state errors, reduced the speed overshoot, and demonstrated a faster settling time with enhanced disturbance rejection capability. Furthermore, two parameter identification methods were designed to estimate the true input gain values online, effectively addressing input gain mismatch issues. The effectiveness and superiority of the proposed approach were thoroughly validated through both simulation and experimental results. Future work will focus on improving the convergence speed and estimation accuracy of the NDOB for lumped disturbances, as well as developing more advanced input gain identification techniques.