Transient High-Frequency Electromagnetic Force Calculation for Linear Induction Motors Under Pulse Width Modulation Current Excitation
Abstract
1. Introduction
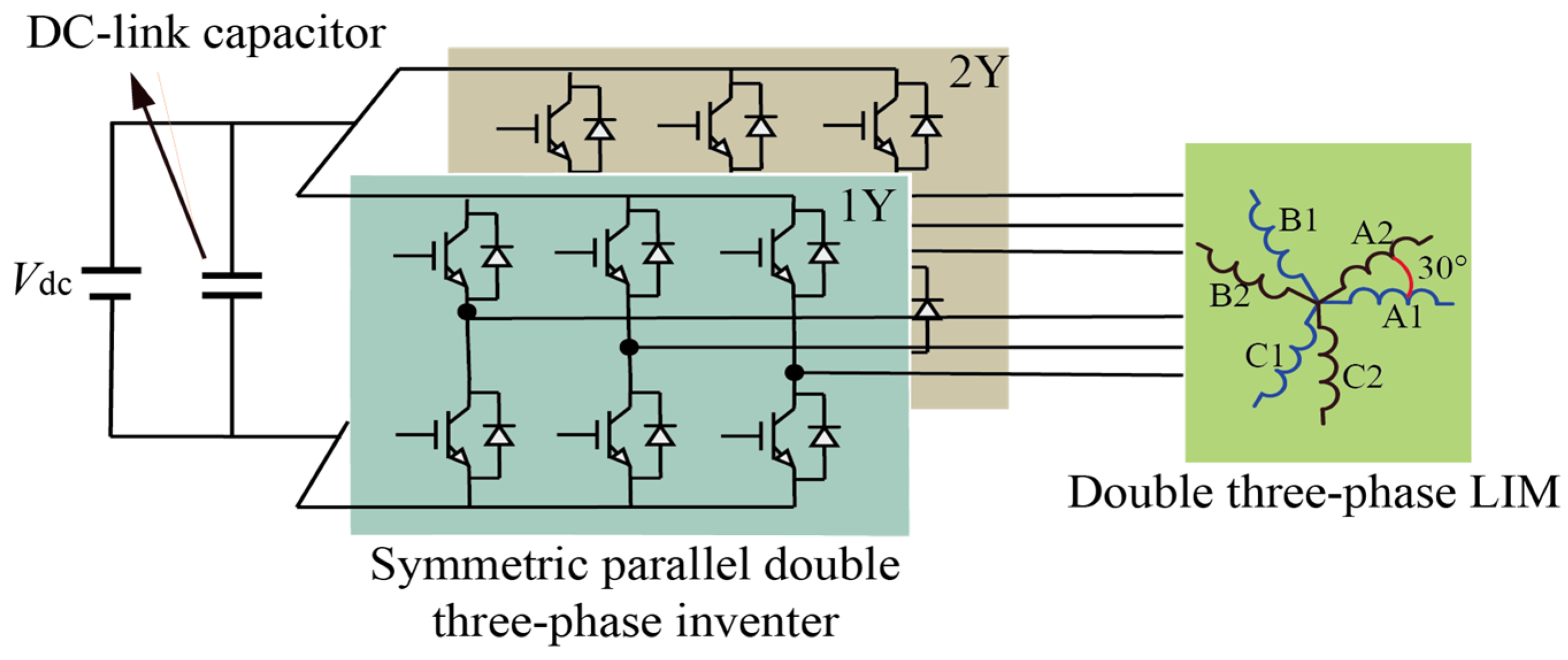
2. System of Double Three-Phase LIM
3. Characteristics of LIM Under High-Frequency Current Excitation
3.1. Characteristics of End Effect Under High-Frequency Current Excitation
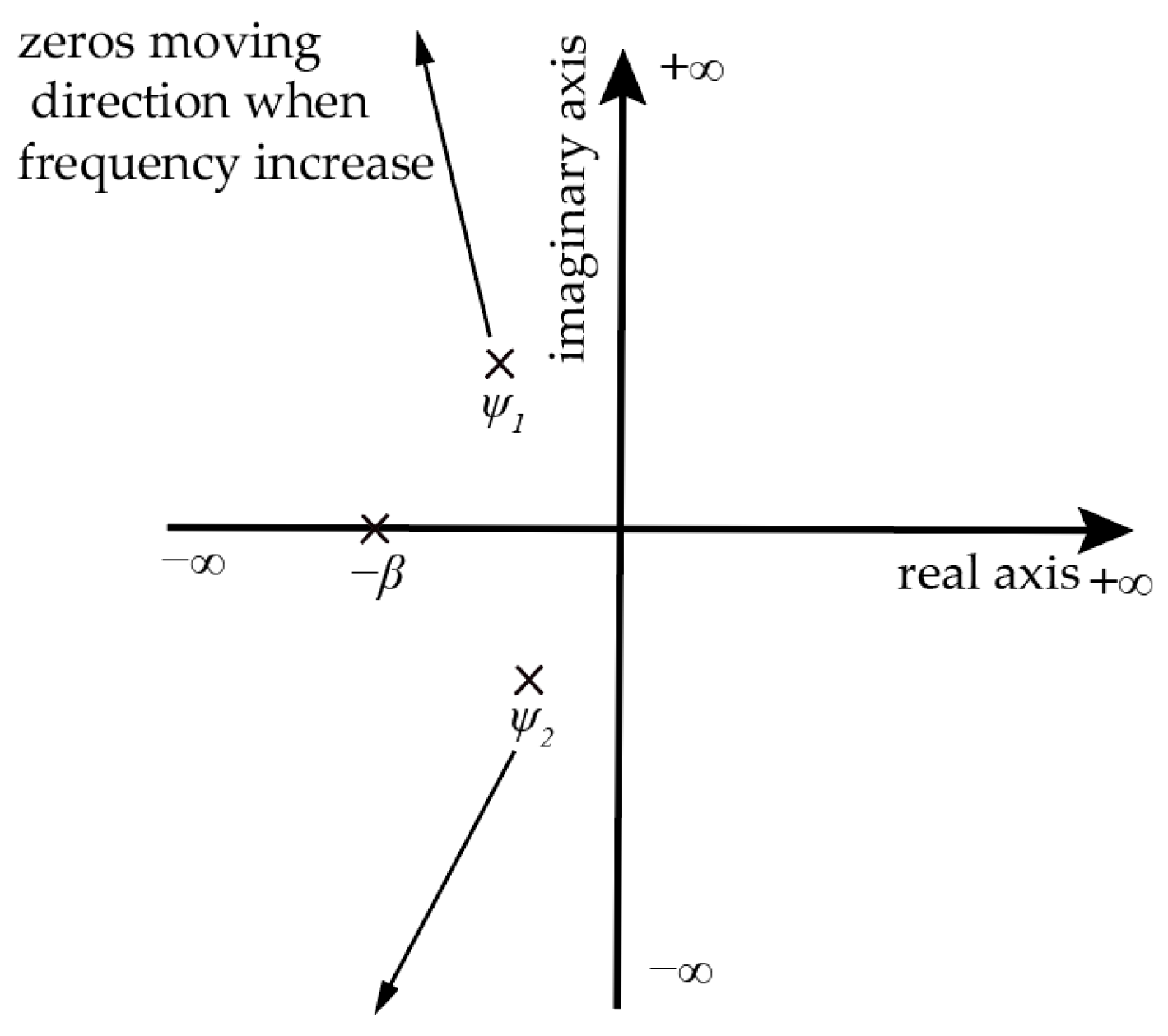
3.1.1. Theoretical Analysis
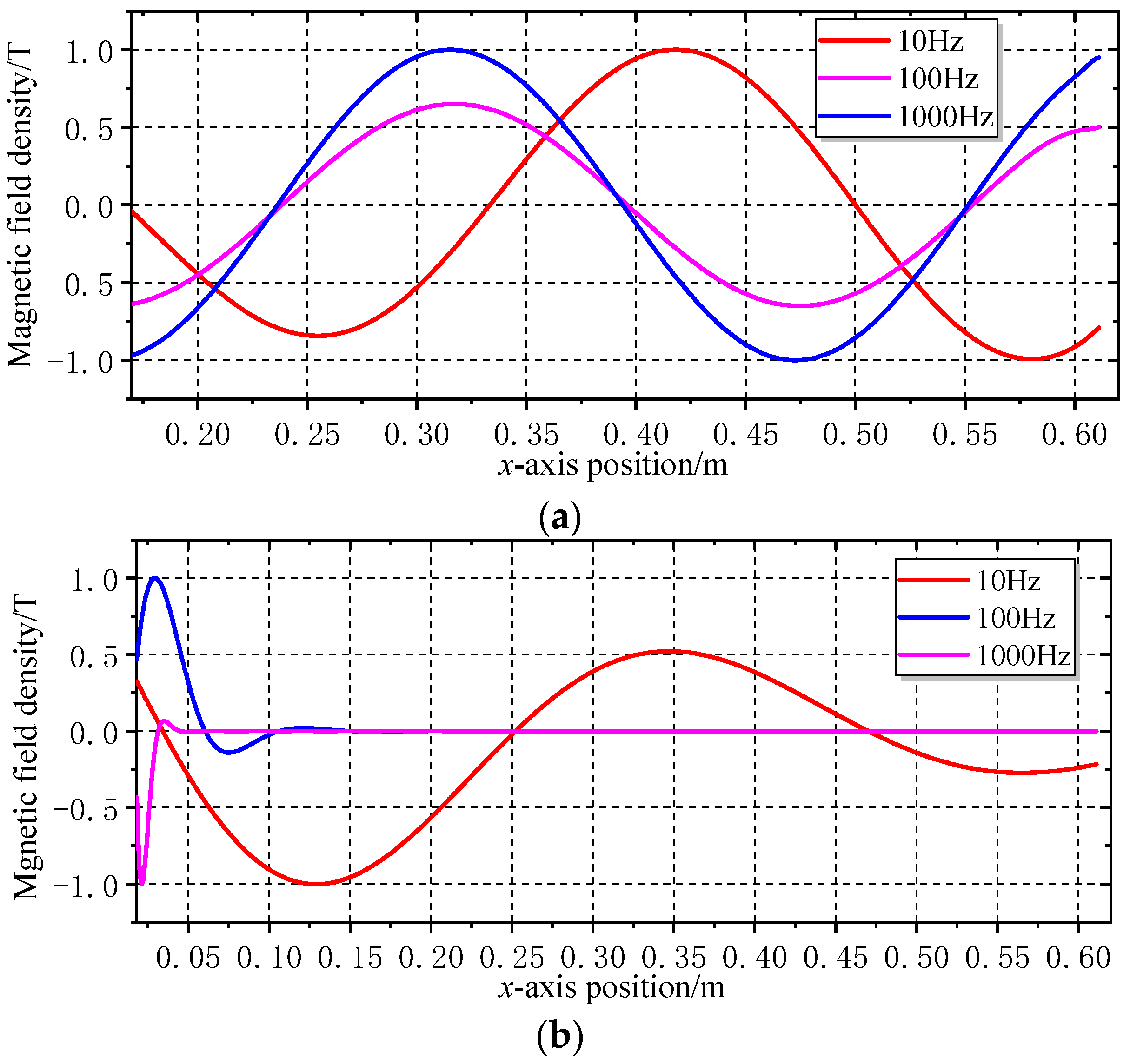
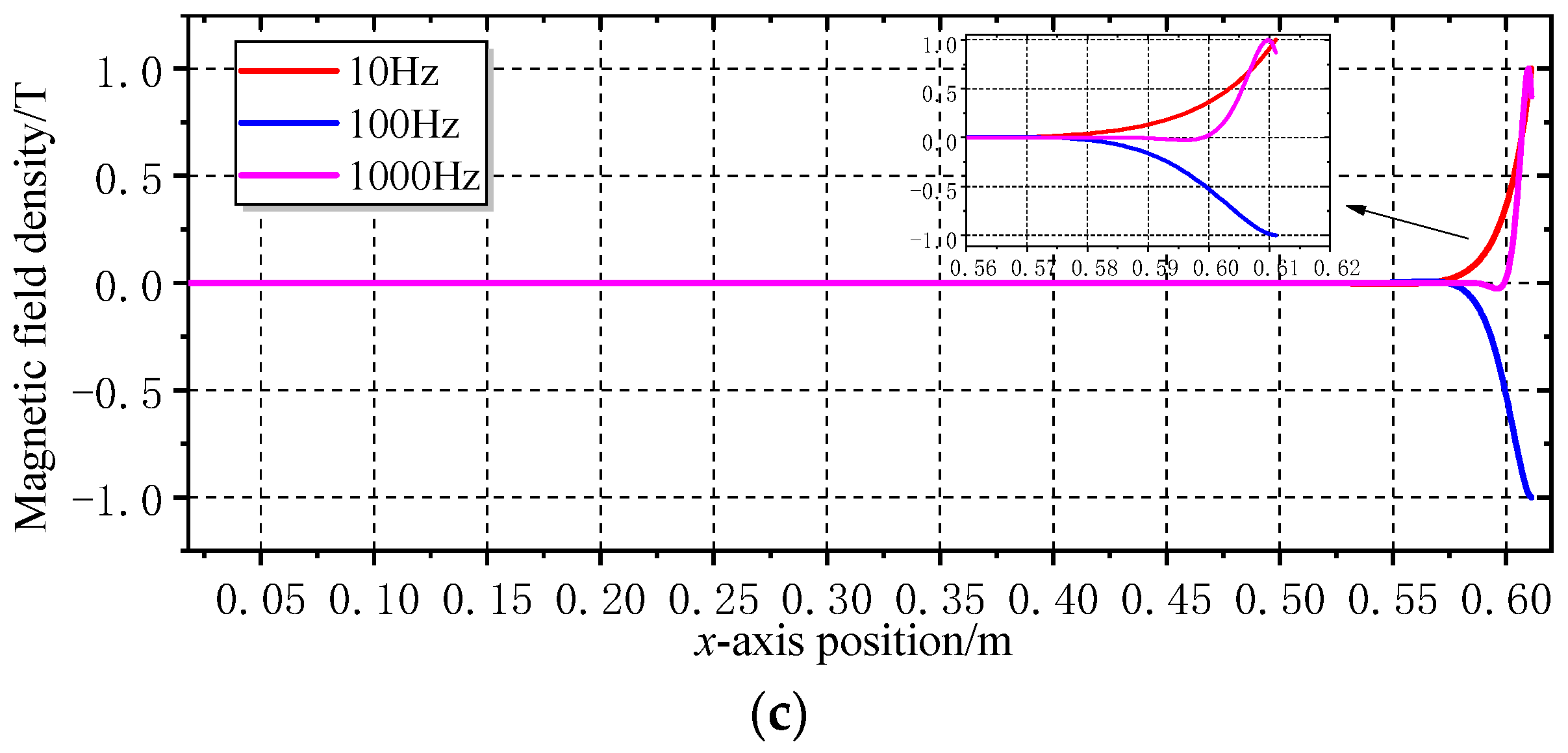
3.1.2. Verification of Analysis Results Based on FEA
3.2. Transient Electromagnetic Characteristic Under High-Frequency Current Excitation
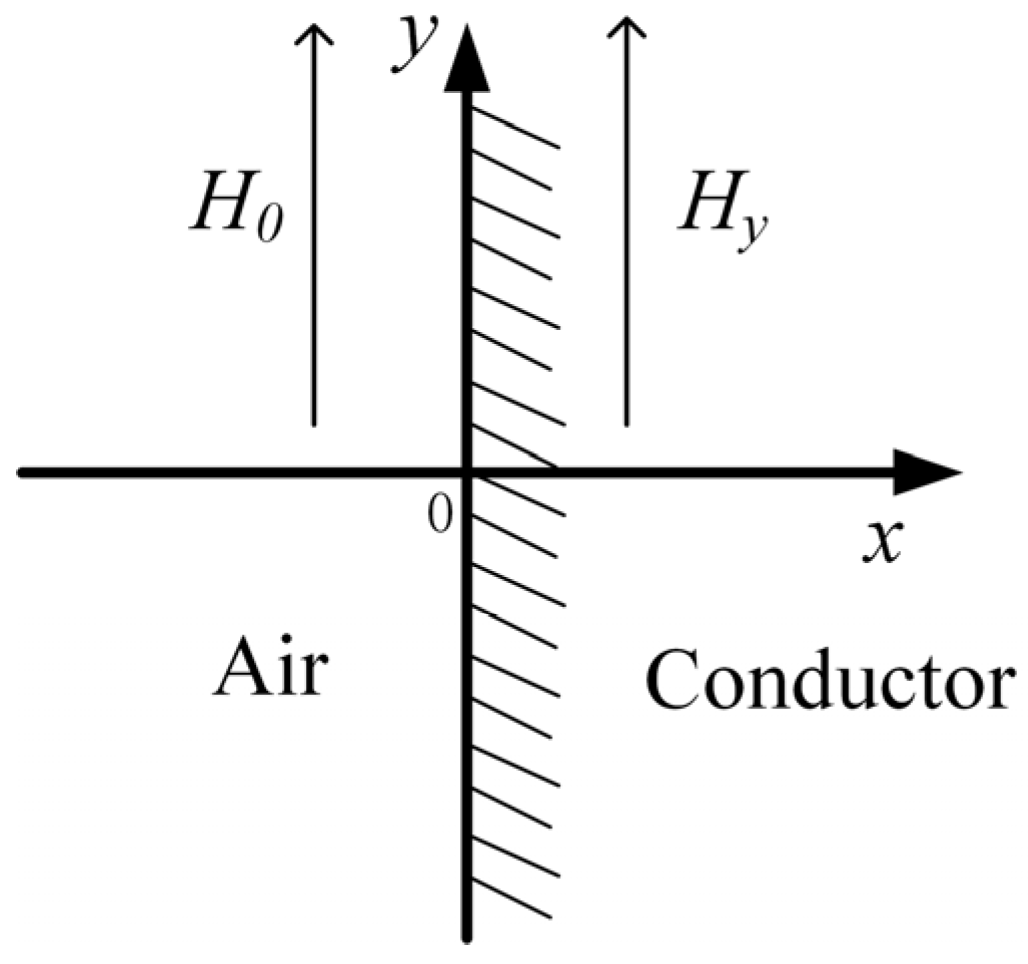
3.2.1. Theoretical Analysis
- When t = 0, Hy(x,0) = 0 (except for x = 0).
- When x = 0, Hy(0,t) = H0.
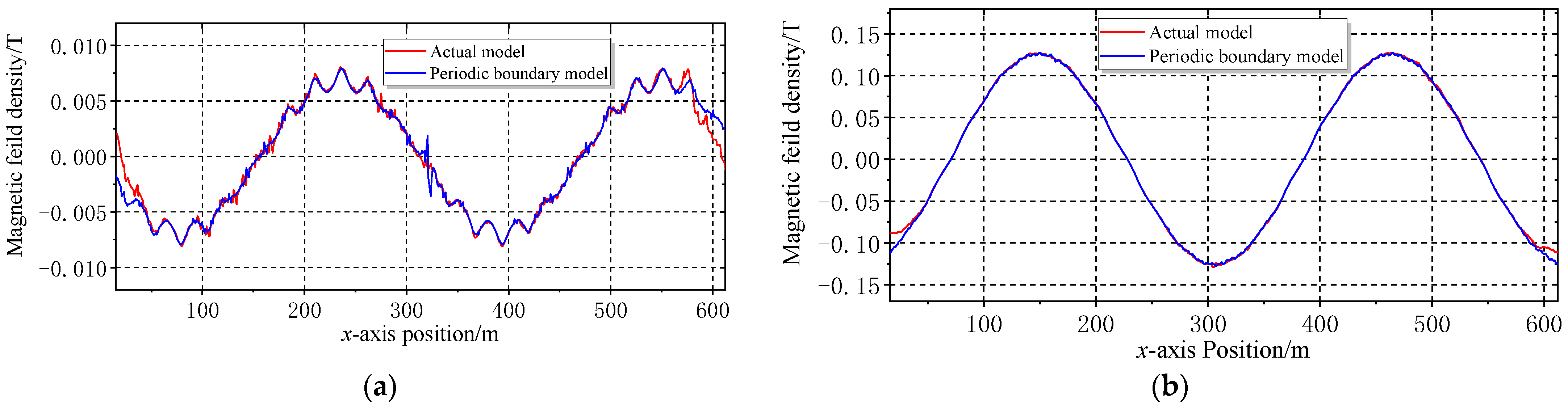
3.2.2. Verification of Analysis Results Based on FEA
4. Novel Simplified Modeling of High-Frequency Electromagnetic Forces in LIMs
4.1. Establishment of High-Frequency MF Analytical Model for LIM
4.1.1. Derivation of Theoretical Formulas
- The currents on the primary current layer and secondary conductive layer have only the z-axis component;
- The primary moves in the positive x-axis direction;
- All field quantities vary sinusoidally with time;
- The magnetic permeability of the primary and secondary cores is infinite.
- When y = 0, Bx1 = 0;
- When y = hco, Bx1 = Bx2, By1 = By2;
- When y = hco + ge, Bx2 = Bx3, By2 = By3;
- When y = hco + ge + hcl, Bx3 = 0.
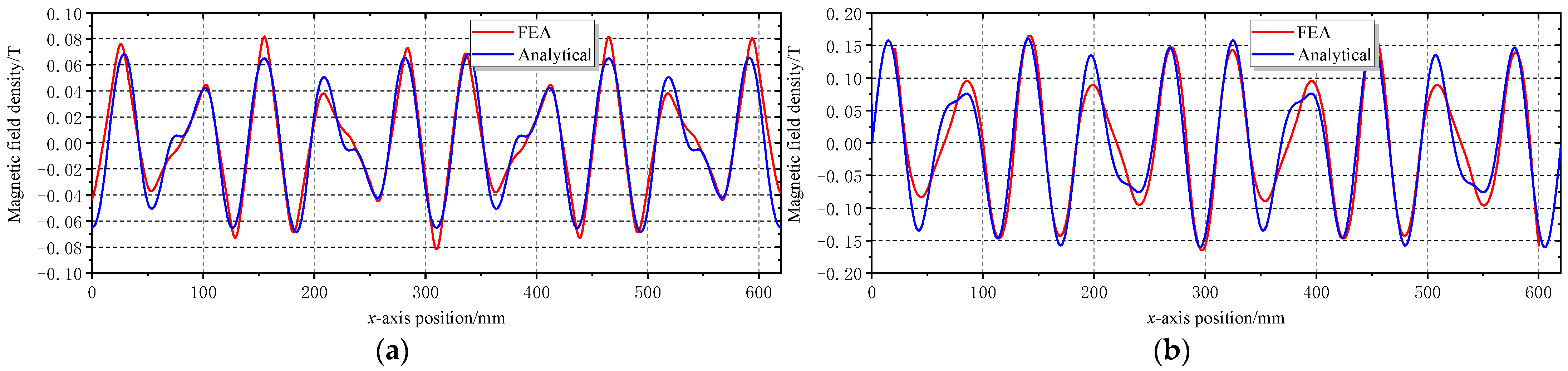
4.1.2. Validated by FEA
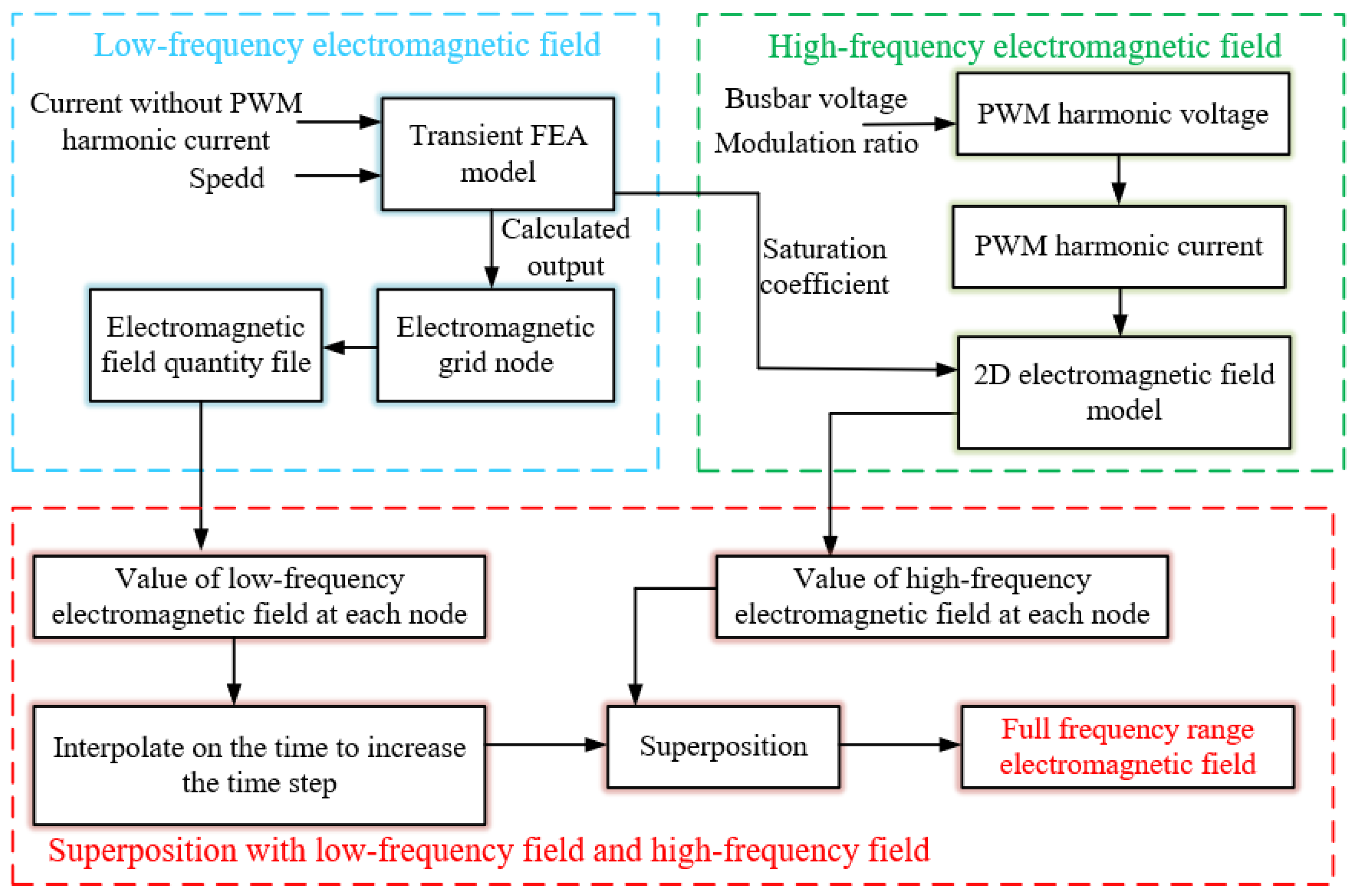
4.2. Calculation Flow of MF Model
4.3. EF Calculation Formula
5. Experimental Validation
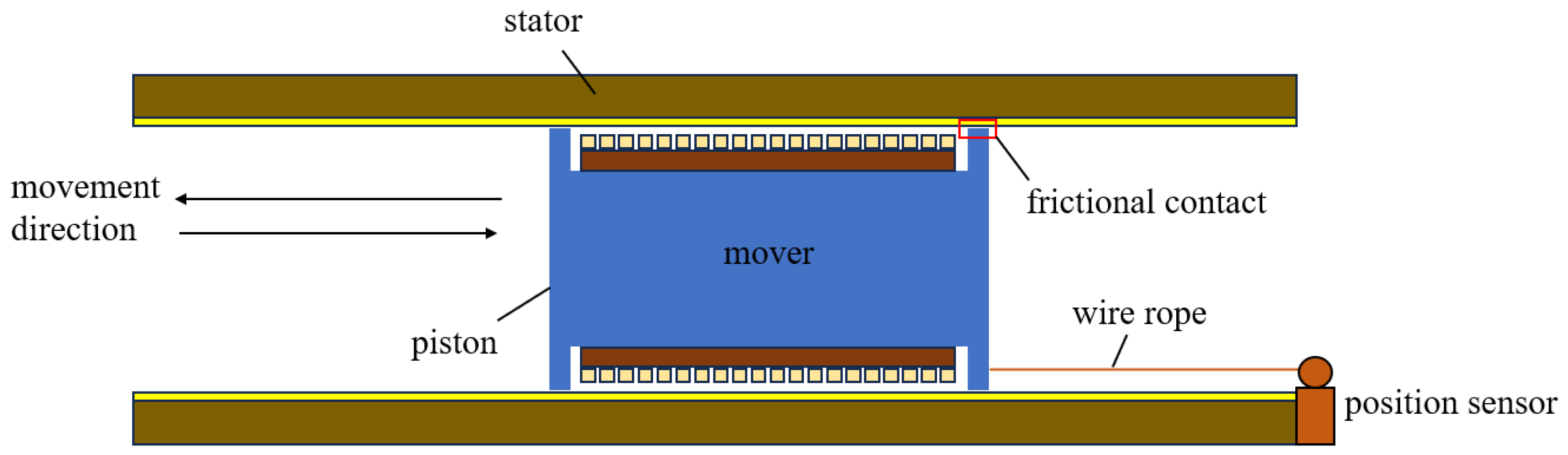
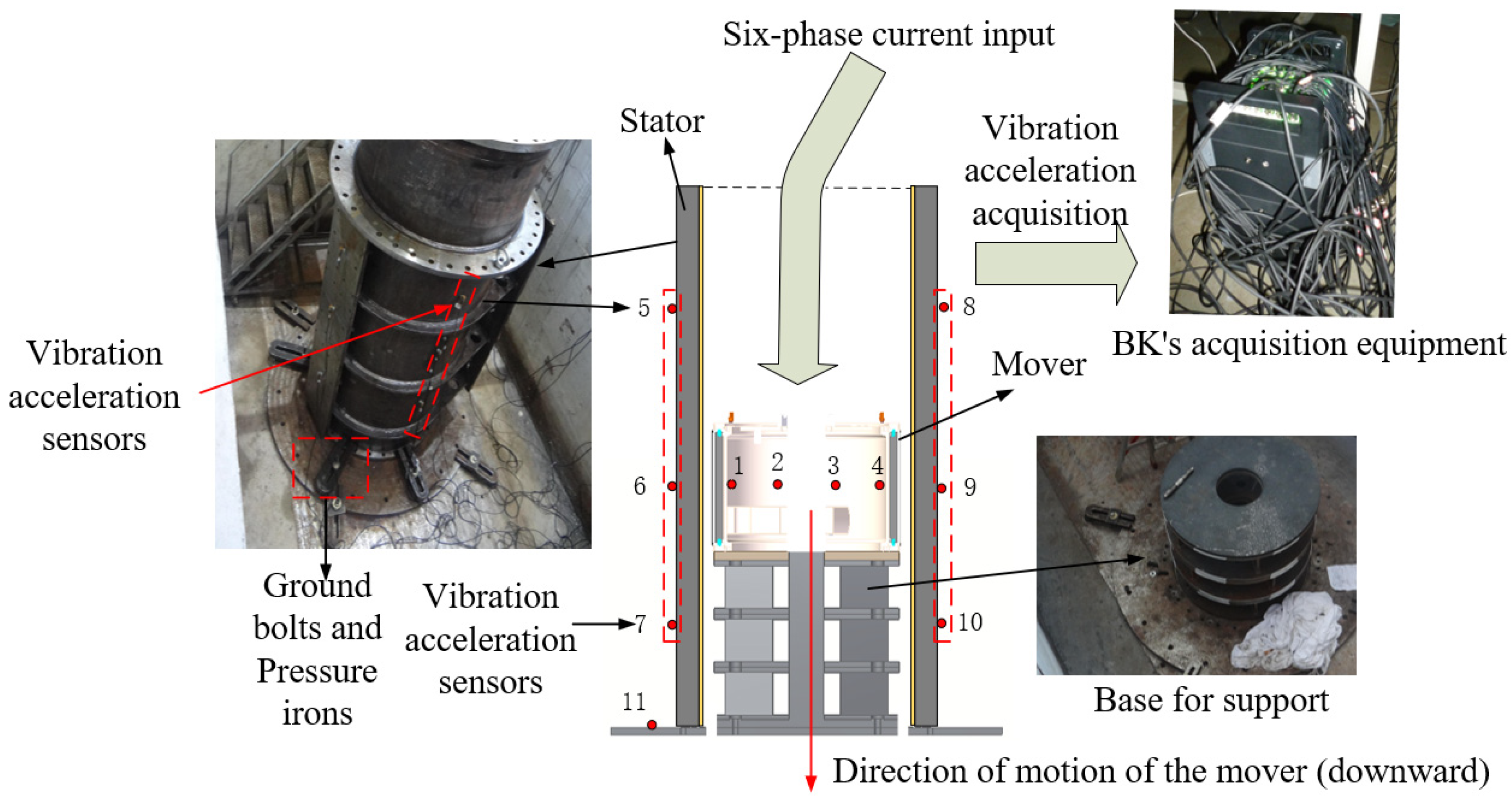
5.1. Experimental Platform
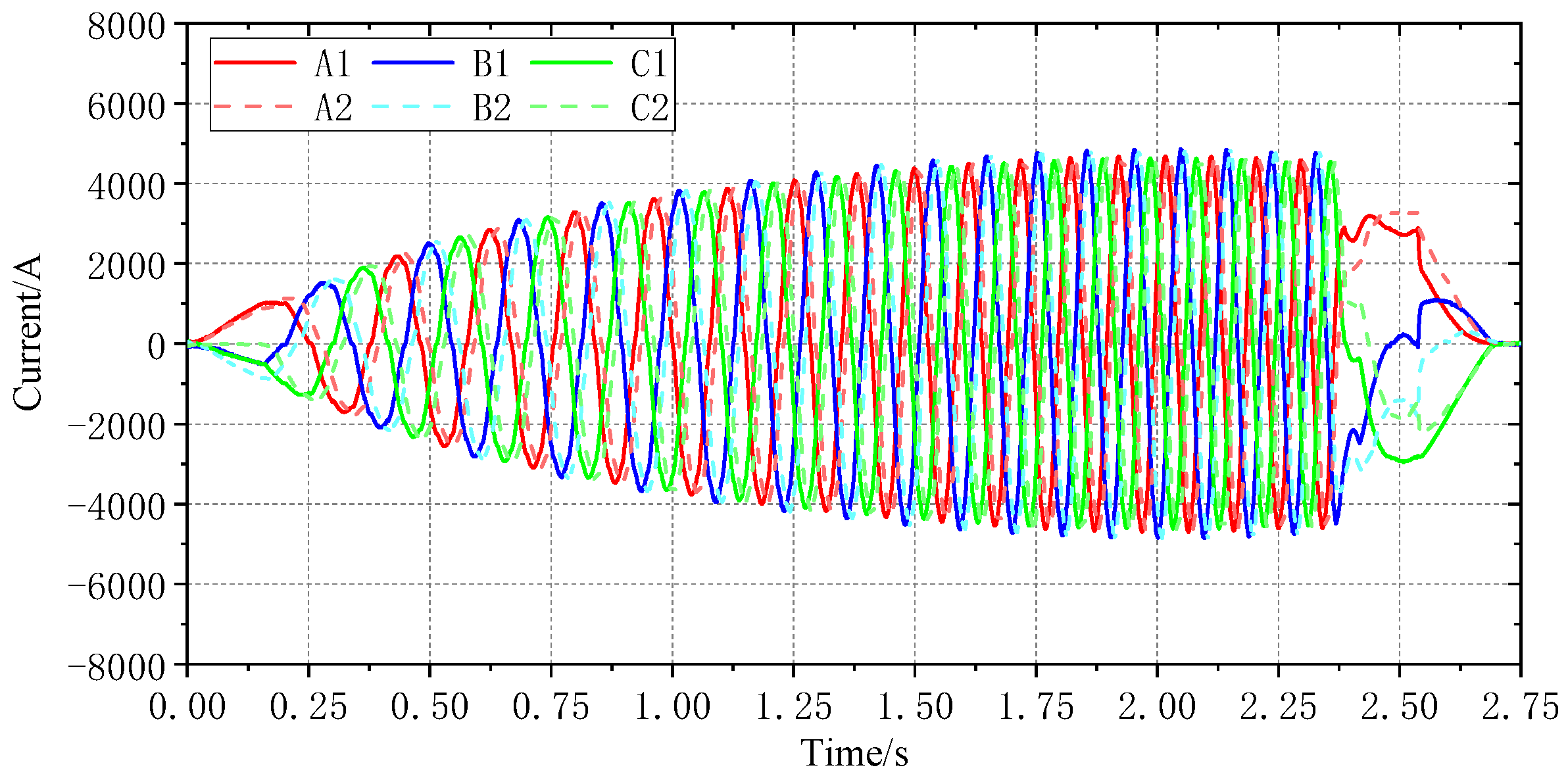
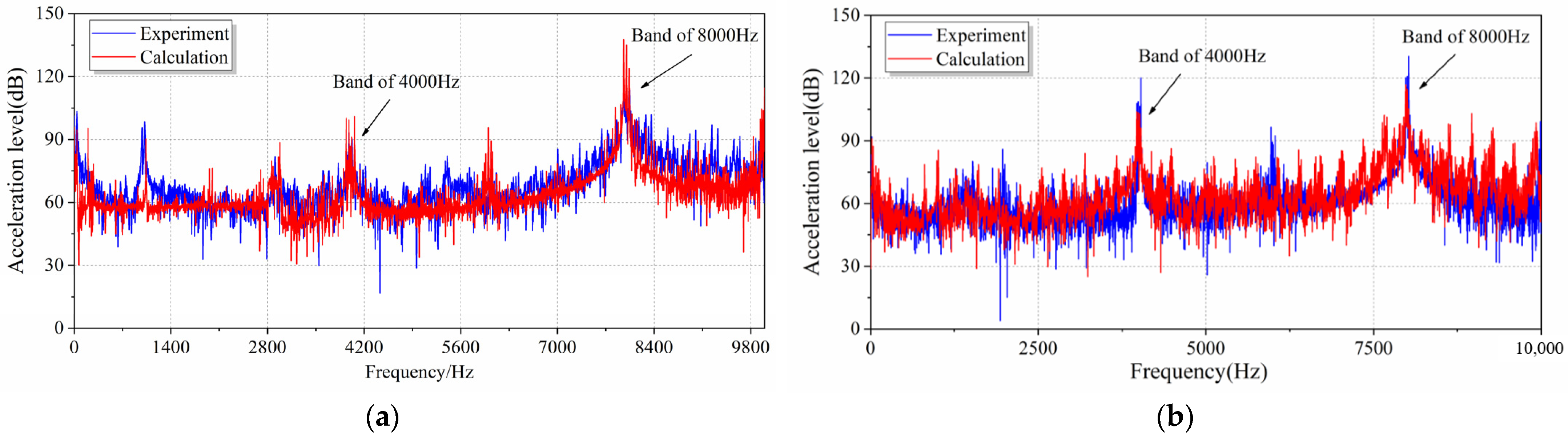
5.2. Experimental Validation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LIM | Linear induction motor |
| PWM | Pulse Width Modulation |
| FEA | Finite element analysis |
| EF | Electromagnetic force |
| MF | Magnetic field |
References
- Zhang, Q.; Zhang, Y. Scheme design of high performance converting control of linear induction motor used for electromagnetic launch. In Proceedings of the 16th International Symposium on Electromagnetic Launch Technology (EML), Beijing, China, 15–19 May 2012. [Google Scholar]
- Zhang, Y.; Zhang, M.; Ma, W.; Xu, J.; Lu, J.; Sun, S. Modeling of a double-stator linear induction motor. IEEE Trans. Energy Convers. 2012, 27, 572–579. [Google Scholar] [CrossRef]
- Schnegas, M.; Jouaneh, M.K. Trajectory Planning for Reciprocating Motion in Integrated Servo Motor Linear Stages. Machnies 2024, 12, 934. [Google Scholar] [CrossRef]
- Yoon, D.S.; Choi, S.B. Adaptive Control for Suspension System of In-Wheel Motor Vehicle with Magnetorheological Damper. Machnies 2024, 17, 433. [Google Scholar] [CrossRef]
- Hoshina, T.; Yamada, T.; Deng, M. Perfect Tracking Control of Linear Sliders Using Sliding Mode Control with Uncertainty Estimation Mechanism. Machnies 2024, 12, 212. [Google Scholar] [CrossRef]
- Ding, A.; Huang, C.; Sun, Z.; Zeng, R.; Mao, Y.; Jia, G. Six-phase cylindrical linear induction motor with high-frequency vibration suppression and experimental study. In Proceedings of the IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022. [Google Scholar]
- Ji, Z.; Cheng, S.; Li, X.; Lv, Y.; Wang, D. An Optimal Periodic Carrier Frequency PWM Scheme for Suppressing High-Frequency Vibrations of Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2023, 38, 13008–13018. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, S.; Fang, H.; Jiang, D.; Qu, R.; Wang, Q. Research on High Frequency Vibration Reduction Using Carrier Phase Shifted PWM for 4-Module 3-Phase Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2022, 58, 7192–7200. [Google Scholar] [CrossRef]
- Han, Z.; Xu, J.; Rui, W.; Zhang, Y.; Li, M. Research on Thrust Ripple of Aperiodic Transient Linear Induction Motors. In Proceedings of the 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021. [Google Scholar]
- Han, Z.; Xu, J.; Rui, W.; Wang, L.; Li, G. Analysis of Electromagnetic Force of Linear Induction Motor with Segmented Power Supply for Electromagnetic Emission. In Proceedings of the 2020 Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 29–31 May 2020. [Google Scholar]
- Chen, M.; Deng, J.; Yang, Y.; Zhou, H.; Tao, T.; Liu, S.; Hua, L. Performance analysis of a floating wind–wave power generation platform based on the frequency domain model. J. Mar. Sci. Eng. 2024, 12, 206. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Z.; Zhang, F. A review of the optimization design and control for ocean wave power generation systems. Energies 2021, 15, 102. [Google Scholar] [CrossRef]
- Ahamed, R.; McKee, K.; Howard, I. A review of the linear generator type of wave energy converters’ power take-off systems. Sustainability 2022, 14, 9936. [Google Scholar] [CrossRef]
- Curto, D.; Franzitta, V.; Guercio, A.; Miceli, R.; Nevoloso, C.; Raimondi, F.M.; Trapanese, M. An experimental comparison between an ironless and a traditional permanent magnet linear generator for wave energy conversion. Energies 2022, 15, 2387. [Google Scholar] [CrossRef]
- Epifanov, A.P.; Kril, D.B. Linear asynchronous electric drive of the monorail transport system for feeding in livestock farms. Izv. St.-Petersburg State Agrar. Univ. 2022, 66, 113–124. [Google Scholar]
- Palka, R.; Woronowicz, K. Linear induction motors in transportation systems. Energies 2021, 14, 2549. [Google Scholar] [CrossRef]
- Prasad, N.; Jain, S. Linear Motor-Based High-Speed Rail Transit System: A Sustainable Approach. Transportation Energy and Dynamics; Singapore: Springer Nature Singapore, 2023; pp. 87–127. [Google Scholar]
- Fironov, A.N.; Kostenko, A.S. Dynamic model of the Moscow monorail transport system using magnetolevitation technology. Mod. Transp. Syst. Technol. 2022, 8, 67–85. [Google Scholar] [CrossRef]
- Abdo, M.M.M.; El-Hussieny, H.; Miyashita, T.; Ahmed, S.M. Design of a new electromagnetic launcher based on the magnetic reluctance control for the propulsion of aircraft-mounted microsatellites. Appl. Syst. Innov. 2023, 6, 81. [Google Scholar] [CrossRef]
- Chi, S.; Yan, J.; Guo, J.; Zhang, Y. Analysis of mechanical stress and vibration reduction of high-speed linear motors for electromagnetic launch system. IEEE Trans. Ind. Appl. 2022, 58, 7226–7240. [Google Scholar] [CrossRef]
- Ji, Z.; Cheng, S.; Ren, Q.; Li, X.; Lv, Y.; Wang, D. The Effects and Mechanisms of Periodic-Carrier-Frequency PWM on Vibrations of Multiphase Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2023, 38, 8696–8706. [Google Scholar] [CrossRef]
- Li, J.; Tong, W.; Wu, S. Analytical Model for No-Load Rotor Bracket Loss of Axial flux Hybrid Excitation Motor based on Subdomain Method. In Proceedings of the 2023 IEEE 6th Student Conference on Electric Machines and Systems (SCEMS), Huzhou, China, 7–9 December 2023. [Google Scholar]
- Tiang, T.L.; Ishak, D.; Lim, C.P.; Jamil, M.K.M. A Comprehensive Analytical Subdomain Model and Its Field Solutions for Surface-Mounted Permanent Magnet Machines. IEEE Trans. Magn. 2015, 51, 8104314. [Google Scholar] [CrossRef]
- Golovanov, D.; Galassini, A.; Transi, T.; Gerada, C. Analytical Methodology for Eddy Current Loss Simulation in Armature Windings of Synchronous Electrical Machines with Permanent Magnets. IEEE Trans. Ind. Electron. 2022, 69, 9761–9770. [Google Scholar] [CrossRef]
- Gu, L.; Bostanci, E.; Moallem, M.; Wang, S.; Devendra, P. Analytical calculation of the electromagnetic field in SRM using conformal mapping method. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016. [Google Scholar]
- Dong, K.; Yu, H.; Hu, M.; Liu, J.; Huang, L.; Zhou, J. Study of Axial-Flux-Type Superconducting Eddy-Current Couplings. IEEE TAS 2017, 27, 0600905. [Google Scholar] [CrossRef]
- Yamazaki, K.; Kuramochi, S.; Fukushima, N.; Yamada, S.; Tada, S. Characteristics Analysis of Large High Speed Induction Motors Using 3-D Finite Element Method. IEEE Trans. Magn. 2012, 48, 995–998. [Google Scholar] [CrossRef]
- Liang, Y.; Bian, X.; Yu, H.; Li, C. Finite-Element Evaluation and Eddy-Current Loss Decrease in Stator End Metallic Parts of a Large Double-Canned Induction Motor. IEEE Trans. Ind. Electron. 2015, 62, 6779–6785. [Google Scholar] [CrossRef]
- Seno, R.; Manabe, T.; Matsutomo, S.; Hidaka, Y. Interactive Motor Design System Using 2-D Finite Element Analysis With Fast Mesh Modification Method. IEEE Trans. Magn. 2022, 58, 7401004. [Google Scholar] [CrossRef]
- Nasar, S.A.; Del Cid, L. Certain approaches to the analysis of single-sided linear induction motors. IEE Proc. 1973, 120, 477–483. [Google Scholar] [CrossRef]
- Li, M.; Xu, J.; Zhang, Y.Z.P.; Han, Z. Calculation and Analysis of PWM Harmonic Current of Multiphase Linear Induction Motor. J. Nav. Univ. Eng. 2024, 36, 105–112. [Google Scholar]
- Ma, C.; Wang, Y.; Chen, H.; Hong, J.; Wang, Y. Analysis of Electromagnetic Vibration in Permanent Magnet Motors Based on Random PWM Technology. Machines 2025, 13, 259. [Google Scholar] [CrossRef]
- Casisa, A.; Lafarge, B.; Lanfranchi, V. Investigations of Vibratory Lines from PWM in Order to Recover Vibratory Energy on an Electric Machine. In Proceedings of the 2024 IEEE International Conference on Industrial Technology (ICIT), Bristol, UK, 25–27 March 2024. [Google Scholar]
- Fan, L.; Liu, Z.; Jiang, D.; Qu, R. Research on High-Frequency Vibration Reduction for Active Magnetic Bearings with Carrier Phase Shifting PWM. IEEE Trans. Ind. Electron. 2025, 72, 5527–5537. [Google Scholar] [CrossRef]
- Lv, Y.; Cheng, S.; Ji, Z.; Li, X.; Wang, D.; Wei, Y. Spatial-Harmonic Modeling and Analysis of High-Frequency Electromagnetic Vibrations of Multiphase Surface Permanent-Magnet Motors. IEEE Trans. Ind. Electron. 2023, 70, 11865–11875. [Google Scholar] [CrossRef]
- Yan, R.; Wang, D.; Wang, C.; Miao, W.; Wang, X. Analytical Approach and Experimental Validation of Sideband Electromagnetic Vibration and Noise in PMSM Drive with Voltage-Source Inverter by SVPWM Technique. IEEE Trans. Magn. 2025, 61, 8200206. [Google Scholar] [CrossRef]
- Kim, J.H.; Won, Y.J.; Lim, M.S. Analysis and Reduction of Radial Vibration of FSCW PMSM Considering the Phase of Radial, Tangential Forces, and Tooth Modulation Effect. IEEE Trans. Transp. Electrif. 2025, 11, 2976–2987. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, J.; Li, M.; Yu, A.; Wu, D. Modelling and analysis of electromagnetic vibration in long sheet secondary tubular linear induction motors. IET Electr. Power Appl. 2023, 17, 1237–1366. [Google Scholar] [CrossRef]
- Guo, G.; Zhao, Y.; Yu, A. Analysis of electromagnetic vibration of submerged tubular linear motors based on wave propagation approach. Wave Motion 2024, 127, 103287. [Google Scholar] [CrossRef]








| Parameter | Symbols | Value | Unit |
|---|---|---|---|
| Primary core thickness | hpc | 40 | mm |
| Primary length | lp | 660 | mm |
| Winding thickness | hco | 15 | mm |
| Air gap | ge | 3 | mm |
| Conductive layer thickness | hcl | 10 | mm |
| Back iron thickness | hbi | 30 | mm |
| Pole pitch | τ | 155 | mm |
| Conductive layer conductivity | σcu | 6.6 × 106 | S/m |
| Pole pair number | P | 2 | -- |
| Reference | Suitable for Linear Motors? | Suitable for Transient Conditions? | Suitable for High-Frequency EF Calculation? | Ability to Calculate All Components | Calculation Speed |
|---|---|---|---|---|---|
| [7] | √ | × | √ | × | fast |
| [32] | √ | × | √ | × | fast |
| [33] | √ | × | √ | × | fast |
| [34] | × | √ | √ | × | fast |
| [35] | √ | × | √ | × | fast |
| [36] | √ | √ | √ | √ | slow |
| [37] | √ | √ | √ | √ | slow |
| This paper | √ | √ | √ | √ | fast |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Xu, J.; Zhu, J.; Wang, Y.; Chen, T. Transient High-Frequency Electromagnetic Force Calculation for Linear Induction Motors Under Pulse Width Modulation Current Excitation. Machines 2025, 13, 409. https://doi.org/10.3390/machines13050409
Li M, Xu J, Zhu J, Wang Y, Chen T. Transient High-Frequency Electromagnetic Force Calculation for Linear Induction Motors Under Pulse Width Modulation Current Excitation. Machines. 2025; 13(5):409. https://doi.org/10.3390/machines13050409
Chicago/Turabian StyleLi, Mingke, Jin Xu, Junjie Zhu, Yuhu Wang, and Tairan Chen. 2025. "Transient High-Frequency Electromagnetic Force Calculation for Linear Induction Motors Under Pulse Width Modulation Current Excitation" Machines 13, no. 5: 409. https://doi.org/10.3390/machines13050409
APA StyleLi, M., Xu, J., Zhu, J., Wang, Y., & Chen, T. (2025). Transient High-Frequency Electromagnetic Force Calculation for Linear Induction Motors Under Pulse Width Modulation Current Excitation. Machines, 13(5), 409. https://doi.org/10.3390/machines13050409






