A Bearing Fault Diagnosis Method Combining Multi-Source Information and Multi-Domain Information Fusion
Abstract
1. Introduction
- A fault diagnosis framework has been developed for variable operating conditions, integrating information from diverse sensor sources and different transformation domains. By effectively integrating features from various signal sources and analysis domains, the framework demonstrates efficient identification of bearing faults under complex operating conditions;
- A novel time–frequency domain conversion method is introduced. The Bessel transform (BT), a novel time–frequency domain conversion method, is employed to facilitate the conversion of time–frequency domain signals, making it suitable for processing non-smooth and complex signals;
- An innovative multi-source feature fusion network is designed. This network leverages a multi-scale CNN, attention mechanism, and residual connections to extract fault features that are insensitive to changes in operating conditions. This approach enhances the model’s adaptability and facilitates the adaptive weighted fusion of information features, further improving fault-sensitive characteristics.
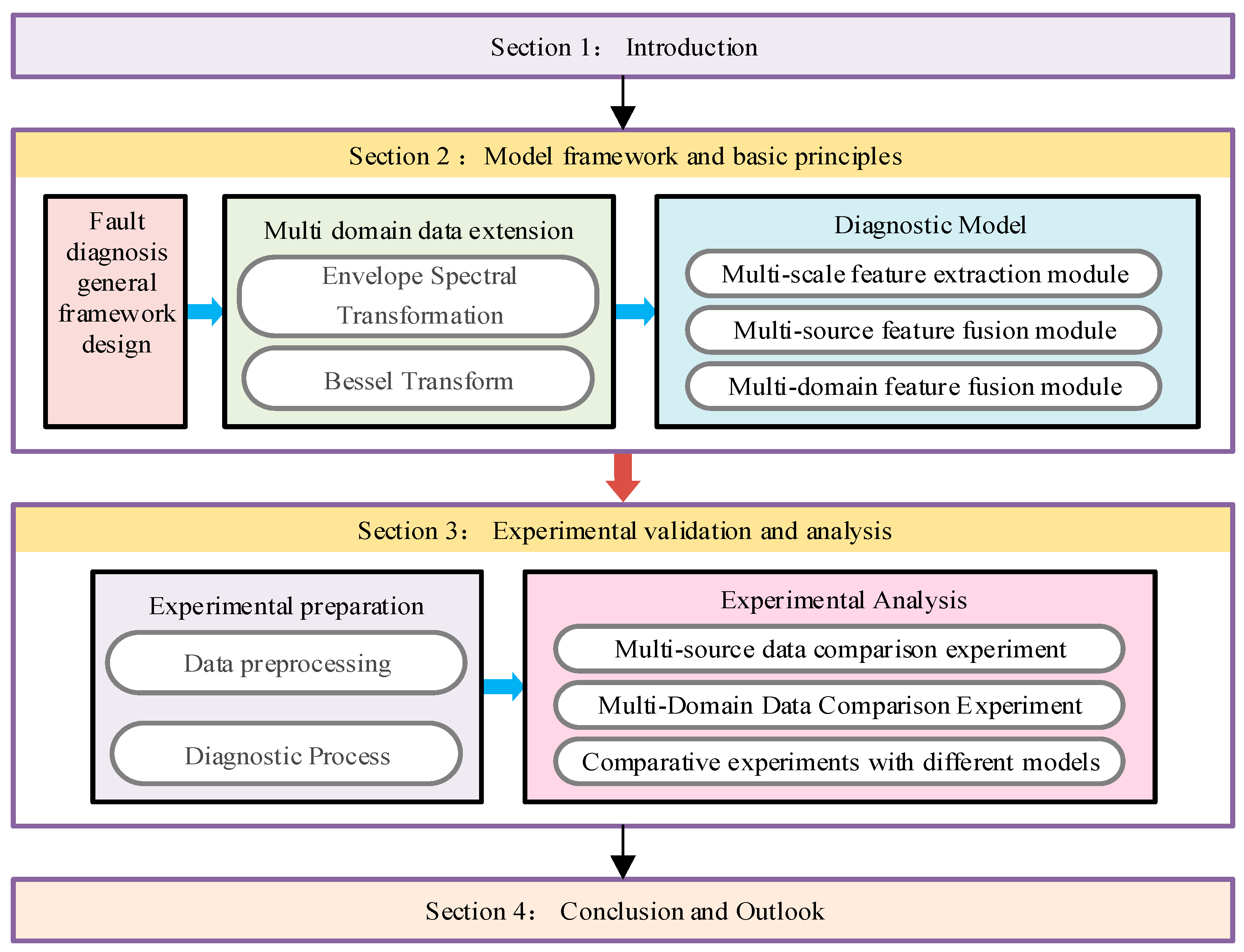
2. Model Framework and Basic Principles
2.1. Fault Diagnosis General Framework Design
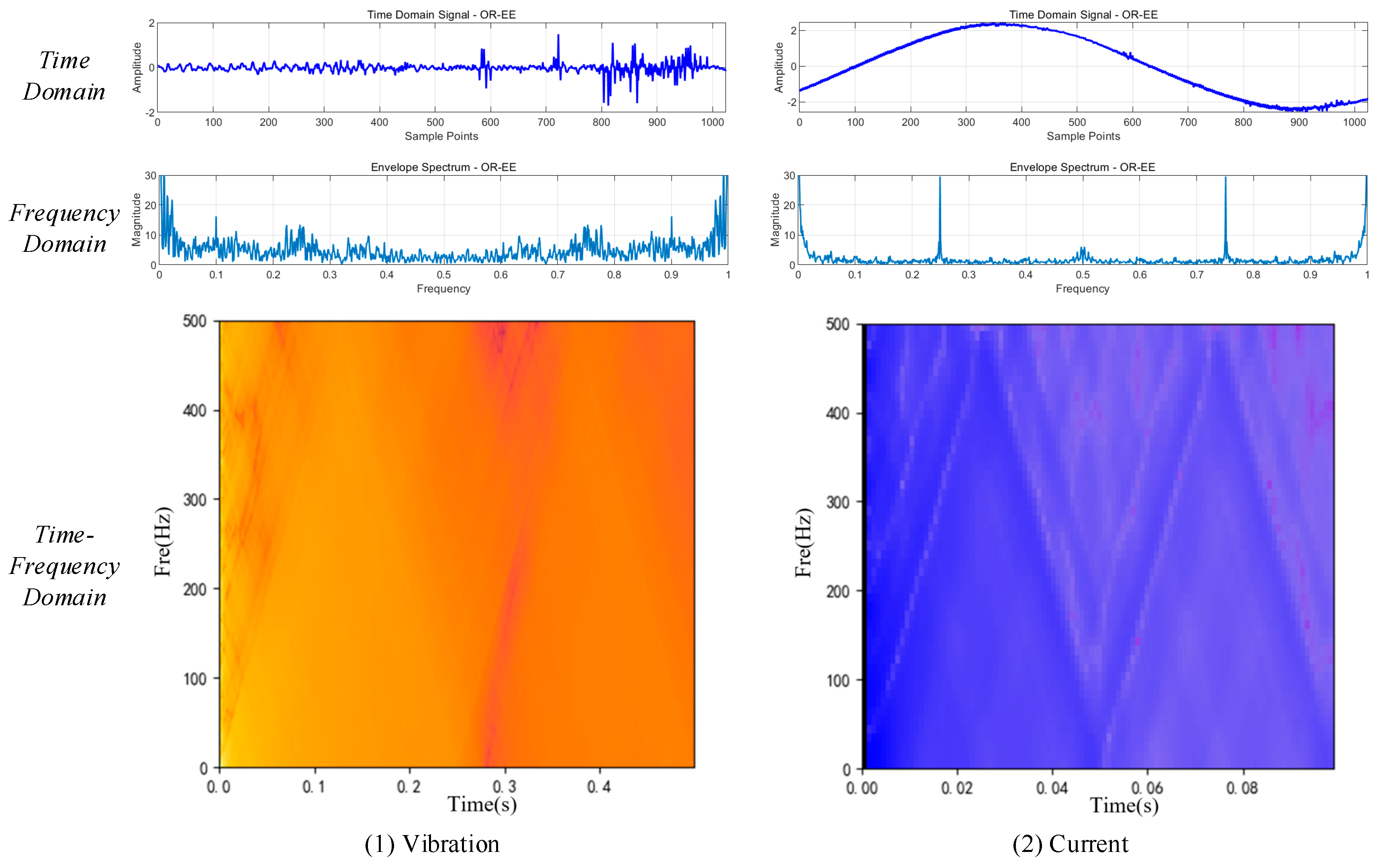
2.2. Multi-Domain Extension of Fault Data
- (1)
- Enveloped Spectral Transform
- (2)
- Bessel transform
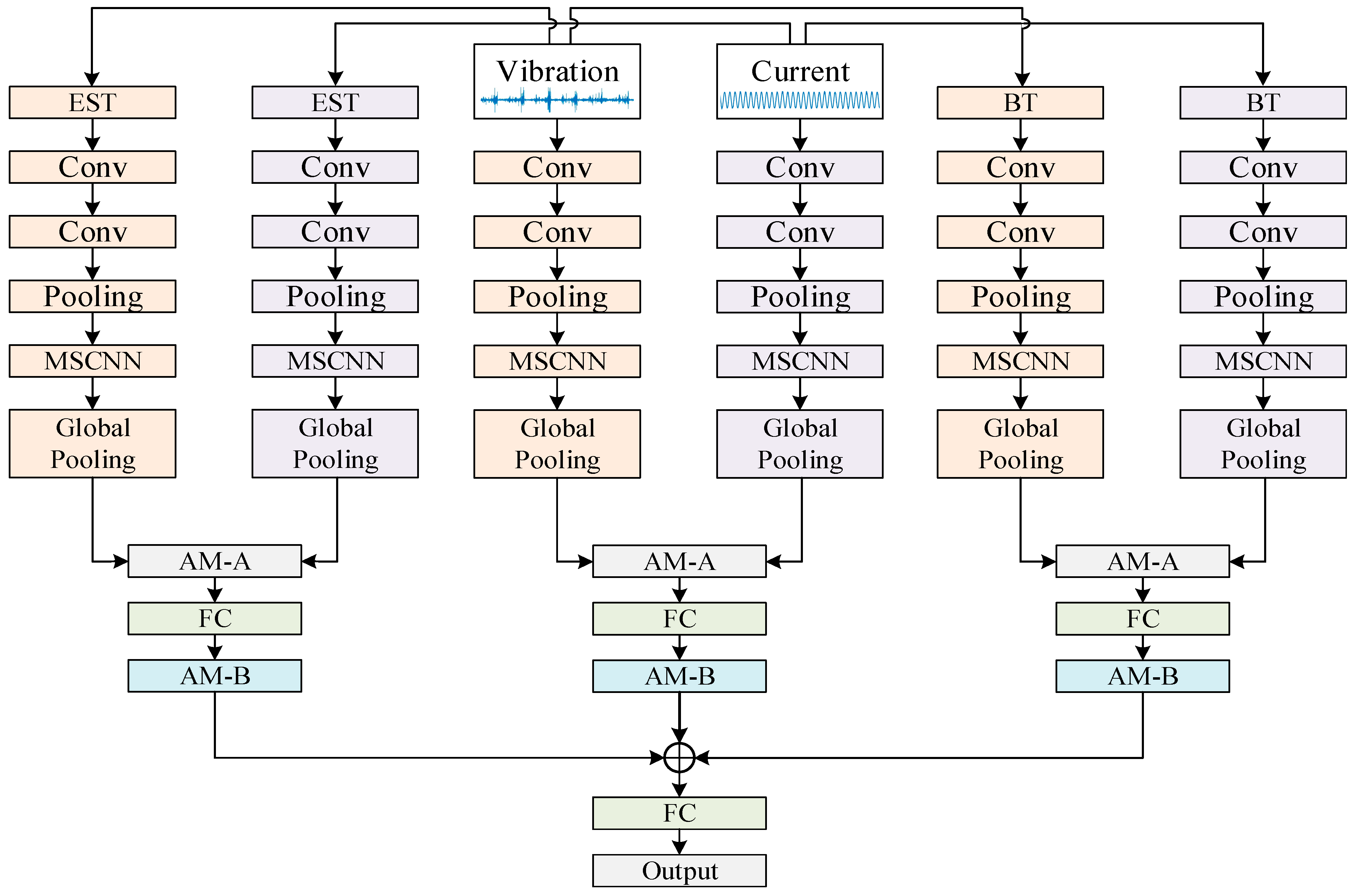
2.3. Multi-Scale Feature Extraction Module
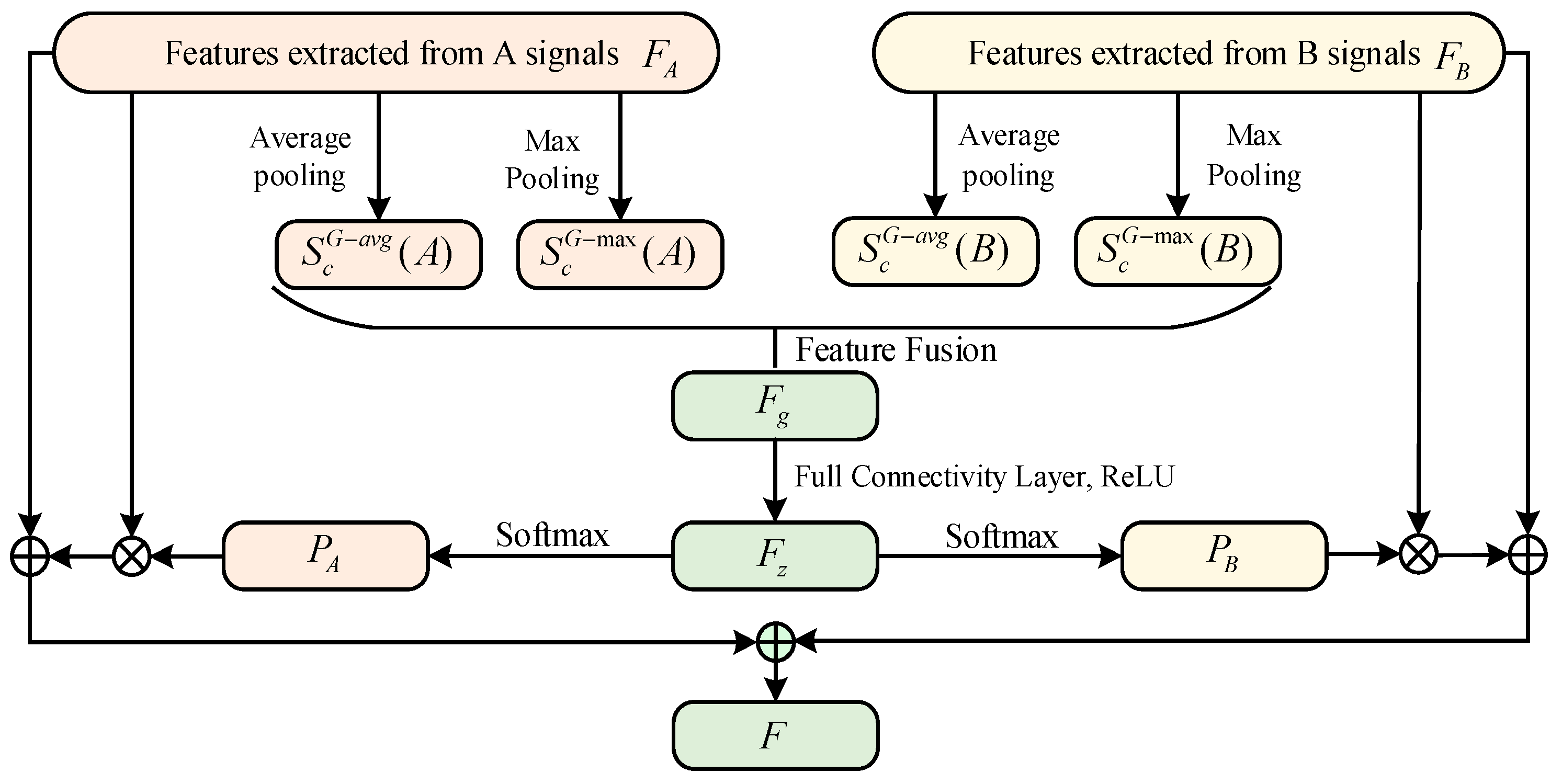
2.4. Feature Fusion Network Based on Attention Mechanism
2.5. Multi-Domain Feature Fusion Module Based on Attention Mechanism
3. Experimental Verification and Results Analysis
3.1. CASE 1
3.1.1. Data Preprocessing for CASE1
3.1.2. Overview of Specific Experimental Parameters
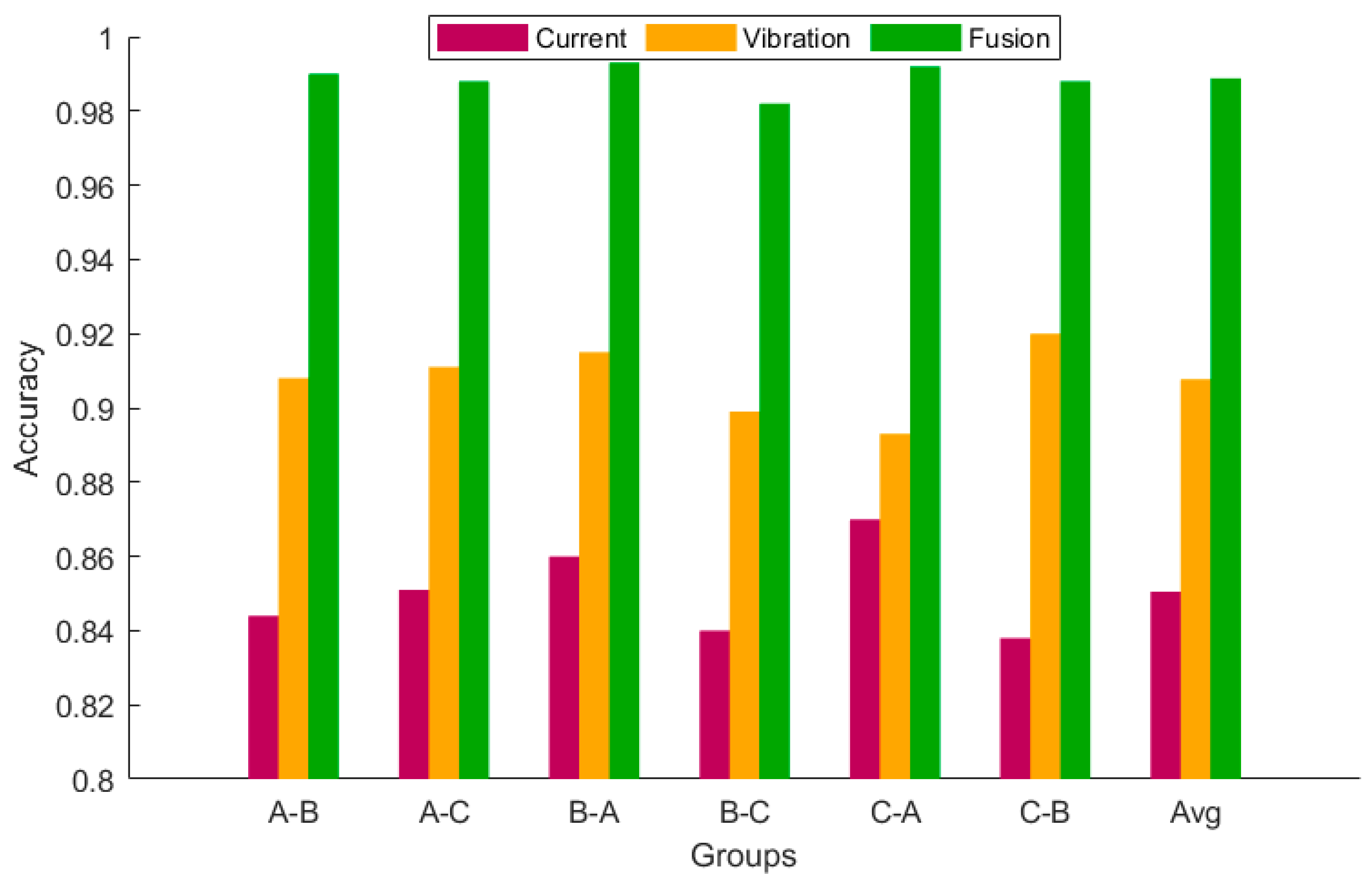
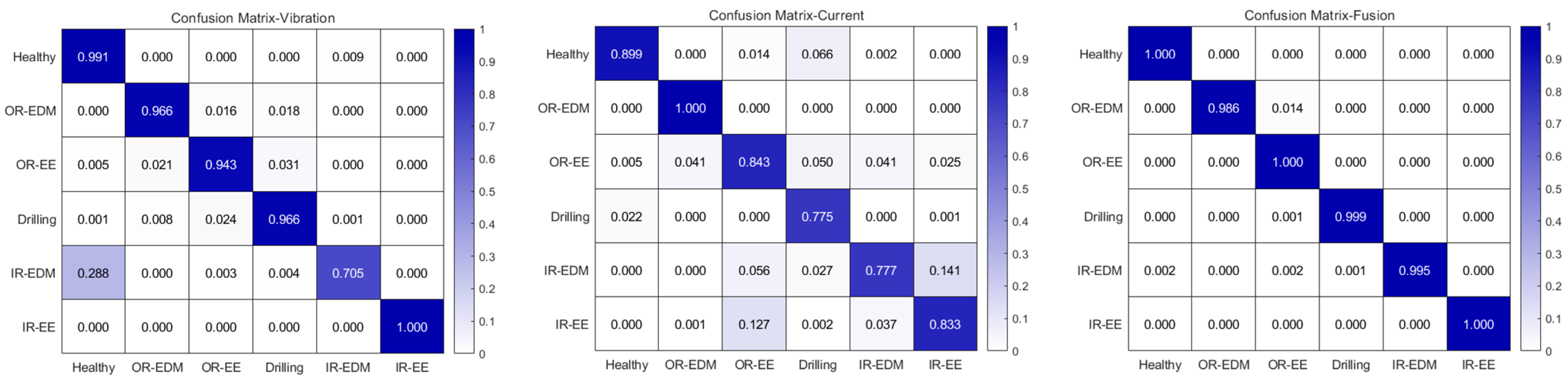
3.1.3. Multi-Source Data Comparison Experiment
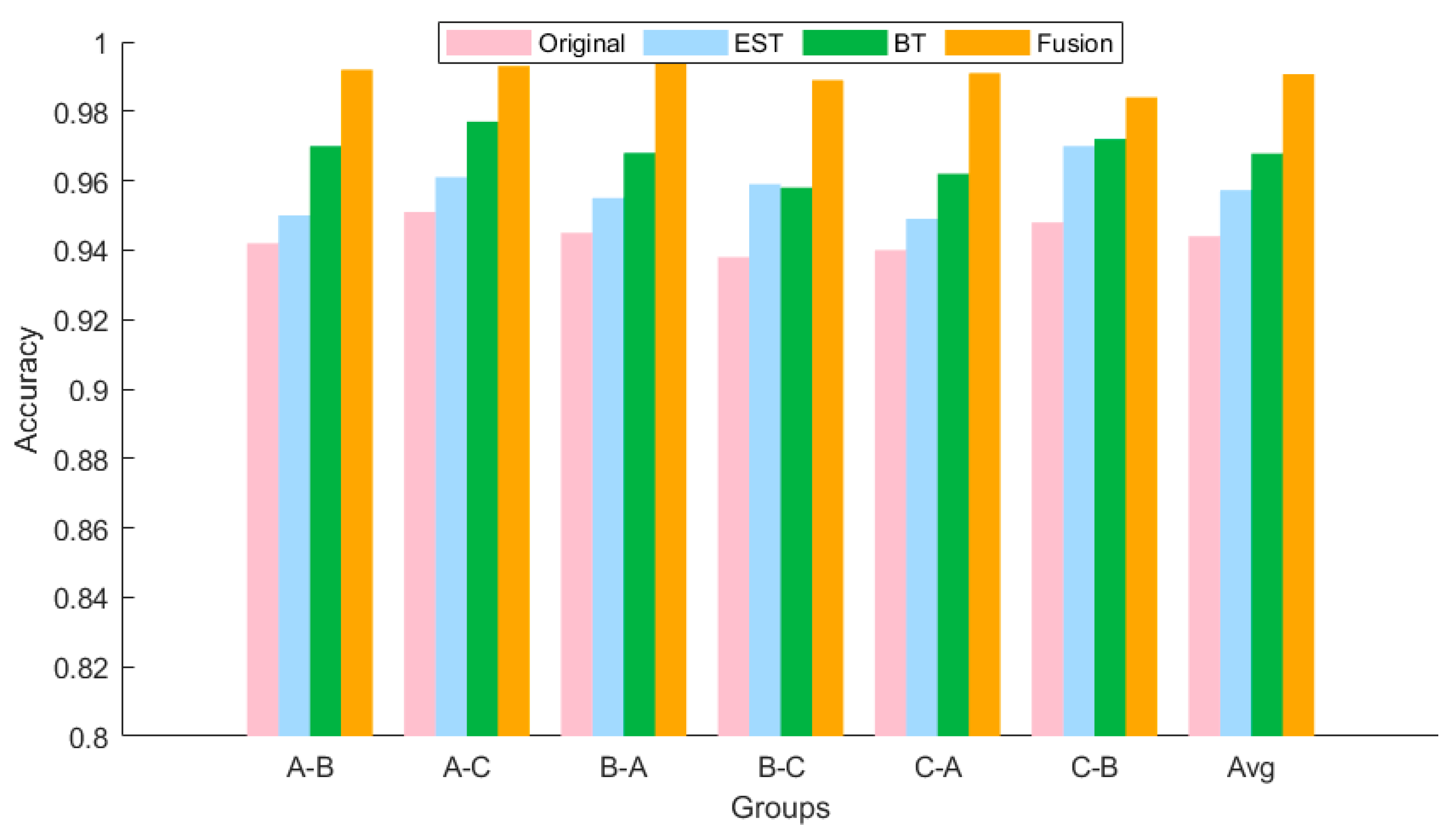
3.1.4. Comparative Experimental Analysis of Multi-Transform Domain Data for CASE1
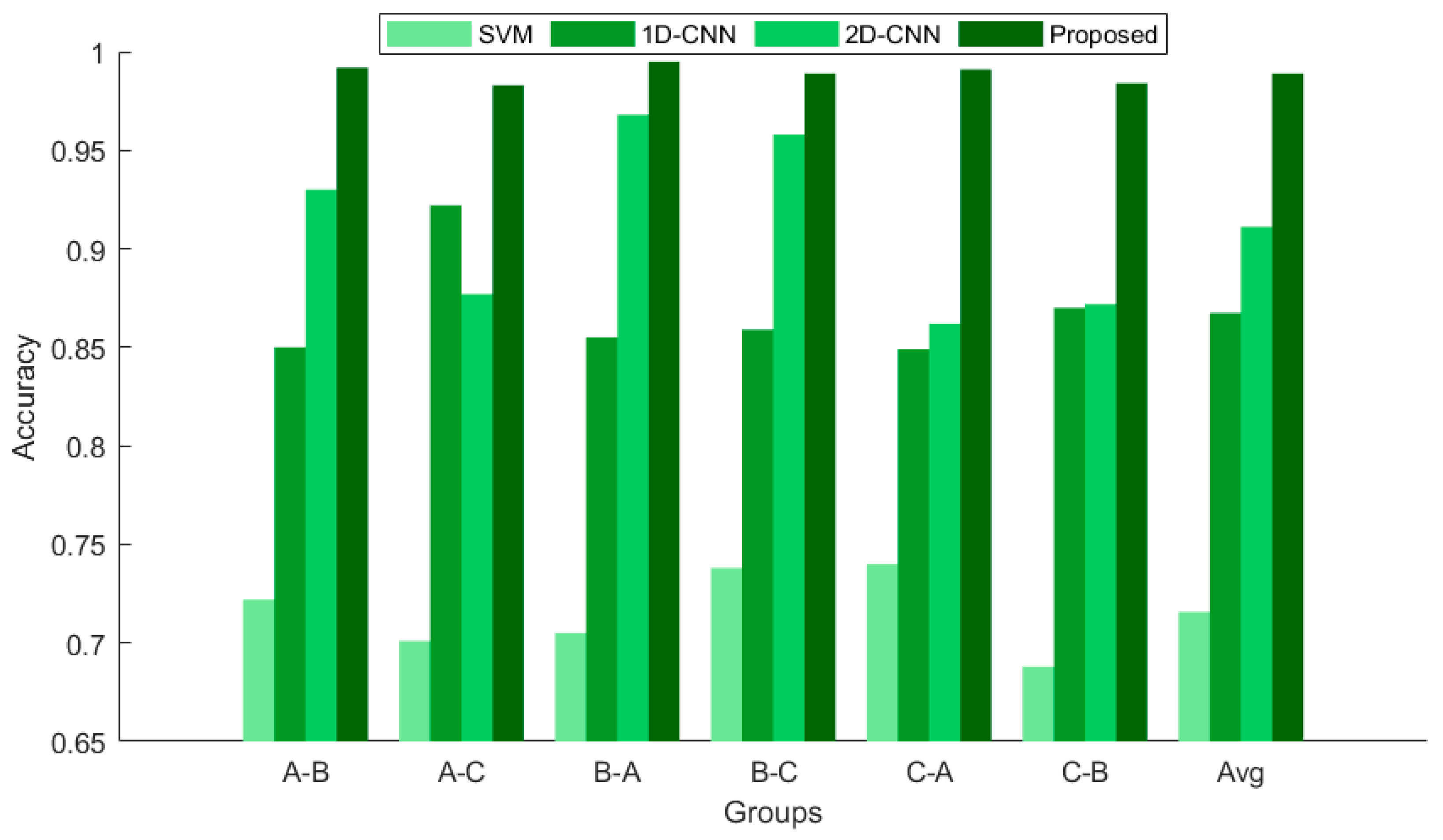
3.1.5. Comparative Experimental Analysis of Different Models for CASE1
3.2. CASE 2
3.2.1. Data Preprocessing for CASE2
3.2.2. Comparative Experimental Analysis of Multi-Source Data
3.2.3. Comparative Experimental Analysis of Multi-Transform Domain Data for CASE2
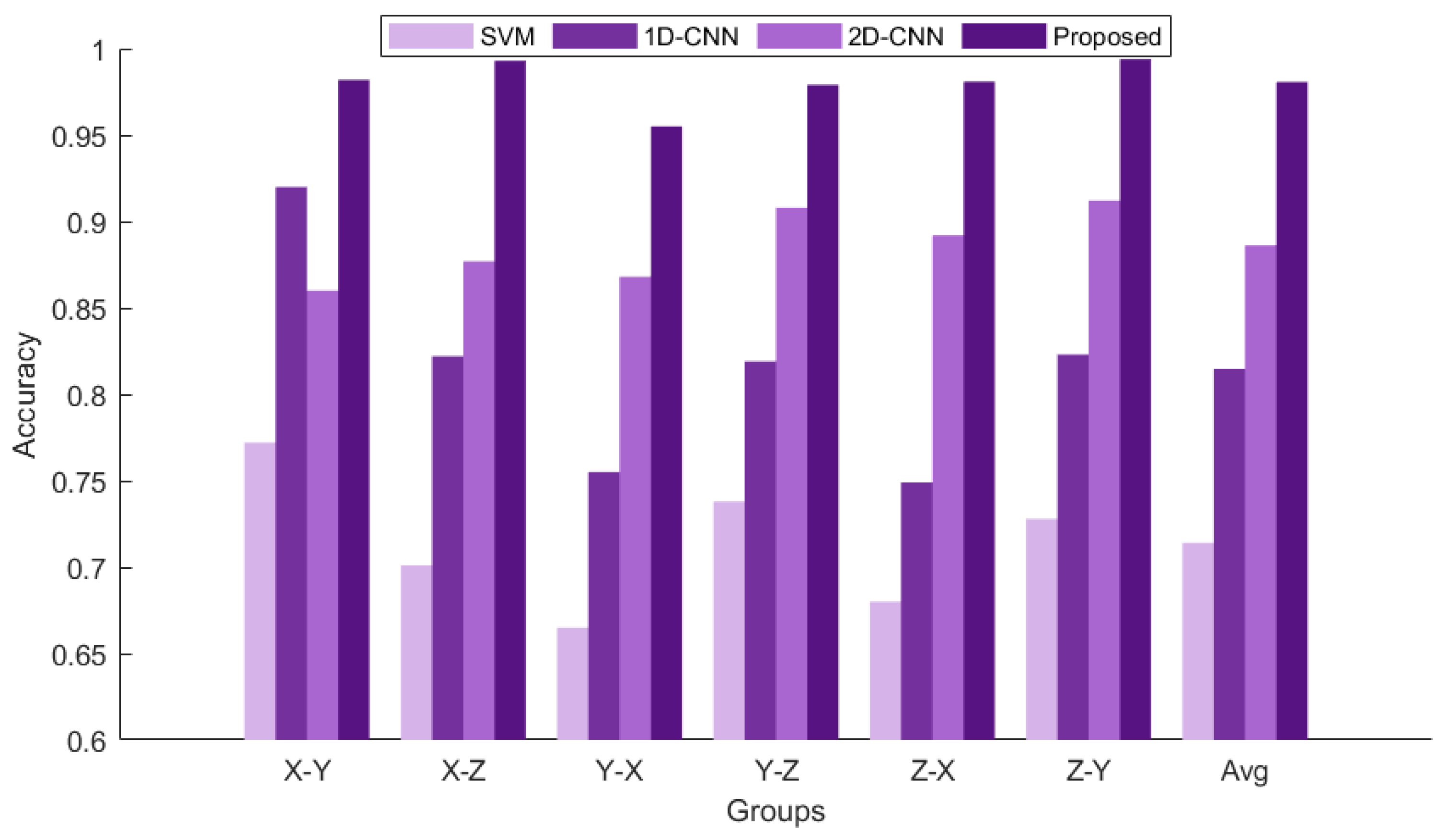
3.2.4. Comparative Experimental Analysis of Different Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, Q.; Yang, M.; Yan, J.; Shi, W. Feature decoupling integrated domain generalization network for bearing fault diagnosis under unknown operating conditions. Sci. Rep. 2024, 14, 30848. [Google Scholar] [CrossRef]
- Sun, Y.; Tao, H.; Stojanovic, V. Pseudo-label guided dual classifier domain adversarial network for unsupervised cross-domain fault diagnosis with small samples. Adv. Eng. Inform. 2025, 64, 102986. [Google Scholar] [CrossRef]
- Qiao, Z.; Yao, D.; Yang, J.; Zhou, T.; Ge, T. MSTD: A framework for rolling bearing fault diagnosis based on multi-scale and soft-threshold denoising. Nondestruct. Test. Eval. 2024, 1–21. [Google Scholar] [CrossRef]
- Zeng, L.; Chang, X.; Chen, J.; Wang, S. An Auxiliary Branch Semi-supervised Domain Generalization Network for Unseen Working Conditions Bearing Fault Diagnosis. IEEE Sens. J. 2024, 24, 42327–42342. [Google Scholar] [CrossRef]
- Snyder, Q.; Jiang, Q. Integrating self-attention mechanisms in deep learning: A novel dual-head ensemble transformer with its application to bearing fault diagnosis. Signal Process. 2025, 227, 109683. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, W.; He, G.; Ding, K.; Chen, Z. Natural Modal Sketching Network: An Interpretable Approach for Bearing Impulsive Feature Extraction. IEEE Trans. Cybern. 2024, 55, 953–968. [Google Scholar] [CrossRef]
- Jiang, L.; Shi, C.; Sheng, H.; Li, X.; Yang, T. Lightweight CNN architecture design for rolling bearing fault diagnosis. Meas. Sci. Technol. 2024, 35, 126142. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, H. Rolling bearing fault diagnosis model based on DSCB-NFAM. Meas. Sci. Technol. 2023, 35, 015029. [Google Scholar] [CrossRef]
- Zhang, D.; Gong, Z.; Zhou, H.; Ma, S.; Li, T.; Huang, Y.; Hu, X. Enhanced Wavelet Transform-Integrated MWRC-ResNet: A Novel Framework for Interpretable and Noise-Robust Rolling Bearing Fault Diagnosis. Meas. Sci. Technol. 2025, 36, 026102. [Google Scholar] [CrossRef]
- Song, L.; Lin, T.; Jin, Y.; Zhao, S.; Li, Y.; Wang, H. Advancements in Bearing Remaining Useful Life Prediction Methods: A Comprehensive Review. Meas. Sci. Technol. 2024, 35, 092003. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, J.; Shen, C.; Huang, W.; Zhu, Z. CycleGAN With Momentum Control for Intelligent Bearing Fault Diagnosis Driven by Dynamic Models. IEEE Sens. J. 2024, 24, 39315–39324. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Zhao, S.; Yao, J.; Li, M. Adaptive Convergent Visibility Graph Network: An interpretable method for intelligent rolling bearing diagnosis. Mech. Syst. Signal Process. 2025, 222, 111761. [Google Scholar] [CrossRef]
- Zhang, M.; He, C.; Huang, C.; Yang, J. A weighted time embedding transformer network for remaining useful life prediction of rolling bearing. Reliab. Eng. Syst. Saf. 2024, 251, 110399. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, L.; Liu, D.; Pan, X. Digital Twin-Driven Graph Convolutional Memory Network for Defect Evolution Assessment of Rolling Bearings. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Ding, L.; Guo, H.; Bian, L. Convolutional Neural Networks Based on Resonance Demodulation of Vibration Signal for Rolling Bearing Fault Diagnosis in Permanent Magnet Synchronous Motors. Energies 2024, 17, 4334. [Google Scholar] [CrossRef]
- You, K.; Lian, Z.; Gu, Y. A performance-interpretable intelligent fusion of sound and vibration signals for bearing fault diagnosis via dynamic CAME. Nonlinear Dyn. 2024, 112, 20903–20940. [Google Scholar] [CrossRef]
- Wang, Y.; Li, D.; Li, L.; Sun, R.; Wang, S. A novel deep learning framework for rolling bearing fault diagnosis enhancement using VAE-augmented CNN model. Heliyon 2024, 10, e35407. [Google Scholar] [CrossRef]
- Thank, P.N.; Cho, M.Y. Advanced AIoT for failure classification of industrial diesel generators based hybrid deep learning CNN-BiLSTM algorithm. Adv. Eng. Inform. 2024, 62, 102644. [Google Scholar] [CrossRef]
- Prawin, J. Deep learning neural networks with input processing for vibration-based bearing fault diagnosis under imbalanced data conditions. Struct. Health Monit. 2024, 24, 883–908. [Google Scholar] [CrossRef]
- Wang, M.; Xu, J.; Niu, X.; Chen, E.; Liu, P. A novel continuous delay hidden layer deep belief network and its application in life prediction of rolling bearings. Meas. Sci. Technol. 2024, 35, 035113. [Google Scholar] [CrossRef]
- Huang, Y.; Yan, C.; Liu, B.; Kang, J.; Shen, Y.; Wu, L. A hybrid deep learning network for diagnosing multipoint faults in rolling bearings under variable operating conditions. J. Mech. Sci. Technol. 2024, 38, 5989–6003. [Google Scholar] [CrossRef]
- Guo, H.; Zhao, X. Intelligent Diagnosis of Dual-channel Parallel Rolling Bearings Based on Feature Fusion. IEEE Sens. J. 2024, 24, 10640–10655. [Google Scholar] [CrossRef]
- Hu, Q.; Fu, X.; Guan, Y.; Wu, Q.; Liu, S. A Novel Intelligent Fault Diagnosis Method for Bearings with Multi-Source Data and Improved GASA. Sensors 2024, 24, 5285. [Google Scholar] [CrossRef]
- Li, T.; Qiao, Z.; Kumar, A.; Xie, C.; Zhang, C.; Lai, Z. A hydraulic motor fault diagnosis method based on weighted multi-channel information fusion. Meas. Sci. Technol. 2024, 36, 015120. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Jing, Z.; Li, H.; Xing, Z.; Yang, Z.; Cao, L.; Zhou, X. Fault diagnosis method of rolling bearing based on SSA-VMD and RCMDE. Sci. Rep. 2024, 14, 30637. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, R.; Li, C.; Lei, N. Remaining useful life prediction of rolling bearings based on time convolutional network and transformer in parallel. Meas. Sci. Technol. 2024, 35, 126102. [Google Scholar] [CrossRef]
- Ding, X.; Wang, J.; Wu, H.; Xu, J.; Xin, M. An Intelligent Fault Diagnosis Framework for Rolling Bearings with Integrated Feature Extraction and Ordering-based Causal Discovery. IEEE Sens. J. 2024, 24, 16374–16386. [Google Scholar] [CrossRef]
- Kulevome, D.K.B.; Wang, H.; Wang, X. Rolling bearing fault diagnostics based on improved data augmentation and ConvNet. J. Syst. Eng. Electron. 2023, 34, 1074–1084. [Google Scholar] [CrossRef]
- Peng, Y. Research on Small Sample Rolling Bearing Fault Diagnosis Method Based on Mixed Signal Processing Technology. Symmetry 2024, 16, 1178. [Google Scholar] [CrossRef]
- Kumar, K.K.; Mandava, S. Real-time bearing fault classification of induction motor using enhanced inception ResNet-V2. Appl. Artif. Intell. 2024, 38, 2378270. [Google Scholar] [CrossRef]
- Rajagopalan, S.; Restrepo, J.A.; Aller, J.M.; Habetler, T.G.; Harley, R.G. Nonstationary motor fault detection using recent quadratic time–frequency representations. IEEE Trans. Ind. Appl. 2008, 44, 735–744. [Google Scholar] [CrossRef]
- Guo, Z.; Durand, L.G.; Lee, H.C. The time-frequency distributions of nonstationary signals based on a Bessel kernel. IEEE Trans. Signal Process. 1994, 42, 1700–1707. [Google Scholar] [CrossRef]
- Athisayam, A.; Kondal, M. A Unified Approach for Compound Gear-Bearing Fault Diagnosis Using Bessel Transform, Artificial Bee Colony-Based Feature Selection and LSTM Networks. J. Vib. Eng. Technol. 2024, 12, 2959–2973. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, Z.; Tang, C.; Sun, J.; Zheng, L.; Qiu, Z.; He, Y.; Li, G. Cross-conditions fault diagnosis of rolling bearings based on dual domain adversarial network. IEEE Trans. Instrum. Meas. 2023, 72, 1–15. [Google Scholar] [CrossRef]
- Xue, Y.; Wen, C.; Wang, Z.; Liu, W.; Chen, G. A novel framework for motor bearing fault diagnosis based on multi-transformation domain and multi-source data. Knowl.-Based Syst. 2024, 283, 111205. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, T.; Wu, F. A fault diagnosis method based on convolutional sparse representation. Digit. Signal Process. 2025, 158, 104940. [Google Scholar] [CrossRef]
- Wu, D.; Chen, D.; Yu, G. New Health Indicator Construction and Fault Detection Network for Rolling Bearings via Convolutional Auto-Encoder and Contrast Learning. Machines 2024, 12, 362. [Google Scholar] [CrossRef]
- Athisayam, A.; Kondal, M. A comprehensive approach with DTW-driven IMF selection, multi-domain fusion, and TSA-based feature selection for compound fault diagnosis. Measurement 2025, 242, 115974. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, Z.; Zhou, F.; Wang, C. A Real-Time Fault Diagnosis Method for Multi-Source Heterogeneous Information Fusion Based on Two-Level Transfer Learning. Entropy 2024, 26, 1007. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Li, J.; Xiang, J. Rotating machinery fault detection using a new version of intrinsic time-scale decomposition. IEEE Sens. J. 2024, 24, 1905–1918. [Google Scholar] [CrossRef]
- Athisayam, A.; Kondal, M. An intelligent compound gear-bearing fault identification approach using Bessel kernel-based time-frequency distribution. Metrol. Meas. Syst. 2023, 30, 83–97. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A.; Liu, W.; et al. Going deeper with convolutions. In Proceedings of the CVPR 2015, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Mu, M.; Jiang, H.; Wang, X.; Dong, Y. Adaptive model-agnostic meta-learning network for cross-machine fault diagnosis with limited samples. Eng. Appl. Artif. Intell. 2025, 141, 109748. [Google Scholar] [CrossRef]
- Yin, C.; Li, Y.; Wang, Y.; Dong, Y. Physics-guided degradation trajectory modeling for remaining useful life prediction of rolling bearings. Mech. Syst. Signal Process. 2025, 224, 112192. [Google Scholar] [CrossRef]
- Chen, P.; Ma, Z.; Xu, C.; Zhang, M.; Li, H.; Zheng, K.; Jin, Y. Scale-aware Domain Adaptation for Surface Defects Detection on Machine Tool Components in Contaminant Measurements. IEEE Trans. Instrum. Meas. 2024, 74, 1–9. [Google Scholar] [CrossRef]
- Yang, T.; Xu, M.; Chen, C.; Wen, J.; Li, J.; Han, Q. DSTF-Net: A novel framework for intelligent diagnosis of insulated bearings in wind turbines with multi-source data and its interpretability. Renew. Energy 2025, 238, 121965. [Google Scholar] [CrossRef]
- Qin, N.; You, Y.; Huang, D.; Jia, X.; Zhang, Y.; Du, J.; Wang, T. AttGAN-DPCNN: An Extremely Imbalanced Fault Diagnosis Method for Complex Signals From Multiple Sensors. IEEE Sens. J. 2016, 24, 38270–38285. [Google Scholar] [CrossRef]
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition Monitoring of Bearing Damage in Electromechanical Drive Systems by Using Motor Current Signals of Electric Motors: A Benchmark Data Set for Data-Driven Classification. In Proceedings of the European Conference of the Prognostics and Health Management Society, Bilbao, Spain, 5–8 July 2016; 2016. [Google Scholar] [CrossRef]
- Jung, W.; Kim, S.-H.; Yun, S.-H.; Bae, J.; Park, Y.-H. Vibration, acoustic, temperature, and motor current dataset of rotating machine under varying operating conditions for fault diagnosis. Data Brief 2023, 48, 109049. [Google Scholar] [CrossRef]






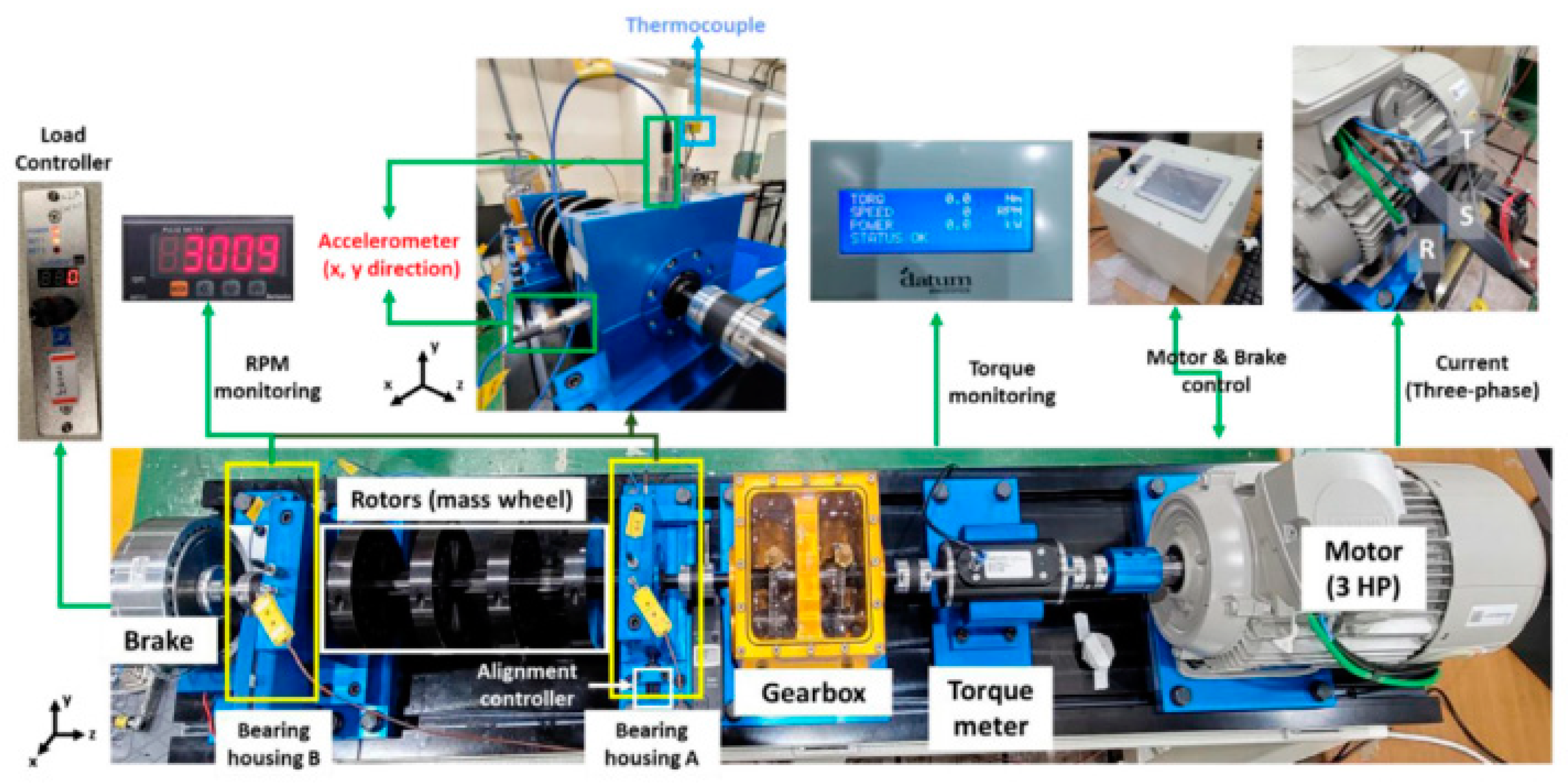

| Types of Failures | Tags |
|---|---|
| Healthy | 0 |
| OR-EDM | 1 |
| OR-EE | 2 |
| OR-Drilling | 3 |
| IR-EDM | 4 |
| IR-EE | 5 |
| Speed (rpm) | Load Torque (N/m) | Radial Force (N) | |
|---|---|---|---|
| A | 900 | 0.7 | 1000 |
| B | 1500 | 0.7 | 1000 |
| C | 1500 | 0.7 | 400 |
| Experiment Name | Training Dataset | Testing Dataset | Number of Samples |
|---|---|---|---|
| AB | A | B | 40,000 |
| AC | A | C | 40,000 |
| BA | B | A | 40,000 |
| BC | B | C | 40,000 |
| CA | C | A | 40,000 |
| CB | C | B | 40,000 |
| Layer Name | Kernel Size/Step | Type |
|---|---|---|
| Conv1 | 3 × 1/2 | BN-Relu |
| Conv1 | 2 × 1/2 | BN-Relu |
| Pooling | 2 × 1/2 | MAXpool |
| Conv_a | 1 × 1/2 | BN-Relu |
| Conv_b | 1 × 1/1 | BN-Relu |
| Conv_b | 3 × 1/2 | BN-Relu |
| Average Pooling_c | 3 × 1/2 | BN-Relu |
| Conv_c | 1 × 1/1 | BN-Relu |
| Conv_c | 5 × 1/1 | BN-Relu |
| Conv_d | 1 × 1/1 | BN-Relu |
| Conv_d | 3 × 1/1 | BN-Relu |
| Conv_d | 3 × 1/2 | BN-Relu |
| Global Pooling | 3 × 1/1 | BN-Relu |
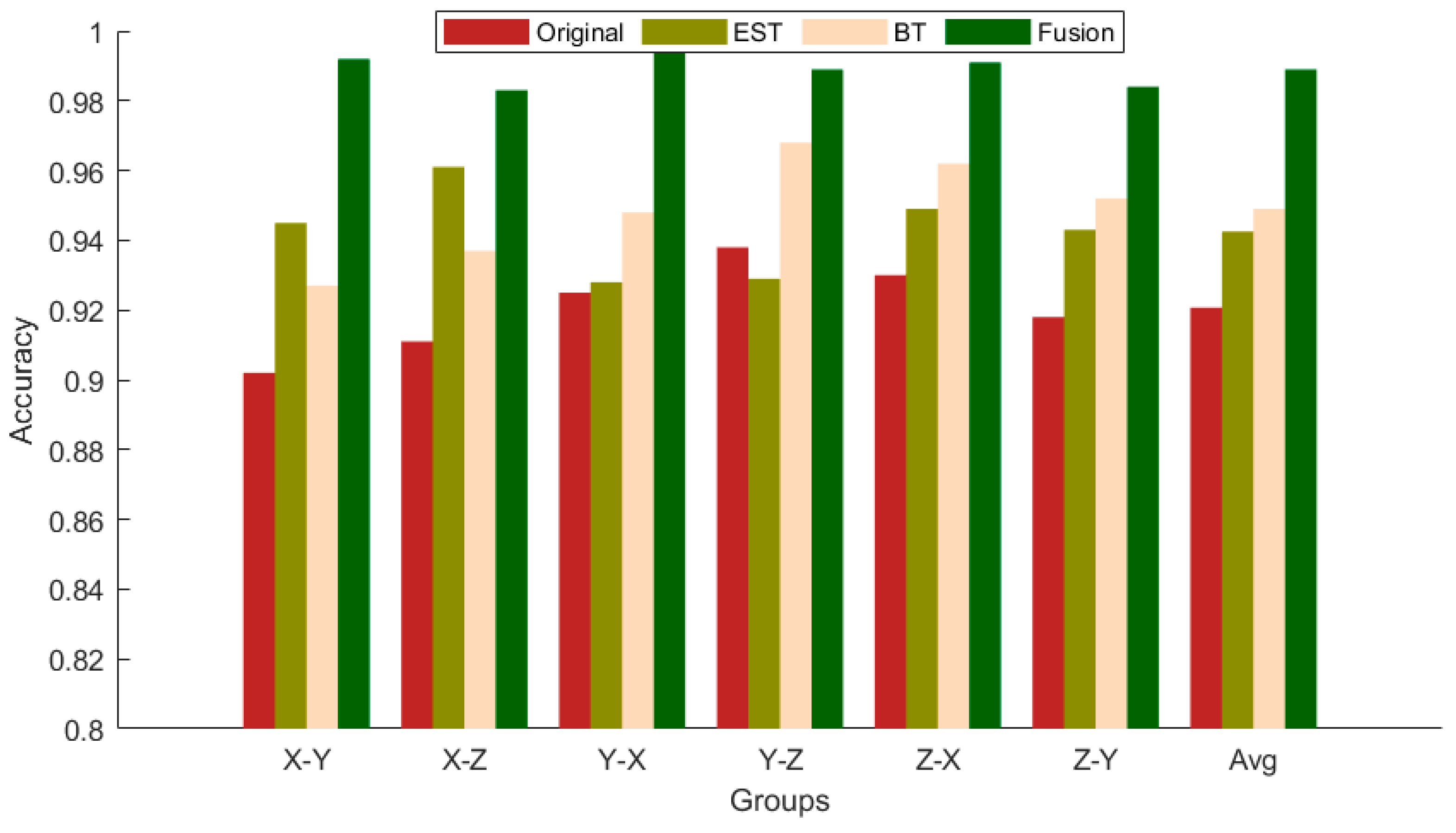
| Experiment Name | Training Dataset | Testing Dataset | Number of Samples |
|---|---|---|---|
| XY | X | Y | 2000 |
| XZ | X | Z | 2000 |
| YX | Y | X | 2000 |
| YZ | Y | Z | 2000 |
| ZX | Z | X | 2000 |
| ZY | Z | Y | 2000 |
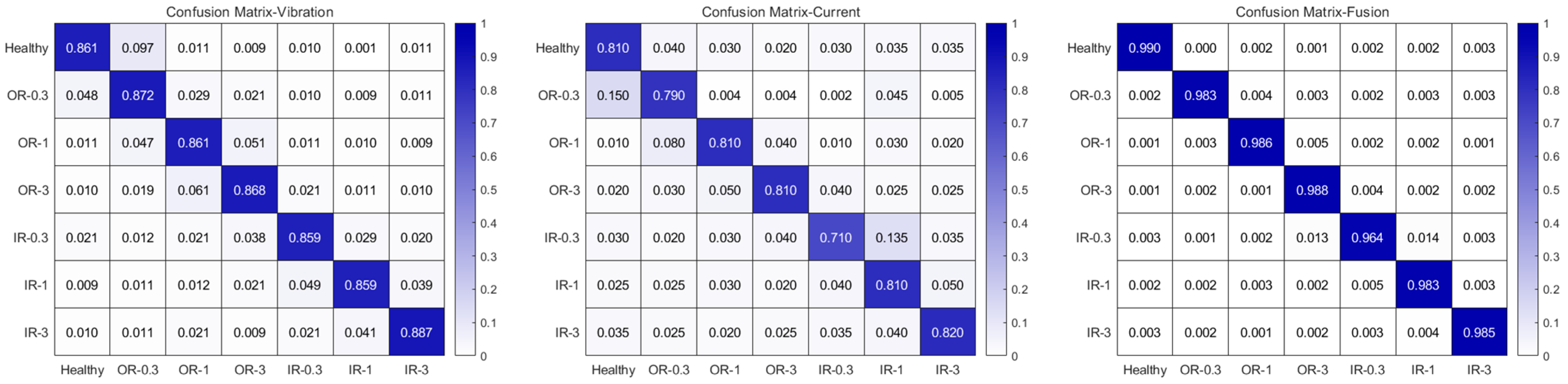
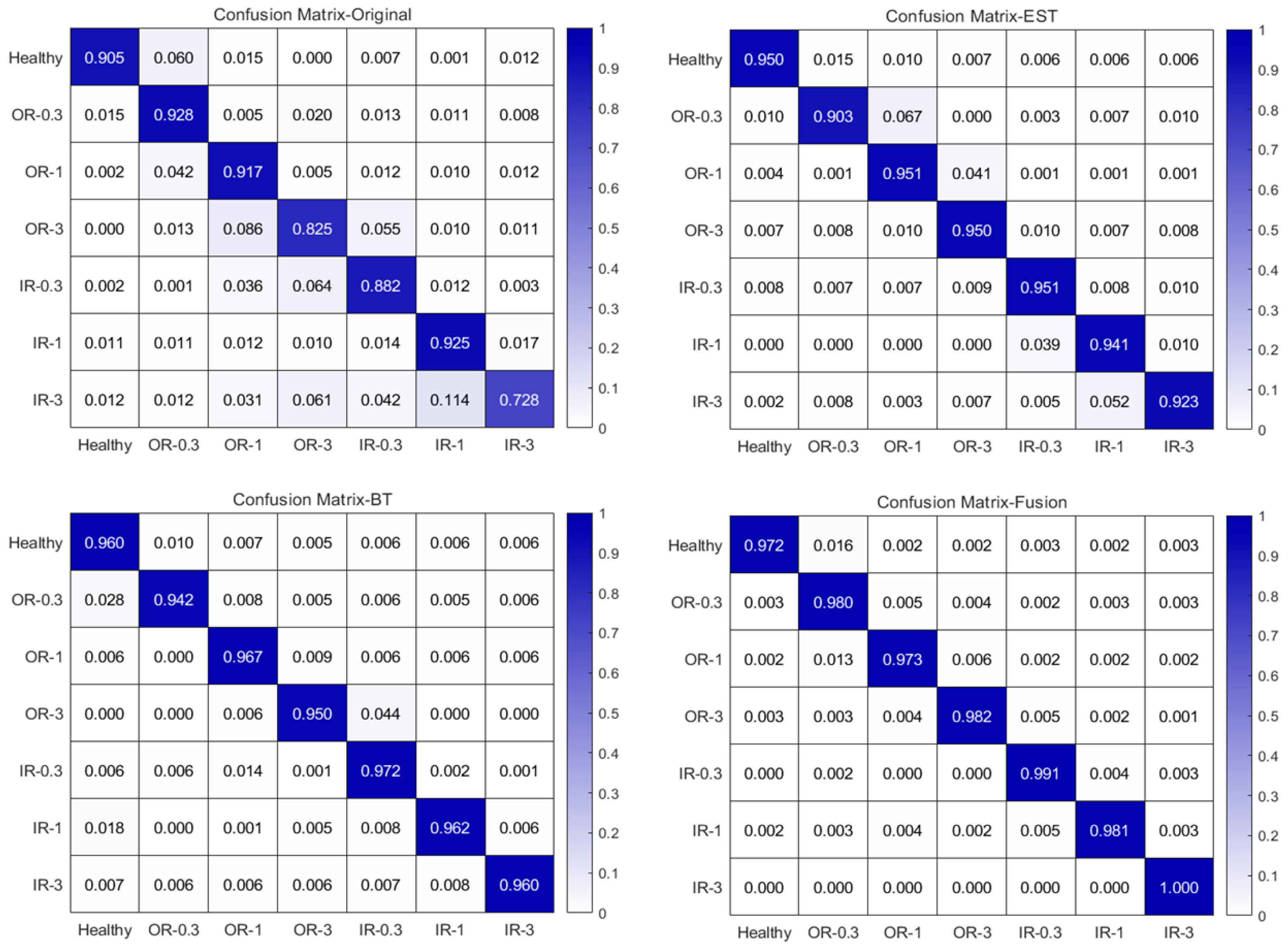
| Types of Failures | Tags |
|---|---|
| Healthy | 0 |
| OR-0.3 | 1 |
| OR-1 | 2 |
| OR-3 | 3 |
| IR-0.3 | 4 |
| IR-1 | 5 |
| IR-3 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, T.; Feng, Y.; Sui, S.; Xie, X.; Li, H.; Liu, X. A Bearing Fault Diagnosis Method Combining Multi-Source Information and Multi-Domain Information Fusion. Machines 2025, 13, 289. https://doi.org/10.3390/machines13040289
Sui T, Feng Y, Sui S, Xie X, Li H, Liu X. A Bearing Fault Diagnosis Method Combining Multi-Source Information and Multi-Domain Information Fusion. Machines. 2025; 13(4):289. https://doi.org/10.3390/machines13040289
Chicago/Turabian StyleSui, Tao, Yixiang Feng, Sitian Sui, Xueran Xie, Hui Li, and Xiuzhi Liu. 2025. "A Bearing Fault Diagnosis Method Combining Multi-Source Information and Multi-Domain Information Fusion" Machines 13, no. 4: 289. https://doi.org/10.3390/machines13040289
APA StyleSui, T., Feng, Y., Sui, S., Xie, X., Li, H., & Liu, X. (2025). A Bearing Fault Diagnosis Method Combining Multi-Source Information and Multi-Domain Information Fusion. Machines, 13(4), 289. https://doi.org/10.3390/machines13040289






