Size Effect on Energy Characteristics of Axial Flow Pump Based on Entropy Production Theory
Abstract
1. Introduction
2. Research Methods
2.1. Numerical Simulation
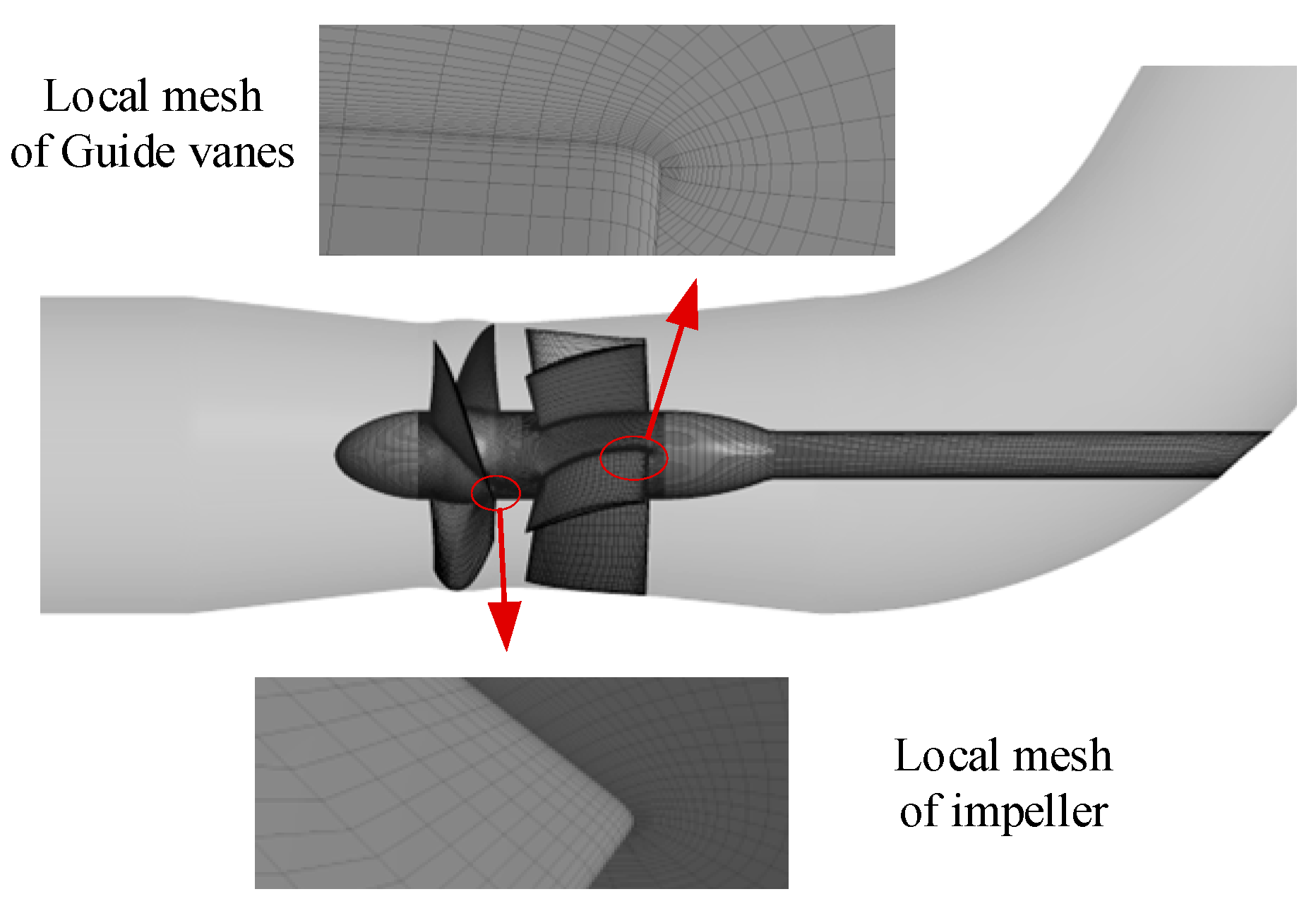
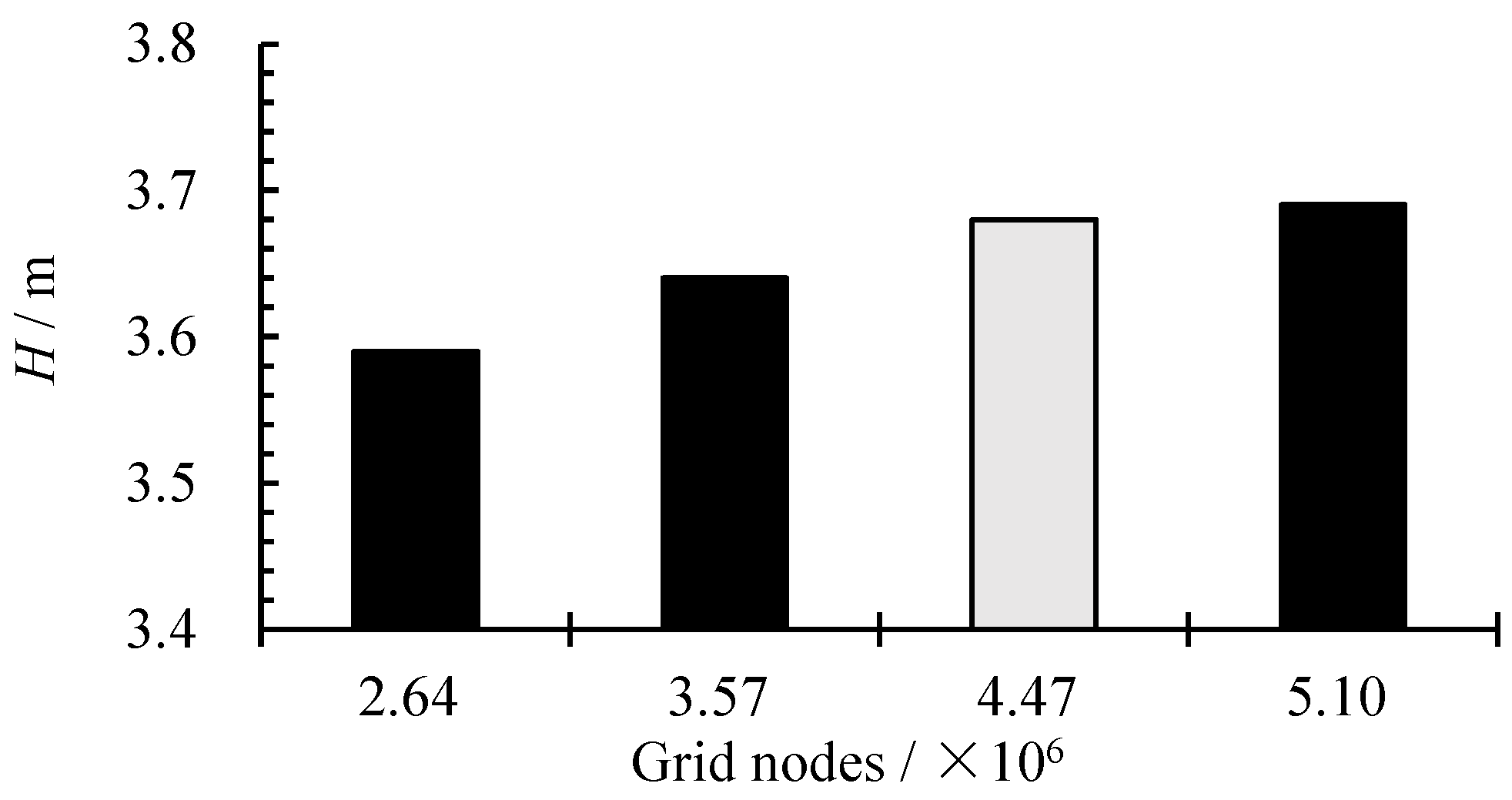
2.1.1. Mesh Generation
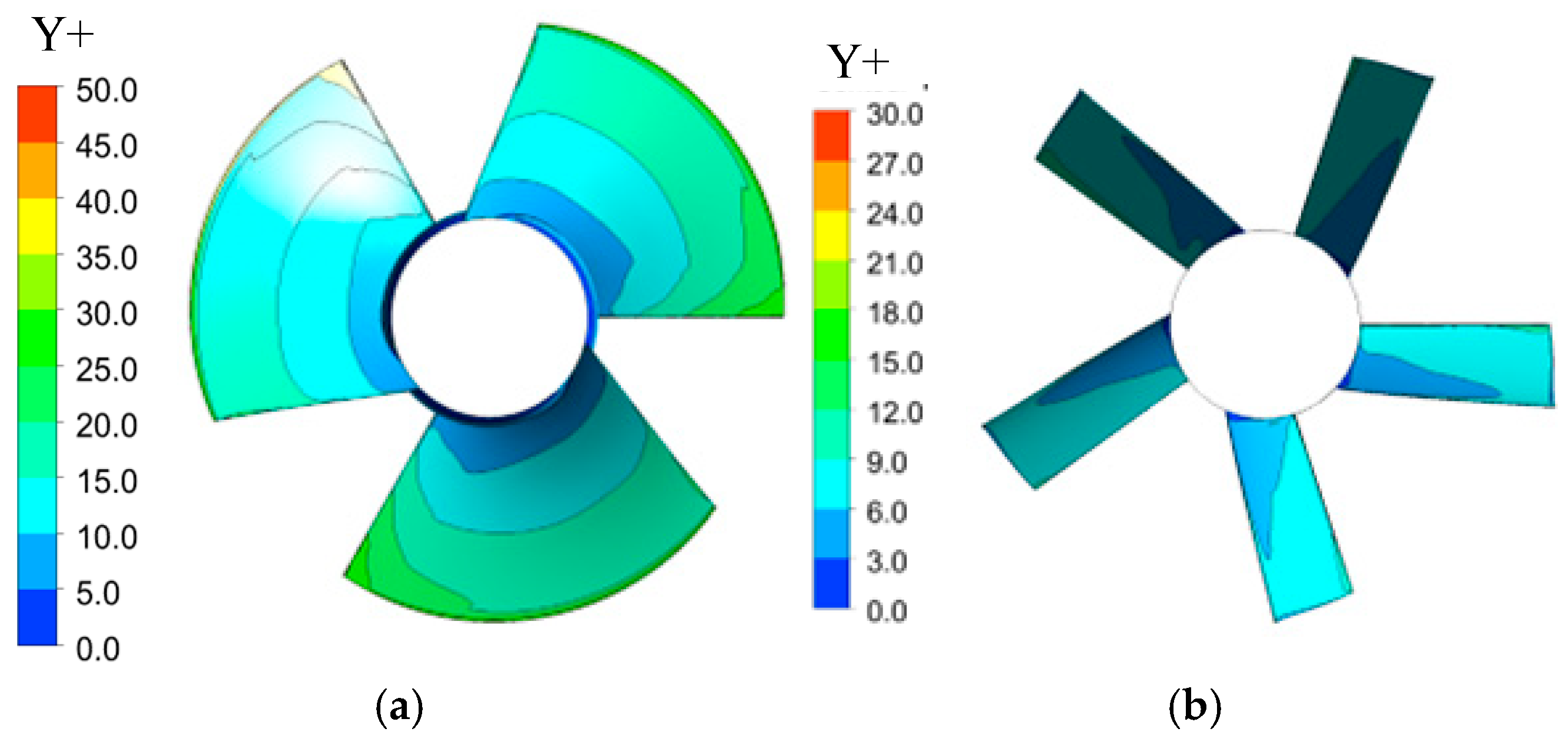
2.1.2. Boundary Condition
2.2. Entropy Production Theory
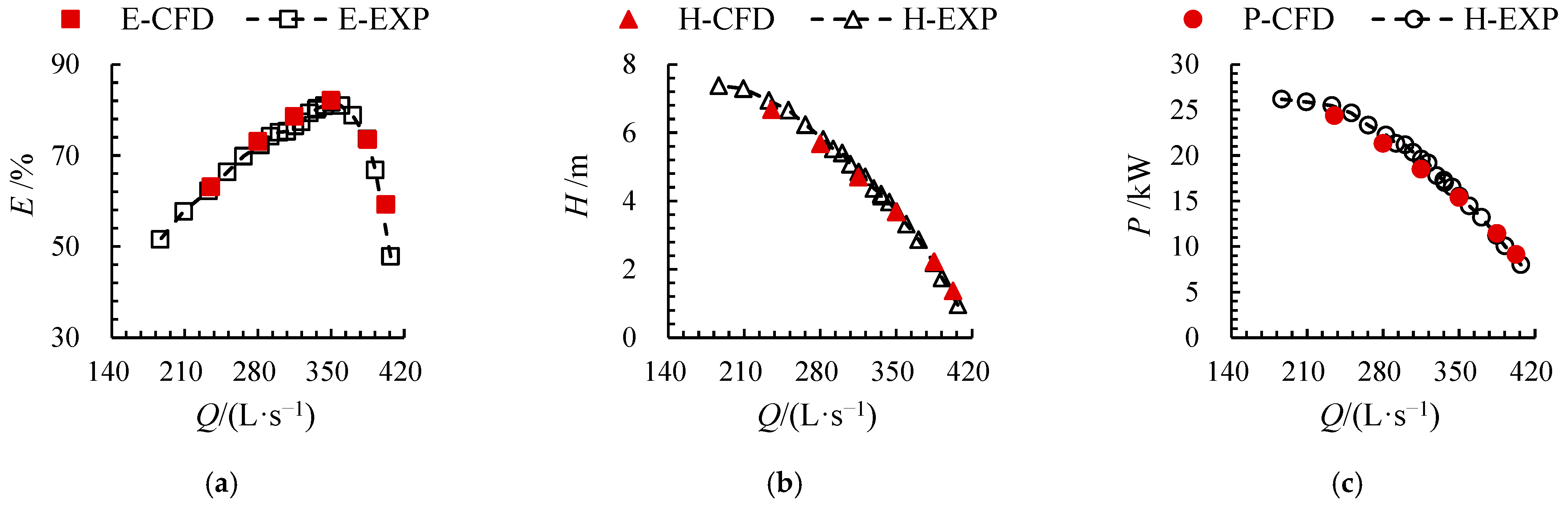
3. Test Verification
4. Results and Discussion
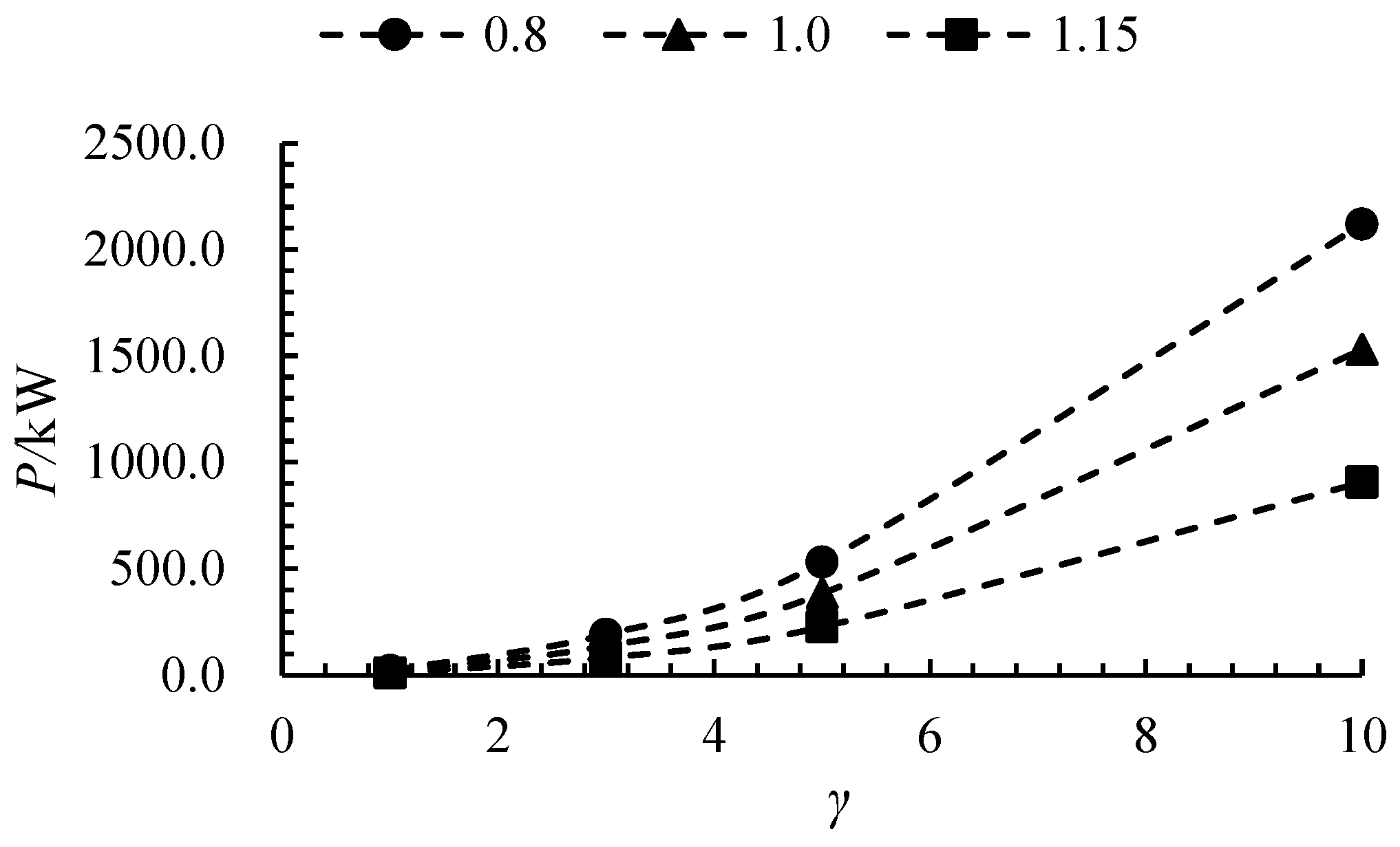
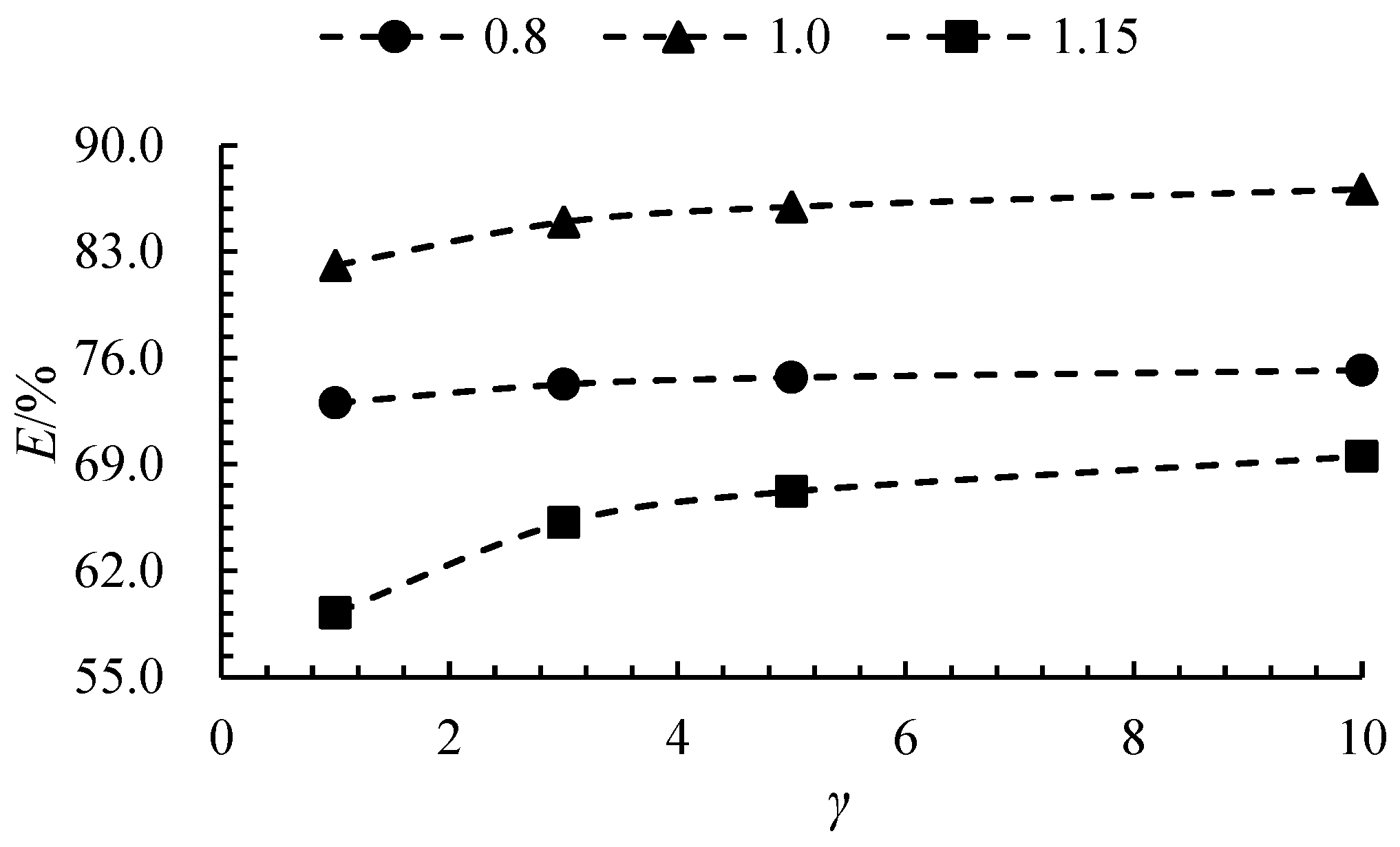
4.1. The Size Effect on External Characteristic Parameters
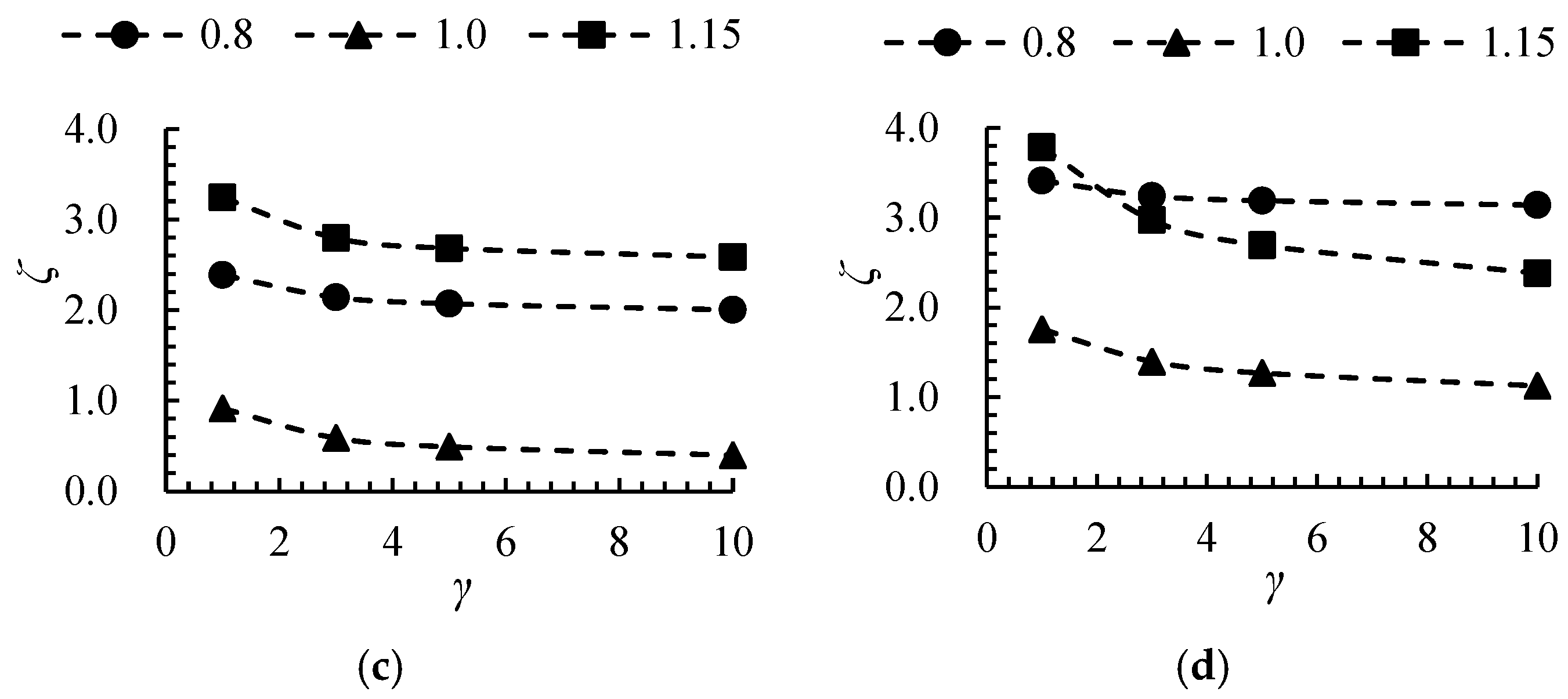
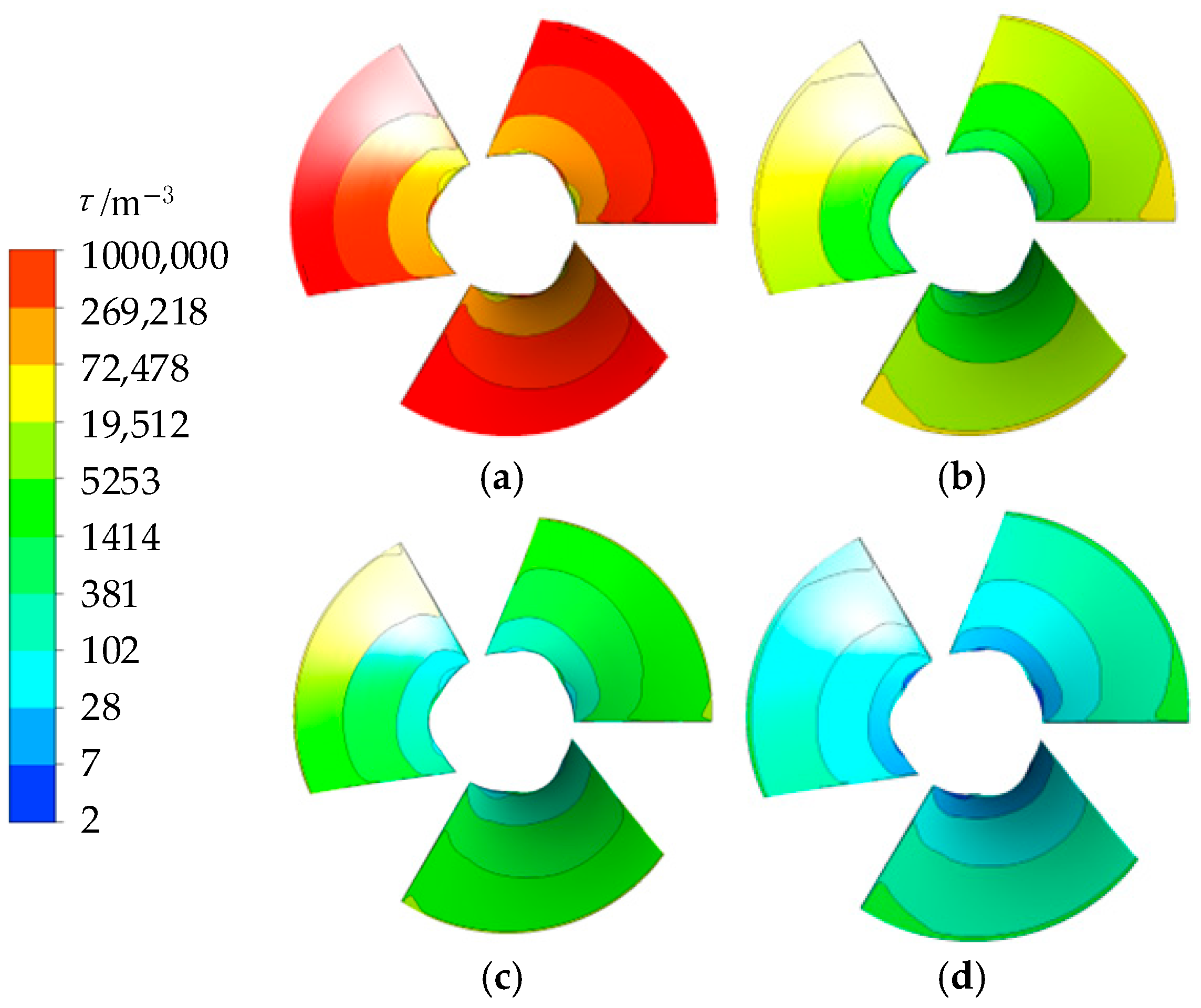
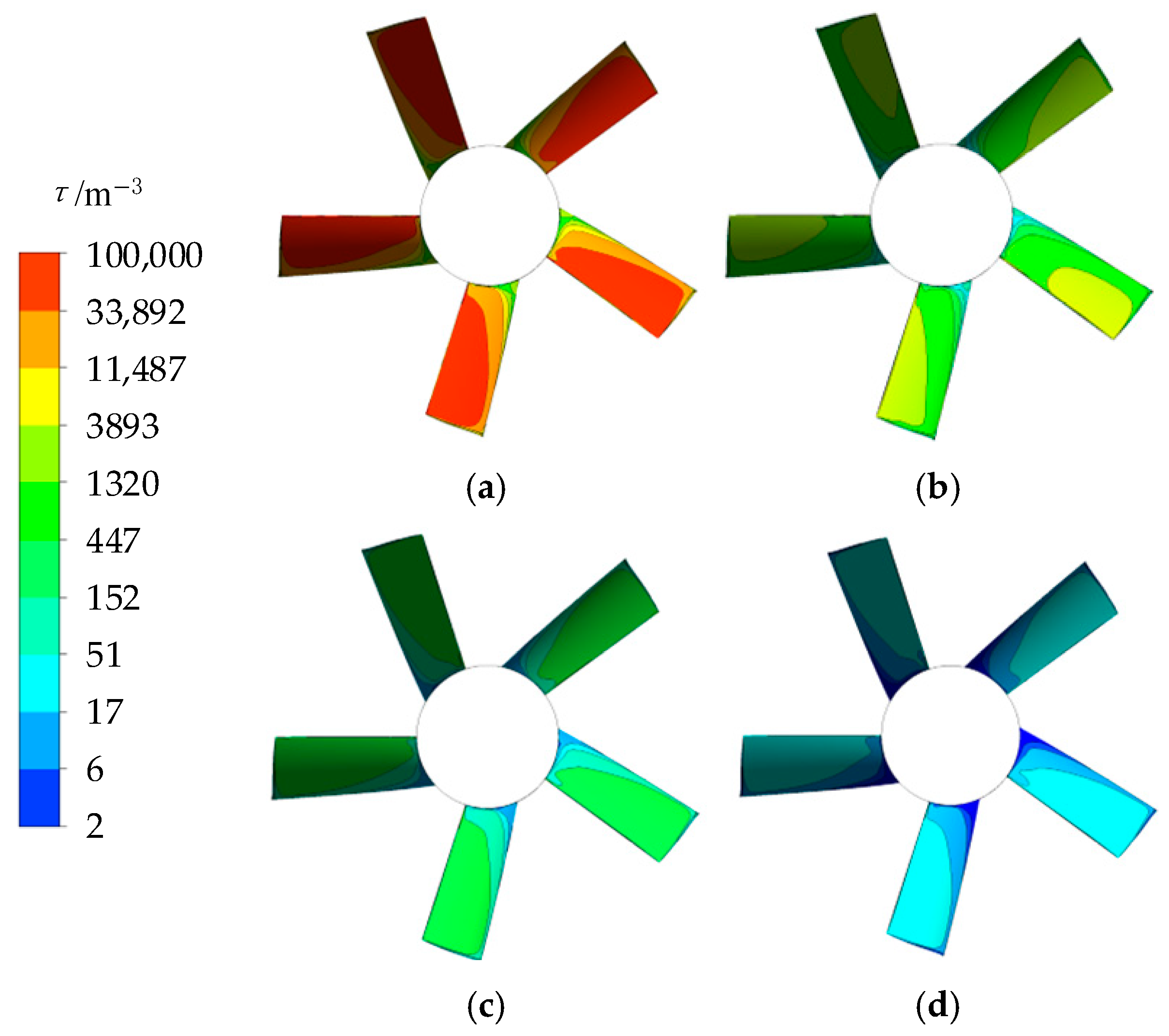
4.2. The Size Effect on Entropy Production
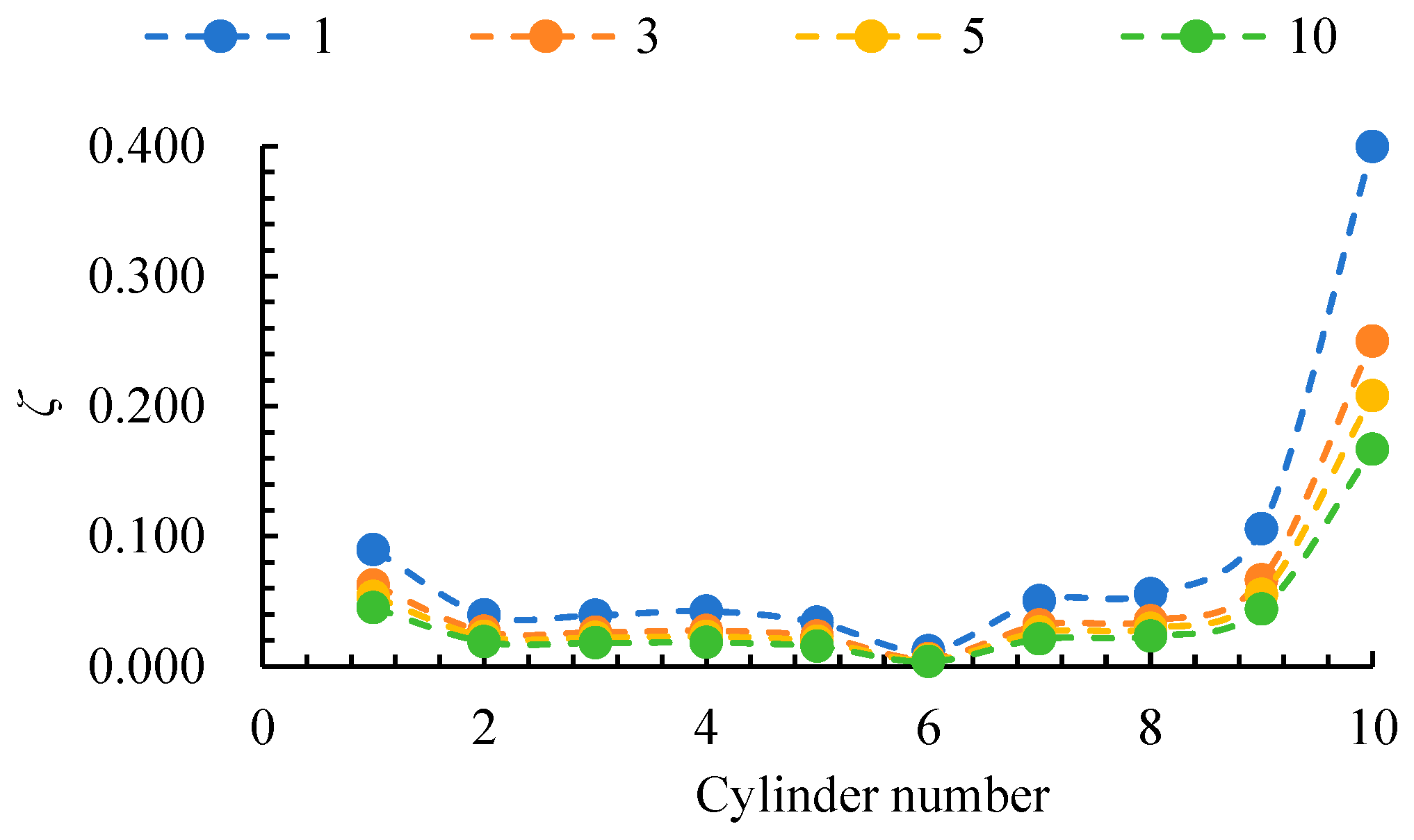
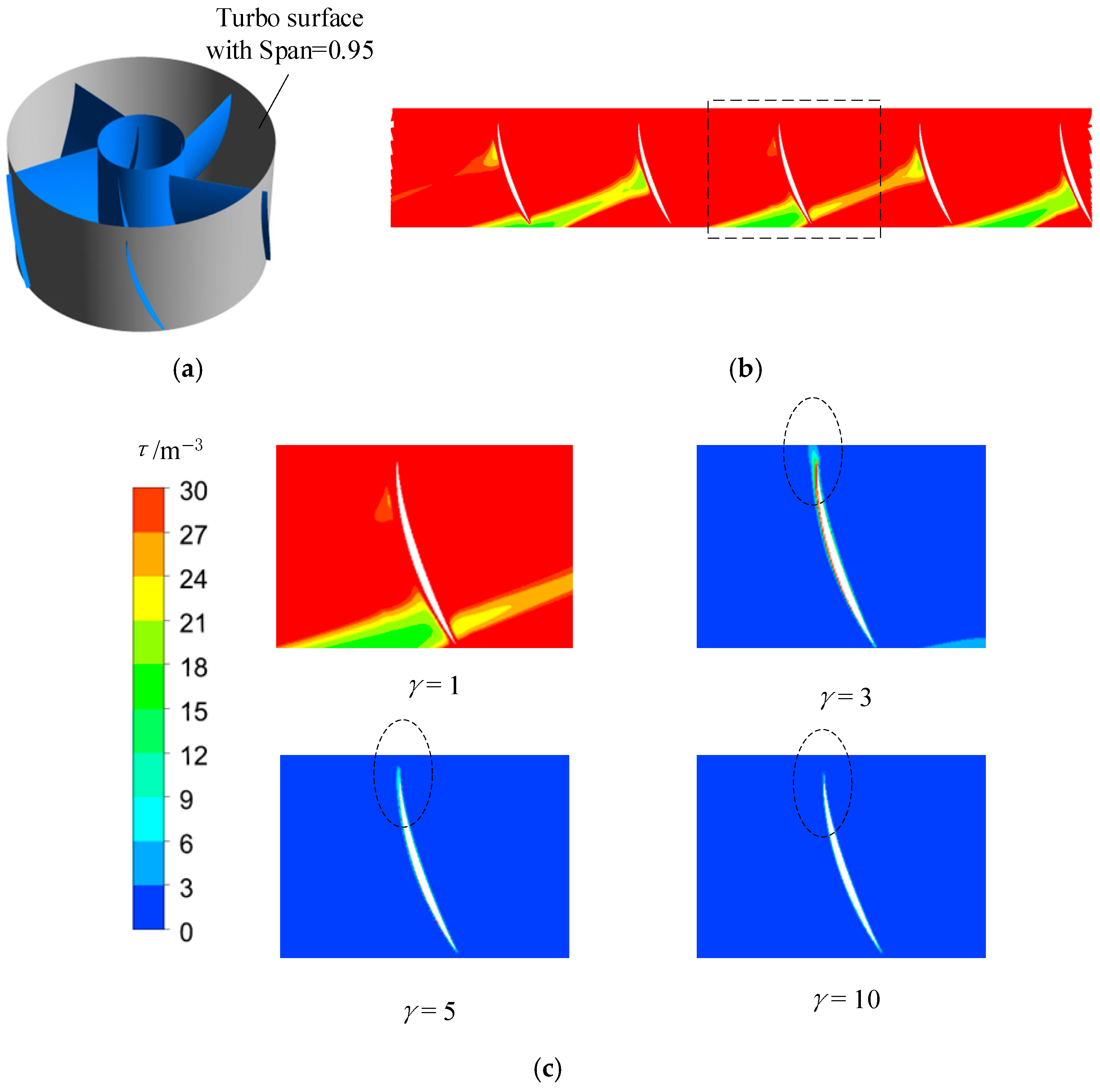
4.3. The Size Effect on Entropy Production Rate
5. Conclusions
- (1)
- The efficiency of axial flow pumps increases with the size ratio, while the head shows a less pronounced upward trend. The efficiency increase is most significant when γ increases from 1 to 5, after which it stabilizes. At 0.8 Qdes, 1.0 Qdes, and 1.15 Qdes, the efficiency for γ = 10 increased by 2.95%, 6.1%, and 17.4%, respectively, compared to γ = 1.
- (2)
- As the size ratio increases, the EPC of all hydraulic components demonstrates a consistent downward trend, with the impeller exhibiting the most pronounced reduction. At the design flow rate, the EPC of the impeller decreased by 55.1% at γ = 10 compared to γ = 1. Furthermore, the EPC inside the impeller increases rapidly in the radial direction from the hub to the rim, with the maximum flow near the rim primarily attributed to tip leakage. Notably, when γ = 10, the EPC near the rim of the impeller decreased by 84.85% compared to γ = 1.
- (3)
- Due to the wall effect, the EPEC near the edges of the impeller and guide vanes is significantly higher. As the size ratio increases, the rotational speed of the impeller decreases, thereby weakening the centrifugal force effect. Consequently, this leads to a sharp reduction in the EPC within the high-EPC regions near the blade leading edge and the guide vane area.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| n | Rotation speed |
| Qdes | Design flow rate |
| ns | Specific rotational speed |
| E | Efficiency |
| H | Head |
| P | Input power |
| T | Temperature |
| Density | |
| Time-averaged entropy production | |
| Fluctuation component of entropy production | |
| Time-averaged velocity components directions of i (x, y, and z) for the Cartesian coordinate system | |
| Velocity fluctuation components in the direction of i (x, y, and z) for the Cartesian coordinate system | |
| Turbulent dissipation rate | |
| Entropy production rate induced by indirect dissipation | |
| Entropy production rate induced by direct dissipation | |
| Overall entropy production | |
| Overall entropy production rate | |
| Entropy production coefficient | |
| Entropy production rate coefficient | |
| URANS | Usteady Reynolds-averaged Navier–Stokes |
| EXP | Experiment |
| CFD | Computational fluid dynamics |
| EPC | Entropy production coefficient |
| EPRC | Entropy production rate coefficient |
References
- Zhang, D.; Shi, W.; Bin, C.; Guan, X. Unsteady flow analysis and experimental investigation of axial-flow pump. J. Hydrodyn. Ser. B 2010, 22, 35–43. [Google Scholar] [CrossRef]
- Shuai, Z.J.; Li, W.Y.; Zhang, X.Y.; Jiang, C.X.; Li, F.C. Numerical study on the characteristics of pressure fluctuations in an axial-flow water pump. Adv. Mech. Eng. 2014, 6, 565061. [Google Scholar] [CrossRef]
- Feng, J.; Luo, X.; Guo, P.; Wu, G. Influence of tip clearance on pressure fluctuations in an axial flow pump. J. Mech. Sci. Technol. 2016, 30, 1603–1610. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, F. Investigation on hydrodynamic characteristics of coastal axial flow pump system model under full working condition of forward rotation based on experiment and CFD method. Ocean Eng. 2022, 253, 111286. [Google Scholar] [CrossRef]
- Kan, N.; Liu, Z.; Shi, G.; Liu, X. Effect of tip clearance on helico-axial flow pump performance at off-design case. Processes 2021, 9, 1653. [Google Scholar] [CrossRef]
- Ge, M.; Petkovšek, M.; Zhang, G.; Jacobs, D.; Coutier-Delgosha, O. Cavitation dynamics and thermodynamic effects at elevated temperatures in a small Venturi channel. Int. J. Heat Mass Transf. 2021, 170, 120970. [Google Scholar] [CrossRef]
- Ge, M.; Manikkam, P.; Ghossein, J.; Subramanian, R.K.; Coutier-Delgosha, O.; Zhang, G. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, A.H.; Wang, Z.N. Fluid Dynamic Characteristics and Flow Distribution Structure Optimization of Axial Piston Pump Considering Cavitation Bubble Evolution. J. Appl. Fluid Mech. 2021, 14, 1603–1616. [Google Scholar]
- Guo, Y.; Yang, C.; Wang, Y.; Lv, T.; Zhao, S. Study on inlet flow field structure and end-wall effect of axial flow pump impeller under design condition. Energies 2022, 15, 4969. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, J.; Wang, L.; Chu, S.; Tang, F.; Jin, Y. Comparative analysis of strength and modal characteristics of a full tubular pump and an axial flow pump impellers based on fluid-structure interaction. Energies 2021, 14, 6395. [Google Scholar] [CrossRef]
- Shi, L.; Yuan, Y.; Jiao, H.; Tang, F.; Cheng, L.; Yang, F.; Jin, Y.; Zhu, J. Numerical investigation and experiment on pressure pulsation characteristics in a full tubular pump. Renew. Energy 2021, 163, 987–1000. [Google Scholar] [CrossRef]
- Jiao, H.; Shan, J.; Yang, G.; Wang, M.; Chen, S. Comparison of the shutdown transitions of the full-flow pump and axial-flow pump. J. Mar. Sci. Eng. 2023, 11, 2129. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Entropy production calculation for turbulent shear flows and their implementation in CFD codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]
- Herwig, H.; Kock, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Liu, H.; Mao, Y.; Wang, Y.; Wang, X.; Jiang, L.; Li, M. Energy characteristic of cavitation in a centrifugal pump based on entropy generation analysis. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 609. [Google Scholar] [CrossRef]
- Pei, J.; Shen, J.; Wang, W.; Yuan, S.; Zhao, J. Evaluating hydraulic dissipation in a reversible mixed-flow pump for micro-pumped hydro storage based on entropy production theory. Renew. Energy 2024, 225, 120271. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Y.; Liang, J.; Chen, P.; Zhang, Y.; Yang, C. Numerical investigation of the vorticity transportation and energy dissipation in a variable speed pump-turbine. J. Energy Storage 2024, 93, 112392. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Liu, H.; Xiao, Y.; Jiang, L.; Li, M. A numerical investigation on energy characteristics of centrifugal pump for cavitation flow using entropy production theory. Int. J. Heat Mass Transf. 2023, 201, 123591. [Google Scholar] [CrossRef]
- Yang, F.; Li, Z.; Hu, W.; Liu, C.; Jiang, D.; Liu, D.; Nasr, A. Analysis of flow loss characteristics of slanted axial-flow pump device based on entropy production theory. R. Soc. Open Sci. 2022, 9, 211208. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, F. Energy loss evaluation of axial flow pump systems in reverse power generation operations based on entropy production theory. Sci. Rep. 2022, 12, 8667. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lin, Q.; Meng, F.; Zheng, Y.; Xu, X. Research on the influence of tip clearance of axial-flow pump on energy characteristics under pump and turbine conditions. Machines 2022, 10, 56. [Google Scholar] [CrossRef]
- Yu, L.; Cheng, L.; Xu, W.; Lei, S. Study on the Influence of Tip Clearance on Cavitation Performance and Entropy Production of an Axial Flow Pump. J. Mar. Sci. Eng. 2024, 12, 101. [Google Scholar] [CrossRef]
- Miao, S.; Tan, X.; Luo, W.; Wang, X.; Yang, J. The mechanism of internal energy losses in double-suction centrifugal pumps under direct and reverse conditions. Energy 2024, 306, 132547. [Google Scholar] [CrossRef]
- Xu, R.; Long, Y.; Wang, D. Effects of rotating speed on the unsteady pressure pulsation of reactor coolant pumps with steam-generator simulator. Nucl. Eng. Des. 2018, 333, 25–44. [Google Scholar] [CrossRef]
- Luo, X.; Ye, W.; Huang, R.; Wang, Y.; Du, T.; Huang, C. Numerical investigations of the energy performance and pressure fluctuations for a waterjet pump in a non-uniform inflow. Renew. Energy 2020, 153, 1042–1052. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Yin, G.; Guan, C. Fluid–structure interaction analysis of fluid pressure pulsation and structural vibration features in a vertical axial pump. Adv. Mech. Eng. 2019, 11, 1687814019828585. [Google Scholar] [CrossRef]
- Yang, F.; Chang, P.; Hu, W.; Mao, B.; Liu, C.; Li, Z. Numerical Study on Pressure Pulsation in a Slanted Axial-Flow Pump Device under Partial Loads. Processes 2021, 9, 1404. [Google Scholar] [CrossRef]
- Meng, F.; Li, Y.; Chen, J. Investigation of energy losses induced by non-uniform inflow in a coastal axial-flow pump. J. Mar. Sci. Eng. 2022, 10, 1283. [Google Scholar] [CrossRef]
- Meng, F.; Qin, Z.; Li, Y.; Chen, J. Investigation of transient characteristics of a vertical axial-flow pump with non-uniform suction flow. Machines 2022, 10, 855. [Google Scholar] [CrossRef]


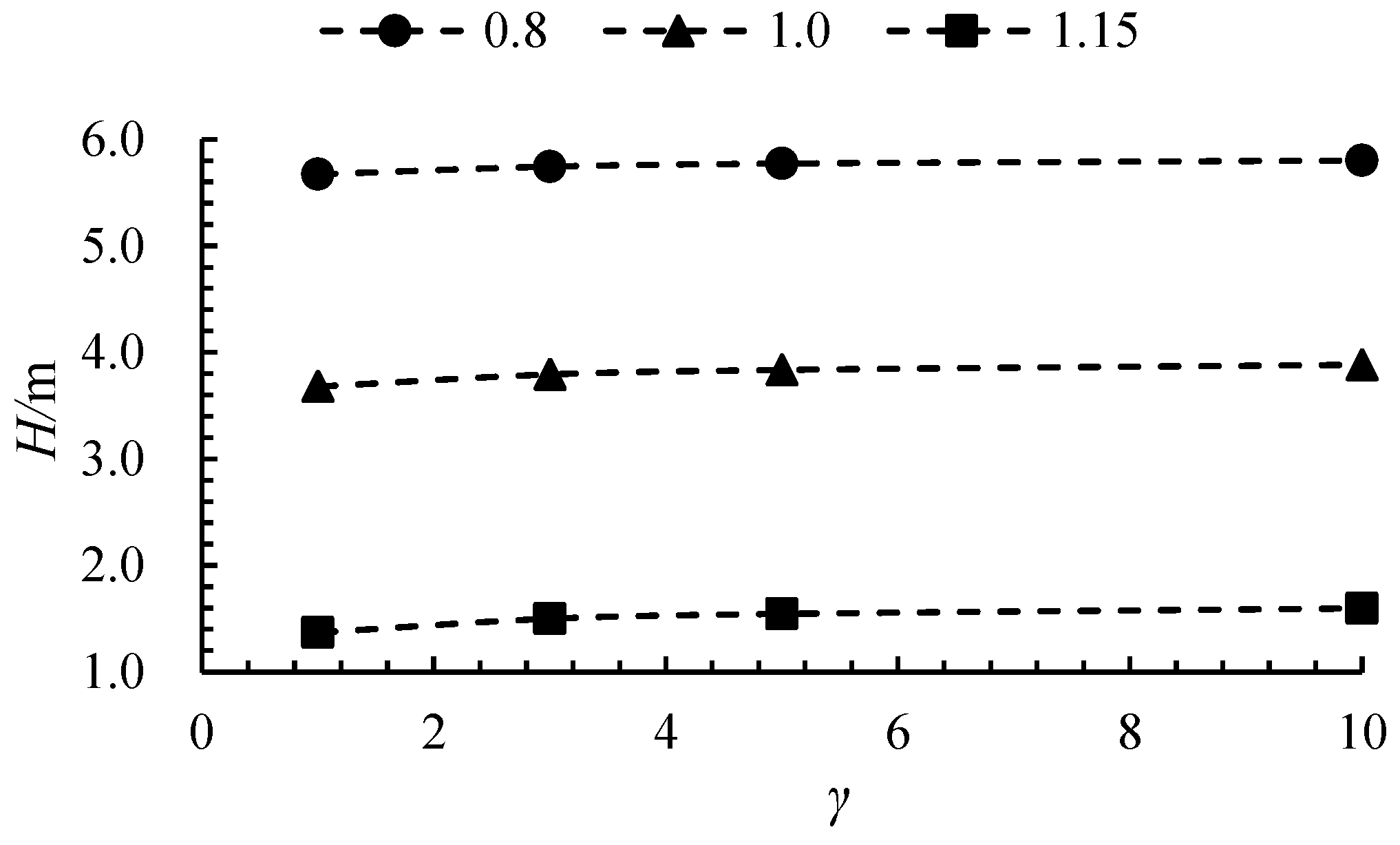
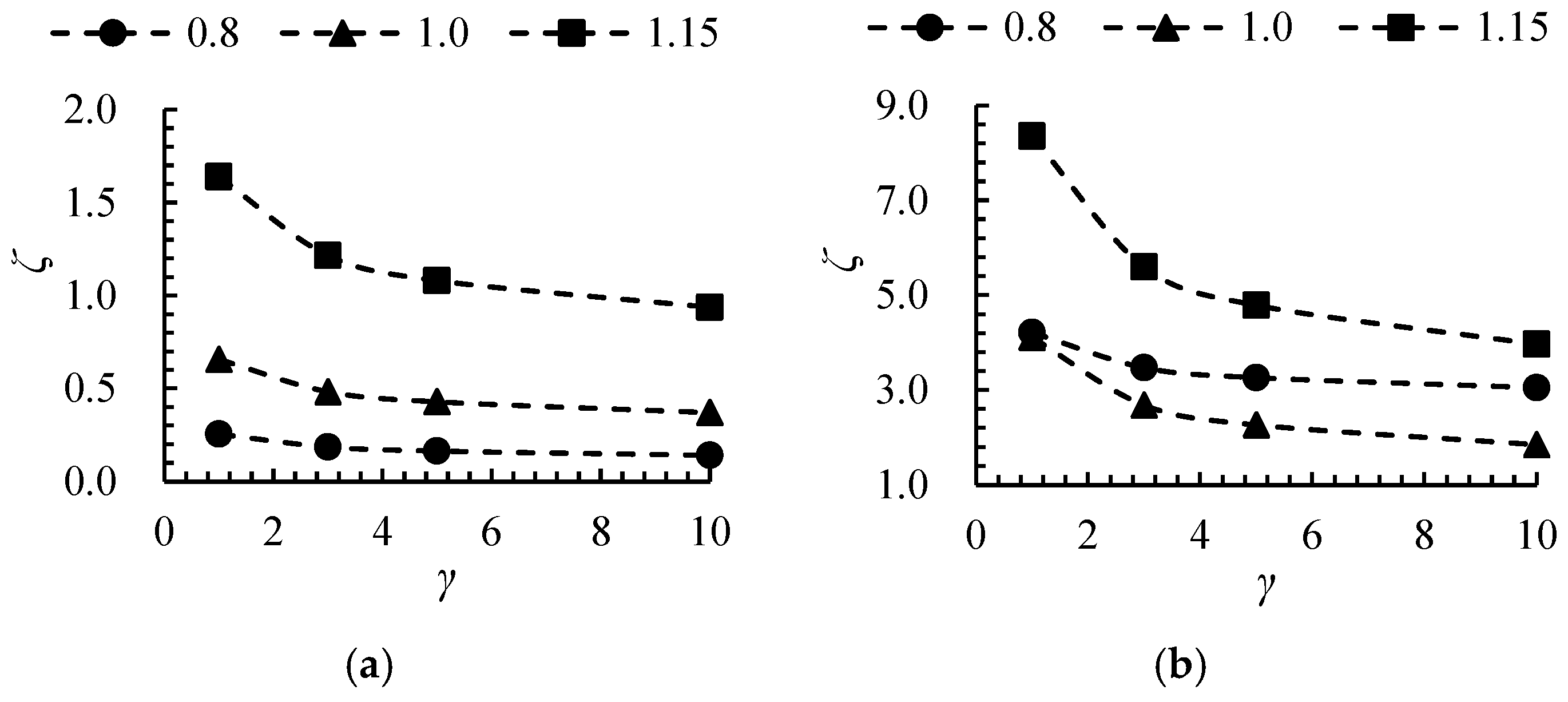
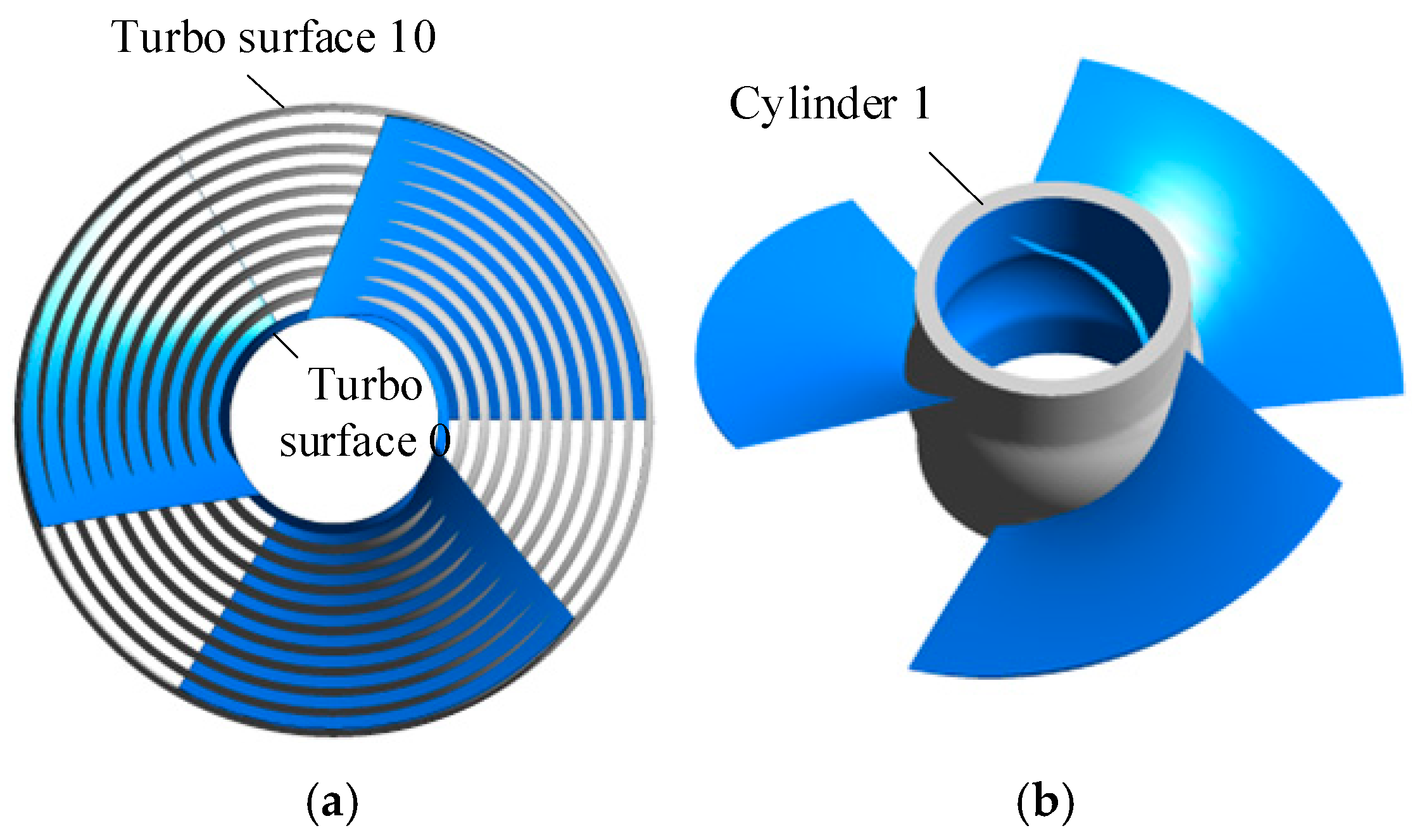

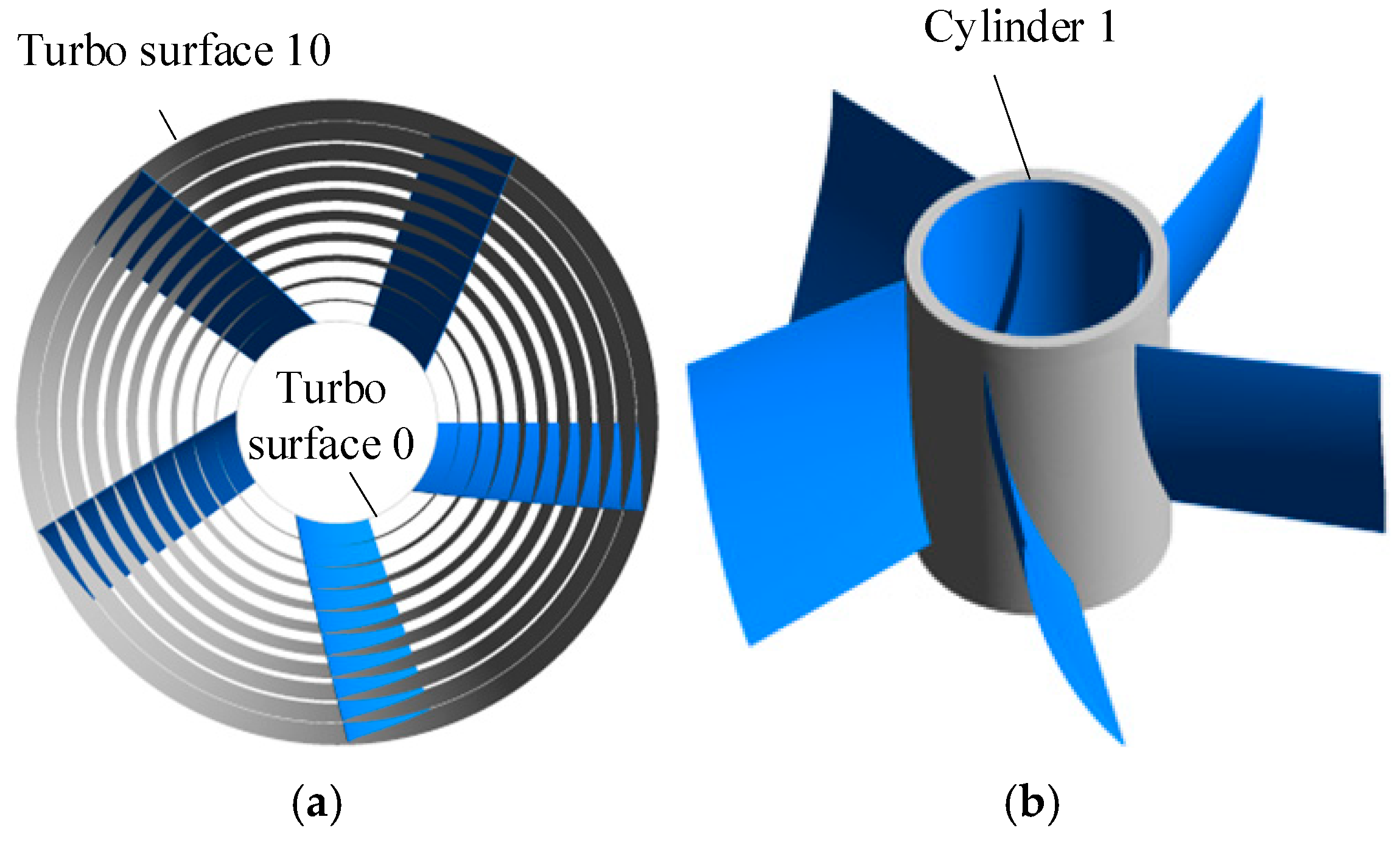

| Scheme 1 (Original Scheme) | Scheme 2 | Scheme 3 | Scheme 4 | |
|---|---|---|---|---|
| Size ratio γ | 1 | 3 | 5 | 10 |
| Qdes/(L·s−1) | 350 | 3150 | 8750 | 35,000 |
| n/(r·min−1) | 1450 | 483.3 | 290 | 145 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wu, X.; Xu, X.; Bian, S.; Meng, F. Size Effect on Energy Characteristics of Axial Flow Pump Based on Entropy Production Theory. Machines 2025, 13, 252. https://doi.org/10.3390/machines13030252
Wang H, Wu X, Xu X, Bian S, Meng F. Size Effect on Energy Characteristics of Axial Flow Pump Based on Entropy Production Theory. Machines. 2025; 13(3):252. https://doi.org/10.3390/machines13030252
Chicago/Turabian StyleWang, Hongliang, Xiaofeng Wu, Xiao Xu, Suhao Bian, and Fan Meng. 2025. "Size Effect on Energy Characteristics of Axial Flow Pump Based on Entropy Production Theory" Machines 13, no. 3: 252. https://doi.org/10.3390/machines13030252
APA StyleWang, H., Wu, X., Xu, X., Bian, S., & Meng, F. (2025). Size Effect on Energy Characteristics of Axial Flow Pump Based on Entropy Production Theory. Machines, 13(3), 252. https://doi.org/10.3390/machines13030252





