The Space Phasors Theory and the Conditions for the Correct Decoupling of Multiphase Machines
Abstract
1. Introduction
2. On the Incorrect Statements as to the Method to Obtain Complete Dynamic Decoupling of Multiphase Machines with Space Harmonics in the General Case
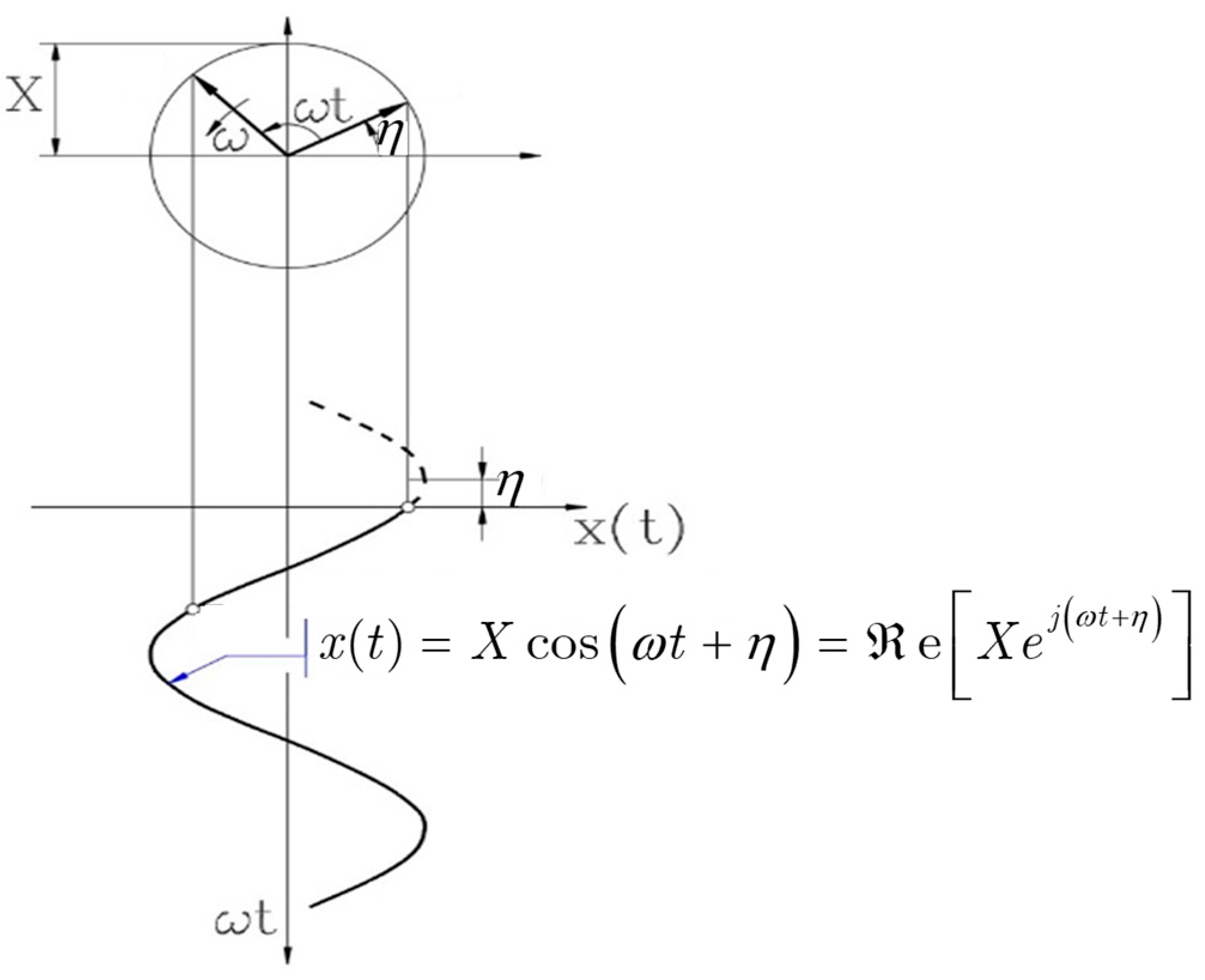
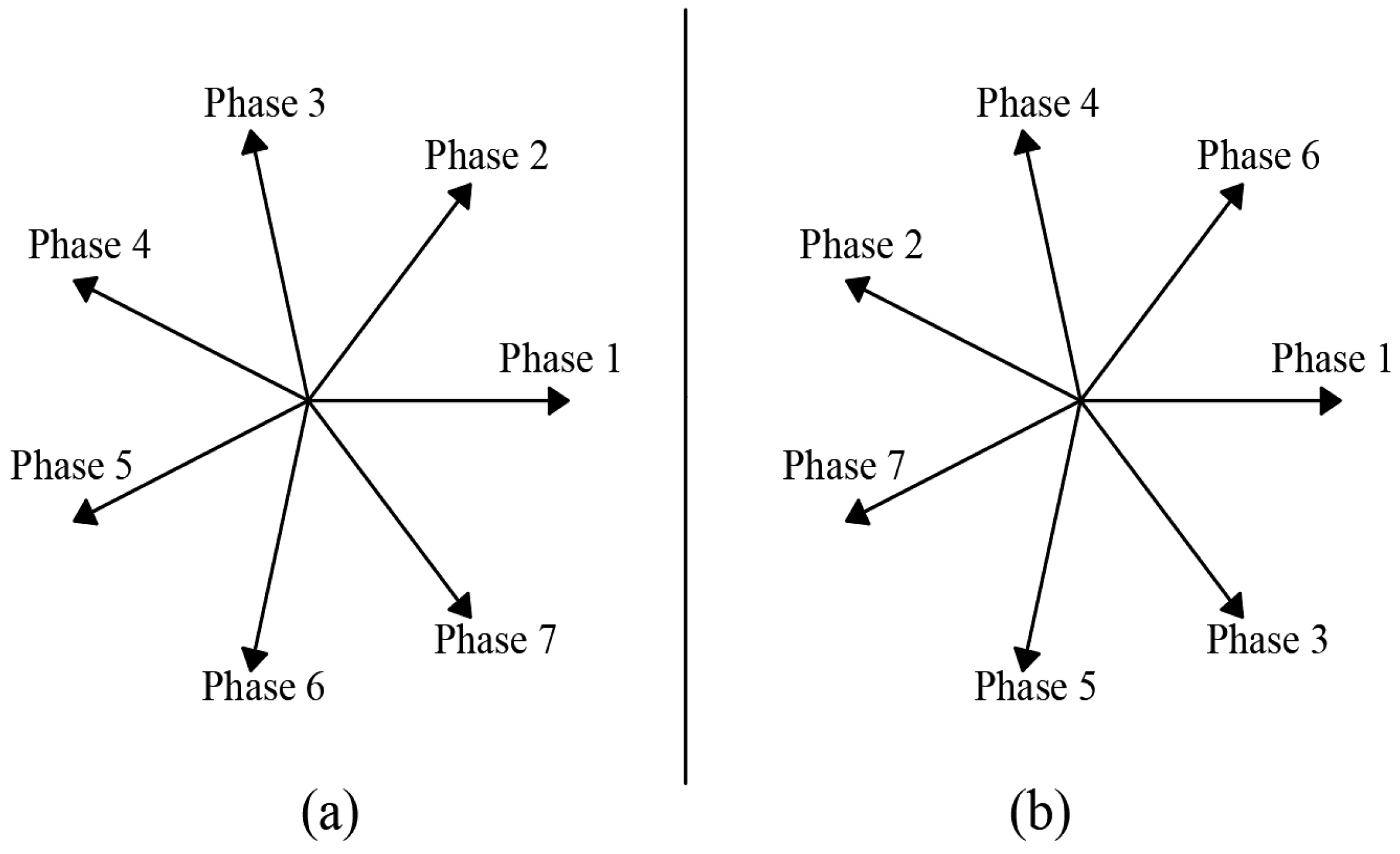
3. Definition of a Dynamic m-Phase System of g Sequence—Extending the Concept of Kapp’s Time Phasor to Dynamic States of m-Phase Systems
4. Dynamic Time Phasors of Symmetrical Multiphase Systems with Arbitrary Currents
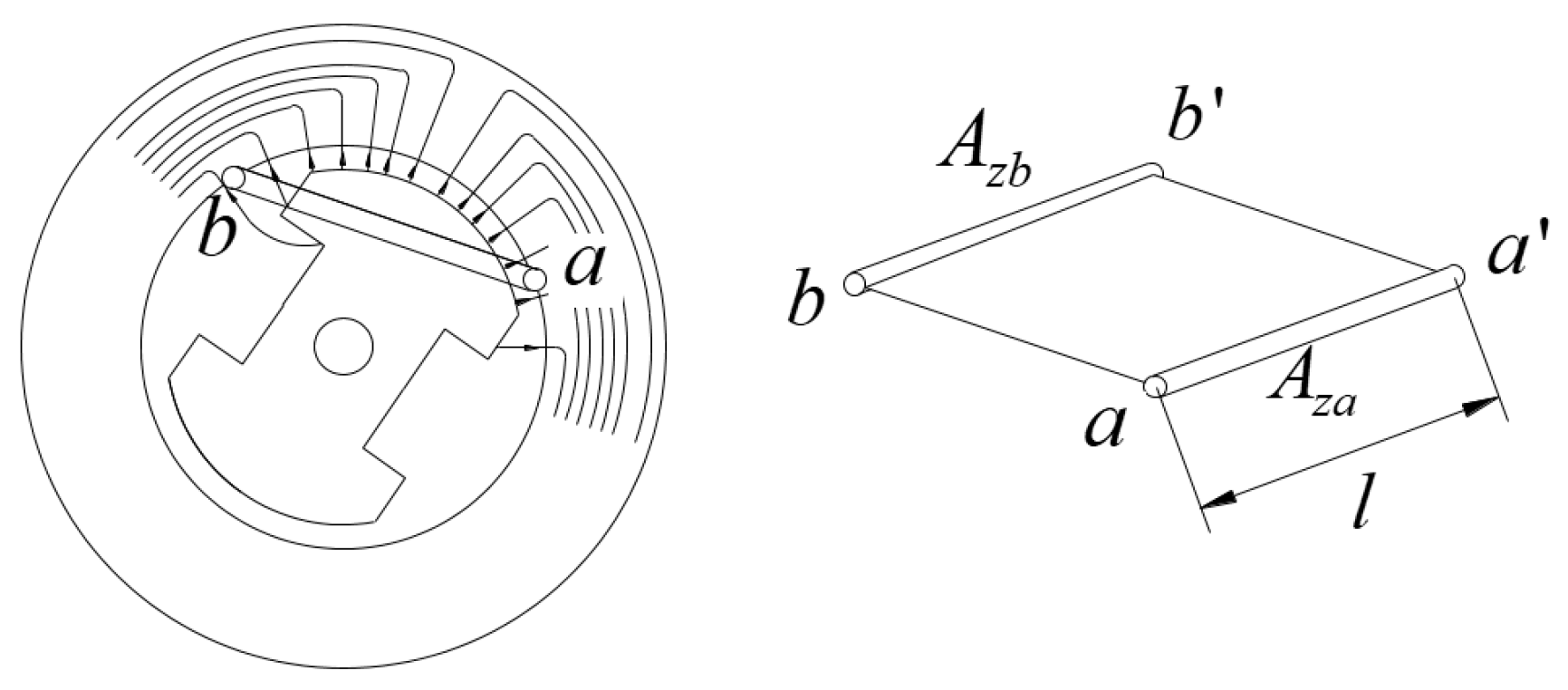
5. The Hard Core of the Space Phasors Theory and the Essential Ψ and U Space Phasors
- Be the most important and dominant ones.
- Be characterized by dynamic space phasors.
- Be easily correlated with their corresponding machine time phase quantities.
6. Untangling the Intricate Structure of the Multiphase Machine
- (a)
- For a three-phase machine, there is only one space phasor U in the stator (all of the corresponding harmonic space waves belong to the same group, h = 3q ± 1 with h odd) and one in the rotor. The same applies to the Ψ and I effective space phasors. These two (U,Ψ, I) triads fully describe the machine behavior.
- (b)
- Each of the (m − 1)/2 U space phasors in the stator (or rotor) characterize an effective voltage space wave in the stator (or rotor). More precisely, they synthesize through an equivalent wave the contribution to the voltages of the stator (or rotor) phases due to a specific group of electric potential difference space waves existing in the stator (or in rotor). Analogous considerations apply to the Ψ and I space phasors.
- (c)
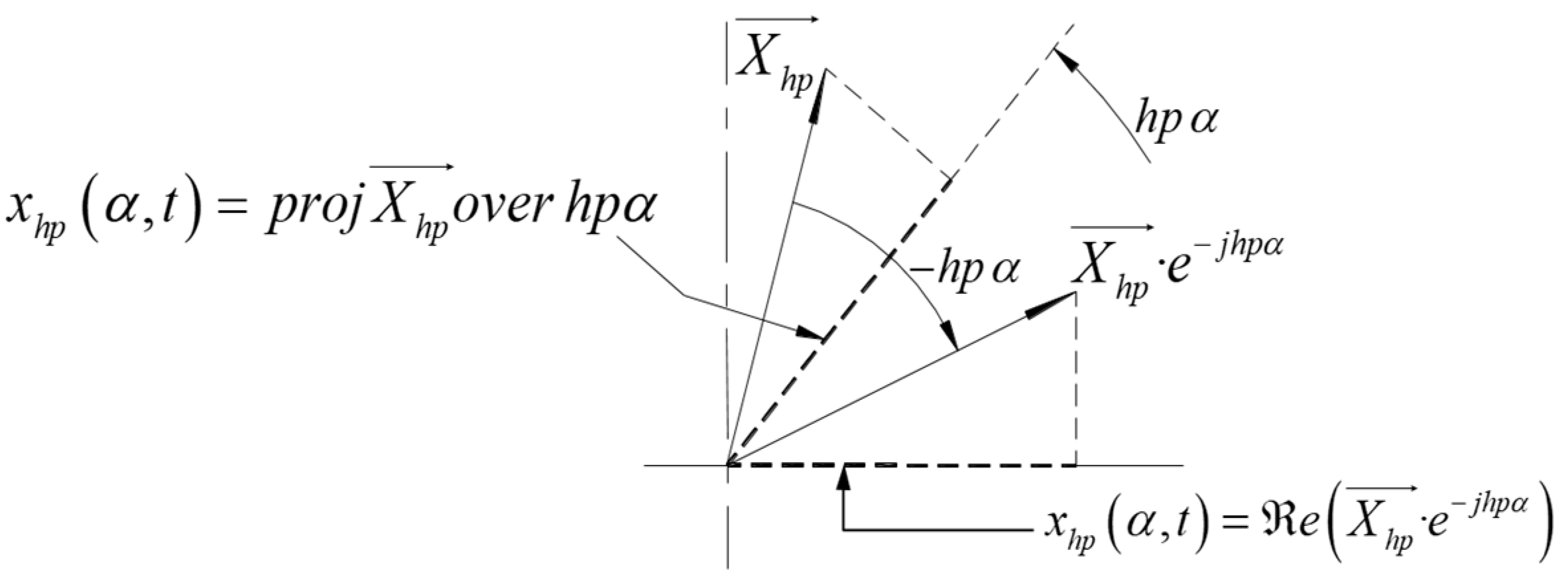
- The mentioned total contribution to a phase of any of the wave groups is obtained through a very simple procedure: by projecting its effective space phasor onto the phase axis.
- (d)
- Each one of the independent groups of space waves in stator, together with its homologous group in rotor, can be associated with a fictitious machine which, therefore, has one only set of phasors (U,Ψ,I) in the stator and one in the rotor, just as in three-phase machines.
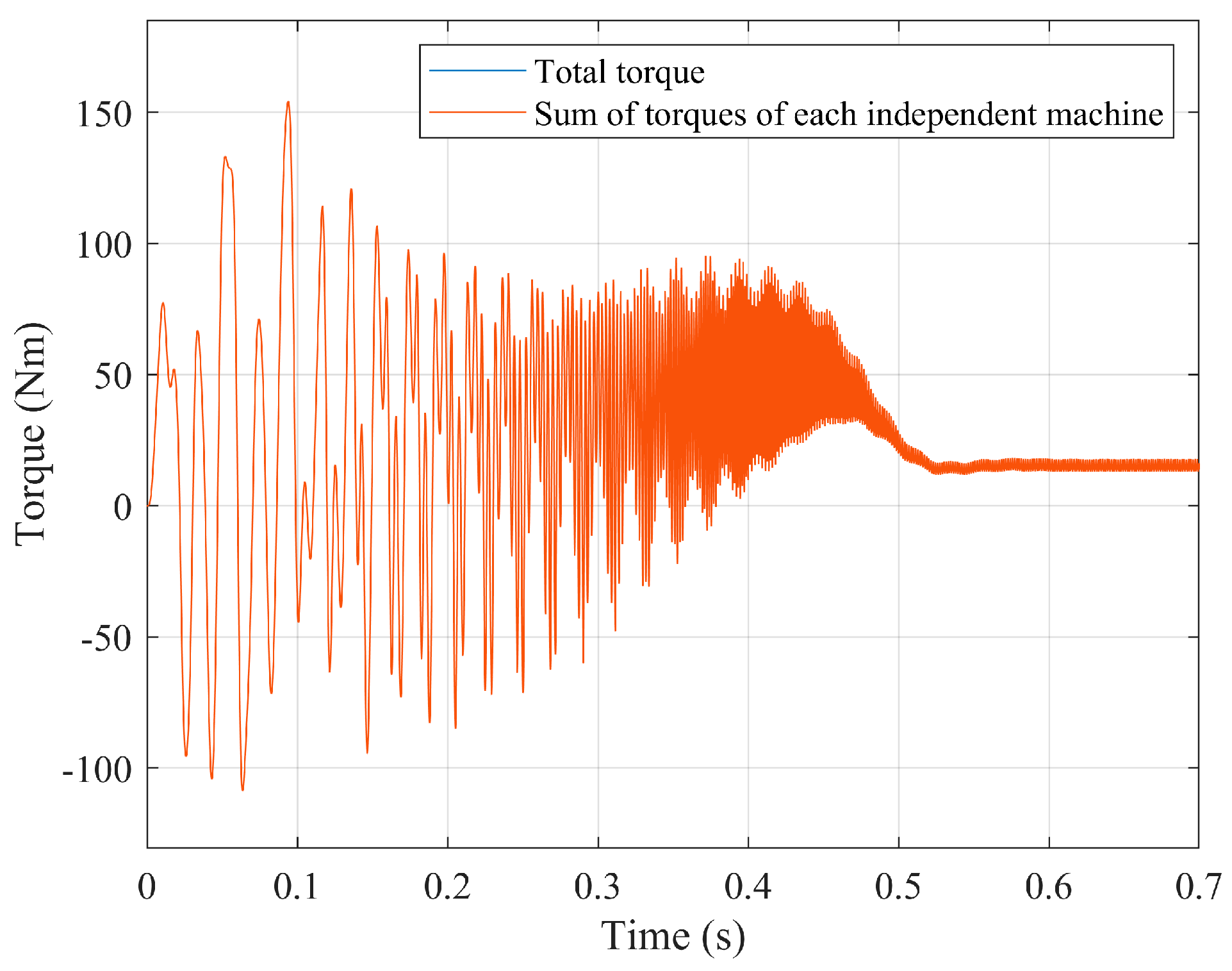
7. Establishing and Verifying the Decoupling Conditions for Constant Air-Gap Multiphase Machines with Space Harmonics
7.1. Precise Decoupling
7.2. Approximate Decoupling Within a Narrow Working Region—Equations of the Multiphase Machine
- (a)
- Space phasors provide a deep physical insight into the machine’s behavior. This enables us to “untangle” its complex structure, and it is just this previous knowledge that allows us to directly write the equations of the machine with space harmonics as the ones of a set of electrically independent machines. Without this knowledge, the machine has to be analyzed as a single global system with a very intricate structure.
- (b)
- The very powerful step from (22) to Equations (23) and (24) is extremely simple and straightforward.
- (a)
- In line with Feynman’s ideas, the space phasors Ψ that appear in (31) are, by far, the most important ones, especially for control studies. In fact, virtually all schemes for very-high-precision torque control are based on them, as commented on in [2].
- (b)
- Ψstr can be easily obtained online by measuring the stator voltages and currents. Indeed, from the general Equation (24), it follows that
8. Conclusions
- (a)
- Always have a clear physical meaning and are not just mere mathematical tools, as usually introduced in the literature.
- (b)
- Easily correlate the machine space waves and their homologous time quantities.
- (c)
- Provide a deep physical insight into the intricate machine structure and how to untangle it.
- (a)
- Introducing and explaining the key concept of a DmPhS of g sequence and its dynamic time phasor, which represents a powerful extension, mathematically and graphically, of the Kapp’s time phasor, which is valid only for sinusoidal steady states and does not include the concept of g sequence.
- (b)
- Presenting an extensive historical and critical review of the ISCs, which makes clear their close relationship to the SPhTh and their two deep physical meanings: (1) They symbolize the linear current density, the electric potential difference, and the magnetic vector potential space waves in the m-phase machine (electric machines viewpoint). (2) They are the set of dynamic time phasors that decouple and fully describe, mathematically and graphically, the time evolution, in the most general case, of the phase quantities in an m-phase symmetrical winding (electric circuits viewpoint).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. On the Space Phasors Theory and Its Relationship to the Park, Clarke, and Instantaneous Symmetrical Components Transformations
- (a)
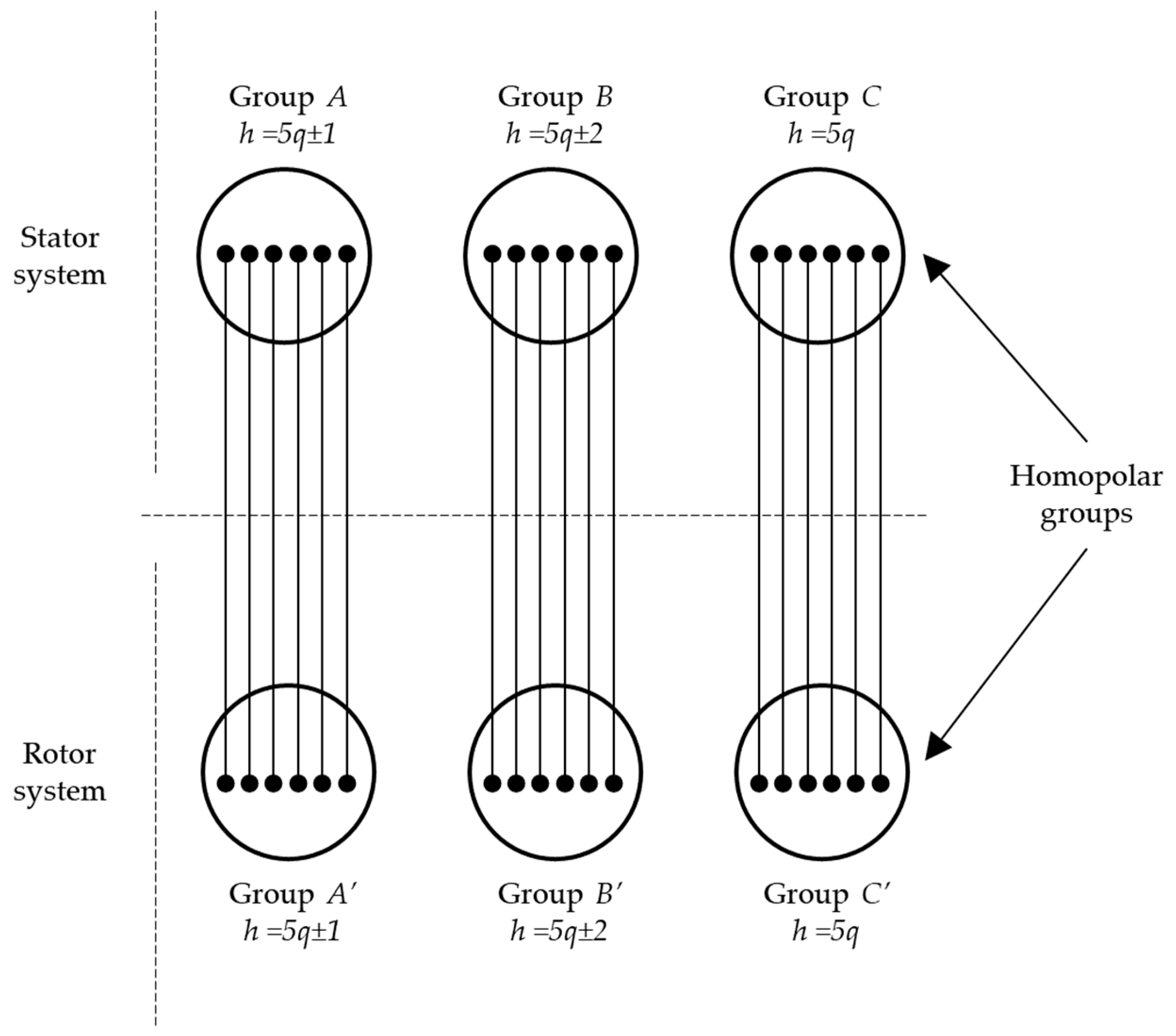
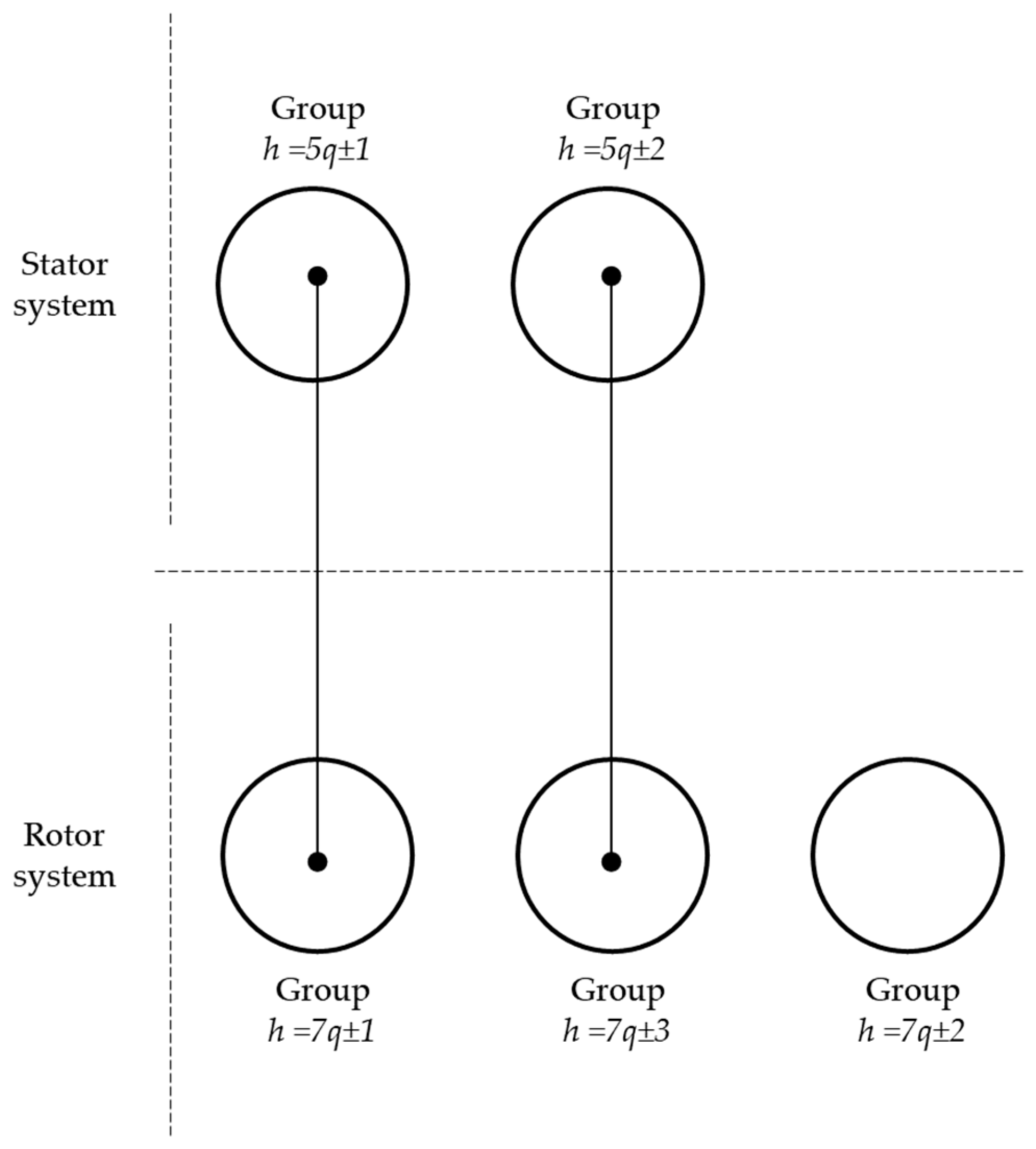
- If mstr = mrot, the machine can be decoupled by means of independent groups of space waves (Figure 6)
- (b)
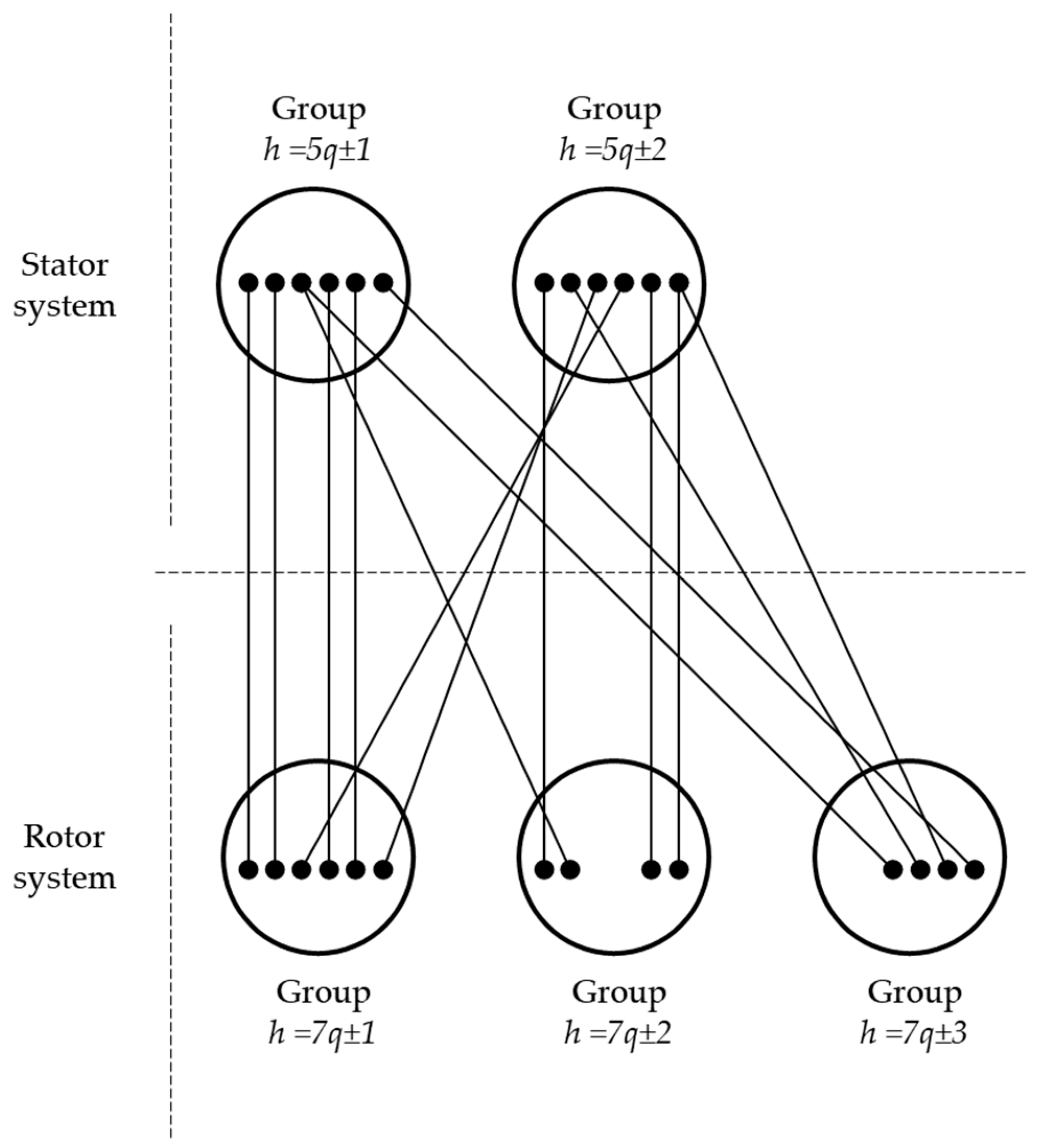
- If mstr ≠ mrot, the machine decoupling is not possible because of the cross-coupling between harrmonic groups (Figure 7).
- (c)
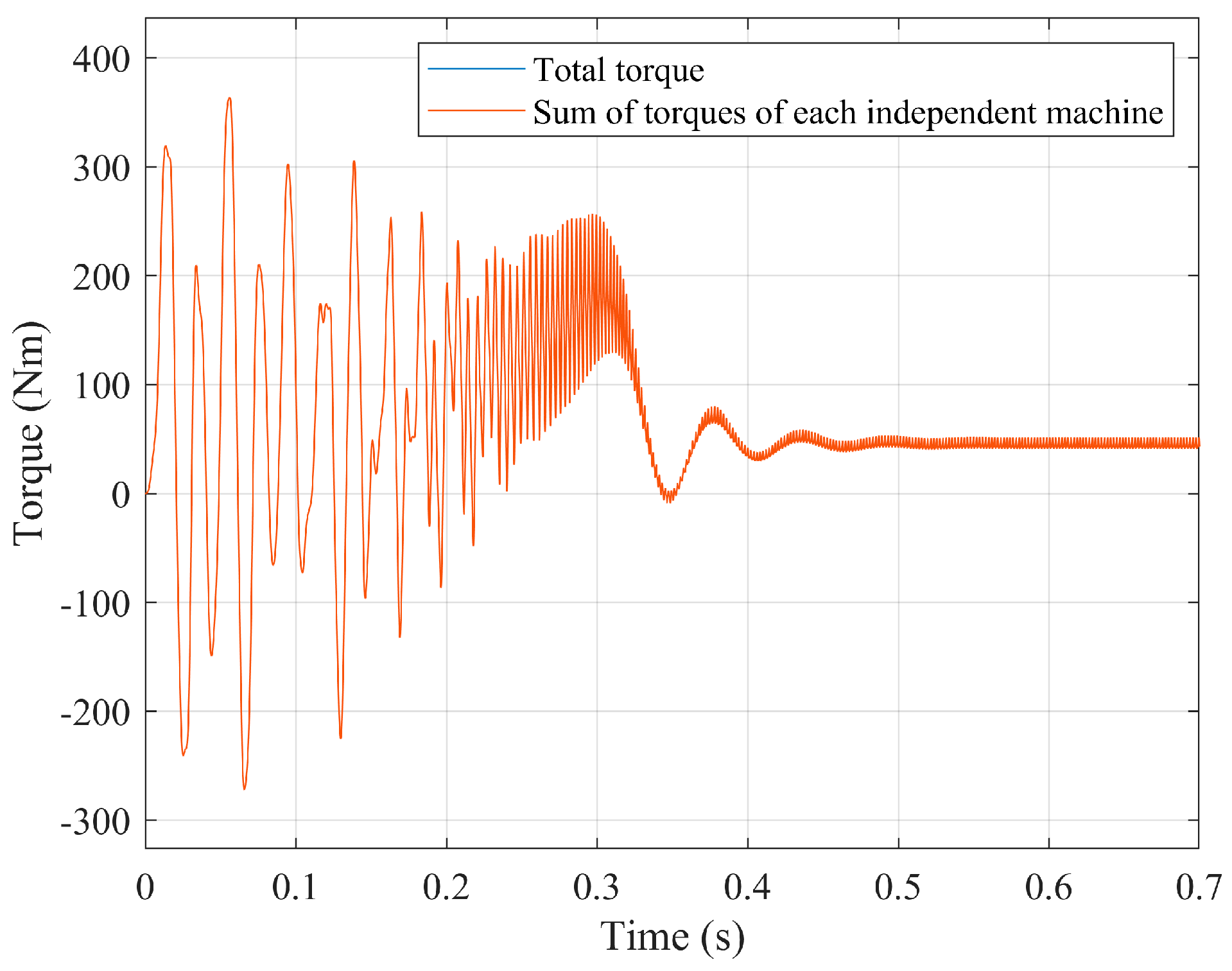
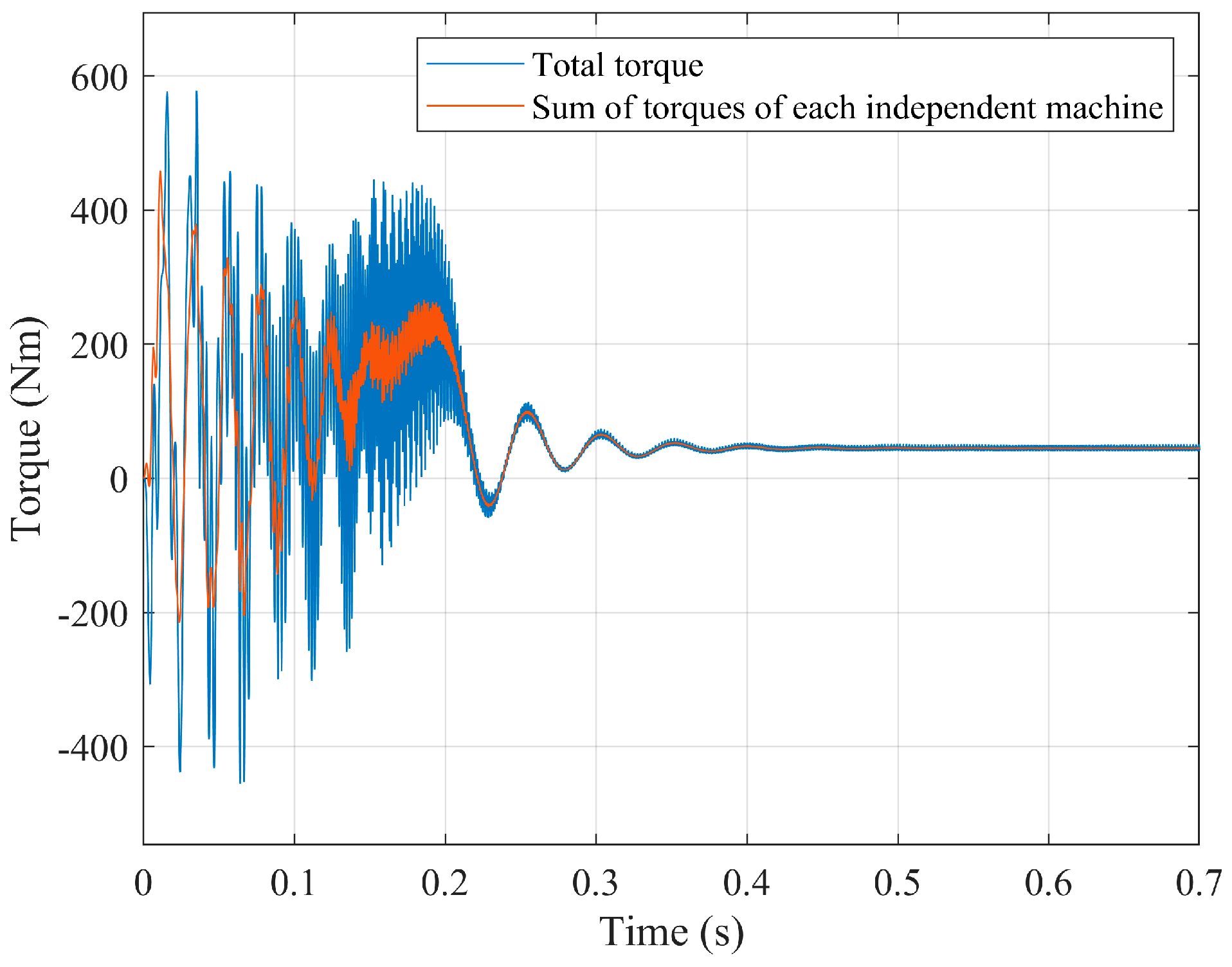
- If the machine working region is restricted to the narrow region of very small slips (e.g., converter-controlled machines), it is possible a practical and approxi-mate machine decoupling even if mstr ≠ mrot (Figure 12).
Appendix B
| Stator | |||
| Rotor |
| Stator | |||
| Rotor | |||
References
- Serrano-Iribarnegaray, L.; Bonet-Jara, J. Physical Meaning of the Multiphase Instantaneous Symmetrical Components and Their Relation to the Space Phasor Theory. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 334–340. [Google Scholar]
- Serrano-Iribarnegaray, L. Space phasor theory and control of multiphase machines through their decoupling into equivalent 3-phase machines. Electr. Eng. (Former Arch. Für Elektrotechnik) 2014, 96, 79–94. [Google Scholar] [CrossRef]
- Fortescue, C.L. Method of symmetrical co-ordinates applied to the solution of polyphase networks. Trans. Am. Inst. Electr. Eng. 1918, 37, 1027–1140. [Google Scholar] [CrossRef]
- Lyon, W.V. Transient Analysis of Alternating-Current Machinery; Technology Press: Cambridge, UK; John Wiley: New York, NY, USA, 1954. [Google Scholar]
- Klima, V. Symmetrische Komponenten, ihr Zusammenang mit trigonometrischer Interpolation, Fourierschen Reihen und Vektorkomponenten. Elektrotech. Maschinenbau 1967, 84, 354–365. [Google Scholar]
- Hochrainer, A. Symmetrische Komponenten in Drehstromsystemen; Springer: Berlin/Heidelberg, Germany, 1957. [Google Scholar]
- White, D.C.; Woodson, H.H. Electromechanical Energy Conversion; John Wiley & Sons: New York, NY, USA, 1959. [Google Scholar]
- Kovács, K.P. Symmetrische Komponenten der Momentanwerte, oder Vektoren der elektrische Grössen? Arch. Für Elek. 1960, 45, 99–117. [Google Scholar] [CrossRef]
- Kovacs, K.P.; Racz, I. Transiente Vorgänge in Wechselstrom-Maschinen; Akademiai Kiado: Budapest, Hungary, 1959. [Google Scholar]
- Park, R.H. Two-Reaction theory of synchronous machines-2. Trans. Am. Inst. Electr. Eng. 1933, 52, 352–355. [Google Scholar] [CrossRef]
- Stepina, J. Die Einzelwellen der Felderregerkurve bei unsymme-trischen Asynchronmaschinen. Arch. Für Elek. 1958, 43, 384–402. [Google Scholar] [CrossRef]
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase induction motor drives—A technology status review. IET Electric. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef]
- Jones, M.; Levi, E.; Vukosavic, S.N.; Toliyat, H.A. A novel nine-phase four-motor drive system with completely decoupled dynamic control. In Proceedings of the IECON’03. 29th Annual Conference of the IEEE Industrial Electronics Society, Roanoke, VA, USA, 2–6 November 2003; Volume 1, pp. 637–642. [Google Scholar]
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Kapp, G. Induction Coils Graphically Treated. Electrician 1887, 18, 502–504, 524–525, 568–571. [Google Scholar]
- Feynman, R.; Leighton, R.; Sands, M. The Feynman lectures on physics. In VOL II. Reading; Addison-Wesley: Boston, MA, USA, 1964. [Google Scholar]
- Simonyi. Theoretische Elektrotechnik; VEB: Berlin, Germany, 1977. [Google Scholar]
- Semail, E.; Bouscayrol, A.; Hautier, J.P. Vectorial formalism for analysis and design of polyphase synchronous machines. Eur. Phys. J. Appl. Phys. 2023, 22, 207–220. [Google Scholar] [CrossRef]
- Bonet-Jara, J.; Morinigo-Sotelo, D.; Duque-Perez, O.; Serrano-Iribarnegaray, L.; Pons-Llinares, J. End-Ring Wear in Deep-Well Submersible Motor Pumps. IEEE Trans. Ind. Appl. 2022, 58, 4522–4531. [Google Scholar] [CrossRef]
- Echeverría-Villar, J.A.; Martínez-Román, J.; Serrano-Iribarnegaray, L. Transient harmonic torques in induction machines: Measurement and impact on motor performance. Electr. Eng. 2012, 94, 67–80. [Google Scholar] [CrossRef]
- Kleinrath, H. Stromrichter Gespeiste Drehfeldmaschinen; Springer: Wien, Austria, 1980. [Google Scholar]
- Figueroa, J.; Cros, J.; Viarouge, P. Generalized transformations for polyphase phase-Modulation motors. IEEE Trans. Energy Convers. 2006, 21, 332–341. [Google Scholar] [CrossRef]
- O’Rourke, C.J.; Qasim, M.M.; Overlin, M.R.; Kirtley, J.L. A Geometric Interpretation of Reference Frames and Transformations: dq0, Clarke, and Park. IEEE Trans. Energy Convers. 2019, 34, 2070–2083. [Google Scholar] [CrossRef]
- Stepina, J. Raumzeiger als Grundlage der Theorie del elektrischen Maschinen. ETZ-A 1967, 88, 584–588. [Google Scholar]
- Zhao, Y.; Lipo, T.A. Space vector PWM control of dual three-phase induction machine using vector space decomposition. IEEE Trans. Ind. Appl. 1995, 31, 1100–1109. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serrano-Iribarnegaray, L.; Bonet-Jara, J. The Space Phasors Theory and the Conditions for the Correct Decoupling of Multiphase Machines. Machines 2025, 13, 107. https://doi.org/10.3390/machines13020107
Serrano-Iribarnegaray L, Bonet-Jara J. The Space Phasors Theory and the Conditions for the Correct Decoupling of Multiphase Machines. Machines. 2025; 13(2):107. https://doi.org/10.3390/machines13020107
Chicago/Turabian StyleSerrano-Iribarnegaray, Luis, and Jorge Bonet-Jara. 2025. "The Space Phasors Theory and the Conditions for the Correct Decoupling of Multiphase Machines" Machines 13, no. 2: 107. https://doi.org/10.3390/machines13020107
APA StyleSerrano-Iribarnegaray, L., & Bonet-Jara, J. (2025). The Space Phasors Theory and the Conditions for the Correct Decoupling of Multiphase Machines. Machines, 13(2), 107. https://doi.org/10.3390/machines13020107






