Enhancing Spraying Performance with Active Stability Control in Multi-Link Mechanisms
Abstract
1. Introduction
2. Materials and Methods
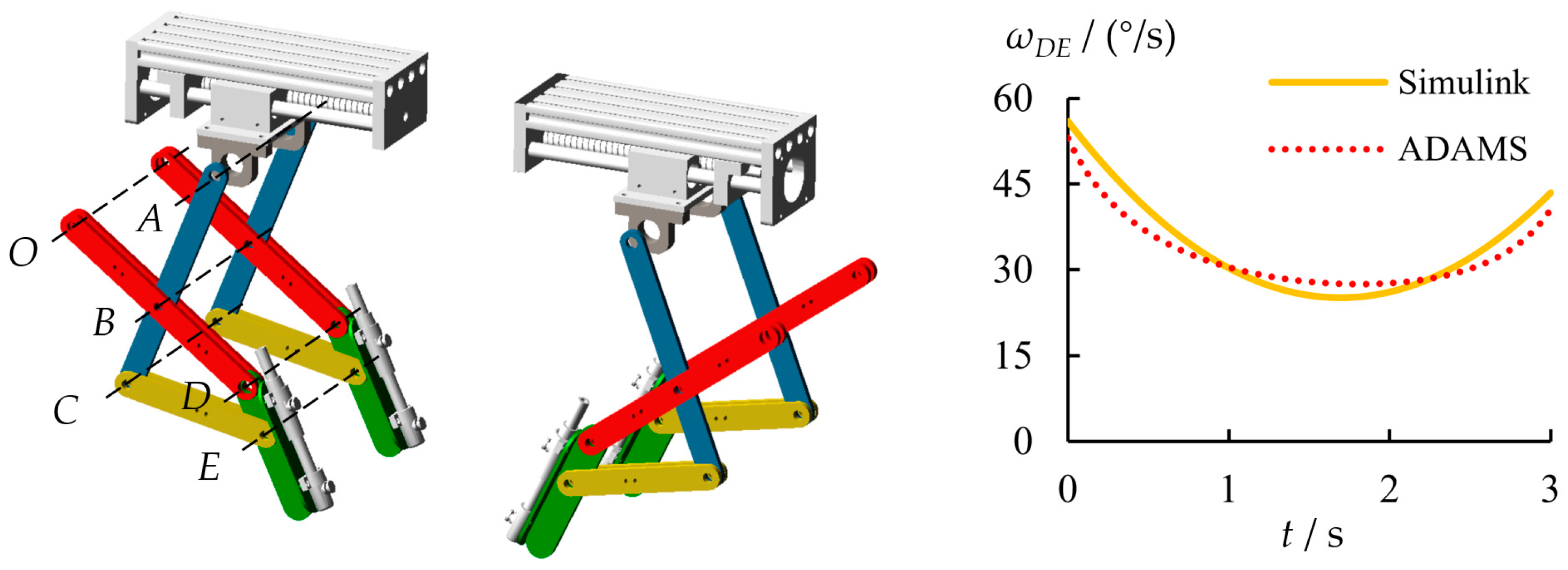
2.1. Structure and Principle of Multi-Link Spraying Machine
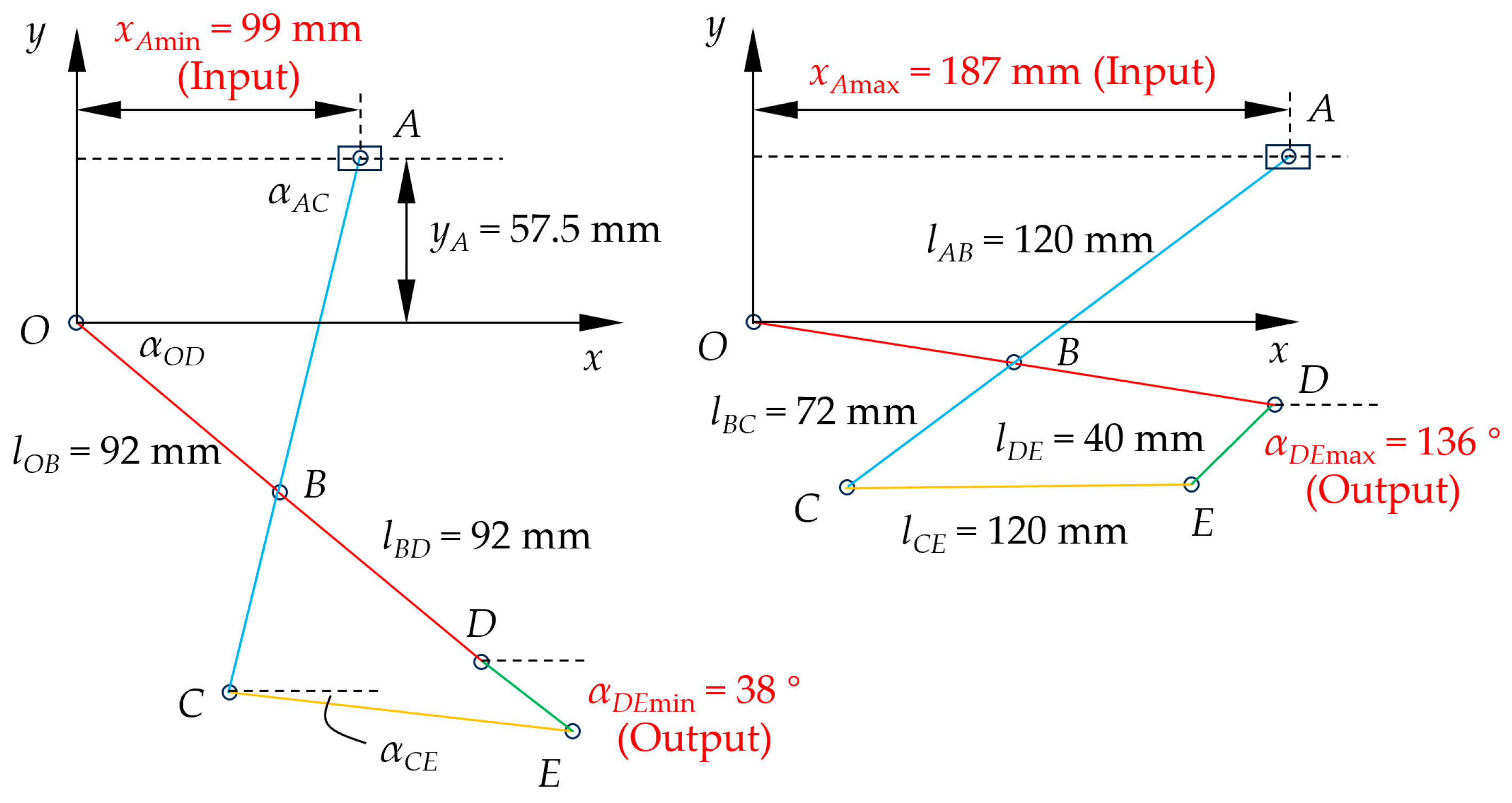
2.2. Modeling and Analysis of Linkage Mechanism
2.3. Establishing Explicit Function Equations and Curve Fitting
2.4. Verification of Consistency Between Simulink and Adams Models
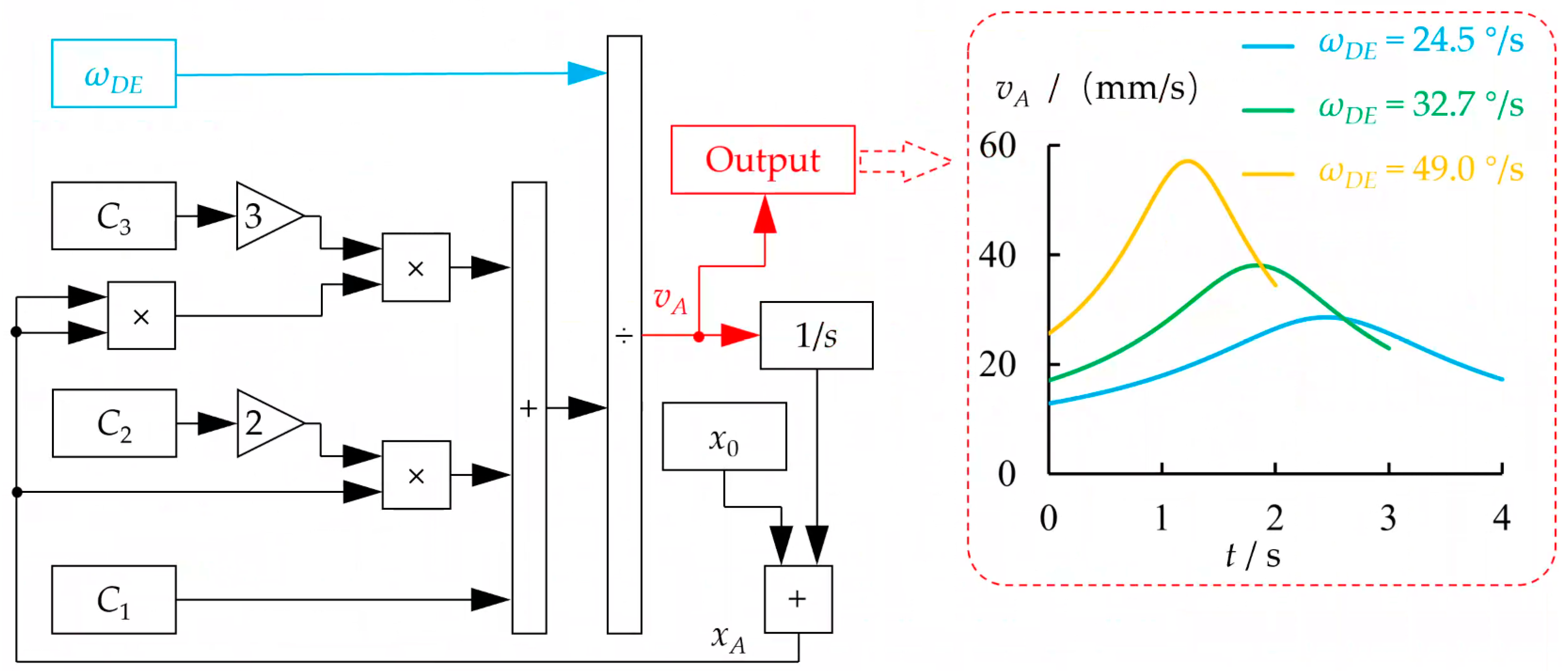
2.5. Solving Input Functions Based on Simulink
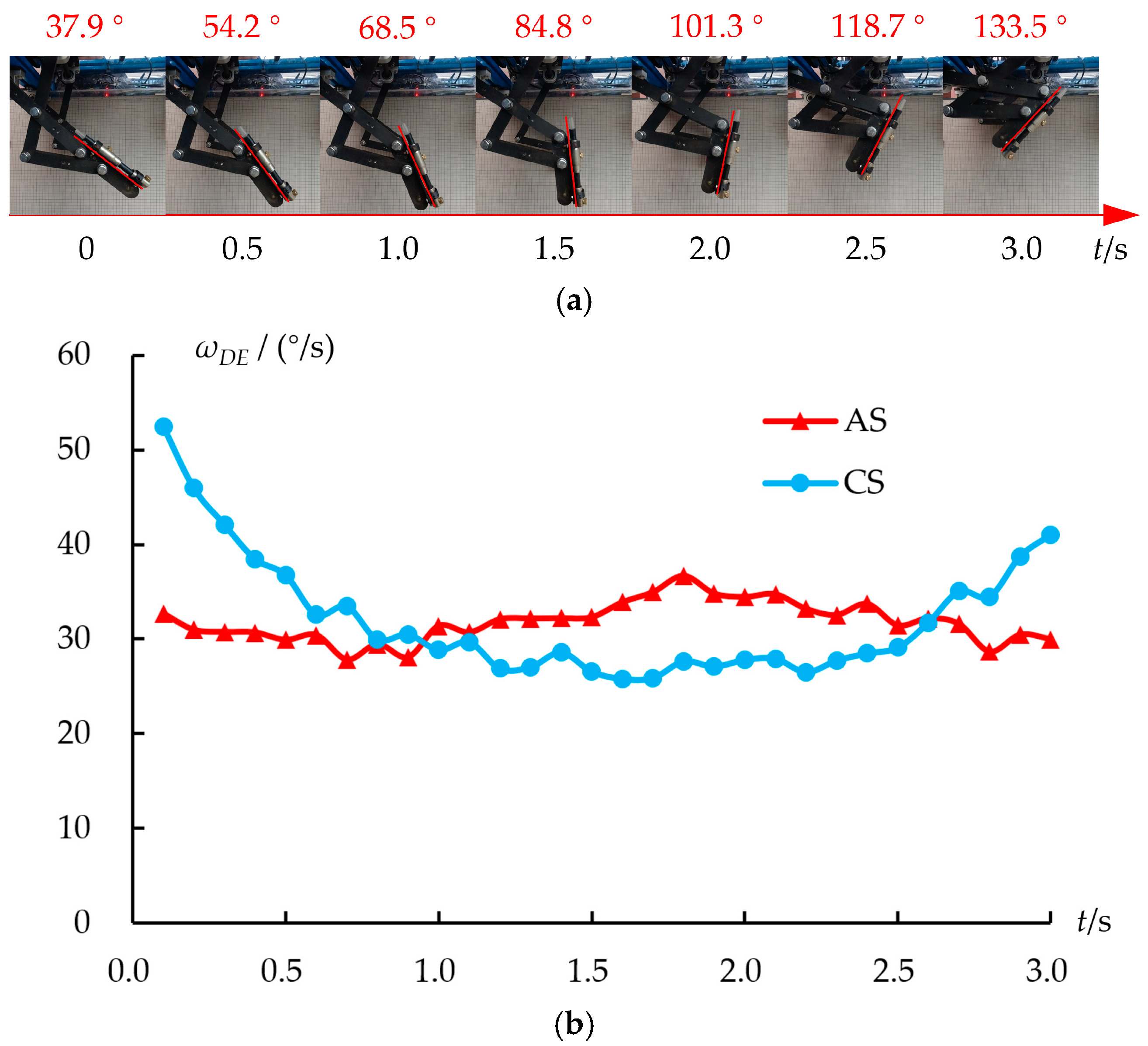
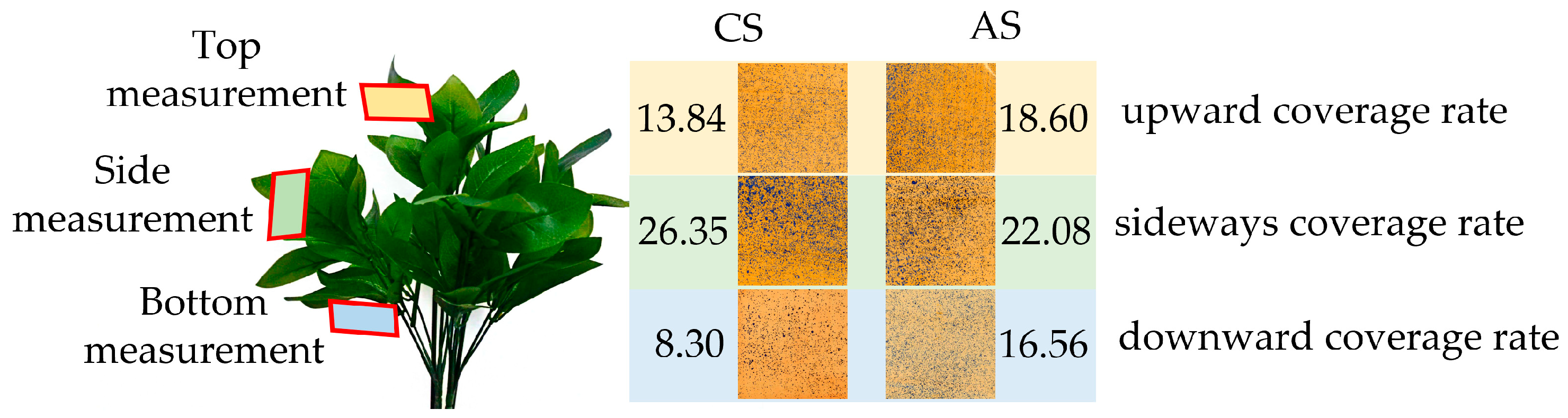
3. Testing, Results, and Analysis
3.1. Testing Plan
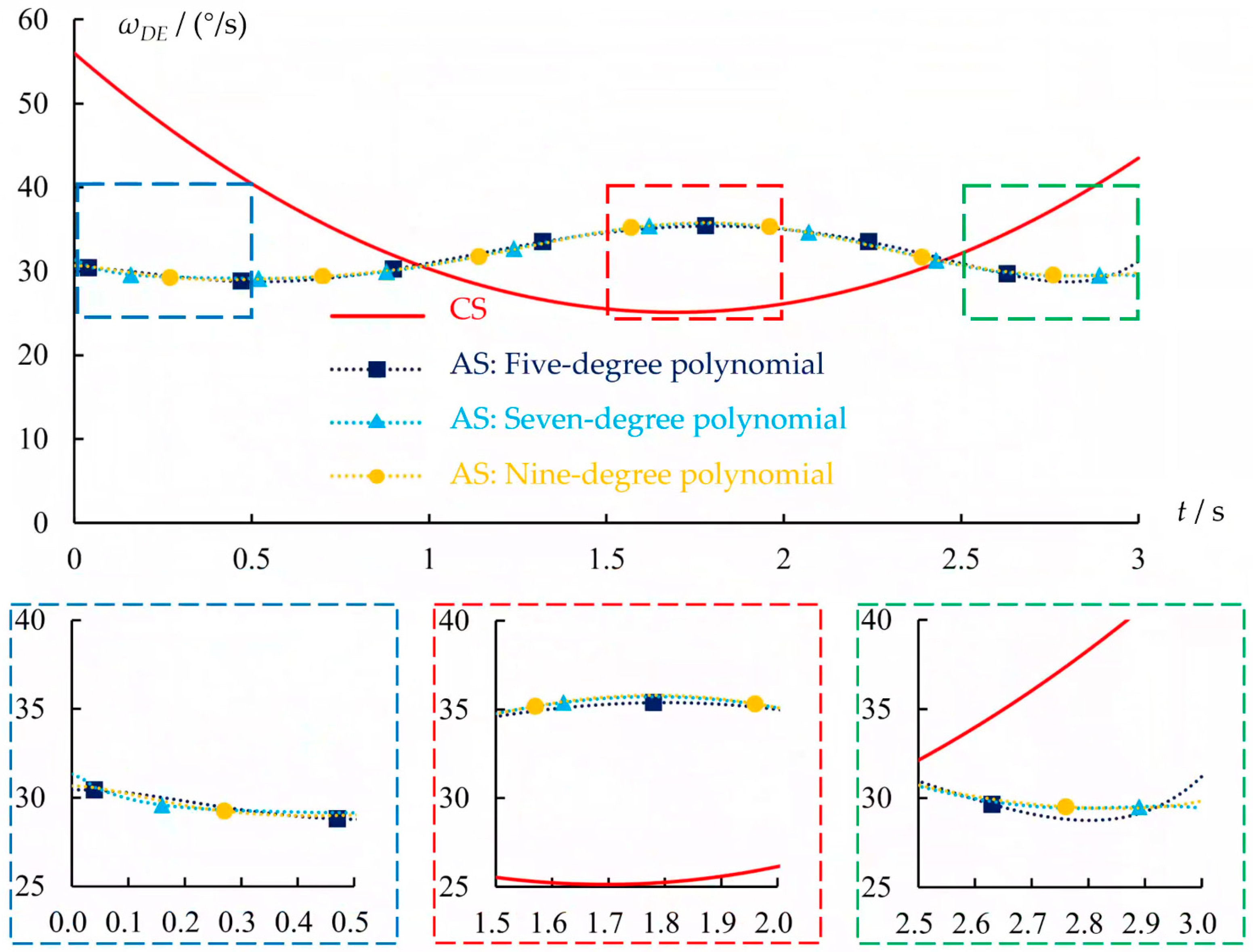
3.2. Comparison and Analysis of Angular Velocity Between CS and AS
3.3. Comparison Test of Spraying with CS and AS
4. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cantelli, L.; Bonaccorso, F.; Longo, D.; Melita, C.D.; Schillaci, G.; Muscato, G. A small versatile electrical robot for autonomous spraying in agriculture. AgriEngineering 2019, 1, 391–402. [Google Scholar] [CrossRef]
- Meshram, A.T.; Vanalkar, A.V.; Kalambe, K.B.; Badar, A.M. Pesticide spraying robot for precision agriculture: A categorical literature review and future trends. J. Field Robot. 2022, 39, 153–171. [Google Scholar] [CrossRef]
- Abbas, I.; Liu, J.; Faheem, M.; Noor, R.S.; Shaikh, S.A.; Solangi, K.A.; Raza, S.M. Different sensor based intelligent spraying systems in Agriculture. Sens. Actuators A Phys. 2020, 316, 112265. [Google Scholar] [CrossRef]
- Zanin, A.R.A.; Neves, D.C.; Teodoro, L.P.R.; Silva Júnior, C.A.; Silva, S.P.; Teodoro, P.E.; Baio, F.H.R. Reduction of pesticide application via real-time precision spraying. Sci. Rep. 2022, 12, 5638. [Google Scholar] [CrossRef] [PubMed]
- Amaya, K.; Bayat, A. Innovating an electrostatic charging unit with an insulated induction electrode for air-assisted orchard sprayers. Crop Prot. 2024, 181, 106701. [Google Scholar] [CrossRef]
- Wei, Z.; Li, R.; Xue, X.; Sun, Y.; Zhang, S.; Li, Q.; Chang, C.; Zhang, Z.; Sun, Y.; Dou, Q. Research status, methods and prospects of air-assisted spray technology. Agronomy 2023, 13, 1407. [Google Scholar] [CrossRef]
- Hussain, N.; Farooque, A.A.; Schumann, A.W.; McKenzie-Gopsill, A.; Esau, T.; Abbas, F.; Acharya, B.; Zaman, Q. Design and development of a smart variable rate sprayer using deep learning. Remote Sens. 2020, 12, 4091. [Google Scholar] [CrossRef]
- Cui, L.F.; Xue, X.Y.; Ding, S.M.; Le, F.X. Development of a DSP-based electronic control system for the active spray boom suspension. Comput. Electron. Agric. 2019, 166, 105024. [Google Scholar] [CrossRef]
- Li, J.Y.; Nie, Z.Y.; Chen, Y.F.; Ge, D.Q.; Li, M.Q. Development of boom posture adjustment and control system for wide spray boom. Agriculture 2023, 13, 2162. [Google Scholar] [CrossRef]
- Appah, S.; Wang, P.; Ou, M.; Gong, C.; Jia, W. Review of electrostatic system parameters, charged droplets characteristics and substrate impact behavior from pesticides spraying. Int. J. Agric. Biol. Eng. 2019, 12, 1–9. [Google Scholar] [CrossRef]
- Dai, S.Q.; Ou, M.X.; Du, W.T.; Yang, X.J.; Dong, X.; Jiang, L.; Zhang, T.; Ding, S.M.; Jia, W.D. Effects of sprayer speed, spray distance, and nozzle arrangement angle on low-flow air-assisted spray deposition. Front. Plant Sci. 2023, 14, 1184244. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.; Alam, M.S.; Roman, M.; Tufail, M.; Khan, M.U.; Khan, M.T. Real-time machine-learning based crop/weed detection and classification for variable-rate spraying in precision agriculture. In Proceedings of the 2020 7th international conference on electrical and electronics engineering (ICEEE), Antalya, Turkey, 14–16 April 2020; pp. 273–280. [Google Scholar]
- Hejazipoor, H.; Massah, J.; Soryani, M.; Vakilian, K.A.; Chegini, G. An intelligent spraying robot based on plant bulk volume. Comput. Electron. Agric. 2021, 180, 105859. [Google Scholar] [CrossRef]
- Liu, X.M.; Li, Y.; Li, M.; Yuan, J.; Fang, Q.Z.; Hou, J.L. Design and test of smart-targeting spraying system on boom sprayer. Trans. Chin. Soc. Agric. Mach. 2016, 47, 37–44. [Google Scholar]
- Luo, Y.H.; Huang, D.F.; Jiang, P.; Xiang, S.L.; Liu, J.F.; Xu, M.Z.; Shi, Y.X. Design and experimental testing of an overhead rail automatic variable-distance targeted spray system for solar greenhouses. Agriculture 2023, 13, 1853. [Google Scholar] [CrossRef]
- Chen, Z.H.; Wang, S.K.; Liu, Q.; Wang, J.Z. Development of sheet palletizing manipulator based on multi-link mechanism. Res. Sq. 2020. [Google Scholar]
- Wei, G.W.; Dai, J.S. A spatial eight-bar linkage and its association with the deployable platonic mechanisms. J. Mech. Robot. 2014, 6, 021010. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhang, L.F.; Wang, W.; Li, Y.M.; Zhang, Q.W. Design and implementation of a two-wheel and hopping robot with a linkage mechanism. IEEE Access 2018, 6, 42422–42430. [Google Scholar] [CrossRef]
- Kim, J.W.; Seo, T.; Kim, J. A new design methodology for four-bar linkage mechanisms based on derivations of coupler curve. Mech. Mach. Theory 2016, 100, 138–154. [Google Scholar] [CrossRef]
- Lin, H.K.; Tekes, A.; Tekes, C. Design, development and modelling of single actuated, compliant and symmetrical multilink hopping mechanism. J. Mech. Sci. Technol. 2020, 34, 555–563. [Google Scholar] [CrossRef]
- Huang, T.C.; Youm, Y. Exact displacement analysis of four-link spatial mechanisms by the direction cosine matrix method. J. Appl. Mech. 1984, 51, 921–928. [Google Scholar] [CrossRef]
- Liu, Y.W.; Wang, H.G.; Li, B.; Zhou, W.J. An optimal method to determine the parameters of anthropomorphic finger based on four-link mechanism. In Proceedings of the 2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; IEEE: Piscataway, NJ, USA; pp. 842–847. [Google Scholar]
- Martini, A.; Troncossi, M.; Carricato, M.; Rivola, A. Elastodynamic behavior of balanced closed-loop mechanisms: Numerical analysis of a four-bar linkage. Meccanica 2014, 49, 601–614. [Google Scholar] [CrossRef]
- Muralidharan, V.; Bose, A.; Chatra, K.; Bandyopadhyay, S. Methods for dimensional design of parallel manipulators for optimal dynamic performance over a given safe working zone. Mech. Mach. Theory 2020, 147, 103721. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Kang, N. Deep generative model-based synthesis framework of four-bar linkage mechanisms with target conditions. J. Comput. Des. Eng. 2024, 11, 318–332. [Google Scholar] [CrossRef]
- Chen, H.C.; Liu, T.K.; Huang, I.M.; Chou, J.H. Multiobjective synthesis of six-bar mechanisms under manufacturing and collision-free constraints. IEEE Comput. Intell. Mag. 2012, 7, 36–48. [Google Scholar] [CrossRef]
- Allmendinger, A.; Spaeth, M.; Saile, M.; Peteinatos, G.G.; Gerhards, R. Precision chemical weed management strategies: A review and a design of a new CNN-based modular spot sprayer. Agronomy 2022, 12, 1620. [Google Scholar] [CrossRef]
- Shi, N.Y.; Chen, Z.; Li, H.; Hua, H.L.; Xu, T.; Ye, J.H. Development and assessment of a novel single-drive variable angle spraying machine. Sci. Rep. 2024, 14, 31264. [Google Scholar] [CrossRef] [PubMed]
- Sinir, B.G. Derivation of governing equations by using vector approach and comparison of analytical solutions of post-buckling behaviors of transverse functionally graded shear deformable beam theories. Arab. J. Sci. Eng. 2023, 48, 4971–4990. [Google Scholar] [CrossRef]
- Corduneanu, E. Expressions of euler angles as functions of the directional cosines of three-orthogonal axes in rigid body kinematics-II. Bull. Polytech. Inst. Iași. Mach. Constr. Sect. 2021, 67, 17–24. [Google Scholar] [CrossRef]
- Wang, W.J. The explicit expression of axis and angle of a rotation matrix. Coll. Math. J. 2021, 52, 39–44. [Google Scholar] [CrossRef]
- Zhang, W.N.; Zhong, S.; Xia, Y.; Xu, D.W. Air vehicle’s attitude control system based on virtual instrument. In Proceedings of the 2007 8th International Conference on Electronic Measurement and Instruments, Xi’an, China, 16–18 August 2007; pp. 3–74. [Google Scholar]
- Ponomarev, A.; Hofmann, J.; Groll, L. Characteristics-based Simulink implementation of first-order quasilinear partial differential equations. In Proceedings of the 10th International Conference on Simulation and Modeling Methodologies, Online, 8–10 July 2020; Volume 1907, p. 13419. [Google Scholar]
- Sánchez-Hermosilla, J.; Rincón, V.J.; Páez, F.; Agüera, F.; Carvajal, F. Field evaluation of a self-propelled sprayer and effects of the application rate on spray deposition and losses to the ground in greenhouse tomato crops. Pest Manag. Sci. 2011, 67, 942–947. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.H.; Wang, J.R.; Yang, J.Q.; Li, J. Dynamic simulation research of adaptive support mechanism of pipeline inspection robot based on ADAMS. J. Phys. Conf. Ser. 2023, 2450, 012047. [Google Scholar] [CrossRef]
- Šarga, P.; Hroncová, D.; Rákay, R. The MSC ADAMS/view and simulation of the crank rocker mechanism. Am. J. Mech. Eng. 2015, 3, 161–164. [Google Scholar]
- Shi, N.Y.; Li, H.; Xu, T.; Hua, H.L.; Ye, J.H.; Chen, Z. Design, analysis, and optimization testing of a novel modular walking device for pipeline robots. Machines 2024, 12, 718. [Google Scholar] [CrossRef]
- Flores-Campos, J.A.; Perrusquía, A.; Hernández-Gómez, L.H.; González, N.; Armenta-Molina, A. Constant speed control of slider-crank mechanisms: A joint-task space hybrid control approach. IEEE Access 2021, 9, 65676–65687. [Google Scholar] [CrossRef]





| Fitting Equations | Parameters | Value |
|---|---|---|
| f(xA) = A4xA4 + A3 xA3 + A2 xA2 + A1 xA + A0 | A4 | −2.826 × 10−7 |
| A3 | 1.401 × 10−4 | |
| A2 | −2.591 × 10−2 | |
| A1 | 1.711 | |
| A0 | 52.165 | |
| R2 | 0.999 | |
| g(xA) = B5xA5 +B4 xA4 + B3 xA3 + B2 xA2 + B1 xA + B0 | B5 | −7.202 × 10−9 |
| B4 | 4.825 × 10−6 | |
| B3 | −1.283 × 10−3 | |
| B2 | 0.167 | |
| B1 | −10.847 | |
| B0 | 323.539 | |
| R2 | 0.999 | |
| h(xA) = C3xA3 + C2 xA2 + C1 xA + C0 | C3 | 1.425 × 10−4 |
| C2 | −6.355 × 10−2 | |
| C1 | 10.302 | |
| C0 | −499.772 | |
| R2 | 0.999 |
| Parameters | Value | ||||
|---|---|---|---|---|---|
| Five-Degree Polynomial | Six-Degree Polynomial | Seven-Degree Polynomial | Eight-Degree Polynomial | Nine-Degree Polynomial | |
| D9 | / | / | / | / | 0.849 |
| D8 | / | / | / | −0.139 | −11.603 |
| D7 | / | / | −1.570 | 0.093 | 64.809 |
| D6 | / | −0.583 | 15.899 | 7.757 | −190.242 |
| D5 | 2.559 | 7.806 | −60.622 | −39.709 | 316.037 |
| D4 | −16.703 | −34.578 | 107.779 | 77.684 | −302.248 |
| D3 | 32.561 | 61.109 | −93.733 | −69.758 | 162.730 |
| D2 | −19.585 | −40.908 | 42.205 | 32.477 | −41.467 |
| D1 | 11.812 | 18.146 | −0.071 | 1.567 | 11.420 |
| D0 | 16.848 | 16.411 | 17.343 | 17.279 | 16.974 |
| R2 | 0.99771 | 0.99812 | 0.99980 | 0.99981 | 0.99997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, N.; Li, H.; Yang, Y.; Hua, H.; Ye, J.; Chen, Z.; Xu, T. Enhancing Spraying Performance with Active Stability Control in Multi-Link Mechanisms. Machines 2025, 13, 104. https://doi.org/10.3390/machines13020104
Shi N, Li H, Yang Y, Hua H, Ye J, Chen Z, Xu T. Enhancing Spraying Performance with Active Stability Control in Multi-Link Mechanisms. Machines. 2025; 13(2):104. https://doi.org/10.3390/machines13020104
Chicago/Turabian StyleShi, Naiyu, He Li, Yongkang Yang, Hongliang Hua, Junhong Ye, Zheng Chen, and Ting Xu. 2025. "Enhancing Spraying Performance with Active Stability Control in Multi-Link Mechanisms" Machines 13, no. 2: 104. https://doi.org/10.3390/machines13020104
APA StyleShi, N., Li, H., Yang, Y., Hua, H., Ye, J., Chen, Z., & Xu, T. (2025). Enhancing Spraying Performance with Active Stability Control in Multi-Link Mechanisms. Machines, 13(2), 104. https://doi.org/10.3390/machines13020104






