Adaptive Multimodal Time–Frequency Feature Fusion for Tool Wear Recognition Based on SSA-Optimized Wavelet Transform

Abstract

Accurate identification of tool wear states is crucial for ensuring machining quality and reliability. However, non-stationary signal characteristics, feature coupling, and limited use of multimodal information remain major challenges. This study proposes a hybrid framework that integrates a Sparrow Search Algorithm–optimized Continuous Wavelet Transform (SSA-CWT) with a Cross-Modal Time–Frequency Fusion Network (TFF-Net). The SSA-CWT adaptively adjusts Morlet wavelet parameters to enhance energy concentration and suppress noise, generating more discriminative time–frequency representations. TFF-Net further fuses cutting force and vibration signals through a sliding-window multi-head cross-modal attention mechanism, enabling effective multi-scale feature alignment. Experiments on the PHM2010 dataset show that the proposed model achieves classification accuracies of 100%, 98.7%, and 98.7% for initial, normal, and severe wear stages, with F1-score, recall, and precision all exceeding 98%. Ablation results confirm the contributions of SSA optimization and cross-modal fusion. External validation on the HMoTP dataset demonstrates strong generalization across different machining conditions. Overall, the proposed approach provides a reliable and robust solution for intelligent tool condition monitoring.

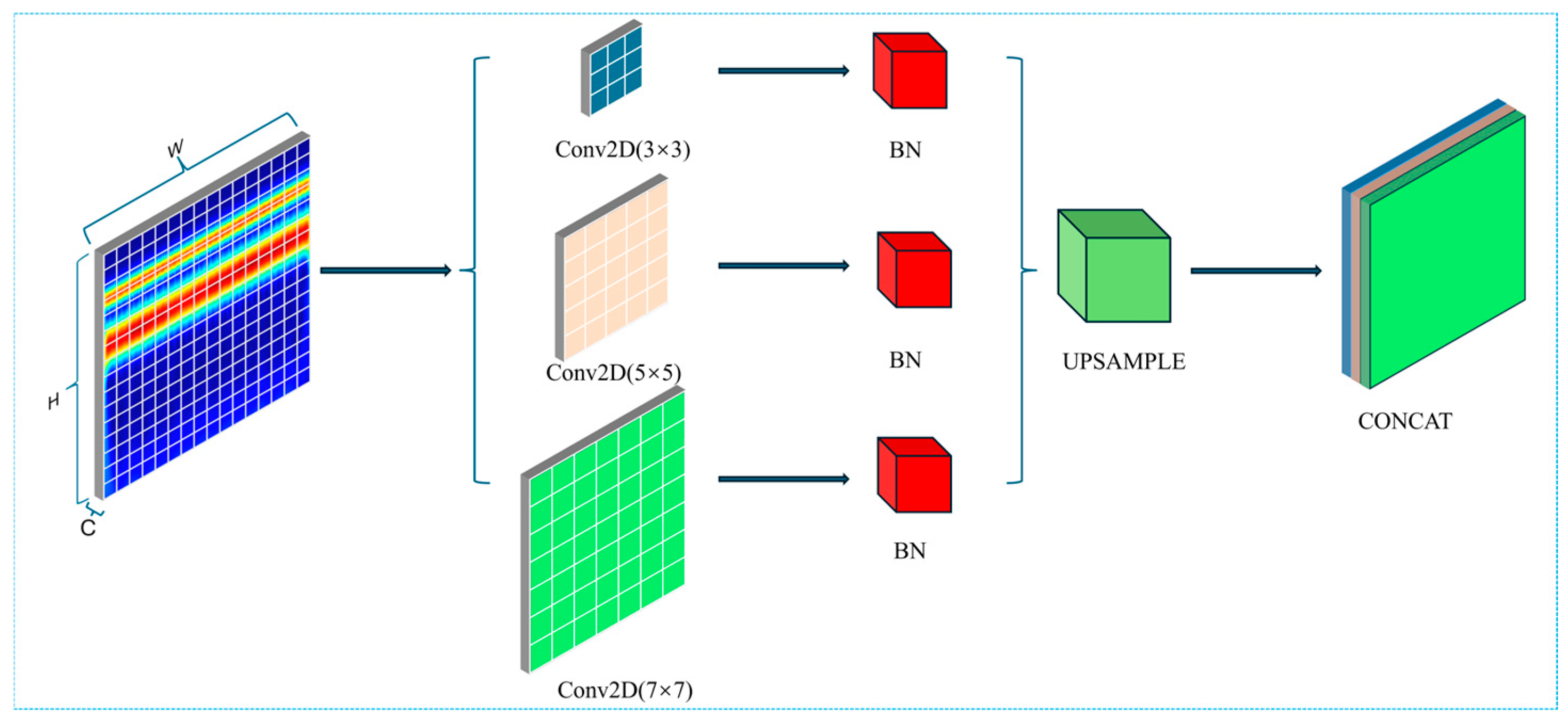
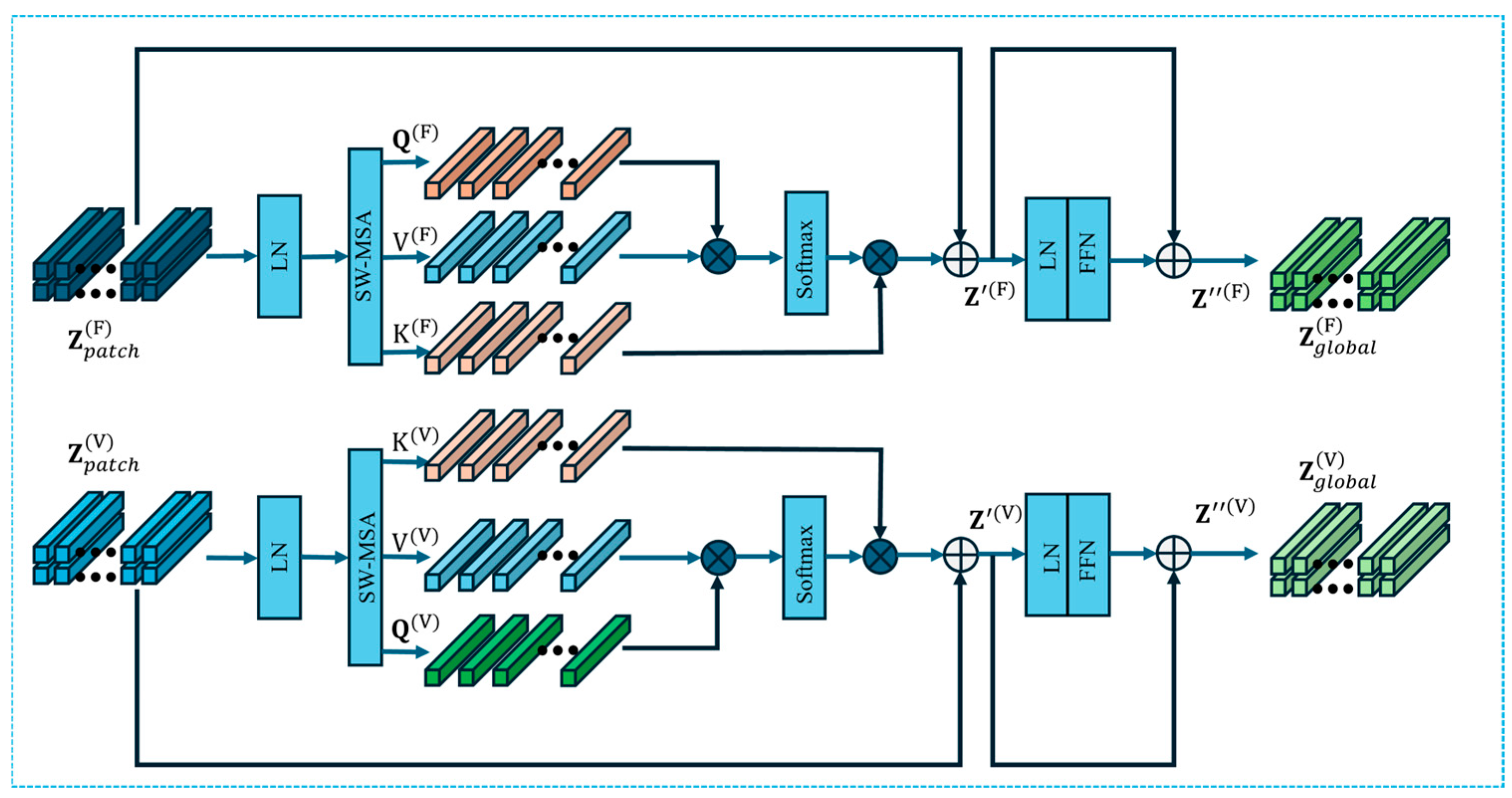
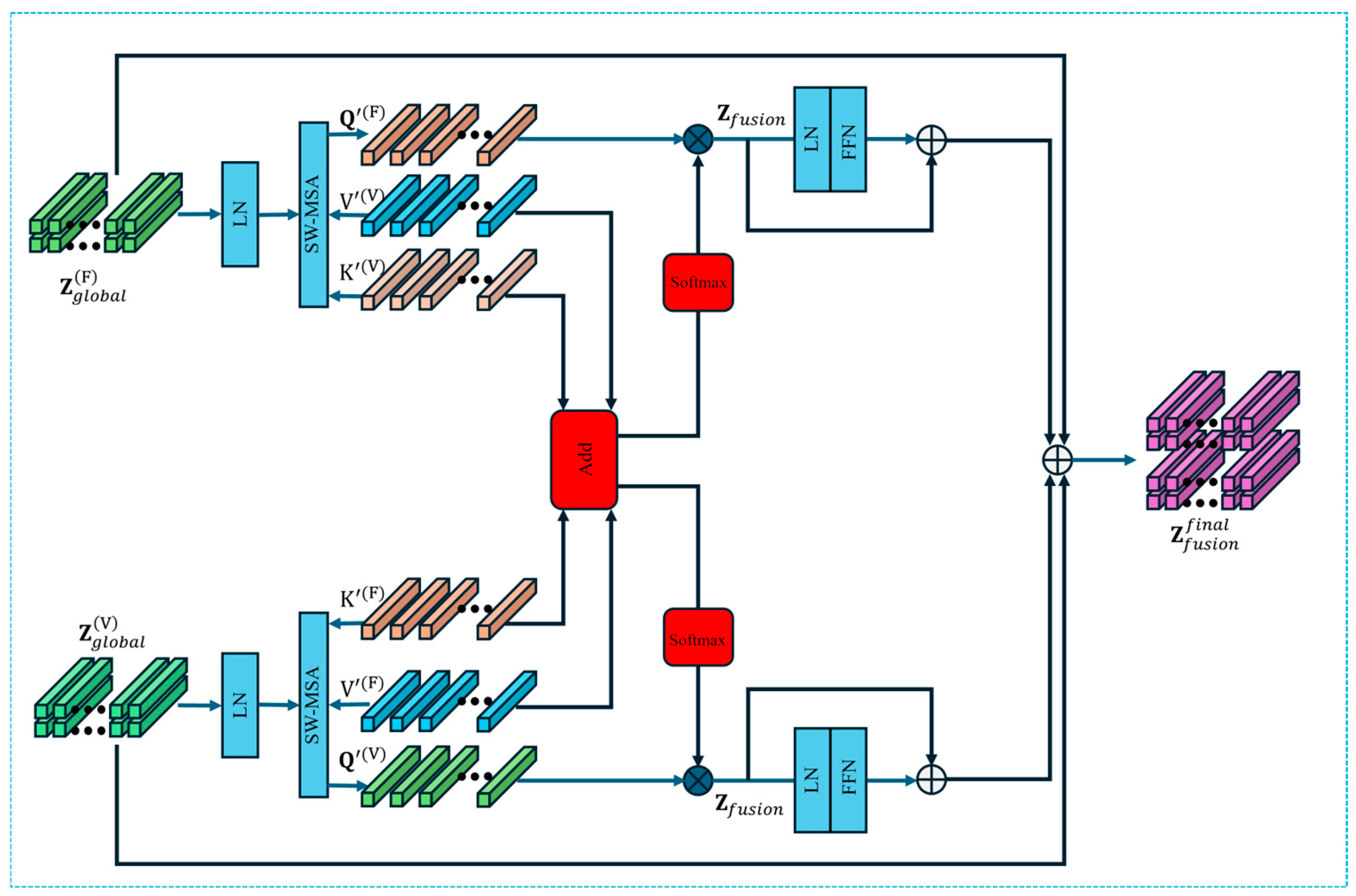
1. Introduction

Driven by the rapid advancement of intelligent manufacturing and Industry 4.0, the global manufacturing industry is progressively evolving toward higher levels of intelligence, automation, and efficiency [1]. As a fundamental pillar of modern production systems, computer numerical control (CNC) machining technology is undergoing a paradigm shift from traditional experience-driven methods to data-driven intelligent optimization [2]. Within this framework, cutting tools, as the core executive components of CNC machine tools, play a decisive role in determining machining precision, surface integrity, and operational stability [3]. However, abnormal tool wear not only deteriorates product quality but may also cause tool breakage, machine damage, or even safety accidents, thereby severely compromising production efficiency and economic performance [4]. Studies indicate that unplanned downtime resulting from tool wear can account for up to 20% of total machine downtime, while tool replacement and maintenance expenses represent approximately 3–12% of total manufacturing costs [5]. Furthermore, due to the inherent complexity, nonlinearity, and irreversibility of the machining process, tool wear behavior varies significantly under different cutting conditions, exhibiting strong uncertainty and nonstationarity [6]. Consequently, the development of real-time, accurate, and reliable tool wear monitoring systems has become a critical scientific and engineering challenge in the field of intelligent manufacturing [7].

Currently, cutting force and vibration signals have become the two most commonly used types of data in tool condition monitoring. Cutting force signals primarily capture the steady-state mechanical variations that occur during machining, while vibration signals are more sensitive to transient dynamic behaviors and high-frequency responses [8]. By integrating additional modalities such as acoustic emission and temperature signals, a more comprehensive characterization of the tool wear process can be achieved [9]. Traditional machine learning algorithms, such as Support Vector Machines (SVM) and Random Forests (RF), have achieved certain success in tool condition classification [10]. However, these approaches rely heavily on handcrafted feature extraction and expert domain knowledge, which limits their adaptability to complex multimodal signal environments and reduces their ability to generalize under varying cutting conditions [11].

To overcome the aforementioned limitations, deep learning techniques have been extensively applied in the field of tool wear monitoring [12]. Compared with traditional approaches, deep learning enables automatic extraction of high-dimensional and complex features through an end-to-end network architecture, effectively eliminating the need for manual feature engineering [13]. Among these methods, convolutional neural networks (CNNs) have demonstrated exceptional performance in processing signal representations such as time–frequency maps and spectrograms, allowing for the in-depth mining of latent correlations between cutting force and vibration signals [14]. For instance, Abdeltawab et al. [15] developed a CNN-based model that integrates continuous wavelet transform (CWT), short-time Fourier transform (STFT), and Gramian angular field (GAF) to convert cutting force signals into two-dimensional time–frequency images for tool wear classification. Sun et al. [16] combined the dual-tree complex wavelet transform (DWT) with CNNs to achieve multi-scale feature extraction from spindle vibration signals. Li et al. [17] further proposed deep models incorporating a dual-channel spatial attention mechanism and a lightweight MobileViT architecture, achieving high-precision tool wear recognition under varying machining conditions. Rezazadeh et al. proposed WaveCORAL-DCCA, an unsupervised domain adaptation framework that integrates discrete wavelet transformation with an enhanced deep canonical correlation analysis network regularized by CORAL loss, achieving around 95% diagnostic accuracy and outperforming several State-of-the-Art UDA benchmarks in cross-domain rotor fault diagnosis [18].

Although deep learning has achieved remarkable progress in single-modal signal analysis, relying on a single source of information remains insufficient to fully characterize the nonlinear degradation patterns of tool wear under complex machining conditions. To address this limitation, researchers have increasingly focused on multimodal information fusion [19]. By integrating heterogeneous signals—such as cutting force, vibration, acoustic emission, and temperature—multimodal frameworks enable feature complementarity and information enhancement, thereby improving the comprehensiveness and robustness of tool condition monitoring systems [19]. For instance, Wei et al. [20] proposed an intelligent wear detection approach based on multi-source data fusion combined with a channel–spatial attention mechanism, which achieved higher recognition accuracy. Hou et al. [21] developed the Swin-Fusion framework, integrating convolutional neural networks (CNNs) with Transformers to realize dynamic wear monitoring through local–global feature extraction and cross-attention fusion. Peng et al. [22] introduced a multi-source information fusion method based on the MKW-GPR model, achieving high-precision monitoring even with small sample sizes. Song et al. [23] enhanced the predictive robustness of multi-signal fusion by combining the Whale Optimization Algorithm (WOA) and XGBoost to optimize the performance of a GRU network. Hao et al. [24] proposed a multimodal information-based monitoring and multi-step prediction framework for ball-end milling tool wear. This framework monitors cutting vibration and spindle power signals and adopts a two-stage deep feature extraction method for real-time wear monitoring., Gao et al. [25] developed a multi-source, multibranch metric ensemble deep transfer learning algorithm (MS-MMEDTL), which employs metric learning to enhance feature discriminability in the target domain and improve cross-condition recognition performance.

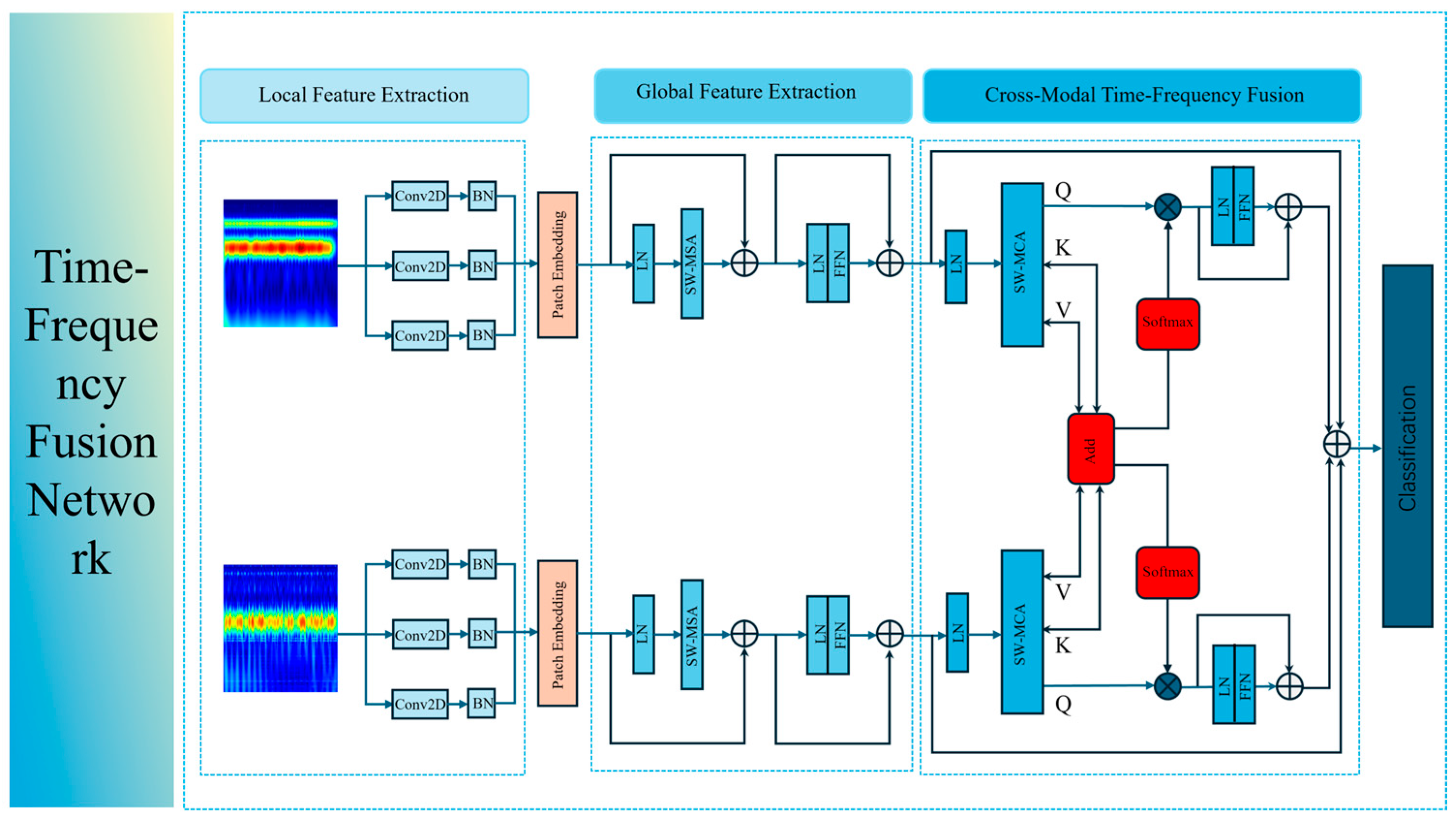
Building upon the aforementioned research, this study proposes a novel tool wear state recognition framework that integrates a Sparrow Search Algorithm (SSA)-optimized Continuous Wavelet Transform (SSA-CWT) with a Cross-Modal Time–Frequency Fusion Network (TFF-Net). To the best of our knowledge, this is the first work that combines SSA with wavelet parameter optimization for time–frequency analysis of tool wear signals, where SSA is specifically employed to adaptively tune the center frequency and bandwidth of the complex Morlet wavelet. By using minimum energy entropy as the optimization objective, the SSA-CWT module yields a more concentrated time–frequency energy distribution while effectively suppressing noise, thereby generating highly discriminative time–frequency representations as inputs for subsequent modeling.

The proposed TFF-Net further combines multi-scale convolutional feature extraction, global representation modeling, and a sliding-window multi-head cross-modal attention mechanism (SW-MCA) to achieve deep fusion of cutting force and vibration signals in the time–frequency domain. In contrast to conventional feature stacking or global attention schemes, the SW-MCA module explicitly models local, window-based cross-modal interactions, enabling more precise temporal alignment between modalities. This design effectively captures inter-modal complementary information and enhances the precision and robustness of tool wear recognition under complex operating conditions.

The main contributions of this study are summarized as follows:

(1)

An adaptive time–frequency analysis method (SSA-CWT) optimized via the Sparrow Search Algorithm is proposed, which automatically adjusts the center frequency and bandwidth of the complex Morlet wavelet based on energy entropy. This enables high energy concentration in critical frequency bands, effective noise suppression, and the generation of highly discriminative time–frequency representations for tool wear signals. To the best of our knowledge, this is the first application of SSA-driven wavelet parameter optimization to tool wear time–frequency analysis.

(2)

A Cross-Modal Time–Frequency Fusion Network (TFF-Net) is developed, which integrates local convolutional feature extraction, global dependency modeling, and a sliding-window multi-head cross-modal attention mechanism. This architecture enables adaptive alignment and deep fusion of cutting force and vibration modalities across multiple scales. Compared with conventional early/late fusion or global attention-based fusion, the proposed SW-MCA module provides a more targeted cross-modal interaction scheme, thereby significantly improving robustness and recognition accuracy under non-stationary machining conditions.

(3)

Extensive experiments on the public PHM2010 dataset demonstrate the superior performance of the proposed framework, achieving recognition accuracies of 100%, 98.7%, and 98.7% for the initial, normal, and severe wear stages, respectively. Ablation studies further validate the specific contributions of SSA-based wavelet optimization and cross-modal fusion, while external validation on the HMoTP dataset confirms strong generalization capability across different tools, materials, and acquisition conditions.

2. Materials and Methods

2.1. Signal Preprocessing

To enhance the quality and stability of the cutting force and vibration signals, a systematic data preprocessing framework was developed, as illustrated in Figure 1. In the experimental setup, a piezoelectric dynamometer and a triaxial accelerometer were mounted on a CNC milling machine to synchronously collect the cutting force and vibration responses during the milling process. The sampling frequency was set to 50 kHz, and the acquired raw data were stored in CSV format for subsequent offline analysis and modeling.

First, for the triaxial measurements (Fx, Fy, Fz, and Vx, Vy, Vz), an energy-adaptive weighted fusion strategy was employed to reduce redundancy and emphasize the dominant directional components. The weights of each axis were assigned based on their respective energy proportions, and the fused signal was calculated as follows:

$$\mathrm{S}\left(\mathrm{t}\right)=\sum _{\mathrm{i}=1}^3{\mathrm{w}}_{\mathrm{i}}{\mathrm{S}}_{\mathrm{i}}\left(\mathrm{t}\right),{\mathrm{w}}_{\mathrm{i}}={\displaystyle \frac{{\sum }_{\mathrm{t}}{\mathrm{S}}_{\mathrm{i}}^2\left(\mathrm{t}\right)}{{\sum }_{\mathrm{j}=1}^3{\sum }_{\mathrm{t}}{\mathrm{S}}_{\mathrm{j}}^2\left(\mathrm{t}\right)}}$$

(1)

where $S_i\left(t\right)$ represents the raw signal of the $i$-th direction, and $w_i$ denotes the corresponding energy weight. This approach ensures that the fused signal preserves the primary mechanical characteristics while effectively suppressing irrelevant directional noise. Consequently, the signal more accurately reflects the dominant energy distribution of the cutting process, providing a physically meaningful input for subsequent time–frequency analysis.

Next, to ensure the representativeness of the analysis segments and to avoid interference from low-energy or idle cutting periods, wavelet decomposition was used to construct the energy curve of the signal. A sliding window cumulative energy search method was then applied to locate the segment with the highest energy concentration, from which a 10,000-point segment was extracted for further analysis. This strategy guarantees that the selected data captures the essential dynamic responses of the cutting process, thereby improving the effectiveness of time–frequency feature extraction.

In the denoising stage, since both cutting force and vibration signals are often affected by transient impulses or isolated outliers, a Hampel filter [26] was applied for robust noise suppression. Within a local window of 1000 points, the median and median absolute deviation (MAD) were computed, and any points deviating by more than three times the MAD were replaced by the local median. This technique effectively eliminates isolated noise spikes while preserving the overall waveform characteristics of the original signal. As a result, the filtered signals exhibit smoother and more stable profiles, providing a reliable foundation for subsequent time–frequency feature extraction and tool wear state classification.

2.2. SSA-CWT

In tool wear monitoring, both cutting force and vibration signals contain rich dynamic characteristics, but their effective extraction largely depends on the selection of appropriate wavelet parameters. The complex Morlet (cmor) wavelet is widely adopted in mechanical signal analysis due to its excellent time–frequency localization and ability to process oscillatory signals. The bandwidth parameter $f_b$ governs the trade-off between time and frequency resolution: a larger $f_b$ improves the discrimination of adjacent frequency components but reduces sensitivity to transient wear impacts, whereas a smaller $f_b$ enhances the detection of rapid variations but sacrifices frequency resolution. The center frequency $f_c$ determines the oscillation period and energy concentration of the wavelet, influencing its adaptability to high-frequency wear shocks and low-frequency cutting trends. Therefore, the proper selection of $(f_b,f_c)$ is crucial for simultaneously capturing both transient wear features and long-term evolution patterns.

To achieve adaptive parameter optimization, this study introduces the Sparrow Search Algorithm (SSA) [27], which simulates the foraging and vigilance behaviors of sparrow populations. SSA dynamically updates the positions of candidate solutions, balancing global exploration and local exploitation capabilities. The optimization objective is defined as the energy entropy based on the wavelet coefficients:

$$\mathrm{H}=-\sum _{\mathrm{i}}{\mathrm{p}}_{\mathrm{i}}\log {\mathrm{p}}_{\mathrm{i}},\hspace{1em}\hspace{1em}{\mathrm{p}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{i}}}{{\sum }_{\mathrm{j}}{\mathrm{P}}_{\mathrm{j}}}}$$

(2)

where $P_i$ denotes the energy of the wavelet coefficient, and $p_i$ is its normalized probability distribution. Energy entropy reflects the concentration of energy in the time–frequency domain—a smaller value indicates more concentrated energy and more discriminative time–frequency features. SSA begins by randomly initializing candidate pairs $(f_b,f_c)$, and through iterative updates of “discoverers,” “joiners,” and “watchers,” it effectively avoids local minima. The final parameter combination that minimizes the energy entropy is selected as the optimal wavelet parameter, achieving adaptive enhancement of time–frequency energy concentration.

To intuitively illustrate the effect of parameter optimization, this study constructs a parameter–energy surface that visualizes the energy distribution across different values of $f_b$ and $f_c$, as shown in Figure 2. The corresponding energy function is defined as follows:

$$\mathrm{E}\left({\mathrm{f}}_{\mathrm{b}},{\mathrm{f}}_{\mathrm{c}}\right)=\sum _{\mathrm{i},\mathrm{j}}{\left|\mathrm{C}\mathrm{W}{\mathrm{T}}_{{\mathrm{f}}_{\mathrm{b}},{\mathrm{f}}_{\mathrm{c}}}\left({\mathrm{S}}_{\mathrm{i},\mathrm{j}}\right)\right|}^2$$

(3)

where $CW{T}_{f_b,f_c}\left(S_{i,j}\right)$ denotes the continuous wavelet transform coefficients of the signal $S$ under parameters $(f_b,f_c)$. By performing a grid search over the parameter space, the energy variation surface can be obtained.

The energy surface not only reveals the overall distribution trend of time–frequency energy but also visually confirms whether the parameters identified by SSA lie within the region of global energy concentration. Consistent with the optimization results of the fitness function, the energy surface analysis provides an intuitive and reliable basis for selecting the optimal wavelet parameters, ensuring both the interpretability and credibility of the optimization process.

After determining the optimal wavelet parameters, the Continuous Wavelet Transform (CWT) [28] was employed to perform time–frequency analysis on the cutting force and vibration signals. The complex Morlet (cmor) wavelet, known for its strong localization properties in both time and frequency domains, was used as the mother wavelet. By incorporating the optimized parameter pair $(f_b,f_c)$ obtained via the Sparrow Search Algorithm (SSA), the CWT achieves an improved balance between time and frequency resolution, resulting in a more concentrated energy distribution within critical frequency bands and enhanced feature discrimination.

Specifically, the optimized wavelet functions were applied to both the cutting force and vibration signals to generate two-dimensional time–frequency energy maps. As shown in Figure 3, the SSA-optimized wavelets (e.g., cmorα–β and cmory–δ) produce representations with stronger energy concentration and lower background noise compared to the traditional cmor3–1 configuration. These improvements enable a clearer visualization of the temporal and spectral evolution of tool wear.

During the initial wear stage, the signal energy is mainly distributed in the mid-to-high frequency range, corresponding to minor cutting impacts at the early contact phase. As wear progresses to the normal and severe stages, the energy gradually shifts toward lower frequencies and forms more stable banded structures, reflecting the increased periodic vibrations caused by tool edge dulling. The SSA-optimized CWT thus provides a more precise and interpretable depiction of the non-stationary behavior of tool wear dynamics, offering high-resolution time–frequency features that serve as reliable inputs for subsequent multimodal fusion and classification tasks.

2.3. Time-Frequency Fusion Network (TFFN)

After completing the signal preprocessing and SSA-optimized Continuous Wavelet Transform (SSA-CWT), a novel Time–Frequency Fusion Network (TFFN) was developed to fully exploit the complementary characteristics embedded in cutting force and vibration signals for accurate tool wear classification. As illustrated in Figure 4, the proposed architecture consists of three main components: Local Feature Extraction, Global Feature Modeling, and Cross-Modal Time–Frequency Fusion, followed by a classification head that outputs the final tool wear state labels.

2.3.1. Local Feature Extraction

In this study, the inputs consist of time–frequency representations of cutting force and vibration signals obtained using the SSA-optimized continuous wavelet transform (SSA-CWT). These inputs are denoted as $X^{\left(m\right)}\in {\mathbb{R}}^{H\times W\times C_0},m\in \{F,V\}$, where $m=F$ and $m=V$ correspond to the force and vibration modalities, respectively. The dimensions $H=W=224$ represent the height and width of the time–frequency maps, and $C_0=3$ indicates a three-channel input.

To effectively extract local spatial–temporal information from different time and frequency scales during tool wear evolution, a multi-scale convolutional neural network (MSCNN) is employed. This module performs feature extraction using convolutional kernels of various sizes to capture both short-term and long-term patterns. The overall architecture and feature flow are illustrated in Figure 5. The convolutional kernel set is defined as $k_b\in \{\mathrm{3,5},7\},b=\mathrm{1,2},3$. Each input $X^{\left(m\right)}$ passes through three parallel convolutional branches, where smaller kernels focus on transient high-frequency impulses, while larger kernels capture low-frequency diffusion trends. The convolution operation is defined as:

$$Z_b^{\left(m\right)}=\varphi \left(\mathrm{BN}\right({\mathrm{Conv}}_{k_b}(X^{\left(m\right)};W_b^{\left(m\right)})\left)\right),b\in \{\mathrm{1,2},3\}$$

(4)

where ${\mathrm{Conv}}_{k_b}$ denotes a 2D convolution with a kernel size of $k_b\times k_b$, $W_b^{\left(m\right)}$ represents the corresponding convolution weights, $\mathrm{BN}(\cdot )$ indicates batch normalization, and $\varphi (\cdot )$ is the GELU activation function.

Since different kernel sizes produce feature maps with varying spatial resolutions, an upsampling operator $U\left(\cdot \right)$ is applied to align features from smaller receptive fields:

$$Z_b^{\prime \left(m\right)}=U\left(Z_b^{\left(m\right)}\right),b\in \{\mathrm{1,2},3\}$$

(5)

Subsequently, features from all scales are concatenated along the channel dimension and fused via a $1\times 1\mathrm{c}$ onvolution to generate the final multi-scale local representation:

$$Z_{\mathrm{local}}^{\left(m\right)}={\mathrm{Conv}}_{1\times 1}\left(\mathrm{Concat}\right[Z_1^{\prime \left(m\right)},Z_2^{\prime \left(m\right)},Z_3^{\prime \left(m\right)}\left]\right)$$

(6)

This multi-scale convolutional framework enables simultaneous learning of local texture information across different time–frequency resolutions, thereby improving the model’s ability to perceive complex tool wear dynamics, such as transient impacts and steady-state variations. The resulting multi-scale features $Z_{\mathrm{local}}^{\left(m\right)}$ provide a high-resolution foundation for subsequent global modeling and cross-modal time–frequency fusion.

2.3.2. Global Feature Extraction

After the multi-scale local features $Z_{\mathrm{local}}^{\left(m\right)}$ are obtained, they are fed into the global feature extraction module to capture long-range dependencies and overall time–frequency patterns. To achieve a seamless transition from 2D spatial representations to sequential Transformer inputs, a convolution-based patch embedding module is introduced. This module partitions the time–frequency maps into non-overlapping semantic tokens while preserving local continuity and structural integrity.

Specifically, the patch embedding layer consists of a 2D convolution followed by layer normalization (LN). Given the following input feature map:

$$Z_{\mathrm{local}}^{\left(m\right)}\in {\mathbb{R}}^{H\times W\times C}$$

(7)

The embedding operation can be formulated as follows:

$$Z_{\mathrm{patch}}^{\left(m\right)}=\mathrm{LN}\left({\mathrm{Conv}}_{P\times P,s=P}\right(Z_{\mathrm{local}}^{\left(m\right)}\left)\right)$$

(8)

where both the kernel size and stride are set to $P$, ensuring that the generated patches are non-overlapping. This convolution operation simultaneously performs downsampling and local feature aggregation, allowing each token to encode contextual neighborhood information. The output dimensions are given by the following:

$$Z_{\mathrm{patch}}^{\left(m\right)}\in {\mathbb{R}}^{H/P\times W/P\times C^{\prime }}$$

(9)

And the flattened sequence for the Transformer input is as follows:

$$Z_0^{\left(m\right)}=\mathrm{Flatten}\left(Z_{\mathrm{patch}}^{\left(m\right)}\right),Z_0^{\left(m\right)}\in {\mathbb{R}}^{N\times C^{\prime }}, N=(H/P)\times (W/P).$$

(10)

Compared with traditional linear patch embedding, the convolution-based strategy better preserves local spatial coherence and boundary continuity, thus improving the robustness of subsequent global modeling.

To model global semantic dependencies in the time–frequency representations, the embedded token sequences $Z_0^{\left(m\right)}$ are fed into an enhanced Swin Transformer architecture. This module employs the Shifted Window Multi-Head Self-Attention (SW-MSA) mechanism, which balances computational efficiency and feature interaction across local and global contexts. As illustrated in Figure 6, each input sequence first undergoes layer normalization:

$$Z_{\mathrm{norm}}^{\left(m\right)}=\mathrm{LN}\left(Z_0^{\left(m\right)}\right),m\in \{F,V\}.$$

(11)

Within each shifted window, self-attention is computed as follows:

$$Q^{\left(m\right)},K^{\left(m\right)},V^{\left(m\right)}=\mathrm{SW}-\mathrm{MSA}\left(Z_{\mathrm{norm}}^{\left(m\right)}\right)$$

(12)

$$Z^{\prime \left(m\right)}=\mathrm{Softmax}\left({\displaystyle \frac{Q^{\left(m\right)}(K^{\left(m\right)}{)}^T}{\sqrt{d_k}}}\right)V^{\left(m\right)}$$

(13)

where $Q^{\left(m\right)}$, $K^{\left(m\right)}$, and $V^{\left(m\right)}$ represent the query, key, and value matrices, respectively, and $d_k$ denotes the dimension of the key vector. The shifted window strategy allows information to propagate across adjacent regions, enabling the model to effectively capture both local dependencies and long-range temporal–frequency relationships.

Finally, a residual connection followed by a feed-forward network (FFN) enhances feature expressiveness and model stability as follows:

$$Z^{″\left(m\right)}=\mathrm{LN}(Z^{\prime \left(m\right)}+Z_{\mathrm{norm}}^{\left(m\right)}),$$

(14)

$$Z_{\mathrm{global}}^{\left(m\right)}=\mathrm{FFN}\left(Z^{″\left(m\right)}\right).$$

(15)

Through this hierarchical process, the global feature extraction module effectively integrates multi-scale local representations with high-level semantic dependencies, forming a unified global embedding that serves as a discriminative input for the subsequent cross-modal time–frequency fusion stage.

2.3.3. Cross-Modal Time–Frequency Fusion

After global feature extraction, the global representations of cutting force and vibration signals, denoted as $Z_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}^{\left(F\right)}$ and $Z_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}^{\left(V\right)}$, are fed into the cross-modal time–frequency fusion module to enhance feature complementarity and inter-modal correlation. The module employs a Shifted Window Multi-Head Cross-Attention (SW-MCA) mechanism to achieve bidirectional interaction between modalities. Specifically, the cutting force features serve as the query while the vibration features act as the key and value:

$$Q^{\left(F\right)}=W_Q{Z}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}^{\left(F\right)},K^{\left(V\right)}=W_K{Z}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}^{\left(V\right)},V^{\left(V\right)}=W_V{Z}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}^{\left(V\right)},$$

(16)

And the cross-modal attention output is computed as follows:

$$A^{F\leftarrow V}=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\hspace{0.17em}\left({\displaystyle \frac{Q^{\left(F\right)}{K^{\left(V\right)}}^{\mathrm{\top }}}{\sqrt{d_k}}}\right)V^{\left(V\right)}$$

(17)

A symmetric operation is applied in the reverse direction to obtain $A^{V\leftarrow F}$.

To further strengthen inter-modal integration, an Adaptive Dual-Addition (ADD) mechanism is introduced. Instead of simple concatenation, ADD performs adaptive additive fusion on the bidirectional attention results, preserving the discriminative patterns of each modality while suppressing redundant or conflicting information. The fusion process is formulated as follows:

$$Z_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}=A^{F\leftarrow V}+A^{V\leftarrow F}+Z_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}^{\left(F\right)}+Z_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}^{\left(V\right)}$$

(18)

This additive design allows each modality to dynamically reinforce the other through learned weighting, improving both the consistency and complementarity of the joint representation.

Finally, the fused feature undergoes layer normalization and a feed-forward network to yield the final representation:

$$Z_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}^{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}=\mathrm{F}\mathrm{F}\mathrm{N}\hspace{0.17em}\left(\mathrm{L}\mathrm{N}\right(Z_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}\left)\right)$$

(19)

As illustrated in Figure 7, the proposed SW-MCA combined with ADD enables efficient cross-modal communication under sliding windows while maintaining a balanced trade-off between local time–frequency structure and global semantic alignment. This design significantly enhances robustness and discriminability in tool wear classification under complex machining conditions.

2.3.4. Tool Wear Classification Head

The Tool Wear Classification Head is responsible for determining the wear condition of the tool based on the integrated features generated by the Cross-Modal Time–Frequency Fusion module. The final fused feature representation $Z_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}^{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}$ is first flattened into a one-dimensional vector to align with the structure required by the fully connected layers. This vector is then processed through several Fully Connected (FC) layers combined with ReLU activation functions, which introduce nonlinear transformations and enhance the network’s ability to capture complex discriminative relationships.

In the output stage, a Softmax layer converts the learned representations into a probability distribution across the three wear categories—initial wear, normal wear, and severe wear—as expressed by the following:

$$P\left(y_i|x\right)={\displaystyle \frac{e^{z_i}}{{\sum }_{j=1}^3{e}^{z_j}}}$$

(20)

where $z_i$ denotes the pre-activation output for the $i$-th class. The predicted wear state is then assigned according to the maximum probability criterion:

$$\widehat{y}=\mathrm{a}\mathrm{r}\mathrm{g} \underset{i}{\mathrm{m}\mathrm{a}\mathrm{x}} P(y_i\mid x)$$

(21)

The training process employs the Cross-Entropy Loss function as the optimization objective:

$$L= - \sum _{i=1}^3{y}_i\log \left(P\left(y_i|x\right)\right)$$

(22)

This minimizes the discrepancy between predicted probabilities and true labels, ensuring stable convergence and improved overall accuracy.

In summary, this classification head provides a compact and effective mapping from the fused multimodal feature space to categorical wear states. By capitalizing on the high-level, complementary information encoded in the fused representations, the model achieves consistent and precise identification of tool wear across multiple degradation stages, highlighting the robustness and scalability of the proposed TFF-Net framework in complex machining scenarios.

3. Results

3.1. PHM2010 Dataset

3.1.1. Experimental Equipment and Parameters

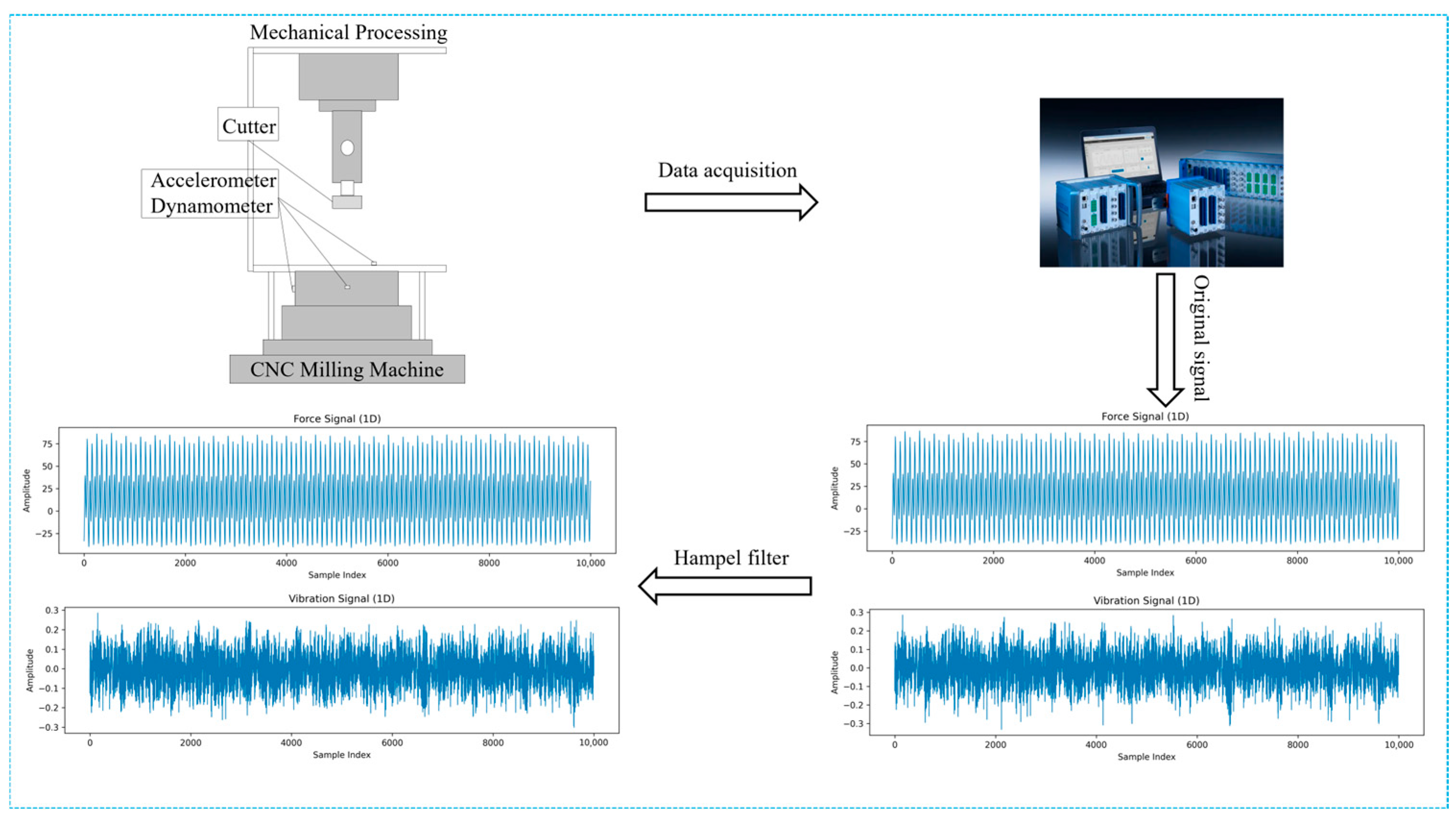
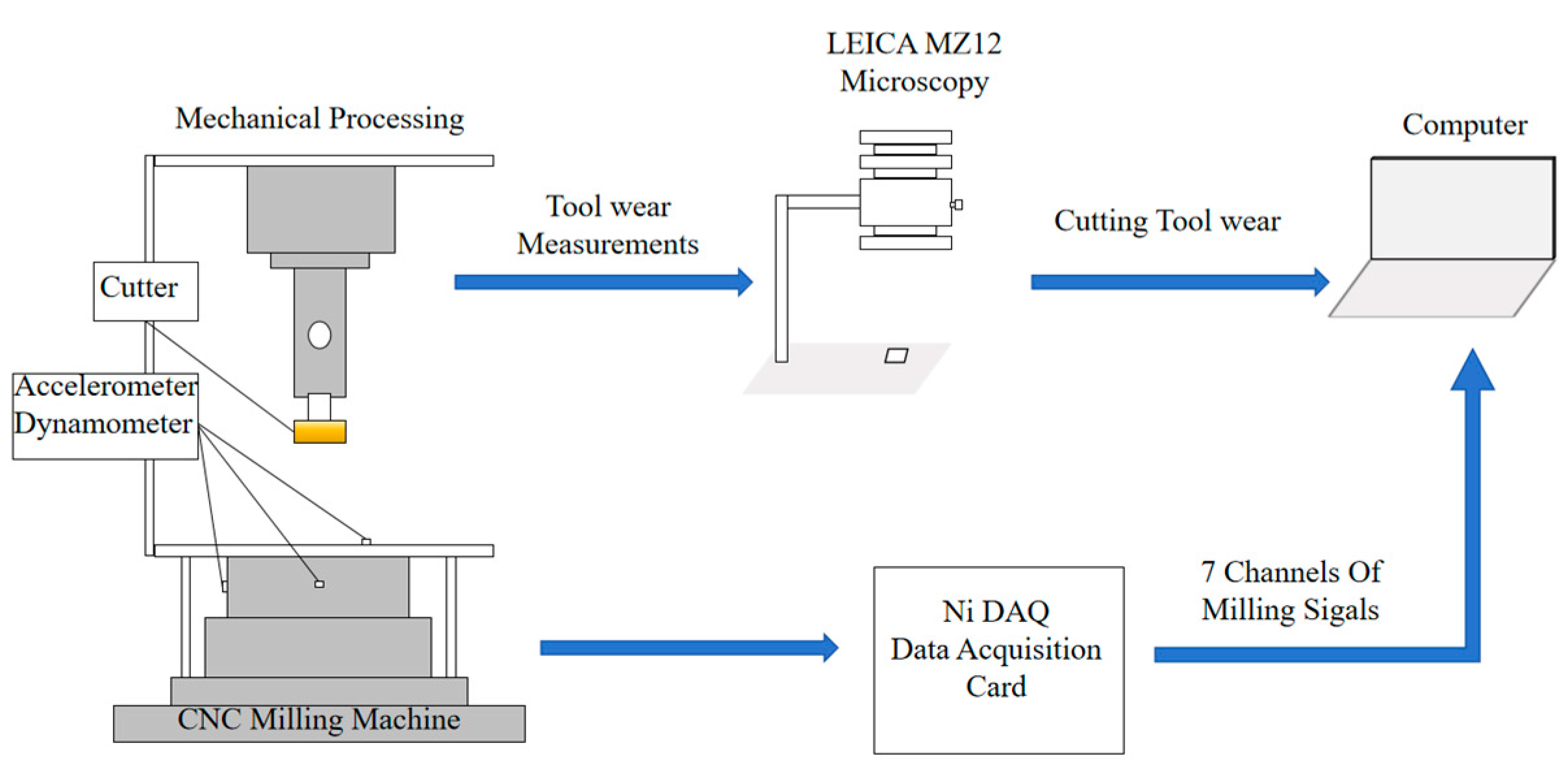
To evaluate the effectiveness and generalization capability of the proposed model, experiments were conducted using the PHM2010 [29] open tool wear dataset. The experimental setup and data acquisition system are illustrated in Figure 8. The workpiece material was Inconel 718, a nickel-based superalloy commonly used in aerospace applications. A 6 mm diameter, three-flute carbide ball-end milling cutter was employed under dry side-milling conditions. All experiments were performed on a Roders Tech RFM760 high-speed CNC milling machine (Röders GmbH & Co. KG, Soltau, Germany).

The signal acquisition system integrated multiple types of sensors. Specifically, a Kistler three-component dynamometer was used to capture the cutting force signals in the x, y, and z directions (Fx, Fy, Fz). A Kistler piezoelectric accelerometer simultaneously collected vibration signals along the same three axes (Vx, Vy, Vz). In addition, an acoustic emission (AE) sensor was used to capture transient high-frequency events associated with tool wear progression. All signals were recorded at a sampling frequency of 50 kHz and conditioned using a Kistler multi-channel charge amplifier(Kistler Instrumente AG, Winterthur, Switzerland). Each cutting trial involved a cutting length of 108 mm, and the milling process was performed in a row-by-row manner on the workpiece surface. The system enabled the real-time acquisition of seven signal channels, including tri-axial force, tri-axial vibration, and AE signals.

Tool wear was measured offline using a LEICA MZ12 optical microscope(Leica Microsystems GmbH, Wetzlar, Germany), where the flank wear width (VB) of the cutter was used as the evaluation metric. Based on the measured VB values, the tool wear condition was categorized into three stages: initial wear, normal wear, and severe wear. The detailed experimental parameters are summarized in

Table 1. Experimental parameters.

Experiment Parameters	Values
Spindle speed (n)	10,400 rpm
Feed per turn (f)	0.003 mm/r
Cutting depth (aP)	0.2 mm
Cutting width (ae)	0.125 mm
Sampling frequency	50 kHz

.

3.1.2. Dataset Division

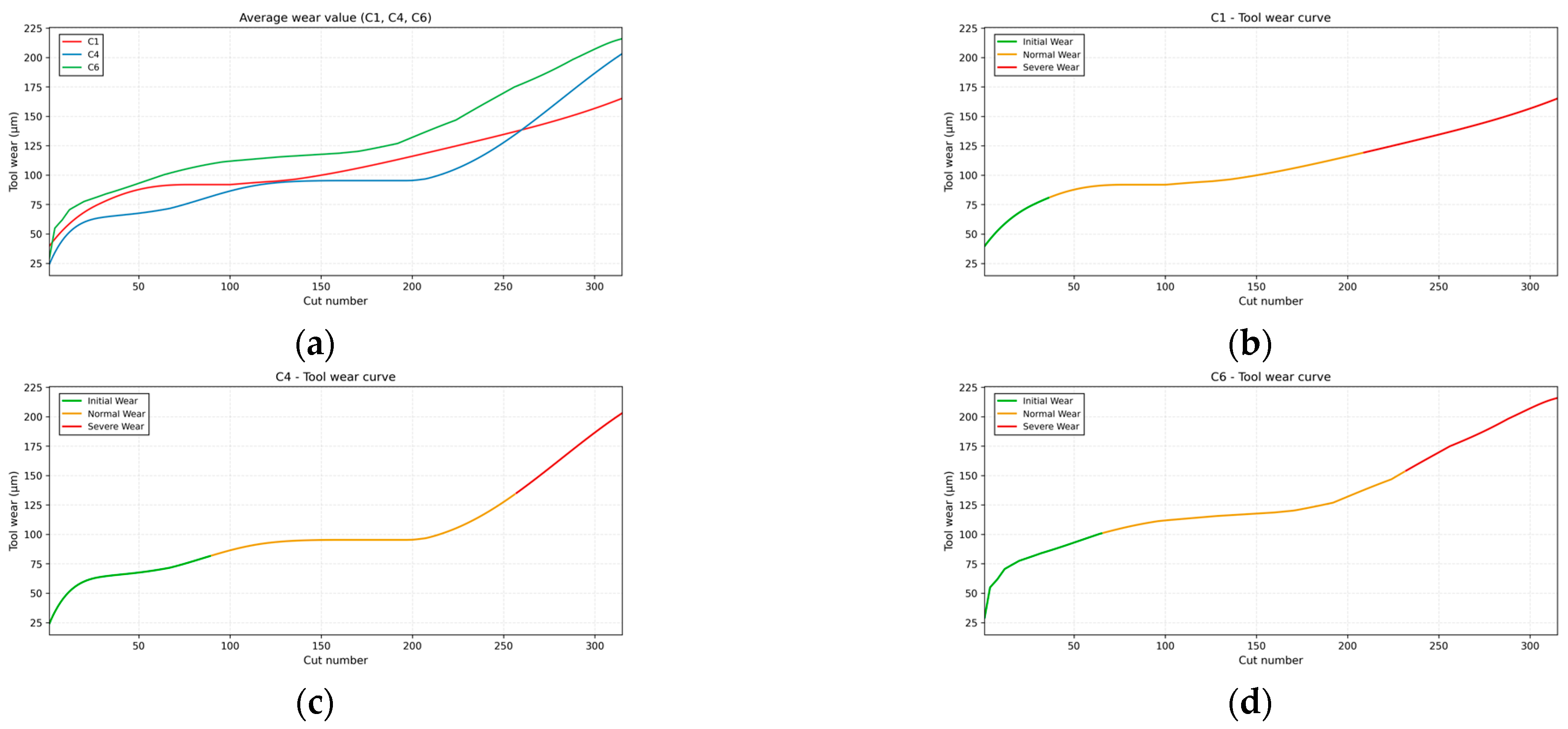
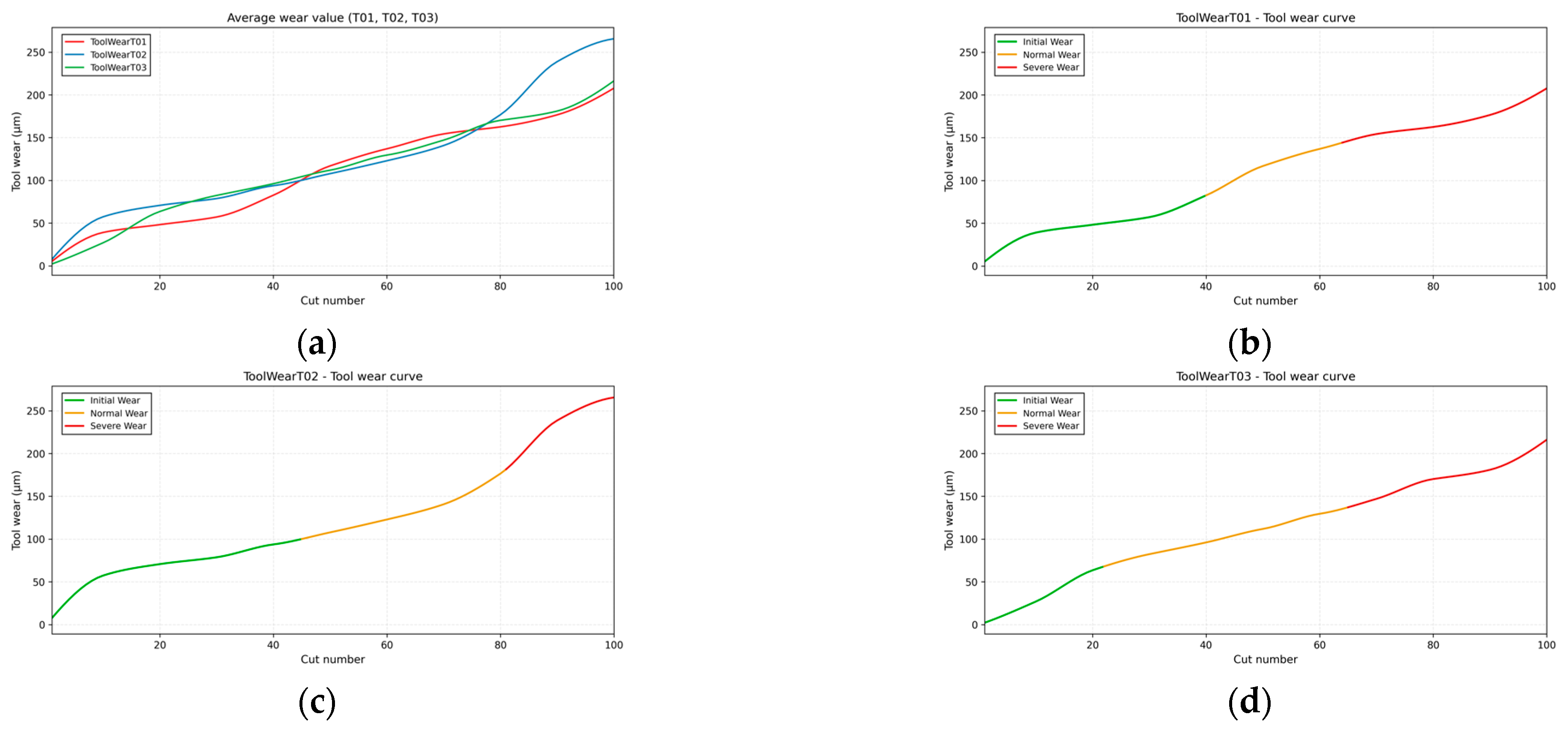
In this study, a total of 315 tool wear data points from three experimental sets, C1, C4, and C6, were used, with each data point consisting of wear values from three cutting edges. Since using the wear value from a single cutting edge does not accurately reflect the overall tool wear, the average wear value of the three cutting edges is used to determine the tool’s wear state. Figure 9a shows the average wear value of each dataset’s three cutting edges, intuitively reflecting the overall wear evolution.

To accurately classify the tool’s wear state, the K-means clustering algorithm was employed to categorize the data from C1, C4, and C6 into three wear states: initial wear, normal wear, and severe wear. Figure 9b–d present the wear curves for each of the three wear states, clearly depicting the evolution of wear across different stages. The classification results are shown in

Table 2. Classification of wear states for C1, C4, and C6 datasets.

Dataset	Initial Wear	Normal Wear	Severe Wear
C1	1–36	37–208	209–315
C4	1–89	90–256	257–315
C6	1–65	66–231	232–315

.

After classification, the datasets were split into training and validation sets in a 7:3 ratio to ensure proper data distribution during the training and validation process.

Table 3. Dataset division for tool wear stages: total samples, training set, and validation set.

Wear Stage	Total Samples	Training Set	Validation Set
Initial wear	190	133	57
Normal wear	505	354	151
Severe wear	250	175	75

provides the specific division of the training and validation datasets. This ensures the accurate classification of tool wear data for subsequent model training and performance evaluation.

3.2. Baseline System Comparison

To ensure the rigor of the experimental methodology, the number of images and the data splitting ratio for each method were kept consistent with the SSA-CWT approach, and all experiments were conducted using the same equipment. The experiments were performed on a computer running Windows 11 64-bit Professional, equipped with a 13th Gen Intel^® Core™ i5-13600KF processor, 32 GB RAM, and an NVIDIA GeForce RTX 4070 GPU (12 GB of VRAM). The programming environment was Python 3.12, with the deep learning framework PyTorch GPU 2.1.0 + cu118 and the GPU acceleration library cuDNN 8.9.5, developed in PyCharm 2024.1.4 (Community Edition).

To evaluate the superiority and effectiveness of the proposed SSA-CWT method in tool wear state recognition, five typical image transformation methods were selected as baseline comparisons. These methods, widely used in the field of tool wear state recognition, include Recursion Plot (RP), Markov Transition Field (MTF), Gram Angular Field (GAF), Short-Time Fourier Transform (STFT), and Continuous Wavelet Transform (CWT). For each of these methods, the cutting force and vibration signals were processed to extract features and generate corresponding time-frequency or feature images, which were then used for performance comparison with the SSA-CWT method. The time-frequency image datasets for cutting force signals are presented in

Table 4. Representative time–frequency transformation methods and spectrograms of cutting force signals.

Transfer Method	Conversion Formula	Initial Wear	Normal Wear	Severe Wear
RP	$\mathrm{R}{\mathrm{P}}_{\mathrm{i}\mathrm{j}}=\mathrm{H}\left(\mathsf{ϵ}-\left|{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}\right|\right)$
MTF	${\mathrm{M}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\sum }_{\mathrm{k}=1}^{\mathrm{N}-1}\left({\mathrm{x}}_{\mathrm{k}}=\mathrm{i}\wedge {\mathrm{x}}_{\mathrm{k}+1}=\mathrm{j}\right)}{{\sum }_{\mathrm{k}=1}^{\mathrm{N}-1}\left({\mathrm{x}}_{\mathrm{k}}=\mathrm{i}\right)}}$
GAF	${\mathrm{G}}_{\mathrm{i},\mathrm{j}}=\cos \left({\mathsf{\phi }}_{\mathrm{i}}-{\mathsf{\phi }}_{\mathrm{j}}\right)$
STFT	$\mathrm{X}\left[\mathrm{m},\mathrm{k}\right]={\displaystyle \sum _{\mathrm{n}=0}^{\mathrm{N}-1}}\mathrm{x}\left[\mathrm{n} \mathrm{m}\mathrm{H}\right]\hspace{0.17em}\mathrm{w}\left[\mathrm{n}\right]\hspace{0.17em}{\mathrm{e}}^{-\mathrm{j}\backslash \mathrm{t}\mathrm{f}\mathrm{r}\mathrm{a}\mathrm{c}2\mathsf{\pi }\mathrm{N}\mathrm{k}\mathrm{n}}$
CWT comr2-1	$\mathrm{C}\mathrm{W}\mathrm{T}\left(\mathrm{s},\mathsf{\tau }\right)={\displaystyle \frac{1}{\sqrt{\left|\mathrm{s}\right|}}}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\left(\mathrm{t}\right)\hspace{0.17em}{\mathsf{\psi }}^{\mathrm{*}}!\left({\displaystyle \frac{\mathrm{t}-\mathsf{\tau }}{\mathrm{s}}}\right)\mathrm{d}\mathrm{t}$

, while the datasets for vibration signals are provided in

Table 5. Representative time–frequency transformation methods and spectrograms of vibration signals.

Transfer Method	Conversion Formula	Initial Wear	Normal Wear	Severe Wear
PR	$\mathrm{R}{\mathrm{P}}_{\mathrm{i}\mathrm{j}}=\mathrm{H}\left(\mathsf{ϵ}-\left|{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}\right|\right)$
MTF	${\mathrm{M}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\sum }_{\mathrm{k}=1}^{\mathrm{N}-1}\left({\mathrm{x}}_{\mathrm{k}}=\mathrm{i}\wedge {\mathrm{x}}_{\mathrm{k}+1}=\mathrm{j}\right)}{{\sum }_{\mathrm{k}=1}^{\mathrm{N}-1}\left({\mathrm{x}}_{\mathrm{k}}=\mathrm{i}\right)}}$
GAF	${\mathrm{G}}_{\mathrm{i},\mathrm{j}}=\cos \left({\mathsf{\phi }}_{\mathrm{i}}-{\mathsf{\phi }}_{\mathrm{j}}\right)$
STFT	$\mathrm{X}\left[\mathrm{m},\mathrm{k}\right]={\displaystyle \sum _{\mathrm{n}=0}^{\mathrm{N}-1}}\mathrm{x}\left[\mathrm{n} \mathrm{m}\mathrm{H}\right]\hspace{0.17em}\mathrm{w}\left[\mathrm{n}\right]\hspace{0.17em}{\mathrm{e}}^{-\mathrm{j}\backslash \mathrm{t}\mathrm{f}\mathrm{r}\mathrm{a}\mathrm{c}2\mathsf{\pi }\mathrm{N}\mathrm{k}\mathrm{n}}$
CWT comr2-1	$\mathrm{C}\mathrm{W}\mathrm{T}\left(\mathrm{s},\mathsf{\tau }\right)={\displaystyle \frac{1}{\sqrt{\left|\mathrm{s}\right|}}}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{x}\left(\mathrm{t}\right)\hspace{0.17em}{\mathsf{\psi }}^{\mathrm{*}}!\left({\displaystyle \frac{\mathrm{t}-\mathsf{\tau }}{\mathrm{s}}}\right)\mathrm{d}\mathrm{t}$

. The core formulas and typical time-frequency spectrograms for each method are also listed in the tables.

To evaluate the effectiveness of different time–frequency feature transformation methods in tool wear state recognition, we compared the performance of six feature representation methods—PR, MTF, GAF, STFT, CWT, and SSA-CWT—in terms of accuracy and loss. All experiments were conducted under the same network architecture and hyperparameter settings. The corresponding hyperparameters are listed in

Table 6. Hyperparameters for model training.

Parameter	Values
Input Image Size	224 × 224
Batch Size	32
Number of Classes	3
Number of Epochs	50
Learning Rate	0.001
Optimizer	AdamW
Weight Decay	1 × 10−4

, and the results are illustrated in Figure 10. Additionally, the confusion matrices for the output results are shown in Figure 11, providing a comprehensive view of the recognition accuracy across different tool wear stages.

3.3. Single-Signal and Multi-Signal Fusion Experiments

To evaluate the effectiveness of the proposed multi-signal fusion strategy, comparative experiments were conducted between single-signal and multi-signal configurations. In the single-signal mode, either vibration or cutting force data was used as the model input. All signals underwent identical preprocessing procedures, including the generation of time–frequency spectrograms using the SSA-optimized Continuous Wavelet Transform (SSA-CWT). These were then fed into a single branch of the Time–Frequency Fusion Network (TFFN), with the cross-modal fusion module disabled to maintain structural consistency. Each configuration was trained and evaluated five times independently, and the average classification accuracy was recorded to ensure statistical stability and reliability.

In the multi-signal mode, both vibration and cutting force signals were simultaneously used as inputs. Each modality passed through the local feature extraction and global feature modeling modules before being fused via the Shifted Window Multi-Head Cross-Attention (SW-MCA) mechanism. This enabled adaptive cross-modal interaction and complementary enhancement in the time–frequency domain. All models shared identical hyperparameters, training epochs, and data partitioning to ensure fair comparison. The experimental results are presented in Figure 12 and

Table 7. Tool wear classification accuracy for different signal input modes across five independent runs.

Signal Type	Tool Wear Classification Accuracy (%)
	1	2	3	4	5
Force Signal	91.15	92.26	91.83	92.56	92.78
Vibration Signal	71.74	72.31	71.47	72.89	71.34
Fusion Signal	97.36	98.45	97.41	97.25	98.73

, while the corresponding confusion matrices for different input configurations are illustrated in Figure 13.

3.4. Ablation Study on SSA-Optimized CWT Parameters

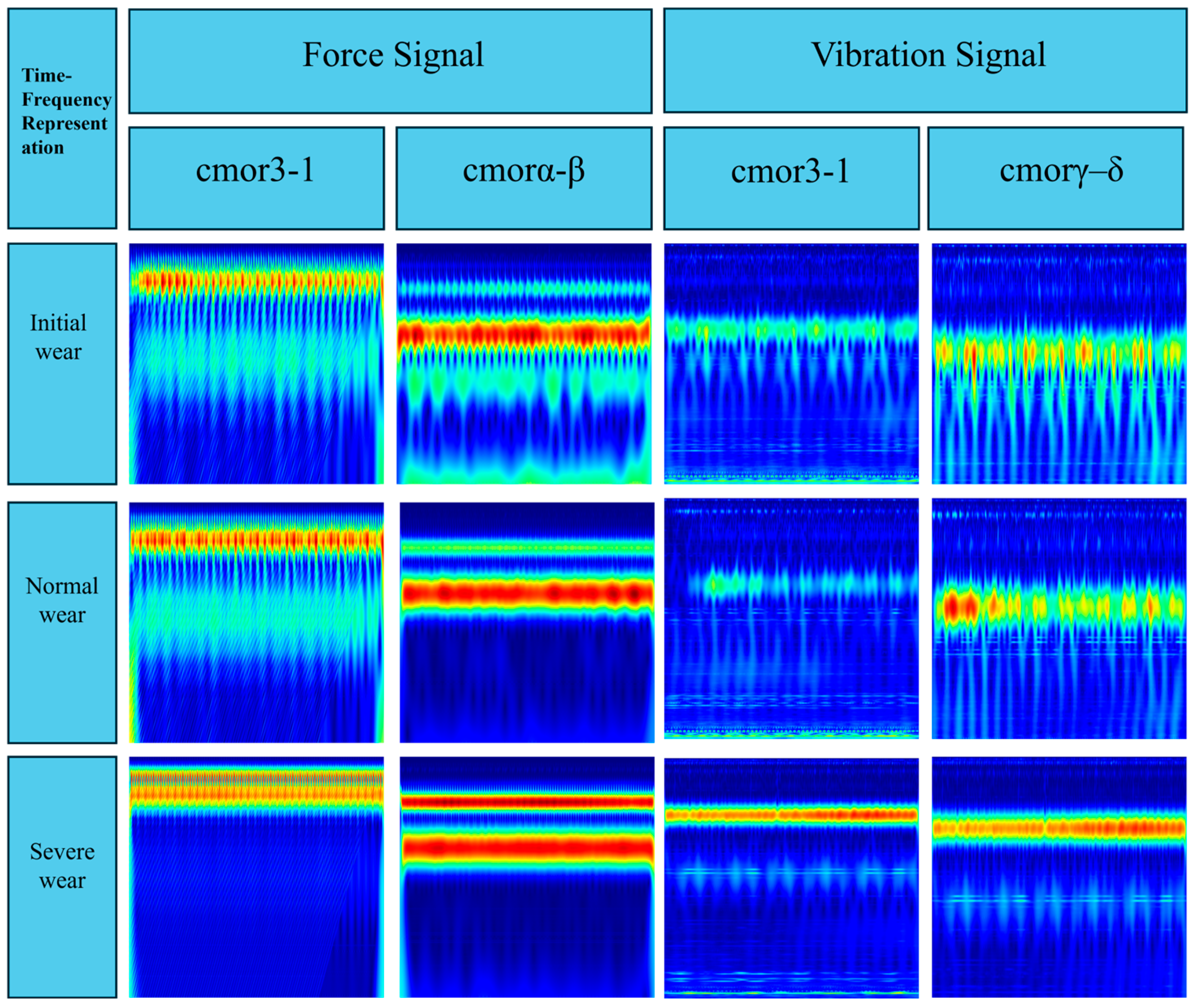
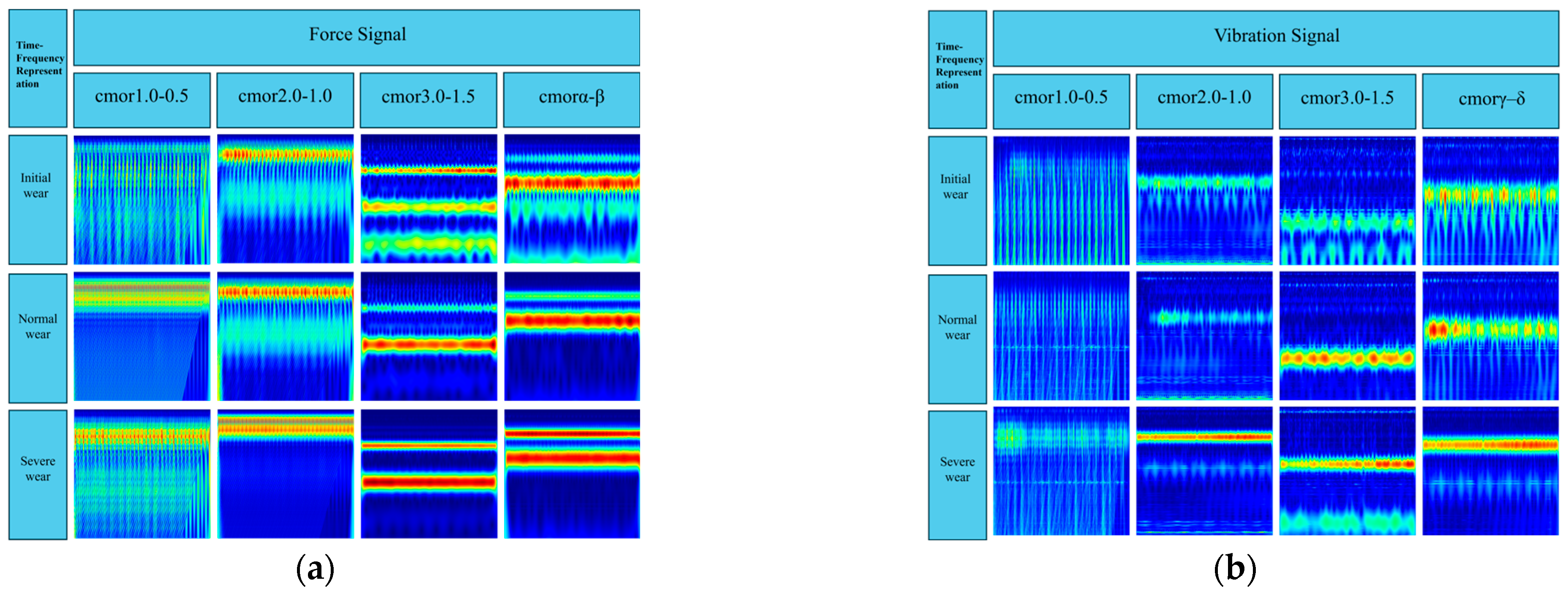
To quantitatively evaluate the impact of CWT parameters on recognition performance and to verify the effectiveness of the proposed SSA-CWT module, an ablation study with four representative complex Morlet (cmor) wavelet configurations was designed based on the time–frequency representations shown in Figure 14a,b. Specifically, Figure 14a illustrates the time–frequency distributions of the cutting force signal under different cmor parameter settings and wear stages, whereas Figure 14b depicts the corresponding results for the vibration signal. Three fixed parameter settings, cmor1.0–0.5, cmor2.0–1.0, and cmor3.0–1.5, were selected as manually designed baseline configurations, and the fourth configuration corresponds to the wavelet parameter pairs optimized by the Sparrow Search Algorithm (SSA), where the cutting force and vibration signals adopt cmorα–β and cmorγ–δ, respectively. For all configurations, an identical multimodal processing pipeline was employed: the three-axis cutting force and vibration signals were first denoised using Hampel filtering and fused by energy-based weighting; high-energy segments were then extracted, and two-dimensional time–frequency representations were obtained via CWT with the corresponding cmor parameters. Finally, the bimodal time–frequency maps of force and vibration were fed into TFF-Net, and all models were trained and tested under the same data partitions and hyperparameter settings to ensure a fair comparison.

For all configurations, an identical multimodal processing pipeline was employed. First, the three-axis cutting force and vibration signals were denoised using Hampel filtering and fused via energy-based weighting. High-energy signal segments were then extracted, and two-dimensional time–frequency representations were obtained by applying CWT with the corresponding cmor parameters. Finally, the bimodal time–frequency maps of force and vibration were fed into TFF-Net, and all models were trained and evaluated under the same data partitions and hyperparameter settings to ensure a fair comparison.

The quantitative results of this ablation study are summarized in

Table 8. Ablation study of tool wear recognition performance under different cmor wavelet parameter configurations.

Config	Wavelet Parameters (Force)	Wavelet Parameters (Vibrations)	Accuracy (%)	F1-Score (%)	Recall (%)	Precision (%)
A	cmor1.0–0.5	cmor1.0–0.5	93.34	93.80	93.56	93.05
B	cmor2.0–1.0	cmor2.0–1.0	95.21	95.74	95.50	95.98
C	cmor3.0–1.5	cmor3.0–1.5	96.08	96.65	96.41	96.92
D	cmorα–β (SSA-optimized)	cmorγ–δ (SSA-optimized)	98.3	98.1	98.0	97.9

, which reports the accuracy, F1-score, recall, and precision of the four parameter configurations on the tool wear recognition task. It can be observed that the three manually designed wavelet parameter settings (Configs A–C) already achieve high recognition performance, while the SSA-optimized configuration D (cmorα–β for the force signal and cmorγ–δ for the vibration signal) attains the highest values across all four evaluation metrics, yielding an overall recognition performance superior to that of the manual baseline Config C.

3.5. Ablation Study of the Proposed Framework

In this section, an ablation study is conducted to evaluate the individual contribution of each component in the proposed framework. Specifically, we investigate the impact of SSA-based wavelet parameter optimization, CWT configuration, preprocessing procedures (Hampel filtering and energy-based fusion), and the cross-modal attention mechanism on tool wear recognition performance. To this end, five model configurations with clearly defined structural differences (Configs A–E) are constructed and trained under identical data partitions and hyperparameter settings to ensure a fair comparison.

Configuration A (Baseline) disables SSA optimization and employs a conventional CWT with fixed cmor3.0–1.5 parameters, without Hampel filtering or energy fusion. The resulting time–frequency representations are directly fed into TFF-Net and serve as the baseline for overall performance comparison. Configuration B corresponds to the full framework without Hampel filtering: the raw three-axis cutting force and vibration signals are first fused by energy-based weighting and then transformed by SSA-optimized CWT before being input to TFF-Net. This setting is used to assess the contribution of Hampel filtering and quantify the effect of noise suppression on feature stability and model robustness. Configuration C retains SSA optimization and Hampel filtering but disables multi-axis energy fusion; instead, only the Fx-axis cutting force component is used as a single-channel input to SSA-CWT and the subsequent network. By comparing this configuration with those using fused multi-axis signals, the benefit of the proposed energy fusion strategy can be quantitatively evaluated. Configuration D preserves SSA optimization, Hampel filtering, and multi-axis energy fusion, but restricts the model to a single modality, i.e., the cutting force signal only, while completely removing the vibration modality and the cross-modal attention mechanism. This design isolates the effect of multimodal interaction and cross-modal attention beyond the influence of preprocessing and time–frequency representation. Finally, Configuration E (Full model) integrates all components of the proposed system, including SSA-optimized CWT, Hampel filtering, energy-based fusion, and the cross-modal attention mechanism, and therefore represents the complete framework and serves as an upper-bound reference.

By comparing the performance of Configurations A–E in terms of accuracy, F1-score, recall, and precision, this ablation study quantitatively reveals the contribution of each module and demonstrates the necessity and effectiveness of SSA optimization, signal preprocessing, multimodal fusion, and cross-modal attention in enhancing tool wear recognition. The corresponding results are summarized in

Table 9. Ablation study results of the proposed framework.

Experiment ID	Accuracy (%)	F1-Score (%)	Recall (%)	Precision (%)
A (Baseline)	92.3	91.8	91.5	92.0
B	93.2	92.7	92.5	93.0
C	94.1	93.7	93.4	93.9
D	95.3	94.9	94.6	95.1
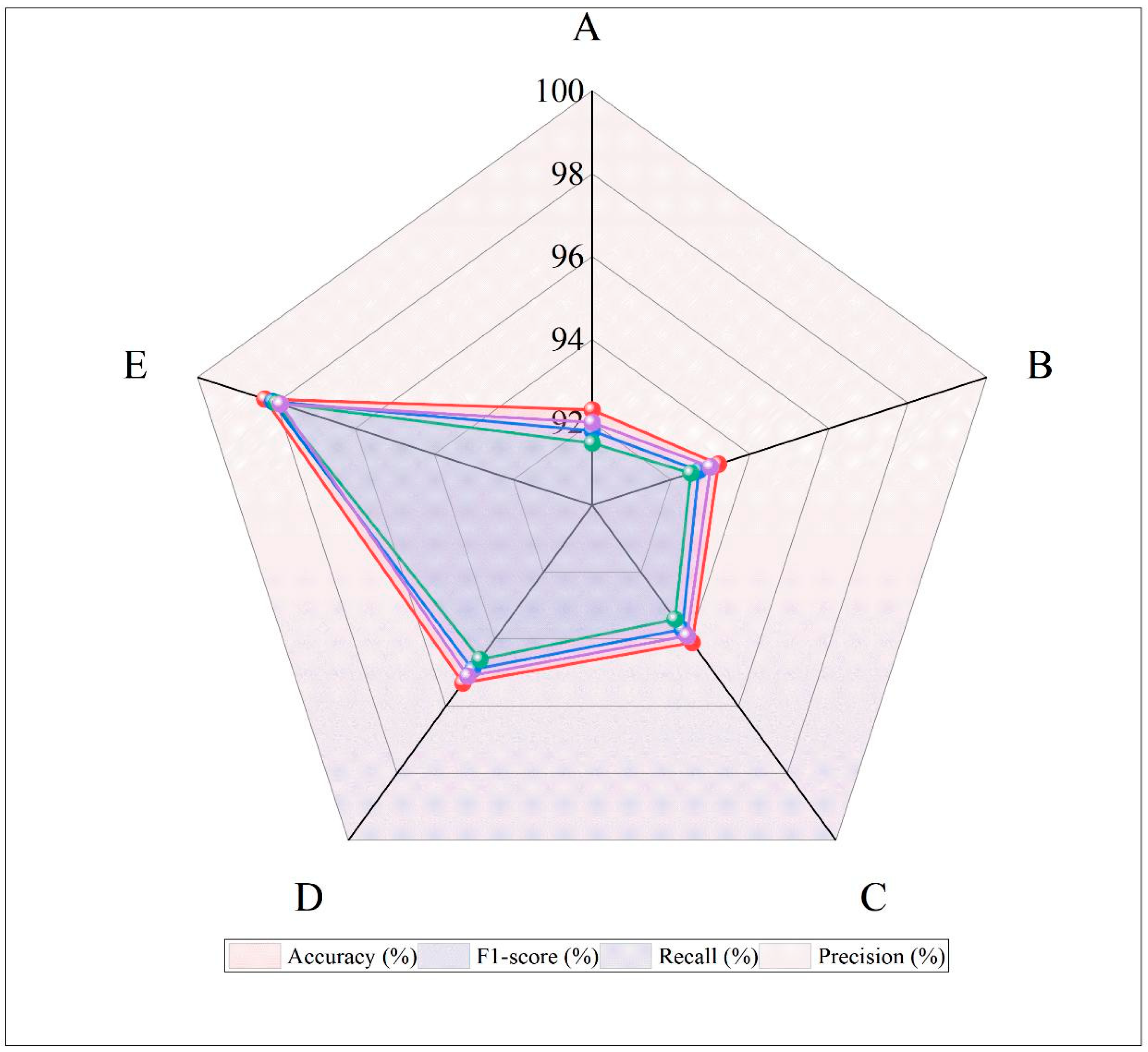
E (Full Model)	98.3	98.1	98.0	97.9

, and the performance comparison across these configurations is visually represented in Figure 15, which illustrates the differences in tool wear recognition performance for each configuration.

3.6. Comparative Study of Cross-Modal Fusion Strategies

To evaluate the fusion effectiveness of the proposed sliding-window multi-head cross-modal attention mechanism (SW-MCA) and to compare it against commonly used cross-modal fusion methods, a dedicated set of experiments on fusion strategies was conducted. In these experiments, the SSA-CWT-based time–frequency representations of cutting force and vibration signals, as well as the backbone architecture of TFF-Net, were kept unchanged, while only the cross-modal fusion module was replaced. In this way, performance differences can be attributed primarily to the choice of fusion strategy rather than changes in feature quality or model capacity. Specifically, five representative cross-modal fusion configurations were constructed: Fusion A (Early Concatenation), in which the time–frequency features of cutting force and vibration are directly concatenated along the channel dimension and fed into the subsequent network; Fusion B (Late Fusion), in which two independent unimodal branches for force and vibration are built, each performing feature extraction and classification, and their logits are combined by weighted averaging before the final softmax layer; Fusion C (Channel-Attention Fusion), where the two modalities are first concatenated along the channel dimension and then passed through an SE-like channel attention module to adaptively reweight the concatenated features; Fusion D (Global Cross-Attention), which applies a standard multi-head cross-modal attention layer over the entire temporal span between the force and vibration feature sequences to model global cross-modal dependencies; and Fusion E (SW-MCA, Proposed), which partitions the time axis into overlapping sliding windows, performs multi-head cross-modal attention within each local window, and subsequently aggregates the window-wise features. All fusion configurations share the same preprocessing pipeline (Hampel filtering and energy-based fusion), SSA-CWT parameter settings, data partition protocol, and training hyperparameters (optimizer, learning rate, batch size, and number of epochs).

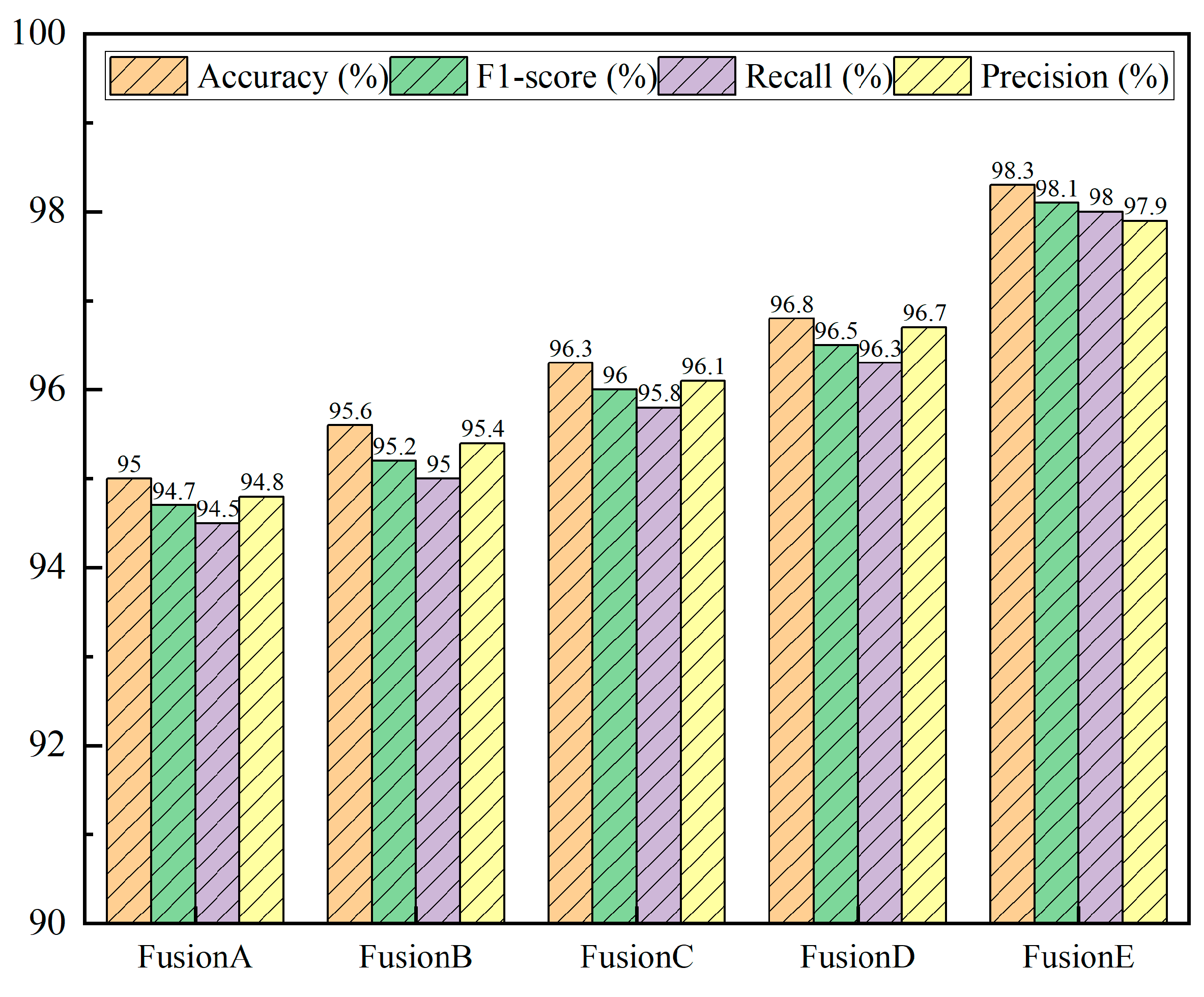
The quantitative results of different cross-modal fusion strategies on the tool wear stage classification task are summarized in

Table 10. Comparison of different cross-modal fusion strategies in tool wear stage classification.

Fusion-Strategy	Accuracy (%)	F1-Score (%)	Recall (%)	Precision (%)
FusionA	95.0	94.7	94.5	94.8
FusionB	95.6	95.2	95.0	95.4
FusionC	96.3	96.0	95.8	96.1
FusionD	96.8	96.5	96.3	96.7
FusionE	98.3	98.1	98.0	97.9

, where accuracy, F1-score, recall, and precision are reported as evaluation metrics. In addition, Figure 16 presents a bar-chart comparison of Fusion A–E across these four metrics, providing an intuitive visualization of the performance levels achieved by each fusion strategy.

3.7. Performance Comparison of Different Network Architectures

To validate the performance advantage of the proposed TFF-Net network structure in multimodal time-frequency feature modeling, a comparative experiment was conducted, selecting three typical deep learning models: ConvMixer [30], Conformer [31], and Moile-Former [32]. All models used the same input features, which are time-frequency representations of the cutting force and vibration signals optimized by SSA-CWT, and were trained under consistent hyperparameters to ensure fairness in the experiment.

Table 11. Tool wear stage classification metrics for different models.

Prediction Model	Tool Wear Stage Classification Metrics
	Accuracy (%)	F1-Score (%)	Recall(%)	Precision (%)	FPS	Total Training Time (50 epochs, min)
ConMixer	90.2	89.7	89.4	90.0	75	6.7
ConFormer	94.1	93.8	93.5	94.0	42	11.7
Moile-Former	95.0	94.7	94.5	94.8	60	8.3
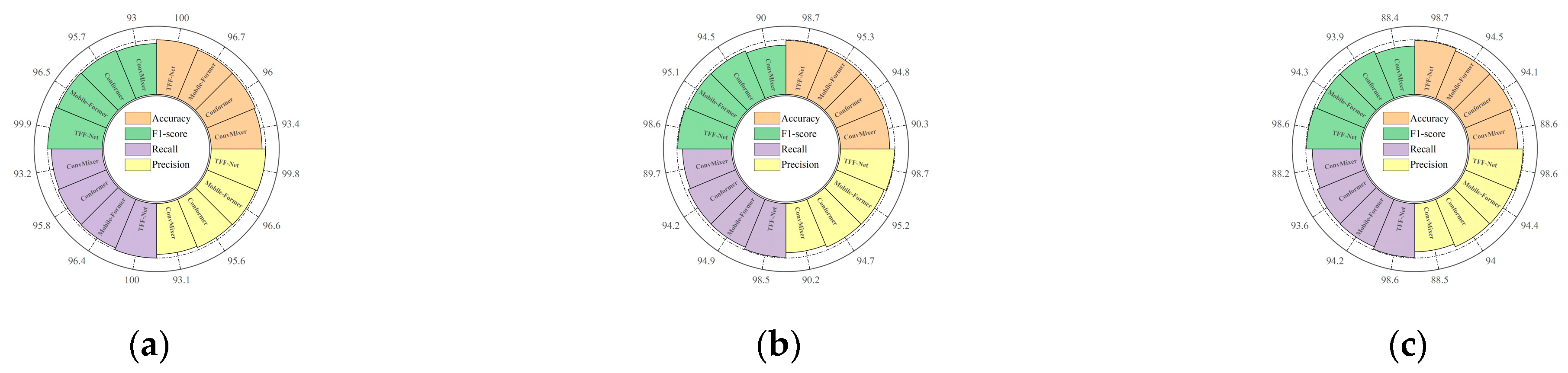
TFF-Net	98.3	98.1	98.0	97.9	35	15.0

presents the comprehensive performance comparison of the four models in the tool wear recognition task, with evaluation metrics including accuracy, F1-score, recall, precision, inference speed (FPS), and total training time. Additionally, Figure 17 illustrates the performance distribution across different wear stages, showing a multi-metric comparison of the four models at each stage.

3.8. External Validation Dataset (HMoTP Dataset) and Experimental Results

3.8.1. Experimental Equipment and Parameters

To further evaluate the generalization capability of the proposed model under different machining conditions and tool types, the HMoTP (High-performance Machining of Thin-walled Parts) open dataset was employed for external validation experiments.This dataset originates from tool wear monitoring experiments conducted during high-speed milling of thin-walled titanium alloy components and is designed to provide multi-source signal data for digital twin research in high-performance manufacturing. The workpiece materials were Ti6Al4V and Al7075, both of which are typical aerospace alloys with distinct mechanical and thermal properties. The cutting tool used was a 14 mm diameter double-insert carbide end mill (insert type APMT1135PDER, coated with (Al,Ti)N), operated under dry side-milling conditions throughout the full tool life. All experiments were performed on a Deckel Maho DMU70V five-axis CNC machining center to ensure machining precision and repeatability.

The signal acquisition system integrated multiple sensors to achieve synchronous multi-channel measurement. A Kistler rotating dynamometer was employed to measure the three-component cutting forces (Fx, Fy, Fz) and the axial bending moment (Mz). A Dytran 3263A1 tri-axial accelerometer, mounted on the back surface of the workpiece, was used to capture vibration signals (Vx, Vy, Vz). All channels were sampled at 5 kHz and transmitted to the host computer through a Kistler 5347A4 wireless acquisition module and a multi-channel charge amplifier for synchronous digitization. Each cutting pass was performed along a fixed toolpath under constant spindle speed and feed rate. In total, seven synchronized channels—cutting force, bending moment, and vibration—were recorded, effectively capturing the multimodal dynamic characteristics associated with tool wear evolution.

Tool wear was measured offline after every ten cutting passes using a LEICA digital microscope. The flank wear width (VB) was adopted as the evaluation metric, and based on the measured VB values, the tool wear states were categorized into three stages: initial wear (VB < 0.1 mm), normal wear (0.1 mm ≤ VB < 0.3 mm), and severe wear (VB ≥ 0.3 mm). The wear measurement point was selected at approximately half the distance from the cutting edge to the tool tip to minimize the influence of built-up edge and coating delamination. The complete experimental parameters are summarized in

Table 12. Experimental parameters.

Experiment Parameters	Values
Spindle speed (n)	8000 rpm
Feed per turn (f)	0.08 mm/r
Cutting depth (aP)	4 mm
Cutting width (ae)	0.2 mm
Sampling frequency	5 kHz

.

3.8.2. Dataset Division

In this study, a total of 300 tool wear samples were selected from three experimental sets (T01, T02, and T03) of the HMoTP dataset and used as an independent test set for external validation. The dataset was preprocessed and feature-extracted following the same procedure as the PHM2010 dataset, enabling direct input into the trained model to evaluate its generalization performance under different machining conditions. Each sample contained synchronized signals from seven sensor channels (Fx, Fy, Fz, Mz, Vx, Vy, and Vz) together with the corresponding flank wear value (VB). Since the wear value obtained from a single cutting edge could not accurately represent the overall tool condition, the average wear value of two cutting edges was adopted to determine the representative wear level, thereby reducing the influence of local wear anomalies on the overall evaluation. Figure 18a illustrates the averaged wear evolution curves of the three experimental sets in the HMoTP dataset, intuitively reflecting the overall wear progression of the tool under various machining conditions.

To ensure consistency with the PHM2010 dataset, the same wear-state division criteria were applied. Based on the averaged VB values, all samples were divided into three wear stages: initial wear (VB < 0.1 mm), normal wear (0.1 mm ≤ VB < 0.3 mm), and severe wear (VB ≥ 0.3 mm). In addition, the K-means clustering algorithm was employed to verify the intra-class compactness and inter-class separability of the samples, ensuring a balanced distribution across the three wear states. Figure 18b–d present the wear curves corresponding to each wear stage, clearly illustrating the gradual evolution of tool wear from mild abrasion to edge degradation. The statistical distribution of the samples in the three wear stages is summarized in

Table 13. Classification of wear states for T01, T02, and T03 datasets.

Dataset	Initial Wear	Normal Wear	Severe Wear
T01	1–40	41–64	65–100
T02	1–45	46–81	82–100
T03	1–22	23–65	66–100

.

3.8.3. Experimental Results

To verify the generalization capability of the proposed model, the trained TFF-Net was directly applied to an independent test set constructed from the HMoTP dataset, without any retraining or fine-tuning. The inference experiments were conducted under the same hardware configuration as in previous experiments to ensure consistency in computational conditions.

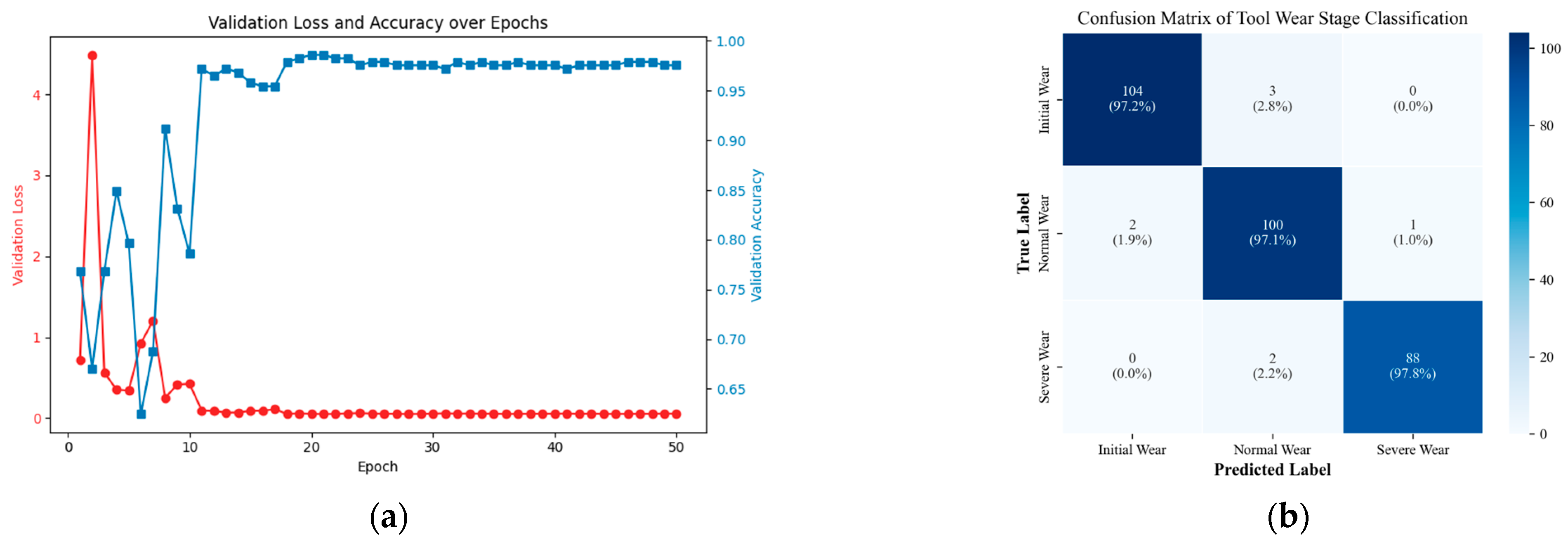
The training and validation performance of the model is illustrated in Figure 19a. During the training process, the validation loss rapidly decreases and stabilizes after approximately ten epochs, while the validation accuracy quickly rises and remains above 97% thereafter, demonstrating stable convergence and effective generalization.

After training, the model was evaluated on the HMoTP independent test set to assess its recognition performance under different machining conditions. The classification results are shown in Figure 19b, which presents the confusion matrix of tool wear stage classification. Out of the 300 test samples, the proposed TFF-Net correctly classified 97.3%, achieving class-wise accuracies of 97.2%, 97.1%, and 97.8% for the initial, normal, and severe wear stages, respectively.

4. Discussion

4.1. Analysis of Baseline System Comparison Results

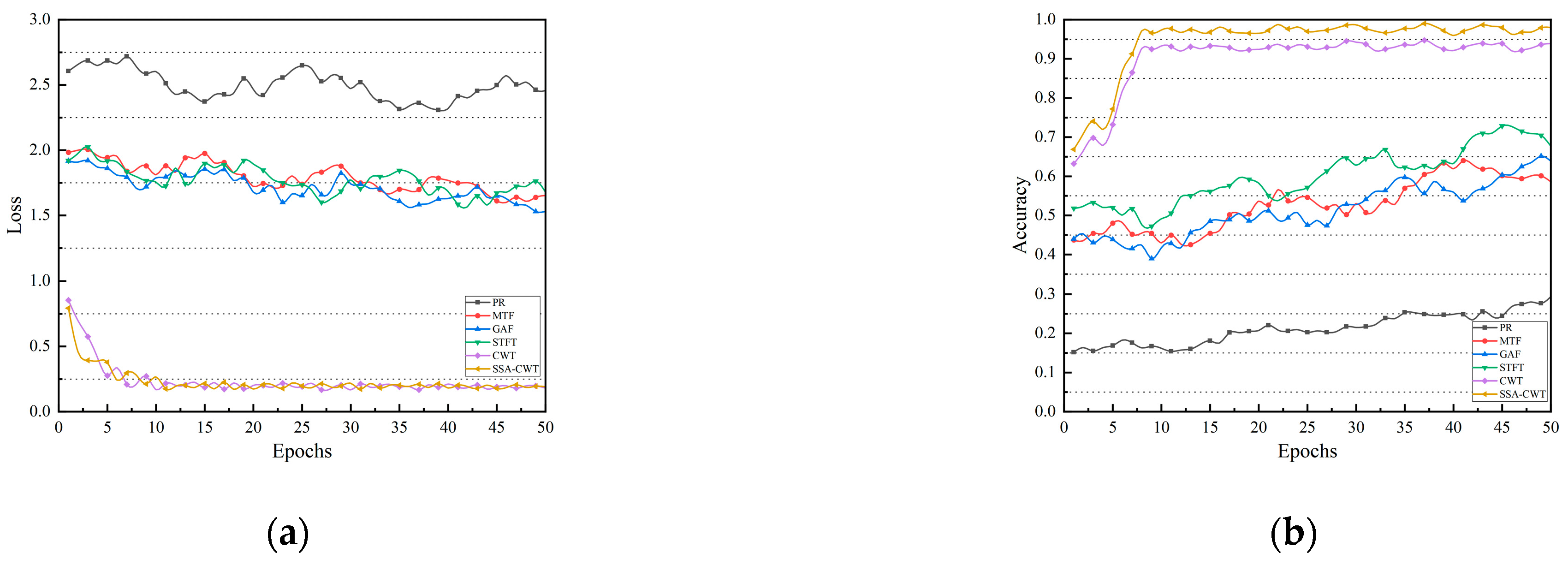
Figure 10b clearly demonstrates the significant differences in accuracy and loss curves between the various methods. The SSA-CWT method exhibits the best classification performance and convergence characteristics throughout the training process. In the early stages of training (around the 5th epoch), the accuracy of SSA-CWT exceeds 0.90 and stabilizes after the 10th epoch, ultimately maintaining between 0.98 and 0.99, almost achieving complete convergence. In contrast, the traditional CWT method shows a similar upward trend, but with a slower pace, stabilizing at 0.94–0.96 after the 10th epoch. The STFT method reaches approximately 0.68–0.70 by the 50th epoch, while the final accuracy for GAF and MTF are 0.62 and 0.58, respectively. The PR method performs the worst, with accuracy remaining between 0.15 and 0.25 throughout the entire training process.

The change in loss curves in Figure 10a further validates these results. SSA-CWT’s training loss drops sharply within the first 5 epochs, from an initial value of around 0.8 to below 0.1, and remains stable with minimal fluctuation throughout the training process. The CWT method’s convergence is slightly slower, with loss dropping to 0.15–0.2 after the 10th epoch and stabilizing. In contrast, the losses for STFT, GAF, and MTF remain in the range of 1.5–1.8, with slow declines and noticeable fluctuations. The loss curve for the PR method shows almost no significant decrease, hovering between 2.4 and 2.7 for most of the training process.

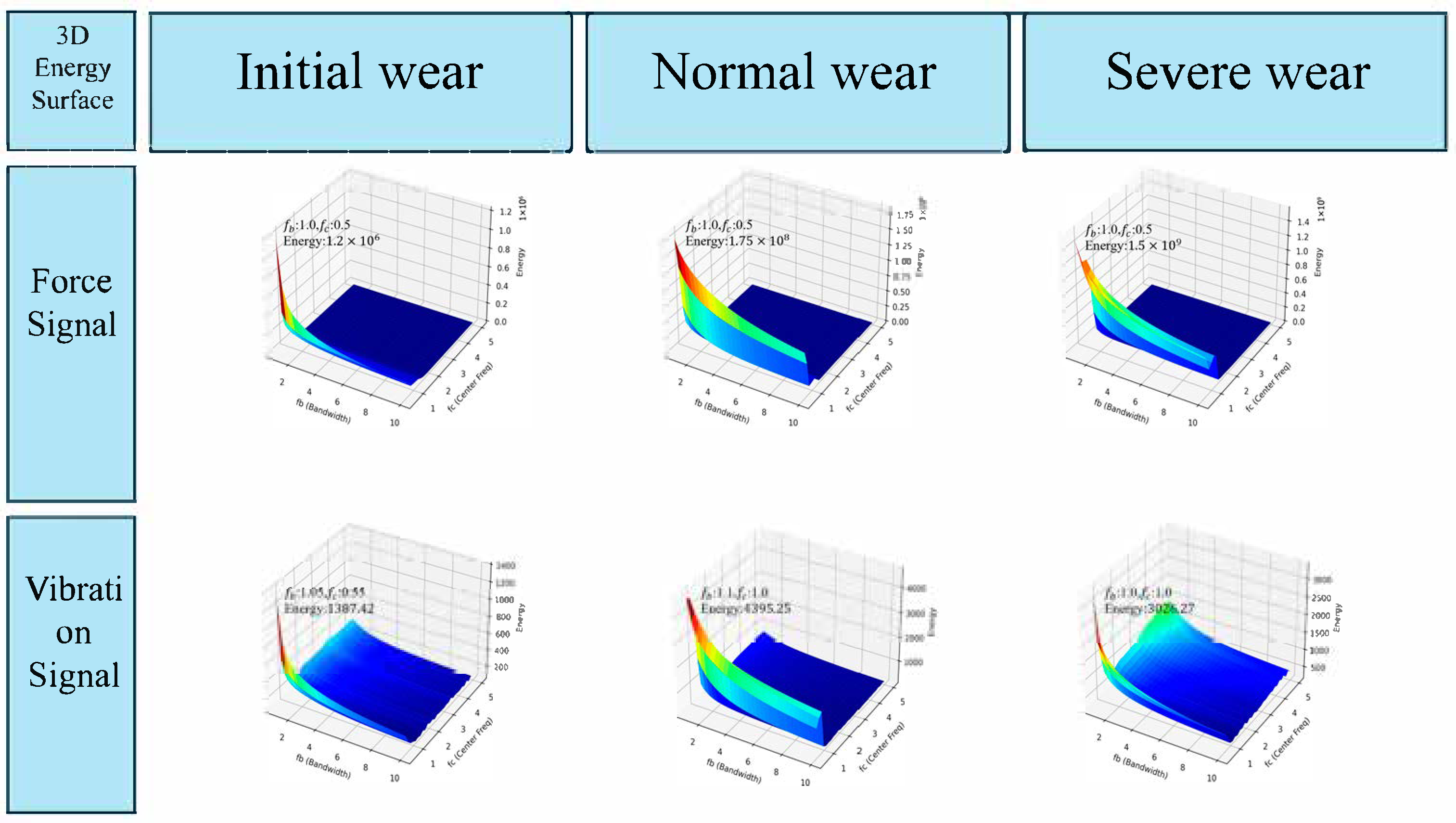
Clearly, SSA-CWT not only achieves the highest accuracy but also demonstrates the lowest loss and the most stable convergence behavior. The significant advantage of SSA-CWT is attributed to its use of the Sparrow Search Algorithm (SSA) for the adaptive optimization of the center frequency $f_c$ and bandwidth $f_b$ of the complex Morlet wavelet. This method minimizes energy entropy as the objective function, performing a global search for the optimal parameter combination on the parameter-energy surface. This results in the concentration of time-frequency energy in key frequency bands and effectively suppresses noise interference, creating clearer energy clustering features in the time-frequency representation. Compared to the fixed parameter CWT method, SSA-CWT not only maintains a balance in time-frequency resolution but also dynamically responds to changes in the frequency distribution of signals at different wear stages, thus capturing transient shocks and non-stationary characteristics of tool wear more effectively.

Therefore, when the time-frequency spectrogram generated by SSA-CWT is used as input to the TFFN, it significantly enhances the discriminability and energy focus of features, enabling the model to converge quickly in the early stages and maintain high accuracy and robustness throughout the training process. Overall, SSA-CWT outperforms PR, MTF, GAF, STFT, and CWT in terms of classification accuracy, convergence speed, and loss stability, demonstrating the effectiveness and superiority of the SSA-optimized wavelet parameter selection strategy in the analysis of tool wear state signals.

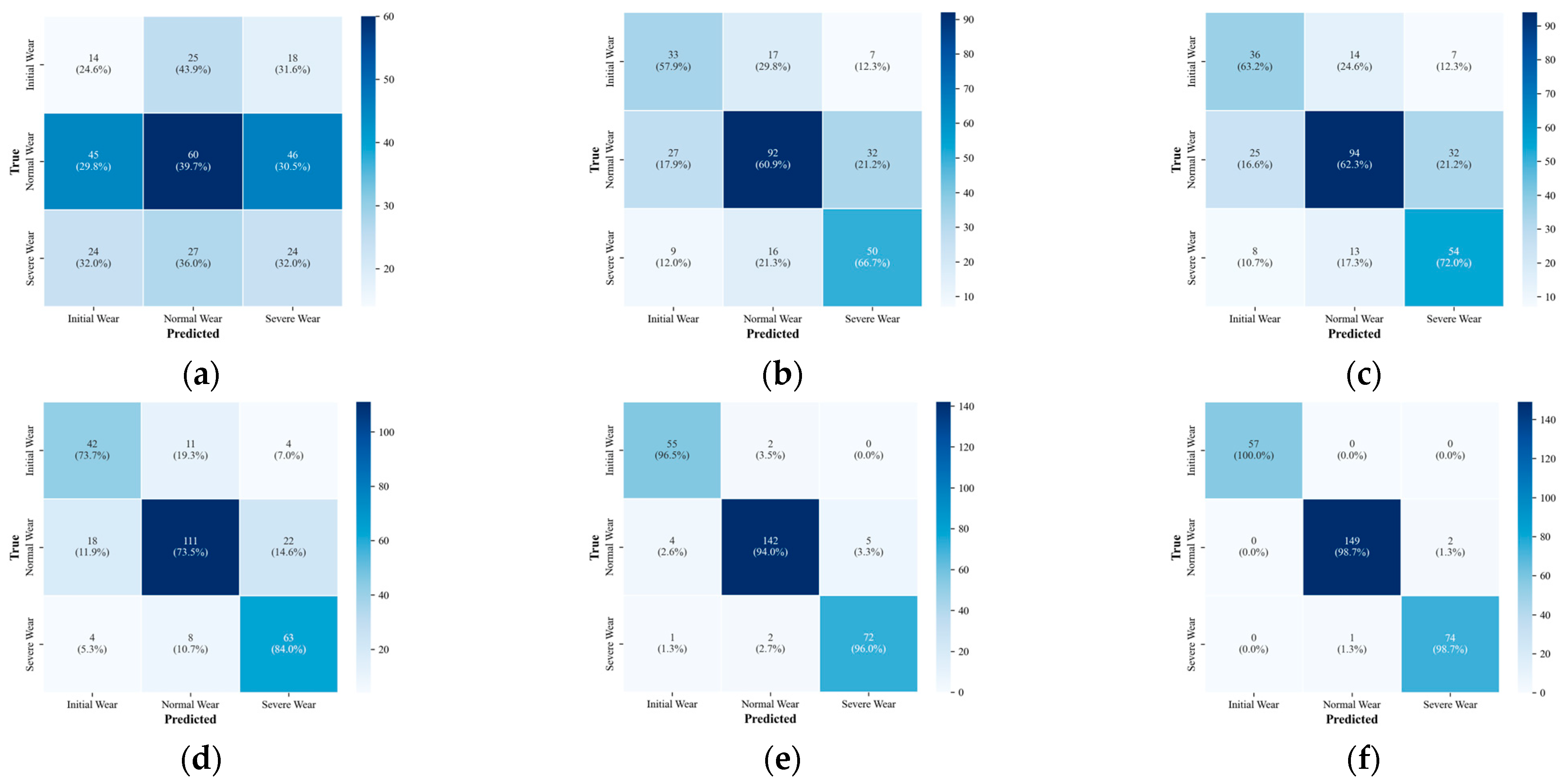
As shown in Figure 11, the six confusion matrices further validate the differences in classification capability among various time–frequency representation methods for tool wear recognition. Overall, SSA-CWT achieved the best performance across all wear stages, with recognition rates of 100% (initial wear), 98.7% (normal wear), and 98.7% (severe wear), and only three minor misclassifications between adjacent categories, demonstrating exceptional accuracy and stability.

In comparison, the CWT method achieved recognition rates of 96.5%/94.0%/96.0%, showing relatively strong overall performance but still exhibiting about 6% boundary confusion between the “normal–severe” classes. This indicates that fixed parameters in conventional CWT struggle to balance the resolution requirements for both high- and low-frequency features. Traditional time–frequency methods such as STFT, GAF, and MTF showed a significant performance drop, particularly in the “normal wear” category, with recognition rates of 73.5%, 62.3%, and 60.9%, respectively. They also exhibited pronounced bidirectional misclassification, reflecting that their energy distributions were overly dispersed and lacked clear inter-class clustering. The PR method performed the worst, with recognition rates below 45% for all wear stages, indicating an inability to effectively capture the non-stationary dynamics of the tool wear signals.

In summary, SSA-CWT, by employing the Sparrow Search Algorithm (SSA) to adaptively optimize the center frequency and bandwidth parameters of the complex Morlet wavelet, achieves highly concentrated signal energy distribution in key frequency bands while effectively suppressing noise. This approach significantly reduces the overlap in the “normal–severe” decision boundary. The proposed optimization strategy not only enhances the energy concentration and feature separability of the time–frequency representation but also improves the discriminative capability and robustness of the model. Consequently, it provides a more reliable and discriminative time–frequency representation framework for tool wear state recognition in complex machining systems.

4.2. Comparison of Single- and Multi-Signal Fusion Experiments

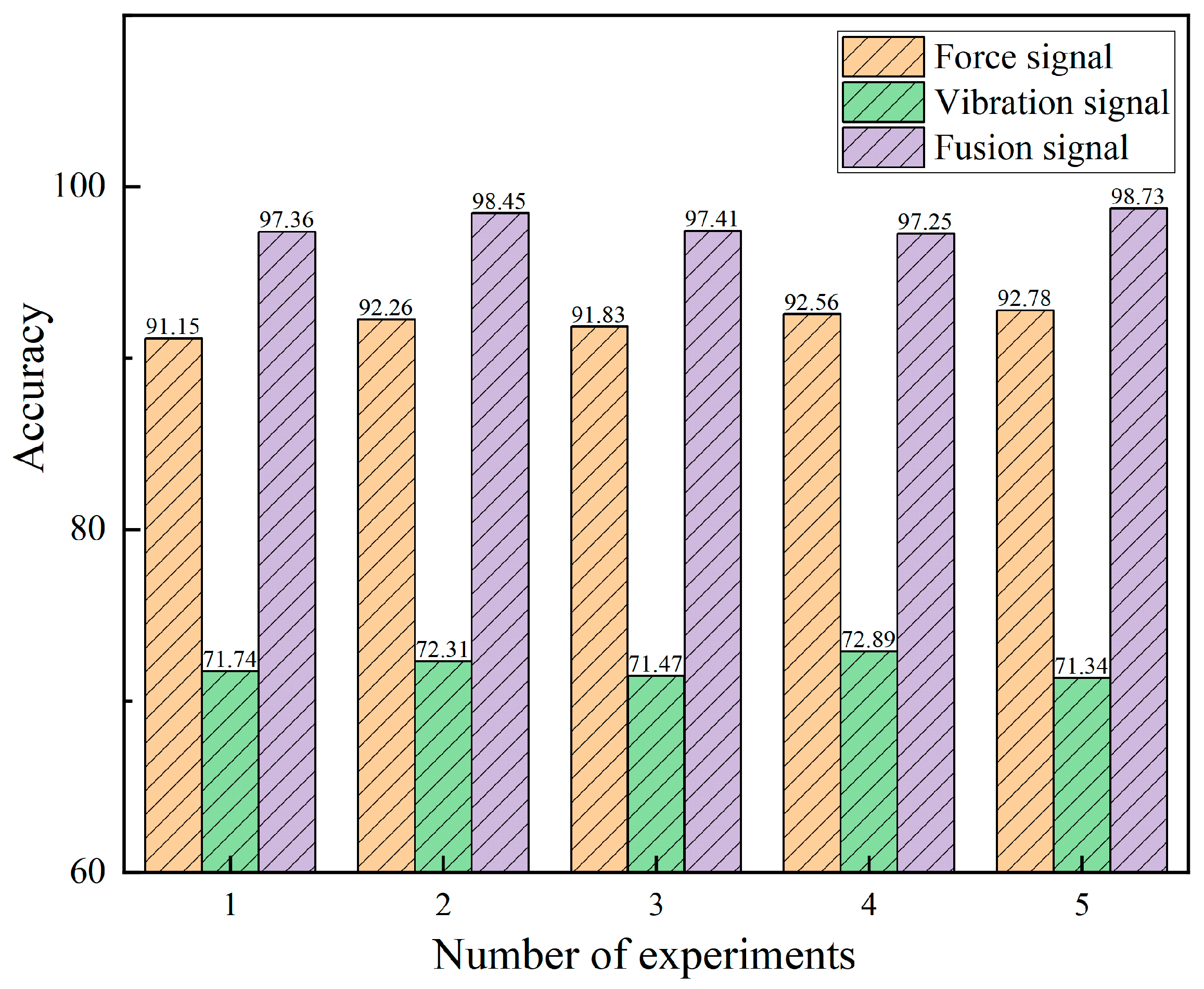
According to the experimental results presented in Table 7, there is a significant difference in the performance of the tool wear classification task between single-signal and multi-signal fusion modes. From the classification accuracy across five experimental runs, the cutting force signal consistently outperforms the vibration signal. The accuracy of the single cutting force signal remains stable between 91.15% and 92.78%, while the accuracy of the vibration signal fluctuates significantly, ranging from 71.34% to 72.89%. This indicates that the single vibration signal has relatively weak discriminative ability in the tool wear classification task and is unable to provide sufficient feature support.

However, when the multi-signal fusion mode is applied, the model’s classification accuracy improves significantly, ranging from 97.25% to 98.73%, with smaller fluctuations in accuracy across the five runs, indicating stronger stability. The complementary characteristics of the vibration and cutting force signals are maximized through the adaptive fusion enabled by the cross-modal attention mechanism (SW-MCA), which greatly enhances the classification performance.

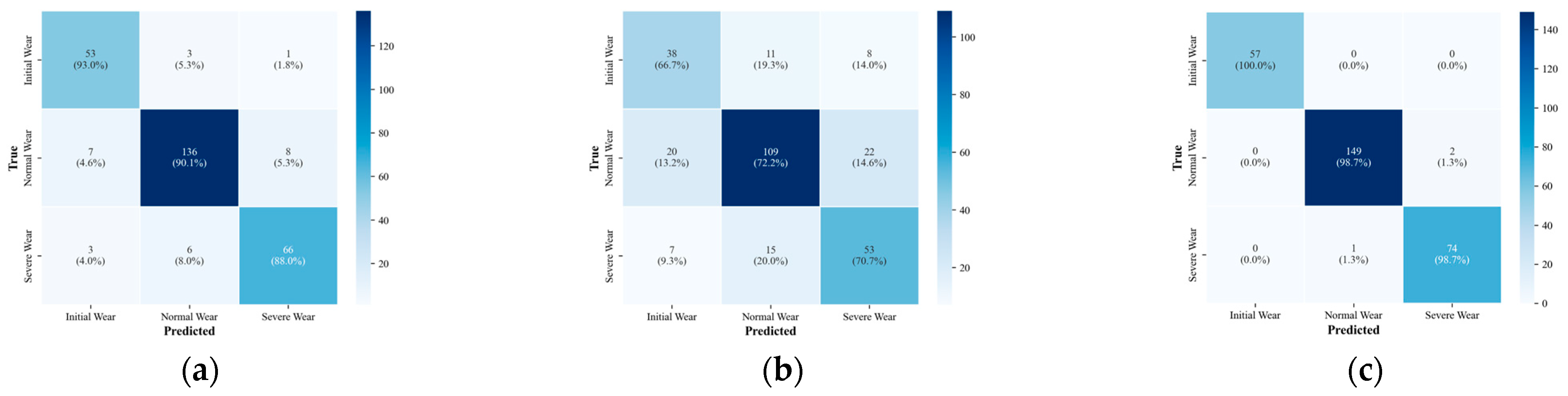
To further verify the effectiveness of the multi-signal fusion strategy, Figure 13 shows the confusion matrix results under different input modes. As shown in Figure 13a, when only the cutting force signal is used, the recognition accuracy for “initial wear” is relatively high (93%), but there is some confusion between the “normal wear” and “severe wear” categories. Figure 13b illustrates that the overall performance of the vibration signal is weaker, with recognition accuracies of 66.7%, 72.2%, and 70.7% for the three wear stages, indicating that its high-frequency features are more susceptible to noise interference, limiting its discriminative ability. In contrast, the multi-signal fusion result in Figure 13c is significantly better than the single-signal modes, with recognition accuracies of 100.0%, 98.7%, and 98.7% for the three wear stages. This improvement is attributed to the complementary characteristics of the cutting force and vibration signals in the time-frequency domain and the adaptive fusion via the cross-modal attention mechanism, enabling the model to fully exploit the feature advantages of both modalities and thereby significantly enhance classification accuracy and robustness.

4.3. Analysis of the Ablation Results on SSA-Optimized CWT Parameters

The ablation results in Table 8 and the time–frequency patterns shown in Figure 14 jointly demonstrate the importance of properly selecting the cmor wavelet parameters for tool wear recognition. Overall, the three manually designed configurations (Configs A–C) already achieve relatively high performance, confirming that CWT-based time–frequency features are effective for modeling the degradation process of the cutting tool. However, the gradual improvement from Config A to Config C also indicates that the recognition performance is sensitive to the choice of $(f_b,f_c)$, and that a suboptimal parameter setting may lead to insufficient feature discrimination.

Specifically, Config A (cmor1.0–0.5) yields the lowest accuracy and F1-score among the four settings. This configuration corresponds to a relatively narrow bandwidth and low center frequency, which tends to over-emphasize certain high-frequency components while introducing noticeable background fluctuations in the time–frequency maps, as seen in Figure 14. As a result, the time–frequency signatures of different wear stages exhibit partially overlapping patterns, and the separability of the learned features is limited. Config B (cmor2.0–1.0) improves the balance between time and frequency resolution, leading to more regular band structures and clearer energy concentrations in the mid-frequency range, which is reflected by the consistent increase in all four evaluation metrics.

Config C (cmor3.0–1.5) represents a manually tuned baseline that provides the best performance among the fixed parameter choices. In this case, the time–frequency representations of both the force and vibration signals show more stable, band-limited structures across wear stages, with reduced background interference and more distinct differences between the initial, normal, and severe conditions. Consequently, the classifier benefits from more discriminative features and achieves higher accuracy, F1-score, recall, and precision compared with Configs A and B.

Nonetheless, the SSA-optimized configuration (Config D, cmorα–β for force and cmorγ–δ for vibration) further improves the recognition performance beyond the manually tuned baseline. By searching the parameter space with energy entropy as the objective, SSA identifies wavelet parameters that yield more compact and stage-dependent energy distributions in the time–frequency plane. This can be clearly observed in Figure 14, where the SSA-based representations exhibit sharper energy bands, cleaner backgrounds, and more pronounced inter-stage contrasts for both modalities. Correspondingly, Config D achieves the highest accuracy, F1-score, recall, and precision among all four configurations, indicating that the automatically optimized CWT parameters enable TFF-Net to exploit more informative and less redundant features.

4.4. Results and Analysis of the Ablation Study

In this section, we present the results of the ablation study, evaluating the contribution of each component in the proposed framework. As shown in Table 9, we compare the performance of five configurations (A–E) in terms of accuracy, F1-score, recall, and precision. The results highlight the impact of each module on tool wear recognition performance and demonstrate the importance of combining SSA optimization, signal preprocessing, multimodal fusion, and the cross-modal attention mechanism.

Configuration A (Baseline) serves as the control experiment, disabling SSA optimization and using a conventional CWT with fixed cmor3.0–1.5 parameters, without Hampel filtering or energy fusion. As expected, it performs the worst across all metrics, with an accuracy of 92.3%, an F1-score of 91.8%, a recall of 91.5%, and a precision of 92.0%. This result underscores the crucial role of SSA optimization and signal preprocessing in improving model performance.

Configuration B introduces SSA optimization and energy fusion while removing Hampel filtering. This configuration results in a noticeable improvement across all metrics, with accuracy reaching 93.2%, F1-score of 92.7%, recall of 92.5%, and precision of 93.0%. This significant performance improvement demonstrates the contribution of SSA optimization and energy fusion to feature extraction and stability.

Configuration C retains SSA optimization and Hampel filtering but disables multi-axis energy fusion, instead using only the Fx-axis cutting force signal as a single-channel input for SSA-CWT and subsequent modeling. This configuration further improves performance, achieving an accuracy of 94.1%, an F1-score of 93.7%, a recall of 93.4%, and a precision of 93.9%. The results highlight the importance of multi-axis fusion in enhancing recognition performance and further validate the necessity of energy fusion for utilizing multi-axis information.

Configuration D preserves SSA optimization, Hampel filtering, and multi-axis energy fusion but restricts the model to a single modality, i.e., the cutting force signal only, while completely removing the vibration modality and the cross-modal attention mechanism. This configuration achieves an accuracy of 95.3%, an F1-score of 94.9%, a recall of 94.6%, and a precision of 95.1%, confirming the positive impact of the cross-modal attention mechanism in multimodal feature interaction and highlighting its significance in processing multimodal signals.

Finally, Configuration E (Full Model) integrates all components of the proposed system, including SSA-optimized CWT, Hampel filtering, energy fusion, and the cross-modal attention mechanism. This configuration performs the best across all metrics, with an accuracy of 98.3%, an F1-score of 98.1%, a recall of 98.0%, and a precision of 97.9%. This result clearly demonstrates that the combination of SSA optimization, preprocessing, multimodal fusion, and cross-modal attention maximizes the model’s tool wear recognition performance.

The results in Table 9 and the visual comparison in Figure 15 further illustrate the gradual performance improvements as more components are incorporated. SSA optimization alone (in Configuration B) leads to a significant performance boost, while additional preprocessing steps, such as Hampel filtering and energy fusion, further enhance the performance. The addition of the cross-modal attention mechanism (in Configuration E) brings the most significant improvement, confirming its crucial role in handling multimodal inputs and enhancing feature interaction.

In conclusion, this ablation study quantitatively demonstrates the necessity and effectiveness of each module in improving overall tool wear recognition performance.

4.5. Results and Discussion on Cross-Modal Fusion Strategies

The comparative results of different cross-modal fusion strategies are reported in Table 10, and their performance distributions are visualized in Figure 16. Overall, all five fusion schemes (Fusion A–E) achieve relatively high recognition performance, confirming the effectiveness of multimodal integration of cutting force and vibration signals for tool wear stage classification. However, clear performance differences can be observed as the fusion mechanism becomes progressively more structured and attention-aware. The simplest early feature concatenation scheme (Fusion A) yields the lowest performance, with an accuracy of 95.0%, F1-score of 94.7%, recall of 94.5%, and precision of 94.8%, indicating that naive stacking of multimodal features without explicit interaction modeling is suboptimal. Late fusion at the decision level (Fusion B) brings a modest improvement (95.6% accuracy), suggesting that independent unimodal experts with score-level aggregation can better exploit complementary information than raw feature concatenation, but still lack fine-grained cross-modal alignment in the feature space.

When channel-attention-based fusion (Fusion C) is adopted, all metrics improve further (96.3% accuracy, 96.0% F1-score), demonstrating that reweighting the concatenated channels helps emphasize more informative feature dimensions across modalities. The global cross-attention scheme (Fusion D) achieves the strongest performance among the baseline fusion strategies, with 96.8% accuracy, 96.5% F1-score, 96.3% recall, and 96.7% precision, showing that explicitly modeling global cross-modal dependencies between force and vibration sequences is more effective than simple concatenation or channel-wise recalibration. The proposed SW-MCA-based fusion (Fusion E) further surpasses all other configurations, achieving 98.3% accuracy, 98.1% F1-score, 98.0% recall, and 97.9% precision. Compared with the best baseline (Fusion D), SW-MCA provides gains of approximately 1.5% in accuracy, 1.6% in F1-score, 1.7% in recall, and 1.2% in precision. These results indicate that introducing sliding-window local cross-modal attention, rather than relying solely on global interactions, enables finer temporal alignment and more effective exploitation of complementary dynamics between cutting force and vibration signals, thereby yielding a more discriminative and robust multimodal representation for tool wear recognition.

4.6. Comparative Analysis of Different Network Architectures

As shown in Table 11 and Figure 17, the overall performance of all models significantly improves after the introduction of multi-source signal fusion, indicating that the joint representation of cutting force and vibration signals effectively enhances the time–frequency characterization and discriminative capability of the models. However, notable differences remain among the network architectures in terms of fusion efficiency and modeling capability, leading to varying degrees of performance improvement.

Among the four compared architectures, ConvMixer primarily relies on convolutional operations with local receptive fields, which limits its ability to capture long-range dependencies. Although multi-signal input slightly improves its classification performance, the model still struggles to fully exploit cross-modal feature correlations, resulting in a relatively low accuracy of 90.2%. Its training process is comparatively fast, requiring only 6.7 min for 50 epochs, but the overall performance improvement remains limited. In contrast, Conformer, which integrates convolutional and Transformer modules, achieves a better balance between local and global feature modeling, reaching an accuracy of 94.1%. However, its fixed fusion mechanism restricts adaptive weighting between modalities, leading to partial redundancy among features. Moreover, its training time is about 11.7 min, reflecting a higher computational complexity. Mobile-Former further enhances feature interaction through lightweight parallel channels and bidirectional communication, achieving both high accuracy (95.0%) and fast inference speed (60 FPS) with a moderate training time of 8.3 min. Nevertheless, the limited depth of cross-modal interaction constrains its ability to model complex nonlinear time–frequency dependencies.

In comparison, the proposed TFF-Net exhibits a distinct advantage in its feature fusion strategy. By incorporating a cross-modal attention mechanism (SW-MCA), the network adaptively allocates feature weights across modalities and achieves multi-scale feature alignment and compensation. The cutting force signal contributes stable low-frequency energy information, while the vibration signal captures high-frequency transient responses. Their complementary properties in the time–frequency domain significantly enhance the discriminability of the fused representation. As a result, TFF-Net achieves the best overall performance across all evaluation metrics—accuracy, F1-score, recall, and precision—all exceeding 98%. Although its inference speed (35 FPS) is slightly lower than that of Mobile-Former (60 FPS) and ConvMixer (75 FPS), and its training time is longer (15.0 min for 50 epochs), the substantial improvement in recognition accuracy and stability under complex operating conditions far outweighs the marginal increase in computational cost, demonstrating an excellent performance–efficiency balance.

Further insights can be drawn from the results at different tool wear stages. As illustrated in Figure 17a–c, TFF-Net consistently outperforms the other models throughout the entire wear process. In the initial wear stage (Figure 17a), where signal variations are minimal, all models exhibit relatively high classification accuracy. Nevertheless, TFF-Net stands out with a perfect 100% accuracy, and its F1-score, recall, and precision all exceed 99%, indicating superior sensitivity to subtle feature variations and excellent feature capture ability. In the normal wear stage (Figure 17b), as signal fluctuations intensify and feature complexity increases, the classification task becomes more challenging. TFF-Net maintains robust performance with an accuracy of 98.7%, showing remarkable stability and generalization. In contrast, Mobile-Former and Conformer show decreased accuracies of 95.3% and 94.8%, respectively, while ConvMixer drops to 90.3%, confirming that TFF-Net possesses stronger adaptability and resistance to dynamic signal perturbations. When entering the severe wear stage (Figure 17c), the energy distribution of the signals becomes highly uneven, and noise interference increases significantly, imposing higher demands on model robustness. Even under such challenging conditions, TFF-Net retains its superior performance, achieving 98.7% accuracy with F1-score, recall, and precision all exceeding 98%. In comparison, Mobile-Former and Conformer reach 94.5% and 94.1%, respectively, while ConvMixer drops to 88.6%, with more pronounced fluctuations.

Overall, TFF-Net achieves the best and most stable performance across all wear stages, fully validating its effectiveness in multi-source signal fusion and time–frequency feature modeling. The proposed architecture demonstrates strong robustness and adaptability, enabling high-precision and reliable recognition of tool wear states under complex operating conditions, thereby providing a promising solution for intelligent manufacturing and equipment health monitoring.

4.7. External Validation Dataset (HMoTP Dataset) and Analysis of Experimental Results

The results obtained from the external validation experiment on the HMoTP dataset demonstrate that the proposed TFF-Net possesses strong generalization and cross-condition adaptability. Despite being trained solely on the PHM2010 dataset, the model achieved a classification accuracy of 97.3% on the independent HMoTP dataset without any retraining or fine-tuning. This confirms that the proposed SSA-CWT + TFF-Net framework can effectively extract discriminative and transferable time–frequency features that remain stable under varying cutting conditions and tool geometries.

The stable validation curve shown in Figure 19a further verifies that the model converges efficiently and maintains high generalization performance. The confusion matrix in Figure 19b indicates that nearly all samples were correctly classified across the three wear stages, with only a few misclassifications between the initial and normal wear stages, where the feature distributions are inherently overlapping. The absence of significant confusion between the normal and severe wear stages implies that the proposed cross-modal time–frequency fusion mechanism effectively captures wear-related degradation patterns.

Overall, these results demonstrate that the proposed method exhibits excellent robustness and transferability across different datasets and machining conditions, providing a reliable basis for intelligent tool wear monitoring in practical industrial applications.

5. Conclusions and Future Work

This study proposes an adaptive multimodal time–frequency fusion framework for tool wear state recognition by integrating the SSA-optimized Continuous Wavelet Transform (SSA-CWT) with a Cross-Modal Time–Frequency Fusion Network (TFF-Net). The experimental results obtained from both the PHM2010 dataset and the external HMoTP dataset verify that the proposed method achieves highly discriminative feature representation, robust cross-modal fusion, and strong generalization capability. The main conclusions are as follows:

(1)

The SSA-CWT module effectively enhances time–frequency representation quality by adaptively optimizing the center frequency and bandwidth of the complex Morlet wavelet through the Sparrow Search Algorithm using energy entropy as the objective function. Compared with conventional CWT, STFT, GAF, MTF, and RP, SSA-CWT yields significantly higher energy concentration, reduced background noise, faster convergence, and improved recognition accuracy, thus providing superior discriminative inputs for deep learning models.

(2)

The proposed TFF-Net realizes efficient multi-source fusion through a hierarchical local–global feature extraction strategy combined with a sliding-window cross-modal attention mechanism. By fully leveraging the complementary properties of cutting force and vibration signals, TFF-Net achieves State-of-the-Art recognition performance across all wear stages, reaching 100% accuracy in initial wear and 98.7% in both normal and severe wear stages. The fusion strategy effectively reduces inter-class overlap and strengthens robustness under complex machining conditions.

(3)

Comprehensive comparisons with representative architectures—including ConvMixer, Conformer, and Mobile-Former—demonstrate the superiority of TFF-Net in both accuracy and robustness. With Accuracy, F1-score, Recall, and Precision all exceeding 98%, and an inference speed of 35 FPS, TFF-Net achieves an excellent balance between computational efficiency and predictive precision, showing strong potential for real-time industrial deployment.

(4)

Ablation experiments validate the necessity and effectiveness of each component of the proposed framework. SSA-based wavelet parameter optimization, Hampel filtering, multi-axis energy fusion, and cross-modal attention all contribute meaningfully to performance improvement. The full model achieves a 6–7% performance gain over the baseline, confirming the synergistic enhancement among signal preprocessing, adaptive time–frequency analysis, and multimodal feature fusion.

(5)

External validation experiments on the HMoTP dataset further verify the generalization capability of the proposed framework. Without retraining, TFF-Net achieves 97.3% accuracy on the independent dataset featuring different cutting tools, materials, and acquisition systems, highlighting the framework’s robustness across varying machining conditions.

Despite the encouraging performance, several directions warrant further investigation:

(1)

Cross-domain adaptive modeling: Developing domain adaptation or meta-learning–based frameworks to handle larger variations in cutting parameters, tool geometries, sensor layouts, and machining environments.

(2)

Lightweight and real-time deployment: Exploring model compression, knowledge distillation, and hardware-friendly architectures to further improve inference speed and meet the requirements of on-machine monitoring.

(3)

Explainable and multi-state diagnostic frameworks: Incorporating interpretable learning methods to enhance model transparency and extending the framework to jointly diagnose tool wear, tool breakage, and abnormal machining conditions.

(4)

Integration with digital twin systems: Combining data-driven modeling with physics-informed mechanisms to develop closed-loop, self-updating digital twins for tool health monitoring and predictive maintenance.