High-Precision Trajectory Tracking Control Strategy for Loader Working Device

Abstract

To improve the automation accuracy and efficiency of the loader working device, this paper proposes a control strategy based on an adaptive backstepping algorithm to address the trajectory tracking control problem under strong nonlinearity, parameter uncertainty, and external load disturbances. Firstly, the working principle of the electro-hydraulic proportional control system of the working device is systematically elaborated, and a nonlinear mathematical model of the system is established. Secondly, an adaptive backstepping tracking controller is designed, which progressively constructs virtual control variables via the backstepping method to ensure system stability, while introducing adaptive laws to estimate uncertain parameters online, thereby compensating for system parameter perturbations and nonlinear disturbances in real time. Finally, an experimental platform for the loader working device is built, and comparative trajectory tracking experiments are conducted. The results demonstrate that, compared to classical PID control, the proposed adaptive backstepping control strategy significantly enhances trajectory tracking accuracy, reducing the maximum displacement error of the bucket tip trajectory by 50.88% and the root mean square error (RMSE) by 56.07%.

1. Introduction

As core equipment in infrastructure construction, mining, and material handling, the level of intelligence and automation of construction machinery directly impacts operational efficiency, safety, and operator comfort. The loader, being one of the most widely used types of construction machinery, relies on its front working device to perform complex operations such as digging, lifting, and dumping. Achieving high-precision, high-dynamic trajectory tracking control of the working device’s end-effector is a key technology for enhancing the automation level of loaders. This advancement holds significant importance in reducing operator workload, improving operational accuracy and efficiency, and lowering energy consumption [1].

The motion control of the working device is primarily realized through its hydraulic drive system. Electro-hydraulic proportional control systems have become the mainstream solution for modern construction machinery due to their advantages of high power density, fast response, relatively high control accuracy, and moderate cost [2,3,4]. However, the loader working device is a typical multi-degree-of-freedom mechanical-hydraulic system characterized by strong nonlinearity, strong coupling, time-varying behavior, and complex external load disturbances. Its dynamic performance is significantly affected by various factors, including the nonlinearity of hydraulic valves, friction in hydraulic cylinders, oil compressibility, load mass variations, and system parameter uncertainties [5,6]. These inherent complexities make it difficult for traditional linear control theory-based methods to achieve satisfactory trajectory tracking performance. Particularly when dealing with large-range motions, abrupt load changes, and system parameter perturbations, issues such as increased tracking errors, response lag, and even instability are prone to occur [7].

To address these challenges, numerous advanced control strategies have been introduced into the field of electro-hydraulic proportional control for construction machinery in recent years. For instance, sliding mode control has attracted attention due to its strong robustness, but its inherent chattering phenomenon may exacerbate system wear and compromise control precision [8,9,10]. While particle swarm optimization and genetic algorithms have been employed to optimize PID parameters, thereby improving parameter self-adaptability, their effectiveness in compensating for the strongly coupled dynamics of hydraulic systems remains limited [11]. Model predictive control predicts system behavior through rolling optimization and feedback correction, yet this method relies on an accurate system model and entails substantial online computational burden [12]. Fuzzy control and neural network control do not require precise models but typically demand extensive empirical knowledge or training data [13,14].

As a systematic nonlinear controller design approach, backstepping is particularly suitable for cascade system control due to its structured design process and effective handling of system nonlinearities [15]. The integration of adaptive mechanisms with backstepping, forming the adaptive backstepping control approach, enables simultaneous treatment of system nonlinearities and parameter uncertainties, thereby significantly enhancing both tracking performance and system robustness [16,17,18]. Although the adaptive backstepping algorithm has demonstrated remarkable success in fields such as robotics and aerospace [19,20,21], its in-depth theoretical research, tailored design, and comprehensive experimental validation remain relatively scarce for trajectory tracking control in complex electro-hydraulic systems like loader working devices, which exhibit unique load characteristics and strong nonlinearities.

Building upon the aforementioned background and analysis, this paper focuses on the high-performance trajectory tracking control problem of loader working devices, proposing a novel control strategy based on an adaptive backstepping algorithm. The main contributions and innovations of this study are manifested in the following aspects:

(1) High-fidelity system modeling: Unlike simplified models commonly used in prior studies, this work establishes a comprehensive fifth-order nonlinear state-space model that explicitly incorporates the dynamics of the electro-hydraulic proportional pressure-reducing valve and the hydraulic control directional valve. This model more accurately captures the high-frequency characteristics and nonlinearities inherent in the loader’s electro-hydraulic system.

(2) Loader-specific adaptive backstepping controller design: A trajectory tracking controller based on the adaptive backstepping algorithm is developed. Its innovation lies in the tailored design of adaptive laws that simultaneously estimate multiple critical time-varying parameters (e.g., viscous damping coefficient, leakage coefficient, load spring stiffness, bulk modulus, directional valve gain, and external load force) unique to the complex operating conditions of loaders. This multi-parameter online estimation provides robust compensation for system uncertainties.

(3) Comprehensive experimental validation: The proposed control strategy is implemented on a rapid-control-prototyping platform and validated through extensive experiments on a real-world loader working device. The performance is rigorously compared against a classical PID controller, quantitatively demonstrating significant improvements in trajectory tracking accuracy under realistic load variations.

The remainder of this paper is organized as follows: Section 2 details the working principle of the electro-hydraulic proportional control system for loader working devices; Section 3 establishes the nonlinear mathematical model of the system; Section 4 presents the trajectory tracking controller design method based on the adaptive backstepping algorithm; Section 5 demonstrates the experimental platform setup and provides detailed results analysis and discussion; finally, Section 6 summarizes the key findings.

2. Working Principle

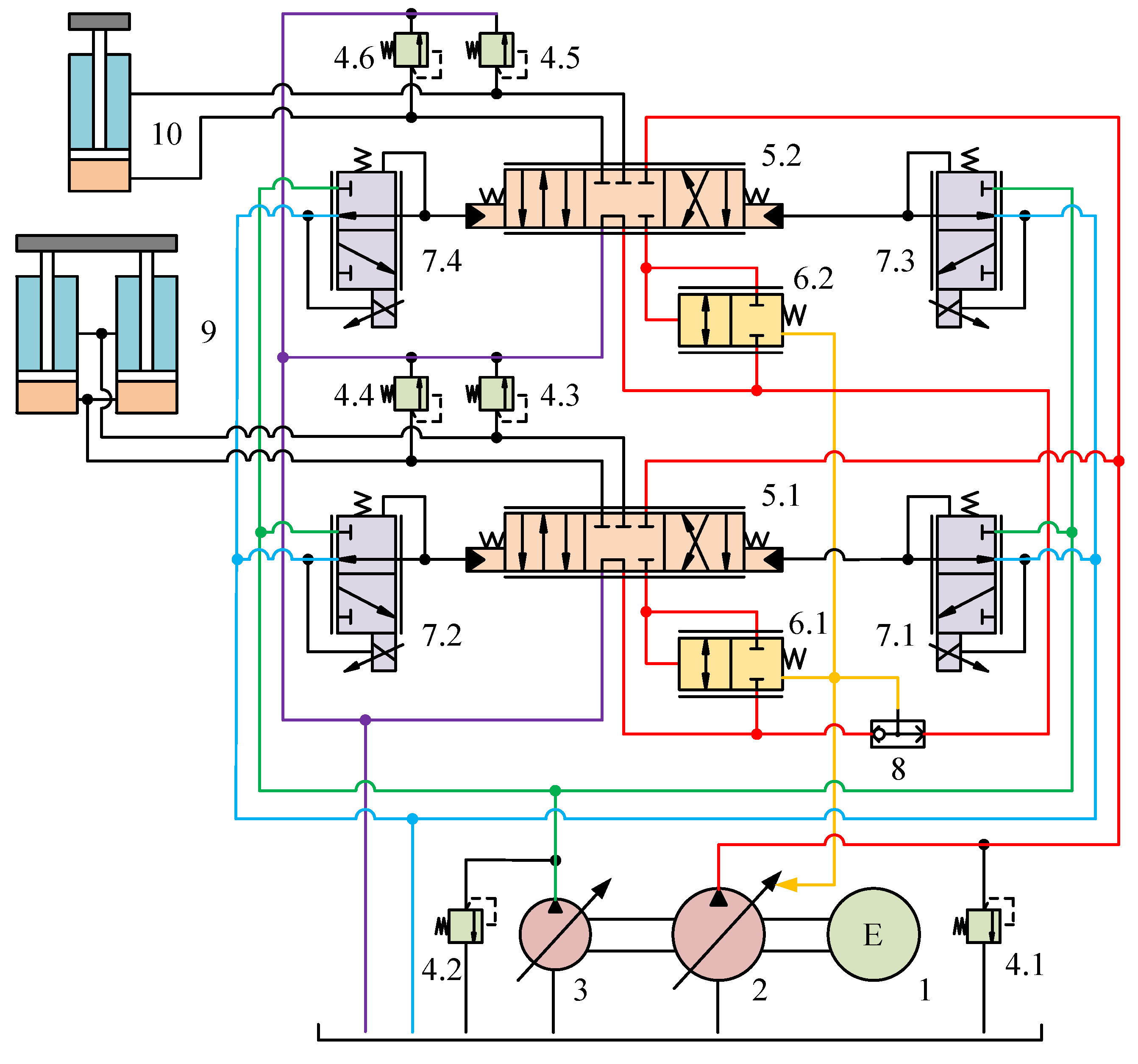
Figure 1 shows the hydraulic schematic diagram of the loader working device. The engine (1) coaxially drives a load-sensing pump (2) and a constant-pressure variable displacement pump (3). The load-sensing pump serves as the main oil supply unit of the system, automatically adjusting its output pressure and flow rate according to the actual working conditions, enabling adaptive matching of power to the load and helping to reduce system energy consumption. The constant-pressure variable displacement pump provides a stable pilot control oil source for the system. The high-pressure oil delivered by the load-sensing pump is distributed to the boom hydraulic cylinder (9) and the bucket hydraulic cylinder (10) after passing through the hydraulic control directional valves (5.1, 5.2) and pressure compensation valves (6.1, 6.2), thereby providing power support for the working device. The multiple relief valves (4.1~4.6) in the system are used to limit the maximum pressure in different circuits, ensuring system safety.

Electro-hydraulic proportional control is the core for achieving precise displacement tracking of the hydraulic cylinders. The pilot oil pressure output by the constant-pressure variable displacement pump is precisely regulated by the electro-proportional pressure-reducing valves (7.1~7.4). These pressure-reducing valves receive electrical command signals from the controller and convert them into corresponding hydraulic control pressures. This pressure acts on the spool control ends of the hydraulic control directional valves, thereby precisely controlling the spool displacement. By adjusting the spool displacement, the flow rate entering the hydraulic cylinders can be accurately controlled, ultimately regulating the motion speed and direction of the cylinders. The pressure compensation valves (6.1, 6.2) are used to maintain a constant pressure differential across the orifices of the hydraulic control directional valves. This ensures that the flow rate through the valve orifices is solely related to the spool opening and remains unaffected by fluctuations in load pressure, thereby improving the control precision of the system. The shuttle valve (8) selects the higher load pressure between the boom cylinder and the bucket cylinder and feeds it back to the displacement mechanism of the load-sensing pump, ensuring the pump’s output pressure consistently adapts to the highest load pressure.

During the loader’s digging operation, the motion control of the working mechanism is achieved through coordinated operation of the boom system and bucket system. The movement trajectory of the working mechanism is typically represented by the bucket tip trajectory. Therefore, based on the optimally planned motion trajectory of the bucket tip, the ideal displacement trajectories of both the boom hydraulic cylinder and bucket hydraulic cylinder can be calculated.

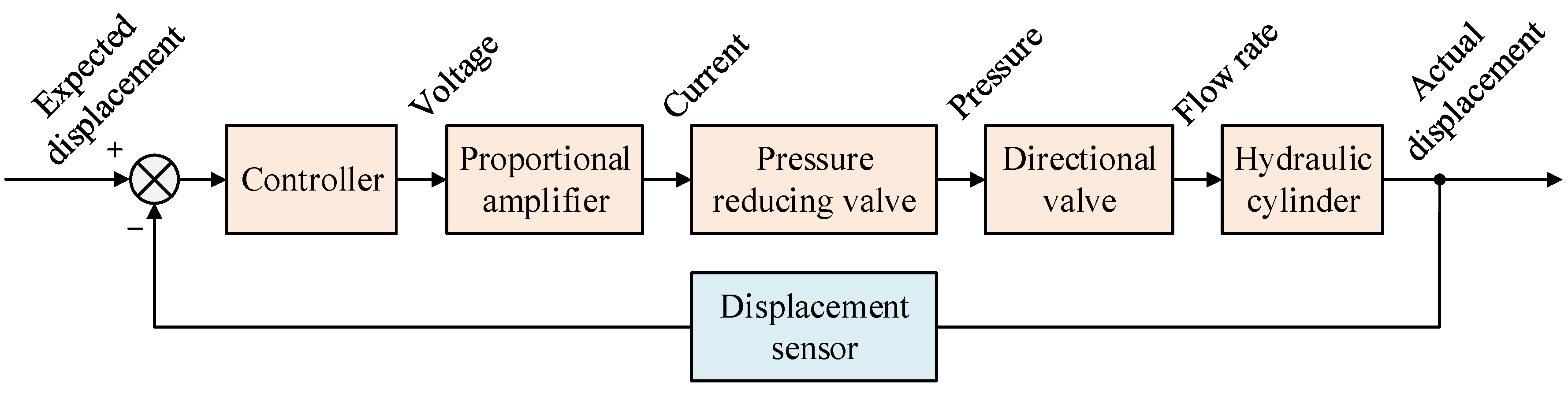
Both the boom and bucket systems employ electro-hydraulic proportional control technology for precise regulation. Figure 2 illustrates the complete control process. Displacement sensors continuously monitor the hydraulic cylinder positions, comparing them with desired displacements to generate error signals that are fed into the controller. After processing, the controller outputs precise voltage command signals, which are converted and amplified by proportional amplifiers to drive the electro-proportional pressure reducing valves. The pressure-reducing valves, responding to input currents, deliver control oil at corresponding pressures to adjust the spool displacement of the hydraulic control directional valves. This precisely regulates the hydraulic oil flow rate, ultimately achieving closed-loop control of the hydraulic cylinder displacements. Through accurate position control of both the boom and bucket hydraulic cylinders, the bucket tip can closely follow the predetermined motion trajectory with high precision.

3. Mathematical Model

To achieve precise trajectory tracking control of the loader working device, a complete mathematical model of the electro-hydraulic proportional control system needs to be established. This model consists of several key submodules, including the proportional amplifier, electro-proportional pressure reducing valve, hydraulic control directional valve, hydraulic cylinder, and displacement sensor. The physical interconnections of these key submodules are shown in the system schematic (Figure 2). The nonlinear mathematical model for each subsystem is established based on first principles of physics and electro-hydraulic system dynamics. This provides the foundational structure for controller design. Here and throughout the manuscript, the Laplace transform of a time-domain variable is denoted by an uppercase letter.

3.1. Proportional Amplifier

The transfer function of the proportional amplifier is:

$${\displaystyle \frac{I_{\mathrm{a}}(s)}{U_{\mathrm{e}}(s)}}=K_{\mathrm{a}}$$

(1)

where $I_{\mathrm{a}}$ is the current output of the proportional amplifier (A), $U_{\mathrm{e}}$ is the voltage input of the proportional amplifier (V), $K_{\mathrm{a}}$ is the proportional gain of the amplifier (A/V).

3.2. Electro-Proportional Pressure Reducing Valve

The transfer function of the electro-proportional pressure reducing valve is:

$${\displaystyle \frac{P_{\mathrm{c}}(s)}{I_{\mathrm{a}}(s)}}=K_{\mathrm{c}}$$

(2)

where $P_{\mathrm{c}}$ is the output pressure of the pressure reducing valve (Pa), $K_{\mathrm{c}}$ is the proportional coefficient of the pressure reducing valve (Pa/A).

3.3. Hydraulic Control Directional Valve

The spool force balance equation of the hydraulic control directional valve is [22]:

$$p_{\mathrm{c}}{A}_{\mathrm{h}}=M_{\mathrm{h}}{\displaystyle \frac{{\mathrm{d}}^2{x}_{\mathrm{h}}}{\mathrm{d}{t}^2}}+B_{\mathrm{h}}{\displaystyle \frac{\mathrm{d}{x}_{\mathrm{h}}}{\mathrm{d}t}}+2K_{\mathrm{h}}{x}_{\mathrm{h}}$$

(3)

where $A_{\mathrm{h}}$ is the effective area of the spool end face (m²), $M_{\mathrm{h}}$ is the spool mass (kg), $x_{\mathrm{h}}$ is the spool displacement (m), $B_{\mathrm{h}}$ is the viscous damping coefficient of the directional valve (N/(m/s)), $K_{\mathrm{h}}$ is the spring stiffness of the spool (N/m).

The load flow rate equation of the hydraulic control directional valve is:

$$Q_{\mathrm{L}}=C_{\mathrm{h}}{W}_{\mathrm{h}}{x}_{\mathrm{h}}\sqrt{{\displaystyle \frac{2}{\rho }}(p_{\mathrm{s}}+{\displaystyle \frac{x_{\mathrm{h}}}{\left|x_{\mathrm{h}}\right|}}{p}_{\mathrm{L}})}$$

(4)

where $Q_{\mathrm{L}}$ is the load flow rate of the directional valve (m³/s), $p_{\mathrm{L}}$ is the load pressure of the directional valve (Pa), $C_{\mathrm{h}}$ is the flow rate coefficient of the directional valve, $W_{\mathrm{h}}$ is the area gradient of the valve orifice (m), $p_{\mathrm{s}}$ is the outlet pressure of the load-sensing pump (Pa), $\rho$ is the density of the hydraulic oil (kg/m³).

Linearizing Equation (4) yields:

$$Q_{\mathrm{L}}=K_{\mathrm{qh}}{x}_{\mathrm{h}}-K_{\mathrm{ph}}{p}_{\mathrm{L}}$$

(5)

where $K_{\mathrm{qh}}$ is the flow rate gain coefficient of the directional valve (m²/s), $K_{\mathrm{ph}}$ is the pressure gain coefficient of the directional valve (m⁵/(N∙s)).

The linearization of Equation (4) is performed around a nominal operating point, and the strict-feedback form is adopted under the assumption that unmodeled nonlinearities (e.g., dead zone, hysteresis, friction) and parameter uncertainties are compensated by the adaptive control law.

Performing Laplace transform on Equations (3) and (5) gives:

$$P_{\mathrm{c}}(s)A_{\mathrm{h}}=M_{\mathrm{h}}{s}^2{X}_{\mathrm{h}}(s)+B_{\mathrm{h}}s{X}_{\mathrm{h}}(s)+2K_{\mathrm{h}}{X}_{\mathrm{h}}(s)$$

(6)

$$Q_{\mathrm{L}}(s)=K_{\mathrm{qh}}{X}_{\mathrm{h}}(s)-K_{\mathrm{ph}}{P}_{\mathrm{L}}(s)$$

(7)

From Equation (6), the transfer function of spool displacement to output pressure of the pressure reducing valve is obtained as:

$${\displaystyle \frac{X_{\mathrm{h}}(s)}{P_{\mathrm{c}}(s)}}={\displaystyle \frac{A_{\mathrm{h}}}{M_{\mathrm{h}}{s}^2+B_{\mathrm{h}}s+2K_{\mathrm{h}}}}$$

(8)

3.4. Hydraulic Cylinder

The flow rate continuity equation of the hydraulic cylinder can be expressed as [23]:

$$Q_{\mathrm{L}}=A_{\mathrm{c}}{\displaystyle \frac{\mathrm{d}{y}_g}{\mathrm{d}t}}+C_{\mathrm{L}}{p}_{\mathrm{L}}+{\displaystyle \frac{V_{\mathrm{e}}}{4{\beta }_{\mathrm{e}}}}{\displaystyle \frac{\mathrm{d}{p}_{\mathrm{L}}}{\mathrm{d}t}}$$

(9)

where $A_{\mathrm{c}}$ is the effective piston area (m²), $y_{\mathrm{g}}$ is the piston displacement (m), $C_{\mathrm{L}}$ is the equivalent leakage coefficient of the hydraulic cylinder (m³/(s∙Pa)), $V_{\mathrm{e}}$ is the equivalent volume of the hydraulic cylinder (m³), ${\beta }_{\mathrm{e}}$ is the equivalent bulk modulus of the hydraulic oil (Pa).

The force balance equation of the hydraulic cylinder can be expressed as:

$$A_{\mathrm{c}}{p}_{\mathrm{L}}=M_{\mathrm{t}}{\displaystyle \frac{d^2{y}_{\mathrm{g}}}{d{t}^2}}+B_{\mathrm{t}}{\displaystyle \frac{d{y}_{\mathrm{g}}}{dt}}+K_{\mathrm{L}}{y}_{\mathrm{g}}+F_{\mathrm{L}}$$

(10)

where $M_{\mathrm{t}}$ is the equivalent mass of the piston and load (kg), $B_{\mathrm{t}}$ is the equivalent viscous damping coefficient of the piston and load (N/(m/s)), $K_{\mathrm{L}}$ is the load spring stiffness (N/m), $F_{\mathrm{L}}$ is the external load force on piston (N).

Performing Laplace transform on Equations (9) and (10) yields:

$$Q_{\mathrm{L}}(s)=A_{\mathrm{c}}s{Y}_g(s)+C_{\mathrm{L}}{P}_{\mathrm{L}}(s)+{\displaystyle \frac{V_{\mathrm{e}}}{4{\beta }_{\mathrm{e}}}}s{P}_{\mathrm{L}}(s)$$

(11)

$$A_{\mathrm{c}}{P}_{\mathrm{L}}(s)=M_{\mathrm{t}}{s}^2{Y}_{\mathrm{g}}(s)+B_{\mathrm{t}}s{Y}_{\mathrm{g}}(s)+K_{\mathrm{L}}{Y}_{\mathrm{g}}(s)+F_{\mathrm{L}}(s)$$

(12)

Combining Equations (7), (11) and (12), while neglecting minimal values, the transfer function of piston displacement to spool displacement is obtained as:

$${\displaystyle \frac{Y_{\mathrm{g}}(s)}{X_{\mathrm{h}}(s)}}={\displaystyle \frac{\frac{K_{\mathrm{qh}}}{A_{\mathrm{c}}}}{s(\frac{s^2}{{\omega }_{\mathrm{h}}^2}+\frac{2{\zeta }_{\mathrm{h}}}{{\omega }_{\mathrm{h}}}s+1)}}$$

(13)

where ${\omega }_{\mathrm{h}}=\sqrt{{\displaystyle \frac{4{\beta }_{\mathrm{e}}{A}_{\mathrm{c}}^2}{M_{\mathrm{t}}{V}_{\mathrm{e}}}}}$, ${\zeta }_{\mathrm{h}}={\displaystyle \frac{K_{\mathrm{ph}}+C_{\mathrm{L}}}{A_{\mathrm{c}}}}\sqrt{{\displaystyle \frac{{\beta }_{\mathrm{e}}{M}_{\mathrm{t}}}{V_{\mathrm{e}}}}}+{\displaystyle \frac{B_{\mathrm{t}}}{4A_{\mathrm{c}}}}\sqrt{{\displaystyle \frac{V_{\mathrm{e}}}{{\beta }_{\mathrm{e}}{M}_{\mathrm{t}}}}}$.

3.5. Displacement Sensor

The transfer function of the displacement sensor is:

$${\displaystyle \frac{U_{\mathrm{f}}(s)}{Y_{\mathrm{g}}(s)}}=K_{\mathrm{f}}$$

(14)

where $U_{\mathrm{f}}$ is the output voltage of the displacement sensor (V), $K_{\mathrm{f}}$ is the proportional coefficient of the displacement sensor (V/m).

3.6. System Transfer Function

Based on the transfer functions of each component, the control block diagram of the electro-hydraulic proportional system is established as shown in Figure 3.

From Figure 3, the transfer function of the hydraulic cylinder piston displacement to the input voltage signal can be derived as:

$$G(s)={\displaystyle \frac{Y_{\mathrm{g}}(s)}{U_{\mathrm{e}}(s)}}={\displaystyle \frac{A_{\mathrm{h}}{K}_{\mathrm{a}}{K}_{\mathrm{c}}\frac{K_{\mathrm{qh}}}{A_{\mathrm{c}}}}{(\frac{s^2}{{\omega }_{\mathrm{h}}^2}+\frac{2{\zeta }_{\mathrm{h}}}{{\omega }_{\mathrm{h}}}s+1)(M_{\mathrm{h}}{s}^2+B_{\mathrm{h}}s+2K_{\mathrm{h}})s}}$$

(15)

The parameters of the electro-hydraulic proportional system were obtained through a combination of manufacturer datasheets, experimental identification, and empirical formulas. Key parameters such as the viscous damping coefficient and the equivalent leakage coefficient of the hydraulic cylinder were identified experimentally using step-response and frequency-domain analysis methods. The accuracy of the established nonlinear mathematical model was verified by comparing the simulated step response of the hydraulic cylinder displacement with the experimental data. The results showed good agreement, confirming the model’s fidelity and providing a reliable foundation for the subsequent controller design.

4. Control Strategy

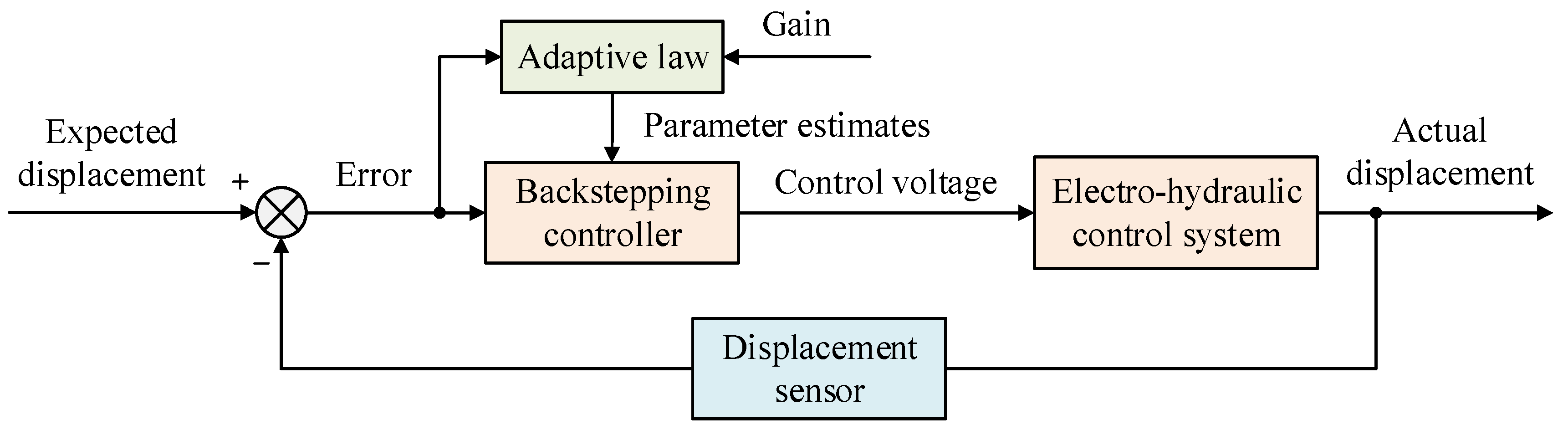
The block diagram of the trajectory tracking control based on the adaptive backstepping algorithm is illustrated in Figure 4. The mathematical model of the electro-hydraulic proportional system is decomposed into a sequence of subsystems in strict feedback form. Using a recursive design approach, the virtual control law is systematically derived starting from the hydraulic cylinder displacement tracking error. Parameter adaptation laws are introduced to estimate unknown system parameters online, while Lyapunov functions are constructed to ensure the stability of each subsystem. Ultimately, the actual control input signal is synthesized to drive the hydraulic cylinder’s actual displacement to asymptotically converge to the desired displacement.

Considering that both the proportional amplifier and electro-proportional pressure reducing valve exhibit proportional characteristics, the system’s input control voltage and the output pressure of the pressure reducing valve maintain a linear relationship. Therefore, this study selects the output pressure $p_{\mathrm{c}}$ of the pressure-reducing valve as the system’s control variable. The system state variables are defined as: hydraulic cylinder displacement $y_{\mathrm{g}}$, hydraulic cylinder velocity ${\dot{y}}_{\mathrm{g}}$, load pressure $p_{\mathrm{L}}$, spool displacement of the directional valve $x_{\mathrm{h}}$, and spool velocity of the directional valve ${\dot{x}}_{\mathrm{h}}$. Letting the state vector $X={\left[x_1,x_2,x_3,x_4,x_5\right]}^{\mathrm{T}}={[y_{\mathrm{g}},{\dot{y}}_{\mathrm{g}},p_{\mathrm{L}},x_{\mathrm{h}},{\dot{x}}_{\mathrm{h}}]}^{\mathrm{T}}$, the state-space equation of the system is obtained as:

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2\hfill \\ {\dot{x}}_2=a_1{x}_3-a_2{x}_2-a_3{x}_1-a_4\hfill \\ {\dot{x}}_3=a_5{x}_4-a_6{x}_3-a_7{x}_2\hfill \\ {\dot{x}}_4=x_5\hfill \\ {\dot{x}}_5=a_8{p}_{\mathrm{c}}-a_9{x}_5-a_{10}{x}_4\hfill \end{array}\right.$$

(16)

where $a_1={\displaystyle \frac{A_{\mathrm{c}}}{M_{\mathrm{t}}}}$, $a_2={\displaystyle \frac{B_{\mathrm{t}}}{M_{\mathrm{t}}}}$, $a_3={\displaystyle \frac{K_{\mathrm{L}}}{M_{\mathrm{t}}}}$, $a_4={\displaystyle \frac{F_{\mathrm{L}}}{M_{\mathrm{t}}}}$, $a_5={\displaystyle \frac{4{\beta }_{\mathrm{e}}{K}_{\mathrm{qh}}}{V_{\mathrm{e}}}}$, $a_6={\displaystyle \frac{4{\beta }_{\mathrm{e}}(K_{\mathrm{ph}}+C_{\mathrm{L}})}{V_{\mathrm{e}}}}$, $a_7={\displaystyle \frac{4{\beta }_{\mathrm{e}}{A}_{\mathrm{c}}}{V_{\mathrm{e}}}}$, $a_8={\displaystyle \frac{A_{\mathrm{h}}}{M_{\mathrm{h}}}}$, $a_9={\displaystyle \frac{B_{\mathrm{h}}}{M_{\mathrm{h}}}}$, and $a_{10}={\displaystyle \frac{2K_{\mathrm{h}}}{M_{\mathrm{h}}}}$.

During actual loader operations, due to complex and variable working environments, dynamically changing load conditions, and inherent hydraulic system characteristics, key system parameters often exhibit significant time-varying properties. These include the viscous damping coefficient of the hydraulic cylinder, leakage coefficient of the hydraulic cylinder, load spring stiffness, bulk modulus of the hydraulic oil, gain coefficient of the directional valve, viscous damping coefficient of the directional valve, and external load force. Accordingly, in establishing the state-space equations, terms containing these unknown parameters are defined as time-varying unknown quantities, including $a_2$, $a_3$, $a_4$, $a_5$, $a_6$, $a_7$ and $a_9$.

The step-by-step design procedure for the trajectory tracking controller based on the adaptive backstepping algorithm is presented as follows:

Define the error equations for each subsystem as:

$$\left\{\begin{array}{l}{z}_1=x_1-x_{\mathrm{d}}\hfill \\ z_2=x_2-{\alpha }_1\hfill \\ \hfill ⋮\hfill \\ z_5=x_5-{\alpha }_4\hfill \end{array}\right.$$

(17)

where $x_{\mathrm{d}}$ is the desired displacement of the hydraulic cylinder, ${\alpha }_i$ is the virtual control variables for subsystems.

Step 1: For the first subsystem

The derivative of $z_1$ is obtained as:

$${\dot{z}}_1=x_2-{\dot{x}}_{\mathrm{d}}$$

(18)

Define the Lyapunov function for the first subsystem as:

$$V_1={\displaystyle \frac{1}{2}}{z}_1^2$$

(19)

The derivative of $V_1$ yields:

$${\dot{V}}_1=z_1(z_2+{\alpha }_1-{\dot{x}}_{\mathrm{d}})$$

(20)

Define the virtual control variable ${\alpha }_1$ for the first subsystem as:

$${\alpha }_1=-c_1{z}_1+{\dot{x}}_{\mathrm{d}}$$

(21)

Further derivation gives:

$${\dot{V}}_1=-c_1{z}_1^2+z_1{z}_2$$

(22)

Step 2: For the second subsystem

The derivative of $z_2$ is obtained as:

$${\dot{z}}_2=a_1{x}_3-a_2{x}_2-a_3{x}_1-a_4-{\dot{\alpha }}_1$$

(23)

Define the estimation errors for $a_2$, $a_3$ and $a_4$ as:

$$\left\{\begin{array}{l}{\tilde{a}}_2=a_2-{\widehat{a}}_2\hfill \\ {\tilde{a}}_3=a_3-{\widehat{a}}_3\hfill \\ {\tilde{a}}_4=a_4-{\widehat{a}}_4\hfill \end{array}\right.$$

(24)

where $a_i$ is the true values of the uncertain parameters, ${\widehat{a}}_i$ is the estimated values of the uncertain parameters.

Define the Lyapunov function for the second subsystem as:

$$V_2=V_1+{\displaystyle \frac{1}{2}}{z}_2^2+{\displaystyle \frac{1}{2k_1}}{\tilde{a}}_2^2+{\displaystyle \frac{1}{2k_2}}{\tilde{a}}_3^2+{\displaystyle \frac{1}{2k_3}}{\tilde{a}}_4^2$$

(25)

The derivative of $V_2$ yields:

$$\begin{array}{cc}\hfill {\dot{V}}_2& =-c_1{z}_1^2+z_2(z_1+a_1{z}_3+a_1{\alpha }_2-{\dot{\alpha }}_1)-a_2({\displaystyle \frac{1}{k_1}}{\dot{\widehat{a}}}_2+z_2{x}_2)-\hfill \\ & a_3({\displaystyle \frac{1}{k_2}}{\dot{\widehat{a}}}_3+z_2{x}_1)-a_4({\displaystyle \frac{1}{k_3}}{\dot{\widehat{a}}}_4+z_2)+{\displaystyle \frac{1}{k_1}}{\widehat{a}}_2{\dot{\widehat{a}}}_2+{\displaystyle \frac{1}{k_2}}{\widehat{a}}_3{\dot{\widehat{a}}}_3+{\displaystyle \frac{1}{k_3}}{\widehat{a}}_4{\dot{\widehat{a}}}_4\hfill \end{array}$$

(26)

To eliminate $a_2$, $a_3$ and $a_4$, let:

$$\left\{\begin{array}{l}{\dot{\widehat{a}}}_2=-k_1{z}_2{x}_2\hfill \\ {\dot{\widehat{a}}}_3=-k_2{z}_2{x}_1\hfill \\ {\dot{\widehat{a}}}_4=-k_3{z}_2\hfill \end{array}\right.$$

(27)

Define the virtual control variable ${\alpha }_2$ for the second subsystem as:

$${\alpha }_2={\displaystyle \frac{1}{a_1}}(-z_1-c_2{z}_2+{\dot{\alpha }}_1+{\widehat{a}}_2{x}_2+{\widehat{a}}_3{x}_1+{\widehat{a}}_4)$$

(28)

Substituting Equations (27) and (28) into Equation (26) yields:

$${\dot{V}}_2=-c_1{z}_1^2-c_2{z}_2^2+a_1{z}_2{z}_3$$

(29)

Step 3: For the third subsystem

The derivative of $z_3$ is obtained as:

$${\dot{z}}_3=a_5{x}_4-a_6{x}_3-a_7{x}_2-{\dot{\alpha }}_2$$

(30)

Define the estimation errors for $a_5$, $a_6$ and $a_7$ as:

$$\left\{\begin{array}{l}{\tilde{a}}_5=a_5-{\widehat{a}}_5\hfill \\ {\tilde{a}}_6=a_6-{\widehat{a}}_6\hfill \\ {\tilde{a}}_7=a_7-{\widehat{a}}_7\hfill \end{array}\right.$$

(31)

Define the Lyapunov function for the third subsystem as:

$$V_3=V_2+{\displaystyle \frac{1}{2}}{z}_3^2+{\displaystyle \frac{1}{2k_4}}{\tilde{a}}_5^2+{\displaystyle \frac{1}{2k_5}}{\tilde{a}}_6^2+{\displaystyle \frac{1}{2k_6}}{\tilde{a}}_7^2$$

(32)

The derivative of $V_3$ yields:

$$\begin{array}{cc}\hfill {\dot{V}}_3& =-c_1{z}_1^2-c_2{z}_2^2+z_3(a_1{z}_2-{\dot{\alpha }}_2)-a_5({\displaystyle \frac{1}{k_4}}{\dot{\widehat{a}}}_5-z_3{x}_4)-\hfill \\ & a_6({\displaystyle \frac{1}{k_5}}{\dot{\widehat{a}}}_6+z_3{x}_3)-a_7({\displaystyle \frac{1}{k_6}}{\dot{\widehat{a}}}_7+z_3{x}_2)+{\displaystyle \frac{1}{k_4}}{\widehat{a}}_5{\dot{\widehat{a}}}_5+{\displaystyle \frac{1}{k_5}}{\widehat{a}}_6{\dot{\widehat{a}}}_6+{\displaystyle \frac{1}{k_6}}{\widehat{a}}_7{\dot{\widehat{a}}}_7\hfill \end{array}$$

(33)

To eliminate $a_5$, $a_6$ and $a_7$, let:

$$\left\{\begin{array}{l}{\dot{\widehat{a}}}_5=k_4{z}_3{x}_4\hfill \\ {\dot{\widehat{a}}}_6=-k_5{z}_3{x}_3\hfill \\ {\dot{\widehat{a}}}_7=-k_6{z}_3{x}_2\hfill \end{array}\right.$$

(34)

Define the virtual control variable ${\alpha }_3$ for the third subsystem as:

$${\alpha }_3={\displaystyle \frac{1}{{\widehat{a}}_5}}(-a_1{z}_2-c_3{z}_3+{\dot{\alpha }}_2+{\widehat{a}}_6{x}_3+{\widehat{a}}_7{x}_2)$$

(35)

Substituting Equations (34) and (35) into Equation (33) yields:

$${\dot{V}}_3=-c_1{z}_1^2-c_2{z}_2^2-c_3{z}_3^2+{\widehat{a}}_5{z}_3{z}_4$$

(36)

Step 4: For the fourth subsystem

The derivative of $z_4$ is obtained as:

$${\dot{z}}_4=x_5-{\dot{\alpha }}_3$$

(37)

Define the Lyapunov function for the fourth subsystem as:

$$V_4=V_3+{\displaystyle \frac{1}{2}}{z}_4^2$$

(38)

The derivative of $V_4$ yields:

$${\dot{V}}_4=-c_1{z}_1^2-c_2{z}_2^2-c_3{z}_3^2+z_4(z_5+{\widehat{a}}_5{z}_3+{\alpha }_4-{\dot{\alpha }}_3)$$

(39)

Define the virtual control variable ${\alpha }_4$ for the fourth subsystem as:

$${\alpha }_4={\dot{\alpha }}_3-{\widehat{a}}_5{z}_3-c_4{z}_4$$

(40)

Further derivation gives:

$${\dot{V}}_4=-c_1{z}_1^2-c_2{z}_2^2-c_3{z}_3^2-c_4{z}_4^2+z_4{z}_5$$

(41)

Step 5: For the fifth subsystem

The derivative of $z_5$ is obtained as:

$${\dot{z}}_5={\dot{x}}_5-{\dot{\alpha }}_4=a_8{p}_{\mathrm{c}}-a_9{x}_5-a_{10}{x}_4-{\dot{\alpha }}_4$$

(42)

Define the estimation error for $a_9$ as:

$${\tilde{a}}_9=a_9-{\widehat{a}}_9$$

(43)

Define the Lyapunov function for the fifth subsystem as:

$$V_5=V_4+{\displaystyle \frac{1}{2}}{z}_5^2+{\displaystyle \frac{1}{2k_7}}{\tilde{a}}_9^2$$

(44)

The derivative of $V_5$ yields:

$$\begin{array}{cc}\hfill {\dot{V}}_5& =-c_1{z}_1^2-c_2{z}_2^2-c_3{z}_3^2-c_4{z}_4^2+\hfill \\ & z_5(z_4+a_8{p}_{\mathrm{c}}-{\dot{\alpha }}_4-a_{10}{x}_4)-a_9({\displaystyle \frac{1}{k_7}}{\dot{\widehat{a}}}_9+z_5{x}_5)+{\displaystyle \frac{1}{k_7}}{\widehat{a}}_9{\dot{\widehat{a}}}_9\hfill \end{array}$$

(45)

To eliminate $a_9$, let:

$${\dot{\widehat{a}}}_9=-k_7{z}_5{x}_5$$

(46)

Define the control variable $p_{\mathrm{c}}$ of the adaptive backstepping controller as:

$$p_{\mathrm{c}}={\displaystyle \frac{1}{a_8}}(-z_4-c_5{z}_5+{\dot{\alpha }}_4+{\widehat{a}}_9{x}_5+a_{10}{x}_4)$$

(47)

Substituting Equations (46) and (47) into Equation (45) yields:

$${\dot{V}}_5=-c_1{z}_1^2-c_2{z}_2^2-c_3{z}_3^2-c_4{z}_4^2-c_5{z}_5^2$$

(48)

where $c_i$ is the backstepping coefficient of the controller, and $c_i>0$.

The adaptive laws in Equations (27), (34) and (46) are modified with a projection operator to ensure parameter boundedness. The closed-loop system is uniformly ultimately bounded, and the tracking error converges to a small residual set.

The global asymptotic stability of the closed-loop system is guaranteed by the Lyapunov stability theory. Consider the final composite Lyapunov function candidate for the entire system:

$$V={\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^5{z}_i^2}+{\displaystyle \frac{1}{2}}{\displaystyle \sum _{j=1}^m\frac{1}{k_j}{\tilde{a}}_j^2}$$

(49)

The derivative of V along the trajectories of the system is:

$$\dot{V}={\displaystyle \sum _{i=1}^5{z}_i{\dot{z}}_i}+{\displaystyle \sum _{j=1}^m\frac{1}{k_j}{\tilde{a}}_j{\dot{\tilde{a}}}_j}$$

(50)

Substituting the error dynamics, the virtual control laws (Equations (21), (28), (35) and (40)), the actual control law (Equation (47)), and the parameter adaptation laws (Equations (27), (34) and (46)), it can be rigorously derived that:

$$\dot{V}\le -{\displaystyle \sum _{i=1}^5{d}_i{z}_i^2}\le 0$$

(51)

Since V is positive definite and $\dot{V}$ is negative semi-definite, V is bounded, which implies that all error signals $z_i$ and parameter estimation errors ${\tilde{a}}_j$ are bounded. Furthermore, from Barbălat’s lemma, it can be concluded that the tracking errors $z_i$ asymptotically converge to zero as time increases. Therefore, the global asymptotic stability of the system is ensured.

In conclusion, when the electro-hydraulic proportional control system of the loader working device adopts the control law shown in Equation (47), combined with the parameter adaptation laws designed in Equations (27), (34), and (46), it ensures that the final position tracking error of the electro-hydraulic proportional control system asymptotically converges to zero.

5. Experiment and Analysis

5.1. Experimental Platform

To validate the effectiveness of the proposed adaptive backstepping control strategy, an experimental platform for the electro-hydraulic proportional control system of a loader working device was established, as shown in Figure 5. The platform consists of four main modules: mechanical system, hydraulic system, measurement system, and control system.

The mechanical system adopts the front working device of a 6-ton wheel loader (WA500-7, KOMATSU, Tokyo, Japan), including the boom, rocker arm, bucket, and linkage mechanism. The hydraulic system comprises a variable displacement pump, electro-hydraulic proportional multi-way valve, boom hydraulic cylinder, and bucket hydraulic cylinder. The measurement system is equipped with high-precision displacement sensors (MTS Temposonics EH series) within the hydraulic cylinders to measure the piston rod displacement in real time. The velocity feedback required by the controller is derived in real-time from the measured displacement signals using a filtered numerical differentiation algorithm. The displacement sensors have a resolution of 0.1 mm and a nonlinearity of ±0.05% full scale. A first-order low-pass filter with a cutoff frequency of 50 Hz was applied to the sensor signals. The control system implements the adaptive backstepping algorithm and classical PID algorithm through MATLAB/Simulink (R2022b), with the compiled control program downloaded to the dSPACE MicroLabBox vehicle control unit. The sampling frequency of the controller was set to 1 kHz. The initial parameter estimates were set to 80% of their nominal values. The controller gains were tuned via simulation and fine-tuned on the experimental platform to ensure stability and performance.

The key parameters of the experimental platform are listed in

Table 1. Parameters of the experimental platform.

Parameters	Values	Parameters	Values
Density of the hydraulic oil	850 kg/m3	Effective end-face area of the directional valve	2.01 × 10−4 m2
Spring stiffness of the directional valve	29,000 N/m	Equivalent piston area of the bucket cylinder	0.0239 m2
Spool mass of the directional valve	0.05 kg	Equivalent piston area of the boom cylinder	0.0189 m2
Flow coefficient of the directional valve	0.62	Orifice area gradient of the directional valve	6.28 × 10−3 m
Viscous damping coefficient of the directional valve	120 N/(m/s)	Equivalent leakage coefficient of the hydraulic cylinder	1 × 10−12 m3/(s∙Pa)

.

The desired bucket tip trajectory for the digging operation is formally defined as a smooth, time-parameterized curve in the Cartesian workspace. It consists of distinct phases: initial penetration, curling, and lifting. The trajectory was designed with consideration for dynamic constraints, including maximum allowable cylinder velocities and system pressure limits. The corresponding desired displacement trajectories for the boom and bucket cylinder are then computed via the inverse kinematics model [24]. These reference signals and their derivatives are continuous and bounded, forming a feasible tracking target for the controller. Subsequently, displacement tracking experiments are conducted using both adaptive backstepping control and PID control. By comparing the tracking errors of the two control algorithms, the performance advantages of the proposed control strategy are quantitatively evaluated.

It should be noted that the current experiments were conducted under a predefined digging trajectory without introducing external load steps or supply pressure disturbances. The robustness of the adaptive backstepping controller is primarily demonstrated through its online parameter estimation capability, which compensates for internal parameter uncertainties.

5.2. Results and Analysis

Using the desired displacement trajectories of the boom and bucket hydraulic cylinders as inputs, the experimental trajectory tracking results for the boom and bucket hydraulic cylinders are shown in Figure 6 and Figure 7, respectively.

Figure 6 and Figure 7 display a 1.4 s segment of the experimental results. This segment was selected as it contains the period of most aggressive motion and the peak tracking error observed during the entire operation, thereby providing a critical comparison of controller performance under the most demanding transient conditions. In the boom cylinder tracking experiments, the PID control yielded a maximum displacement error of 4.93 mm and a root mean square error (RMSE) of 1.69 mm. The adaptive backstepping control reduced these values to 1.82 mm and 0.71 mm, corresponding to reductions of 63.08% and 57.98%, respectively. Similarly, for the bucket cylinder tracking experiments, the PID control produced a maximum error of 5.81 mm and an RMSE of 3.83 mm, which were optimized to 2.72 mm and 1.45 mm by the adaptive backstepping control, corresponding to reductions of 53.18% and 62.14%, respectively. These single-cylinder experimental results consistently demonstrate the superior control precision of the adaptive backstepping algorithm.

The bucket tip trajectory tracking curves and errors, derived from the forward kinematics model, are presented in Figure 8. The adaptive backstepping control achieved a maximum displacement error of 7.80 mm and an RMSE of 3.29 mm, compared to 15.88 mm and 7.49 mm for PID control. This represents accuracy improvements of 50.88% and 56.07%, respectively, confirming the enhanced tracking performance of the adaptive backstepping algorithm in bucket tip trajectory control during digging operations.

In addition to tracking accuracy, the control effort was quantified to provide a comprehensive performance evaluation. The Integrated Absolute Control Effort, defined as ${\displaystyle \int \left|u(t)\right|}\mathrm{d}t$ over the trajectory duration, was calculated for both controllers, where u(t) represents the controller output. The results showed that for the boom hydraulic cylinder and the bucket hydraulic cylinder, the control effort of the adaptive backstepping controller was reduced by 15.2% and 9.2%, respectively, compared to that of the PID controller. This indicates that the performance improvement of the adaptive backstepping control is attributed to more sophisticated and efficient coordination of the control action rather than merely increased actuation intensity.

Comprehensive experimental results demonstrate that the adaptive backstepping control exhibits significant advantages in tracking control performance for both the boom cylinder, bucket cylinder, and bucket tip trajectory. Notably, for the critical bucket tip trajectory that determines operational accuracy, both maximum error and RMSE were reduced by over 50%. These experimental results fully validate the superiority of the adaptive backstepping algorithm in hydraulic system control. By effectively compensating for nonlinearities and adapting to parameter variations, the algorithm successfully mitigates the impact of hydraulic system uncertainties, thereby achieving higher-precision trajectory tracking control.

6. Conclusions

This study proposes and validates an adaptive backstepping control strategy to address the high-precision trajectory tracking requirements of loader working devices under strong nonlinearities, parameter uncertainties, and external load disturbances. Through systematic theoretical analysis, controller design, and experimental investigation, the following conclusions are drawn:

(1) The designed adaptive backstepping tracking controller guarantees global asymptotic stability of the closed-loop system via Lyapunov stability theory, while incorporating adaptive laws for real-time online estimation of key uncertain parameters. This significantly enhances robustness against parameter variations and external disturbances.

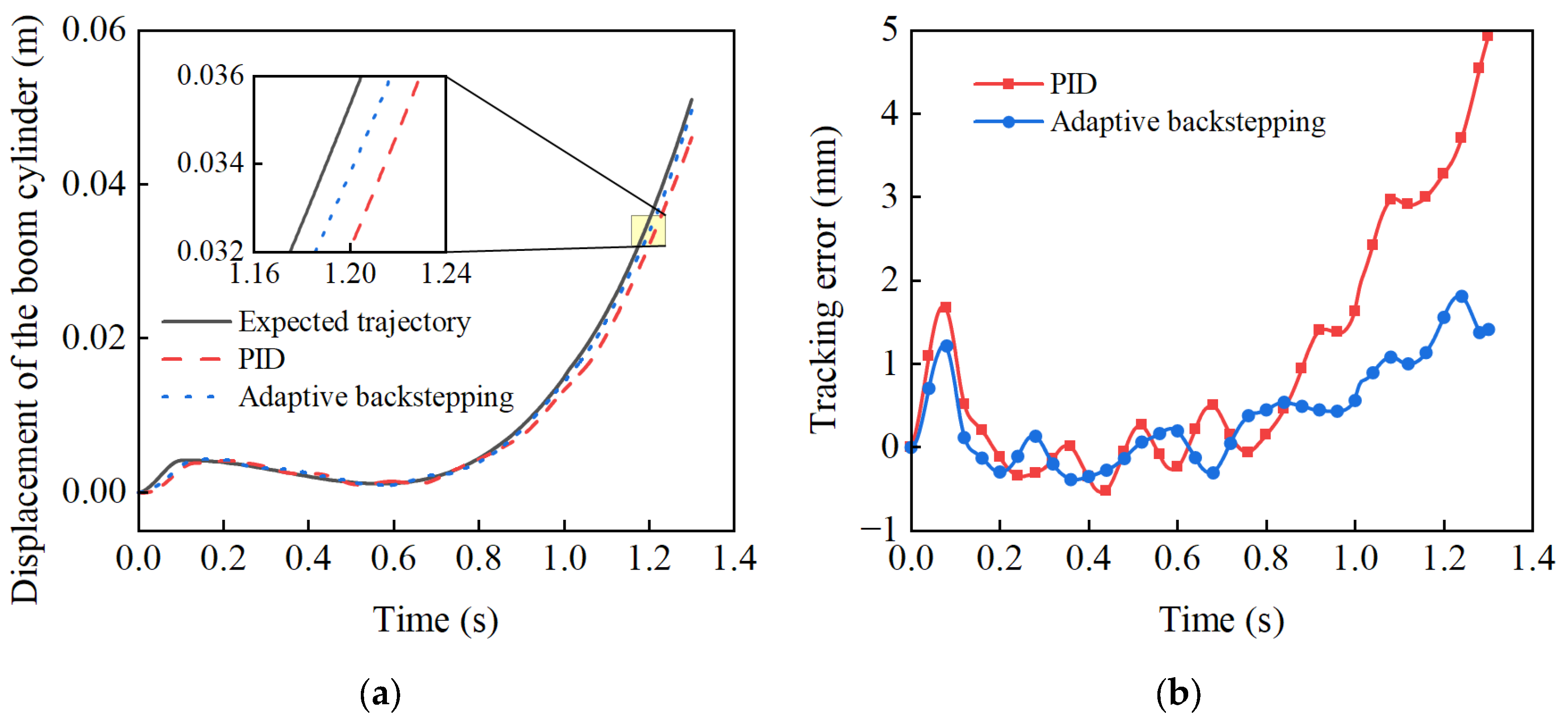
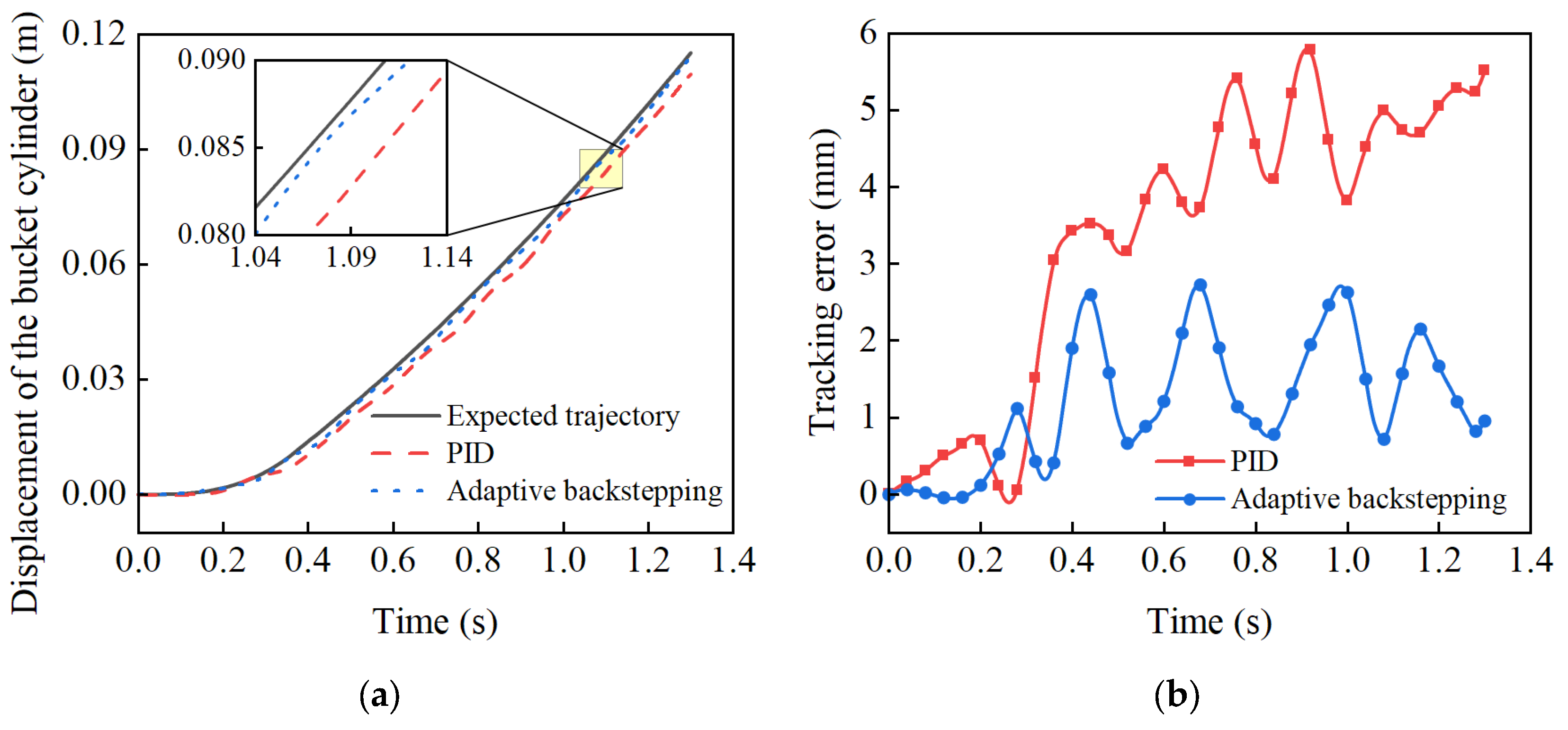
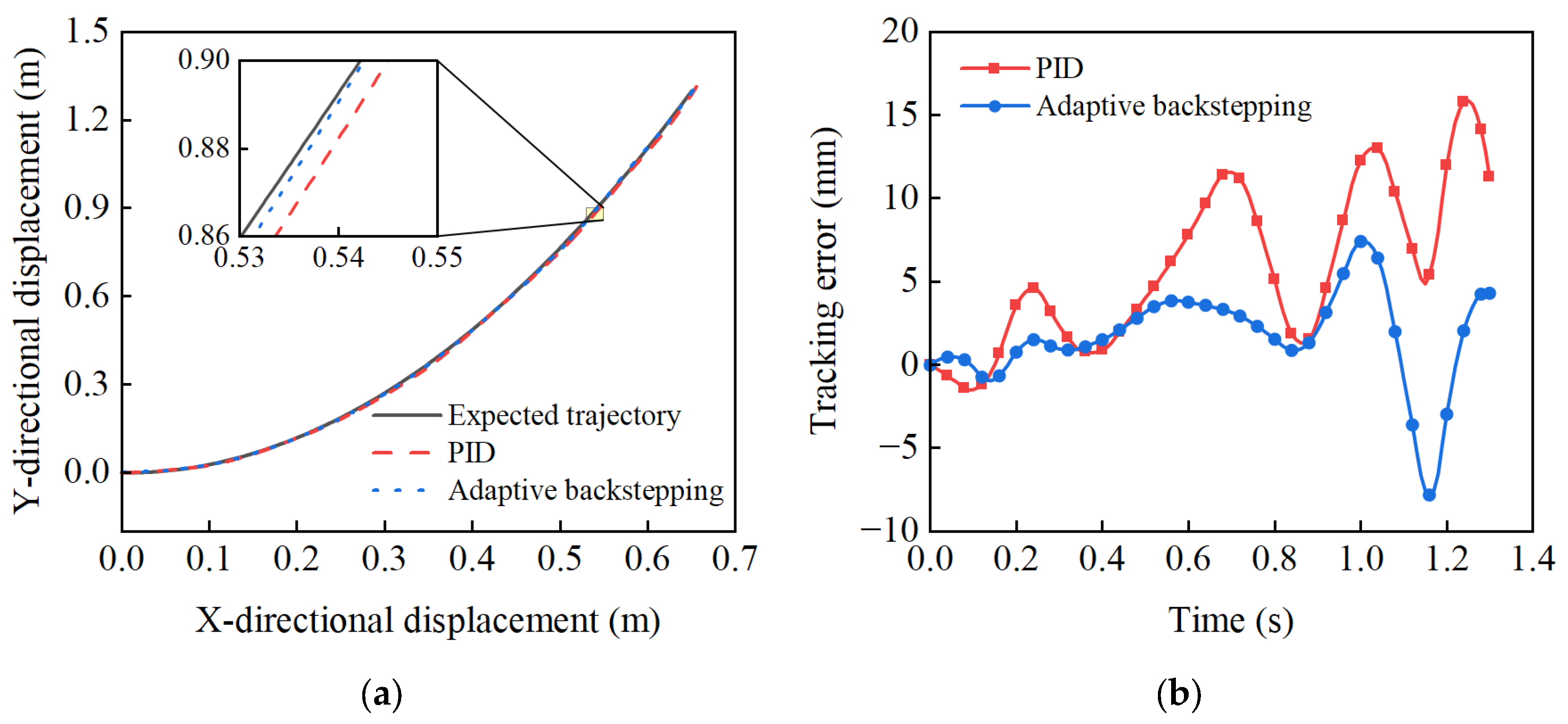
(2) The experimental results based on a representative mining trajectory show that, compared with classical PID control, the proposed method reduced the maximum tracking error and the RMSE for the boom cylinder by 63.08% and 57.98%, and for the bucket cylinder by 53.18% and 62.14%, respectively. Most importantly, for the critical bucket tip trajectory, the corresponding improvements reached 50.88% and 56.07%,conclusively demonstrating its superior performance in improving trajectory tracking accuracy.

The proposed adaptive backstepping control strategy shows promise in improving trajectory tracking accuracy for loader electro-hydraulic systems. The methodological framework can serve as a reference for intelligent control of similar construction machinery. Future research will focus on embedded real-time algorithm optimization and integration with intelligent control methods.