Experiment Study on Flow-Induced Vibration of O-Type Ball Valve
Abstract
1. Introduction
2. Experimental Design and Setup
2.1. Experimental Platform Design
2.2. Experimental Setup
2.3. Analysis Methods of Experimental Data
3. Results and Discussion
3.1. Verification of Vibration Isolation
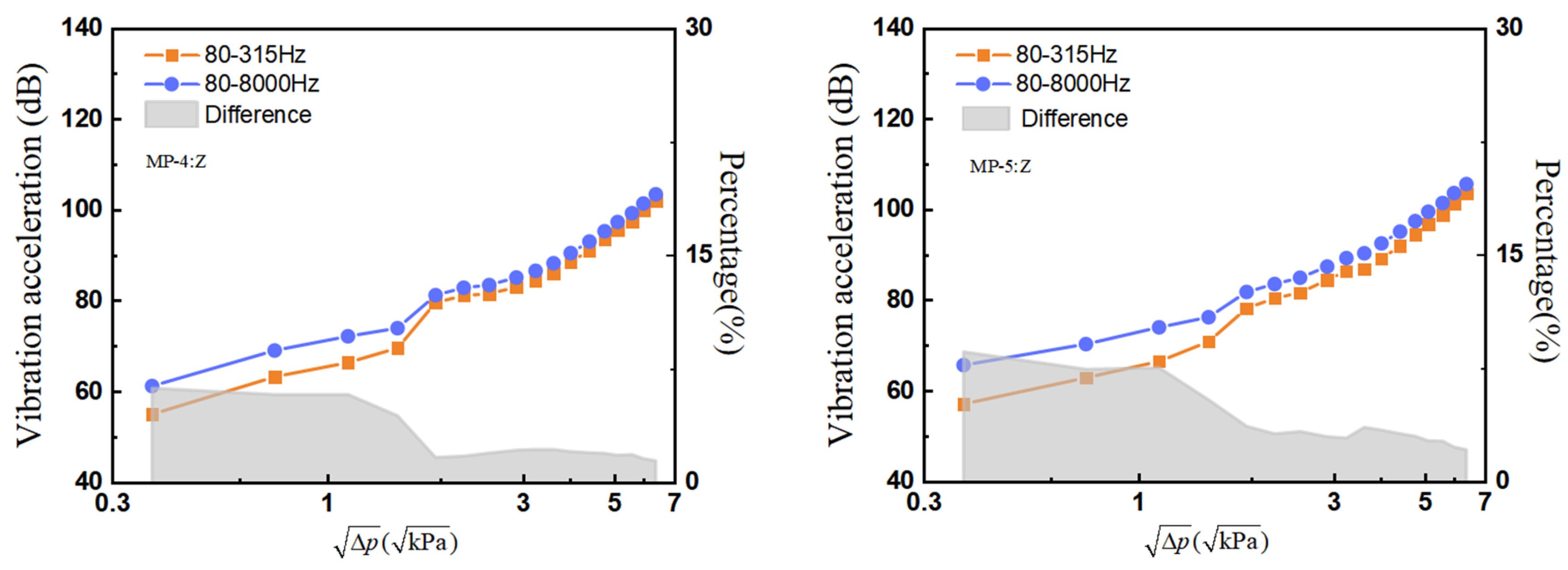
3.1.1. Low Flow Velocities
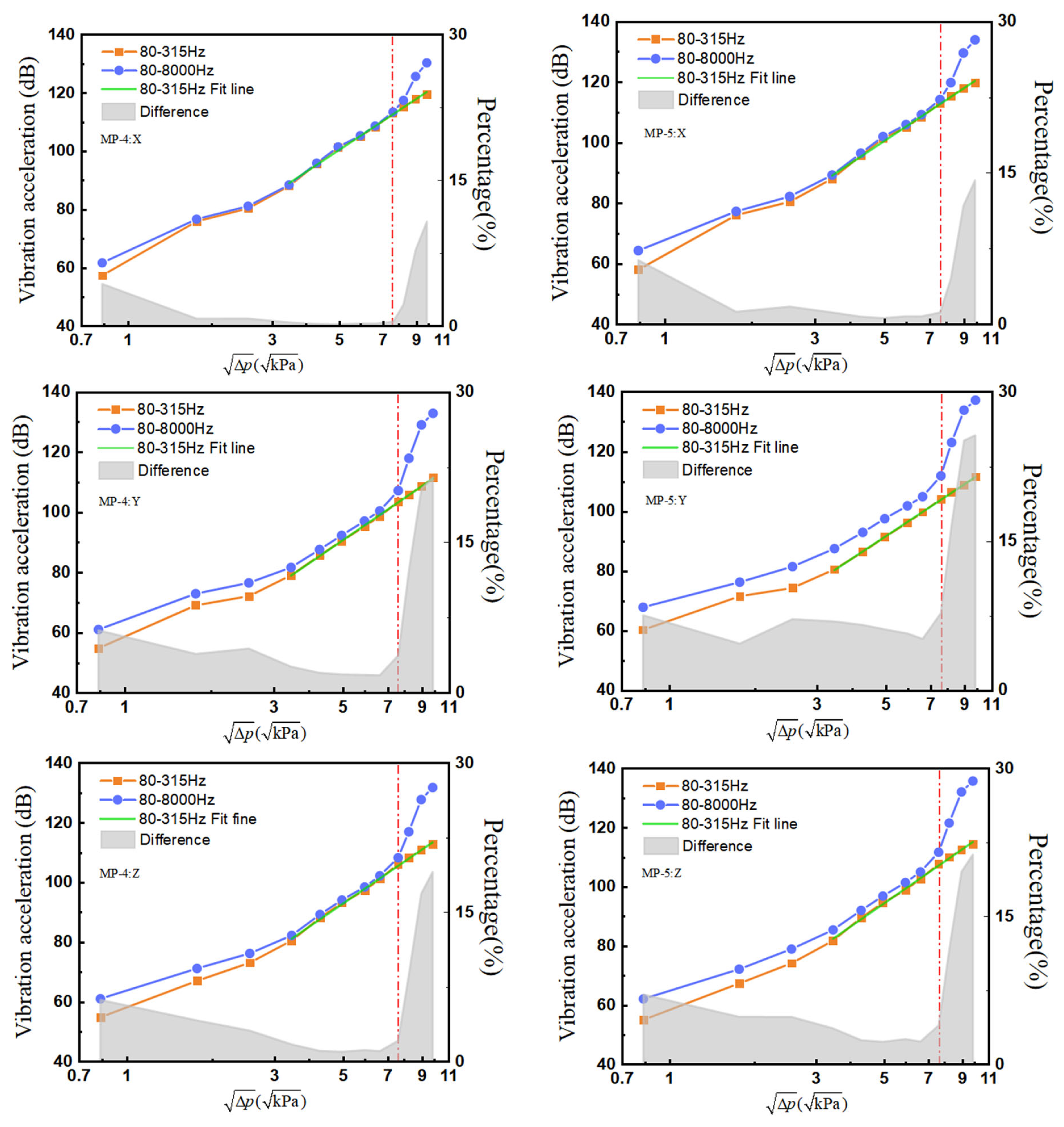
3.1.2. High Flow Velocities
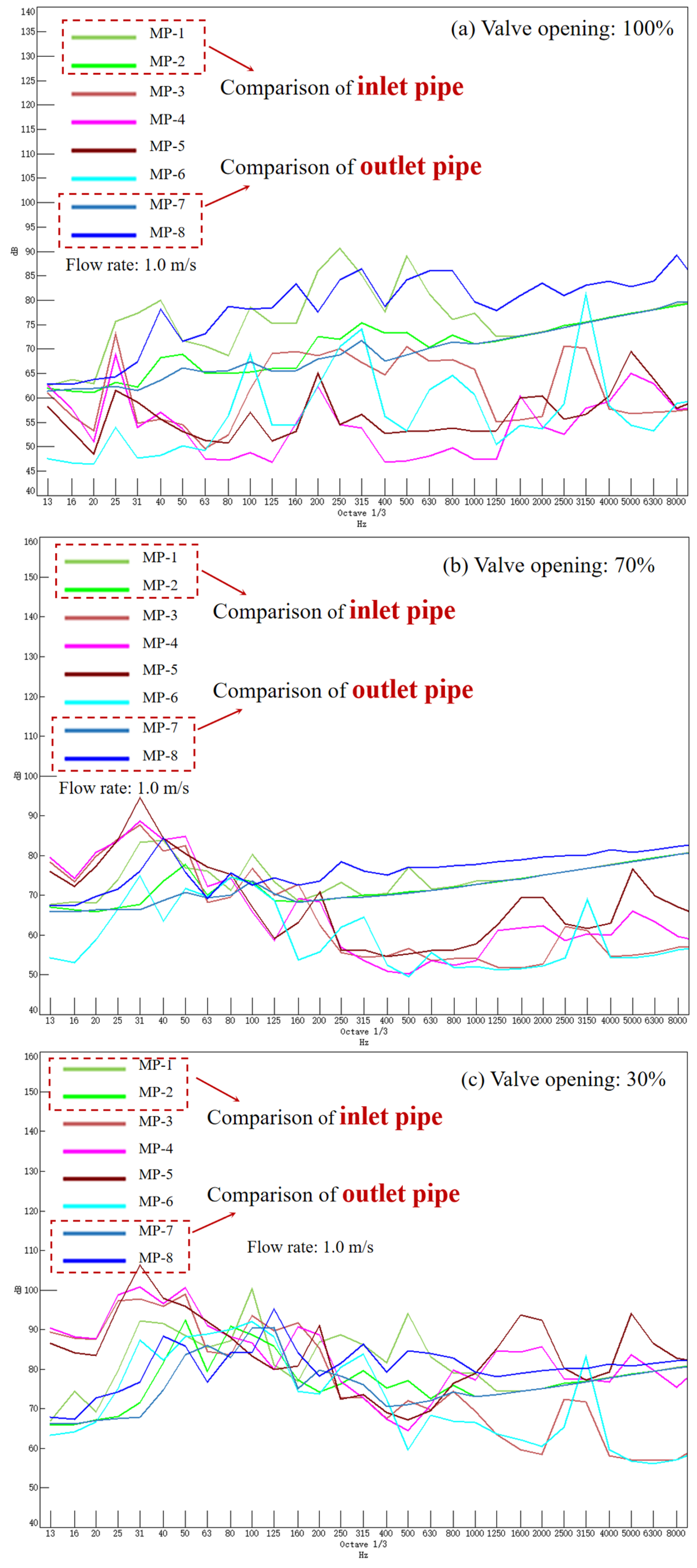
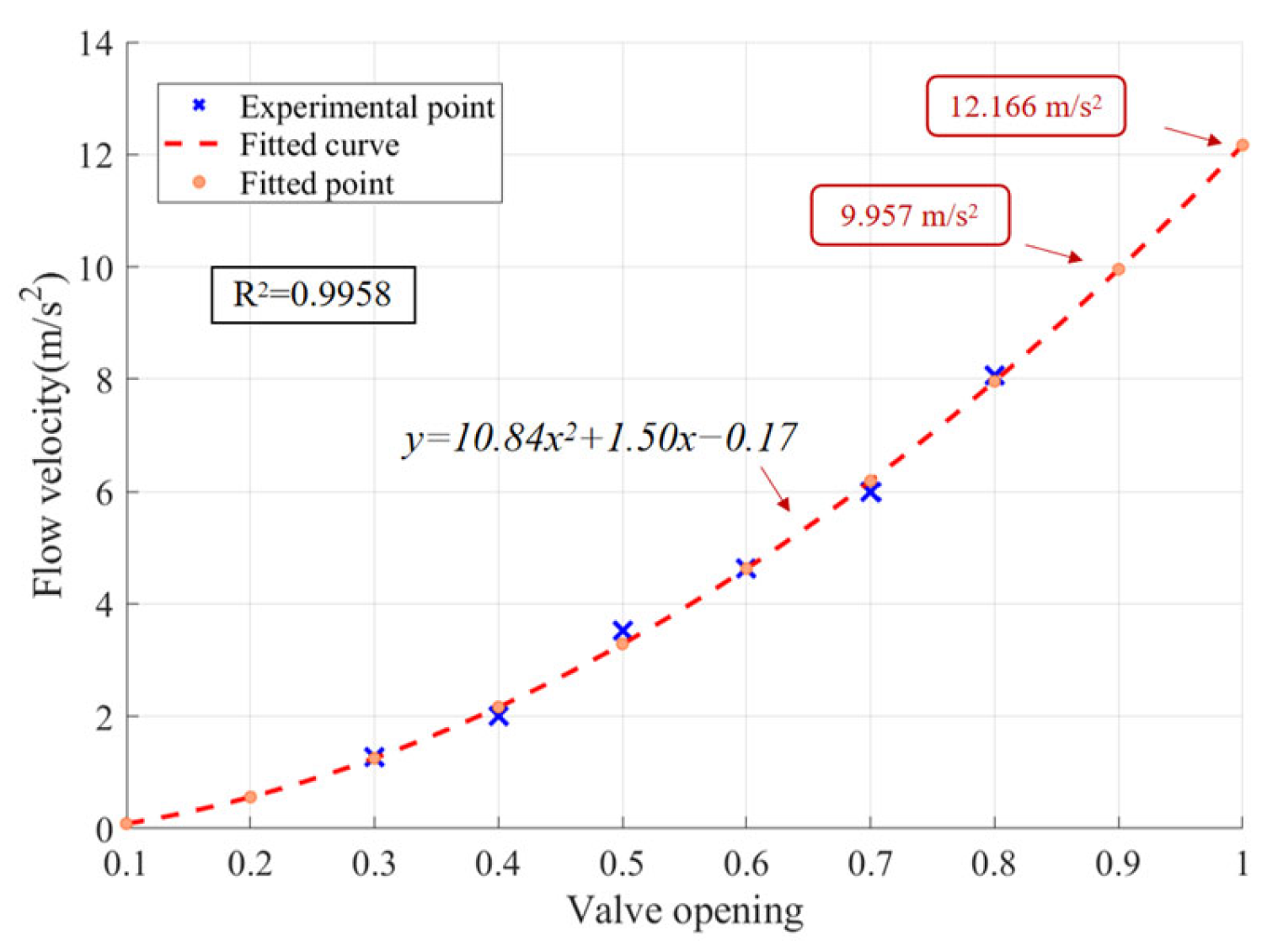
3.2. Effects of Flow Velocities on Vibration
3.2.1. Non-Cavitation Conditions
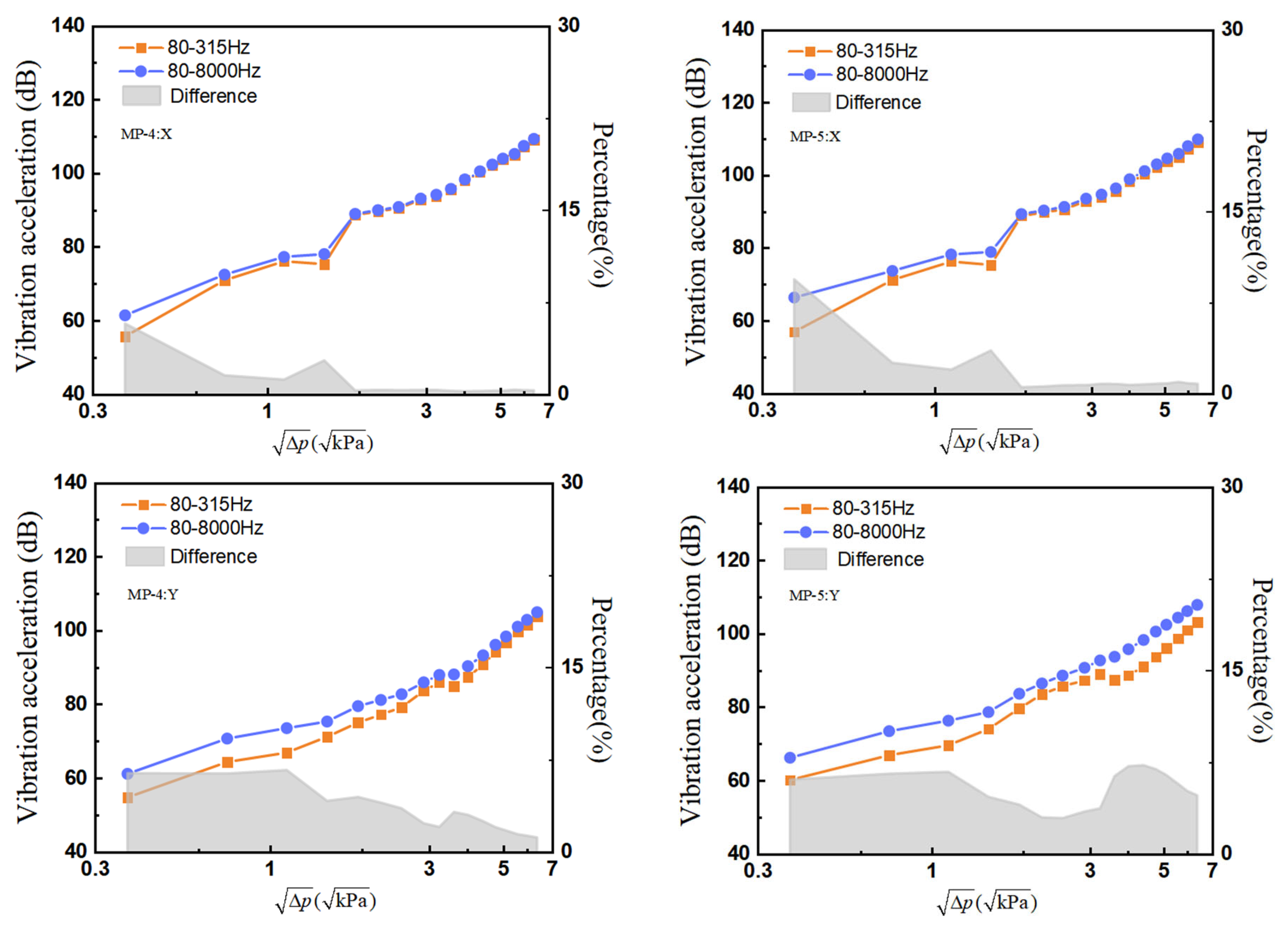
3.2.2. Cavitation Conditions
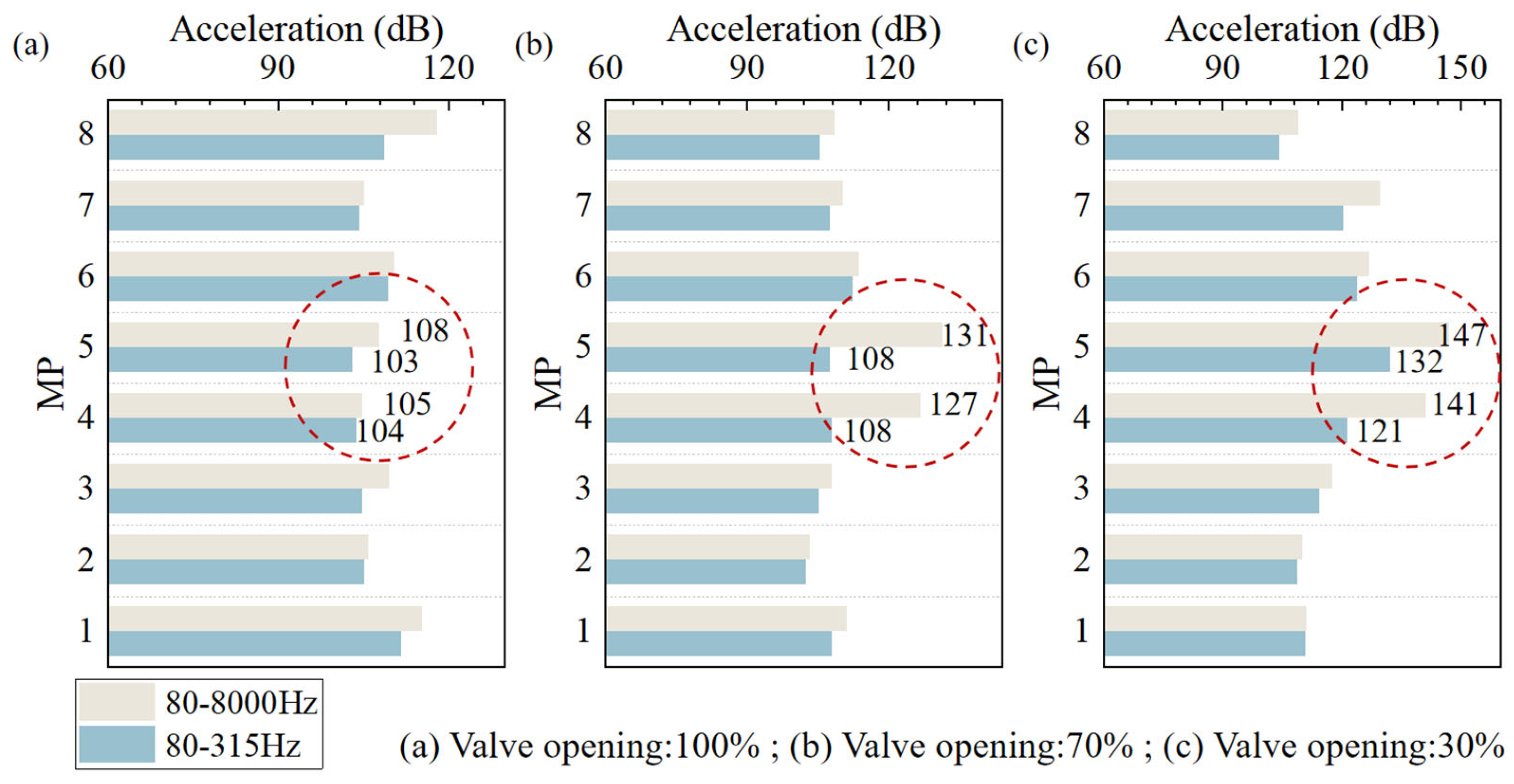
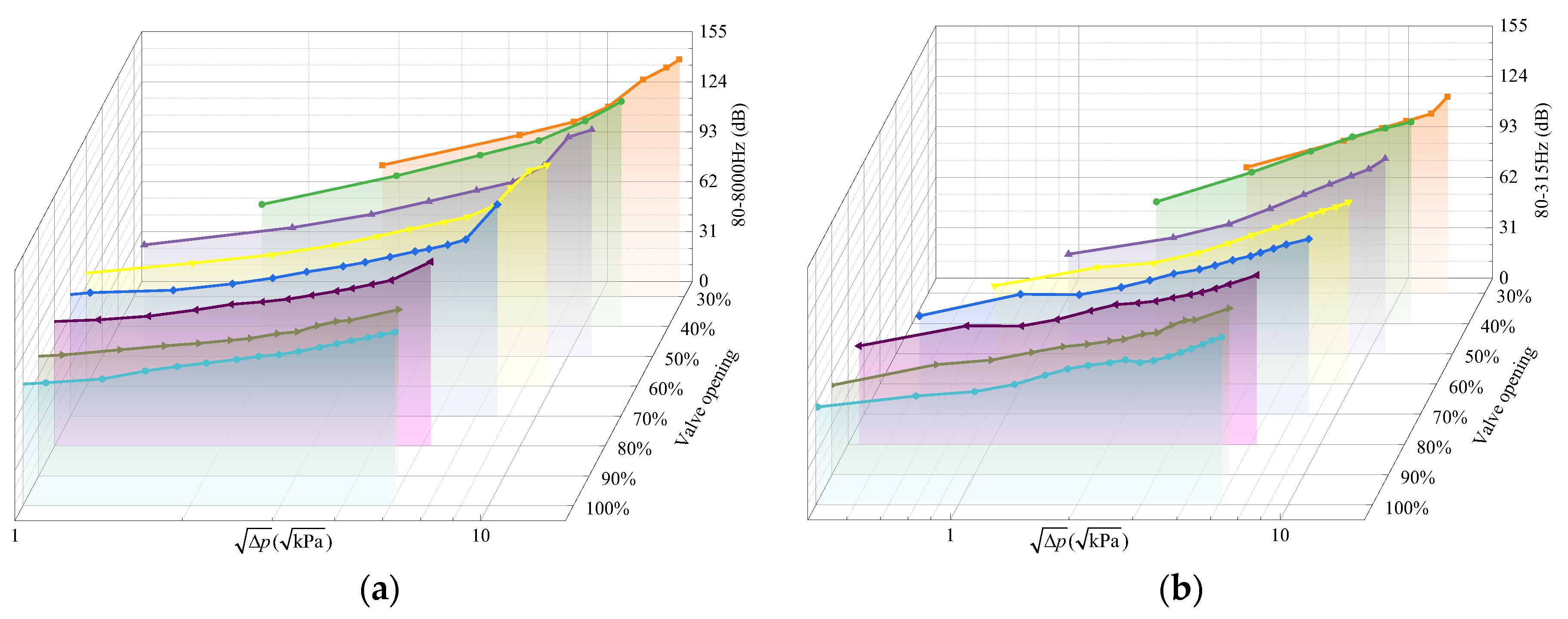
3.3. Effects of Valve Openings on Vibration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Qu, J.; Liu, L.; Tan, X.; Guo, J.; Li, Y.; Zhang, J.; Liu, X.; Yu, J.; Ji, G.; et al. Design and Flow Characteristics of a Gravity-Driven Flow Control Valve. Machines 2025, 13, 654. [Google Scholar] [CrossRef]
- Asok, S.P.; Vijayaragavan, B.; Sundararajan, T.; Manikandan, G.R. Development of a Hydraulic Conical Valve for the Linearization of Flow. Machines 2025, 13, 866. [Google Scholar] [CrossRef]
- Wei, A.B.; Gao, R.; Zhang, W.; Wang, S.H.; Zhou, R.; Zhang, X.B. Computational fluid dynamics analysis on flow-induced vibration of a cryogenic poppet valve in consideration of cavitation effect. J. Zhejiang Univ.-Sci. A 2022, 23, 83–100. [Google Scholar] [CrossRef]
- Yang, L.; Li, S.; Hou, J. A Comprehensive Review of Flow-Induced Vibration and Fatigue Failure in the Moving Components of Control Valves. Machines 2025, 13, 766. [Google Scholar] [CrossRef]
- ISO 10767-1:2015; Hydraulic Fluid Power—Determination of the Pressure Ripple Levels Generated in Systems and Components—Part 1: Method for Determining Source Flow Ripple and Source Impedance of Pumps. International Organization for Standardization: Geneva, Switzerland, 2015.
- Stosiak, M.; Yatskiv, I.; Prentkovskis, O.; Karpenko, M. Reduction of Pressure Pulsations over a Wide Frequency Range in Hydrostatic Systems. Machines 2025, 13, 25. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M. The influence of the hydropneumatic accumulator on the dynamic and noise of the hydrostatic drive operation. Eksploat. Niezawodn.–Maint. Reliab. 2024, 26, 186169. [Google Scholar] [CrossRef]
- Chen, P.; Liu, Z.; Xu, R.; Liu, J. Comparative investigation and test verification of cavitation and turbulence models of injector control ball valve. Int. J. Heat Fluid Flow 2024, 109, 109557. [Google Scholar] [CrossRef]
- Iravani, M.; Toghraie, D. Design a high-pressure test system to investigate the performance characteristics of ball valves in a compressible choked flow. Measurement 2020, 151, 107200. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, S.; Yang, G.; Zhang, H. Simulation study on the cavitation distribution in the ball valve of a common rail injector. Int. J. Engine Res. 2024, 25, 1575–1587. [Google Scholar] [CrossRef]
- Miao, X.; Chang, A.B.; Zheng, J.; Chen, X.; Guo, L.; Xia, S.; Di, Y. Flow analysis of a control ball valve in a common rail fuel injector. Int. J. Engine Res. 2024, 25, 1013–1023. [Google Scholar] [CrossRef]
- Zhao, Z.; Gao, X.; Liu, Y. The optimized design of a ball valve with large stroke and high precision. Flow Meas. Instrum. 2024, 96, 102545. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, Y.; Gao, X.; Tong, S. Design of a high-precision linear regulating ball valve. Flow Meas. Instrum. 2024, 100, 102708. [Google Scholar] [CrossRef]
- Arora, K.; Uppal, A.S.; Singh, A.K. Experimental investigation into magnetorheological finishing of polymer valve seat surface for ball valve performance. Surf. Rev. Lett. 2024, 32, 2550002. [Google Scholar] [CrossRef]
- Teles, D.B.; Gouveia, S.M.; Clarke, T.G. Identification of leakage in ball valves by analysis of pressure and torque signatures in cyclical tests under critical operating conditions. Eng. Fail. Anal. 2020, 117, 104828. [Google Scholar] [CrossRef]
- Shi, M.; Deng, L.; Yang, B.; Qin, L.; Gu, L. Research on internal leakage detection of the ball valves based on stacking ensemble learning. Meas. Sci. Technol. 2024, 35, 095109. [Google Scholar] [CrossRef]
- Sotoodeh, K. Why packing adjustment cannot stop leakage: Case study of a ball valve failing to seal after packing adjustment during fugitive emission as per ISO 15848–1. Eng. Fail. Anal. 2021, 130, 105751. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, J.; Ming, L.; Zhang, G.; Lin, Z.; Li, H. Study on gas–liquid–solid multiphase flow and erosion in ball valves. Eng. Fail. Anal. 2025, 167, 108945. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Zhang, M.; Li, M.; Zhao, Z.; Liu, L. Failure analysis of the outlet pipeline and ball valve of the circulating pump in the desulfurization liquid concentration tower. Eng. Fail. Anal. 2024, 161, 108338. [Google Scholar] [CrossRef]
- Chemaa, K.; Kezrane, M.; Hassani, S.; Abd-El-Yazid, K.; Benmaamar, Z. Austenite stainless steel multilayers coatings on ball valves for tribological behavior improvement. Appl. Phys. A 2022, 128, 616. [Google Scholar] [CrossRef]
- Moses, D.; Haider, G.; Henshaw, J. An investigation of the failure of a 1/4″ ball valve. Eng. Fail. Anal. 2019, 100, 393–405. [Google Scholar] [CrossRef]
- Zhu, H.; Lin, X.; Xue, X.; Zhang, Y.; Wang, L.; Ning, Y.; Fang, X. Laser cladding of stainless-steel ball valves by a high-power diode laser source with a rectangular beam spot. Opt. Laser Technol. 2024, 169, 110123. [Google Scholar] [CrossRef]
- Awad, H.; Parrondo, J. Turbine inlet valve’s self-excited vibrations risk the safe operation of hydropower plants. J. Vib. Eng. Technol. 2024, 12, 3355–3371. [Google Scholar] [CrossRef]
- Lv, X.; Chen, B.; Zhang, Y.; Li, S. Vibration suppression of an armature assembly in hydraulic servo valve based on distributed parameters mathematical models. J. Vib. Control 2023, 30, 4801–4813. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Prentkovskis, O.; Deptuła, A.; Skačkauskas, P. Research of vibrations effect on hydraulic valves in military vehicles. Def. Technol. 2023, 30, 111–125. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Deptuła, A.; Urbanowicz, K.; Skačkauskas, P.; Deptuła, A.M.; Łapka, M. Research of vibration effects on a hydraulic valve in the pressure pulsation spectrum analysis. J. Mar. Sci. Eng. 2023, 11, 301. [Google Scholar] [CrossRef]
- Wang, H.; Lai, Z.; Wu, D.; Zhang, K.; Zheng, M. Investigation of the friction-induced vibration of a novel four-way reversing valve using spectral kurtosis and number of peaks spectrum. Mech. Syst. Signal Process. 2022, 166, 108425. [Google Scholar] [CrossRef]
- Musselman, M.; Xie, H.; Djurdjanovic, D. Nonstationary signal analysis and support vector machine based classification for vibration based characterization and monitoring of slit valves in semiconductor manufacturing. J. Intell. Manuf. 2019, 30, 1099–1110. [Google Scholar] [CrossRef]
- Lyu, F.; Cao, C.; Zhao, D.; Li, C.; Su, J.; Zhao, X.; Jia, X. Vibration characteristics analysis of high-pressure long-distance dense paste pipeline transporting with hydraulic active check valve. Alex. Eng. J. 2023, 71, 669–677. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Y.; Xu, Q.N.; Han, D. Novel structure for waveform control of twin rotary flowrate valve controlled vibration exciter. IEEE/ASME Trans. Mechatron. 2020, 26, 1183–1188. [Google Scholar] [CrossRef]
- Schröders, S.; Fidlin, A. Asymptotic analysis of self-excited and forced vibrations of a self-regulating pressure control valve. Nonlinear Dyn. 2021, 103, 2315–2327. [Google Scholar] [CrossRef]
- Miyaki, Y.; Tsukagoshi, H. Self-excited vibration valve that induces traveling waves in pneumatic soft mobile robots. IEEE Robot. Autom. Lett. 2020, 5, 4133–4139. [Google Scholar] [CrossRef]
- Ordoñez, V.; Arcos, R.; Romeu, J.; Josefsson, A. Investigation on electromagnetic vibration energy harvesting in water distribution control valves. IEEE Sens. J. 2020, 21, 2734–2741. [Google Scholar] [CrossRef]
- Kovacevic, S.; Agarwal, V.; Buttles, J.W. Numerical and Experimental Vibration Analysis of an Additive Manufactured Sensor Mounting Unit for a Wireless Valve Position Indication Sensor System. Nucl. Technol. 2022, 208, 468–483. [Google Scholar] [CrossRef]
- Zhong, Q.; Jia, T.; Xu, E.; Yao, Z.; Li, Y.; Yang, H. A Vibration-Based Measurement Method for Dynamic Characteristic of Solenoid Switching Valve. IEEE Trans. Instrum. Meas. 2023, 73, 7500810. [Google Scholar] [CrossRef]
- Wang, P.; Yang, C.Y.; Yuan, Y.Y.; Fu, Y.C.; Ding, W.F.; Xu, J.H.; Chen, Y. Study on the mechanism of burr formation in ultrasonic vibration-assisted honing 9Cr18MoV valve sleeve. Adv. Manuf. 2024, 13, 606–619. [Google Scholar] [CrossRef]
- Lu, Y.; Tan, L.; Zhao, X.; Ma, C. Experiment on cavitation-vibration correlation of a centrifugal pump under steady state and start-up conditions in energy storage station. J. Energy Storage 2024, 83, 110763. [Google Scholar] [CrossRef]
- Mousmoulis, G.; Karlsen-Davies, N.; Aggidis, G.; Anagnostopoulos, I.; Papantonis, D. Experimental analysis of cavitation in a centrifugal pump using acoustic emission, vibration measurements and flow visualization. Eur. J. Mech.-B/Fluids 2019, 75, 300–311. [Google Scholar] [CrossRef]
- Feng, J.; Zhao, N.; Zhu, G.; Wu, G.; Li, Y.; Luo, X. Cavitation identification in a hydraulic bulb turbine based on vibration and pressure fluctuation measurements. Mech. Syst. Signal Process. 2024, 208, 111042. [Google Scholar] [CrossRef]
- Liu, D.; Li, G.; Sun, N.; Zhu, G.; Cao, H.; Wang, T.; Gu, F. Vibration-induced cavitation in cylinder liners caused by piston slaps. Int. J. Mech. Sci. 2024, 267, 109025. [Google Scholar] [CrossRef]
- Ouyang, T.; Li, Y.; Tian, H.; Wang, J.; Zhang, N. Cavitation mechanism of high-speed helical gears induced by vibration. Tribol. Int. 2024, 193, 109440. [Google Scholar] [CrossRef]
- Kristian, A. Elimination of cavitation induced vibrations in orifice plates. Exp. Comput. Multiph. Flow 2022, 4, 310–317. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Cheng, H.; Ji, B.; Long, X. Experimental study of the cavitation noise and vibration induced by the choked flow in a Venturi reactor. Ultrason. Sonochem. 2020, 67, 105183. [Google Scholar] [CrossRef] [PubMed]
- McKee, K.K.; Forbes, G.L.; Mazhar, I.; Entwistle, R.; Hodkiewicz, M.; Howard, I. A vibration cavitation sensitivity parameter based on spectral and statistical methods. Expert Syst. Appl. 2015, 42, 67–78. [Google Scholar] [CrossRef]
- Lin, Z.H.; Hou, C.W.; Zhang, L.; Guan, A.Q.; Jin, Z.J.; Qian, J.Y. Fluid-structure interaction analysis on vibration characteristics of sleeve control valve. Ann. Nucl. Energy 2023, 181, 109579. [Google Scholar] [CrossRef]

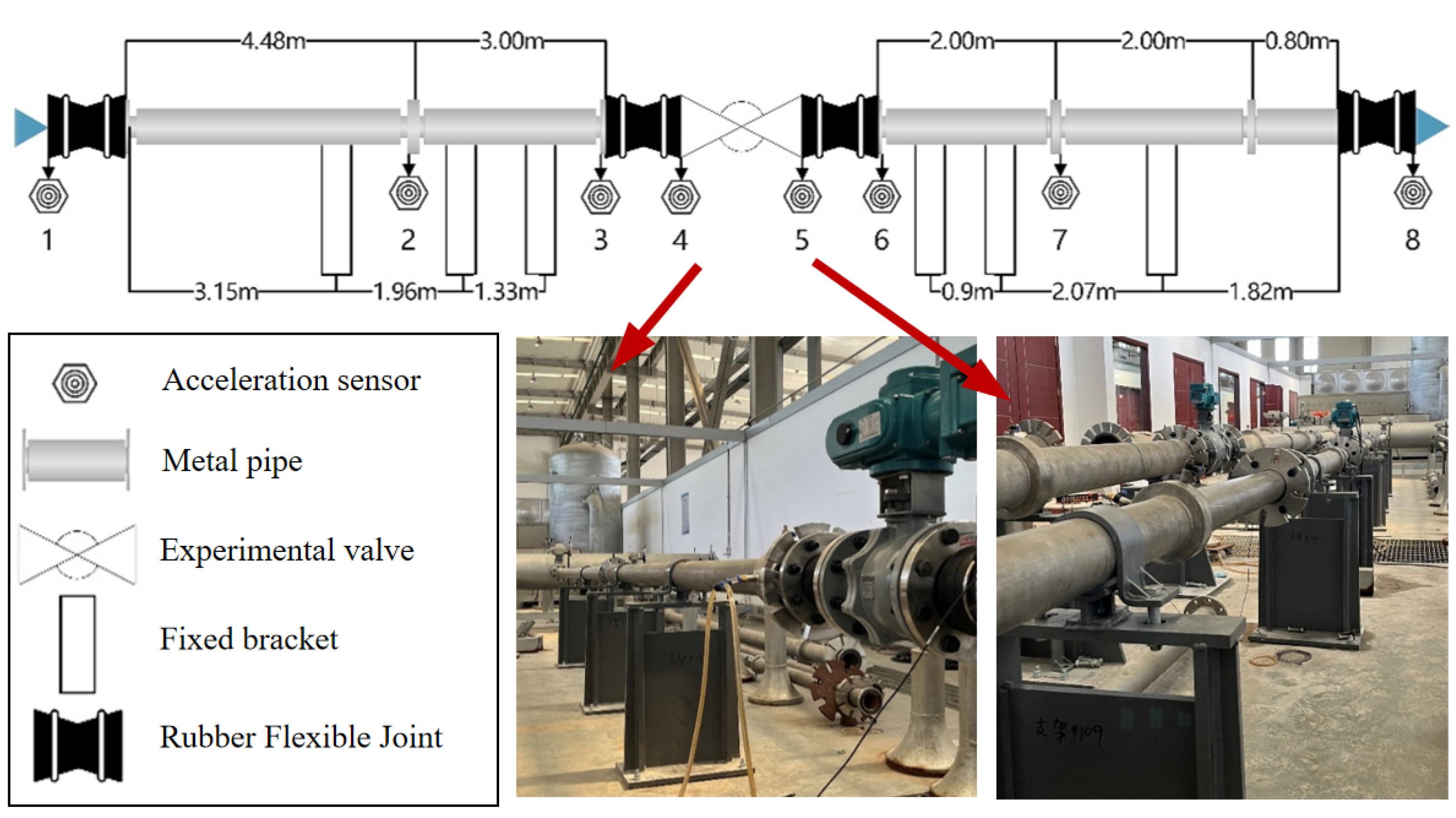


| Measurement Point (MP) | Acceleration Channel | Measurement Direction | Abbreviations |
|---|---|---|---|
| 1 | 1-Y | Horizontal radial | MP-1:Y |
| 2 | 2-Y | Horizontal radial | MP-2:Y |
| 3 | 3-X | Axial | MP-3:X |
| 3-Y | Horizontal radial | MP-3:Y | |
| 3-Z | Vertical radial | MP-3:Z | |
| 4 | 4-X | Axial | MP-4:X |
| 4-Y | Horizontal radial | MP-4:Y | |
| 4-Z | Vertical radial | MP-4:Z | |
| 5 | 5-X | Axial | MP-5:X |
| 5-Y | Horizontal radial | MP-5:Y | |
| 5-Z | Vertical radial | MP-5:Z | |
| 6 | 6-X | Axial | MP-6:X |
| 6-Y | Horizontal radial | MP-6:Y | |
| 6-Z | Vertical radial | MP-6:Z | |
| 7 | 7-Y | Horizontal radial | MP-7:Y |
| 8 | 8-Y | Horizontal radial | MP-8:Y |
| Device | Device Model | Quantity |
|---|---|---|
| Acceleration sensors | BK-4535-B-001 | 4, MP-3~6 |
| PCB-356A25 | 4, MP-1~2, MP-7~8 | |
| Data-acquisition device | LMS SCADAS Mobile (Siemens, Munich, Germany) | 1 |
| Valve Opening (%) | 100 | 70 | 30 | |||
|---|---|---|---|---|---|---|
| Overall Level (dB) | 80–315 Hz | 80–8000 Hz | 80–315 Hz | 80–8000 Hz | 80–315 Hz | 80–8000 Hz |
| MP1:Y | 93.10 | 95.45 | 92.77 | 97.04 | 101.02 | 102.13 |
| MP2:Y | 79.20 | 87.22 | 79.36 | 87.36 | 94.06 | 95.06 |
| MP3:Y | 76.17 | 79.85 | 84.40 | 86.16 | 97.27 | 97.35 |
| MP4:Y | 64.32 | 70.68 | 70.99 | 73.57 | 95.02 | 96.81 |
| MP5:Y | 66.88 | 73.44 | 73.67 | 76.55 | 93.71 | 100.14 |
| MP6:Y | 76.79 | 82.75 | 77.58 | 84.05 | 95.64 | 95.93 |
| MP7:Y | 76.53 | 86.64 | 77.18 | 87.32 | 94.19 | 95.06 |
| MP8:Y | 90.75 | 96.71 | 91.64 | 96.94 | 96.78 | 98.23 |
| Acceleration Channel | Fitting Equation |
|---|---|
| MP-4:X | y = 52.41856 + 68.67104x |
| MP-4:Y | y = 41.17538 + 70.84909x |
| MP-4:Z | y = 43.38455 + 70.88041x |
| MP-5:X | y = 52.47205 + 68.70526x |
| MP-5:Y | y = 43.7786 + 68.52023x |
| MP-5:Z | y = 44.207 + 71.77222x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, D.; Sheng, K.; Zhang, S.-Z.; Han, J.; Gu, X.-J.; Yang, L.; Qian, J.-Y. Experiment Study on Flow-Induced Vibration of O-Type Ball Valve. Machines 2025, 13, 1065. https://doi.org/10.3390/machines13111065
Wei D, Sheng K, Zhang S-Z, Han J, Gu X-J, Yang L, Qian J-Y. Experiment Study on Flow-Induced Vibration of O-Type Ball Valve. Machines. 2025; 13(11):1065. https://doi.org/10.3390/machines13111065
Chicago/Turabian StyleWei, Dong, Kan Sheng, Shen-Zhe Zhang, Jie Han, Xuan-Jie Gu, Liang Yang, and Jin-Yuan Qian. 2025. "Experiment Study on Flow-Induced Vibration of O-Type Ball Valve" Machines 13, no. 11: 1065. https://doi.org/10.3390/machines13111065
APA StyleWei, D., Sheng, K., Zhang, S.-Z., Han, J., Gu, X.-J., Yang, L., & Qian, J.-Y. (2025). Experiment Study on Flow-Induced Vibration of O-Type Ball Valve. Machines, 13(11), 1065. https://doi.org/10.3390/machines13111065







