Profit-Oriented Multi-Objective Dynamic Flexible Job Shop Scheduling with Multi-Agent Framework Under Uncertain Production Orders

Abstract

In the highly competitive manufacturing environment, customers are increasingly demanding punctual, flexible, and customized deliveries, compelling enterprises to balance profit, energy efficiency, and production performance while seeking new scheduling methods to enhance dynamic responsiveness. Although deep reinforcement learning (DRL) has made progress in dynamic flexible job shop scheduling, existing research has rarely addressed profit-oriented optimization. To tackle this challenge, this paper proposes a novel multi-objective dynamic flexible job shop scheduling (MODFJSP) model that aims to maximize net profit and minimize makespan on the basis of traditional FJSP. The model incorporates uncertainties such as new job insertions, fluctuating due dates, and high-profit urgent jobs, and establishes a multi-agent collaborative framework consisting of “job selection–machine assignment.” For the two types of agents, this paper proposes adaptive state representations, reward functions, and variable action spaces to achieve the dual optimization objectives. The experimental results show that the double deep Q-network (DDQN), within the multi-agent cooperative framework, outperforms PPO, DQN, and classical scheduling rules in terms of solution quality and robustness. It achieves superior performance on multiple metrics such as IGD, HV, and SC, and generates bi-objective Pareto frontiers that are closer to the ideal point. The results demonstrate the effectiveness and practical value of the proposed collaborative framework for solving MODFJSP.

1. Introduction

Over the past few decades, economic globalization has reshaped industrial and value chains with unprecedented depth and breadth. While unlocking economies of scale and accelerating technological diffusion, it has also continuously exposed traditional manufacturing to uncertainties such as demand fluctuations and factor price shocks [1]. As the cornerstone of industrial systems and the macroeconomy, the capacity of the manufacturing sector directly reflects a nation’s comprehensive strength and international competitiveness [2]. With the advancement of intelligent manufacturing technologies, manufacturing paradigms are shifting from uniformity to diversification, imposing higher demands on enterprises’ production organization and management [3].

The job shop scheduling problem (JSP) is one of the most fundamental and frequently deliberated decision-making issues in enterprise production management [4]. Its essence lies in arranging task sequences and allocating resources under limited time and resource constraints, with the aim of minimizing production cycles, reducing costs, and maximizing efficiency [5]. As a significant extension of JSP, the flexible job shop scheduling problem (FJSP) allows each operation to be processed on multiple alternative machines and enables flexible adjustment of process routes according to task requirements [6]. This feature not only enhances the flexibility and resource utilization of production systems but also alleviates bottlenecks, enabling enterprises to maintain high production efficiency and delivery reliability even under complex scenarios such as fluctuating order structures and tight due dates [7]. Consequently, FJSP has become an indispensable tool for modern production scheduling optimization and enterprise operation management, and it has been widely applied in high-demand industries such as semiconductor manufacturing, automotive production, and metallurgical processing [8].

In real-world production, enterprises under fierce market competition and increasing customer demands are often required to simultaneously shorten production cycles and enhance profits [9]. However, the production process is frequently accompanied by dynamic events such as job insertions, machine breakdowns, and due date changes, which transform the scheduling problem from a static FJSP into a dynamic FJSP (DFJSP), thereby significantly increasing decision-making complexity [10]. Moreover, a single optimization objective can no longer meet the needs of modern manufacturing systems, and thus the DFJSP has further evolved into the multi-objective flexible job shop scheduling problem (MODFJSP) [11].

For the MODFJSP, researchers have proposed various heuristic, metaheuristic, and machine learning approaches [12,13,14]. Although metaheuristic algorithms can effectively cope with uncertainties, they often require re-tuning when applied to new production lines or disturbances, thus limiting their generalization ability [9]. Deep reinforcement learning (DRL) offers advantages in adaptability and real-time responsiveness, and in particular, multi-agent DRL (MADRL) has demonstrated greater robustness and scalability in solving MODFJSP [15]. However, existing MADRL-based studies mainly focus on minimizing production time and reducing costs, while placing insufficient emphasis on profit maximization. Especially under uncertain production orders, how to simultaneously ensure production efficiency and maximize net profit remains an urgent challenge. The main contributions of this research are as follows.

• For the MODFJSP with dynamic new job arrivals, high-profit urgent jobs, and fluctuating due dates, an optimization model is constructed with two objectives: minimizing makespan and maximizing net profit.
• A sequential multi-agent collaborative framework of “job selection → machine assignment” is constructed: the job agent first decides the job to be processed, and the machine agent then assigns the pending operation of the selected job to a feasible machine set, thereby enabling efficient solution of the proposed MODFJSP.
• Customized reward functions are designed for the two agents with the objectives of maximizing profit and minimizing makespan, accompanied by adaptive state representations and variable action output mechanisms, which significantly enhance learning efficiency and enable multi-objective collaborative optimization.
• The system conducts a comparative analysis of various mainstream DRL algorithms and classical dispatching rules in solving the proposed MODFJSP, thereby identifying the optimal DRL-based solution.

2. Literature Review

In this section, we first review JSP-related studies focusing on cost or profit, then summarize the research contributions on solving FJSP using DRL, and finally highlight the existing research gaps.

2.1. Research on Production Scheduling Problems Considering Cost or Profit

In recent years, an increasing number of researchers have focused on the JSP with energy cost considerations under time-of-use (TOU) electricity pricing, aiming to reduce operating expenses for manufacturing enterprises [16]. For example, Shen et al. [17] studied the TOU mechanism by optimizing operation start times, sequencing, and machine assignments, demonstrating that even with a slight increase in makespan, energy costs can be effectively reduced. The study provided a rigorous and practical basis for cost reduction and efficiency improvement in FJSP under TOU pricing. Similarly, Park and ham [18] incorporated TOU pricing and planned machine downtime to minimize makespan and total energy cost, employing integer linear programming and constraint programming approaches to effectively lower energy consumption in manufacturing.

By contrast, fewer studies have approached scheduling from a profit-oriented perspective, considering the combined impact of scheduling decisions on enterprise revenue and cost. Zouadi et al. [19] innovatively addressed profit orientation and order acceptance by applying a robust decomposition method to maximize production profit, particularly suitable for industries with volatile prices and fragmented customer demand. In the existing FJSP literature, profit-oriented research remains scarce. However, thanks to the dual flexibility of jobs and machines, FJSP still holds substantial potential for profit improvement. Moreover, the MODFJSP can further embed various dynamic events to achieve global adaptive optimization of production and profit. This study innovatively incorporates enterprise profit into the MODFJSP framework, thereby enhancing the effectiveness of scheduling decisions.

2.2. Research on Solving FJSPs with DRL

With the increasing complexity of scheduling problems and the presence of multiple dynamic disturbances (such as job insertions and price fluctuations), traditional heuristic algorithms can hardly provide efficient responses [12]. DRL, leveraging its trial-and-error mechanism and adaptive policy learning, offers a new decision-making paradigm for such high-dimensional, dynamic, and non-stationary environments [20]. In the field of FJSP, an increasing number of researchers have proposed various solutions for FJSP [21]. For example, Luo [22] designed a Deep Q-Network (DQN) algorithm to address DFJSP by incorporating new job insertions to reduce delays. Lu et al. [23] applied a Double Deep Q-Network (DDQN) to solve DFJSP with dynamic job arrivals and urgent job insertions, aiming to minimize makespan (C_max) and average tardiness. Lei et al. [12] proposed a proximal policy optimization (PPO) algorithm with a multi-pointer graph network (MPGN) structure to reduce makespan in FJSP. Existing studies have further verified that when solving FJSP with single-agent DRL methods, the state–action space often suffers from combinatorial explosion, whereas adopting a multi-agent approach can effectively alleviate this issue [15].

Therefore, multi-agent deep reinforcement learning has been widely applied to solve DFJSP [24]. For example, Liu et al. [25] focused on DFJSP with dynamic job arrivals, aiming to minimize total tardiness. Yan et al. [26] also considered DFJSP with dynamic job arrivals and employed a DQN-based multi-agent framework to address factory selection, job allocation, and operation sequencing, achieving the objective of minimizing total tardiness through agent collaboration. Ref. [27] proposed a multi-agent deep reinforcement learning based scheduling framework to address the complex scheduling problem in flexible job shops with the integration of automated guided vehicles (AGVs), achieving collaborative optimization of production and transportation resources.

Table 1. Studies on DRL-based flexible job shop scheduling problems.

Work	RL Algorithm	Agent	Problem	Dynamic Events	Objectives
[22]	DQN	Single	DFJSP	New job insertions	Tardiness
[23]	DDQN	Single	MODFJSP	New job insertions and urgent job insertions	Cmax, Tardiness
[12]	PPO	Single	FJSP	None	Cmax
[25]	DDQN	Multiple	DFJSP	New job insertions	Total tardiness
[26]	DQN	Multiple	DFJSP	New job insertions	Total tardiness
[27]	PPO	Multiple	FJSP with AGVs	None	Makespan; Average lateness; Max lateness
Our work	DDQN	Multiple	MODFJSP	New job insertions, high-profit urgent job insertions, and due day changes	Cmax, Total net Profit

summarizes the above studies on applying deep reinforcement learning methods to FJSP, along with our proposed approach.

2.3. Research Gaps

By summarizing the existing studies, three research gaps can be identified:

• Most cost- or profit-oriented FJSP studies mainly focus on electricity costs under TOU pricing policies, while giving insufficient attention to the penalty costs incurred by tardiness.
• Most studies focus solely on cost; however, in practice, some jobs differ in the remuneration offered by customers due to process complexity or specific requirements. How to incorporate such heterogeneous profits into DFJSP and maximize net profit remains to be further investigated.
• Most DRL-based studies on DFJSP primarily consider dynamic events such as new job insertions, while neglecting profit and due date fluctuations. Moreover, when targeting profit maximization and makespan minimization, further technical challenges arise in the design of scheduling strategies and reward functions to improve agent learning efficiency.

3. Problem Description for MODFJSP

In this section, to illustrate the considered MODFJSP, we first provide a detailed description. Next, the notations and constraints are presented. Finally, the mathematical model is formulated.

3.1. Problem Description

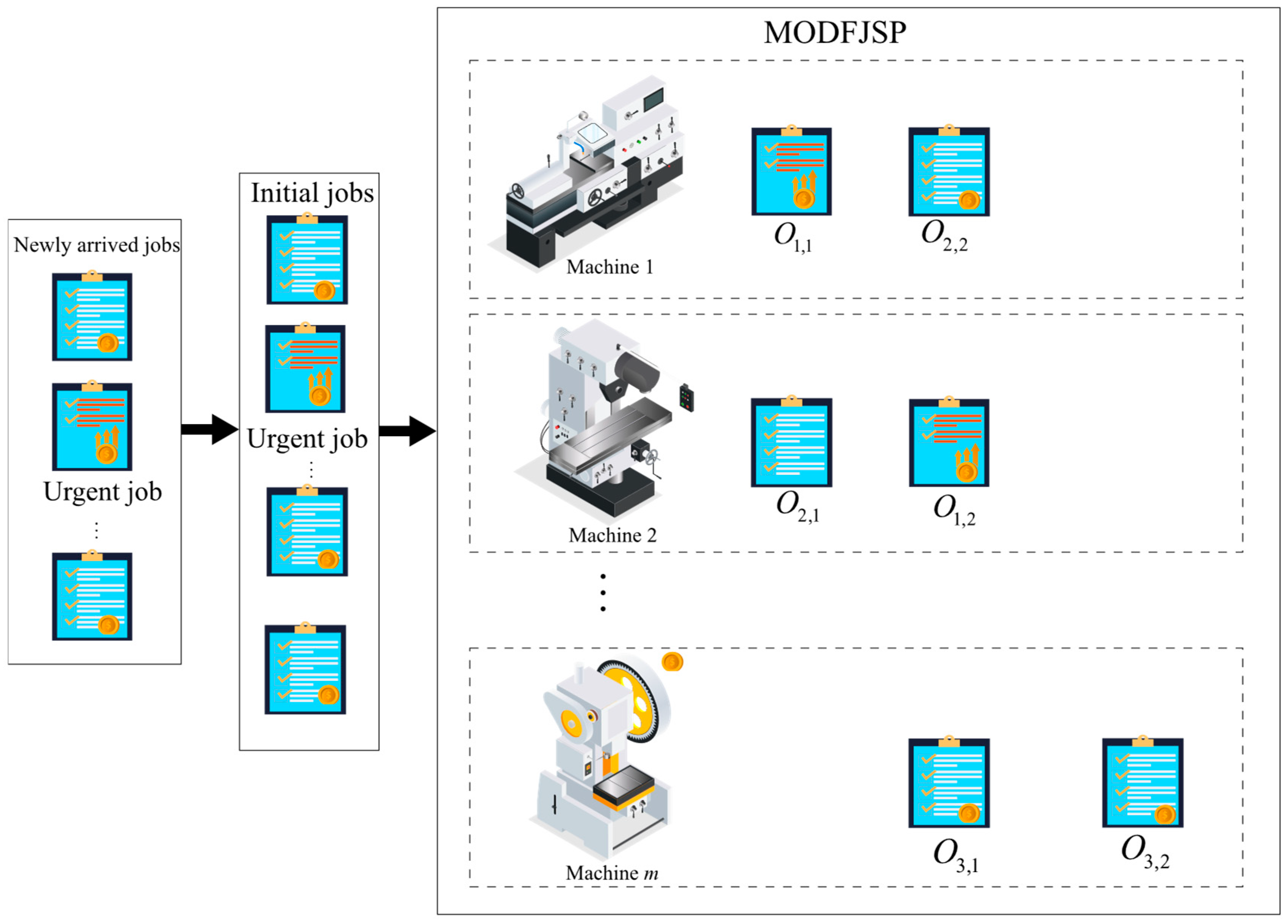
The MODFJSP considered in this study can be defined as follows. A set of n consecutively arriving jobs J = {1, 2, …, n} must be processed on m machines M = {1, 2, …, m}. Each job i consists of n_i operations O_i = {1, …, n_i}, where O_i,j denotes the jth operation of job i. Each operation O_i,j can be processed on any machine selected from its predefined feasible machine set M_i,j (M_i,j⊆M). The processing time of operation O_i,j on machine k is denoted as t_i,j,k. The arrival time and due date of job i are denoted as A_i and D_i, respectively. S_i,j,k and C_i,j,k represent the actual start time and completion time of operation O_i,j on machine k, respectively. The system consists of initial orders and dynamically arriving ${Job}_{new}$ new jobs. Due dates are adjusted according to environmental changes, and some jobs are urgent, generating higher revenue but incurring stricter tardiness penalties. The energy consumption cost is calculated based on TOU electricity pricing. The objectives are to maximize net profit and minimize makespan under resource constraints. The decision process proceeds in two steps: first, selecting the job to be processed, and second, assigning its next operation to a machine. 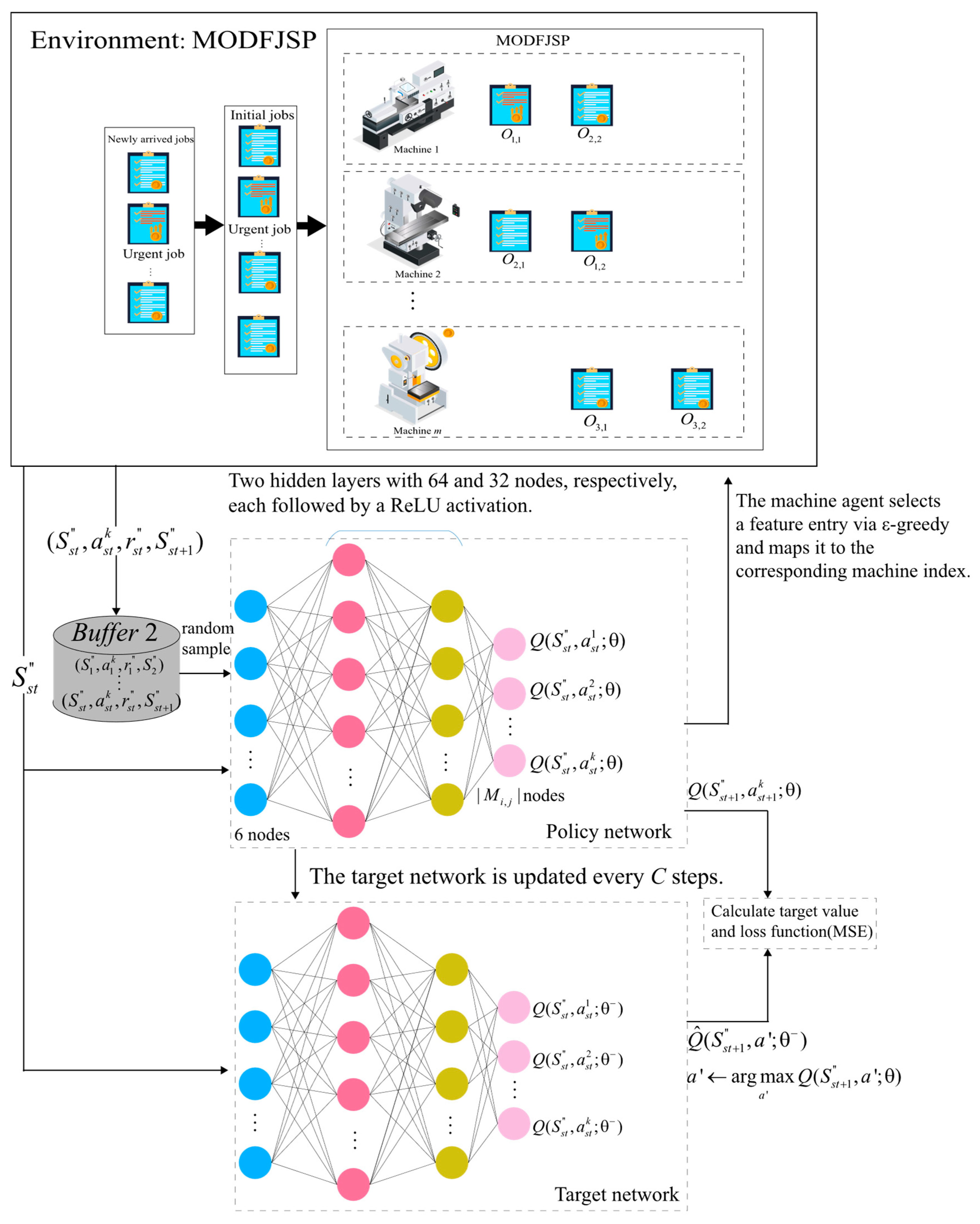For ease of understanding, Figure 1 illustrates the considered MODFJSP.

3.2. Mathematical Model

Before presenting the mathematical model of MODFJSP, we provide a detailed description of the notations used.

Table 2. Notations for the mathematical model.

Parameters	Description
$J$	Set of n jobs, with $J$ = {1, 2, …, n}.
$M$	Set of machines, with M = {1, 2, …, m}.
$O_i$	Set of operations of job i, with $O_i$ = {1, …, ni}.
$T$	Set of all time points within the entire scheduling time horizon, with T = {1,2, 3, …, Cmax}.
$U{C}_{st}^{job}$	Set of unfinished jobs at decision point st.
$U_i$	Set of urgent jobs.
$t_{i,j,k}$	Processing time of operation Oi,j on machine k, $i\in J$, $k\in M$, $j\in O_i$.
${Job}_{new}$	Number of newly arrived jobs.
$M_{i,j}$	The set of available machines for operation, $i\in J$, $j\in O_i$.
$p_i$	Selling price of job i, i.e., the price offered by the customer, $i\in J$.
$c_t$	TOU electricity price (yuan/kWh) at time t, $t\in T$.
$T{D}_i$	Tardiness of job i, $i\in J$.
$e_k$	Energy processing consumption of machine k (kW), $k\in M$.
$e_{ki}$	Idle power consumption of machine k (kW), $k\in M$.
$e_t$	Total power consumption of the shop at time t (kW): $e_t={\displaystyle \sum _{k\in M}{\displaystyle \sum _{i\in J}{\displaystyle \sum _{j\in O_i}{x}_t^{i,j,k}\cdot e_k+\left(b_t^k-x_t^{i,j,k}\right)\cdot {\mathrm{e}}_{ki}}}}$, including both processing and idle power consumption, $i\in J$, $k\in M$, $j\in O_i$.
$U{f}_i$	Urgency level of urgent jobs, $i\in U_i$, $U{f}_i\in \left[\mathrm{0,1}\right]$.
$T{P}_i$	Net profit of job i, $i\in J$.
$O_{s_t}^i$	Index of the operation of job i completed at scheduling point st, $i\in J$.
$penalt{y}_i$	Tardiness penalty of job i, $i\in J$.
Ci	Completion time of job i.
Ci,j	Completion time of operation Oi,j.
Variables	Description
$x_t^{i,j,k}$	Time-related task and resource allocation variables: at time t, operation Oi,j of job j being processed on machine k is 1.
$b_t^k$	Equal to 1 if and only if machine k is in the ON state.

summarizes these notations, including the variables related to jobs, machine resources, processing times, and scheduling decisions.

In real-world production, production efficiency is often reflected in the reduction in C_max. Job processing generates electricity consumption costs, while delivery delays incur penalties, which are even higher for urgent orders. Due to differences in process complexity, customer remuneration varies across jobs, and energy consumption also differs among machines. Based on these considerations, this study proposes a bi-objective model aiming to minimize C_max and maximize net profit. The objectives and constraints are summarized as follows.

$$F_1=\mathrm{Minimize}\left(C_{max}\right)$$

(1)

$$F_2=\mathrm{Maximum}(\sum _{i\in J}T{P}_i)=\mathrm{Maximum}(\sum _{i\in J}{p}_i-\sum _{t\in T}{c}_t\cdot e_t-\sum _{i\in J}penalt{y}_i)$$

(2)

Subject to:

$$\sum _{i\in J}{x}_t^{i,j,k}\le 1, \forall t\in T,k\in M_{i,j},j\in O_i$$

(3)

$$b_t^k\ge x_t^{i,j,k}, \forall t\in T,k\in M_{i,j},i\in J, j\in O_i$$

(4)

$$C_i\ge 0,\forall i\in J$$

(5)

$$t_{i,j,k}>0,\forall i\in J,j\in O_i,k\in M_{i,j}$$

(6)

$$(C_{i,j}-t_{i,j,k}-C_{i,j-1})\cdot x_t^{i,j,k}\ge 0, \forall i\in I_n,j\in J_i,k\in M_{i,j}$$

(7)

$$(C_{i,1}-t_{i,1,k}-A_i)\cdot x_t^{i,1,k}\ge 0, \forall i\in I_n,k\in M_{i,j}$$

(8)

Objective Equation (1) minimizes the C_max, while Objective Equation (2) maximizes net profit after accounting for energy costs under TOU pricing and tardiness penalties. Constraint Equation (3) ensures that each job can be processed on at most one machine at any given time. Constraint Equation (4) specifies that if a job is assigned to machine k at time t, then the machine must be in the “on” state at that time. Constraint Equation (5) requires that the completion time of each job be non-negative. Constraint Equation (6) ensures that the processing time of each operation is non-negative. Constraint Equation (7) guarantees that the operations of each job are executed in sequence. Constraint Equation (8) ensures that jobs can only be processed after their arrival time.

4. Multi-Agent Collaboration Framework for the Proposed MODFJSP

Table 3. Explanation of variables covered in Section 4.

Parameters	Description
$S_{st}^{\prime }$	At decision point st, the set of job states. $S_{st}^{\prime }$ = {$s_{st}^1,s_{st}^2,\dots ,s_{st}^i,\dots$}
$s_{st}^i$	The state corresponding to job i at the decision point, where $i\in U{C}_{st}^{job}$
$S_{st}^{″}$	At decision point st, the set of available machine statuses for the next machining operation of the selected job. $S_{st}^{″}$ = {$s_{st}^1,s_{st}^2,{\dots ,s}_{st}^k,\dots$}
$s_{st}^k$	The state corresponding to machine k, ${k\in M}_{i,j}$
$O_{st}^i$	Index of completed machining operations for job i, where $i\in U{C}_{st}^{job}$
$r_{st}^{\prime }$	Job agent reward
$r_{st}^{″}$	Machine agent reward
${\mathit{TD}}_i$	Job i delay time
$Action space\prime$	Action space of the job agent
$Action space″$	Action space of machine agent
$a_{st}^i$	At decision point st, the action taken by the job agent is to select the job state with the highest Q-value.
$i_{st}$	At decision point st, the job index corresponding to the job state selected by $a_{st}^i.$
$a_{st}^k$	At decision point st, the action taken by the machine agent is the selection of the machine state with the highest Q-value.
$k_{st}$	At decision point st, the machine index corresponding to $a_{st}^k.$
$\tau$	DDQN soft update parameters.

provides the explanations of the variables and notations used in this section, serving as a reference for the subsequent content. This section first explains the symbols and notations used, then introduces the core algorithms adopted by the multi-agent collaboration framework. Subsequently, it elaborates on the design of each agent’s state inputs, reward functions, and action spaces. Finally, it presents the complete implementation process and technical details for solving the MODFJSP.

4.1. The DRL Algorithm for the Multi-Agent Cooperative Framework

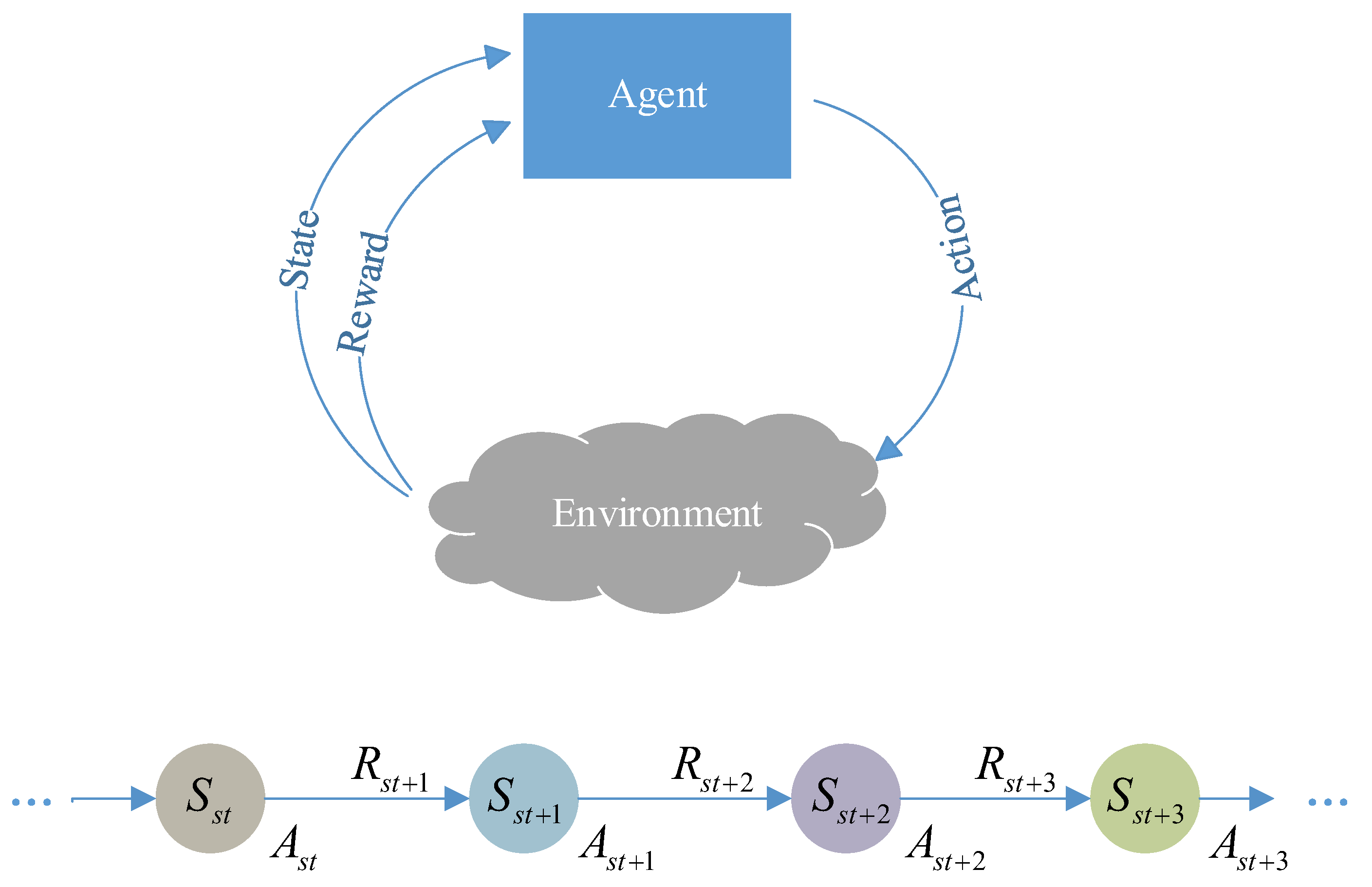
The interaction between reinforcement learning and the scheduling environment is modeled as a Markov Decision Process (MDP) [28]. MDP is the standard framework for sequential decision-making problems and is typically represented as a four-tuple (S, A, P, R) [29]. Here, S denotes the state space, A the action space, R the reward function, and P the state transition function. Figure 2 illustrates the workflow of reinforcement learning (RL) under the MDP framework [30]. DRL is an extension of RL that integrates deep neural networks into state representation and policy learning. Its main challenge lies in how to stably and efficiently optimize the policy to maximize cumulative rewards, for which various algorithmic strategies (e.g., DQN, DDQN, PPO) have been proposed [15]. Among them, DDQN is an improvement over DQN designed to alleviate the overestimation of Q-values [31]. DDQN introduces two networks: the action-selection network (policy network) and the target-evaluation network (target network), thereby decoupling action selection from value estimation [32]. The target update formula is given as

$$y_{st}^{DDQN}=r_{st}+\gamma Q(s_{st+1},\underset{a^{\prime }}{argmax}Q(s_{st+1},a^{\prime };\theta );{\theta }^{-})$$

(9)

Here, $\theta$ denotes the parameters of the online network (policy network), and ${\theta }^{-}$ denotes the parameters of the target network. First, the online network is used to select the optimal action at the next decision point st + 1, i.e., $\underset{a^{\prime }}{argmax}Q(s_{st+1},a^{\prime };{\theta }^{\prime })$. a′ presents candidate action from the action space. Then, the target network evaluates the Q-value of this action.

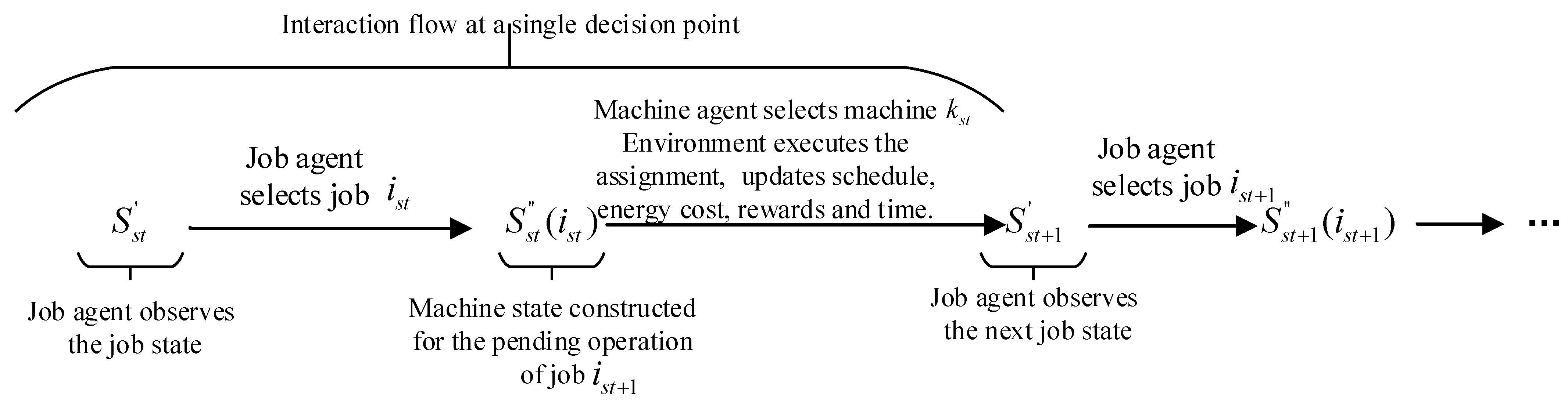
4.2. Definition of DRL Problem

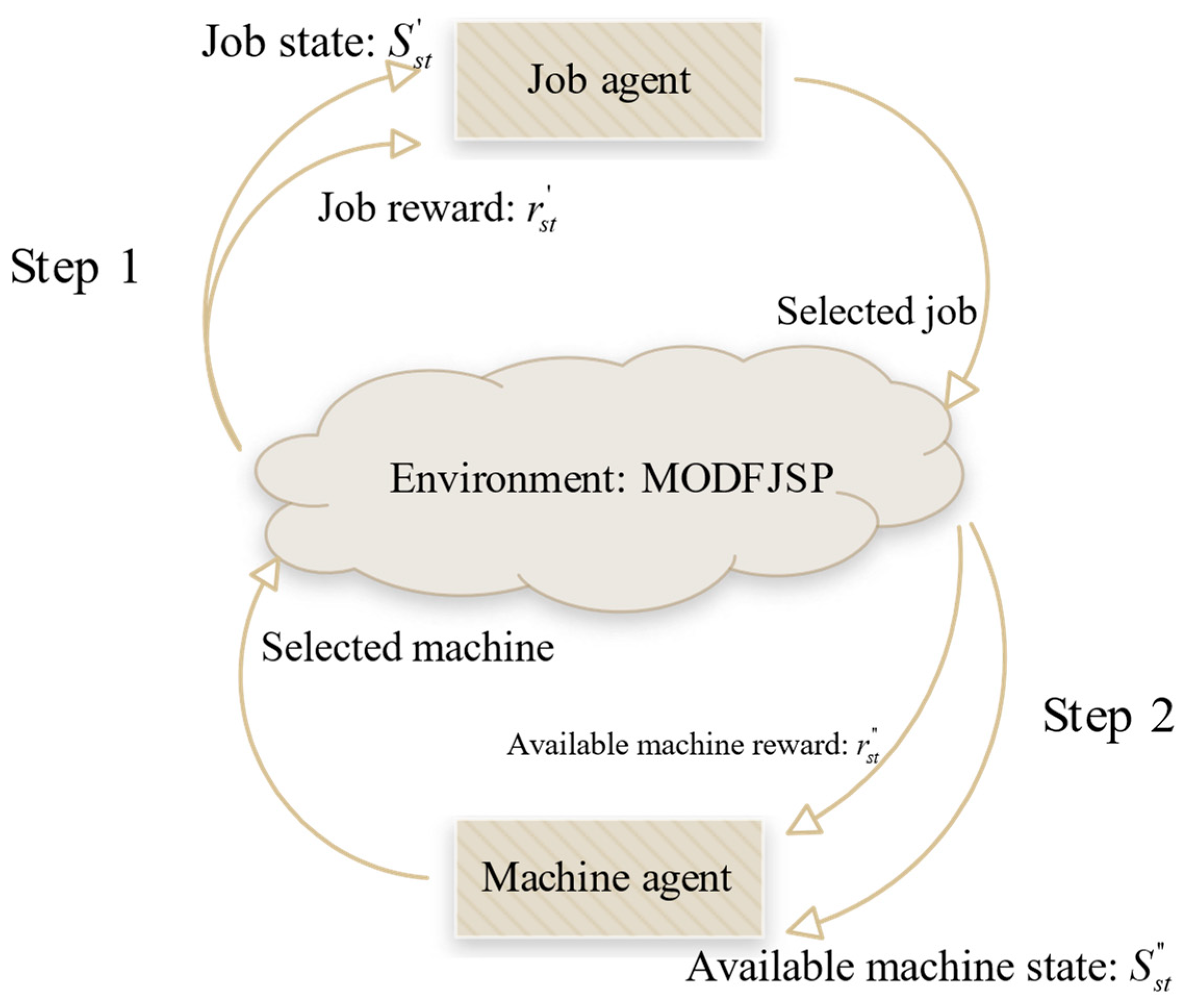
Given the characteristics of FJSP, this study applies DDQN to solve the MOFJSP by employing a new multi-agent framework with a sequential decision-making process: first, the job agent selects the job to be processed and interacts with the MODFJSP environment constructed in this study; then, the environment generates the candidate machine states for the current operation of the selected job; finally, the machine agent chooses an appropriate machine based on this information, forming a “job selection–machine assignment” multi-agent collaborative framework. The overall process is illustrated in Figure 3, which provides a more intuitive representation of the cooperation between agents.

For the above components, this section sequentially introduces the state inputs, reward functions, and action spaces of the two agents, followed by the detailed procedure of the complete multi-agent solution for MODFJSP.

4.3. State Input

In existing DRL-based studies for solving MODFJSP, the processing status of all jobs is often abstracted into a set of variables [33], through which agents perceive the shop-floor environment. However, such approaches usually lack fine-grained characterization of unfinished jobs. Based on the characteristics of FJSP and the optimization objectives, this study treats the relevant features of each unfinished job $i\in U{C}_{st}^{job}$ and its pending operation on each candidate machine k ∈ M_i,j as variable states, which are then recognized by the job agent and the machine agent. This variable state design enables agents to enhance their decision-making capabilities more effectively.

4.3.1. State Input of the Job Agent

To support the job agent’s decision-making in job selection, the job state $S_{st}^{\prime }$ is defined. Each unfinished job state $s_{st}^i$ within it varies with ${\mathit{UC}}_{st}^{job}$ and can be expressed as

$$S_{st}^{\prime }=\left\{s_{st}^i\right|i\in {\mathit{UC}}_{st}^{job}\}, s_{st}^i=[i,R_i^{op},T_i^{rem},{\mathit{TD}}_i^{norm},U{f}_i,I_i^{urg},{\mathit{TP}}_i^{norm}]$$

(10)

Except for the job index i, all other features are normalized to enhance the feature discriminability and convergence efficiency of the neural network. A detailed description is provided in

Table 4. Descriptions of the state input variables of the job agent.

Features	Description
$i$	Job index, where ${\mathit{UC}}_{st}^{job}$ denotes the set of unfinished jobs.
$R_i^{op}$	Ratio of the remaining operations to the total operations of the job.
$T_i^{rem}$	Estimated remaining processing time intensity based on the average operation processing time, normalized.
$U{f}_i$	Urgency level of the job, set to 0 if it is not an urgent job.
$I_i^{urg}$	Urgent job indicator: 1 if job i belongs to the urgent job set, and 0 otherwise.
${\mathit{TP}}_i^{norm}$	Normalized profit of job i.

.

4.3.2. State Input of the Machine Agent

For the selected job $i_{st}$ and its pending operation $j\leftarrow O_{st}^{i_{st}}+1$, the machine agent constructs a state vector for each available machine ${k\in M}_{i,j}$:

$$S_{st}^{″}=\{s_{st}^k,k\in M_{i_{st},j}\}, s_{st}^k=[k,e_k^{norm},t_{i_{st},j,k}^{norm},\mathit{Cos}{t}_k^{norm},A_k^{norm},T{P}_{i_{st}}^{norm}]$$

(11)

Table 5. Descriptions of the available machine state variables.

Features	Description
k	Machine index, ${k\in M}_{i_{st},j}$
$e_k^{norm}$	Power of the machine when processing the operation, normalized by the maximum power
$t_{i_{st},j,k}^{norm}$	Processing time of machine k for operation $O_{i_{st},j}$, normalized by the maximum processing time among its available machines
$\mathrm{Cos}{t}_k^{norm}$	Estimated electricity cost incurred by processing on machine k.
$A_k^{norm}$	Available start time of machine k for processing the pending operation $j\leftarrow O_{st}^{i_{st}}+1$ of job $i_{st}$, normalized by the maximum available time of all machines.
${\mathit{TP}}_{i_{st}}^{norm}$	Estimated profit generated by processing on machine k, normalized by the maximum profit among all candidates.

summarizes the detailed descriptions of the available machine state variables.

4.4. Reward Functions

4.4.1. Reward Function of the Job Agent

The job agent takes into account the effects of tardiness and job urgency. If a job is urgent and incurs tardiness, the reward function provides stronger positive guidance while imposing penalties on the degree of tardiness. In this way, under the same conditions, jobs with higher urgency and existing tardiness are prioritized, thereby reducing overall tardiness penalties and improving delivery reliability. Algorithm 1 presents the pseudocode of the reward function.

Algorithm 1 Reward function of the job agent
Input: Selected job $i_{st}$, $U_i,{\mathit{TD}}_{i_{st}}$; $U{f}_{i_{st}}$
Output: $r_{st}^{\prime }$
1.	$r_{st}^{\prime }\leftarrow 0$
2.	${TD}_{max}\leftarrow {argmax}_{i\in J}\left\{{TD}_i\right\}$
3.	$T{D}_{i_{st}}^{norm}\leftarrow {\displaystyle \frac{T{D}_{i_{st}}}{T{D}_{max}+\epsilon }}, \epsilon$ = 1 × 10−6
4.	if selected job $i_{st}$$\in$$U_i$then
5.	$r_{st}^{\prime }$+ = ${\omega }_1·U{f}_{i_{st}}$− ${\omega }_2 · {\mathit{TD}}_{i_{st}}^{norm}$
6.	else
7.	$r_{st}^{\prime }-={\mathit{TD}}_{i_{st}}^{norm}$
8.	end if
9.	return $r_{st}^{\prime }$

4.4.2. Reward Function of the Machine Agent

When selecting machines, the machine agent comprehensively considers processing profit, electricity cost, and tardiness impact. First, these three factors are normalized as ${TP}_{i_{st}}^{norm},{Cost}^{norm}$, and $T{D}_{i_{st}}^{norm}$, respectively. In the decision-making process, profit is assigned the highest weight, followed by electricity cost from energy consumption, and finally the impact on tardiness. The electricity cost is normalized as the ratio of the actual electricity cost to the benchmark of the “highest electricity price,” where $c^{high}$ denotes the maximum unit price in the TOU tariff. Algorithm 2 presents the pseudocode of the reward function for machine selection.

Algorithm 2 Reward function of the machine agent
Input: Selected job ist and machine kst, ${TP}_{i_{st}},T{D}_i$
1.	${TD}_{max}\leftarrow {argmax}_{i\in J}\left\{{TD}_i\right\}$
2.	${Cost}_{k_{st}}^{norm}\leftarrow {\displaystyle \frac{\sum _{t\in [s_{i_{st},j,k_{st}},c_{i_{st},j,k_{st}}]}{c}_t·e_t}{\sum _{t\in [s_{i_{st},j,k_{st}},c_{i_{st},j,k_{st}}]}{c}^{high}·e_t}}$
3.	${TP}_{i_{st}}^{norm}\leftarrow {\displaystyle \frac{{TP}_{i_{st}}}{{argmax}_{i\in J}\left\{{TP}_i\right\}}}$, ${TP}_{i_{st}}$ is calculated according to Equation (2)
4.	$T{D}_{i_{st}}^{norm}\leftarrow {\displaystyle \frac{T{D}_{i_{st}}}{T{D}_{max}+\epsilon }}, \epsilon$ = $1\times {10}^{-6}$
5.	$r_{st}^{″}={\omega }_3·{TP}_{i_{st}}^{norm}-{\omega }_4·{Cost}_{k_{st}}^{norm}-T{D}_{i_{st}}^{norm}$
6.	return $r_{st}^{″}$

4.5. Definition of Action Spaces

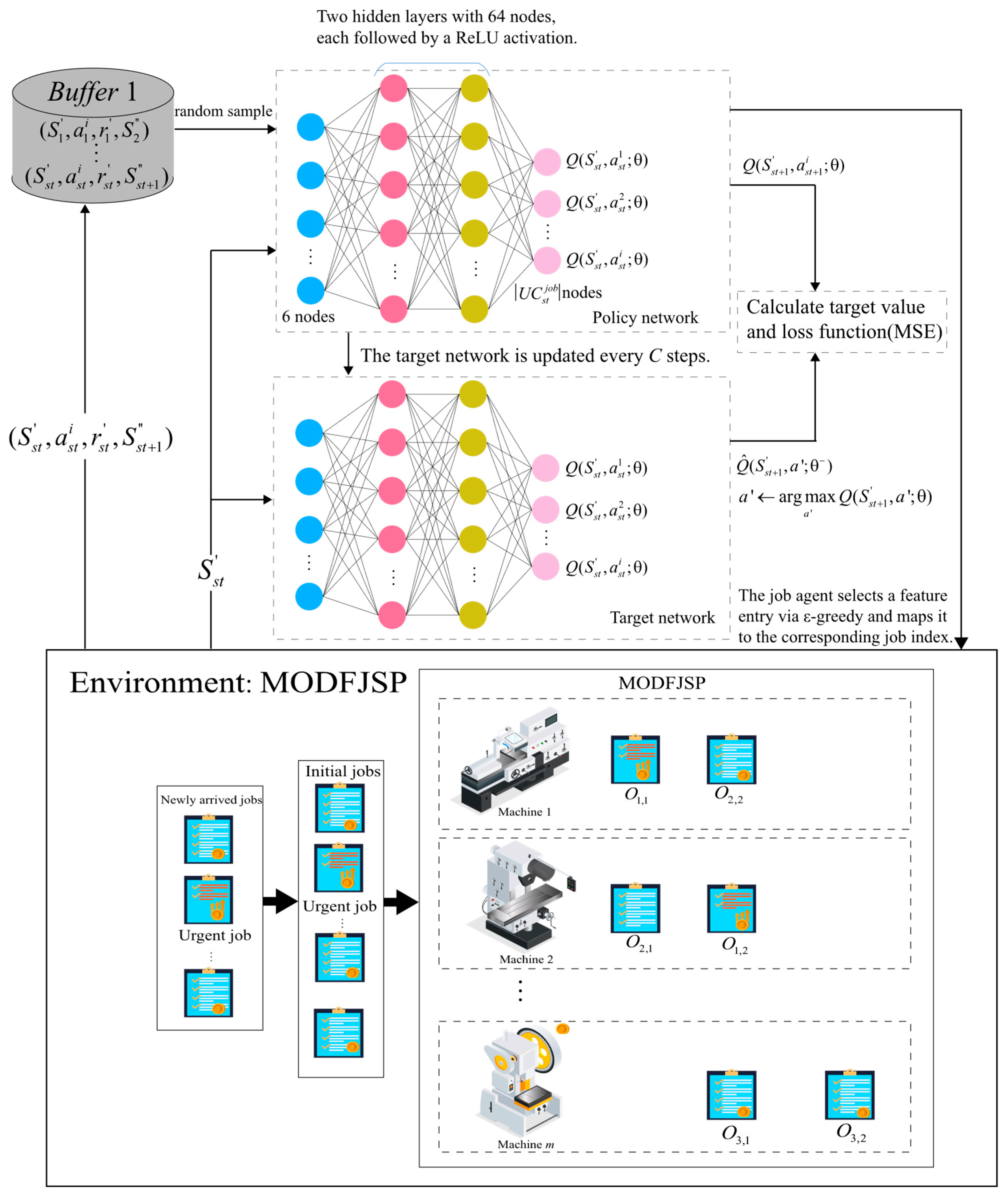
4.5.1. Action Space of the Job Agent

In the decision-making process, the job agent constructs its action space from the states of unfinished jobs, computes the corresponding action values, and then selects the optimal action using the ϵ-greedy strategy. The job index corresponding to the chosen action is the job actually scheduled.

$$Action {space}^{\prime }=\left\{s_{st}^i\right|i\in U{C}_{st}^{job}\}$$

(12)

$$a_{st}^i=\underset{i\in U{C}_{st}^{job}}{argmax}Q(s_{st}^i;\theta )$$

(13)

Figure 4 presents the overall structure of the job agent and its interaction process with the environment. At each decision point st, the job agent first identifies the states of unfinished jobs as input. The policy network outputs Q-value estimates for all actions, and actions are selected using a greedy strategy. The target network has the same structure as the policy network but is updated differently: the policy network parameters are updated via gradient descent based on the mean squared error (MSE) loss function, while the target network parameters are gradually migrated from the policy network through soft updates, thereby improving training stability and convergence. Meanwhile, DDQN introduces an experience replay mechanism, in which the state transition samples $(S_{st}^{\prime },a_{st}^i,r_{st}^{\prime },S_{st}^{\prime })$ obtained from environment interactions are stored in a replay buffer. During training, mini-batches of samples are randomly drawn to break data correlations and improve sample efficiency.

4.5.2. Action Space of the Machine Agent

The action space of the machine agent is composed of the set of state feature vectors of all candidate machines capable of processing the job.

$$Action {space}^{″}=\left\{s_{st}^k\right|k\in M_{i_{st},j}\}$$

(14)

The machine agent computes the corresponding action values based on the given features and selects the optimal action using the ϵ-greedy strategy. The machine index corresponding to the chosen action is then assigned as the processing machine for $O_{i_{st},j}.$

$$a_{st}^k=\underset{k\in M_{i_{st},j}}{argmax}Q(s_{st}^k;\theta )$$

(15)

The network structure of the machine agent is illustrated in Figure 5. At each scheduling point st, after the job agent selects the job to be processed, the MODFJSP environment provides the machine states of the candidate machine set $M_{i_{st},j}$ for its pending operation. The policy network then outputs Q-value estimates for all candidate machine features, and a greedy strategy is adopted for action selection. The target network has the same structure as the policy network, and its update and sampling procedures are identical to those of the job agent.

4.6. Multi-Agent Collaborative Framework for the Proposed MODFJSP

The two agents learn and update independently but collaborate in the same environment following the sequence of “job selection → machine assignment.” Multi-agent DDQN(MADDQN), experience replay, and soft updates of the target network are employed to enhance stability and reduce overestimation bias. The detailed procedure is given in Algorithm 3. For further illustration, Figure 6 demonstrates the process: the environment provides job states → the job agent selects a job $i_{st}$ → the environment provides feasible machine states $S_{st}^{″}\left(i_{st}\right)$ → the machine agent selects a machine $k_{st}$ → the environment updates the schedule and computes energy consumption and tardiness → the transition is stored in the replay buffer and the networks are updated, and this cycle continues until all jobs are scheduled.

Algorithm 3 Pseudocode of the training process for solving MODFJSP using MADDQN
1.	Initialize job agent replay memory buffer 1 to capacity N, and machine agent buffer 2 to capacity N′
2.	Initialize job agent’s online network Q with random weight $\theta$ and target network ${\theta }^{-}$
3.	Initialize machine agent’s online network Q with random weight $\theta$ and target network ${\theta }^{-}$
4.	for epoch = 1: L do
5.	Generate the job agent state $S_{st}^{\prime }=\left\{s_{st}^i\right|i\in U{C}_{st}^{job}\}, s_{st}^i=[i,\mathrm{0,0},\mathrm{0,0},\mathrm{0,0}]$
6.	for $st$ = 1:${\sum }_{i\in J}{n}_i$ do//where $st$ represents a decision point corresponding to an operation completion    or the arrival of a new job
7.	Job agent execute action $a_{st}^i$ to obtain the selected job $i_{st}$; the environment then provides the      available machine state $S_{st}^{″}$ for the pending operation ($j\leftarrow O_{st}^{{ i}_{st}}+1$).
8.	The machine agent makes the decision $a_{s_t}^k$, interacts with the environment to assign the selected      machine $k_{st}$, and then the environment updates to provide the next job agent state $S_{st+1}^{\prime }$. The next      available machine state $S_{st+1}^{″}$ is observed after the job agent selects next job $i_{st+1}$.
9.	Compute the reward function $r_{st}^{\prime }$ for job agent and $r_{st}^{″}$ for machine agent based on Section 4.4.1      and Section 4.4.2. buffer 1←($S_{st}^{\prime },a_{st}^i,r_{st}^{\prime },S_{st+1}^{\prime }$), buffer 2← ($S_{st}^{″},a_{st}^k,r_{st}^{″},S_{st+1}^{″})$.
10.	If the size of buffer 1 $\ge$ batch size 1 then:
11.	Sample minibatch from buffer 1
12.	for each sample:
13.	$y_{st}^{DDQN}=r_{st}^{\prime }+\gamma Q\left(S_{st+1}^{\prime },\underset{a^{\prime }}{\arg \max }Q(S_{st+1}^{\prime },a^{\prime };\theta );{\theta }^{-}\right)$//Use target network to evaluate target value
14.	end for
15.	$L_{loss}$ = MSE$(y_{st}^{DDQN}, Q(S_{st}^{\prime }, a_{st}^i; \theta \left)\right)$//Compute job agent loss
16.	Update $\theta$ by minimizing $L_{loss}. {\theta }^{-}$← (1 − $\tau$)${\theta }^{-}+\tau ·\theta$//Soft update of job agent’s target network
17.	end if
18.	If the size of buffer 2 $\ge$ batch size 2 then:
19	Sample minibatch from buffer 2
20.	for each sample:
21.	$y_{st}^{DDQN}=r_{st}^{″}+\gamma Q\left(S_{st+1}^{″},\underset{a^{\prime }}{\arg \max }Q(S_{st+1}^{″},a^{\prime };\theta );{\theta }^{-}\right)$//Use target network to evaluate target value
22.	end for
23.	$L_{loss}$ = MSE$(y_{st}^{DDQN}, Q(S_{st}^{″}, a_{st}^k; \theta \left)\right)$//Compute machine agent loss
24.	Update $\theta$ by minimizing $L_{loss}. {\theta }^{-}$← (1-$\tau$)${\theta }^{-}+\tau ·\theta$//Soft update of machine agent’s target network
25.	end if
26.	end for
27.	end for

5. Numerical Experiments

This section first introduces the method of generating numerical simulation instances, followed by a description of the multi-objective evaluation metrics and the necessary parameter settings to ensure the validity of the experiments. To verify the effectiveness of the proposed multi-agent collaborative model in solving MODFJSP, it is compared with commonly used multi-agent reinforcement learning algorithms as well as classical scheduling rules suitable for this study, thereby further demonstrating the advantages of the approach. Finally, the optimization results are visualized to provide more intuitive research insights.

5.1. Generation of Numerical Instances

Since classical FJSP benchmark instances do not contain information on job arrival times or due dates, this study randomly generates numerical simulation instances for training and testing the proposed multi-agent collaborative model. Following the method in [22], the inter-arrival times of newly inserted jobs are assumed to follow an exponential distribution, Exponential (1/${\lambda }_{new}$). The due date of job i is calculated as the sum of its arrival time $A_i$ and the average processing time, scaled by a due date tightness factor (DDT): $D_i=A_i+DDT\cdot \sum _{j=1}^{n_i}{\displaystyle \frac{\sum _{k\in M_{i,j}}{t}_{i,j,k}}{\left|M_{i,j}\right|}}$ = $A_i+DDT\cdot \sum _{j=1}^{n_i}{\overline{t}}_{i,j},$ where ${\overline{t}}_{i,j}$ denotes the average processing time of operation O_i,j over its feasible machine set M_i,j. By combining different values of ${\lambda }_{new}$ and DDT, a total of 24 numerical instances are generated. For urgent jobs, customers provide higher prices. The detailed experimental settings are summarized in

Table 6. Parameter settings of numerical simulation instances.

Parameters	Value
Set of the number of initial jobs ${Job}_{initial}$	{15, 30, 50, 100}
Set of the number of new inserted jobs ${Job}_{new}$	{10, 6, 12}
Processing time $t_{i,j,k}$ per operation	U {1, 50}
Set of the number of total machines m	{8, 10, 20, 30}
Processing energy consumption $e_k$	U {12, 17}KW
Idle power $e_{ki}$	$e_{ki}=$ 30% × $e_k$
Due date tightness DDT	{0.5, 1, 1.5}
λnew	{20, 50}
Number of available machines of each operation	U {1, m − 1}
Number of operations belonging to a job	U {1, 5}
Number of urgent jobs	20% of total jobs
Non-urgent profit $P_i$	$p_i=a\cdot {\displaystyle \sum _{j=1}^{n_i}}\underset{k\in M_{i,j}}{max}(t_{i,j,k})\cdot c^{high}+b$
Profit adjustment for urgent jobs	${p_{urgent}=p}_i\times \mathrm{U}\left[\mathrm{1.3,1.7}\right]$
Tardiness penalty for job i	$penalt{y}_i=\beta \cdot T{D}_i\cdot (1+U{f}_i)$

. Electricity costs are calculated based on the TOU pricing scheme referenced in [34], with specific settings provided in

Table 7. TOU price.

	TOU Power $\mathbf{Price} {\mathit{c}}_{\mathit{t}}$	Period of Time
Electricity purchase price (yuan/kWh)	Peak: 1.241	9:00~12:00; 17:00~22:00
	Flat: 0.779	8:00~9:00; 12:00~17:00; 22:00~23:00
	Valley: 0.488	0:00~8:00; 23:00~24:00

.

5.2. Evaluation Metrics

Three indicators are used to evaluate the proposed method in the multi-objective optimization problem: Set Coverage (SC) [35], Inverted Generational Distance (IGD) [36], and Hypervolume (HV) [37].

(1)

IGD

It is used to measure the closeness and coverage of a solution set generated by an algorithm relative to the true Pareto Front. However, due to the complexity of MODFJSP, the ideal Pareto Front P* is unknown, and thus the Pareto front approximated from the non-dominated solutions obtained by all algorithms is used as P* [38]. Moreover, a lower IGD value indicates that the solutions derived from the evaluated algorithm exhibit better convergence and diversity. It is calculated using Equation (16).

$$IGD(Q,P^{*})={\displaystyle \frac{{\displaystyle \sum _{p_i\in P^{*}}\underset{q\in Q}{\min }‖p_i-q‖}}{\left|P^{*}\right|}}$$

(16)

$P^{*}=\{p_1,p_2,...,p_N\}$: the true Pareto front. $Q=\left\{q_1,q_2,...,q_V\right\}:$ the set of non-dominated solutions generated by the algorithm. ${\mathit{min}}_{q\in Q}‖p_i-q‖$: the Euclidean distance from a true solution $p_i$ to its closest point in the approximate solution set $Q$.

(2)

HV

In multi-objective optimization, HV is a metric frequently used to measure the volume of the objective space covered by a set of solutions. Specifically, it represents the union of hyper-rectangular regions formed between each non-dominated point $q_i$ and a reference point r. A larger HV value indicates that the solution set is closer to the Pareto front, has broader coverage, and is of higher quality. It is calculated by applying Equation (17).

$$HV(Q,r)=Volume(\underset{q_i\in Q}{\cup }[q_i,r])$$

(17)

The reference point is set as r = (1, 1, 1).

(3)

SC

It is used to measure the dominance relationship between two sets of non-dominated solutions, i.e., to compare their relative quality and convergence. Here, U denotes the non-dominated solution set generated by the current algorithm, and V denotes that generated by the comparison algorithm. u dominates v means that u is no worse in all objectives and strictly better in at least one.

• SC(U,V) = 1: all solutions in U dominate all solutions in V → clear superiority.
• SC(U,V) = 0: none of the solutions in V are dominated by any solution in U → clear inferiority.
• 0 < SC(U,V) < 1: the solution set U has a certain degree of dominance over V.

The closer the value of SC(U,V) is to 1, the higher the solution quality of the current algorithm and the stronger its dominance advantage. Conversely, the closer it is to 0, the weaker the advantage, even indicating inferiority.

$$SC(U,V)={\displaystyle \frac{\left|\{v\in V|\exists u\in U,u\prec v\}\right|}{\left|V\right|}}$$

(18)

To facilitate measurement and reduce the influence caused by differences in units or magnitudes among objectives, all objective values are normalized using Equation (19). In this case, $f_g$ represents the original value of the gth objective, while $f_g^{min}$ and $f_g^{max}$ denote the minimum and maximum values of the gth objective across all solutions [39]. By unifying the scale, this normalization procedure improves the reliability and comparability of multi-objective performance measures.

$$\widehat{f_g}={\displaystyle \frac{f_g-f_g^{\min }}{f_g^{\max }-f_g^{\min }}}, g\in \{1,2\}$$

(19)

5.3. Experimental Parameter Settings

The numerical model was coded in Python 3.10.0 and executed on a Windows 11 system equipped with a 2.30 GHz Intel Core i7-12700H processor and 16 GB of RAM. Both the proposed algorithm and the baseline algorithms are implemented in Python. To realize the proposed approach, Python is employed as the primary programming language, supported by several libraries: Pytorch = 1.12.0 is used to construct and train neural networks, while NumPy = 1.23.0 handles numerical computations and data processing, and matplotlib (3.5.3) is employed for result visualization.

Unlike heuristic algorithms, RL relies on agents continuously exploring and trying actions to achieve convergence; therefore, the number of training epochs is crucial for deep reinforcement learning [40]. We conducted experiments with different epoch settings on an instance with ${Job}_{initial}=15, {Job}_{new}=10, m=8, {\lambda }_{new}=20,DDT=20$. For each epoch setting, 10 runs were performed to calculate the HV metric in order to determine the optimal epoch number. A boxplot, as a statistical tool, was used to characterize data dispersion and accurately describe the stability of optimization performance [4]. 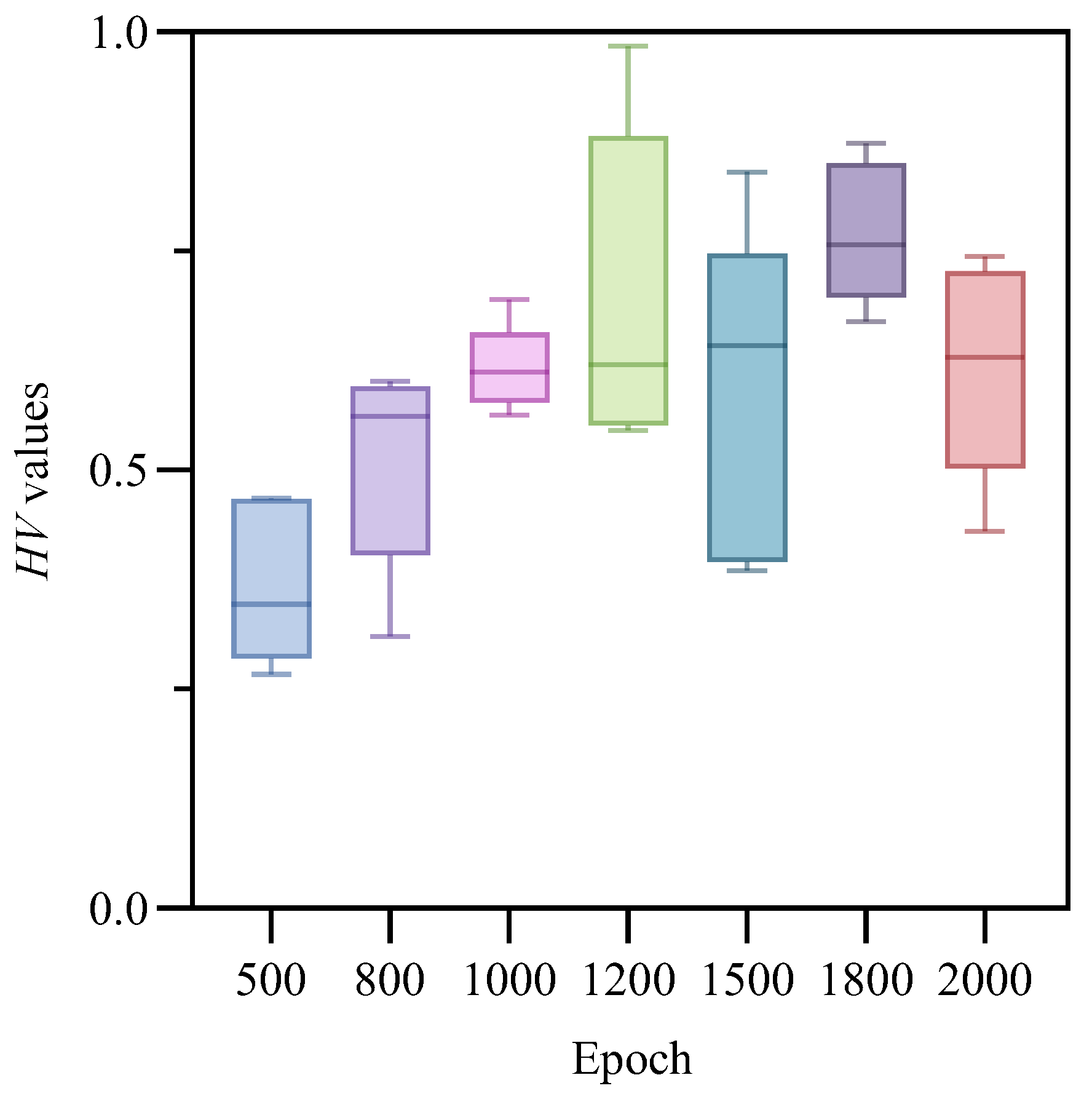Figure 7. box plots of HV values under different training epochs; different colors represent different numbers of training epochs. As shown in Figure 7, across 10 runs of the algorithm, the model trained with 1800 epochs achieved an average HV value of 0.767600375, which was higher than the other six settings (0.370214, 0.510288, 0.616378, 0.696846, 0.585371, and 0.617534, respectively). Therefore, the model trained for 1800 epochs overall produced the best results and demonstrated greater stability across multiple runs.

In addition, the hyperparameters of the two agents were tuned, and the optimal values were determined by monitoring the cumulative reward in each training epoch.

Table 8. Job agent parameter settings.

Hyperparameters	Value
Number of training epochs L	1800
Learning rate	1 × 10−3
Discount factor γ	0.99
ε-greedy exploration rate	0.1
Minimum ε-value	0.05
Batch size 1	64
Buffer capacity	10,000
Soft update coefficient $\tau$	0.01
Optimizer	Adam
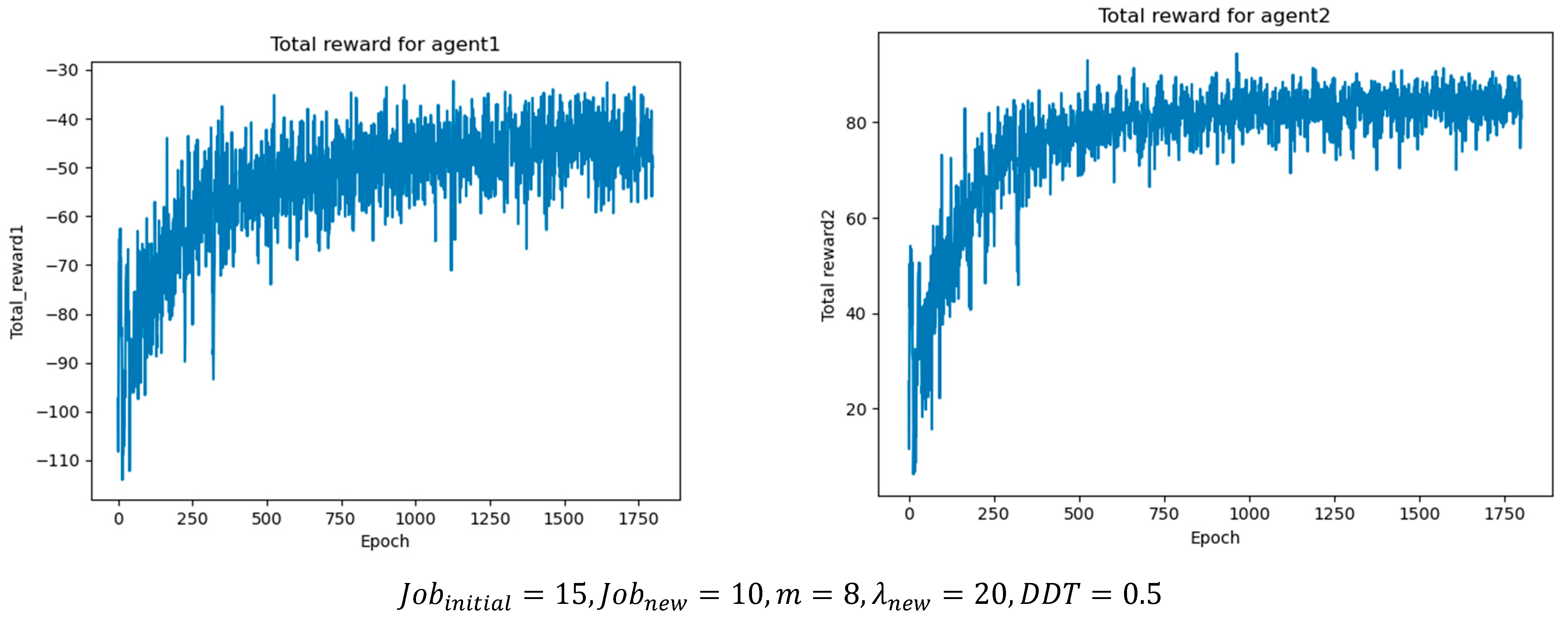
Weight parameters in the reward function: ${\omega }_1, {\omega }_2$	6, 4

and

Table 9. Machine agent parameter settings.

Hyperparameters	Value
Number of training epochs L	1800
Learning rate	1 × 10−3
Discount factor γ	0.99
ε-greedy exploration rate	0.1
Minimum ε-value	0.05
Batch size 2	64
Buffer capacity	10,000
Soft update coefficient $\tau$	0.01
Optimizer	Adam
Weight parameters in the reward function: ${\omega }_3, {\omega }_4$	5, 4

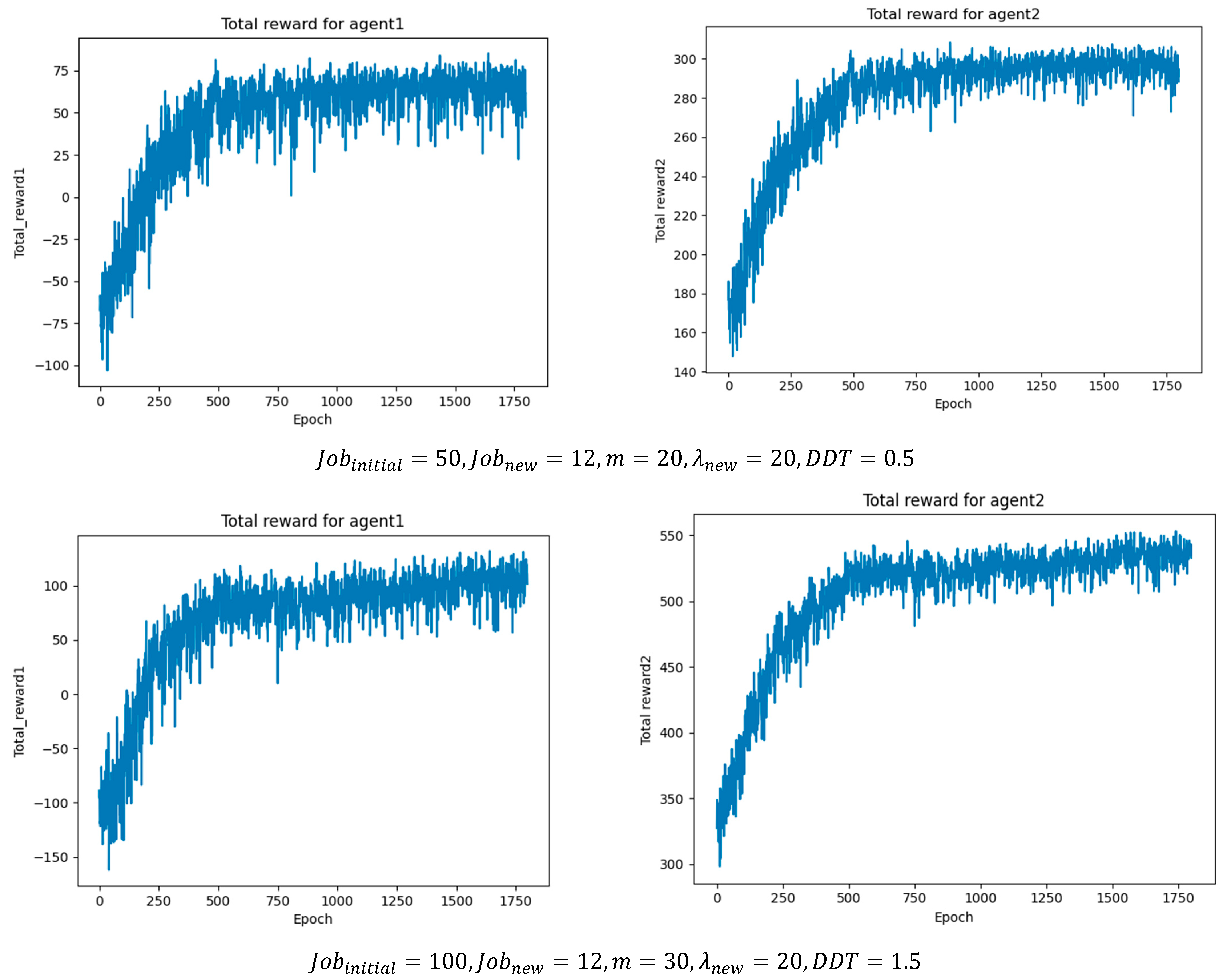
summarize the optimal parameter settings obtained from the experiments, while Figure 8 illustrates the cumulative reward results per epoch under different job batch sizes, where agent1 represents the job agent and agent2 represents the machine agent. As the batch size increases, the number of scheduling operations and optimal actions also rises, leading to higher cumulative rewards. This demonstrates that the proposed method can achieve stable convergence under different operating conditions.

5.4. Experimental Results

5.4.1. Comparison of Results

To evaluate the effectiveness and stability of the proposed multi-agent reinforcement learning framework in solving the MODFJSP described in this study, commonly used DRL baselines in the FJSP domain (PPO, DQN, DDQN) are selected for comparison [12,25,26].

Table 10. Description of compared algorithms.

Algorithms	Description
DDQN-DDQN	Our method: Job agent with DDQN; Machine agent with DDQN
DDQN-DQN	Job agent with DDQN; Machine agent with DQN
PPO-DDQN	Job agent with PPO; Machine agent with DDQN
PPO-PPO	Job agent with PPO; Machine agent with PPO

lists several typical combinations of cooperative agents. In addition, classical scheduling rules applicable to the context of this study, as shown in

Table 11. Description of scheduling rules.

Rules	Priority Description
EDD-SPT-M	Job selection: EDD prioritizes the job with the earliest due date; Machine selection: SPT-M prioritizes the machine with the shortest processing time.
FIFO-EAM	Job selection: FIFO prioritizes the earliest arriving job; Machine selection: EAM prioritizes the earliest available machine.
Random	Randomly select both job and machine.

, are introduced as benchmarks [22]. A systematic evaluation of solution quality is then conducted based on three evaluation metrics, with particular emphasis on maximizing net profit and minimizing makespan.

In this study, each method is independently executed 10 runs on 24 instances, and the average IGD and HV values as well as the SC metric are calculated to comprehensively evaluate the advantages and disadvantages of the proposed method compared with other approaches. Moreover, the dominance relationships between the non-dominated solutions generated by our method and those of the comparison methods are analyzed. The evaluation results are presented in

Table 12. IGD values for solutions obtained by DDQN–DDQN, DDQN–DQN,PPO-DDQN, PPO-PPO and classical scheduling rules.

${\mathit{\lambda }}_{\mathit{n}\mathit{e}\mathit{w}}$	DDT	${\mathbf{(}\mathit{J}\mathit{o}\mathit{b}}_{\mathit{i}\mathit{n}\mathit{i}\mathit{t}\mathit{i}\mathit{a}\mathit{l}}\mathbf{,}{\mathit{J}\mathit{o}\mathit{b}}_{\mathit{n}\mathit{e}\mathit{w}}\mathbf{,}\mathit{m}\mathbf{)}$	DDQN-DDQN	PPO-DDQN	PPO-PPO	DDQN-DQN	FIFO-EAM	EDD-SPT-M	Random
20	0.5	(15,10,8)	0.054859	0.057435	0.173360	0.061103	0.380170	0.490278	0.289240
		(30,6,10)	0.042265	0.051395	0.104919	0.0445135	0.420481	0.483181	0.300935
		(50,12,20)	0.022450	0.039487	0.149944	0.027592	0.494244	0.411686	0.405403
		(100,12,30)	0.000510	0.010893	0.093641	0.002407	0.338582	0.537263	0.437711
	1	(15,10,8)	0.053759	0.074556	0.084140	0.056995	0.352341	0.439906	0.154800
		(30,6,10)	0.044555	0.064114	0.084884	0.052853	0.360538	0.542772	0.305371
		(50,12,20)	0.029263	0.048181	0.107453	0.032112	0.436225	0.451014	0.361074
		(100,12,30)	0.097993	0.071701	0.019414	0.105504	0.04047	0.405968	0.110002
	1.5	(15,10,8)	0.060887	0.089392	0.160640	0.050309	0.332754	0.447768	0.185778
		(30,6,10)	0.042315	0.070105	0.117966	0.044867	0.408433	0.46043	0.323373
		(50,12,20)	0.054425	0.061335	0.071502	0.044325	0.044744	0.790365	0.399020
		(100,12,30)	0.049678	0.040152	0.106691	0.015308	0.090093	0.104488	0.092739
50	0.5	(15,10,8)	0.047233	0.063687	0.274370	0.05187	0.417043	0.464195	0.301849
		(30,6,10)	0.048418	0.052739	0.061828	0.042306	0.355806	0.595167	0.268373
		(50,12,20)	0.034162	0.061210	0.080823	0.050394	0.044621	0.740737	0.264720
		(100,12,30)	0.037861	0.04037	0.07939	0.040909	0.044794	0.400768	0.441831
	1	(15,10,8)	0.045325	0.064684	0.161846	0.059643	0.365292	0.492496	0.331768
		(30,6,10)	0.394420	0.060557	0.076853	0.048337	0.387177	0.433037	0.309464
		(50,12,20)	0.062509	0.076393	0.086067	0.054579	0.333961	0.782902	0.372529
		(100,12,30)	0.070671	0.039404	0.066345	0.060627	0.333424	0.215337	0.267733
	1.5	(15,10,8)	0.055236	0.078507	0.077265	0.058287	0.350005	0.478642	0.126799
		(30,6,10)	0.040968	0.093851	0.063894	0.049112	0.391466	0.503196	0.189945
		(50,12,20)	0.041931	0.071664	0.08153	0.061443	0.031274	0.783230	0.188447
		(100,12,30)	0.073273	0.084930	0.076034	0.105645	0.090458	0.113773	0.151171

,

Table 13. HV values for solutions obtained by DDQN–DDQN, DDQN–DQN, PPO-DDQN, PPO-PPO and classical scheduling rules.

${\mathit{\lambda }}_{\mathit{n}\mathit{e}\mathit{w}}$	DDT	${\mathbf{(}\mathit{J}\mathit{o}\mathit{b}}_{\mathit{i}\mathit{n}\mathit{i}\mathit{t}\mathit{i}\mathit{a}\mathit{l}}\mathbf{,}{\mathit{J}\mathit{o}\mathit{b}}_{\mathit{n}\mathit{e}\mathit{w}}\mathbf{,}\mathit{m}\mathbf{)}$	DDQN-DDQN	PPO-DDQN	PPO-PPO	DDQN-DQN	FIFO-EAM	EDD-SPT-M	Random
20	0.5	(15,10,8)	0.767600	0.744720	0.731368	0.758419	0.623297	0.055088	0.590809
		(30,6,10)	0.77246	0.743107	0.722714	0.765869	0.588382	0.012006	0.683379
		(50,12,20)	0.873795	0.843027	0.806715	0.847061	0.752313	0.009377	0.564390
		(100,12,30)	0.899389	0.876845	0.810713	0.893988	0.868386	0.875418	0.777251
	1	(15,10,8)	0.705976	0.675435	0.690266	0.690535	0.514127	0.081000	0.595298
		(30,6,10)	0.792162	0.791562	0.786056	0.782185	0.582115	0.012874	0.528932
		(50,12,20)	0.825888	0.832226	0.772855	0.827112	0.702721	0.025889	0.567808
		(100,12,30)	0.995241	0.942097	0.771155	0.993896	0.789911	0.858213	0.793605
	1.5	(15,10,8)	0.686472	0.678807	0.698275	0.699047	0.530544	0.084557	0.560230
		(30,6,10)	0.793845	0.774062	0.752306	0.785848	0.605827	0.014820	0.618818
		(50,12,20)	0.794735	0.793765	0.781856	0.801739	0.712925	0.038169	0.678874
		(100,12,30)	0.993544	0.95656	0.674900	0.858861	0.747503	0.881494	0.702293
50	0.5	(15,10,8)	0.714744	0.705503	0.713064	0.706853	0.492632	0.051258	0.668093
		(30,6,10)	0.768952	0.786448	0.761735	0.778419	0.595167	0.008706	0.590771
		(50,12,20)	0.825685	0.811636	0.791437	0.823030	0.701750	0.009807	0.612933
		(100,12,30)	0.998798	0.983789	0.740564	0.997938	0.823208	0.899702	0.815501
	1	(15,10,8)	0.773239	0.749264	0.768887	0.753430	0.580352	0.037332	0.517169
		(30,6,10)	0.799822	0.769466	0.778661	0.788496	0.550567	0.010945	0.502802
		(50,12,20)	0.814062	0.828795	0.795007	0.838231	0.745097	0.027127	0.600298
		(100,12,30)	0.987041	0.937499	0.748739	0.985659	0.814192	0.853308	0.744819
	1.5	(15,10,8)	0.646318	0.601106	0.635441	0.636972	0.516858	0.028875	0.492524
		(30,6,10)	0.613633	0.613161	0.613002	0.613548	0.610379	0.010002	0.414054
		(50,12,20)	0.814149	0.779443	0.777327	0.816031	0.707079	0.003183	0.772396
		(100,12,30)	0.966884	0.920609	0.680371	0.956579	0.773687	0.788774	0.730839

and

Table 14. SC values for solutions obtained by DDQN–DDQN, DDQN–DQN, PPO-DDQN, PPO-PPO and classical scheduling rules.

			DDQN-DDQN (U) vs. DDQN-DQN (V)		DDQN-DDQN (U) vs. PPO-DDQN (V)		DDQN-DDQN (U) vs. PPO-PPO (V)		DDQN-DDQN (U) vs. EDD-SPT-M (V)		DDQN-DDQN (U) vs. FIFO-EAM (V)		DDQN-DDQN (U) vs. Random (V)
${\mathit{\lambda }}_{\mathit{n}\mathit{e}\mathit{w}}$	DDT	${\mathbf{(}\mathit{J}\mathit{o}\mathit{b}}_{\mathit{i}\mathit{n}\mathit{i}\mathit{t}\mathit{i}\mathit{a}\mathit{l}}\mathbf{,}{\mathit{J}\mathit{o}\mathit{b}}_{\mathit{n}\mathit{e}\mathit{w}}\mathbf{,}\mathit{m}\mathbf{)}$	SC(U,V)	SC(V,U)	SC(U,V)	SC(V,U)	SC(U,V)	SC(V,U)	SC(U,V)	SC(V,U)	SC(U,V)	SC(V,U)	SC(U,V)	SC(V,U)
20	0.5	(15,10,8)	0.353	0.462	0.478	0.346	0.759	0.154	1.000	0.000	1.000	0.000	1.000	0.115
		(30,6,10)	0.625	0.333	0.821	0.1875	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000
		(50,12,20)	0.591	0.263	1.000	0.000	0.957	0.000	1.000	0.000	1.000	0.000	0.500	0.184
		(100,12,30)	0.000	0.667	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000
	1	(15,10,8)	0.583	0.250	0.842	0.000	0.773	0.100	1.000	0.000	1.000	0.000	1.000	0.000
		(30,6,10)	0.538	0.53125	0.857	0.09375	0.941	0.0625	1.000	0.000	1.000	0.000	0.545	0.031
		(50,12,20)	0.618	0.263	0.952	0.026	0.926	0.000	1.000	0.000	1.000	0.000	1.000	0.000
		(100,12,30)	0.000	1.000	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000
	1.5	(15,10,8)	0.500	0.581	0.864	0.000	0.667	0.667	1.000	0.000	1.000	0.000	0.182	0.000
		(30,6,10)	0.576	0.207	0.909	0.000	0.957	0.000	1.000	0.000	0.207	0.000	1.000	0.000
		(50,12,20)	0.500	0.342	0.903	0.079	0.800	0.105	1.000	0.000	0.026	0.000	0.364	0.053
		(100,12,30)	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000
50	0.5	(15,10,8)	0.667	0.186	0.871	0.056	0.636	0.056	1.000	0.000	1.000	0.000	1.000	0.000
		(30,6,10)	0.216	0.750	0.911	0.100	0.931	0.050	1.000	0.000	1.000	0.000	0.500	0.000
		(50,12,20)	0.444	0.237	0.903	0.000	0.857	0.000	1.000	0.000	0.000	0.000	0.583	0.089
		(100,12,30)	0.333	0.000	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000
	1	(15,10,8)	0.679	0.241	0.913	0.034	0.722	0.172	1.000	0.000	1.000	0.000	0.414	0.000
		(30,6,10)	0.697	0.406	0.931	0.000	0.840	0.061	1.000	0.000	1.000	0.000	0.750	0.061
		(50,12,20)	0.622	0.394	0.926	0.091	0.500	0.091	1.000	0.000	0.000	0.000	0.636	0.152
		(100,12,30)	1.000	0.000	1.000	0.000	1.000	0.000	1.000	0.000	0.000	0.000	1.000	0.000
	1.5	(15,10,8)	0.423	0.375	0.917	0.038	0.781	0.115	1.000	0.000	1.000	0.000	1.000	0.000
		(30,6,10)	0.600	0.182	1.000	0.000	0.778	0.200	1.000	0.000	1.000	0.000	0.158	0.120
		(50,12,20)	0.069	0.692	0.971	0.026	0.762	0.103	1.000	0.000	0.000	0.077	0.200	0.128
		(100,12,30)	0.833	0.000	1.000	0.000	1.000	0.000	0.000	0.000	1.000	0.000	1.000	0.000

, with the best values highlighted in bold.

First, for fixed composite scheduling rules such as EDD–SPT-M and FIFO–EAM, the lack of adaptability to optimization objectives often leads to repeatedly generating similar solutions for the two objectives, thereby limiting their optimization potential. Although random selection of jobs and machines provides exploratory capability, the strong randomness in decision-making makes it difficult to form a stable learning process and achieve convergence. In addition, among the reinforcement learning combinations, our proposed DDQN–DDQN method performs slightly worse than DDQN–DQN in large-scale scenarios with higher DDT values and a larger number of jobs. Nevertheless, their HV and IGD values remain close, indicating only minor differences in the overall quality of the Pareto front. Finally, although PPO has shown advantages in some FJSP studies, in this work its instability and low sample efficiency are amplified by the variable action sets and complex state representations, resulting in inferior overall performance compared with other reinforcement learning methods.

5.4.2. Visual Comparison of Results

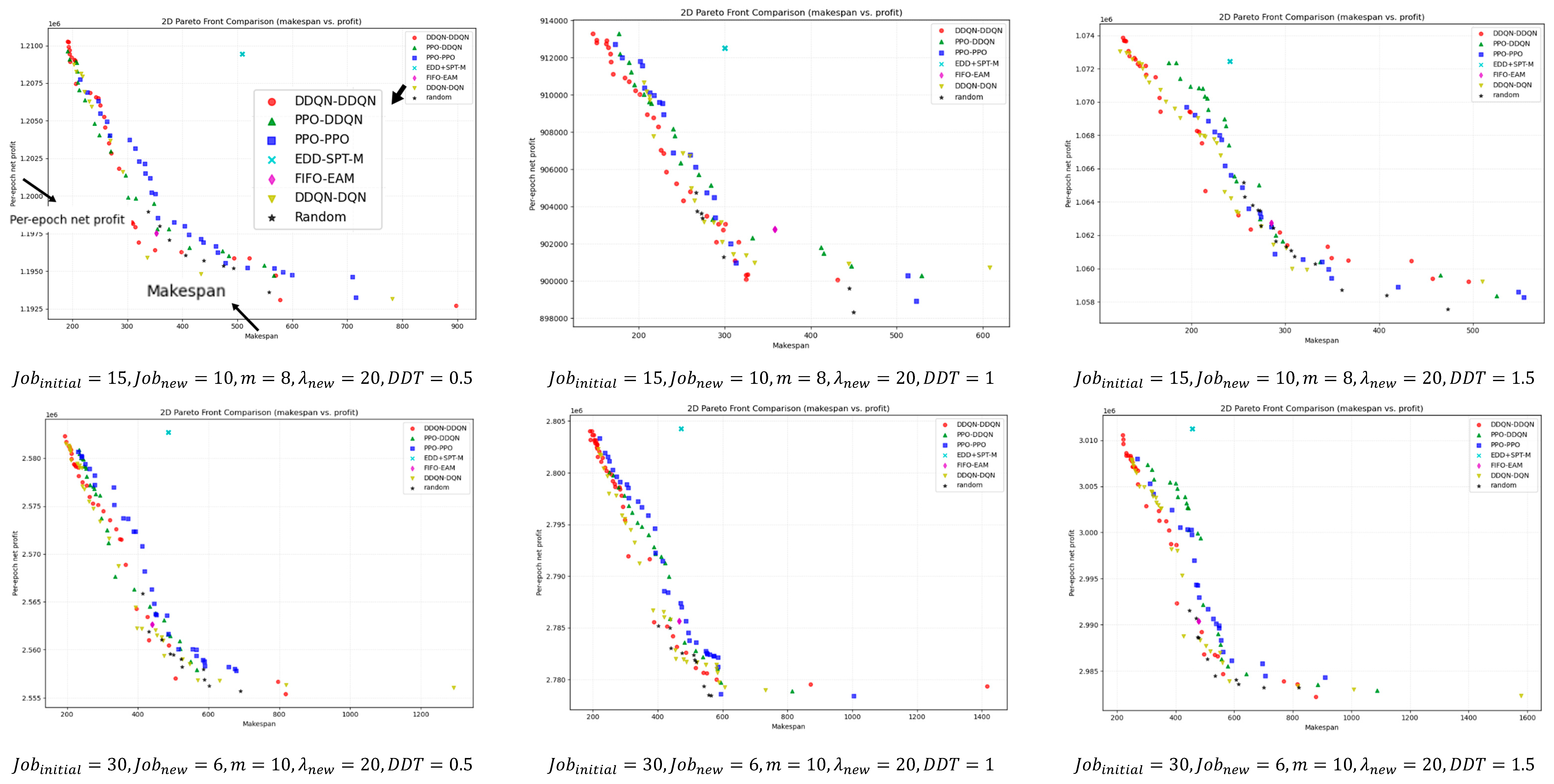
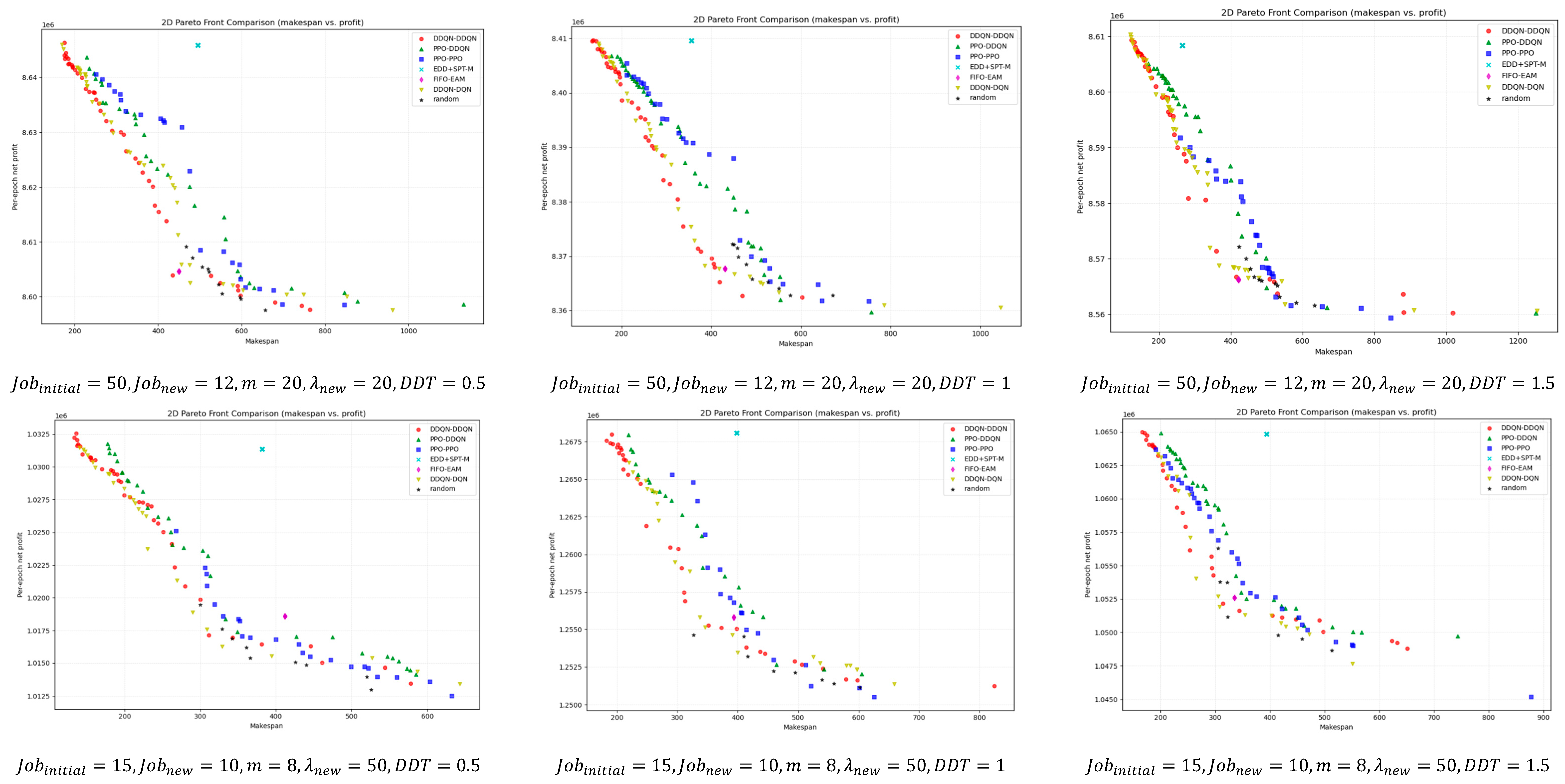
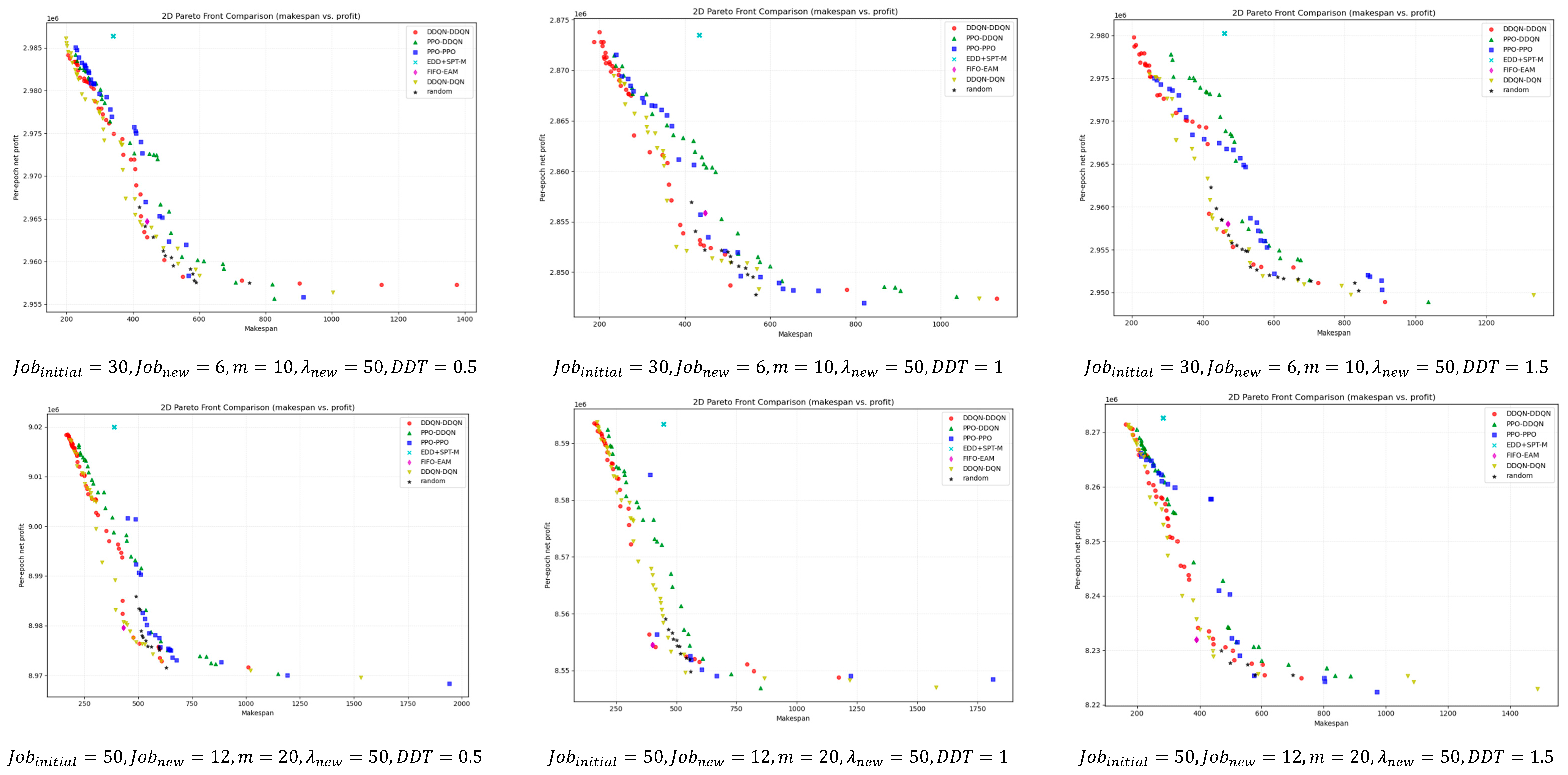
For a deeper comparison, Figure 9 illustrates the bi-objective Pareto fronts obtained after non-dominated filtering for different instance scales. Overall, DDQN–DDQN is closer to the ideal point in most instances and maintains good front coverage. Even in the few cases where it does not outperform in terms of HV, IGD, or SC metrics, its pareto front remains close to that of the best-performing method, with only minor visual differences.

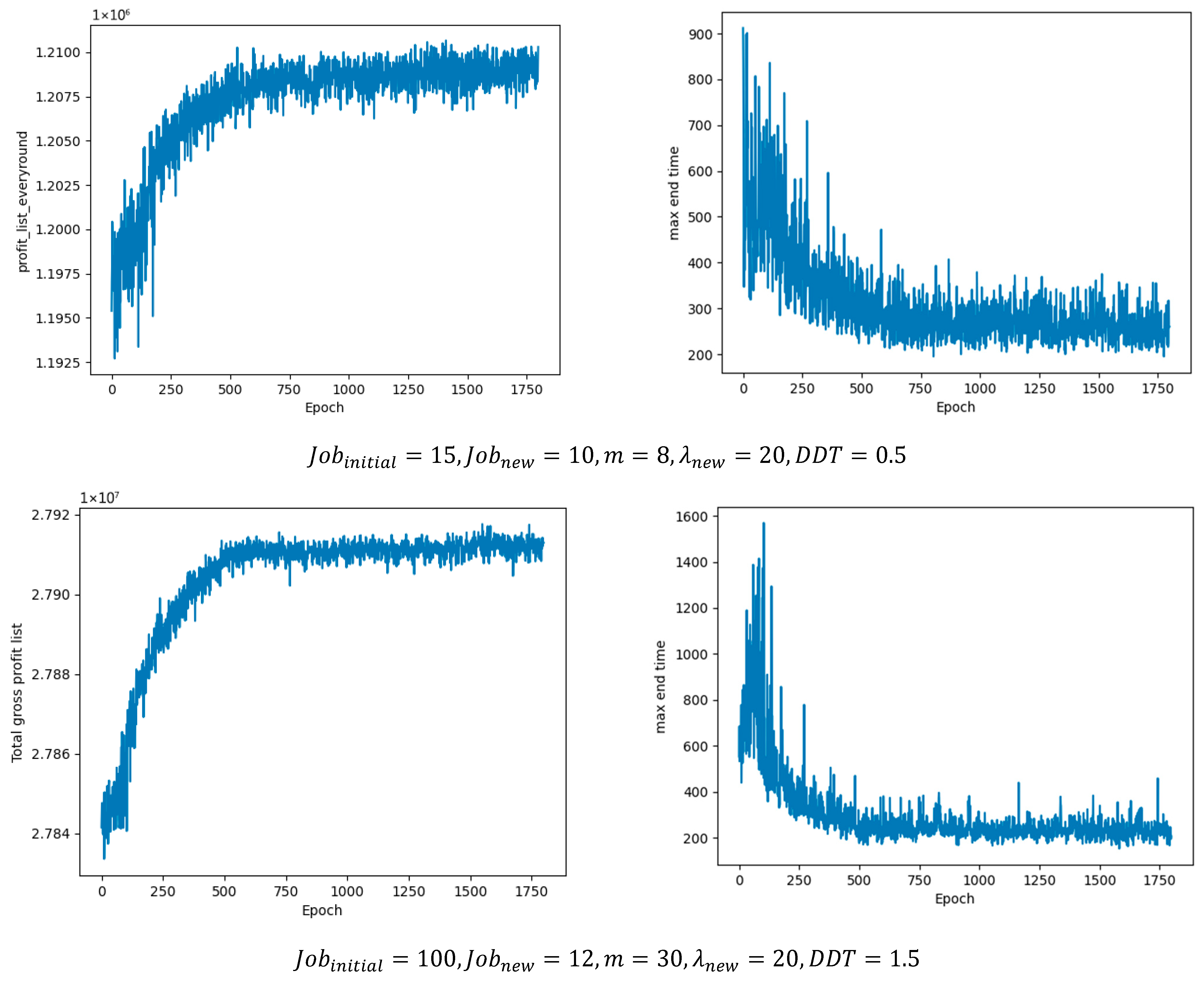
Unlike intelligent optimization algorithms that can generate multiple candidate solutions in parallel, DRL produces one scheduling solution per epoch. Guided by the reward functions and through continuous iterations, it can eventually approach the optimal solution. Specifically, the DRL agent interacts with the environment through actions, generating one scheduling solution in each training epoch; under the guidance of reward signals, it updates iteratively, gradually improving solution quality and finally converging to a (near-)optimal solution. As shown in Figure 10, the proposed collaborative multi-agent method quickly explores high-reward solutions in the early training stage under reward-driven guidance, and subsequently stabilizes and converges to an approximately optimal solution.

5.5. Decision Support Module

Due to inherent conflicts between the two objectives, such as an excessive pursuit of low C_max potentially increasing the number of jobs processed simultaneously, thereby driving up electricity costs and reducing profits; conversely, maximizing profits may delay certain processes to off-peak electricity periods, consequently increasing C_max. To comprehensively evaluate the potential of the proposed model, the technique for order preference by similarity to ideal solution (TOPSIS) method is employed to identify optimal or near-optimal solutions among the non-inferior solutions [41,42].

Table 15. The Pareto solutions of the case study.

Pareto Solution Numbers	Cmax	${\displaystyle \mathbf{\sum }_{\mathit{i}\mathbf{\in }\mathit{J}}{\mathit{TP}}_{\mathit{i}}}$
S1	400	1,069,352
S2	261	1,063,606
S3	262	1,064,400
S4	402	1,069,528
S5	269	1,067,695
S6	353	1,068,191
S7	320	1,067,856
S8	382	1,068,462

presents representative non-dominated solutions obtained by the algorithm.

Decision-makers can obtain the most satisfactory solution from non-inferior solutions using the TOPSIS method [43]. First, establish weight vectors based on decision-makers’ preferences: C_max priority W1 = [0.7, 0.3], profit priority W2 = [0.3, 0.7].

Based on the Pareto solution design decision matrix X in Table 15

$$X=\left(\begin{array}{c}\begin{array}{c}\begin{array}{cc}400& 1069352\end{array}\\ \begin{array}{cc}261& 1063606\end{array}\\ \begin{array}{cc}262& 1064400\end{array}\end{array}\\ \begin{array}{c}⋮\\ \begin{array}{cc}353& 1068191\end{array}\\ \begin{array}{cc}320& 1067856\end{array}\\ \begin{array}{cc}382& 1068462\end{array}\end{array}\end{array}\right)$$

Due to the differing dimensions of various objectives, it is challenging to evaluate performance metrics. By normalizing different values, a normalized decision matrix Y is constructed.

$$Y=\left(\begin{array}{cc}0.420782& 0.354204\\ 0.274560& 0.352301\\ ⋮& ⋮\\ 0.371340& 0.353819\\ 0.336625& 0.353708\\ 0.401846& 0.353909\end{array}\right)$$

Given a weight vector reflecting decision-maker preferences, the normalized matrix Y is weighted row by row to obtain the weighted normalized matrix:

$${\mathit{V}}^{\left(1\right)}=\left({\mathit{v}}_{\mathit{m},\mathit{n}}^{\left(1\right)}\right)= \mathit{Y}·\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left(\mathit{W}1\right), {\mathit{V}}^{\left(2\right)}=\left({\mathit{v}}_{\mathit{m},\mathit{n}}^{\left(2\right)}\right)= \mathit{Y}·\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left(\mathit{W}2\right), m = 1, \dots , 8, n = 1, 2.$$

Since one objective should be as small as possible while the other should be as large as possible, the ideal solution and negative ideal solution can be defined as

$$A^{*}=\{v_1^{*\left(k\right)},v_2^{*\left(k\right)}\},{ A}^{-}=\{v_1^{-\left(k\right)},v_2^{-\left(k\right)}\}$$

Among them,

$$\left\{\begin{array}{c}{v}_1^{*\left(k\right)}=\underset{m}{min}{v}_{m,1}^{\left(k\right)},{ v}_1^{-\left(k\right)}=\underset{m}{max}{v}_{m,1}^{\left(k\right)}, \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e} \mathrm{f}\mathrm{o}\mathrm{r} C_{max}\hfill \\ v_2^{*\left(k\right)}=\underset{m}{max}{v}_{m,2}^{\left(k\right)},{ v}_2^{-\left(k\right)}=\underset{m}{min}{v}_{m,2}^{\left(k\right)}, \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{f}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e} \mathrm{f}\mathrm{o}\mathrm{r} {\displaystyle \sum _{i\in J}}{\mathit{TP}}_i\end{array}\right.$$

Calculate the Euclidean distance between the ideal solution and the negative ideal solution:

$$D_m^{*\left(k\right)}=\sqrt{(v_{m,1}^{\left(k\right)}-v_1^{*\left(k\right)}{)}^2+(v_{m,2}^{\left(k\right)}-v_2^{*\left(k\right)}{)}^2}, D_m^{-\left(k\right)}=\sqrt{(v_{m,1}^{\left(k\right)}-v_1^{-\left(k\right)}{)}^2+(v_{m,2}^{\left(k\right)},v_2^{-\left(k\right)}{)}^2}$$

Define the relative closeness coefficient using the TOPSIS method:

$$C_m^{\left(k\right)}={\displaystyle \frac{D_m^{-\left(k\right)}}{D_m^{*\left(k\right)}+D_m^{-\left(k\right)}}}, m=1, \dots , 8, 0\le C_m^{\left(k\right)}\le 1$$

The larger $C_m^{\left(k\right)}$, the better the plan, which means it is based on the decision-maker’s preferences. Therefore,

Table 16. Examples of optimal solutions in non-inferiority solution sets based on preference mechanisms.

Pareto Solution Numbers	Cmax	${\displaystyle \mathbf{\sum }_{\mathit{i}\mathbf{\in }\mathit{J}}{\mathit{TP}}_{\mathit{i}}}$	${\mathit{C}}_{\mathit{m}}^{\mathbf{\left(}\mathbf{1}\mathbf{\right)}}$	${\mathit{C}}_{\mathit{m}}^{\mathbf{\left(}\mathbf{2}\mathbf{\right)}}$
S1	400	1,069,352	0.015197	0.032514
S2	261	1,063,606	0.994364	0.970063
S3	262	1,064,400	0.991388	0.972908
S4	402	1,069,528	0.005636	0.029937
S5	269	1,067,695	0.943237	0.942523
S6	353	1,068,191	0.347535	0.348040
S7	320	1,067,856	0.581564	0.581684
S8	382	1,068,462	0.141909	0.143759

shows that the weight vector W1 corresponds to “C_max priority,” and the optimal solution calculated based on this weight is S2; the weight vector W2 corresponds to “profit priority,” and the optimal solution calculated based on this weight is S3.

6. Conclusions

In this study, for the MODFJSP, we construct a “job selection–machine assignment” multi-agent collaborative framework that comprehensively considers factors such as dynamic job arrivals, fluctuating due dates, and high-profit urgent orders, with the dual objectives of maximizing net profit and minimizing makespan. In terms of method design, variable state representations, reward functions, and variable action spaces are customized for the two types of agents to enhance learning efficiency and stability. Systematic experiments are then conducted on 18 instances, comparing the proposed framework with PPO, DQN, and other deep reinforcement learning algorithms as well as classical scheduling rules. The results show that the proposed framework demonstrates a certain advantage in solution quality and robustness. Statistics indicate that, compared with other algorithms and scheduling rules, it can achieve a 0.368% increase in profit.

The profit function employed by this research does not account for labor, maintenance, inventory, or other financial factors, thus retaining a certain gap from real-world business metrics. Furthermore, the methodology has not yet been validated against traditional heuristic algorithms, and its effectiveness and advantages require further exploration.

Subsequent work will focus on integrating more practical profit functions and introducing more robust and efficient multi-agent reinforcement learning algorithms to optimize the overall trade-off between profitability and timeliness in dynamic and uncertain industrial environments. Additionally, flexible profit models may be considered, enabling users to adjust profit parameters according to actual needs, thereby enhancing the model’s applicability and practical value.