Adaptive Backstepping Control of an Unmanned Aerial Manipulator
Abstract
1. Introduction
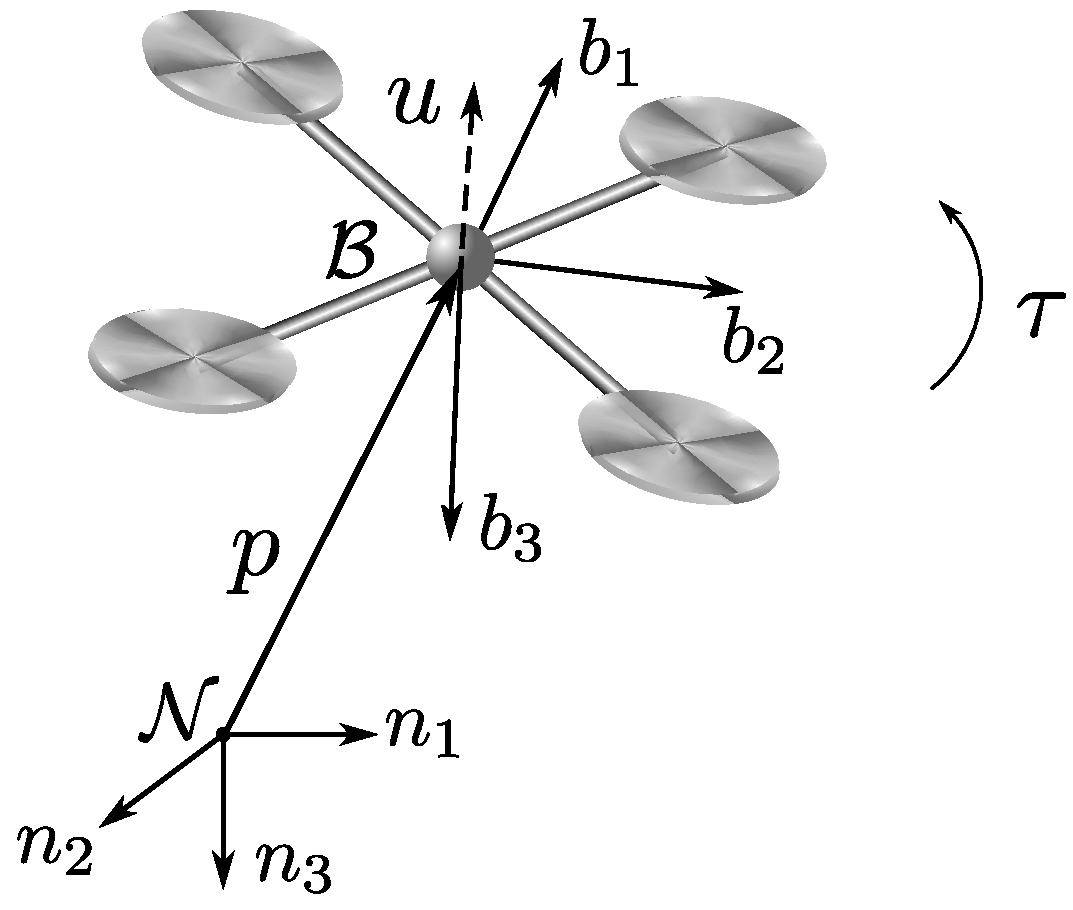
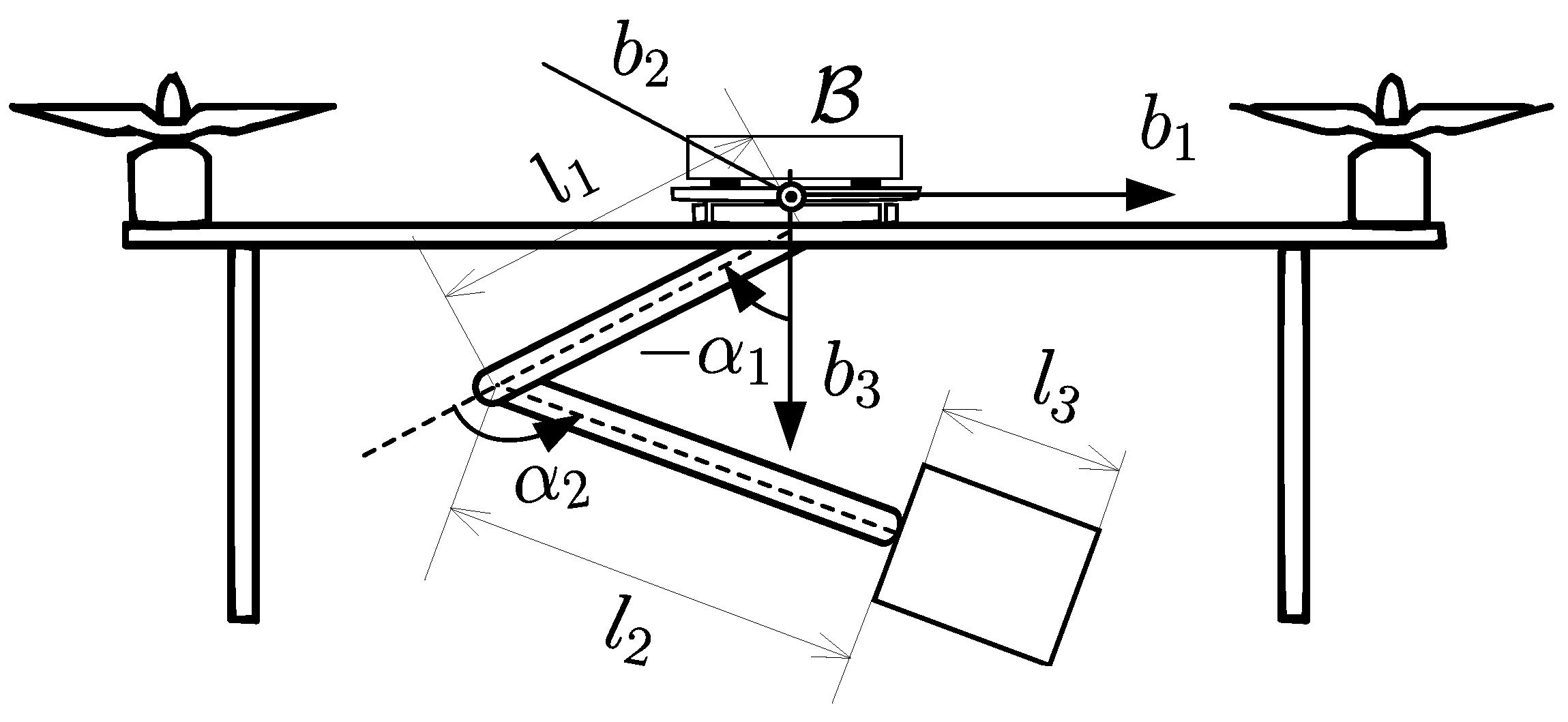
2. Modeling
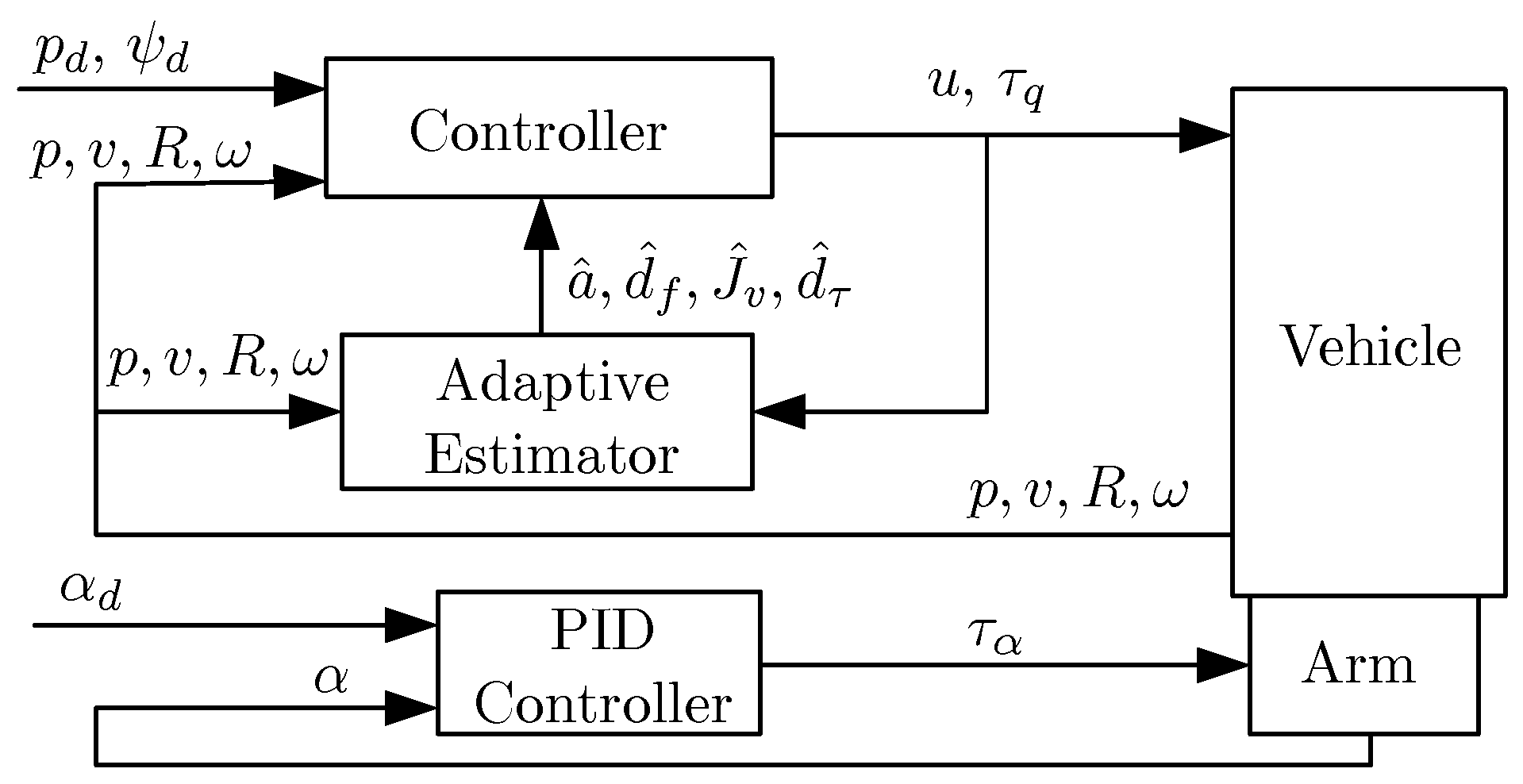
3. Control Design
3.1. Position Tracking Control
3.2. Position and Yaw Tracking Control
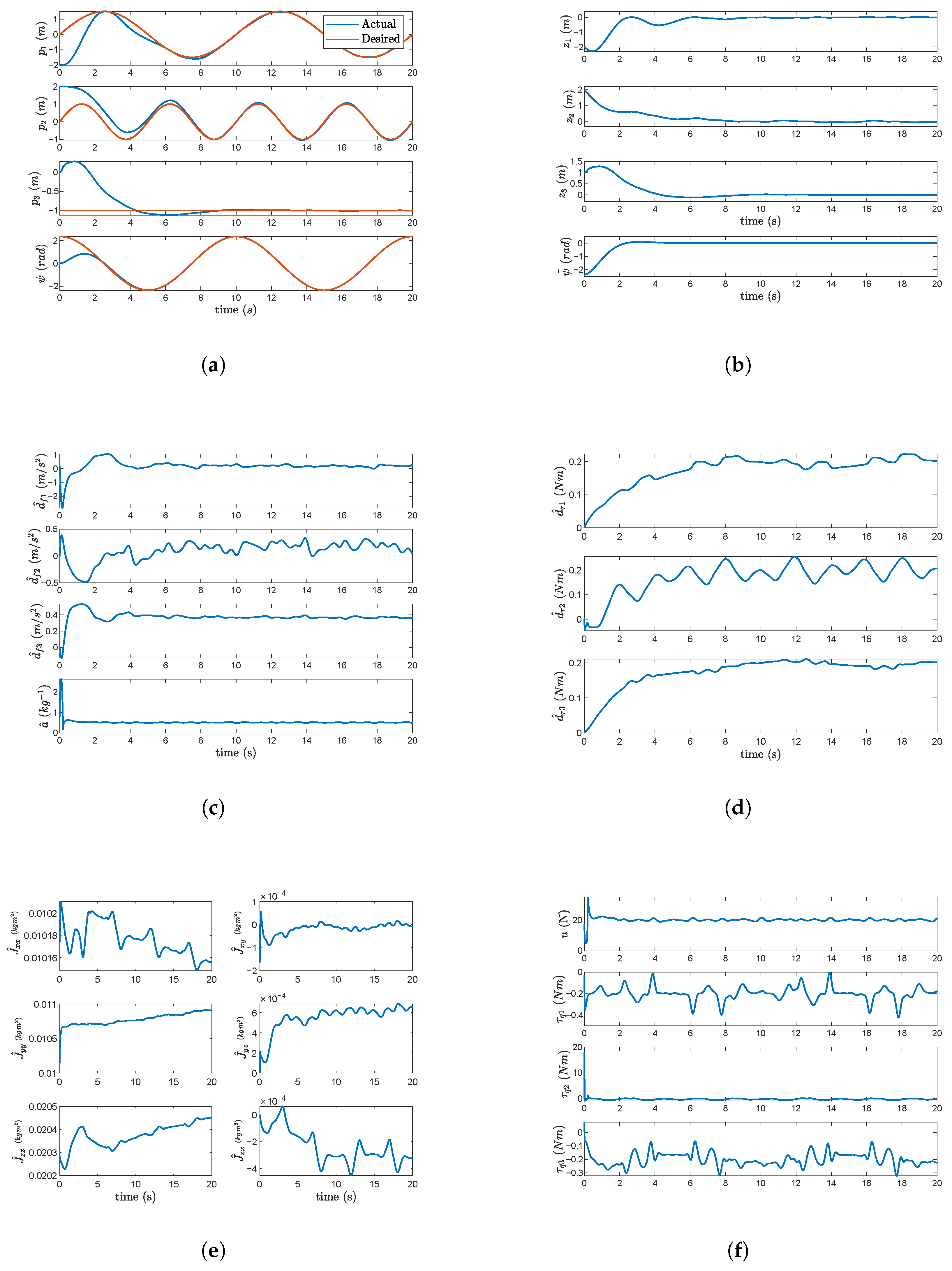
4. Simulation Results
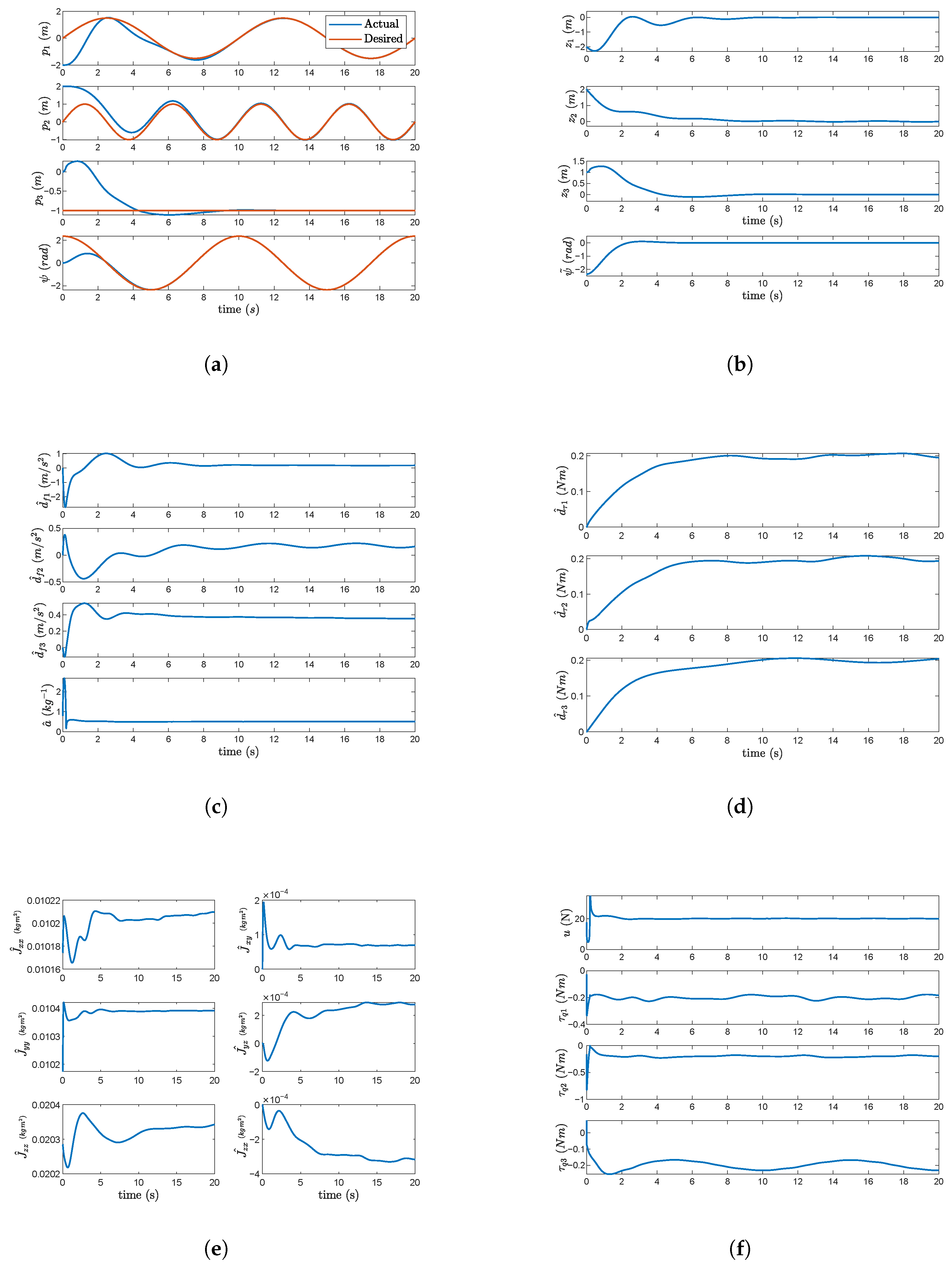
4.1. Figure-of-Eight Reference Trajectory
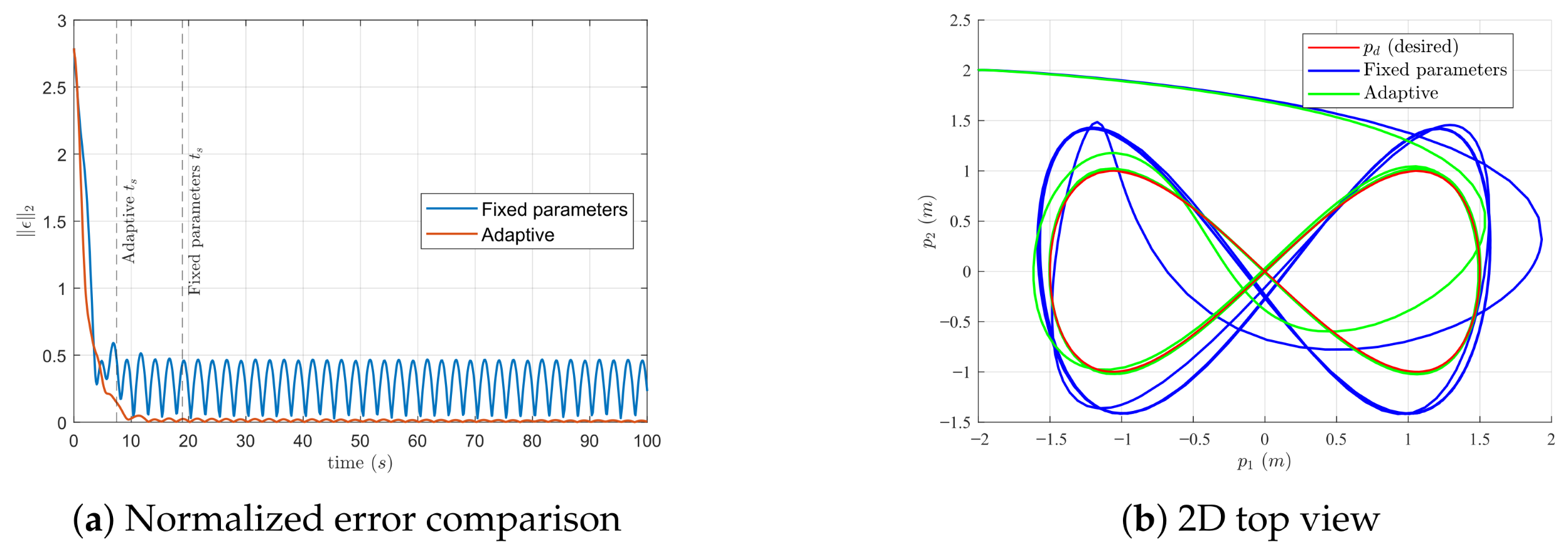
4.2. Adaptation Comparison with Fixed-Parameter Case
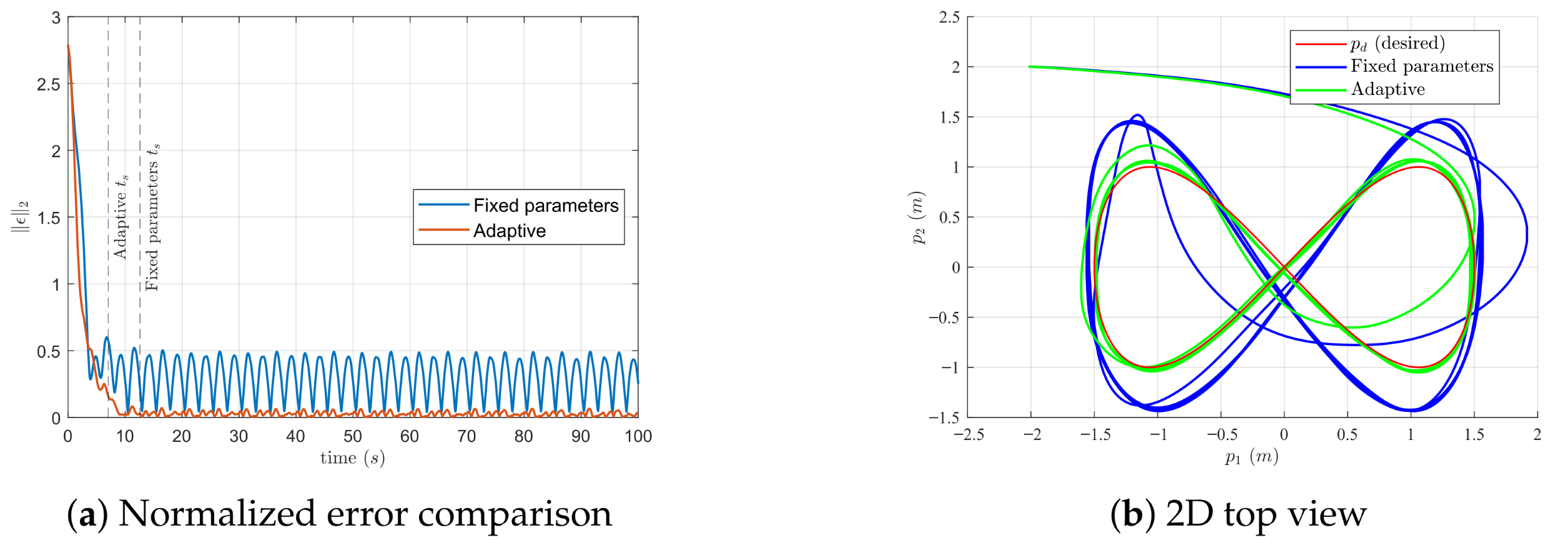
4.3. Robustness to Parameter Variation
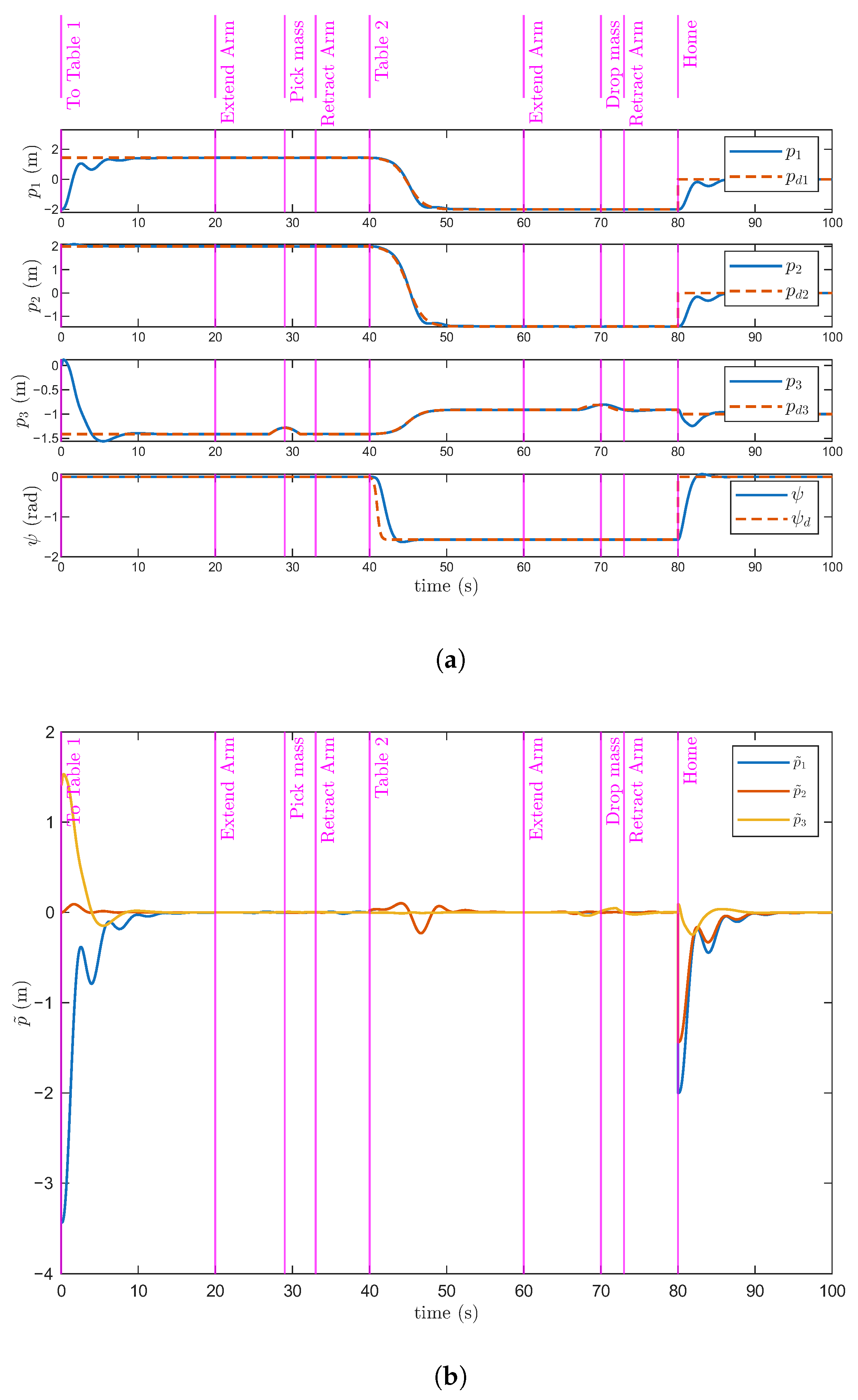
4.4. Pick-and-Place
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Villa, D.K.D.; Brandão, A.S.; Sarcinelli-Filho, M. A Survey on Load Transportation Using Multirotor UAVs. J. Intell. Robot. Syst. 2020, 98, 267–296. [Google Scholar] [CrossRef]
- Watson, R.J.; Pierce, S.G.; Kamel, M.; Zhang, D.; MacLeod, C.N.; Dobie, G.; Bolton, G.; Dawood, T.; Nieto, J. Deployment of Contact-Based Ultrasonic Thickness Measurements Using Over-Actuated UAVs. In European Workshop on Structural Health Monitoring, Proceedings of the European Workshop on Structural Health Monitoring (EWSHM 2020), Palermo, Italy, 6–9 July 2020; Lecture Notes in Civil Engineering; Rizzo, P., Milazzo, A., Eds.; Springer: Cham, Switzerland, 2021; Volume 127, pp. 683–694. [Google Scholar] [CrossRef]
- Bonyan Khamseh, H.; Janabi-Sharifi, F.; Abdessameud, A. Aerial manipulation—A literature survey. Robot. Auton. Syst. 2018, 107, 221–235. [Google Scholar] [CrossRef]
- Ollero, A.; Tognon, M.; Suarez, A.; Lee, D.; Franchi, A. Past, Present, and Future of Aerial Robotic Manipulators. IEEE Trans. Robot. 2022, 38, 626–645. [Google Scholar] [CrossRef]
- Albers, A.; Trautmann, S.; Howard, T.; Nguyen, T.A.; Frietsch, M.; Sauter, C. Semi-autonomous flying robot for physical interaction with environment. In Proceedings of the IEEE Conference on Robotics, Automation and Mechatronics, Singapore, 28–30 June 2010; pp. 441–446. [Google Scholar] [CrossRef]
- Nguyen, H.; Lee, D. Hybrid force/motion control and internal dynamics of quadrotors for tool operation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 3458–3464. [Google Scholar] [CrossRef]
- Mersha, A.Y.; Stramigioli, S.; Carloni, R. Variable impedance control for aerial interaction. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 3435–3440. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S.; Kim, H.; Shin, J.; Shim, H.; Kim, H.J. Robust Control of an Equipment-Added Multirotor Using Disturbance Observer. IEEE Trans. Autom. Control 2018, 26, 1524–1531. [Google Scholar] [CrossRef]
- Jimenez-Cano, A.E.; Martin, J.; Heredia, G.; Ollero, A.; Cano, R. Control of an aerial robot with multi-link arm for assembly tasks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 4916–4921. [Google Scholar] [CrossRef]
- Korpela, C.; Orsag, M.; Pekala, M.; Oh, P. Dynamic stability of a mobile manipulating unmanned aerial vehicle. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 4922–4927. [Google Scholar] [CrossRef]
- Kannan, S.; Olivares-Mendez, M.A.; Voos, H. Modeling and Control of Aerial Manipulation Vehicle with Visual sensor. IFAC Proc. Vol. 2013, 46, 303–309. [Google Scholar] [CrossRef]
- Kannan, S.; Alma, M.; Olivares-Mendez, M.A.; Voos, H. Adaptive control of Aerial Manipulation Vehicle. In Proceedings of the IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 28–30 November 2014; pp. 273–278. [Google Scholar] [CrossRef]
- Khalifa, A.; Fanni, M.; Ramadan, A.; Abo-Ismail, A. Modeling and control of a new quadrotor manipulation system. In Proceedings of the First International Conference on Innovative Engineering Systems, Alexandria, Egypt, 7–9 December 2012; pp. 109–114. [Google Scholar] [CrossRef]
- Samadikhoshkho, Z.; Lipsett, M. Decoupled Control Design of Aerial Manipulation Systems for Vegetation Sampling Application. Drones 2023, 7, 110. [Google Scholar] [CrossRef]
- Ding, L.; Zhu, G.; Li, Y.; Wang, Y. Cable-Driven Unmanned Aerial Manipulator Systems for Water Sampling: Design, Modeling, and Control. Drones 2023, 7, 450. [Google Scholar] [CrossRef]
- Lippiello, V.; Ruggiero, F. Exploiting redundancy in Cartesian impedance control of UAVs equipped with a robotic arm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 3768–3773. [Google Scholar] [CrossRef]
- Lippiello, V.; Ruggiero, F. Cartesian Impedance Control of a UAV with a Robotic Arm. In Proceedings of the 10th International IFAC Symposium on Robot Control, Dubrovnik, Croatia, 5–7 September 2012; pp. 704–709. [Google Scholar]
- Kim, S.; Choi, S.; Kim, H.J. Aerial manipulation using a quadrotor with a two DOF robotic arm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 4990–4995. [Google Scholar] [CrossRef]
- Yang, H.; Lee, D. Dynamics and control of quadrotor with robotic manipulator. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5544–5549. [Google Scholar] [CrossRef]
- Korpela, C.; Orsag, M.; Oh, P. Towards valve turning using a dual-arm aerial manipulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 3411–3416. [Google Scholar] [CrossRef]
- Samadikhoshkho, Z.; Ghorbani, S.; Janabi-Sharifi, F.; Zareinia, K. Nonlinear control of aerial manipulation systems. Aerosp. Sci. Technol. 2020, 104, 105945. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Wu, T.; Dong, C.; Xu, Q.; Yang, Y.; Yu, X. A Novel Active Anti-Disturbance Control Strategy for Unmanned Aerial Manipulator Based on Variable Coupling Disturbance Compensation. Electronics 2024, 13, 1477. [Google Scholar] [CrossRef]
- Lee, K.; Back, J.; Choy, I. Nonlinear disturbance observer based robust attitude tracking controller for quadrotor UAVs. Int. J. Control Autom. Syst. 2014, 12, 1266–1275. [Google Scholar] [CrossRef]
- Baraban, G.; Sheckells, M.; Kim, S.; Kobilarov, M. Adaptive Parameter Estimation for Aerial Manipulation. In Proceedings of the American Control Conference, Denver, CO, USA, 1–3 July 2020; pp. 614–619. [Google Scholar] [CrossRef]
- Alvarez-Munoz, J.; Marchand, N.; Guerrero-Castellanos, J.F.; Tellez-Guzman, J.J.; Escareno, J.; Rakotondrabe, M. Rotorcraft with a 3DOF Rigid Manipulator: Quaternion-based Modeling and Real-time Control Tolerant to Multi-body Couplings. Int. J. Autom. Comput. 2018, 15, 547–558. [Google Scholar] [CrossRef]
- Park, C.; Ramirez-Serrano, A.; Bisheban, M. Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators. Aerospace 2024, 11, 671. [Google Scholar] [CrossRef]
- Petrlík, M.; Báča, T.; Heřt, D.; Vrba, M.; Krajník, T.; Saska, M. A robust UAV system for operations in a constrained environment. IEEE Robot. Autom. Lett. 2020, 5, 2169–2176. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Q.; Ren, B. Wind turbine crack inspection using a quadrotor with image motion blur avoided. IEEE Robot. Autom. Lett. 2023, 8, 1069–1076. [Google Scholar] [CrossRef]
- Ullah, S.; Alghamdi, H.; Algethami, A.; Alghamdi, B.; Hafeez, G. Robust Control Design of Under-Actuated Nonlinear Systems: Quadcopter Unmanned Aerial Vehicles with Integral Backstepping Integral Terminal Fractional-Order Sliding Mode. Fractal Fract. 2024, 8, 412. [Google Scholar] [CrossRef]
- Moeini, A.; Lynch, A.F.; Zhao, Q. Exponentially Stable Motion Control for Multirotor UAVs with Rotor Drag and Disturbance Compensation. J. Intell. Robot. Syst. 2021, 103, 15. [Google Scholar] [CrossRef]
- Moeini, A.; Rafique, M.A.; Xue, Z.; Lynch, A.F.; Zhao, Q. Disturbance Observer-Based Integral Backstepping Control for UAVs. In Proceedings of the the International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 382–388. [Google Scholar] [CrossRef]
- Imran, I.; Wood, K.; Montazeri, A. Adaptive Control of Unmanned Aerial Vehicles with Varying Payload and Full Parametric Uncertainties. Electronics 2024, 13, 347. [Google Scholar] [CrossRef]
- Rafique, M.A. Adaptive Nonlinear Control for Unmanned Aerial Vehicles: Visual Servoing and Aerial Manipulation. Ph.D. Thesis, University of Alberta, Edmonton, AB, Canada, 2022. [Google Scholar] [CrossRef]
- Bangura, M. Aerodynamics and Control of Quadrotors. Ph.D. Thesis, College of Engineering and Computer Science, The Australian National University, Canberra, ACT, Australia, 2017. [Google Scholar]
- Bouabdallah, S. Design and Control of Quadrotors with Application to Autonomous Flying. Ph.D. Thesis, Ecole Polytechnique Federale de Luasanne, Lausanne, Switzerland, 2007. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Bisgaard, M.; la Cour-Harbo, A.; Dimon Bendtsen, J. Adaptive control system for autonomous helicopter slung load operations. Control Eng. Pract. 2010, 18, 800–811. [Google Scholar] [CrossRef]
- Huber, F.; Kondak, K.; Krieger, K.; Sommer, D.; Schwarzbach, M.; Laiacker, M.; Kossyk, I.; Parusel, S.; Haddadin, S.; Albu-Schäffer, A. First analysis and experiments in aerial manipulation using fully actuated redundant robot arm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 3452–3457. [Google Scholar] [CrossRef]
- Meier, L.; Honegger, D.; Pollefeys, M. PX4: A node-based multithreaded open source robotics framework for deeply embedded platforms. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 6235–6240. [Google Scholar] [CrossRef]
- Jiang, Z.; Yu, Y.; Lynch, A. Nonlinear Motion Control of a Multirotor Slung Load System: Experimental Results. In Proceedings of the American Control Conference, Toronto, ON, Canada, 10–12 July 2024; pp. 2851–2857. [Google Scholar] [CrossRef]
- Lawati, M.A.; Zhang, Z.; Yan, E.; Lynch, A.F. Nonlinear Control of a Multi-Drone Slung Load System. In Proceedings of the American Control Conference, Denver, CO, USA, 8–10 July 2025; pp. 1989–1996. [Google Scholar]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 1.6 | , | 0.03 |
| 0.05 | , , | 0.0 |
| Parameter | Link 1 | Link 2 | Link 3 |
|---|---|---|---|
| Joint Type | Revolute | Revolute | Fixed |
| Mass () | 0.1 | 0.1 | 0.1 |
| Length () | 0.2 | 0.3 | 0.1 |
| Inertia () |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.4 | 0.5 | ||
| 0.5 | 7 | ||
| 1 | 3 | ||
| 0.001 | 5 | ||
| 1 |
| Case | (s) | SS nRMSE (%) |
|---|---|---|
| Fixed parameters | 18.93 | 33.34 |
| Adaptive | 7.45 | 1.37 |
| Case | (s) | SS nRMSE (%) |
|---|---|---|
| Fixed parameters | 12.60 | 33.57 |
| Adaptive | 7.04 | 1.96 |
| Case | Fixed Arm | Moving Arm | ||
|---|---|---|---|---|
| (s) | SS nRMSE (%) | (s) | SS nRMSE (%) | |
| 1 | 7.39 | 1.73 | 6.77 | 2.64 |
| 2 | 7.25 | 1.80 | 6.80 | 2.42 |
| 3 | 7.93 | 1.26 | 7.81 | 1.56 |
| 4 | 7.55 | 2.20 | 7.28 | 2.38 |
| 5 | 7.63 | 1.52 | 7.33 | 2.07 |
| 6 | 7.39 | 1.51 | 6.89 | 1.92 |
| 7 | 7.33 | 1.47 | 6.84 | 2.04 |
| 8 | 7.64 | 1.57 | 7.43 | 2.18 |
| 9 | 7.54 | 1.64 | 7.44 | 2.12 |
| 10 | 7.16 | 1.54 | 6.83 | 2.05 |
| STD | 0.25 | 0.26 | 0.29 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafique, M.A.; Elshaar, M.E.; Lynch, A.F. Adaptive Backstepping Control of an Unmanned Aerial Manipulator. Machines 2025, 13, 915. https://doi.org/10.3390/machines13100915
Rafique MA, Elshaar ME, Lynch AF. Adaptive Backstepping Control of an Unmanned Aerial Manipulator. Machines. 2025; 13(10):915. https://doi.org/10.3390/machines13100915
Chicago/Turabian StyleRafique, Muhammad Awais, Mohssen E. Elshaar, and Alan F. Lynch. 2025. "Adaptive Backstepping Control of an Unmanned Aerial Manipulator" Machines 13, no. 10: 915. https://doi.org/10.3390/machines13100915
APA StyleRafique, M. A., Elshaar, M. E., & Lynch, A. F. (2025). Adaptive Backstepping Control of an Unmanned Aerial Manipulator. Machines, 13(10), 915. https://doi.org/10.3390/machines13100915






