Abstract
Board games like chess serve as an excellent testbed for human–robot interactions, where advancements can lead to broader human–robot cooperation systems. This paper presents a chess-playing robotic system to demonstrate controlled pick and place operations using a 3-DoF manipulator with image and speech recognition. The system identifies chessboard square coordinates through image processing and centroid detection before mapping them onto the physical board. User voice input is processed and transcribed into a string from which the system extracts the current and destination locations of a chess piece with a word error rate of 8.64%. Using an inverse-kinematics algorithm, the system calculates the joint angles needed to position the end effector at the desired coordinates actuating the robot. The developed system was evaluated experimentally on the 3-DoF manipulator with a voice command used to direct the robot movement in grasping a chess piece. Consideration was made involving both the own pieces as well as capturing the opponent’s pieces and moving the captured piece outside the board workspace.
1. Introduction
Human–robot interaction is one of many applications seeking to leverage the recent advances in technology to realize the operation of robots in a shared space with people. Based on the review in [1], human–robot interaction is enhanced through the combination of modalities such as voice, vision [2], text, touch, and bio-signals [3] as methods of intercommunication. Some of the collaboration efforts have been directed towards elderly care, addressing the challenges of aging populations [4,5], in addition to physically assistive robots [6]. Board games, such as chess and checkers, provide a rich domain for researching human–robot cooperation due to their structured yet flexible nature [7]. Chess, a two-player strategy board game played on a checkered board in an 8 × 8 grid, serves as an excellent testbed for developing general human–robot cooperation systems requiring perception, reasoning, and manipulation of physical pieces. It is characterized by turn-taking in moving pieces to either an unoccupied square or one occupied by an opponent’s piece. The defined and easy to understand rules make chess an appealing choice for incorporating robotic systems. Progress made on the incorporation of robots in board games can in turn pave the way for more general human–robot cooperation systems, not only in industrial applications but also in health, entertainment, and educational fields [8]. Chess is also one of the few games and sports allowing everyone, including disabled individuals, to compete equally under the same standards, fostering an inclusive environment where ratings and international titles are awarded similarly.
The essential requirements to develop a robotic system for board games can be summarized as recognizing the board state, deciding the optimal move, and controlling the robot to execute the desired move [9]. In this research, speech recognition was considered as one of the methods that can be used to address the challenges faced in the inclusion of marginalized individuals with physical disabilities, by using a voice command from a human player to decide the desired move for a robot system. A voice command-based robotic system can prove to be useful for individuals with physical impairments such as amputated arms, motor disabilities making hand–eye coordination difficult, and neurological disorders such as cerebral palsy. While the availability of virtual chess playing platforms through computer games partially addresses some of the challenges such as remote playing, a higher level of involvement and corresponding enjoyment is observed to arise from face to face playing with a human or with a robot [10]. Physical embodiment is therefore a key factor in chess playing and one which is also promoted by using an assistive robot system in this research.
Voice command-based robot execution provides an inclusive and accessible chess-playing experience and aims to further propose potential solutions for human equality while at the same time advancing the efforts towards human–robot collaboration, furthering the recommendations presented in [11]. The system is directed at the aforementioned marginalized group affected by motor disabilities such as cerebral palsy, the most common motor disability in childhood [12,13]. The inclusion of physically disabled individuals in various aspects of life is a significant research focus [14], often encapsulated by the phrase “physical disability is not inability”. Advances in technology, such as self-driving cars and gesture-controlled appliances, have improved accessibility and this work aims to make a step towards this end.
In this research, a low-cost semi-autonomous chess-playing robot prototype was implemented. The system incorporated a 3-DoF robot manipulator, image segmentation, and speech recognition. The system receives a voice command containing the location of the desired chess piece location from the chess player, which is then processed through the Microsoft Azure Speech Services API. As an intermediate step, color-based image segmentation translates the command-derived coordinates into the detected coordinates on the robot workspace, allowing individuals with motor disabilities to interact with the system seamlessly. The output to the system is the piece movement by the robot manipulator, with the manipulator functioning as an assistive grasping system of the chess pieces. Integration of speech and image recognition ensures a smooth, accessible human–robot interaction providing for physical presence, which is lacking in normal computer chess played against a computer, a contributing factor to the enjoyment of the game in addition to cognitive benefits.
The research work is organized in four sections, as follows: Section 2 looks at the related works. Section 3 describes the architecture of the robot used, methods considered in robot kinematics, image processing, and speech recognition, as well as the specifications of the software and hardware in the experimental setup. One of the main differences from the works presented in Section 2 is the inclusion of speech processing in the implementation scheme, leading to a human-assistive robot applied in board games, while reducing the complexity and increased computational power associated with including a chess engine for autonomous execution. Section 4 describes the results and discussion, with Section 5 presenting the conclusions based on the research work.
2. Related Works
Modern robots, equipped with sensors mimicking human sensory functions, have revolutionized the manufacturing industry and extended their applications to tasks such as welding, painting, drilling, and complex pick and place operations. The applications range from performing repetitive tasks, working in hazardous environments, and in numerous industrial operations [15,16,17]. A significant advancement in this field is machine vision, enabling robots to gather environmental data by integrating computer vision and thus enhancing their flexibility and adaptability [18]. With increasing computer processing power and the affordability of advanced motors and sensory equipment, autonomous robots are now poised to transition from industrial settings to household tasks and entertainment.
Remarkable advancements that have been made in the application of robotics in board games are the coupling of robotic arms with other technologies, such as speech recognition and image processing. Most automated chess-playing systems are divided into three basic building blocks: the input, the processor, and the output (which is the move to be made). One of the notable types of research works looking at the automation of chess playing includes the use of Hall sensors as the input, an Arduino Nano as the microcontroller, and a custom designed Printed Circuit board for the detection of chess positions [19]. The limitation to this is the use of a custom, expensive chess board and pieces, where it becomes a challenge since most chess players have their own boards. Castling moves and the allowed en passant moves are also not executable, and therefore limiting gameplay.
In [20] a simple autonomous robotic manipulator for playing chess against any opponent in real time was presented. Image processing using the OpenCV library determined the current orientation of the board given the previous orientations. The image processing algorithm used the Shi-Tomasi corner detection algorithm to detect the four corners of the chessboard and the Canny edge detection algorithm to detect the edges of the chess pieces. The counter move was determined using the GNU Chess engine free software and implemented using a robot arm. Gambit [7], an autonomous chess-playing robotic system, is another noteworthy application of robotics in board games. The Gambit system consists of a low-cost Kinetic-style visual sensor and a custom 6-DoF robot manipulator. To recognize the chess pieces on the board, Gambit utilizes machine learning—in particular, Support Vector Machines (SVMs). Gambit then utilizes the difference between two consecutive board game states to determine the move made by an opponent alongside the GNU engine. Another approach uses the KUKA KR6 R900 sixx (Agilus),a robot made in Augsburg, Germany and classified as one of the fastest industrial robots worldwide [21]. The system is integrated with a PLC-controlled conveyor belt and a vacuum cup with a venturi nozzle designed for sucking and picking up the custom chess pieces.
In realizing controlled robot motion, motion planning is necessary to ensure no collisions or singularities occur during motion execution. Motion planning is defined as the process of generating a sequence of intermediate points to be followed by a manipulator as it moves from an initial point to a desired goal point whilst satisfying a set of boundary conditions. The sequence of intermediate points is referred to as a trajectory. Some of the techniques used in generating a trajectory are outlined in [22,23], with quadrinomial and quintic polynomials used in [24] for the trajectory planning of a biped robot simulating the human gait. A quintic polynomial was preferred in producing a trajectory for this research since it gives a simple solution, satisfying boundary conditions on velocity, acceleration, and position through successive differentiation.
In presenting the application of an intelligent and collaborative robotic system for playing checkers, ref. [9] highlights three essential requirements in developing a robotic system for playing checkers or chess; namely, board recognition, decision on optimal move, and robot-controlled execution. Chess and checkers are highly correlated, with both being played on an 8 × 8 square board, and the main difference being in the rules of play and the pieces used in gameplay. The implementation of the robot system considers a Franka Emika robot with seven degrees of freedom, utilizing a decision-making checkers algorithm in combination with computer vision to determine the board state. The computer vision algorithm requires the user to manually point a camera to the position of the board corners in the image in obtaining the board image. Any imprecision in positioning the camera is corrected due to the regularity in the squares on a board. The inclusion of an AI-based game engine determines the best move for the robot to play, based on the Italian checkers rules. The complete system can be used to play against a human opponent, as demonstrated in the research.
Some of the works preceding [9] and related to the implementation of this current proposal include [25], where a humanoid robot plays chess using visual control. The color-space mapping is based on OpenCV and a Harris corner detection algorithm to identify the corners of the square boxes. The humanoid robot employed in this research is the NAO robot by Softbank Japan, an autonomous but expensive robot selling at more than $12,000 as of writing this paper. In [26] an autonomous robot system is implemented in playing checkers using image processing to learn the game state. This system uses a modified electromagnetic system to realize the gameplay. The implementation uses materials that can easily be 3D-printed, therefore making it cheaper and more accessible. However, the system required manually inputting the coordinates of the destination point, with image processing only detecting the current board state.
In realizing the game state of board games, the utilization of various image processing techniques, ranging from corner detection algorithms to color space mapping as in [9,20,25,26], highlighted the importance of image processing. In [27], an image recognition method based on convolutional neural networks is presented. The research then develops a dataset and a transfer learning method to allow for the portability of the developed system to a new board by requiring taking only two images of the new board.
Human–robot collaboration is a landmark research area that requires care in the implementation due to the possibility to inflict physical damage to people in the surrounding workspace. As a result, in proactive human–robot collaboration work, ref. [8] presents perspectives that should be considered towards human-centric development. These include mutual cognition of the environment, predictability, and self-organizing capabilities where techniques for adaptiveness, perception, and collision avoidance are presented. Use cases of robots in human–robot collaboration for elderly care and as physically assistive robots in feeding a person are presented in [4] and [6], respectively. Speech processing integration stands out as being useful in the development of assistive robots. The authors of [11] investigated the key engineering advances needed to realize effective integration of speech processing in robotics. One of the factors is the need for real-time processing in ensuring effective interaction between robots and humans.
Table 1 briefly shows the recent developments integrating various robotics systems to checkers or chess, furthering the approach used in [9]. A comparison of these works with this current proposal in terms of the cost effectiveness and the application scope is outlined.

Table 1.
Review of recent developments in robotic systems for playing board games.
3. Robot Architecture and Methods
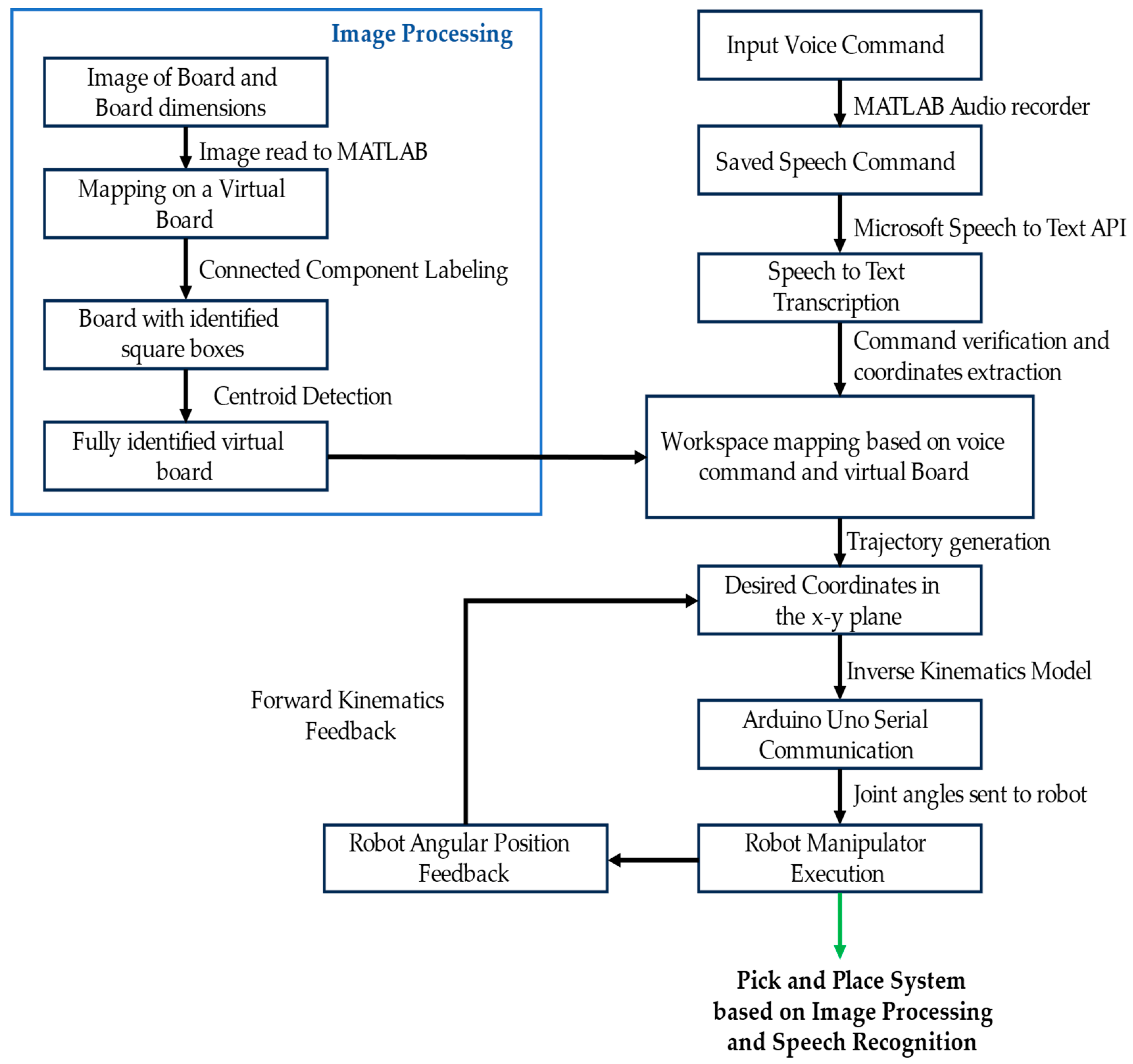
The complete system is a pick and place control, based on image and pattern recognition, for a 3-DoF robot manipulator. This pick and place operation is the foundation upon which the chess-playing robot prototype, which uses voice input to locate the source and destination of the chess pieces, is implemented. The flowchart showing the general overview of the execution base and interdependence of the various modules considered in the methods is shown in Figure 1.
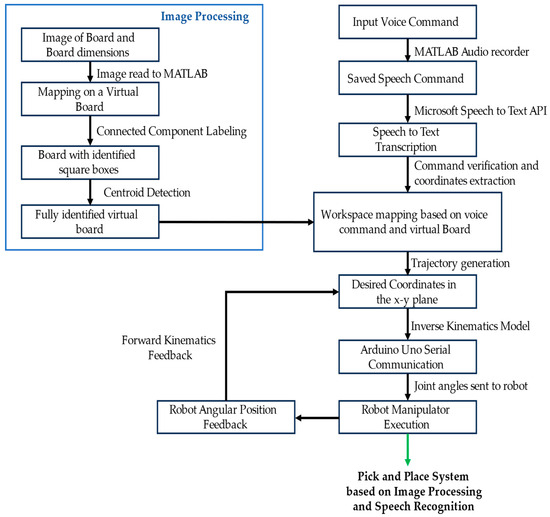
Figure 1.
Algorithm for the general execution sequence based on the methodology.
The hardware and software tools used in realizing the general execution and developing the complete system are shown in Table 2.

Table 2.
Software and hardware tools used in proposed system.
3.1. Robot Arm and Kinematics
The main actuator of the pick and place-based chess-playing robot prototype was the MeArm, as shown in Figure 2, a 3-DoF low-cost open-source robot arm that uses a “double parallelogram” mechanism of operation. The parallel structure allows the servos to be mounted on the base while still allowing them to be moved independently. The MeArm had four SG90 micro servos, each having a weight of 9 g, rotation of 0°–180°, and a torque of 1.3 kg/cm. It is worth noting that this task could be completed by a large variety of robots, including those described previously [7,20,28]. The requirements needed for a robotic arm to be viable in the domain of playing board games are related to the workspace, end effector type, accuracy, and cost.

Figure 2.
MeArm robot, as applied to pick and place in chess playing.
The workspace of the robotic arm should be such that it can reach any target on the chess board and extend outside to remove captured pieces. The end effector should be able to effectively pick and place the pieces within the board grids or squares while realizing a good enough accuracy. The cost of the robot arm should not be too expensive, as the solution should be economically manageable, ensuring inclusivity for the physically challenged.
In achieving control of the 3-DoF robot manipulator with 4 servo motors, including the gripper opening and closing servo, an Arduino Uno was used as the microcontroller, through which commands for actuation could be sent to the manipulator due to its simplicity and execution efficiency. The Arduino was connected to MATLAB through serial communication, allowing data transfer between the two interfaces. MATLAB was used as the interface on which the robot-based control algorithm was designed, due to its high computational capability. Kinematics, trajectory generation, speech, and image processing phases of the project were implemented in the MATLAB environment. The Arduino input data comprised of joint angles based on the inverse kinematics calculation, which then led to servo motor rotation.
Kinematics is the science of motion that treats the subject without regard to the forces that cause it. A manipulator may thus be thought of as a set of bodies (links) connected in a chain by joints. Forward kinematics (FK) involves computing the position and orientation of the end effector given a set of joint angles. The forward kinematics were performed in accordance with the Denavit–Hartenberg (D–H) convention. By considering the physical architecture and motion of the 3-DoF MeArm robot, the relations between the robot base frame in the workspace, and the moving frame at the joint locations, the D–H parameters can be calculated, and are represented as in Table 3.

Table 3.
D–H parameter representation for the 3-DoF MeArm robot.
Each homogeneous transformation Ai is represented as a product of four basic transformations, which evaluates to a 4 × 4 matrix that is used to transform a point from frame n to n-1 such that:
The homogenous transformation matrix of each link was then obtained as:
The total homogenous transformation is obtained as the product of the individual link transformations, from which the cartesian coordinates representing the end effector positions are determined. This total transformation is represented as:
The position of the end effector (x, y, z) could be determined based on the total homogeneous transformation (6) as:
where is the joint angle with relation to links 1, 2, and 3 respectively.
The FK equation was helpful in determining the position of the end effector given a set of joint angles; however, in the given research problem, verifying the correctness of the forward kinematics was conducted through physical confirmation of the end effector position. The process in the verification included actuating the robot based on desired input angles and physically measuring the end effector position relative to the base frame. The FK was then used to mathematically determine the end effector positions corresponding to these input angles. A comparison of the two methods was conducted and equivalent results were obtained. In the complete pick and place system, forward kinematics were used as feedback mechanism following the motion of the robot based on the inverse kinematics.
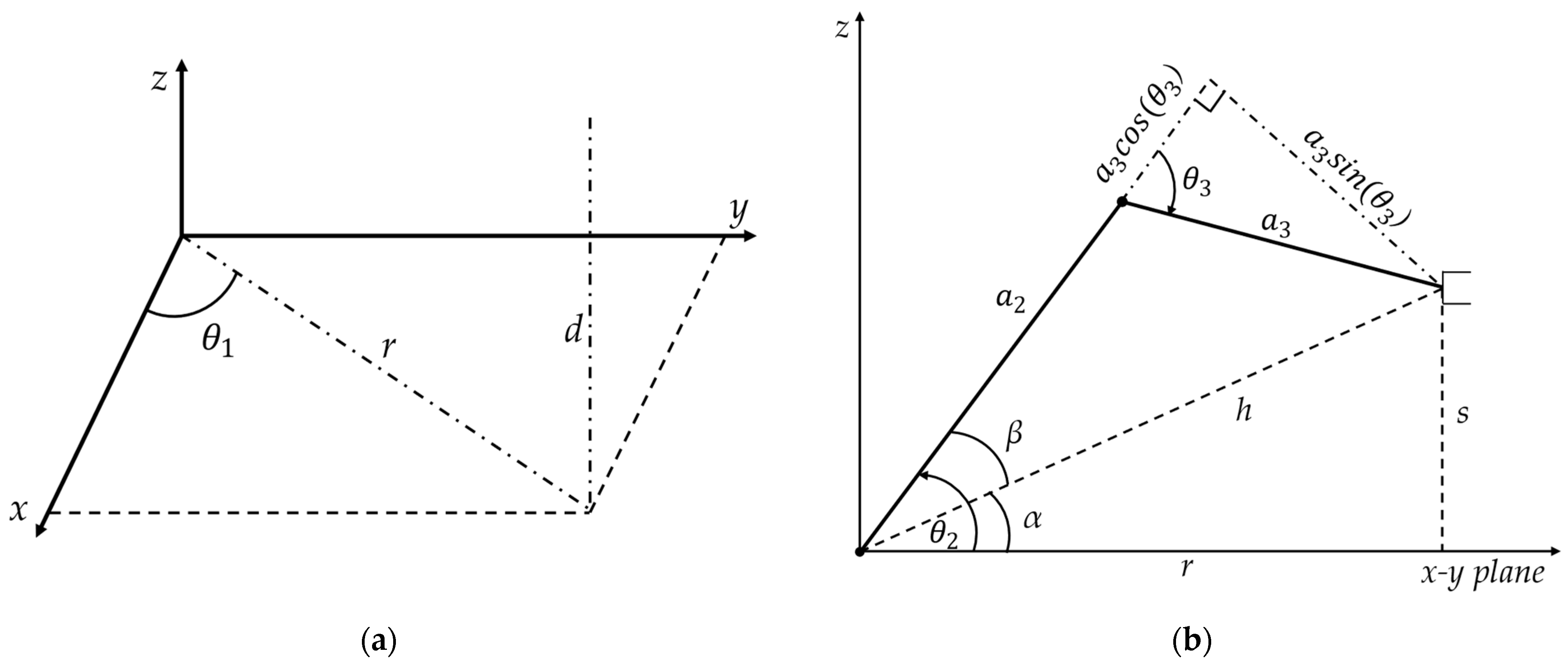
Inverse kinematics involves computing the joint angles given the position and orientation of the end effector. Inverse kinematics were the most suitable control method, since for most pick and place applications, the desired end effector position is the known variable, while joint angles are to be determined. In the implementation of the research, inverse kinematics involved determining the x-y coordinates of a chess piece located on a chess square, translating those positions into joint angles, and then sending those angles to the manipulator servos to move the robot arm to that desired position. In determining the inverse kinematics, a geometric approach was used to decompose the spatial geometry into several plane-geometry problems including the sine rule and the cosine rule, as shown in Figure 3.
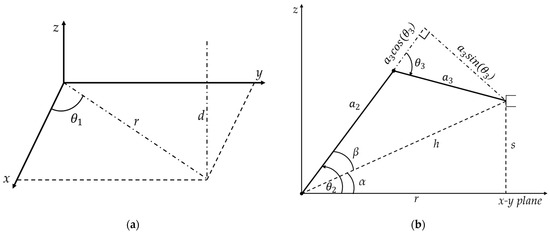
Figure 3.
Inverse kinematics based joint angle determination: (a) determining angle θ1; (b) determining angles θ2 and θ3.
The angle θ1 was determined by considering the base servo rotation. The triangle x, y, r formed at the base as shown in Figure 3a allows θ1 to be calculated, using the arctangent as:
The hypotenuse r, connecting x and y was obtained using the Pythagoras theorem as:
The angle θ2 formed between the shoulder and the arm was obtained by considering the plane formed by the second and third link, as shown in Figure 3b. Angle θ2 is responsible for the horizontal movement of the end effector. In this plane, s is the difference between z (the distance of the end effector from the base) and d (the offset of the shoulder from the base). Angle θ2 can thus be calculated as the sum of angles α and β, and α can be found using the arctangent by considering the right triangle formed by s, h, and r.
The angle θ3, made by the forearm, was also obtained by considering the plane formed by the second and third link, as shown in Figure 3b. Angle θ3 is responsible for the vertical movement of the end effector.
Any position within the reachable workspace of the manipulator can ideally be attained by calculating the joint angles θ1, θ2, and θ3. Angle θ1 determines the length of the arc made by the shoulder, angle θ2 determines how much the end effector moves in the forward and backward direction, and angle θ3 determines the height of the end effector from the base. Once the servo angles θ1, θ2, and θ3 were determined from the inverse kinematics, they were later fed into the forward kinematics equation as part of feedback mechanism, to verify if the manipulator had moved to the desired coordinates.
From inverse kinematics, the initial and final motor angles responsible for orienting our manipulator as desired were obtained. However, for the purposes of control, there arose the need to generate a continuous time-varying pose that moves smoothly in translation and rotation over the duration of motion execution. Smoothness in this context alludes to the fact that the trajectory’s first few derivatives are continuous. Therefore, we define a trajectory over the execution period for the manipulator, spanning the range between the initial and final angles.
To generate a trajectory, a quintic (fifth order) polynomial commonly used in motion planning problems was used to give solutions satisfying the temporal constraints on position, velocity, and acceleration [16].
The quintic polynomial used is given as:
where: 0 ≤ t ≤ T.
These are the initial and final positions, (S(t = 0)) and (S(t = T)), respectively, of the motor angles being defined as the boundary conditions. The equations for the angular velocity and angular acceleration in determining the trajectory generation are as in (13).
The boundary conditions for the first derivative, , and second derivative, , were set to the angular velocity value which were constant and zero, respectively, in obtaining the coefficients of A, B, C, and D. Evaluation was then conducted at t = 0 and t = T. This evaluation yielded the six trajectory governing equations written in matrix form as:
The resultant matrix was a square matrix and the coefficients were obtained by making the coefficient vectors (A, B, C, D, E, F) the subject of the formula. These foundational principles of the trajectory generation algorithm discussed above were realized by utilizing the MATLAB robotics toolbox by Peter Corke. The trajectory was used in obtaining a set of intermediate angles between the initial and final angle positions for three of the servo motors, excluding the gripper servo motor. This was used as the path for the robot motion where, after completion of execution, feedback depicting the actual manipulator movements during the execution cycle was sent back from the Arduino microcontroller to MATLAB.
3.2. Image Processing
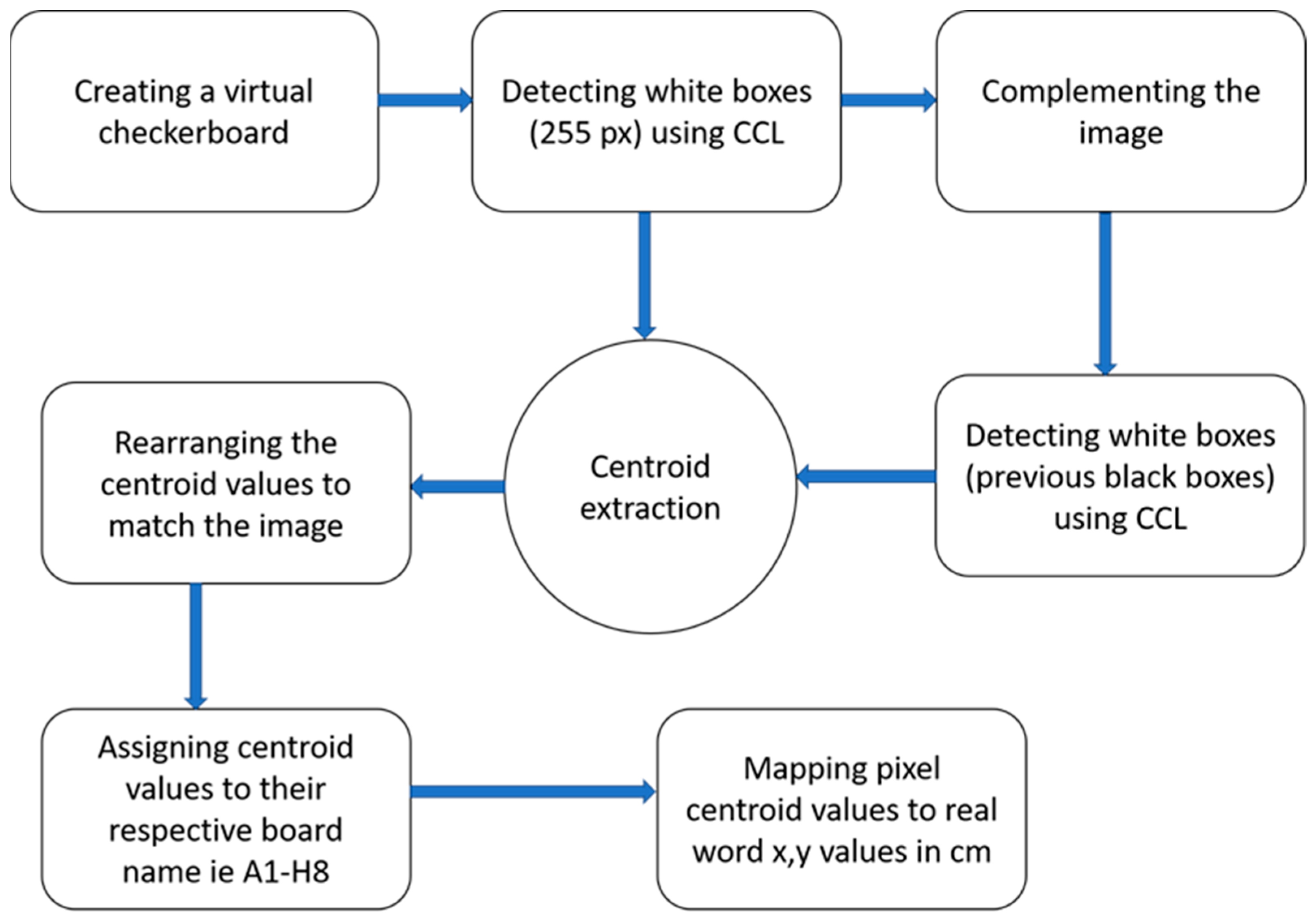
Image processing was implemented to make the robot adaptable to various kinds of chess boards by mapping out the x-y coordinates of the board. The approach used in this research only required an image of the checkerboard and the real dimensions (length and width) of the chessboard. A virtual board created in MATLAB sufficed in mapping out the real x-y coordinates of the board, thus eliminating the need for a camera in real-time as the focus was not on tracking the game state. At a high-level overview, the algorithm was tasked with detecting the white squares and then determining their centroid coordinates, complementing the image to detect the black squares, and then determining their centroid coordinates, rearranging the coordinate values to match the checkerboard image, mapping the pixel coordinates to the board coordinates, and then assigning a name to each individual square. The key features of this algorithm are connected component labeling, centroid extraction, and pixel translation to x-y cm values.
Connected component labeling, CCL, is an algorithmic application of graph theory, where subsets of connected components are uniquely labeled based on a given heuristic. CCL is used in computer vision to detect connected regions in binary digital images with black equal to pixel zero and white equal to 255. A 640 × 640 pixel checkerboard served as the start of the image processing task. The checkerboard consisted of an 8 × 8 square binary image with each side of the square having 80 pixels, and with clear and distinct color segmentation making it easier to detect the individual squares in subsequent operations. CCL uses a 4-connected component for binary images to detect connected pixels [29]. Two pixels were considered as connected if their edges touch, and are part of the same object if they are connected along both the vertical and horizontal directions. In this research problem, CCL was used to identify the individual checkerboard squares by using a flood-fill algorithm to label all the pixels in the connected component containing an unlabeled pixel. This was first conducted for the white squares and then the black squares by complementing the initially detected white squares. After this process, the 64 successfully detected and extracted squares were notated by a unique coordinate pair consisting of a letter and a number based on international chess notations. The horizontal squares (files) were between the letters ‘A’ and ‘H’ and the vertical squares (ranks) from ‘1’ to ‘8’. All the squares on the chess board could then be identified, and actuation carried out based on the voice command. The overview of the image processing process is presented in Figure 4.
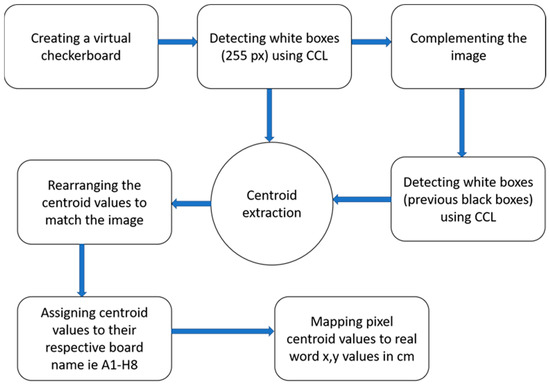
Figure 4.
Block diagram for the image processing task.
3.3. Speech Processing
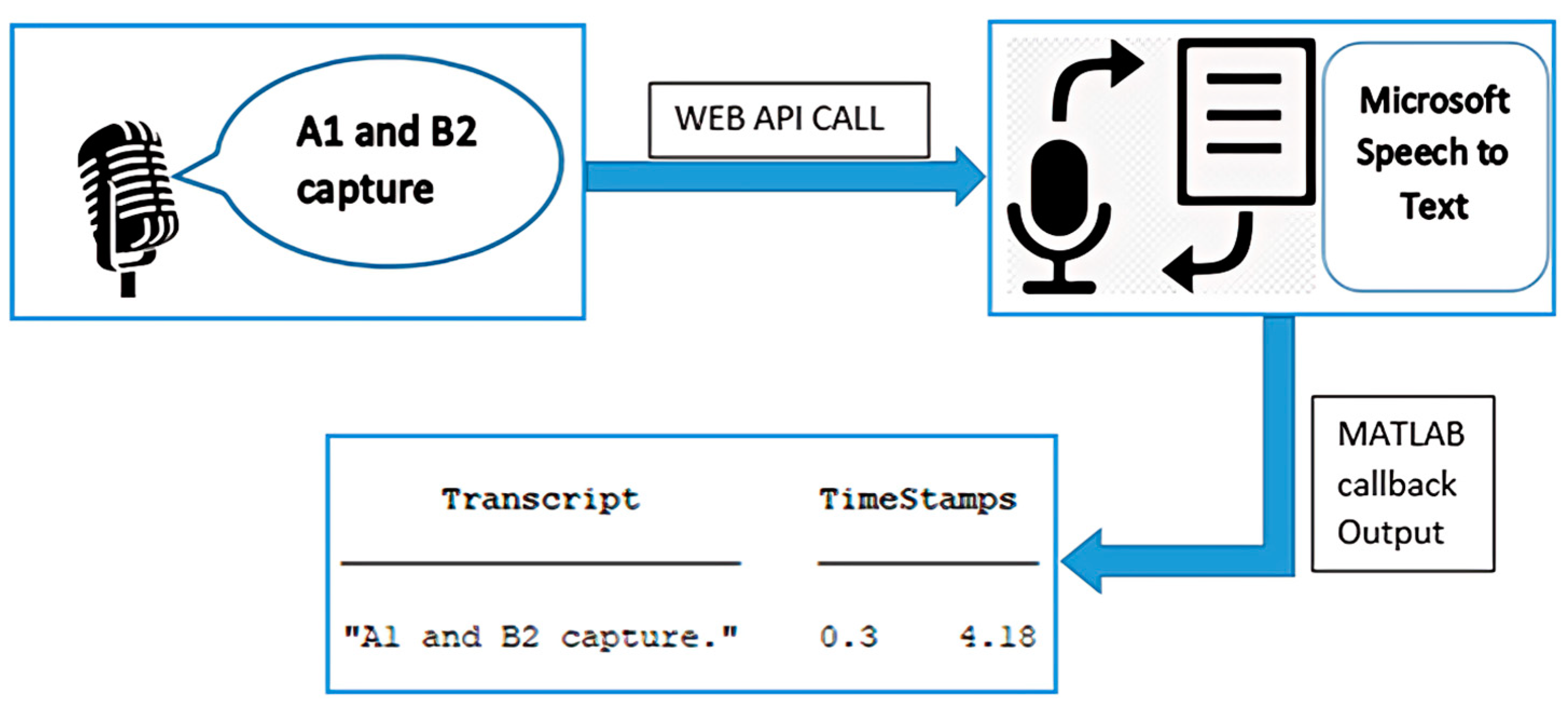
The final objective for the speech processing system was to achieve the transfer of a voice input by the human player into specific coordinates on the board, which would then be mapped onto the manipulator workspace, as in image processing. The MeArm robot would then execute the movement of the piece following the calculation of the joint angles from the inverse kinematics. The computer microphone was used in capturing the voice command by the user, utilizing the MATLAB-based “audio recorder” object at a sampling frequency of 16 kHz. The input command was passed onto the speech to text translation. The translation of the captured voice input into text was conducted using a speech to text package on MATLAB, speech2text. This package provides the ability to use third party APIs to perform the speech to text transcription. This package is free and compatible with MATLAB once the package contents are added to the MATLAB path during setup.
For this application, the Microsoft Azure Speech Services API was used while utilizing the credits given per month for a student’s account, for a high accuracy model with a low word error rate. The student account was free for 5 h per month of speech to text transcription, which was adequate given the brevity of the input commands with a maximum command time of 5 s. For the transcription, a speech to text resource group was created in the Microsoft Speech to Text cognitive service [30]. The API was initialized and verified by using subscription keys. On MATLAB R2019b, a speech client was created, and the speech object called, resulting in a http request that, on being successful, had an output of the translated transcription. The process is represented in Figure 5.
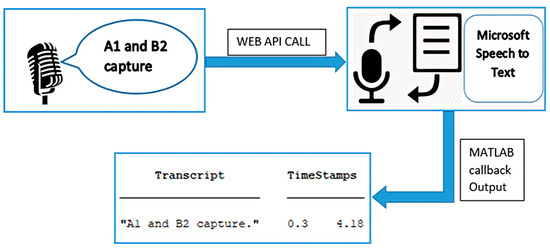
Figure 5.
Speech to text transcription based on MATLAB API call.
Pattern recognition was used in constituting the voice input command where either a three-word or four-word execution sentence based on the 8 × 8 chess board and on whether a ‘normal’ or ‘opponent capture’ chess move was desired. In characterizing the desired pick and place operation, a ‘normal’ move contained the initial chess piece location and followed by the desired location of the piece as in “B3 and C4”. The order for the ‘opponent piece capture’ command move was the same as the ‘normal’ move, with the word capture appended after the coordinate containing the piece to capture, as in: “B3 and C4 capture”, where C4 in this case is the coordinate for the piece to capture. The command format for the letters could either be said using the letters ‘A to H’ or using the corresponding NATO phonetic alphabets. The transcribed command in the format above was finally mapped onto the virtual chess board pixel locations by using the centroid determined in the image processing section.
3.4. Robot Manipulator Execution
From the image processing and speech processing, the current and final piece locations were obtained on the two-dimensional virtual board via the pixel locations obtained from the images of the board, before conversion into the equivalent workspace coordinates corresponding to the locations of the chess pieces on the board. These locations mark the end effector position on the board, with the inverse kinematics described above being used to determine the joint angles necessary to actuate the robot. On completion of the joint motion, the gripper opens to pick up the chess piece in the current piece location, closes upon picking it, and moves it to the desired piece location. In the case of ‘opponent piece capture’, the execution is conducted in four steps. The first step is capturing the opponent’s piece, which is conducted by having the first end effector position being the desired piece location. The opponent’s piece is picked followed by placing it outside the board on one side as the second step. The third and fourth steps, same as the ‘normal’ piece motion, involve picking the ‘own’ piece from the current location to the desired location. The manipulator then retreats to its home position awaiting further commands. The execution of these steps is iterated each time the player voices a command to the manipulator in the required order, hence leading to a pick and place motion of the manipulator, akin to that of a human player’s hand. Figure 6 shows the physical representation of the robot using a pre-defined ‘home’ position, representing the origin of the manipulator execution, and with the gripper open at one of the identified square boxes.

Figure 6.
Robot orientation with respect to the chess board: (a) at the home position; (b) at the chess board square box D3.
4. Results and Discussion
As evidenced by the literature review, research in robotics applied to board games, particularly those requiring perception and manipulation, serves as a valuable testbed for advancing real-world robot adoption and enhancing human–robot interaction.
The ability to effectively calculate forward kinematics, inverse kinematics, trace a trajectory, and ensure effective human–robot interaction is key to the success of incorporating robots in board games. To this end, this research presents a low-cost 3-DoF robot arm based on a pick and place operation as applied to the development of a chess-playing robot prototype.
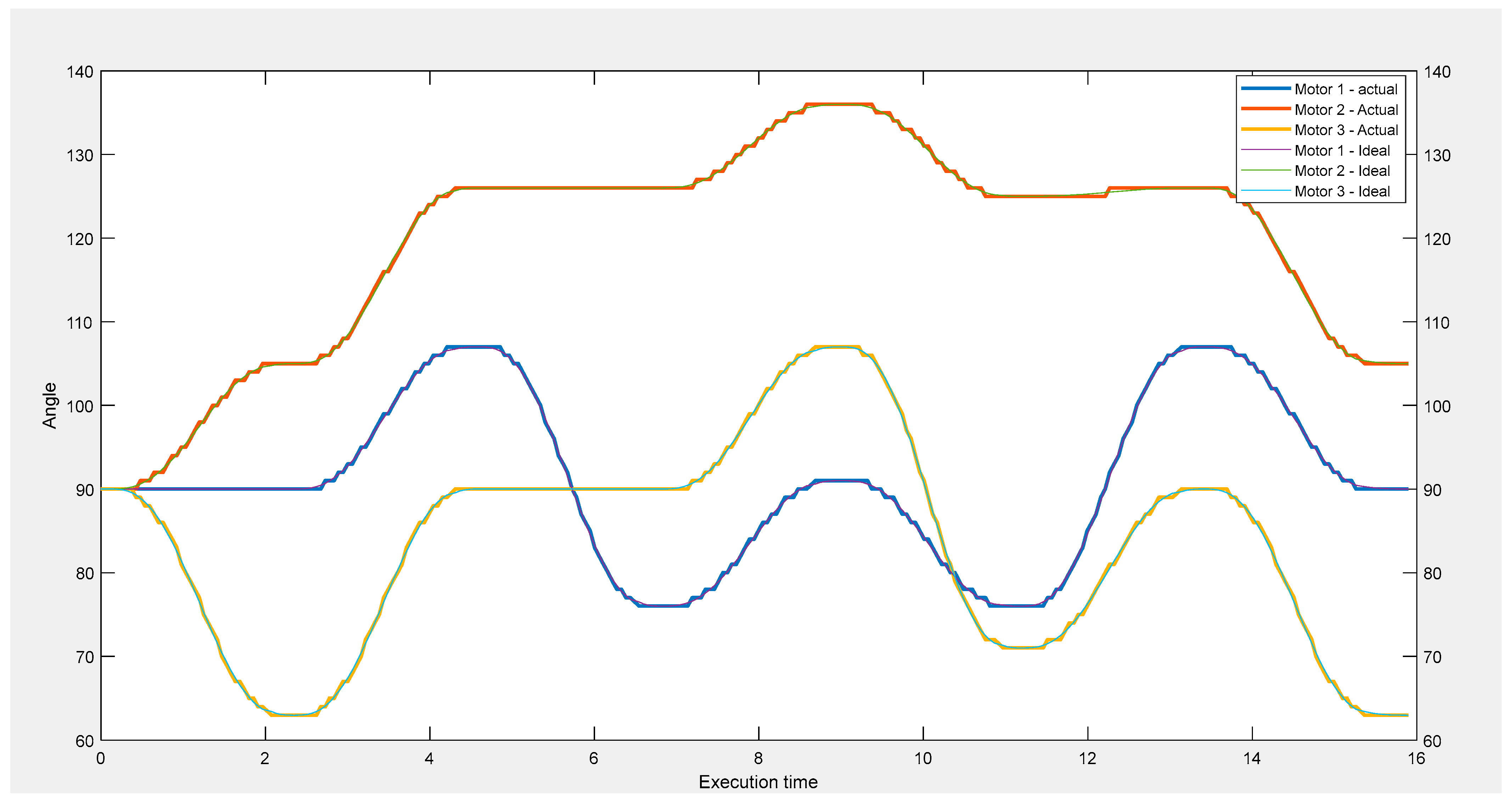
The inclusion of trajectory generation considering the quintic 5th order polynomial ensured a smooth and controlled motion of the robot. This is achieved by interpolating between the initial and final coordinate points. Figure 7 shows the joint angle variation obtained for a given set of coordinates, with the ‘ideal’ representing the trajectory generated path based on the quintic polynomial, while the ‘actual’ shows the output based on the real-time motion of the robot.
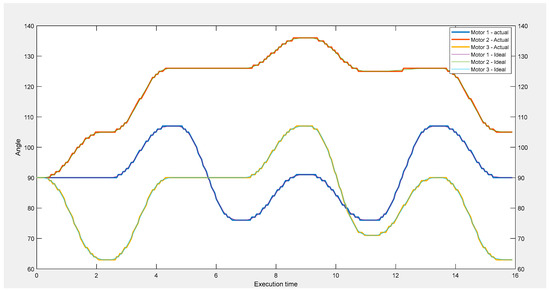
Figure 7.
Comparison between actual and ideal trajectories based on a command sequence.
The sequence for the board positions considered in the trajectory generated in Figure 7 was:
Home position − C2 – F2 – E3 – F1 – C2 – Home position
In the sequence, the aim is to realize a set of joint angles that can be traced by the robot arm. The quintic polynomial is used to interpolate for any two points in the sequence, such as, in the first actuation step, the “Home position” being the initial position and “C2” the final position. In the second actuation step, “C2” becomes the initial position and “F2” the final position. The process is repeated until the sequence is completed.
The initial joint angles are obtained by using inverse kinematics to convert the positional coordinates on the board into joint angles. The execution path starts from a “Reset” with the three servo motors having joint angles initialized to 90 degrees. The “Home position” denotes a defined set of workspace coordinates representing the start and end points for a complete sequence. Based on the execution sequence, the comparison showing the ideal and actual variation of the angles presents the resemblance and correlation between the ideal path based on ideal values against that of the actual execution by the robot manipulator for the given trajectory path. The x-axis represents the actual time it takes for the manipulator to complete the execution of a given x-y trajectory. The actual manipulator trajectory represented the real-time position of each of the three motors, with the differences observed between the smooth ideal and erratic actual curves being due to servo motor limitations. This was because the SG90 servo motors are limited to a rotational accuracy of 1 degree, resulting in the differences shown in Figure 7.
Analysis based on the sequence above can be verified in Figure 7 by considering the estimated time stamps in seconds based on the execution time, as follows:
The trajectory begins from the “Reset” position and proceeds to the “Home position” at 2 s. This is followed by position “C2” at 4.5 s, “F2” at 6.5 s, “E3” at 8.5 s, “F1” at 10.5 s, “C2” at around 12.5 s, and “Home position” as the last execution, ending at around 16 s.
The significance of trajectory generation is that it results in a smooth and consequently more controlled robot motion between any two points, especially for longer displacements. This is because it eliminates the jerky motion experienced when the distance between any two joint angles is large, where the motor can overshoot due to inertial forces. Trajectory generation is therefore crucial for achieving smooth and controlled robot motion, especially for pick and place operations where precision is paramount.
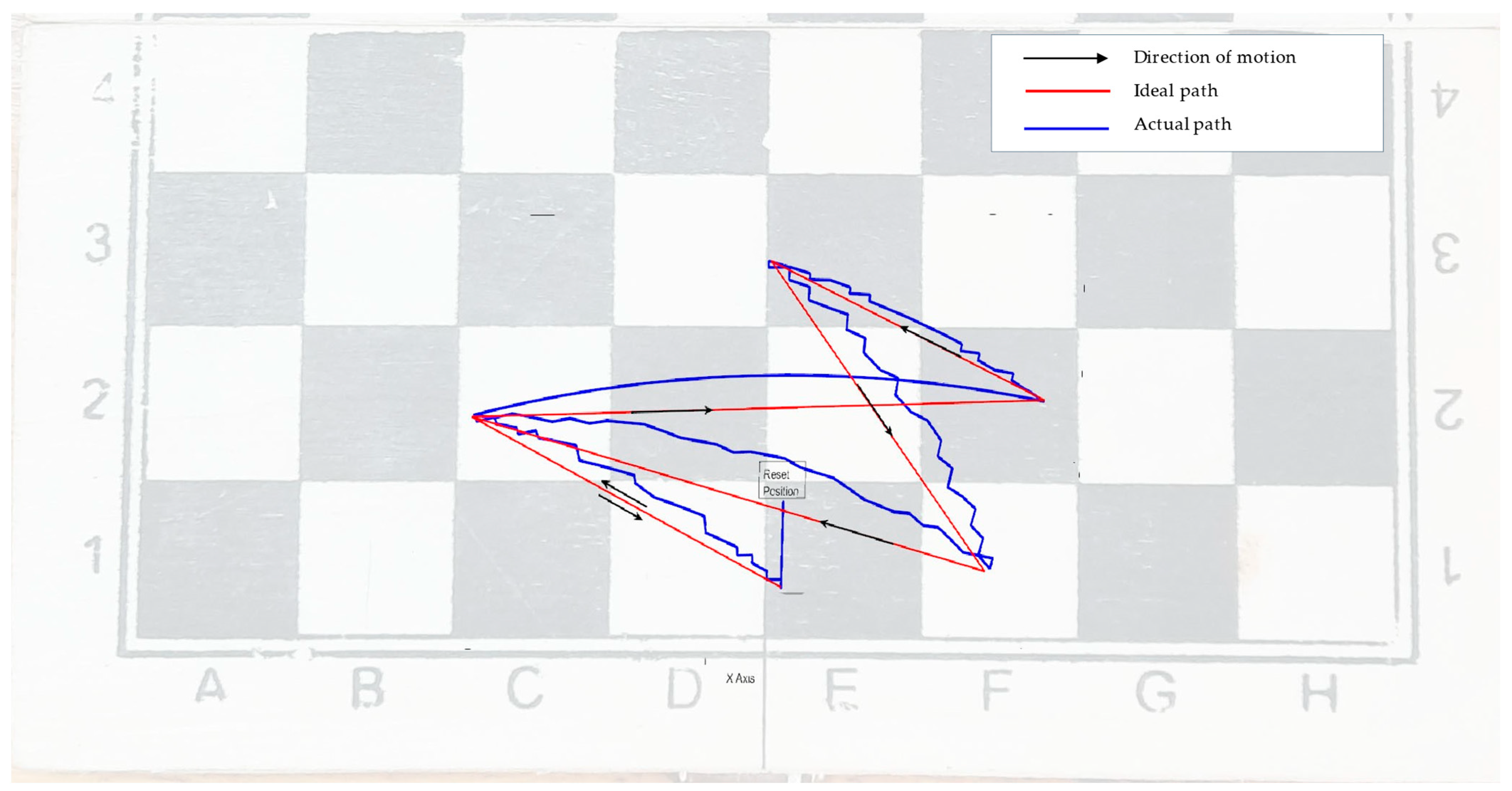
From the trajectory data presented in Figure 7, it was possible to compare the actual trajectory traced by the robot against the ideal trajectory generated by the quintic polynomial. Forward kinematics were used in transforming the angles based on the trajectory into end effector positions for comparison between the ideal and actual paths. The path traced on the robot workspace and corresponding to the base frame’s Cartesian coordinates x and y was obtained, as shown in Figure 8.
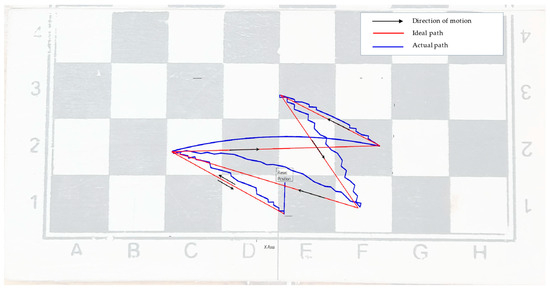
Figure 8.
Real-time robot execution in the workspace based on a generated trajectory.
Figure 8 shows the “Ideal path” (red) which is determined as being the shortest path between any two points, which, in the case of a two-dimensional workspace, is a line. The arrows on the “Ideal path” curve denote the direction of movement of the robot motion where, notably, the trajectory generation results in a continuous path from the start to the end without any undesired discontinuity. The “Actual execution path” (blue) curve shows the exact path followed by the end effector of the robot in real-time. This execution path was determined by obtaining feedback from the Arduino to MATLAB and based on the serial communication protocol. The servo reset position is a characteristic of the SG90 micro servos, where whenever the Arduino restarts following the port opening on MATLAB, the servo motors are initialized to 90 degrees.
While the correctness of the algorithm used in the system is demonstrated, in developing a real-life chess-playing system, it would be necessary to consider using higher resolution motors to ensure a higher precision.
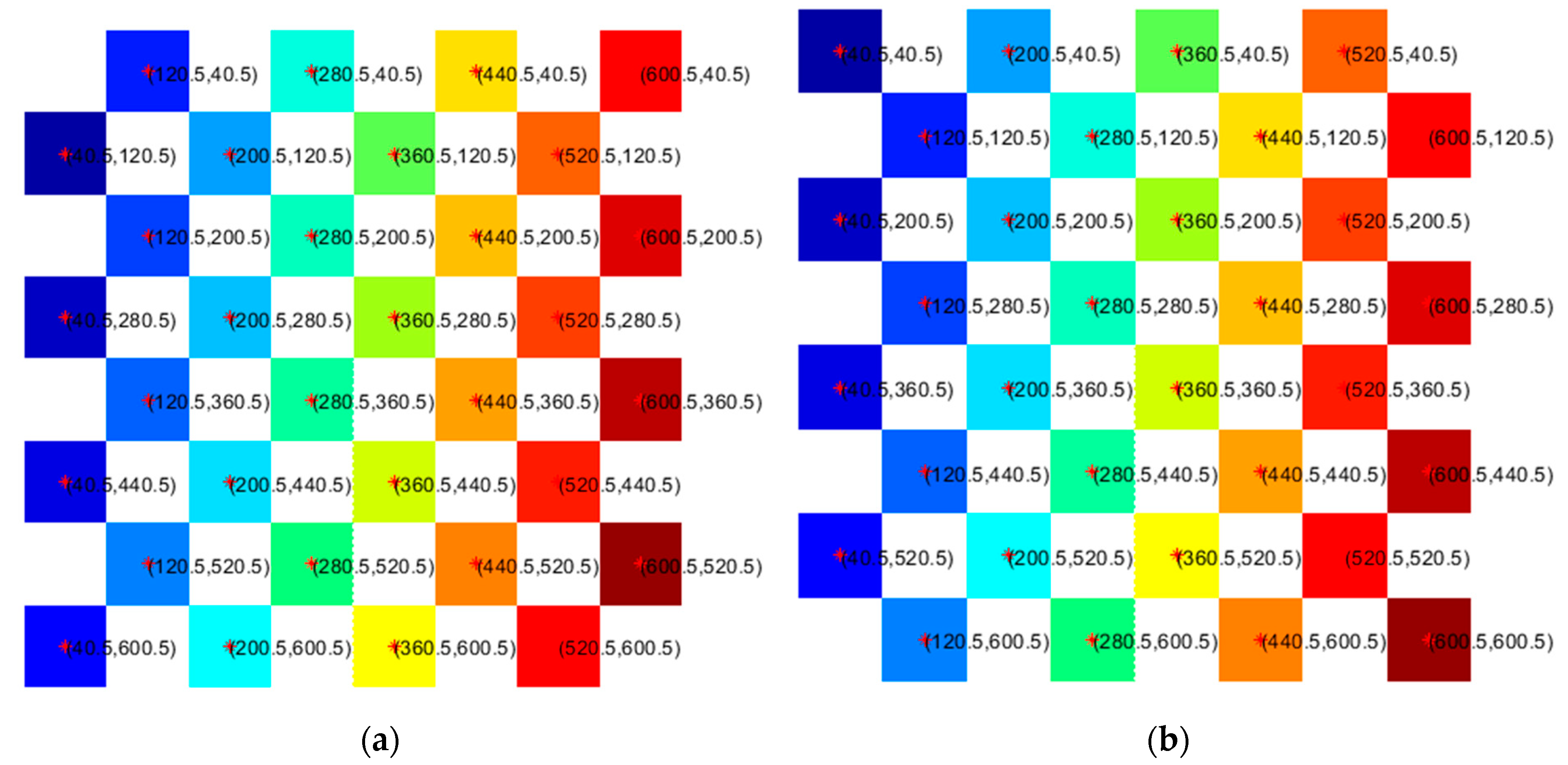
In image processing, after each box was identified using connected component labeling, the extraction of the centroid pixel coordinates of each detected box was conducted by averaging the x-y coordinates of their pixels. All the detected boxes were then assigned a different color for distinction. This is as shown in Figure 9.
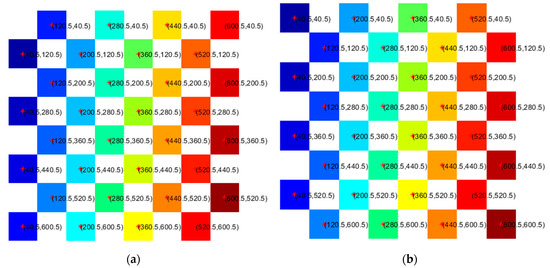
Figure 9.
Detected centroids on grid with distinct colors and pixel locations: (a) for white squares; (b) for black squares.
With all the boxes detected and their centroid pixel values known, the boxes could then be named according to the algebraic notation. The algebraic notation is the standard method for recording and describing the moves in a game of chess. A unique coordinate pair—a letter and a number from “A1” to “H8” identifies each square of the chessboard. Based on this convention, the boxes were named sequentially as the centroid coordinate values increased from [40.5, 40.5] (A1) to [600.5, 600.5] (H8), as shown in Figure 9. The centroid pixels were then mapped and translated to their corresponding real-world x-y coordinates. The image processing algorithm was therefore successful in achieving the specific objective of mapping out the chessboard in terms of the real-world centroid coordinates of each box. This served as a stepping stone for the subsequent modules of our research, such as speech input. For instance, when a speech command “H3” is given, the box name is already associated with specific coordinates and an inverse kinematics algorithm can then be applied to generate servo angles that will move the arm to the desired box.
The correctness of the image processing step was verified by observing the centroid locations based on the virtual board. This is due to the uniformity of the square boxes in the board games, as presented in [27]. The determined centroids with the corresponding box name could then be assigned to any board based on knowledge of the board dimensions, which is the height and weight. Since the human player is also responsible for determining the execution move, it is not necessary to monitor the game state in real-time, hence minimizing the computational power.
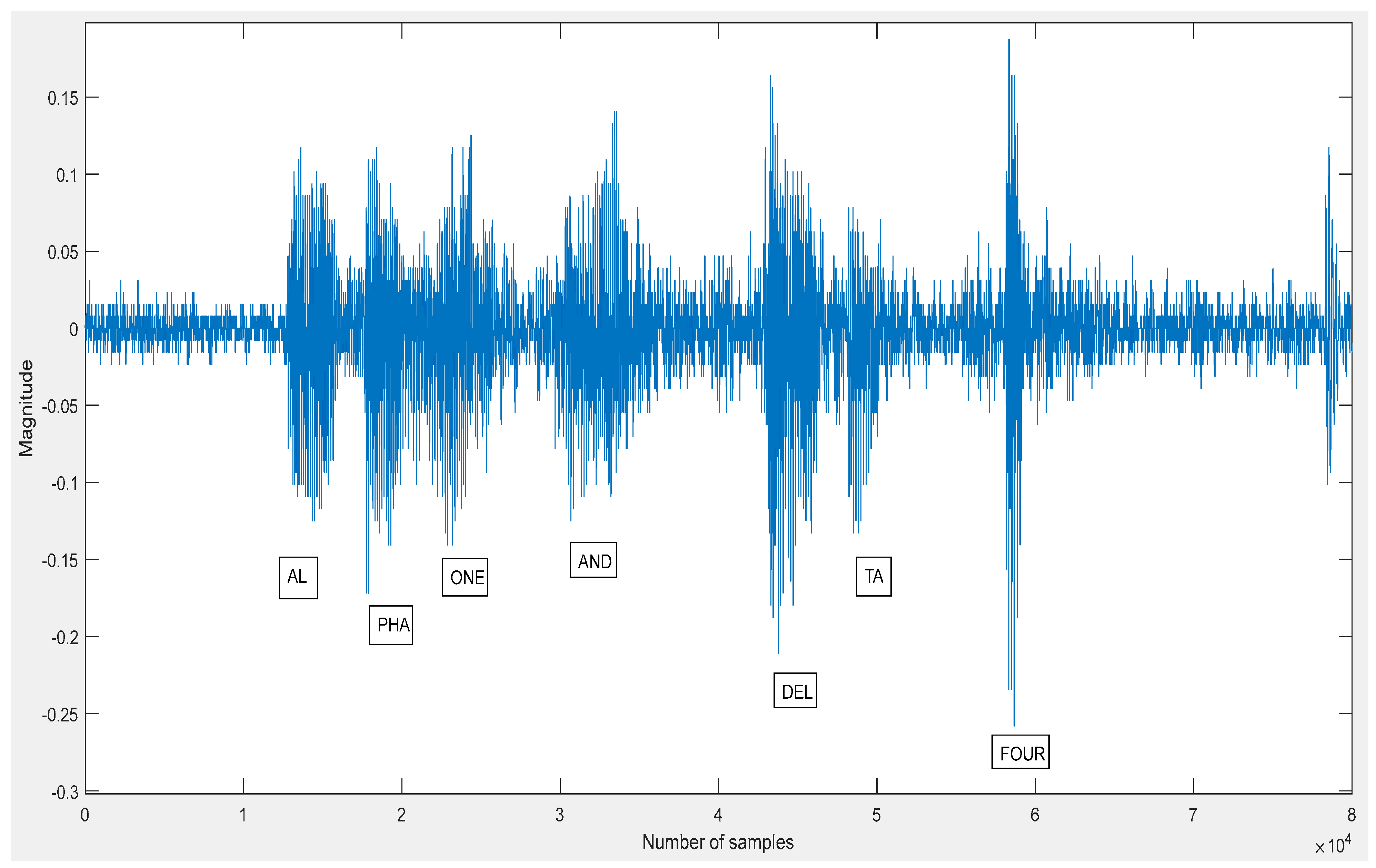
The speech magnitude spectrum obtained before transcription for a sample audio signal “Alpha 1 and Delta 4,” alternatively represented as “A1 and D4”, is shown in Figure 10. While Microsoft Azure Speech Services boast a high word error rate of around 5%, from the magnitude spectrum it is evident that it was necessary to properly articulate the command distinctively, which is why having the option to use the NATO phonetic alphabet was beneficial.
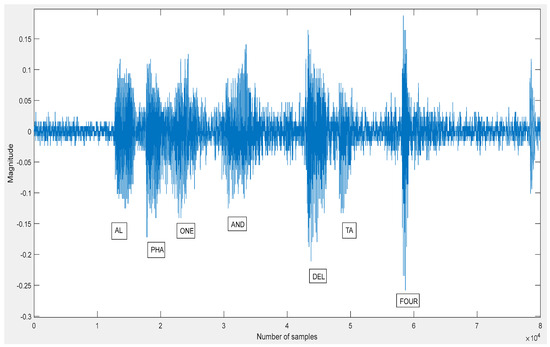
Figure 10.
Magnitude spectrum for the input voice command “Alpha 1 and Delta 4”.
The post-processing steps after the speech to text transcription in Figure 5, had two major outcomes. The first outcome was to obtain the coordinates representing the start and final destinations, and this was derived in text from the transcribed command statement.
The second outcome was to determine the execution sequence of the robot manipulator based on the type of move, as applied in the chess application of pick and place. The type of move could be either a normal move executed in two steps by moving the piece at start position to the final coordinate position, or it could be a capture move as described in the transcription above. The execution sequence of the capture move was conducted in four steps, beginning with the picking of the opponent’s piece, placing it outside the board, and then executing the normal two-step move sequence. As an example, the capture moves could be broken down as in Table 4. The “OUT” coordinate was a value that is outside the board workspace but within the robot workspace. The coordinates obtained from the speech processing are then handed over to the image processing for mapping onto the board space.

Table 4.
Output coordinate sequence from transcription.
The verification for correctness in terms of the speech processing was a two-fold process based on visual confirmation by the human player on the transcribed text, as well as the program-based command check. The confirmation by the human player issuing the command allowed for cancellation of a command based on issuing an incorrect command or in case of a mispronunciation. The program-based error check was based on two options: The first option was on whether the desired move was a ‘normal’ or ‘capture’ move. The ‘normal’ move had three keywords comprising the two coordinates connected by the ‘and’ keyword. The capture move had the same order, with one additional keyword ‘capture’ appended. The verification was conducted by confirming the command size and presence of keywords, in addition to being a coordinate existing in the workspace.
A word error rate of 8.64% was obtained in the experimental set up based on a sizeable dataset. While this was a little higher than the proposed benchmark of 5%, it was still within the 5–10% range considered as good quality [31] considering the three evaluation categories: insertions, deletion, and substitution. Table 5 below represents an example of the transcriptions containing the three categories considered in determining the WER:

Table 5.
Transcriptions containing the three categories for word error rate.
The independent development and verification of the image processing and speech recognition modules, as described, in addition to the forward kinematics-based feedback for verifying the inverse kinematics used in the pick and place, meant that a high certainty in the performance of the pick and place was ensured and experimentally observed.
The developed system serves as a low-cost improvement to the approach presented in [9], which used a game engine to autonomously play checkers. While G. Fabris et al. in [9] considered developing a robot capable of autonomously playing checkers by integrating image processing techniques with robotics, this research proposes a method to realize a voice command control of robotics aimed at assistive works, in addition to implementing image processing. Considering this proposal, the integration of image processing and speech recognition enhanced the usability of robots for collaborative activities while furthering inclusivity in applications of robotics to board games. This current proposal presents a unique perspective for the use of an assistive robot, allowing for the inclusion of people with motor disabilities in board games, specifically chess. This leads to reduced complexity in the implementation, realizing chess playing without a game engine. This is because the human player, aware of the rules of the game, issues the command move. This research also considers a low-cost MeArm robot, costing less than $500, which further leads to accessibility and portability. While industrial robots such as the Franka Emika Robot and NAO robot are highly accurate and present state-of-the-art precision and control, affordability is a big concern, especially in assistive robots aimed at marginalized groups.
5. Conclusions
This research successfully implemented a 3-DoF robot manipulator for controlled pick and place operations using speech and image recognition. A chess-playing robotic task was selected as the testbed of our research, whereby we explored the possibility of using image and speech input to play chess. By providing voice-based control and achieving a high degree of accuracy in chess piece manipulation based on image processing, this system demonstrates the potential of affordable, assistive robotics, especially for physically impaired individuals. Although the system’s workspace is currently limited, future improvements in manipulator precision and workspace range can extend its functionality. This research paves the way for further exploration of inclusive robotic systems, particularly in gaming and education, fostering new opportunities for human–robot collaboration.
The use of image processing led to the realization of an accurate mapping of the centroid locations from a virtual board to the robot workspace, ensuring that the system could be extended to various board sizes with minimal modifications. The incorporation of speech recognition, on the other hand, resulted in a good word error rate of 8.64%. The possibility to use the NATO phonetic alphabet led to an alternative to the determination of the desired moves, based on commands that could be misidentified such as “G” and “D” based on individual accents. The speech recognition also led to an assistive robot that works independently of a game engine to realize robot-assisted chess playing. The MeArm being low-cost and light leads to the advantages of affordability, portability, and safety by not posing any danger of harm to human beings.
Future works based on this research may include the realization of a full execution of the chess-playing system by further developing the robot to achieve a higher accuracy. Higher resolution motors would be included in the design, leading to improved performance. Design for a bigger but lightweight 3D-printed robot that could fit into bigger board sizes is also one of the targets in building a prototype that will be implemented outside the research environment. Game state tracking using a camera and computer vision algorithms would also be beneficial in helping players review their performance after a game. Research towards more applications aimed at human–robot collaboration and enhancing automation also constitutes future works.
Some of the limitations encountered while implementing this project include the limited reachable workspace of the manipulator, where chess play was limited to only the first four rows of the chessboard. The accuracy of the SG90 micro servo was limited to 1 degree, hindering the manipulator from tracing the ideal and smooth trajectory completely.
Author Contributions
Conceptualization, J.M., W.N. and M.S.; methodology, S.K., E.W. and I.M.; software, S.K., E.W. and I.M.; validation, S.K., E.W. and I.M.; formal analysis, S.K., E.W., I.M. and W.N.; writing—original draft preparation, S.K., E.W. and I.M.; writing—review and editing, S.K., E.W., I.M., and J.M.; supervision, W.N. and M.S.; resources and funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. It was conducted at the Dedan Kimathi University of Technology, Kenya, in the department of Electrical and Electronic Engineering.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Su, H.; Qi, W.; Chen, J.; Yang, C.; Sandoval, J.; Laribi, M.A. Recent advancements in multimodal human–robot interaction. Front. Neurorobotics 2023, 17, 1084000. [Google Scholar] [CrossRef] [PubMed]
- Shahria, M.T.; Sunny, M.S.H.; Zarif, M.I.I.; Ghommam, J.; Ahamed, S.I.; Rahman, M.H. A Comprehensive Review of Vision-Based Robotic Applications: Current State, Components, Approaches, Barriers, and Potential Solutions. Robotics 2022, 11, 139. [Google Scholar] [CrossRef]
- Rückert, P.; Wallmeier, H.; Tracht, K. Biofeedback for human-robot interaction in the context of collaborative assembly. Procedia CIRP 2023, 118, 952–957. [Google Scholar] [CrossRef]
- Fahn, C.-S.; Chen, S.-C.; Wu, P.-Y.; Chu, T.-L.; Li, C.-H.; Hsu, D.-Q.; Wang, H.-H.; Tsai, H.-M. Image and Speech Recognition Technology in the Development of an Elderly Care Robot: Practical Issues Review and Improvement Strategies. Healthcare 2022, 10, 2252. [Google Scholar] [CrossRef] [PubMed]
- Obo, T.; Kasuya, C.; Sun, S.; Kubota, N. Uman-robot interaction based on cognitive bias to increase motivation for daily exercise. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics, SMC, Banff, AB, Canada, 5–8 October 2017. [Google Scholar] [CrossRef]
- Padmanabha, A.; Yuan, J.; Gupta, J.; Karachiwalla, Z.; Majidi, C.; Admoni, H.; Erickson, Z. VoicePilot: Harnessing LLMs as Speech Interfaces for Physically Assistive Robots. arXiv 2024, arXiv:abs/2404.04066v2. [Google Scholar] [CrossRef]
- Matuszek, C.; Mayton, B.; Aimi, R.; Deisenroth, M.P.; Bo, L.; Chu, R.; Kung, M.; LeGrand, L.; Smith, J.R.; Fox, D. Gambit: An autonomous chess-playing robotic system. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar] [CrossRef]
- Li, S.; Zheng, P.; Liu, S.; Wang, Z.; Wang, X.V.; Zheng, L.; Wang, L. Proactive human–robot collaboration: Mutual-cognitive, predictable, and self-organising perspectives. Robot. Comput. Manuf. 2023, 81, 102510. [Google Scholar] [CrossRef]
- Fabris, G.; Scalera, L.; Gasparetto, A. Playing Checkers with an Intelligent and Collaborative Robotic System. Robotics 2024, 13, 4. [Google Scholar] [CrossRef]
- Pereira, A.; Martinho, C.; Leite, I.; Paiva, A. ICat, the chess player: The influence of embodiment in the enjoyment of a game. In Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS, Estoril, Portugal, 12–16 May 2008. [Google Scholar]
- Marge, M.; Espy-Wilson, C.; Ward, N.G.; Alwan, A.; Artzi, Y.; Bansal, M.; Blankenship, G.; Chai, J.; Daumé, H.; Dey, D.; et al. Spoken language interaction with robots: Recommendations for future research. Speech Lang. 2022, 71, 101255. [Google Scholar] [CrossRef]
- Patel, D.R.; Neelakantan, M.; Pandher, K.; Merrick, J. Cerebral palsy in children: A clinical overview. Transl. Pediatr. 2020, 9, S125–S135. [Google Scholar] [CrossRef] [PubMed]
- Amankwah, N.; Oskoui, M.; Garner, R.; Bancej, C.; Manuel, D.G.; Wall, R.; Finès, P.; Bernier, J.; Tu, K.; Reimer, K. Cerebral palsy in Canada, 2011–2031: Results of a microsimulation modelling study of epidemiological and cost impacts. Health Promot. Chronic Dis. Prev. Can. 2020, 40, 25–37. [Google Scholar] [CrossRef] [PubMed]
- de Saille, S.; Kipnis, E.; Potter, S.; Cameron, D.; Webb, C.J.R.; Winter, P.; O’neill, P.; Gold, R.; Halliwell, K.; Alboul, L.; et al. Improving Inclusivity in Robotics Design: An Exploration of Methods for Upstream Co-Creation. Front. Robot. AI 2022, 9, 731006. [Google Scholar] [CrossRef] [PubMed]
- Ito, K.; Hatta, Y.; Yamada, T.; Sato, J.; Shiroyama, Y.; Hamajima, T. High Precision Machining Force Control of VCM-driven Deburring Equipment. In Proceedings of the 2022 IEEE 17th International Conference on Advanced Motion Control (AMC), Padova, Italy, 18–20 February 2022. [Google Scholar] [CrossRef]
- Njeri, W.; Sasaki, M.; Matsushita, K. Two degree-of-freedom vibration control of a 3D, 2 link flexible manipulator. Adv. Sci. Technol. Eng. Syst. J. 2018, 3, 412–424. [Google Scholar] [CrossRef][Green Version]
- Ito, H.; Nakamura, S. Rapid prototyping for series of tasks in atypical environment: Robotic system with reliable program-based and flexible learning-based approaches. ROBOMECH J. 2022, 9, 7. [Google Scholar] [CrossRef]
- Kosiba, D.A.; Kasturi, R. Machine vision. In Microelectronics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Susac, F.; Aleksi, I.; Hocenski, Z. Digital chess board based on array of Hall-Effect sensors. In Proceedings of the 2017 40th International Convention on Information and Communication Technology, Electronics and Microelectronics, MIPRO 2017, Opatija, Croatia, 22–26 May 2017. [Google Scholar] [CrossRef]
- Banerjee, N.; Saha, D.; Singh, A.; Sanyal, G. A Simple Autonomous Robotic Manipulator for playing Chess against any opponent in Real Time. In Proceedings of the International Conference on Computer Vision and Robotics, Bhubaneshwar, India, 6 October 2012. [Google Scholar]
- Lukač, D. Playing chess with the assistance of an industrial robot. In Proceedings of the 2018 3rd International Conference on Control and Robotics Engineering, ICCRE 2018, Nagoya, Japan, 20–23 April 2018. [Google Scholar] [CrossRef]
- Ganeshmurthy, M.S.; Suresh, G.R. Path planning algorithm for autonomous mobile robot in dynamic environment. In Proceedings of the 2015 3rd International Conference on Signal Processing, Communication and Networking, ICSCN 2015, Chennai, India, 26–28 March 2015. [Google Scholar] [CrossRef]
- Montiel, O.; Sepúlveda, R.; Orozco-Rosas, U. Optimal Path Planning Generation for Mobile Robots using Parallel Evolutionary Artificial Potential Field. J. Intell. Robot. Syst. Theory Appl. 2015, 79, 237–257. [Google Scholar] [CrossRef]
- Dunn, E.R.; Howe, R.D. Towards smooth bipedal walking. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994. [Google Scholar] [CrossRef]
- Juang, L.H. Humanoid robots play chess using visual control. Multimedia Tools Appl. 2021, 81, 1545–1566. [Google Scholar] [CrossRef]
- Manurung, E.B. Gantry Robot System Checkers Player. ADI J. Recent Innov. 2023, 5, 9–19. [Google Scholar] [CrossRef]
- Wölflein, G.; Arandjelović, O. Determining chess game state from an image. J. Imaging 2021, 7, 94. [Google Scholar] [CrossRef] [PubMed]
- Ómarsdóttir, F.Y.; Ólafsson, R.B.; Foley, J.T. The Axiomatic Design of Chessmate: A Chess-playing Robot. Procedia CIRP 2016, 53, 231–236. [Google Scholar] [CrossRef][Green Version]
- He, L.; Ren, X.; Gao, Q.; Zhao, X.; Yao, B.; Chao, Y. The connected-component labeling problem: A review of state-of-the-art algorithms. Pattern Recognit. 2017, 70, 25–43. [Google Scholar] [CrossRef]
- Xiong, W.; Wu, L.; Alleva, F.; Droppo, J.; Huang, X.; Stolcke, A. The Microsoft 2017 Conversational Speech Recognition System. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar] [CrossRef]
- Urban, E.; Mehrotra, N. Test Accuracy of a Custom Speech Model. Available online: https://learn.microsoft.com/en-us/azure/ai-services/speech-service/how-to-custom-speech-evaluate-data?pivots=speech-studio (accessed on 20 August 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).