A New Zero Waste Design for a Manufacturing Approach for Direct-Drive Wind Turbine Electrical Generator Structural Components

Abstract

An integrated structural optimization strategy was produced in this study for direct-drive electrical generator structures of offshore wind turbines, implementing a design for an additive manufacturing approach, and using generative design techniques. Direct-drive configurations are widely implemented on offshore wind energy systems due to their high efficiency, reliability, and structural simplicity. However, the greatest challenge associated with these types of machines is the structural optimization of the electrical generator due to the demanding operating conditions. An integrated structural optimization strategy was developed to assess a 100-kW permanent magnet direct-drive generator structure. Generated topologies were evaluated by performing finite element analyses and a metal additive manufacturing process simulation. This novel approach assembles a vast amount of structural information to produce a fit-for-purpose, adaptative, optimization strategy, combining data from static structural analyses, modal analyses, and manufacturing analyses to automatically generate an efficient model through a generative iterative process. The results obtained in this study demonstrate the importance of developing an integrated structural optimization strategy at an early phase of a large-scale project. By considering the typical working condition loads and the machine’s dynamic behavior through the structure’s natural frequencies during the optimization process coupled with a design for an additive manufacturing approach, the operational range of the wind turbine was maximized, the overall costs were reduced, and production times were significantly diminished. Integrating the constraints associated with the additive manufacturing process into the design stage produced high-efficiency results with over 23% in weight reduction when compared with conventional structural optimization techniques.

1. Introduction

Energy demand has been drastically increasing on a global scale and to accomplish a sustainable future, the development of renewable energy systems is necessary [1]. To tackle climate change on a large scale, it needs to be acknowledged that our global economic system is mainly based on fossil fuels, more specifically, oil for all the transportation sector, and coal and gas for electricity generation. However, while fossil fuels become scarcer, the method used to obtain these resources turns more extreme and aggressive with our ecosystem. In today’s technology, we can find the right tools and techniques to develop a more sustainable energy landscape [2]. The research of innovative optimization strategies and the implementation of new technologies for renewable energy systems is crucial for sustainable development. Wind energy is considered one of the most efficient and cost-effective renewable energy sources, with offshore wind farm projects increasing in recent years due to their vast energy density and reliability [3,4]. The implementation of direct-drive generator structures for offshore applications is common for producing more efficient systems, preventing the use of a gearbox, reducing the weight of the structure, and decreasing failure rates. In open sea locations, the simplification of the system is an important factor to account for considering the harsh environmental conditions and inaccessibility [5]. The costs of development of offshore wind turbine farms are high and the optimization of these projects at an early stage is of significant interest to developers and manufacturers [6]. New and more innovative optimization approaches for offshore wind turbine projects are in high demand to overcome the challenges involved in the design of the different components integrating these systems [7,8,9,10,11] and the current supply chain issues.

1.1. Direct-Drive Wind Turbine Generators

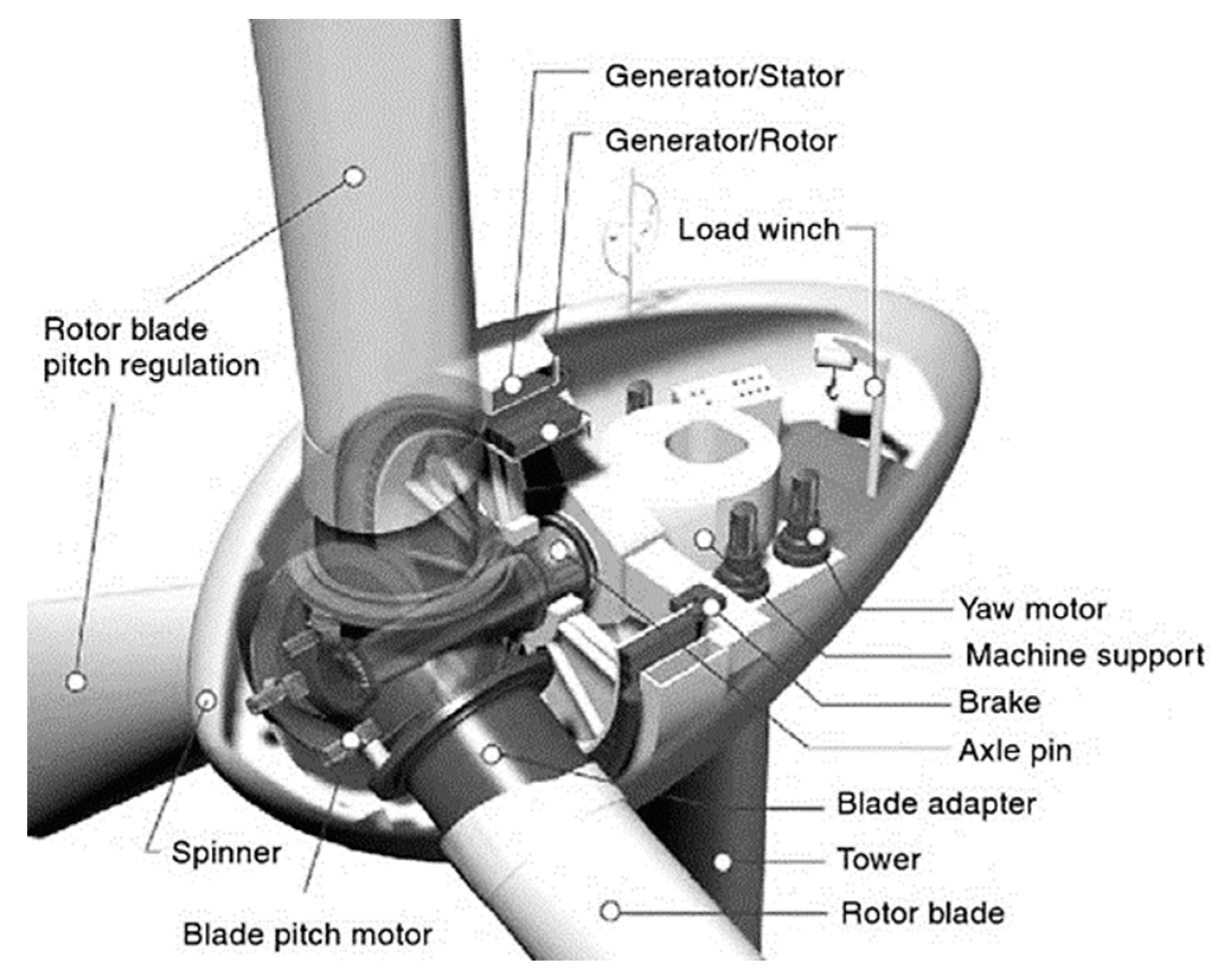
Large direct-drive generators are rotational electrical machines operating under high electromagnetic and gravitational loads. In Figure 1, we can observe a representation of a direct-drive, wind turbine, electrical machine configuration with different components forming the design.

Direct-drive generators are AC synchronous electrical machines and can be excited electrically or through permanent magnets. These types of generators are classified depending on the direction of the magnetic flux crossing between the rotor and the stator structure; the three different configurations are axial flux, transverse flux, and radial flux, with the former configuration representing the most popular choice for offshore wind turbine generators [13,14]. Direct-drive generator structures work under high torques while rotating at low speed, and this requires high levels of structural stiffness to keep the deformation below the established limits of 10% through the air gap length “z” between the rotor and stator of the generator [12].

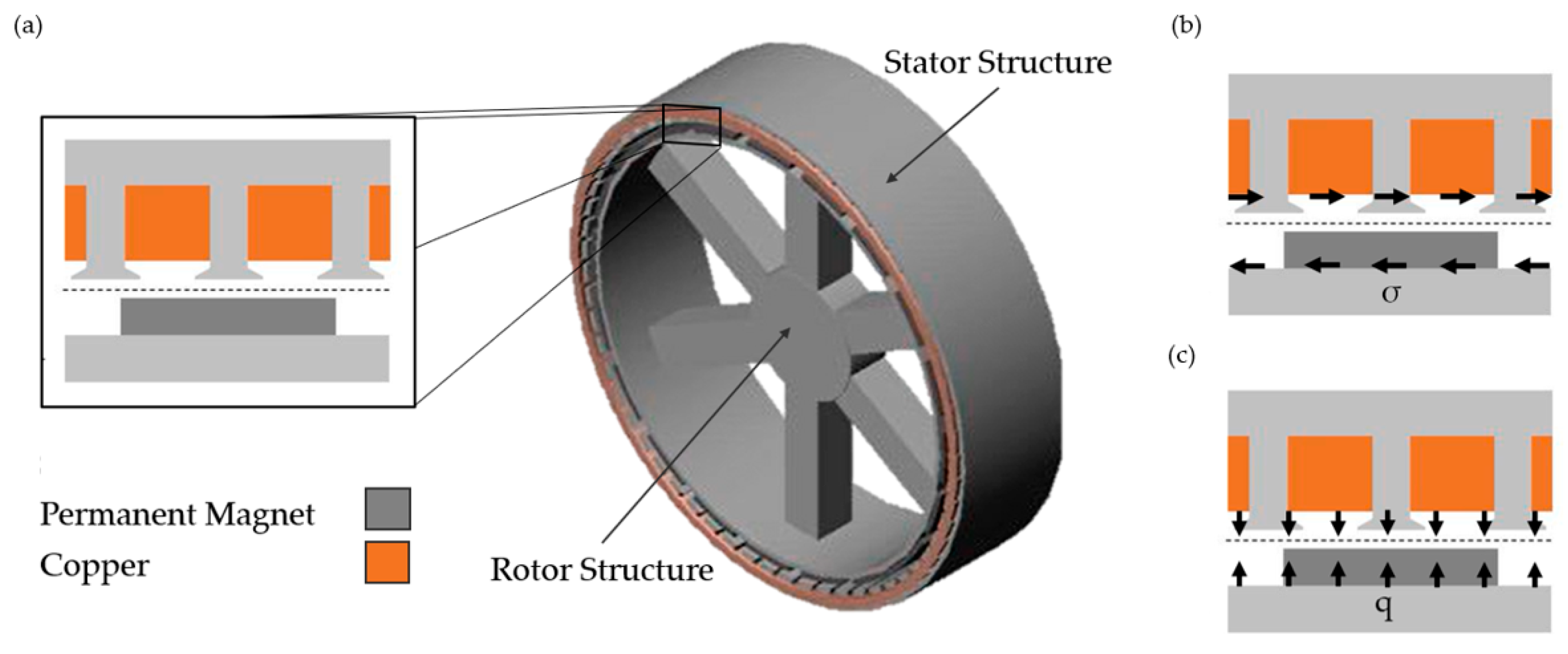
The main loads generated upon a direct-drive generator structure under working conditions are represented in Figure 2. Maxwell stress “q”, or normal stress, is the electromagnetic force generated in the direction of the magnetic flux across the air gap between the rotor and the stator, having a typical value of 200–400 kPa for these electrical machines. Shear stress “σ” is the force generated perpendicular to the magnetic flux, having a value of 25–50 kPa. The third main load to consider for the structural analysis of direct-drive generators is the gravitational load [13].

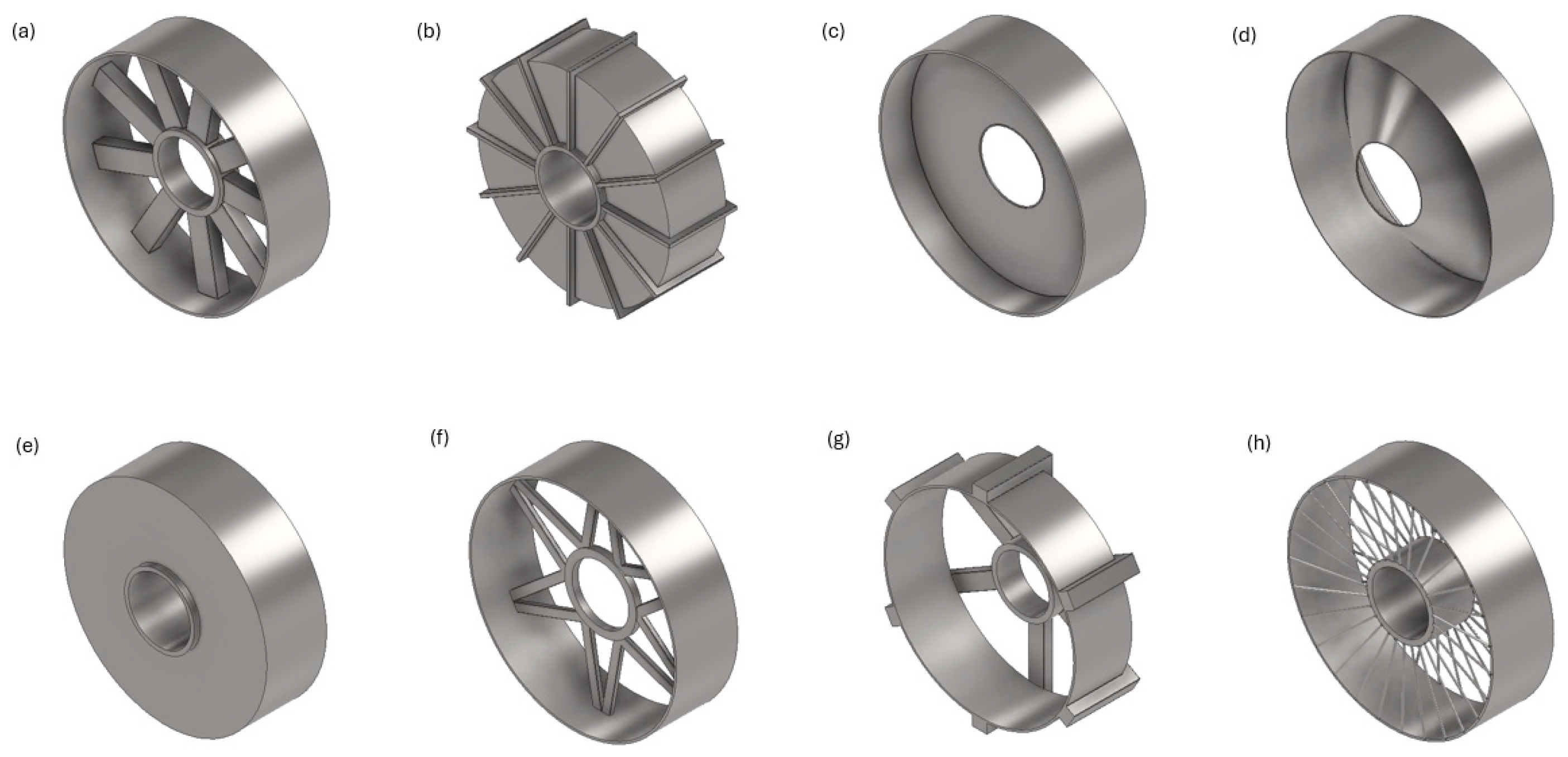
Direct-drive generator structures are large components typically made of steel, which account for over 60% of the overall mass of the system, opening the door to ambitious optimizations through high-performance structural analysis strategies. These specific requirements and the harsh operational conditions constitute a great challenge to the structural design of these machines [12]. Different support structures for direct-drive generators have been explored through the implementation of simple topologies (discs, cones, and arms) designed to be manufactured commonly in cast iron [15]. The representation of a review of conventional structures can be observed in Figure 3. Advanced optimization techniques such as generative design constitute an innovative approach to overcoming complex multi-objective structural challenges of direct-drive generators and have been implemented to discover nonconventional structural configurations [16,17].

1.2. Additive Manufacturing

New optimization methods allow engineers to explore nonconventional topologies and, with the development of innovative manufacturing techniques, for the fabrication of these novel topologies to become a reality in the form of high-performance and lightweight structures.

Additive manufacturing is a general term used to describe a fabrication process, which generates, layer-by-layer, a physical object from model data [18]. Additive manufacturing is capable of generating highly efficient, complex parts, that are otherwise unfeasible to obtain by conventional manufacturing methods. This process of manufacturing consists of adding material through the process of building up a three-dimensional model directly from computer-aided design software, in opposition to conventional manufacturing, which focuses on subtracting techniques [19]. New progress in additive manufacturing technologies allows the production of nonconventional structural configurations. The recent development of metal additive manufacturing has experienced significant growth, driving innovation in design optimization techniques across different high-profile sectors, such as the aerospace industry, the automotive industry, and the energy sector [20]. In Figure 4, we can observe the result of the implementation of additive manufacturing processes for different high-performance components. Complex designs can be achieved through additive manufacturing methods coupled with advanced optimization strategies linked to algorithmic methods, such as generative design, to efficiently redistribute the mass of the part, which improves mechanical, thermal, and dynamic performance [16].

Laser powder bed fusion (L-PBF) is one of the most popular metal additive manufacturing processes, characterized by a high level of precision and short lead times with a minimum feature size of 0.2 mm and large building volume, with new commercial machines achieving just under 1 m³ of volume. The laser powder bed fusion process uses powerful lasers, with some commercial machines having up to 12 lasers of 1000 W each [21], to melt layers of metal powder and using materials such as steel alloys, aluminum alloys, and nickel and iron superalloys [22].

Figure 4. Implementation of additive manufacturing approaches for the development of high-efficiency components over diverse disciplines [22]; (a) Prototype rocket nozzle featuring internal cooling channels; (b) F1 heat exchanger; (c) Hyperganic prototype rocket nozzle featuring internal cooling channels and an external lattice; (d) Liquid hydrogen and liquid oxygen turbopumps by NASA.

Figure 4. Implementation of additive manufacturing approaches for the development of high-efficiency components over diverse disciplines [22]; (a) Prototype rocket nozzle featuring internal cooling channels; (b) F1 heat exchanger; (c) Hyperganic prototype rocket nozzle featuring internal cooling channels and an external lattice; (d) Liquid hydrogen and liquid oxygen turbopumps by NASA.

Understanding the additive manufacturing process is fundamental to achieving the full potential of this new technology. Acknowledging the energy efficiency of a manufacturing process is important to assess the energy usage during the full manufacturing process. To evaluate additive manufacturing processes in comparison to conventional subtracting processes, it is necessary to establish different parameters, such as production costs or environmental impact [23]. In

Table 1. Energy consumption through the different stages of an SLM process for a single part and a batch of 12 parts of aluminum [24].

SLM Process	Energy Consumption (MJ)
	Single Part	Batch (12 Parts)
Aluminum powder production	0.57	6.80
Argon gas production	0.41	4.87
Preheating of chamber	2.88	2.11
Printing of parts	26.81	245.00
Laser cooler by chiller	31.45	140.81
Idle period between prints	1.34	1.34
Cool down process	6.19	6.23
Part removal by EDM separation method	33.45	142.46
Cleaning of build chamber by vacuum immersion separator	0.15	0.15
Recycling/sieving to filter large AI particles	0.05	0.05
Total energy consumption	103.29	549.83
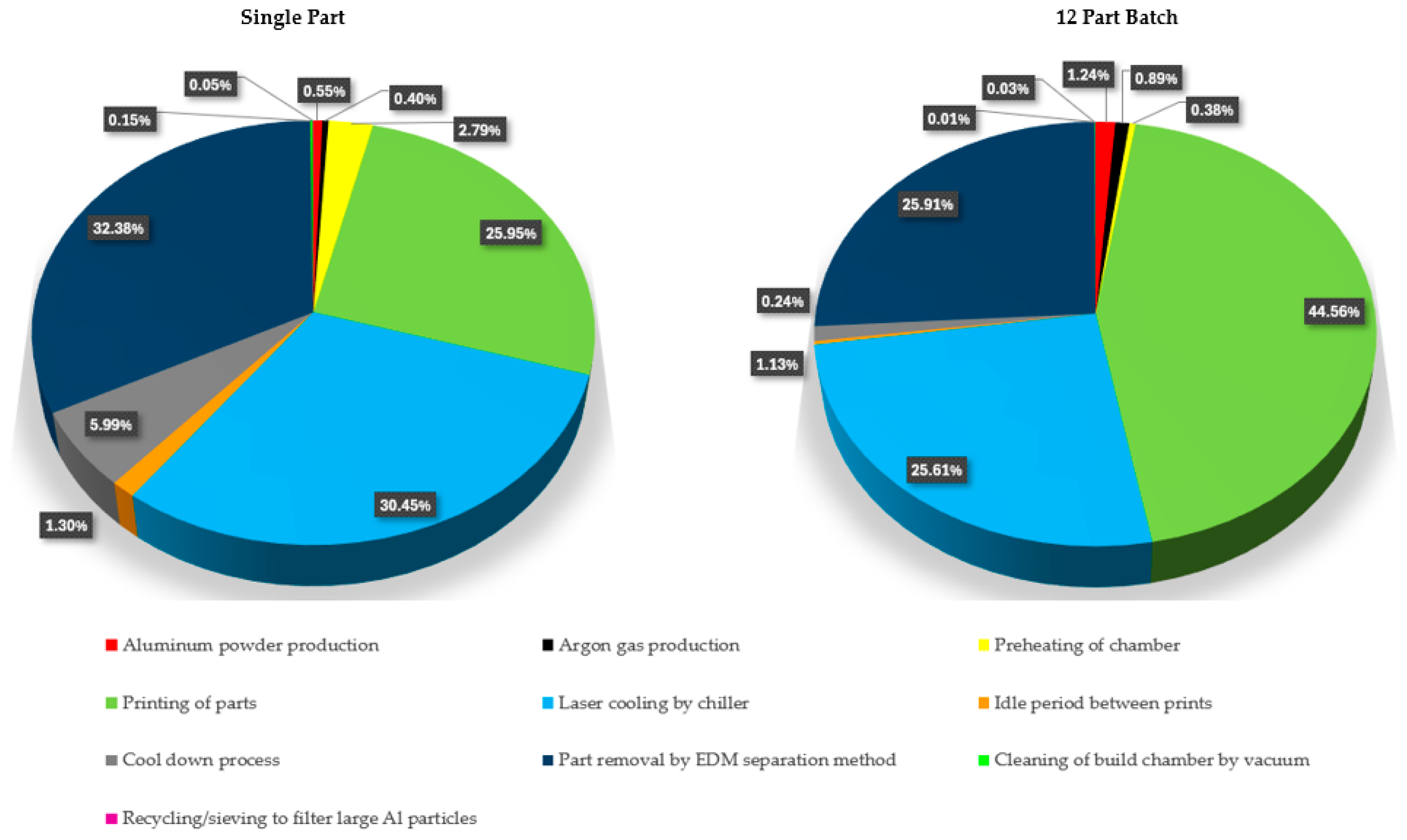
Total energy consumption per part	103.29	45.82

, the energy consumption for each stage of a selective laser melting process is described for the production of a single part and for the production of a batch of 12 parts [24]. In Figure 5, an example of energy efficiency assessment has been addressed with a visualization of the energy consumption percentages for a metal additive manufacturing process using selective laser melting (SLM) technology and AlSi10Mg as printing material. Figure 5 shows the importance of the build volume optimization during an SLM process on the energy efficiency of the production of the printed part, with a 55.64% total energy consumption reduction per part when producing a batch of 12 parts against a single part production.

The consideration of a design for an additive manufacturing (DfAM) approach during a structural optimization strategy in order to improve the efficiency of the production and the sustainability of the process is essential. Integrating additive manufacturing constraints into structural optimization strategies allows the development of more efficient, sustainable, and fit-for-purpose processes. Simulation-driven design for additive manufacturing and, more precisely, selective laser melting processes, such as laser powder bed fusion (L-PBF), represents a breakthrough in the fields of design optimization for metal 3D printing components. L-PBF possess multiple advantages in comparison with conventional manufacturing methods for structural optimization methods of highly efficient metal components. Some benefits of L-PBF applied to optimization processes are a decrease in lead times, waste material reduction, design flexibility, and on-demand production, with great performance on lightweight applications. The recent development of L-PBF commercial machines allows the comparison of metal additive manufacturing against conventional manufacturing techniques and highlights the advantages of using this process [25,26]. SLM commercial machines such as the NXG XII 600 present a step further toward metal additive manufacturing mass production and incrementing the number of lasers up to 12 to achieve a process 20 times faster in comparison with other SLM machines. This new technology development has been addressed in several academic and industrial investigations across different fields in the last few years [27].

In [24], the energy efficiency of the additive manufacturing process is discussed, where manufacturing parameters such as additional support structure could increase energy efficiency by over 45% and bulk part production optimization pushing the energy efficiency even further. Optimization strategies focusing on metal additive manufacturing at a design stage could revolutionize the industry, drastically reducing material waste, energy consumption, and production costs [28]. The implementation of additive manufacturing constraints over design optimization strategies has a direct impact on the manufacturing stage and the overall sustainability of the production [29].

Additive manufacturing has been applied for the structural optimization of direct-drive generators in [30,31], where triply periodic minimal surfaces were employed for the generation of the lattice topology using evolutionary algorithms, and mass reduction of the generator structure was observed.

1.3. Potential Applications: Multirotor Wind Turbines

The power rate and scale of the systems within traditional horizontal axis wind turbines have been substantially increased recently. Some of the most important logistical challenges of these large wind turbines are those associated with large-scale blades of over 100 m long and structural components, such as the big steel structures of direct-drive generators [32]. The multirotor configuration demonstrates an improvement in efficiency and a reduction in overall loads, although it introduces a larger number of moving parts in the system [33]. The multirotor wind turbine concept offers an alternative to increasing the power output of the machine by combining multiple rotors into a single wind turbine. This configuration has been assessed to be 80% of the cost of an equivalent power rate single rotor wind turbine and over 8% higher on power output than a single rotor with an equivalent swept area. The major advantage of this configuration is the standardization offering a modular design in which the systems could be upscaled or adapted to the environmental conditions of the location, with standardized components being easily replaceable [34]. Due to the advantages presented by the multirotor wind turbine system, new companies such as Myriad Wind Energy Systems [35], as well as established multinationals, such as Vestas [33], are adopting this unconventional wind turbine configuration. Figure 6 shows a multirotor wind turbine built and tested by Vestas as part of the review performed for future emerging technologies in the wind power sector [33].

A small generator structure implemented on the Vestas multirotor wind turbine opens the door to alternative and innovative manufacturing processes, such as additive manufacturing, as part of a modular, efficient, and more sustainable wind turbine configuration. In [36,37], steel structures and structures made with composite materials are explored for direct-drive generators. The 100-kW generator considered in this study is based on the electrical machine explored in [36] and possesses a rotor diameter of 0.5 m with a cylinder width of 150 mm. The challenges associated with the design of the support structure of a permanent magnet direct-drive electrical generator (PMDD) require the careful assessment of the design parameters in order to develop an efficient structural optimization strategy. The high torques generated in these electrical machines demand a great level of structural stiffness. The parameters of a 3-MW and a 100-kW PMDD electrical generator are described in

Table 2. Wind turbine generator parameters [16,17,36,37,38].

Rated Power	3-MW	100-kW
Generator excitation	Permanent magnet	Permanent magnet
Permanent magnet topology	Radial flux	Radial flux
Drivetrain	Direct-drive	Direct-drive
Axial length “l”	1.2 m	0.150 m
Rotor diameter “R”	4 m	0.5 m
Airgap limit “z”	0.5 mm	0.208 mm
Pole pairs	60	60
Electromagnetic working loads
Maxwell stress “q”	400 kPa	400 kPa
Shear stress “σ”	30 kPa	30 kPa
Excitation frequencies
Rotational frequency	1P	1P
Electrical frequency	fe	fe
Rotor blades frequency	3P, 6P	3P, 6P

, following the considerations in [16,17,36,37].

New commercial metal additive manufacturing machines integrate building envelopes big enough to manufacture the generator structure of these wind turbine rotors as one single part. One example of a large-envelope metal additive manufacturing machine is the SLM NGX XII 600, with a building envelope of 600 × 600 × 600 mm [21]. The 3-MW generator support structure, with a 2-m rotor diameter, represents a challenge to be manufactured by current commercial additive manufacturing methods due to its size. A modular design with a design for an additive manufacturing approach holds great potential for future research on 3-MW generators.

1.4. Structural Optimization Strategy

An integrated structural optimization strategy consists of a large set of design analysis data involving the selected structure and its environmental conditions [17]. Performing a complex three-dimensional structural optimization requires an advanced stress package embedded in a modelling piece of software, such as the one used in this study, ANSYS Workbench 2022. Structural optimization is a combination of multiple mathematical algorithms representing different aspects of the design specifications, optimization objectives, dynamic behavior, boundary conditions, or manufacturing constraints [39].

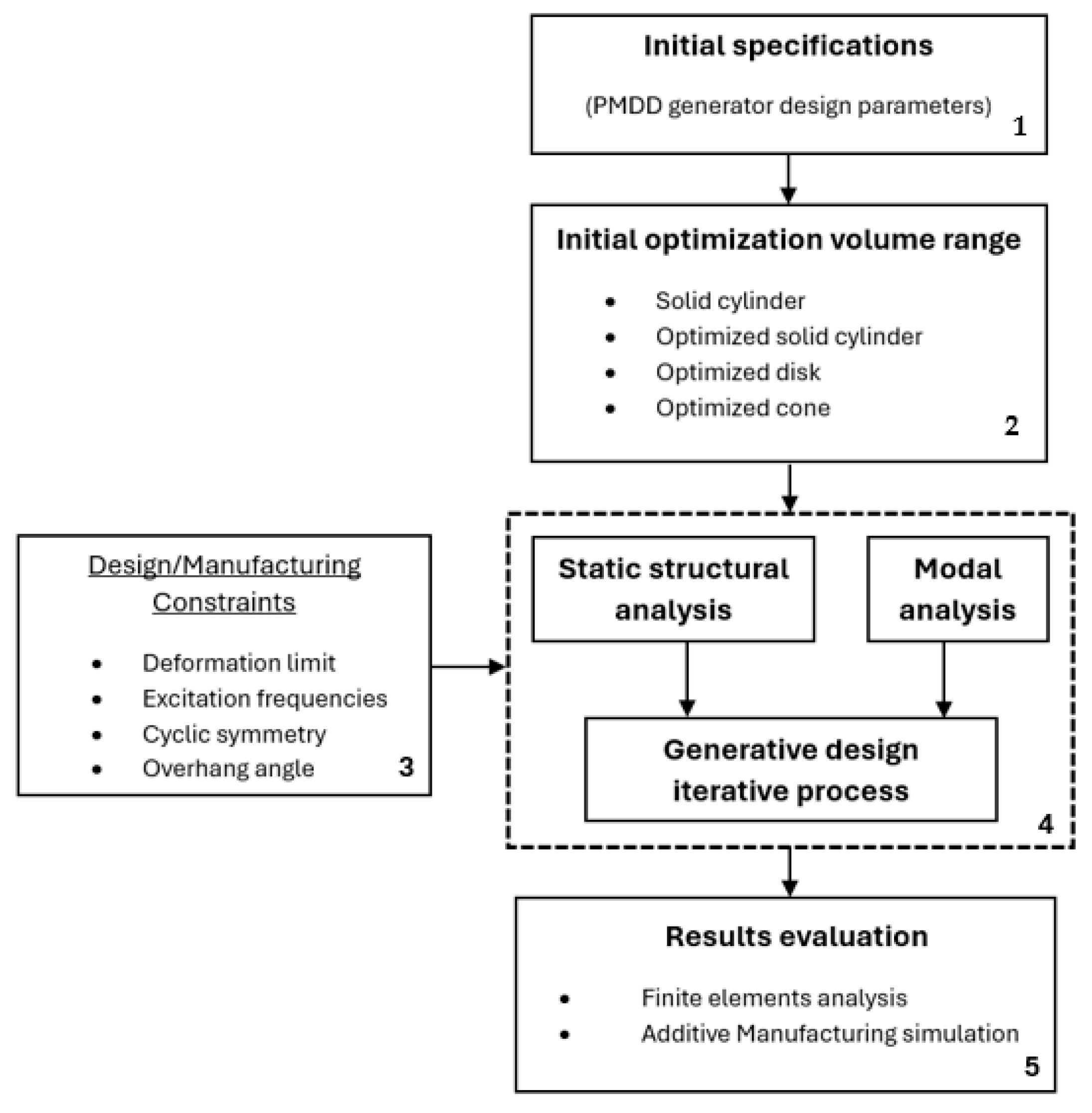
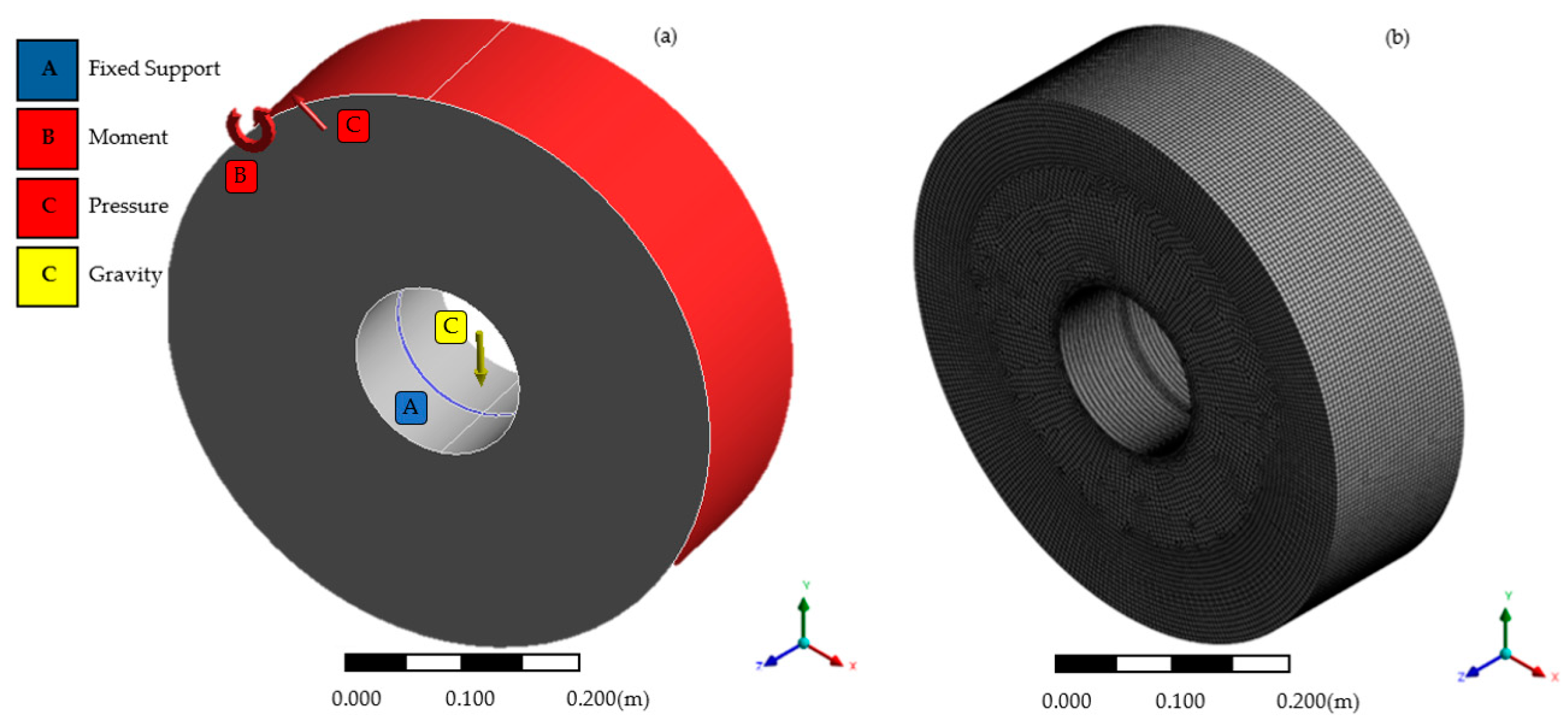
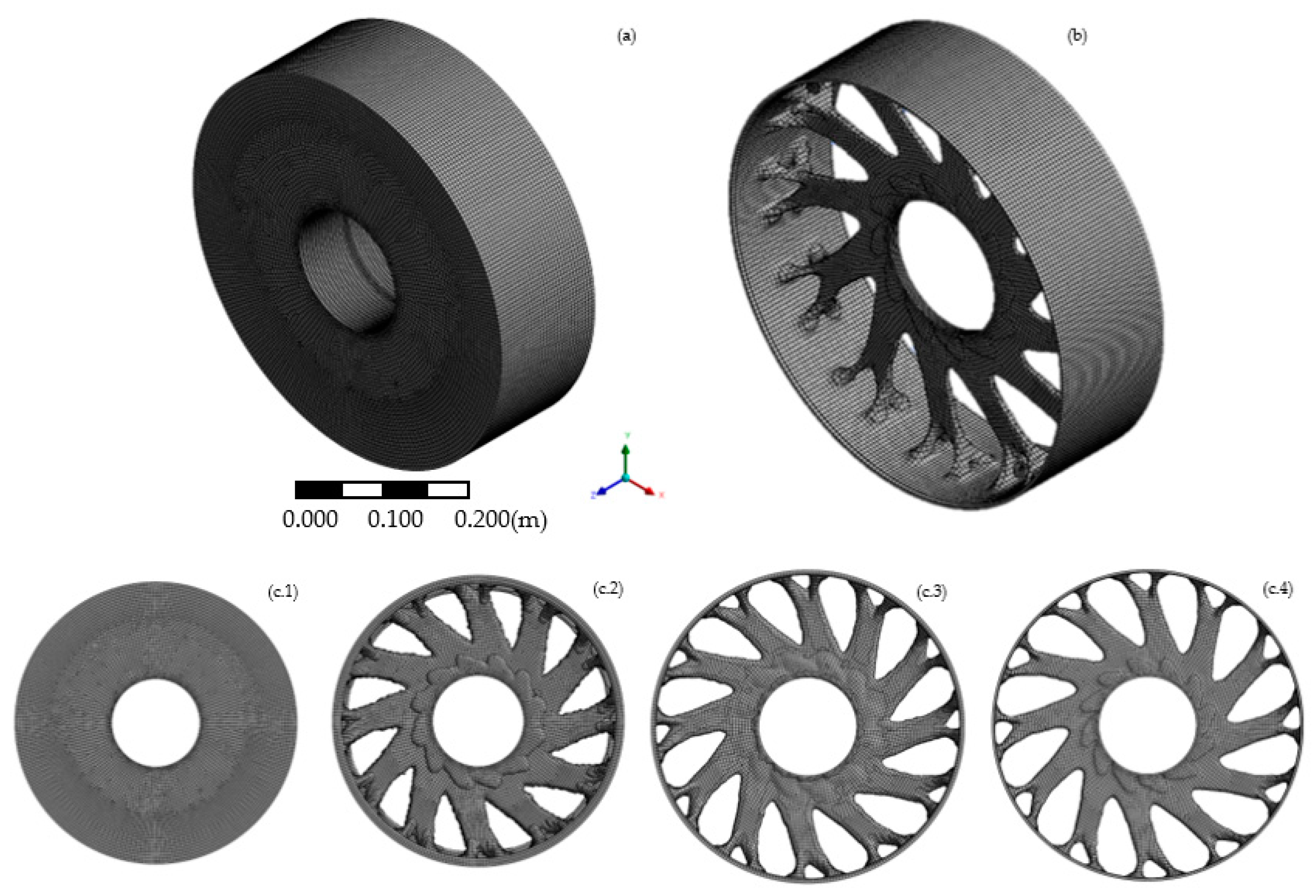
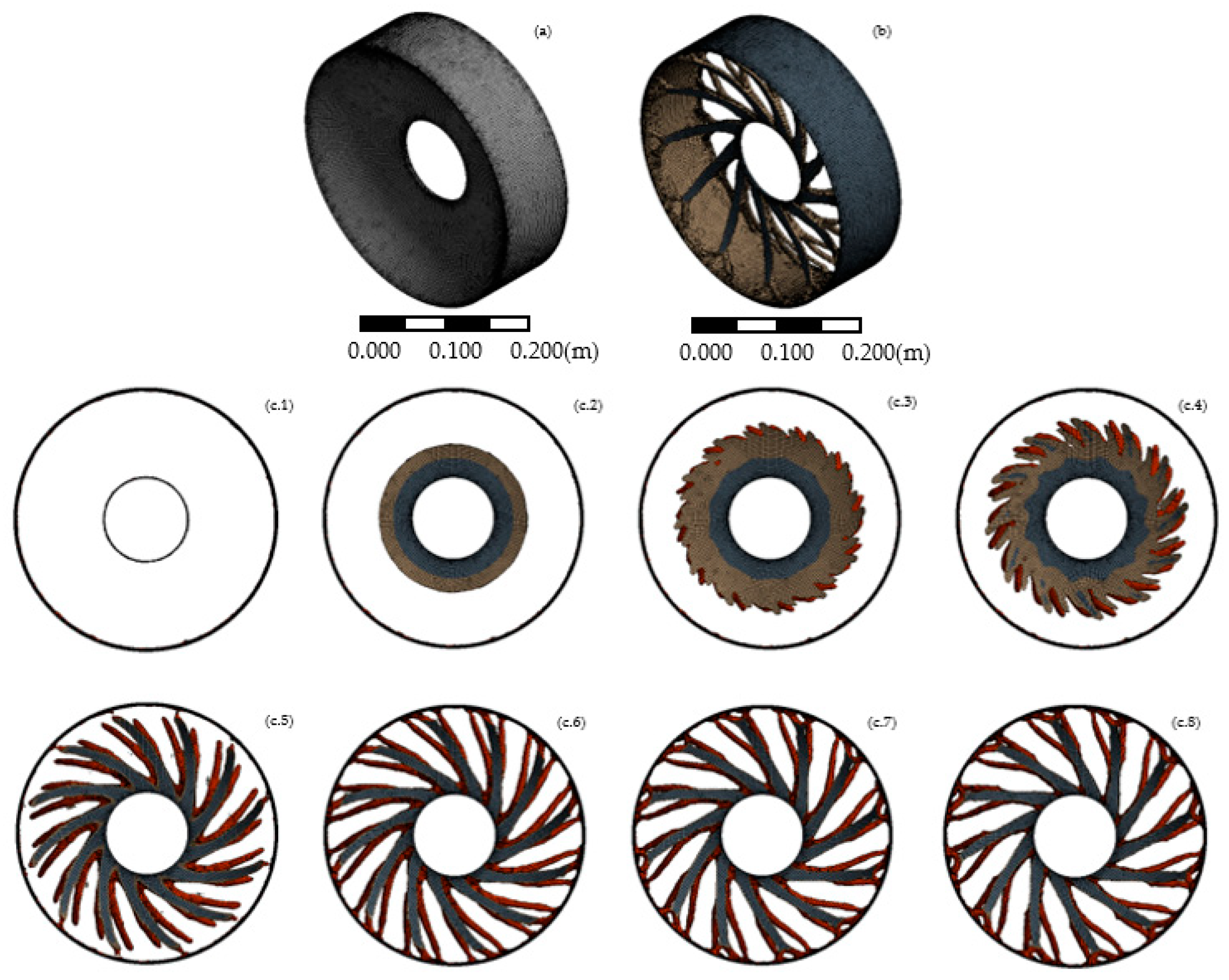
In a structural optimization process, the initial optimization volume represents the range of volume in which the software performs the optimization study. Depending on the software or the parameters, this volume can be described, or the software can determine it automatically. The initial optimization volume range is represented in Figure 7.

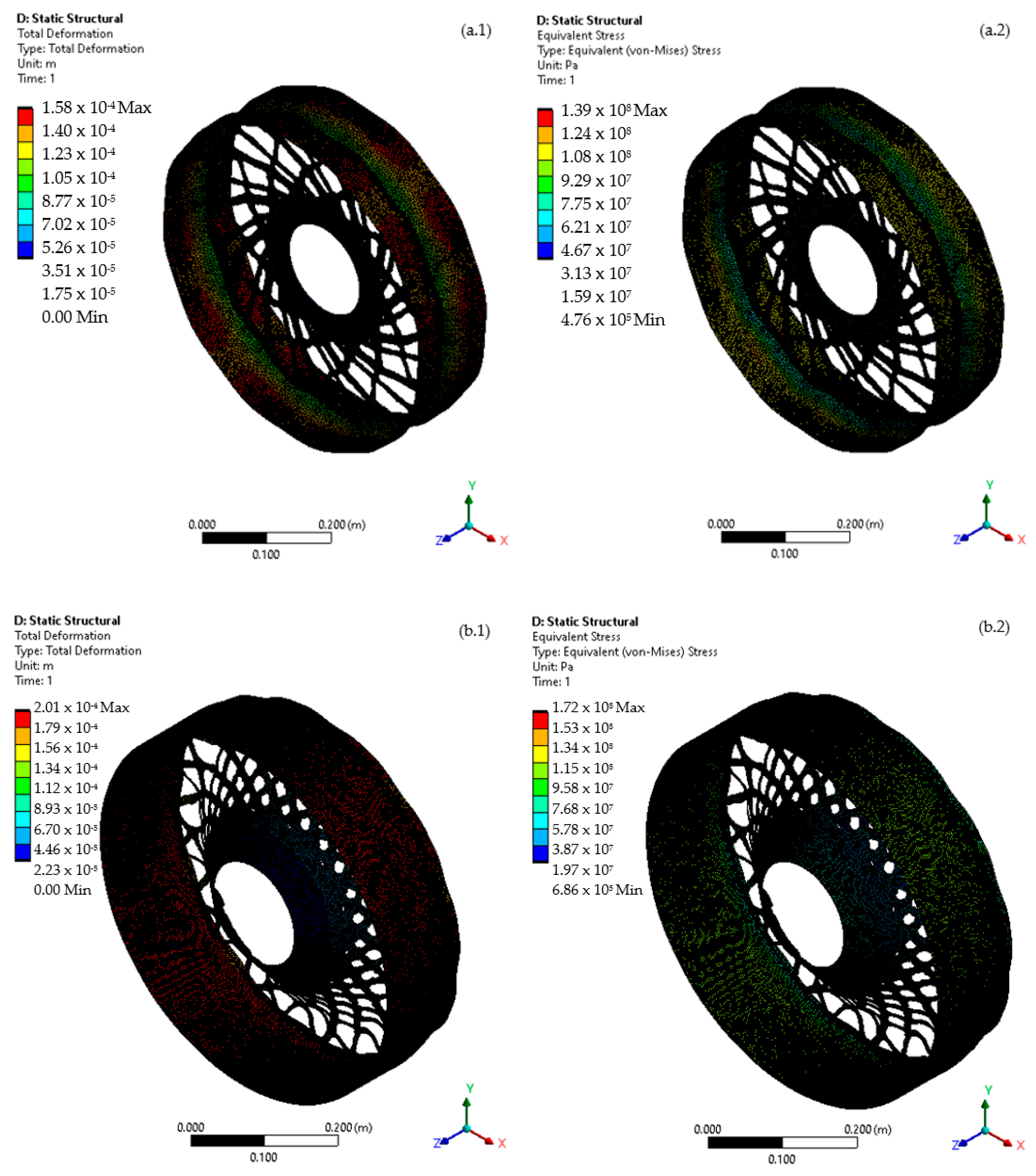
On a structural optimization strategy for a direct-drive generator structure, maintaining the air gap deformation is crucial. Therefore, the primary criteria for the structural optimization strategy, as in [17], is determined by the limit of deformation through the air gap between the rotor and the stator. In Equation (1), we can see a strain-based function used in structural optimization, where “Ω_mat” represents the volume of the material, “ε” represents the strain, “u” is the displacement, and “σ” is the density [39].

$$\min \underset{{\mathrm{\Omega }}_{mat}}{\int }{\epsilon \left(\overrightarrow{u}\right)}^T\sigma \left(\overrightarrow{u}\right)d{\mathrm{\Omega }}_{mat}$$

(1)

The considerations of structural vibrations of a rotational machine are fundamental for the optimization strategy. A modal analysis needs to be performed and integrated into the optimization strategy in order to identify and modify the natural frequencies of the structure and avoid the effect of resonance. Vibrations on rotating machinery need to be minimized to avoid fatigue, noise generation, and ultimately catastrophic system failure [17]. The major excitation frequencies to consider for a direct-drive wind turbine generator are the turbine rotation speed “1P”, the electrical frequency “f_e”, and the frequencies generated by the rotor blades “3P” and “6P” [38].

A complex three-dimensional model requires the assessment of a modal analysis, in which the natural frequencies of the structure are identified and compared against the excitation frequencies of the system. The method used by the modal analysis to identify the frequency modes affecting the dynamic behavior of the structure is known as the effective mass participation factor (EMPF), in which the mass participation for a specific direction can be determined for each natural frequency mode of the structure. A frequency mode is identified as dangerous when over 1% of the participation mass is contributing within the operational range of the wind turbine [17]. A modal analysis is integrated as part of the advanced structural optimization strategy to optimize the structure, avoiding dangerous frequency modes [40].

An example of the algorithm used in the modal analysis can be seen in Equation (2), where “η_r“ is the generalized mass of mode r, “Ω_mat” represents the volume of the material, “φ_r” is the load participation factor of mode r, “f_mag” is the spatial distribution of the displacement and magnetic force, “ω_r” is the frequency of mode r, and “ω_ext” is the harmonic excitation frequency [39].

$${\eta }_r={\displaystyle \frac{\underset{{\mathrm{\Omega }}_{mat}}{\int }\overrightarrow{{\phi }_r}·{\overrightarrow{f}}_{mag}d{\mathrm{\Omega }}_{mat}}{{\omega }_r^2-{\omega }_{ext}^2}}$$

(2)

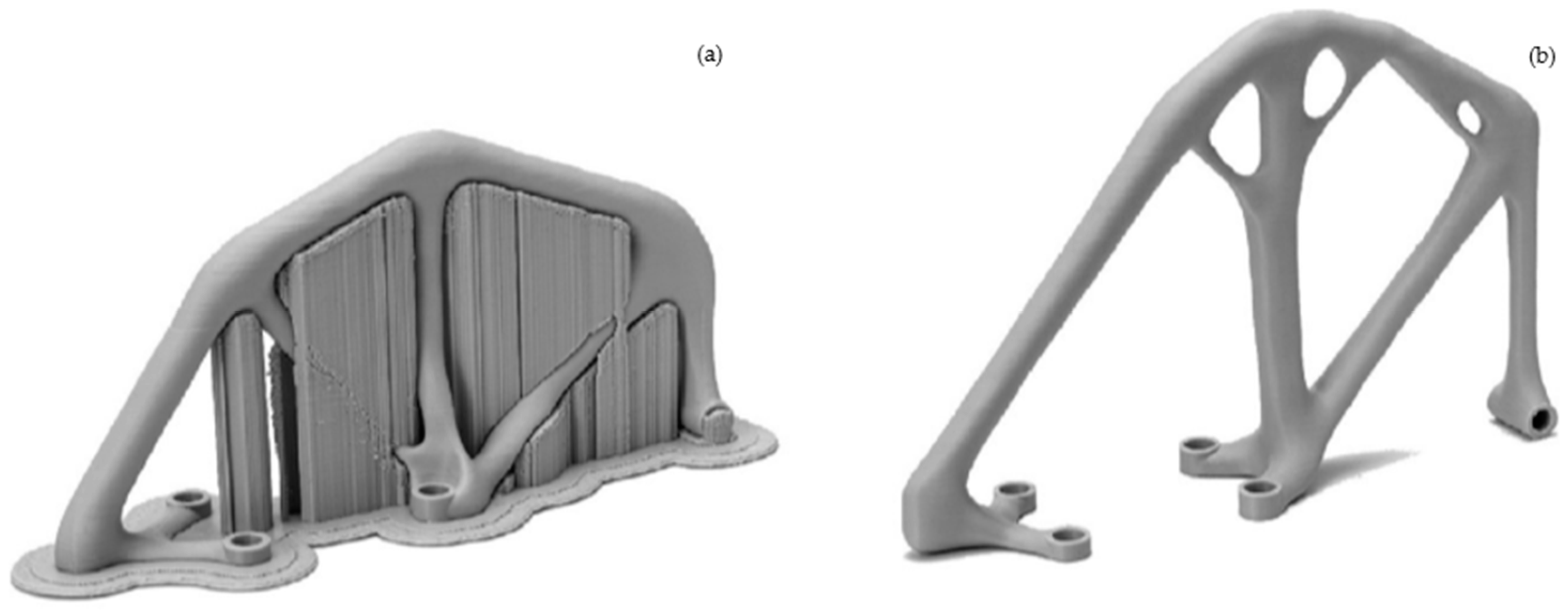
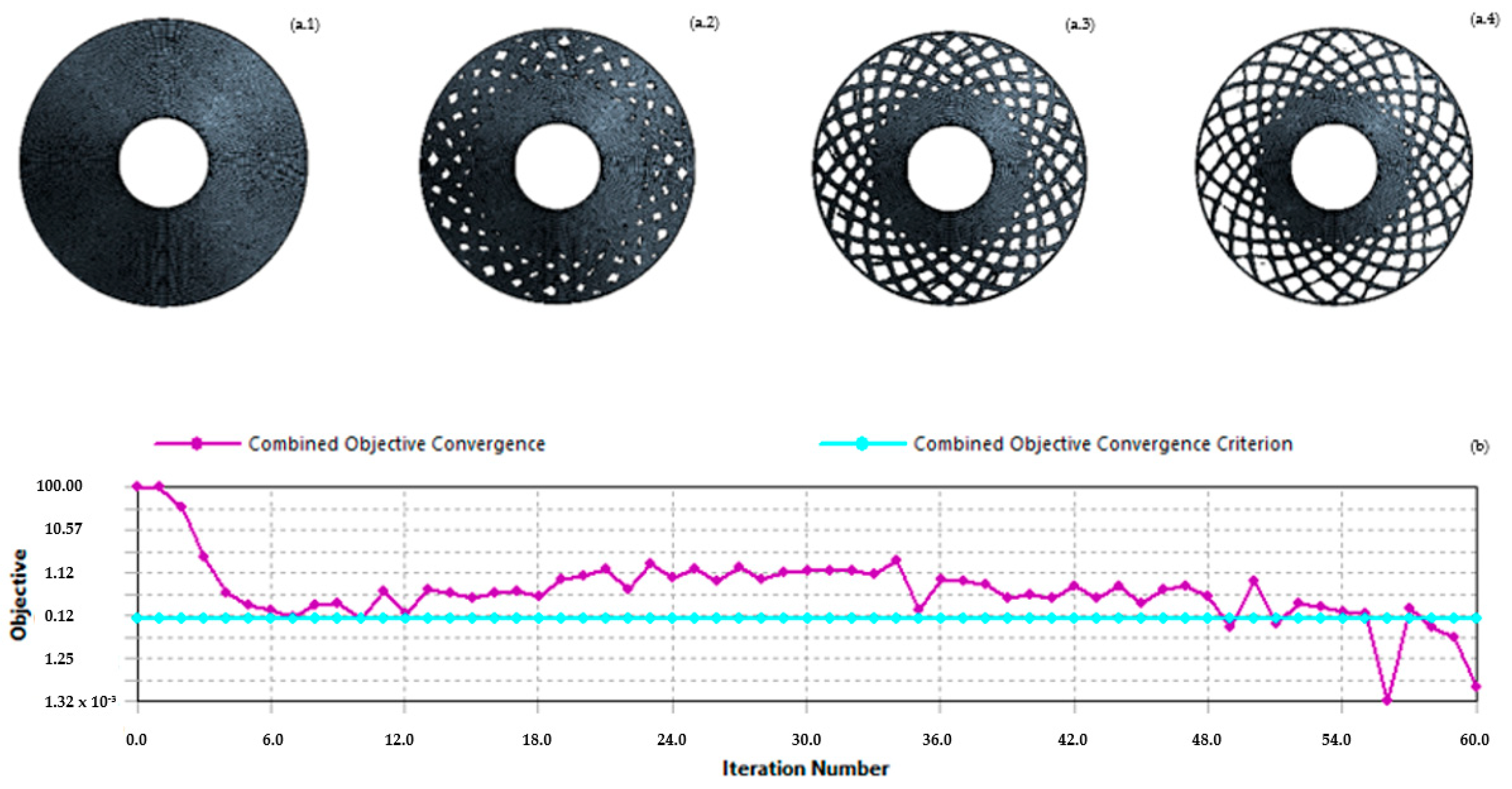
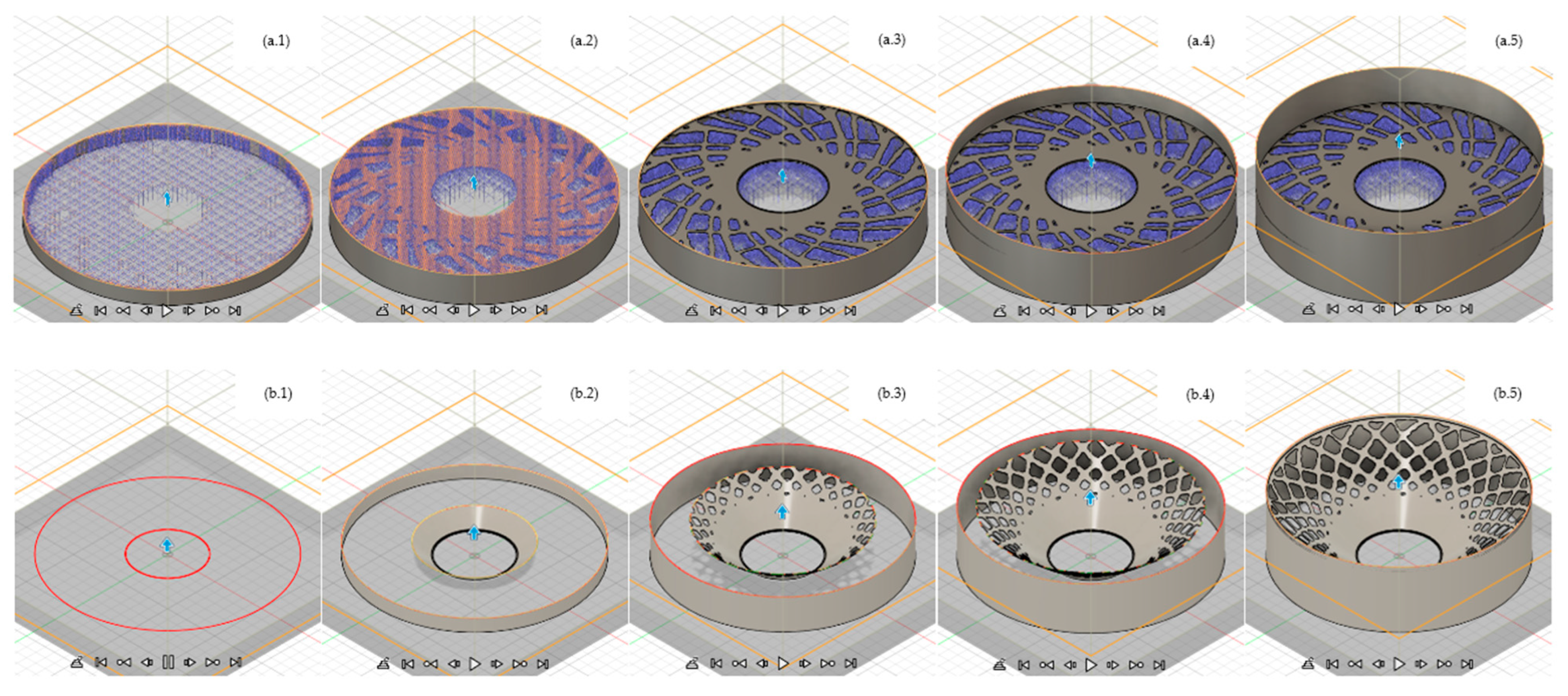
Introducing additive manufacturing constraints into the structural optimization strategy is fundamental to achieving an optimal result model. The implementation of design for additive manufacturing (DfAM) practices is essential to incorporating this new manufacturing knowledge into advanced structural optimization techniques for high-efficiency results [41]. In Figure 8, different additive manufacturing tests, such as design guidance, can be observed.

Manufacturing constraints such as overhang angle are essential to produce efficient result models while performing structural optimization techniques for additive manufacturing applications. The overhang angle constraint represents the minimum angle to accomplish the design performance required, obtaining the minimum surface finish intended or avoiding part failure. In Figure 8b, we can observe the results at various overhang angle values. Considering design for additive manufacturing while developing a structural optimization strategy centered on the use of generative design techniques is an efficient approach that can lead to the generation of complicated designs. An example of the design for additive manufacturing is shown in Figure 9, where the consideration of additive manufacturing constraints generates a self-supported structure, avoiding the need for additional supporting structure and reducing waste material, production costs, and manufacturing time.

Adding all the previously mentioned functions and constraints into an advanced, multi-objective, structural optimization strategy produced an adaptable and efficient method of analysis. Nonetheless, the complexity of the optimization strategy is proportional to the computing cost needed and needs to be considered through the iteration process [42].

An integrated structural optimization strategy has been developed based on the studies [16,17] for a 100-kW permanent magnet direct-drive, wind turbine generator structure [36]. A generative design process has been used, combining a static structural analysis and a modal analysis using the commercial software packages ANSYS for the structural optimization process and Fusion 360 for the additive manufacturing process simulation.

The process starts by determining the electrical generator design parameters and specifications, the considerations for the diverse optimization volume ranges for the different approaches, and the integrated structural optimization strategy, including the static structural analyses, the modal analyses, and the design and manufacturing constraints as part of the iterative generative design stage.

A workflow of the structural optimization strategy developed in this study has been represented in Figure 10, where we can see the different steps followed during the process. The structural optimization strategy consists of:

• The initial specification parameters of the direct-drive generator structure to be optimized.
• The consideration of the different initial optimization volume ranges for the diverse approaches.
• The design and manufacturing constraints strategy as objectives for the structural optimization process.
• The development of the iterative generative design process integrating static structural analyses and modal analyses.
• The evaluation of the results obtained from finite element analysis techniques and a metal additive manufacturing process simulation study.

The aim of this study is to develop an advanced structural optimization strategy based on the methodology produced in the investigations presented in [16,17], making use of generative design techniques that consider static structural and modal analyses and include a design for the additive manufacturing approach.

This novel design and manufacturing structural optimization strategy represents a zero-waste approach that integrates not only the optimization of the structures but also the optimization of the intended manufacturing process, virtually reducing the material waste to zero and significantly reducing the energy and water usage during fabrication. The integrated consideration of the latest developments in technology, both for computational structural optimization and manufacturing techniques, is a novel approach for complex engineering applications, such as the design of the support structures of permanent magnet direct-drive electrical generators.

2. Methodology

The integrated structural optimization strategy with generative design techniques developed in the studies [16,17] produced efficient results for the application of multi-MW permanent magnet direct-drive wind turbine generators. Nevertheless, due to the large scale of offshore wind turbine generator structures, the additive manufacturing process was unfeasible to implement with commercial metal additive manufacturing machines. The most organic-like topologies produced by the generative design process were avoided by controlling different design parameters of the process, such as the cyclic symmetry, to generate a more standard outcome adapted for conventional manufacturing processes such as casting. Based on the potential of multirotor wind turbine concepts and the use of smaller generator structures in these systems, suitable for the building envelope of commercial metal additive manufacturing machines, a 100-kW permanent magnet direct-drive generator structure was chosen for this study [33]. A comparison between a 3-MW and a 100-kW direct-drive generator structure is performed in [36], where a 100-kW generator with a rotor diameter of 0.5 m and a cylinder width of 150 mm was assessed. The deformation limit calculated for this structure across the air gap between the rotor and stator was 0.208 mm.

The approach chosen for this study is founded on the knowledge acquired in the previous studies [16,17], where the initial optimization volume range would be varied from a wider volume to a pre-optimized volume, with the intention of giving flexibility to the generative design process to produce more adaptative topologies. The material used for this study is Inconel 625. This material is widely used in aerospace, chemical, and marine industries, demonstrating good mechanical properties for harsh environmental conditions [43]. Inconel 625 owns an excellent combination of yield, creep, and fatigue strength, with good frictional wear and corrosion resistance, which makes it ideal for marine systems applications. Inconel alloys also have printable and weldable suitable characteristics for selective laser melting (SLM) additive manufacturing processes [44]. The mechanical properties of the material are excellent for the optimization of the generator support structure and the additive manufacturing process, with a Young’s modulus “E” of 2.07 GPa, a density “σ” of 8440 kg/m³, and a Poisson’s ratio “ν” of 0.278–0.312.

The integrated structural optimization strategy was developed using the finite element analysis package of ANSYS Workbench 2022, adapting the mesh analysis to each of the initial optimization volume ranges with local mesh control applied to the fixed support surface and a mesh analysis method of hexahedron elements. A single fixed support is used in the structural optimization strategy on the generator shaft axis, and the three loads considered for the static structural analysis (normal stress, shear stress, and gravitational load) are applied following the process utilized in [16,17].

A representation of the mesh analysis and boundary conditions can be observed in Figure 11. The parameters selected for the iterative process were set with a limit of 100 iterations and a convergence rate of 0.1%, obtaining computational times of 60 to 560 min throughout the different simulations. As part of the multi-objective optimization, a displacement limit across the air gap between the rotor and stator structures of the generator was set as a primary criterion with a value of 0.208 mm. Moreover, cyclic symmetry was set as a design constraint due to the impact of mass distribution on inertia for rotating machinery. The cyclic symmetry is a crucial design parameter for the structural optimization strategy as an uneven distribution of mass on rotating machines could produce a system malfunction through vibration reducing the lifespan and provoking structural failure [40]. In [17], the manufacturing constraint of cyclic symmetry was explored as a variable for the structural optimization strategy. The impact on the dynamic behavior and mass reduction for the generated topologies was assessed using this method. Based on the knowledge acquired in [16,17] a cyclic symmetry of 12 sectors was assumed for this study.

The simulation studies have been performed on a standard workstation HP Z2 Intel^® Core^TM i7-9700K (12 MB Cache, 3.6 GHz) with 64 GB of memory RAM, and the methodology has been adapted to the capabilities of the system with the aim of optimizing computational times. In

Table 3. Structural optimization strategy parameters.

Mesh Analysis	Structural Optimization	Design and Manufacturing Constraints
Element size: 5 mm	<100 iterations	Displacement limit: 0.208 mm
Local mesh: 1 mm	Convergence: 0.1%	Cyclic symmetry: 12
Method: Hexahedrons	Computational time: 60–540 min	Overhang angle: 35 degrees
Number of elements: 150,000–2,500,000

, the general parameters for the structural optimization strategy are described.

The first analysis was developed using a solid cylinder structure as an initial optimization volume range, allowing the generative design process more flexibility but decreasing computational efficiency considerably. Figure 11 represents the structural loads with boundary conditions (a) and mesh analysis (b).

Due to large computational times and low-efficient optimization results, the initial optimization volume range was modified. In Figure 12, the representation of different initial optimization volume ranges is described.

In order to evaluate the manufacturability of the generated models produced by the structural optimization strategy, an additive manufacturing process simulation was performed with a virtual machine in Fusion 360. The additive manufacturing virtual machine selected for the evaluation of the results was the commercial metal additive manufacturing laser powder bed fusion (L-PBF) machine SLM NGX XII 600 due to its high performance and large build envelope. The specifications of the metal additive manufacturing virtual machine and its setup are given in

Table 4. Metal additive manufacturing virtual machine SLM NGX XII 600 configurations.

Machine Model	Technology	Specifications
SLM NXG XII 600	Laser beam PBF	Build envelope: 600 × 600 × 600 mm
	Number of lasers: 12	Build volume: 216 L
	Laser power: 1000 W	Build rate: 1000 cm/h
		Build spot size: 160 μm

. As mentioned, the SLM NGX XII 600 is a laser powder bed fusion (L-PBF) commercial machine with high-power multi-laser technology. With a quick production time of a build-up rate of 1000 cm/h and its large volume build envelope available, it represents a revolution in metal additive manufacturing [21].

3. Discussion of Results

3.1. First Approach: Solid Cylinder as Initial Volume Range

The results of the first approach of the structural optimization strategy with a solid cylinder as the initial optimization volume range can be seen in Figure 13, where the iterative optimization process (c.1–c.4) and the resulting model of the generative design (b) can be observed. The wide initial volume of the optimization strategy produced a time-consuming iterative process.

In

Table 5. Structural optimization strategy with a solid cylinder.

Initial Volume Range	Generative Design Structural Optimization	Mass
Solid cylinder	93 iterations	Original: 208.62 kg
	Convergence: 0.1%	Final: 19.06 kg
	Time: 9 h 23 m	Percentage of mass reduction: 90.86%

, the details for the iterative process are described, where it can be observed that the computational time exceeded 9 h of simulation. This is due to the large percentage of mass to reduce, starting with an original mass of 208.62 kg for the solid cylinder as the initial optimization volume range and generating a topology with a final mass of 19.06 kg, representing a mass reduction in relation to the original mass of 90.86%.

The results observed in Figure 13 and Table 5, represent the structural optimization strategy with a solid cylinder as the initial optimization volume range. This method generates a high percentage of mass reduction, producing a fully functional support structure throughout an automated iterative process. The automation of the process and the integration of multiple optimization objectives and design constraints represent an advantage against more time-consuming conventional parametric optimization strategies. However, as demonstrated in previous investigations [16,17], the preoptimization of the initial optimization volume range proved to achieve more efficient results on the optimization of the support structure of the PMDD generator.

The additive manufacturing constraint of the overhang angle was suppressed, as the simulation process with this manufacturing constraint actively produced a nonconvergence result for this first approach. The nonconvergence result when implementing the additive manufacturing overhang constraint can be seen in Figure 14, with a topological resemblance to the pre-optimized conical structure study in [16].

3.2. Second Approach: Pre-optimized Solid Cylinder as Initial Volume Range

The second approach was developed with an initial optimization volume range of a pre-optimized solid cylinder. The iterative process of the structural optimization strategy can be seen in Figure 15, where one can observe the resulting model of the generative design process (b) and the iterative generative design optimization process (c). The structural optimization strategy produced a very organic-like structure, and how the structure grows throughout the iterative generative design process to comply with the requirements established can be observed.

In

Table 6. Structural optimization strategy with pre-optimized solid cylinder.

Initial Volume Range	Generative Design Structural Optimization	Mass
Pre-optimized solid cylinder	76 iterations	Original: 83.50 kg
	Convergence: 0.1%	Final: 15.05 kg
	Time: 9 h 47 m	Percentage of mass reduction: 81.98%

, the details of the generative design iterative process are described. It can be seen that, even though the initial optimization volume range has decreased, the computational time still exceeds 9 h of simulation. The starting mass of the pre-optimized solid cylinder structure was 83.50 kg, and the final generated topology mass was 15.05 kg, i.e., 81.98% mass reduction in comparison with the original mass.

3.3. Third Approach: Pre-Optimized Disk as Initial Volume Range

In the third approach, a pre-optimized disk has been used as the initial optimization volume range based on the results obtained in the previous study [16,17]. The use of pre-optimized structures, including the disk structure, for the initial optimization volume range was observed to generate more efficient results for the structural optimization strategy on the processes developed in [16,17]. The results of the iterative process of the structural optimization strategy can be seen in Figure 16, including the generative design iterative process (a) and the combined objective convergence diagram (b). The details of the process are described in

Table 7. Structural optimization strategy with pre-optimized disk.

Initial Volume Range	Mesh Analysis	Structural Optimization	Mass
Pre-optimized disk	Element Size: 5 mm	52 iterations	Original: 3.26 kg
	Method: Hexahedrons	Convergence: 0.1%	Final: 2.57 kg
	Nodes: 172,502	Time: 53 m 4 s	Percentage of mass reduction: 21.27%
	Elements: 39,936

, where one can see the mesh information and the computational process, achieving a simulation of under an hour of computational time with a number of 52 iterations and a final mass of 2.57 kg, representing a mass reduction of 21.27%.

3.4. Fourth Approach: Pre-Optimized Cone as Initial Volume Range

In the fourth and last approach, a pre-optimized conical structure has been used as an initial optimization volume range due to the dynamic performance and mass reduction of this type of topology based on the results obtained in the previous study [16], where conical and disk support structures are explored. The use of pre-optimized structures, including the conical structure, for the initial optimization volume range was observed to generate more efficient results for the structural optimization strategy on the process developed in [16]. The iterative process of the structural optimization strategy can be seen in Figure 17. The details of the process, such as the mesh information, are described in

Table 8. Structural optimization strategy with pre-optimized cone.

Initial Volume Range	Mesh Analysis	Structural Optimization	Mass
Pre-optimized cone	Element size: 5 mm	60 iterations	Original: 3.67 kg
	Method: Hexahedrons	Convergence: 0.1%	Final: 2.84 kg
	Nodes: 177,053	Time: 1 h 25 m	Percentage of mass reduction: 22.50%
	Elements: 41,353

. The optimization process accounts for just under an hour and a half of computational time with 60 iterations and a final mass of 2.84 kg, representing a mass reduction of 22.50%.

3.5. Analysis Validation

The most promising results were obtained from the pre-optimized structures as initial optimization volume range, as seen in the previous studies [16,17]. The results obtained from the pre-optimized disk and cone structures have been evaluated using a finite elements analysis technique with ANSYS Workbench 2022 and a metal additive manufacturing process simulation with Fusion 360.

In Figure 18, we can observe the graphical representation of the finite element analysis static structural results for the GD disk and GD cone-generated topologies for total deformation and total von Mises stress under working load and boundary conditions.

In

Table 9. Results for the structural optimization strategy with pre-optimized disk and cone.

Initial Model	GD Optimization	Mass	Static Structural	Modal Analysis
Pre-optimized disk	52 iterations	Original: 3.26 kg	Total deformation: 0.15 mm	Mode 3: 17.07 Hz
	Convergence: 0.1%	Final: 2.57 kg	von-Mises: 139.07 MPa	Mode 12: 169.5 Hz
	Time: 53 m 4 s	Mass reduction: 21.27%
Pre-optimized cone	60 iterations	Original: 3.67 kg	Total deformation: 0.201 mm	Mode 17: 349.3 Hz
	Convergence: 0.1%	Final: 2.84 kg	von-Mises: 171.88 MPa	Mode 18: 349.3 Hz
	Time: 1 h 25 m	Mass reduction: 22.50%

, it can be observed that the deformation across the air gap between the rotor and the stator structures is kept under the limit of 0.208 mm (10% of the air gap length “z”) and the von-mises stress under the safety factor of 200MPa for both of the disk and cone pre-optimized structures [16,36]. The GD pre-optimized disk result achieved a final mass of 2.57 kg with a total deformation of 0.15 mm and a value for the von Mises stress of 139.07 MPa; however, the frequency mode 3 of the generated structure with 17.07 Hz interfered with the operational range of the wind turbine generator. The GD pre-optimized cone result achieved a final mass of 2.84 kg with a total deformation of 0.201 mm and a value for the von Mises stress of 171.88 MPa. The dynamic behavior of the natural frequencies of the generated cone structure was found to be safe under working conditions, with modes 17 and 18 at 349.3 Hz, far away from the excitation frequencies for the operational range of the wind turbine generator.

The metal additive manufacturing process simulation with the virtual machine SLM NGX XII 600 has been performed with the results generated from the pre-optimized disk and the pre-optimized cone using the software Fusion 360.

In Figure 19, the simulation for the metal additive manufacturing process is presented for the GD results of the pre-optimized disk structure (a), and the pre-optimized cone structure (b).

In

Table 10. Results for the additive manufacturing process simulation with pre-optimized disk and cone.

Model	Setup	Supports	Statistics	Print Time
GD disk	SLM NXG XII 600	Self-supported structure: no	Layer count: 943	16:16:18
	Material: Inconel 625	Support volume: 210.141 cm3	Height: 150.880 mm
	Build spot size: 160 μm	Support type: lattice volume
GD cone	SLM NXG XII 600	Self-supported structure: yes	Layer count: 937	8:40:29
	Material: Inconel 625	Support volume: 0.000 cm3	Height: 150.880 mm
	Build spot size: 160 μm	Support type: n/a

, the details of the results of the additive manufacturing process simulation with the virtual machine SLM NGX XII 600 are described. It can be observed that the implementation of design for additive manufacturing approaches, such as overhangs and support structure considerations with design and manufacturing constraints as an integrated part of the structural optimization process, can achieve more efficient results.

The additive manufacturing process of the GD disk structure has a printing process time of over 16 h and 210.141 cm³ of waste material as a support structure. This is an example of the lack of compliance by the design for additive manufacturing constraint of overhang angle. As we can see in the additive manufacturing process simulation for the optimized disk structure in Figure 19b, an extra support structure needs to be created (represented in blue) during the manufacturing process to support the generated disk topology as it surpasses the limit of the overhang angle of 35 degrees.

In comparison, the GD cone structure has a printing process of under 9 h and does not require extra material as the support structure due to its self-supported performance.

3.6. Discussion

The implementation of additive manufacturing considerations as part of the structural optimization strategy of direct-drive generator structures using generative design techniques has been demonstrated to produce highly efficient and adaptative results. Additionally, metal additive manufacturing has rapidly developed in recent years, particularly laser powder bed fusion (L-PBF) [42]. New commercial metal additive manufacturing L-PBF machines possess high production capabilities and can gain efficiency over conventional subtracting manufacturing processes if adequate manufacturing parameters are considered during optimization processes [21].

We can observe that the development of an integrated structural optimization strategy generates efficient fit-for-purpose structures when integrating relevant design parameters. As seen in [16], the use of a pre-optimized initial optimization volume range performed more efficiently in order to achieve a reduction in structural mass when compared with a wider initial optimization volume range, with an additional reduction in computational processing time. The topology characteristics of the conical structure represent a higher efficiency for an additive manufacturing process due to the unnecessary use of extra support material, resulting in a self-supported structure with minimal production time and material waste [42]. On top of that, conical structures achieve higher dynamic performance against excitation frequencies of direct-drive electrical generators.

An integrated structural optimization process requires full control and understanding of all aspects affecting the integrity of the structure to obtain efficient results, including the manufacturing process parameters affecting the mechanical and thermophysical properties of the final manufactured component. Increasing the understanding of metal additive manufacturing processes and the relevant parameters will boost mechanical design optimization strategies. Integrating additive manufacturing as a crucial element in optimization processes and the research of material parameters and quality assessment on additive manufacturing processes will enhance the capabilities of structural optimization techniques [22].

4. Conclusions

In this study, the integration of additive manufacturing as part of the structural optimization strategy with generative design techniques for direct-drive generator structures has been demonstrated to be a revolutionary and cost-effective method to produce highly efficient results. The flexibility of an integrated optimization process allows the development of an adaptative process to fit the application required. An optimized, lightweight structure has been generated, integrating not only the working condition loads and dynamic frequencies of the structure but also the manufacturing constraints tailored for our application. Controlling high-adaptative optimization strategies such as generative design techniques with an adequate understanding of additive manufacturing processes represents a revolution in structural optimization methods for direct-drive generator structures. Exploring these new integrated optimization techniques could provide a breakthrough in sustainable outcomes, not only in the efficiency of the final optimized components but also in the sustainability of the manufacturing process used.

Recent advances in metal additive manufacturing technologies represent an improvement in cost-effectiveness compared with conventional manufacturing subtractive processes for small-volume production, showing a great future prospect for the field of structural optimization strategies for high-performance topologies. However, a better understanding of design for additive manufacturing approaches is needed as it represents a complete reversal in thinking in comparison to conventional manufacturing processes, as most mechanical design optimization techniques are based on subtracting knowledge.

The integrated structural optimization strategy with generative design techniques and additive manufacturing constraints produced a fit-for-purposed result with a weight reduction of over 22% in comparison with conventional structural optimization techniques, while improving the dynamic behavior of the structure against the excitation frequencies of the generator and maximizing the sustainability of the manufacturing process.