Deep Learning-Based Real-Time 6D Pose Estimation and Multi-Mode Tracking Algorithms for Citrus-Harvesting Robots

Abstract

In the agricultural sector, utilizing robots for tasks such as fruit harvesting poses significant challenges, particularly in achieving accurate 6D pose estimation of the target objects, which is essential for precise and efficient harvesting. Particularly, fruit harvesting relies heavily on manual labor, leading to issues with an unstable labor supply and rising costs. To solve these problems, agricultural harvesting robots are gaining attention. However, effective harvesting necessitates accurate 6D pose estimation of the target object. This study proposes a method to enhance the performance of fruit-harvesting robots, including the development of a dataset named HWANGMOD, which was created using both virtual and real environments with tools such as Blender and BlenderProc. Additionally, we present methods for training an EfficientPose-based model for 6D pose estimation and ripeness classification, and an algorithm for determining the optimal harvest sequence among multiple fruits. Finally, we propose a multi-object tracking method using coordinates estimated by deep learning models to improve the robot’s performance in dynamic environments. The proposed methods were evaluated using metrics such as $ADD$ and $ADDS$, showing that the deep learning model for agricultural harvesting robots excelled in accuracy, robustness, and real-time processing. These advancements contribute to the potential for commercialization of agricultural harvesting robots and the broader field of agricultural automation technology.

1. Introduction

The agricultural sector faces significant challenges due to an aging farming population and the increasing reliance on manual labor, particularly in tasks such as fruit harvesting. These challenges lead to an unstable labor supply and rising operational costs, necessitating innovative technological solutions to maintain productivity and sustainability in agriculture [1]. Among these solutions, agricultural harvesting robots have gained significant attention for their potential to address these issues by enabling fast and accurate harvesting [2]. However, the effectiveness of these robots is heavily dependent on their ability to accurately estimate the 6D pose of fruits, which is crucial for recognizing and optimally approaching the target for harvesting [3].

Despite the progress made in developing 6D pose estimation techniques, the existing methods often face limitations when applied in the dynamic and unstructured environments typical of agriculture. Previous studies have predominantly focused on industrial applications where the environmental conditions are controlled, and the objects are more uniform in shape. These approaches often struggle with the variability of lighting, occlusions, and the complex geometries of fruits found in agricultural settings. As a result, inaccuracies in pose estimation can lead to reduced efficiency and effectiveness in robotic harvesting systems.

In recent research, various approaches have been developed to enhance robotic harvesting systems. For instance, a study proposed a method based on a single-stage object detector (SSD) to detect apples, leveraging stereo cameras and inverse kinematics for harvesting [4,5]. Another study introduced rotated YOLO (R-YOLO) based on YOLOv3, which predicts rotated bounding boxes to improve the accuracy of strawberry harvesting points [6,7]. Additionally, other studies employed Mask R-CNN for instance segmentation, obtaining pixel-level position information on crops to assist in precise fruit harvesting [8,9,10,11]. These studies demonstrated significant progress in the field but still faced challenges related to real-time accuracy and adaptability in unstructured environments.

In comparison with these studies, this study emphasized the innovation of our approach by focusing on the specific challenges posed by agricultural environments. We propose a more robust and adaptable 6D pose estimation model that can overcome the limitations of existing systems. This study not only addresses real-time accuracy and adaptability in unstructured environments but also contributes to developing a more efficient robotic harvesting process. In a comparison of the proposed research plan with the state-of-the-art methods, the novelty and significance of our work became even more evident.

The objective of this study was to develop a deep learning model that accurately estimates the 6D pose of fruits, thereby improving the performance and accuracy of fruit-harvesting robots. This research aimed to overcome the limitations identified in previous studies by addressing the specific challenges posed by agricultural environments. By constructing datasets in both virtual and real environments, and employing advanced deep learning techniques, this study sought to improve the robustness and accuracy of pose estimation models used in agricultural robotics. Additionally, we propose a method for labeling the harvesting order and efficiently tracking targets in situations where there are multiple suitable fruits, based on the recognition of ripeness. Ultimately, this research contributes to the advancement of agricultural automation technology and enhances the commercialization potential of agricultural harvesting robots.

This article proposes several approaches to enhance the performance of fruit-harvesting robots. First, we propose a method to build a dataset named HWANGMOD. This method can be used in both virtual and real environments and utilizes Blender and BlenderProc to automatically generate large-scale fruit datasets in virtual environments. Furthermore, the method includes techniques for collecting data from real-world environments via a mapping process between 2D images and 3D objects and can effectively build a variety of large datasets required for the model’s training.

Second, the article provides a detailed explanation of the training process and hyperparameter settings for the EfficientPose-based 6D pose estimation model. This process was designed to enable accurate ripeness classification and 6D pose estimation of fruits, playing a crucial role in allowing the robot to identify and harvest ripe fruits.

Third, an algorithm for determining the harvest sequence among multiple suitable fruits with estimated 6D poses is proposed. This algorithm allows for the creation of efficient harvesting plans based on the camera coordinate system of the agricultural harvesting robot, helping the robot to systematically and efficiently harvest the fruits.

Finally, we propose a method to track multiple citrus objects by leveraging the coordinates estimated by deep learning models. This tracking method enhances the robot’s ability to effectively recognize and navigate toward multiple fruits while in motion, improving its performance in dynamic environments.

In the experiments, the proposed methods were evaluated by comparing the performance of the EfficientPose model and the YOLOv5-6D model on a single-object dataset using the $ADD$ (average distance of the model’s points) and $ADDS$ (average distance of the model’s points for symmetric objects) metrics. YOLO stands for you only look once, which is a popular object detection model that has been extended in this case to support 6D pose estimation. Subsequently, the effectiveness of the proposed model’s 6D pose estimation and ripeness classification, and the proposed harvesting and tracking algorithms were assessed in real-time scenarios involving multiple objects in both virtual and real environments. The experimental results demonstrated that the EfficientPose model excelled in accuracy, robustness, and real-time processing capability, proving to be a critical factor for the practical deployment of agricultural harvesting robots.

2. Related Work

2.1. Camera Calibration

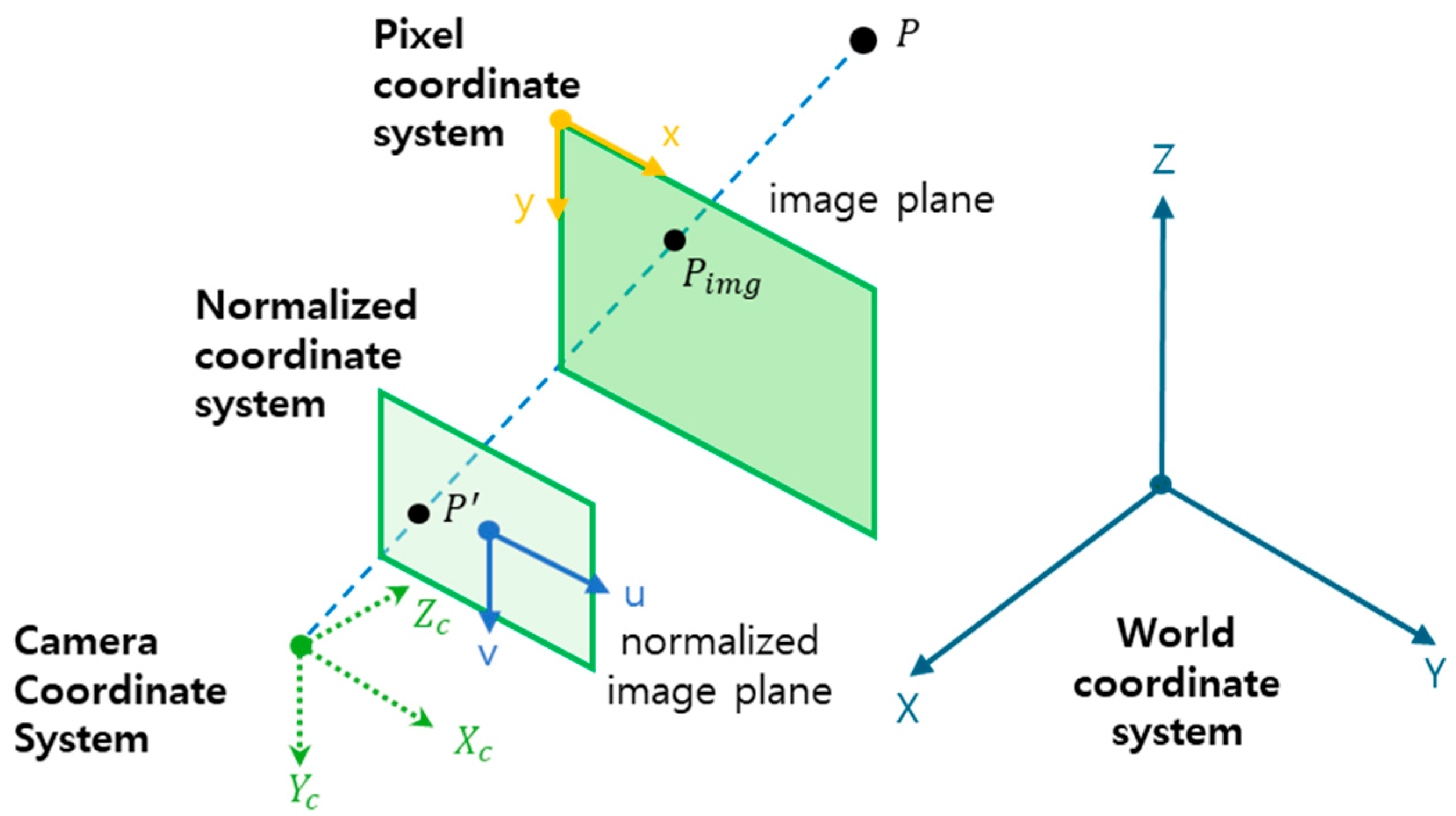
The real world is three-dimensional, but the world shot with a camera transforms into a two-dimensional image. The point at which a 3D point is projected onto an image is influenced by the position and orientation of the camera at the time of capture. The actual image is affected by the mechanical parts inside the camera, such as the lens, the distance to the image sensor, and the angle. Therefore, to accurately calculate the projected positions of 3D points in the image or to reconstruct the 3D spatial coordinates from the image’s positions, it is necessary to remove the internal factors of the camera [1].

In this study, we used the Intel Realsense D435i, a stereo camera system that includes two individual cameras. Each camera can be modeled using the pinhole camera model. The stereo camera’s setup allows for depth estimation by calculating the disparity between the images captured by the left and right cameras, which are separated by a known baseline distance.

Camera images are obtained by projecting points in 3D space onto a 2D plane image. The transformation relationship between the 3D world coordinates and the 2D image’s coordinates in the pinhole camera model can be expressed as Equation (1).

$$s\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& skew\_c{f}_x& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_1\\ r_{21}& r_{22}& r_{23}& t_2\\ r_{31}& r_{32}& r_{33}& t\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]=A\left[R|t\right]\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right],$$

(1)

where $X,Y,Z$ is the coordinate of a 3D point in the world coordinate system, $\left[R|t\right]$ is the rotation and translation matrix for transforming the world coordinates to the camera coordinates and represents the external parameters of the camera, and $A$ denotes the internal parameters of the camera. The internal parameters include the focal lengths $f_x$ and $f_y$ along the $x$ and $y$ axes, the coordinates of the principal point $c_x$ and $c_y$, and $skew\_c{f}_x$, which accounts for any skewness between the $x$ and $y$ axes. $A$ and $\left[R|t\right]$ are collectively called the camera matrix. The internal parameters include the intrinsic parameters of the camera, such as the focal length, aspect ratio, and principal point. The extrinsic parameters were optimized by minimizing the reprojection error, which is the difference between the projected 2D points calculated using the estimated parameters and the actual observed 2D points on the checkerboard. This optimization ensures that the camera model accurately represents the real-world setup, leading to more precise 3D-to-2D point transformations in subsequent processes. The external parameters are related to the geometric relationship between the camera and the external space, such as the camera’s installation height, pan, and tilt [2]. Camera calibration using these variables involves finding the transformation relationships and parameters between the 3D spatial coordinates and the 2D image coordinates, as shown in Figure 1.

Figure 1. The camera and world coordinate systems.

As shown in Figure 1, 3D coordinate transformation is the process of representing the position of a point or object in space from one coordinate system to another [3]. Specifically, it provides a method for transforming the 3D world coordinate system to the camera coordinate system. This transformation aims to convert a point $X,Y,Z$ defined in the world coordinate system to a point $X_c,Y_c,Z_c$ in the camera coordinate system. The world coordinate system is defined with the ground as the $X,Y$ plane and the $Z$ axis pointing upwards. In contrast, the camera coordinate system is defined with the optical axis of the camera as the $Z_c$ axis, the right direction as the $X_c$ axis, and the downward direction as the $Y_c$ axis. The position of the camera is defined as the point $x_1,y_1,z_1$ in the world coordinate system. The angles of the camera are defined as roll, pitch, and yaw. Roll is the rotation angle of the camera up and down, pitch is the rotation angle left and right, and yaw is the rotation angle around the optical axis. This transformation is performed by combining a series of rotational transformation matrices. It involves constructing rotation matrices for the $X,Y$, and $Z$ axes using the camera’s yaw, pitch, and roll angles, and combining them to obtain the final transformation matrix. Figure 2 assumes that the camera and world coordinate systems, which are 3D coordinate systems, are fixed, as shown in the figure. When converting this to a single coordinate system, the method above is used when constructing a dataset.

Figure 2. The 3D coordinate system of the camera and the world.

2.2. 3D Model Extraction

To utilize a deep learning model, it is crucial to refine and optimize the dataset. Additionally, the coordinate system of the 3D object model of the harvested fruit is important for the robot to manipulate and reach the harvest point based on the estimated 6D pose. Based on the calibration between the 3D object, camera, and 2D image mentioned earlier, this section explains the extraction of 3D object models and the structure of the dataset for training the deep learning model. The structure of this dataset forms the basis for constructing a customized dataset for agricultural harvesting robots.

To estimate the 6D pose of an object, it is essential to extract the 3D model of the object. Therefore, a portable high-precision 3D scanner, EinScan Pro 3D, was used to perform scanning in various modes. Using the scanner and an automatic turntable, the point cloud data of the object were obtained eight times per full rotation utilizing various markers on the turntable, thus extracting the 3D object model. Figure 3 shows the process of creating a 3D fruit object using a 3D scanner and a turntable.

Figure 3. Extracting a 3D model from a real fruit.

The 3D object model obtained using the 3D scanner was stored in PLY (Stanford Triangle Format) file format. PLY is a computer file format used to store three-dimensional data from 3D scanners. Its structure is based on a list of flat polygons, allowing for a relatively simple description of a single object. PLY format provides the flexibility to store various attributes such as color, transparency, the normal surface, texture coordinates, and data confidence values. Additionally, one of the features of the PLY file format is the ability to assign different properties to the front and back of polygons, enabling more precise modeling. There are two versions of the PLY file format: ASCII (American Standard Code for Information Interchange) and binary. The ASCII version stores data in a text-based format that is human-readable. This format makes it easier to understand and edit the file content but can result in larger file sizes and slower processing speeds. In contrast, the binary version stores data in binary format, reducing the file’s size and increasing the reading/writing speeds. This study used the ASCII version of the PLY file format to process 3D objects for input into the deep learning model [12].

After extraction of the 3D object model using the scanner, the model was textured, the axis and origin were modified, and ASCII format and triangulation were performed to adjust the number of polygons. This was achieved using Blender. Blender is a powerful open-source 3D graphics software widely used for modeling, rendering, animation, simulation, video editing, and game creation [13]. It provides users with a complete 3D pipeline and offers strong functionality, particularly in 3D modeling and texturing.

The post-processing steps for the 3D object model extracted with the scanner using Blender were as follows. Texturing enhanced the visual quality of the model. Blender’s texture mapping function was used to give the model a realistic appearance. This process can add colors, patterns, or other visual details to the model, allowing it to represent the fruit realistically. Modifying the axis and origin of the object is crucial for adjusting the model’s placement and orientation. Blender allowed the adjustment of the model’s origin (center) and the rotation of the axes to change the model’s direction. This is important for setting a consistent axis when the model is transferred to other 3D environments or applications.

Converting the model to an ASCII format file using Blender was a step to enhance data compatibility. ASCII format files, being text-based, increase compatibility with other software or systems. The triangulation process in Blender involves splitting complex polygon meshes into triangles to improve their rendering efficiency. This is essential for enabling real-time rendering and is important when creating datasets in an automated rendering environment. Finally, Blender’s mesh optimization tools can be used to reduce the number of polygons and adjust the model’s size. This process maintains the model’s detail while reducing the file’s size and shortening the rendering time. These steps are crucial for efficient memory usage and fast loading times. Figure 4 illustrates the 3D coordinates of the fruit modeled in Blender after scanning with the 3D scanner.

Figure 4. Coordinate system of 3D fruit model.

To implement a method for 6D pose estimation of objects using deep learning, a large-scale training dataset composed of various parameters, including input images and ground truth labels, is required. However, generating relative motion and rotation information in 3D space from 2D images is highly inaccurate and challenging. Therefore, this article presents a method for constructing a dataset by automatically rendering a large-scale virtual dataset and combining it with real-world datasets in appropriate proportions. The parameters included in each dataset and the structure of the datasets are explained.

The structure of the dataset for training the proposed model follows the BOP (Benchmark for 6D Object Pose estimation) dataset format, a benchmark for 6D object pose estimation. BOP datasets are used to accurately estimate the position and orientation of objects in various real-world environments. BOP datasets are provided in various forms depending on the purpose, such as Linemod, T-LESS, ITODD, and YCB-V. Among these, the Linemod dataset plays a significant role in 6D object pose estimation. This dataset includes 15 household objects with different colors, shapes, and sizes but no textures [14]. However, the Linemod dataset provides images with various backgrounds but can only estimate one type of object and cannot estimate the 6D pose when the object is occluded.

To address these limitations, the HWANGMOD dataset was proposed to estimate multiple objects’ poses simultaneously and determine the optimal time for harvesting. Furthermore, it could accurately estimate the 6D pose of fruits even when they were partially obscured by obstacles such as leaves. While the Linemod dataset focuses on basic 6D pose estimation, HWANGMOD is better suited for complex scenarios in open-field environments where agricultural harvesting robots operate, considering the occlusion of multiple fruits. Unlike traditional benchmark datasets, the proposed dataset includes a text data file that indicates the presence or absence of each object class. This file provides refined information on the inclusion of various fruit classes in each scene and details how many times each fruit appears in the entire dataset. In this article, we refer to this information as “valid poses”, and this approach allowed the inclusion of occlusion data in the training dataset.

2.3. Deep Learning Model

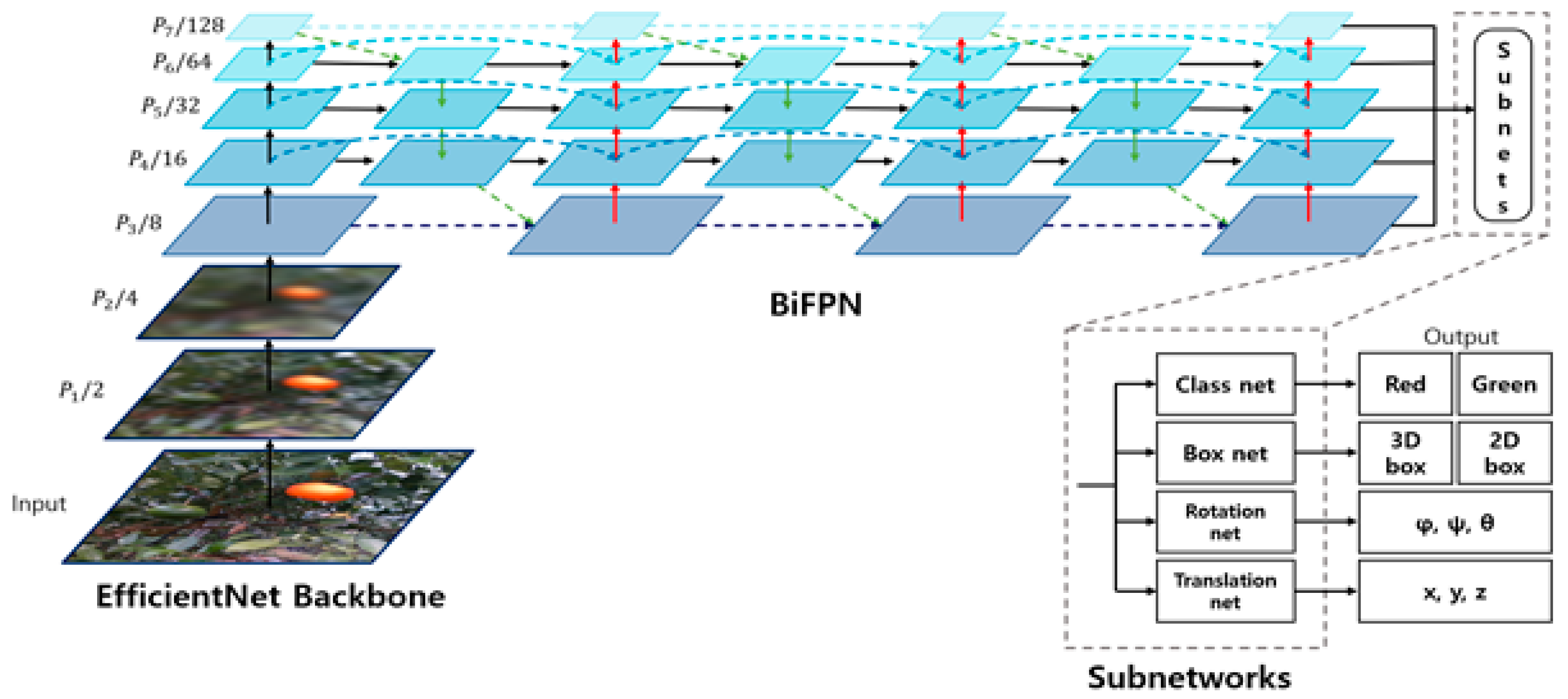
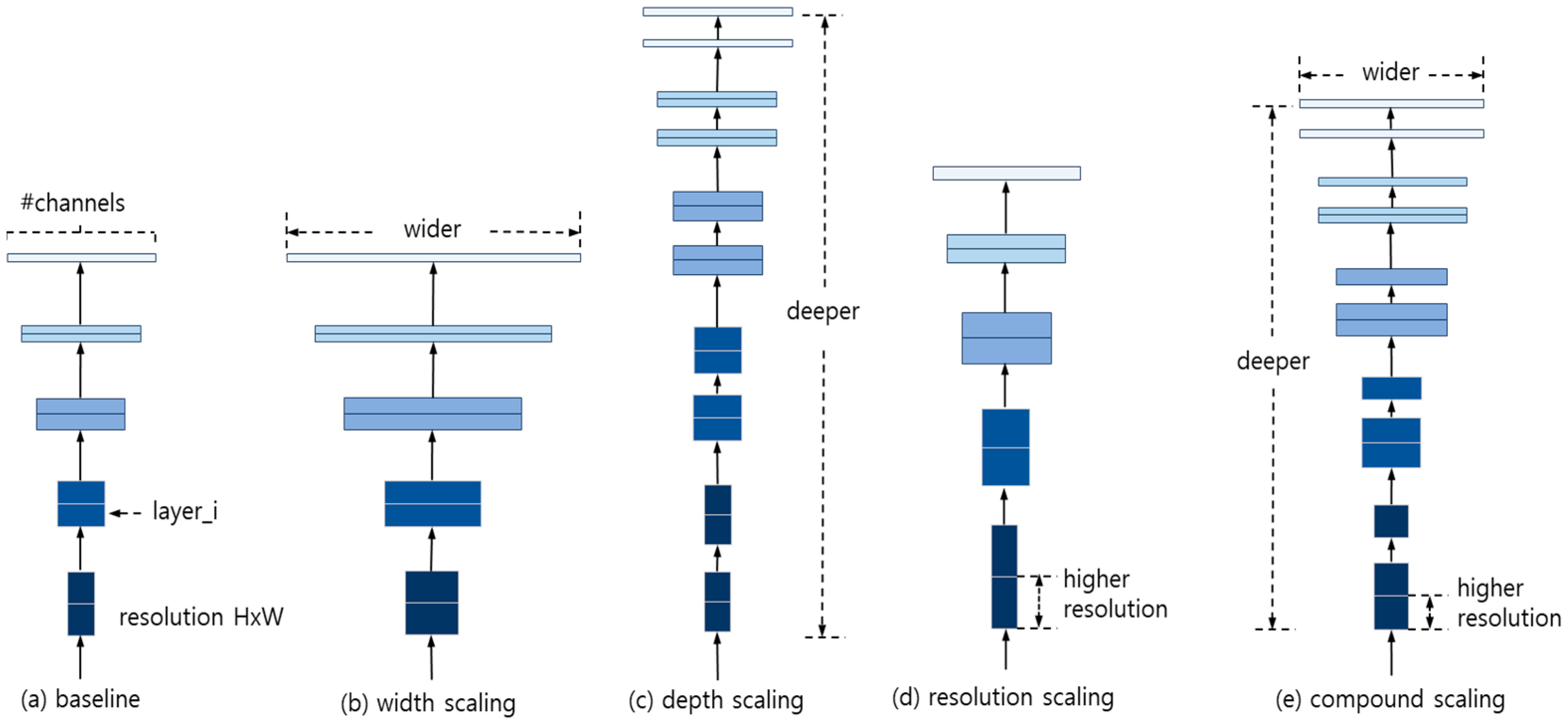
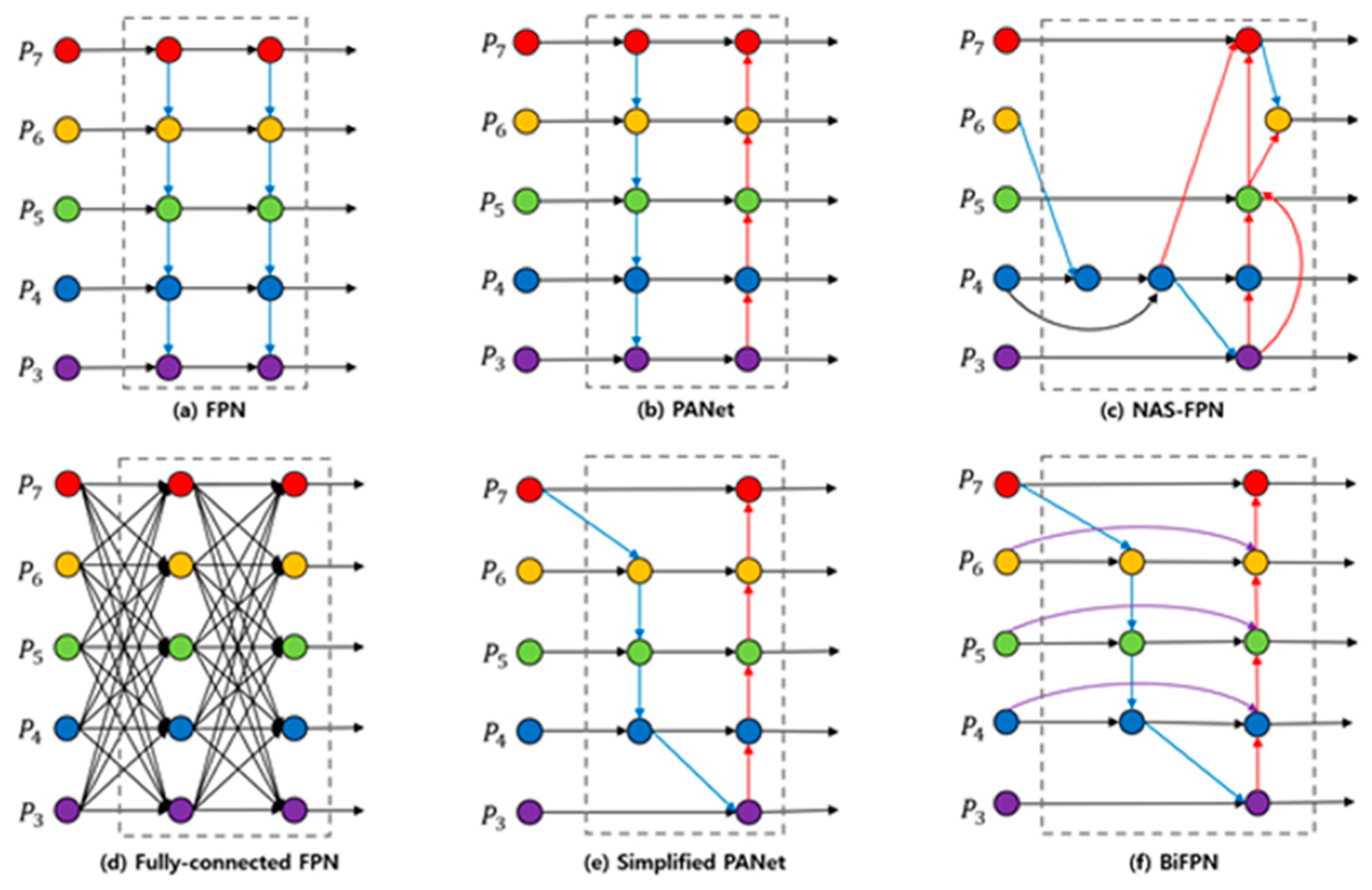
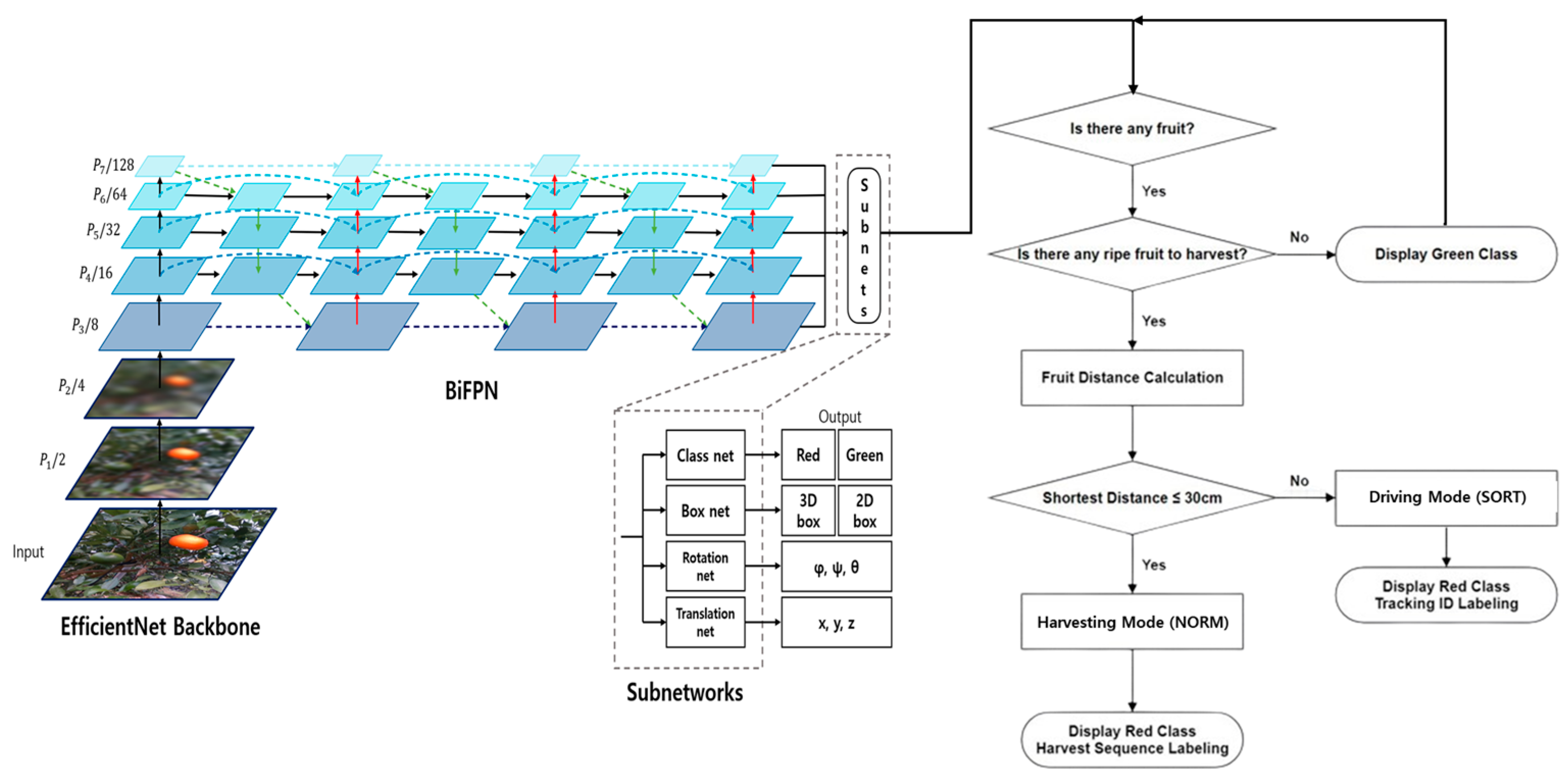
The deep learning model proposed in this article was based on EfficientPose [15], a model that accurately estimates the 6D pose of objects in real-time using RGB data. Instead of expanding the existing network structure in the image classification part, this model adopts the compound scaling strategy of EfficientNet [16], which introduced a compound scaling mechanism to balance the network’s depth, width, and input image resolution through a single factor. Additionally, it effectively performs feature extraction and information fusion for objects of various sizes and shapes by utilizing the bidirectional feature pyramid network (BiFPN) [17]. Using the feature maps obtained from the BiFPN at various levels, it can accurately predict the 6D pose of objects without separate post-processing.

EfficientNet is one of the deep learning models that excel in image classification. Previous studies scaled either the depth, width, or image size to enhance the model’s performance. However, EfficientNet introduces a compound scaling mechanism that balances the relationship between depth, width, and image size, as shown in Figure 5. This allows EfficientNet to achieve higher accuracy with fewer parameters compared with other models, which generally increase their accuracy with more parameters.

Figure 5. Scaling all three factors.

The features and information extracted through the compound scaling mechanism of the backbone model require a fusion process. BiFPN, which extends the feature pyramid network (FPN), effectively fuses information by delivering features bidirectionally. This process enables the extraction and utilization of features for objects of various sizes and shapes more effectively.

BiFPN simplifies the pyramid of feature maps, where the size of all the feature maps and the depth of the network layers differ, by proposing a method for bidirectional fusion of the feature maps. This involves adding edges from the input features to the output nodes at the same level without additional computation, reducing the computational cost while achieving high performance. Figure 6 shows various attempts to improve the structure of the feature pyramid network, and it confirms that the BiFPN structure is a bidirectional structure using both top-down and bottom-up pathways.

Figure 6. Various structures based on feature pyramid network (a–f). The different colors of the dots represent feature maps at various pyramid levels (P3 to P7), corresponding to distinct spatial resolutions for detecting objects of different sizes.

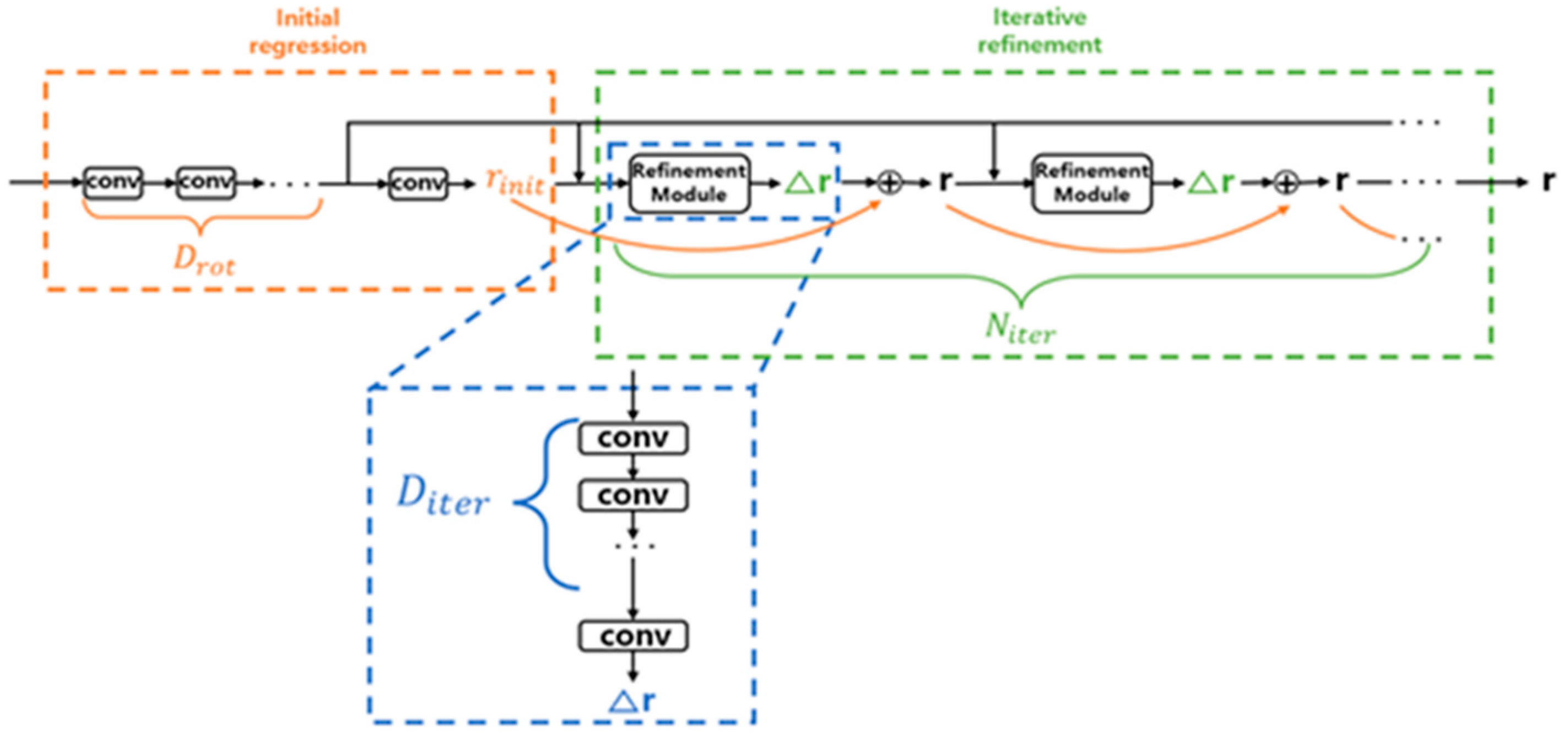
Using the feature maps obtained from the BiFPN, the 6D pose of objects and the 2D bounding boxes and classes were predicted. Following the backbone and the bidirectional feature pyramid network, the EfficientDet model included four sub-networks. This allowed for highly accurate 6D pose estimation without the need for separate post-processing. The prediction of 2D bounding boxes and classes followed the same approach as the EfficientDet model, while the rotation and translation sub-networks for 6D pose estimation were as follows. The rotation network used axis angles, which offer better performance and fewer parameters compared with quaternions. The architecture of the rotation network, serving as an initial regression and iterative refinement module, is shown in Figure 7 [15]. Each convolutional block consists of depth-wise separable convolution layers followed by group normalization and SiLU activation. Additionally, the architecture of the refinement module of the rotation network is depicted in the blue section at the bottom of Figure 7. The refinement module’s architecture also consists of depth-wise separable convolution layers, followed by group normalization and SiLU activation.

Figure 7. The rotational network’s architecture with the initial regression and iterative refinement modules.

The translation network, which had a structure similar to the rotation network, output a 3D translation vector $t$ for each anchor box. Instead of predicting $t={(t_x,t_y,t_z)}^T$ directly, it used an approach inspired by PoseCNN [18]. It predicted the center point $c={(c_x,c_y)}^T$ of the 2D image and the distance $t_z$. This means that it predicted the relative values of $t_x,t_y,t_z$ rather than the absolute 3D translation vector $t$. The relative 3D translation vector extraction method used the center point $c_x,c_y$ of the 2D image and the distance $t_z$. Additionally, the model predicted the pixel-wise offset from the center of the anchor box to the center point of the object, as shown in Figure 8.

Figure 8. Process of center point estimation in the 2D image plane including fruit.

2.4. Object Labeling Based on Driving and Harvesting Mode

To operate the agricultural robot, it is necessary to provide recognition results according to the harvesting and driving modes. To this end, technologies for sorting the harvesting order and tracking multiple fruits during driving were added to the deep learning model.

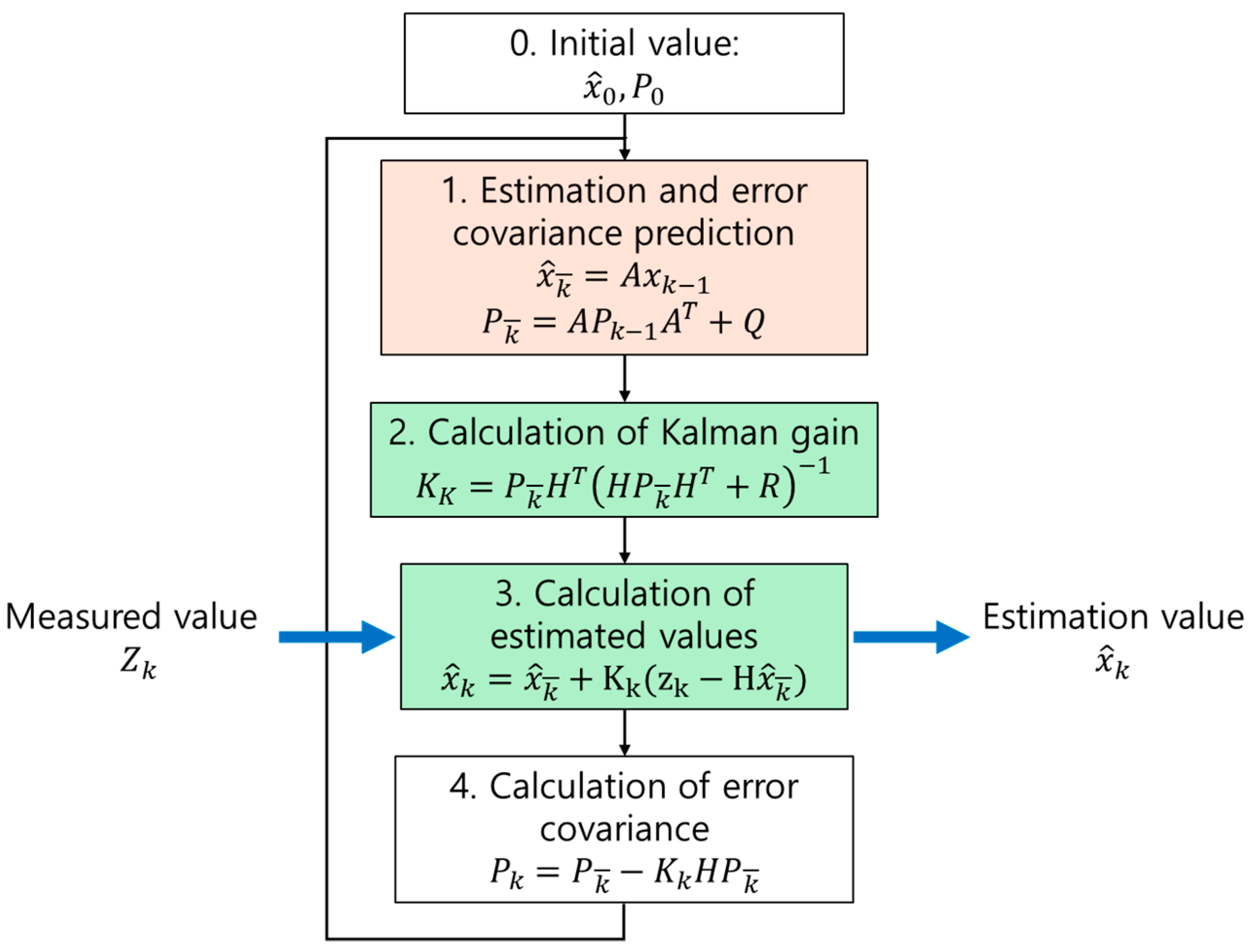
After the model had recognized fruits, the SORT (Simple Online and Realtime Tracking) algorithm was used to sort the harvesting order during the harvesting process of the agricultural robot. The fruits were recognized and represented by 2D bounding boxes, allowing each fruit to be tracked in real time. SORT tracks objects by finding the association between objects in the previous frame and the current frame, creating a movement path. It uses a Kalman filter to predict the current position of objects based on their previous position [19].

The Kalman filter operates via the following steps. First, in the prediction step, the Kalman filter predicts the current state and error covariance based on the previous state. This is mathematically represented by the equations ${\widehat{x}}_{\overline{k}}=A{x}_{k-1}$ for predicting the state and $P_{\overline{k}}=A{p}_{k-1}{A}^T+Q$ for predicting the error covariance. In this step, the system estimates the fruit’s current position based on its previous position and the motion model. Next, in the correction step, the Kalman gain $K_k=P_{\overline{k}}{H}^T{(H{P}_{\overline{k}}{H}^T+R)}^{-1}$ is calculated, and the estimated state is corrected by incorporating the actual measurement. This is achieved using the equation ${\widehat{x}}_k={\widehat{x}}_{\overline{k}}+K_k(z_k-H{\widehat{x}}_{\overline{k}})$. In this step, the difference between the predicted position and the actual measured position is used to refine the estimate.

The algorithm flow is shown in Figure 9. Because it is based on measurements over time, accurate estimation is possible. Each estimation operation is divided into two steps: prediction, which calculates the expected state, given the previous time’s input, and correction, which calculates the difference between the predicted state and the actual measured state [20].

Figure 9. Flowchart of the Kalman filter.

Using the bounding box coordinates $x\_\min$, $y\_\min$, $x\_\max$, and $y\_\max$ of the 2D bounding box estimated through the real-time camera image, the state of the 2D bounding box was modeled as shown in Equation (2)

$$X={[u,v,s,r,\dot{u},\dot{v},\dot{s}]}^T,$$

(2)

where $u$ represents the horizontal position of the object’s center pixel, $v$ represents the vertical position of the object’s center pixel, $s$ represents the area of the object’s 2D bounding box, and $r$ represents the aspect ratio of the object’s 2D bounding box. The target state $\dot{u},\dot{v},\dot{s}$ of the next frame was then predicted.

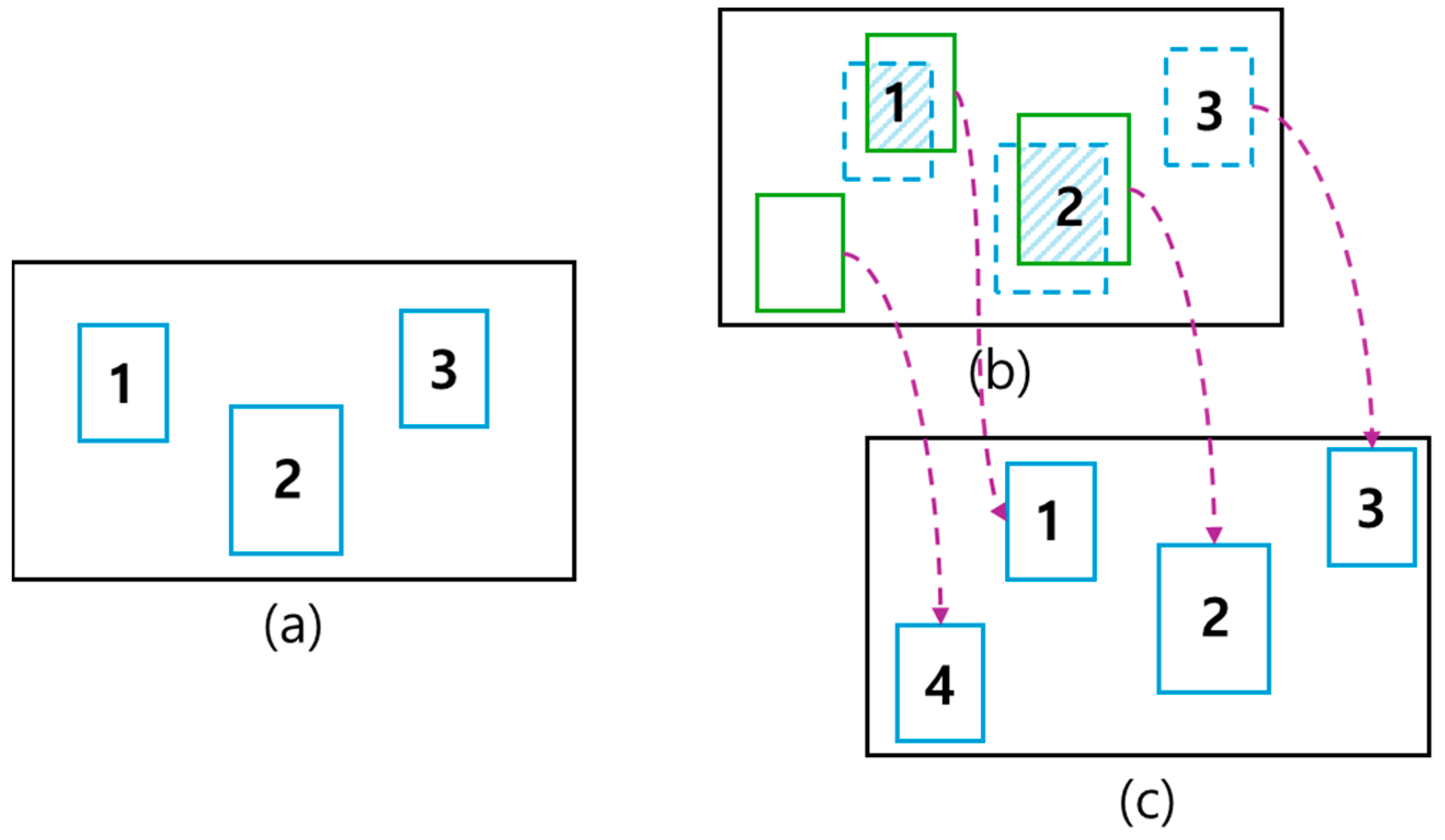
When the object of recognition was associated with the target object, the detected 2D bounding box was used to update the target object’s state, and the velocity component was optimized through the Kalman filter. If the target object was not associated with the object recognition, a linear velocity model was used to predict a simple state. If the object recognition was not associated with the target object, the target object’s ID was deleted.

After predicting the target object using the Kalman filter as described above, the Hungarian algorithm was used to optimize the data’s association. The predicted values obtained through the Kalman filter were associated with newly recognized objects in the next frame. The association was obtained by calculating the assignment cost matrix using the $IoU$ (intersection over union) distance between the recognized value of each existing target and all predicted 2D bounding boxes. The Hungarian algorithm was then used for assignment [21]. The $IoU$ is calculated as follows:

$$IoU={\displaystyle \frac{\left|A\cap B\right|}{\left|A\cup B\right|}},$$

(3)

If the overlap area of the recognized object was smaller than $Io{U}_{\min }$, it was not assigned and $Io{U}_{\min }$ was applied. If a target was temporarily occluded by another object, the $IoU$ distance preferred similar-sized distances, thus only the occluding object was detected. This meant that the occluded object was not associated as before, and both targets could be adjusted along with the occluding object. Figure 10 shows the association of the object recognition results from the previous frame through the Kalman filter with the object recognition results from the current frame using the Hungarian algorithm, assigning IDs to each of the objects.

Figure 10. The association of the fruit object recognition results. (a) Result from the previous Kalman filter, where numbers 1, 2, and 3 represent the tracked fruit objects. (b) The green box represents the current detection results, and after performing $IoU$ between these two (where 1, 2, and 3 refer to the previous objects and 4 is the newly detected object), a pair is found using the Hungarian filter, and an ID is assigned as shown in (c).

To determine the harvest sequence, the commonly used Euclidean distance was utilized to calculate the distance between two points. However, since the extracted harvest-ready fruits had positions in 3D space $x,y$ and $z$, it was necessary to define the Euclidean space using the Euclidean distance and then extract the corresponding Euclidean norm [22]. Assuming the camera was located at the origin of the world coordinate system, the Euclidean norm from the origin to the position $x,y,z$ of the harvest-ready fruit could be computed. Each coordinate represents the actual distance between the camera and the fruit. Using this information, the harvesting robot could accurately determine the position of each fruit and move along the optimal path. By utilizing the Euclidean norm, the algorithm prioritized the closest fruit for harvesting among multiple fruits.

3. Proposed Method

3.1. Building a Dataset

In this study, the creation of a large-scale dataset, including automatically renderable virtual datasets, utilized the BlenderProc pipeline, which combines Blender and PyTorch [23]. This enabled the generation and processing of the large-scale 3D datasets necessary for training deep learning models for 6D object pose estimation. The following describes the rendering process, the data used, and the structure and content of the generated dataset.

In the Blender environment, the 3D fruit models of the ripe fruit class (red) and un-ripe fruit class (green), previously scanned, were uploaded. Then, the position coordinates and rotation angles were randomly rendered. Thresholds were set to ensure that the two fruit objects did not exceed a certain cubic volume, and images of the two objects, background, and lighting were captured through the camera. Additionally, the camera’s 6D pose was randomly arranged to ensure that both fruits could be captured. If one object was completely occluded by another, it was named an occlusion dataset with the class name “valid poses” and rendered automatically.

This automatic rendering algorithm generated $n$ scenes, each captured twice by the camera, resulting in $2n$ scenes being stored. An automatic rendering environment was established to automatically obtain the internal and external parameters of the camera. Thus, $2n$ RGB and depth images, a camera.json file containing the camera’s parameters used for rendering, a scene_camera.json file containing the camera’s parameters for each image, and a scene_gt.json file containing the parameters of the relationship between the camera and objects in the scene were automatically generated. Additionally, the mask and mask_visib were represented by a single image showing the information on the mask for each object in the $2n$ scenes, expressed in grayscale from 0 to 255. The mask’s information was extracted using RGB and depth images, storing information on whether all objects were present in the scene or which class was occluded. Subsequently, a scene_gt_info.json file containing the ground-truth pose’s metadata, such as the bbox_obj parameter with the 2D bounding box information $(x,y,h,w)$ and the px_count_all parameter with the pixel count of the object’s silhouette, was generated to construct the virtual dataset. Figure 11 shows the automatic rendering environment established using Blender and BlenderProc. Figure 12 illustrates the RGB and mask images from the automatically rendered dataset in the virtual environment.

Figure 11. Auto rendering of virtual environment using Blender.

Figure 12. RGB and mask images automatically rendered in the virtual environment.

Extracting the 6D pose values of objects in a virtual environment yields accurate results, but datasets from real environments are also necessary to achieve high recognition rates. Therefore, we proposed a dataset construction environment using SolvePnP and QT Creator to match 3D object models and extract 6D poses from 2D images.

SolvePnP estimates the 6D pose (position and orientation) of an object using the camera’s internal parameters and several points on the 2D image. This method is widely used in computer vision and is essential for obtaining 3D information from 2D images. By utilizing point matching, the 3D object model of the scanned fruit is matched with corresponding points on the 2D image [24]. Pose estimation is then carried out using the SolvePnP algorithm, and the 6D pose of the fruit is estimated based on the matched points. The internal parameters of the camera used to capture the actual data are utilized to extract accurate 6D poses.

To efficiently perform the algorithm that extracts the pose of the 3D fruit model using point-to-point matching in 2D images, a graphical user interface (GUI) was developed using QT Creator. QT Creator is used for cross-platform development of GUI applications and provides a user-friendly interface to facilitate the matching process. This interface includes algorithms for loading and displaying images, a 3D object viewer, matching tools, and saving the matched results in a dataset format.

In the proposed method, images were loaded and displayed by accessing the 2D image location of fruits containing two classes that were acquired. The 3D fruit objects to be point-to-point matched were then visualized, and coordinate systems were also brought in to match the positional and rotational information. Interactive tools are essential for connecting corresponding points by adjusting the rotation, depth, and position to align the 3D fruit object with the image’s pose during point-to-point matching. This interactive tool interface was constructed using QT Creator.

Finally, a tool was developed for precise matching between the 3D object model and the 2D image by integrating the two algorithms mentioned above. This tool was used to estimate the accurate 6D pose (position and orientation) of the 3D object. By selecting points on the 3D model and linking them with corresponding points on the 2D image using the user-friendly interface, the pose of the 3D object was calculated and output to a data file, enabling construction of a dataset in real environments. Figure 13 shows the interface environment built for constructing the actual dataset. Figure 14 illustrates the RGB and mask images extracted from the real dataset in an actual environment.

Figure 13. Actual dataset construction using SolvePnP and QT Creator.

Figure 14. RGB and mask images constructed through point-to-point matching in a real environment.

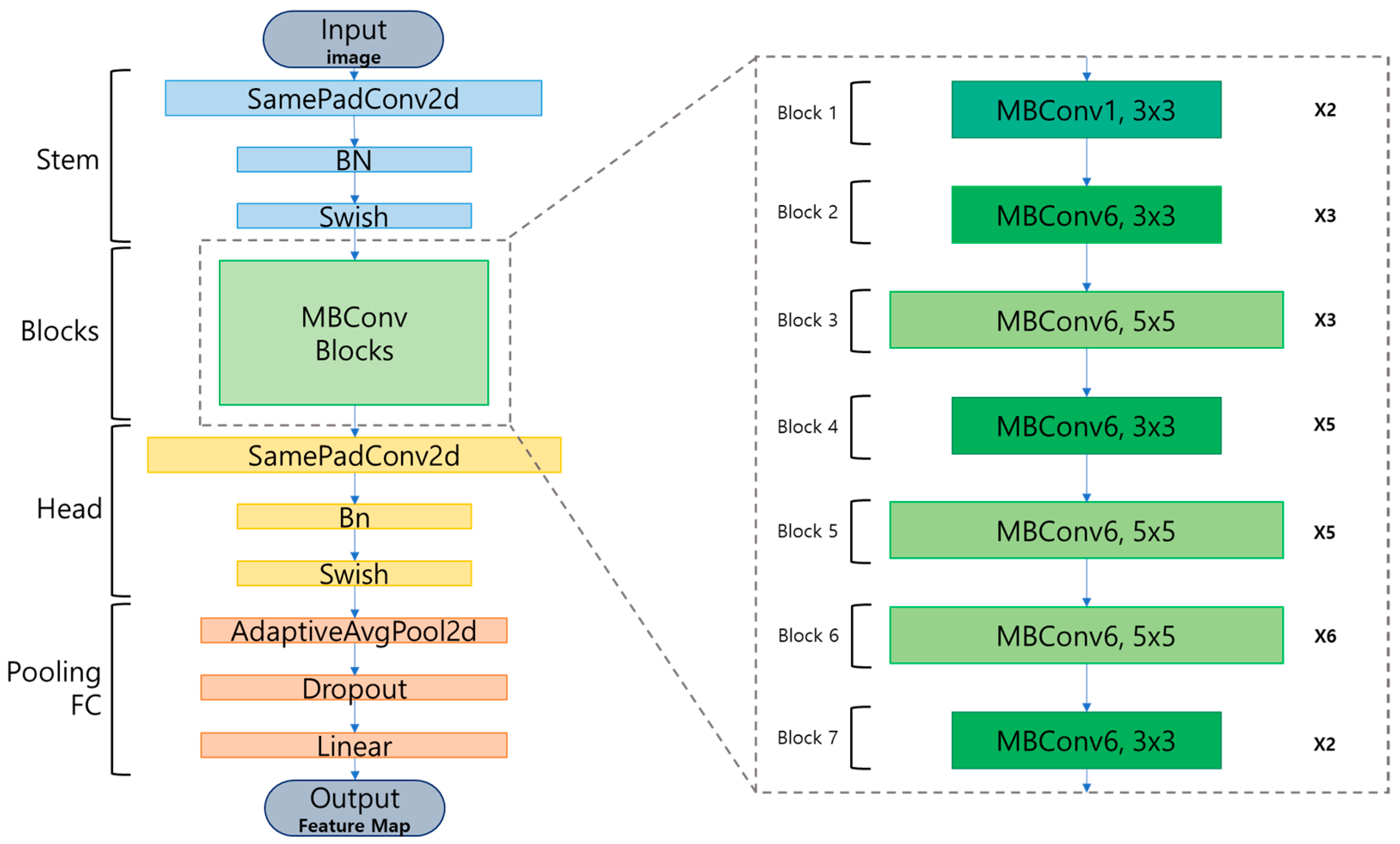
3.2. Deep Learning Model Architecture

The proposed model, based on EfficientPose, could distinguish between harvest-ready fruits (red class) and unripe fruits (green class). Additionally, the 6D pose of each fruit class was extracted for harvesting operations by agricultural robots. Training was possible using the HWANGMOD dataset, which includes both real and virtual datasets. The proposed model allows for flexible adjustment of image resolution according to the model’s backbone. Therefore, if the internal parameters of the camera used to create the dataset are known, it is possible to build and train the model on both real and virtual datasets without being restricted by the image resolution output by the camera, enabling the application of the model to various objects.

The EfficientPose model referenced in this study was originally developed for TensorFlow version 1. The backbone components of the algorithm, including EfficientNet, BiFPN, and the sub-networks, were designed to operate only on TensorFlow version 1. However, this imposed a limitation in utilizing the latest graphics processing units (GPUs). Therefore, the proposed model was modified to function on TensorFlow version 2, updating all the model’s functions and structures accordingly. This upgrade allows the core components of the model, including the backbone network, BiFPN, and sub-networks, to be utilized on the latest GPUs.

EfficientNet, used as the backbone in EfficientPose, is a network for feature extraction, as shown on the left side of Figure 15. The backbone structure responsible for feature extraction employs the model described earlier, with the compound coefficient $\varphi$ set to 3 to utilize compound scaling for depth, width, and resolution. During compound scaling, the parameters were adjusted to be 1.4 times deeper, 1.2 times wider, and with an input resolution of 896 × 896 compared with the base backbone model, forming a model with seven blocks. The seven blocks used as the backbone in the proposed model are shown on the right side of Figure 15. The model’s depth, width, and input image resolution varied, depending on the parameters used for compound scaling. Consequently, the model could be trained on the HWANGMOD dataset, which includes more complex and occluded data compared with models using the Linemod dataset that classify only one type of object, improving the accuracy of simultaneous multi-object tracking.

Figure 15. Backbone structure.

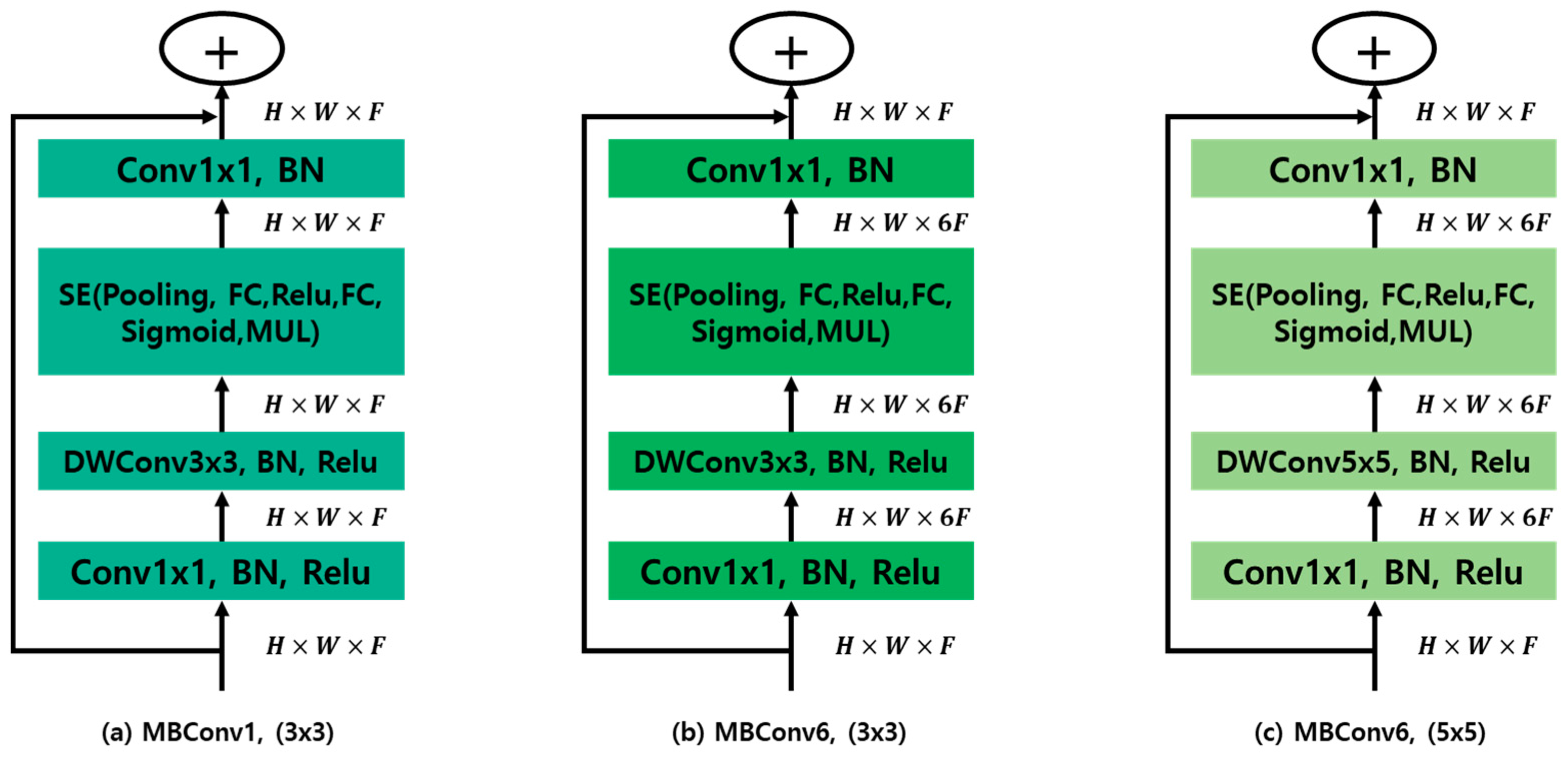
The MBConv blocks utilized in the proposed model were mobile inverted bottleneck convolution blocks. MBConv was designed as a lightweight block that optimizes the performance relative to the computational cost, making it ideal for efficient modeling. MBConv consists of three main components.

The first component is the 1 × 1 convolution layer (Conv1×1). This layer expands or reduces the number of input channels, adjusting the depth of each feature map to alleviate bottlenecks. Additionally, a batch normalization (BN) layer follows this layer, enhancing the network’s stability and speeding up learning. The second component is the depth-wise convolution layer [25]. This layer extracts spatial features by applying filters independently to each input channel. It significantly reduces the computational cost while maintaining performance. As shown in Figure 16, a 3 × 3 depth-wise convolution is typically used, but a 5 × 5 depth-wise convolution can also be used to capture a broader range of features. This layer is followed by BN and ReLU activation functions [26]. The third component is the SE (squeeze and excitation) block [27]. This block learns channel-wise interactions to emphasize the important features. The SE block consists of pooling fully connected layers (FC), ReLU, sigmoid, and multiplication operations. It learns and adjusts the importance of each channel, enhancing the model’s representational capabilities. Each MBConv block ends with an addition operation with the original input. This prevents information loss as the network deepens, and mitigates the problem of a vanishing gradient during backpropagation. This structure allows the model to optimize its performance while minimizing the computational cost. By employing these MBConv blocks, the proposed model can effectively balance computational efficiency and high performance, making it well-suited for applications in agricultural robotics, particularly for tasks requiring real-time processing and accuracy.

Figure 16. The MBConv structure used in the backbone.

The EfficientPose model can estimate 6D poses through four sub-networks from an input image. However, this model operates only in TensorFlow version 1 and cannot utilize high-resolution input images. Therefore, the proposed model addressed these limitations by utilizing the latest features and APIs of TensorFlow 2 to improve the performance and efficiency. Additionally, it increased the depth of the backbone through compound scaling parameters and optimized the flow of information between the features in the BiFPN part to enable more accurate object detection and segmentation. This improvement also leverages new functions in TensorFlow 2. Finally, the sub-networks, which perform predictions in the final stage of the model, were enhanced using TensorFlow 2’s improved performance to provide more precise predictions and reduce training time. These upgrades allowed the model to operate faster and more efficiently, taking advantage of the various benefits of the latest TensorFlow version to enhance the overall performance.

The proposed model has several advantages over the basic EfficientPose by modifying the data generator part. The model can accept high-resolution images as input. Additionally, it can simultaneously recognize multiple objects in real-time, outputting various labeled classes of fruits, and can also recognize occluded objects through dataset transformations. Therefore, the proposed deep learning model can determine the harvest readiness of fruits and estimate the 6D poses of various objects using the created datasets, regardless of the resolution.

Figure 17 shows the structure of the proposed model. The model comprises seven compound-scaled blocks as the backbone, BiFPN for fusion of the feature maps at various levels, and four sub-networks for the outputs (class, bounding box, rotation, and translation). The class network allows simultaneous estimation of multiple objects. In this study, this part was used to determine that some fruit was harvest-ready if its class was “red” and not harvest-ready if its class was “green”. The bounding box network estimates 2D bounding boxes of objects and combines them with 3D object information from the dataset to estimate the 3D bounding boxes. The rotation network estimates the rotation values of the 6D poses for each detected object. Finally, the translation network estimates the position values of the 6D poses for each detected object.

Figure 17. The model’s structure.

3.3. Object Labeling and Tracking According to the Driving and Harvesting Mode

In this study, we applied the SORT algorithm to predict the 2D bounding boxes for object tracking in a fruit-harvesting robot. The SORT algorithm integrates an object detector, a Kalman filter, $IoU$ distance calculation, and the Hungarian algorithm to enable real-time object tracking. The object detector predicts the position of objects in each frame by generating bounding boxes in the format $[x,y,a,h]$, where $x$ and $y$ represent the center coordinates of the bounding box, a is the aspect ratio, and h is the height. Using the information on bounding boxes from previously tracked objects, the Kalman filter predicts the object’s position in the current frame. The Kalman filter estimates the object’s trajectory and provides a corrected position to maintain tracking continuity, resulting in predictions of the bounding boxes for the next frame.

Next, we calculated the $IoU$ values between the detected bounding boxes in the current frame and the predicted bounding boxes from the Kalman filter to compute matching scores. $IoU$ represents the overlap ratio between two bounding boxes, with higher values indicating greater similarity. Based on these matching scores, the Hungarian algorithm optimally matches the detected objects with the predicted objects. The Hungarian algorithm minimizes the matching cost, assigning tracking IDs to each object and maintaining object continuity across frames.

The proposed algorithm’s workflow is as follows. The Kalman filter uses the detection results from the previous frame to predict the current frame’s object positions while simultaneously performing new detections. $IoU$ distances are calculated to match the predicted and detected bounding boxes. Unmatched detections are treated as new objects, while unmatched predictions are considered to be tracking failures. Matched objects update their state via the Kalman filter, while unmatched objects are either deleted or added as new objects, enabling real-time object tracking.

This proposed algorithm for tracking 2D bounding boxes of fruits is utilized during the robot’s navigation mode when the target is farther than the threshold distance. Hence, it is an essential component for a fruit-harvesting robot to help it accurately navigate toward the target fruit. Figure 18 represents the overall workflow of the tracking algorithm used in the fruit-harvesting robot. In recognizing multiple classes of fruits through the detector in the previous and current frames, ripe fruits are indicated by blue boxes, and unripe fruits are indicated by orange boxes. Subsequently, real-time object tracking can be performed as described for the previous process.

Figure 18. Overall operational flow of the tracking algorithm for citrus-harvesting robots.

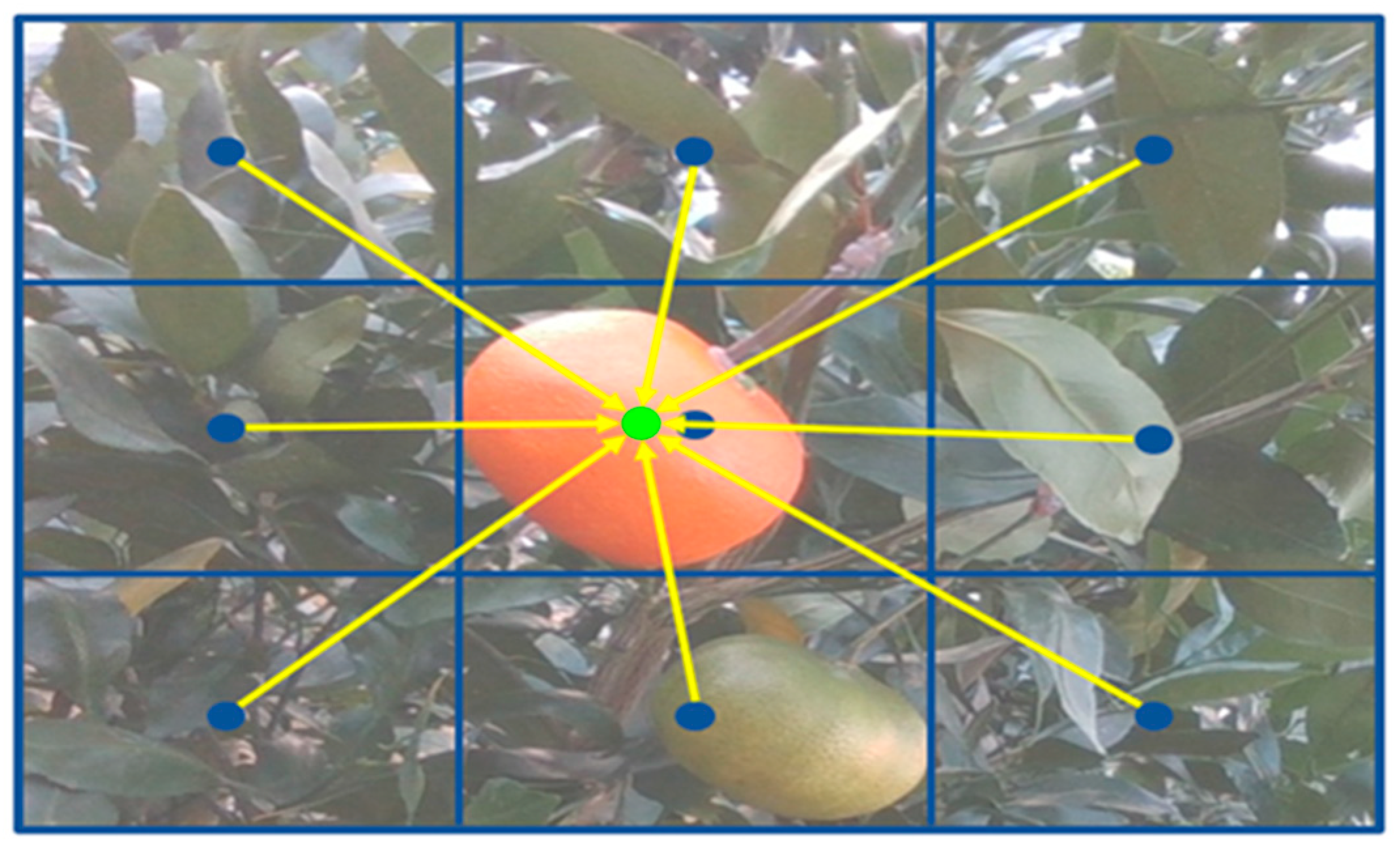
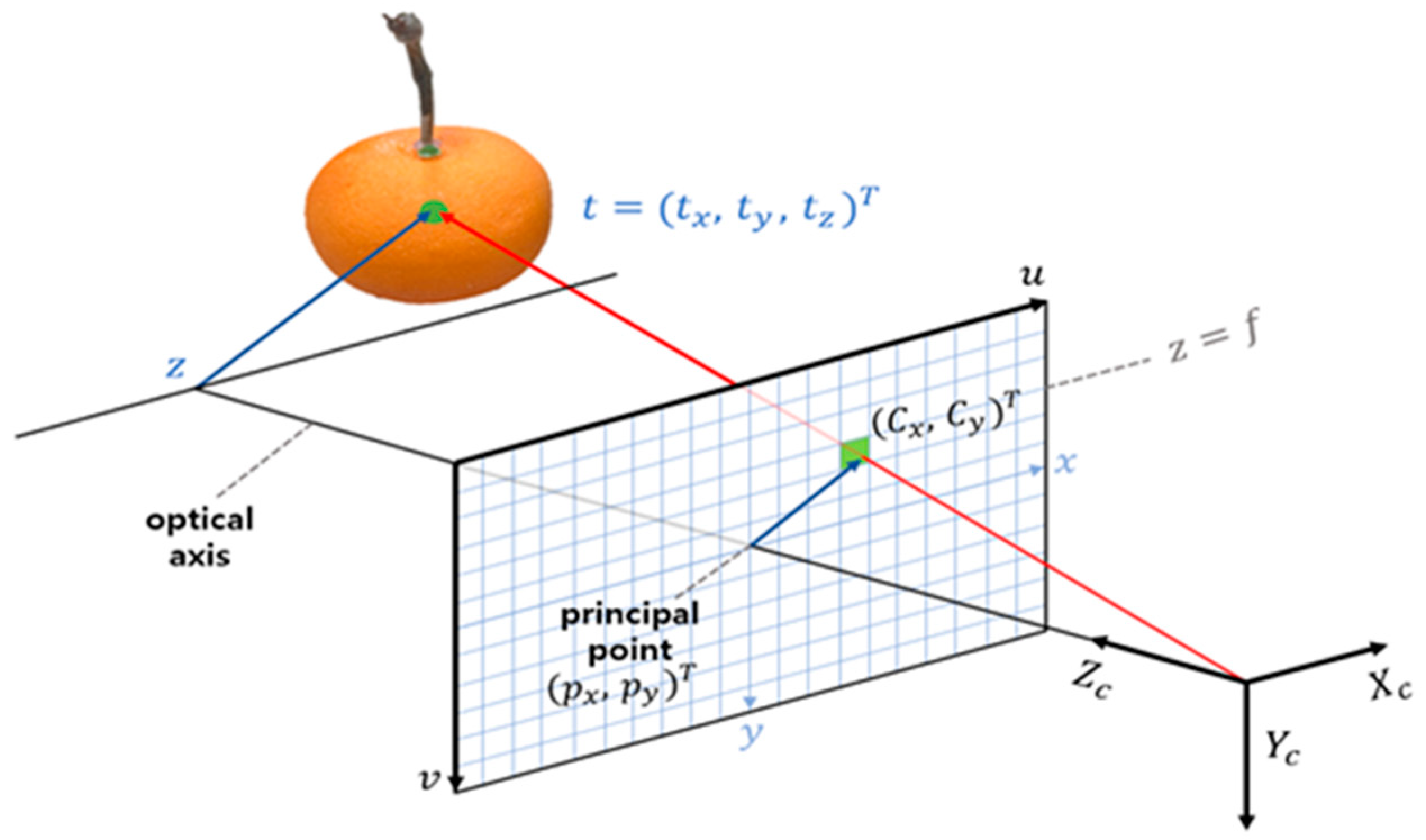
We propose an algorithm that utilizes the 6D coordinates of objects to sort the harvesting order so that the fruit-harvesting robot can effectively harvest multiple ripe fruits. This enables the robot to harvest the fruits in the most efficient path, optimizing the harvesting task. Figure 19 shows the schematic of estimating the position of a fruit in three-dimensional space using a geometric model of the camera. Based on this, an algorithm can be proposed to sort the harvesting order using the 6D coordinates of the objects. This algorithm helps the robot harvest multiple fruits in the most efficient path, optimizing the harvesting task. In the camera coordinate system, the fruit’s position is represented as $t=(t_x,t_y,t_z)$, which is projected onto the image plane from the principal point. The camera is aligned with the optical axis, and the principal point is the center of the camera’s image sensor. The image plane of the camera is set at $z=f$ in the camera coordinate system, where $f$ is the focal length of the camera. The 3D coordinates of the fruit are projected onto the image plane along the optical axis, resulting in the image coordinates $(c_x,c_y)$. This projection process uses the camera’s internal and external parameters to calculate and convert 3D coordinates to image coordinates $(c_x,c_y)$.

Figure 19. Schematic for labeling the harvesting order.

Through the four sub-networks of the previously explained deep learning model, the class, 2D bounding box, rotation, and translation of the objects can be extracted. We propose an algorithm that labels the harvesting order using the class and translation values of the objects when they are ready for harvesting. The determination of whether an object is ready for harvesting is made based on the extracted class ID of the object. If the recognized object’s class is “red” and its ID is 0, it is considered ready for harvesting; if the class is “green” and its ID is 1, it is considered unready for harvesting. When multiple objects of either class are recognized on the tree, the agricultural harvesting robot may become confused about which ripe object to harvest first. Therefore, an algorithm for labeling the harvesting order is necessary. By using the Euclidean distance formula, the translation values of multiple ripe objects are utilized to calculate the distance in the 3D space for each object. The Euclidean distance formula is as follows:

$$d=\sqrt{{(t_x-X_c)}^2+{(t_y-Y_c)}^2+{(t_z-Z_c)}^2},$$

(4)

Finally, we propose an algorithm that controls the harvest and navigation modes using a threshold to enable the fruit-harvesting robot to effectively harvest multiple fruits. The proposed algorithm calculates the Euclidean distance of the detected fruits and applies the harvest mode when the distance to the nearest fruits is within the threshold of 30 cm, and applies the navigation mode when it exceeds this threshold.

The overall flow of the algorithm is as follows. First, the robot checks if there are any detected fruits. If fruits are detected, it then determines whether there are any ripe fruits ready for harvest. If no ripe fruits are detected, it displays “green class”. If ripe fruits are present, it proceeds to the distance calculation stage. Using the Euclidean distance, it calculates the distance to each fruit. If the distance to the nearest fruits is within 30 cm, it applies the harvest mode (SORT) and displays “red class harvest sequence labeling” to label the harvesting order. Conversely, if the distance to the nearest fruits exceeds 30 cm, it applies the navigation mode (NORM) and displays “red class tracking ID labeling”.

Figure 20 shows the overall structure of the model, which includes the algorithm for estimating the 6D pose of fruits, determining the harvest-readiness of multiple objects, and switching between harvest and navigation modes depending on the distance. The algorithm first checks for detected fruits, then determines if there are any ripe fruits. It then calculates the distance to the nearest fruits and compares it with the 30 cm threshold to decide between the harvest and navigation modes. This algorithm is integrated into the overall deep learning model. The deep learning model is based on the EfficientNet Backbone and BiFPN network and extracts the object’s class, 2D bounding box, rotation, and translation through four sub-networks. The extracted data are fed into the proposed algorithm to determine the harvest and navigation modes.

Figure 20. Algorithm for switching between harvesting and navigation modes for a fruit-harvesting robot.

4. Experimental Results

In this study, three experiments were conducted to evaluate the performance of the fruit-harvesting robot. The first experiment compared $ADD$ and $ADDS$ for the Yolov5-6D [28] model and the EfficientPose model using an optimized dataset of single fruits. The second experiment was to validate the recognition rate of recognition for multiple citrus fruits, including ripe and unripe citrus, using multi-object virtual and real datasets. The third experiment compared the FPS (frames per second) and recognition rate of the overall model, including the algorithm for switching between harvest and navigation modes, based on the results of recognition.

$ADD$ and $ADDS$ were used as performance evaluation metrics for object recognition [29]. All experiments were conducted using two 3090ti GPUs. These two metrics were used to evaluate the accuracy of a model in predicting the 6D position and pose of an object. $ADD$ was used for asymmetric objects and calculated the average distance between the predicted 6D pose and the actual 6D pose of the model’s points. The formula for $ADD$ is as follows

$$ADD={\displaystyle \frac{1}{m}}{\displaystyle \sum _{x\in M}\Vert (R_x+T)-({\widehat{R}}_x+\widehat{T})\Vert },$$

(5)

where $M$ is the set of the 3D model’s points; $m$ is the number of the model’s points, $R$ and $T$ are the actual rotation matrix and translation vector of the object, respectively; $\widehat{R}$ and $\widehat{T}$ are the predicted rotation matrix and translation vector, respectively; and $x$ represents the model’s points. $ADD$ indicated how closely the predicted pose matched the actual pose, with smaller values indicating higher accuracy. $ADDS$ was used for symmetric objects and calculated the shortest distance between the predicted pose and the actual pose for each point in the model, averaging these distances. The formula for $ADDS$ is as follows

$$ADDS={\displaystyle \frac{1}{m}}{\displaystyle \sum _{x_1\in M}{\min }_{x_2\in M}\Vert (R_{x_1}+T)-({\widehat{R}}_{x_2}+\widehat{T})\Vert },$$

(6)

where $x_1$ and $x_2$ are points in the set of points in the model $M$, and the other symbols have the same meaning as in $ADD$. $ADDS$ takes symmetry into account and calculates the average distance between the predicted pose and the actual pose, making it a more accurate metric for evaluating symmetric objects.

To evaluate performance, FPS and recognition accuracy of the entire model were measured. FPS is a metric that evaluates the real-time processing performance of a model, representing the number of frames processed per second [30]. A high FPS indicates the model’s capability to operate in real-time, ensuring the robot’s fast and accurate operation. In the experiments, the FPS of the entire system based on Yolov5-6D and EfficientPose models was measured and compared. The recognition rate of fruits suitable for harvesting evaluated how accurately the model classified the suitability of fruits for harvesting, using the confusion matrix components of TP (true positive), FP (false positive), TN (true negative), and FN (false negative) [31]. The recognition rate indicated the percentage of classes correctly recognized by the model, calculated using the confusion matrix.

In the first experiment, we compared the 6D pose accuracy of a single ripe citrus object using the Yolov5-6D model and the proposed model with $ADD$ and $ADDS$ metrics. The Yolov5-6D model is a deep learning model based on the YOLO (you only look once) architecture, which detected 2D objects and subsequently estimated their 6D pose. In contrast, the proposed model directly estimated the 6D pose in an end-to-end manner from the input image. Both models were trained using the dataset of single citrus objects automatically rendered in a virtual environment that was proposed in this study. The dataset was divided into 80% (8000 images) for training and 20% (2000 images) for validation. Table 1 shows the performance evaluation metrics for single objects of the harvestable “Red” class and the non-harvestable “Green” class. The comparison used the 10% $ADD$ and $ADDS$ metrics, evaluating the models with the criterion that errors within 10% of the size of the modeled object were acceptable. This means that the accuracy of the 6D pose estimation was considered to be successful if the error in predicting the object’s position and orientation was within 10% of the object’s total size. By using this 10% threshold, the experiment ensured that the models are robust enough to perform accurate pose estimation in scenarios where slight deviations are permissible, reflecting real-world applications where perfect accuracy may not always be necessary but the accuracy must be within a tolerable range

Table 1. Performance evaluation for a single object using the 10% $ADD$ and $ADDS$ metrics.

Method	YOLOv5-6D	EfficientPose ($\mathit{\varphi }$ = 0)
Red	97.87	98.25
Green	95.15	96.98
Average	96.51	97.615

Figure 21 and Figure 22 illustrate the ground truth of the 6D pose and the predicted 6D pose for a single object, represented as 3D bounding boxes.

Figure 21. YOLOv5-6D’s performance on the virtual dataset of single red fruits: correct (green box) and predicted (blue box) 6D poses.

Figure 22. EfficientPose’s performance on the virtual dataset of single red fruits: correct (green box) and predicted (blue box) 6D poses.

In the second experiment, a combined dataset of virtual and real environments was used to simultaneously recognize ripe and unripe citrus fruits. The dataset consisted of 10,000 images, with virtual and real images mixed in a 7:3 ratio. All 10,000 images were used for training. The validation was performed on an independent dataset of 4000 images obtained from outdoor environments in Jeju Island. The backbone structure of the model was set with a compound coefficient of 3 to recognize multiple objects in a more complex structure. Table 2 shows the recognition accuracy of multi-object class classification in both virtual and real environments through a confusion matrix. The ripeness classification of fruits involved assigning each of the multiple objects a class (red or green) and distinguishing them. To evaluate the performance of the ripeness classification, 10 scenes each containing 10 citrus fruits were filmed, comprising 8 fruits suitable for harvest and 2 unsuitable ones. In total, 100 citrus fruits were evaluated using a confusion matrix. The results were categorized into harvest-suitable success (true positive, TP), harvest-suitable failure (false negative, FN), harvest-unsuitable success (false positive, FP), and harvest-unsuitable failure (true negative, TN).

Table 2. Recognition rate for the confusion matrix after 10 rounds of evaluating performance in discriminating ripeness.

Scene	TP	FN	FP	TN
1	100	0	100	0
2	100	0	50	50
3	100	0	100	0
4	100	0	100	0
5	75	25	100	0
6	100	0	100	0
7	100	0	100	0
8	100	0	100	0
9	100	0	100	0
10	100	0	100	0
Recognition rate (%)	97.5	2.5	95	5

Figure 23 is one of the scenes from the maturity recognition experiment shown in Table 2. Figure 24 shows the results of estimating 6D poses for green and red objects photographed in three different scenes from an actual environment in Jeju.

Figure 23. Experimental results of determination of the ripeness of multiple objects, represented as harvestable (blue boxes) and unharvestable (red boxes).

Figure 24. Accurate poses (green boxes) and predicted poses (blue and red boxes) of 6D pose estimations for citrus fruits in three different scenes from a real environment of a Jeju Island farm.

In the final experiment, we evaluated the processing performance of the required harvest and driving modes in an agricultural harvesting robot using the weights learned from previous experiments. We utilized the same training results as in the second experiment. If the closest object was within the threshold distance, this corresponded to the robot’s harvest mode, and the harvest order IDs for multiple objects were sorted. Conversely, if the object was beyond the threshold distance, this corresponded to the robot’s driving mode, and tracking was performed. On the basis of this algorithm, we verified the inference time per frame from the RGB input to the classification of multiple objects, extraction of 2D and 3D bounding boxes, classification of the objects’ translation and rotation, and, finally, the proposed sorting and order.

The experimental results showed that using the model with a compound coefficient of 3, which utilized a relatively complex backbone, processing 4000 images took 236.13 s. Among the 4000 images, the number of images that were correctly recognized was 3998. Thus, a performance of approximately 16.94 FPS was verified. Figure 25 and Figure 26 show the application of the tracking function in driving mode and the function of classifying the harvesting order in harvesting mode in an agricultural harvesting robot.

Figure 25. Assigning a harvesting order to harvestable citrus fruits in harvest mode.

Figure 26. Tracking the same objects in driving mode compared with the previous frame.

5. Discussion

Our experimental results provided a comprehensive understanding of the performance and practical applicability of the EfficientPose-based model for fruit-harvesting robots. The EfficientPose-based model outperformed the YOLOv5-6D model across all key metrics. In the first experiment, the EfficientPose model achieved higher accuracy in 6D pose estimation, with an average $ADD$ and $ADDS$ of 97.615% compared with 96.51% for the YOLOv5-6D model. This improvement was attributed to the end-to-end architecture of EfficientPose, which directly estimated the 6D pose from input images, thereby reducing the errors associated with the intermediate steps in the YOLOv5-6D model.

In the second experiment, the model successfully recognized and classified ripe and unripe citrus fruits in both virtual and real environments, achieving a recognition rate of 97.5% for ripeness. The high true positive (TP) rate demonstrated the model’s robustness in accurately identifying harvestable fruits, while the relatively low false negative (FN) and false positive (FP) rates underscored its precision in distinguishing between ripe and unripe fruits. This precision is crucial for optimizing the harvesting process and minimizing damage to unripe fruits.

The third experiment validated the model’s real-time processing capabilities, with an average FPS of 16.94. This indicated that the model can effectively support the dynamic and fast-paced requirements of an agricultural harvesting robot. The ability to switch between harvesting and navigation modes based on the proximity of target objects should ensure efficient operation and reduce downtime.

In conclusion, the EfficientPose-based model presents a viable solution for enhancing the performance and efficiency of fruit-harvesting robots. The integration of advanced deep learning techniques and comprehensive dataset construction methods significantly contributes to the advancement of agricultural automation technology, demonstrating the potential for commercial deployment and real-world application in diverse agricultural settings.

6. Conclusions

We developed and validated a deep learning model specifically designed for agricultural robots, with a focus on improving the efficiency and accuracy of fruit harvesting. A key contribution of this research is the creation and validation of the HWANGMOD dataset, which includes both virtual and real-world data. This dataset was instrumental in enabling the model to accurately extract 6D pose information for multiple fruits in real-time, and to assess the ripeness of each fruit.

One of the distinguishing features of our proposed model is its ability to switch between navigation and harvesting modes according to a predefined threshold. When the distance between the robot and the target fruit exceeds this threshold, the model utilizes the SORT algorithm to track multiple objects, ensuring efficient navigation toward the fruits. As the robot approaches the fruits and the distance falls below the threshold, the model transitions to harvesting mode. In this mode, the Euclidean distance is employed to prioritize the fruits based on their proximity to the robot, allowing the robot to harvest the fruits in the most efficient sequence.

This dynamic mode-switching capability, driven by real-time 6D pose estimation and threshold-based decision-making, significantly enhances the robot’s operational efficiency. By accurately distinguishing between ripe and unripe fruits and adapting its behavior according to the proximity of the target, the robot can optimize both its navigation and harvesting processes. The integration of these advanced techniques contributes to the development of more autonomous and effective agricultural robots, paving the way for their practical deployment in diverse agricultural environments.

Additionally, we proposed a model that includes 6D pose estimation and tracking algorithms for switching between harvesting and navigation modes to improve the performance of fruit-harvesting robots. The proposed model was designed to perform 6D pose estimation and determine the ripeness of fruits in real-time. To achieve this, we constructed virtual and real datasets to accurately estimate the 6D pose of fruits and developed an algorithm to efficiently determine the harvesting order by distinguishing between ripe and unripe fruits.

In a comparison of the $ADD$ and $ADDS$ metrics on an optimized fruit dataset using the Yolov5-6D model and the EfficientPose model, the EfficientPose model achieved higher accuracy in 6D pose estimation. The model successfully recognized and classified ripe and unripe fruits in both virtual and real environments, achieving a recognition rate of 97.5% for suitability for harvesting. The high true positive rate and low false negative and false positive rates demonstrated the model’s robustness and precision. The model’s real-time processing capability was validated with an average FPS of 16.94. This indicated that the model can effectively support the dynamic and fast-paced requirements of agricultural harvesting robots, allowing efficient operation by switching between the harvesting and navigation modes depending on the proximity of the target objects.

This study suggests that the development of a robust and efficient 6D pose estimation model can significantly impact the commercialization of agricultural harvesting robots. The ability to accurately identify and harvest ripe fruits in real time can lead to substantial improvements in productivity and cost-efficiency. Additionally, integrating virtual and real datasets for training enhanced the model’s adaptability to various environmental conditions, supporting practical deployment in diverse agricultural settings.

While the current study has demonstrated promising results, further research is needed to address certain limitations. Future work should focus on improving the model’s performance under varying lighting conditions and in more complex environments. Additionally, integrating other sensory data, such as depth information, could enable accurate pose estimation regardless of the fruits’ characteristics and improve the rotational accuracy. Expanding the dataset to include a wider variety of fruit types and sizes could also enhance the model’s generalizability and robustness.