Design and Testing of a Fully Automatic Aquatic Plant Combing Machine for Crab Farming
Abstract
1. Introduction
2. Materials and Methods
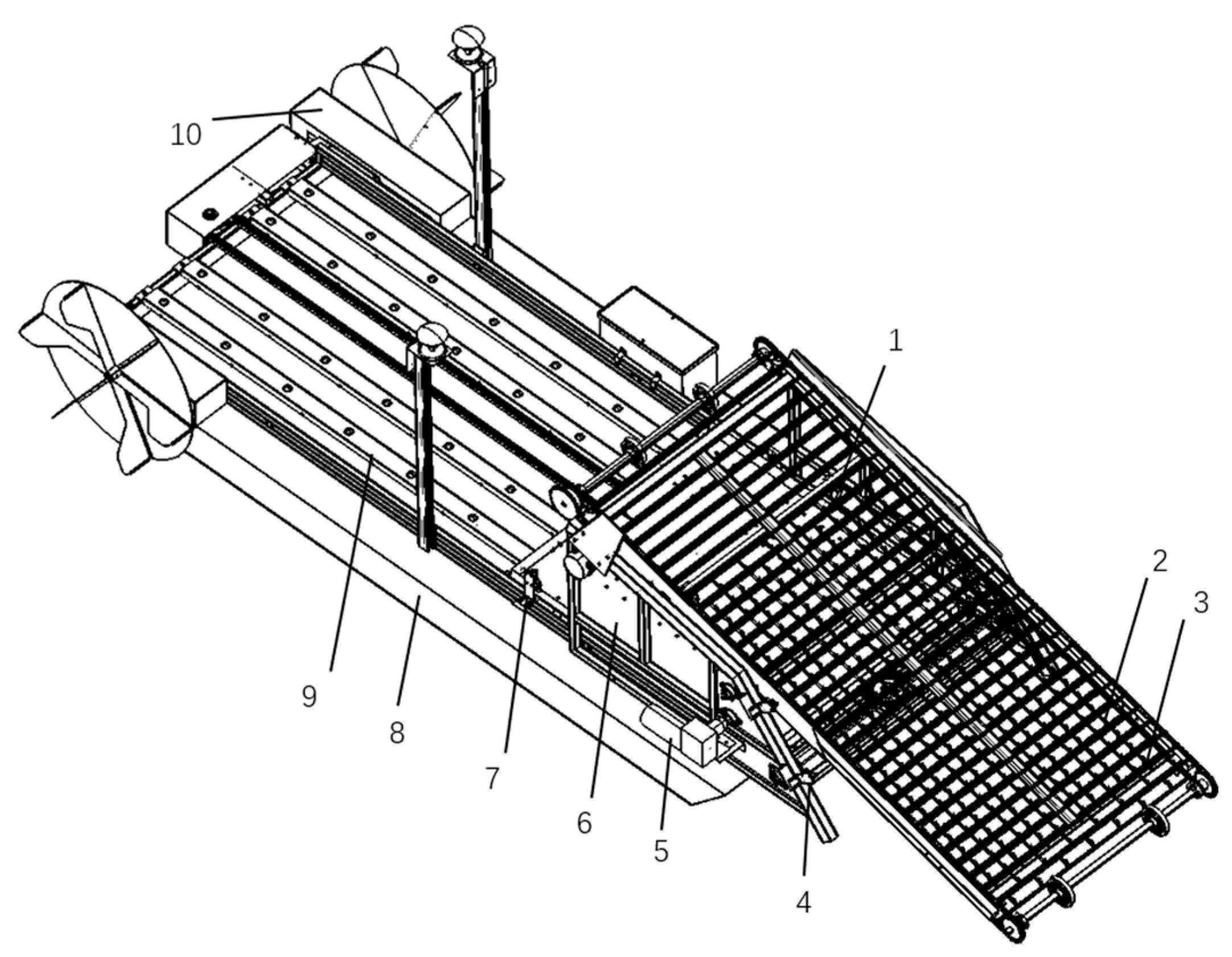
2.1. Overall Structure and Working Principles of Fully Automatic Aquatic Plant Combing Machine
2.1.1. Overall Structure
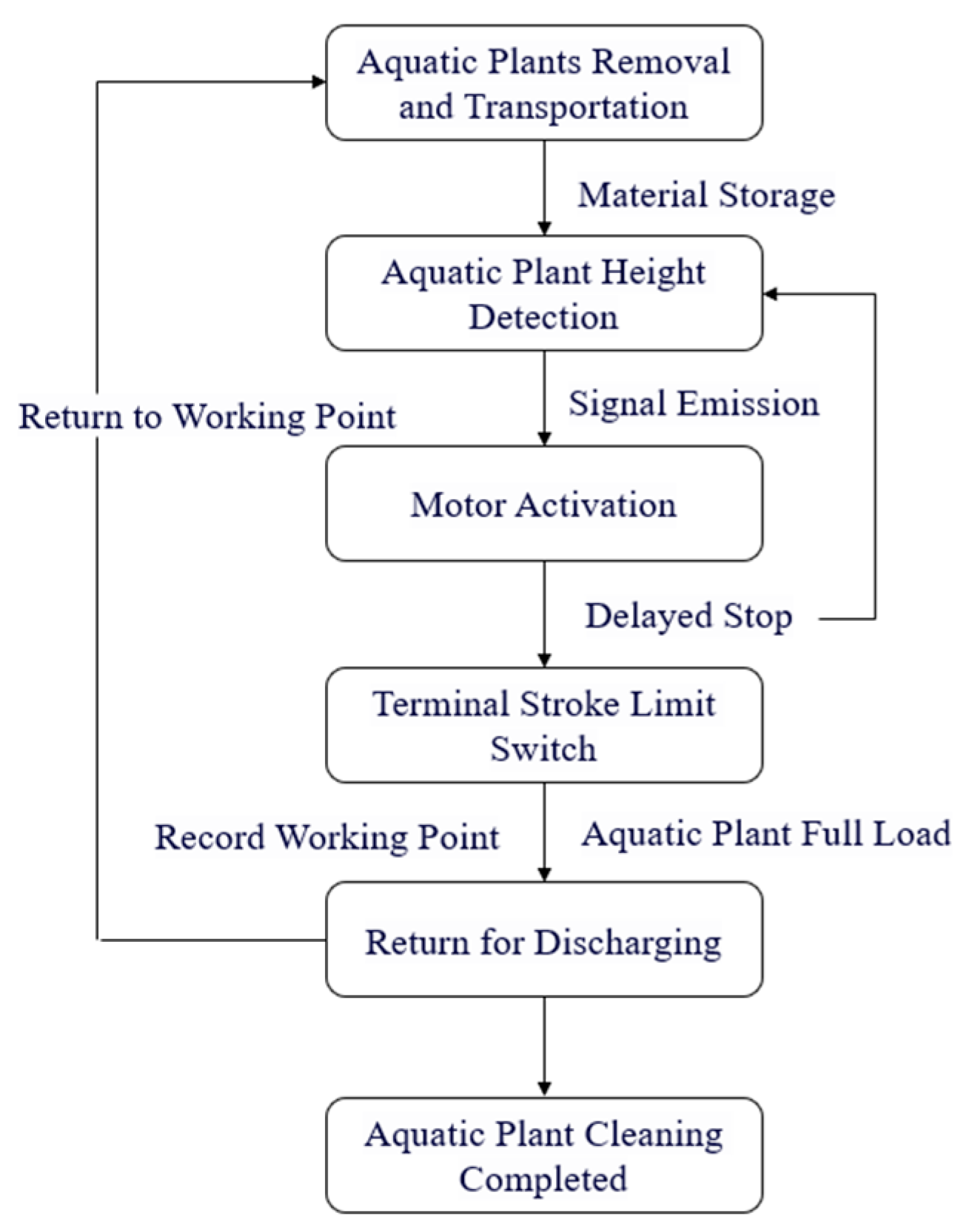
2.1.2. Working Principles
2.2. Design of Key Components and Parameters Determination
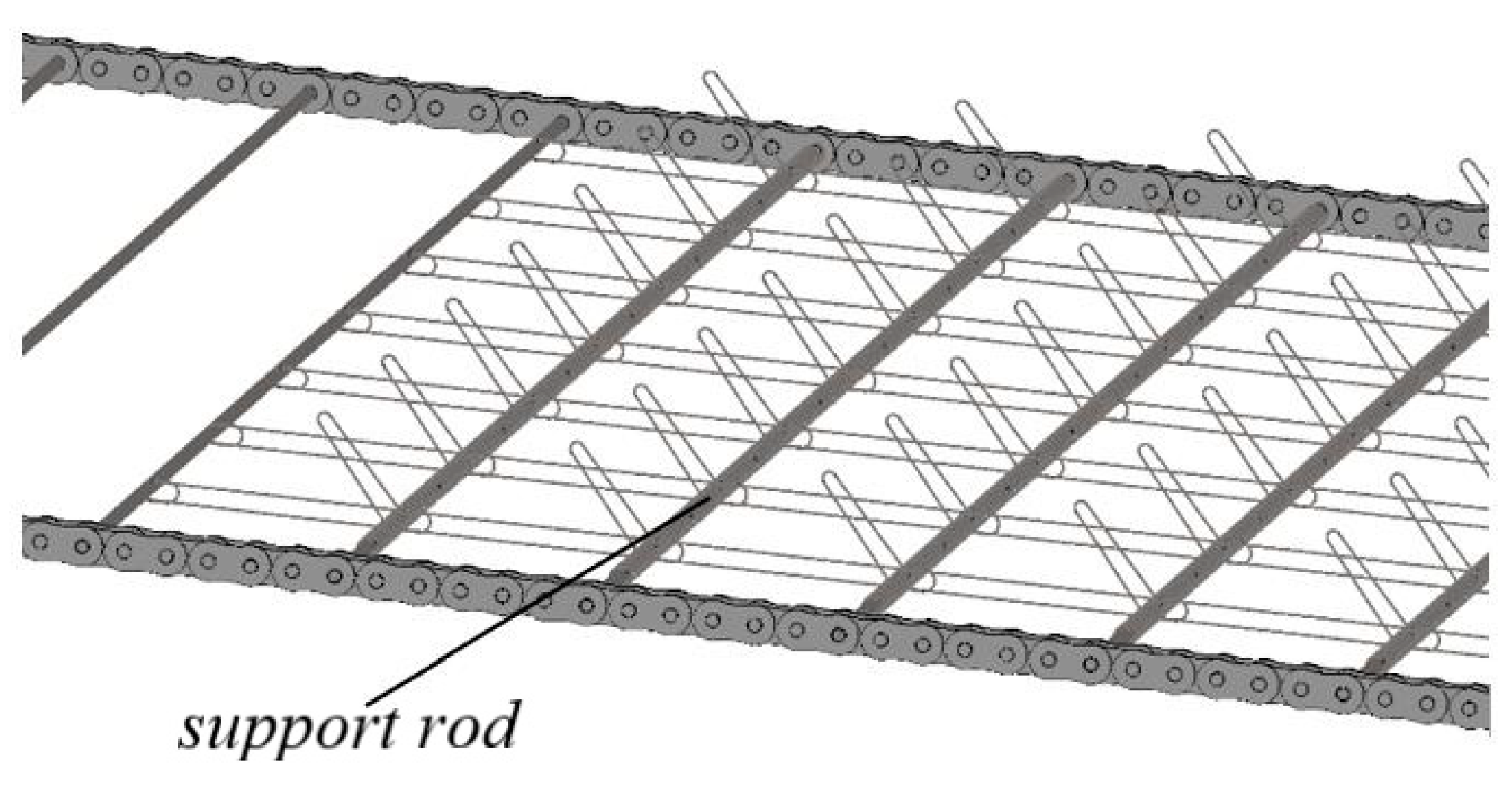
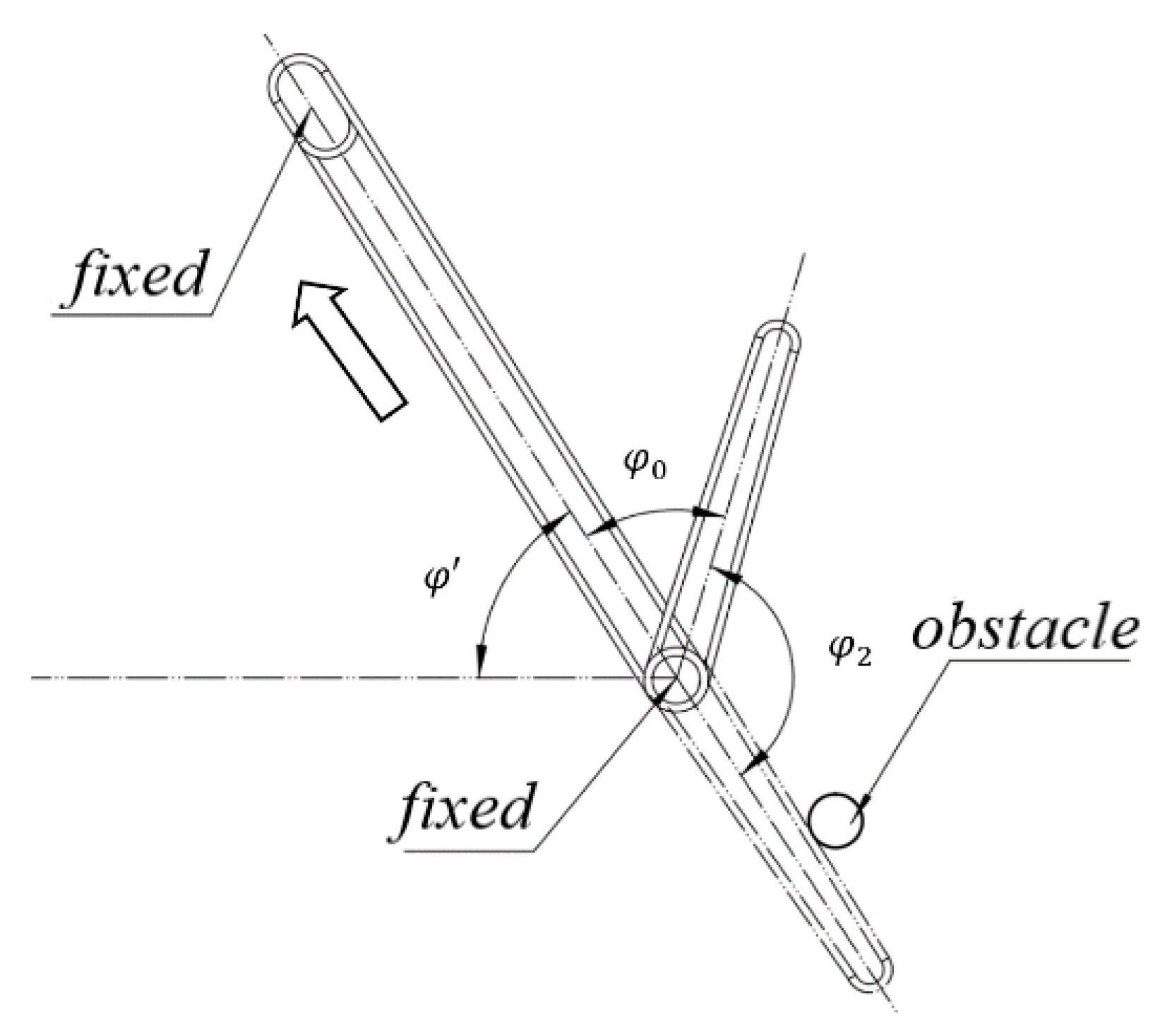
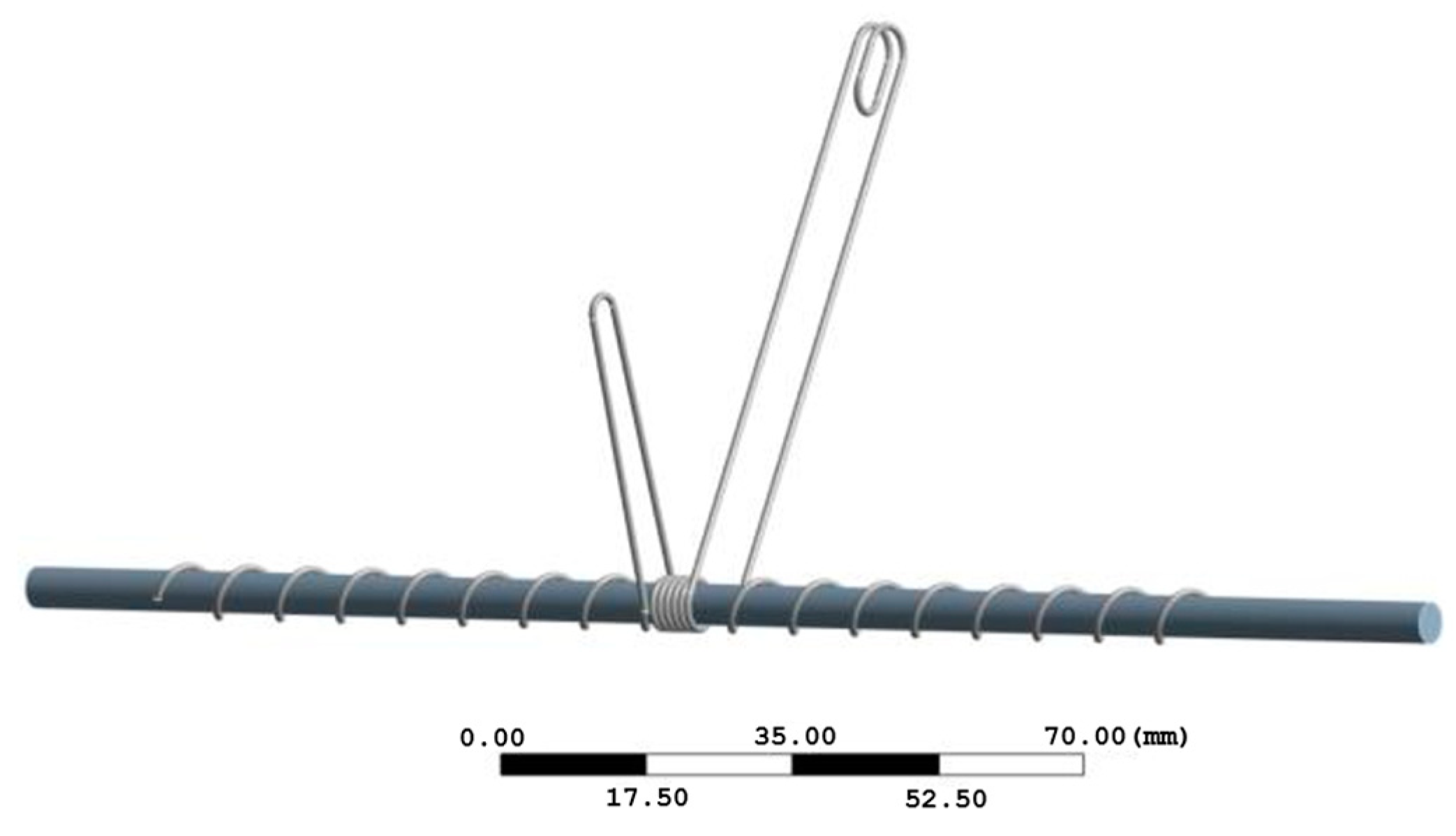
2.2.1. Design of Torsion Spring Hooks
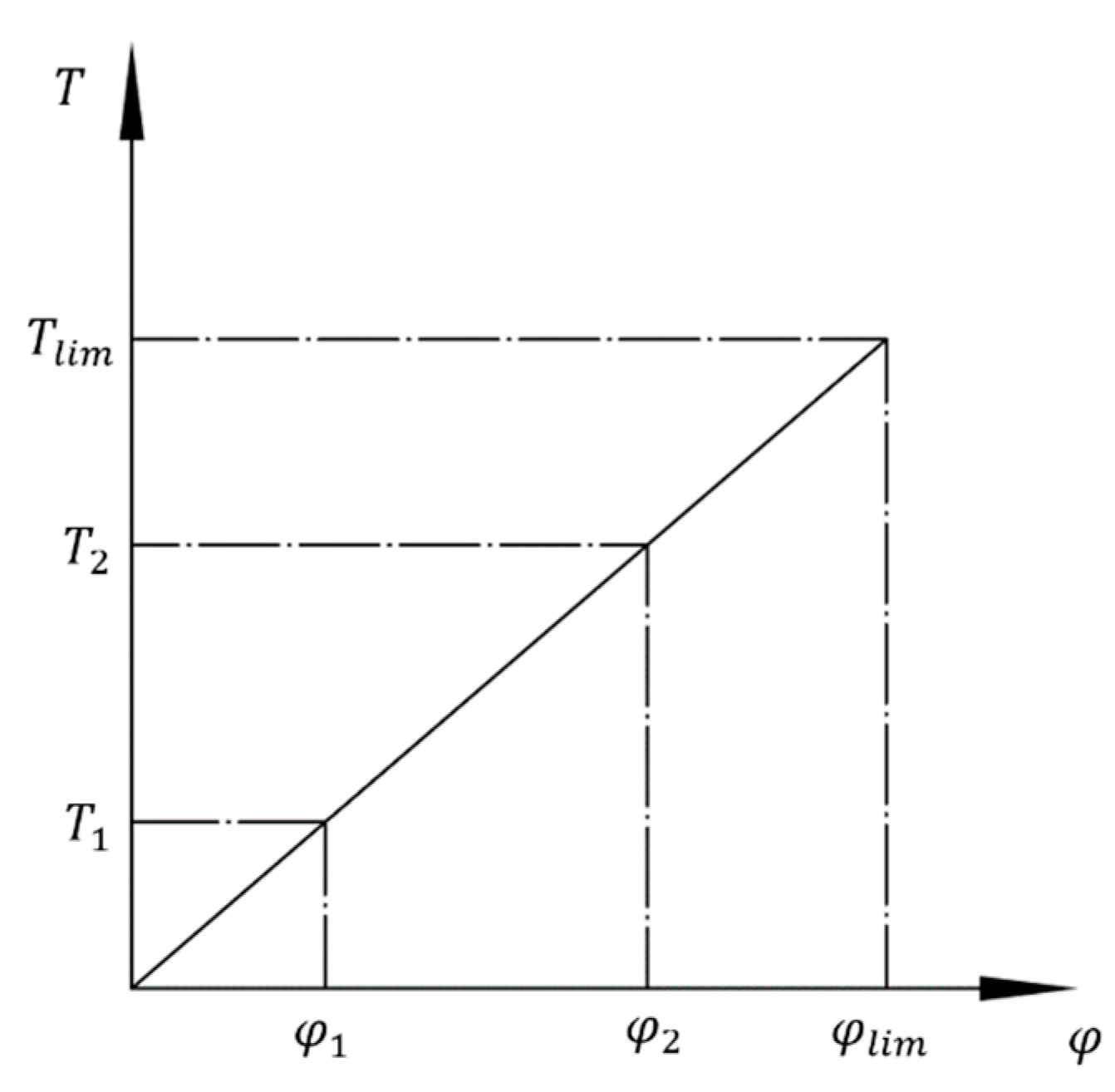
2.2.2. Theoretical Analysis and Calculation
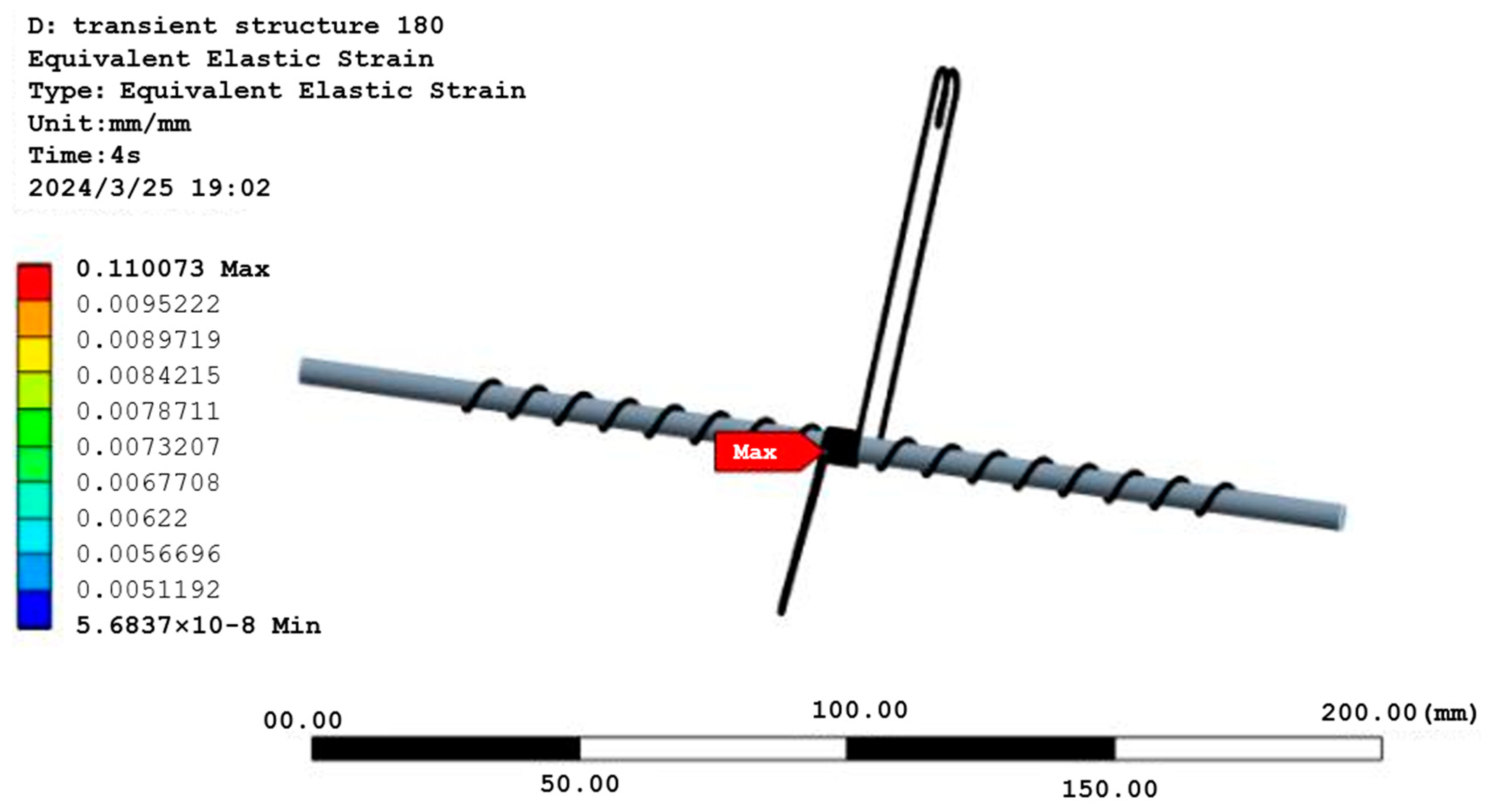
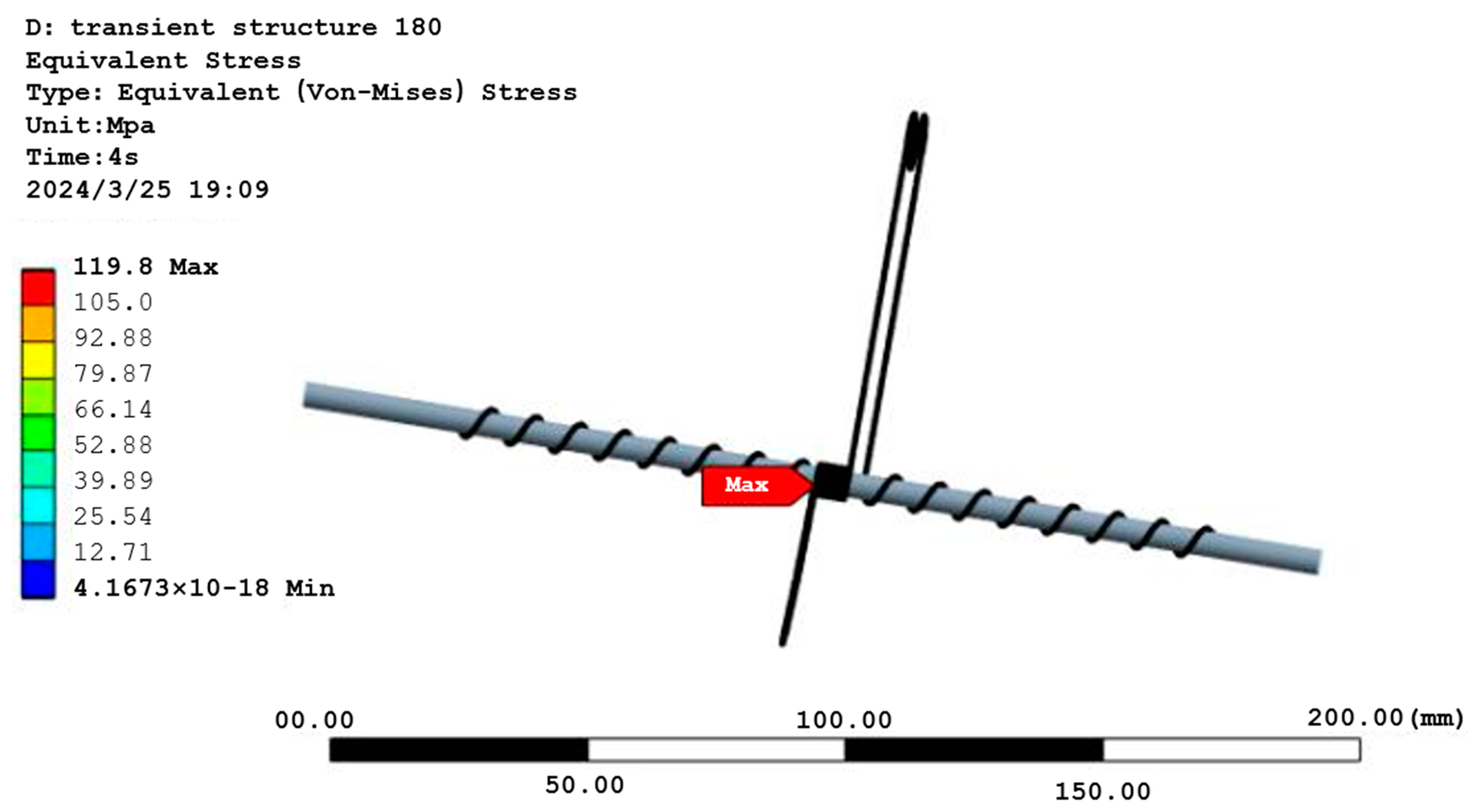
2.3. Transient Dynamics Simulation
2.4. Performance Testing of Torsion Spring Hooks
2.5. Comprehensive Performance Test in Water
- (1)
- Basic tests of the prototype
- (2)
- Aquatic plant harvesting efficiency
- (3)
- Missed clearing rate of aquatic plants and injury rate of river crabs
3. Results and Discussions
3.1. Analysis of Transient Dynamics Simulation
3.2. Performance Testing Results of Torsion Spring Hooks
3.3. Comprehensive Performance Test Results in Water
- (1)
- Basic tests of the prototype
- (2)
- Aquatic plant harvesting efficiency
- (3)
- Missed clearing rate of aquatic plant and injury rate of river crabs
4. Conclusions
- (1)
- A fully automated aquatic plant combing and clearing machine for river crab farming is developed, which consists of two main parts: an aquatic plant combing and clearing device and a fully automated aquatic plant spreading mechanism. The aquatic plant combing and clearing device comprises a combing mechanism and a water depth adjustment mechanism. The fully automated aquatic plant spreading mechanism includes a drawer-type material warehouse, a material warehouse support, a damping mechanism, a guide rail, a hull, a transmission system, and other components.
- (2)
- A method for aquatic plant clearing using torsion spring hooks instead of traditional cutting blades is proposed. This method causes minimal damage to the aquatic plant, does not harm the river crabs, and allows for better control of aquatic plant density. The torsion spring hooks were theoretically analyzed and calculated based on the maximum breaking force of the aquatic plant to ensure that they meet the design requirements. Transient dynamics simulations were performed using ANSYS to verify the theoretical calculations. Finally, experimental verification was conducted, and the results showed that the torsion force generated within a certain range of torsion angles can break the aquatic plant, and the torsion spring hooks can avoid obstacles through their own deformation.
- (3)
- Prototype and Experimental Research: The processing and assembly of the prototype were completed, and basic performance tests as well as comprehensive performance tests in water were conducted. The basic performance test verified that the torsion spring hook can meet the design requirement of breaking off aquatic plants when the torsion angle is less than 20°, and can avoid obstacles through its own deformation. The comprehensive performance tests in water confirmed that the prototype operates smoothly and the stability of water depth adjustment is good. The average clearing efficiency of aquatic plant is 4.92 mu/h, the missed clearing rate of aquatic plants is 0.44%, and the injury rate of river crabs is 0.028%, all meeting the design requirements.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Lu, Y.; Li, J.; Zhang, X.; Zheng, P.; Meng, Y.; Luan, K.; Xian, J.; Gu, Z. Research progress of astaxanthin used in culture of shrimp and crab. China Feed 2023, 34, 79–85. [Google Scholar]
- Lin, H.; Huang, C.; Pan, J.; Peng, G.; Zhou, J.; Li, X.; Fu, L. The investigation and analysis of cost and benefit of the Chinese mitten crab breeding in Jiangsu province. J. Aquac. 2020, 41, 14–18. [Google Scholar]
- Chen, L.; Du, Z.; Hu, Q.; Huang, C.; Li, J. Design and experiment on crab ecological culture system using internal circulation and self-purification in a pond. Trans. Chin. Soc. Agric. Eng. 2021, 37, 227–234. [Google Scholar]
- Wang, J.; Liu, Q.; Huo, W.; Han, J.; Liu, T. High Density Breeding Technology of Chinese Mitten Crab and Key Points of Prevention and Control of “Milk Disease”. Mod. Agric. Res. 2023, 29, 128–131. [Google Scholar]
- Wu, K.; Ma, X.; Wang, Y.; Wang, W.; Lang, Y. Effect of three water plants decomposition on water quality. J. Shanghai Ocean Univ. 2016, 25, 726–734. [Google Scholar]
- Wang, Y.; Shen, W. Harvesting process of aquatic for shrimp-crab-pond. J. Shanghai Ocean Univ. 2011, 20, 938–942. [Google Scholar]
- Zhang, G.; Jiang, X.; Cheng, W.; Zhou, W.; Lou, M.; Wu, X. Effect of submerged macrophytes planting mode on performance and economic profit of all-male adult Eriocheir sinensis culture. South China Fish. Sci. 2023, 19, 107–115. [Google Scholar]
- Li, Z.; Zhu, H.; Wu, G.; Chen, L.; Chen, Y. Design and test on the navigation control system of the aquatic plants comb collect boat. J. Shanghai Ocean Univ. 2023, 32, 932–942. [Google Scholar]
- Chen, H.; Zhou, Y.; Xu, D. Development of A Small-scale Battery-driven Remote-controllable Weed Harvester. J. Anhui Agric. Sci. 2010, 38, 14791–14792. [Google Scholar]
- Liu, H.; Zhao, D.; Sun, Y.; Zhang, J.; Wu, B. Control System for Automatic Aquatic Plant Cleaning Ship. Trans. Chin. Soc. Agric. Mach. 2014, 45, 281–286. [Google Scholar]
- Hu, Q.; Zhu, H.; Li, J. Research progress and development trend of mechanization of shrimp and crab breeding pond. J. Shanghai Ocean Univ. 2022, 31, 1216–1223. [Google Scholar]
- Xu, Y. Design and Experimental Study on Cutting-Transport-Feeding System of Amphibious Aquatic Plants Harvesting Ship; Jiangsu University: Zhenjiang, China, 2019. [Google Scholar]
- Kaizu, Y.; Shimada, T.; Takahashi, Y.; Igarashi, S.; Yamada, H.; Furuhashi, K.; Imou, K. Development of a small electric robot boat for mowing aquatic weeds. Trans. ASABE 2021, 64, 1073–1082. [Google Scholar] [CrossRef]
- Bian, H. Desing and Research of Deformable Amphibious Cleaup Based on Parallel Mechanism; Shanghai University of Engineering Science: Shanghai, China, 2016. [Google Scholar]
- Zhang, L.; Chen, J.; Li, J.; Zhang, Y. Development of SCSGJ-2.6 typeharvester of aquatic weed. J. Northwest A F Univ. 2008, 36, 229–234. [Google Scholar]
- Wang, X. Design of a Small Aquatic Cutting Machine; Shanghai Ocean University: Shanghai, China, 2014. [Google Scholar]
- Chen, X. Design and Test of Automatic Harvesting Equipment for Water Grass in Crab Pond. Master’s Thesis, Nanjing Agricultural University, Nanjing, China, 2021. [Google Scholar]
- Qi, H. Study and Design of Self-Cruising Mowing Boat System for Shrimp and Crab Culture Based on IMU/DGPS; Jiangsu University: Zhenjiang, China, 2021. [Google Scholar]
- Rodusky, A.J.; Sharfstein, B.; East, T.L.; Maki, R.P. A Comparison of Three Methods to Collect Submerged Aquatic Vegetation in a Shallow Lake. Environ. Monit. Assess. 2005, 110, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Huang, Z.; Mu, Y.; He, J. Influence of The Pitch of Cylindrical Spiral Torsion Spring on Rigidity and Stress. Machinery 2021, 59, 47–50. [Google Scholar]
- Xu, Z.; Deng, Y.; Zhou, J.; Li, X.; Lu, Q.; Chen, F.; Zhou, G. Structural and functional characteristics of microbial communities in aquaculture ponds of Chinese mitten crab Eriocheir sisensis L. Chin. J. Ecol. 2021, 40, 2223–2233. [Google Scholar]
- Liu, L.; Li, J.; Kong, K. Influence of End Fixing Method on Breaking Force of Overhead Insulated Cable. Wire Cable 2024, 67, 40–42. [Google Scholar]
- Cheng, D. Mechanical Design Manual, 5th ed.; Chemical Industry Press: Beijing, China, 2016; pp. 11–44. [Google Scholar]
- Zhang, H.; Hu, R.; Kang, S. ANSYS 12.0 Finite Element Analysis: From Beginner to Proficient; China Machine Press: Beijing, China, 2010. [Google Scholar]
- Li, F.; Zhang, H.; Li, Y.; Zhang, Z. Transient Dynamic Analysis for Cam Mechanism of the Spindle-Picking Cotton. Mach. Des. Manuf. 2013, 51, 128–130. [Google Scholar]
- Jiang, H. Study of Fatigue Life and Failure Mechanism of Titanium Alloy Torsion Springs; Shaanxi University of Technology: Xi’an, China, 2022. [Google Scholar]









| Density /kg/cm3) | Yield Strength /Mpa) | Tensile Strength /Mpa) | Modulus of Elasticity (E/Gpa) | Shear Modulus (G/Gpa) | Poisson’s Ratio () |
|---|---|---|---|---|---|
| 7930 | 255 | 515 | 193 | 82.3 | 0.285 |
| Wire Type | Stainless Steel Wire for Springs | ||
|---|---|---|---|
| Torsion spring | Test bending stress | ||
| Static load allowable bending stress | |||
| Dynamic load allowable bending stress | Finite fatigue life | ||
| Infinite fatigue life | |||
| Serial Number | Torsional Force/N | Maximum Breaking Force of Aquatic Plant/N | Difference/N |
|---|---|---|---|
| 1 | 18.94 | 16.41 | 2.53 |
| 2 | 18.88 | 2.47 | |
| 3 | 19.04 | 2.63 | |
| 4 | 18.99 | 2.58 | |
| 5 | 18.91 | 2.5 | |
| 6 | 18.93 | 2.52 | |
| 7 | 19.06 | 2.65 | |
| 8 | 18.94 | 2.53 | |
| 9 | 19.01 | 2.6 | |
| 10 | 18.96 | 2.55 |
| Number of Tests | Free Angle after Test/(°) | Initial Free Angle/(°) | Difference/(°) |
|---|---|---|---|
| 5 | 45 | 45 | 0 |
| 10 | 45 | 0 | |
| 20 | 45 | 0 | |
| 30 | 45 | 0 | |
| 50 | 45 | 0 | |
| 60 | 45.02 | 0.02 | |
| 70 | 45.02 | 0.02 | |
| 80 | 45.04 | 0.04 | |
| 90 | 45.04 | 0.04 | |
| 100 | 45.08 | 0.08 |
| Operational Stability (30 min) | Water Depth Adjustment Stability (30 min) | No-Load Speed (m/s) | Full Load Speed (m/s) | Battery Worktime/h |
|---|---|---|---|---|
| good | good | 1.32 | 1.05 | 7.6 |
| Test Pond | Area (mu) | Clearing Time/h | Clearing Efficiency/h |
|---|---|---|---|
| Pond 1 | 6 | 1.23 | 4.88 |
| Pond 2 | 6.5 | 1.31 | 4.96 |
| Pond 3 | 7 | 1.42 | 4.93 |
| Average | / | / | 4.92 |
| Test Pond | Number of Uncleared Aquatic Plant Stems/m2 | Number of Injured River Crabs/Crab/mu | Missed Clearing Rate of Aquatic Plants (%) | Injury Rate of River Crabs (%) |
|---|---|---|---|---|
| Pond 1 | 1 | 0 | 1.33% | 0% |
| Pond 2 | 0 | 1 | 0 | 0.083% |
| Pond 3 | 0 | 0 | 0.44% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, S.; Xu, J.; Yuan, H.; Ku, J.; Liu, Z. Design and Testing of a Fully Automatic Aquatic Plant Combing Machine for Crab Farming. Machines 2024, 12, 639. https://doi.org/10.3390/machines12090639
Yuan S, Xu J, Yuan H, Ku J, Liu Z. Design and Testing of a Fully Automatic Aquatic Plant Combing Machine for Crab Farming. Machines. 2024; 12(9):639. https://doi.org/10.3390/machines12090639
Chicago/Turabian StyleYuan, Shijie, Jintao Xu, Hao Yuan, Jinsheng Ku, and Zexin Liu. 2024. "Design and Testing of a Fully Automatic Aquatic Plant Combing Machine for Crab Farming" Machines 12, no. 9: 639. https://doi.org/10.3390/machines12090639
APA StyleYuan, S., Xu, J., Yuan, H., Ku, J., & Liu, Z. (2024). Design and Testing of a Fully Automatic Aquatic Plant Combing Machine for Crab Farming. Machines, 12(9), 639. https://doi.org/10.3390/machines12090639





