Abstract
To obtain an optimal range of structural parameters for dry-gas seals with good performance, this study employed advanced sensing technology to monitor and analyze the internal flow characteristics of dry-gas seals in real time. Additionally, the validity of the calculation program was verified through experimentation. Using steady-state performance parameters as evaluation indices, a calculation model with lubrication characteristics was developed. The results indicate that when there are 12 grooves, the gas film pressure distribution is uniform and has a high value. At pressures greater than 2 MPa, the opening force, leakage, and gas film stiffness change significantly due to enhanced dynamic pressure effects with high-pressure differences, which reduces the local contact forces and frictional forces. At a constant speed, decreasing the gas film thickness increases the pressure difference while increasing both the opening force and film stiffness; however, at higher rotational speeds where the gas flow becomes non-uniform, the stability of the gas film is affected, leading to increased frictional forces. When there are between 10 and 16 grooves with depths ranging from 5.0 to 6.0 μm, dynamic pressure effects caused by pressure gradients become apparent, resulting in good dry-gas sealing performance being achieved. This research provides a theoretical reference for optimizing the design of dry-gas seals, as well as their steady-state seal performance.
1. Introduction
Dry-gas sealing is an advanced sealing technology developed based on the dynamic pressure effect of gas bearings. Dry-gas seals are widely used in shaft-end sealing devices in rotating machinery due to their advantages of low wear, long lifespan, and low energy consumption [1,2]. The end face of the sealing pairs in the rotating machinery unit is susceptible to wear failure during start-up, shutdown, and under high-pressure operating conditions. This can lead to leakage and compromise the reliability and service life of the sealing device. Consequently, this not only results in energy waste and pollution but also severely hampers the rapid development of high-performance rotating machinery [3]. To address these issues, the dynamic characteristics of dry-gas seals [4], flow characteristics of gas films [5], and coordinated optimal design of gas seals [6,7] have been evaluated.
The investigation of gas film flow characteristics in seal pairs is crucial for the theoretical research on shaft-end sealing technology for rotating machinery. The dynamic pressure effect exerted by fluids on the end face of the seal pair is closely associated with the groove structure. In 1968, Gardner [8] pioneered the development of dry-gas seals with circular spiral grooves. These seals have been successfully employed in high-pressure and high-speed compressors because they can withstand pv (pressure and velocity) fluctuations without affecting the sealing properties of secondary materials. In 1979, Gabriel [9] investigated the influence of structural parameters and operating conditions on the dry-gas seal’s performance and derived formulas for calculating performance parameters, thereby establishing a foundation for subsequent theoretical research on dry-gas seals.
With the rapid development of computer technology, the flow characteristics and sealing performance of dry-gas seals have been analyzed using various calculation methods. In 2010, Wang et al. [10] numerically calculated the flow field law of dry-gas seals with spiral grooves. They revealed the effects of hydrodynamic lubrication, as well as large bearing capacity and low friction of dry-gas seals. Subsequently, Wang et al. [11,12], Chávez [13], Garcia [14], and Du et al. [15] used numerical methods in CFD to obtain the pressure distribution rule of seal rings. They considered the microscale heat transfer effect and heat–flow–structure interaction to analyze the influence of different working parameters on the performance of dry-gas seals with spiral grooves. Results revealed that the gas film exhibited a larger bearing capacity at a spiral angle of 15°. Ren et al. [16], Wang et al. [17], and Ran et al. [18] used various design methods to develop a more accurate model and obtain an optimum operating point of the calculation program, as well as the performance parameters of dry-gas seals with varying groove depth and rotation speeds. Based on these results, Xu [19] and Wang et al. [20] considered the influence of a real gas on the pressure characteristics and temperature distribution of dry-gas seals with spiral grooves to propose a new method for accurately predicting the flow state of their rotating flow field based on a three-dimensional velocity component. As the clearance film was only a few microns thick, the fluid in the rotating flow field was considered a complex three-dimensional flow. In recent years, the steady-state performance and flow dynamics of dry gas seals have been experimentally investigated under real operating conditions. Moreover, their designs have been optimized based on specific experimental data. In 2020, Yuan et al. [21] verified the accuracy of a numerical model using experimental data and calculated the sealing performance parameters for structures with different spiral angles. Sun et al. [22] used the finite volume method, shear stress k-ω model, and response surface methodology of a central composite design to modify the boundary parameters of an end inlet. Hahn et al. [23] proposed an improved Reynolds equation by considering the effects of laminar flow, turbulence, and slip behavior and verified its accuracy using experimental data. Zheng et al. [24] introduced comprehensive evaluation factors and used orthogonal tests to optimize the structural parameters of the sealing surface. The research presents the historical development and research methodologies of spiral groove dry-gas sealing technology. Initially, researchers primarily employed theoretical calculations and numerical analyses to address the flow field characteristics and sealing performance parameters under various influences. However, with the emergence of demanding operating conditions in large-scale and high-precision rotating machinery, particularly in high-parameter and micro-scale scenarios, a certain discrepancy between theoretical research and practical engineering applications of dry-gas seals has been identified. To obtain an accurate model depicting the lubrication characteristics of dry-gas seals, two aspects were investigated as follows: (1) Multiscale modeling and simulation: A combination of multiscale numerical simulation methods with experimental verification was utilized to delve into both micro-level and macro-level features within complex flows occurring inside dry gas seals. This approach aims to enhance prediction accuracy while ensuring practicality. (2) Application of novel sensing technologies: Advanced sensing technologies such as high-speed cameras and pressure sensors were employed for real-time monitoring and analysis of internal flow characteristics within dry-gas seals, thereby exploring new data acquisition techniques along with analysis methods.
This study focused on the structure of spiral groove dry-gas seals. Numerical calculations coupled with experimental verification were performed to evaluate the steady-state performance parameters as evaluation indices. Moreover, the influence of working condition parameters and structural factors on the lubrication performance of the gas film in dry-gas seals in calculation models was analyzed to determine optimal parameter ranges. This study thus offers a theoretical reference and scientific foundation for optimal design coordination pertaining to high-parameter applications of dry-gas seals.
2. Theoretical Model
2.1. Structure and Principle of Dry-Gas Seals
The assembly of a dry-gas seal is shown in Figure 1a, which is mainly composed of a sealing house, split clasps, a shaft sleeve, springs, gaskets, and other parts. The rotating ring is fixed on the shaft by the shaft sleeve for its rotation, and the stationary ring and spring are installed in the spring seat. Gaskets and O-rings are used for secondary sealing. The functioning of the stationary ring primarily depends on the loading spring load and the guiding role of the stationary ring seat, which can move freely along the axis. The sealing structure comprises a dynamic ring, stationary ring, and gas film. The rotating ring is generally composed of tungsten carbide with high toughness and strength or silicon carbide with good corrosion resistance, whereas the stationary ring is composed of antimony-impregnated graphite. The end face of the sealing pairs and the dynamic pressure formation principle are shown in Figure 1b. The gas entering the seal face is compressed as it encounters the sealing weir, resulting in a hydrodynamic pressure effect when the rotating ring rotates with the shaft. The pressure reaches a certain value, and the stationary ring is pushed away by the end face of the rotating ring due to hydrodynamic and static pressures. A thin gas film is formed in the clearance of the sealing pairs. The gas film has a certain stiffness, which enables a dynamic axial force balance and maintains the clearance of the sealing pairs in a noncontact operating state [25].
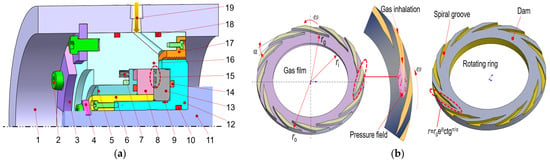
Figure 1.
Structure and working principle of dry-gas seals: (a) dry-gas sealing device; (b) structure of end face of sealing pairs and formation of a dynamic pressure effect. 1—Sealing house; 2—Fixing bolt; 3—Outer split clasp; 4—Inner split clasp; 5—Thrust collar; 6—Pressing sleeve; 7—Spring; 8—Stationary ring; 9—Gasket; 10—O-ring; 11—Rotating shaft; 12—Shaft sleeve; 13—Rotating ring; 14—O-ring; 15—Gas film; 16—Spring seat; 17—Labyrinth seal; 18—O-ring; 19—Gas inlet.
In the proposed calculation model, the spiral groove is processed on the end face of the rotating ring, the gas effect on the sealing performance is ignored, and the air is considered the fluid medium. Table 1 shows the specific initial calculation parameters.

Table 1.
Initial parameters of dry-gas seal.
2.2. Mathematical Model
2.2.1. Governing Equation
- (1)
- Basic assumptions
- (a)
- The volume force and inertia force of the gas are ignored;
- (b)
- The flow process is approximately isothermal continuous flow, assuming constant fluid viscosity;
- (c)
- The gas is an ideal gas, and its flow is laminar;
- (d)
- The influence of surface roughness is not considered.
- (2)
- Establishment of Reynolds equation
As shown in Figure 1, the end face has an annular structure, and the two seal ends are not in contact due to a gas film in the gap. The gas film thickness is uniform on the smooth seal surface, and the rectangular coordinate system is converted to the column coordinate system. Based on these assumptions, the dimensionless Reynolds equation of the gas film pressure on the end face of the dry-gas seal was obtained as follows [26,27,28]:
Dimensionless parameters were defined as follows:
- (3)
- Dimensionless gas film thickness governing equation
2.2.2. Setting of Boundary Conditions
- (1)
- Pressure boundary condition
- (2)
- Periodic pressure conditions along the circumference
2.3. Calculation of Sealing Performance Parameters
By solving the governing equation and boundary conditions, the gas film pressure distribution in the end face of the seals, as well as the steady-state performance parameters, can be determined.
Opening force of sealing pairs end face:
Gas leakage of the end face of the seal pairs:
Gas film friction:
Gas film stiffness:
2.4. Numerical Calculation and Process
Figure 2 shows the numerical calculation flow. The Reynolds equation was discretely analyzed using the finite difference method while determining boundary conditions and iterative solutions. By performing axial force balance analysis, the influence patterns and mechanisms of working condition parameters, as well as structural parameters on the dry-gas seal clearance performance, were investigated. Furthermore, relevant structural parameters of the end face were coordinated and optimized while developing a corresponding calculation program. The Reynolds equation is a non-linear differential equation that poses challenges in obtaining an analytical solution. Therefore, the flexible and computationally feasible finite difference method was used to solve the Reynolds equation. Figure 3 shows the grid division diagram of the central difference scheme, where p(i,j) denotes the gas film pressure at any point on the circular sealing end face. By adopting polar coordinates and dividing the circumferential and radial grids into n and m grids, respectively, a control model was established for the end-shape groove based on the gas film lubrication theory.
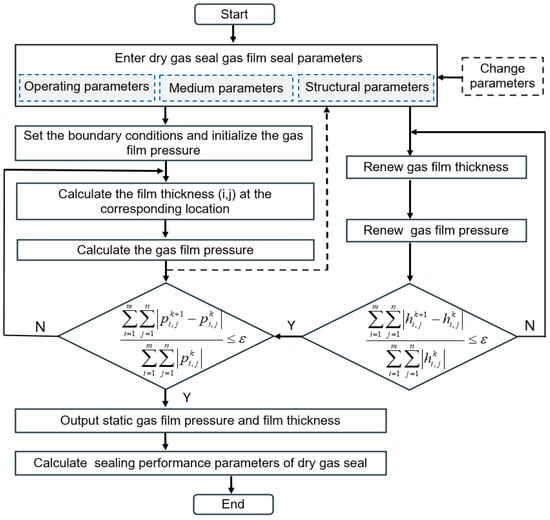
Figure 2.
Numerical calculation flow.
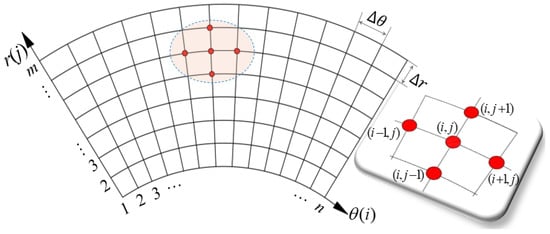
Figure 3.
Calculate area mesh.
3. Experimental Research
3.1. Sealing Tests System
The dry-gas seal’s lubrication was tested to assess its performance indicators and design effectiveness. The test system is shown in Figure 4, which comprises a sealing system, gas path system, power system, and test system. A comprehensive experimental test setup was established for the spiral groove dry-gas seals in rotating machinery to evaluate the performance parameters under controlled operating conditions such as pressure, temperature, and speed. An intermediate intake mode of operation was adopted for testing, wherein a compressor supplied high-pressure buffer gas through the control valve along the gas path system to provide suitable conditions for the dry gas seal. The motor, combined with a control cabinet, regulated the operating speed. Other instruments and sensors monitored and transmitted data signals related to temperature, pressure, speed, and leakage to a computer for analysis and processing.
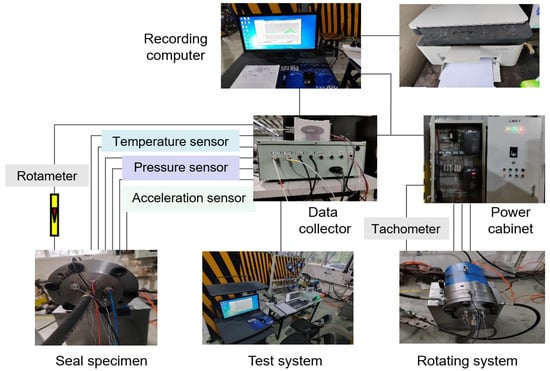
Figure 4.
Sealing system of dry-gas seals.
The dry-gas seal test bench consists primarily of a compressor, a high-pressure gas storage tank, a pressure-reducing valve, a filter, a gas test system, a test control system, a motor, an ultra-high-speed seal test bench and its accessories, several connecting pipelines, and the test system. After passing through the filter, the air is pressurized by the compressor and stored in the gas storage tank via pipeline connections for pressure preservation. It is then controlled by the pressure-reducing valve as it enters the sealed chamber. Additionally, pressure gauges are installed on the pipelines as necessary in order to monitor pressure changes and measure leakage rates using high-precision flowmeters. The pipelines also have necessary valves for controlling fluid pressures and flows of processes, while their speeds are regulated by inverters in the control system.
3.2. Test Technology and Method
The layout of the dry-gas seal test piece and sensor is depicted in Figure 5. A high-speed tester, pressure sensor, and other advanced sensing technologies are employed for the real-time monitoring and analysis of the internal flow characteristics of dry-gas seals. The moving and static rings were composed of cemented carbide and antimony graphite, respectively. The leakage test was used to evaluate the performance of dry gas seals. To ensure measurement accuracy, the KROHNE H250 metal tube float flowmeter with an accuracy class of 1.5 and a measuring range of 16 Nm3/h was used. To assess the opening force of the sealing device and monitor its real-time working status, as well as adjust and optimize its working parameters promptly for achieving the optimal sealing effect, the eddy-current displacement sensor model ZH220601, with a measuring range of 0.5 mm, was used.

Figure 5.
Test pieces for dry-gas seals.
3.3. Experimental Verification
3.3.1. Grid Independence Verification
Different mesh densities were employed and analyzed to investigate the impact of mesh sizes on the accuracy of numerical calculation. Figure 6 shows the results of grid independence verification. As the number of grids increased, the error in performance parameter calculations gradually decreased. Upon reaching a certain threshold at 135 × 135 grid nodes, the variation in the amplitude of sealing performance parameter errors stabilized at 5.22%. However, further increasing the number of grids prolonged the code solution convergence time. Considering calculation model complexity and effective computation time for enhancing the efficiency of numerical analysis within an acceptable accuracy range, 155 × 155 grids were used herein.
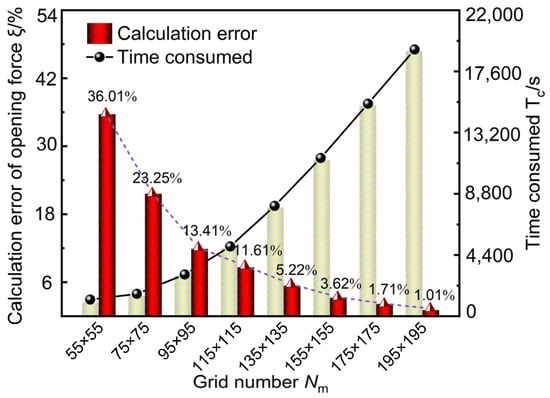
Figure 6.
Grid numbers independence verification.
3.3.2. Validity Verification of the Calculation Model
Figure 7 shows the verified results of the numerical model. The calculation program used for spiral-groove dry-gas seals with geometrical parameters (Table 1) was validated using a dry-gas seal testing device. The numerical calculation results, literature references [29], and experimental data were compared and analyzed to determine the impact of operational parameters on performance indicators. Figure 7a shows that when the pressure of the spiral groove increases from 2.0 MPa at rotation speeds of 2000–22,000 r∙min−1, the opening force and leakage rate gradually increase. This behavior can be attributed to an increase in the dynamic pressure effect with the increase in speed, which results in the formation of a stiff gas film at the clearance of the end face. This film reduces the friction force and opening force impact. Simultaneously, the dynamic pressure effect offsets part of the external load pressure applied on the seal, thereby reducing its opening force and leading to relatively insensitive changes in the steady-state performance parameter with varying speeds. Figure 7b shows the variations in the opening force and leakage rate at a constant rotational speed of 20,000 r∙min−1 and varying pressure at the inlet of the dynamic pressure tank from 2.0 to 4.0 MPa in range-wise gradient increments. As the pressure gradient increases, the gas flow within the seal gap increases, causing a sharp increase in the opening force and leakage.
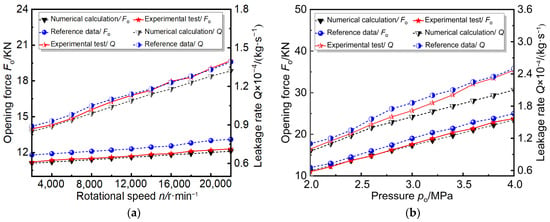
Figure 7.
Verified numerical model calculation results: (a) sealing performance under different rotational speeds; (b) sealing performance under different pressures.
The relative errors of the calculation performance parameters in numerical simulations when compared to the experimental test data and literature data at different speeds were as follows: an opening force of 1.65% and 8.26% and a leakage rate of 6.1% and 5.3%. Furthermore, the maximum errors between the numerical calculations and both experimental data and literature data for these performance parameters under varying pressures were as follows: an opening force of 3.4% and 6.5% and a leakage rate of 17.6% and 19.3%. These discrepancies can be attributed to deformation in the sealing component caused by additional loading at higher pressures, which subsequently affects its normal functioning, leading to an increase in both the opening force and leakage rate. The relative error between calculated values obtained in this study and corresponding experimental values falls within a reasonable range, thus validating our numerical simulation results.
4. Results and Analysis
4.1. Gas Film Pressure Distribution
The three-dimensional diagram in Figure 8 illustrates the pressure distribution of the gas film on the end face of a spiral-groove dry-gas seal under different pressures. The calculation was performed using the following working parameters: a rotational speed of 20,000 r∙min−1 and pressures of 1.4 MPa, 1.8 MPa, 2.2 MPa, and 2.6 MPa, as shown in Figure 8a–d, respectively. With an increase in pressure, the gas film pressure also increases accordingly. When the gas enters through the outer diameter of the spiral groove, it is obstructed by the sealing weir and compressed, leading to an enhanced dynamic pressure effect with maximum film pressure occurring at half of the groove root position. However, there is no dynamic pressure groove in the dam area of the seal end face, resulting in a similar circumferential pressure gradient along with variations in gas film thicknesses throughout this region. Changes in pressure can affect uniformity in the dry-gas seal film pressure distribution as well; lower pressures tend to cause an uneven distribution and significant local differences, while higher pressures help to homogenize the film pressure distribution.
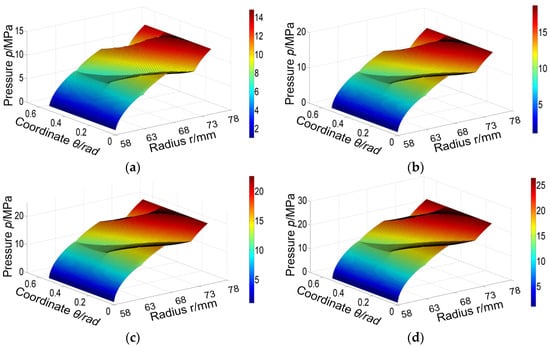
Figure 8.
Distribution of film pressure under different pressures: (a) po = 1.4 MPa; (b) po = 1.8 MPa; (c) po = 2.2 MPa; (d) po = 2.6 MPa.
The three-dimensional diagram in Figure 9 illustrates the pressure distribution of the gas film on the end face of a spiral-groove dry-gas seal at different speeds. The calculation was conducted using the following working parameters: a pressure of 1.4 MPa and a speed of 8000 r∙min−1, 14,000 r∙min−1, 20,000 r∙min−1, or 26,000 r∙min−1. The gas film pressure distribution at different speeds is shown in Figure 9a–d. Overall, there is a noticeable variation trend of gas film pressure from the inlet to the outlet side, with distinct pressure limits observed in areas such as the sealing dam area, spiral groove area, and sealing weir area. At lower rotational speeds, an insufficient dynamic pressure effect leads to lower gas film pressures. As the rotation speed increases, the enhanced gas flow velocity and dynamic pressure effects within the seal gap give rise to more complex gas phenomena, resulting in irregular changes in the gas film pressure distribution. Simultaneously, centrifugal force effects become stronger with the increase in speed, leading to an uneven distribution of gas pressures within the seal gap, causing radial variations in film pressure distribution; that is, an increase in the difference between the inner and outer film pressures occurs. When the speed reaches a certain value, a greater radial gradient appears in the gas film pressure distribution, which affects stability and sealing performance.
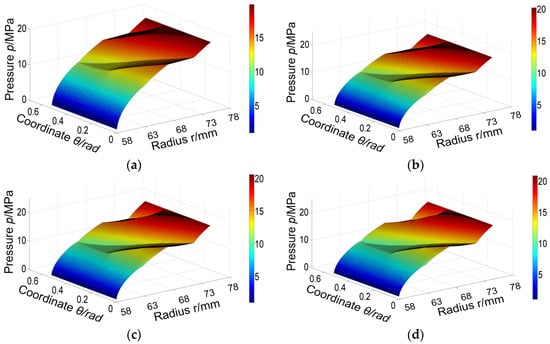
Figure 9.
Distribution of film pressure at different rotational speeds: (a) n = 8000 r∙min−1; (b) n = 14,000 r∙min−1; (c) n = 20,000 r∙min−1; (d) n = 26,000 r∙min−1.
Figure 10 shows a three-dimensional diagram of the gas film pressure distribution on the end face of the dry-gas seal with different numbers of grooves. The calculation parameters are as follows: at a rotational speed of 20,000 r∙min−1, the number of grooves is 4, 12, 20, or 28, and the gas film pressure distributions are shown in Figure 10a–d, respectively. When there are only four grooves, the pressure in each groove increases and results in an uneven pressure distribution due to prominent pressure concentration areas. As the number of grooves increases, the force exerted by the sealing film becomes more evenly distributed among them. At a groove count of 12, a higher atmospheric film pressure is observed. With an increase in the groove count, the pressure distribution becomes more uniform, and local fluctuations decrease because more grooves effectively disperse airflow and reduce local pressure concentration phenomena. However, increasing the groove count also leads to increased complexity in gas flow between grooves while ensuring structural stability and meeting sealing performance requirements, thus resulting in higher atmospheric film pressures when there are exactly 12 grooves.
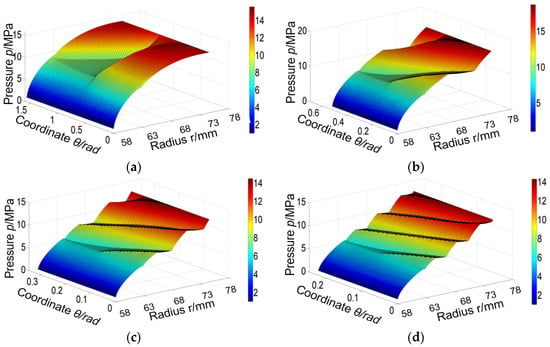
Figure 10.
Distribution of film pressure for different numbers of grooves: (a) Ng = 4; (b) Ng = 12; (c) Ng = 20; (d) Ng = 28.
4.2. Sealing Characteristic Analysis of Dry-Gas Seals
The dry-gas seal structure was chosen for the calculation model. The dynamic pressure effect of the seal pairs clearance was determined based on the working conditions and structural parameters. Air was considered the medium gas, and the initial calculation parameters are shown in Table 1.
4.2.1. Effect of Speed Changes on the Sealing Performance
The influence of the changing speed of the moving ring on the sealing performance is illustrated in Figure 11. The numerical calculation model considers gas film thicknesses of 3 μm, 4 μm, 5 μm, and 6 μm, with rotation speeds ranging from 8000 r∙min−1 to 28,000 r∙min−1. As depicted in Figure 11a,b,d, the dynamic pressure effect gradually increases with higher moving-ring speeds, leading to improved sealing performance parameters. At a constant speed, decreasing the gas film thickness results in an increase in both the opening force and gas film stiffness due to the increased gas film pressure difference; notably, larger values are observed when the film thickness is at its minimum of 3 μm. Conversely, when the film thickness reaches its maximum value of 6 μm, a further increase may compromise gas film stability and lead to increased leakage as a result. Figure 11c demonstrates that variations in the gas film thickness have minimal impact on the formation and maintenance of the gas film itself. However, a reduced gas film thickness leads to increased contact between sealing surfaces at a given speed, while higher rotational speeds alter flow characteristics by inducing uneven flow patterns and turbulence effects that affect gas film stability and elevate friction forces accordingly. At a rotational speed of 20,000 r∙min−1, the maximum frictional increase across different film thicknesses amounts to only about 1.33%. Additionally, it should be noted that the steady-state performance of dry-gas seals can be influenced by factors such as seal material selection, design considerations, and operating pressures, and the rotational ring speed represents only one among several factors, albeit having a relatively minor impact.
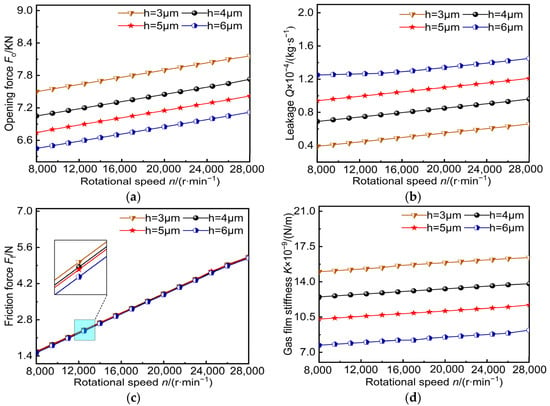
Figure 11.
Influence of speed changes on sealing performance: (a) opening force; (b) leakage; (c) friction force; (d) gas film stiffness.
4.2.2. Effect of Pressure Changes on the Sealing Performance
The effect of pressure changes on seal performance is illustrated in Figure 12. In the numerical calculation model, the gas film thickness ranges from 3 μm to 6 μm, and the pressure varies between 1.4 MPa and 2.7 MPa. Figure 12a,d demonstrates that an increase in pressure enhances the dynamic pressure effect on seal clearance, leading to significant changes in the opening force and gas film stiffness. Pressure directly influences the deformation and pressure distribution of the gas film, causing it to deform with higher seal gap pressure differences, thereby reducing sealing performance stability and increasing leakage. At a speed of 20,000 r∙min−1, compared with different gas film thicknesses, there is a maximum increase of 1.56% in leakage, indicating that while thicker gas films provide more flow channels, they also contribute to increased leakage. Film thickness has relatively little influence on the gas film deformation and pressure distribution at the same speed, as shown in Figure 12c. As depicted by Figure 12c, as pressure increases, the atmospheric film force intensifies, resulting in an expansion of the contact area between the gas film and seal surface, which further elevates frictional forces exerted during operation. When pressures exceed 2.0 MPa, lubrication effects are enhanced due to high-pressure gases, resulting in better formation of lubricating films between the gas film and sealing surfaces, thus reducing local contact pressures, which subsequently slows down friction trends. The variation in the gas film stiffness with respect to changing pressures can be observed in Figure 12d. An increase in pressure leads to greater forces acting upon the gas films, consequently altering their stiffness properties significantly; for instance, when considering a film thickness of only 3 μm, there is a relative increase in force by approximately 3.51% from 1.5 MPa to 2.0 MPa and an increase of over 50% from 2.0 MPa to 2.5 MPa. Therefore, it can be seen from the figure that with the increase in pressure, the change in sealing performance is prominent.
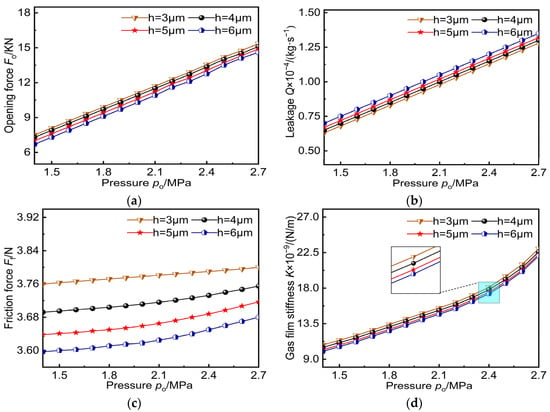
Figure 12.
Influence of pressure variation on sealing performance: (a) opening force; (b) leakage; (c) friction force; (d) gas film stiffness.
4.2.3. Influence of the Groove Depth Variation on the Sealing Performance
Figure 13 shows the effect of the groove depth variation on the sealing performance. The numerical calculation model assumes the following: the gas film thickness is 3 μm, 4 μm, 5 μm, or 6 μm, and the groove depth of the spiral groove is 3–9.5 μm. Figure 13a shows that with the increase in groove depth, the dynamic pressure effect between seal faces is enhanced. When the groove depth is greater than 6 μm, the maximum change in the opening force is 6.1%. Figure 13b shows that the leakage varies significantly with the increase in the tank depth. The leakage with a 6 μm tank depth is 0.15 × 10−4 kg∙s−1, while that with a 9 μm tank depth increases to 2.8 × 10−4 kg∙s−1 due to the combined influence of the gas film thickness and tank depth. Figure 13c shows that the friction force changes little when the groove depth is 3–3.5 μm. With the increase in the spiral groove depth, the gas in the groove is compressed, and the flow is weakened, resulting in an increase in friction force. Figure 13d shows that increasing the groove depth of the spiral groove is conducive to increasing the stiffness of the gas film, but the groove depth exceeding a certain value causes gas flow instability, thus affecting the sealing performance. According to the calculation model, when the groove depth is 5.0–6.0 μm, the dynamic pressure effect caused by the pressure gradient is obvious, and good dry-gas sealing performance can be obtained.
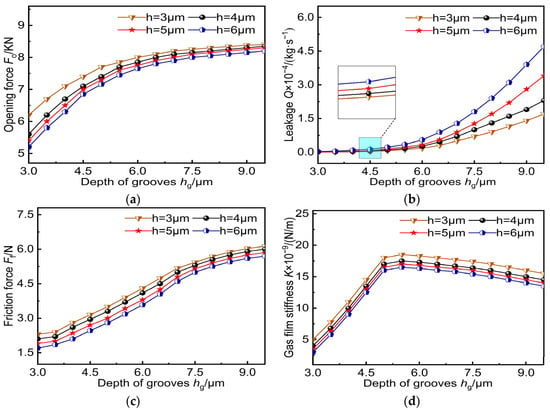
Figure 13.
Influence of groove depth variation on sealing performance: (a) opening force; (b) leakage; (c) friction force; (d) gas film stiffness.
4.2.4. Effect of the Number of Spiral Grooves on the Sealing Performance
Figure 14 shows the effect of the number of slots on the sealing performance. Gas film thicknesses of 3 μm, 4 μm, 5 μm, and 6 μm are included in the numerical calculation model, and the number of spiral grooves is 4–30. It can be seen from Figure 14a,d that the pressure difference between the end faces of the sealing width increases with the increase in the number of grooves. At the same speed, the opening force and the stiffness of the gas film have larger values when the film thickness is 3 μm. When the number of grooves is 4–10, the opening force and gas film stiffness change obviously, and when the number of slots is greater than 12, the change trend gradually becomes smooth. Figure 14b shows that the leakage volume increases with the increase in the number of slots. When the number of slots is unchanged, the leakage volume increases with the increase in film thickness. Figure 14c shows that as the number of grooves increases, the change in friction force presents a non-linear trend, and as the number of grooves continues to increase, the friction force gradually becomes stable. In summary, when the number of grooves is greater than 10, the change in steady-state performance parameters of the dry-gas seal decreases. Considering that the processing difficulty increases with the number of slots, the number of slots was selected to be 10–16 after comprehensively considering the processing and manufacturing and the performance of the high-stability and low-leakage seal. In addition, the number of symmetrical spiral grooves designed can further ensure the balance of the spiral grooves when the working condition changes, which helps to reduce the poor sealing performance caused by asymmetry in order to maximize the steady-state performance of the dry-gas seal.
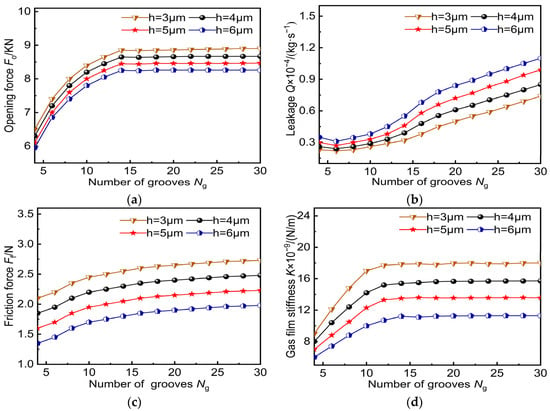
Figure 14.
Influence of the number of spiral grooves on sealing performance: (a) opening force; (b) leakage; (c) friction force; (d) gas film stiffness.
5. Conclusions
In this study, a calculation program method was utilized and experimentally verified to validate its effectiveness. The steady-state performance parameters of the dry-gas seal were utilized as evaluation indices to derive the distribution patterns of film pressure with lubrication characteristics and the variation patterns of different steady-state performance parameters.
- (1)
- The effectiveness of the calculation program was validated through experiments. Advanced sensing technology was applied in the experiment to monitor and analyze real-time internal flow characteristics of dry-gas seals while exploring new data acquisition technology and analysis methods. Additionally, the central difference method was used to solve the governing equations for gas film pressure and thickness, establishing a computational model for spiral groove dry-gas seals.
- (2)
- Distribution patterns of membrane pressure for different parameters were obtained. When operating at low pressures, the film pressure distribution becomes non-uniform with local variations in pressure differences; however, an increase in pressure helps to homogenize the film pressure distribution. As rotational speed increases, centrifugal effects intensify, resulting in radial gradients in gas film pressures. When there are 12 grooves present, the gas film pressure distribution becomes uniform with higher values.
- (3)
- The variation rules of steady-state performance parameters under different operating conditions were determined. When the gas film thickness remains constant, the steady-state performance parameters increase with an increase in the operating condition parameters. However, when the film thickness is 6 μm, an increase in the gas film thickness easily leads to a deterioration in gas film stability and subsequently increases leakage. Significant changes in the opening force, leakage, and gas film stiffness are observed for a film thickness of 3 μm and pressure greater than 2.0 MPa. Simultaneously, with high-pressure differences, an increase in the dynamic pressure effect reduces the local contact force and, consequently, the friction force. A decrease in the gas film thickness at the same rate results in an increase in gas film pressure difference, which further causes an increase in the opening force and gas film stiffness. However, as the rotational speed increases, non-uniformity of the gas flow occurs, leading to an increased friction force that affects the stability of the gas film.
- (4)
- A range of structural parameters yielding improved performance was identified. Optimal dry-gas sealing performance can be achieved when there are 10–16 grooves with depths ranging from 5.0 to 6.0 μm, where dynamic pressure effects caused by the pressure gradient become evident.
Author Contributions
Conceptualization, X.D.; methodology, L.Z.; formal analysis, S.W.; investigation, S.Z.; resources, S.W.; data curation, B.C.; writing—original draft preparation, L.Z.; visualization, S.W.; supervision, S.Z.; project administration, B.C. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the National Natural Science Foundation of China (No. 51565029).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to the reviews for their careful and detailed comments.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| A | Spiral groove region |
| Fo, Ff | Opening force, KN, Friction force, N |
| H, h0 | Dimensionless gas film thickness, Dimensionless gas film thickness, μm |
| hg | Spiral groove depth, μm |
| K | Gas film stiffness, N/m |
| Ng | Number of grooves |
| n | Rotating ring speed, r·min−1 |
| P, p | Dimensionless pressure, Dimensionless pressure, MPa |
| Q | Leakage, kg·s−1 |
| R, r | Dimensionless radius, radius at any point of the seal end face, mm |
| rg | Radius at the root, mm |
| ri, ro | Inner radius of moving ring, mm, outer radius of moving ring, mm |
| ur | Radial velocity, m·s−1 |
| α | Spiral Angle, ° |
| δ | The thickness of the gas film in the dimensional groove, μm |
| θ | Development Angle, rad |
| μ | Fluid viscosity, pa·s |
| ρ | Fluid density, kg·m−3 |
| ω | Angular velocity of rotation, rad/s |
| Δθ | θ-direction dimensionless difference step length |
| Δr | r-direction dimensionless difference step length |
| dθ | The minor component of Angle theta |
| dz | The z component |
References
- Fairuz, Z.M.; Jahn, I.; Abdul-Rahman, R. The Effect of Convection Area on the Deformation of Dry Gas Seal Operating with Supercritical CO2. Tribol. Int. 2019, 137, 349–365. [Google Scholar] [CrossRef]
- Li, S.; Zhu, Q.; Cai, J.; Zhang, Q.; Jin, Z. Regulation Performance of Regulatable Dry Gas Seal. Trans. Fluid Mech. 2016, 11, 18–24. [Google Scholar]
- Jiang, P.; Tian, Y.; Wang, B.; Guo, C. Numerical Study on Rotor Cooling of Turbine in Supercritical Carbon Dioxide Cycle. ACS Omega 2022, 7, 39325–39334. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Wang, S.; Zhang, S.; Ding, J. Research Progress on the Dynamic Stability of Dry Gas Seals. Processes 2024, 12, 575. [Google Scholar] [CrossRef]
- Yan, R.; Chen, H.; Zhang, W.; Hong, X.; Bao, X.; Ding, X. Calculation and Verification of Flow Field in Supercritical Carbon Dioxide Dry Gas Seal Based on Turbulent Adiabatic Flow Model. Tribol. Int. 2022, 165, 107275. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhao, W.; Jin, J.; Peng, X. A Comprehensive Multi-Objective, Multi-Parameter and Multi-Condition Optimization of a Spiral Groove in Dry Gas Seals. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 206. [Google Scholar] [CrossRef]
- Wang, L.; Sun, J. Performance Analysis and Bi-Objective Optimization Study on Diffuser Self-pumping Hydrodynamic Mechanical Seal. Tribology 2024, 44, 947–959. [Google Scholar]
- Gardner, J.; Basu, P.; Muraki, R. Analysis, Design, Laboratory Testing of a High Pressure, High Speed, Reduced Axial Length Gas Seal. In Fluid Sealing; Springer: Dordrecht, The Netherlands, 1992; pp. 389–409. [Google Scholar]
- Gabriel, R.P. Fundamentals of Spiral Groove Noncontacting Face Seals. Lubr. Eng. 1994, 50, 215–224. [Google Scholar]
- Wang, H.; Zhu, W.; Wang, Q.; Huang, Z.; Zhang, C. Numerical Simulation on Flow Field of Spiral Grooved Dry Gas Seals. In Proceedings of the 2010 International Conference on Computer Design and Applications, Qinhuangdao, China, 25–27 June 2010; Volume 5, pp. V5-227–V5-230. [Google Scholar]
- Wang, B.; Zhang, H. Numerical Analysis of a Spiral-Groove Dry-Gas Seal Considering Micro-Scale Effects. Chin. J. Mech. Eng. 2011, 24, 146–153. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, H.; Cao, H. Flow Dynamics of a Spiral-Groove Dry-Gas Seal. Chin. J. Mech. Eng. 2013, 26, 78–84. [Google Scholar] [CrossRef]
- Chávez, A.; De Santiago, O. Experimental Measurements of the Thermo Elastic Behavior of a Dry Gas Seal Operating with Logarithmic Spiral Grooves of 11° and 15°. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 1807–1819. [Google Scholar] [CrossRef]
- Garcia, J.C.; Reyes, R.; De Santiago Duran, O.; Ramirez, J.A.R.; Espinosa, F.S.; Pensado, M.B. Numerical Computation of Flow Field in the Spiral Grooves of Steam Turbine Dry Seal. Am. J. Aerosp. Eng. 2017, 4, 54–58. [Google Scholar] [CrossRef]
- Du, Q.; Gao, K.; Zhang, D.; Xie, Y. Effects of Grooved Ring Rotation and Working Fluid on the Performance of Dry Gas Seal. Int. J. Heat Mass Transf. 2018, 126, 1323–1332. [Google Scholar] [CrossRef]
- Ren, B.; Hao, M. Performance Analysis and Software Development of Spiral Groove Dry Gas Seal Based on Semi-Analytical Method. J. Chem. Pharm. Eng. 2019, 40, 55–59. [Google Scholar]
- Wang, Y.; Ge, Y.; Huang, G.; Hu, Q.; Xiao, Y.; Hu, P. The Logic Relationship between Macroscopic Characteristics and Mesoscopic Velocity Field of High-Speed Rotating Flow Field of Dry Gas Seal. Tribology 2020, 40, 364–377. [Google Scholar]
- Ran, R.; Ding, X.; Xu, J.; Yu, S.; Ding, J. The Influence Analysis of Centrifugal Inertia Force Effect on the Flow Field and Sealing Characteristics of Supercritical Carbon Dioxide Dry Gas Seal. Tribology 2020, 40, 781–791. [Google Scholar]
- Xu, H.; Song, P.; Mao, W.; Deng, Q. The Performance of Spiral Groove Dry Gas Seal under Choked Flow Condition Considering the Real Gas Effect. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 554–566. [Google Scholar] [CrossRef]
- Wang, Y.; Ge, Y.; Huang, G.; Hu, Q.; Hu, P. Microscale Flow Field Analysis and Flow Prediction Model Exploration of Dry Gas Seal. IEEE Access 2020, 8, 52663–52675. [Google Scholar] [CrossRef]
- Yuan, T.; Li, Z.; Li, J.; Yuan, Q. Effect of Spiral Structure on the Shaft End Dry Gas Seal Performance for Supercritical Carbon Dioxide Compressors. J. Xi’an Jiaotong Univ. 2020, 54, 37–45. [Google Scholar]
- Sun, X.; Song, P.; Hu, X.; Mao, W.; Deng, Q.; Xu, H. Cross-Scale Flow Field Analysis of Sealing Chamber and End Face Considering the CO2 Real Gas Effect. J. Appl. Fluid Mech. 2021, 14, 979–991. [Google Scholar]
- Hahn, M.; Park, Y.; Kang, M.; Jun, S.; Jang, G. Effects of Laminar, Turbulent, and Slip Conditions in a Fluid Film on a Dry Gas Seal. Machines 2022, 10, 954. [Google Scholar] [CrossRef]
- Zheng, W.; Sun, J.; Ma, C. Comprehensive Performance of Diffused Self-Pumping Hydrodynamic Mechanical Seal. Tribology 2024, 44, 686–695. [Google Scholar]
- Jiang, Z.; Chen, Q. Comparison of Spiral Groove Dry Gas Sealing Performance and Optimization of Structure. Jilin Inst. Chem. Technol. 2021, 38, 13–17. [Google Scholar]
- Huang, P. Numerical Calculation of Lubrication: Methods and Programs; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Miller, B.A.; Green, I. Semi-Analytical Dynamic Analysis of Spiral-Grooved Mechanical Gas Face Seals. J. Tribol. 2003, 125, 403–413. [Google Scholar] [CrossRef]
- Miller, B.A.; Green, I. Numerical Formulation for the Dynamic Analysis of Spiral-Grooved Gas Face Seals. J. Tribol. 2001, 123, 395–403. [Google Scholar] [CrossRef]
- Jiang, X.; Gu, B. Characteristic of Gas Film between Spiral Groove Dry Gas Seal Faces. CIESC J. 2005, 56, 1419–1425. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).