Abstract
To optimize the production scheduling of a flexible job shop, this paper, based on the NSGA-II algorithm, proposes an adaptive simulated annealing non-dominated sorting genetic algorithm II with enhanced elitism (ASA-NSGA-EE) that establishes a multi-objective flexible job shop scheduling model with the objective functions of minimizing the maximum completion time, processing cost, and carbon emissions generated from processing. The ASA-NSGA-EE algorithm adopts an adaptive crossover and mutation genetic strategy, which dynamically adjusts the crossover and mutation rates based on the evolutionary stage of the population, aiming to reduce the loss of optimal solutions. Additionally, it incorporates the simulated annealing algorithm to optimize the selection strategy by leveraging its cooling characteristics. Furthermore, it improves the elite strategy through incorporating elite selection criteria. Finally, by simulation experiments, the effectiveness of the improved NSGA-II algorithm is validated by comparing it with other algorithms.
1. Introduction
In recent years, with the nation’s economy continuing to grow, the intelligent manufacturing sector has reached its full potential. As the core of the manufacturing industry, production workshop scheduling is crucial for increasing productivity and reducing production costs. The green production workshop scheduling has become an indispensable development direction because of the importance of comprehensive consideration of economic benefits and environmental protection, and the research on green workshop scheduling has become the focus [1].
The MOFJSP (multi-objective flexible job shop scheduling problem) is the most challenging and production environment-focused problem in workshop scheduling optimization [2], and it has been proven to be an NP-hard problem [3]. As a critical production management task, it can maximize production efficiency and resource utilization, effectively addressing the requirements of a low-carbon economy. Therefore, research on multi-objective flexible job shop scheduling is of great significance. Currently, there are many algorithms for the MOFJSP, such as particle swarm optimization (PSO) [4,5,6], ant colony optimization (ACO) [7,8], grey wolf optimization (GWO) [9,10], and so on. Among all algorithms, the NSGA-II algorithm has shown good performance [11]. It was proposed by Indian scientist Deb [12] in 2002 and showed good performance in many fields; it also performs well on the MOFJSP problem. Nowadays, the NSGA-II algorithm is one of the most widely used and influential multi-objective evolutionary algorithms, but it also has issues such as slow convergence and susceptibility to falling into a local optimal solution. At present, a large number of scholars both domestically and internationally are beginning to turn the objective to the optimization of the NSGA-II algorithm to solve the multi-objective workshop scheduling problem, and numerous research findings have been obtained. Liu et al. proposed a combined neighborhood search algorithm [13] based on the NSGA-II algorithm according to the characteristics of multiple types and small batches of aviation part processing, taking the completion time, total load of the machine, and energy consumption of the machine as the target. They improved the search ability of the algorithm through a variety of neighborhood search operators. Jiang et al. [14] improved the population initialization, cross mutation rate, and elite retention strategy in the NSGA-II algorithm with energy consumption and processing cost as the target, and verified the effectiveness of the algorithm through practical cases. Liang et al. introduced constructive heuristic algorithm [15] in the initial population stage to improve the initial population quality of the NSGA-II algorithm. Jauny et al. [16] proposed a trust region interior point algorithm for solving multi-objective optimization problems, effectively balancing the conflicts between multiple objectives and demonstrating superior performance. Anh et al. [17] explored the robust degraded completion time scheduling problem in single-machine scheduling. They proposed a linear-time algorithm and a polynomial-time combinatorial algorithm, effectively addressing the challenge of achieving a specified degraded completion time under uncertain cost conditions. Wang et al. [18] optimized the NSGA-II algorithm by using a non-dominated fast sorting operator and competitive operator to select a descendant operator with processing period, delay penalty, and processing cost as the target. Vital-Soto et al. [19] improved the NSGA algorithm with innovative operators by minimizing the maximum completion time, the maximum worker workload, and the weighted tardiness as optimization objectives, including probabilistically selecting from three different crossover strategies during the crossover operation. Liu [20], aiming at the diversity of the NSGA-II algorithm in screening out non-dominated solutions, proposed a crowding distance elimination method. Ren et al. [21] proposed a hybrid algorithm combining particle swarm optimization and the genetic algorithm to optimize the production efficiency and energy consumption during processing. Luan et al. [22] established models of completion time, delay time, and power consumption, and combined sparse theory with the NSGA-II algorithm to enhance the population diversity and improve the uniformity in optimal solution distribution. It is evident that in recent years, researchers have often combined the NSGA-2 algorithm with other heuristic methods to enhance search efficiency and speed, expanding optimization objectives beyond time to include dimensions such as energy consumption and processing costs. However, we observe that studies considering time, processing costs, and carbon emissions simultaneously are still rare, and there is a lack of validation in real production environments.
In this paper, the energy consumption of equipment startup and shutdown, idle energy consumption, and operation energy consumption are taken as the sources of carbon emission in the production process of the workshop. Considering the processing cost and raw material cost generated by the operation of the machine, aiming at minimizing the carbon emission, production cost, and maximum completion time, a low-carbon flexible operation workshop scheduling model is established, and an ASA-NSGA-EE algorithm is proposed for the model. The feasibility of the proposed algorithm is verified by a practical case. The remainder of this paper is organized as follows: Section 2 provides a detailed introduction to the mathematical model approach used for the problem. Section 3 de-scribes the enhanced ASA-NSGA-EE algorithm, including key improvements. Section 4 presents the experiments conducted and an analysis of their results to verify the algorithm’s effectiveness. Finally, Section 5 concludes this paper by summarizing the main findings and suggesting directions for future research.
2. MOFJSP Scheduling Model
2.1. Description of MOFJSP Problem
The multi-objective flexible workshop scheduling problem can be described as follows: there are n to-be-machined workpieces in the processing workshop, denoted as job set J (), and there are m sets of processable equipment, denoted as equipment set M (). Each workpiece J includes multiple processes. Each process can be processed by one or more pieces of equipment on the machine set . The processing time, processing cost, and carbon emission of the same process on different machines are different. Different equipment can process different workpiece at the same time. The objective of this paper is to determine the processing equipment used in each process and the processing sequence of the workpiece on each equipment, so as to achieve the optimal combination of carbon emission, production cost, and processing time.
In this paper, the MOFJSP is subject to the following constraints:
(1) Each machine can process only one type of workpiece within a certain time period.
(2) The processing of workpieces is strictly scheduled according to the sequence of operations.
(3) The machine cannot be stopped processing once it has begun until the task is finished.
(4) The carbon emissions during machine processing are independent of the type of workpiece, and carbon emissions can also occur when the machine is idle.
2.2. MOFJSP Mathematical Model
During the manufacturing process, machines operate in various states, such as startup, preheating, running, and idling, with different carbon emissions for each state. Therefore, this paper considers energy consumption, job completion time, and processing costs in various machine operating states to develop a multi-objective green job shop scheduling model that accounts for energy consumption in the production process. Table 1 shows the notations and descriptions for modelling the MOFJSP. The objective functions can be calculated by Equation (3).

Table 1.
Notations of the proposed MOFJSP.
2.2.1. The Model of Makespan
2.2.2. The Model of Cost
means the material cost of the to-be-machined workpiece. means the costs incurred by equipment and machines during the processing of workpieces.
2.2.3. The Model of Carbon Emission
In this paper, machine energy consumption is considered as the source of carbon emissions.
means carbon emission factor. means the total energy consumption during the machine operation.
Total EC (): The total EC generated during the machine production process consists of three parts: processing EC, idle EC, and start-stop EC. can be calculated based on Equation (7).
Processing EC (): This refers to the energy consumed by equipment and machines during the processing of workpieces. can be calculated based on Equation (8).
Idle EC (): This refers to the energy consumed through equipment and machines when they are in standby mode or not processing workpieces. can be calculated based on Equation (9).
Start–stop EC (): This refers to the energy lost during the startup and shutdown processes of machines. can be calculated based on Equation (10).
3. The ASA-NSGA-EE Algorithm
The NSGA-II algorithm is an improved genetic algorithm based on Pareto-optimal solutions, with the goal of resolving multi-objective optimization issues. In order to improve the operational efficiency and optimization capability of the algorithm, this paper proposed an ASA-NSGA-EE algorithm, which will improve the NSGA-II algorithm in three aspects, tournament selection, elite retention strategy, and crossover and mutation, as shown in the ASA-NSGA-EE basic flow in Figure 1.
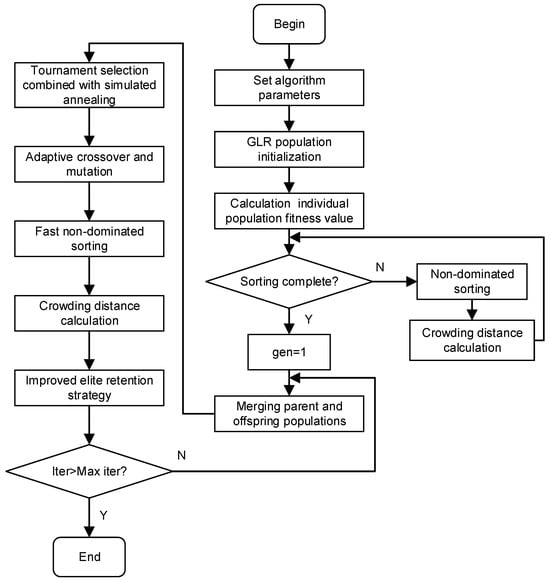
Figure 1.
The basic flow of ASA-NSGA-EE.
3.1. Population Initialization
In the NSGA-II algorithm, both the solving speed and the search quality are strongly impacted by the quality of solutions produced by the initial population. Typically, scholars use random population initialization methods. Based on [23], the ASA-NSGA-EE algorithm adopted a GLR population initialization method that models total completion time, carbon emissions, and processing costs.
3.2. Encoding and Decoding
In this paper, we use a two-layer real-number encoding method. In the process layer encoding, different encoding values represent different workpieces. The same workpiece’s different processes are represented by the same value, and the sequence and frequency of the same encoding value indicate the process order of the workpiece. In the machine layer encoding, each gene value represents the machine number selected for the corresponding process in the set of processing machines. For instance, in Figure 2, the first number 4 in the machine layer indicates the machine number in the optional machine set for its corresponding process. Compared to other encoding methods like permutation or discrete encoding, this approach reduces decoding complexity and errors, making it more adaptable to flexible job shop scheduling problems of varying scales and complexities, while maintaining robust performance under challenging scheduling conditions. For instance, in Figure 1, the first number 4 in the machine layer indicates that its corresponding process is processed by machine number in the optional machine set . The last number 3 indicates that its corresponding process is processed by machine number in the optional machine set .
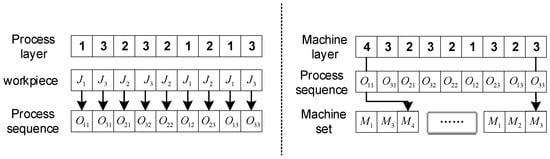
Figure 2.
Example of coding.
Decoding involves translating the chromosomes obtained by the algorithm back into feasible solutions for the original problem. This paper employs active decoding and fully active decoding, with the detailed process described in Reference [24].
3.3. Fast Non-Dominated Sorting and Crowding Distance Calculation
The Pareto-optimum solution set is the main challenge in multi-objective optimization. Fast non-dominated sorting categorizes solutions into different non-dominated levels by comparing their dominance relationships. All individuals in the population are ranked according to their non-dominated relationships. Those at level 0 form the optimal layer, and all individuals in this layer are extracted. The levels are incremented until all individuals are extracted. The specific steps are as follows:
(1) Initialize the set of solutions to be sorted.
(2) Compare each pair of individuals within the solution set. If solution A dominates solution B, it indicates that A is at least equal to B in all objective functions and superior to B in at least one objective function.
(3) Based on the obtained dominance relationships, divide all solutions into different non-dominated levels, and assign each solution to its corresponding non-dominated level.
(4) Recombine all non-dominated level solutions into a new set of solutions. Select and retain higher-level non-dominated solutions while gradually discarding lower-level non-dominated solutions to maintain diversity and convergence of the solution set.
(5) Repeat step 2 to 4 until all individuals are compared.
3.4. Improved Tournament Selection
The selection operation involves selecting some superior individuals from the current population to enter the next generation, an important step to promote the evolution of the solution set. Generally, the binary tournament selection method is used, but this method has limitations such as a lack of diversity and difficulty in retaining excellent individuals. Thus, in this paper, we introduce an improve elite selection strategy combined with the Metropolis criterion into the general binary tournament selection. In the early stages of algorithm iteration, solutions with lower-quality are retained with a higher probability to increase population diversity. In the later stages, higher-quality solutions are retained with a higher probability to accelerate the convergence of the population. When the fitness values of two individuals cannot determine the dominance relationship, a temperature-controlled selection pressure is used, still allowing for a certain probability of selecting better individuals. This achieves a dynamic balance between diversity and convergence. The specific process is shown in Figure 3.
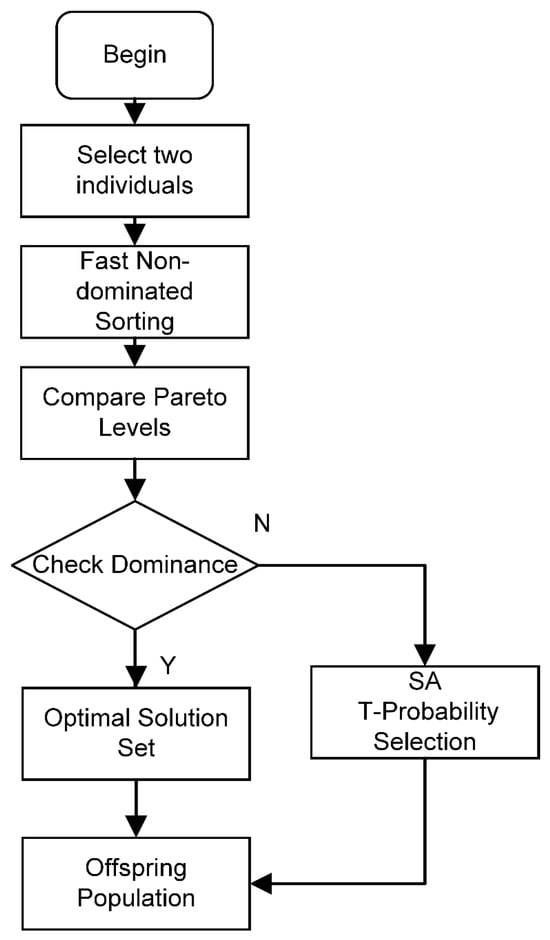
Figure 3.
The basic flow of the improved tournament selection.
3.5. Crossover and Mutation Operation Design Program
The crossover operation generates new offspring individuals by combining the genetic information of parent individuals, which facilitates the global search of the algorithm. This paper employs improved position-based crossover (IPOX) and uniform crossover (UX) for the process part and the equipment selection part, respectively.
The crossover process for operation codes uses IPOX, as shown in Figure 4a. The specific steps are as follows: randomly select two individuals from the parent population and designate their operation codes as Parent 1 and Parent 2. Then, randomly divide all workpieces into sets and . While maintaining their positions, copy the genes from Parent 1 that are in to Offspring 1 and the genes from Parent 2 that are in to Offspring 2. Then, sequentially place the genes from Parent 1 that are in into Offspring 2, and the genes from Parent 2 that are in into Offspring 2, thus completing the generation of the offspring.
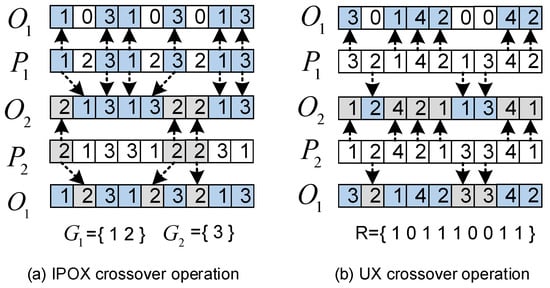
Figure 4.
Crossover operation.
The crossover process for machine codes uses UX, as shown in Figure 4b. This method generates diverse offspring by randomly selecting gene positions from parent individuals. The specific steps are as follows:
First, generate a binary string R of the same length as the parent chromosomes. Next, copy all genes from Parent 1’s chromosome at positions corresponding to the binary string R to Offspring 1’s chromosome. Similarly, copy all genes from Parent 2’s chromosome at positions corresponding to the binary string R to Offspring 2’s chromosome. Finally, copy the remaining genes from Parent 1’s chromosome to Offspring 2’s chromosome in order, and the remaining genes from Parent 2’s chromosome to Offspring 1’s chromosome in order, thus completing the crossover.
This paper uses a two-point gene swap method for operation code mutation. Two genes in the parent operation code chromosome are randomly selected and swapped to obtain the mutated offspring operation code chromosome, as shown in Figure 5a.

Figure 5.
Mutation operation.
A double-gene mutation method is used for equipment code mutation. Two genes in the parent equipment code chromosome are randomly selected, and then another machine is chosen from the optional equipment set for the mutation operation, as shown in Figure 5b.
3.6. Improved Adaptive Crossover and Mutation Operation
The crossover rate and mutation rate have a significant impact on the global convergence of the algorithm. In the typical NSGA-II algorithm, the crossover probability and mutation probability often use fixed values. For individuals with fitness above the population average, fixed crossover and mutation rates struggle to protect the superior genetic material. This approach has the drawbacks of failing to balance the needs of multi-objective optimization problems and causing the algorithm to prematurely converge to suboptimal solutions. Therefore, this paper improves the method proposed in the literature by adaptively adjusting the crossover probability and mutation probability . The expressions are as follows:
In the equations, is the maximum fitness value of the population, is the average fitness value of the population, is the fitness value of the better individual in the crossover, and f is the fitness value of the mutated individual. Generally, after several experimental validations, we take , ,, and .
This method uses larger and values for individuals that deviate from the average fitness value to generate new individuals closer to the optimal solution, thereby increasing the search speed. For individuals close to the average fitness value, smaller and values are used to protect the genes of superior individuals, allowing for all individuals in the population to gradually approach the global optimal solution.
3.7. Improved Elite Retention Strategy
The standard NSGA-II algorithm’s elitism strategy directly incorporates the best individuals into the next generation’s parent population. While this method can increase the algorithm’s convergence speed, it can also affect the diversity of the next generation’s population, leading the algorithm to get stuck in local optima. This paper improves on this by introducing an elite selection criterion to limit the number of elite solutions from each non-dominated front entering the next generation’s parent population, and then randomly selecting several non-elite solutions to join the next generation’s parents. The elite selection criterion is shown in the following equation:
In the equation, represents the number of individuals in the non-dominated front, is the number of individuals selected from the non-dominated front, and is a random real number between 0.8 and 1.
4. Test Simulation
This paper compares the performance of the ASA-NSGA-EE algorithm, the traditional NSGA-II algorithm, the MOGWO algorithm using the MK series scheduling examples provided by Brandimarte (the specific data can be downloaded from the following website: https://people.idsia.ch/~monaldo/fjsp.html#ProblemInstances, accessed on 20 August 2024), and a case study from a gear shaft workshop in a manufacturing company.
The operational environment was Windows 11, and MATLAB R2020b was used for algorithm implementation. The algorithm parameters were set as follows: The population for all three algorithms was set to 150, with 100 iterations. The crossover probability for NSGA-II and ASA-NSGA-EE was set at 0.9, and the mutation probability at 0.2. For ASA-NSGA-EE, the population initialization ratios for GS, LS, and RS were 0.6, 0.3, and 0.1
4.1. Performance Evaluation Index of Algorithm
To provide a detailed comparison demonstrating the improved NSGA-II algorithm’s superior distribution and convergence, this paper evaluates the algorithm’s performance using the IGD, HV, and C-metric indicators.
The IGD indicator reflects the average distance between each reference point and the closest solution. A lower IGD value indicates better overall algorithm performance. Its specific definition is as follows:
represents the minimum distance from each non-dominated solution in the objective space to the true Pareto front, and is the number of non-dominated solutions.
The C-metric indicator reflects the dominance relationship between two sets of non-dominated solutions. It is defined as follows:
In this equation, A and B are two sets of non-dominated solutions to be compared; a represents an individual in A. indicates the proportion of individuals in B that are dominated by or equal to at least one individual in A. If = 1, all individuals in B are dominated by or equal to individuals in A; conversely, if = 0, none of the individuals in B are dominated by individuals in A.
The HV indicator is used to obtain the volume of the objective space region enclosed by the non-dominated solution set and the reference points [25,26]. It comprehensively reflects the algorithm’s convergence and diversity. The larger the HV indicator, the better the overall performance of the algorithm. The specific definition is as follows:
In the equation, represents the Lebesgue measure used to measure volume, represents the hypervolume formed by the reference point and the individuals in the solution set, and denotes the number of non-dominated solutions. This paper selects the maximum value of each objective function as the reference point.
Each of the three algorithms was run 20 times with consistent parameter settings, and the best metrics were recorded, as shown in Table 2. The bold font indicates the better results for the same instances. The results show that, in terms of the COV indicator, the ASA-NSGA-EE algorithm described in this paper outperformed the other two algorithms in all ten instances. Most of the solutions obtained by ASA-NSGA-EE dominate the solution sets of the comparison algorithms, demonstrating the superior optimization capability and solution quality of ASA-NSGA-EE. In terms of the HV indicator, the ASA-NSGA-EE algorithm also outperformed the comparison algorithms, indicating that the solution sets obtained have better convergence and diversity. Regarding the IGD indicator, it is evident that the solution sets obtained by the ASA-NSGA-EE algorithm are closer to the true Pareto front and have more uniform distribution.

Table 2.
Comparison of algorithm performance evaluation indexes.
4.2. Enterprise Case
To put the ASA-NSGA-EE algorithm presented in this paper to further testing, a gear shaft from a manufacturing workshop was taken as the research object. Based on the actual data from the workshop, the processing information is shown in Table 3. This workshop contains various lathes, drilling machines, milling machines, boring machines, CNC machines, and machining centers, encompassing turning, milling, and drilling processes, representing a typical flexible job shop. Processing costs consist of workers’ wages and the consumed electricity resources. Based on the policy released by the Zhejiang Provincial Development and Reform Commission in April 2024, the average industrial electricity price is set at 0.8118 yuan/(kW·h). Carbon emissions are related to the electricity resources consumed during processing and the carbon emission factor. According to the Ministry of Ecology and Environment’s “Notice on the Management of Greenhouse Gas Emission Reports for the Power Generation Industry for 2023–2025,” the national grid’s average emission factor for 2024 is determined to be 0.5703 kgCO2/kWh.

Table 3.
Processing data for gear shaft FJSP instance.
Under the same parameter settings, the three algorithms were run, and the convergence curves of each optimization objective were plotted, as shown in Figure 6. It can be seen that the ASA-NSGA-EE algorithm proposed in this paper achieved the optimal values for makespan, production cost, and carbon emissions. Additionally, it converged to the optimal solution more quickly, verifying the reliability of the proposed algorithm.
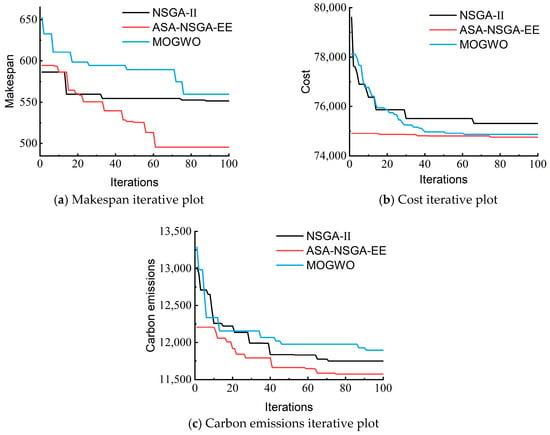
Figure 6.
Iterative chart plot.
To more intuitively analyze the differences in results among the three algorithms for solving the gear shaft scheduling problem, a three-dimensional Pareto front distribution map was plotted with processing cost, completion time, and carbon emissions as optimization objectives after running each algorithm once.
From Figure 7a, it can be seen that the gear shaft scheduling problem studied in this paper does not have an exact solution but rather a Pareto front composed of a series of discrete solutions distributed along the Pareto-optimal frontier. To more accurately determine the correlation among the optimization objectives, three 2D scatter plots from different perspectives were drawn. Figure 7b shows that the solutions obtained by the ASA-NSGA-EE algorithm are more diverse, achieving lower carbon emissions and processing costs. Figure 7c indicates that as the completion time increases, the processing cost decreases, and the convergence effect is superior to that of the other two algorithms. Figure 7d shows that the ASA-NSGA-EE algorithm can find shorter completion times and lower carbon emissions.
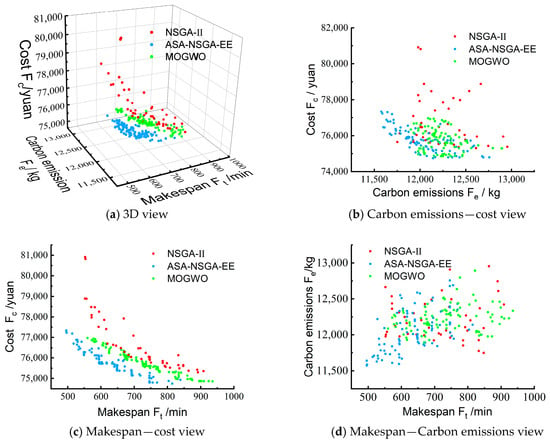
Figure 7.
Pareto front scatter.
In summary, under the same parameter settings, the solutions obtained by the algorithm described in this paper are of higher quality across all objective dimensions. Additionally, a Gantt chart for gear shaft scheduling generated by the ASA-NSGA-EE algorithm is provided in Figure 8.
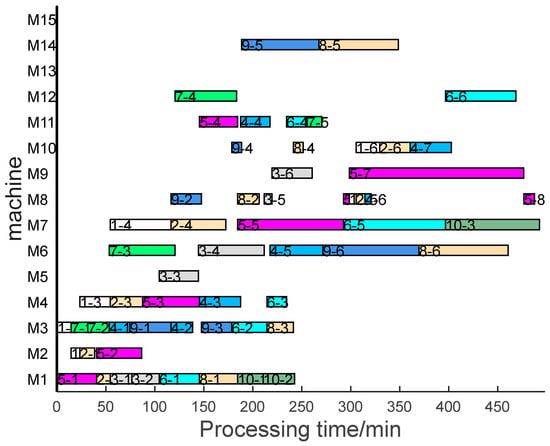
Figure 8.
The Gantt chart of the ASA-NSGA-EE for gear shaft instance.
5. Conclusions
In this paper, we propose an ASA-NSGA-EE algorithm based on the NSGA-II algorithm to solve the multi-objective low-carbon flexible job shop scheduling optimization model in the context of green intelligent manufacturing, aiming to minimize makespan, processing cost, and carbon emissions by utilizing GLR population initialization and active decoding to generate a high-quality initial population and design an adaptive crossover and mutation strategy to dynamically adjust the crossover and mutation rates during crossover and mutation operation. In addition, we combined the tournament selection process with the simulated annealing algorithm to probabilistically select better individuals, and the elitism preservation strategy was also improved. Finally, the algorithm was validated using Brandimarte’s MK series scheduling instances and a real-life case study. Comparisons with the traditional NSGA-II algorithm and the MOGWO algorithm demonstrated the effectiveness of the ASA-NSGA-EE algorithm in solving multi-objective low-carbon job shop scheduling problems. It can be widely applied in industrial production, simultaneously reducing carbon emissions and environmental pollution while enhancing economic efficiency. The results of this study not only offer an effective solution for flexible job shop scheduling but also provide new insights and inspiration for future researchers in the fields of algorithm optimization and industrial applications. Finally, although this study has achieved significant success in addressing the flexible job shop scheduling problem, there are still some limitations. Firstly, this study does not consider the more complex disruptive factors present in real-world environments. Secondly, the performance of the algorithm on larger and more complex problems requires further validation. These limitations suggest that we need to make adaptive adjustments based on specific production environments in practical applications. Meanwhile, these limitations also provide directions for future scholars’ research.
Future work will further explore the application of the algorithm to problems of varying scales and complexities, incorporating dynamic changes in real production environments, such as considering transportation time and tool wear as more realistic production constraints. Additionally, efforts will be made to integrate the ASA-NSGA-EE algorithm with other intelligent optimization algorithms to further enhance solving efficiency and accuracy, thereby boosting the economic benefits for enterprises.
Author Contributions
Data curation, Z.M.; Funding acquisition, Y.L.; Supervision, Y.L. and L.L.; Writing—original draft, Z.M.; Writing—review and editing, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Key R&D Projects of Zhejiang Province (2022C01242) and the Project of Longgang Research Institute of Zhejiang Sci-Tech University (LGYJY2021004).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
On behalf of all authors, the corresponding author states that there are no conflicts of interest.
References
- Destouet, C.; Tlahig, H.; Bettayeb, B.; Mazari, B. Flexible job shop scheduling problem under Industry 5.0: A survey on human reintegration, environmental consideration and resilience improvement. J. Manuf. Syst. 2023, 67, 155–173. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S.; Sethi, R. The complexity of flowshop and jobshop scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
- Fattahi, P.; Bagheri Rad, N.; Daneshamooz, F.; Ahmadi, S. A new hybrid particle swarm optimization and parallel variable neighborhood search algorithm for flexible job shop scheduling with assembly process. Assem. Autom. 2020, 40, 419–432. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Amirteimoori, A.; Mahdavi, I.; Solimanpur, M.; Ali, S.S.; Tirkolaee, E.B. A parallel hybrid PSO-GA algorithm for the flexible flow-shop scheduling with transportation. Comput. Ind. Eng. 2022, 173, 108672. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Jeon, H.W.; Lee, S.; Wang, C. Minimizing total energy cost and tardiness penalty for a scheduling-layout problem in a flexible job shop system: A comparison of four metaheuristic algorithms. Comput. Ind. Eng. 2020, 141, 106295. [Google Scholar] [CrossRef]
- Demir, H.I.; Erden, C. Dynamic integrated process planning, scheduling and due-date assignment using ant colony optimization. Comput. Ind. Eng. 2020, 149, 106799. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Ahmed, R.; Nazir, A.; Mahadzir, S.; Shorfuzzaman, M.; Islam, J. Niching grey wolf optimizer for multimodal optimization problems. Appl. Sci. 2021, 11, 4795. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Xin, B.; Dou, L. Solving multi-objective multi-stage weapon target assignment problem via adaptive NSGA-II and adaptive MOEA/D: A comparison study. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 3132–3139. [Google Scholar]
- Kalyanmoy, D. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Z.; Chen, W.; Hu, Z. Aerial Accessory Flexible Job Shop Scheduling Optimization Considering Carbon Low Emissions. Aeronaut. Sci. Technol. 2024, 35, 47–57. [Google Scholar]
- Jiang, Y.; Ji, W.; He, X.; Su, X. Low-carbon Scheduling of Multi-objective Flexible Job-shop Based on Improved NSGA-Ⅱ. China Mech. Eng. 2022, 33, 2564–2577. [Google Scholar] [CrossRef]
- Liang, X.; Chen, J.; Gu, X.; Huang, M. Improved adaptive non-dominated sorting genetic algorithm with elite strategy for solving multi-objective flexible job-shop scheduling problem. IEEE Access 2021, 9, 106352–106362. [Google Scholar] [CrossRef]
- Ghosh, D.; Upadhayay, A.; Ansari, Q.H. A Trust-Region Interior-Point Technique to Solve Multi-Objective Optimization Problems and Its Application to A Tuberculosis Optimal Control Problem. J. Nonlinear Var. Anal. 2022, 6, 675–691. [Google Scholar]
- Anh, L.Q.; Le, H.M.; Nguyen, K.T.; Thanh, L.X. AN ALGORITHMIC APPROACH TO THE ROBUST DOWNGRADING MAKESPAN SCHEDULING PROBLEM. Appl. Set-Valued Anal. Optim. 2024, 6, 263–273. [Google Scholar]
- Yahui, W.; Ling, S.; Cai, Z.; Liuqiang, F.; Xiangjie, J. NSGA-II algorithm and application for multi-objective flexible workshop scheduling. J. Algorithms Comput. Technol. 2020, 14, 1748302620942467. [Google Scholar] [CrossRef]
- Vital-Soto, A.; Baki, M.F.; Azab, A. A multi-objective mathematical model and evolutionary algorithm for the dual-resource flexible job-shop scheduling problem with sequencing flexibility. Flex. Serv. Manuf. J. 2023, 35, 626–668. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X. An improved NSGA-II algorithm based on crowding distance elimination strategy. Int. J. Comput. Intell. Syst. 2019, 12, 513–518. [Google Scholar] [CrossRef]
- Ren, W.; Wen, J.; Yan, Y.; Hu, Y.; Guan, Y.; Li, J. Multi-objective optimisation for energy-aware flexible job-shop scheduling problem with assembly operations. Int. J. Prod. Res. 2021, 59, 7216–7231. [Google Scholar] [CrossRef]
- Luan, F.; Zhao, H.; Liu, S.Q.; He, Y.; Tang, B. Enhanced NSGA-II for multi-objective energy-saving flexible job shop scheduling. Sustain. Comput. Inform. Syst. 2023, 39, 100901. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, G.; Wang, X. Intelligent Algorithm of Flexible Job Shop Scheduling and Its Application; Huazhong University of Science and Technology Press: Wuhan, China, 2012; pp. 154–196. [Google Scholar]
- Zhang, C.; Guan, Z.; Liu, Q.; Shao, X.; Li, P. New Scheduling Type Applied to Solving Job-shop Scheduling Problem. J. Mech. Eng. 2008, 44, 24–31. [Google Scholar] [CrossRef]
- Zheng, J.; Li, K.; Li, M.; Wen, S. Adaptive Neighbor Multi-Objective Evolutionary Algorithm Based on Hypervolume Indicator. J. Comput. Res. Dev. 2012, 49, 312–326. [Google Scholar]
- Shang, K.; Ishibuchi, H.; He, L.; Pang, L.M. A survey on the hypervolume indicator in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2020, 25, 1–20. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).