Detection of Demagnetization Faults in Electric Motors by Analyzing Inverter Based Current Data Using Machine Learning Techniques
Abstract
1. Introduction
2. Background to Demagnetization
2.1. Demagnetization Mechanism in PMSMs
2.2. State of the Art for Detection of Demagnetization
3. Simulative Investigations
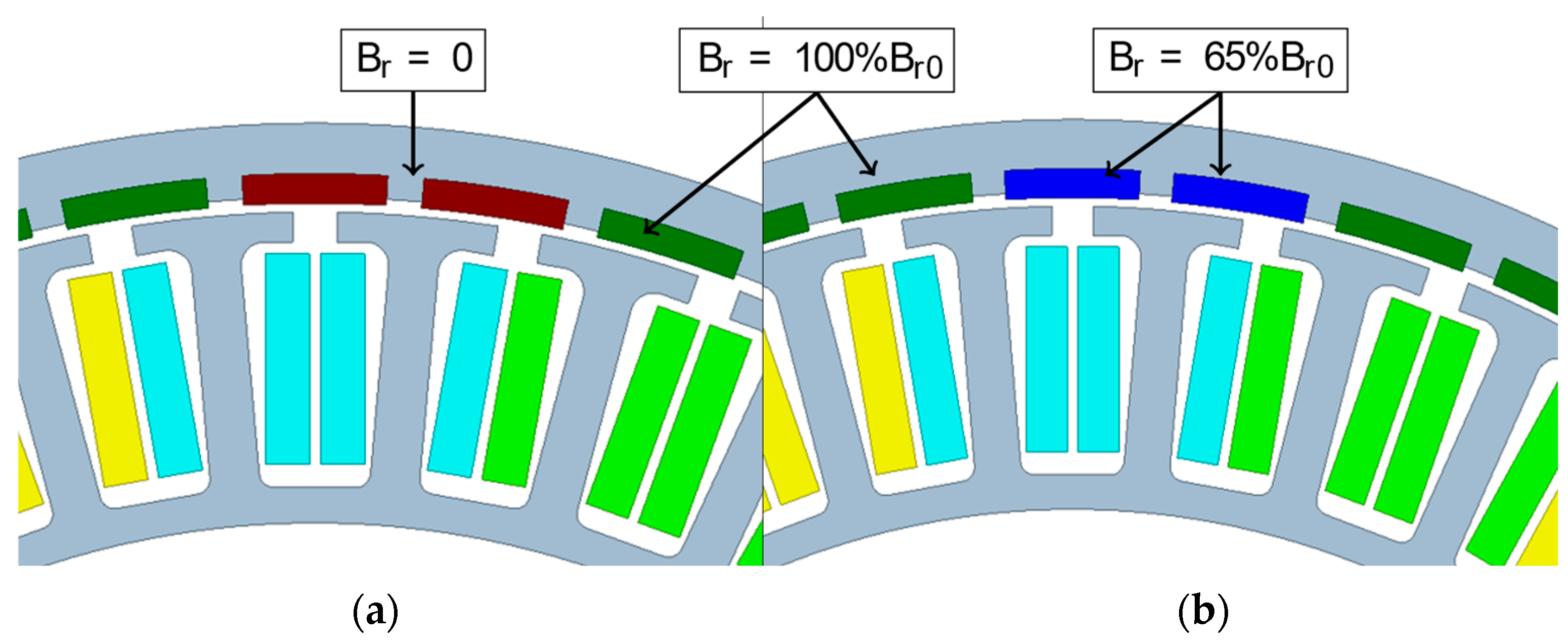
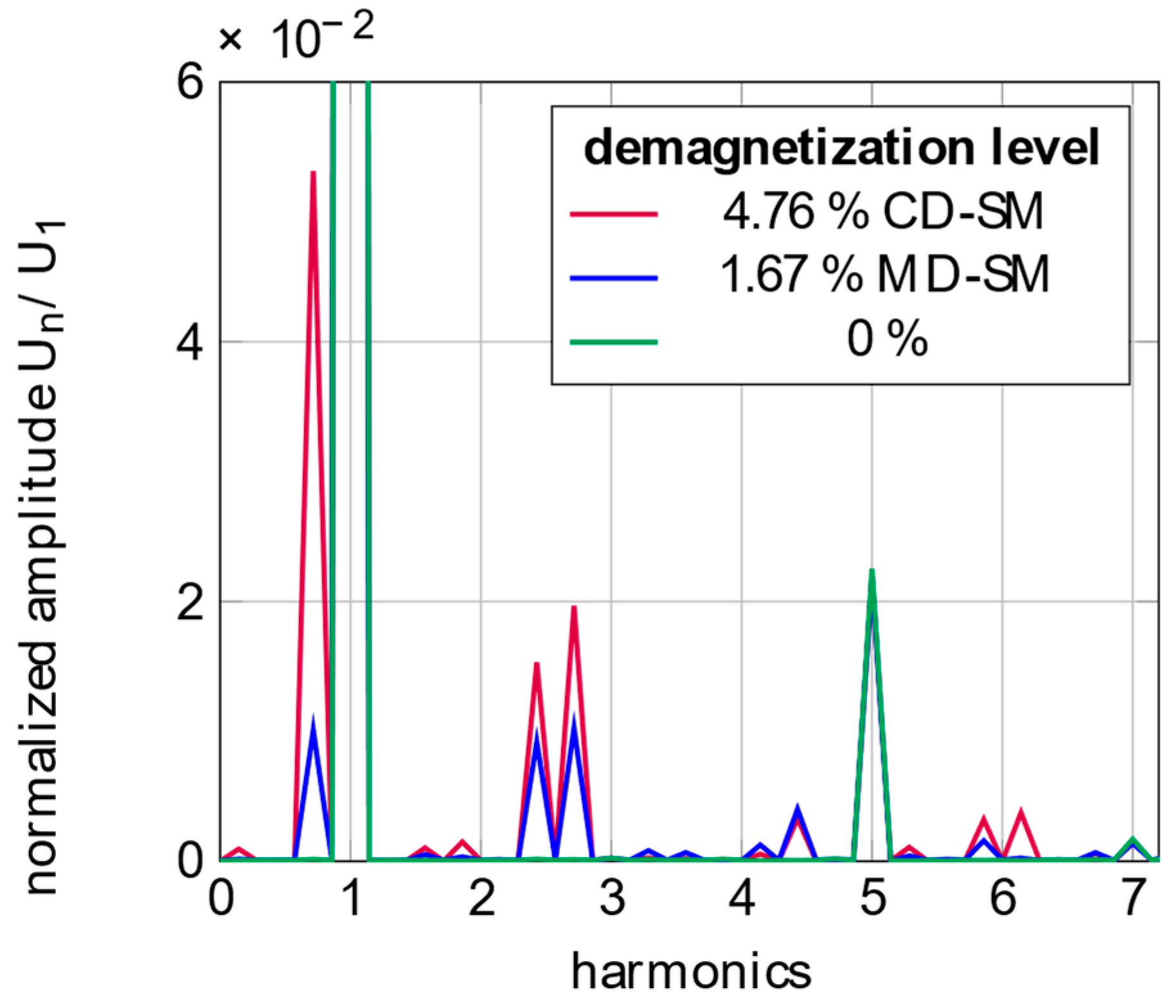
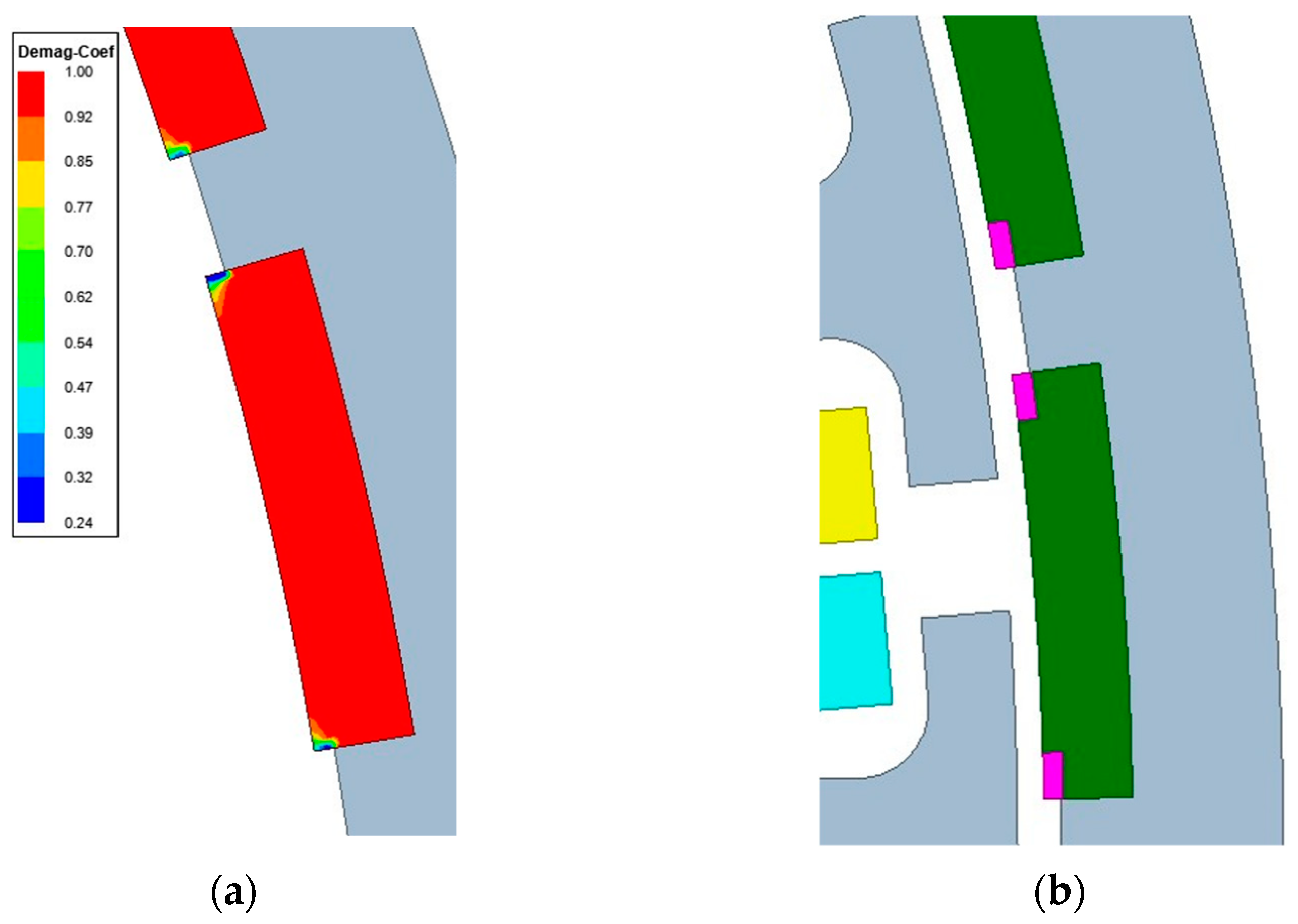
3.1. Partial Demagnetization
3.2. Uniform Demagnetization
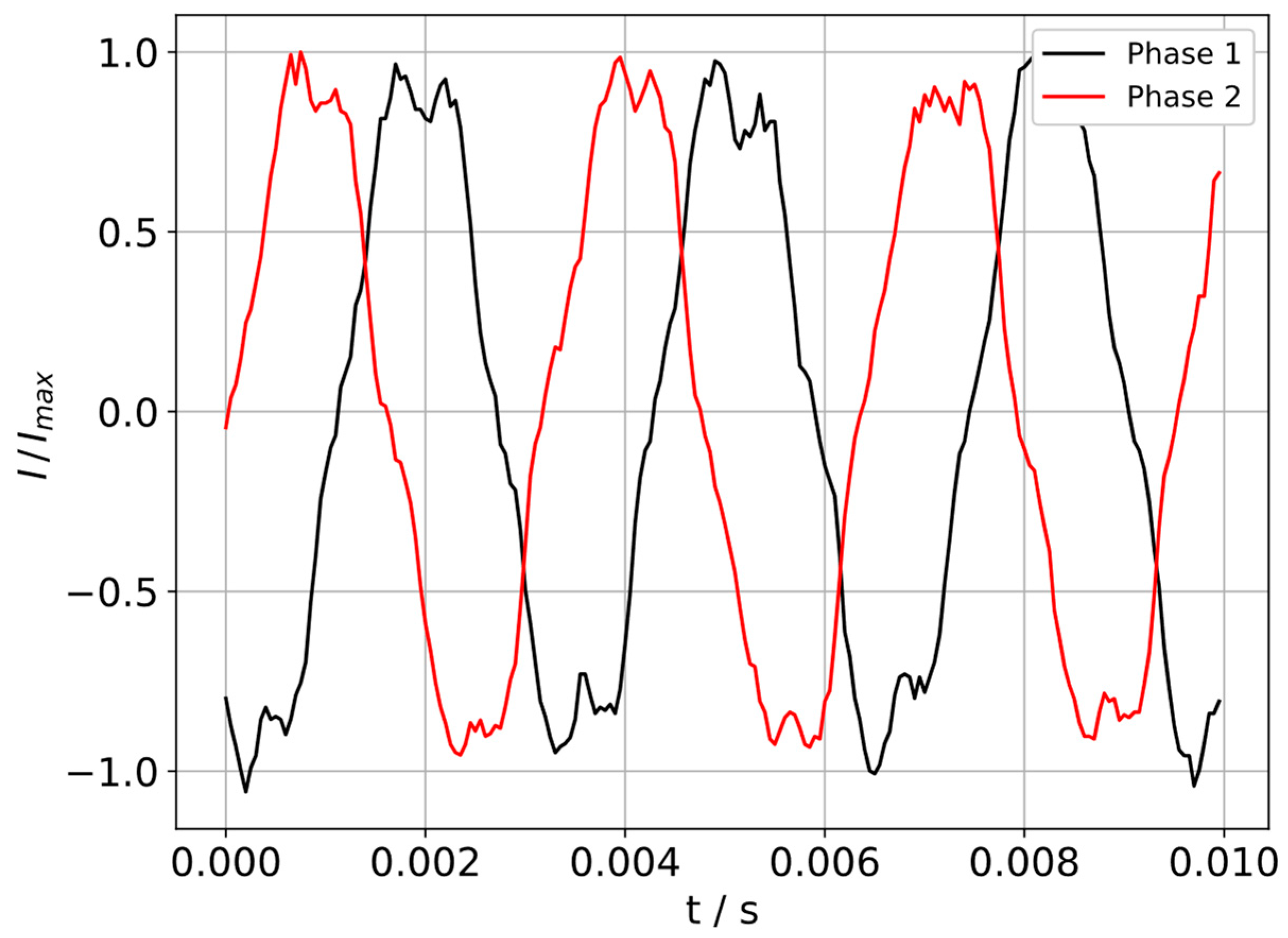
4. Experimental Investigations
4.1. Experimental Setup for the Investigation of Electric Drives
4.2. Explored Demagnetization Faults
5. Machine Learning Pipeline
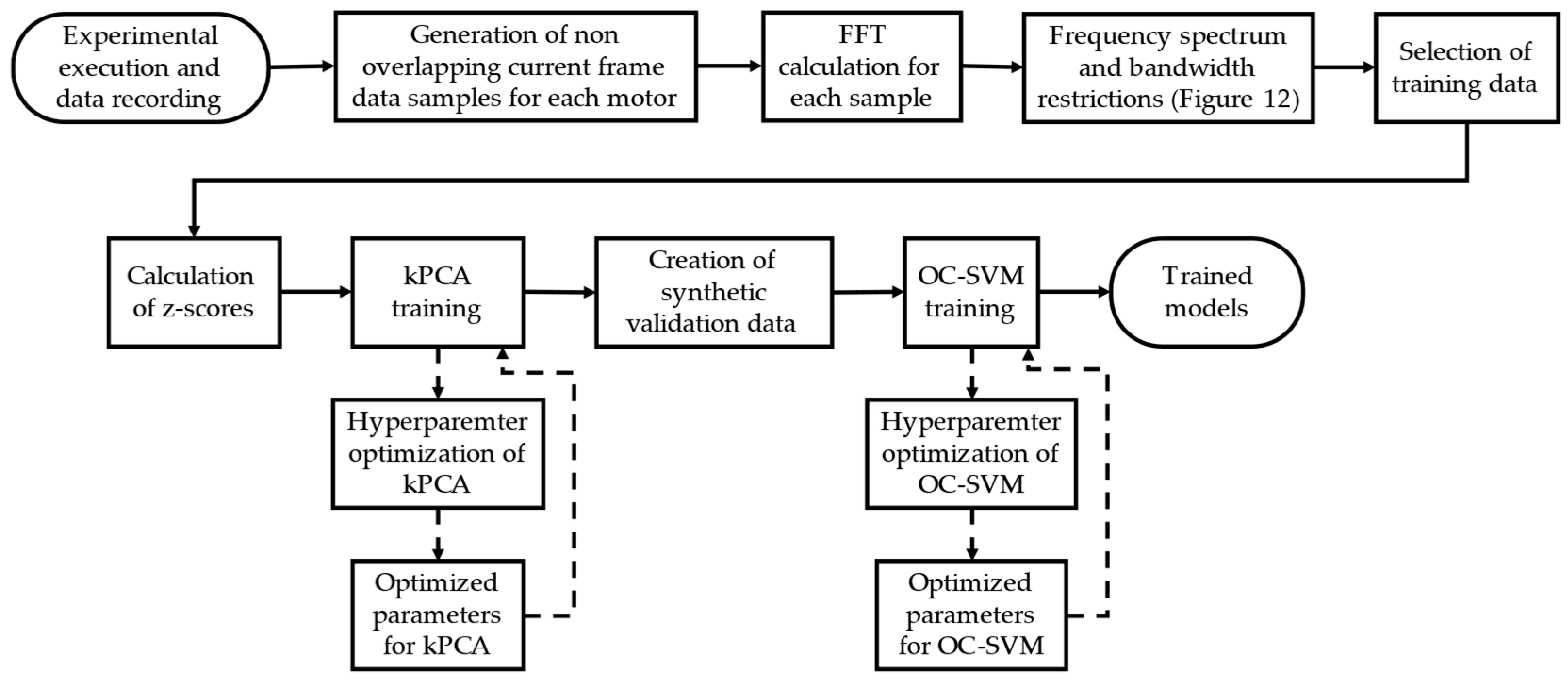
5.1. Analysis Approach
5.2. Data Preprocessing
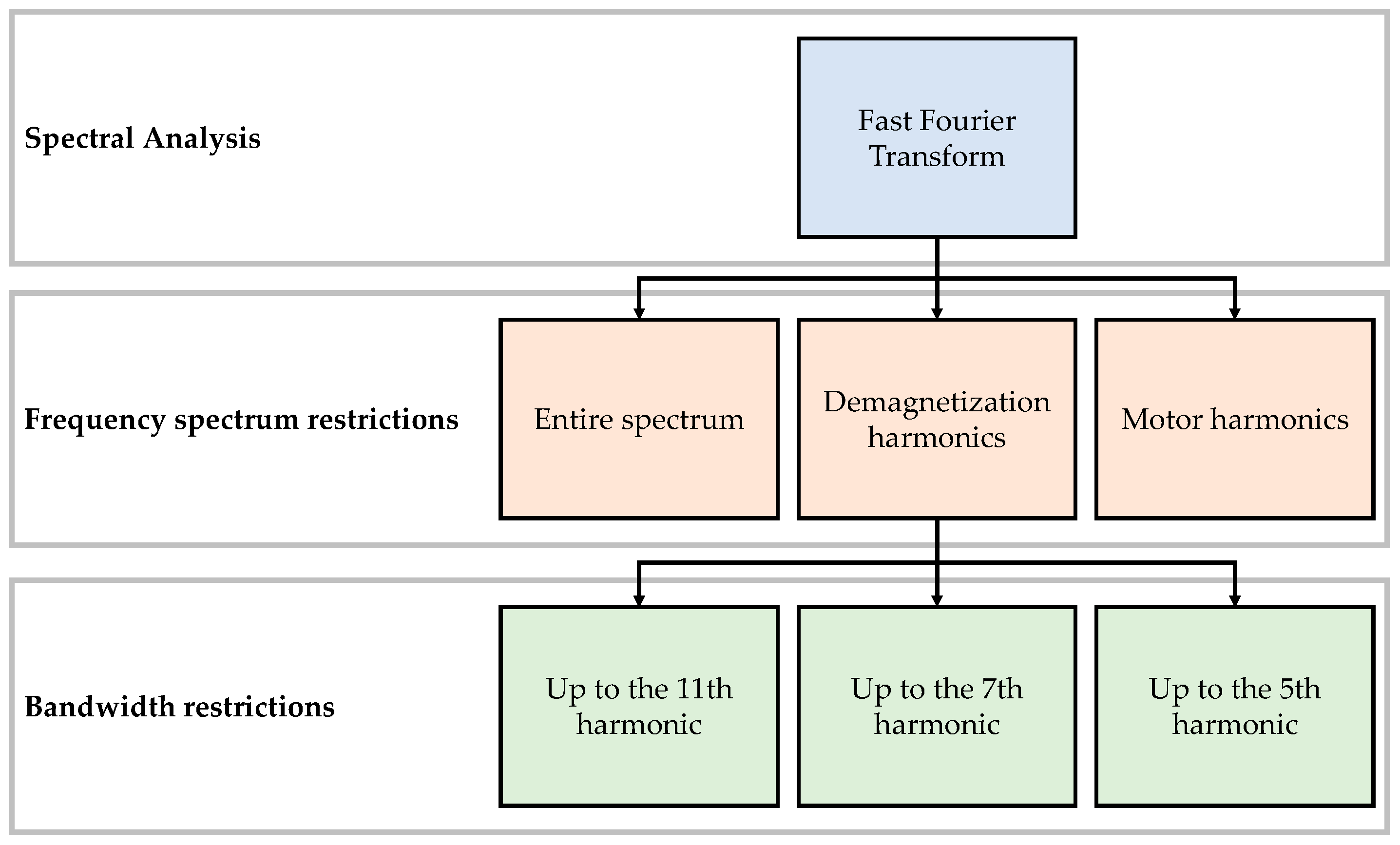
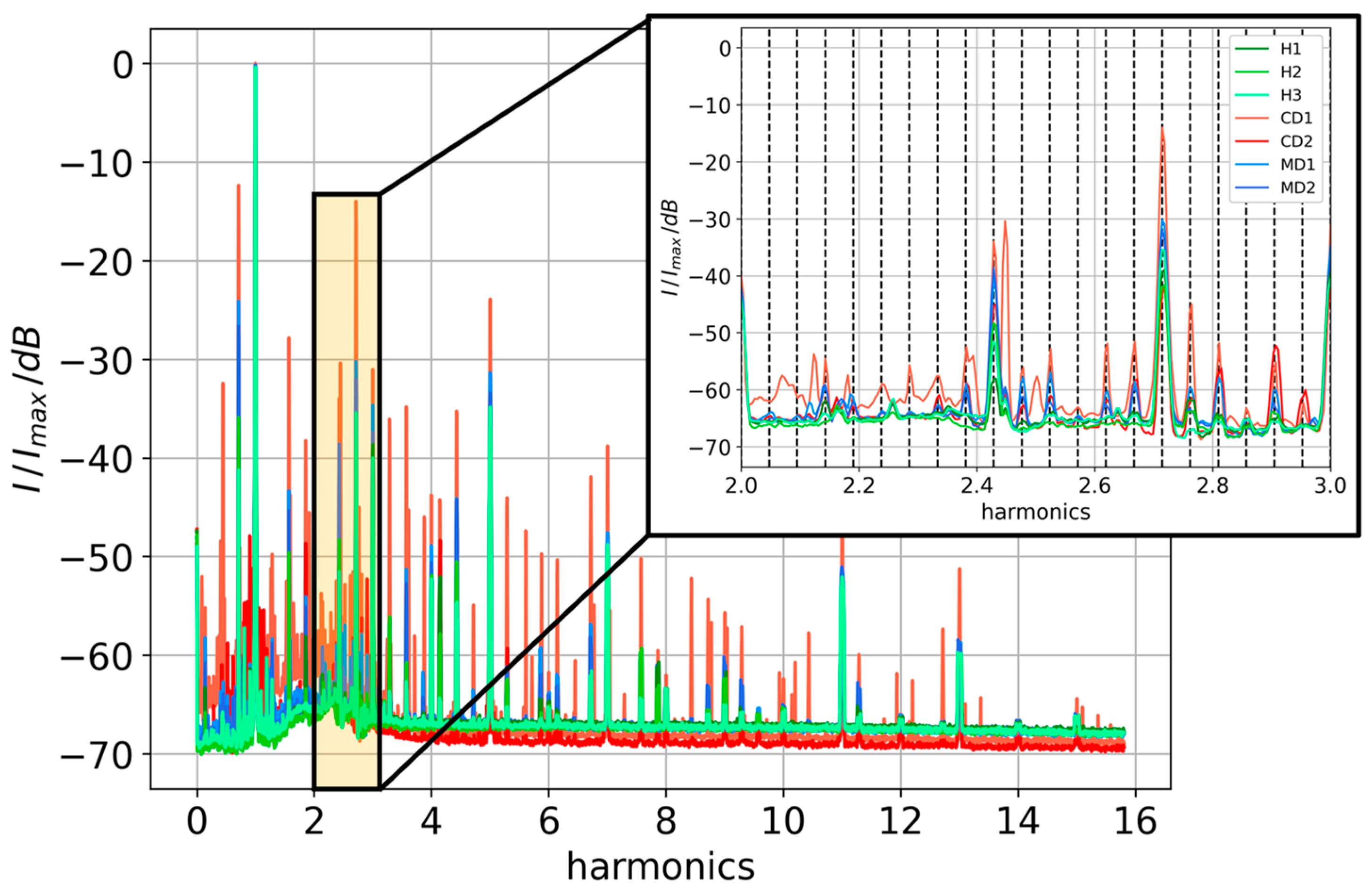
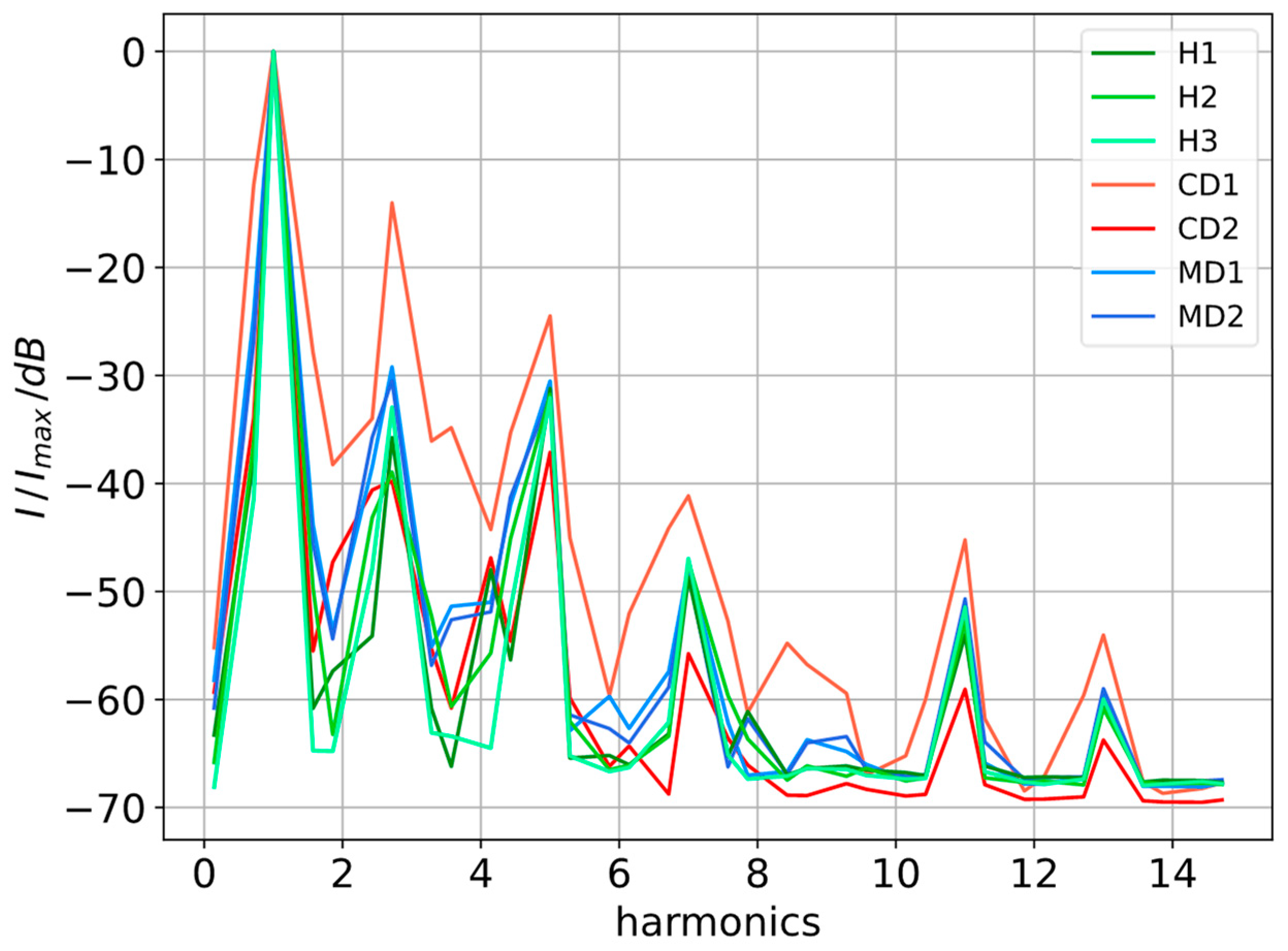
5.3. Spectral Analysis
- Up to the 11th harmonic
- Up to the 7th harmonic
- Up to the 5th harmonic
5.4. General Machine Learning Approach
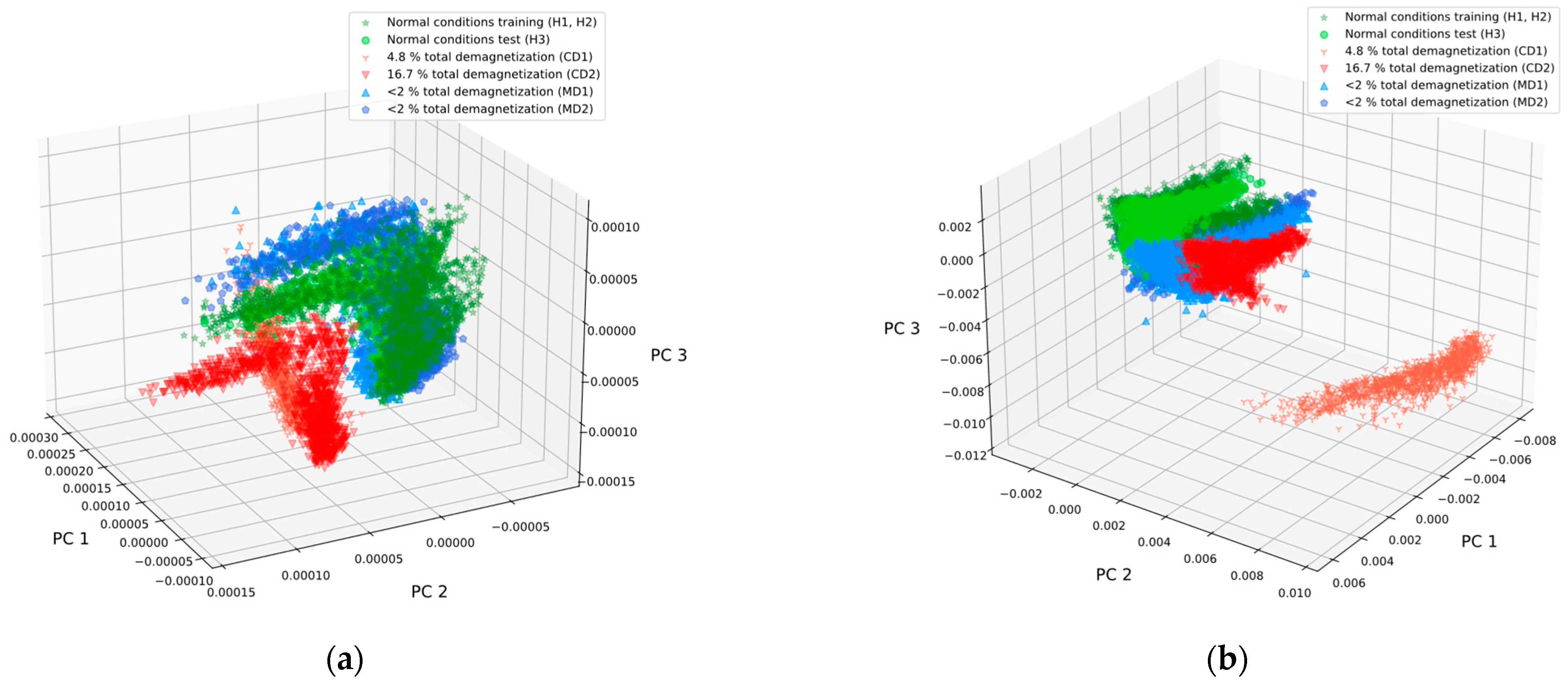
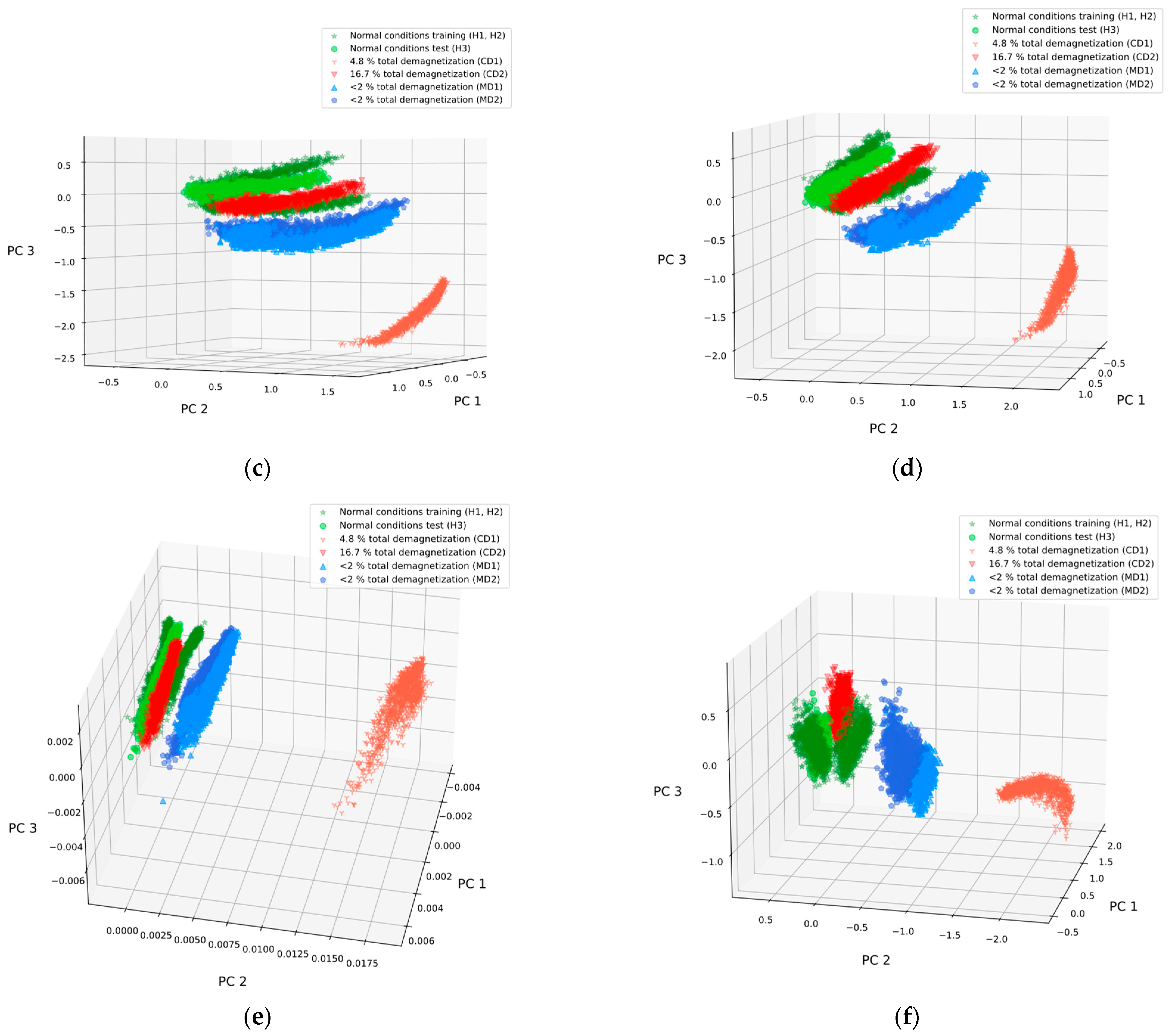
5.4.1. Dimensionality Reduction
5.4.2. Anomaly Detection
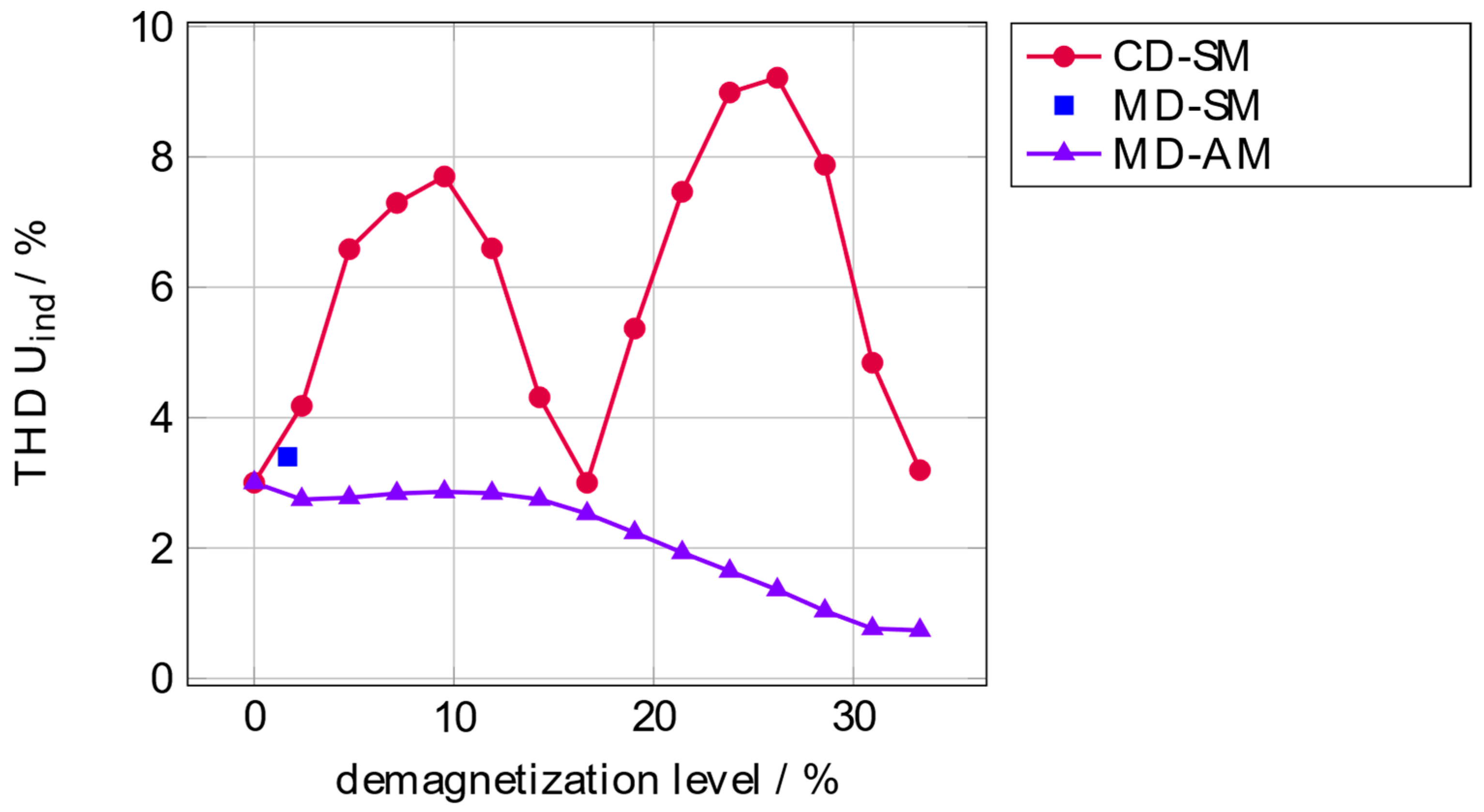
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El Hadraoui, H.; Zegrari, M.; Chebak, A.; Laayati, O.; Guennouni, N. A Multi-Criteria Analysis and Trends of Electric Motors for Electric Vehicles. World Electr. Veh. J. 2022, 13, 65. [Google Scholar] [CrossRef]
- Constantinides, S. The Important Role of Dysprosium in Modern Permanent Magnets. 2017. Available online: https://www.arnoldmagnetics.com/wp-content/uploads/2017/10/Important-Role-of-Dysprosium-in-Modern-Permanent-Magnets-150906.pdf (accessed on 13 May 2024).
- Orlowska-Kowalska, T.; Wolkiewicz, M.; Pietrzak, P.; Skowron, M.; Ewert, P.; Tarchala, G.; Krzysztofiak, M.; Kowalski, C.T. Fault Diagnosis and Fault-Tolerant Control of PMSM Drives–State of the Art and Future Challenges. IEEE Access 2022, 10, 59979–60024. [Google Scholar] [CrossRef]
- Lang, W.; Hu, Y.; Gong, C.; Zhang, X.; Xu, H.; Deng, J. Artificial Intelligence-Based Technique for Fault Detection and Diagnosis of EV Motors: A Review. IEEE Trans. Transp. Electrif. 2022, 8, 384–406. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, S.; Li, W.; Liang, H.; Wang, C. Faults and Diagnosis Methods of Permanent Magnet Synchronous Motors: A Review. Appl. Sci. 2019, 9, 2116. [Google Scholar] [CrossRef]
- Niu, G.; Dong, X.; Chen, Y. Motor Fault Diagnostics Based on Current Signatures: A Review. IEEE Trans. Instrum. Meas. 2023, 72, 3520919. [Google Scholar] [CrossRef]
- Schellenberger, M.; Lorentz, V.; Eckardt, B. Cognitive Power Electronics—An Enabler for Smart Systems. In PCIM Europe 2022; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management; VDE: Nuremberg, Germany, 2022. [Google Scholar]
- Rao, D.; Bagianathan, M. Selection of Optimal Magnets for Traction Motors to Prevent Demagnetization. Machines 2021, 9, 124. [Google Scholar] [CrossRef]
- Aguilar-Zamorate, I.S.; Galluzzi, R.; Ibarra, L.; Amati, N. A Method to Compute the Irreversible Demagnetization Temperature in Permanent Magnets. In Proceedings of the 2023 International Symposium on Electromobility (ISEM), Monterrey, Mexico, 26–28 October 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Choi, S.; Haque, M.S.; Bin Tarek, T.; Mulpuri, V.; Duan, Y.; Das, S.; Garg, V.; Ionel, D.M.; Masrur, M.A.; Mirafzal, B.; et al. Fault Diagnosis Techniques for Permanent Magnet AC Machine and Drives—A Review of Current State of the Art. IEEE Trans. Transp. Electrif. 2018, 4, 444–463. [Google Scholar] [CrossRef]
- Navarro-Navarro, A.; Ruiz-Sarrio, J.E.; Biot-Monterde, V.; Antonino-Daviu, J.A.; Becker, V.; Urschel, S. Application of Transient Analysis Techniques to Fault Diagnosis in Low- and Medium-Power Synchronous Machines. Machines 2023, 11, 288. [Google Scholar] [CrossRef]
- Nejadi-Koti, H.; Faiz, J.; Demerdash, N.A.O. Uniform demagnetization fault diagnosis in permanent magnet synchronous motors by means of cogging torque analysis. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Ullah, Z.; Lee, S.-T.; Siddiqi, M.R.; Hur, J. Online Diagnosis and Severity Estimation of Partial and Uniform Irreversible Demagnetization Fault in Interior Permanent Magnet Synchronous Motor. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1682–1686. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Lee, H.; Park, Y.; Bin Lee, S.; Fernandez, D.; Diaz-Reigosa, D.; Briz, F. A Simple Method for Identifying Mass Unbalance Using Vibration Measurement in Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2021, 69, 6441–6444. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Khang, H.V.; Senanayaka, J.; Robbersmyr, K.G.; Panadero, R. A two-stage Fault Diagnosis Scheme of Partial Demagnetization Faults in PMSMs with Low Labelled Rates. In Proceedings of the 2023 IEEE International Electric Machines & Drives Conference (IEMDC), San Francisco, CA, USA, 15–18 May 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Du, B.; Huang, W.; Cheng, Y.; Chen, J.; Tao, R.; Cui, S. Fault Diagnosis and Separation of PMSM Rotor Faults Using Search Coil Based on MVSA and Random Forests. IEEE Trans. Ind. Electron. 2024, 1–11. [Google Scholar] [CrossRef]
- Mohammad-Alikhani, A.; Vahedi, A.; Mahmouditabar, F.; Rahnama, M. Demagnetization Fault Diagnosis of FSPM Motor Based on ReliefF and SVM. In Proceedings of the 2019 International Power System Conference (PSC), Tehran, Iran, 9–11 December 2019; pp. 95–99. [Google Scholar] [CrossRef]
- Blechinger, C.; Hofmann, M.; Walch, D.; Steinmetz, H.-F.; Schellenberger, M. Cognitive Power Electronics for Detection of Demagnetization in Electric Drives. In Proceedings of the 2023 13th International Electric Drives Production Conference (EDPC), Regensburg, Germany, 29–30 November 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Peng, W.; Kun, W.; Meng, F. Demagnetization Study of Permanent Magnet Machine Under Three Phase Short Circuit. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 2705–2710. [Google Scholar] [CrossRef]
- Chen, S.; Hsiao, C.-Y.; Yao, L.; Yu, F.; Wang, Y.; Shen, J.-X. Comparative Analysis of Magnet Demagnetization in FSCW and ISDW IPM Machines with Various Rotor Topologies. In Proceedings of the 2020 23rd International Conference on Electrical Machines and Systems (ICEMS), Hamamatsu, Japan, 24–27 November 2020. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Alam, M.A.; Fukumizu, K. Hyperparameter selection in kernel principal component analysis. J. Comput. Sci. 2014, 10, 1139–1150. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Q.; Zhu, E.; Porikli, F.; Yin, J. Hyperparameter selection of one-class support vector machine by self-adaptive data shifting. Pattern Recognit. 2018, 74, 198–211. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar] [CrossRef]







| Physical Parameter | Demagnetization Features | Classification Algorithm | ||
|---|---|---|---|---|
| Time Domain | Frequency Domain | Time-Frequency Domain | ||
| magnetic flux | mean | FFT | STFT | convolutional neural network |
| induced voltage/EMF | median | cepstrum | CWT | Bayesian neural network |
| current | standard deviation | envelope | DWT | probabilistic neural network |
| torque | RMS | HHT | random forest | |
| vibration | clearance factor | WVT | support vector machine | |
| acoustics | shape factor | CWD | ||
| kurtosis | ||||
| skewness | ||||
| impulse factor | ||||
| crest factor | ||||
| Degree of Demagnetization Level | |||
|---|---|---|---|
| Total (Br/Br0 = 0) | Variable (0 < Br/Br0 < 1) | ||
| number of affected magnets | all magnets | complete demagnetization of all magnets (CD-AM) | moderate demagnetization of all magnets (MD-AM) |
| some magnets | complete demagnetization of some magnets (CD-SM) | moderate demagnetization of some magnets (MD-SM) | |
| Parameter | Value |
|---|---|
| Topology | PMSM with external rotor |
| Rated output power (W) | 320 |
| Nominal voltage (V) | 24 |
| Outer diameter (mm) | 86 |
| Number of phases m | 3 |
| Number of slots Q | 36 |
| Number of pole pairs p | 21 |
| Magnet material | N45 |
| Motor | Damaged Magnets | Extend of Damage | Total Demagnetization |
|---|---|---|---|
| H1 | 0 | - | 0% |
| H2 | 0 | - | 0% |
| H3 | 0 | - | 0% |
| CD1 | 2 | Complete demagnetization | 4.8% |
| CD2 | 7 | Complete demagnetization | 16.7% |
| MD1 | 2 | Moderate demagnetization | ~1.67% |
| MD2 | 2 | Moderate demagnetization | ~1.67% |
| Approach | Precision | SPC | Precision-SPC Mean | Accuracy | Share of CD2 in False Negatives |
|---|---|---|---|---|---|
| Entire spectrum | 93.4% | 83.8% | 88.6% | 62.3% | 10.8% |
| All demagnetization harmonics | 95.2% | 85.1% | 90.1% | 75.8% | 33.2% |
| Up to the 11th demagnetization harmonic | 98.1% | 93.1% | 95.6% | 90.1% | 98.8% |
| Up to the 7th demagnetization harmonic | 97.7% | 91.8% | 94.7% | 88.6% | 99.7% |
| Up to the 5th demagnetization harmonic | 98.6% | 95.9% | 97.2% | 75.4% | 64.1% |
| All motor harmonics | 99.4% | 98.1% | 98.8% | 86.6% | 100.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walch, D.; Blechinger, C.; Schellenberger, M.; Hofmann, M.; Eckardt, B.; Lorentz, V.R.H. Detection of Demagnetization Faults in Electric Motors by Analyzing Inverter Based Current Data Using Machine Learning Techniques. Machines 2024, 12, 468. https://doi.org/10.3390/machines12070468
Walch D, Blechinger C, Schellenberger M, Hofmann M, Eckardt B, Lorentz VRH. Detection of Demagnetization Faults in Electric Motors by Analyzing Inverter Based Current Data Using Machine Learning Techniques. Machines. 2024; 12(7):468. https://doi.org/10.3390/machines12070468
Chicago/Turabian StyleWalch, Daniel, Christoph Blechinger, Martin Schellenberger, Maximilian Hofmann, Bernd Eckardt, and Vincent R.H. Lorentz. 2024. "Detection of Demagnetization Faults in Electric Motors by Analyzing Inverter Based Current Data Using Machine Learning Techniques" Machines 12, no. 7: 468. https://doi.org/10.3390/machines12070468
APA StyleWalch, D., Blechinger, C., Schellenberger, M., Hofmann, M., Eckardt, B., & Lorentz, V. R. H. (2024). Detection of Demagnetization Faults in Electric Motors by Analyzing Inverter Based Current Data Using Machine Learning Techniques. Machines, 12(7), 468. https://doi.org/10.3390/machines12070468







