Abstract
High-density 3D warehousing is the future cornerstone of modern logistics storage. It aims to efficiently manage and store various types of goods by utilizing 3D space and automation technology. The accurate and fast docking algorithm of the four-way shuttles, as a core method of carrying the goods in high-density 3D warehousing, has become an increasingly important technical challenge. Inaccurate docking will result in a failure to change direction, while long docking time will affect the operation efficiency of the four-way shuttle. To overcome these obstacles, this paper presents an accurate and rapid docking algorithm for four-way shuttles. Firstly, the deceleration and jerk of a four-way shuttle in the braking stage are initialized according to the motion parameter set calculated by the docking motion model. Then, the four-way shuttle starts to move until the stop signal has been detected. If the system fails to detect the stop signal, the distance compensation is needed to ensure that the four-way shuttle can arrive at the stop point. Finally, the four-way shuttle stops immediately by way of amplifying the deceleration when reaching the stop point. The result shows that the accuracy of rapid docking is superior to that of direct docking. Compared with crawling docking, rapid docking reduces the braking time by 3.99s and stops at a speed lower than the crawling speed. The rapid docking algorithm not only enhances the throughput of high-density 3D warehousing but also improves the service life of four-way shuttles.
1. Introduction
With the development of the e-commerce industry, logistics and warehousing have a certain scale, and the traditional storage solutions cannot meet the needs of the high-density 3D warehousing environment. Generally, there are two solutions for high-density 3D warehousing: an automated storage/retrieval system (AS/RS) or automated vehicles storage/retrieval system (AVS/RS) [1]. The former, with its simple implementation method but low throughput of goods, relies heavily on trustworthy hardware equipment, such as stackers [2] and high-rack shelves. The stacker is responsible for moving in the vertical plane to carry the goods to the high-rack shelves. The latter, with its low cost for expanding goods slots and high throughput of goods due to the multiple storage entrances available, is developed based on the AS/RS system, consisting of a four-way shuttle, grid shelves, and elevator. The four-way shuttle is a key component of the AVS/RS system, responsible for transporting and docking goods in three-dimensional space. Operating on fixed tracks [3], the four-way shuttle can achieve higher speeds and more precise positioning, making operational control simpler and more user-friendly. Additionally, the four-way shuttle system has relatively low requirements for warehouse height and 3D structure, making construction and maintenance more cost-effective. Due to their efficiency, flexibility, and strong adaptability, four-way shuttles are increasingly applied in modern warehousing applications. The elevator manages to lift goods into high shelves.
Although the throughput of the AVS/RS system is higher and the cost of expanding the goods slots is lower than in the AS/RS system, the motion control of the four-way shuttle is very complex, especially in terms of docking. Inaccurate docking will result in a failure to change direction, and long docking time will affect the operational efficiency of the four-way shuttle, which become obstacles to improving the throughput of high-density 3D warehousing. Automated guided vehicles (AGVs) are capable of automatic material transportation without the need for a driver. The employment of AGVs is a capital investment that requires the analysis of station locations, optimal route design, determination of the optimal number of AGVs, AGV positioning, assignment of the AGVs to collection requests, AGV routing and dispatch, and other factors [4]. Among them, docking is also an aspect that needs to be discussed. There are two traditional docking methods of four-way shuttles: direct docking and crawling docking. Under the position mode [5] of a servo motor in the deceleration stage, direct docking means that the four-way shuttle directly decelerates from a high speed to 0 and just reaches the target position, so it is also called zero speed docking. Crawling docking indicates that the four-way shuttle first slows down to the crawling speed, runs at the crawling speed, and slows down to zero immediately upon finding the sensor stop signal in the deceleration stage.
Direct docking has a short docking time but cannot accurately dock without a specific hardware environment and a large amount of experimental debugging. Crawling docking can achieve accurate docking with a stop signal generated by a photoelectric sensor, but crawling docking has an obvious crawling process in the braking stage. Generally, the four-way shuttle movement depends on the track distance information obtained by the photoelectric sensor in advance, that is, the guiding distance. Moreover, direct docking sets the predetermined braking distance according to the guiding distance to complete the docking task. Due to the delay error of the photoelectric sensor, direct docking requires an amount of experimental debugging and more sophisticated hardware equipment to achieve accurate docking.
Overall, the current docking methods, whether direct docking or crawling docking, have significant limitations in terms of speed and precision. These limitations not only affect the overall throughput and operational efficiency of the system but also worsen the mechanical wear on the shuttles, shortening their lifespan. To address these issues and reduce the docking time while improving the docking accuracy, this paper proposes a rapid docking algorithm. Firstly, the algorithm obtains and initializes the deceleration and jerk of the four-way shuttle in the braking stage, which is calculated by the rapid docking motion model. Then, the four-way shuttle moves and starts to detect the stop signal during the braking stage, the same as crawling docking. If the stop signal is detected, the four-way shuttle stops immediately by way of amplifying the deceleration. If the stop signal is not detected, the four-way shuttle requires continuous distance compensation to ensure that it can arrive at the stop point. Finally, the four-way shuttle will report a motion error if the value of the distance compensation exceeds the preset threshold. Especially, the rapid docking motion model and distance compensation are the core and most difficult section of the algorithm. The former constructs the relationship between distance, deceleration, and jerk based on kinematic principles to obtain the motion parameter set in the braking stage. The latter is achieved by the position mode of the servo motor; that is, the preset position of the servo motor is continuously adjusted to reach the stopping point. The two cooperate with each other to complete the accurate and fast docking of the four-way shuttle.
The main contributions of this paper include the following:
- (1)
- We propose a new rapid docking algorithm that combines optimized deceleration and jerk calculations with a real-time distance compensation mechanism, significantly reducing docking time. The experiments show that this algorithm reduces the braking time by approximately 3.99 s compared to the traditional methods.
- (2)
- The precision and reliability of the docking process have been enhanced through a real-time distance compensation mechanism, which reduces the dependence on high-precision hardware and cumbersome debugging. This also minimizes the mechanical vibrations, ensuring the safety of the goods and extending the lifespan of the four-way shuttles.
2. Related Work
Many researchers have presented a few useful solutions for docking algorithms. Kei [6] and Uchida [7] achieved direct docking by hardware devices, but the cost of the hardware devices was high. Song et al. [8] proposed a deep learning-based approach to adjust autonomous docking for AGV systems. By utilizing deep learning to recognize the environmental features and adjust the docking behaviors accordingly, AGVs can efficiently and precisely complete docking tasks in unstructured environments. However, this method requires extensive training data and might struggle with scenarios outside the trained conditions. Li [9] proposed a docking system and airborne visual perception system based on a parallel mechanism. The new compact self-assembling mobile modular robot (SMMRob modules) can dock with each other based on relative positioning, which employs the visual perception of passive markers or active infrared signals in different localizations. Rajvanshi [10] used an RGBD camera and visual processing techniques to propose an automatic docking method that includes modules for scene segmentation, point cloud generation, and path planning. This approach addresses the problem of shuttle vehicles in coal mines docking with continuous mining machines in GPS-denied underground environments. Hou [11] mentioned a magnetic docking device system that allows multiple parts of a quadruped structure (three or more) to be connected, significantly improving the robot’s flexibility and responsiveness. He [12] addressed the efficiency of AGV’s automatic docking at intersections by proposing models based on mean value analysis (MVA) and a Fork/Join queueing network (FJQN). These models optimize the vehicle service rates, enhancing the overall performance at logistical operations at intersections. Lin [13] introduced a wireless indoor positioning and navigation method for AGVs with measurement uncertainty. Reis [14] analyzed the sensor and perception technologies used for AGV position control over the past five years, highlighting the potential of machine vision sensors in enhancing docking response capabilities.
In addition to hardware-based and environmental perception systems, advancements in speed control and precision docking strategies have significantly improved the docking performance. Hu [15] utilized a combined localization method based on ultra-wideband (UWB) and visual guidance. The mean compensation method is used to correct the positioning data of the UWB to obtain a consistent and accurate positioning trajectory. Fu [16] developed a vehicle motion model and applied the Stanley-PID control algorithm to reduce the docking response time and minimize path error fluctuations. However, this approach may lack the flexibility to adapt to highly nonlinear or rapidly changing environments. Ren [17] combined a hybrid intelligent real-time optimal control method based on deep neural networks (DNNs) to improve the autonomy and intelligence of automated guided vehicle (AGV) navigation control. Yadegar [18] proposed a navigation strategy-based method to solve the issue of the precise docking of mobile robots in industrial settings. This approach allows the robot to dock without a complete stop by aligning the direction and distance between the robot and the docking station. Tsiogas [19] introduced a vision-based approach that enables the safe and autonomous operation of pallet moving vehicles, and Ding [20] proposed a combination of the double-wheel chassis model (DCM) and PID control strategy to enhance the precision and stability during docking. Moreover, visual strategies are applied for accurate docking alignment. Wang [21] introduced an EKF-based relative attitude estimation algorithm to handle noise and intermittent observations. During docking, a solution integrating motion planning and control was proposed, enhancing the docking precision and stability in static environments. Despite its benefits, EKF can perform poorly with non-Gaussian noise or highly nonlinear dynamics and requires accurate initial state estimates. Yilmaz [22] applied a multi-stage localization method and a scan-matching-based method in the docking stage. Yu [23] addressed the nonlinear and time-varying uncertainties of motors by proposing an improved PID control method based on BP neural networks combined with an inertia factor. Guney [24] resolved the movement coordination issue of a fleet of AGVs in a confined industrial facility. To address the speed variation control issues in manned AGVs during acceleration and braking, Liu [25] employed an S-curve speed control method. This approach significantly improved the operational smoothness of the AGVs while ensuring rapid operational performance. However, the S-curve method may not always provide optimal responses under sudden or unpredictable speed changes. Some scholars calculated the operation efficiency of different docking modes and provided a reference for the research of docking algorithms. Gong [26] proposed a method for achieving efficient docking during wireless charging through real-time path planning and fast nonlinear model predictive control (FNMPC). This method significantly improves the docking accuracy in complex dynamic environments. However, the computational complexity of FNMPC might limit its real-time application in highly dynamic settings. Skulstad [27] offered a hybrid prediction method combining LSTM neural networks and a ship dynamic model, improving the docking position prediction accuracy for ships. However, the computational complexity of FNMPC might limit its real-time application in highly dynamic settings. Romanov [28] proposed a robust and easy-to-configure algorithm based on ArUco detection, improving the positioning and orientation accuracy of mobile robots docking with charging stations.
3. Docking Algorithm Flow and Motion Stage
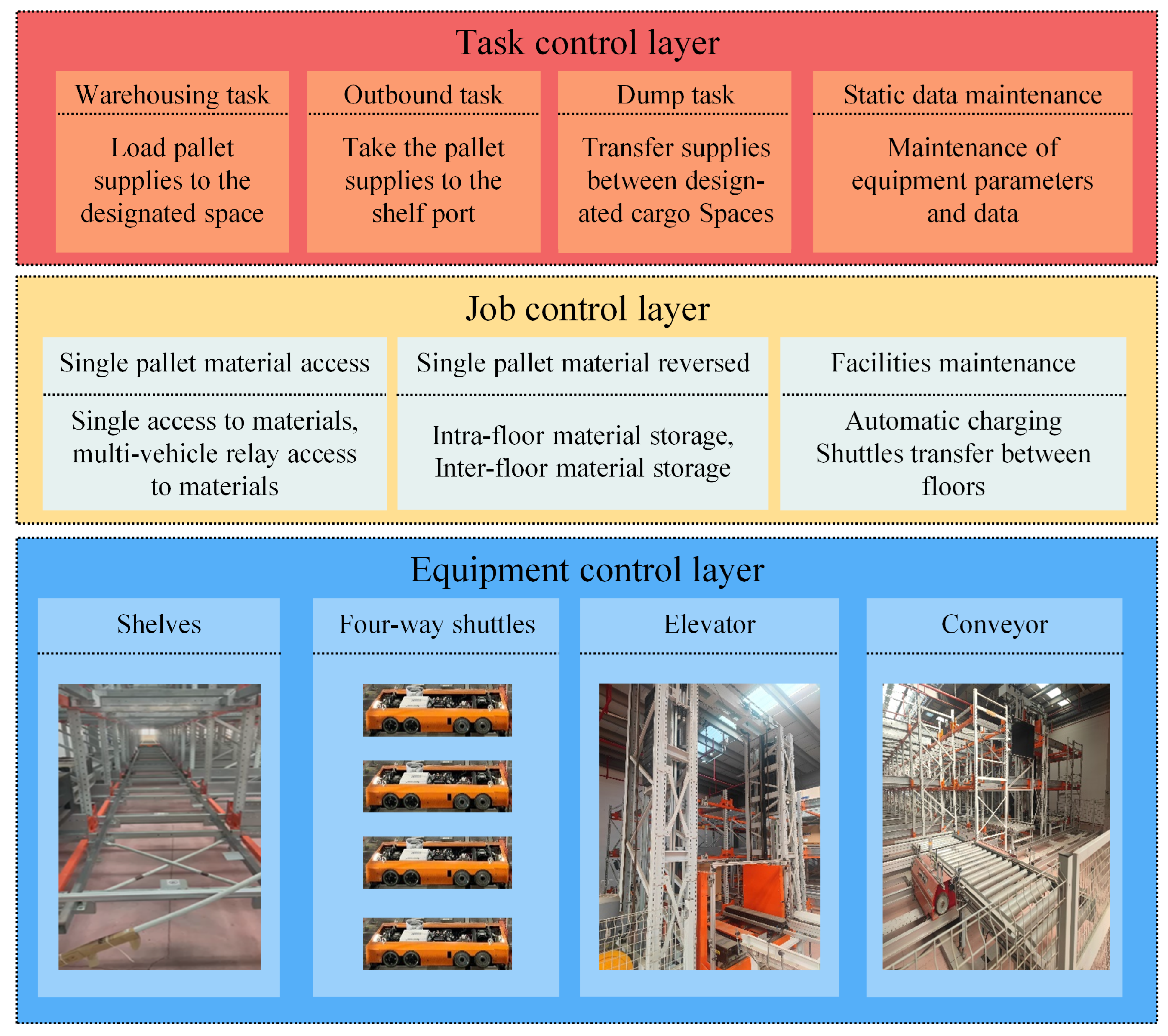
The entire system comprises a task control layer, a job control layer, and an equipment control layer, primarily overseeing warehousing operations such as inbound and outbound processes. The task control layer manages the storage and retrieval operations, along with maintaining static data. Meanwhile, the job control layer handles the access of palletized goods and the charging of shuttles. The equipment control layer within the WCS includes hardware components like shelves, four-way shuttles, elevators, and conveyors, in addition to scheduling equipment control software. See Figure 1.
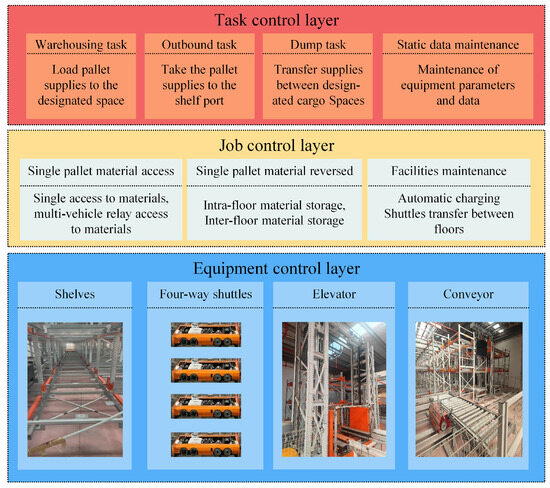
Figure 1.
Overall structure of the system.
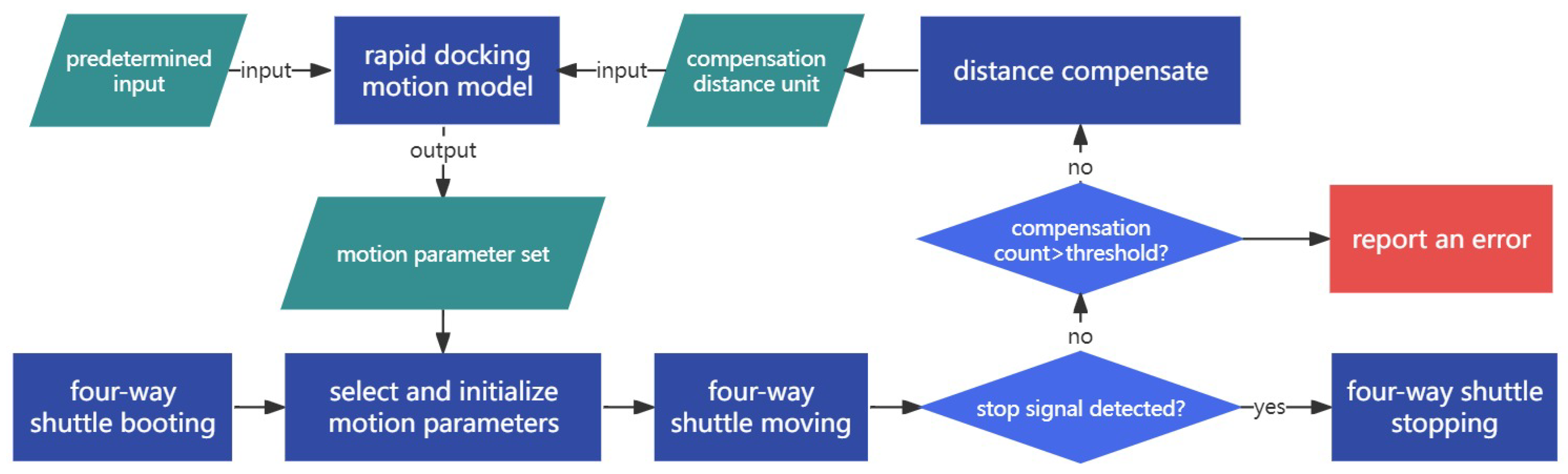
After the four-way shuttle boots, the rapid docking model calculates the motion parameter set according to the predetermined input, including load capacity, predetermined transfer speed, and predetermined braking distance. The appropriate initial motion parameters of the four-way shuttle are randomly selected from the motion parameter set. Then, the four-way shuttle starts to move and detects the stop signal in the braking stage. If the stop signal is detected, the four-way shuttle stops immediately by way of boosting the deceleration. Otherwise, the next round of motion parameters calculation and docking signal detection is performed until the four-way shuttle arrives at the stop point. See Figure 2.
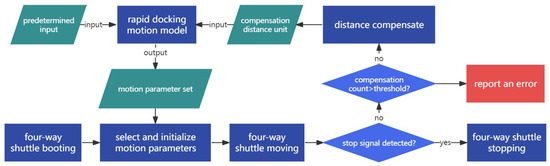
Figure 2.
Flowchart of the rapid docking algorithm.
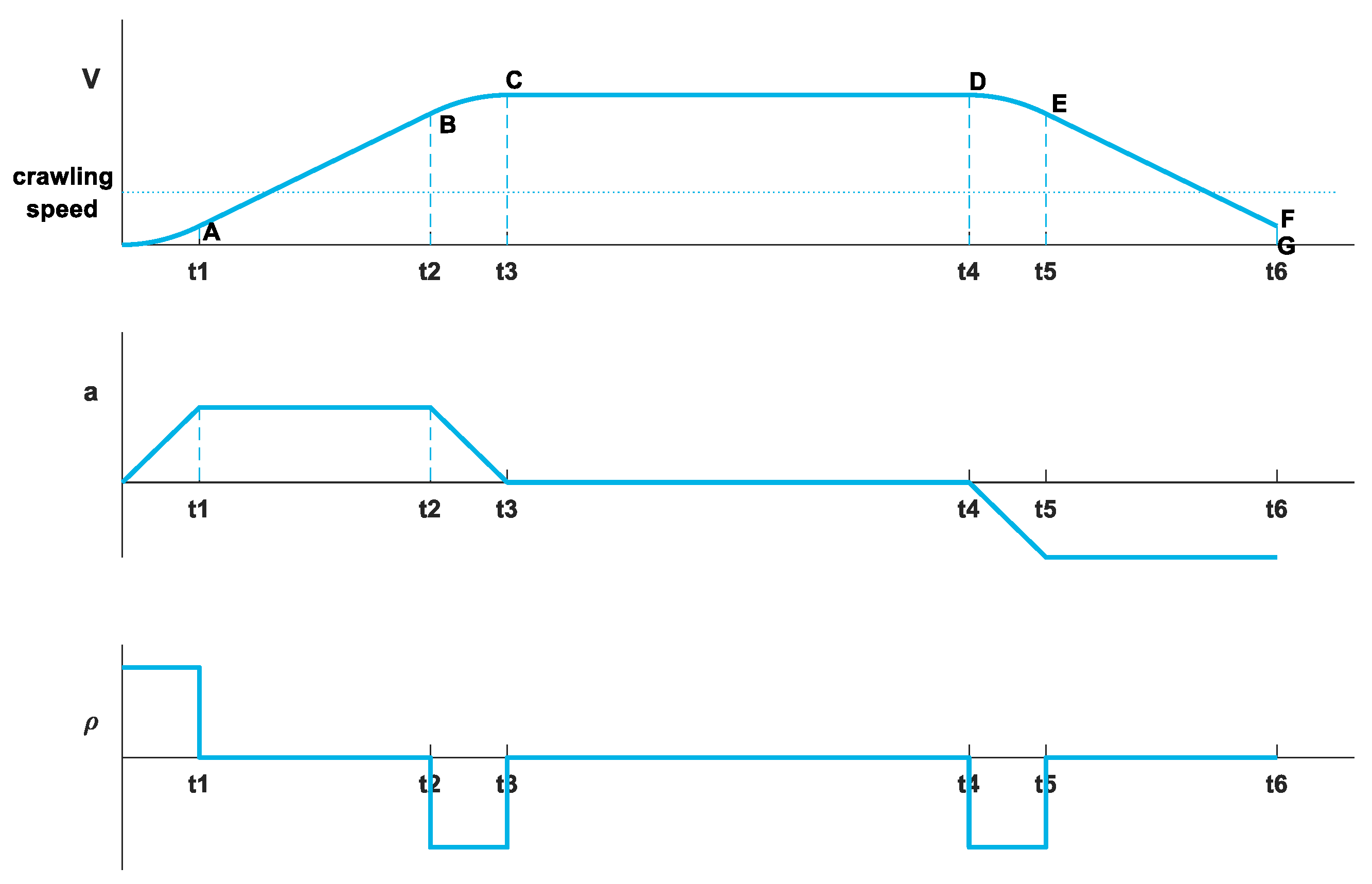
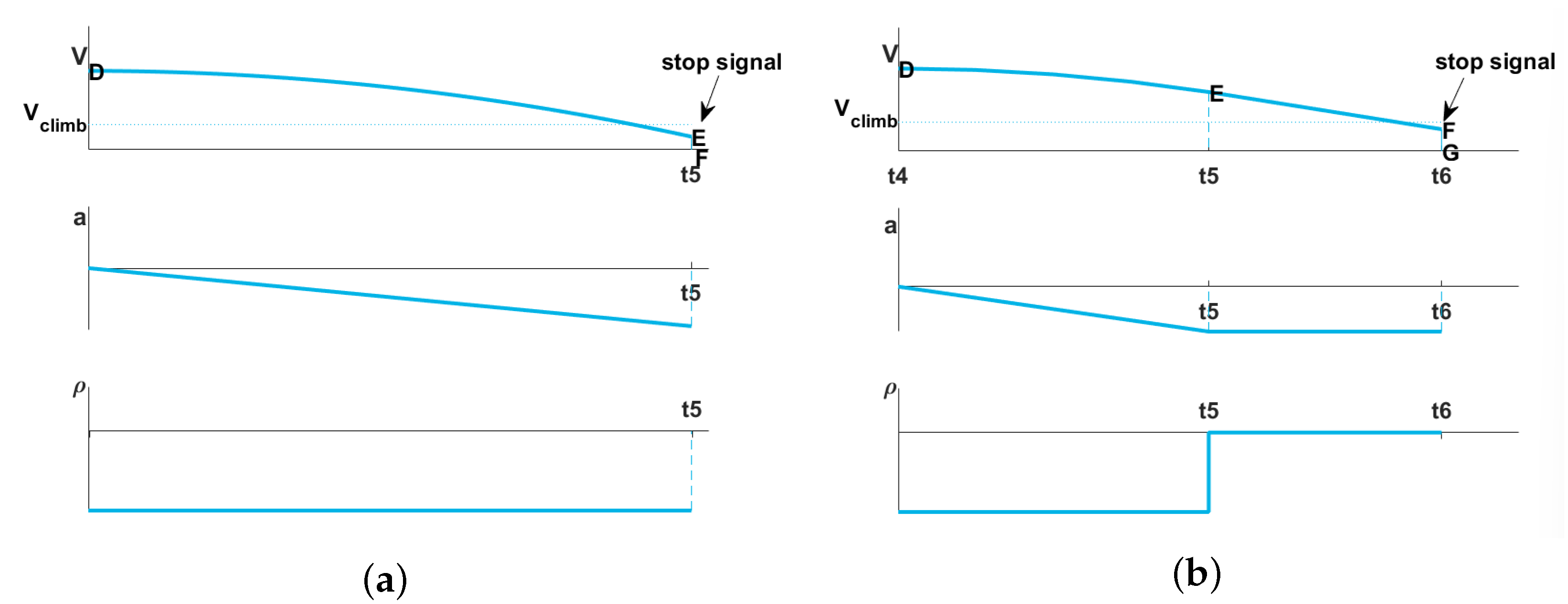
The rapid docking algorithm can be divided into the following 3 stages. Phases OA, AB, and BC belong to the starting stage. The high-speed movement is performed in phase CD. The braking stage consists of phases DE, EF, and FG. These phases are shown in Figure 3, where V is the real-time speed, a denotes the acceleration, and represents the jerk. The whole motion process is open-loop.
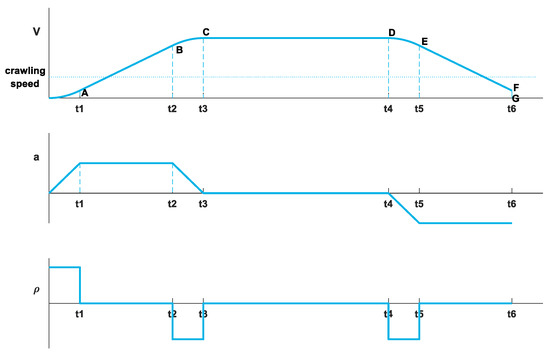
Figure 3.
Speed, acceleration, and jerk in different phases.
The following points should be noted in the braking process:
- Distance compensation is carried out in phase DF.
- When the movement speed is lower than the crawling speed, the four-way shuttle starts to detect the docking signal.
Since this research mainly optimizes the braking stage, the starting stage and high-speed movement stage of the four-way shuttles are not analyzed in detail.
4. Rapid Docking Motion Model
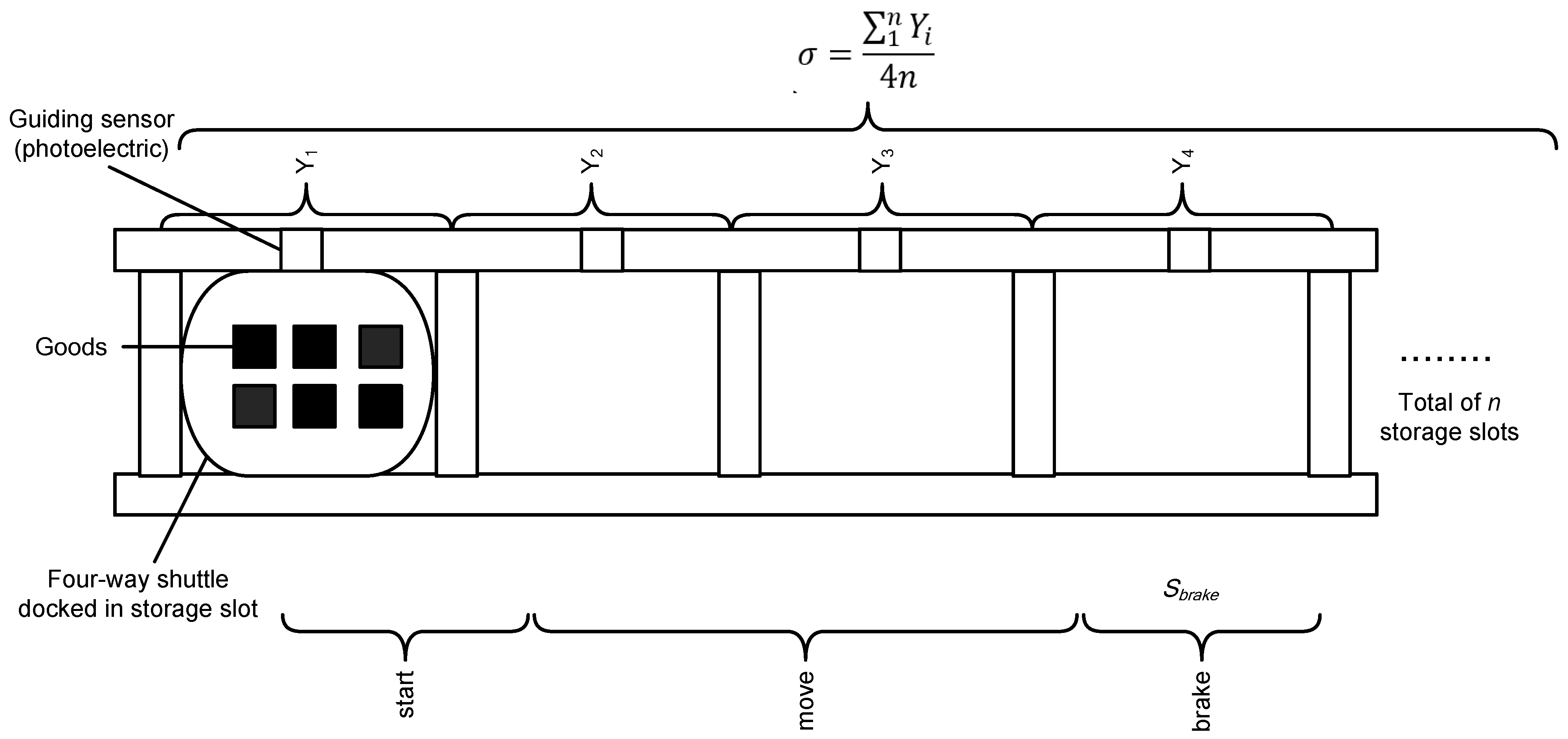
The rapid docking algorithm is mainly optimized by distance compensation in braking stage to shorten the docking time (see Figure 4). The four-way shuttle reaches the stopping point through continuous distance compensation in the braking stage, so the actual maximum braking distance of the four-way shuttle is formulated as
where is the width of the slot of number i, n stands for the number of slots on the motion track, denotes the predetermined braking distance, k is the number of distance compensation times, and represents the compensation distance unit, which is generally 1/4 goods slot width.
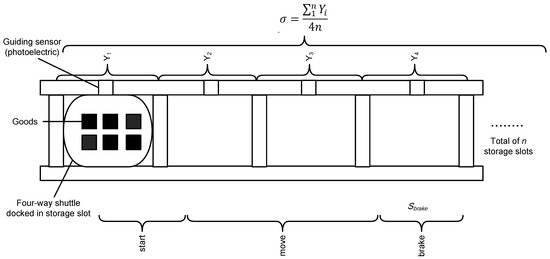
Figure 4.
Illustration of different stages.
Due to the two deceleration movements in the braking stage, the rapid docking model can be discussed as the following two situations.
4.1. Situation I
When the four-way shuttle detects the stopping signal during the variable deceleration motion (phase DE), there is no need to perform the uniform deceleration motion, as shown in Figure 5a. The relationship among jerk , deceleration a, real-time velocity V, and the actual braking distance S at this time is analyzed as follows:
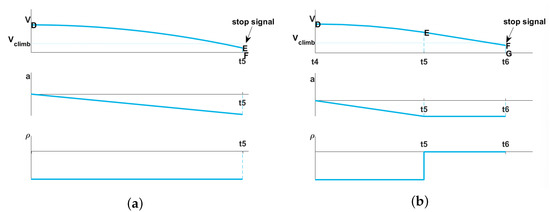
Figure 5.
Two deceleration motions in the braking stage. (a) Situation I. (b) Situation II.
At point E:
where is the jerk, represents the predetermined transfer velocity, refers to the braking distance in phase DE, and denotes the velocity at point E. Since , phase DF is the emergency braking stage, indicating that the four-way shuttle stops at , where its motion distance is ignored. Therefore, the acceleration of point E and the braking distance can be simplified as
4.2. Situation II
The stop signal of the four-way shuttle is detected during the uniform deceleration motion (phase EF). As shown in Figure 5b, the relationship among jerk , deceleration a, real-time velocity V, and the braking distance S at this time is analyzed as follows. In phase DE:
At point E:
where is the deceleration of phase EF. From the uniform deceleration motion of phase EF, we can conclude the following:
At point F:
where is the velocity of point F. Phase FG is the emergency braking stage; that is, the four-way shuttle stops at , with its movement distance ignored. By , is simplified as follows:
4.3. Overall Situation I, II
In this situation, the formula of braking distance is
where is known as the predetermined transfer velocity and , is the allowable acceleration of the maximum load capacity. The larger the load capacity, the smaller the the allowable acceleration . Therefore, the domain D of the is .
According to Formula (7), where , the four-way shuttle has detected the stop signal and stops immediately when it is just at . The four-way shuttle has detected the stop signal during phase DE, where . It is required for the uniform deceleration where , showing that the four-way shuttle has detected the stop signal during phase EF.
According to Formula (23), the solution set R for is
The initial jerk and initial deceleration in the braking stage are selected from the solution set R to control stop of the four-way shuttle.
5. Experimental Analysis
5.1. Experimental Setup
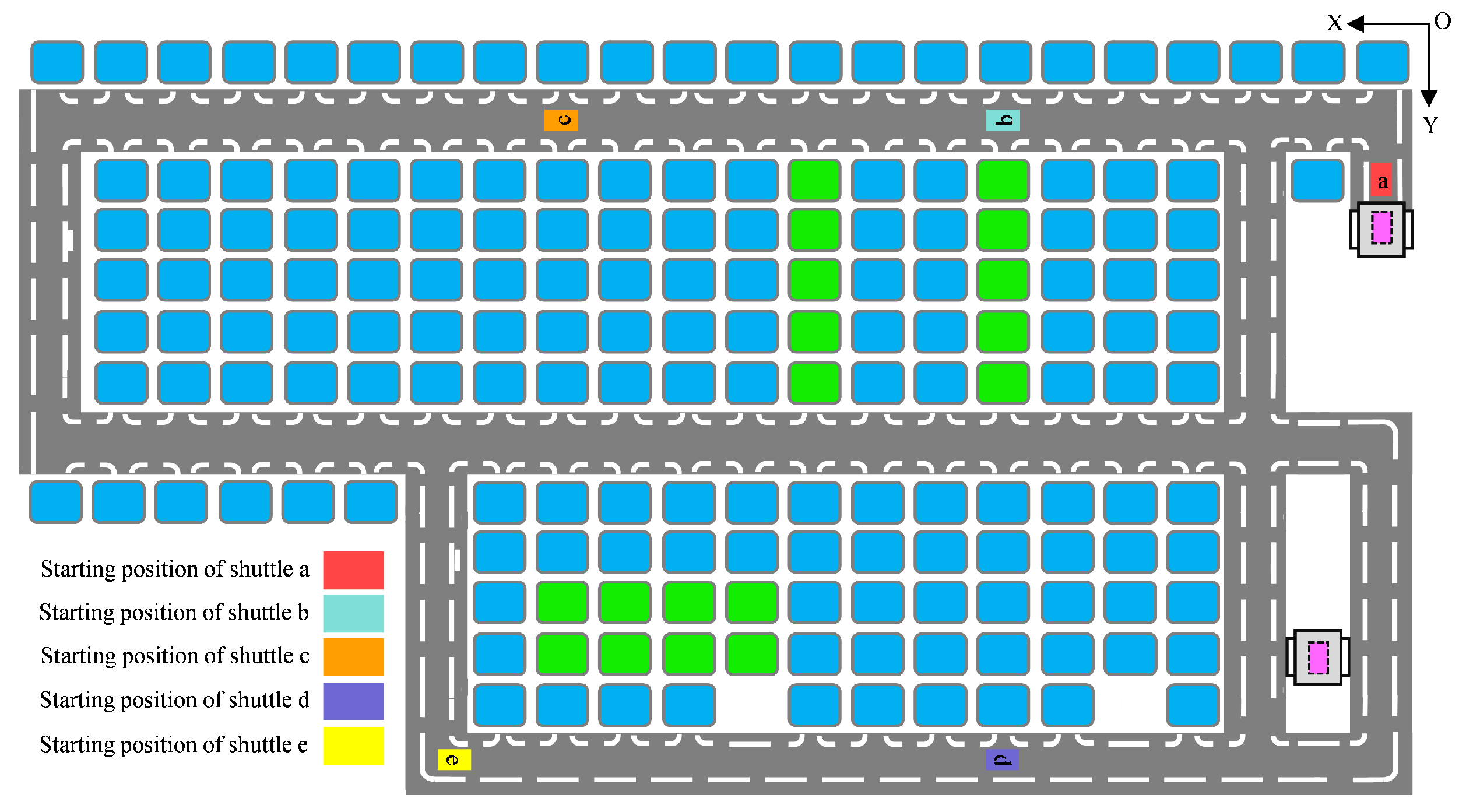
Within the factory’s warehouse, the whole system consists of main alleys, sub-alleys, storage shelves, conveyors, four-way shuttles, and elevators, with entry and exit ports on each level (see Figure 6). Various shuttles are chosen, and the positions for stored goods as well as the locations for goods to be stored are randomly selected. Figure 7 provides an example of one floor in the warehouse with four-way shuttles.

Figure 6.
Illustration of the warehouse.
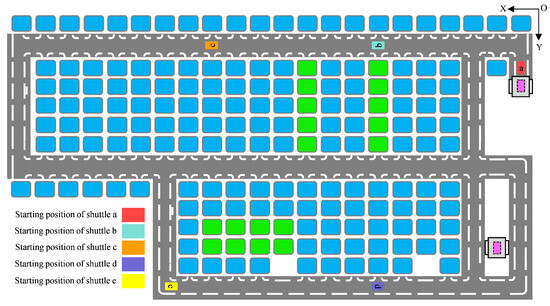
Figure 7.
Illustration of different four-way shuttles on the same floor of the warehouse. The blue rounded rectangles represent available storage locations, while the green rounded rectangles stand for occupied storage locations.
5.2. Results and Analysis
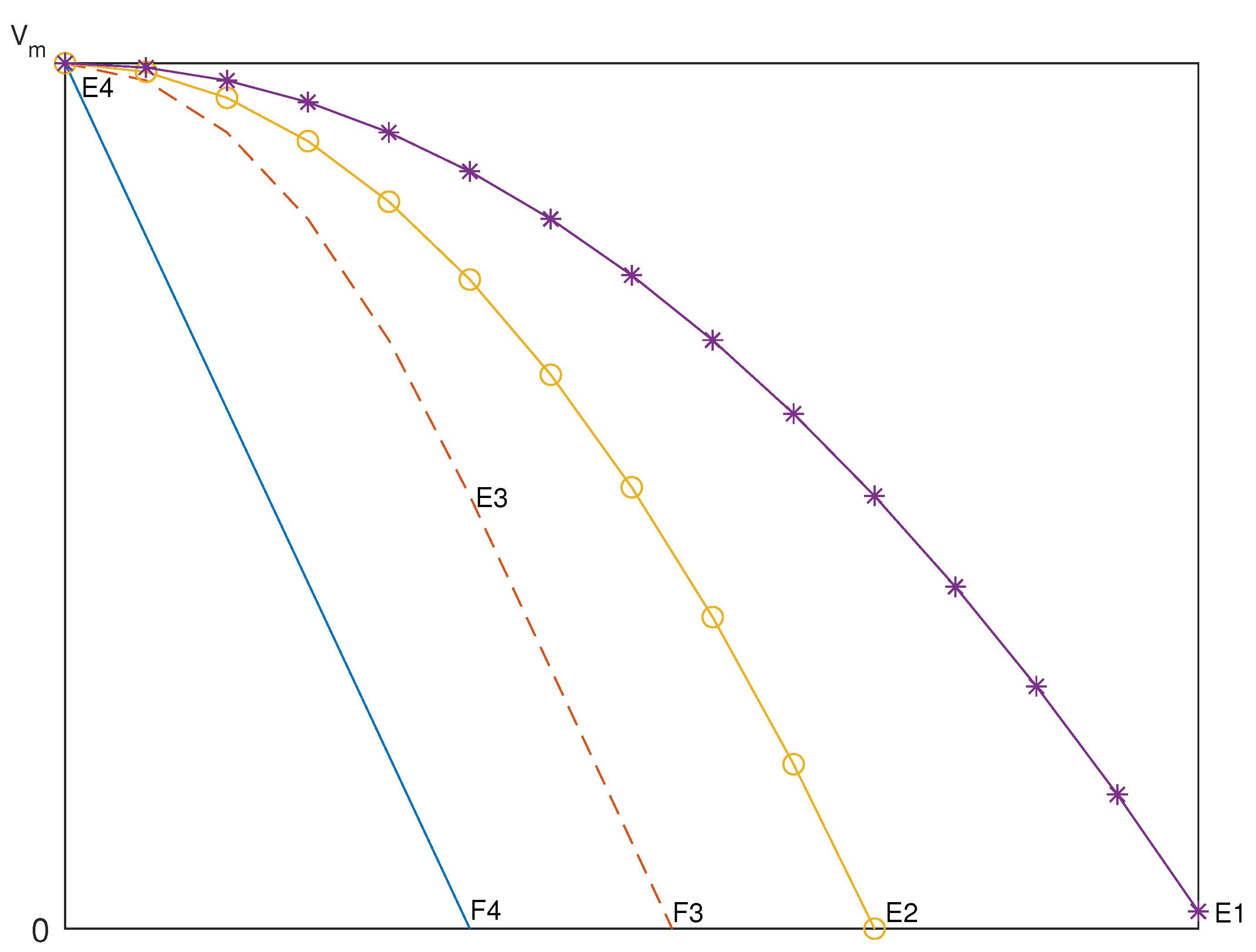
When m/s, , = 2, = 4, = 8, and approaches infinity, the speed curves during the braking stage are shown in Figure 8. or 4 conforms to situation I. conforms to situation II. The variable deceleration motion is neglected where tends to infinity; it can be regarded as just the uniform deceleration motion. The deceleration methods for different braking speed curves are referenced in Table 1.
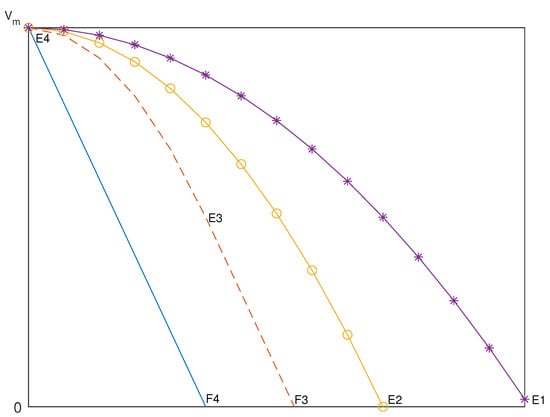
Figure 8.
Speed curves for = 2, = 4, = 8, and approaching infinity.

Table 1.
Deceleration methods for different braking speed curves (V: variable deceleration; C: constant deceleration).
When m/s, , and , during the braking stage, only variable deceleration is performed, and there is no need for a constant deceleration stage. For m/s, , and , variable deceleration is completed, and the four-way shuttle is about to start the constant deceleration stage. With m/s, , and , after completing the variable deceleration, the four-way shuttle enters the constant deceleration phase. When m/s, , and , the four-way shuttle can instantly reach the set maximum deceleration value, and the variable deceleration stage can be neglected, approximating it as only undergoing constant deceleration. Figure 8 illustrates the changes in the deceleration method of the four-way shuttle under different values of .
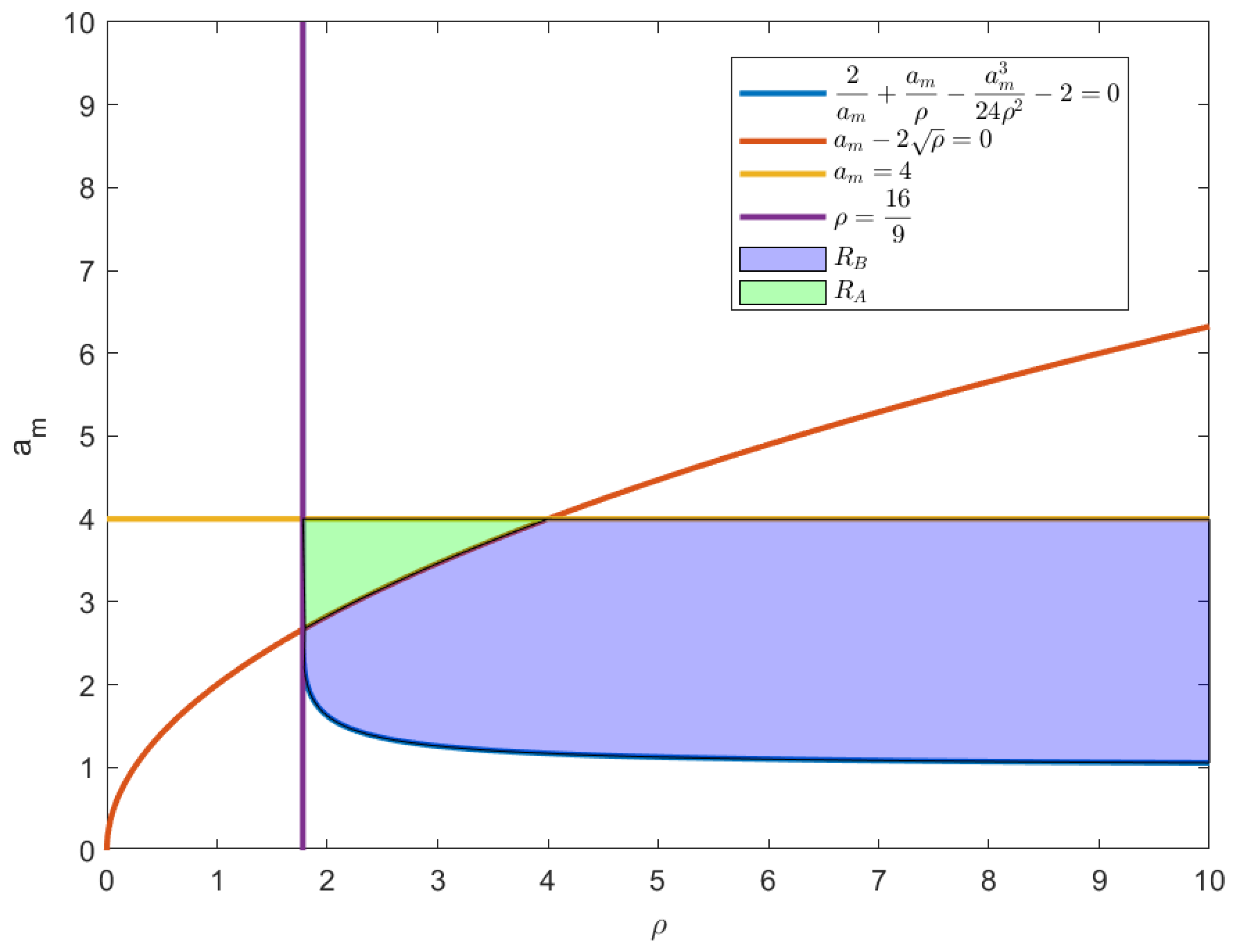
When m/s, , and the maximum threshold of braking distance , according to Formulas (24) and (25), the solution set R is
The solution set of is , as shown in Figure 9. Due to the need to keep the braking distance of the four-way shuttle within a reasonable range, based on , , and the maximum threshold of the braking distance , the deceleration and jerk during the braking stage can be determined. The solution set range for and is established, and one solution is selected to initialize the four-way shuttle’s motion parameters during the braking stage. The green area corresponds to the case when m/s, , and , the light purple area corresponds to the case when m/s, , and , and the brown boundary line indicates the case when m/s, , and .
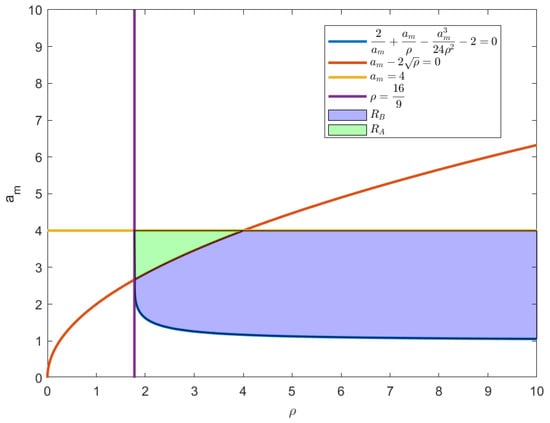
Figure 9.
Braking distance solution set region diagram.
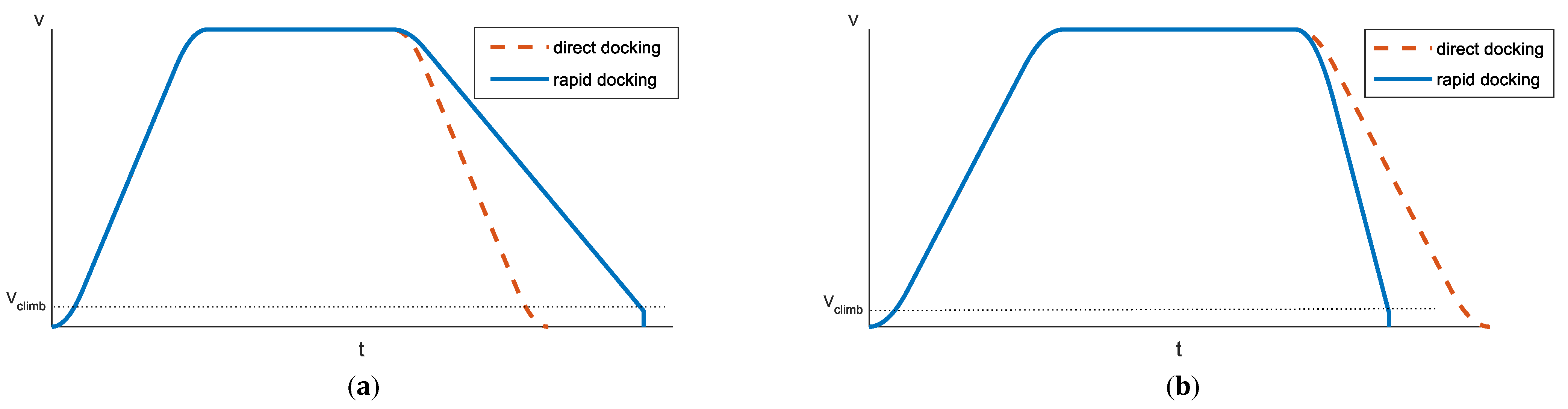
Compared with direct docking, when the real distance exceeds the guiding distance, direct docking cannot reach the target position. When the real distance does not exceed the guiding distance, the direct docking will pass the target position. The velocity curves of the rapid docking and direct docking are shown in Figure 10.
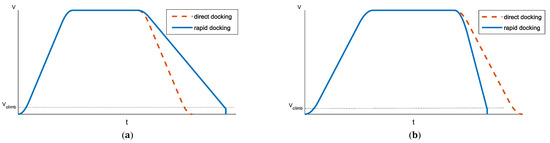
Figure 10.
The velocity curves of rapid docking and direct docking. (a) The real distance is longer than the guiding distance. (b) The real distance is shorter than the guiding distance.
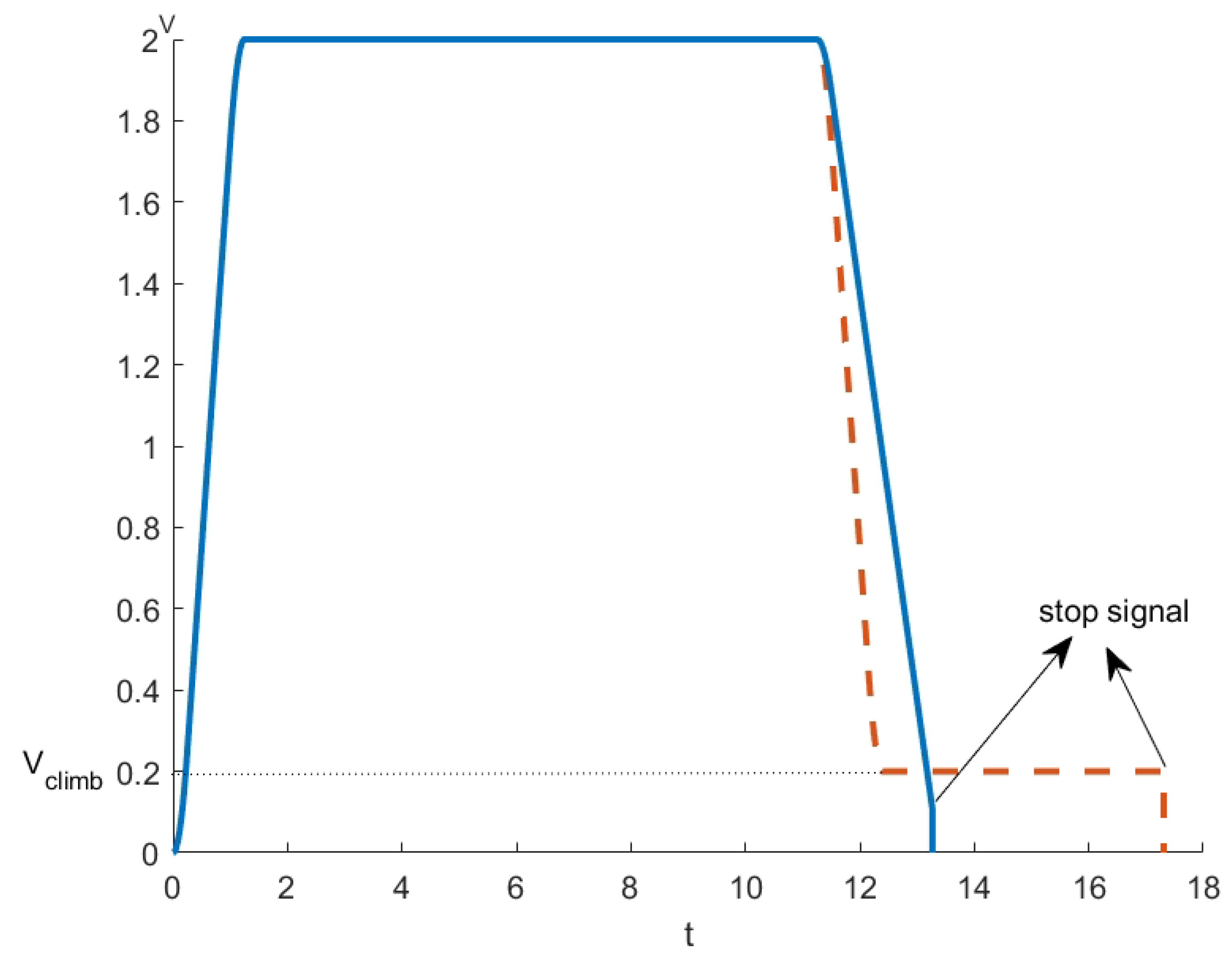
Compared with crawling docking, although both rapid docking and crawling docking stop by way of detecting the stop signal, rapid docking replaces the crawling process through distance compensation; that is, there is no need to preset the crawling distance, and there is no need to wait for the crawling process, which greatly shortens the braking time of the four-way shuttle. The velocity curves of the rapid docking and crawling docking processes are shown in Figure 10. Where m/s, , , and m/s, the braking time of the rapid docking is 3.99 s shorter than that of the crawling docking, and the four-way shuttle stops at a speed lower than the crawling speed, and the working efficiency and service life of the four-way shuttle have been improved. The key difference between crawling docking and direct docking lies in the use of docking signals in crawling docking, ensuring precise docking to the target position. While both crawling docking and rapid docking use docking signals, the proposed rapid docking method substitutes crawling with positional compensation, ensuring precise docking while reducing the docking time. See Figure 11.
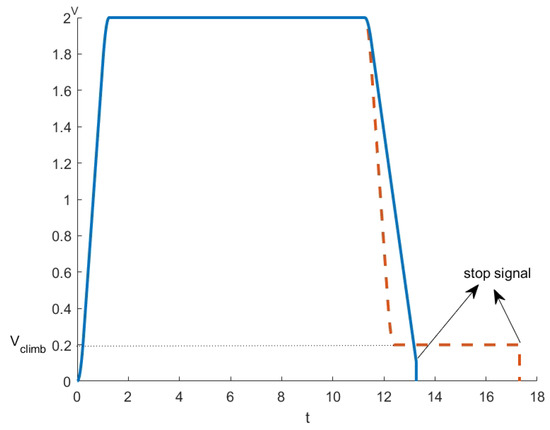
Figure 11.
The velocity curves of rapid docking and crawling docking.
6. Conclusions
The docking control of four-way shuttles is one of the important factors to improve the throughput of dense 3D storage. Inaccurate docking and extremely long parking time will affect the operation efficiency of the four-way shuttle. This paper proposes a rapid docking algorithm based on the docking motion model and distance compensation, which shortens the docking time, improves the user experience, and tackles the failure to change direction caused by inaccurate docking. In addition, the four-way shuttle stops at a speed lower than the crawling speed by the rapid docking algorithm, which not only prevents the goods from rolling off but also improves the service life of a four-way shuttle by reducing the mechanical vibration.
Although the rapid docking algorithm has good operation efficiency in dense 3D storage environments, the delay of the photoelectric sensor has a great impact on the detection of the location of goods slots and the docking signal. Therefore, this model may not work effectively in a warehouse with strong illumination. How to enhance the detection of the location of goods slots and docking signals needs to be further studied.
Author Contributions
Conceptualization, X.L. (Xiangpeng Liu) and X.L. (Xun Liu); methodology, X.L. (Xun Liu); software, X.L. (Xun Liu); validation, X.L. (Xun Liu) and Y.H.; formal analysis, Y.S.; investigation, Y.H.; resources, Y.S.; data curation, X.L. (Xun Liu); writing—original draft preparation, X.L (Xiangpeng Liu), X.L. (Xun Liu) and L.Z.; writing—review and editing, X.L. (Xiangpeng Liu) and L.Z.; visualization, X.L. (Xun Liu) and Y.H.; supervision, X.L. (Xiangpeng Liu); project administration, X.L. (Xiangpeng Liu) and X.X.; funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shanghai Normal University (SK202123).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ekren, B.Y. A multi-objective optimisation study for the design of an AVS/RS warehouse. Int. J. Prod. Res. 2021, 59, 1107–1126. [Google Scholar]
- Wu, W.; Chen, Z.; Wu, J.; Wang, Y. Safety analysis of small rail roadway stacker based on parametric design. Machines 2023, 11, 8. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S. Structural design and modeling of four-way shuttle car for automated warehouse systems. In Proceedings of the Ninth International Symposium on Sensors, Mechatronics, and Automation System (ISSMAS 2023), Nanjing, China, 11–13 August 2023; pp. 1590–1595. [Google Scholar]
- Şenaras, O.M.; Solmaz, E.; Öztürk, N.; Öztürk, F. Determination of the fleet size of AGVs with AGV pools using a genetic algorithm and artificial intelligence. Appl. Sci. 2023, 13, 7994. [Google Scholar] [CrossRef]
- Debnath, D.; Malla, P.; Roy, S. Position control of a DC servo motor using various controllers: A comparative study. Mater. Today Proc. 2022, 58, 484–488. [Google Scholar] [CrossRef]
- Kei, T.W.; Mang, V.; Un, C.S. Design of S-Curve direct landing position control system for elevator using microcontroller. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 24–26 October 2012; pp. 24–26. [Google Scholar]
- Uchida, T.; Sato, S.; Nakagawa, T. A proposal of control method for an elevator emergency stop device with a magnetic rheological fluid damper. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Song, K.T.; Chiu, C.W.; Kang, L.R.; Sun, Y.X.; Meng, C.H. Autonomous docking in a human-robot collaborative environment of automated guided vehicles. In Proceedings of the 2020 IEEE International Conference on Automatic Control (CACS), Shanghai, China, 6–8 November 2020; pp. 1–6. [Google Scholar]
- Li, H.; Wang, H.; Cui, L.; Li, J.; Wei, Q.; Xia, J. Design and experiments of a compact self-assembling mobile modular robot with joint actuation and onboard visual-based perception. Appl. Sci. 2022, 12, 3050. [Google Scholar] [CrossRef]
- Rajvanshi, A.; Krasner, A.; Sizintsev, M.; Chiu, H.P.; Sottile, J.; Agioutantis, Z.; Rose, J. Autonomous docking using learning-based scene segmentation in underground mine environments. In Proceedings of the 2022 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Seville, Spain, 8–10 November 2022; pp. 327–334. [Google Scholar]
- Hou, J.; Xue, Z.; Liang, Y.; Sun, Y.; Zhao, Y.; Chen, Q. Self-configurable centipede-inspired rescue robot. Appl. Sci. 2024, 14, 2331. [Google Scholar] [CrossRef]
- He, X.; Prabhu, V.V. Design and analysis of AGV-based cross-docking operations using analytical models. PMR 2022, 10, 428–449. [Google Scholar] [CrossRef]
- Lin, P.T.; Liao, C.A.; Liang, S.H. Probabilistic indoor positioning and navigation (PIPN) of autonomous ground vehicle (AGV) based on wireless measurements. IEEE Access 2021, 9, 25200–25207. [Google Scholar] [CrossRef]
- dos Reis, W.P.N.; Morandin Junior, O. Sensors applied to automated guided vehicle position control: A systematic literature review. Int. J. Adv. Manuf. Technol. 2021, 113, 21–34. [Google Scholar] [CrossRef]
- Hu, X.; Luo, Z.; Jiang, W. AGV localization system based on ultra-wideband and vision guidance. Electronics 2020, 9, 448. [Google Scholar] [CrossRef]
- Fu, W.; Liu, Y.; Zhang, X. Research on accurate motion trajectory control method of four-wheel steering AGV based on stanley-PID control. Sensors 2023, 16, 7219. [Google Scholar] [CrossRef]
- Ren, Z.; Lai, J.; Wu, Z.; Xie, S. Deep neural networks-based real-time optimal navigation for an automatic guided vehicle with static and dynamic obstacles. Neurocomputing 2021, 443, 329–344. [Google Scholar] [CrossRef]
- Yadegar, M.; Kashi, Z.; Ghaderi, H.; Meskin, N.; Noorizadeh, M. Autonomous target docking with obstacle avoidance and final velocity control for non-holonomic mobile robots. IEEE Trans. Autom. Sci. Eng. 2024, 1–12. [Google Scholar] [CrossRef]
- Tsiogas, E.; Kleitsiotis, I.; Kostavelis, I.; Kargakos, A.; Giakoumis, D.; Bosch-Jorge, M.; Ros, R.J.; Tarazón, R.L.; Likothanassis, S.; Tzovaras, D. Pallet detection and docking strategy for autonomous pallet truck AGV operation. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3444–3451. [Google Scholar]
- Ding, H.; Huang, Y.; Shi, J.; Shi, Q.; Yang, Y. A novel industrial AGV control strategy based on dual-wheel chassis model. Assem. Autom. 2022, 42, 306–318. [Google Scholar] [CrossRef]
- Wang, Y.; Shan, M.; Yue, Y.; Wang, D. Autonomous target docking of nonholonomic mobile robots using relative pose measurements. IEEE Trans. Ind. Electron. 2020, 68, 7233–7243. [Google Scholar] [CrossRef]
- Yilmaz, A.; Temeltas, H. A multi-stage localization framework for accurate and precise docking of autonomous mobile robots (AMRs). Robotica 2024, 1–24. [Google Scholar] [CrossRef]
- Yu, J.; Liang, M.; Peng, W.; Wu, T.; Rong, C.; Zhang, D. Speed control based on an improved PID controller with BP neural network for two wheel differential AGV System. In Proceedings of the 2023 IEEE 6th Student Conference on Electric Machines and Systems (SCEMS), Huzhou, China, 7–9 December 2023; pp. 1–5. [Google Scholar]
- Guney, M.A.; Raptis, I.A. Dynamic prioritized motion coordination of multi-AGV systems. Rob. Auton. Syst. 2021, 139, 103534. [Google Scholar] [CrossRef]
- Liu, J.; Li, M.; Wang, Z. AGV variable speed control for human body adaptability. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; pp. 1473–1478. [Google Scholar]
- Gong, L.; Wu, Y.; Gao, B.; Sun, Y.; Le, X.; Liu, C. Real-time dynamic planning and tracking control of auto-docking for efficient wireless charging. IEEE Trans. Intell. Veh. 2022, 8, 2123–2134. [Google Scholar] [CrossRef]
- Skulstad, R.; Li, G.; Fossen, T.I.; Vik, B.; Zhang, H. A hybrid approach to motion prediction for ship docking—Integration of a neural network model into the ship dynamic model. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Romanov, A.M.; Tararin, A.A. An automatic docking system for wheeled mobile robots. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), Moscow, Russia, 26–29 January 2021; pp. 1040–1045. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).