Advanced Waterjet Technology for Machining Beveled Structures of High-Strength and Thick Material

Abstract

The bevel cutting of large-thickness plates is a key process in modern industries. However, traditional processing method such as air-arc gouging bevel cutting or laser bevel cutting may cause serious deformation and rough surface quality due to the defects of the thermal cutting method. In order to improve the quality and efficiency of bevel processing, the abrasive waterjet cutting method is used in this research to overcome the challenge for bevel machining of high-strength DH40 steel plates with a large thickness. For different kinds of beveled structures, a 3D camera is used to measure the reference points defined on the workpiece and the SVD registration algorithm is adopted to transform the theoretical coordinate system to the actual coordinate system. Furthermore, the distance between the nozzle and the workpiece surface is also measured and compensated for to ensure the consistency of the bevel width. Finally, experiments are carried out for different kinds of bevels to verify the feasibility of the proposed method for high precision processing for beveled structures. The developed method has been effectively applied in the actual shipbuilding industry.

1. Introduction

Shipbuilding is a comprehensive industry that provides technical equipment for shipping, marine exploration, national defense construction, and other fields [1,2,3]. Its manufacturing technology reflects the overall industrial strength of a country. There is a significant demand for bevel cutting of steel plates and tubes in the shipbuilding process, accounting for about 8% to 12% of the total workload of ship construction. The quality and precision of cutting seriously affect the level of shipbuilding [4,5]. Generally, the manufacturers rely on beveling as part of the welding preparation process, as illustrated in Figure 1. The beveled edge produces a sturdier type of welding to support the massive weight and loads on such machines and structures [6]. However, the traditional beveling processing methods such as flame cutting or plasma cutting usually produce rough machined surfaces with deep dents and cuts [7]. What is more, these thermal cutting methods are likely to cause serious thermal deformation of the workpiece. Thus, the process of inverse deformation is required, which has always been a difficulty in improving the efficiency of bevel processing. Under the urgent needs of industrial applications, abrasive waterjet cutting (AWJC) technology is introduced for the processing and manufacturing of beveled structures [8,9].

AWJC technology is an emerging unconventional cutting method that can cut different kinds of materials such as high-strength steels [10], composites [11,12], rocks [13], glasses [14], foams [15], and so on. The waterjet is accelerated by a streamline intensifier high-output pump that can provide water pressure up to 413.7 MPa (60,000 psi), and is ejected from an orifice with a tiny diameter of 0.33 mm [16,17,18]. The abrasive particles are mixed with the high-speed waterjet in the focusing tube to form the continuous abrasive waterjet and be sprayed at a speed of over 600 m/s. Compared with other machining technologies, AWJC technology offers a higher material removal rate than the flame cutting process. It is reported that AWJC can cut large thickness materials up to 250 mm. Also, the surface integrity produced by AWJC is better than thermal machining methods like plasma cutting or laser cutting [19,20,21]. As a kind of cold machining method, the cutting quality of the abrasive waterjet machining is not affected by thermal deformations. Thus, it can cut intricate shapes with better dimensional accuracy [22]. Compared with other high energy fluid jet machining (HEFJet-Mach) methods such as laser cutting [23], an abrasive waterjet can cut almost any material, while laser cutting is less effective for some reflective materials such as aluminum and copper. In addition, waterjet cutting does not generate high temperatures, so it will not cause thermal damage to the material, while laser cutting will produce a heat-affected zone, which may cause material deformation or microstructural changes. Moreover, the abrasive waterjet is an environmentally friendly processing technology that does not produce harmful gases or fumes, while laser cutting may produce harmful gases and require fume treatment. However, the abrasive waterjet also has its own processing disadvantages. For example, for thin materials, the speed of laser cutting is usually faster than that of an abrasive waterjet, and laser cutting can usually achieve higher precision and smaller kerf width. At present, the widely accepted theory is that AWJC has significant advantages in cutting quality and material adaptability, but the initial investment and operating costs are high. According to the survey, the abrasive consumption cost is high (about USD 10–20 per hour), and the high-pressure equipment maintenance cost is high, especially the high-pressure pump and nozzle; however, the water and electricity consumption cost is relatively low. Thus, AWJC is suitable for occasions that require high precision and high-quality cutting.

Furthermore, AWJC can also be applied in other large-scale industries such as automotive manufacturing and rail transportation due to its flexibility and high precision, showing great potential for industrial application. AWJC is used in the aerospace industry [24] to cut titanium alloys, aluminum alloys, carbon fiber composite materials [25], etc., which are used to manufacture aircraft fuselages, engine components, and spacecraft structures. However, composite materials such as carbon fiber reinforced polymer (CFRP) are composed of different layers of materials. The abrasive waterjet will be affected by the different properties of each layer during the cutting process, resulting in uneven cutting force and easy delamination. Moreover, as the jet penetrates deeper into the material, its energy gradually weakens, causing the cutting seam to gradually narrow and form a tapered section. The cutting width at the exit is usually smaller than that at the entrance, resulting in geometric deviation. With the development of high-precision waterjet cutting technology, high-precision turbine blades, structural frames, and other complex-shaped parts are manufactured. In this study, AWJC technology is applied in the high-precision manufacturing of bevels with complex structures.

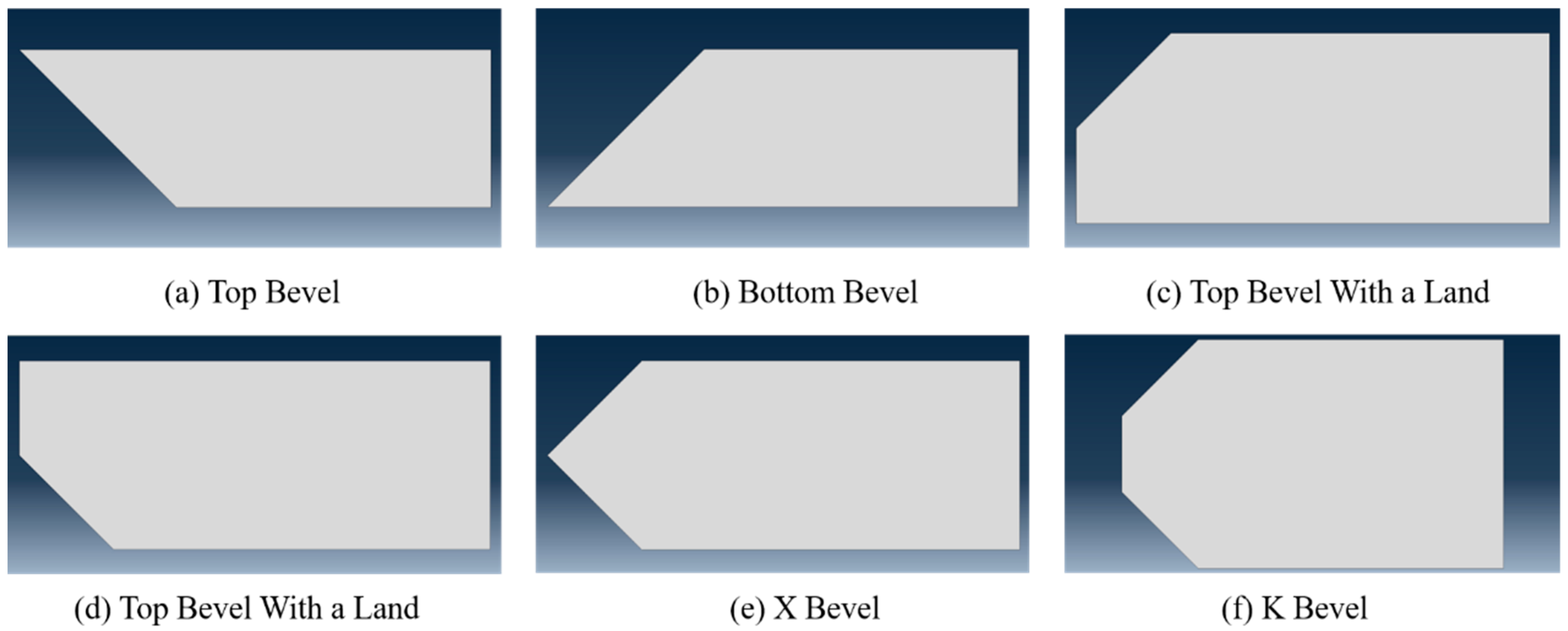
There are many challenges in the process of abrasive waterjet cutting bevels. The first step in delivering a precise bevel cut is to determine the right direction of the bevels. In fact, there are various kinds of bevels as illustrated in Figure 2. Also, it may become even more complicated when the bevels are specified on pipes or curved surfaces. The cutting directions of these bevels gradually change over the entire cutting track [26]. It is impossible to realize precise bevel cutting on curved surfaces without the help of the parametric modeling method. In the actual production of these complex bevel structures, it mainly relies on manual operations, which greatly reduces the cutting efficiency. Furthermore, the bevel cutting machine tools such as plasma cutting and gouging systems cannot be applied to a cramped processing environment like the shipbuilding industry. In order to break through the difficulty of bevel cutting on curved panel parts, different types of bevel models of curved panels are constructed based on the three-dimensional modeling software CATIA V5 according to the constraints of the product drawings. In addition, the bevel modeling process has been developed as a software module, which greatly facilitates factory applications.

Another vital issue in the bevel cutting process of abrasive waterjet machining is to ensure bevel shape accuracy. As we all know, AWJC technology has limitations [8,9]. The quality of the workpiece produced is affected by defects such as taper and jet lag because of the energy dissipating when the waterjet penetrates through the workpiece. Eliminating the deformation error of AWJC has always been a research hotspot. Process parameters have a significant impact on the kerf geometry and surface roughness. Optimizing the process parameters of abrasive waterjet machining requires comprehensive consideration of factors such as cutting depth, kerf width, and surface roughness [12]. Generally speaking, the energy of the waterjet impacting the workpiece can be increased by adjusting the water pressure, abrasive flow rate, traverse speed, abrasive particle size, nozzle diameter, and working distance, which can improve cutting efficiency while ensuring machining quality. Hlavac [27] proposed the method of nozzle tilting to reduce the distortion of the circular shape of AWJC. Similarly, Chen [28] analyzed the reasons for the corner error of the square trajectory and proposed a method to compensate for this error. In addition, Chen [29] also pointed out a guideline setting method in AWJC, which reduced the shape error caused by the cutting-in/cut-out process. Moreover, Wu et al. [26] analyzed the main reasons that cause the jet point to deviate from the cutting path, including the linear motion error of the X-axis and Y-axis, the rotation error of the cutting head, and the change in the standoff distance. Thus, a target distance tracker was used to keep the standoff distance constant, and the motion errors of the machine tool were compensated for. Although these pioneer researchers have put much effort into improving the cutting accuracy of AWJC, there were few scholars to study the bevel cutting problems on curved structures especially for the cutting of high-strength and thick materials.

The challenge of bevel cutting on curved structures has been one of the most urgent problems that need to be broken through in AWJC technology. Therefore, a new method for precisely cutting bevels on curved plates by AWJC is proposed in this article. The newly developed method has been applied in the shipbuilding industry successfully. Compared with traditional bevel machining methods, it can not only achieve high quality but also improve processing efficiency. The roots of beveling are evenly retained and bevel widths are uniform with acceptable surface roughness. The rest of the article is structured as follows. Section 2 describes the bevel types and analyzes the causes of the deformation error. In Section 3, the key technologies to ensure bevel cutting accuracy are introduced. In Section 4, experiments are carried out. In Section 5, the experimental data are analyzed in accordance with the process quality requirements. Finally, the article is concluded in Section 6.

2. Bevel Types and Cutting Error Analysis

2.1. Different Bevel Types Specified on Curved Surfaces

2.1.1. Characteristics of Bevel Structures

The abrasive waterjet cutting for bevel structures in this paper refers to the beveling specified on curved surfaces such as pipes, ship parts, and so on. The experimental objects in the paper are high-strength steel plates with a radius of 3500 mm and a thickness of 30 mm. The diameter of the opening hole is ∅350 mm, and the bevel style is like the K-shaped bevel or X-shaped bevel structures illustrated in Figure 2. The difficulties we meet in the bevel machining process are to realize the typically shaped bevels specified on radial holes and non-radial holes. A radial hole refers to the type of opening where the central axis of the hole coincides with the diameter direction of the circular workpiece, while a non-radial hole means that the center of the hole is perpendicular to the ground, as shown in Figure 3. It can be known by analyzing the geometric characteristics that the structure of a radial hole is symmetrical, but as for the bevel structure of a non-radial hole, the inclined angles gradually change along the entire track, which increases the geometric modeling difficulties directly.

2.1.2. Technical Requirements for Bevel Processing

The cutting qualities of bevel structures have significant influences on the properties of the subsequent welding process. Therefore, there are specific regulations for bevel processing, which are shown in Figure 4. It is seen that the positioning accuracy of the hole is required to be ±1 mm, and the geometric shape accuracy is required to be 0~2 mm. A tolerance of ±1 mm is demanded for the depth of the bevel (H) and the width of the bevel (K). The tilt angle of the bevel surface (α) is required to be 40~50°, and the angle error is less than 2.5°. The retained root of the bevel (P) is requested to be ±1 mm. In addition, the surface roughness of beveling is asked to be Ra ≤ 12.6. Finally, it is worth noting that the bevel depth (H) and the bevel width (K) are determined according to the thickness of the workpiece, as listed in

Table 1. Technical requirements for workpieces with different thicknesses.

Parameters	Value Ranges (mm)
Workpiece thickness Δ	20~22	24~26	28~30	32~35
Bevel depth T	6	7	11	13
Bevel width K	16	19	19	23

.

2.2. Factors Causing the Deviation of Bevel Cutting Quality

In the bevel machining method of today’s shipbuilding industry, the hole is opened by manually cutting and polishing, while the bevel is manufactured by the carbon arc gouging method. Thus, a large amount of smoke and dust is generated during the manufacturing process, which causes some damage to the health of the operators. Moreover, for large-thickness plates, multiple gouging procedures are needed to cut through the boards, so that the machining efficiency is low. In order to improve the traditional bevel processing mode in the shipbuilding industry and realize automatic bevel cutting for complex bevel shapes on curved surfaces, three-dimensional models of bevels are established, especially for the bevel cutting model of non-radial holes. Furthermore, the modeling process has been developed into a software module, which greatly facilitates the modeling for the operators. In addition, the simulation of bevel cutting is conducted based on offline programming software to calculate whether the singular postures of the robot or unreachable points are exited on the planned trajectory.

Whether it is a radial hole or a non-radial hole, the key to ensuring the accuracy of waterjet bevel cutting lies in the determination of the direction and position of the trajectory point, as illustrated in Figure 5. Since the center point of the opened hole is now determined mainly by manual operations, the positioning accuracy is low. Further, the measurement deviation leads to the reference error directly, which in turn causes the mistaken position of the hole center. Therefore, a 3D camera with a measuring accuracy of less than 0.1 mm is used to identify the reference points set on the workpiece. Additionally, the SVD decomposition method is adopted to perform coordinate conversions from the theoretical coordinate system to the actual processing coordinate system to ensure the correctness of the bevel directions. More importantly, in order to eliminate the manufacturing accuracy of the curved workpieces, the standoff distance is also measured and compensated for, which can not only improve bevel processing accuracy but also increase manufacturing efficiency.

3. Key Technologies to Ensure the Bevel Cutting Quality in AWJC

At present, the main cutting and processing methods for large ship parts are manual marking and flame cutting, resulting in large manual marking positioning errors and trajectory cutting errors.

Thus, based on a robot high-pressure abrasive waterjet processing system, this paper adopts AWJC to cut thick ship parts. In order to optimize the existing processing process, the main functional modules include workpiece hoisting and positioning, visual measurement and station establishment, processing hole position correction, and abrasive waterjet cutting. Firstly, the workpiece is hoisted into place to determine the initial radial and axial positions of the parts. Then, visual measurement and station establishment are performed, and the transfer station matrix is calculated through reference point measurement to determine the positional relationship of the workpiece relative to the processing system. Subsequently, the surface deformation of the processing area is detected, and the offline trajectory program of the three-dimensional model is corrected at the point position to meet the quality requirements of trajectory cutting. After the hole position correction step is completed, the high-pressure abrasive waterjet trajectory cutting program can be implemented to cut and process different types of ship parts.

3.1. Modeling Procedures for Bevel Structures

The 3D model of the cylindrical workpiece is firstly constructed depending on the parameters such as diameter, thickness, length, and so on. Then, the holes are opened in accordance with the requirements of the drawings. In addition, it is worth noting that radial holes and non-radial holes are distinguished according to the orientations of the axes of the holes. On the basis of the opened holes, parametric modeling of the bevel is carried out, as shown in Figure 6. In particular, the modeling process of a non-radial bevel is challenging because of the continuously changing bevel directions along the entire trajectory. The realization for modeling non-radial bevels in this paper is a breakthrough in the shipbuilding industry. In addition, it is worth noting that the modeling of procedures determines the theoretical posture of the bevel points. Since large hull parts may deform during the manufacturing process, the theoretical direction and position of the bevel points need to be compensated for, as described in Section 3.2 and Section 3.3, respectively.

3.2. Determination of the Direction of Beveling

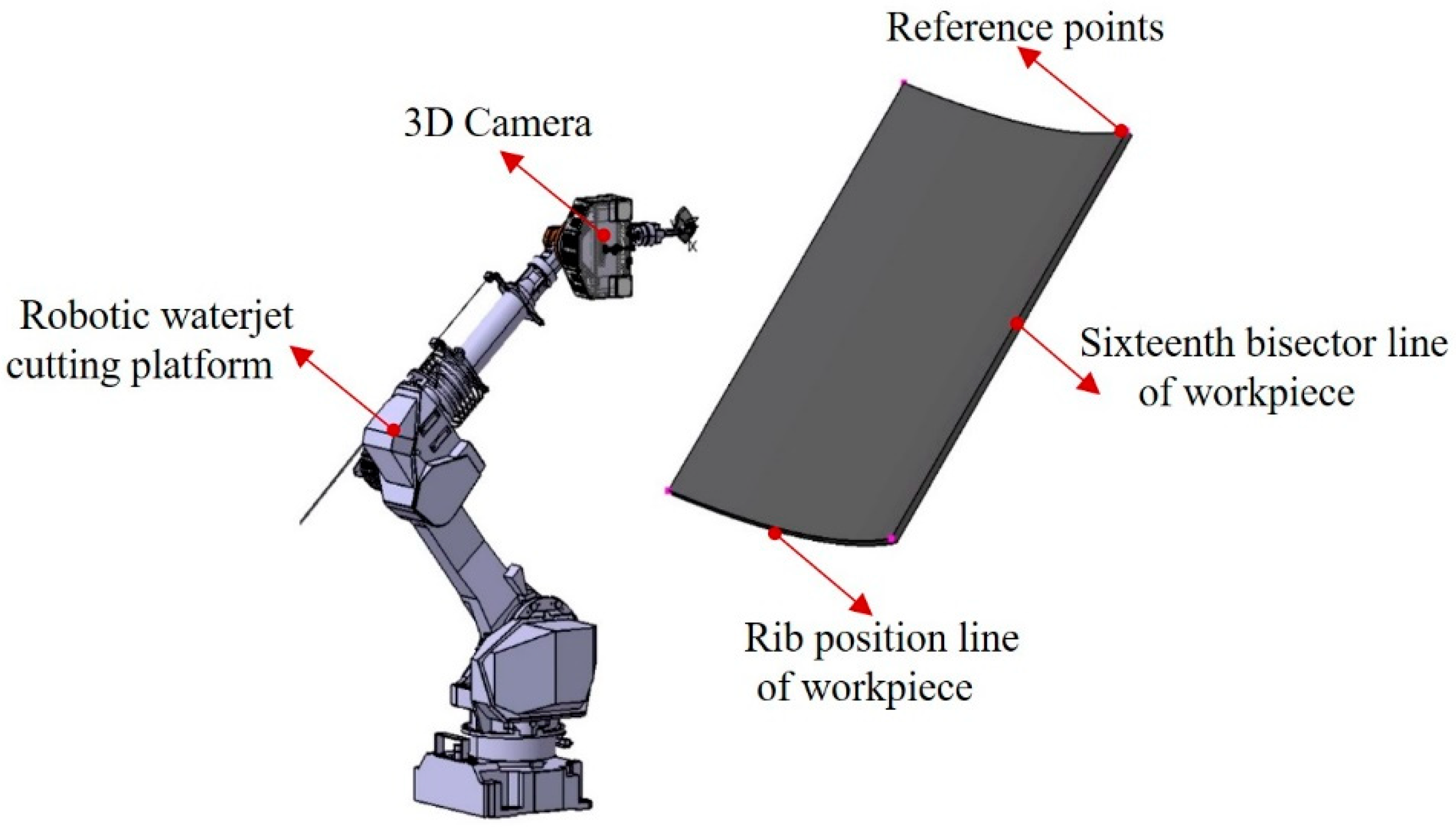
The accurate determination of the bevel direction has an important impact on the product qualities, which is regarded as another challenge in bevel machining. In this paper, the determination of the bevel direction refers to the use of a 3D camera system to establish the relative positional relationship between the workpiece (the hull panel) and the equipment (the waterjet cutting system). Firstly, a 3D camera is used to measure the positions of the reference points pre-set on the workpiece. Then, the processing coordinate system of the workpiece is acquired by the weighted singular value decomposition (SVD) algorithm [30]. As shown in Figure 7, the reference points are defined at the vertices of the processing area, which are the intersections of the reference lines (the two-dimensional curves on the surface) and the welds (the three-dimensional space features). Thus, the robot equipped with a 3D camera measures the four reference points sequentially in different postures. The coordinate transformation matrix between the processing coordinate system of the on-site workpiece and the theoretical coordinate system is calculated as:

$${\sum }^2=\left({\displaystyle \sum _{i=1}^4{w}_i^2}{\Vert P_{Bi}-\left(R·P_{Ai}+t\right)\Vert }^2\right)$$

(1)

where P_Bi and P_Ai represent the theoretical coordinate value and the actual coordinate value of the reference point i, respectively. R is the 3 × 3 rotation transformation matrix, and t is the 3 × 1 translation transformation matrix; w_i represents the weight parameter of the reference point i. The conversion matrices R and t are solved under the optimization goal of the minimum registration error. Therefore, the actual posture v_Ai of the track point is calculated as:

$$v_{Ai}=R·v_{Bi}+t$$

(2)

where v_Bi = (α, β, γ, x, y, z) is the theoretical posture of the discrete point i setting on the beveling cutting trajectory. In addition, the conversion error has been calculated in the experiments below.

3.3. Compensation for Standoff Distance

It is worth noting that the formation for curved high-strength steel plates with large thickness is really a heavy duty. Thus, there are manufacturing errors on the product surfaces, which will cause the deviations of beveling, as illustrated in Figure 5. Therefore, it is necessary to measure the surface deformation in the bevel-cutting area and compensate for the standoff distances of the points on the cutting tracks in time, as illustrated in Figure 8. A laser tracker has been used to measure the actual positions of the points,. and then the offset errors are compensated for to ensure the constant bevel width of the target.

4. Experiments

4.1. Experimental Setup

For the proposed abrasive waterjet bevel cutting procedure, relevant experiments have been conducted in this section to verify the feasibility and effectiveness of the method. As depicted in Figure 9, the high-pressure pump was provided by Hypertherm, whose maximum pressure was up to 60,000 psi (413 Mpa). The nozzle was assembled by standard accessories (KMT) including a ruby orifice with the diameter of 0.33 mm, and a focusing tube with a diameter of 1.02 mm and a length of 76.2 mm. An 80-mesh almandine garnet sand was selected as the abrasive type. In addition, the six-axis robot (FANUC M710ic/70, Oshino, Japan) was configured with an error compensation package (iRCalibration Signature, FANUC) so that a high positioning accuracy of ±0.05 mm was achieved. In addition, the experimental methods, techniques, testing technologies, and data processing of the abrasive waterjet cutting tests conducted in this study are in accordance with the national standard “Ultra-High Pressure Waterjet Cutting Machine” (GB/T 26136—2018) [31] and the industry standard “Robot Ultra-High Pressure Waterjet Cutting Machine” (JB/T 13245—2017) [32]. A sample of 20 mm thick high-strength steel (DH40) was used as the test workpiece. The DH40 material produced by Baosteel (Shanghai, China), is a high-strength marine steel, mainly used in the shipbuilding industry. The chemical composition and mechanical properties of DH40 are shown in

Table 2. Chemical composition of DH40 [33,34].

Material	Chemical Composition (%)
DH40	C	Si	Mn	Cr	Ni	Cu	S	P	Nb	Mo	V	Ti
	12	27	145	2	1	4	0.3	1.2	3.2	0.5	0.3	1.2

and

Table 3. Mechanical properties of DH40 [33,34].

Parameters	Range
Yield strength (N/mm2)	415
Tensile strength (N/mm2)	515
Elongation (%)	31.5
Impact toughness J (−2 °C)	158

, separately. Specimens of dimension 2500 mm × 1400 mm were machined from a large curved panel with a diameter of 7000 mm.

The high-precision measurements were conducted by a 3D structured light camera TrueD2305Md supported by HANCHINE (Hangzhou, China). The 3D camera could supply a resolution of 1920 × 1200 px, a visual field of 150.5 × 113.4 mm², and an accuracy of ±0.092 mm in the X/Y direction, ± 0.03 mm in the Z direction. A laser tracker (Leica AT930, Heerbrugg, Switzerland) is utilized to measure the actual position of the workpiece feature points with an accuracy of ±5 ppm. In addition, the surface roughness of the workpiece was detected by a Mitutoyo SJ-410 roughness measuring instrument, whose measuring scope was from 0.0125 μm to 800 μm. The measuring instruments are pictured in Figure 10. According to the technical requirements for bevel cutting, the roughness at the outlet of the cutting section is measured. The measurement points should be the same as the dimension measurement points. Perform three repeated measurements at each measurement point, and record the average of the results from all measurement points as the experimental result. The entire roughness measurement process follows the ISO 25178-6 standard [35].

4.2. Experimental Design

Cutting tests of the complex bevel structures specified on radial holes and the non-radial holes were carried out to verify the effectiveness of the waterjet bevel cutting process proposed in this paper. It is worth noting that the quality requirements are shown in Figure 4 above. Furthermore, the positions of the reference points at the four vertices of the workpiece were measured by the 3D camera, and then the conversion matrix was solved according to the weighted singular value decomposition algorithm as Equation (1). In addition, the positions of the cutting path points detected by the 3D camera were compared with the laser tracker to verify the position and direction accuracies of these points. Also, the standoff distances of the cutting path points were measured and compensated for. Finally, the bevel cutting qualities such as deviations of the hole shape, the bevel depth, the bevel width, and the tilt angle direction were measured to evaluate the bevel processing qualities by the AWJC method. The measurement diagram for the cutting path points is depicted in Figure 11.

Parameter optimization experiments were performed first to obtain the optimal process parameters for high-strength steel (DH40) panels with a thickness of 30 mm. Thus, the response surface method (RSM) was adopted to design the experiments with three five-level factors as outlined in

Table 4. Experimental variables.

Parameters	Range
Jet Pressure P (MPa)	260, 290, 320, 350, 380
Abrasive mass flow rate ${\dot{m}}_a$ (g/min)	350, 400, 450, 500, 550
Jet traverse speed u (mm/min)	15, 18, 21, 24, 27

, resulting in 20 experimental runs. Analysis of variance (ANOVA) was performed based on Design-Expert 13 software. Finally, the optimal process parameters were solved under the goals of minimum kerf width and surface roughness (≤Ra 12.6).

5. Results

5.1. Measurement Accuracy of the Reference Points

The experiments were conducted to verify the feasibility of the robotic abrasive waterjet automated cutting process and assess the measurement accuracy of the reference points. The workpiece used was a curved metal plate with scribed lines. The theoretical coordinates of the visual reference point on the curved panel were measured by a laser tracker. The target ball of the laser tracker was placed on a special base shown in Figure 12b, and the spatial coordinates of the four visual reference points were measured, respectively. The measurement layout of the instrument is shown in Figure 12, and the results of the theoretical coordinate point ^wp of the reference point are shown in

Table 5. Measurement results of the reference points.

Point	tp (x, y, z)T
1	(3049.94, −360.94, 874.60)
2	(3049.52, 364.50, 875.11)
3	(3046.90, 385.77, 134.00)
4	(3056.02, −305.20, 137.37)

.

The robot with the 3D camera was moved to the positions of the reference points, thus the reference points (^cp) were measured in the camera coordinate system. In addition, the coordinate system of the robot pose ^bT_c was also recorded. According to the above process, the positions of the four reference points are recorded in

Table 6. The coordinates of reference point ^cp and robot pose ^bT_c.

Point	cp (x, y, z)T	bTc (x, y, z, w, p, r)T
1	(123.97, 12.55, 494.80)	(636.66, −219.59, 1616.90, 75.11, 1.90, 67.70)
2	(161.22, −8.73, 506.93)	(669.36, 217.31, 1585.88, 77.40, −22.07, 103.75)
3	(155.85, −20.68, 498.04)	(712.33, 235.85, 834.68, 74.35, −22.11, 104.23)
4	(118.12, 6.11, 502.11)	(657.43, −253.75, 932.89, 77.22, 15.23, 75.43)

.

According to the data in Table 6, the coordinates ^bp of the reference points in the robot base coordinate system are obtained as shown in

Table 7. The reference points in the robot base coordinate system.

Point	bp (x, y, z)T
1	(1124.87, −280.91, 1751.99)
2	(1125.36, 443.23, 1741.04)
3	(1157.69, 453.32, 999.36)
4	(1166.45, −236.53, 1014.78)

.

The position of the workpiece theoretical coordinate system in the base coordinate system is determined by the rigid body pose transformation algorithm as:

$${}^{b}T_w=\left(\begin{array}{cccc}0.9989& 0.0007& 0.0476& -1879.522\\ -0.00002& 0.9999& 0.0158& 65.8457\\ 0.0476& -0.0158& 0.9987& 727.3267\\ 0& 0& 0& 1\end{array}\right)$$

(3)

Therefore, the measurement error vector e (∆x, ∆y, ∆z) of reference points could be defined as:

$$e={}^{b}R_w{}^{w}p+{}^{b}t_w-{}^{b}p$$

(4)

The calculated error e is shown in

Table 8. Conversion error of the reference points (mm).

No.	∆x	∆y	∆z	$\sqrt{\left|\right|\mathit{e}|{|}^2}$
1	0.2019	−0.4124	−0.3457	0.5748
2	−0.1715	0.8054	−0.3342	0.8887
3	0.1551	0.2941	0.7077	0.7819
4	−0.1855	−0.6870	−0.0277	0.7122

.

The results show that the average error of the reference points is 0.74 mm, the minimum error is 0.57 mm, and the maximum error is 0.89 mm, which is less than 2.00 mm, meeting the technical requirements. The above experimental process was repeated two additional times. Thus, the conversion error of the reference points is shown in Figure 13, which can be seen that the maximum value of the visual reference point coordinate system conversion error is 0.89 mm.

5.2. Compensation Results of the Standoff Distance

The program interface of the key points measurement is shown in Figure 14, which mainly includes the button window and the data display window. The button window is responsible for implementing operations related to point measurement, and the data display window is responsible for visual collection of data. The corresponding six-axis end pose of the robot is obtained through the data display interface button, and is automatically loaded into the interface data display button after clicking, which can effectively provide a safety guarantee in case of collision of peripheral equipment. A total of nine different robot system pose data were collected. The camera pose data calculated based on the pictures and point clouds of each pose are shown in

Table 9. Camera pose data.

No.	cTt	No.	cTt
1	$\left(\begin{array}{ccc}-0.999& 0.012& \begin{array}{cc}-0.042& 179.511\end{array}\\ -0.013& -0.999& \begin{array}{cc}0.012& 42.148\end{array}\\ -0.041& 0.012& \begin{array}{cc}0.999& 497.492\end{array}\end{array}\right)$	6	$\left(\begin{array}{ccc}-0.976& -0.001& \begin{array}{cc}-0.213& 166.351\end{array}\\ -0.000& -0.999& \begin{array}{cc}0.006& 40.571\end{array}\\ -0.213& 0.007& \begin{array}{cc}0.977& 513.759\end{array}\end{array}\right)$
2	$\left(\begin{array}{ccc}-0.991& -0.085& \begin{array}{cc}0.102& 186.292\end{array}\\ 0.086& -0.996& \begin{array}{cc}0.005& 31.803\end{array}\\ 0.101& 0.013& \begin{array}{cc}0.995& 482.541\end{array}\end{array}\right)$	7	$\left(\begin{array}{ccc}-0.975& 0.033& \begin{array}{cc}0.217& 194.018\end{array}\\ -0.028& -0.999& \begin{array}{cc}0.023& 45.336\end{array}\\ 0.217& 0.017& \begin{array}{cc}0.976& 469.181\end{array}\end{array}\right)$
3	$\left(\begin{array}{ccc}-0.977& 0.109& \begin{array}{cc}-0.184& 169.687\end{array}\\ -0.111& -0.994& \begin{array}{cc}0.005& 52.189\end{array}\\ -0.183& 0.025& \begin{array}{cc}0.983& 511.263\end{array}\end{array}\right)$	8	$\left(\begin{array}{ccc}-0.989& -0.057& \begin{array}{cc}0.131& 188.609\end{array}\\ 0.076& -0.986& \begin{array}{cc}0.143& 42.332\end{array}\\ 0.121& 0.152& \begin{array}{cc}0.981& 481.406\end{array}\end{array}\right)$
4	$\left(\begin{array}{ccc}-0.998& -0.003& \begin{array}{cc}-0.046& 178.917\end{array}\\ -0.005& -0.983& \begin{array}{cc}0.185& 53.385\end{array}\\ -0.05& 0.185& \begin{array}{cc}0.982& 499.278\end{array}\end{array}\right)$	9	$\left(\begin{array}{ccc}-0.988& 0.120& \begin{array}{cc}-0.087& 177.397\end{array}\\ -0.109& -0.986& \begin{array}{cc}-0.124& 43.314\end{array}\\ -0.101& -0.113& \begin{array}{cc}0.988& 501.057\end{array}\end{array}\right)$
5	$\left(\begin{array}{ccc}-0.999& 0.026& \begin{array}{cc}-0.034& 180.319\end{array}\\ -0.021& -0.986& \begin{array}{cc}-0.161& 31.576\end{array}\\ -0.038& -0.161& \begin{array}{cc}0.986& 493.733\end{array}\end{array}\right)$

. The pose transformation matrix is represented by three rows and four columns.

The pose data of the robot are shown in

Table 10. Robot six-axis end data.

No.	tx/mm	ty/mm	tz/mm	θx/∘	θy/∘	θz/∘
1	542.482	34.353	1537.782	−89.490	−0.482	−88.666
2	545.761	65.842	1549.295	−90.523	−6.923	−92.778
3	545.778	95.414	1549.286	−90.524	−6.924	−99.258
4	545.821	−77.589	1546.391	−90.525	−6.923	−79.333
5	557.436	−27.076	1593.581	−97.724	0.447	−90.137
6	531.556	−27.097	1449.165	−80.360	−2.081	−90.798
7	531.590	−94.503	1417.656	−78.348	−1.946	−84.123
8	531.614	16.089	1618.290	−95.871	−3.222	−92.876
9	596.749	−124.861	1679.712	−101.310	−4.431	−77.888

.

Due to the measurement error of the binocular structured light camera, the hand–eye matrix error, and the robot pose error, the actual measurements are not exactly the same. Therefore, the absolute error is used to access the accuracy of the measurements, which can be calculated as:

$$e_p=\frac{1}{C_k^2}{\displaystyle \sum _{i=1}^k\sqrt{\left|\right|{}^b\widehat{p}^{(i)}-{}^b\overline{p}|{|}^2}}$$

(5)

where k is the number of robot poses, ${}^b\widehat{p}^{(i)}$ is the measurement value of the robot pose under base coordination. The absolute measurement error (e_p) distribution of the key points is shown in Figure 15. The average relative measurement error is 0.45 mm and the maximum value is 0.47 mm.

5.3. Bevel Cutting Results

In the parameter optimization experiments (RSM), the optimization goals are to minimize the kerf width and the surface roughness [36]. The optimal parameters that can meet the machining quality requirements are that the abrasive mass flow rate is 549.112 g/min, the nozzle traverse speed is about 17.340 mm/min, and the water pressure is 373.071 MPa. The optimized process parameters are used for bevel cutting process. The bevel cutting qualities are evaluated from the hole shape, bevel depth and width, bevel tilt angle, root retention, and surface roughness. The workpiece after cutting is shown in Figure 16.

The schematic diagram of measurement points is illustrated in Figure 17, and the measured results of the cutting holes are shown in

Table 11. Circular trajectory bevel cutting test results (mm).

Point	Ac	Bc	Cc	Dc	Ec	Fc	Gc	Hc
Diameter	142.00	141.10	141.60	141.50	142.06	141.05	141.80	141.40
Vertex	134.30	134.80	134.72	134.80	134.31	134.84	134.73	134.82
Height	10.50	10.33	10.82	9.94	10.35	10.75	12.30	10.95
Angle	20.4°	19.6°	18.7°	19.0°	19.0°	18.2°	18.9°	19.0°

. It can be seen from the experimental data that the variation range of the upper surface diameter is 141.10~142.00 mm, with an amplitude of 0.90 mm; the inner diameter formed by the K-shaped vertexes is 134.30~134.80 mm, and the amplitude is 0.50 mm. Thus, the geometry of the bevel is acceptable within the tolerance of 2 mm. Moreover, the G_c point vibrates violently, so the overall change range is 9.94~12.30 mm, with an amplitude of 2.36 mm; after removing the G_c point, the overall change range is 9.94~10.95 mm, with an amplitude of 1.01 mm.

Similarly, the cutting quality of the oval hole is measured and the relevant data are outlined in

Table 12. Elliptical trajectory bevel cutting test results (mm).

Point	Ae	Be	Ce	De	Ee	Fe	Ge	He
Diameter	129.50	130.80	129.80	130.50	—	—	—	—
Vertex	124.00	123.60	123.72	123.80	—	—	—	—
Height	11.08	10.8	11.75	11.16	11.28	10.23	11.66	10.45
Angle	17.5°	17.8°	17.8°	18.2°	19.3°	19.3°	19.7°	19.6°

. It can be seen from the experimental results that the bevel angle of the oval hole is gradually changing, while the upper bevel diameter ranges from 129.50 mm to 130.80 mm, while the middle K-shaped diameter is 123.60 mm to 124.00 mm. What is more, the bevel height is 10.23 mm to 11.75 mm with amplitude 1.52 mm. The bevel angle variation ranges from 17.5° to 19.7°, and the amplitude is 2.2°.

Furthermore, the cutting quality of the square hole is outlined in

Table 13. Square trajectory bevel cutting test results (mm).

Point	As	Bs	Cs	Ds	Es	Fs	Gs	Hs
Diameter	140.80	140.60	140.26	140.10	140.58	140.67	140.31	140.63
Vertex	133.80	133.70	134.00	134.20	133.68	133.77	134.21	134.29
Height	11.75	11.40	10.05	10.45	11.50	11.40	10.95	10.92
Angle	19.5°	19.5°	19.6°	19.6°	18.2°	18.2°	18.0°	19.6°

. The upper bevel diameter variation range is 140.10 mm to 140.80 mm and the amplitude is 0.70 mm, while the K-shaped apex is 133.70 mm to 134.20 mm with amplitude 0.50 mm. Because of the obvious vibration marks at points C_s and D_s, the overall change range is 10.92~11.75 mm, with an amplitude of 1.70 mm. After removing points C_s and D_s, the overall change range is 10.92~11.75 mm, and the amplitude decreases to 0.83 mm. The bevel angle variation range is 18.0~19.6°, and the angle change of the entire trajectory is 1.6°. It can be concluded from the experimental results that the machining method proposed in this paper for complex bevel cutting on curved surfaces is effective and can be further applied in the shipbuilding industry. In addition, due to the lack of rigidity of the robot, the waterjet can be unstable during the cutting process, resulting in an increase in the trajectory error and surface roughness. In subsequent research, the optimized trajectory can be developed to avoid sharp turns and reduce vibration.

In summary, abrasive waterjet bevel cutting technology has significant advantages and broad development prospects in the manufacturing of ship parts. The process proposed in this paper will be combined with CNC technology in the future to achieve automated processing, and improve production efficiency and processing consistency.

6. Conclusions

In this paper, the complex bevel structures specified on curved surfaces of high-strength steel have been successfully machined by AWJC within the quality requirements. The proposed bevel cutting method has been applied in the shipbuilding industry and greatly facilitated the operators. According to the detailed experimental results, the following conclusions can be obtained:

(1)

The four reference points are measured by the 3D camera, and the weighted singular value decomposition algorithm is adopted to obtain the processing coordinate system of the workpiece. The maximum position error of reference points is 0.89 mm;

(2)

The key points on the cutting path are measured by the 3D camera, and the maximum measurement error is 0.47 mm;

(3)

The machined bevel structures by AWJC can meet the technical requirements with 0.9 mm hole shape deviation, 1.7 mm bevel depth deviation, and 2.2° bevel direction error.