Digital Simulation of Coupled Dynamic Characteristics of Open Rotor and Dynamic Balancing Test Research
Abstract
1. Introduction
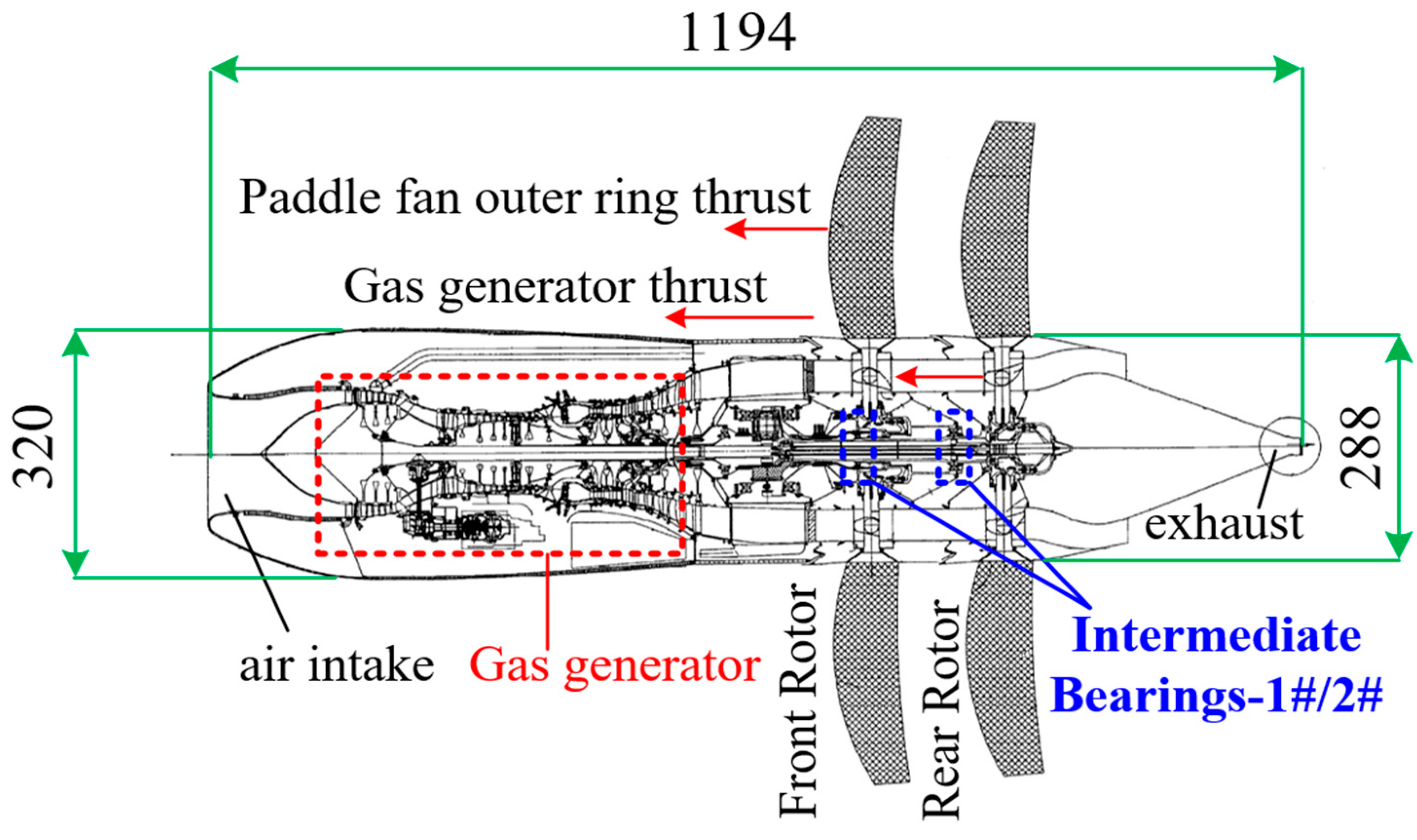
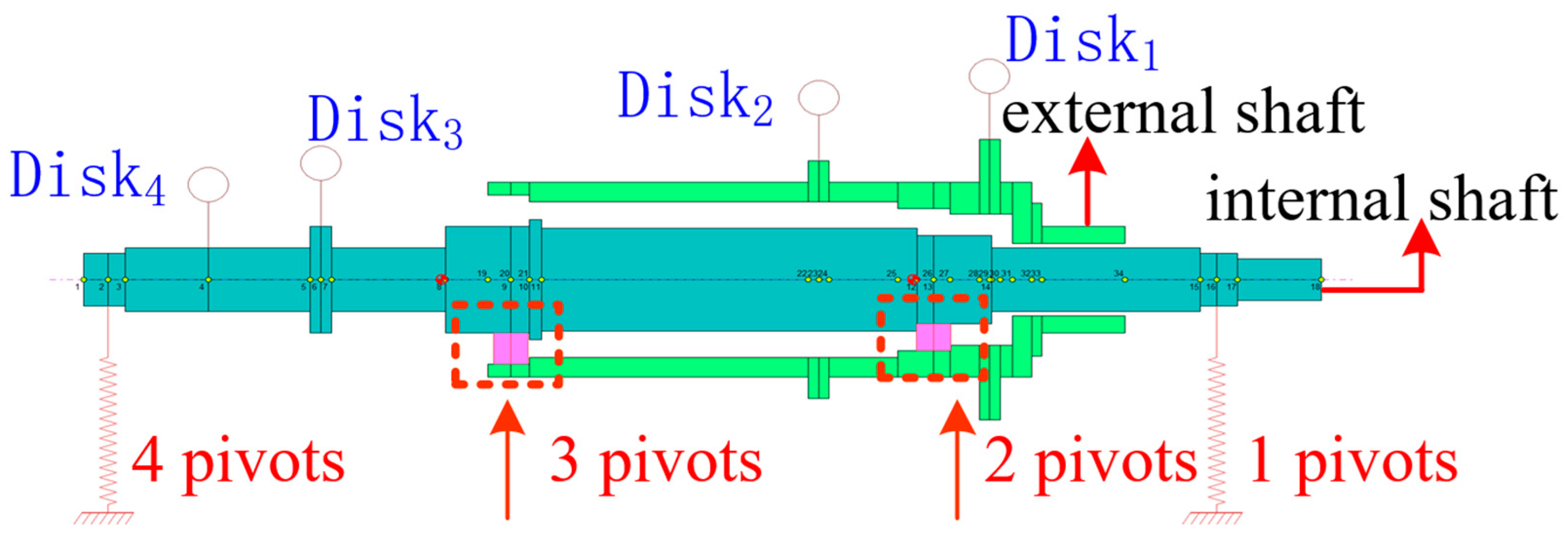
2. Simulation of Double-Row Open Rotor Structure
3. Simulation of Open Rotor Coupling Dynamics
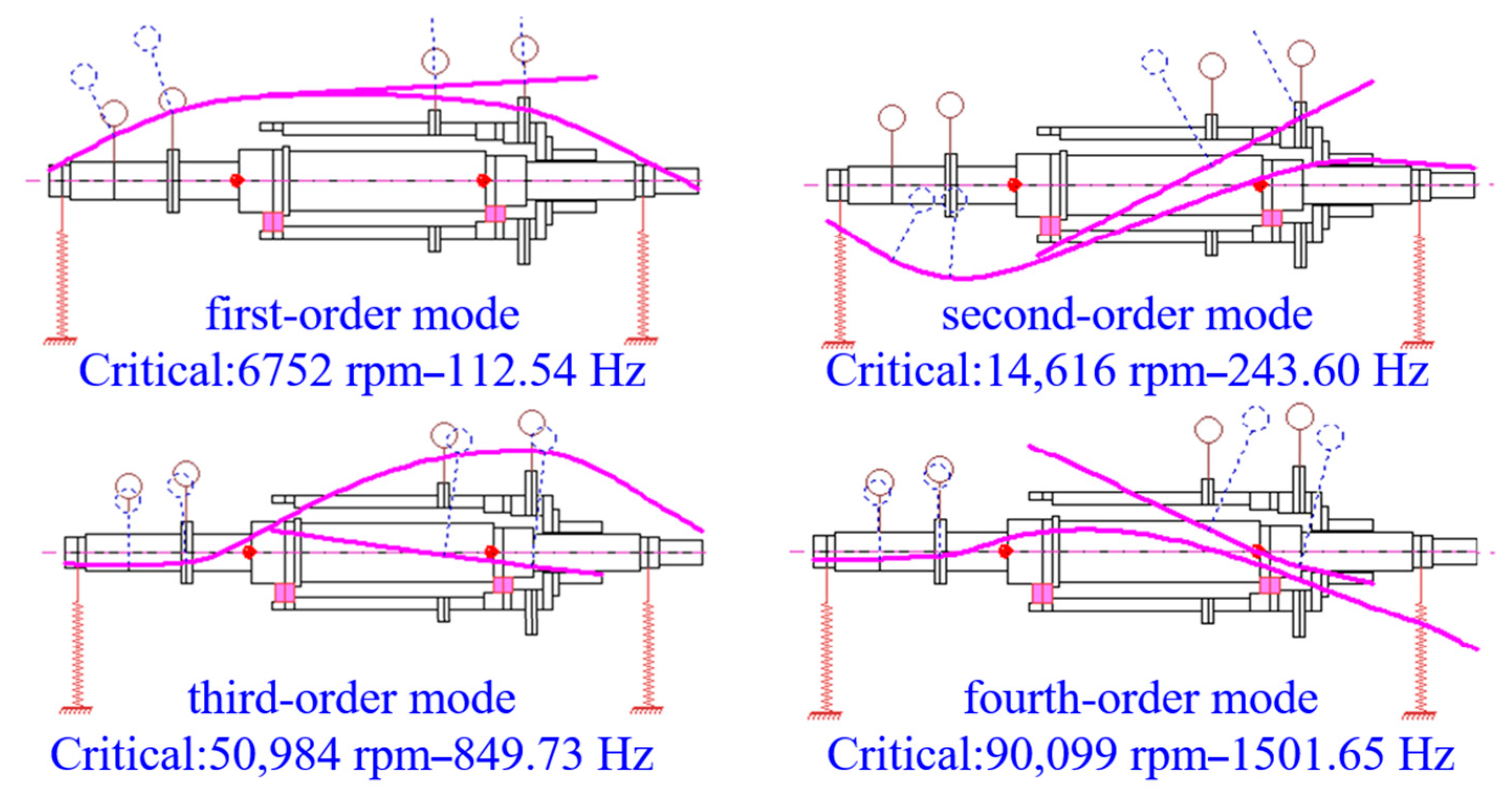
3.1. Twin Rotor Modal Simulation
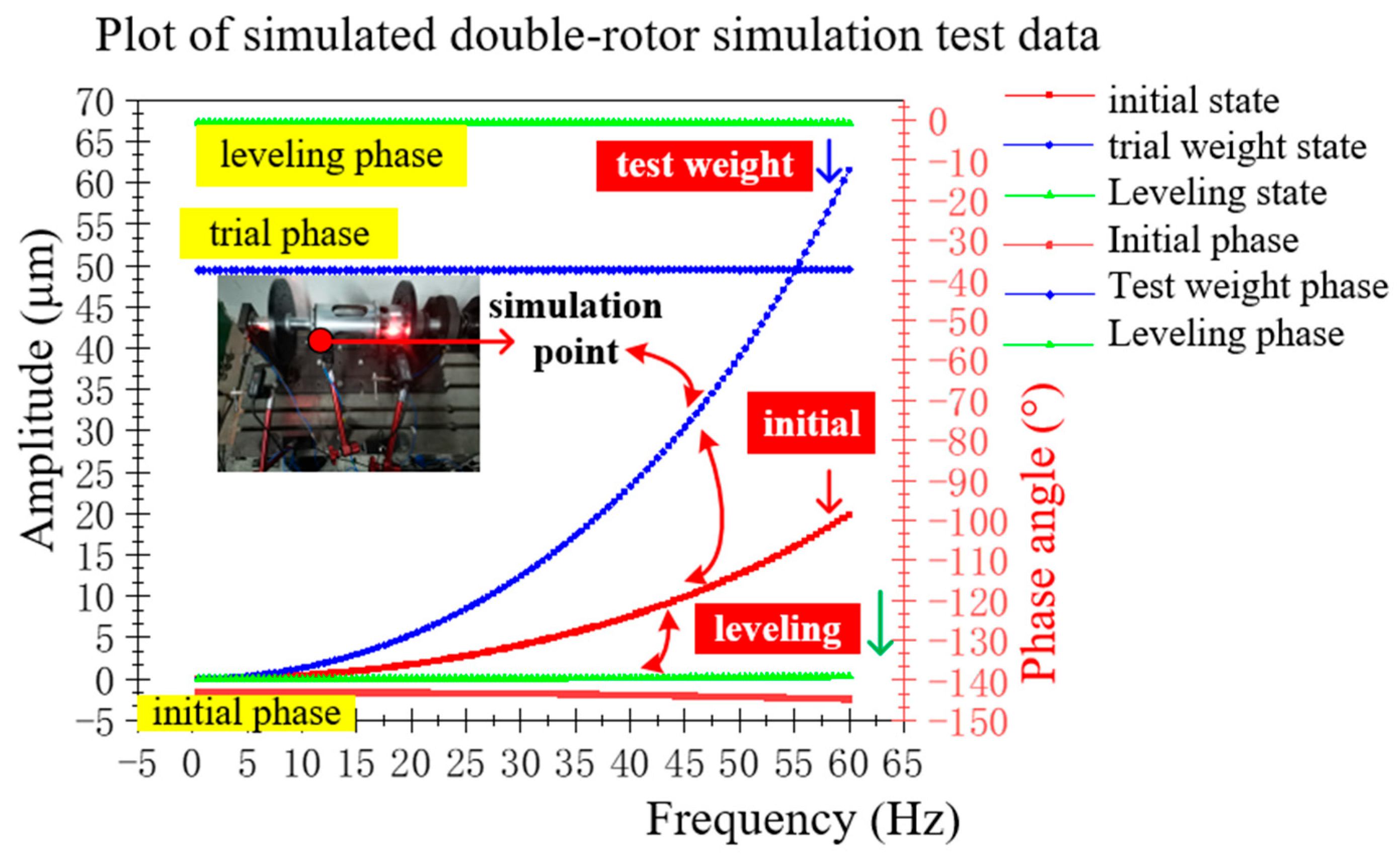
3.2. Twin Rotor Steady-State Response Sweep
4. Coupled Vibration Mechanism of Counter-Rotating Double Rotor
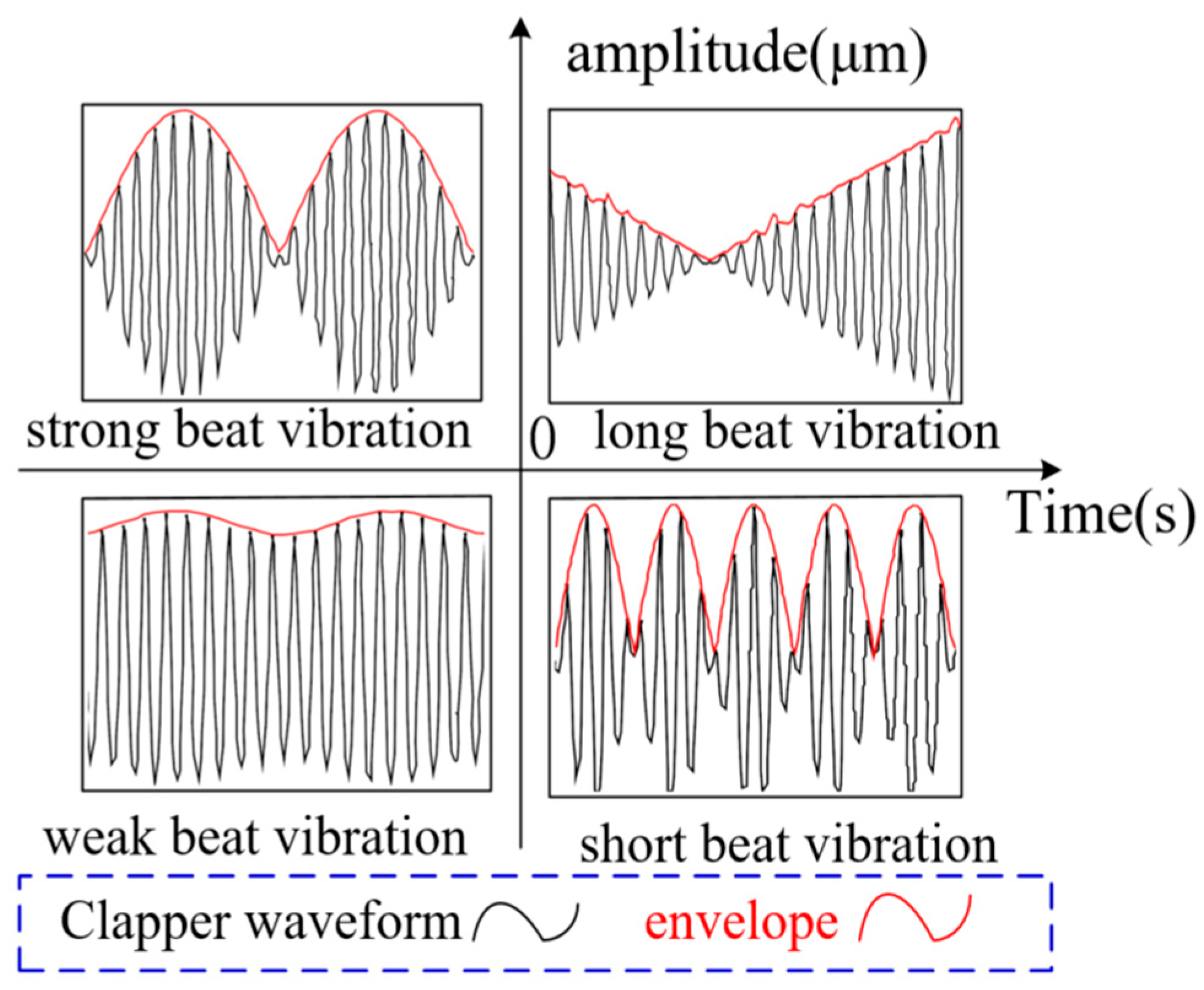
4.1. Theory and Properties of Pattern Oscillation
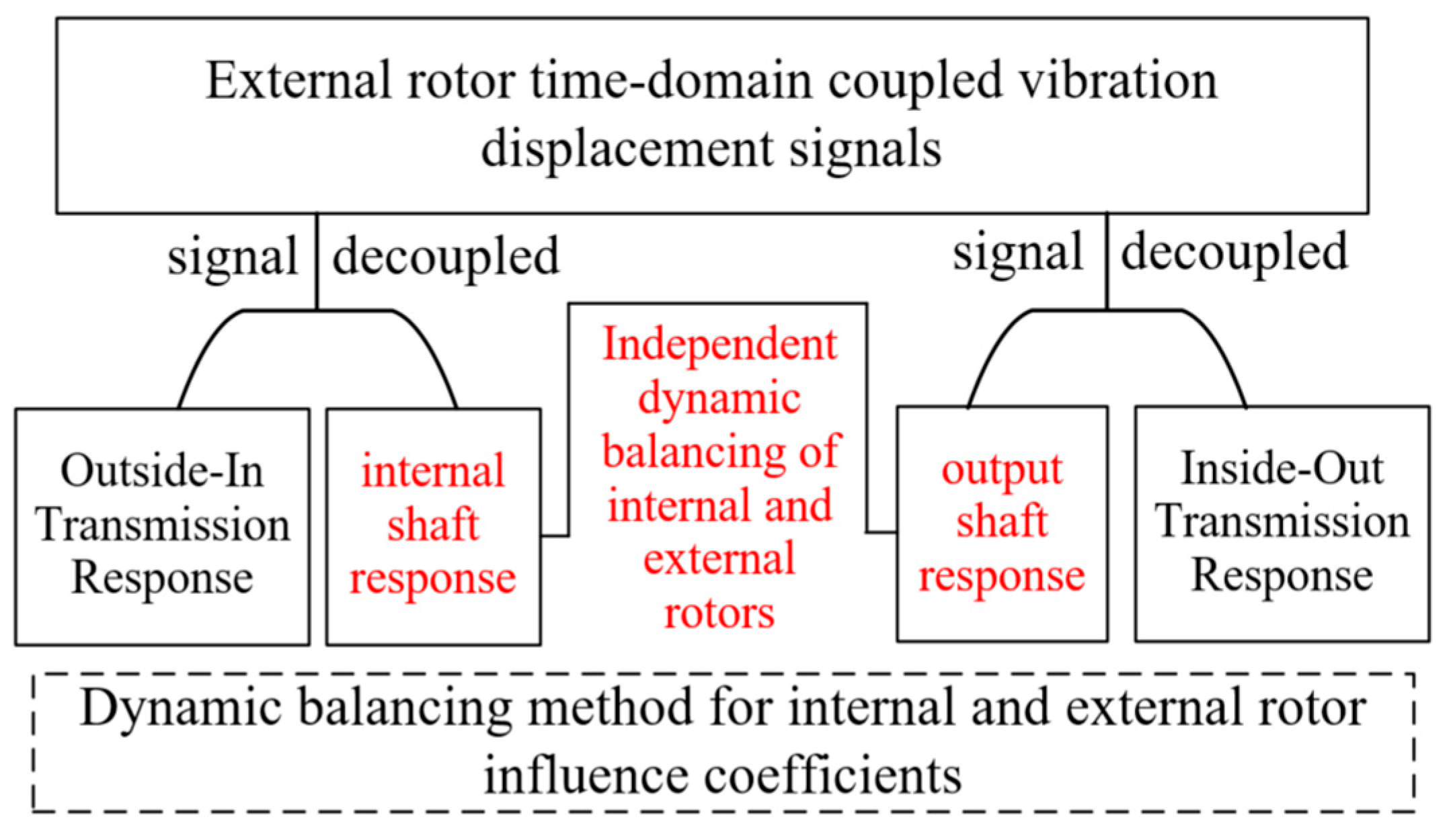
4.2. Coupled Vibration Identification and Decoupling
4.2.1. Coupling Mechanism and Identification of Double Rotor Vibration Signals
4.2.2. Separation and Decoupling of Two-Rotor Coupled Vibration Signals
5. Counter-Rotating Double Rotor Dynamic Balance Test
5.1. Open Rotor Simulation Test System
5.2. Simulated Double Rotor Take-Off Speed Condition Dynamic Balancing Test
5.3. Simulated Dual-Rotor Cruise Speed Condition Dynamic Balancing Test
5.4. Open Rotor Simulation Tester for High-Speed Dynamic Balancing Test
6. Conclusions
- Aiming at the typical dual-rotor structure mechanical system of aerospace and civil equipment, the dual-rotor coupled vibration separation algorithm can accurately identify the respective unbalance response information of the inner and outer rotors (a sensor can obtain the vibration information of two rotors), and make technical reserves for the subsequent dual-rotor dynamic balancing;
- Under the premise of ensuring the accuracy of the model, the calculation results of the finite element twin model in the virtual space can be used to guide the physical reality of the structure of the on-site test, the simulation modeling calculations are basically the same as the results of the real test, and the simulation results of the twin-rotor finite element modeling can be used as a theoretical basis for the actual structural test;
- Based on the independently designed and constructed simulated dual-rotor test bench, dynamic balancing tests with coaxial counter-rotating dual-plane dual influence coefficients were carried out. Beneficial vibration reduction effects were achieved for both the inner and outer rotors under three typical working conditions, further proving the accuracy of the identification algorithm, which meets the requirements for dynamic balancing accuracy of the equipment and stable operation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, C.Z. Open Rotor Engines; Aviation Industry Press: Beijing, China, 2016. [Google Scholar]
- Zhang, Z.X.; Jing, T.; Chen, A.P. Development and research on portable micro-velocity difference double rotor system intelligent whole machine dynamic balancer. J. Vib. Eng. 2003, 16, 62–66. [Google Scholar]
- Zhang, Z.X.; Jin, Z.J.; He, S.Z. Research on dynamic balancing method of coaxial micro-speed differential double rotor system. J. Mech. Eng. 2004, 40, 40–44. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, Y.F.; Jiang, Z.N.; Feng, K. Evaluation of vibration coupling effects in a two-rotor system with intermediate bearings. J. Aeronaut. 2021, 42, 401–412. [Google Scholar]
- Feng, G.Q.; Zhou, B.Z.; Luo, G.H. An analytical approach to the vibration characteristics of a counter-rotating twin-rotor engine. Trans. Nanjing Univ. Aeronaut. Astronaut. 2012, 29, 33–39. [Google Scholar]
- Wang, Q.H.; Zhou, L.; Wang, Z.X. Pneumatic design methodology for counter-rotating open rotors. J. Aerodyn. 2024, 39, 138–149. [Google Scholar]
- Chen, Z.W.; Jiang, Y.B.; Zhao, Y.; Lu, X.Y.; Tong, F. Wind tunnel test techniques for counter-rotating propeller aerodynamic and aerodynamic noise. J. Aerodyn. 2022, 1–10. [Google Scholar] [CrossRef]
- Song, Z.Y.; Hong, J.; Wang, Y.F.; Ma, Y.H. Vibration coupling mechanism and response characteristics of a common support-twin rotor system. J. Aerodyn. 2023, 38, 11. [Google Scholar] [CrossRef]
- Wei, G.S. Research on the Analytical Method of Coupled Dynamics of Internal and External Twin Rotor System of Aircraft Development. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Tang, Z.H.; Mi, D.; Lu, Y.; Long, L.; Tang, Y. Study on the coupled vibration characteristics of bearing common cavity-twin rotor system. Adv. Technol. 2022, 43, 246–255. [Google Scholar]
- Qu, X.X. Research on Blind Separation Technique of Rotor Coupling Fault Vibration Signals. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar]
- Miao, H.; Wang, K.M.; Zhai, X.; Mu, P. Finite element analysis of the dynamic characteristics of a counter-rotating twin-rotor system. J. Shenyang Univ. Aeronaut. Astronaut. 2011, 28, 27–32. [Google Scholar]
- Zhang, D.Y.; Liu, Y.H.; Hong, J.; Ma, Y.H. Dynamic modeling and vibration characterization of aero-engine complete machine. Propuls. Technol. 2015, 36, 768–773. [Google Scholar]
- Ouyang, Y.F.; Ming, Y. Vibration characterization of aero-engine twin-rotor system with touch-and-go faults. Mech. Eng. 2016, 11, 65–71. [Google Scholar]
- Zhang, T.C. Bending-Torsion Coupling Vibration Analysis of Aero-Engine Twin-Rotor System Under Touch-and-Go Failure. Master’s Thesis, Tianjin University, Tianjin, China, 2018. [Google Scholar]
- Wang, F.; Luo, G.H.; Cui, H.T. Effect of speed ratio on nonlinear dynamic characteristics of a two-rotor system. J. Nanjing Univ. Aeronaut. Astronaut. 2018, 50, 367–374. [Google Scholar]
- Long, L.; Li, J.; Zhao, Y.M.; Wang, D. Coupled vibration characteristics of the power driving shaft-casing system. Sci. Technol. Eng. 2021, 21, 14422–14427. [Google Scholar]
- Zhong, W.C.; Wang, Y.; Song, J.; Zhang, H.; Song, J. A novel correction method for aero-engine mathematical models. J. Aerodyn. 2023, 38, 2776–2784. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D.; Xu, H. Dynamic characteristics analysis of a dual-rotor system with inter-shaft bearing. J. Aerosp. Eng. 2019, 233, 1147–1158. [Google Scholar] [CrossRef]
- Hai, P.M.; Bonello, P. An impulsive receptance technique for the time domain computation of the vibration of a whole aero-engine model with nonlinear bearings. J. Sound Vib. 2008, 318, 592–605. [Google Scholar] [CrossRef]
- Guskov, M.; Sinou, J.-J.; Thouverez, F. Multi-dimensional harmonic balance applied to rotor dynamics. Mech. Res. Commun. 2008, 35, 537–545. [Google Scholar] [CrossRef]
- Sun, C.; Chen, Y.; Hou, L. Steady-state response characteristics of a dual-rotor system induced by rub-impact. Nonlinear Dyn. 2016, 86, 91–105. [Google Scholar] [CrossRef]
- Hou, L.; Chen, Y.; Fu, Y.; Chen, H.; Lu, Z.; Liu, Z. Application of the HB–AFT method to the primary resonance analysis of a dual-rotor system. Nonlinear Dyn. 2017, 88, 2531–2551. [Google Scholar] [CrossRef]
- Pi, J.; Chang, J.Z.; Liu, G.C. Analysis of aero-engine vibration signals. J. Syst. Simul. 2020, 32, 525–532. [Google Scholar]
- Zhao, Y.H.; Zhang, H.Y.; Shi, X.Z. An effective vibration signal separation algorithm. Noise Vib. Control. 2002, 22, 13–16. [Google Scholar]
- Feng, G.Q.; Zhu, X.G. Vibration characteristics of rotor systems with initial bending. Aeroengine 2003, 1, 20–22. [Google Scholar]
- Chen, M.L.; Li, S.M.; Wen, W.D.; Liu, J.Y.; Du, J.J. Multi-source beat vibration analysis methods and tests. Vib. Test Diagn. 2011, 31, 202–206. [Google Scholar]
- Bian, B.; Liu, S.Q.; He, S.Y.; Li, D.G. Analysis of beat vibration phenomenon in the electric spindle of magnetic levitation bearing grinding machine. J. Shandong Univ. 2012, 42, 133–142. [Google Scholar]
- Zhao, Q.; Jia, M.P.; Huang, Y.G.; Fang, K.R. Analysis of beat frequency in rotating machine vibration. J. Southeast Univ. 2003, 33, 312–315. [Google Scholar]
- Ding, X.F.; Liao, M.F.; Cao, H.; Dong, C. Analysis of vibration fluctuation problem caused by multi-source beat vibration in aero-engine. In Proceedings of the Abstracts of the 14th National Vibration Theory and Application Conference, Tianjin, China, 22–24 October 2021; Chinese Society of Vibration Engineering: Nanjing, China, 2021; p. 66. [Google Scholar] [CrossRef]
- Xiao, N.; Liu, K. Numerical simulation calculation and test of transient heat transfer in aero-engine heating. China Sci. Technol. Inf. 2022, 1, 38–40. [Google Scholar]
- Song, X.P.; Liao, M.F. Separation test technique for vibration signals of twin rotor aero-engine. Mech. Sci. Technol. 2006, 25, 487–490. [Google Scholar]
- Liu, X.F. Research on Vibration Signal Separation Technology of Twin Rotor Aero-Engine. Master’s Thesis, Shenyang Institute of Aeronautics and Astronautics, Shenyang, China, 2009. [Google Scholar]
- Bai, J.F. Modern Signal Processing Methods and Their Application in Engine Vibration Signal Analysis. Master’s Thesis, Northwestern Polytechnical University, Xi’an, China, 2004. [Google Scholar]
- Han, J.; Gao, D.P.; Hu, X.; Chen, G.J. Beat vibration analysis of aero-engine twin rotor system. J. Aeronaut. 2007, 28, 1369–1373. [Google Scholar]
- Han, J.; Gao, D.P.; Hu, X. A model-based fault diagnosis method for double rotor imbalance. J. Aerosp. Dyn. 2008, 23, 932–938. [Google Scholar]
- Luciano, P.P.; Geraldo, C.; Joao, C.M. Simplified procedure for vibration analysis and dynamic balancing in mechanical systems with beats frequency. Measurement 2021, 174, 109056. [Google Scholar]
- Vencl, A.; Gašić, V.; Stojanović, B. Fault tree analysis of most common rolling bearing tribological failures. IOP Conf. Ser. Mater. Sci. Eng. 2017, 174, 012048. [Google Scholar] [CrossRef]
- Philip, B.; Pham, M.H. A receptance harmonic balance technique for the computation of the vibration of a whole aero-engine model with nonlinear bearings. J. Sound Vib. 2009, 324, 221–242. [Google Scholar]
- Ronny, R.; Volker, D.; Peter, M.; Carsten, S.; Adrian, R. Inverse imbalance reconstruction in rotordynamics. J. Appl. Math. Mech. 2010, 86, 385–399. [Google Scholar]
- Sembiring, A.; Lubis, A. Numerical Study for Comparison of Pseudo Modal and Direct Method in Predicting Critical Speed of Coaxial Dual Rotor System. Mater. Sci. Eng. 2020, 990, 012028. [Google Scholar] [CrossRef]
- An, S.L.; Jin, W.H.; Dong, H.C. Coupled lateral and torsional vibration characteristics of a speed increasing geared rotor-bearing system. J. Sound Vib. 2003, 263, 725–742. [Google Scholar]
- Nandi, A. Reduction of finite element equations for a rotor model on non-isotropic spring support in a rotating frame. Finite Elem. Anal. Des. 2004, 40, 935–952. [Google Scholar] [CrossRef]
- Ferraris, G.; Maisonneuve, V.; Lalanne, M. Prediction of The Dynamic Behavior of Non-Symmetric Coaxial Co-Or Counter-Rotating Rotors. J. Sound Vib. 1996, 195, 649–666. [Google Scholar] [CrossRef]
- Su, S.K.; Lv, L. ANSYS Finite Element Structural Analysis and Example Analysis; Chemical Industry Press: Beijing, China, 2014. [Google Scholar]
- Yang, J.; Zhou, B.T. Study on the vibration signal separation method of micro-velocity difference double rotor system. China Mech. Eng. 2002, 8, 86–89+6. [Google Scholar]
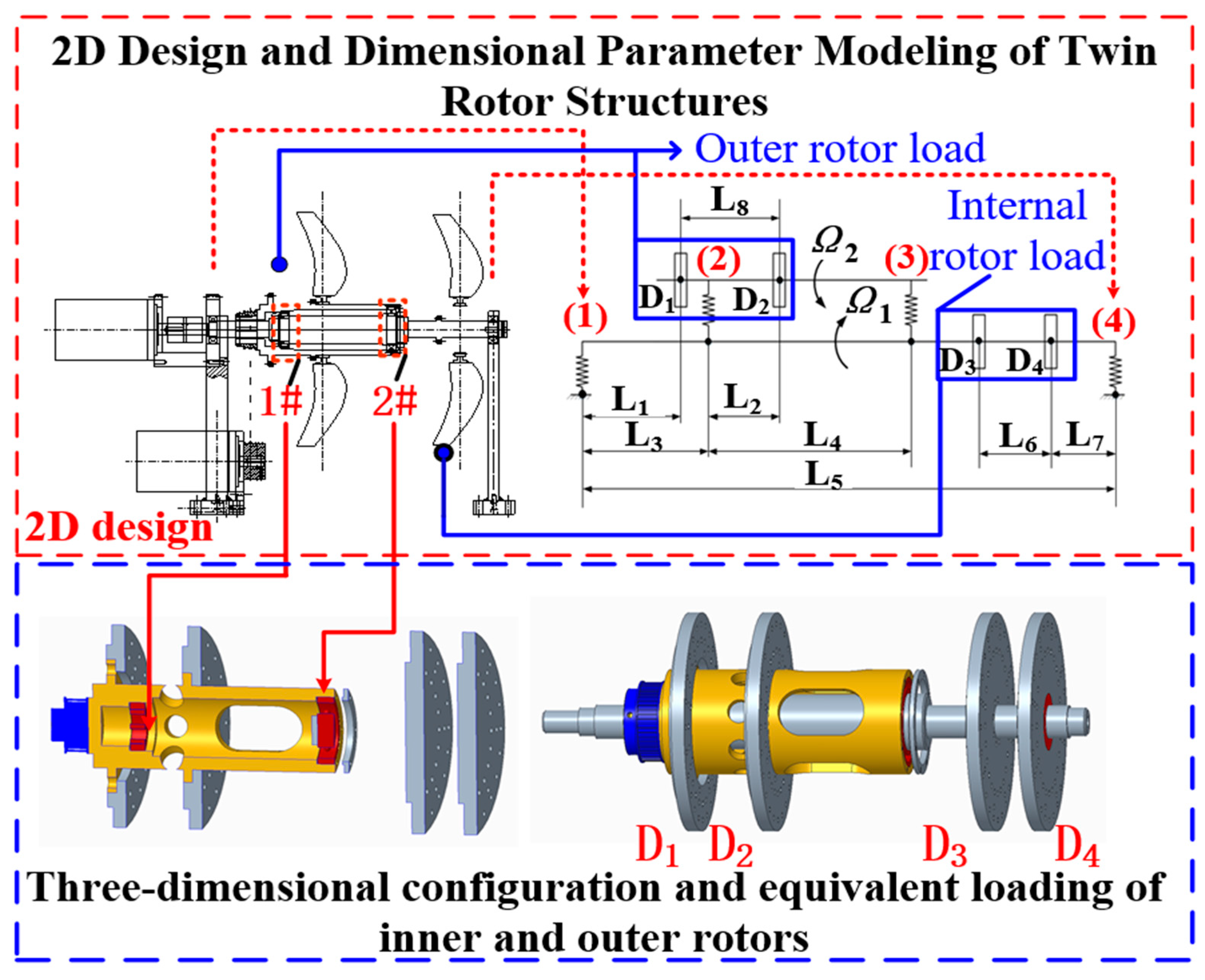
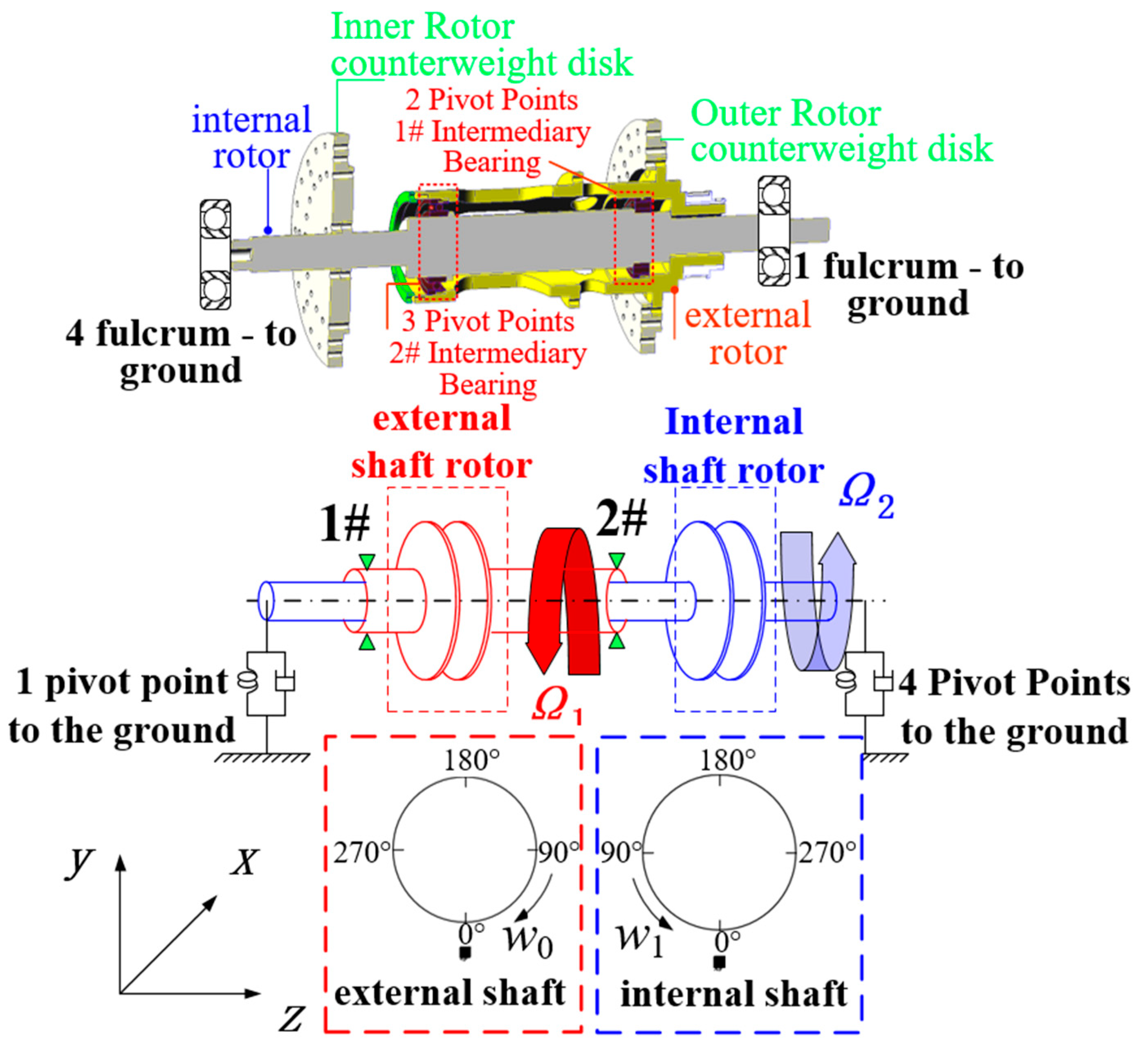




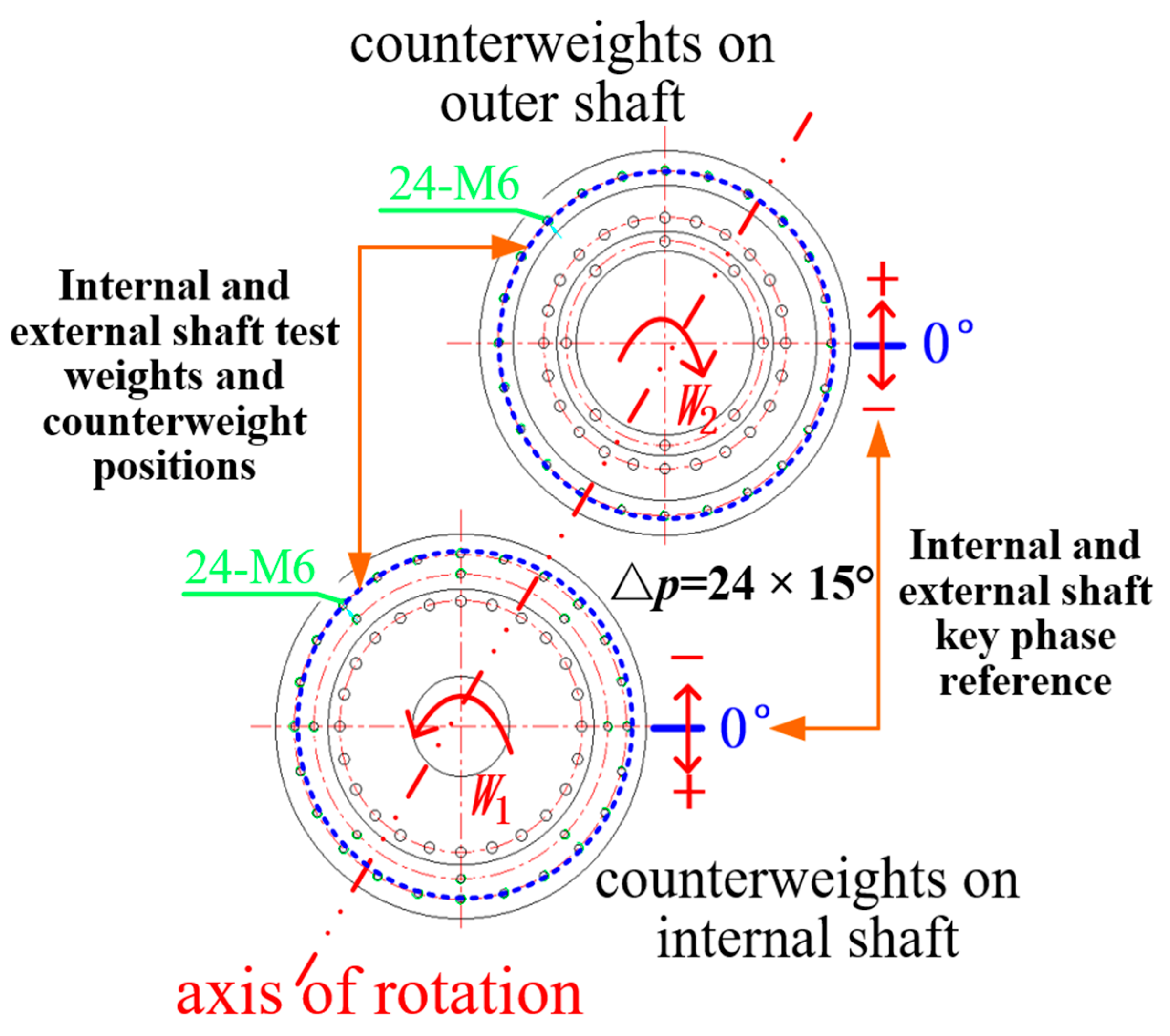
| Parameter Meaning | Symbolic | Dimensions/(mm) |
|---|---|---|
| 1 fulcrum-D1 | L1 | 119 |
| 2 fulcrum-D2 | L2 | 63 |
| 1 fulcrum- 2 fulcrum | L3 | 138 |
| 2 fulcrum- 3 fulcrum | L4 | 202 |
| 1 fulcrum- 4 fulcrum | L5 | 536 |
| D3–D4 | L6 | 56 |
| D4-4 fulcrum | L7 | 43 |
| D1–D2 | L8 | 82 |
| Pivot Stiffness | 1 Fulcrum | 2 Fulcrum | 3 Fulcrum | 4 Fulcrum |
|---|---|---|---|---|
| Kxx/(N·mm−1) | 1.00 × 104 | 2.00 × 105 | 2.00 × 105 | 1.00 × 104 |
| Kyy/(N·mm−1) | 1.00 × 104 | 2.00 × 105 | 2.00 × 105 | 1.00 × 104 |
| Disk Unit | Nodal Position | Disk Mass/kg | Diameter Inertia/(kg·m2) | Polar Moment of Inertia/(kg·m2) |
|---|---|---|---|---|
| Disk1 | 29 | 12.34 | 0.132 | 0.2572 |
| Disk2 | 23 | 1.31 | 0.005 | 0.0106 |
| Disk3 | 6 | 12.25 | 0.131 | 0.2548 |
| Disk4 | 4 | 1.69 | 0.005 | 0.0109 |
| Model Number | Probe Size | Range | Midpoint Voltage | Sensitivity | Power Supply Voltage |
|---|---|---|---|---|---|
| ZA-21 | 8 mm | 2 mm | −10 V | 8 mV/μm | −24 V |
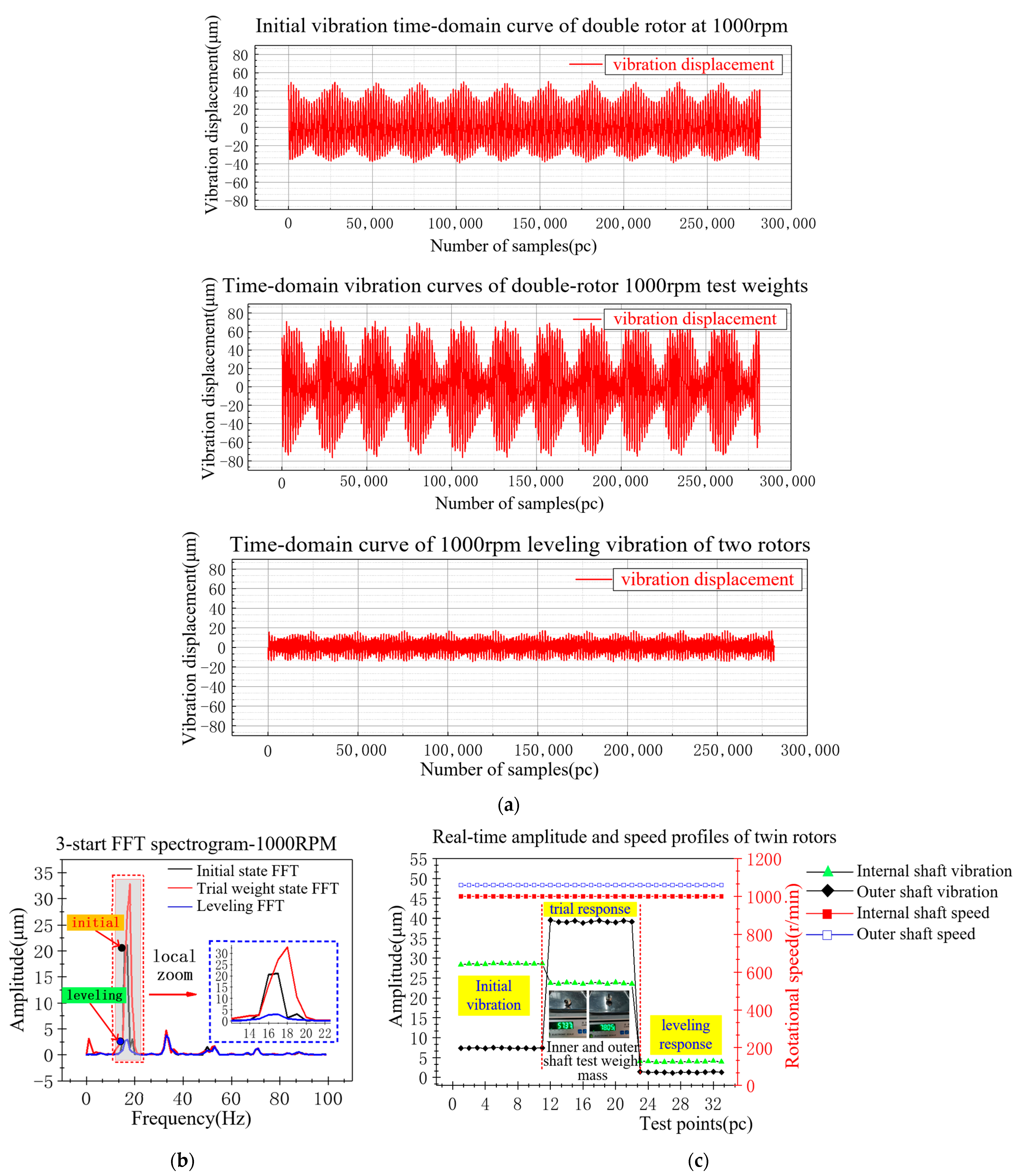
| 1000 rpm Experimental | Test Weights | Measured Rotor Response | Amplitude (μm) | Phase (°) | Impact Factor | Lag Angle | Counterweight Position |
|---|---|---|---|---|---|---|---|
| internal shaft | 57.67 g | initial response | 28.70 | 212.70 | 0.85 μm/g | 33.38 g | |
| ∠−45.00° | test weight response | 23.70 | 70.80 | ∠94.90° | ∠−62.00° | ||
| outer shaft | 67.57 g | initial response | 7.40 | 58.60 | 0.49 μm/g | 15.06 g | |
| ∠30.00° | test weight response | 39.30 | 31.40 | ∠−4.40° | ∠−117.00° | ||
| Internal Shaft: 1000 rpm Outer Shaft: 1060 rpm | Initial Vibration | Leveling Vibration | Percentage of Vibration Reduction |
|---|---|---|---|
| inner rotor | 28.52 μm | 3.93 μm | 86.20% |
| outer rotor | 7.47 μm | 1.26 μm | 83.10% |
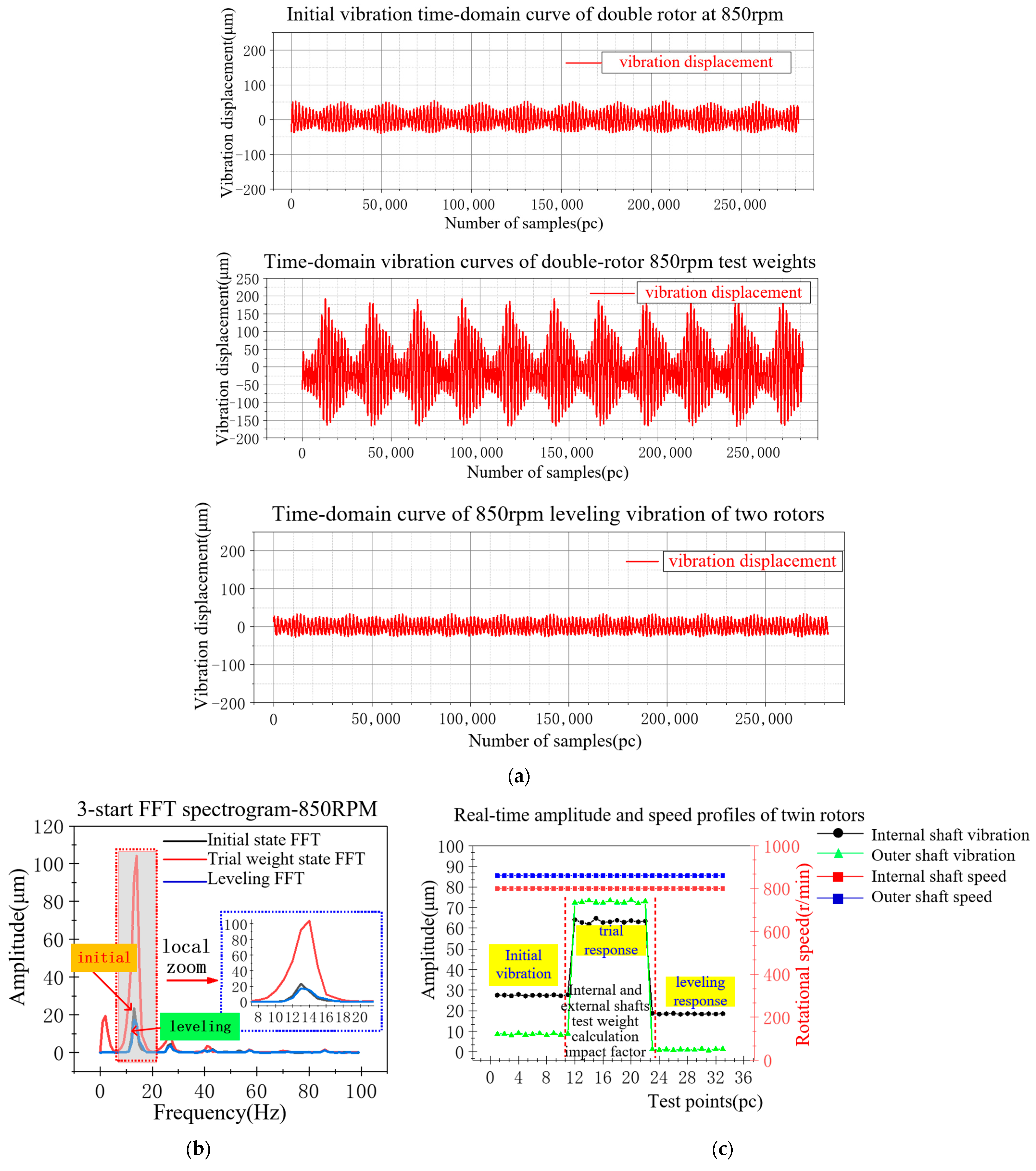
| 850 rpm Experimental | Test Weights | Measured Rotor Response | Amplitude (μm) | Phase (°) | Impact Factor | Lag Angle | Counterweight Position |
|---|---|---|---|---|---|---|---|
| internal shaft | 78.19 g | initial Response | 27.70 | 216.30 | 0.88 μm/g | 31.56 g | |
| ∠30.00° | test weight Response | 63.50 | 127.70 | ∠73.90° | ∠−38.00° | ||
| outer shaft | 108.18 g | initial Response | 8.90 | 60.90 | 0.61 μm/g | 15.08 g | |
| ∠45.00° | test weight Response | 72.50 | 35.20 | ∠−13.30° | ∠−106.00° | ||
| Internal Shaft: 800 rpm Outer Shaft: 860 rpm | Initial Vibration | Leveling Vibration | Percentage of Vibration Reduction |
|---|---|---|---|
| inner rotor | 27.53 μm | 18.21 μm | 33.90% |
| outer rotor | 8.57 μm | 1.46 μm | 82.90% |
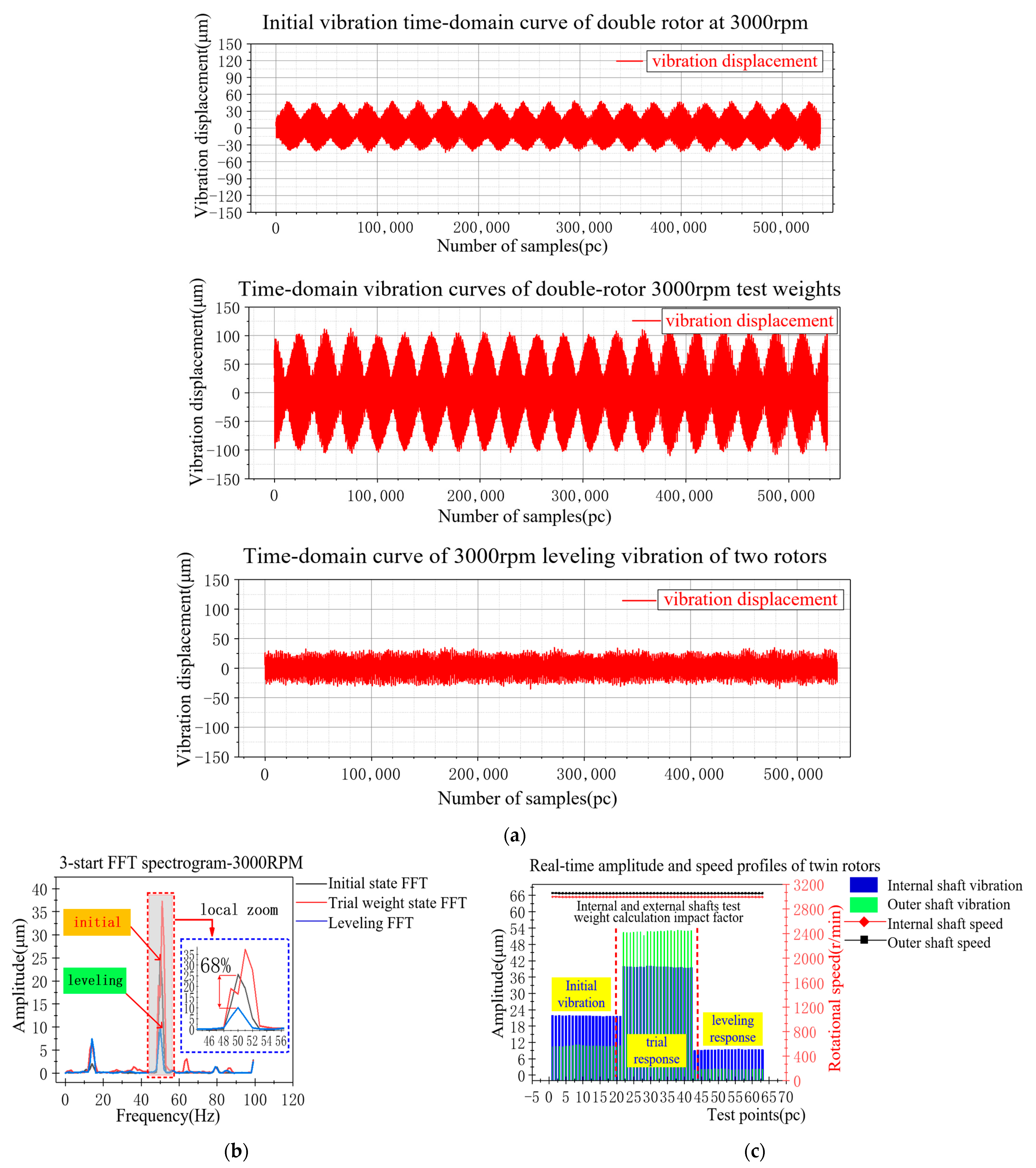
| 3000 rpm Experimental | Test Weights | Measured Rotor Response | Amplitude (μm) | Phase (°) | Impact Factor | Lag Angle | Counterweight Position |
|---|---|---|---|---|---|---|---|
| internal shaft | 17.06 g | initial response | 21.70 | 226.50 | 2.41 μm/g | 9.02 g | |
| ∠45.00° | test weight response | 39.20 | 147.30 | ∠70.90° | ∠−24.00° | ||
| outer shaft | 27.12 g | initial response | 11.10 | 72.10 | 1.59 μm/g | 6.94 g | |
| ∠30.00° | test weight response | 53.20 | 92.20 | ∠67.30° | ∠−175.00° | ||
| Internal Shaft: 3000 rpm Outer Shaft: 3060 rpm | Initial Vibration | Leveling Vibration | Percentage of Vibration Reduction |
|---|---|---|---|
| inner rotor | 21.94 μm | 9.47 μm | 56.80% |
| outer rotor | 10.78 μm | 1.94 μm | 82.10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Chen, L.; Long, Y.; Zhang, X. Digital Simulation of Coupled Dynamic Characteristics of Open Rotor and Dynamic Balancing Test Research. Machines 2024, 12, 391. https://doi.org/10.3390/machines12060391
Guo Y, Chen L, Long Y, Zhang X. Digital Simulation of Coupled Dynamic Characteristics of Open Rotor and Dynamic Balancing Test Research. Machines. 2024; 12(6):391. https://doi.org/10.3390/machines12060391
Chicago/Turabian StyleGuo, Yixiang, Lifang Chen, Yuda Long, and Xu Zhang. 2024. "Digital Simulation of Coupled Dynamic Characteristics of Open Rotor and Dynamic Balancing Test Research" Machines 12, no. 6: 391. https://doi.org/10.3390/machines12060391
APA StyleGuo, Y., Chen, L., Long, Y., & Zhang, X. (2024). Digital Simulation of Coupled Dynamic Characteristics of Open Rotor and Dynamic Balancing Test Research. Machines, 12(6), 391. https://doi.org/10.3390/machines12060391






