On the Integrity of Large-Scale Direct-Drive Wind Turbine Electrical Generator Structures: An Integrated Design Methodology for Optimisation, Considering Thermal Loads and Novel Techniques
Abstract
1. Introduction
2. Materials and Methods
- Quantify the production of heat within the generator and determine the consequences this has on the structural integrity of the rotor.
- Incorporate and evaluate the effectiveness of heat mitigation devices.
- Produce a rotor structure optimised according to the current understanding of generator loads using innovative techniques.
- Quantify the financial and environmental impacts of producing the optimised rotor.
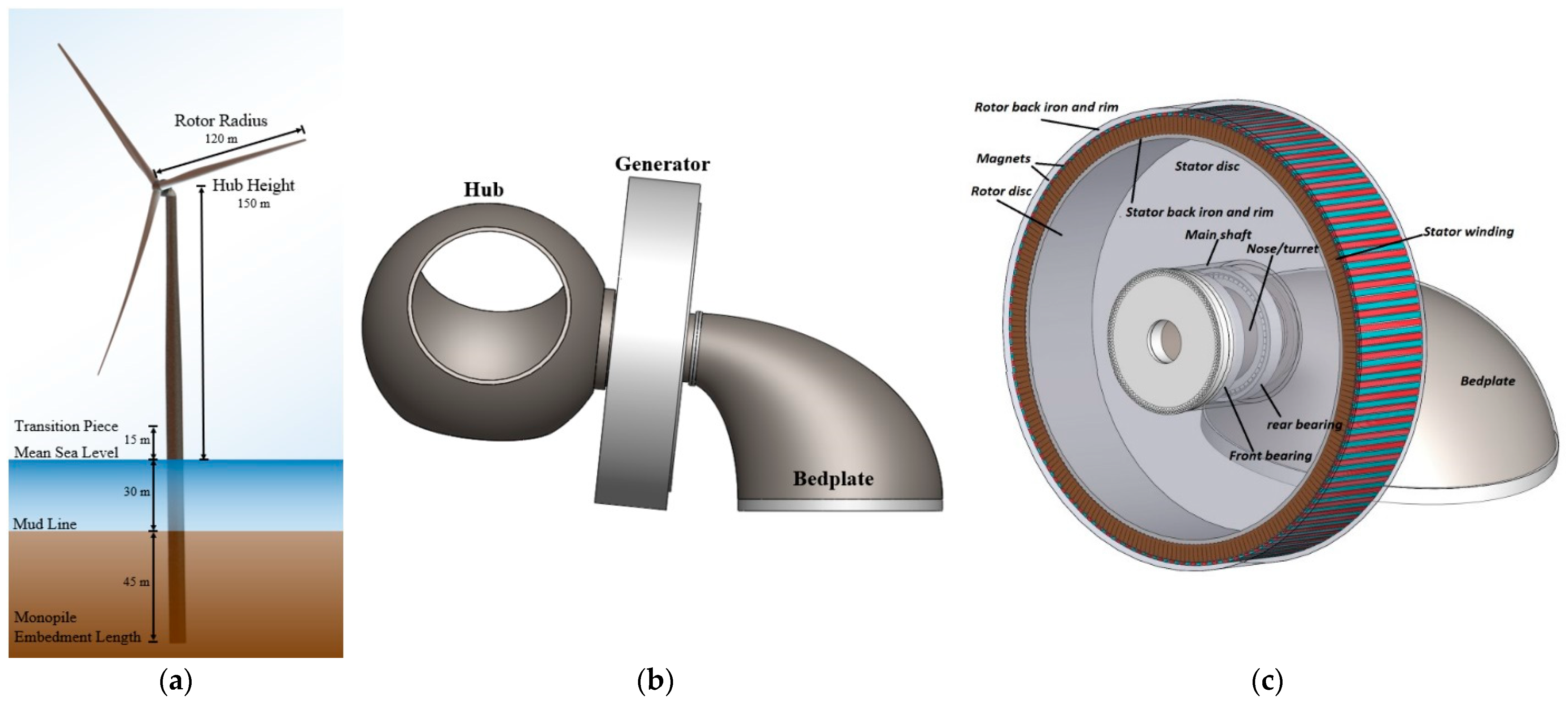
2.1. Direct-Drive Generator Operation
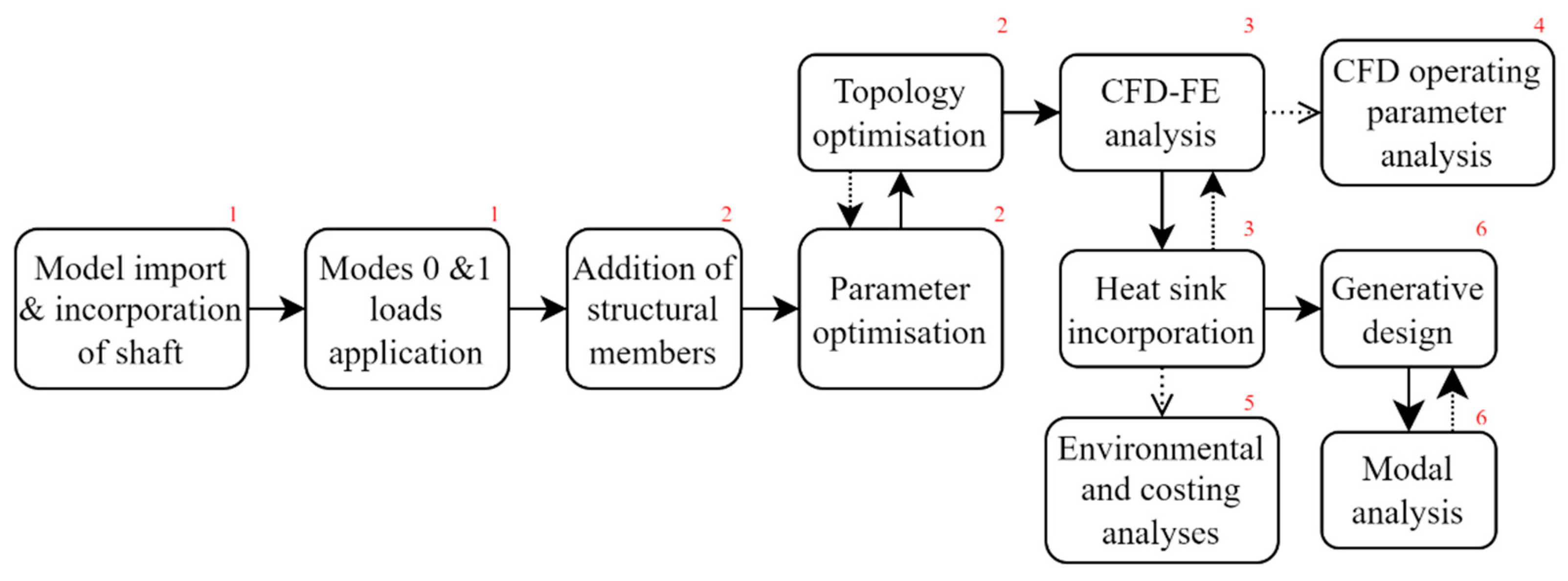
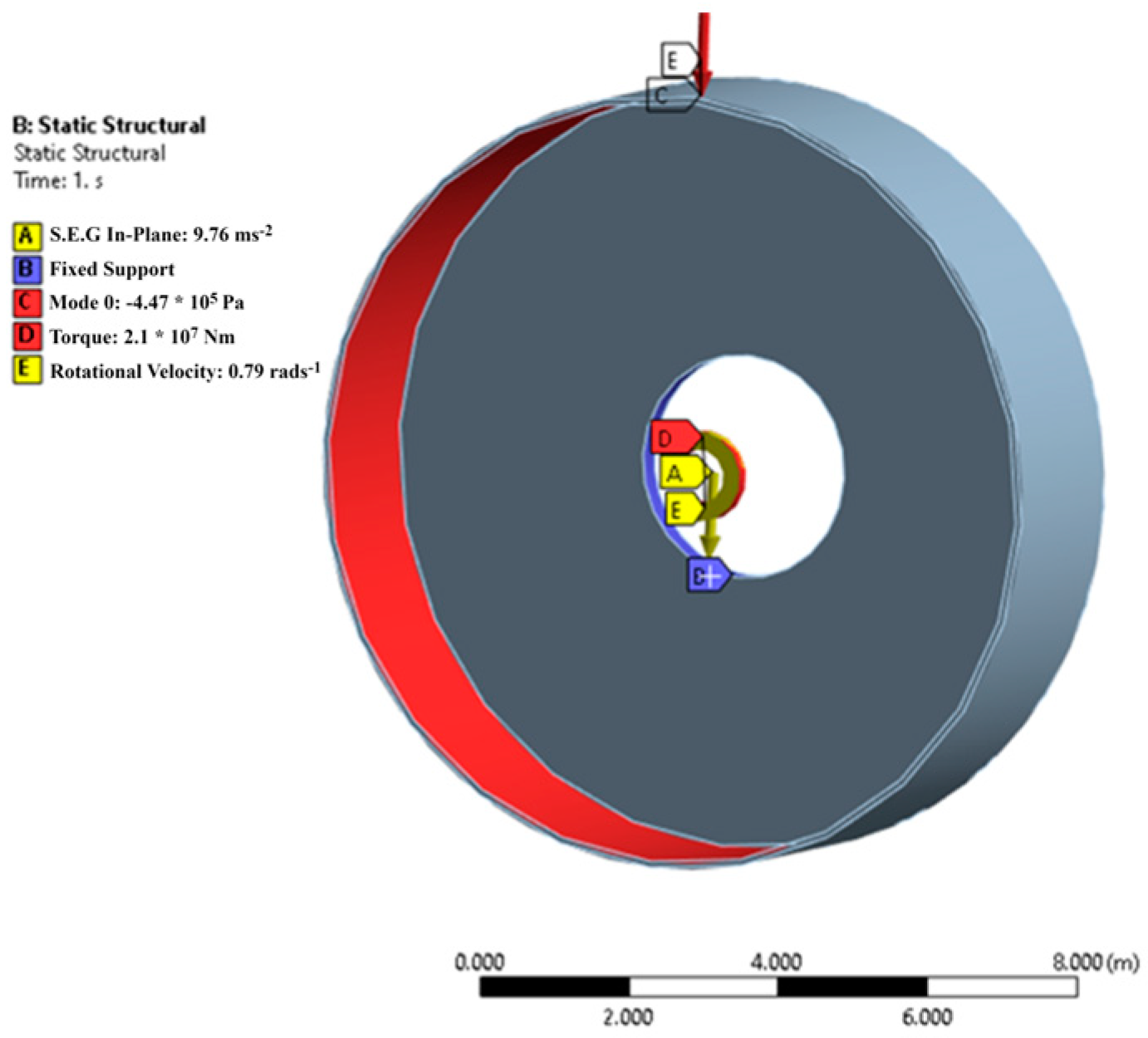
2.2. Facilitation of Simulation, Optimisation, and Performance Analysis
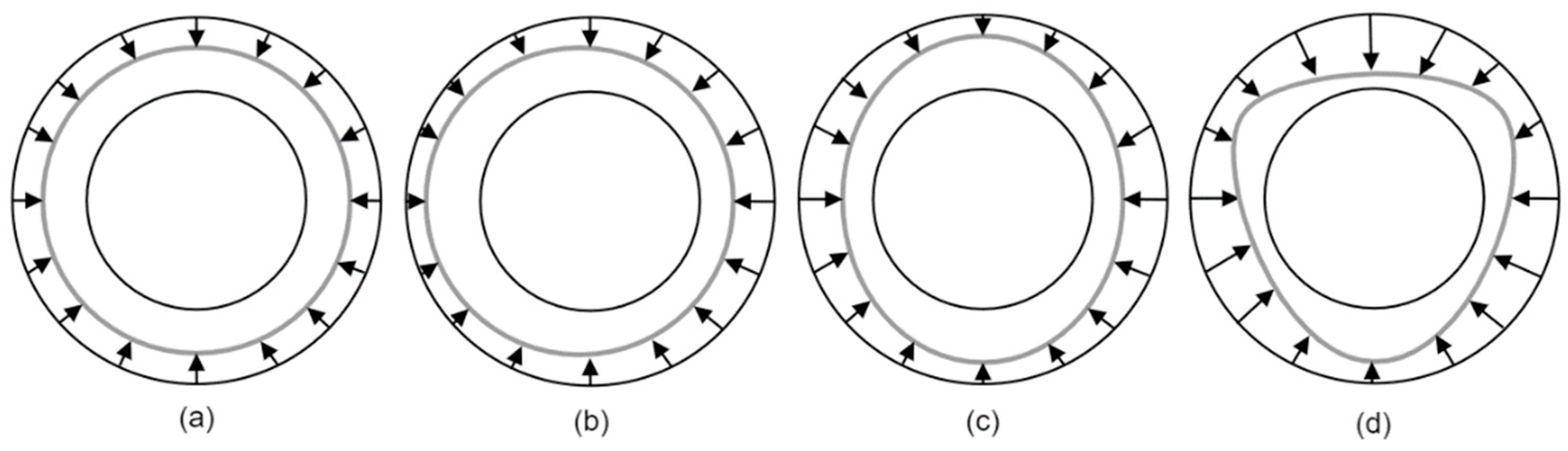
2.2.1. Mode 0
2.2.2. Mode 1
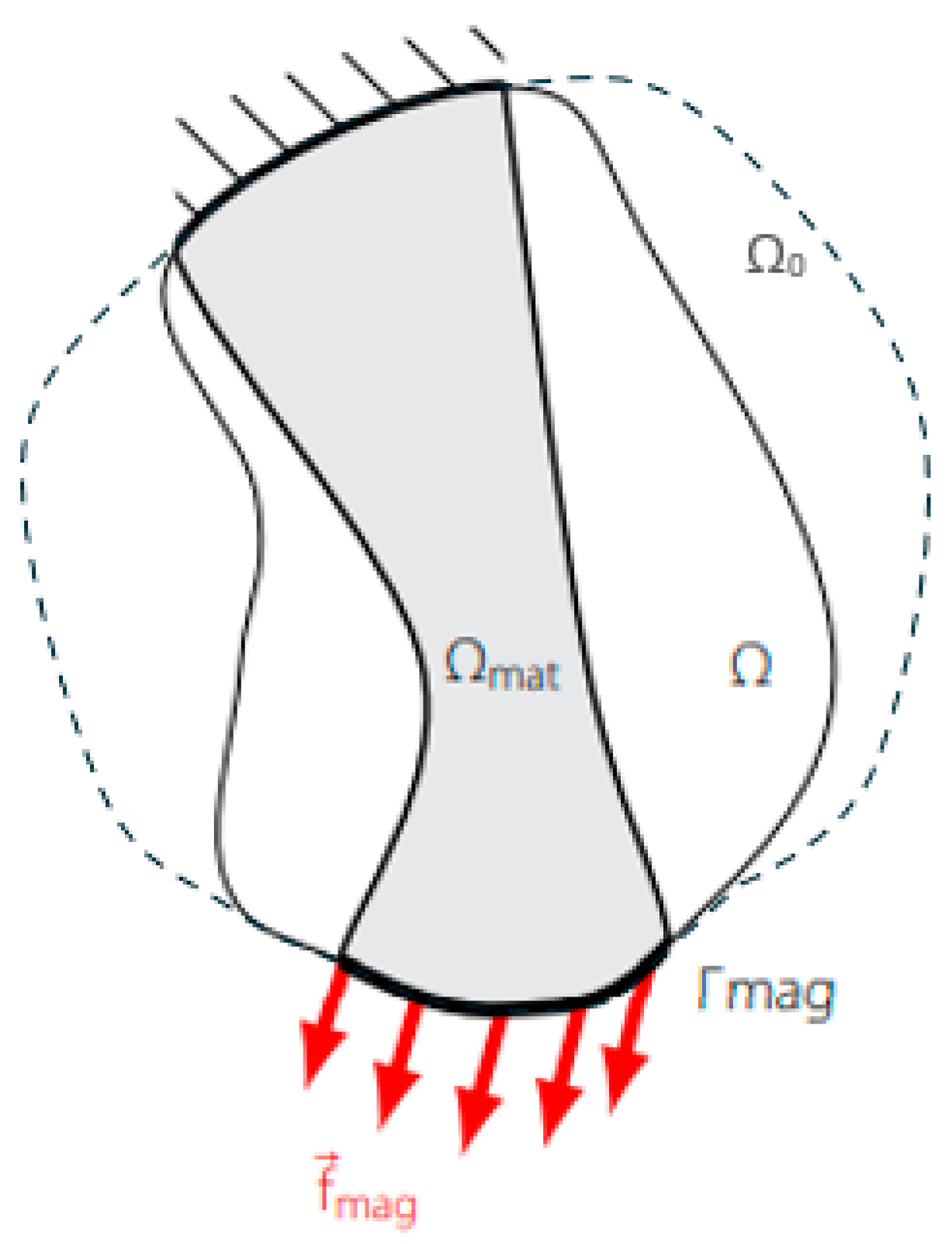
2.3. Structural Optimisation Process
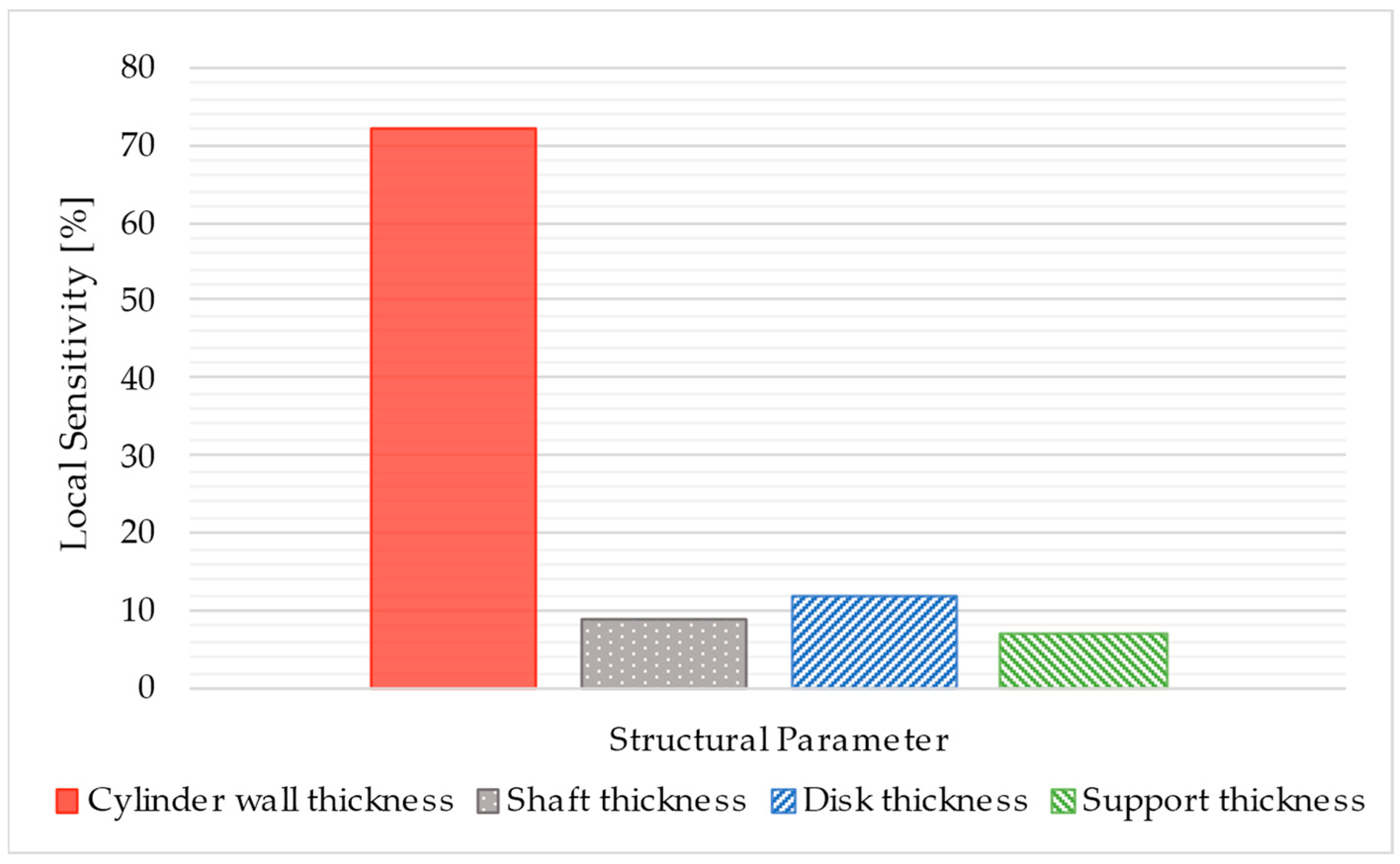
2.3.1. Parameter Optimisation
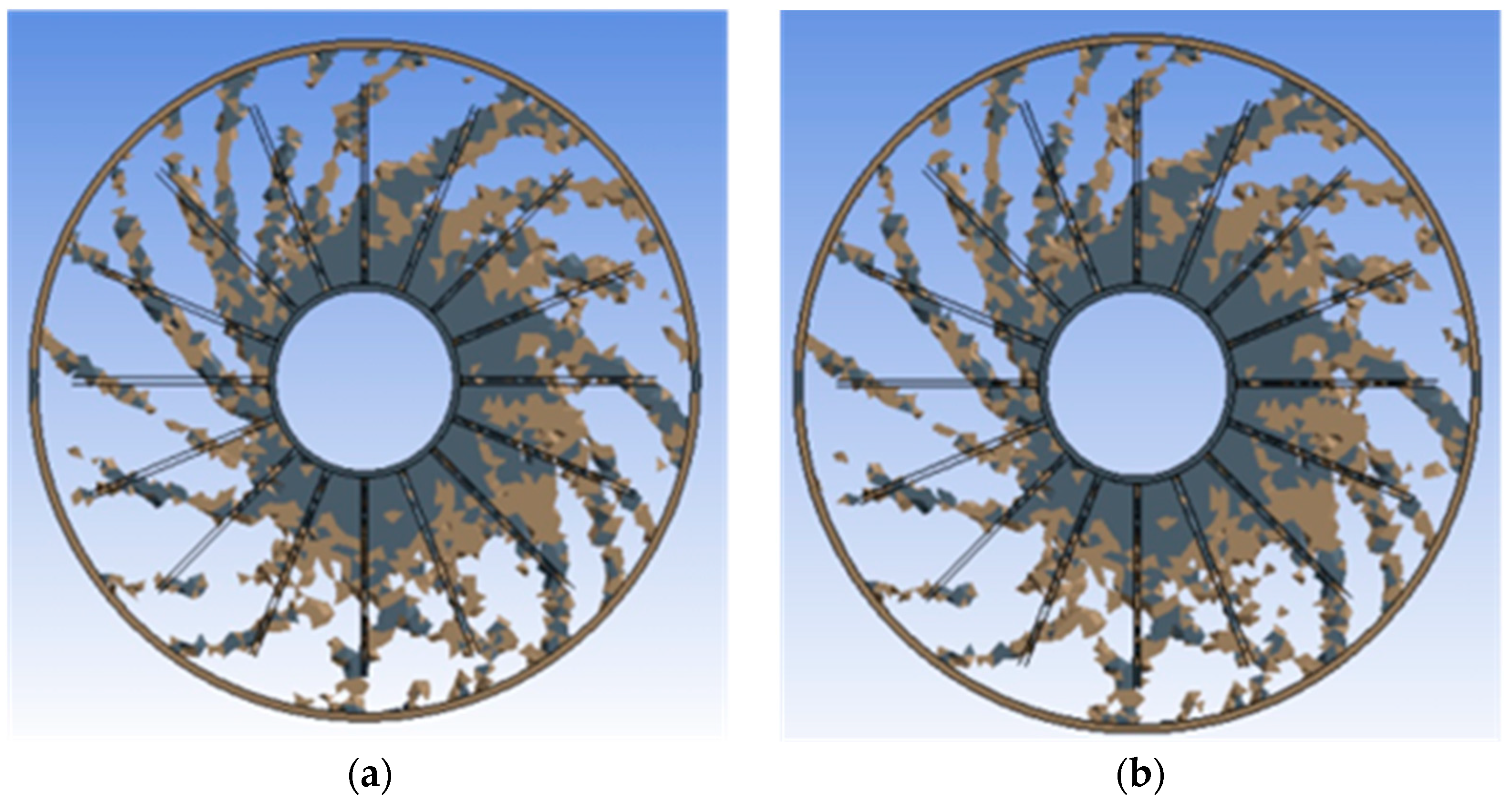
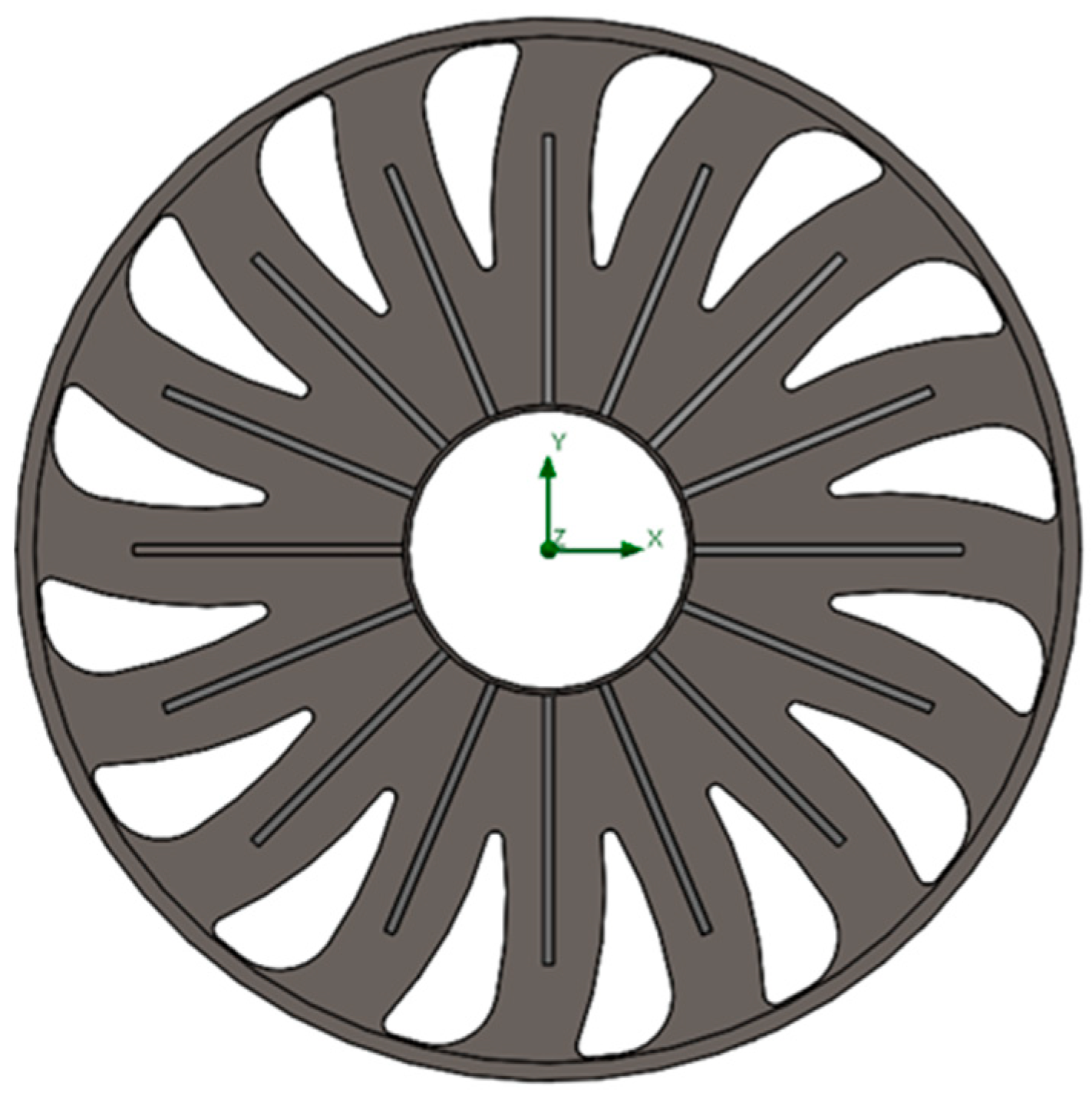
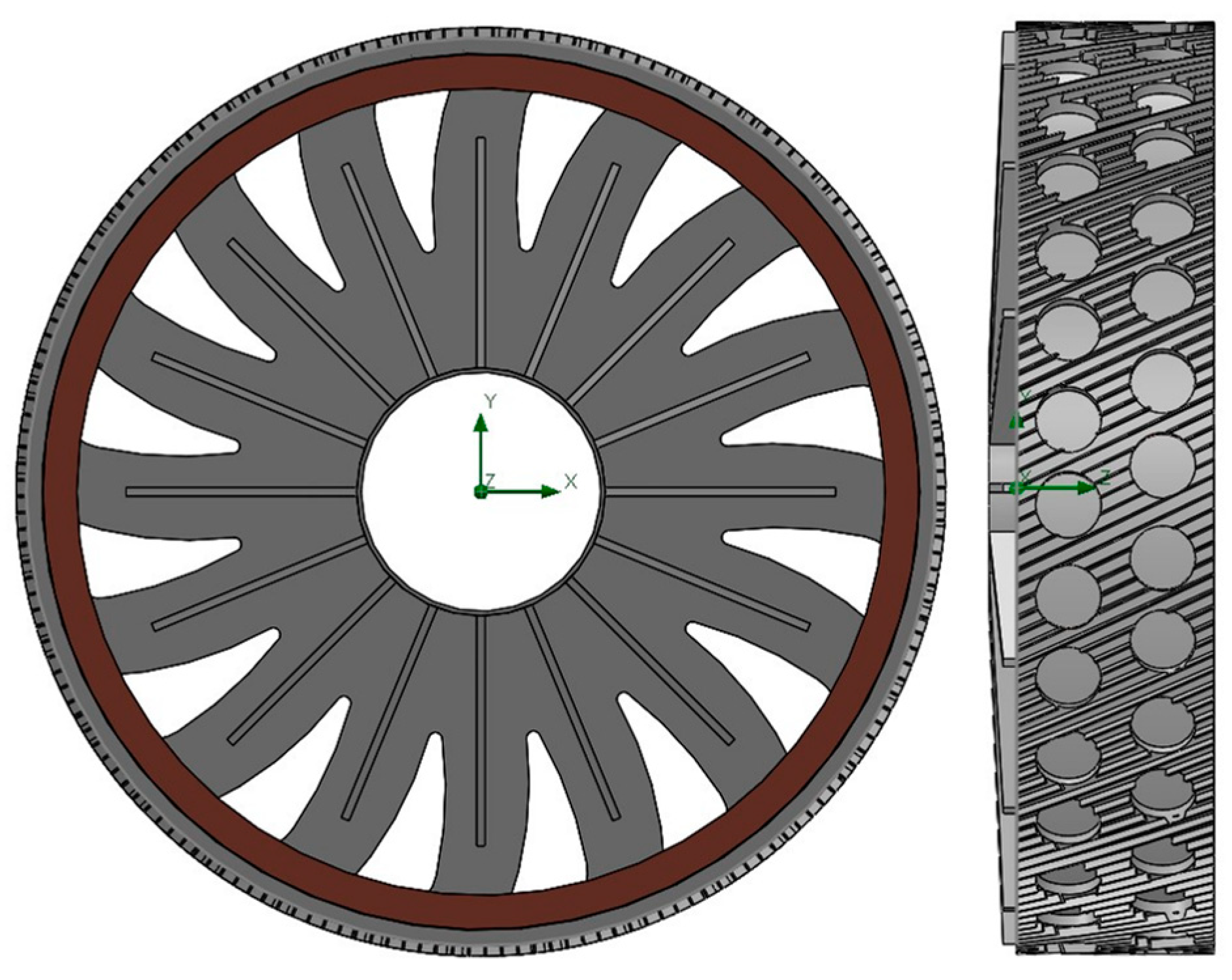
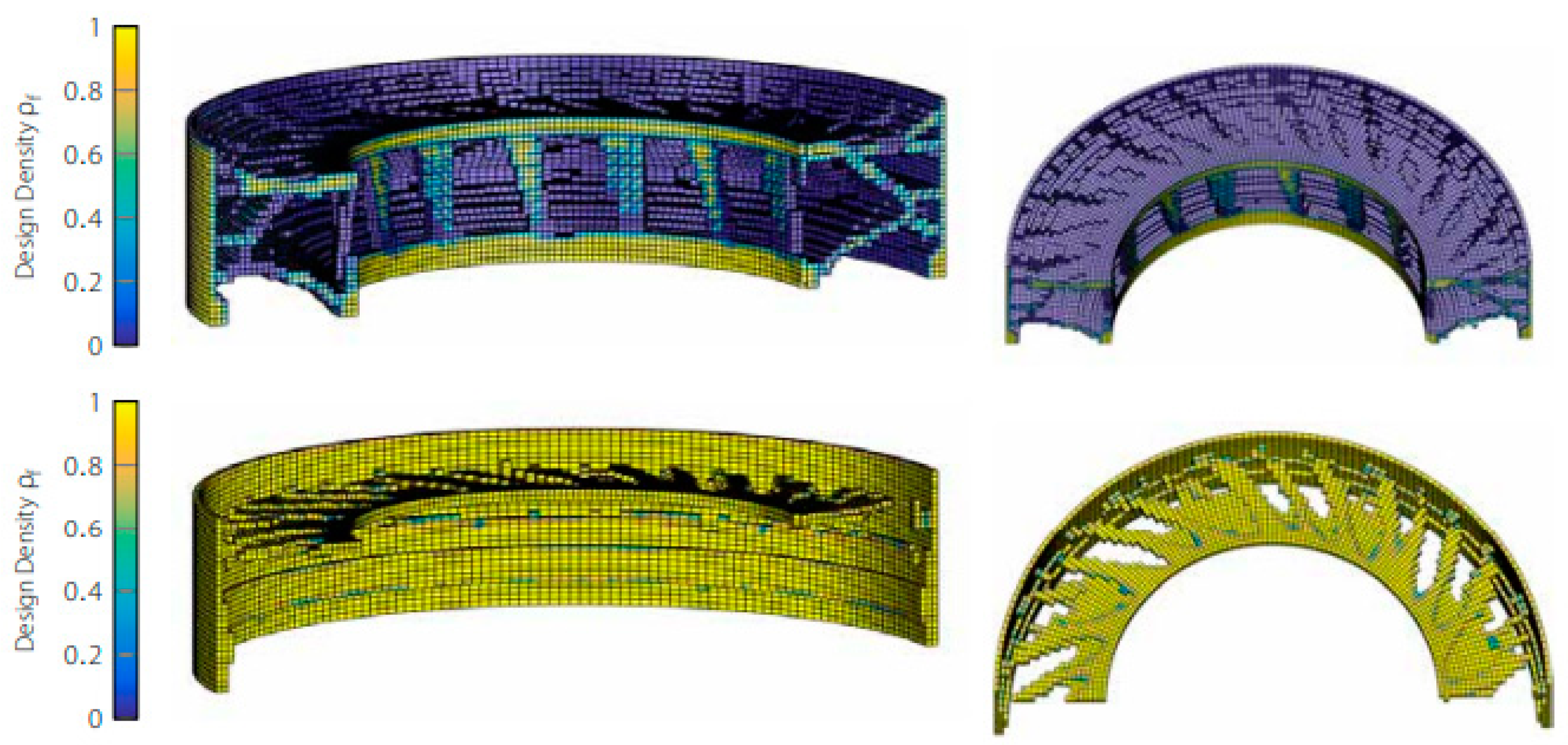
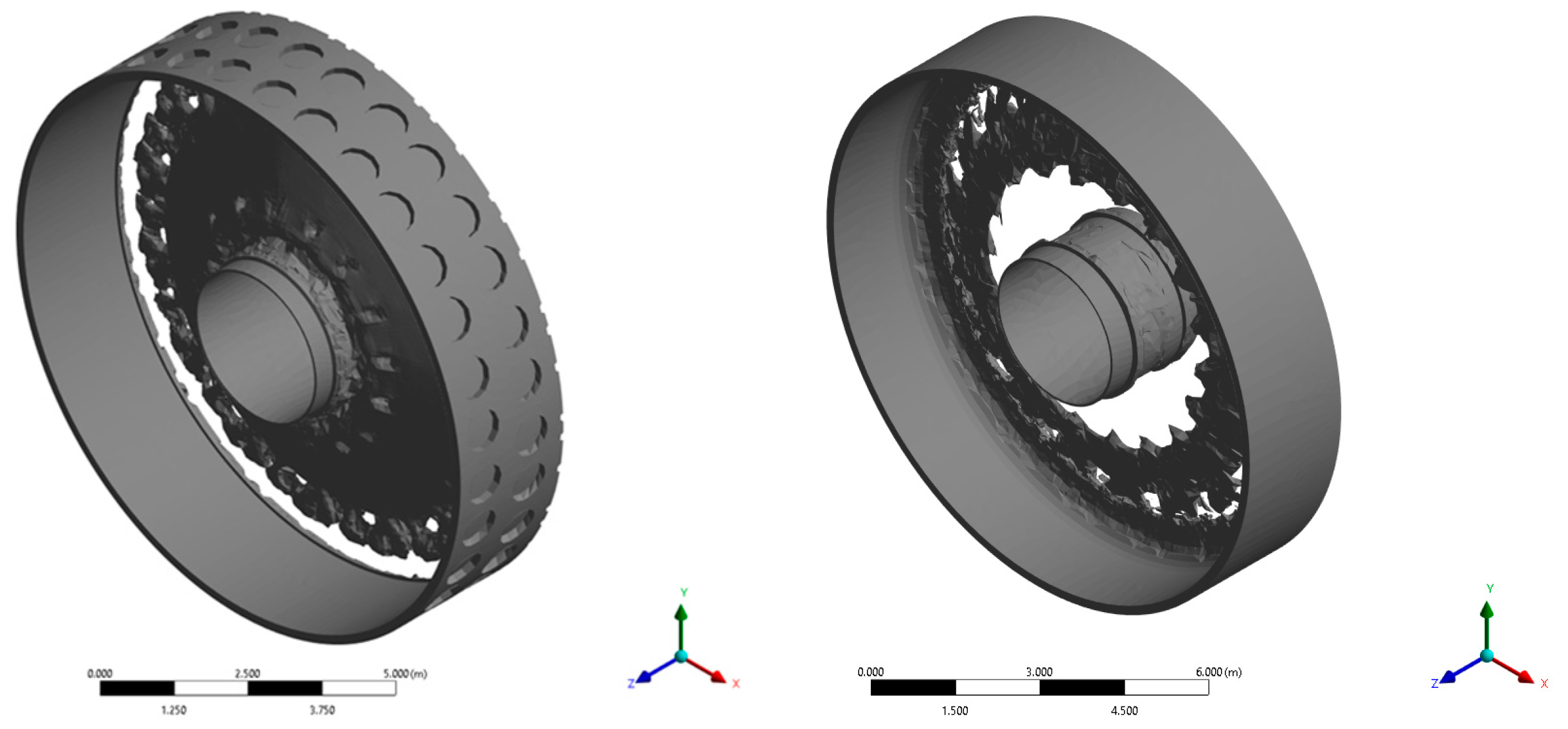
2.3.2. Topology Optimisation and Addition of Structural Members
2.4. CFD-FEA Simulation Development
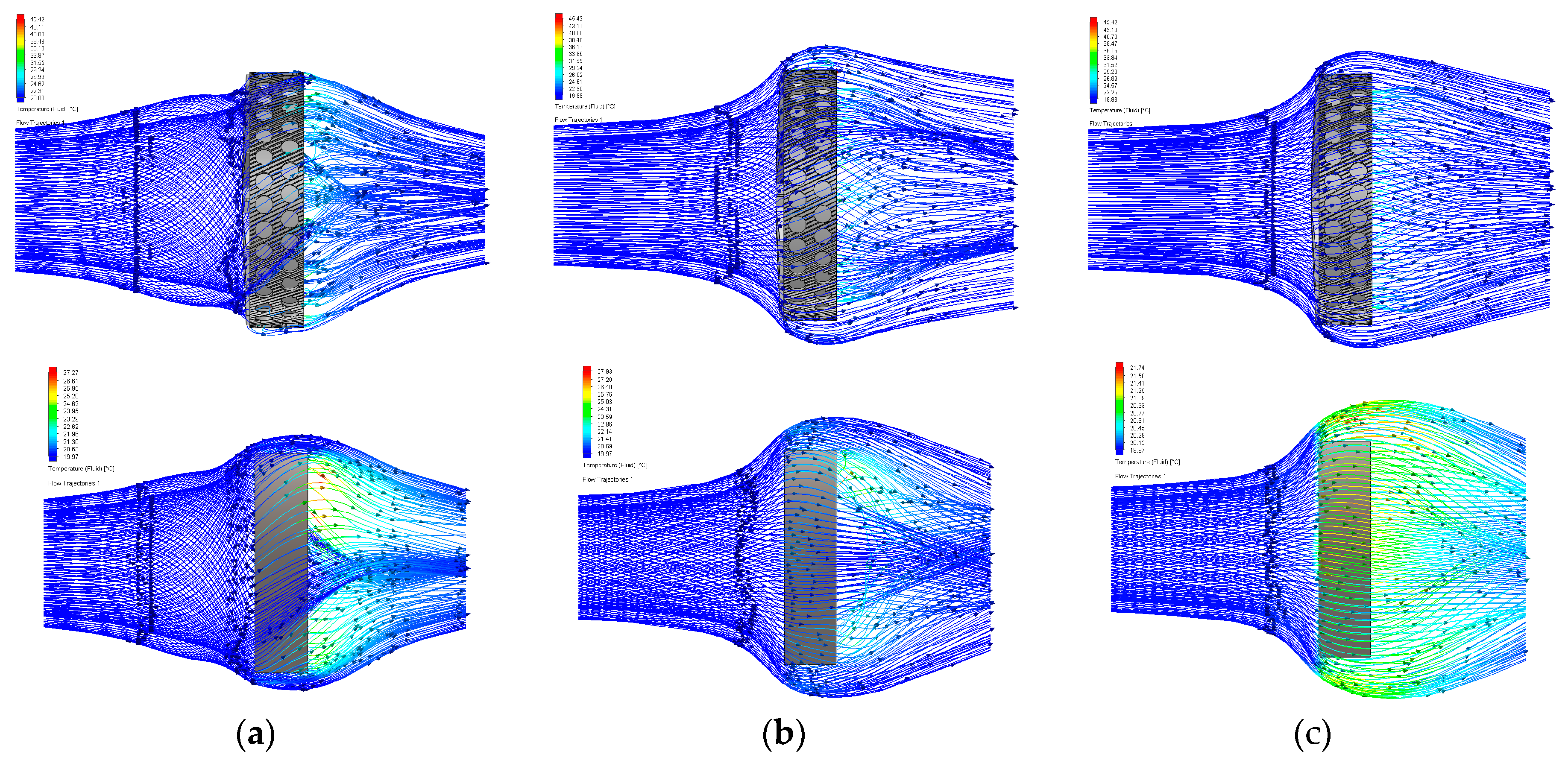
2.5. Incorporation of Heatsinks
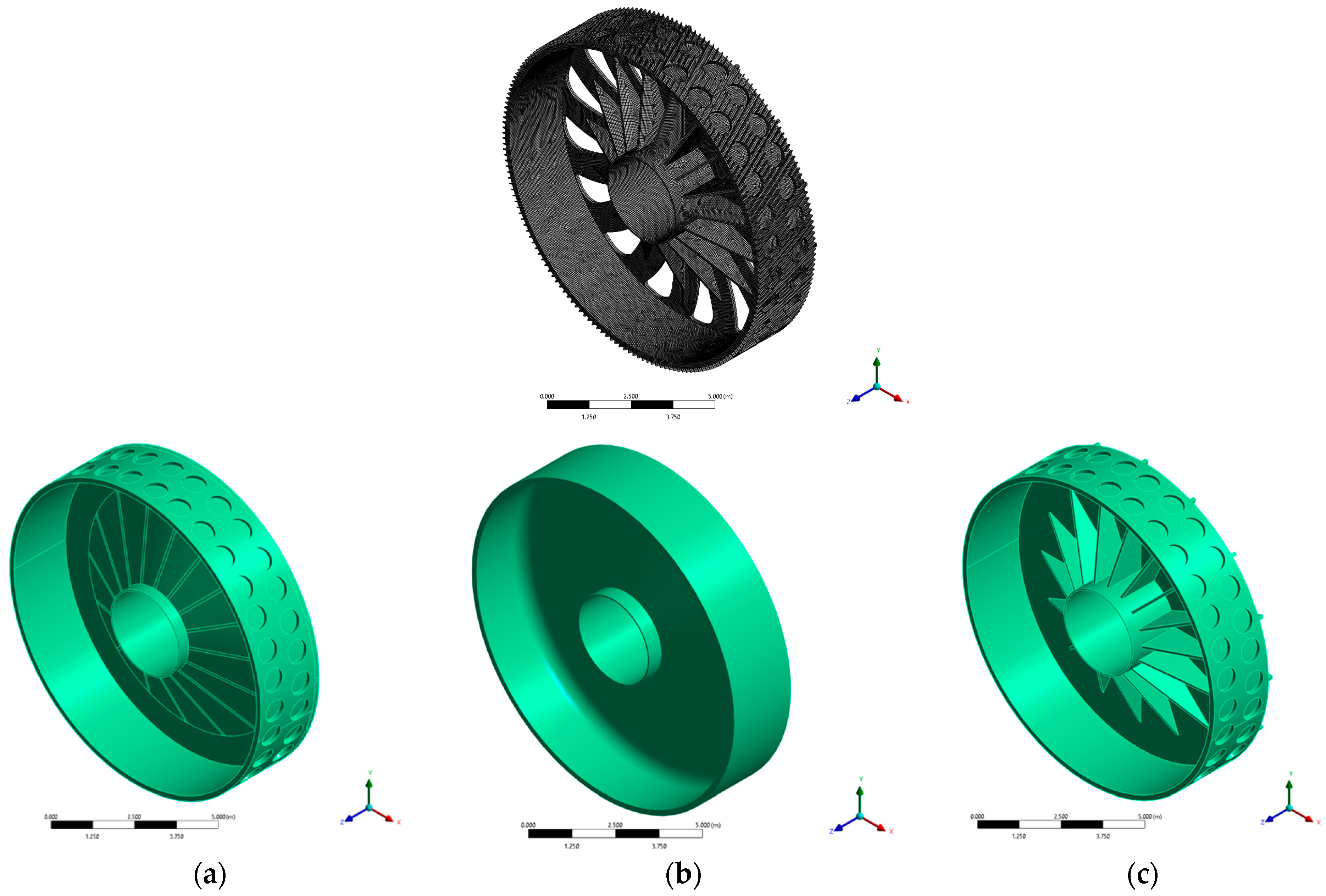
2.6. Generative Design
3. Results
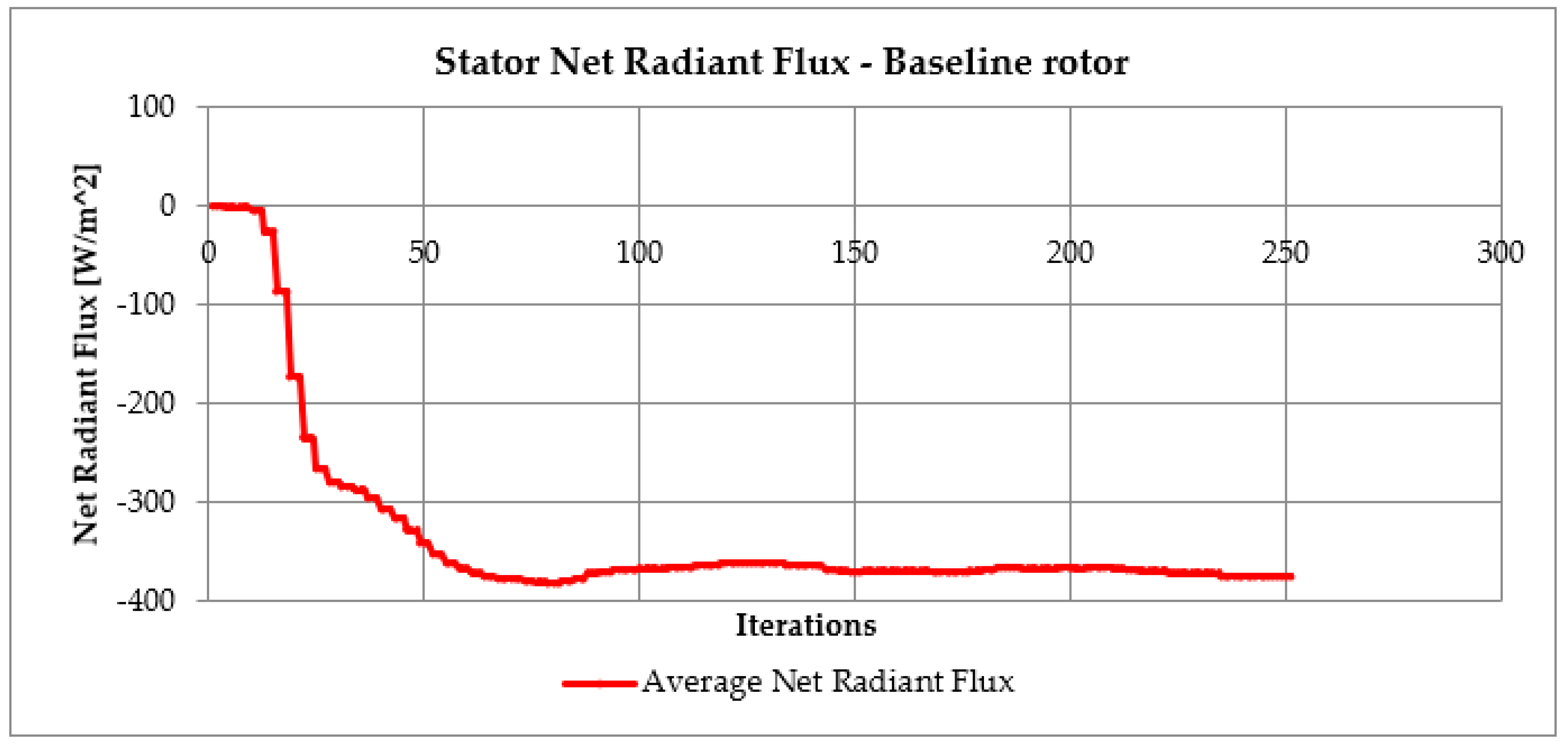
3.1. Mesh Independence Study
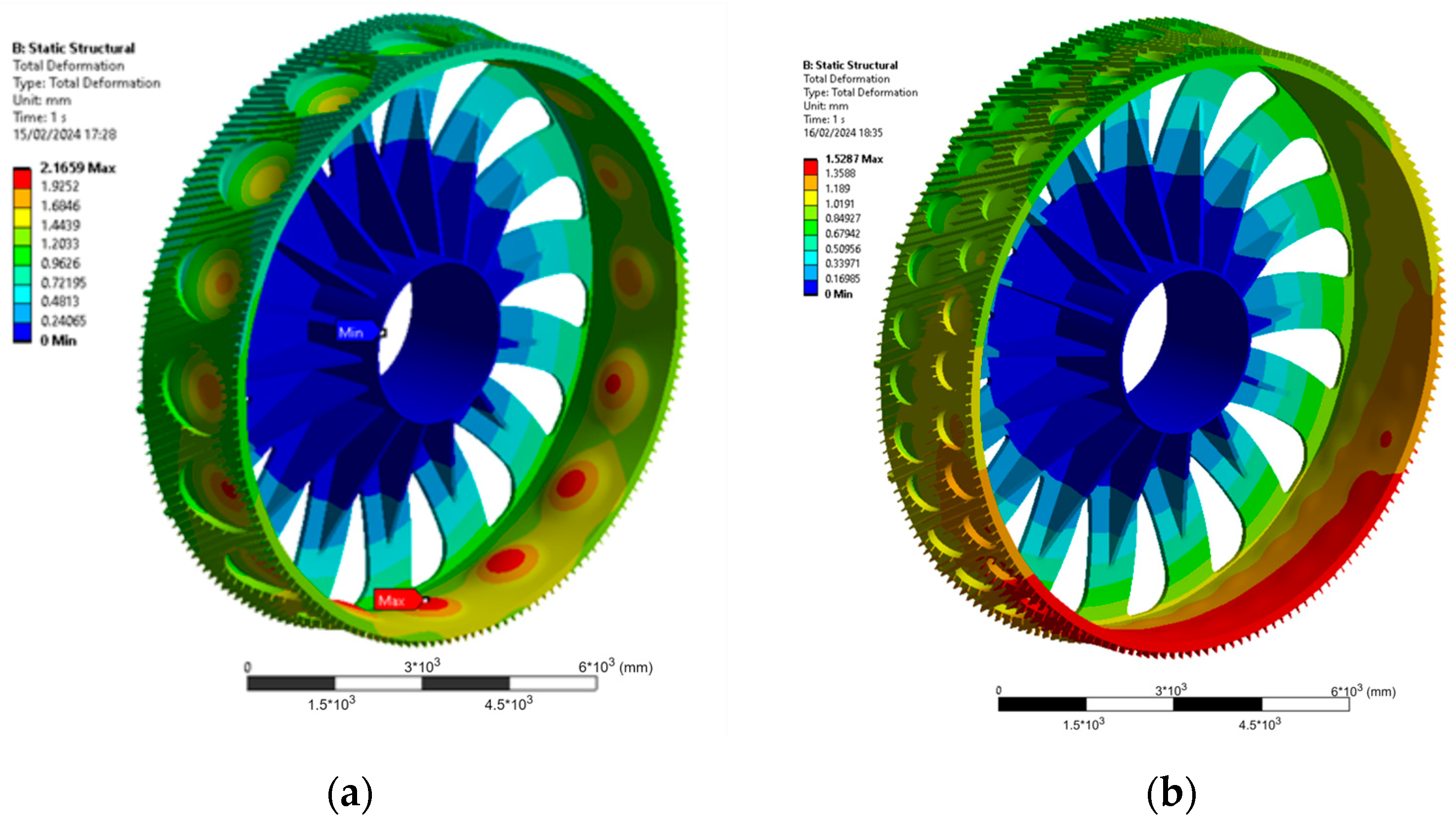
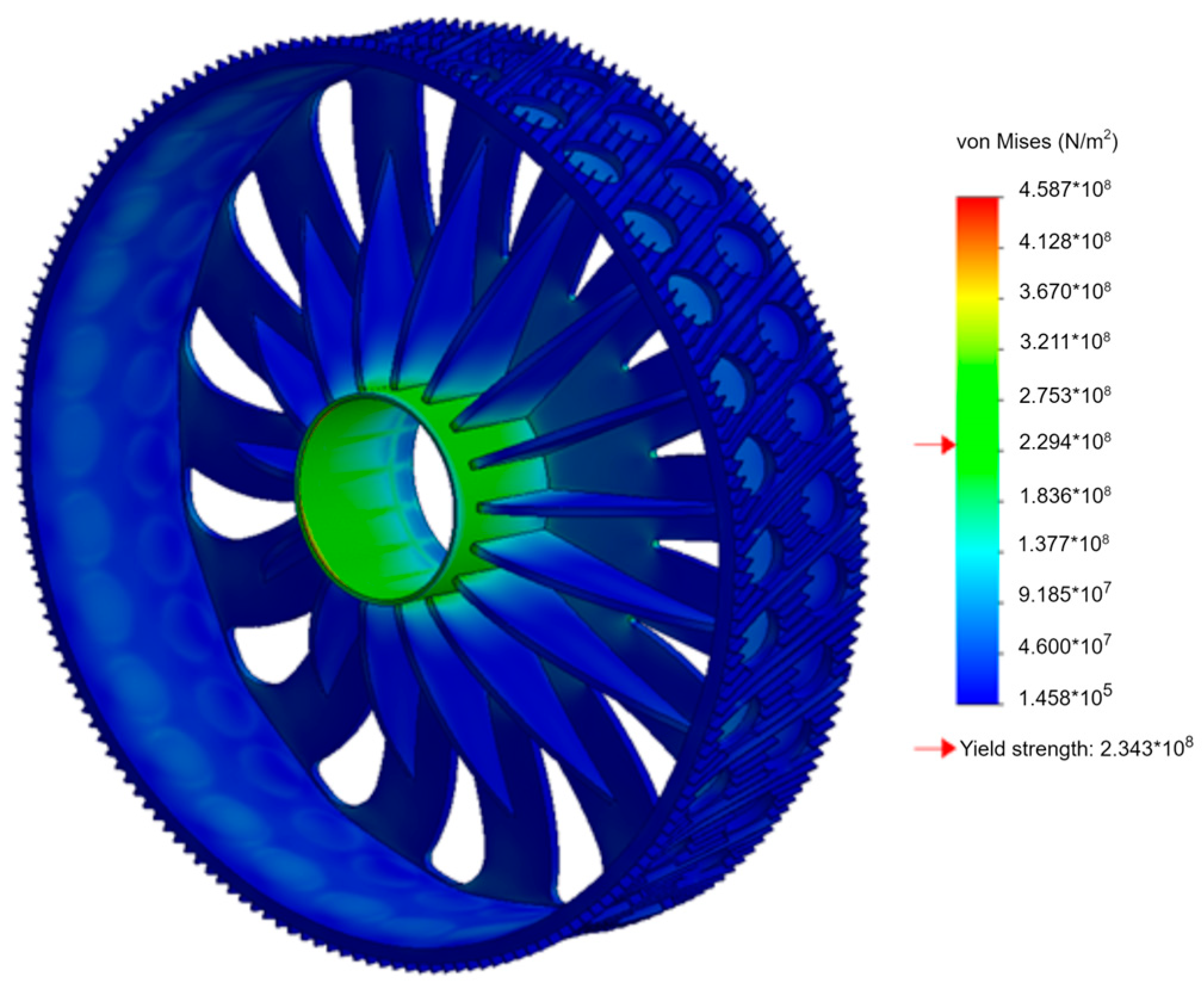
3.2. Rotor Optimisation Results
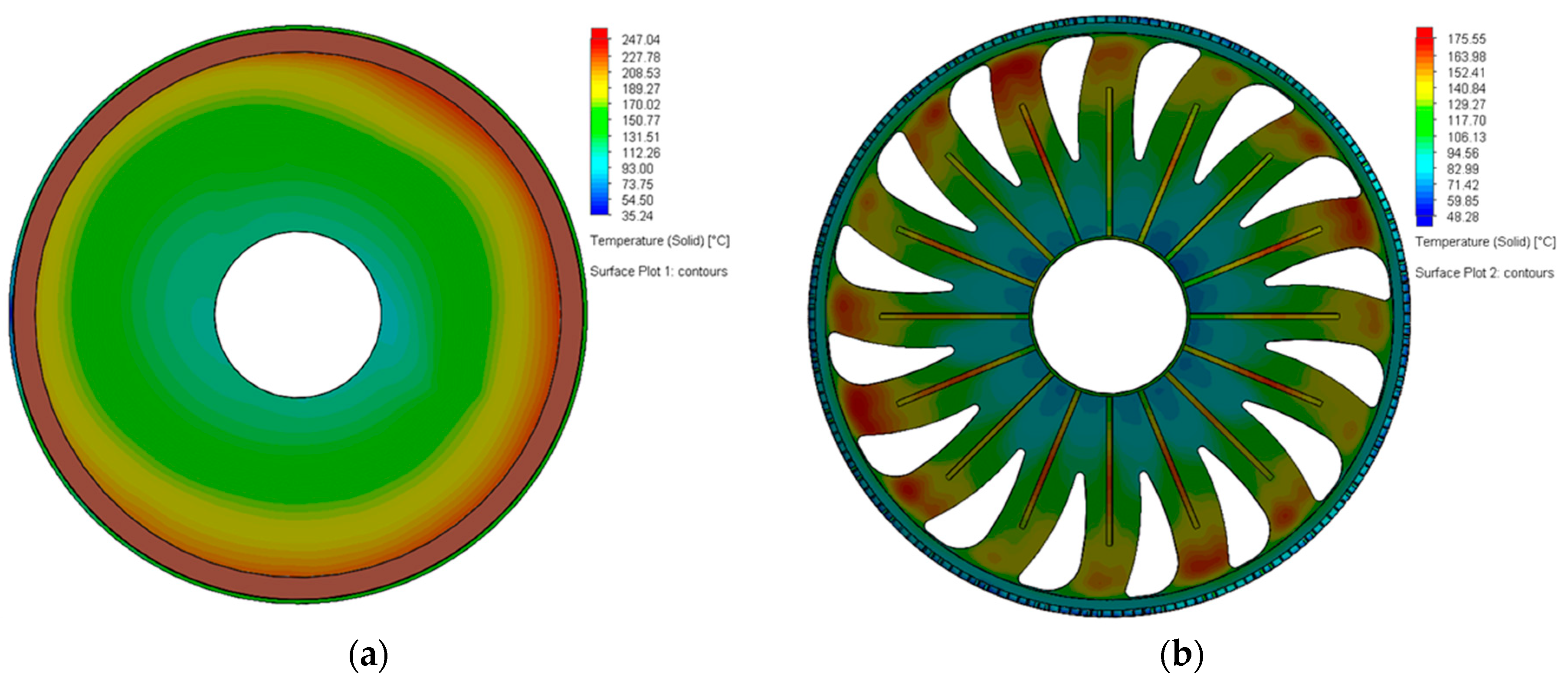
3.3. CFD-FE Analysis
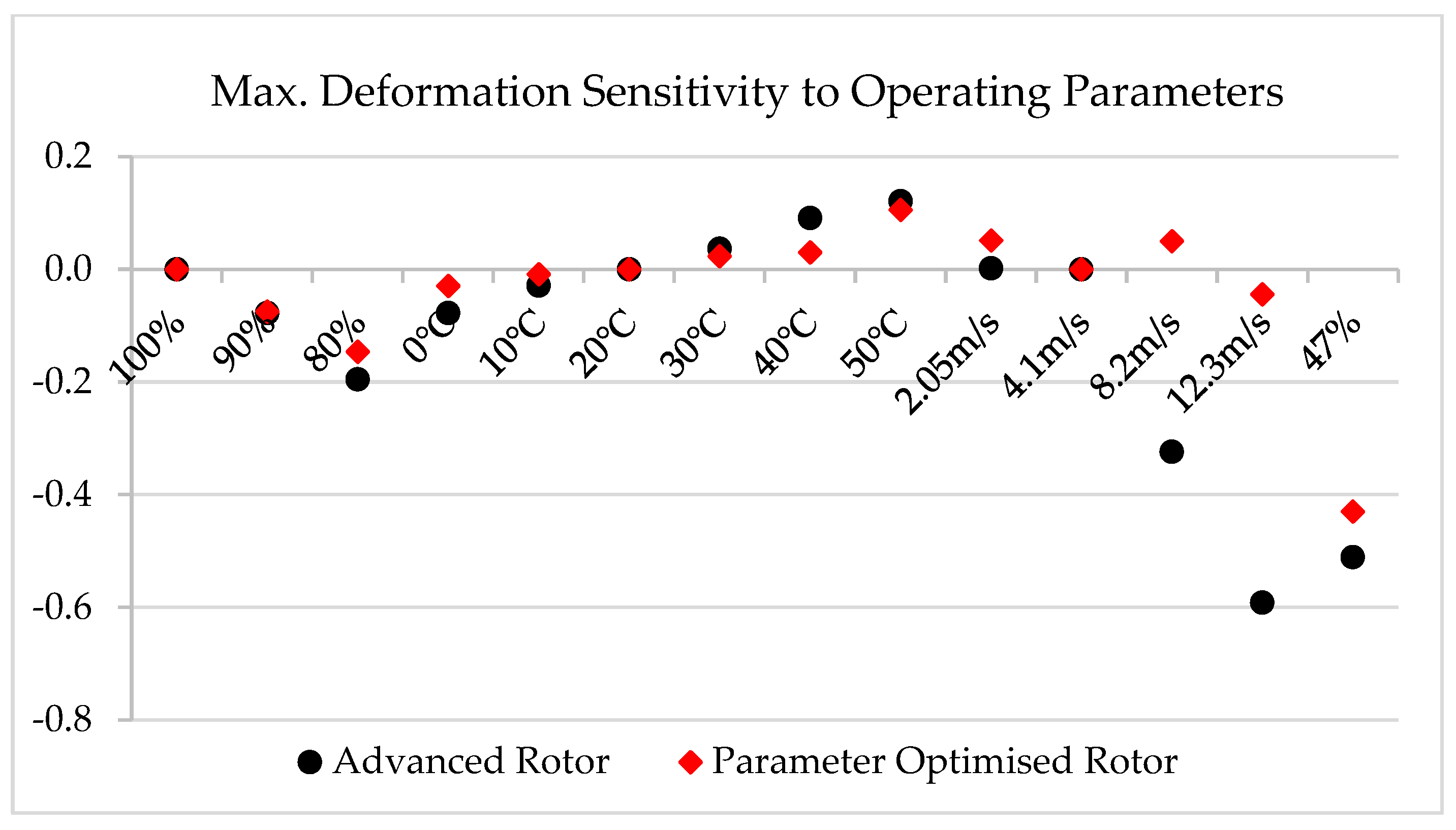
3.4. Operating Parameter Analysis
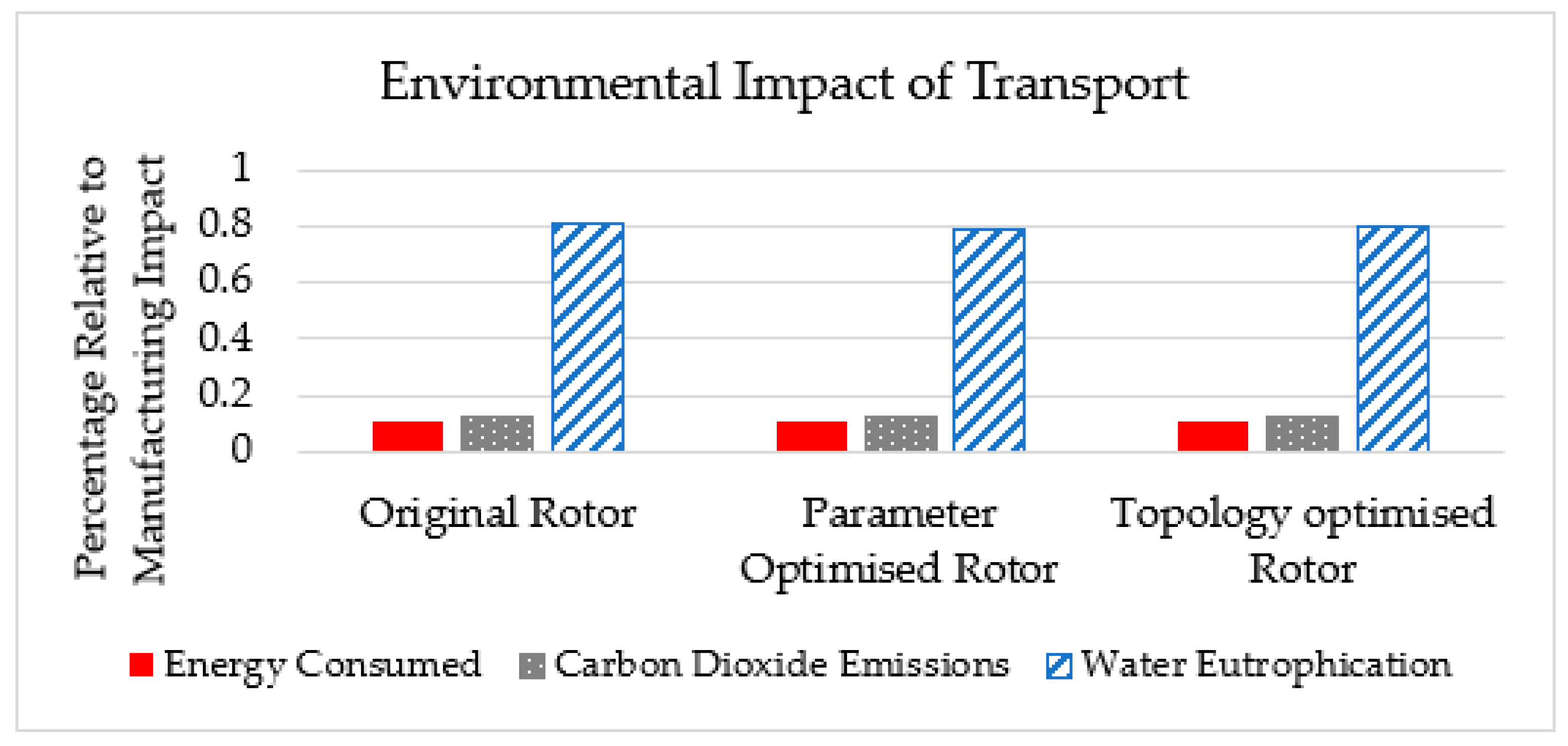
3.5. Environmental Performance Analysis
3.6. Costing Analysis
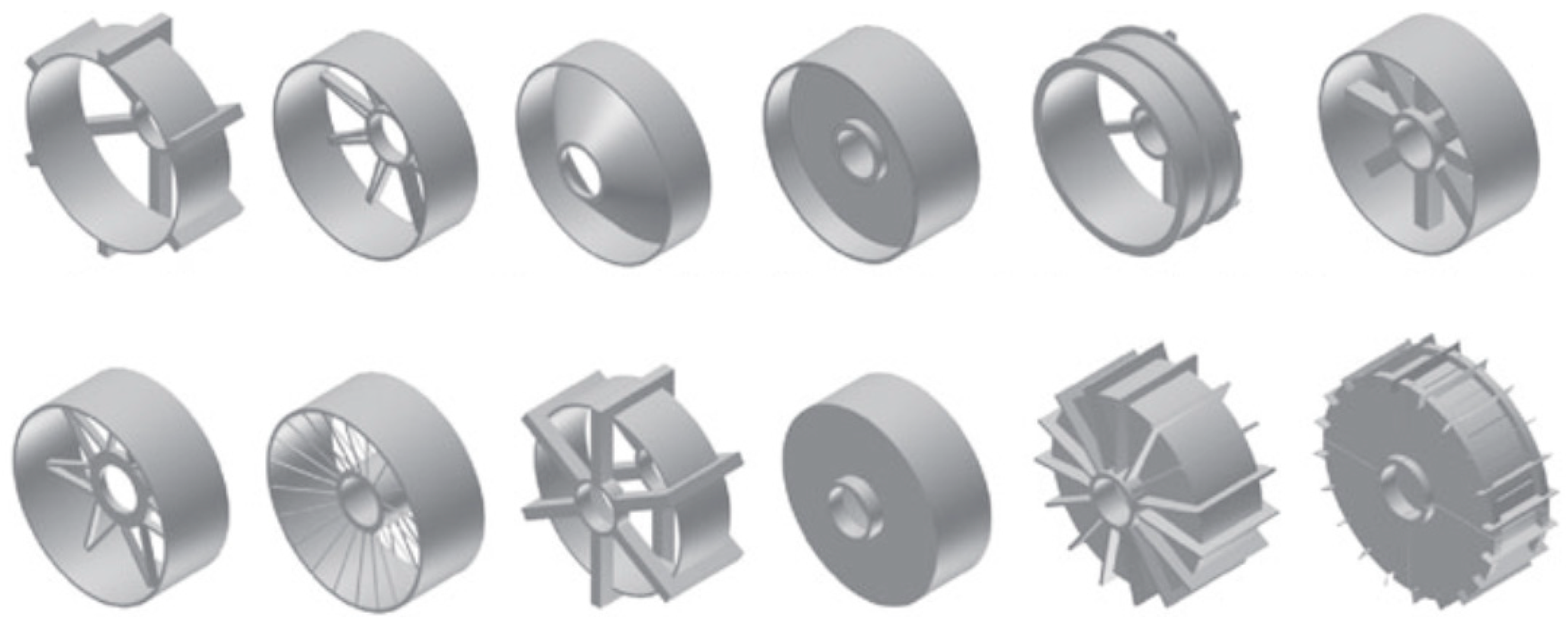
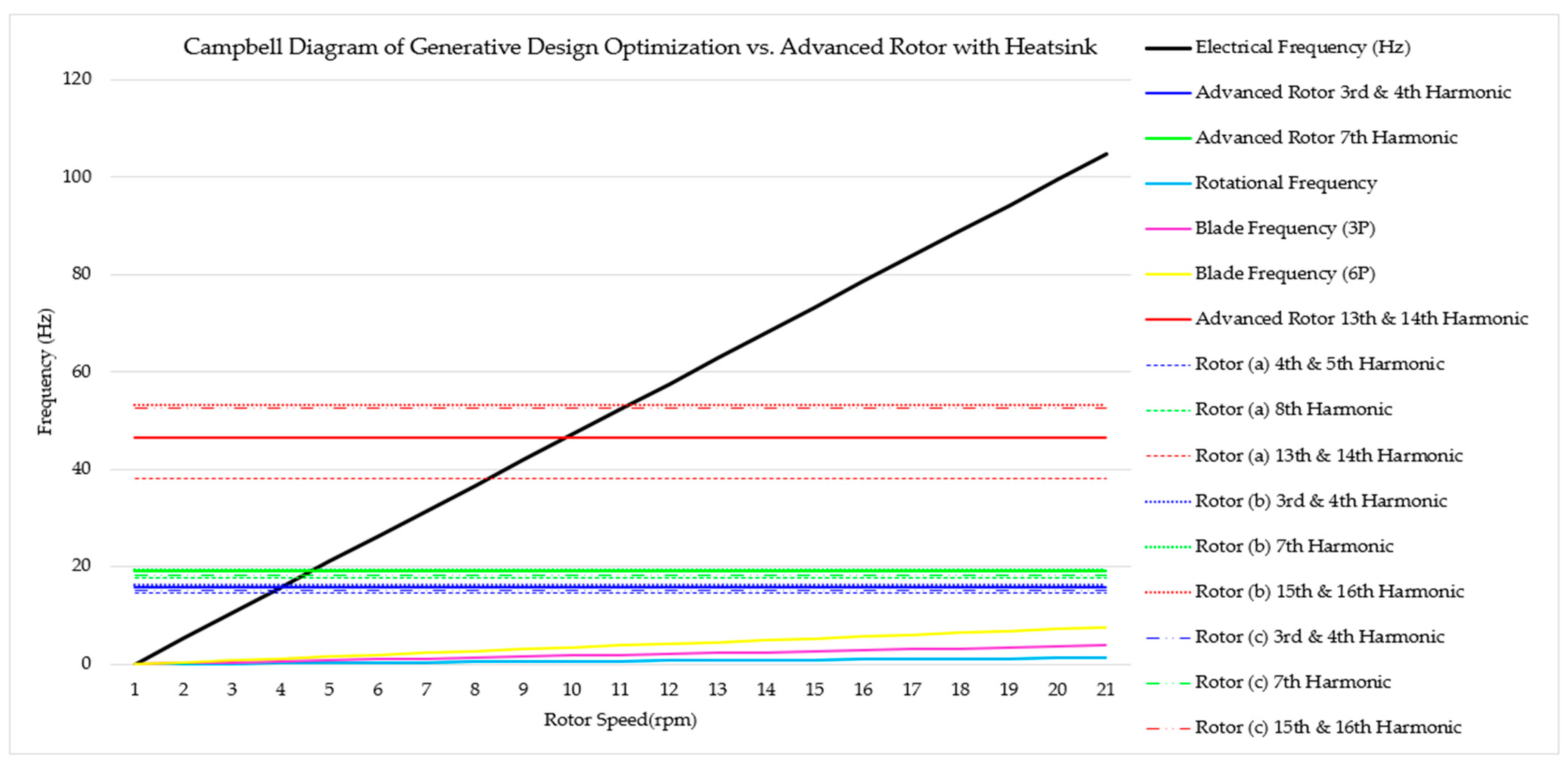
3.7. Generative Design and Modal Analysis Results
4. Discussion
5. Conclusions
- The removal of the cylinder wall material achieves a significant reduction in mass and despite increasing maximum deformation when paired with the addition of disk supports and the heatsink device, justifies its use and ongoing study.
- Retrofit heatsinks were found to reduce the rotor structure’s operating temperatures; however, integrated designs were found to outperform the retrofit models whilst providing structural support.
- A primary benefit of the CFD-FE simulation produced in this paper is the ability to accurately identify thermal hotspots on the rotor structure that may increase the severity of cyclic thermal stresses on the generator structure and to quantify their effects.
- Although the advanced rotor structure outperformed the parametrically optimised rotor in terms of deformation in the CFD-FEA simulation, it was subject to greater variations in deformation as conditions were varied, implying that the advanced rotor structure may be subject to greater levels of dynamic thermal loading fatigue.
- Further savings in environmental and financial factors are thought possible through the advent of high-capacity additive manufacturing or investment casting as eliminating additional milling steps required of the complex design would reduce the mass of initial material to be cast.
- Generative design was shown to yield considerable improvements to an already complex structure, finding mass reductions of 2.3% and 7.6% while considerably reducing deformation and maximum stress in the first instance and further reducing deformation at the cost of increased maximum stress in the second instance. Its potential for substantial design improvements over topology optimisation techniques necessitates its use and future investigation.
- By reducing the rotor structure’s temperature through the incorporation of heatsinks, stator temperatures were consequently reduced, which may in turn increase generator lifespans and efficiencies. It is apparent that the inverse is also true, i.e., active cooling of the generators’ components likewise benefits its structural components, reducing stress and deformation across the structure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Baseline Rotor | Advanced Rotor | |||||
|---|---|---|---|---|---|---|
| ANSYS | SolidWorks | Difference (%) | ANSYS | SolidWorks | Difference (%) | |
| Mode 0, 20 °C | ||||||
| Maximum Deformation (mm) | 1.47 | 1.46 | 0.68% | 1.5246 | 1.540429 | −1.04% |
| Maximum Von Mises Stress (Pa) | 38.77 | 38.66 | 0.28% | 68.01 | 67.779152 | 0.34% |
| Mode 0, 55.7 °C | ||||||
| Maximum Deformation (mm) | 2.1 | 2.17 | −3.33% | 2.3907 | 2.393144 | −0.10% |
| Maximum Von Mises Stress (Pa) | 185.7 | 192.1 | −3.45% | 206.85 | 241.88168 | −16.94% |
| Variable | Average Heat Generation Rate (°C) | Maximum Heat Generation Rate (°C) | Average Rotor Volume Temperature (°C) | Average Rotor Surface Temperature (°C) | Maximum Rotor Surface Temperature (°C) |
|---|---|---|---|---|---|
| 100% extrapolated losses (1108.5 kW) | 404.5705 | 415.428444 | 118.068925 | 116.298406 | 180.80674 |
| 90% extrapolated losses (997.7 kW) | 383.6046 | 393.560494 | 109.330937 | 107.862391 | 164.647565 |
| 80% extrapolated losses (886.8 kW) | 359.4766 | 367.459624 | 99.7267309 | 98.559667 | 146.681904 |
| Environmental temperature: 0 °C | 399.6924 | 410.603192 | 104.659817 | 102.815426 | 168.443351 |
| Environmental temperature: 10 °C | 402.7004 | 413.503268 | 111.720373 | 109.970155 | 174.152592 |
| Environmental temperature: 20 °C | 404.5705 | 415.428444 | 118.068925 | 116.298406 | 180.80674 |
| Environmental temperature: 30 °C | 407.9513 | 417.775446 | 124.952048 | 123.237336 | 187.321608 |
| Environmental temperature: 40 °C | 410.5165 | 420.916036 | 131.308137 | 129.665143 | 193.551724 |
| Environmental temperature: 50 °C | 413.242 | 422.750595 | 136.938565 | 135.287998 | 199.352458 |
| Airflow velocity: 2.05 m/s | 397.0629 | 411.294731 | 108.661729 | 106.72026 | 167.798051 |
| Airflow velocity: 4.1 m/s | 404.5705 | 415.428444 | 118.068925 | 116.298406 | 180.80674 |
| Airflow velocity: 8.2 m/s | 352.2316 | 360.295474 | 83.259744 | 81.8573649 | 132.407794 |
| Airflow velocity: 12.3 m/s | 298.9707 | 306.482525 | 56.0123885 | 55.121305 | 86.5987422 |
| Defined generator losses (517.5 kW) | 261.12 | 269.19 | 65.82 | 75.66 | 97.4 |
| Variable | Maximum Total Deformation (mm) | Maximum Von Mises Stress (Pa) | Maximum Airgap Deformation (mm) | Minimum Airgap Deformation (mm) |
|---|---|---|---|---|
| 100% extrapolated losses (1108.5 kW) | 7.3982 | 717,986,688 | 7.104675 | 5.173855 |
| 90% extrapolated losses (997.7 kW) | 6.824816 | 646,424,576 | 6.564463 | 4.841605 |
| 80% extrapolated losses (886.8 kW) | 5.9527 | 600,393,152 | 5.728301 | 4.313871 |
| Environmental temperature: 0 °C | 6.822642 | 655,258,496 | 6.564501 | 4.366 |
| Environmental temperature: 10 °C | 7.1834 | 686,678,656 | 6.92293 | 4.9578 |
| Environmental temperature: 20 °C | 7.3982 | 717,986,688 | 7.104675 | 5.173855 |
| Environmental temperature: 30 °C | 7.6684 | 729,111,744 | 7.37527 | 5.571075 |
| Environmental temperature: 40 °C | 8.07005 | 756,542,912 | 7.736152 | 5.847183 |
| Environmental temperature: 50 °C | 8.292427 | 801,503,168 | 7.946857 | 6.152822 |
| Airflow velocity: 2.05 m/s | 7.410163 | 628,218,944 | 6.968168 | 4.4833 |
| Airflow velocity: 4.1 m/s | 7.3982 | 717,986,688 | 7.104675 | 5.173855 |
| Airflow velocity: 8.2 m/s | 5.0029 | 458,688,160 | 4.875976 | 3.064497 |
| Airflow velocity: 12.3 m/s | 3.0203 | 275,507,296 | 2.951388 | 1.669598 |
| Defined generator losses (517.5 kW) | 3.618967 | 316,771,776 | 3.436346 | 2.35124 |
| Variable | Average Heat Generation Rate (°C) | Maximum Heat Generation Rate (°C) | Average Rotor Volume Temperature (°C) | Average Rotor Surface Temperature (°C) | Maximum Rotor Surface Temperature (°C) |
|---|---|---|---|---|---|
| 100% extrapolated losses (1108.5 kW) | 414.9 | 431.53 | 168.53 | 179.52 | 247.36 |
| 90% extrapolated losses (997.7 kW) | 394.506783 | 410.806871 | 159.368551 | 170.858066 | 235.120326 |
| 80% extrapolated losses (886.8 kW) | 370.669538 | 386.0827 | 146.835913 | 158.289781 | 220.483813 |
| Environmental temperature: 0 °C | 409.963443 | 429.367567 | 161.034199 | 171.519854 | 244.346557 |
| Environmental temperature: 10 °C | 412.760377 | 429.736599 | 165.153835 | 179.31847 | 245.326211 |
| Environmental temperature: 20 °C | 414.9 | 431.53 | 168.53 | 179.52 | 247.36 |
| Environmental temperature: 30 °C | 417.981289 | 433.843892 | 174.130672 | 186.754466 | 250.585765 |
| Environmental temperature: 40 °C | 422.026752 | 436.026212 | 179.595431 | 192.060718 | 254.889108 |
| Environmental temperature: 50 °C | 421.568573 | 433.6744 | 177.980684 | 192.012944 | 249.236399 |
| Airflow velocity: 2.05 m/s | 418.249814 | 428.835087 | 161.777553 | 179.768922 | 248.82763 |
| Airflow velocity: 4.1 m/s | 414.9 | 431.53 | 168.53 | 179.52 | 247.36 |
| Airflow velocity: 8.2 m/s | 415.626512 | 432.006217 | 168.704913 | 182.382952 | 247.547985 |
| Airflow velocity: 12.3 m/s | 404.969776 | 419.809132 | 146.623846 | 164.195795 | 231.913276 |
| Defined generator losses (517.5 kW) | 273.796534 | 286.034418 | 100.234433 | 111.230527 | 163.0137 |
| Variable | Maximum Total Deformation (mm) | Maximum Von Mises Stress (Pa) | Maximum Airgap Deformation (mm) | Minimum Airgap Deformation (mm) |
|---|---|---|---|---|
| 100% extrapolated losses (1108.5 kW) | 11.776982 | 506,168,672 | 11.605173 | 3.089048 |
| 90% extrapolated losses (997.7 kW) | 10.895239 | 466,471,904 | 10.744861 | 2.557209 |
| 80% extrapolated losses (886.8 kW) | 10.056499 | 372,834,496 | 9.919287 | 2.774552 |
| Environmental temperature: 0 °C | 11.43097 | 465,074,240 | 11.266694 | 1.976938 |
| Environmental temperature: 10 °C | 11.6743 | 488,489,536 | 11.505387 | 6.233285 |
| Environmental temperature: 20 °C | 11.791964 | 507,118,144 | 11.623928 | 3.761743 |
| Environmental temperature: 30 °C | 12.049924 | 525,310,848 | 11.888286 | 4.058718 |
| Environmental temperature: 40 °C | 12.133654 | 556,985,088 | 11.955224 | 4.653414 |
| Environmental temperature: 50 °C | 13.018543 | 558,268,992 | 12.844136 | 8.293615 |
| Airflow velocity: 2.05 m/s | 12.380209 | 425,423,424 | 12.202521 | 6.332108 |
| Airflow velocity: 4.1 m/s | 11.776982 | 506,168,672 | 11.605173 | 3.089048 |
| Airflow velocity: 8.2 m/s | 12.365489 | 476,877,664 | 12.212373 | 6.329225 |
| Airflow velocity: 12.3 m/s | 11.255186 | 388,515,936 | 11.106085 | 6.606413 |
| Defined generator losses (517.5 kW) | 6.715411 | 251,927,744 | 6.614156 | 1.644034 |
References
- BEIS. Renewable Energy Planning Database (REPD): April 2023; Department for Business, Energy and Industrial Strategy: London, UK, 2023. [Google Scholar]
- Kaiser, M.J.; Snyder, B.F. Offshore Wind Energy Cost Modeling; Springer: London, UK, 2012; ISBN 9781608054220. [Google Scholar]
- Ren, Z.; Shankar Verma, A.; Li, Y.; Teuwen, J.J.E.; Jiang, Z. Offshore Wind Turbine Operations and Maintenance: A State-of-the-Art Review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
- Nejad, A.R.; Keller, J.; Guo, Y.; Sheng, S.; Polinder, H.; Watson, S.; Dong, J.; Qin, Z.; Ebrahimi, A.; Schelenz, R.; et al. Wind Turbine Drivetrains: State-of-the-Art Technologies and Future Development Trends. Wind Energy Sci. 2022, 7, 387–411. [Google Scholar] [CrossRef]
- Carroll, J.; McDonald, A.; Dinwoodie, I.; McMillan, D.; Revie, M.; Lazakis, I. Availability, Operation and Maintenance Costs of Offshore Wind Turbines with Different Drive Train Configurations. Wind Energy 2017, 20, 361–378. [Google Scholar] [CrossRef]
- Hayes, A.; Sethuraman, L.; Dykes, K.; Fingersh, L.J. Structural Optimization of a Direct-Drive Wind Turbine Generator Inspired by Additive Manufacturing. Procedia Manuf. 2018, 26, 740–752. [Google Scholar] [CrossRef]
- Hayes, A.C.; Whiting, G.L. Reducing the Structural Mass of Large Direct Drive Wind Turbine Generators through Triply Periodic Minimal Surfaces Enabled by Hybrid Additive Manufacturing. Clean Technol. 2021, 3, 227–242. [Google Scholar] [CrossRef]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. Definition of the IEA 15 MW Offshore Reference Wind Turbine; National Renewable Energy Laboratory: Golden, CO, USA, 2020. [Google Scholar]
- Gonzalez-Delgado, D.; Jaen-Sola, P.; Oterkus, E. Design and Optimization of Multi-MW Offshore Direct-Drive Wind Turbine Electrical Generator Structures Using Generative Design Techniques. Ocean Eng. 2023, 280, 114417. [Google Scholar] [CrossRef]
- Wang, S.; Xing, Y.; Balakrishna, R.; Shi, W.; Xu, X. Design, Local Structural Stress, and Global Dynamic Response Analysis of a Steel Semi-Submersible Hull for a 10-MW Floating Wind Turbine. Eng. Struct. 2023, 291, 1116474. [Google Scholar] [CrossRef]
- Wang, S.; Nejad, A.R.; Moan, T. On Design, Modelling, and Analysis of a 10-MW Medium-Speed Drivetrain for Offshore Wind Turbines. Wind Energy 2020, 23, 1099–1117. [Google Scholar] [CrossRef]
- Isidori, A.; Mario Rossi, F.; Blaabjerg, F.; Ma, K. Thermal Loading and Reliability of 10-MW Multilevel Wind Power Converter at Different Wind Roughness Classes. IEEE Trans. Ind. Appl. 2014, 50, 484–494. [Google Scholar] [CrossRef]
- Bichan, M.; Jaen-Sola, P.; Jack, A. Establishing the Importance of Operating Temperature in the Structural Integrity of Large-Scale Direct-Drive Wind Turbine Generators. Machines 2023, 11, 780. [Google Scholar] [CrossRef]
- Bywaters, G.; Mattila, P.; Costin, D.; Stowell, J.; John, V.; Hoskins, S.; Lynch, J.; Cole, T.; Cate, A.; Badger, C.; et al. Northern Power NW 1500 Direct-Drive Gnerator: April 12, 2001–September 30, 2006; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2007. [Google Scholar]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.; Abbas, N.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. IEAWindTask37/IEA-15-240-RWT: 15MW Reference Wind Turbine Repository. Available online: https://github.com/IEAWindTask37/IEA-15-240-RWT (accessed on 10 April 2023).
- McDonald, A.; Jaen-Sola, P. A Stiffness Approach for Coupling Structural and Magnetic Models for the Sustainable Design, Optimisation and Real-Time Structural Integrity Assessment of Radial Flux Permanent Magnet Generators for Direct-Drive Wind Turbines. Sustainability 2024, 16, 2393. [Google Scholar] [CrossRef]
- Stander, J.N.; Venter, G.; Kamper, M.J. Review of Direct-Drive Radial Flux Wind Turbine Generator Mechanical Design. Wind Energy 2012, 15, 459–472. [Google Scholar] [CrossRef]
- BOVIA. Dassault Systèmes BOVIA Solidworks 2022, Version 29.3.0.0059; Dassault Systèmes: San Diego, CA, USA, 2022.
- ANSYS. ANSYS ® Academic Research Mechanical 2022, Release 2022R2; ANSYS: Canonsburg, PA, USA, 2022.
- BOVIA. Dassault Systèmes BOVIA SOLIDWORKS Sustainability Overview. Available online: https://help.solidworks.com/2020/english/SolidWorks/sldworks/c_Sustainability_Overview.htm (accessed on 24 April 2023).
- BOVIA. Dassault Systèmes BOVIA SOLIDWORKS Costing Overview. Available online: https://help.solidworks.com/2018/english/SolidWorks/sldworks/c_costing_top.htm (accessed on 24 April 2023).
- Alexandrova, Y.; Semken, R.S.; Pyrhönen, J. Permanent Magnet Synchronous Generator Design Solution for Large Direct-Drive Wind Turbines: Thermal Behavior of the LC DD-PMSG. Appl. Therm. Eng. 2014, 65, 554–563. [Google Scholar] [CrossRef]
- ANSYS. SOLID227. 3-D 10-Node Coupled-Field Solid. Available online: https://www.mm.bme.hu/~gyebro/files/ans_help_v182/ans_elem/Hlp_E_SOLID227.html#elem227structmat (accessed on 16 April 2024).
- ANSYS. ANSYS ® Granta Selector 2022, Release 2022R1; ANSYS: Canonsburg, PA, USA, 2022.
- Kirschneck, M. Mastering Electro-Mechanical Dynamics of Large Off-Shore Direct-Drive Wind Turbine Generators Proefschrift. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Donald, A.M.C.; Mueller, M.; Zavvos, A. Electrical Drives for Direct Drive Renewable Energy Systems. Chapter 3: Electrical, Thermal and Structural Generator Design and Systems Integration for Direct Drive Renewable Energy Systems; Mueller, M., Polinder, H., Eds.; Woodhead Publishing Limited: Cambridge, UK, 2013. [Google Scholar]
- McDonald, A.S.; Mueller, M.A.; Polinder, H. Structural Mass in Direct-Drive Permanent Magnet Electrical Generators. Proc. IET Renew. Power Gener. 2008, 2, 3–15. [Google Scholar] [CrossRef]


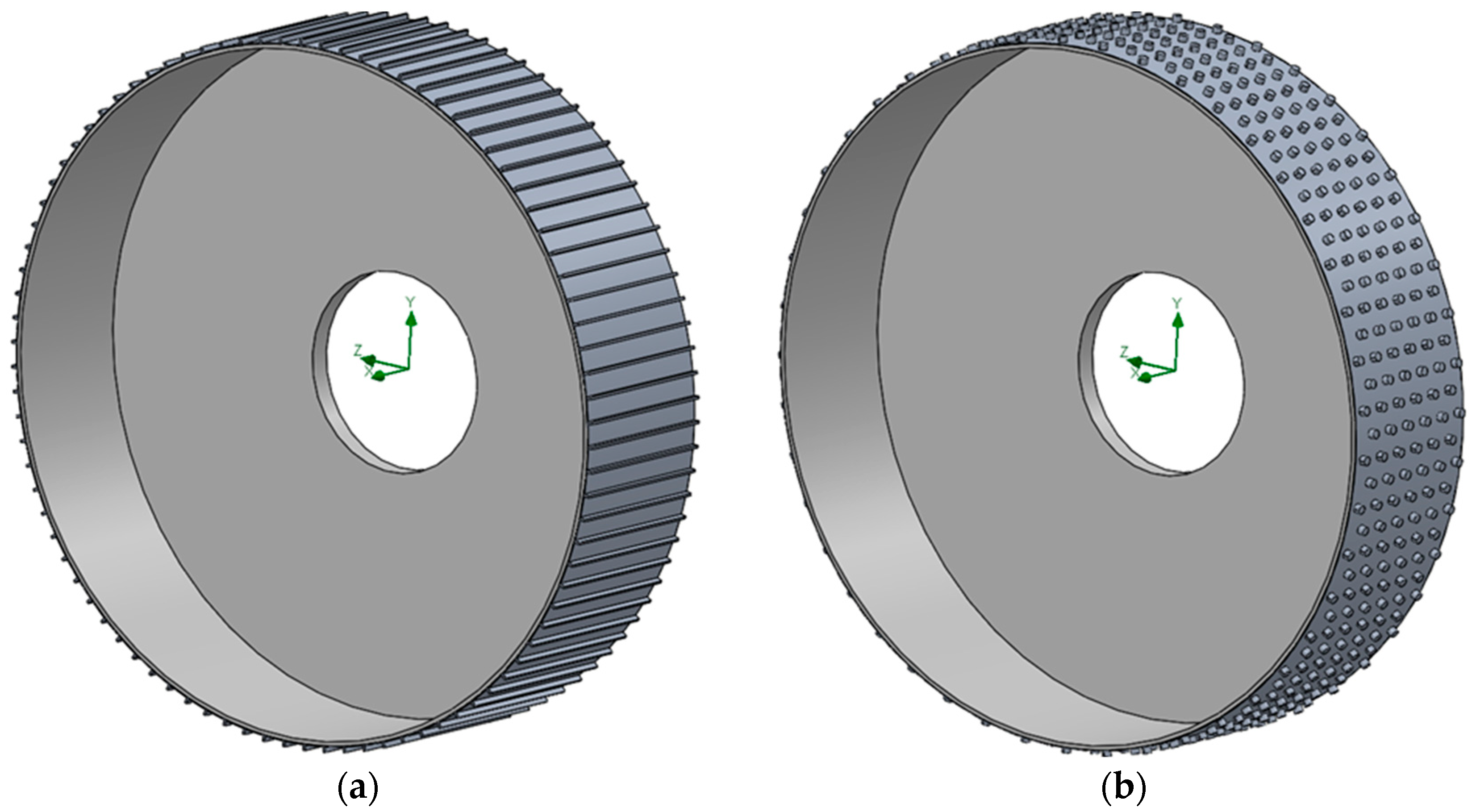
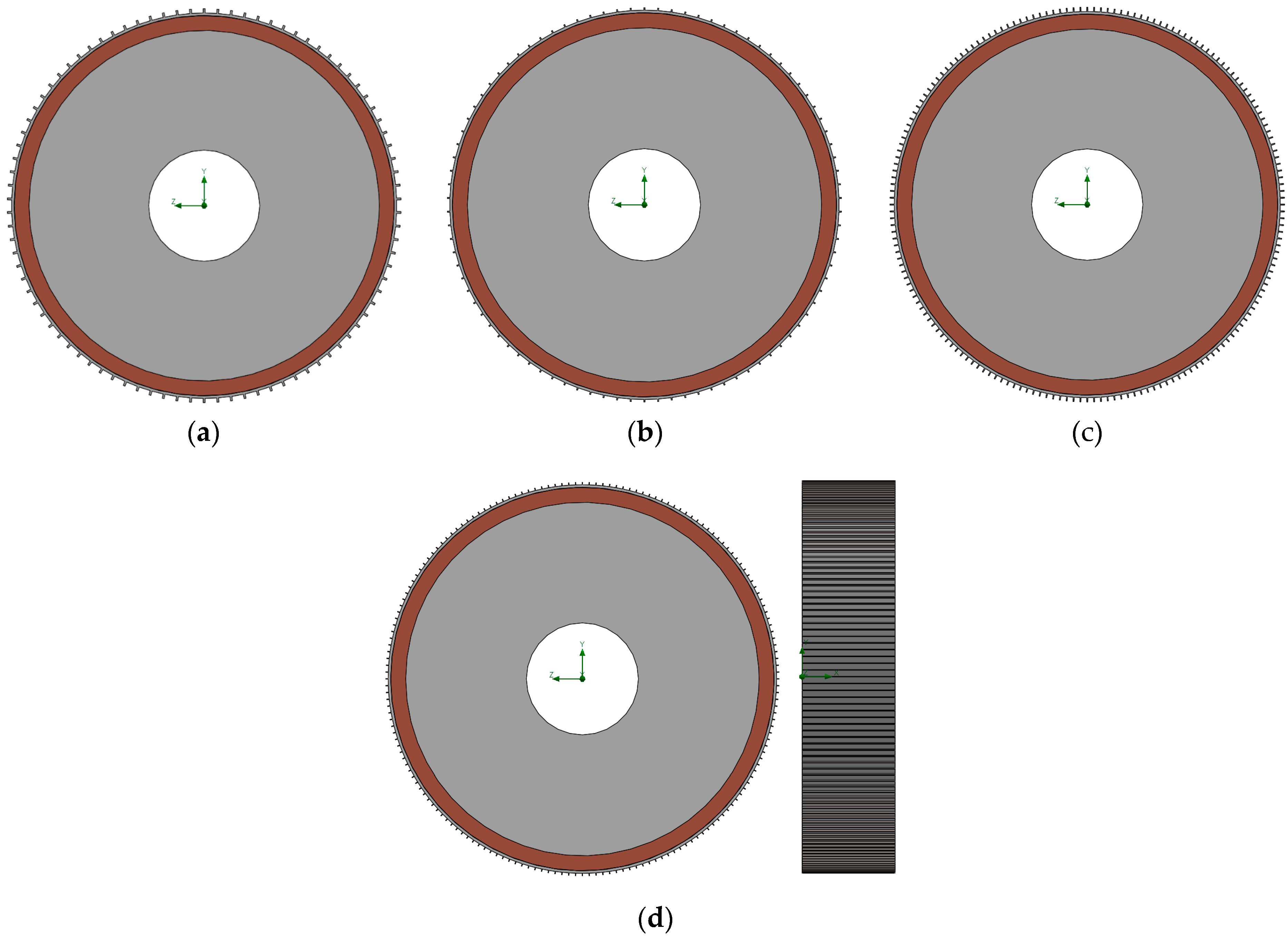





| Design Name | Heatsink Composition | Nature | Number of Fins | Total (Heatsink) Mass [t] | Total (Heatsink) Volume [m3] | Total (Heatsink) Surface Area [m2] |
|---|---|---|---|---|---|---|
| Parameter Optimised Rotor | None | None | None | 234.9 | 30.03 | 310.55 |
| Small-90 | Carbon Steel SA216 | Fins—integrated | 90 | 238.4 | 30.47 | 340.34 |
| Large-90 | Carbon Steel SA216 | Fins—integrated | 90 | 245.5 | 31.37 | 364.22 |
| Small-180 | Carbon Steel SA216 | Fins—integrated | 180 | 238.4 | 30.47 | 369.77 |
| Large-180 | Carbon Steel SA216 | Fins—integrated | 180 | 245.5 | 31.37 | 416.78 |
| Retrofit Fins | Aluminium | Fins—external | 90 | 239.2 (4.19) | 31.58 (1.55) | 511.96 (201.41) |
| Retrofit Pins | Aluminium | Pins—external | 90 rows 540 pins | 239.0 (4.04) | 31.53 (1.50) | 495.48 (184.93) |
| Advanced Rotor | Carbon Steel SA216 | Fins—integrated, helix | 176 | 174.2 | 22.27 | 500 |
| Mesh Analysis | |
| Elements | 300,000–1,500,000 |
| Mesh control method | Hexahedron |
| Element size | 0.2 m |
| Local mesh control (optimisation volume) | 0.1 m |
| Multi-Objective Criteria | Objective Weight |
| Primary criterion: Airgap displacement limit (2.0 mm) | (5) |
| Mass reduction | (3) |
| Minimise total displacement | (1) |
| Maximise frequency modes | (1) |
| Optimisation Process | |
| Convergence rate | 0.2% |
| Number of iterations | 50–500 |
| Response constraint | Mass reduction %; Primary criterion |
| Manufacturing constraints | Cyclic symmetry; pull-out direction; and AM overhang angle |
| Description | Unaltered IEA Rotor | Previous Parameter Optimised Rotor [13] | Parameter Optimised Baseline | Advanced Rotor | Limits |
|---|---|---|---|---|---|
| Disk thickness (mm) | 82.21 | 416.18 | 326.21 | 116 | - |
| Cylinder thickness (mm) | 129.06 | 224.32 | 65.37 | 183.8 | - |
| Mass (kg) | 1.2255 × 105 | 3.9802 × 105 | 2.3498 × 105 | 1.7425 × 105 | - |
| Mode 0 Max. Eq. Von-Mises Stress (MPa) | 69.32 | 12.99 | 38.77 | 68.01 | 200 |
| Mode 0 Max. Total Deformation (mm) | 20.45 | 0.93 | 1.47 | 1.52 | 2.03 |
| Mode 1 Max. Eq. Von-Mises Stress (MPa) | 100.10 | 13.40 | 40.03 | 59.98 | 200 |
| Mode 1 Max. Total Deformation (mm) | 30.68 | 1.08 | 1.78 | 1.72 | 2.03 |
| Candidate | Outside Cylinder Radius (mm) | Outside Shaft Radius (mm) | Disk Thickness (mm) | Support Thickness (mm) | Mass (tonne) | Deformation (mm) |
|---|---|---|---|---|---|---|
| 1 | 5322.1 | 1451.6 | 115 | 99.635 | 206.39 | 1.099 |
| 2 | 5328.9 | 1452.1 | 114.44 | 99.709 | 210.09 | 1.098 |
| 3 | 5334.5 | 1458.7 | 114.48 | 98.502 | 213.81 | 1.098 |
| 4 | 5322.7 | 1459.1 | 114.61 | 101.71 | 207.82 | 1.095 |
| 5 | 5322.7 | 1459.1 | 114.61 | 101.71 | 207.82 | 1.095 |
| 6 | 5320.1 | 1452 | 116.09 | 98.69 | 205.75 | 1.096 |
| 7 | 5328.1 | 1475 | 114.4 | 99.051 | 211.97 | 1.100 |
| 8 | 5322.9 | 1473 | 114.88 | 99.294 | 209.07 | 1.100 |
| 9 | 5330.3 | 1452.2 | 115.17 | 99.113 | 211.25 | 1.093 |
| 10 | 5320.4 | 1453 | 115.72 | 99.935 | 206.12 | 1.095 |
| Modification | Rotor + Inner Disk Supports | Disk Cuts | Cylinder Cuts | Outer Disk Supports | Heatsink | Overall Change |
|---|---|---|---|---|---|---|
| Total Mass (t) | 208.62 | 190.32 | 156.75 | 168.46 | 174.25 | −34.37 |
| Mass (%) | - | −8.77 | −17.64 | +7.47 | +3.44 | −16.47 |
| Deformation (mm) | 11.09 | 1.56 | 1.75 | 1.59 | 1.53 | +0.43 |
| Rotor | Average Heat Generation Rate | Maximum Heat Generation Rate | Average Rotor Temperature | Maximum Rotor Temperature |
|---|---|---|---|---|
| Unaltered Rotor | 431.7 °C | 448.5 °C | 169.5 °C | 245.6 °C |
| Unaltered Rotor w/Magnets | 414.1 °C | 430.7 °C | 172.4 °C | 263.6 °C |
| Parameter Optimised Rotor | 415.5 °C | 432.6 °C | 170.2 °C | 249.0 °C |
| Small-90 | 413.9 °C | 425.2 °C | 162.1 °C | 232.6 °C |
| Large-90 | 412.9 °C | 424.8 °C | 161.4 °C | 230.0 °C |
| Small-180 | 410.9 °C | 422.4 °C | 159.1 °C | 227.8 °C |
| Large-180 | 409.2 °C | 419.0 °C | 147.9 °C | 215.5 °C |
| External Fins | 412.8 °C | 424.4 °C | 161.8 °C | 231.9 °C |
| External Pins | 412.5 °C | 423.0 °C | 184.0 °C | 227.3 °C |
| Advanced Rotor | 404.3 °C | 413.7 °C | 117.9 °C | 179.9 °C |
| No Temperature Considerations | 55.7 °C Operating Temperature | CFD Import | ||||
|---|---|---|---|---|---|---|
| Max. Cylinder Deformation (mm) | Stress (Pa) | Max. Cylinder Deformation (mm) | Stress (Pa) | Max. Cylinder Deformation (mm) | Stress (Pa) | |
| Parameter Optimised Rotor | 1.46 | 3.867 × 107 | 2.17 | 1.921 × 108 | 11.10 | 4.858 × 108 |
| Small-90 | 1.53 | 4.613 × 107 | 2.18 | 1.847 × 108 | 10.24 | 4.519 × 108 |
| Large-90 | 1.69 | 4.494 × 107 | 2.30 | 1.846 × 108 | 10.63 | 4.492 × 108 |
| Small-180 | 1.53 | 4.757 × 107 | 2.18 | 1.848 × 108 | 9.44 | 4.461 × 108 |
| Large-180 | 1.70 | 4.480 × 107 | 2.31 | 1.846 × 108 | 9.84 | 4.107 × 108 |
| External Fins | 1.50 | 3.747 × 107 | 2.65 | 1.847 × 108 | 11.19 | 4.531 × 108 |
| External Pins | 1.46 | 3.844 × 107 | 2.48 | 1.923 × 108 | 11.62 | 4.499 × 108 |
| Advanced Rotor | 1.54 | 6.778 × 107 | 2.30 | 2.419 × 108 | 7.10 | 7.180 × 108 |
| Unaltered IEA Rotor | Parameter Optimised Rotor | Advanced Rotor | ||
|---|---|---|---|---|
| Energy (TJ) | Casting | 1.63 | 2.86 | 2.48 |
| Machining | N/A | N/A | 0.04 | |
| (% change) | - | +75.5 | +54.6 | |
| Carbon Dioxide (t) | Casting | 98.22 | 171.82 | 149.16 |
| Machining | N/A | N/A | 2.52 | |
| (% change) | - | +74.9 | +54.4 | |
| Water (Litres) | Casting | 3.76 × 106 | 6.57 × 106 | 5.70 × 106 |
| (% change) | - | +74.7 | +51.6 |
| Unaltered Rotor | Parameter Optimised Baseline Rotor | Advanced Rotor | ||
|---|---|---|---|---|
| Manufacturing cost | GBP (USD) | 97,600 (123,400) | 172,400 (218,000) | 193,100 (244,100) |
| Change from original | % | - | +76.6 | +97.8 |
| Financial impact | GBP (USD) | 58,200 (73,600) | 114,000 (144,200) | 131,500 (166,200) |
| Change from original | % | - | +95.9 | +125.9 |
| Total | GBP (USD) | 155,800 (197,000) | 286,400 (362,200) | 324,600 (410,300) |
| Change from original | % | - | +83.8 | +108.3 |
| T: 55.7 °C | Advanced Rotor with Heatsink | (a) | (b) | (c) |
|---|---|---|---|---|
| Total Mass (t) | 174.25 | 139.49 | 169.56 | 161.95 |
| Mass (%) | N/A | −24.92% | −2.77% | −7.59% |
| Deformation (mm) | 2.30 | 2.057 | 1.782 | 1.808 |
| Max. Eq. Von-Mises Stress (MPa) | 241.90 | 295.77 | 214.32 | 340.16 |
| Effective Mass Participation Factor | |||||
|---|---|---|---|---|---|
| Model | Frequency Mode | Frequency (Hz) | X-Direction | Y-Direction | Axial Z-Direction |
| Advanced rotor with Heatsink | |||||
| 3 | 15.77 | 5.58 | 2.10 | 0.00 | |
| 4 | 15.77 | 2.10 | 5.58 | 0.00 | |
| 7 | 19.07 | 0.00 | 0.00 | 69.38 | |
| 13 | 46.57 | 46.34 | 9.06 | 0.00 | |
| 14 | 46.57 | 9.06 | 46.34 | 0.00 | |
| (a) | 4 | 14.59 | 4.45 | 6.27 | 0.00 |
| 5 | 14.60 | 6.28 | 4.46 | 0.00 | |
| 8 | 17.73 | 0.00 | 0.00 | 74.63 | |
| 13 | 38.08 | 55.38 | 6.17 | 0.00 | |
| 14 | 38.09 | 6.17 | 55.38 | 0.00 | |
| (b) | 3 | 16.22 | 6.17 | 0.38 | 0.00 |
| 4 | 16.22 | 0.38 | 6.17 | 0.00 | |
| 7 | 19.36 | 0.00 | 0.00 | 69.44 | |
| 15 | 53.10 | 52.23 | 6.09 | 0.00 | |
| 16 | 53.10 | 6.09 | 52.22 | 0.00 | |
| (c) | 3 | 15.16 | 2.47 | 4.23 | 0.00 |
| 4 | 15.16 | 4.23 | 2.47 | 0.00 | |
| 7 | 18.13 | 0.00 | 0.00 | 72.97 | |
| 15 | 52.62 | 49.95 | 9.72 | 0.00 | |
| 16 | 52.62 | 9.72 | 49.95 | 0.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bichan, M.; Jaen-Sola, P.; Gonzalez-Delgado, D.; Oterkus, E. On the Integrity of Large-Scale Direct-Drive Wind Turbine Electrical Generator Structures: An Integrated Design Methodology for Optimisation, Considering Thermal Loads and Novel Techniques. Machines 2024, 12, 277. https://doi.org/10.3390/machines12040277
Bichan M, Jaen-Sola P, Gonzalez-Delgado D, Oterkus E. On the Integrity of Large-Scale Direct-Drive Wind Turbine Electrical Generator Structures: An Integrated Design Methodology for Optimisation, Considering Thermal Loads and Novel Techniques. Machines. 2024; 12(4):277. https://doi.org/10.3390/machines12040277
Chicago/Turabian StyleBichan, Magnus, Pablo Jaen-Sola, Daniel Gonzalez-Delgado, and Erkan Oterkus. 2024. "On the Integrity of Large-Scale Direct-Drive Wind Turbine Electrical Generator Structures: An Integrated Design Methodology for Optimisation, Considering Thermal Loads and Novel Techniques" Machines 12, no. 4: 277. https://doi.org/10.3390/machines12040277
APA StyleBichan, M., Jaen-Sola, P., Gonzalez-Delgado, D., & Oterkus, E. (2024). On the Integrity of Large-Scale Direct-Drive Wind Turbine Electrical Generator Structures: An Integrated Design Methodology for Optimisation, Considering Thermal Loads and Novel Techniques. Machines, 12(4), 277. https://doi.org/10.3390/machines12040277










