Study on the Evolution of Sealing Performance during the Start-Up Process of Dynamic Pressure Seals Based on Three-Dimensional Fractal Functions
Abstract
1. Introduction
2. Dynamic Pressure Seal Structure and Sealing Principle
3. The Model for the Evolution of Seal Performance during Seal Initiation
3.1. Asperity-Asperity Thermoelastic-Plastic Contact Deformation Analysis
3.2. Thermoelastic Deformation Analysis of the Bases
3.3. Microfluidic Characterization of Thin Films with Sealing Gaps
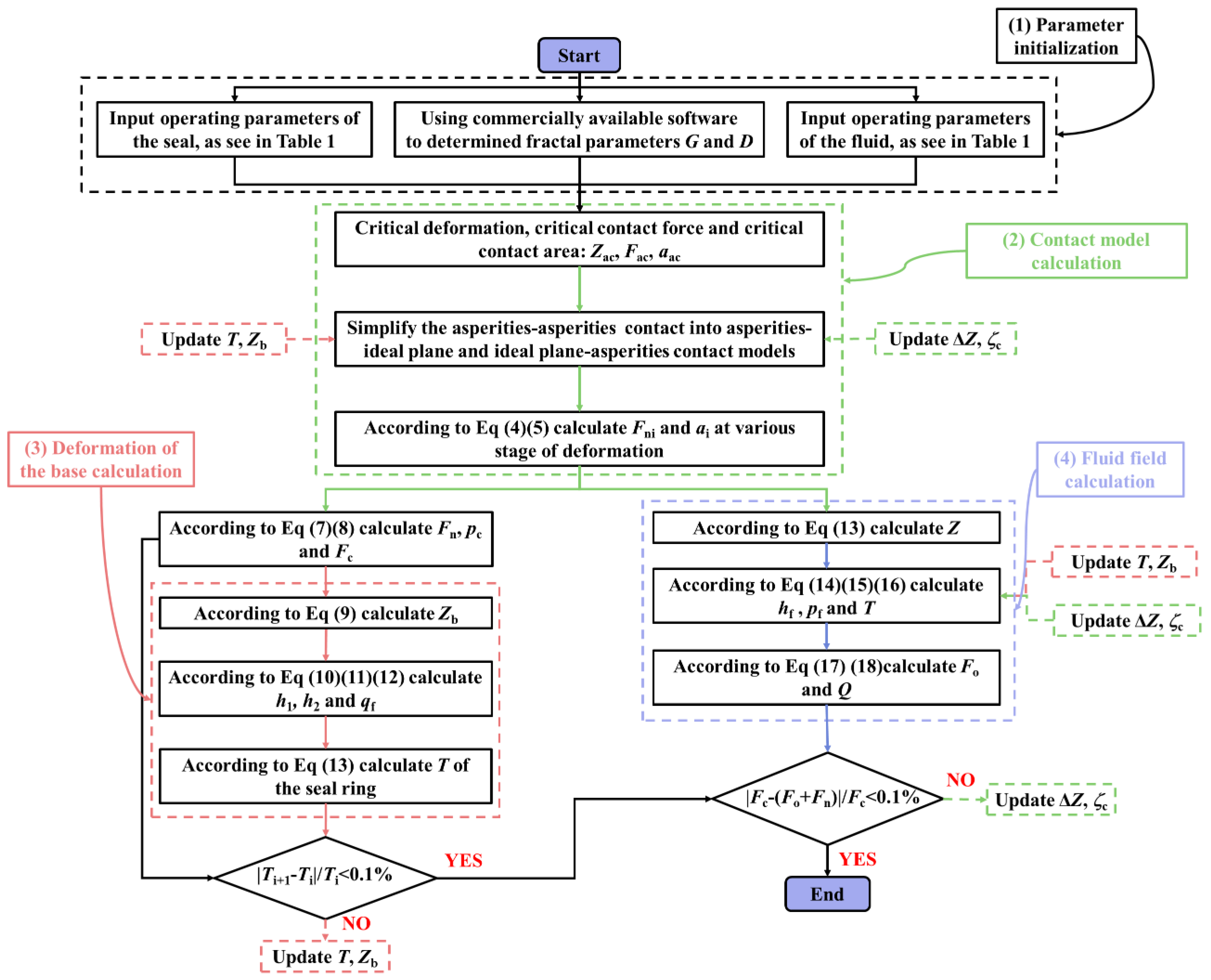
3.4. Coupled Analysis Process
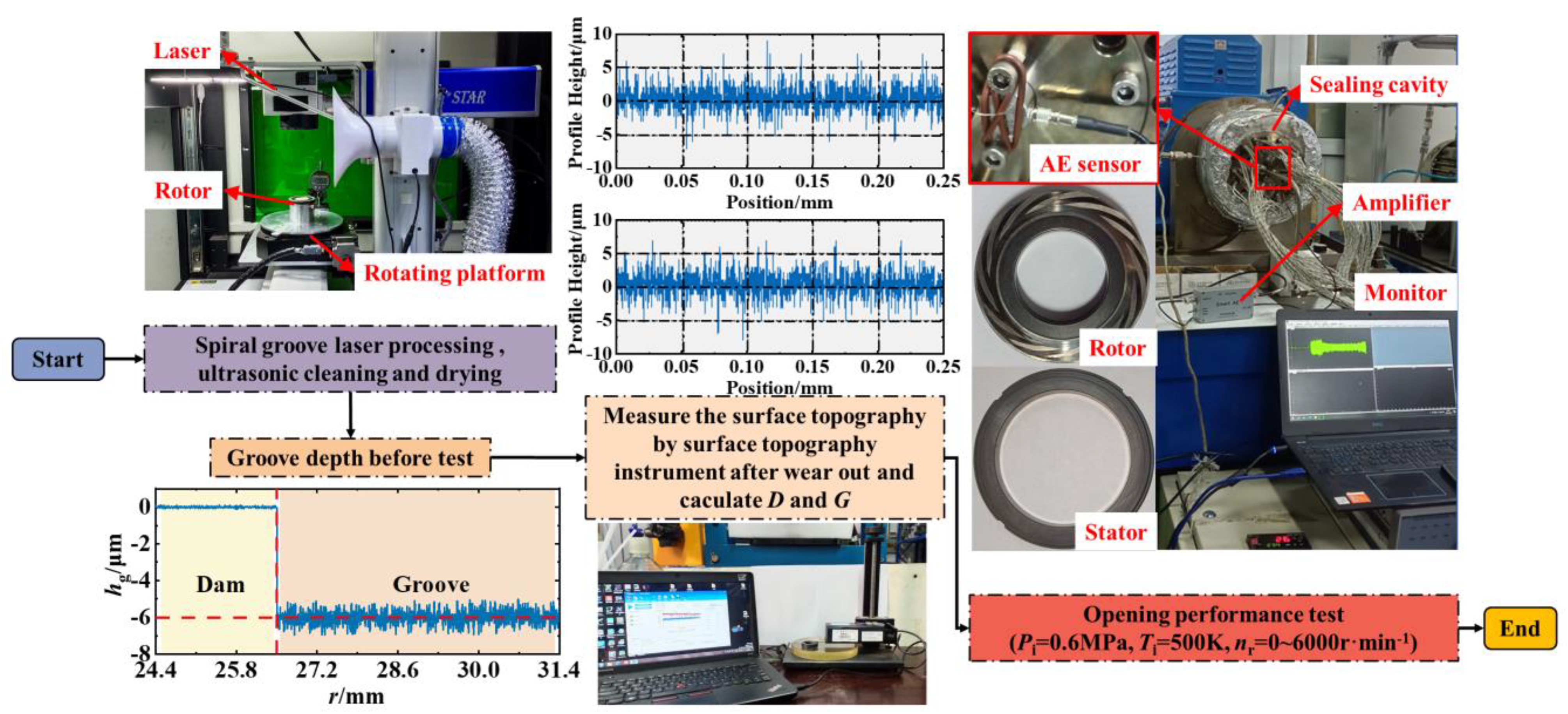
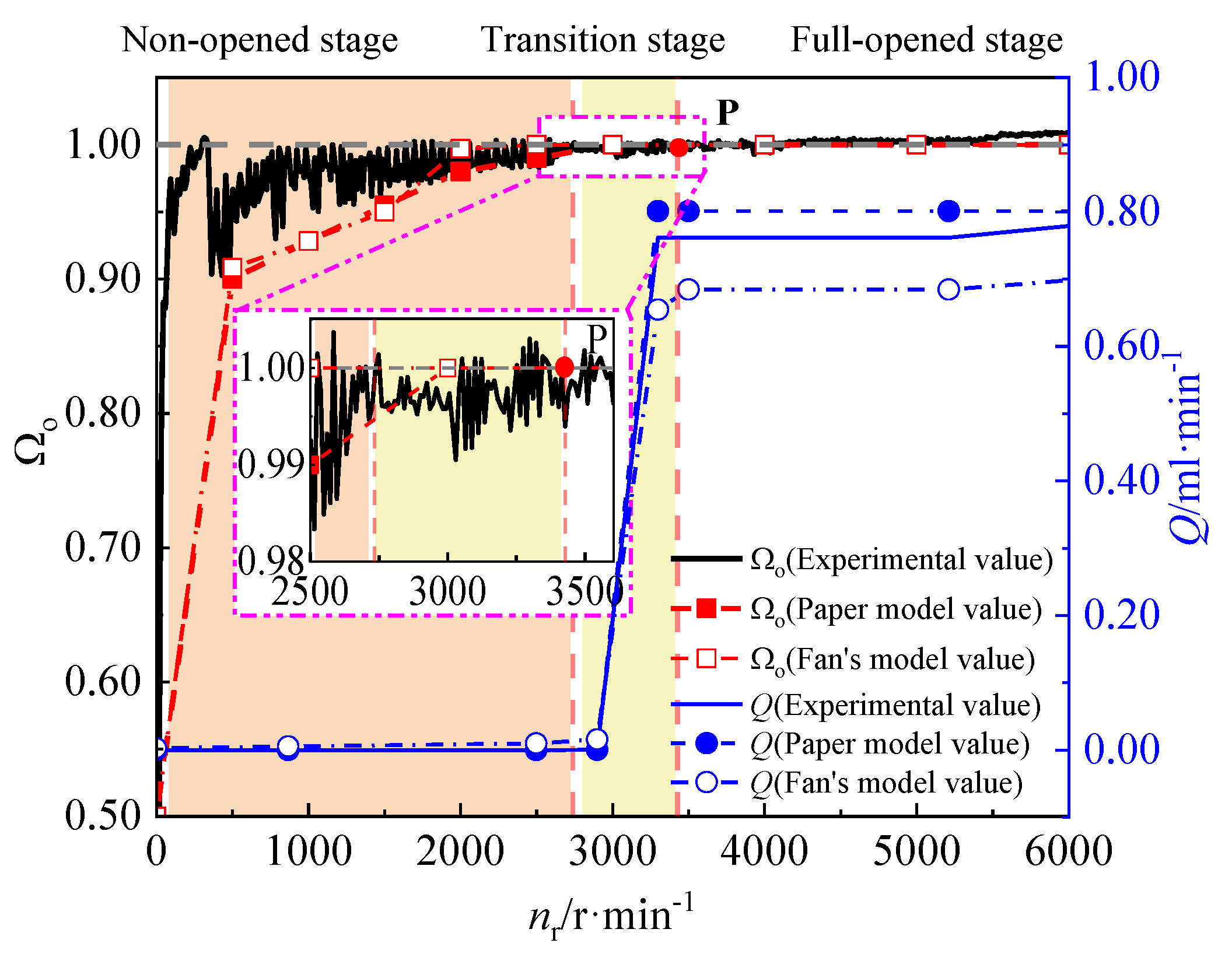
3.5. Model Validation
4. Discussion
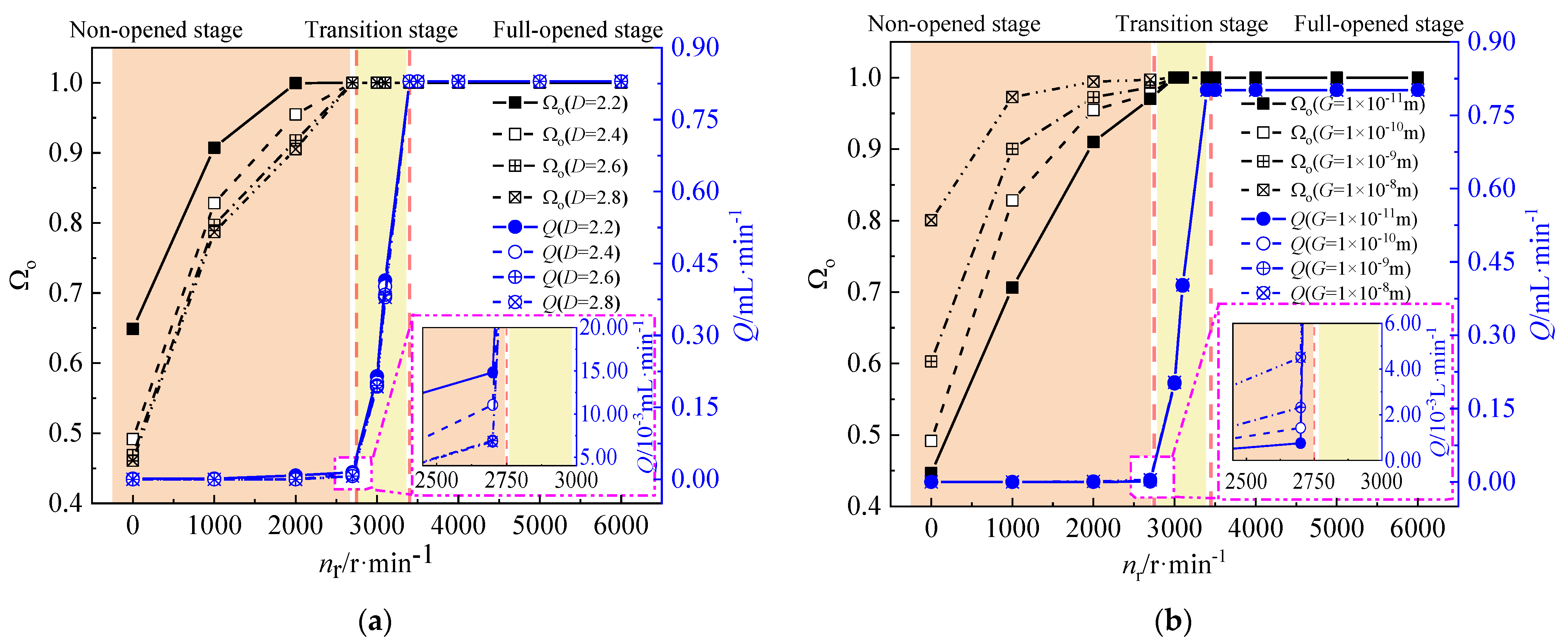
4.1. Effect of Fractal Parameters on the Sealing Performance during the Start-Up Process
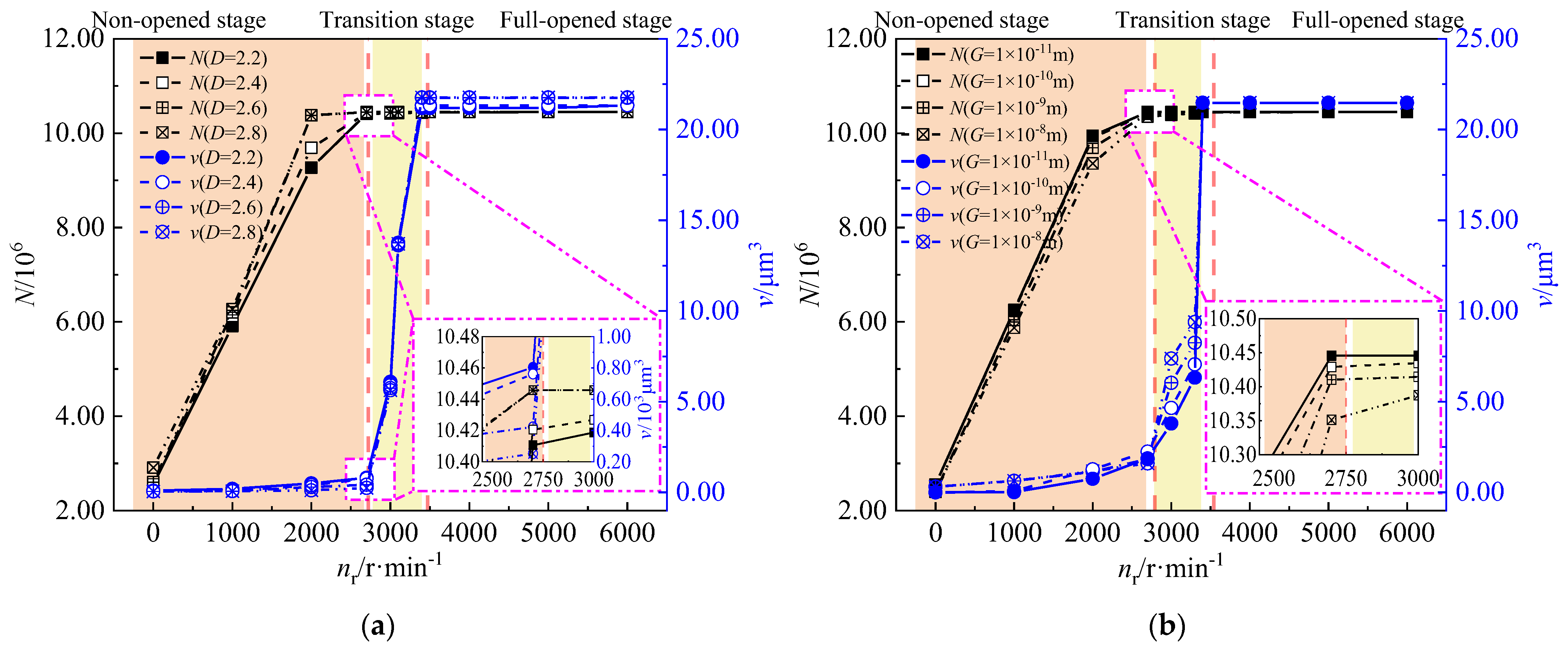
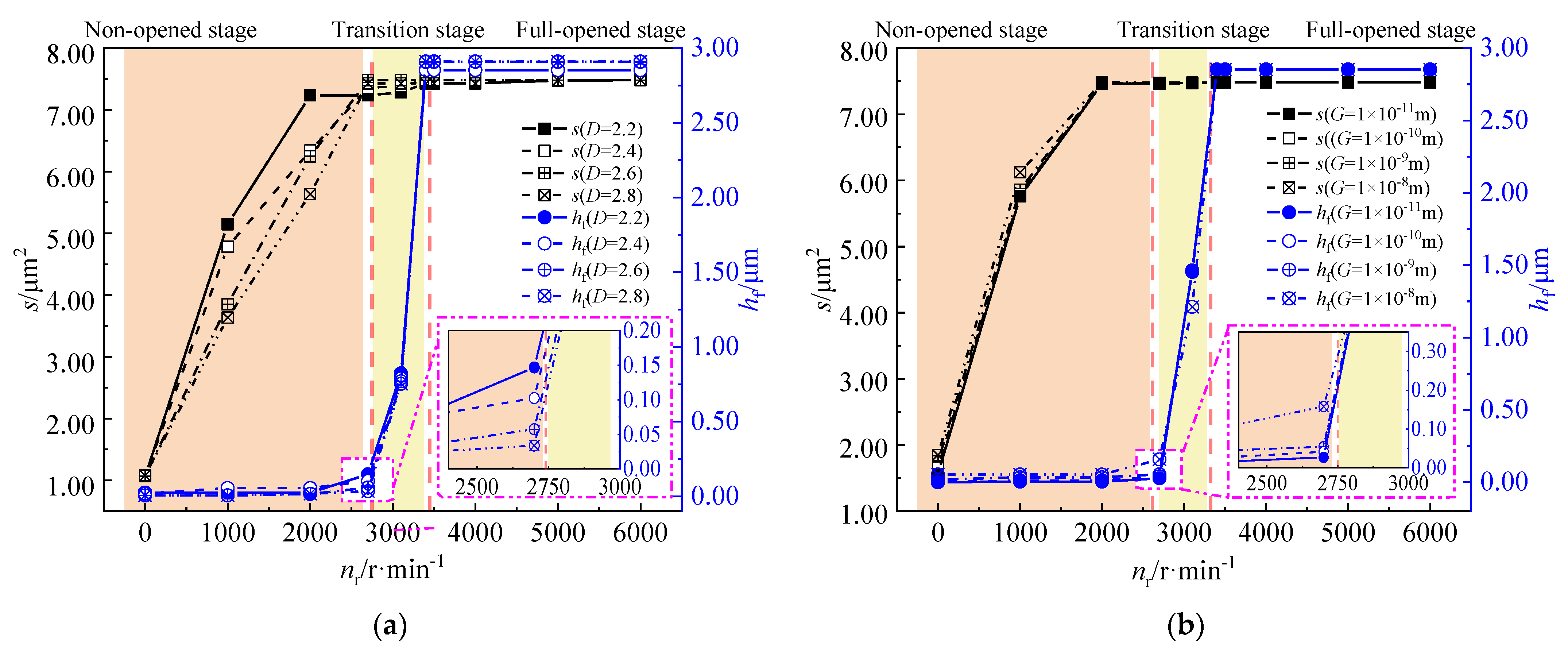
4.2. Effect of Fractal Parameters on the Micro-Features on End-Faces during Start-Up Process
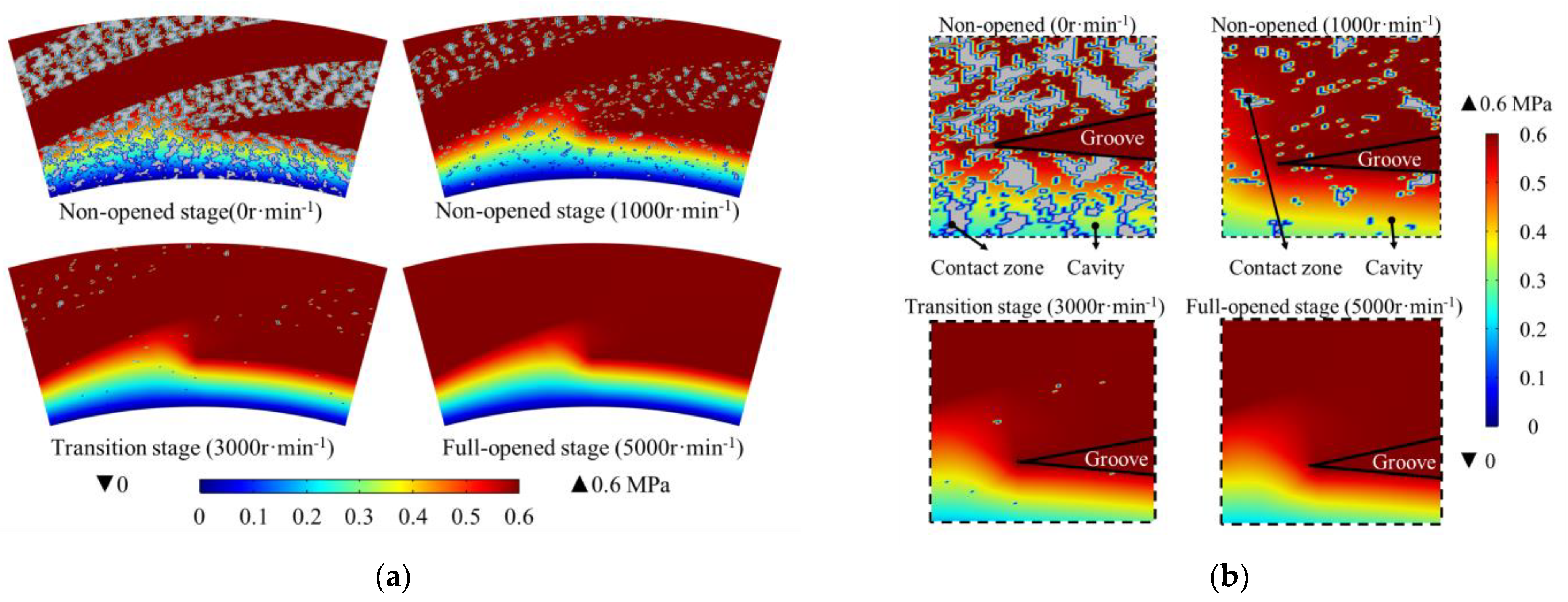
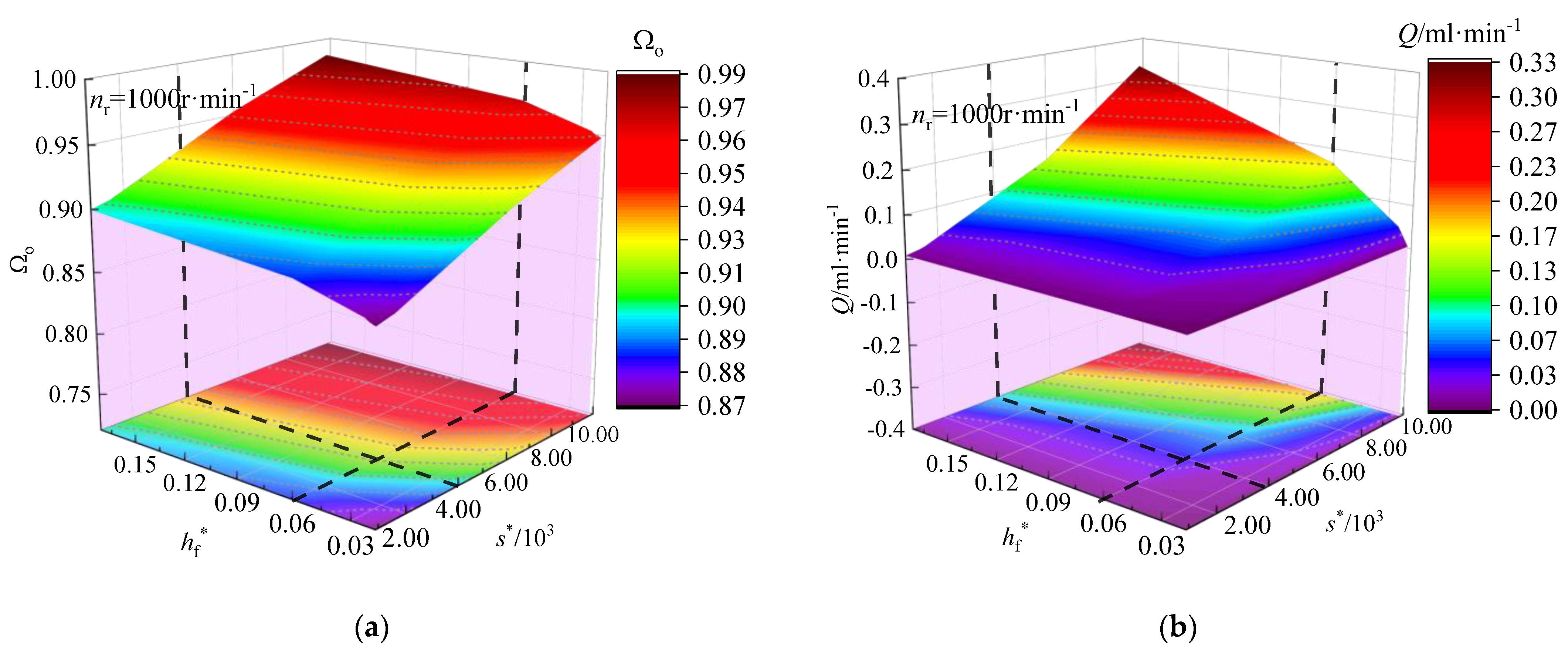
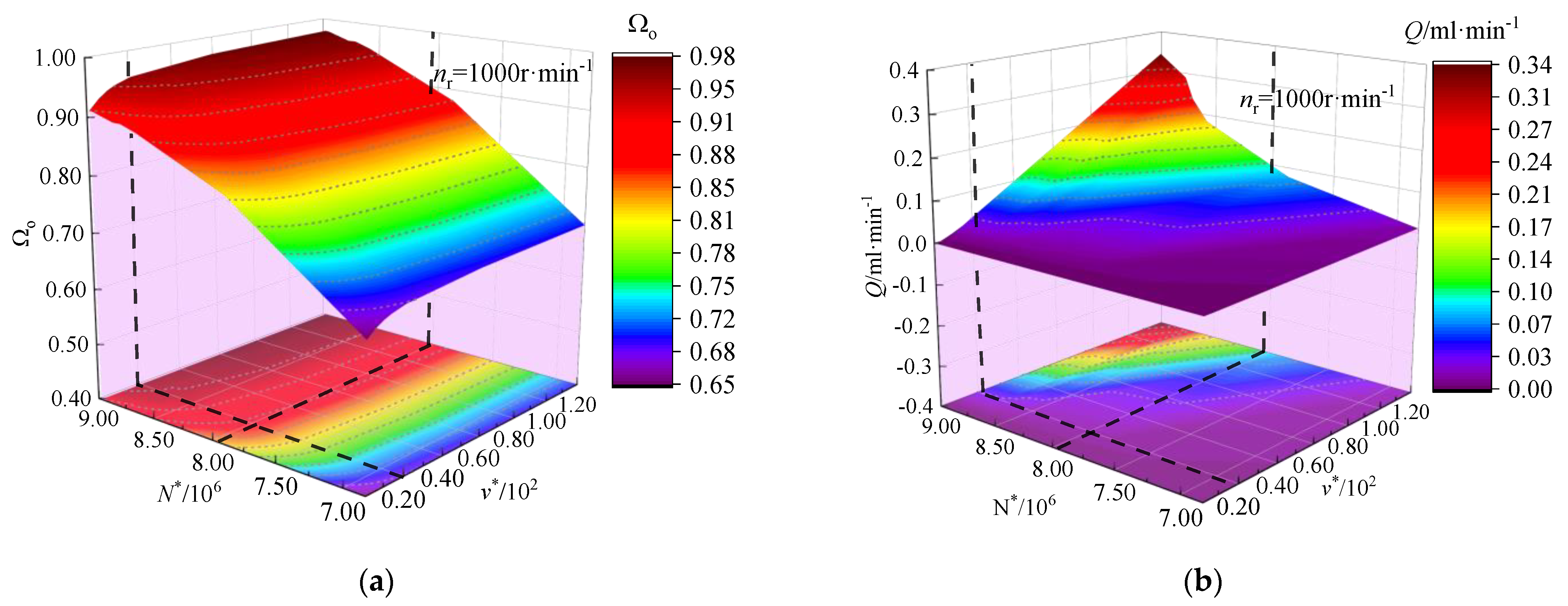
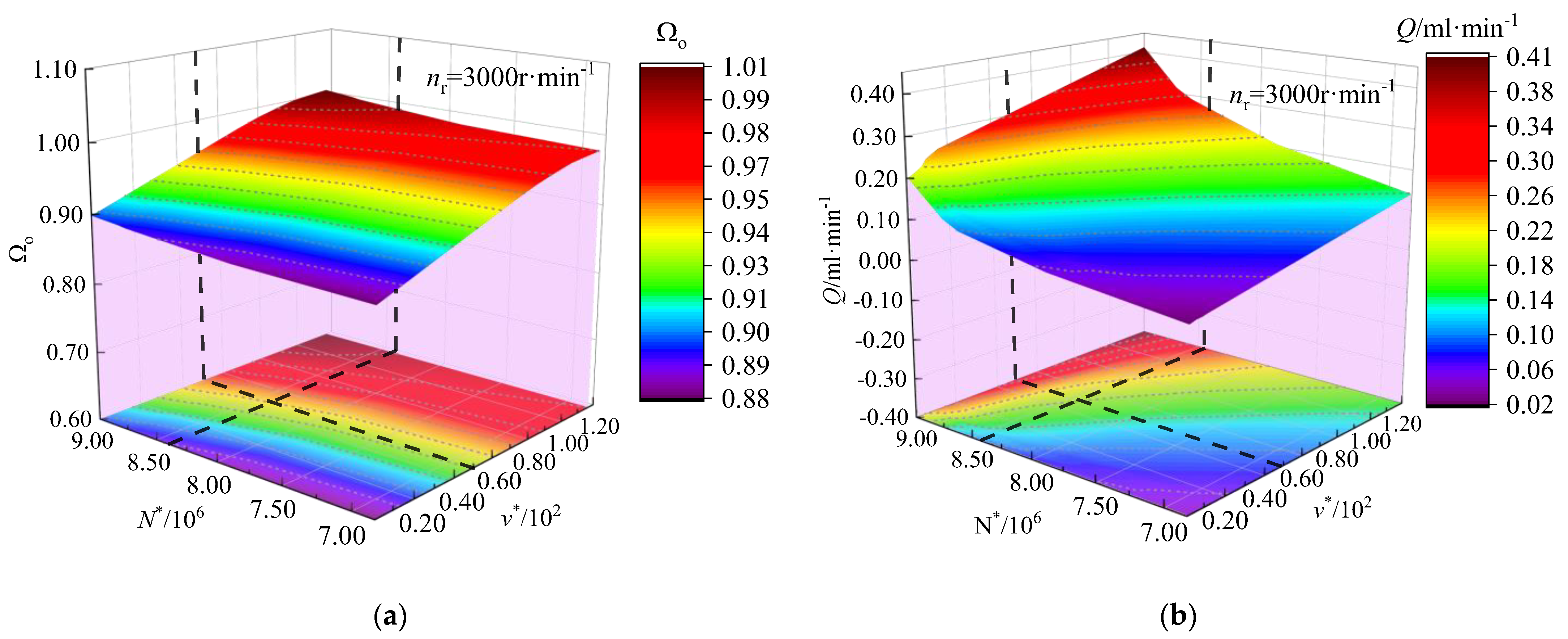
4.3. Effect of the Micro-Features on the Sealing Performance during the Start-Up Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhuo, Z.Y.; Chen, Y.; Li, Y.T.; Wang, B.Q.; Peng, X.D. Intelligent Prediction of Control Force of Active Hydrodynamic Pressure Dry Gas Seal under Random Conditions and Comparative Study of Its Algorithm Performance. Tribology 2023, 43, 1370–1380. [Google Scholar] [CrossRef]
- Park, Y.; Hahn, M.; Jang, G. Effect of Laminar, Turbulent and Slip Conditions on the Dynamic Coefficients of a Dry Gas Seal. Lubricants 2023, 11, 98. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.B.; Peng, X.D. Numerical analysis of supercritical CO dry gas seals with phase transitions. Ind. Lubr. Tribol. 2022, 74, 780–787. [Google Scholar] [CrossRef]
- Zhai, X.; Yang, X.C.; Chen, J.L.; Ding, X.X. Elastic-plastic contact stiffness model of dry gas seal friction interface. J. Vib. Shock. 2023, 42, 165–171. [Google Scholar] [CrossRef]
- Bai, S.X.; Song, Y.S.; Yang, J. Elastic deformation of liquid spiral groove face seals operating at high speeds and low pressure. Int. J. Mech. Sci. 2022, 226, 107397. [Google Scholar] [CrossRef]
- Li, Q.Z.; Li, S.X.; Zheng, R.; Jiang, L.; Zeng, Y.; Zhu, M.Y. Friction and Wear Performance of Oil-gas Miscible Reflux Pumping Seal During Start-up. Aeroengine 2023, 49, 167–174. [Google Scholar] [CrossRef]
- Su, W.T.; Hu, S.H.; Wang, L.; Feng, X.D. Performance analysis and optimized model selection of wavy hydrodynamic mechanical seals. J. China Univ. Pet. (Ed. Nat. Sci.) 2023, 47, 138–145. [Google Scholar] [CrossRef]
- Yin, T.; Wei, D.; Wang, T.; Xie, Z. Thermal compression and accumulation effect on lubrication regime transition mechanism of water seal. Tribol. Int. 2023, 181, 108285. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Li, X.Y.; Wang, Z.L.; Yu, B.; Hao, M.M. Steady-State Performance of Liquid Film Seal Considering Dissolution of Methane. Tribology 2023, 43, 645–656. [Google Scholar] [CrossRef]
- Hu, Z.L.; Fan, X.; Diao, D.F. Facilitation of sp2 nanocrystallites on the formation of transfer films for stable low friction with in-situ TEM nanofriction study. Tribol. Int. 2022, 174, 107713. [Google Scholar] [CrossRef]
- Chen, W.; Song, P.Y.; Xu, H.J.; Sun, X.J. Study on Startup Process of Carbon Dioxide with Impurities Lubricating Dry Gas Seal. Lubr. Eng. 2022, 47, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Hao, M.; Li, X.; Liu, K. The effect of thermal-elastic deformation on the sealing performance of supercritical CO dry gas seal. Ind. Lubr. Tribol. 2023, 75, 950–958. [Google Scholar] [CrossRef]
- Hossain Bhuiyan, M.M.; Sakib, A.N.; Corral, A.B.; Siddique, Z. Investigating the influence of operating variables on sealing performance of a V-ring seal stack in the oil and gas industry for enhanced environmental and operational performance. Polym. Test. 2024, 131, 108346. [Google Scholar] [CrossRef]
- Cui, Y.; Yu, Y.; Zhong, J.; Wang, Y. Prediction of sealing interface leakage based on porous medium model considering effective porosity. Tribol. Int. 2022, 174, 107695. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, W.; Dong, R.; Cao, Z. Multi-scale dimensionless prediction model of PEMFC sealing interface leakage rate based on fractal geometry. Int. J. Hydrogen Energy 2023, 48, 5276–5287. [Google Scholar] [CrossRef]
- Bai, L.Q.; Zhang, P.C.; Ahmad, K.Z. Semi Salix Leaf Textured Gas Mechanical Face Seal with Enhanced Opening Performance. Materials 2021, 14, 7522. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, X.D.; Wang, B.Q.; Jiang, J.B.; Li, J.Y. Experimental and theoretical investigations on dry gas seal transient performance and its disparity with steady performance. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 1661–1673. [Google Scholar] [CrossRef]
- Li, Y.F.; Brunetière, N.; Hao, M.M.; Li, T.Z.; Liu, F.Y. Experimental study on transient frictional features of herringbone-grooved mechanical face seals in start-up and stop stages. Tribol. Int. 2022, 175, 107790. [Google Scholar] [CrossRef]
- Mutellip, A.; Runsheng, Y. Coupling analysis of thermal-solid deformation for spiral groove mechanical seal. In Proceedings of the International Conference on Mechanical Design and Simulation (MDS 2022), Wuhan, China, 18–20 March 2022; Volume 12261, p. 122610E. [Google Scholar] [CrossRef]
- Xu, W.; Tian, Y.; Song, Y.; Xu, Y. Bidirectional Trapezoidal Versus Unidirectional Spiral Groove Performance in Dry Gas Seals. Int. J. Fluid Mach. Syst. 2021, 14, 220–228. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, Z.; Gu, C.H.; Wang, J.H. Thermo-mechanical coupling analysis of the end faces for a mechanical seal under dry friction. Tribol. Int. 2021, 160, 107050. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.B.; Zhao, W.J.; Jin, J.; Peng, X.D. A comprehensive multi-objective, multi-parameter and multi-condition optimization of a spiral groove in dry gas seals. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 206. [Google Scholar] [CrossRef]
- Fan, Y.; Song, P.Y.; Xu, H.J. Study on startup operation of dry gas seal with steam lubrication. CIESC J. 2020, 71, 3671–3680. [Google Scholar] [CrossRef]
- Zhang, H.B.; Izhak, E. Evolution of adhesive wear and friction in elastic-plastic spherical contact. Wear 2021, 478–479, 203915. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal Model of Elastic-Plastic Contact Between Rough Surfaces. J. Tribol. 1991, 113. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Yuan, Y.; Cheng, Y.; Liu, K.; Gan, L. A revised Majumdar and Bushan model of elastoplastic contact between rough surfaces. Appl. Surf. Sci. 2017, 425, 1138–1157. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Ding, X.X.; Zhang, L.X.; Li, N.; Si, J.X. Fractal wear prediction model and numerical analysis of floating ring seal face. CIESC J. 2022, 73, 5526–5536. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, X.; Xu, J.; Jiang, H.; Li, N.; Si, J. A study on building and testing fractal model for predicting end face wear of Aeroengine’s floating ring seal. Wear 2023, 532–533, 205079. [Google Scholar] [CrossRef]
- Nordhagen, E.M.; Sveinsson, H.A.; Malthe-Sørenssen, A. Diffusion-Driven Frictional Aging in Silicon Carbide. Tribol. Lett. 2023, 71, 95. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Nikhil, C.; Rao, S.; Mandal, S.; Ganguly, R.; Rao, M.S.R.; Arunachalam, N. Tribological behavior of diamond coated reaction-bonded silicon carbide under dry and seawater environment. Surf. Coat. Technol. 2024, 476, 130204. [Google Scholar] [CrossRef]
- Zhao, W.; He, W.F.; Liang, X.Q.; Huang, Z.B.; Zhou, Q.; Pang, Z.C.; Song, J.D.; Hu, S.; Cui, L.Q.; Luo, S.H. Enhancing elevated-temperature fretting wear performance of GH4169 by tuning wear mechanism through laser shock peening. Tribol. Int. 2024, 192, 109215. [Google Scholar] [CrossRef]
- Wang, S. Real Contact Area of Fractal-Regular Surfaces and Its Implications in the Law of Friction. J. Tribol. 2004, 126, 1–8. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Ding, X.X.; Wang, S.P. Prediction of Leakage Rate and Film Thickness of Mechanical Seal Based on Fractal Contact Theory. Lubr. Eng. 2022, 47, 156–163. [Google Scholar] [CrossRef]
- Ding, J.H.; Yu, S.R.; Liu, Z.; Wang, S.P.; Lu, J.J. Fault Diagnosis of Dry Gas Seal Operation Status Based on Acoustic Emission Monitoring. Lubricants 2024, 12, 2075–4442. [Google Scholar] [CrossRef]
- Hu, F.M.; He, Q.; Huang, W.F.; Yin, Y.; Wen, X.; Liu, Y.; Wang, Y.M. Face grooves for state monitoring in dry gas seals. Tribol. Int. 2023, 189, 108950. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, X.; Xu, P.; Liu, H.; Tian, J.; Wang, Z.; Hao, M. Research on friction state monitoring method of liquid film seal during start-up based on acoustic emission. Appl. Acoust. 2023, 210, 109424. [Google Scholar] [CrossRef]
- Bi, H.C.; Hao, M.M.; Ren, B.J.; Sun, X.H.; Li, Y.F.; Li, T.Z.; Liu, F.Y.; Li, X.Y. Frictional Evolution of Contact Mechanical Seals with Hybrid Lubrication. Tribology 2023, 43, 1241–1253. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Outer radius of the end-face ro/mm | 31.4 | Specific heat capacity of the fluid / | 1006 |
| Inner radius of the end-face /mm | 24.4 | Thermal conductivity of the fluid / | 0.026 |
| Thickness of the ring /mm | 8.0 | Density of the rotor material / | 8190 |
| Radius of the groove root /mm | 26.5 | Specific heat capacity of the rotor material / | 481.4 |
| Balance radius of the seal /mm | 26.0 | Thermal conductivity of the rotor material / | 13.4 |
| Angle of the land /rad | Modulus of elasticity of the rotor material /GPa | 539 | |
| Angle of the groove /rad | Hardness of the rotor material /GPa | 1.54 | |
| Depth of the groove /μm | 0.6 | Poisson’s ratio of the rotor material | 0.3 |
| Inlet pressure /MPa | 0.0 | Expansion coefficient of the rotor material | 11.8. |
| Outlet pressure /MPa | 350 | Density of the stator material / | 3210 |
| Inlet temperature /K | 293.15 | Specific heat capacity of the stator material / | 650 |
| Outlet temperature /K | 6000 | Thermal conductivity of the stator material / | 490 |
| Rotation speed / | 69.78 | Modulus of elasticity of the stator material /GPa | 481 |
| Acceleration of start-up / | 0.80 | Hardness of the stator material /GPa | 21 |
| Density of the fluid / | 1.29 | Poisson’s ratio of the stator material | 0.25 |
| Viscosity of the fluid / | 17.9 | Expansion coefficient of the stator material / | 4.4 |
| Rotor | Stator | |||||
|---|---|---|---|---|---|---|
| Fractal dimension D | 2.69 | 2.70 | 2.72 | 2.51 | 2.52 | 2.53 |
| Characteristic coefficient | 1.69 | 1.72 | 1.70 | 21.20 | 21.18 | 21.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, E.; Li, S.; Zhang, J.; Liu, A. Study on the Evolution of Sealing Performance during the Start-Up Process of Dynamic Pressure Seals Based on Three-Dimensional Fractal Functions. Machines 2024, 12, 269. https://doi.org/10.3390/machines12040269
Bi E, Li S, Zhang J, Liu A. Study on the Evolution of Sealing Performance during the Start-Up Process of Dynamic Pressure Seals Based on Three-Dimensional Fractal Functions. Machines. 2024; 12(4):269. https://doi.org/10.3390/machines12040269
Chicago/Turabian StyleBi, Enzhe, Shuangxi Li, Jiangteng Zhang, and An Liu. 2024. "Study on the Evolution of Sealing Performance during the Start-Up Process of Dynamic Pressure Seals Based on Three-Dimensional Fractal Functions" Machines 12, no. 4: 269. https://doi.org/10.3390/machines12040269
APA StyleBi, E., Li, S., Zhang, J., & Liu, A. (2024). Study on the Evolution of Sealing Performance during the Start-Up Process of Dynamic Pressure Seals Based on Three-Dimensional Fractal Functions. Machines, 12(4), 269. https://doi.org/10.3390/machines12040269





