A Novel Hole System Dimension Analysis Tool Based on the Combination of the Process Path and Design Path
Abstract
1. Introduction
- (1)
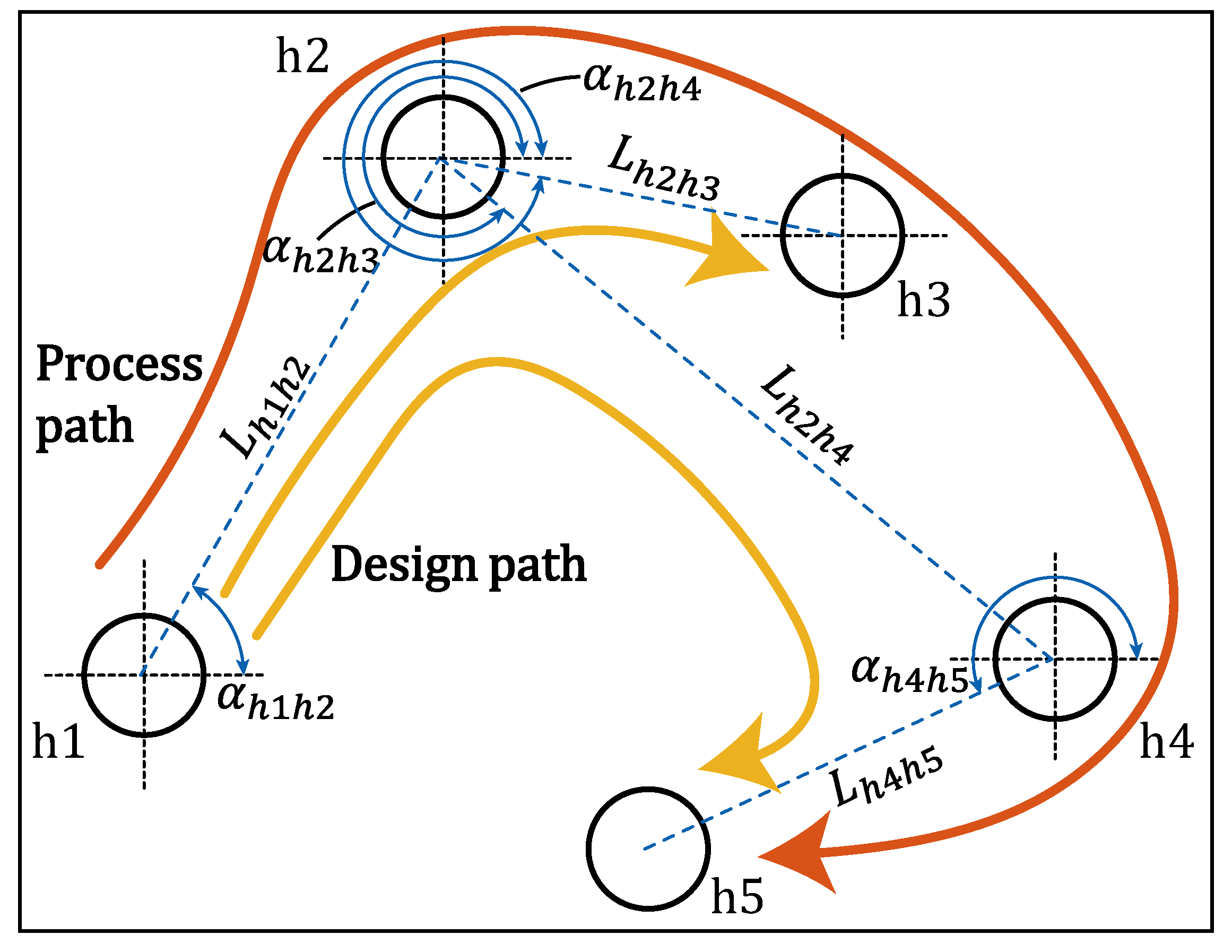
- The process path is combined with the design path to establish a system of vector equations and generate the corresponding mathematical model to calculate the process dimensions, obtaining the process dimensions with vector characteristics, which expresses the dimensional relationship and also clearly expresses the process sequence and machining datum;
- (2)
- Based on the system of vector equations established by combining the process path and the design path, the process dimension chain and the dimension chain function are directly generated, and the differential principle is applied to calculate the tolerance of process dimensions, which avoids the drawing of the dimension chain diagram and the judgment of the increase or decrease in the rings. By determining the number of rings in the dimensional chain and adopting different calculation methods to calculate the tolerance of process dimensions, the tolerance range is enlarged on the basis of guaranteeing the accuracy, which is more in line with the actual production situation;
- (3)
- CATIA CAA secondary development technology is used to establish a set of automated calculation systems for the dimensions of the process system for the machining of hole parts, to make up for the shortcomings of manual calculations that are prone to errors and inefficiency.
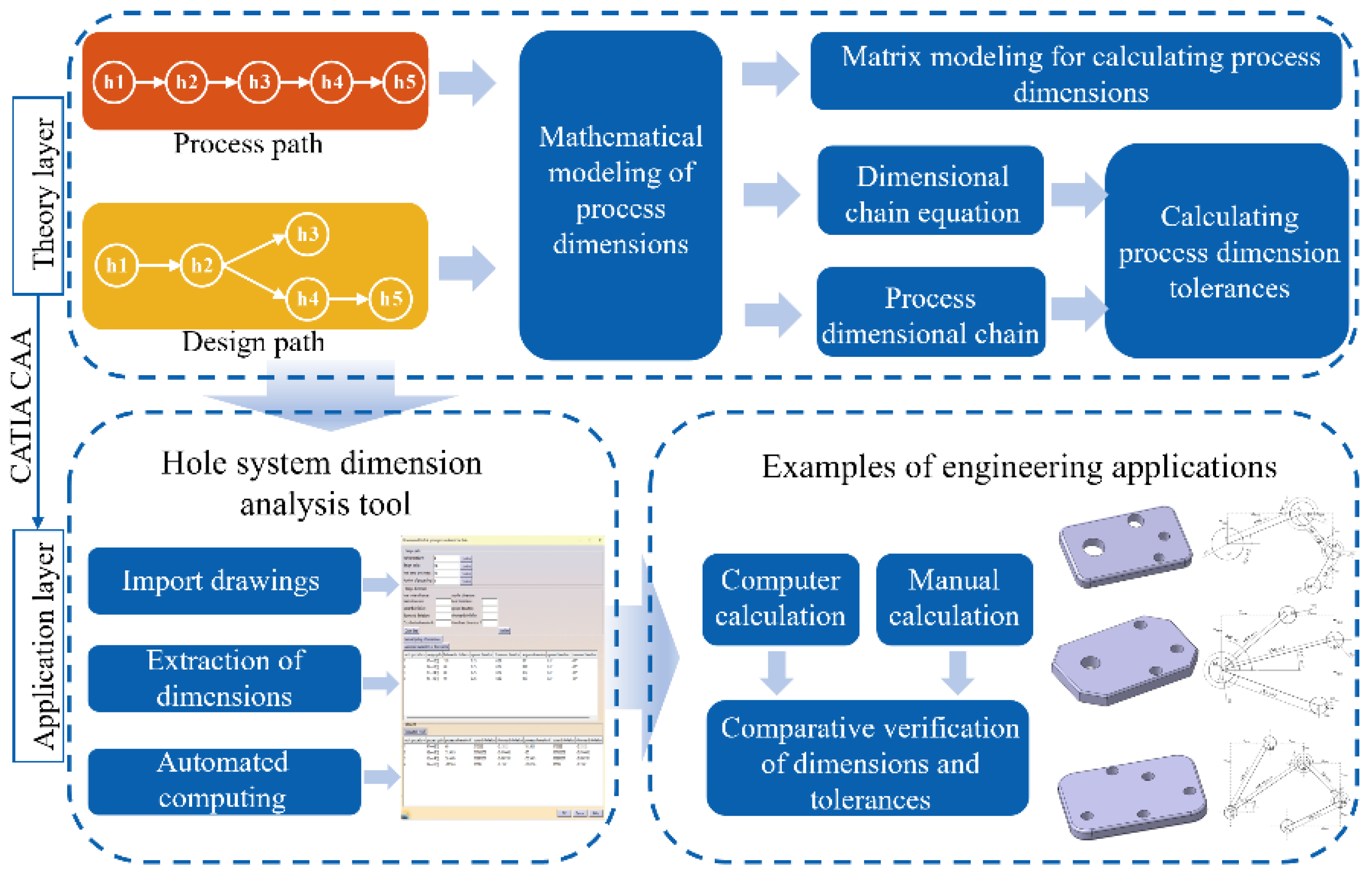
2. Calculation of Process Dimensions and Tolerances of Process Dimensions
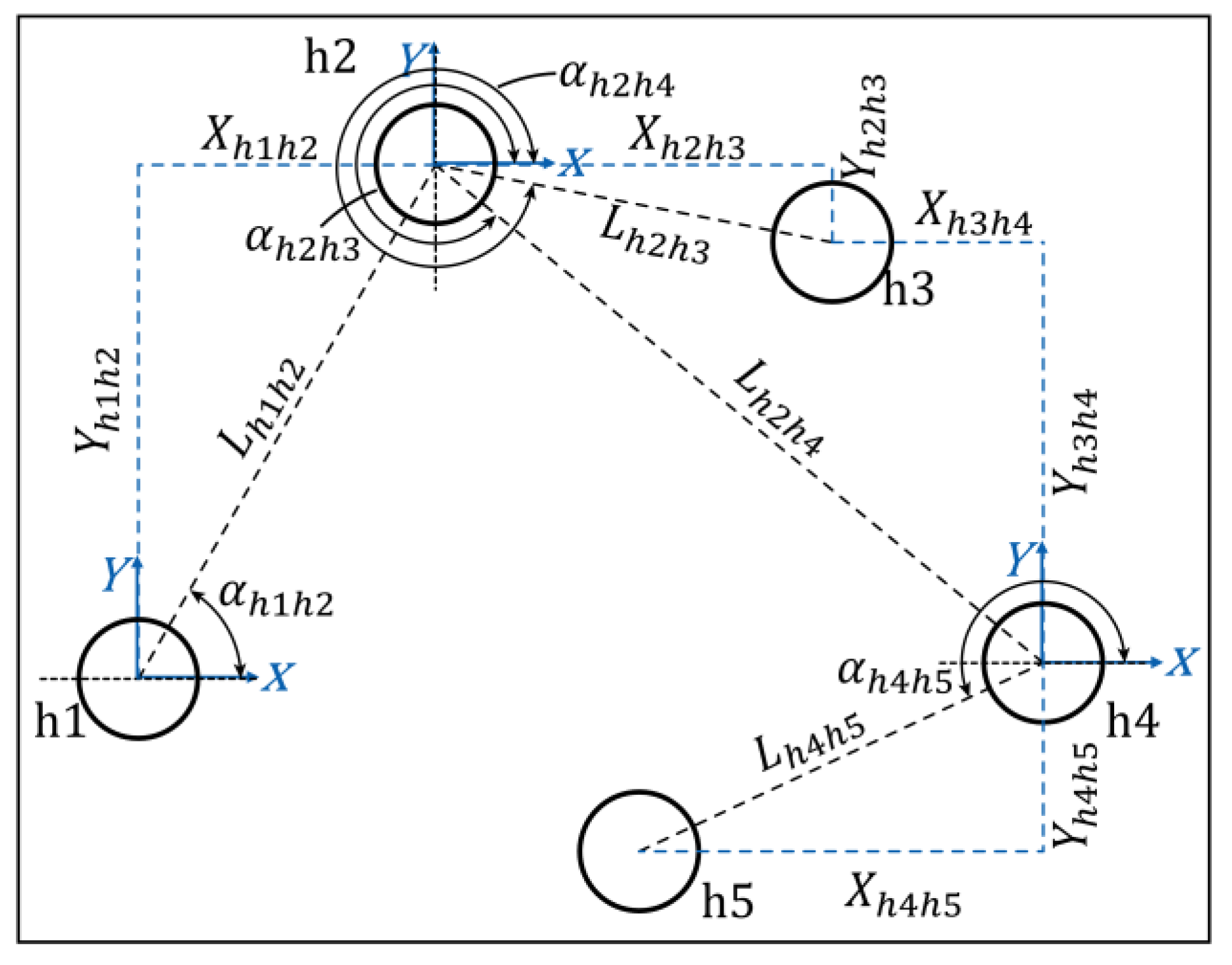
2.1. Mathematical Modeling of Dimensions
2.2. Calculation of Process Dimensions
2.3. Calculation of Tolerances of Process Dimensions
3. Automated Calculation System for Process Dimensions
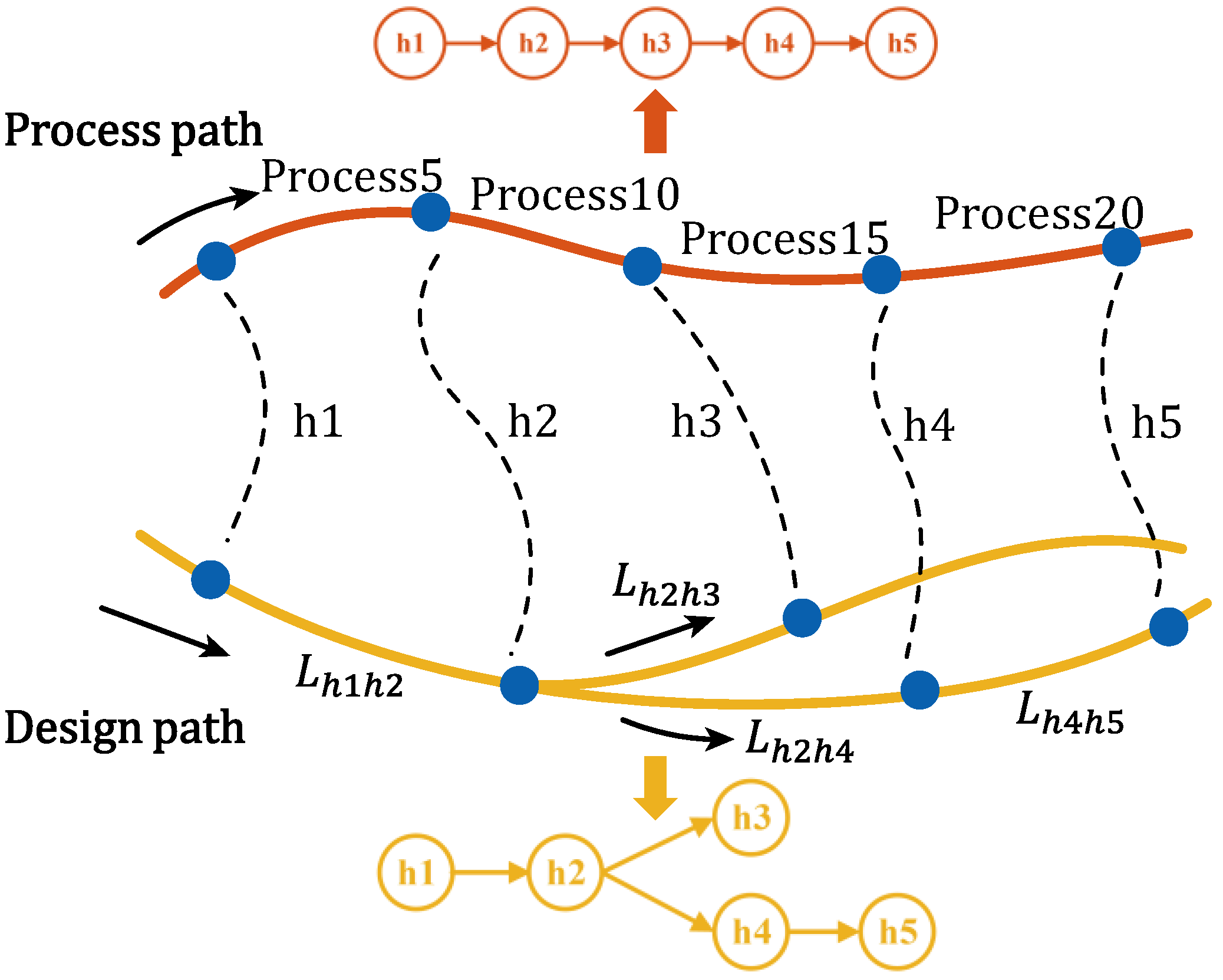
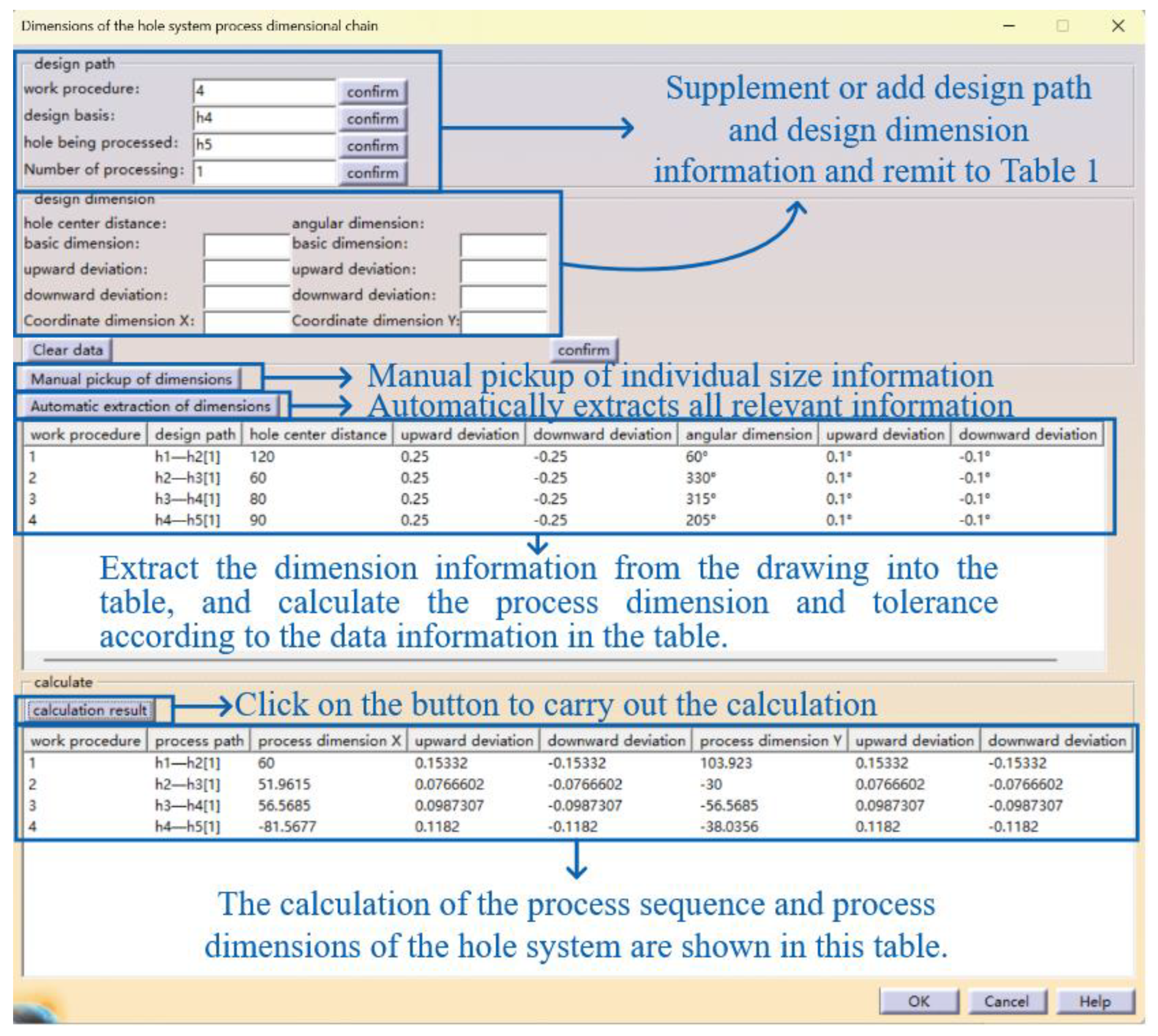
3.1. Automatic Extraction of Design Dimensions and Paths
- (1)
- Obtain the number of holes in the engineering drawing, denoted as n; obtain the set P of the labeling information of the hole centers in the engineering drawing;
- (2)
- Take the center of the first hole being machined, h1, as the starting point. Search for the dimension associated with h1, and judge that the end node of the dimension exists in the set P. If it exists, output the start node, size information, and angle information of the dimension to the dimension information table, and at the same time, mark the dimension.
- (3)
- When the unmarked dimension cannot be searched, the center h2 of the second hole to be machined is selected as the starting point and Step (2) is repeated until all holes are searched.
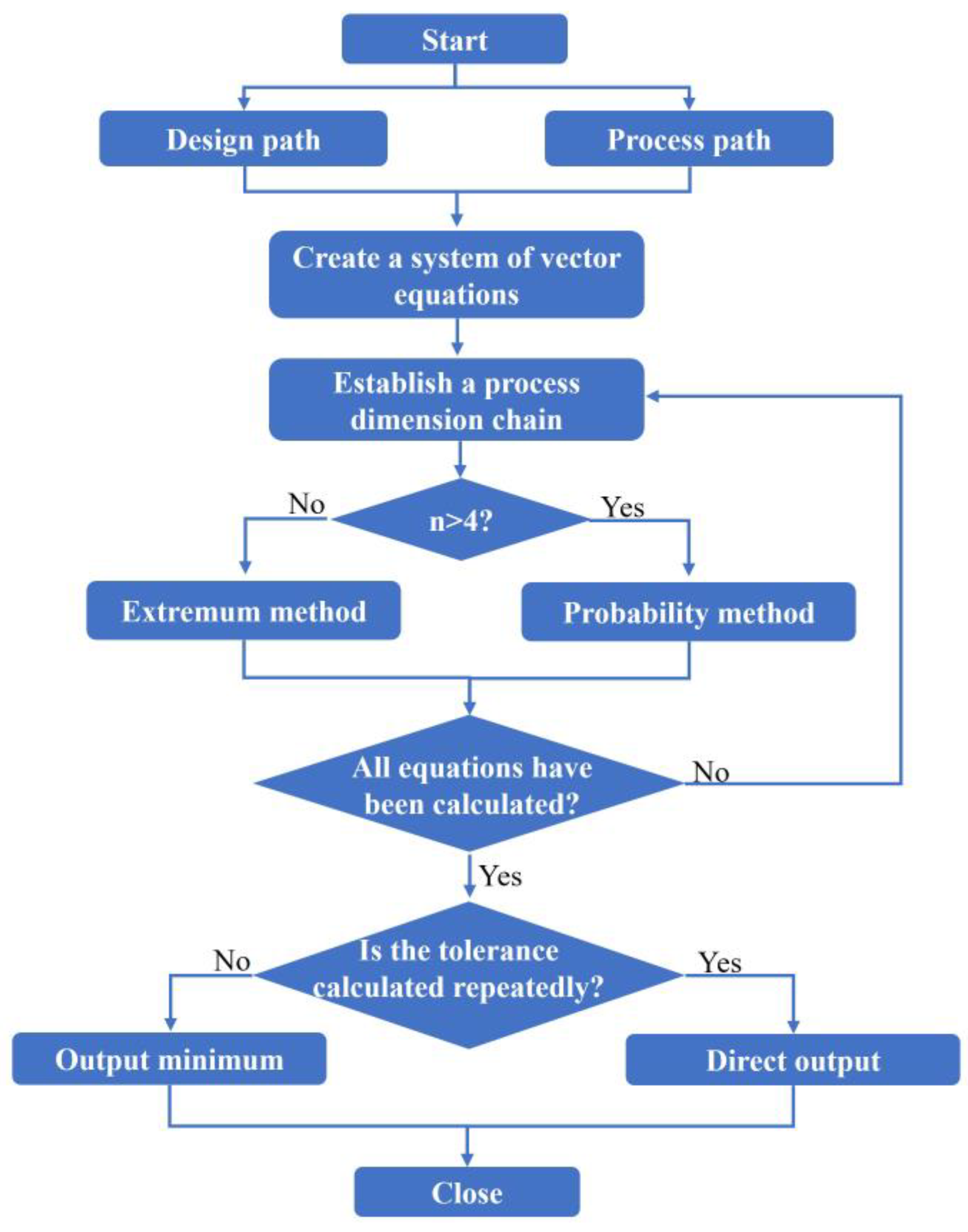
3.2. System Calculation Flow
- (1)
- Establish a system of equations based on the design path as well as the process path in the dimension information table, and establish the process dimensional chain and dimensional chain equations through the vector equations;
- (2)
- Determine whether the number of dimensional chain rings is greater than 4, and use Equations (6) and (8) to calculate if it is greater than 4, otherwise use Equations (7) and (8) to calculate;
- (3)
- Determine whether there are repeated calculations of dimensional tolerances; if so, take the minimum value output to the calculation of the results of the information table; if not, directly output the results to the calculation of the results of the information table.
3.3. Interactive Interface Design
4. Examples of Engineering Applications
4.1. Example of Calculation
4.2. Comparison of Results
5. Experimental Verification
6. Conclusions
- (1)
- Combining the process path with the design path not only expresses the dimensional relationship between two holes, but also describes the machining datum and process sequence between holes. By establishing the mathematical model of process dimension through the process path and design path, all process dimensions with directionality can be solved at once;
- (2)
- The mathematical model established according to the process path and design path can directly generate the process dimensional chain and dimensional chain calculation function, avoiding the drawing of the dimensional chain and the judgment of the increase and decrease in the ring, simplifying the analysis process and reducing the likelihood of making mistakes. The number of rings in the dimensional chain is determined and different calculation methods are used for the calculation of process dimension tolerance, so that the resulting tolerance is enlarged by about 50%, which is more in line with the actual situation of production and reduces the production cost;
- (3)
- An automated process dimension calculation tool for porous parts has been developed to make up for the time-consuming and labor-intensive traditional manual calculations, which are prone to errors and need to be repeatedly verified, and to improve the efficiency of the calculations. Therefore, this tool is feasible and significant for analyzing and calculating process dimensions in the machining of complex porous parts;
- (4)
- Not all users have access to or are proficient in the use of CATIA, and in order to increase the popularity of the tool and broaden its applicability, the development of a stand-alone version of the system will be considered in subsequent studies. This would enable a wider group of users, including those without a background in CATIA, to utilize the tool for design and manufacturing analysis. In addition, the development of a stand-alone version should also be considered to include more flexible interfaces and algorithms to ensure that it can be effectively applied in different design and manufacturing environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Groover, M.P. Fundamentals of Modern Manufacturing: Materials, Processes, and Systems; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Hong, Y.S.; Chang, T.C. A comprehensive review of tolerancing research. Int. J. Prod. Res. 2002, 40, 2425–2459. [Google Scholar] [CrossRef]
- Meguid, S.A. Integrated Computer-Aided Design of Mechanical Systems; Springer Science & Business Media: Berlin, Germany, 1987. [Google Scholar]
- Xue, J.; Ji, P. Process tolerance allocation in angular tolerance charting. Int. J. Prod. Res. 2004, 42, 3929–3945. [Google Scholar] [CrossRef]
- González Contreras, F.; Rosado, P. An alternative method to tolerance transfer for parts with 2D blueprint. Int. J. Prod. Res. 2007, 45, 5309–5328. [Google Scholar] [CrossRef]
- Ji, P.; Xue, J.B. Process tolerance control in a 2D angular tolerance chart. Int. J. Adv. Manuf. Technol. 2002, 20, 649–654. [Google Scholar] [CrossRef]
- Li, K.L.; Wang, Z.Y.; Li, J.F.; Geng, J. The parallel-chain in the machining-process-dimension-chain and application. Appl. Mech. Mater. 2008, 10, 615–620. [Google Scholar] [CrossRef]
- Ji, P.; Xue, J. Extending the algebraic method to identify dimensional chains for angular tolerance charting. Int. J. Prod. Res. 2002, 40, 1597–1612. [Google Scholar] [CrossRef]
- Pan, Y.R.; Tang, G.R. Computer-aided tolerance charting for products with angular features. Int. J. Adv. Manuf. Technol. 2001, 17, 361–370. [Google Scholar] [CrossRef]
- Masyagin, V.; Bazhenov, R.; Artyukh, R. Calculation of linear technological dimensions with adaptation. MATEC Web Conf. 2018, 224, 01072. [Google Scholar] [CrossRef][Green Version]
- Pang, L.; Liu, Y.; Fu, R.; Ji, L.; Li, Y. Research on the method of UG secondary development to the calculating plane dimension chain. In Proceedings of the 2nd International Conference on Electronic & Mechanical Engineering and Information Technology, Shenyang, China, 7 September 2012; pp. 1534–1537. [Google Scholar]
- Ji, L.; Liu, L.Q.; Mei, X.F. Calculation of dimension chain through AutoCAD secondary development technique based on dimension tracking method. Appl. Mech. Mater. 2012, 101, 631–634. [Google Scholar] [CrossRef]
- Lin, Y.H.; Ting, Y.H.; Huang, Y.C.; Cheng, K.L.; Jong, W.R. Integration of Deep Learning for Automatic Recognition of 2D Engineering Drawings. Machines 2023, 11, 802. [Google Scholar] [CrossRef]
- Jiang, N.; Wang, S.; Yang, A.; Zhou, W.; Zhang, J. Transmission Efficiency of Cycloid–Pinion System Considering the Assembly Dimensional Chain. Appl. Sci. 2022, 12, 11917. [Google Scholar] [CrossRef]
- Dong, Y.; Su, F.; Sun, G.; Liu, Y.; Zhang, F. A feature-based method for tire pattern reverse modeling. Adv. Eng. Softw. 2018, 124, 73–89. [Google Scholar] [CrossRef]
- Yougao, F.; Xiaoyu, D.; Jianhua, L.; Zhiqiang, Z. A method of automatic generation of assembly dimension chains based on information cells. J. Comput. Aided Des. Comput. Graph. 2016, 28, 1989–1999. [Google Scholar]
- Fang, H.M.; Zhao, G.; Zhang, G.Z.; Xiao, P. The Research and the Development of the 3D System Platform of Shafting Parts Based on CAA. Key Eng. Mater. 2016, 693, 1886–1892. [Google Scholar] [CrossRef]
- Zhang, G.G.; Chang, Z.B.; Liu, H.T. Parametric modeling for globoidal cam based on CATIA/CAA. Appl. Mech. Mater. 2011, 88, 236–239. [Google Scholar] [CrossRef]
- Shen, Z.; Ameta, G.; Shah, J.J.; Davidson, J.K. A comparative study of tolerance analysis methods. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005. [Google Scholar]
- Li, K. Dimension Chain of Machining Process; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Chahbouni, M.; Elmouden, M.; Miskin, M.; Boutahari, S.; Amegouz, D. Tolerance analysis with the 1D angular dimension chain: Application. In Proceedings of the 2020 IEEE 13th International Colloquium of Logistics and Supply Chain Management (LOGISTIQUA), Fez, Morocco, 2–4 December 2020; pp. 1–6. [Google Scholar]
- Hu, B.; Wu, Y. CATIA Software Modeling and Secondary Development of CAA Beijing; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2018; pp. 75–82. [Google Scholar]
- Bao, J.R.; Ding, Y.; Hu, S.B.; Hu, P. A study on intelligent parting line design of vehicle door based on CATIA CAA. Adv. Mater. Res. 2014, 902, 357–363. [Google Scholar] [CrossRef]
- Hao, B.; Liu, F.; Liu, M. Variant design of typical aircraft parts based on CATIA technology. J. Phys. Conf. Ser. 2020, 1605, 012064. [Google Scholar] [CrossRef]
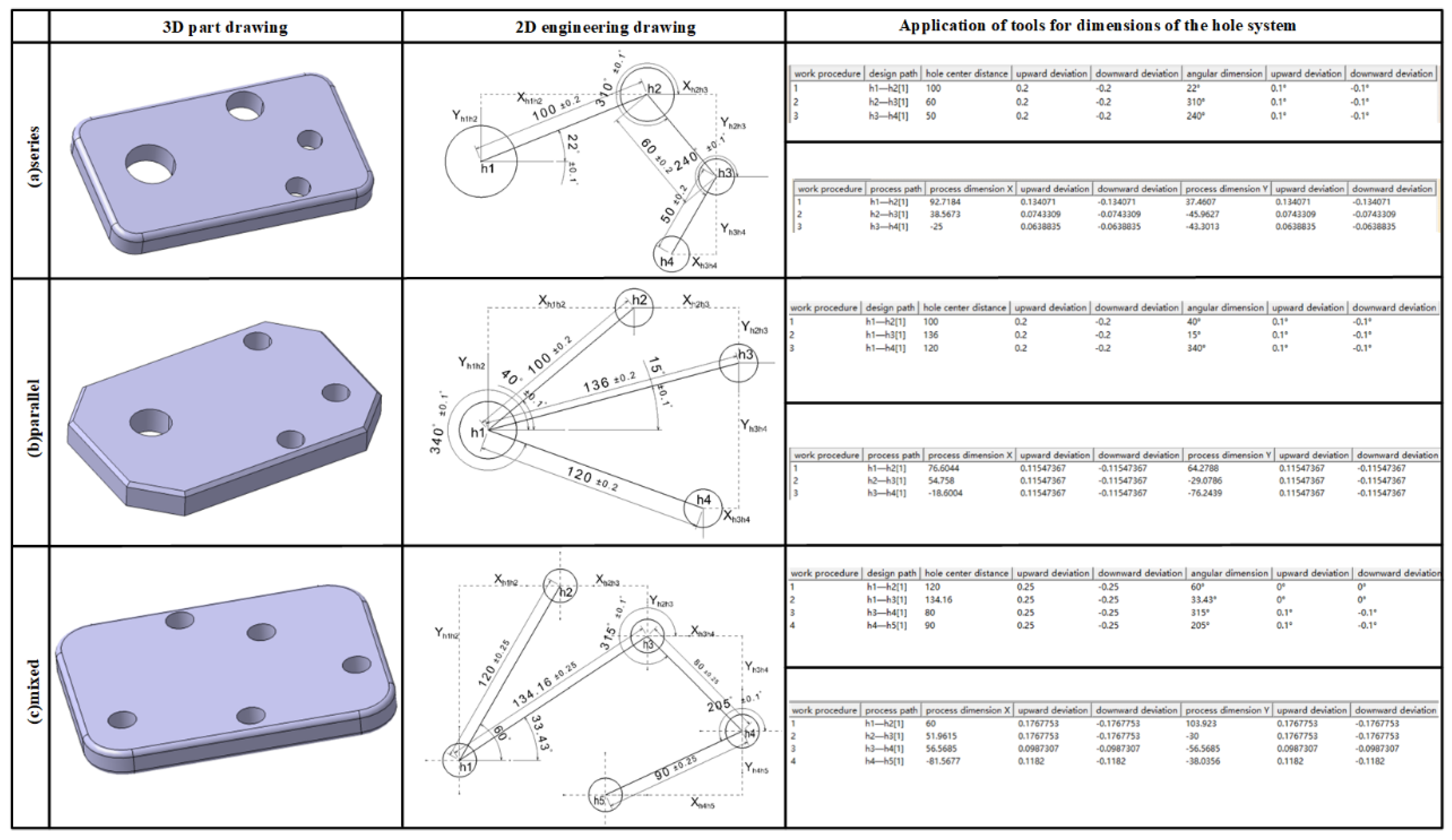



| Dimensions and Tolerances | Traditional Method | Proposed Method |
|---|---|---|
| 92.72 ± 0.134071 | 92.72 ± 0.134071 | |
| 37.46 ± 0.134071 | 37.4607± 0.134071 | |
| 38.57 ± 0.07433 | 38.5673 ± 0.0743309 | |
| 45.96 ± 0.07433 | −45.9627 ± 0.0743309 | |
| 25 ± 0.06388 | −25 ± 0.0638835 | |
| 43.30 ± 0.06388 | −43.3013 ± 0.0638835 |
| Dimensions and Tolerances | Traditional Method | Proposed Method |
|---|---|---|
| 76.60 ± 0.052016 | 76.6044 ± 0.11547367 | |
| 64.28 ± 0.052016 | 64.2788 ± 0.11547367 | |
| 54.758 ± 0.052016 | 54.758 ± 0.11547367 | |
| 29.08 ± 0.052016 | −29.0786 ± 0.11547367 | |
| 18.60 ± 0.052016 | −18.6004 ± 0.11547367 | |
| 76.24 ± 0.052016 | −76.2439 ± 0.11547367 |
| Dimensions and Tolerances | Traditional Method | Proposed Method |
|---|---|---|
| 60 ± 0.090218 | 60 ± 0.17677531 | |
| 103.92 ± 0.090218 | 103.923 ± 0.17677531 | |
| 51.96 ± 0.090218 | 51.6915 ± 0.17677531 | |
| 30 ± 0.090218 | −30 ± 0.17677531 | |
| 56.57 ± 0.0987307 | 56.5685 ± 0.0987307 | |
| 56.57 ± 0.0987307 | −56.5685 ± 0.0987307 | |
| 81.57 ± 0.1182 | −81.5677 ± 0.1182 | |
| 38.04 ± 0.1182 | −38.0356 ± 0.1182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Yang, J.; Xue, S.; Wang, Z. A Novel Hole System Dimension Analysis Tool Based on the Combination of the Process Path and Design Path. Machines 2024, 12, 245. https://doi.org/10.3390/machines12040245
Ma X, Yang J, Xue S, Wang Z. A Novel Hole System Dimension Analysis Tool Based on the Combination of the Process Path and Design Path. Machines. 2024; 12(4):245. https://doi.org/10.3390/machines12040245
Chicago/Turabian StyleMa, Xingyu, Jiong Yang, Shuncong Xue, and Zhichao Wang. 2024. "A Novel Hole System Dimension Analysis Tool Based on the Combination of the Process Path and Design Path" Machines 12, no. 4: 245. https://doi.org/10.3390/machines12040245
APA StyleMa, X., Yang, J., Xue, S., & Wang, Z. (2024). A Novel Hole System Dimension Analysis Tool Based on the Combination of the Process Path and Design Path. Machines, 12(4), 245. https://doi.org/10.3390/machines12040245






