Abstract
This study aims to develop, evaluate, and improve a polygeneration system that combines solar and Brayton cycle technologies and focuses on the sequential integration of heat. In this configuration, the exhaust gases from the Al-Qayyarah gas turbine power plant and the parabolic trough collector (PTC) array generate steam through a high recovery steam generation process. An absorption refrigeration system also supplies the Brayton circuit with low-temperature air. This process is evaluated from a 3E perspective, which includes exergy, energy, and exergoeconomic analyses for two different configurations. These configurations are integrated solar combined cycle (ISCC) with and without absorption systems (ISCC and ISCC-ARC). In addition, a comprehensive analysis was carried out to assess the impact of critical factors on the output generated, the unit cost of the products, and the exergy and energy efficiency for each configuration. The results revealed that the power produced by the ISCC-ARC and ISCC systems is 580.6 MW and 547.4 MW, respectively. Accordingly, the total energy and exergy efficiencies for the ISCC-ARC are 51.15% and 49.4%, respectively, while for the ISCC system, they are 50.89% and 49.14%, respectively. According to the results, the total specific costs for the ISCC-ARC system increased from 69.09 $/MWh in June to 79.05 $/MWh in December. ISCC’s total specific costs also fluctuate throughout the year, from 72.56 $/MWh in June to 78.73 $/MWh in December.
1. Introduction
The urgency and significance of incorporating multiple energy production units into the use of a shared primary energy input effectively have been heightened due to the escalating concerns around global warming and fossil fuel depletion. In thermal power plants, such as gas turbine plants, fossil fuels are the principal energy source for electricity generation. Additionally, the waste flue gases produced during this process can be effectively utilized to power various other thermal cycles, including the steam and organic Rankine cycles, desalination cycles, absorption refrigeration cycles, and heating units, as well as other cycles. The field of integrated multi-energy production is now gaining significant attention and is considered a developing topic of study [1,2,3].
Although the demand for electricity has increased recently, there has been a noticeable shift towards sustainability. This shift is driven by heightened environmental consciousness, concerns regarding global warming, the depletion of natural resources, and the quest for energy autonomy. According to the Ministry of Energy’s annual report in Iraq, Iraq has experienced a rapid annual growth in energy demand, growth reaching 4.5%. As a developing nation, Iraq boasts significant economic potential and a range of investment opportunities [1,4]. New power plants have been installed at an annual rate of 8%, pushing to fill the gap.
A study on the Iraqi electricity sector reveals that nearly 25% of electricity is produced by thermal plants, at 40% efficiency with 60% as wasted heat. Gas turbines, contributing 47% of Iraq’s electricity, face efficiency challenges due to high temperatures. Implementing inlet air cooling systems is a recognized method for substantial electricity savings. Vapor Absorption Cooling technology [5] offers potential energy-saving solutions, yet remains unimplemented in Iraq’s power plants.
High ambient temperatures in the inlet air result in a 6–10% decline in output power for every 10 °C temperature rise, with specific heat consumption increasing [6,7]. Although the Iraqi Ministry of Electricity encourages researchers to study the possibilities of improving current power plants and using renewable energy, there has been little research in this field.
Saeed et al. [8] examined the potential options for the replacement of fossil fuels in Iraq, with a particular emphasis on renewable energy sources and nuclear plants, and evaluated their viability for practical implementation. They provided a comprehensive analysis of how the implementation of alternative energy sources may effectively mitigate the current electricity supply deficit and make a significant contribution towards the reduction of greenhouse gas emissions resulting from the use of fossil fuel-based generators.
Hassan et al. [9] presented the feasibility of building solar photovoltaic power plants with a 20 MW capacity to generate energy. Their evaluation included four major cities in Iraq.
Kazem and Chaichan [10] researched the electrical shortages and a number of issues in Iraq. According to the results of this study, solar, wind, and biomass energy were all underutilized at the time; however, they have the potential to contribute significantly to Iraq’s renewable energy future.
Talal and Akroot [11] presented an exergoeconomic study that was conducted to justify implementing an integrated solar combined cycle, ISCC, system utilizing the concentrated solar tower technology at the Al-Qayyarah power plant in Iraq.
Faisal et al. [12] presented an energy and exergy analysis carried out on a General Electric (GE) gas turbine unit in the Shatt Al-Basra power plant located in Basra, Iraq. Their analysis showed that the maximum thermal and exergy efficiencies occurred in February. According to the data, the best month to maximize thermal and exergy efficiency is February.
Salah et al. [13] analyzed the energy and exergy of the Kirkuk gas power plant to study the losses incurred under real operating circumstances.
Ahmed et al. [14] conducted a study on the energy and exergy analysis of a 150 MW gas turbine plant. The study used a Dataflow sheet and Kirkuk unit for the examination, in which the energy and exergy were investigated to assess the losses occurring under natural operating settings.
The study conducted by Alaa et al. [15] centered on the exergoeconomic analysis of the Taji power plant located in Baghdad. The selection of this station was motivated by the objective of mitigating the release of environmentally harmful waste gases, given its proximity to a residential area. Additionally, it aimed to enhance the generation of electrical power, addressing the longstanding issue of energy scarcity in Iraq.
By installing an absorption air refrigeration system at the compressor inlet, the incoming air can be treated at below ambient temperature. This improves the operating efficiency of the system, especially during times of high ambient temperatures [16,17,18]. It was observed that changes in ambient temperature have a significant effect on the productivity of gas turbines [19]. Researchers have noted that for every additional degree of the surrounding temperature, the performance and power production of the gas turbine diminished by approximately 0.07%, resulting in a reduction of 1.47 MW in power generation. This temperature-dependent behavior underscores the need for precise thermal management systems in gas turbine facilities to optimize their performance and maintain consistent power output, especially in regions with fluctuating climatic conditions [20].
To maximize the effectiveness of the interconnected systems, the solar Rankine cycle is designed to operate in tandem with a gas turbine power plant and the absorption refrigeration cycle. To define the implementation of this approach, various significant research papers are described in the following paragraphs.
A performance study of an integrated gas-, steam-, and organic fluid-cycle thermal power plant (IPP) was conducted by Oko and Njoku [21]. An integrated power plant is designed to harness the waste heat generated by the exhaust of a pre-existing 650 MW combined-cycle power plant (CCPP) that utilizes gas and steam. This waste heat was used to drive an organic Rankine cycle (ORC) unit, thereby enhancing the overall efficiency of the power generation process. The findings indicate that the waste heat-fired ORC unit produces an additional 12.4 MW of electric power. The exergy and energy efficiency of the integrated power plant (IPP) showed a significant increase compared to the extant combined cycle power plant (CCPP), with improvements of 1.95% and 1.93%, respectively.
Shukla and Singh [22] proved that gas turbine capacity can be increased by using an absorption chiller powered by waste heat, which could result in an 8–13% increase in power output. Compared to the expensive alternative of constructing a new gas turbine unit, this economical method increases the turbine’s capacity by 11%, which is advantageous for energy producers in arid and tropical areas.
Elberry et al. [16] integrated an exhaust gas waste-heat-powered combined cycle with a Lith Br & Water absorption intake air refrigeration system. With model results verified by actual plant performance, this integration increases the electricity output by 11% when cooling down the inlet air from 30 °C to 10 °C. This also produces 3.5 g of condensed fresh water for every kilogram of intake air at 60% humidity.
Karaali [23] studied ammonia–water power cycles that efficiently utilize solar and waste heat and low-temperature heat sources. By conducting an energetic evaluation of a shared power and refrigeration cycle, they emphasized the use of ammonia (NH3) with water mixes for independent power and cooling. This increase in a turbine’s inlet pressure decreases both its energy and exergy efficiencies and its exergy efficiency.
Settino et al. [24] examined a gas combined cycle power plant integrated with solar energy. According to their analysis of the effect of the intercooler on power efficiency and CO2 releases, a single-stage intercooler design with a ratio of compression reaching 17.9 provides a solar energy efficiency of 33% and a net electrical efficiency of 69.5%. The actual operating conditions in various cities result in annual efficiency of s solar energy to electricity around 32% and significant natural gas emissions of 7.7% to 5.8%.
Roshanzadeh et al. [25] examined the procedural operations of the combined cycle of a power plant at elevated temperatures and found reduced energy production. To address this issue, the use of solar-powered intake air cooling systems was explored to maintain performance and efficiency effectively. The ideal combination of vacuum plate collectors and double-acting absorption units was deemed economically attractive, with a return money period of 2.96 annually.
The aim of this article is to combine the absorption refrigeration cycle and solar-driven Rankine cycle with the Al-Qayyarah gas turbine power plant. This combined sysem merges solar energy, gas engine power, and cutting-edge cooling technologies to make the most of energy efficiency, reduce damage to the environment, and ensure a steady supply of electricity. This system is intended to cool the compressor’s intake air and is driven by exhaust flue gases from the Heat Recovery Steam Generator (HRSG). This new method not only uses green energy sources but also makes the best use of traditional power production. The result is a more reliable and eco-friendly power plant that can keep abreast of the growing demand for electricity in Iraq. The Al-Qayyarah gas turbine power plant was selected as a case study. The power plant consists of six units with a capacity of 125 megawatts. In the current study, all calculations are performed for three units only. By applying the proposed solution model, this research has attempted to provide performance estimates for the completed integrated plant, considering different operating situations and local climates.
2. System Description
Figure 1 presents the configuration of the Al-Qayyarah gas-fired power plant. It consists of six 125-megawatt gas turbines, but we only use three units in this simulation. A gas turbine works very simply: air is compressed and mixed with fuel before being ignited to produce a high-temperature, high-pressure gases. This gases then expands in a turbine and extracts energy from it to drive the compressor and generate helpful energy.
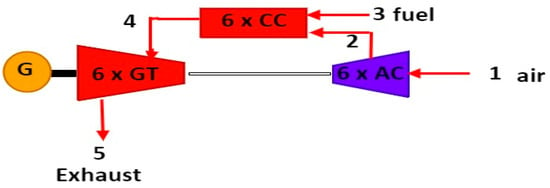
Figure 1.
Al-Qayyarah gas power plant.
The exhaust gases from the gas turbine are routed through the steam generation process with heat recovery to generate additional electricity using the Rankine cycle and improve the system’s overall efficiency. Figure 2 shows the integration of the combined cycle of Al-Qayyarah’s gas turbines with parabolic trough collectors (PTCs) to increase the power plant’s output by increasing steam generation in the HRSG. Only three units of gas turbine are used in this simulation.
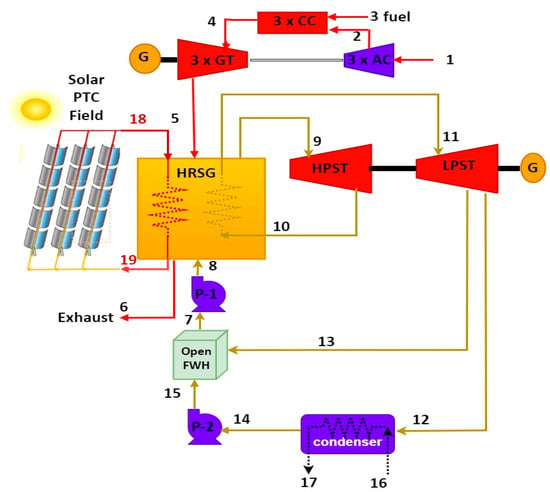
Figure 2.
Al-Qayyarah integrated solar combined cycle.
Figure 3 presents the integrated solar combined cycle and the absorption refrigeration cycle (ISCC-ARC). The ARC cycle plays a central role as it uses the exhaust gases from the gas turbine in the HRSG unit as a heat source and lowers the temperature of the ambient air to 283 K before it enters the air compressors of the gas turbine units. The power generated by the ISCC-ARC system increases by reducing the power consumed by the air compressors, especially in summer.
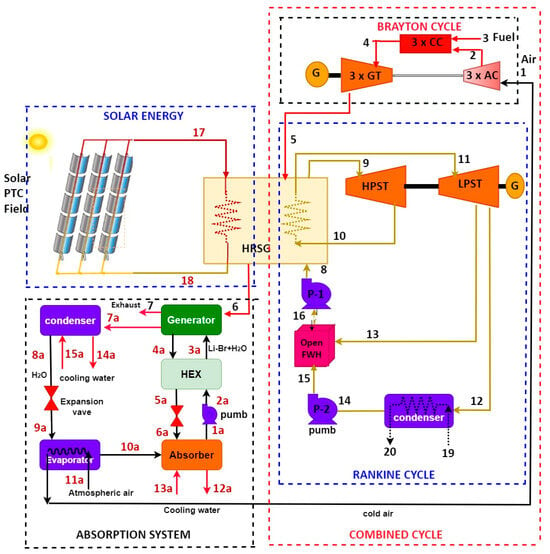
Figure 3.
Integrated solar combined cycle with the absorption refrigeration cycle (ISCC-ARC).
3. Thermodynamics Model
This assessment uses the Engineering Equation Solver (EES) software version 10.2 for simulation and analysis. This program computes thermodynamic properties, such as pressure, temperature, entropy, and exergy. The assumptions made for this analysis are as follows:
- The system operates in a steady-state condition.
- Air is classified as an ideal gas.
- The pressure drop, heat loss, and friction effect of the pipe network and heat exchangers are all negligible.
- There are no changes in kinetic and potential energy, and the energies remain at zero.
- Compressors, turbines, and pumps are mathematically represented using adiabatic models that include a certain isentropic efficiency.
3.1. PTC System Model
The thermal power inlet to the accumulators’ absorber is derived by [26]
The symbol represents the efficiency of the PTC, with denoting the specific zone covered by the solar area. DNI refers to the direct normal irradiance recorded in Mosul (43.17° E, 35.33° N) during the relevant year. The primary function of the PTC involves the transmission of a fraction of the sunlight to the chief receiver in the form of solar isolation, and is denoted thus [27]:
3.2. Thermodynamic Analysis
The mass and energy balance equations for each control volume (device) of the ISCC-ARC system may be expressed using the following relations [28]:
where , , , and are the rates of heat transfer, work, and specific enthalpy at the intake and the outlet per unit mass, respectively. The exergy destruction of each part is its magnitude, calculated using the equilibrium calculation of the exergy:
where and are, respectively, the exergy destruction rate, heat loss exergy rate, and the exergy of power. and are calculated thus:
The energy and exergy stability relationships for all components of the ISCC-ARC system are shown in Table 1.

Table 1.
Energy and exergy balance equations for all components of the ISCC-ARC system.
Energy performance, , can be estimated as follows [29]:
Exergy efficiency, , is a measure of the system’s quality and may be calculated using the following formula:
3.3. Investment Cost of the Main Equipment
Analysis of exergoeconomics involves establishing the price equilibrium for every component within the system. The essential equation used for the price equilibrium of every system section in thermoeconomics is depicted as follows [30]:
where is the cost rate ($/h) and is the entire cost rate related to capital investment and the operation and maintenance costs component k. The total investment cost rate is determined using the following formula:
In this context, φ represents the maintenance factor, which is assigned a value of 1.06. N refers to the system’s total number of operating hours in a year, namely 8000 h [31]. The Capital Recovery Factor (CRF) is a numerical value used to indicate the recovery of capital investment, and calculated thus:
The interest rate, denoted as ‘i’ and the system life, denoted as ‘n’ are assumed to be 10% and 20 years, respectively [31]. The explicit equations for the cost balance of each component in this integrated system are listed in Table 2, together with their corresponding auxiliary equations and underlying assumptions. Furthermore, Table 3 lists the capital investment cost functions for each individual component in this system. The exergoeconomic analysis employs certain performance metrics to assess the system. The cost per unit exergy of fuel and product, the exergy destruction cost rate, and the exergoeconomic factor are defined as follows:

Table 2.
Cost analysis.

Table 3.
Capital investment cost functions [27,32,33,34].
The total cost of the investment can be computed using the following equation [35]:
The entire power price (electricity) over energy, $/MJ, is calculated from the following formula [32]:
4. Results and Discussion
The exergoeconomic findings of the current integrated system are provided in three steps. In the first step, the integrated system functions according to selected circumstances, which serve as the base case. The second step involves conducting parametric experiments to analyze the behavior of this system under different scenarios, and the third step includes validating the integrated model by comparing this model with previous studies.
4.1. Base Case
The system is simulated in the Engineering Equation Solver (EES) program. Table 4 presents the primary parameters and simulation settings of the proposed ISCC-ARC system.

Table 4.
Input values used for the ISCC-ARC system model [36,37,38].
The thermodynamic properties of the state points in the ISCC-ARC system model are presented in Table 5. This system model relies heavily on these characteristics when calculating exergy and energy. Also, the summary of the energy analysis is presented in Table 6.

Table 5.
Properties for each state of the ISCC-ARC in ideal conditions.

Table 6.
Output quantities produced by the integrated system model.
The primary exergy analysis findings for the various components of the performance and economics of the ISCC and ISCC-ARC are outlined in Table 7, offering comprehensive insights into the fuel, product, and destruction exergies associated with each specific element. Additionally, the table presents specific data on and Ψ percentages, allowing for a detailed assessment of exergy performance. Notably, the net output power shows a standing corresponding to approximately 586.3 MW, followed by overall thermal efficiency ratios of 50.94%. Furthermore, the planned ISCC-ARC achieves a total of 49.19%, with the electricity cost of the cycle being changed from 6876 $/h to 6708 $/h and the cost for each megawatt from 72.86 $/h to 71.16 $/h.

Table 7.
Exergy analysis of the ISCC-ARC system model.
Exergoeconomic analysis is a useful approach for evaluating the efficiency of a thermal system. The results of the exergoeconomic analysis for the ISCC-ARC system are shown in Table 8. The data suggest that the combustion chamber and air compressor had the greatest values, respectively. The evaluation of the exergoeconomic component reveals that 58.9% of the total cost can be attributed to investment expenses, whereas only 42.1% can be attributed to the cost of exergy destruction.

Table 8.
Exergoeconomic results of the components of the ISCC-ARC system.
4.2. Results of the Parametric Studies
In this subsection, the findings of the conducted parametric studies on these integrated systems will be discussed. Figure 4 shows the effect of the pressure ratio (Pr) on the overall work and price of each component of the cycle. As shown in Figure 4a, Pr has a destructive impact on the of every component in the cycle. When the Pr is high, the work consumed by the compressors increases. in the ISCC-ARC system drops from 619.8 MW to 537.4 MW after the Pr is raised from 6 to 18. The results show that the of the ISCC drops from 607.5 MW to 511.5 MW. Moreover, the results show that the performance of the ISCC with an absorption refrigeration cycle is higher than that of the ISCC system, because the absorption refrigeration system decreases the power consumed by the air compressors.
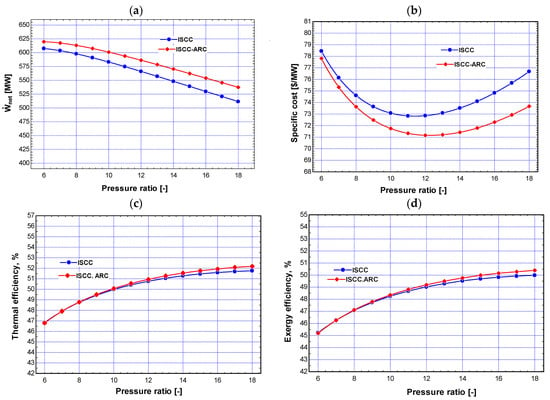
Figure 4.
(a–d) Impact of the pressure ratio on the performance and cost of both systems.
As shown in Figure 4b, the specific cost for both systems reduced as the Pr rose, peaked, and then increased with the further increase in the Pr. The figure also shows that Pr = 12 is the optimal pressure ratio. The specific cost of the ISCC-ARC system was 71.1 $/MWh at Pr = 12 compared to 72.8 $/MWh for the ISCC system. As the pressure ratio grows, both the investment cost rate of the BC components and the power consumed by the compressors also increase simultaneously. This increases the cost rate after reaching a pressure ratio of Pr = 12.
It is evident from Figure 4c,d that Pr has an impact on the overall efficiencies of both systems. The diagrams illustrate how the overall efficiencies for both systems improve as the Pr rises. Depending on the results, when the Pr increases from 6 to 18, increases from 46.8% to 52.18%, and increases from 45.19% to 50.39% for the ISCC-ARC system. Similarly, for the ISCC system, increases can be observed in from 46.84% to 51.76%, and in from 45.23% to 49.98%.
Figure 5 shows the overall performance and costs of the ISCC-ARC and ISCC systems linked to the gas turbine inlet temperature (GTIT). These data demonstrate the influence of the GTIT on both the cost and performance of the gas cycle. The GTIT improves the effectiveness of the Rankine and Brayton cycles by raising the temperature of the exhaust gases and thermal energy at the gas turbine intake. Figure 5a shows the increasing from 473.6 MW to 779.4 MW for the ISCC-ARC and from 452.7 MW to 758.6 MW for the ISCC system when the GTIT changes from 1250 K to 1550 K. The specific cost for both systems decreases when the GTIT rises, reaching a minimum value when the GTIT reaches 1517 K and increasing for a second time when the GTIT rises further (see Figure 5b). As the GTIT increases, the costs of the CC and GT likewise increase, leading to a corresponding rise in the specific costs of the systems. The specific cost of the ISCC-ARC system is 65.96 $/MWh at 1517 K of GTIT, while it is 67.17 $/MWh for the ISCC system.
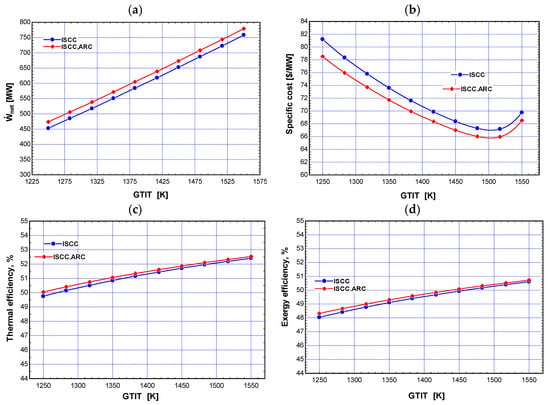
Figure 5.
(a–d) Impact of GTIT on the performance and cost of both systems.
The results shown in Figure 5c,d indicate that increasing the GTIT may enhance the thermal and exergy efficiencies of both systems. This is because a greater amount of energy input is effectively transformed into useful work, resulting in less energy being lost as low-quality heat.
The effect of changing the pressure at the inlet of the HPST () on the work net, efficiencies, and cost of the ISCC-ARC and ISCC systems are shown in Figure 6. Increasing the increases the , , and reduces the specific costs of both systems. The performance of the systems is boosted at a higher due to the increase in the enthalpy. Figure 6a presents that, when rises from 80 bar to 125 bar, the of the ISCC-ARC system rises from 578.2 MW to 584.4 MW. Likewise, the of the ISCC system increases from 557.4 MW to 563.6 MW. As illustrated in Figure 6b, the specific cost for the ISCC-ARC system varies from 72.08 $/MWh to 70.43 $/MWh compared to the specific cost for the ISCC system changing from 73.94 $/MWh to 72.2 $/MWh. The overall efficiencies for both systems grow gradually when the rises, as seen in Figure 6c,d. When is raised from 80 bar to 125 bar, the in the ISCC-ARC system improves from 50.85% to 51.39%, and the rises from 49.1% to 49.62%. In the ISCC system, the increases from 50.63% to 51.19%, while the rises slightly from 48.89% to 49.43%.
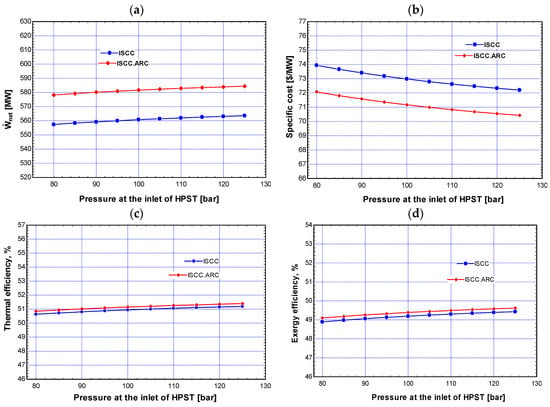
Figure 6.
(a–d) Impact of on the performance and cost of both systems.
Figure 7 illustrates the effect of changing the condenser temperature () from 25 °C to 70 °C on the overall efficiencies, specific costs, and work net for both systems. The findings revealed that the increase in has a negative impact on the performance and specific cost of both systems. When the is high, the system’s output is reduced, and the specific cost increases. Figure 7a shows that when the is raised from 25 °C to 70 °C, the decreases from 587.4 MW to 561 MW for the ISCC-ARC system and drops from 566.6 MW to 540.2 MW for the ISCC system. The specific cost rose from 69.72 $/MWh to 77.04 $/MWh for the ISCC-ARC system, while it increased from 71.46 $/MWh to 79.15 $/MWh for the ISCC design, as presented in Figure 7b. Figure 7c,d illustrate a decline in the overall efficiencies of both designs due to a fall in the as the Tcond increases. The results demonstrate that increasing the from 25 °C to 70 °C leads to a decrease in the from 51.66% to 49.33%, and a decrease in the from 49.88% to 47.64% for the ISCC-ARC system. Furthermore, the in the ISCC system drops from 51.47% to 49.07%, while the decreases from 49.7% to 47.38%.
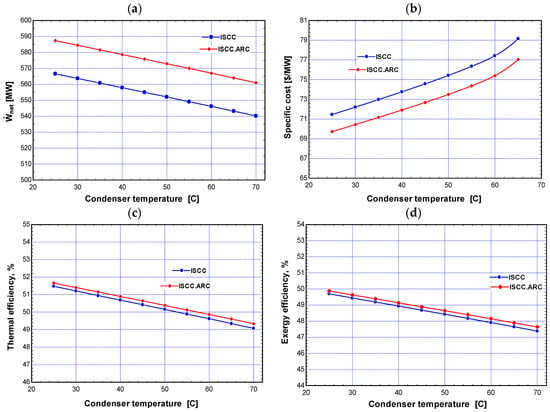
Figure 7.
(a–d) Impact of on the performance and cost of both systems.
Figure 8 shows the proportion of monthly power production produced by both systems. The findings show that the power production of the ISCC system is better in the winter months due to the reduction in the atmospheric temperature and the gas turbine cycles, producing a maximum allowable work net. The ISCC system produced a maximum work net in March (557.7 MW). Conversely, the ISCC-ARC system exhibits enhanced power generation during the summer months due to the ability of the ARC system to lower the intake temperature of the air compressor and the high levels of direct normal irradiance (DNI). These settings optimize the outputs of the system throughout the summer months. In June, the ISCC system had its highest work net output of 591.4 MW.
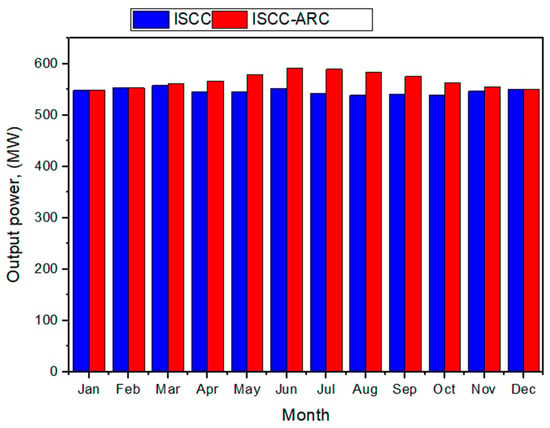
Figure 8.
Total monthly output power from both systems.
Figure 9 illustrates the monthly specific costs of both systems. The visual representation makes it evident that changes in climate conditions exert a noticeable influence in terms of thermodynamic work on these cycles. Our study findings indicate that the overall specific costs for the ISCC-ARC system vary between 69.09 $/MWh in June and 79.05 $/MWh in December. Similarly, the overall specific costs for the ISCC vary from 72.56 $/MWh in June to 78.73 $/MWh in December.
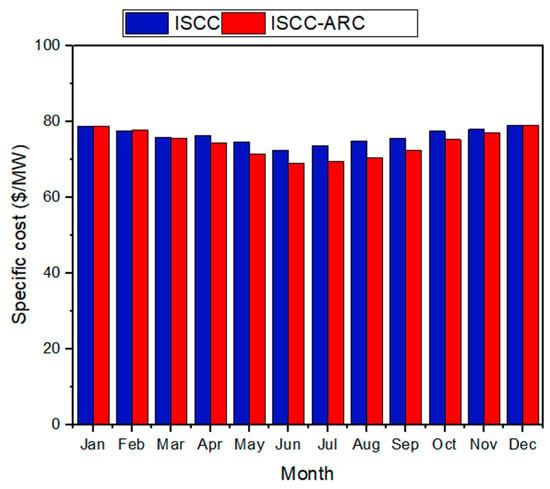
Figure 9.
Monthly specific costs of both systems.
4.3. Validation Study Results
Table 9 presents a comparison between the production from Brayton model employed here in the study and the designated factors of the Brayton units within Al-Qayyarah station, illustrating the consistency. Correspondingly, as delineated in Table 9 the regenerative Rankine cycle (RC) model underwent a comparative analysis with the analogous cycle outlined in focusing on the validation of energy and efficiency [36].

Table 9.
Validation results for the gas turbine’s combined cycle.
The Schedule encompasses the operating environments utilized in the justification typical along with corresponding mathematical outcomes, affirming the robustness of the proposed model in contrast to the referenced findings.
5. Conclusions and Recommendations
This paper conducted a feasibility analysis of a new solar-assisted Brayton cycle (BC)-based Rankine cycle (RC) with an absorption refrigeration system (ARC). The integrated solar combined cycle with absorption refrigeration system was introduced and examined from the perspectives of exergoeconomics, exergy, and energy. The proposed model was composed of three gas turbine units, solar-based parabolic trough collectors, a Rankine cycle, and an absorption refrigeration system. The primary objective of the arranged system is to substantially augment the electricity generation capacity of the Qayyarah power plant, thereby addressing and mitigating the prevalent energy deficit in Iraq. The arranged system is also designed to optimize the operational efficiency of the Qayyarah station, implementing advanced technologies and methodologies to increase electricity output. The EES software was used to simulate and analyze the system. The essential findings are classified as follows:
- Adding the absorption refrigeration cycle improves the , , and of the ISCC-ARC system, the performance of which is far better than that of the ISCC system at keeping the temperature at the inlet of the air compressor at 10 °C, enhancing the , , and of the ISCC-ARC system. In contrast, the , , and of the ISCC system reduce with the increase in the ambient temperature. The work input to the compressor decreases from 315.2 MW to 271.5 MW due to maintaining the temperature of the intake air for the AC at 10 °C.
- The ISCC produces 547.4 MW, while the ISCC-ARC produces 581.6 MW. Adding an ARC to the system increases the produced output by 34.2 MW.
- The thermal and exergy efficiencies and ) are, respectively, 50.89% and 49.14% for the ISCC system, whereas they increase to 51.15% and 46.4%, respectively, for the ISCC-ARC system.
- The highest exergy destruction of the elements in both systems is related to the combustion chambers because of their chemical reaction. The for each element of the ISCC-ARC system is lower than that for the ISCC, except for the CC because the increase in the flow rate of fuel in the ISCC-ARC system causes an elevation in the for the CC.
- A high steam turbine inlet pressure positively impacts cycle performance because the efficiencies and of both systems increase as the PHPST.in increases.
- The gas turbine inlet temperature increases the thermal energy for the exhaust gases at the inlet of the GT, which leads to an increase in the and efficiencies of both cycles.
- The overall specific costs for the ISCC-ARC system range from 69.09 $/MWh in June to 79.05 $/MWh in December. The overall specific costs of the ISCC also fluctuate during the year, from 72.56 $/MWh in June to 78.73 $/MWh in December.
Author Contributions
Conceptualization, W.T.; Methodology, W.T. and A.A.; Software, W.T. and A.A.; Validation, W.T.; Formal analysis, W.T. and A.A.; Resources, W.T.; Data curation, A.A.; Writing—original draft, W.T.; Writing—review & editing, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Area of the solar field (m2) | |
| Cost rate ($/h) | |
| DNI | Direct normal irradiance of the sun |
| Exergy rate (kJ) | |
| Exergy destruct | |
| Heat loss exergy | |
| Exergy of power | |
| Mass flow rate (kg/s) | |
| h | Specific enthalpy (kJ·kg−1) |
| i | Interest rate |
| N | Number of operating hours |
| Lower heating value of fuel | |
| Heat transfer rate (kW) | |
| T | Temperature |
| Tcond | Condenser temperature |
| DNI sun temperature | |
| Power (kW) | |
| Entire cost rate | |
| Greek Symbols | |
| Energy efficiency | |
| Energy performance | |
| Exergy efficiency | |
| Maintenance factor | |
| Exergy efficiency | |
| Subscripts | |
| D | Destruction |
| e | Exit |
| i | Inlet |
| f | Fuel |
| p | Product |
| q | Related to heat |
| w | Related to work |
| tot | Total |
| Therminol VP-1 | |
| Abbreviations | |
| AC | Air compressor |
| ARC | Absorption refrigeration cycle |
| BC | Brayton cycle |
| CC | Combustion chamber |
| CCPP | Combined cycle power plant |
| Con | Condenser |
| CRF | Capital Recovery Factor |
| CSP | Concentrating Solar Power |
| EES | Engineering Equation Solver |
| GE | General Electric |
| GT | Gas turbine |
| GTIT | Gas turbine inlet temperature |
| HRSG | Heat Recovery Steam Generation |
| HPST | High-pressure steam turbine |
| ISCC | Integrated solar combined cycle |
| ISCC-ARC | Integrated solar combined cycle with an absorption refrigeration cycle |
| LiBr | Lithium bromide |
| LPST | Low-pressure steam turbine |
| ORC | Organic Rankine cycle |
| Pr | Pressure ratio |
| PTC | Parabolic trough collector |
References
- Ibraheem, W.E.; Abdulraheem, A.A. Design of 5MW PV Power Plant in Iraq in Al-Sharqiyah Diyala Substation. In Proceedings of the 2021 Fourth International Conference on Electrical, Computer and Communication Technologies (ICECCT), Erode, India, 15–17 September 2021; pp. 1–7. [Google Scholar]
- Dawood, T.A.; Raphael, R.; Barwari, I.; Akroot, A. Solar Energy and Factors Affecting the Efficiency and Performance of Panels in Erbil/Kurdistan. Int. J. Heat Technol. 2023, 41, 304–312. [Google Scholar] [CrossRef]
- Khudhur, J.; Akroot, A.; Al-samari, A. Experimental Investigation of Direct Solar Photovoltaics that Drives Absorption Refrigeration System. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 1, 116–135. [Google Scholar] [CrossRef]
- Abed, F.M.; Al-Douri, Y.; Al-Shahery, G.M. Review on the energy and renewable energy status in Iraq: The outlooks. Renew. Sustain. Energy Rev. 2014, 39, 816–827. [Google Scholar] [CrossRef]
- Abusaibaa, G.Y.; Al-Aasam, A.B.; Al-Waeli, A.H.A.; Al-Fatlawi, A.W.A.; Sopian, K. Performance analysis of solar absorption cooling systems in Iraq. Int. J. Renew. Energy Res. 2020, 10, 223–230. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration (EIA). International Energy Outlook 2016. Available online: http://www.eia.gov/forecasts/ieo/ (accessed on 1 October 2023).
- Haseeb, Q.S.; Yunus, S.M.; Shoshan, A.A.A.; Aziz, A.I. A study of the optimal form and orientation for more energy efficiency to mass model mult-istorey buildings of Kirkuk city, Iraq. Alex. Eng. J. 2023, 71, 731–741. [Google Scholar] [CrossRef]
- Saeed, I.M.; Ramli, A.T.; Saleh, M.A. Assessment of sustainability in energy of Iraq, and achievable opportunities in the long run. Renew. Sustain. Energy Rev. 2016, 58, 1207–1215. [Google Scholar] [CrossRef]
- Hassan, Q.; Hafedh, S.A.; Hasan, A.; Jaszczur, M. Evaluation of energy generation in Iraqi territory by solar photovoltaic power plants with a capacity of 20 MW. Energy Harvest. Syst. 2022, 9, 97–111. [Google Scholar] [CrossRef]
- Kazem, H.A.; Chaichan, M.T. Status and future prospects of renewable energy in Iraq. Renew. Sustain. Energy Rev. 2012, 16, 6007–6012. [Google Scholar] [CrossRef]
- Talal, W.; Akroot, A. Exergoeconomic Analysis of an Integrated Solar Combined Cycle in the Al-Qayara Power Plant in Iraq. Processes 2023, 11, 656. [Google Scholar] [CrossRef]
- Faisal, S.H.; Naeem, N.K.; Jassim, A.A. Energy and exergy study of Shatt Al-Basra gas turbine power plant. J. Phys. Conf. Ser. 2021, 1773, 012020. [Google Scholar] [CrossRef]
- Salah, S.A.; Abbas, E.F.; Ali, O.M.; Alwan, N.T.; Yaqoob, S.J.; Alayi, R. Evaluation of the gas turbine unit in the Kirkuk gas power plant to analyse the energy and exergy using ChemCad simulation. Int. J. Low-Carbon Technol. 2022, 17, 603–610. [Google Scholar] [CrossRef]
- Ahmed, A.H.; Ahmed, A.M.; Hamid, Q.Y. Exergy and energy analysis of 150 MW gas turbine unit: A case study. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 67, 186–192. [Google Scholar]
- Kareem, A.F.; Akroot, A.; Wahhab, H.A.A.; Talal, W.; Ghazal, R.M.; Alfaris, A. Exergo–Economic and Parametric Analysis of Waste Heat Recovery from Taji Gas Turbines Power Plant Using Rankine Cycle and Organic Rankine Cycle. Sustainability 2023, 15, 9376. [Google Scholar] [CrossRef]
- Elberry, M.; Elsayed, A.; Teamah, M.; Abdel-Rahman, A.; Elsafty, A. Performance improvement of power plants using absorption cooling system. Alex. Eng. J. 2018, 57, 2679–2686. [Google Scholar] [CrossRef]
- Santos, A.P.P.; Andrade, C.R.; Zaparoli, E. Comparison of different gas turbine inlet air cooling methods, World Academy of Science. Eng. Technol. 2012, 6, 1–6. [Google Scholar]
- Kwon, H.M.; Kim, T.S.; Sohn, J.L.; Kang, D.W. Performance improvement of gas turbine combined cycle power plant by dual cooling of the inlet air and turbine coolant using an absorption chiller. Energy 2018, 163, 1050–1061. [Google Scholar] [CrossRef]
- Javanfam, F.; Ghiasirad, H.; Khoshbakhti Saray, R. Efficiency Improvement and Cost Analysis of a New Combined Absorption Cooling and Power System; Springer International Publishing: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Sa, A.D.; Zubaidy, S.A. Gas turbine performance at varying ambient temperature. Appl. Therm. Eng. 2011, 31, 2735–2739. [Google Scholar] [CrossRef]
- Oko, C.O.C.; Njoku, I. Performance analysis of an integrated gas-, steam- and organic fluid-cycle thermal power plant. Energy 2017, 122, 431–443. [Google Scholar] [CrossRef]
- Shukla, A.K.; Singh, O. Effect of Compressor Inlet Temperature & Relative Humidity on Gas Turbine Cycle Performance. Eng. Environ. Sci. 2014, 5, 664–671. [Google Scholar]
- Karaalı, R. Exergy analysis of a combined power and cooling cycle. Acta Phys. Pol. A 2016, 130, 209–213. [Google Scholar] [CrossRef]
- Settino, J.; Ferraro, V.; Morrone, P. Energy analysis of novel hybrid solar and natural gas combined cycle plants. Appl. Therm. Eng. 2023, 230, 120673. [Google Scholar] [CrossRef]
- Roshanzadeh, B.; Asadi, A.; Mohan, G. Technical and Economic Feasibility Analysis of Solar Inlet Air Cooling Systems for Combined Cycle Power Plants. Energies 2023, 16, 5352. [Google Scholar] [CrossRef]
- Nami, H.; Mahmoudi, S.M.A.; Nemati, A. Exergy, economic and environmental impact assessment and optimization of a novel cogeneration system including a gas turbine, a supercritical CO2 and an organic Rankine cycle (GT-HRSG/SCO2). Appl. Therm. Eng. 2017, 110, 1315–1330. [Google Scholar] [CrossRef]
- Bakhshmand, S.K.; Saray, R.K.; Bahlouli, K.; Eftekhari, H.; Ebrahimi, A. Exergoeconomic analysis and optimization of a triple-pressure combined cycle plant using evolutionary algorithm. Energy 2015, 93, 555–567. [Google Scholar] [CrossRef]
- Akroot, A.; Namli, L. Performance assessment of an electrolyte-supported and anode-supported planar solid oxide fuel cells hybrid system. J. Ther. Eng. 2021, 7, 1921–1935. [Google Scholar] [CrossRef]
- Nourpour, M.; Manesh, M.K. Evaluation of novel integrated combined cycle based on gas turbine-SOFC-geothermal-steam and organic Rankine cycles for gas turbo compressor station. Energy Convers. Manag. 2022, 252, 115050. [Google Scholar] [CrossRef]
- Köse, A.; Koç, Y.; Yağlı, H. Energy, exergy, economy and environmental (4E) analysis and optimization of single, dual and triple configurations of the power systems: Rankine Cycle/Kalina Cycle, driven by a gas turbine. Energy Convers. Manag. 2021, 227, 113604. [Google Scholar] [CrossRef]
- Mohammadkhani, F.; Shokati, N.; Mahmoudi, S.; Yari, M.; Rosen, M. Exergoeconomic assessment and parametric study of a Gas Turbine-Modular Helium Reactor combined with two Organic Rankine Cycles. Energy 2014, 65, 533–543. [Google Scholar] [CrossRef]
- Cavalcanti, E.J.C. Exergoeconomic and exergoenvironmental analyses of an integrated solar combined cycle system. Renew. Sustain. Energy Rev. 2017, 67, 507–519. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Jing, Y. Exergoeconomic analysis of solar absorption-subcooled compression hybrid cooling system. Energy Convers. Manag. 2017, 144, 205–216. [Google Scholar] [CrossRef]
- Xie, N.; Xiao, Z.; Du, W.; Deng, C.; Liu, Z.; Yang, S. Thermodynamic and exergoeconomic analysis of a proton exchange membrane fuel cell/absorption chiller CCHP system based on biomass gasification. Energy 2023, 262, 125595. [Google Scholar] [CrossRef]
- Musharavati, F.; Khanmohammadi, S.; Pakseresht, A. A novel multi-generation energy system based on geothermal energy source: Thermo-economic evaluation and optimization. Energy Convers. Manag. 2021, 230, 113829. [Google Scholar] [CrossRef]
- Sachdeva, J.; Singh, O. Thermodynamic analysis of solar powered triple combined Brayton, Rankine and organic Rankine cycle for carbon free power. Renew. Energy 2019, 139, 765–780. [Google Scholar] [CrossRef]
- Lugand, P.; Parietti, C. Combined Cycle Plants with Frame 9F Gas Turbines; American Society of Mechanical Engineers: New York, NY, USA, 1990; Volume 4, pp. 1–8. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D. Fundamentals of Engineering Thermodynamics; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).