DC Series Arc Fault Diagnosis Scheme Based on Hybrid Time and Frequency Features Using Artificial Learning Models
Abstract
1. Introduction
2. Arc Failure Generation, Specifications, and Characteristics
3. Feature Extraction in Time and Frequency Domains, and Artificial Learning Models
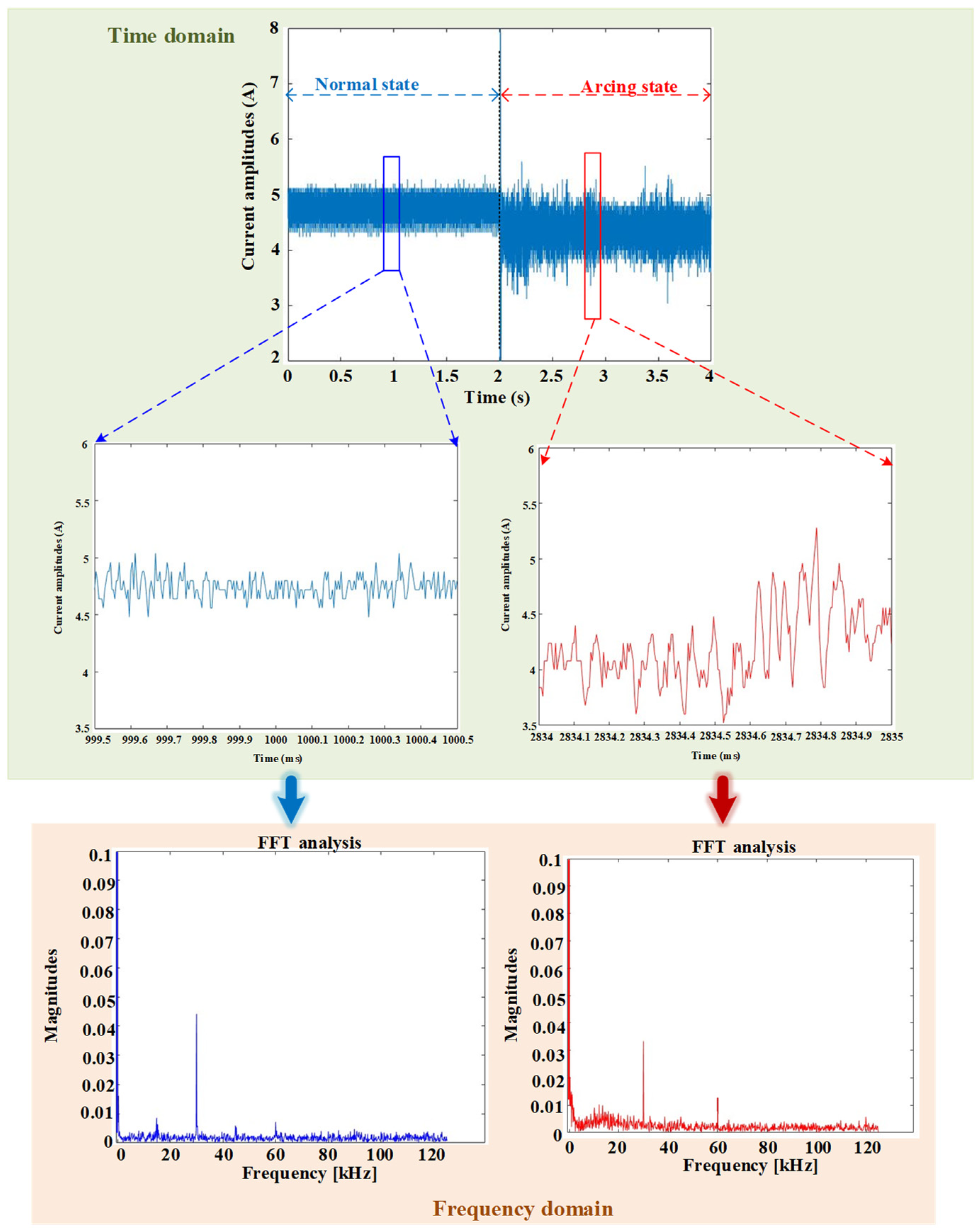
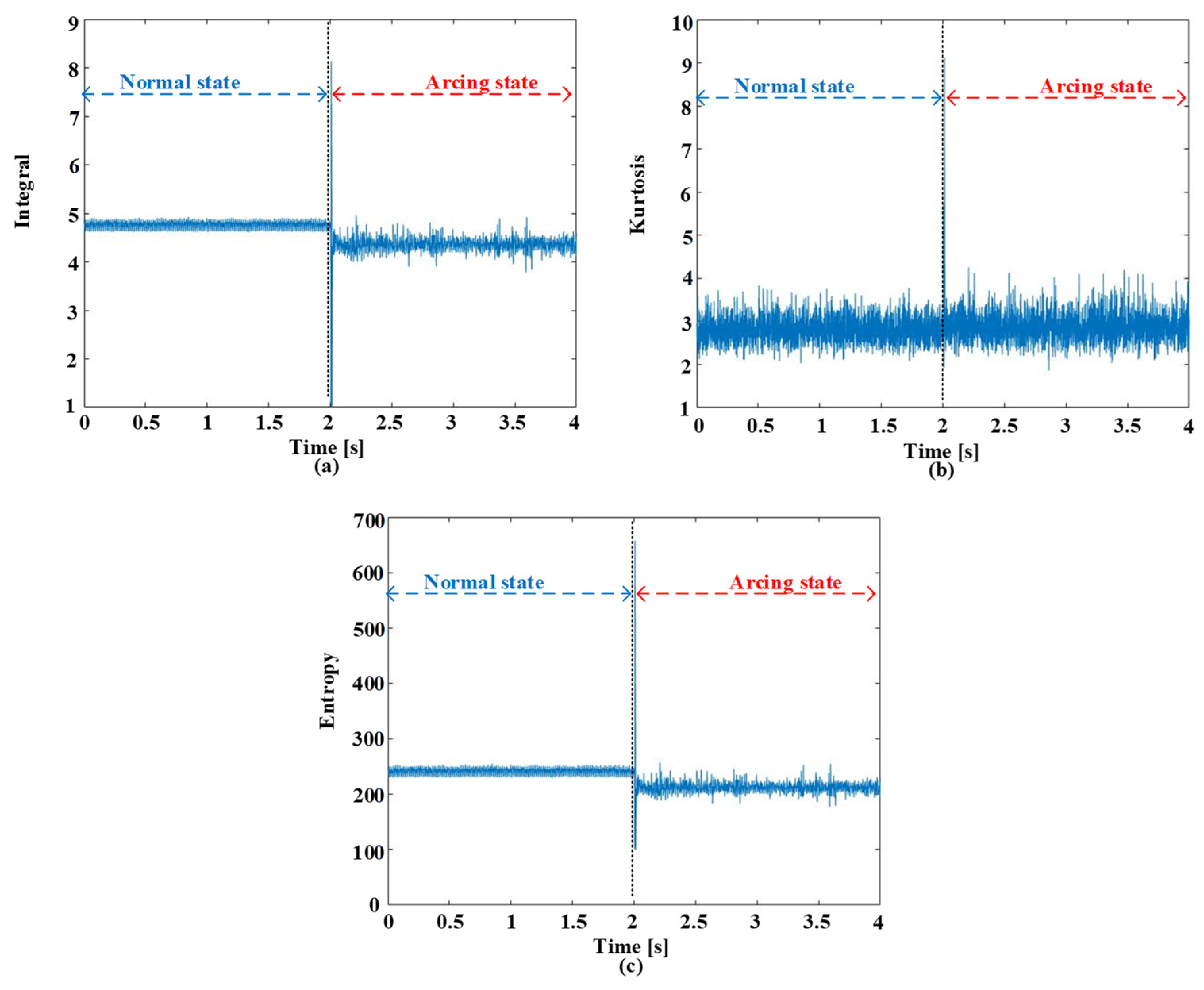
3.1. Feature Extraction in Time Domain
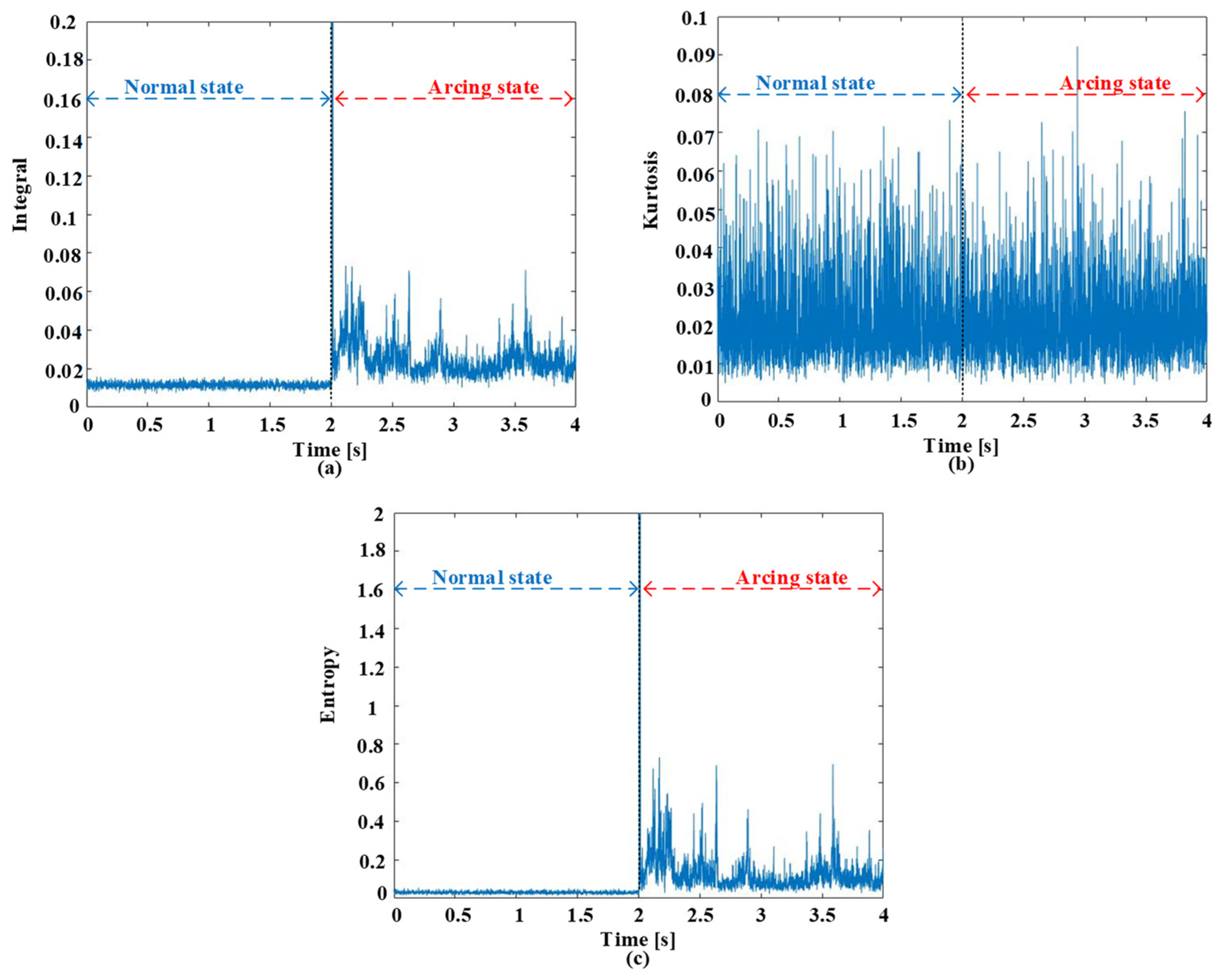
3.2. Feature Extraction in Frequency Domain
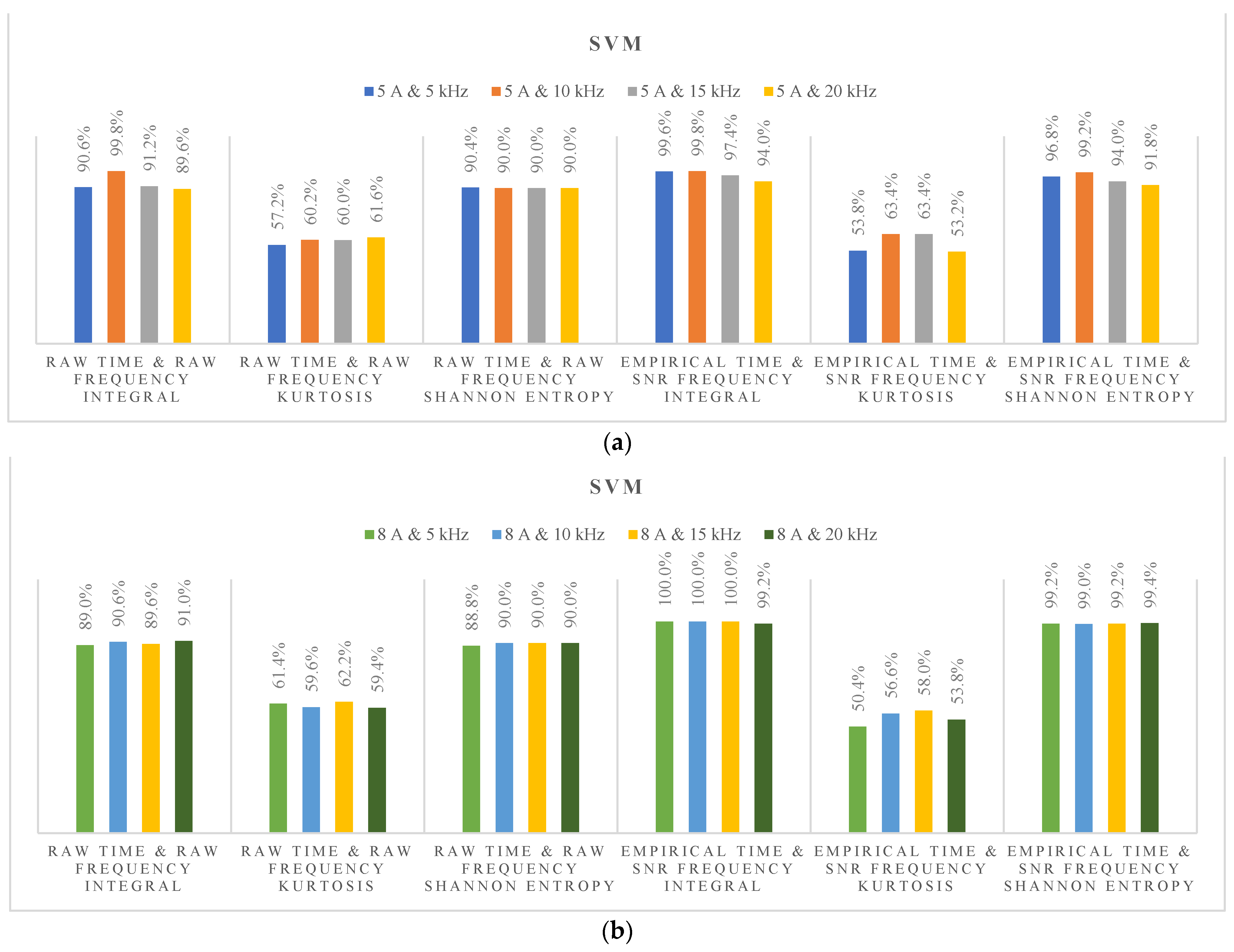
3.3. Artificial Learning Models (ALMs)
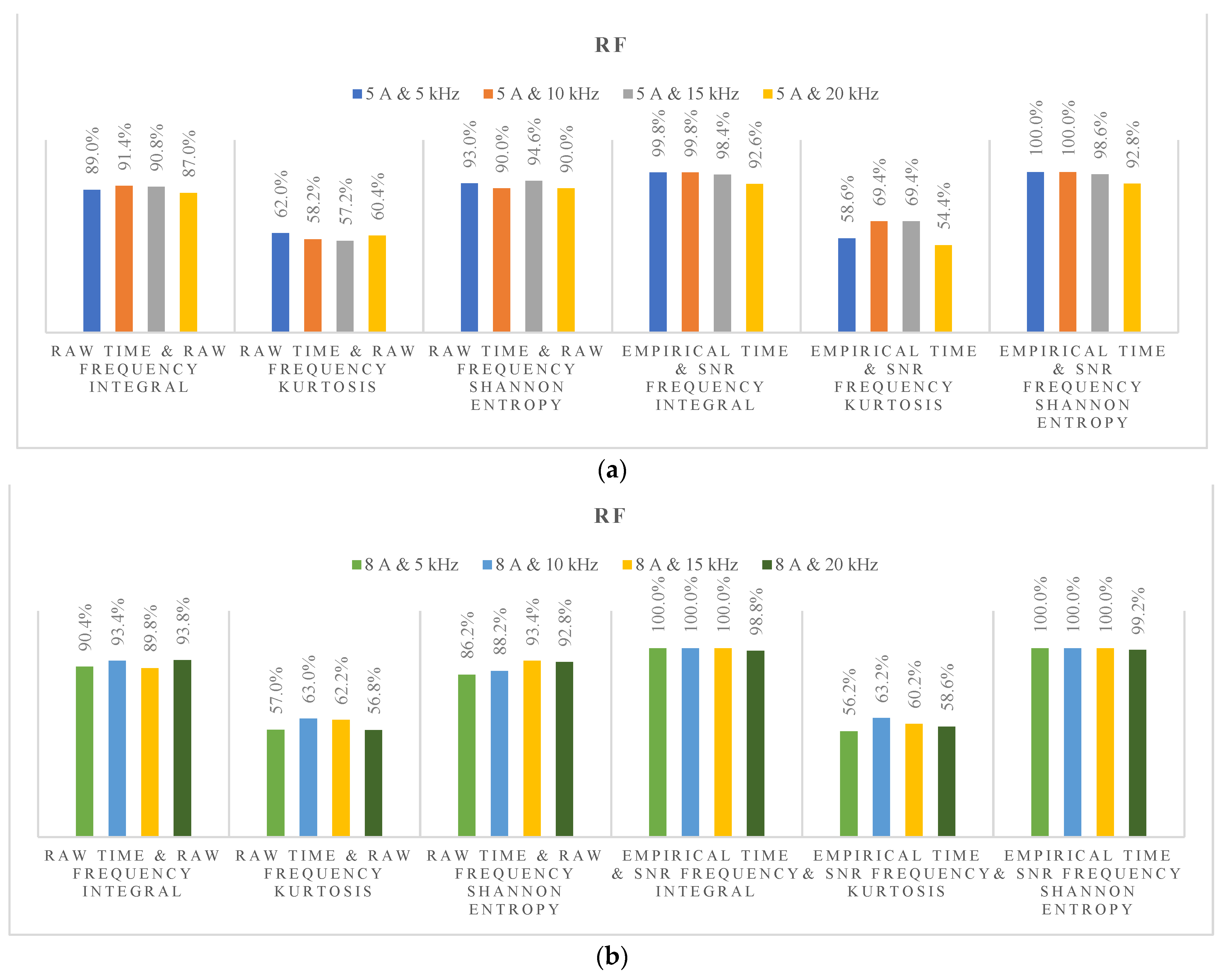
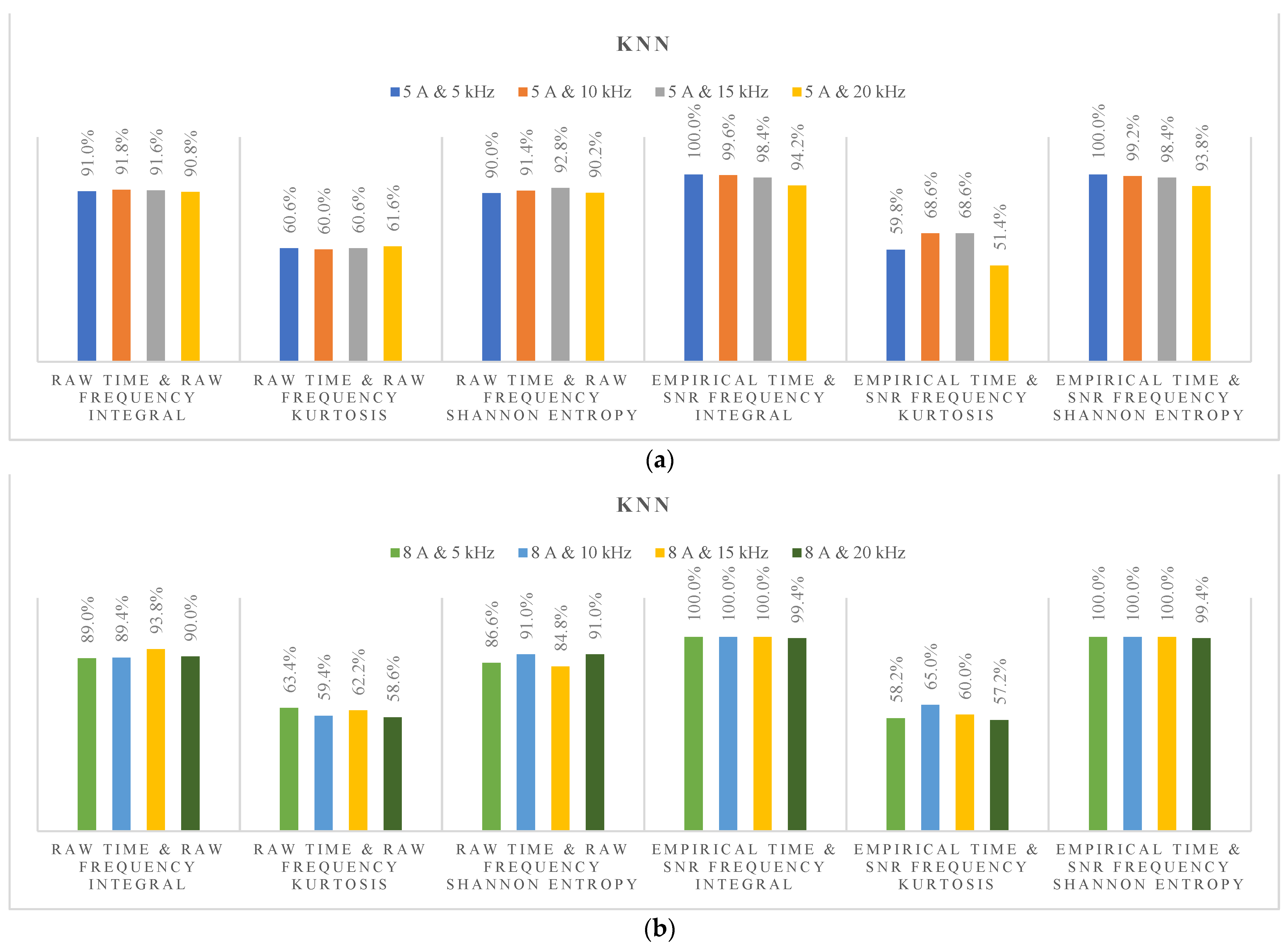
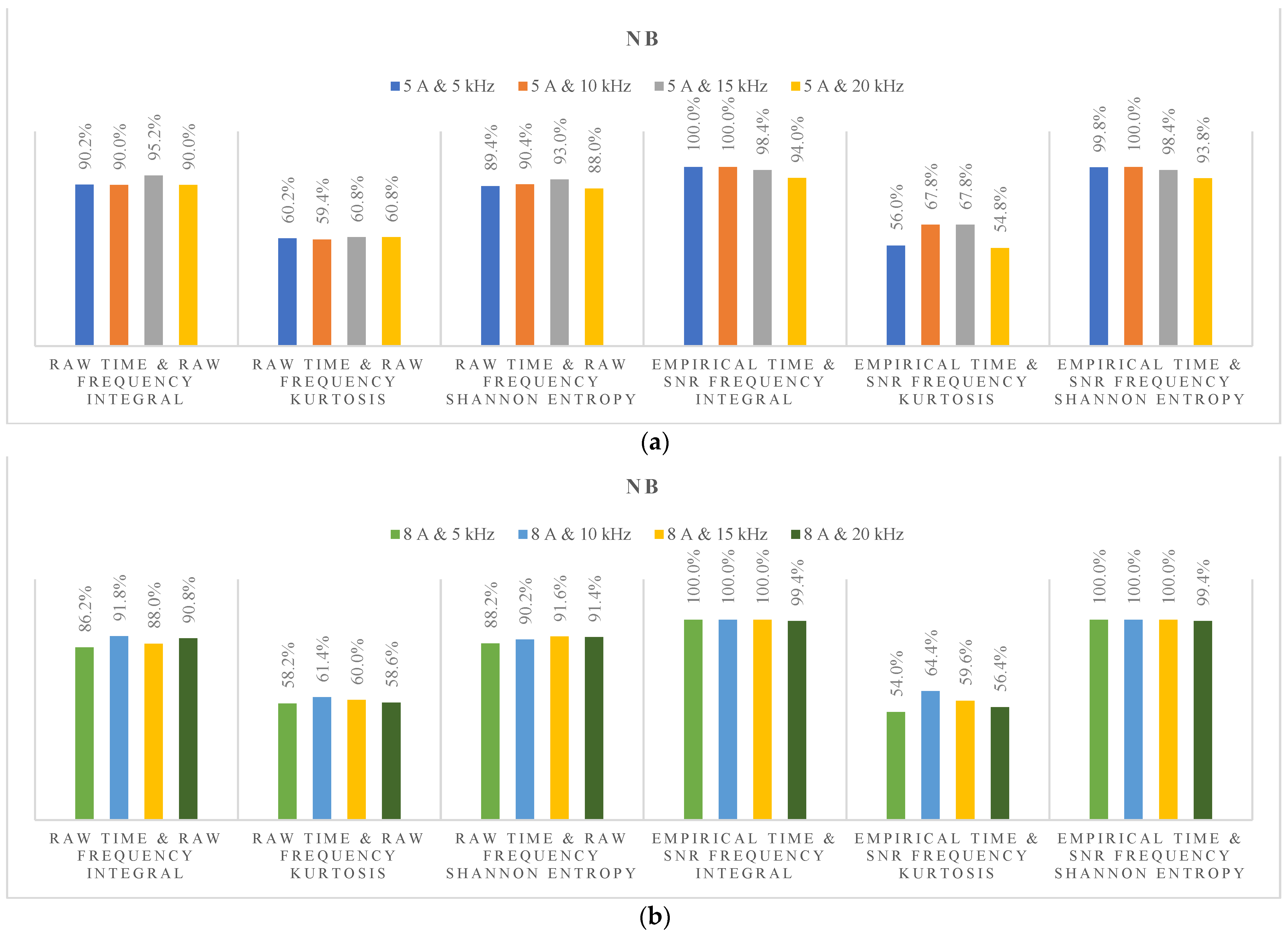
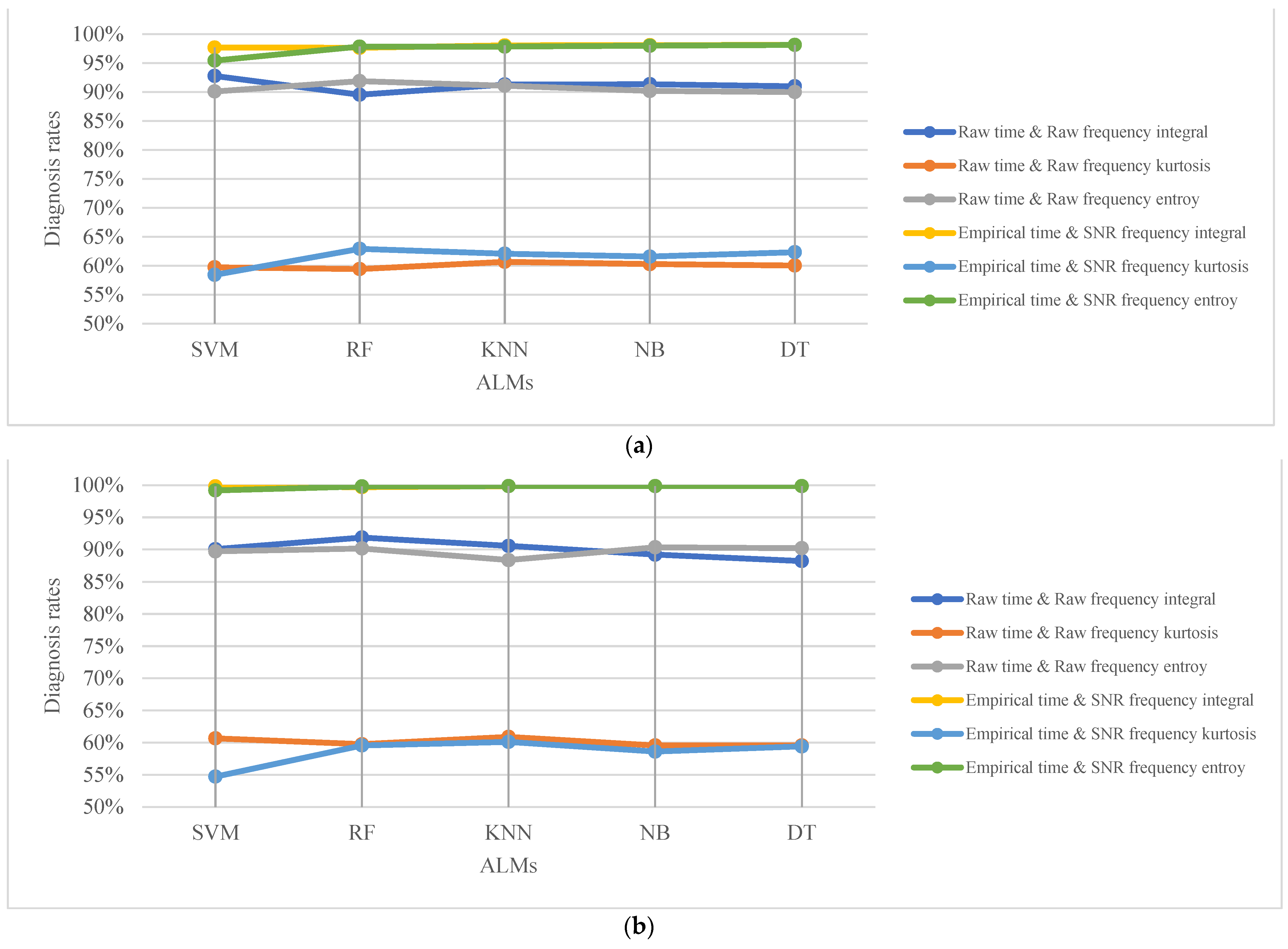
4. DC Series Arc Fault Diagnosis Based on Hybrid Time and Frequency Features Using Artificial Learning Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, Z.; Wang, L.; Yang, S.; Gao, Y. A Series Arc Fault Diagnosis Method in DC Distribution Systems Based on Multiscale Features and Random Forests. IEEE Sens. J. 2022, 23, 2605–2617. [Google Scholar] [CrossRef]
- Xing, L.; Wen, Y.; Xiao, S.; Zhang, D.; Zhang, J. A Deep Learning Approach for Series DC Arc Fault Diagnosing and Real-Time Circuit Behavior Predicting. IEEE Trans. Electromagn. Compat. 2021, 64, 569–579. [Google Scholar] [CrossRef]
- Jalil, M.; Samet, H.; Ghanbari, T.; Tajdinian, M. Development of Nottingham Arc Model for DC Series Arc Modeling in Photovoltaic Panels. IEEE Trans. Ind. Electron. 2021, 69, 13647–13655. [Google Scholar] [CrossRef]
- Yao, X.; Herrera, L.; Wang, J. Impact evaluation of series dc arc faults in dc microgrids. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 2953–2958. [Google Scholar]
- Yao, X. Study on DC arc faults in ring-bus DC microgrids with constant power loads. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar]
- Pillai, D.S.; Rajasekar, N. A comprehensive review on protection challenges and fault diagnosis in PV systems. Renew. Sustain. Energy Rev. 2018, 91, 18–40. [Google Scholar] [CrossRef]
- Xiang, W.; Yang, S.; Adam, G.P.; Zhang, H.; Zuo, W.; Wen, J. DC Fault Protection Algorithms of MMC-HVDC Grids: Fault Analysis, Methodologies, Experimental Validations, and Future Trends. IEEE Trans. Power Electron. 2021, 36, 11245–11264. [Google Scholar] [CrossRef]
- Ahn, J.-B.; Jo, H.-B.; Ryoo, H.-J. Real-Time DC Series Arc Fault Detection Based on Noise Pattern Analysis in Photovoltaic System. IEEE Trans. Ind. Electron. 2022, 70, 10680–10689. [Google Scholar] [CrossRef]
- Chen, S.; Wu, H.; Meng, Y.; Wang, Y.; Li, X.; Zhang, C. Reliable Detection Method of Variable Series Arc Fault in Building Integrated Photovoltaic Systems Based on Nonstationary Time Series Analysis. IEEE Sens. J. 2023, 23, 8654–8664. [Google Scholar] [CrossRef]
- Georgijevic, N.L.; Jankovic, M.V.; Srdic, S.; Radakovic, Z. The Detection of Series Arc Fault in Photovoltaic Systems Based on the Arc Current Entropy. IEEE Trans. Power Electron. 2015, 31, 5917–5930. [Google Scholar] [CrossRef]
- Rabla, M.; Tisserand, E.; Schweitzer, P.; Lezama, J. Arc Fault Analysis and Localisation by Cross-Correlation in 270 V DC. In Proceedings of the 2013 IEEE 59th Holm Conference on Electrical Contacts (Holm 2013), Newport, RI, USA, 22–25 September 2013; pp. 1–6. [Google Scholar]
- Yao, X.; Herrera, L.; Ji, S.; Zou, K.; Wang, J. Characteristic Study and Time-Domain Discrete- Wavelet-Transform Based Hybrid Detection of Series DC Arc Faults. IEEE Trans. Power Electron. 2013, 29, 3103–3115. [Google Scholar] [CrossRef]
- Wang, Z.; Balog, R.S. Arc fault and flash detection in photovoltaic systems using wavelet transform and support vector machines. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 3275–3280. [Google Scholar]
- He, C.; Mu, L.; Wang, Y. The Detection of Parallel Arc Fault in Photovoltaic Systems Based on a Mixed Criterion. IEEE J. Photovolt. 2017, 7, 1717–1724. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Z.; Balog, R.S. Real time arc fault detection in PV systems using wavelet decomposition. In Proceedings of the 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016; pp. 1761–1766. [Google Scholar]
- Gajula, K.; Herrera, L. Detection and Localization of Series Arc Faults in DC Microgrids Using Kalman Filter. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 2589–2596. [Google Scholar] [CrossRef]
- Li, W.; Liu, Y.; Li, Y.; Guo, F. Series Arc Fault Diagnosis and Line Selection Method Based on Recurrent Neural Network. IEEE Access 2020, 8, 177815–177822. [Google Scholar] [CrossRef]
- Jalayer, M.; Orsenigo, C.; Vercellis, C. Fault detection and diagnosis for rotating machinery: A model based on convolutional LSTM, Fast Fourier and continuous wavelet transforms. Comput. Ind. 2020, 125, 103378. [Google Scholar] [CrossRef]
- Thakur, K.; Dwivedi, D.; Babu, K.; Parimi, A.M.; Yemula, P.K.; Chakraborty, P.; Pal, M. Advancements in Arc Fault Detection for Electrical Distribution Systems: A Comprehensive Review from Artificial Intelligence Perspective. arXiv 2023, arXiv:2311.16804. [Google Scholar]
- Dang, H.-L.; Kwak, S.; Choi, S. DC Series Arc Failure Diagnosis Using Artificial Machine Learning With Switching Frequency Component Elimination Technique. IEEE Access 2023, 11, 119584–119595. [Google Scholar] [CrossRef]
- Dang, H.-L.; Kwak, S.; Choi, S. Empirical Filtering-Based Artificial Intelligence Learning Diagnosis of Series DC Arc Faults in Time Domains. Machines 2023, 11, 968. [Google Scholar] [CrossRef]
- Dang, H.-L.; Kwak, S.; Choi, S. Different Domains Based Machine and Deep Learning Diagnosis for DC Series Arc Failure. IEEE Access 2021, 9, 166249–166261. [Google Scholar] [CrossRef]
- Pukelsheim, F. The Three Sigma Rule; The American Statistician: Alexandria, VA, USA, 1994; Volume 48, pp. 88–91. [Google Scholar]
- Gu, J.-C.; Lai, D.-S.; Wang, J.-M.; Huang, J.-J.; Yang, M.-T. Design of a DC Series Arc Fault Detector for Photovoltaic System Protection. IEEE Trans. Ind. Appl. 2019, 55, 2464–2471. [Google Scholar] [CrossRef]
- UL 1699B; Outline of Investigation for Photovoltaic (PV) dc Arc-Fault Circuit Protection, Issue 2. Underwriters Laboratories, Inc.: Northbrook, IL, USA, 2013.
- Borges, F.A.; Fernandes, R.A.; Silva, I.N.; Silva, C.B.S. Feature Extraction and Power Quality Disturbances Classification Using Smart Meters Signals. IEEE Trans. Ind. Inform. 2015, 12, 824–833. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F.; Zhang, X.; Zhang, S. Series AC Arc Fault Detection Method Based on Hybrid Time and Frequency Analysis and Fully Connected Neural Network. IEEE Trans. Ind. Inform. 2018, 15, 6210–6219. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computation Learning Theory (COLT’92), Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Statistics/Probability Series; Wadsworth and Brooks: Belmont, CA, USA, 1984. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Langley, P.; Iba, W.; Thompson, K. An analysis of Bayesian classifiers. In Proceedings of the 10th National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; pp. 223–228. [Google Scholar]
- Lu, W.; Liang, B.; Cheng, Y.; Meng, D.; Yang, J.; Zhang, T. Deep Model Based Domain Adaptation for Fault Diagnosis. IEEE Trans. Ind. Electron. 2016, 64, 2296–2305. [Google Scholar] [CrossRef]
- Sung, Y.; Yoon, G.; Bae, J.-H.; Chae, S. TL–LEDarcNet: Transfer Learning Method for Low-Energy Series DC Arc-Fault Detection in Photovoltaic Systems. IEEE Access 2022, 10, 100725–100735. [Google Scholar] [CrossRef]
- Lu, S.; Sirojan, T.; Phung, B.T.; Zhang, D.; Ambikairajah, E. DA-DCGAN: An Effective Methodology for DC Series Arc Fault Diagnosis in Photovoltaic Systems. IEEE Access 2019, 7, 45831–45840. [Google Scholar] [CrossRef]



| ALMs | SVM | KNN | DT | RF | NB |
|---|---|---|---|---|---|
| Core principles | Finding the hyperplane that maximizing the margin between classes. | Similar things are possess neighboring closeness. | A tree structure starts with a root node and ends with a decision made by leaves. | Consists of many individual decision trees that operate as an ensemble. | Based on Bayes’ theorem with assumption that all features are conditionally independent. |
| Approach | Input Domain(s) | Data Size | Learning Type—Structure Complexity | Overall Accuracy |
|---|---|---|---|---|
| DAFD [33] | Time domain | Large | Deep learning—High | 95.76% |
| TL-LEDArcNet [34] | Time and frequency domains | Large | Deep learning—High | 95.8% |
| DA-DCGAN [35] | Time domain | Large | Deep learning—High | 98.5% |
| Proposed method | Time and frequency domains | Small | Machine learning—Medium | 98.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, H.-L.; Kwak, S.; Choi, S. DC Series Arc Fault Diagnosis Scheme Based on Hybrid Time and Frequency Features Using Artificial Learning Models. Machines 2024, 12, 102. https://doi.org/10.3390/machines12020102
Dang H-L, Kwak S, Choi S. DC Series Arc Fault Diagnosis Scheme Based on Hybrid Time and Frequency Features Using Artificial Learning Models. Machines. 2024; 12(2):102. https://doi.org/10.3390/machines12020102
Chicago/Turabian StyleDang, Hoang-Long, Sangshin Kwak, and Seungdeog Choi. 2024. "DC Series Arc Fault Diagnosis Scheme Based on Hybrid Time and Frequency Features Using Artificial Learning Models" Machines 12, no. 2: 102. https://doi.org/10.3390/machines12020102
APA StyleDang, H.-L., Kwak, S., & Choi, S. (2024). DC Series Arc Fault Diagnosis Scheme Based on Hybrid Time and Frequency Features Using Artificial Learning Models. Machines, 12(2), 102. https://doi.org/10.3390/machines12020102






