Research on a Bearing Fault Diagnosis Method Based on a CNN-LSTM-GRU Model
Abstract
1. Introduction
- The vibration signal processing method relies on data sample quality and a weak generalization ability in bearing fault diagnosis. The CNN-LSTM-GRU deep learning network model proposed in this paper is used for bearing fault diagnosis, providing new ideas for fault diagnosis.
- To provide the diagnostic model with a stable time series prediction ability and an efficient comprehensive spatiotemporal feature extraction ability, this study optimizes the network hierarchy structure of a convolutional neural network (CNN) to strengthen the extraction of spatial features. At the same time, it integrates a long short-term memory network (LSTM) network to model the long-term trends of the time series. In addition, a gated recurrent unit (GRU), which efficiently processes medium- and short-length sequences, is introduced to locally fine-tune the long time series, enabling better management and maintenance of the long-term time series prediction results.
- The proposed model was evaluated using comparative experiments. This method can effectively prevent gradient vanishing and data overfitting compared to other models, and has higher robustness, with a comprehensive diagnostic accuracy of 99.34%.
2. Related Work
2.1. Convolutional Neural Network (CNN)
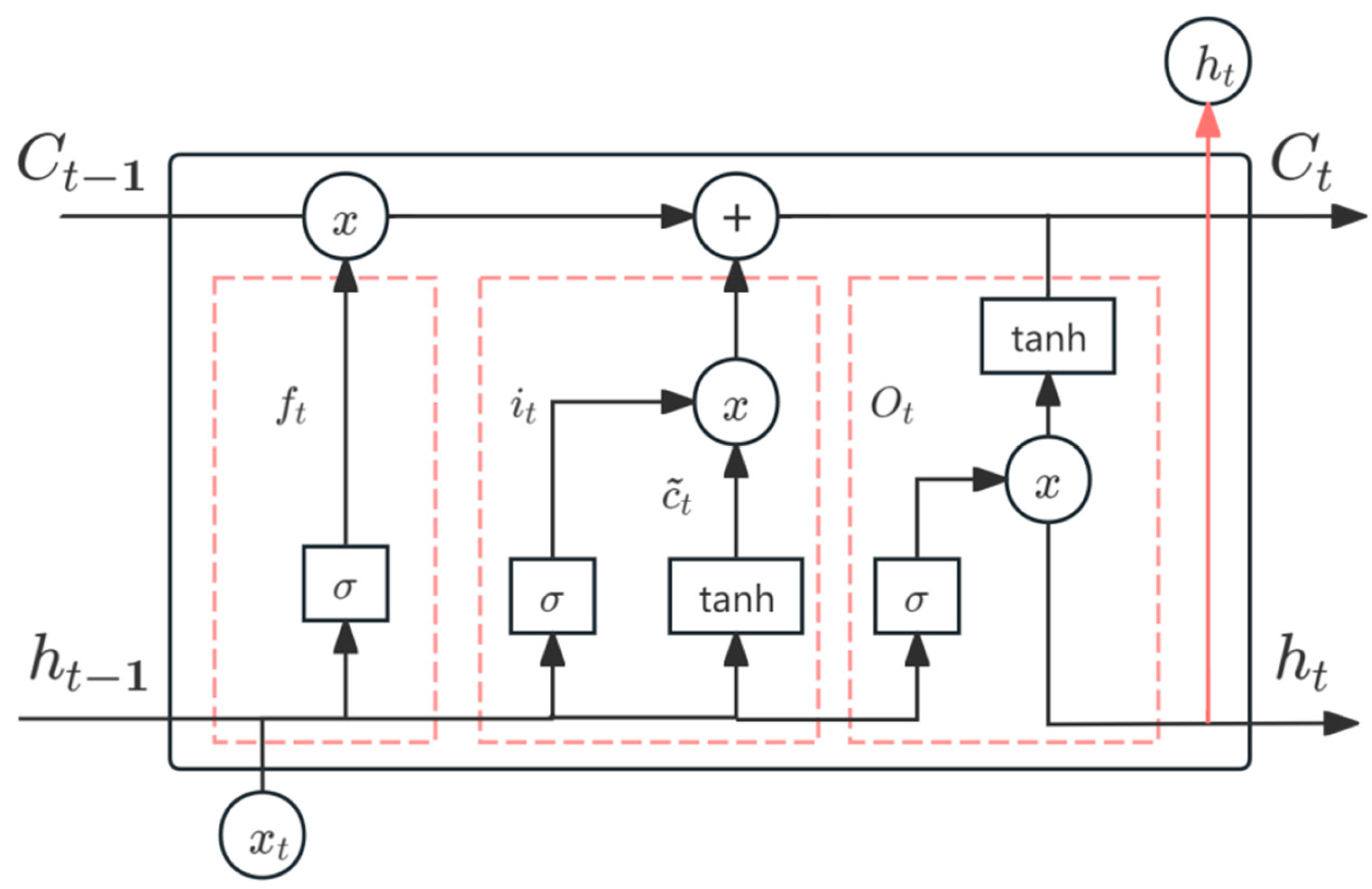
2.2. Long Short-Term Memory (LSTM) Network
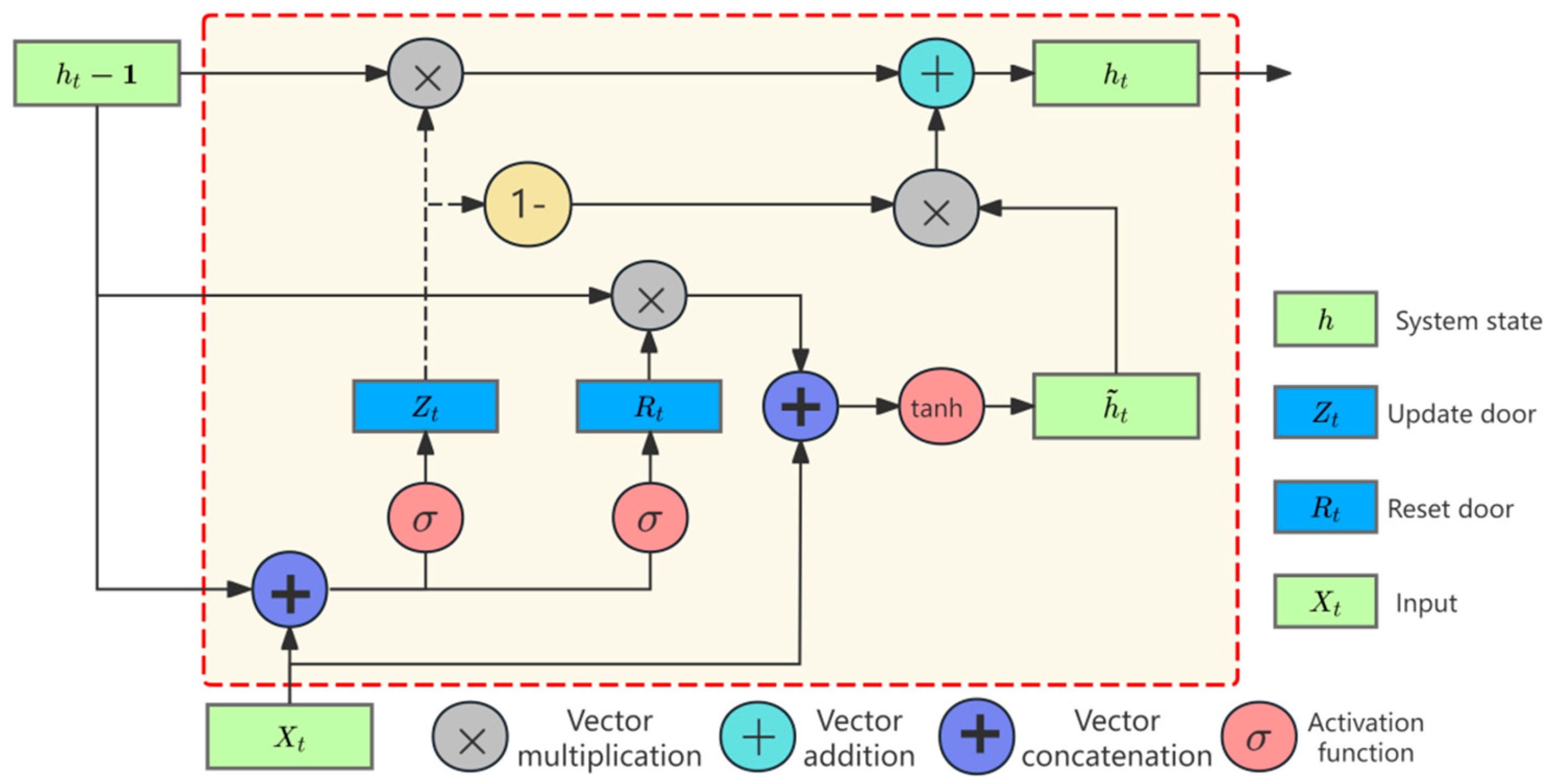
2.3. Gated Recurrent Unit (GRU)
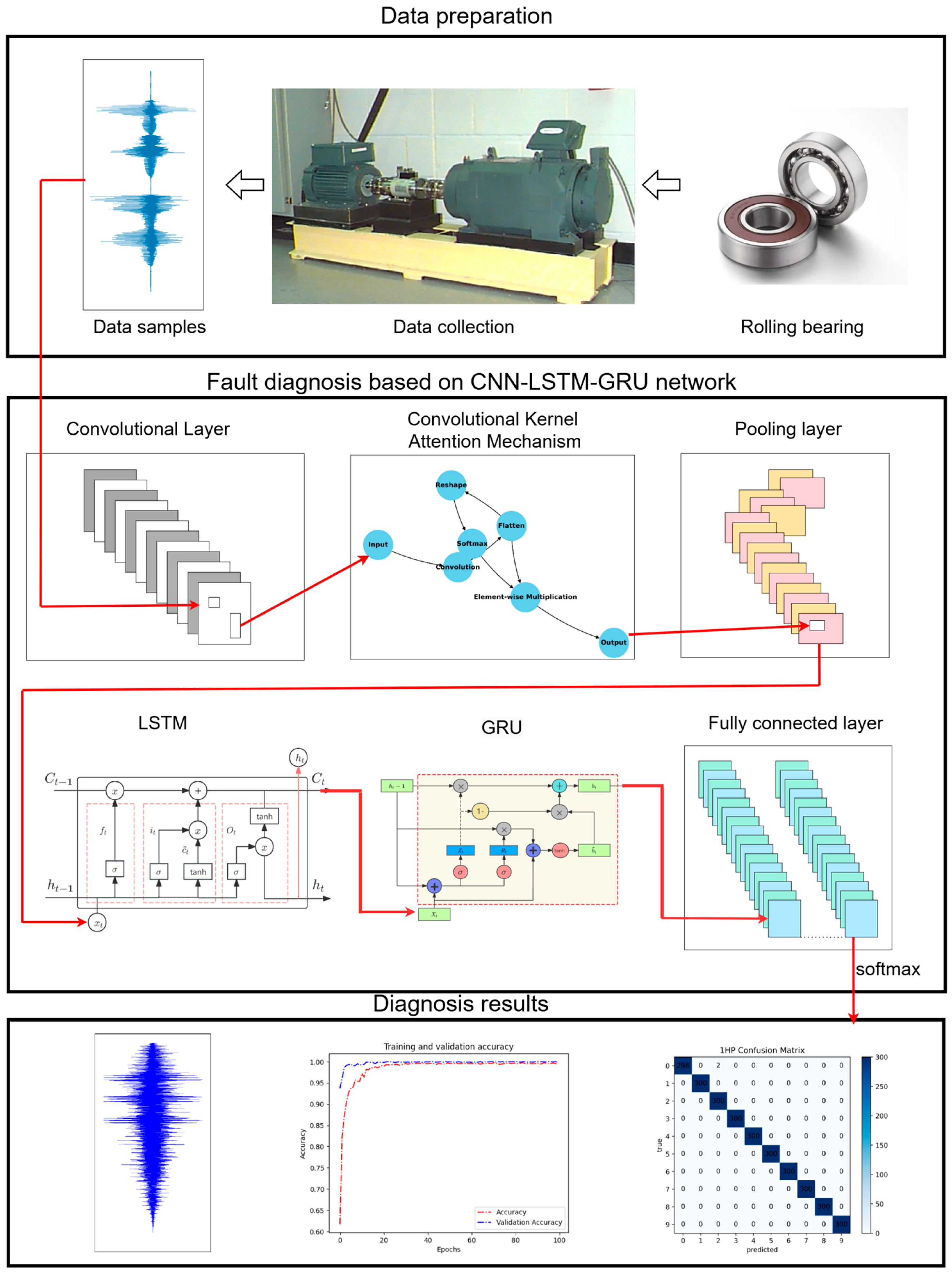
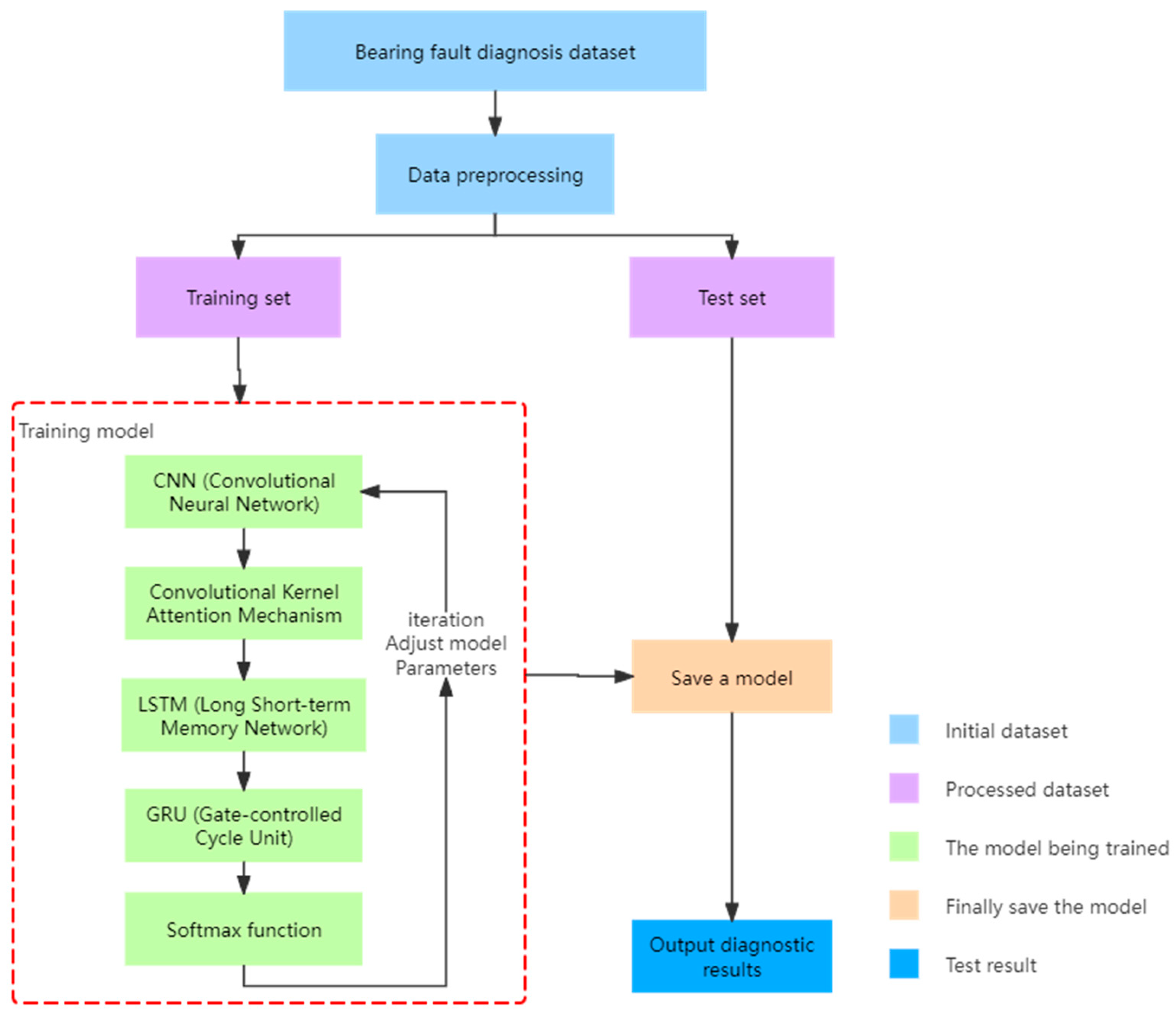
3. Fault Diagnosis Model for Rolling Bearings
3.1. A Bearing Diagnosis Model Based on a CNN-LSTM-GRU Model
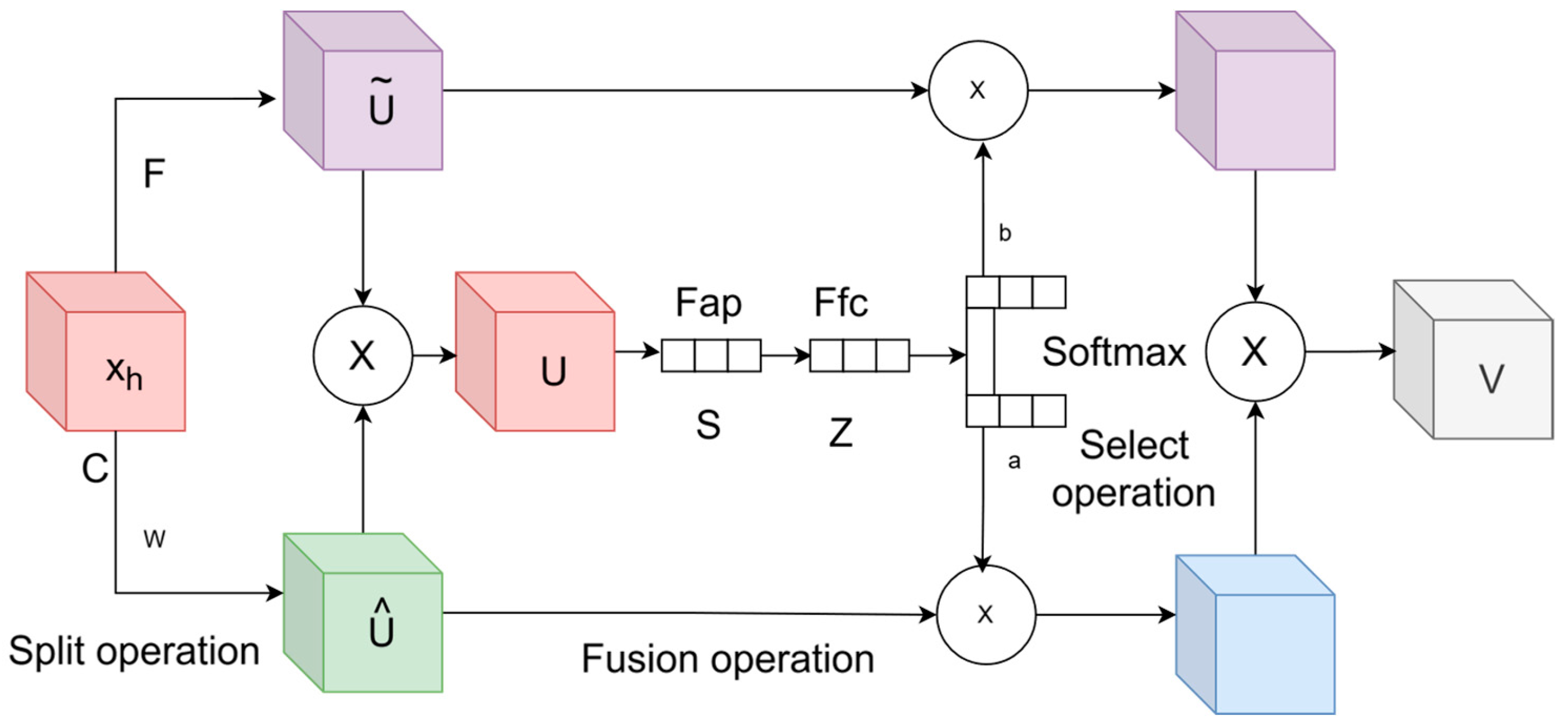
3.2. Convolutional Kernel Attention Mechanism
3.3. Softmax Activation Function
4. Experimental Study
4.1. Introduction to the CWRU Dataset
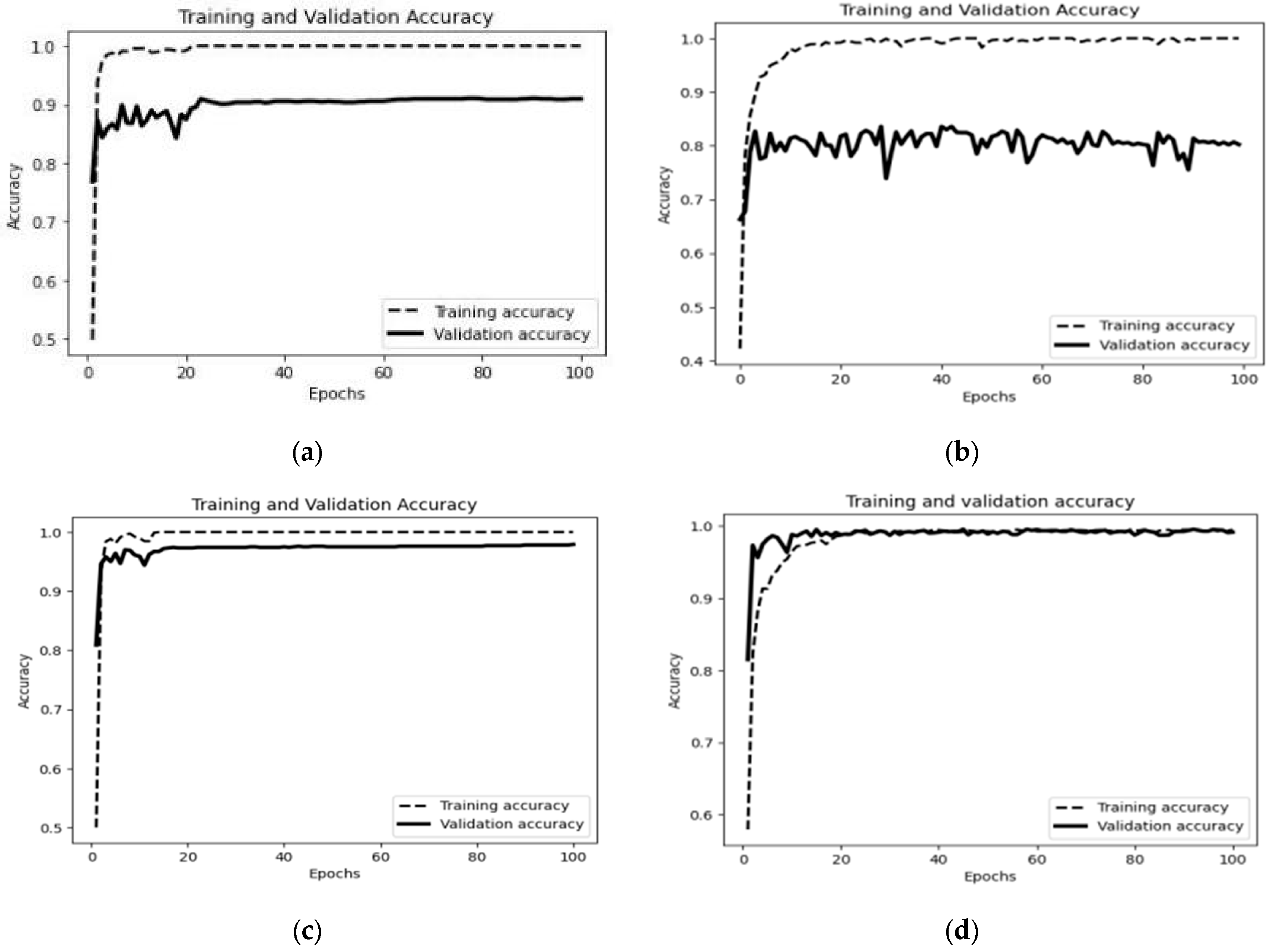
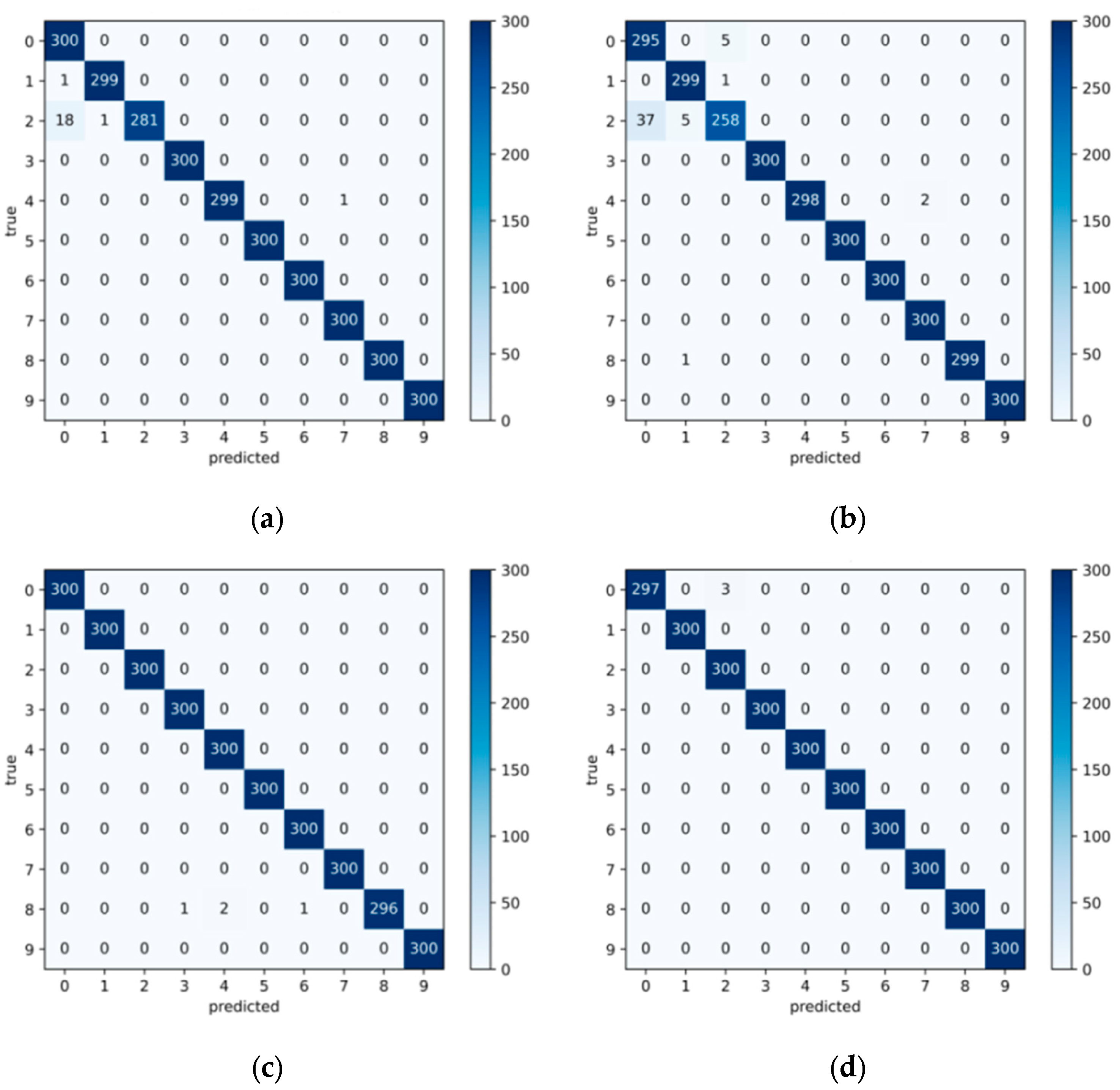
4.2. Experimental Comparison and Result Analysis
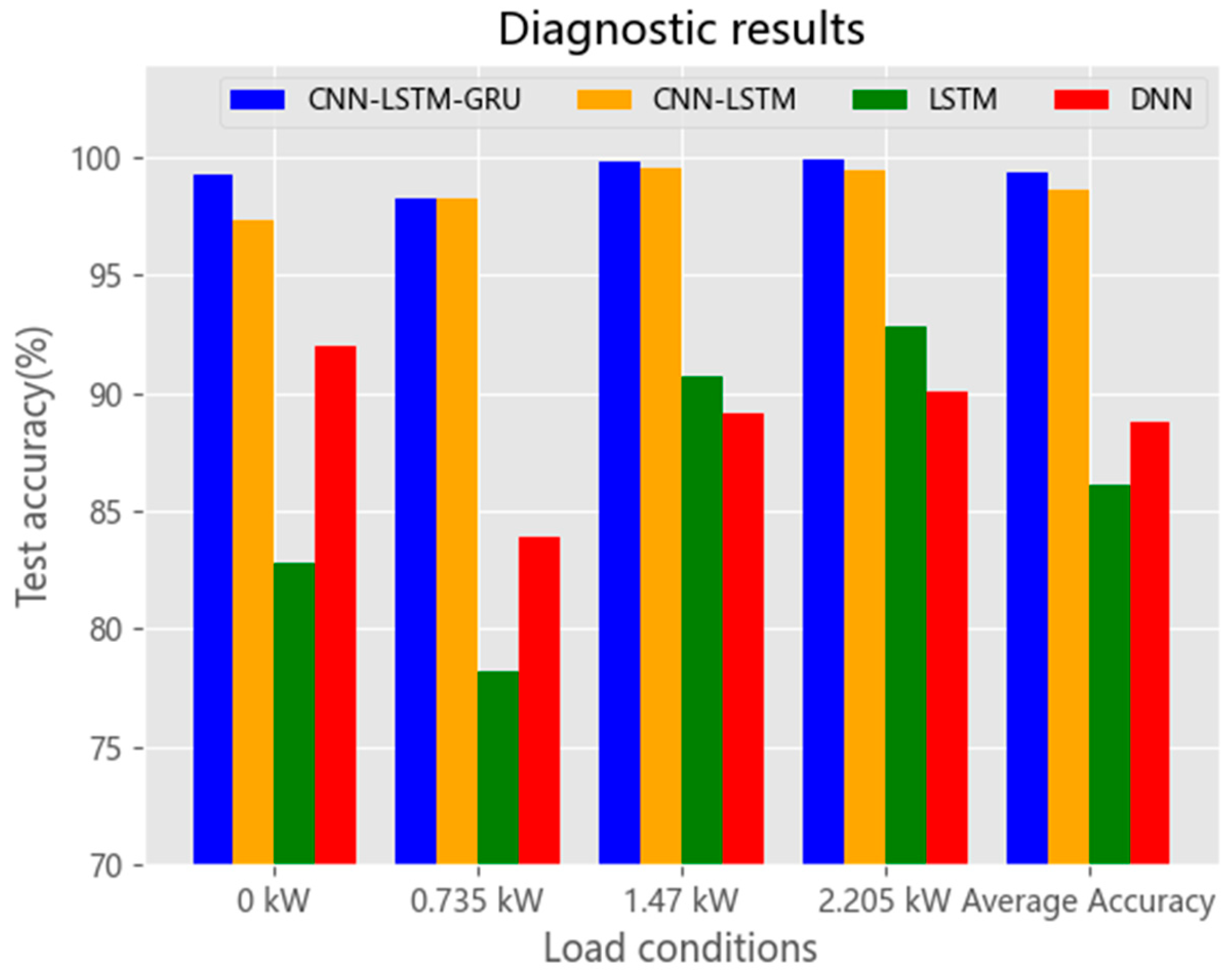
4.2.1. Diagnosis Comparison Experiments Under a Stable Environment
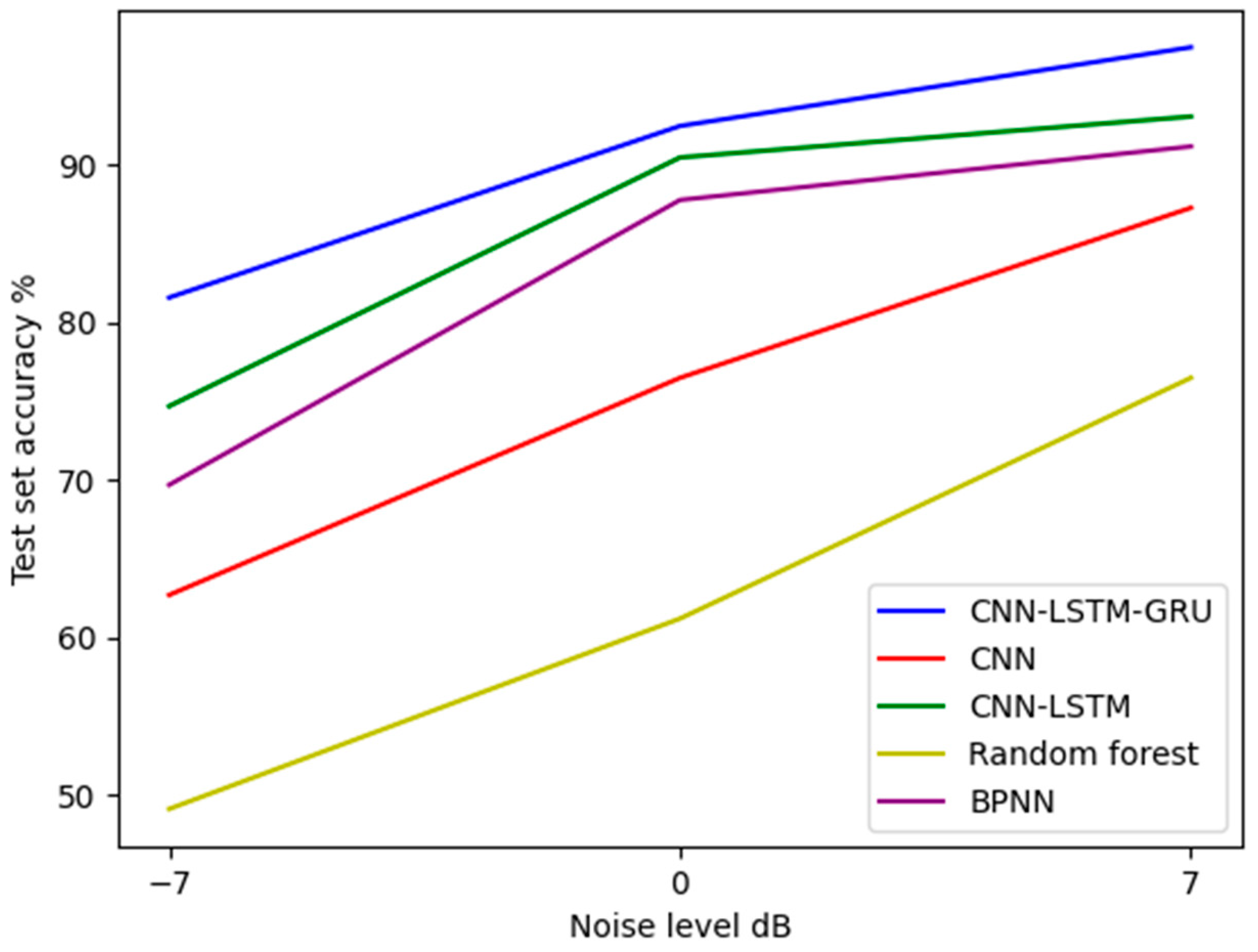
4.2.2. Comparative Experiment of Diagnosis in a Noisy Environment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Desnica, E.; Ašonja, A.; Radovanović, L.; Palinkaš, I.; Kiss, I. Selection, Dimensioning and Maintenance of Roller Bearings. In 31st International Conference on Organization and Technology of Maintenance (OTO 2022); Blažević, D., Ademović, N., Barić, T., Cumin, J., Desnica, E., Eds.; OTO 2022. Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 592. [Google Scholar] [CrossRef]
- Pastukhov, A.; Timashov, E.; Stanojević, D. Temperature Conditions and Diagnostics of Bearings. Appl. Eng. Lett. 2023, 8, 45–51. [Google Scholar] [CrossRef]
- Shi, R.; Wang, B.; Wang, Z.; Liu, J.; Feng, X.; Dong, L. Research on Fault Diagnosis of Rolling Bearings Based on Variational Mode Decomposition Improved by the Niche Genetic Algorithm. Entropy 2022, 24, 825. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Hua, T.; Xu, S.; Zhao, X. A Novel Rolling Bearing Fault Diagnosis Method Based on BLS and CNN with Attention Mechanism. Machines 2023, 11, 279. [Google Scholar] [CrossRef]
- Lee, S.; Kim, S.; Kim, S.J.; Lee, J.; Yoon, H.; Youn, B.D. Revolution and peak discrepancy-based domain alignment method for bearing fault diagnosis under very low-speed conditions. Expert Syst. Appl. 2024, 251, 124084. [Google Scholar] [CrossRef]
- Kulevome, D.K.B.; Wang, H.; Cobbinah, B.M.; Mawuli, E.S.; Kumar, R. Effective time-series Data Augmentation with Analytic Wavelets for bearing fault diagnosis. Expert Syst. Appl. 2024, 249 Pt A, 123536. [Google Scholar] [CrossRef]
- Ma, H.; Li, S.; Lu, J.; Gong, S.; Yu, T. Impulsive wavelet based probability sparse coding model for bearing fault diagnosis. Measurement 2022, 194, 110969. [Google Scholar] [CrossRef]
- Biao, H.; Qin, Y.; Luo, J.; Yang, W.; Xu, L. Impulse feature extraction via combining a novel voting index and a variational model penalized by center frequency constraint. Mech. Syst. Sig. Process. 2023, 186, 109889. [Google Scholar] [CrossRef]
- Yin, L.; Wang, Z. Bi-level binary coded fully connected classifier based on residual network 50 with bottom and deep level features for bearing fault diagnosis. Eng. Appl. Artif. Intell. 2024, 133 Pt D, 108342. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, H.; Wu, Z.; Yang, Q. Adaptive variational autoencoding generative adversarial networks for rolling bearing fault diagnosis. Adv. Eng. Inf. 2023, 56, 102027. [Google Scholar] [CrossRef]
- Shi, H.; Guo, L.; Tan, S.; Bai, X. Rolling bearing initial fault detection using long short-term memory recurrent network. IEEE Access 2019, 7, 171559–171569. Available online: https://ieeexplore.ieee.org/document/8905994 (accessed on 9 January 2024). [CrossRef]
- Ruan, D.; Wang, J.; Yan, J.; Gühmann, C. CNN parameter design based on fault signal analysis and its application in bearing fault diagnosis. Adv. Eng. Inform. 2023, 55, 101877. [Google Scholar] [CrossRef]
- Zhang, S.; Qiu, T. Semi-supervised LSTM ladder autoencoder for chemical process fault diagnosis and localization. Chem. Eng. Sci. 2022, 251, 117467. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lu, N.; Xing, S. Deep normalized convolutional neural network for imbalanced fault classification of machinery and its understanding via visualization. Mech. Syst. Sig. Process. 2018, 110, 349–367. [Google Scholar] [CrossRef]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Sig. Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Grezmak, J.; Zhang, J.; Wang, P.; Loparo, K.A.; Gao, R.X. Interpretable convolutional neural network through layer-wise relevance propagation for machine fault diagnosis. IEEE Sens. J. 2020, 20, 3172–3181. Available online: https://ieeexplore.ieee.org/document/8930493 (accessed on 9 January 2024). [CrossRef]
- Yu, W.; Zhao, C. Online Fault Diagnosis for Industrial Processes with Bayesian Network-Based Probabilistic Ensemble Learning Strategy. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1922–1932. [Google Scholar] [CrossRef]
- Meng, Z.; Cao, W.; Sun, D.; Li, Q.; Ma, W.; Fan, F. Research on fault diagnosis method of MS-CNN rolling bearing based on local central moment discrepancy. Adv. Eng. Inform. 2022, 54, 101797. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Broad Convolutional Neural Network Based Industrial Process Fault Diagnosis with Incremental Learning Capability. IEEE Trans. Ind. Electron. 2020, 67, 5081–5091. [Google Scholar] [CrossRef]
- Da, T.N.; Thanh, P.N.; Cho, M.-Y. Novel cloud-AIoT fault diagnosis for industrial diesel generators based hybrid deep learning CNN-BGRU algorithm. Internet Things 2024, 26, 101164. [Google Scholar] [CrossRef]
- Zhao, H.; Sun, S.; Jin, B. Sequential fault diagnosis based on LSTM neural network. IEEE Access 2018, 6, 12929–12939. Available online: https://ieeexplore.ieee.org/document/8272354 (accessed on 10 January 2024). [CrossRef]
- Chadha, G.S.; Panambilly, A.; Schwung, A.; Ding, S.X. Bidirectional deep recurrent neural networks for process fault classification. ISA Trans. 2020, 106, 330–342. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Zhao, C.; Huang, B.; Xie, M. An Unsupervised Fault Detection and Diagnosis with Distribution Dissimilarity and Lasso Penalty. IEEE Trans. Control Syst. Technol. 2024, 32, 767–779. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, C.; Peng, Z.; Dong, X.; Meng, G. Detecting the early damages in structures with nonlinear output frequency response functions and the CNN-LSTM model. IEEE Trans. Instrum. Meas. 2020, 69, 9557–9567. Available online: https://ieeexplore.ieee.org/document/9130164 (accessed on 10 January 2024). [CrossRef]
- Zhao, S.; Duan, Y.; Roy, N.; Zhang, B. A deep learning methodology based on adaptive multiscale CNN and enhanced highway LSTM for industrial process fault diagnosis. Reliab. Eng. Syst. Saf. 2024, 249, 110208. [Google Scholar] [CrossRef]
- Song, B.; Liu, Y.; Fang, J.; Liu, W.; Zhong, M.; Liu, X. An optimized CNN-BiLSTM network for bearing fault diagnosis under multiple working conditions with limited training samples. Neurocomputing 2024, 574, 127284. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C.; Wang, J. Gated recurrent units based neural network for time heterogeneous feedback recommendation. Inf. Sci. 2018, 423, 50–65. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Ren, Z.; Yan, K.; Kang, W. A novel weak fault diagnosis method for rolling bearings based on LSTM considering quasi-periodicity. Knowl.-Based Syst. 2021, 231, 107413. [Google Scholar] [CrossRef]
- Andermatt, S.; Pezold, S.; Amann, M.; Cattin, P.C. Multi-dimensional Gated Recurrent Units for Automated Anatomical Landmark Localization. arXiv 2017, arXiv:1708.02766. [Google Scholar] [CrossRef]
- Shan, X.; Ma, T.; Shen, Y.; Li, J.; Wen, Y. KAConv: Kernel attention convolutions. Neurocomputing 2022, 514, 477–485. [Google Scholar] [CrossRef]
- Martins, A.F.T.; Astudillo, R.F. From Softmax to Sparsemax: A Sparse Model of Attention and Multi-Label Classification. arXiv 2016, arXiv:1602.02068. [Google Scholar] [CrossRef]




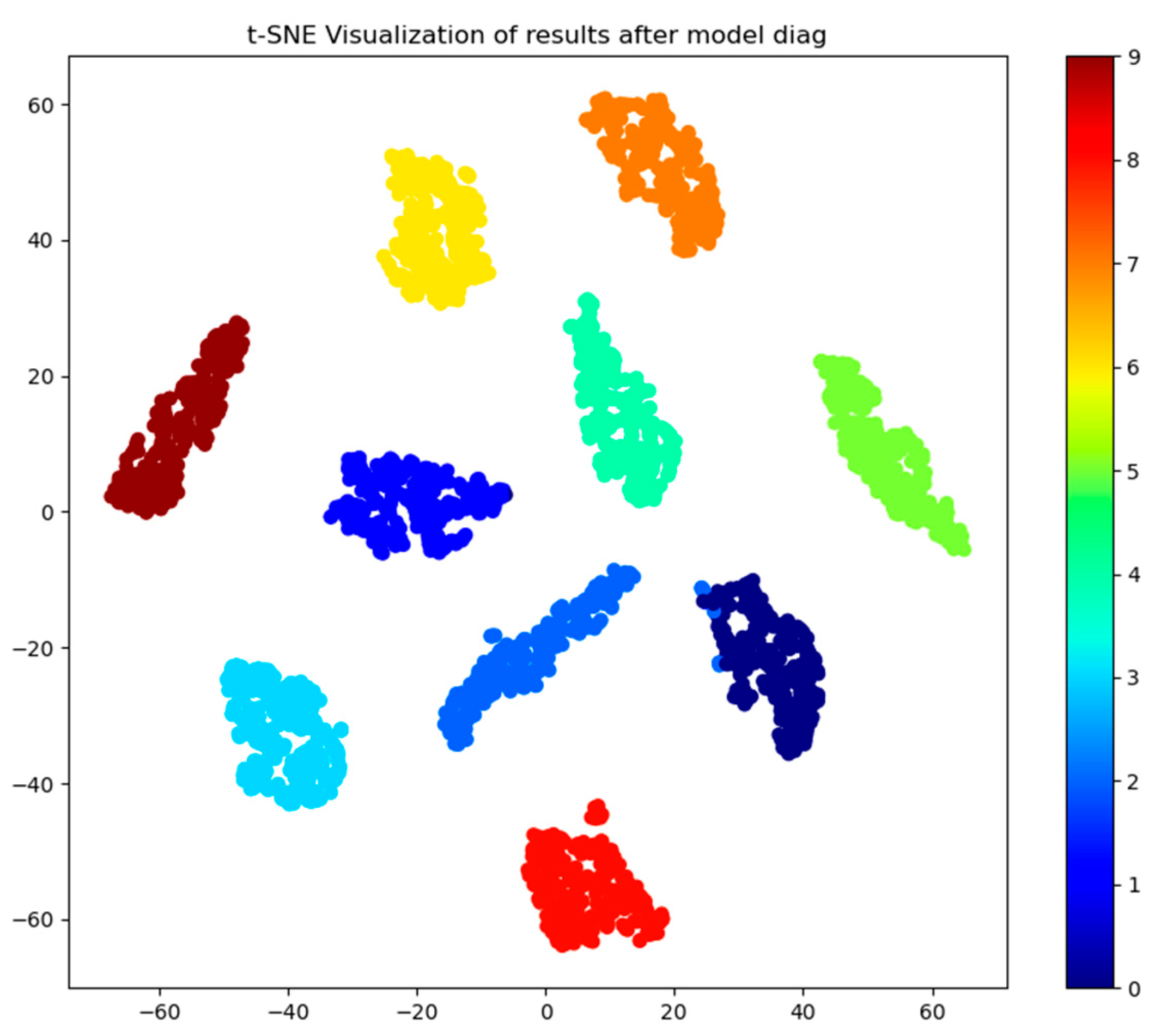
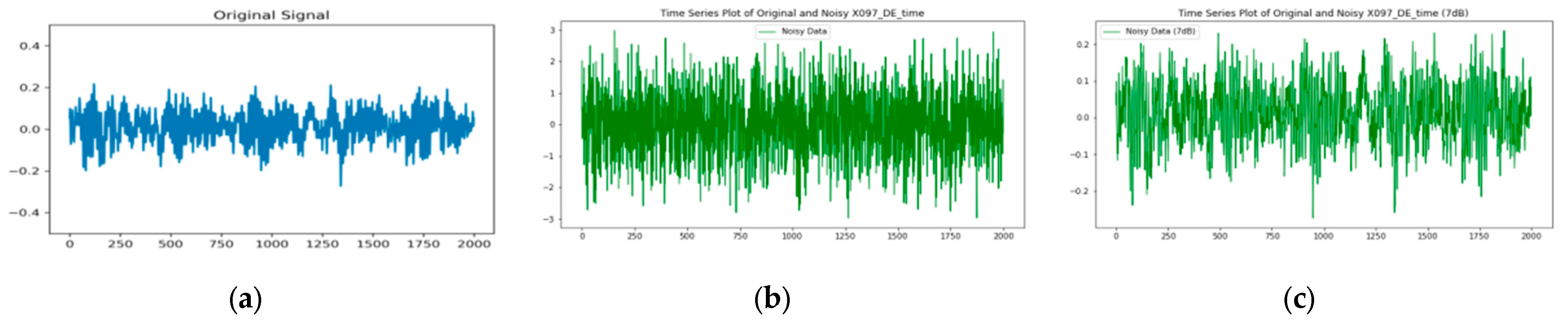
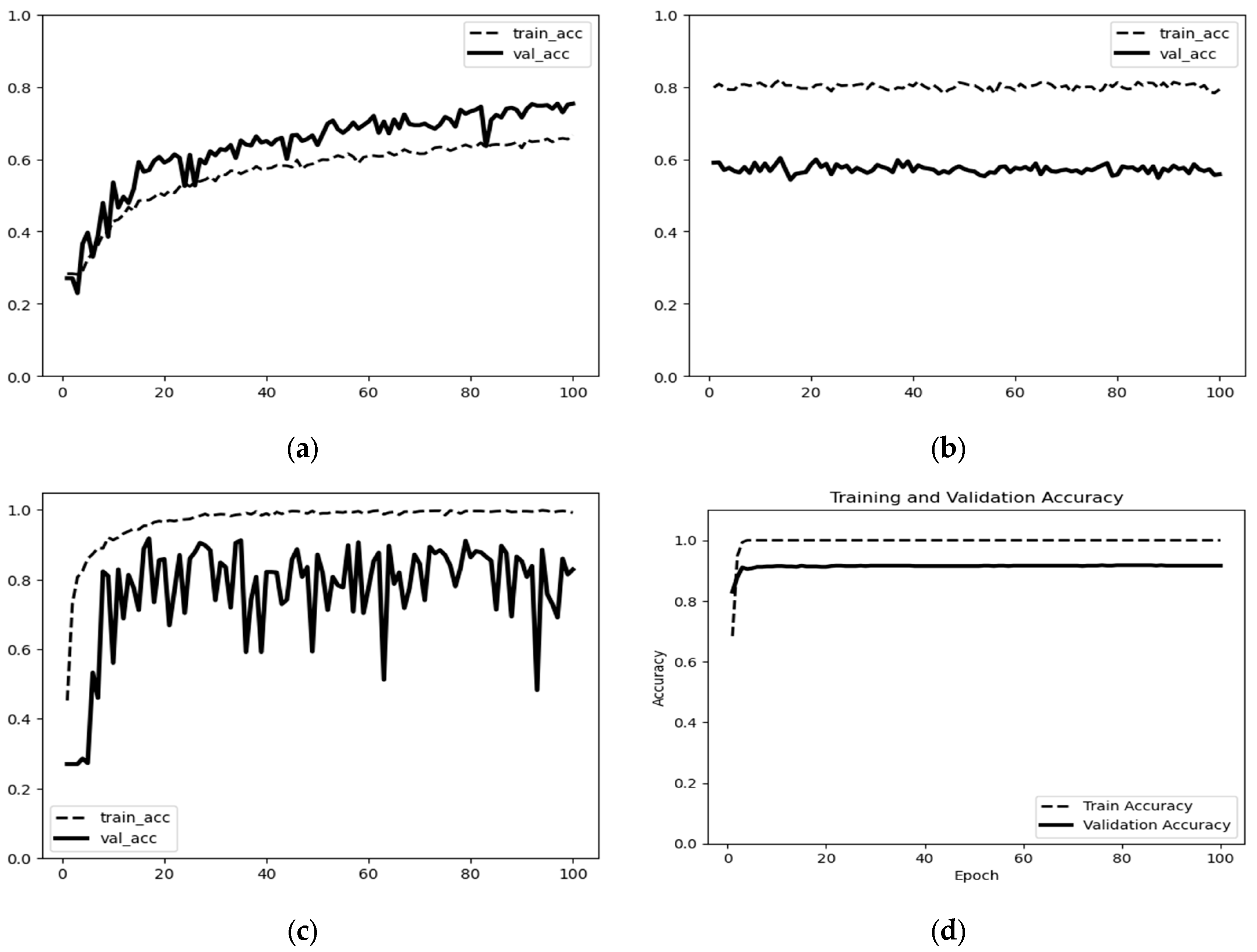

| Label | Damage Location | Damage Diameter | Training Set | Test Set |
|---|---|---|---|---|
| 0 | Rolling element damage | 0.178 | 700 | 300 |
| 1 | Rolling element damage | 0.356 | 700 | 300 |
| 2 | Rolling element damage | 0.533 | 700 | 300 |
| 3 | Inner ring damage | 0.178 | 700 | 300 |
| 4 | Inner ring damage | 0.356 | 700 | 300 |
| 5 | Inner ring damage | 0.533 | 700 | 300 |
| 6 | Outer ring damage | 0.178 | 700 | 300 |
| 7 | Outer ring damage | 0.356 | 700 | 300 |
| 8 | Outer ring damage | 0.533 | 700 | 300 |
| 9 | Normal | 0.000 | 700 | 300 |
| Load | Accuracy | Number of Iterations |
|---|---|---|
| 0 kW | 99.29% | 100 |
| 0.735 kW | 98.29% | 100 |
| 1.47 kW | 99.86% | 100 |
| 2.205 kW | 99.90% | 100 |
| Model | Load | Average Accuracy | |||
|---|---|---|---|---|---|
| 0 kW | 0.735 kW | 1.47 kW | 2.205 kW | ||
| CNN-LSTM-GRU | 99.29% | 98.29% | 99.86% | 99.90% | 99.34% |
| CNN-LSTM | 97.36% | 98.27% | 99.53% | 99.43% | 98.65% |
| LSTM | 82.77% | 78.23% | 90.71% | 92.82% | 86.13% |
| DNN | 92.01% | 83.91% | 89.11% | 90.10% | 88.78% |
| Algorithm | CNN-LSTM-GRU | CNN-LSTM | CNN | BPNN | Random Forest |
|---|---|---|---|---|---|
| −7 dB | 81.6% | 74.7% | 62.7% | 69.7% | 49.1% |
| 0 dB | 92.5% | 90.5% | 76.5% | 87.8% | 61.2% |
| 7 dB | 97.2% | 93.1% | 87.3% | 91.2% | 76.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, K.; Wang, W.; Guo, J. Research on a Bearing Fault Diagnosis Method Based on a CNN-LSTM-GRU Model. Machines 2024, 12, 927. https://doi.org/10.3390/machines12120927
Han K, Wang W, Guo J. Research on a Bearing Fault Diagnosis Method Based on a CNN-LSTM-GRU Model. Machines. 2024; 12(12):927. https://doi.org/10.3390/machines12120927
Chicago/Turabian StyleHan, Kaixu, Wenhao Wang, and Jun Guo. 2024. "Research on a Bearing Fault Diagnosis Method Based on a CNN-LSTM-GRU Model" Machines 12, no. 12: 927. https://doi.org/10.3390/machines12120927
APA StyleHan, K., Wang, W., & Guo, J. (2024). Research on a Bearing Fault Diagnosis Method Based on a CNN-LSTM-GRU Model. Machines, 12(12), 927. https://doi.org/10.3390/machines12120927





