Meshing Characteristic Analysis of CBR Reducer Considering Tooth Modification and Manufacturing Error
Abstract
1. Introduction
2. Modeling of VISPM of CBR
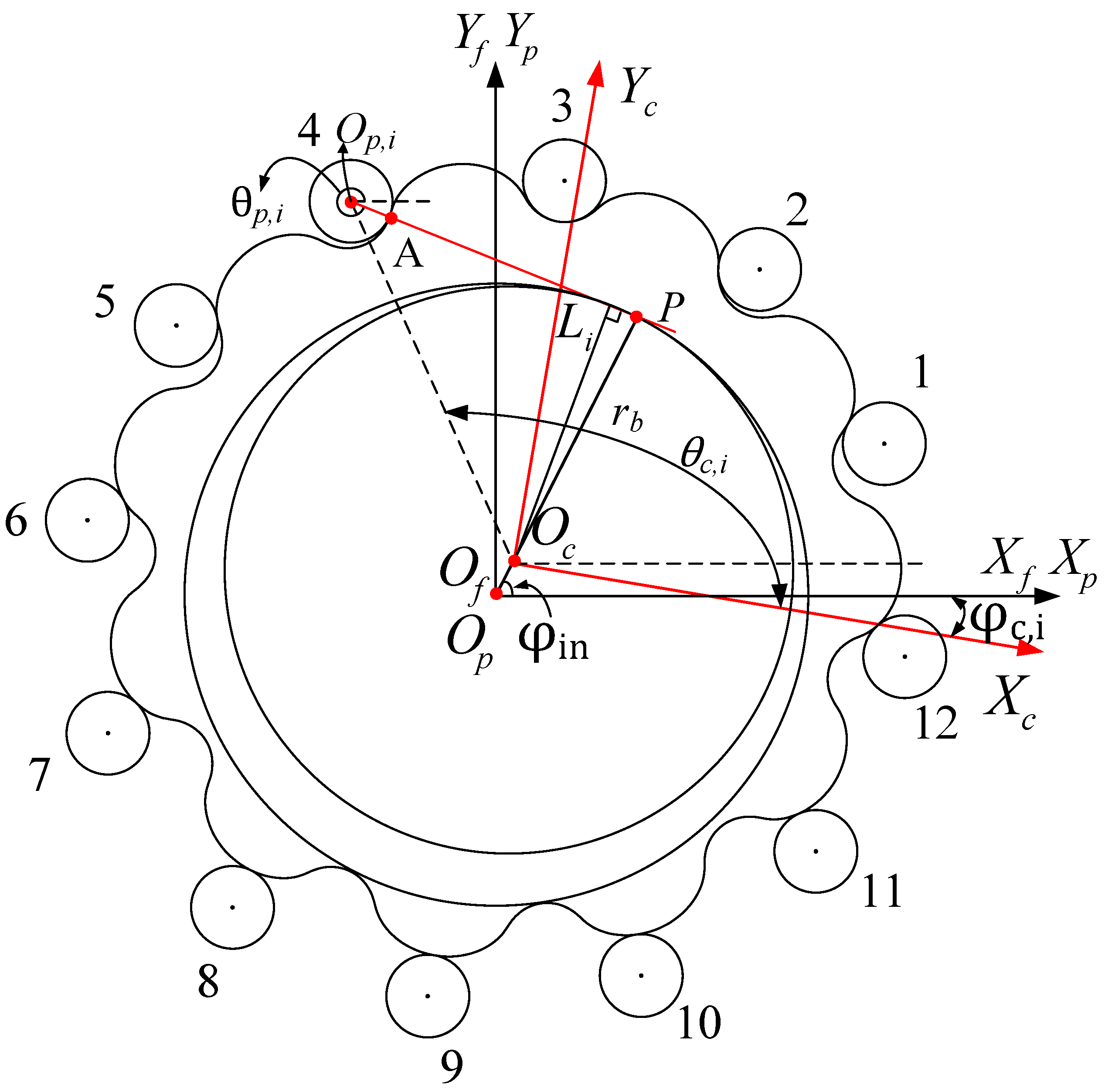
2.1. Structure of CBR
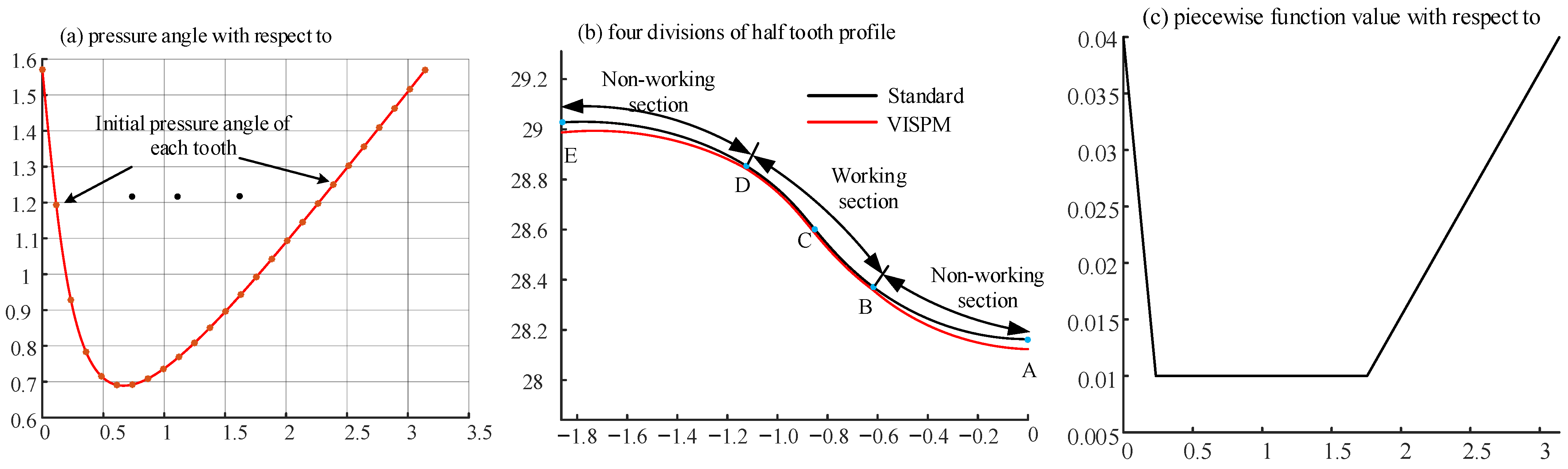
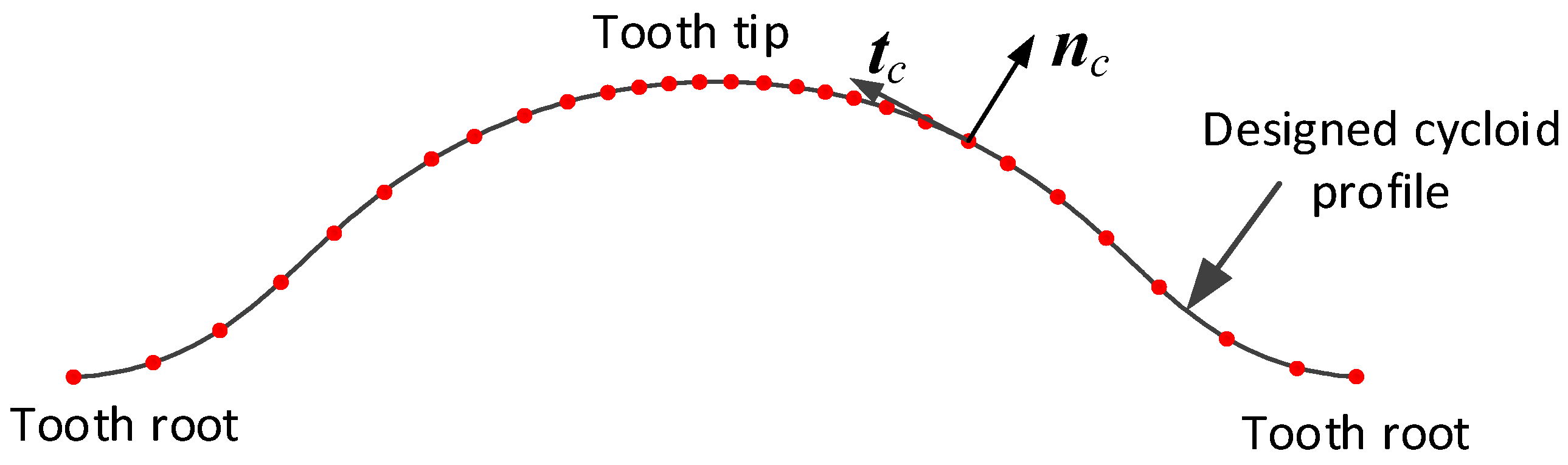
2.2. Tooth Profile Equation of Cycloid Gear with VISPM
3. TCA Both Considering VISPM and Manufacturing Error
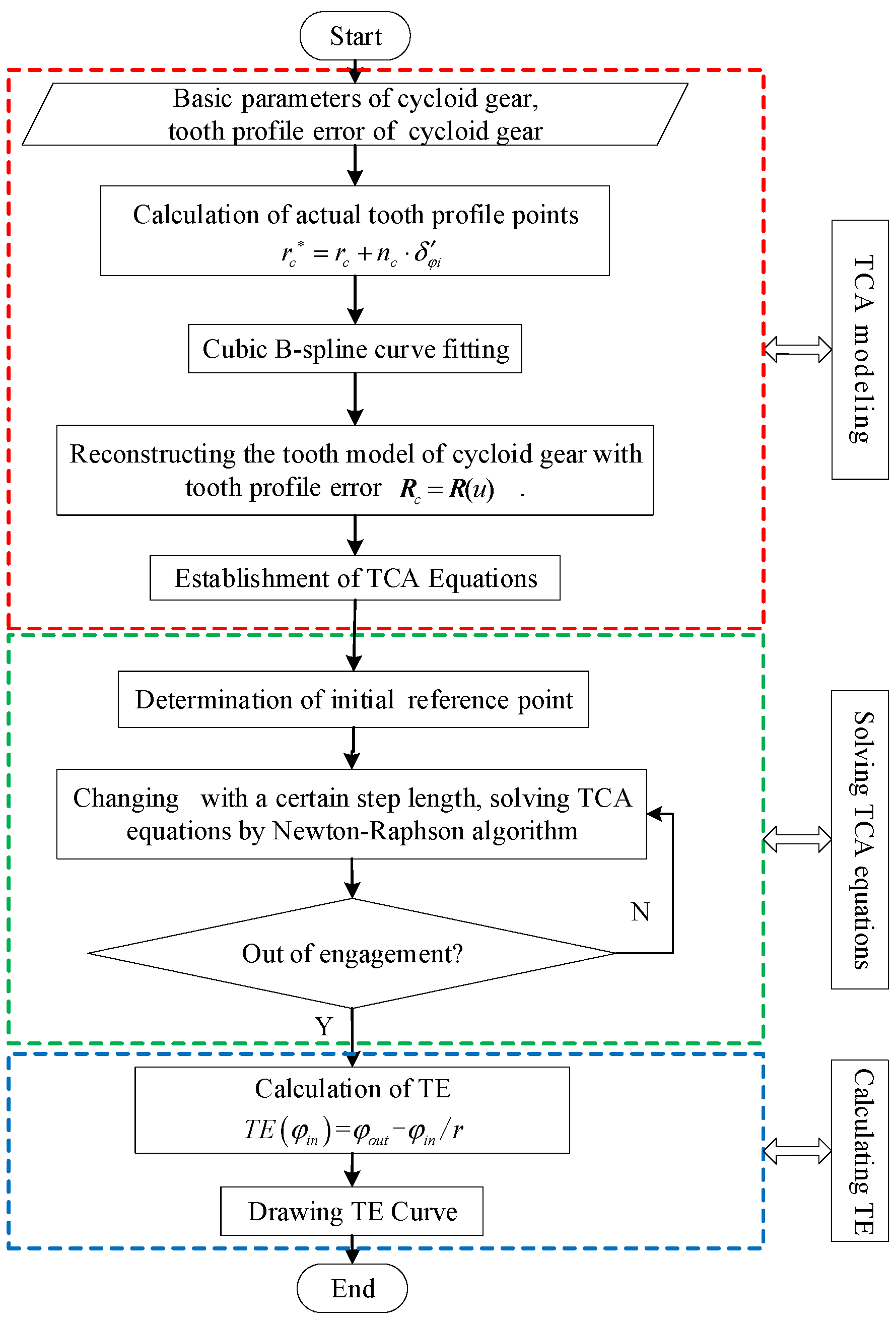
3.1. Modeling and Solving TCA and TE with VISPM
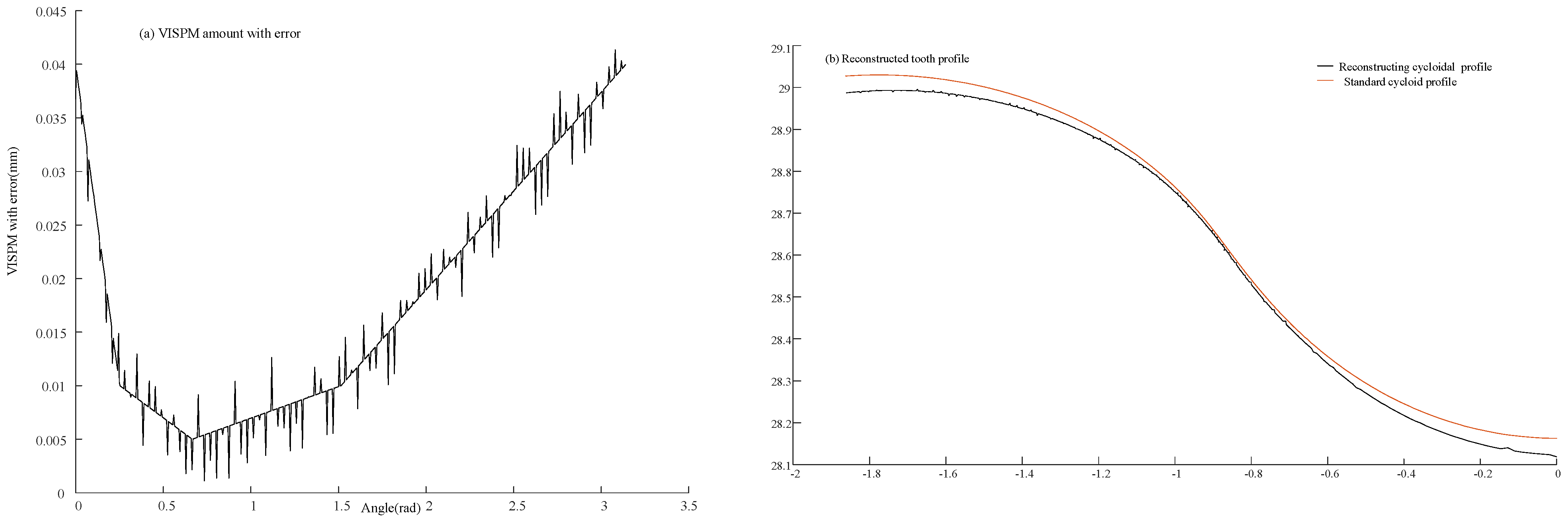
3.2. Reconstructing Cycloid Tooth Profile with Tooth Profile Error
- (1)
- Coordinate calculation of discrete points on cycloid gear profile with tooth profile error
- (2)
- Reconstruction of the cycloid gear profile with tooth profile error
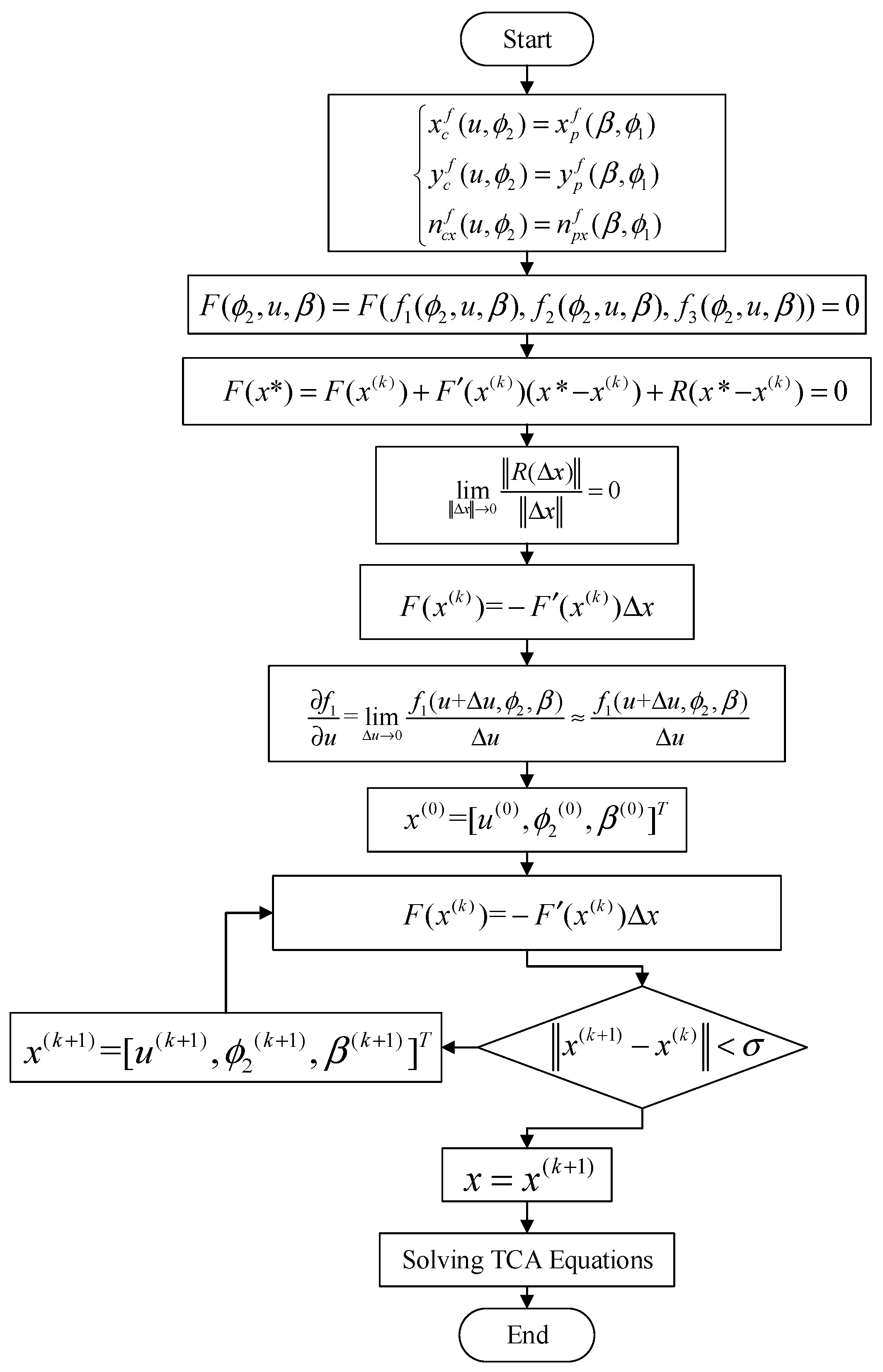
3.3. Solving the TCA with Tooth Profile Error (ETCA)
Newton–Raphson Algorithm for Solving TCA Equations with Tooth Profile Error
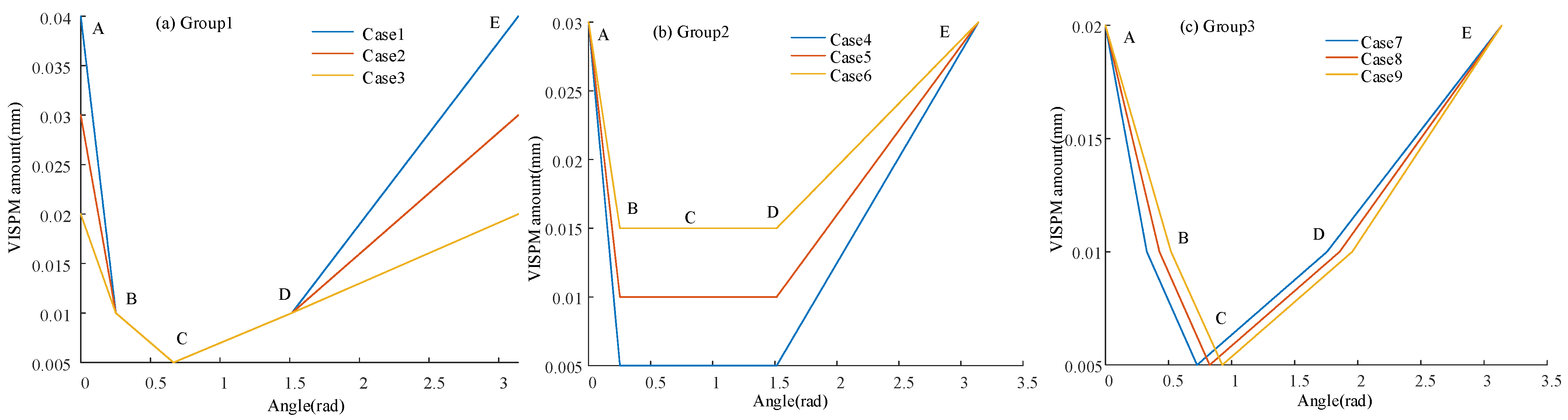
3.4. Meshing Characteristic of VISPM
4. Optimization of VISPM Based on PSO
4.1. Optimization Model
- (1)
- Objective Function
- (2)
- Design variables
- (3)
- Constraint conditions
- (4)
- Mathematical model
4.2. Solving the Optimization Model
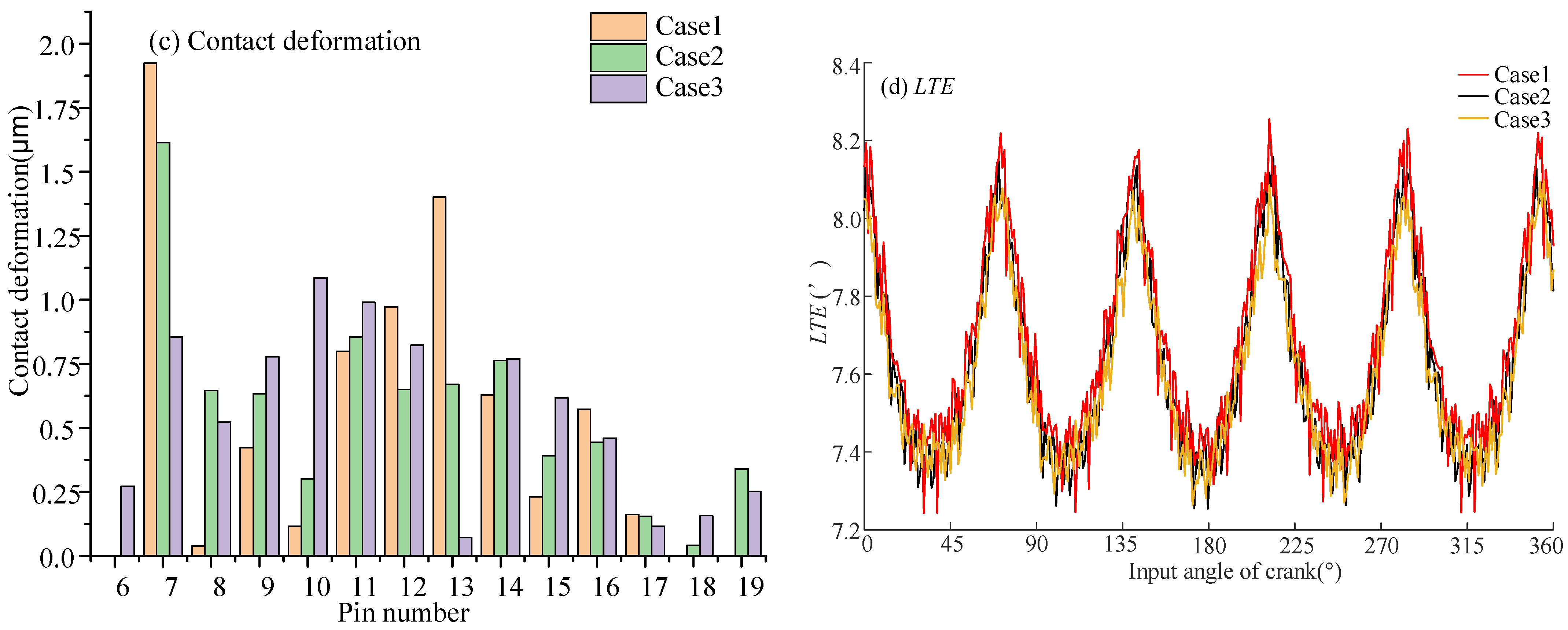
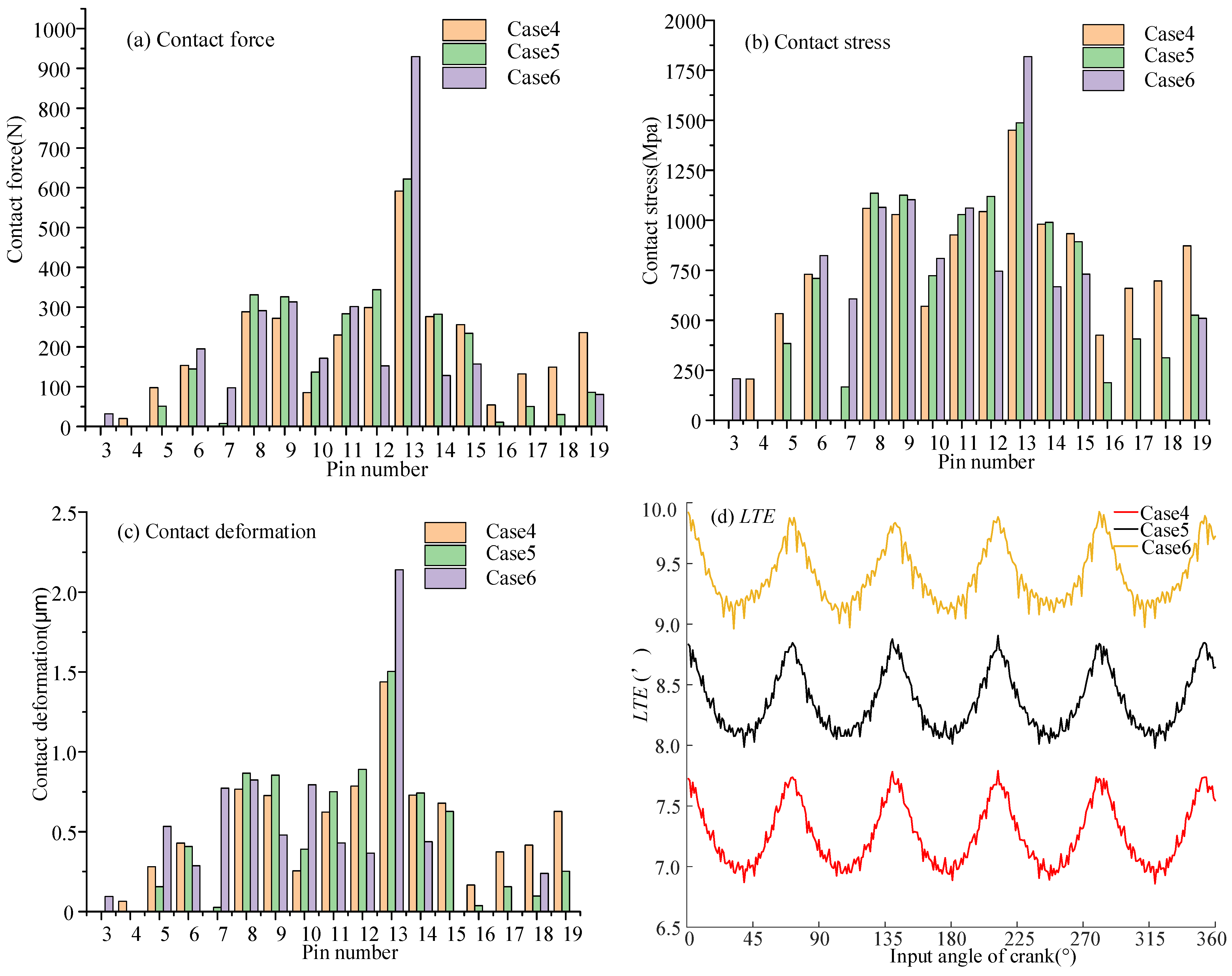
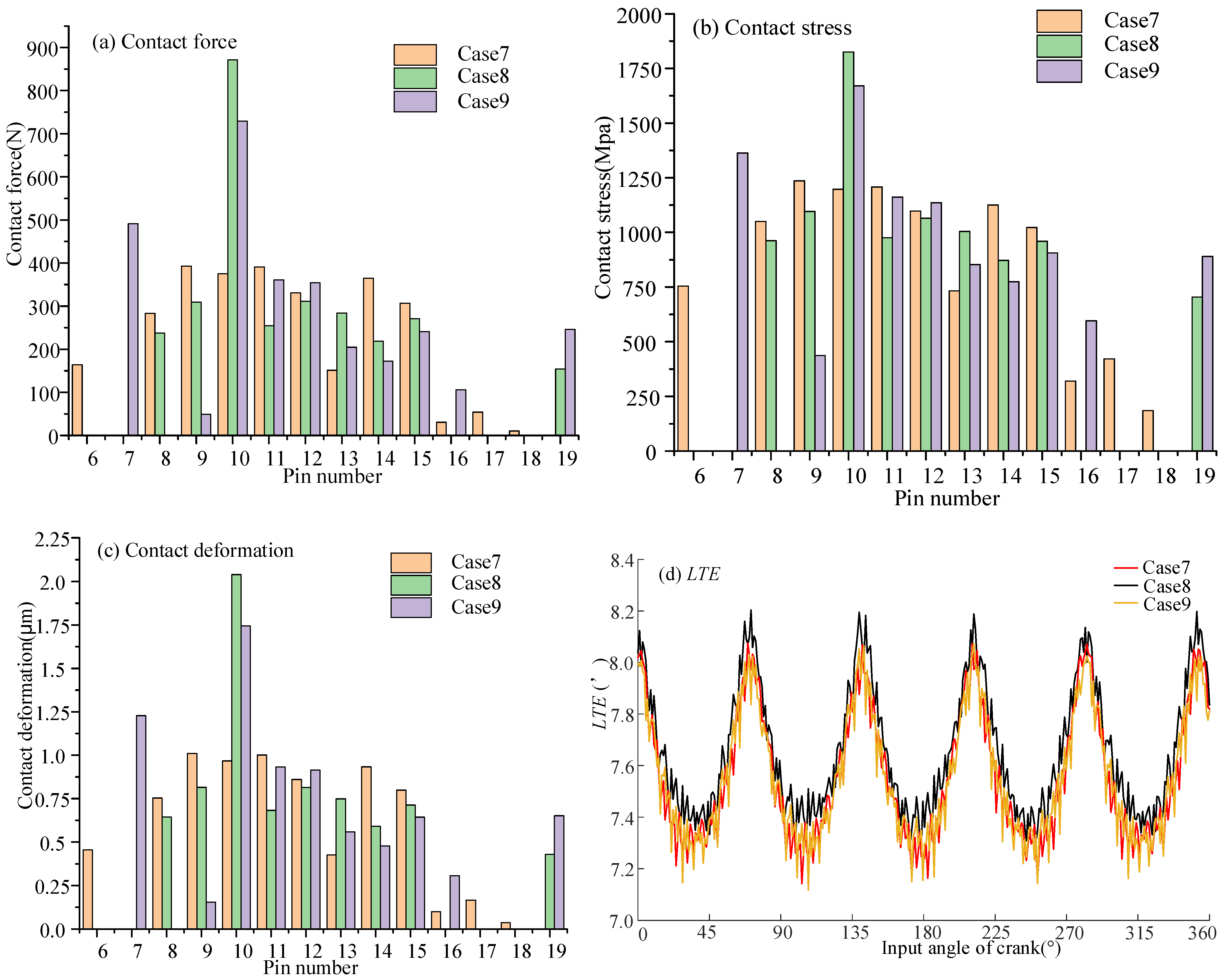
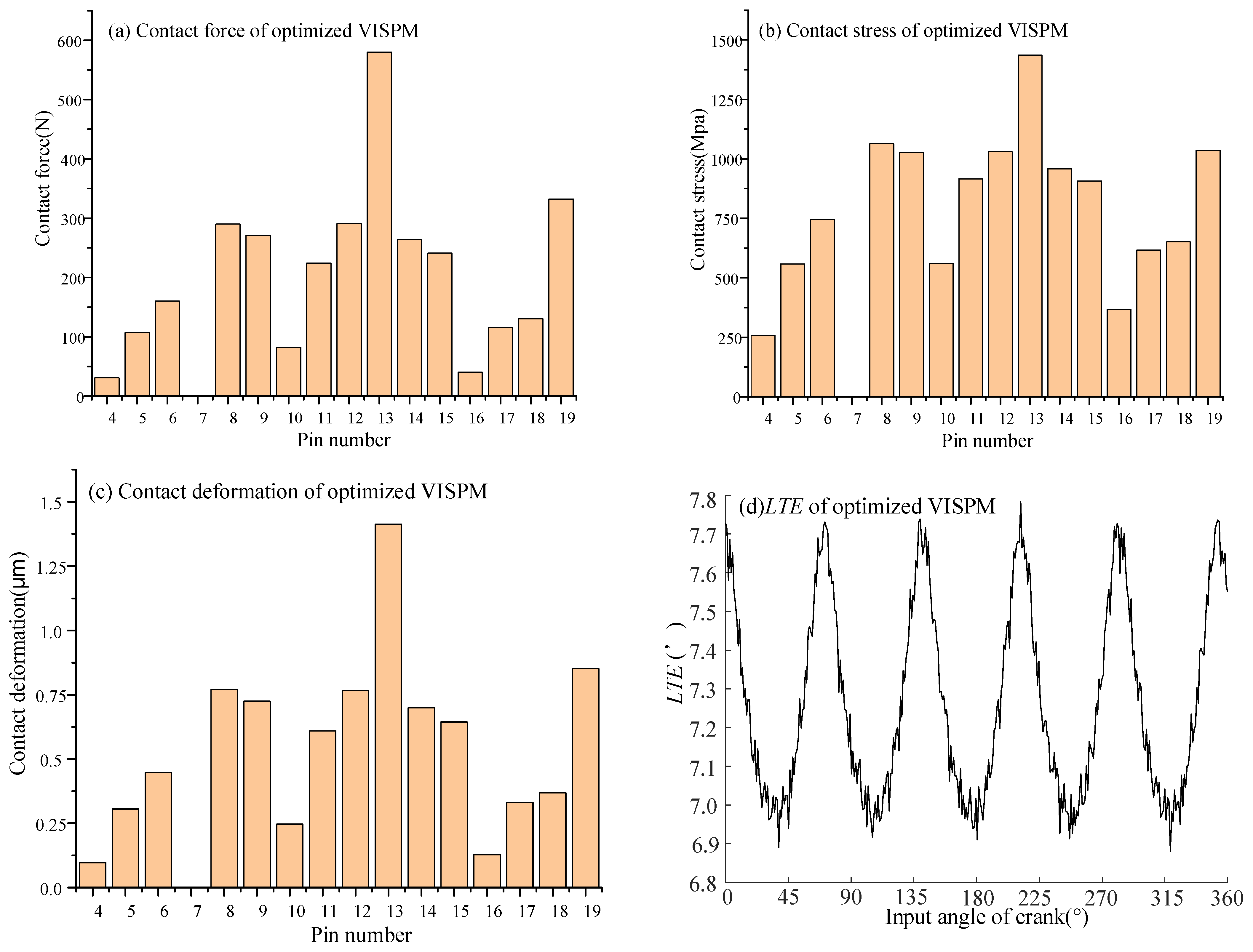
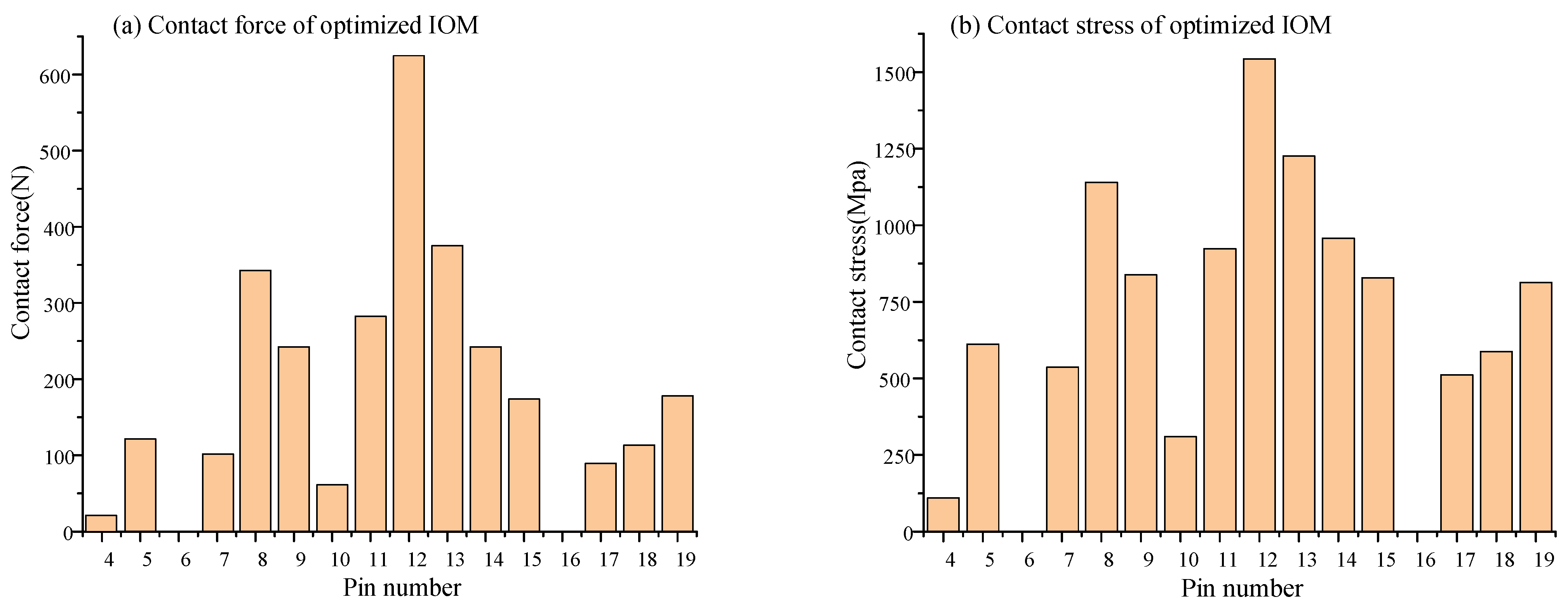
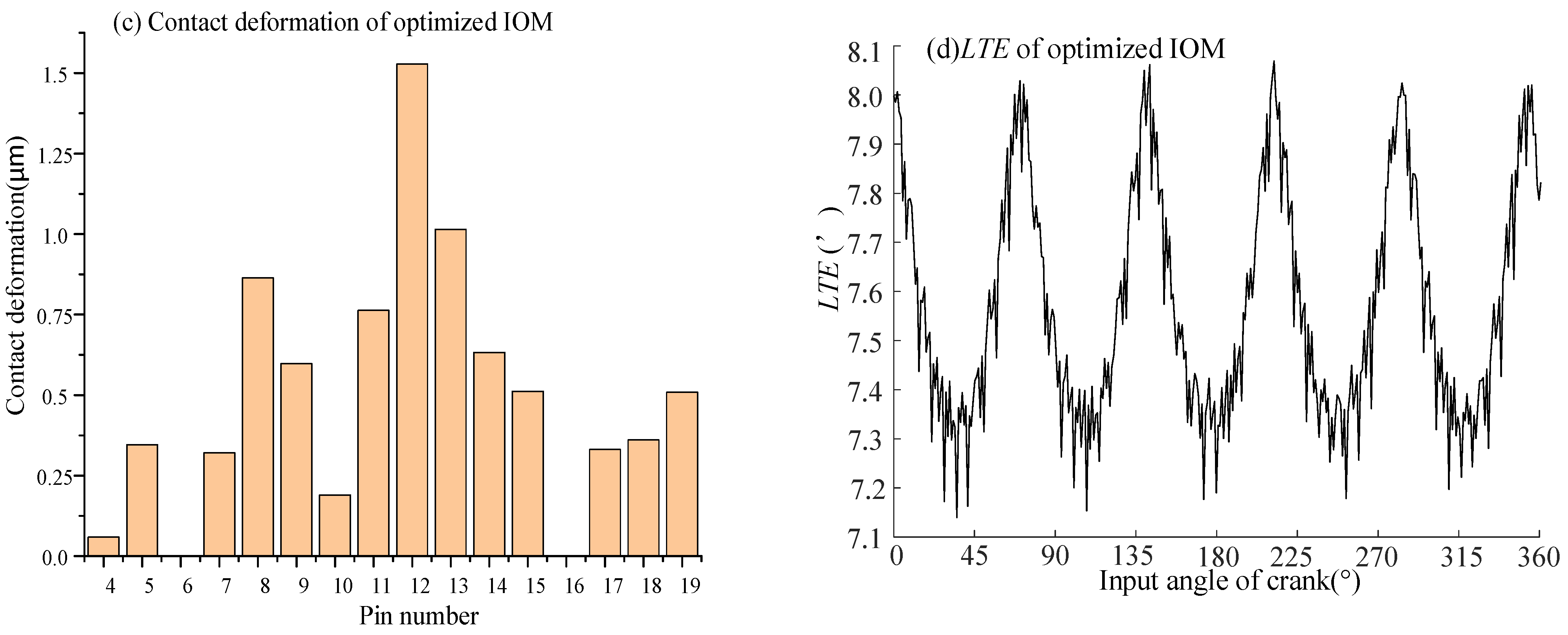
4.3. Example Analysis
5. Experimental Tests
5.1. Test Platform
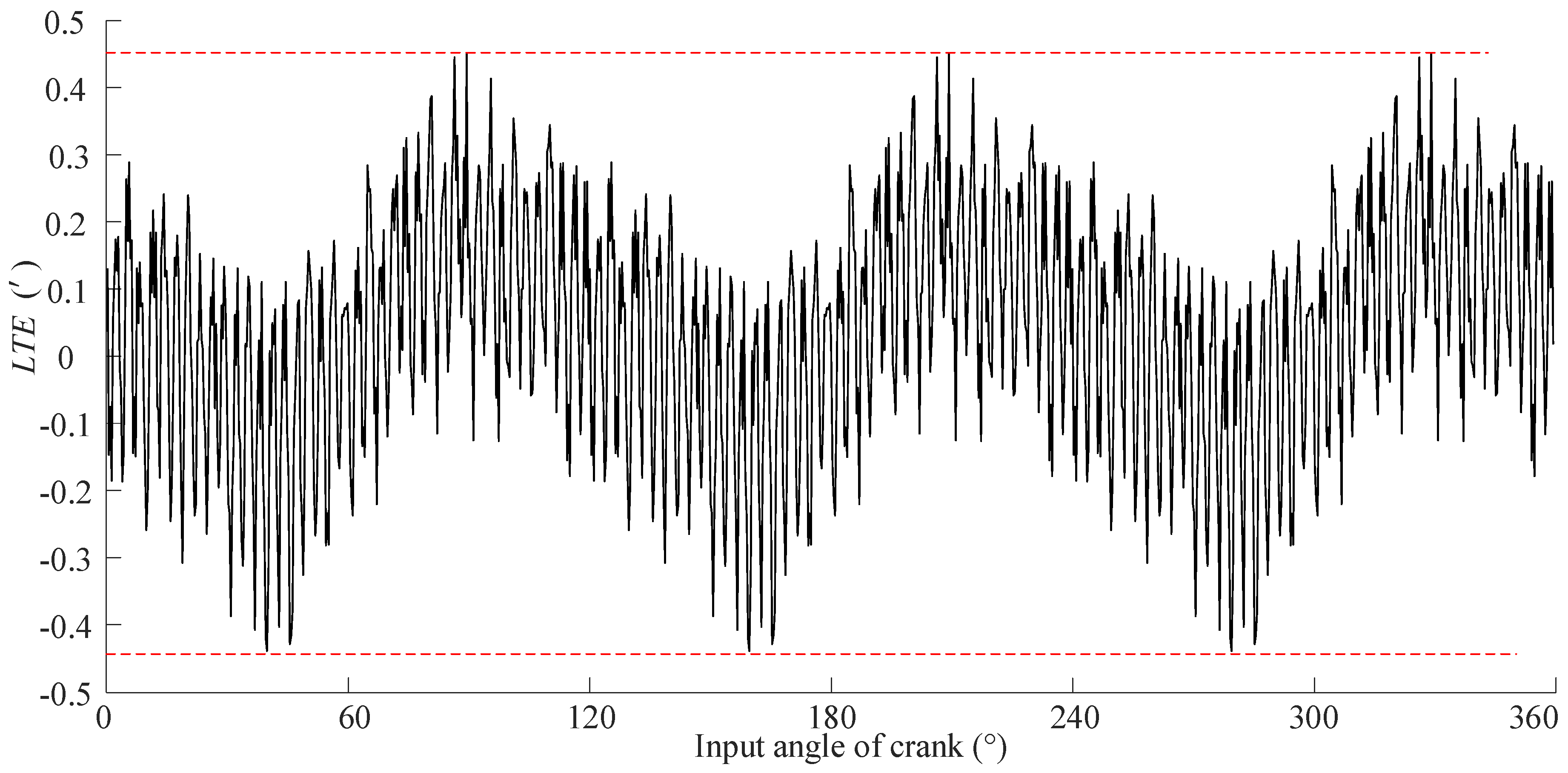
5.2. LTE Testing of CBR25 Prototype
6. Conclusions
- (1)
- The VISPM can accurately control the modification amount of the working section and non-main working section of the tooth profile. The working section was selected according to the contact pressure angle to improve the loading capacity of the CBR reducer. The gap of the non-working section had little effect on the backlash and TE. The working section clearance had a significant effect on the backlash. But it had little effect on the TE. When the working section clearance was large, it had the maximum contact force, contact stress, and contact deformation. When the phase angle of the working section was different, it had little influence on the backlash and TE. When the pressure angle corresponding to the phase angle of the working section was small, it had the minimum contact force, contact stress, and contact deformation.
- (2)
- Taking the TE as the optimization objective, both the VISPM and IOM methods are optimized by the PSO algorithm for the CBR25. The maximum contact force, maximum contact stress, and maximum TE of the VSIPM method were all less than those of the IOM method, with reductions of 5.26%, 5.55%, and 5.31%, respectively. This indicates that the VSIPM method is superior to the IOM method in enhancing meshing characteristics.
- (3)
- The prototype of the CBR25 was manufactured with optimal VISPM and IOM, and the TE was tested on the testing bench. The test results demonstrate that the ETCA method was corrected for cycloid drive analysis, and the new VISPM method significantly enhanced the transmission performance of the CBR reducer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Rotation angle of cycloid gear | |
| Rotation angle of roller gear | |
| Transmission ratio of cycloid gear and roller gear | |
| Teeth number of cycloid gear | |
| Teeth number of roller gear | |
| Radius of roller gear | |
| Radius of the roller | |
| Eccentricity of the input crank shaft | |
| Value of offset modification | |
| Value of isometric modification | |
| Fixed coordinate system in center of roller gear | |
| Moving coordinate system in center of roller gear | |
| Moving coordinate system in center of cycloid gear | |
| Origin of | |
| Origin of | |
| Value of variable isometric modification | |
| Modification amount of point A and E | |
| Modification amount of point C | |
| Modification amount of point B and D | |
| Position of points B | |
| Position of point C | |
| Position of point D | |
| Unit normal vector in for the contact point on the i-th point | |
| Unit normal vector of the i-th cycloid gear in | |
| Coordinate transformation matrix from to | |
| Contact point on the i-th cycloid gear in | |
| Contact point on the i-th pin in | |
| Angle parameter of cycloid gear | |
| Meshing angle of cycloid gear at initial reference point | |
| Meshing angle of pin gear at initial reference point | |
| Pitch circle radius of the cycloid gear | |
| Pitch circle radius of the roller gear | |
| Input crank angle | |
| Output angle of cycloid gear corresponding to i-th roller | |
| Angle parameter of i-th roller | |
| Parametric angle of cycloid gear corresponding to i-th roller | |
| Output angle of cycloid gear | |
| Cycloidal gear tooth profile deviation at each measuring point | |
| B-spline curve function | |
| Basis function | |
| Control point | |
| Pressure angle |
References
- Blanche, J.G.; Yang, D.C.H. Cycloid drives with machining tolerances. J. Mech. Transm. Autom. Des. 1989, 111, 337–344. [Google Scholar] [CrossRef]
- Yang, D.C.H. Design and Application Guidelines for Cycloid. Mech. Mach. Theory 1990, 25, 487–501. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, W.; Zhi, Y.; Hou, N.; Li, H.; Wang, C.; Li, T.; Zhang, Y.; Zhang, H.; Chen, J. Optimization of Tooth Profile Modification and Backlash Analysis of Multi-tooth Mesh Cycloid Transmission. Manuf. Technol. 2024, 24, 154–163. [Google Scholar] [CrossRef]
- Song, X.; Chen, Y.; Yang, J. Study of the Transmission Characteristics of the Cycloid Gear Based on a Multi-Objective Optimization Modification. Machines 2023, 11, 775. [Google Scholar] [CrossRef]
- Lin, W.S.; Shih, Y.P.; Lee, J.J. Design of a two-stage cycloidal gear reducer with tooth modifications. Mech. Mach. Theory 2014, 79, 184–197. [Google Scholar] [CrossRef]
- Hong-Liu, Y.; Jin-hua, Y.; Xin, H.; Ping, S. Study on teeth profile modification of cycloid reducer based on non-hertz elastic contact analysis. Mech. Res. Commun. 2013, 48, 87–92. [Google Scholar] [CrossRef]
- Sun, X.; Han, L.; Wang, J. Design and transmission error analysis of CBR reducer. J. Mech. Des. 2019, 141, 082301. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Wang, Y.; Chen, B.; Lim, T.C. Analysis of a cycloid speed reducer considering tooth profile modification and clearance-fit output mechanism. J. Mech. Des. 2017, 139, 033303. [Google Scholar] [CrossRef]
- Wu, S.; Guo, R.; Li, X. Quasi-Static Force Analysis and Tooth Profile Modification Optimization of the Cycloid Speed Reducer. Appl. Sci. 2024, 14, 845. [Google Scholar] [CrossRef]
- Sun, X.; Han, L.; Wang, J. Tooth modification and loaded tooth contact analysis of china bearing reducer. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6240–6261. [Google Scholar] [CrossRef]
- Ren, Z.-Y.; Mao, S.-M.; Guo, W.-C.; Guo, Z. Tooth modification and dynamic performance of the cycloidal drive. Mech. Syst. Signal Process. 2017, 85, 857–866. [Google Scholar] [CrossRef]
- Lin, K.-S.; Chan, K.-Y.; Lee, J.-J. Kinematic error analysis and tolerance allocation of cycloidal gear reducers. Mech. Mach. Theory 2018, 124, 73–91. [Google Scholar] [CrossRef]
- Sensinger, J.W. Unified Approach to Cycloid Drive Profile, Stress, and Efficiency Optimization. J. Mech. Des. 2010, 132, 024503. [Google Scholar] [CrossRef]
- Sensinger, J.W. Efficiency of High-Sensitivity Gear Trains, Such as Cycloid Drives. J. Mech. Des. 2013, 135, 71006. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, J.; He, W. Multi-objective optimization of cycloidal gear based on segmental modification of pressure angle. J. Mech. Sci. Technol. 2022, 36, 3535–3545. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Y.; Li, Y.; Ji, S.; Wei, T.; Wang, Z. Piecewise Modification of Cycloidal Gear in RV Reducer: Application of Spline Interpolation Theory and Comparison with a Combination Modification Optimization Method. Int. J. Precis. Eng. Manuf. 2024. [Google Scholar] [CrossRef]
- Tran, T.L.; Pham, A.D.; Ahn, H.-J. Lost motion analysis of one stage cycloid reducer considering tolerances. Int. J. Precis. Eng. Manuf. 2016, 17, 1009–1016. [Google Scholar] [CrossRef]
- Li, T.; Tian, M.; Xu, H.; Deng, X.; An, X.; Su, J. Meshing contact analysis of cycloidal-pin gear in rv reducer considering the influence of manufacturing error. J. Braz. Soc. Mech. Sci. 2020, 42, 133. [Google Scholar] [CrossRef]
- Wang, J.; Lv, H. Modification and Optimization of Cycloidal Gear Tooth Profile Based on Machining Error Compensation. Appl. Sci. 2023, 13, 2581. [Google Scholar] [CrossRef]
- Antoniak, P.; Bednarczyk, S. Determination of Mechanical Power Loss of the Output Mechanisms with Serially Arranged Rollers in Cycloidal Gears While Taking into Account Manufacturing Tolerances. Machines 2024, 12, 345. [Google Scholar] [CrossRef]
- Xu, L.X. A dynamic model to predict the number of pins to transmit load in a cycloidal reducer with assembling clearance. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4247–4269. [Google Scholar] [CrossRef]
- Sun, X. Design Theory and Experimental Research of CBR Reducer for Robot. Ph.D. Thesis, School of Mechanical Engineering, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Qi, F.; Wilcox, L. New developments in tooth contact analysis (TCA) and loaded TCA for spiral bevel and hypoid gear drives. Gear Tech. 2007, 24, 26–35. [Google Scholar]
- Demenego, A.; Vecchiato, D.; Litvin, F.L.; Nervegna, N.; Manc, S. Design and simulation of meshing of a cycloidal pump. Mech. Mach. Theory 2002, 37, 311–332. [Google Scholar] [CrossRef]
- Shuaifeng, L.; Xiaozhong, D.; Tianxing, L.; Changlu, W.; Jingzhao, Y. Tooth contact analysis of cycloidal pinwheel drive in rv reducer of robot. J. Mech. Trans. 2017, 41, 17–22. [Google Scholar]
- Jingzhao, Y. Load Contact Analysis of Cycloidal-Pin Gear Drive of Robot RV Reducer. Master’s Thesis, Henan University of Science and Technology, Luoyang, China, 2018. [Google Scholar]
- Lixin, X.; Yuhu, Y. A general method for multi-tooth contact analysis of cycloid-pin gear transmission. China Mech. Eng. 2016, 27, 1382–1388. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book, 2nd ed.; Springer: Berlin, Germany, 1997. [Google Scholar]
- Ma, K.; Han, L.; Sun, X.; Liang, C.; Zhang, S.; Shi, Y.; Wang, X. A path planning method of robotic belt grinding for workpieces with complex surfaces. IEEE-ASME T. Mech. 2020, 25, 728–738. [Google Scholar] [CrossRef]
- Zhenglin, W.; Chun, G.; Qian, H. Proficient in MATLAB Scientific Computing; Publishing House of Electronics Industry: Beijing, China, 2009. [Google Scholar]
- GB/T18254; High-Carbon Chromium Bearing Steel. China Iron and Steel Association: Beijing, China, 2016.


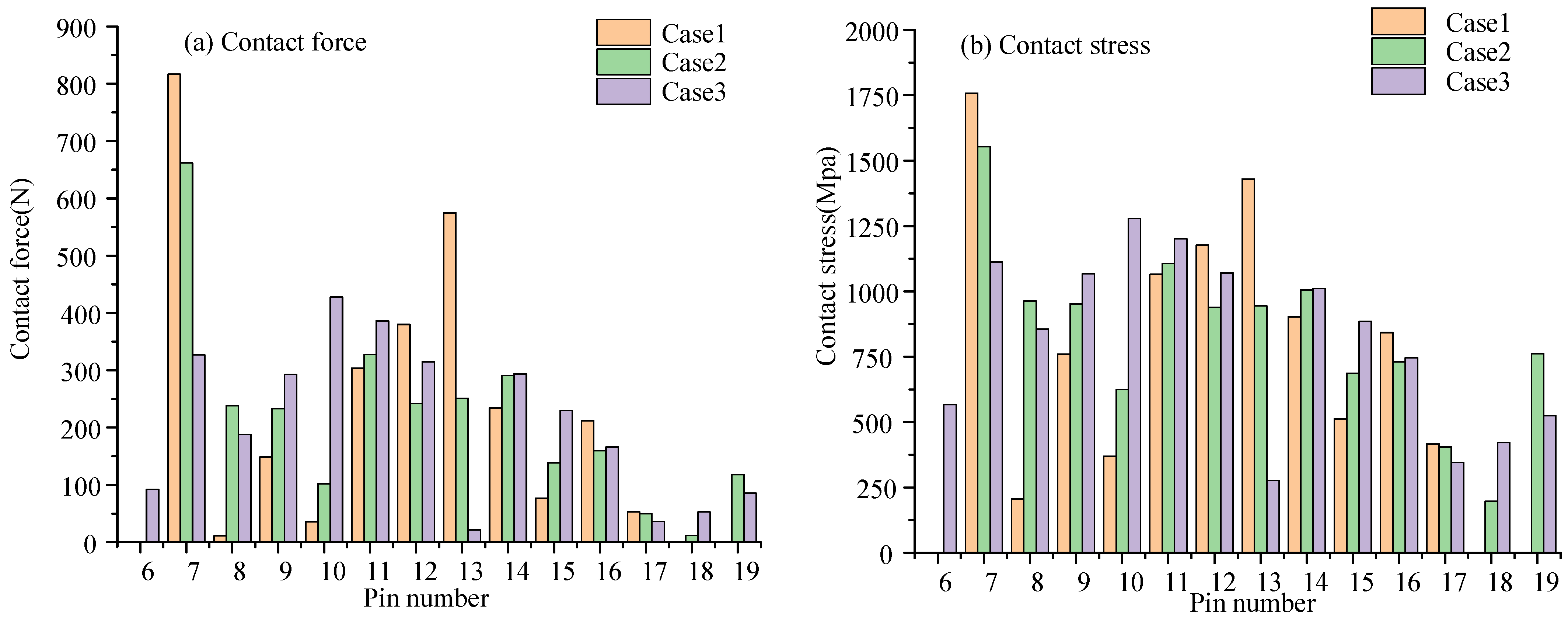





| Name | Parameter Value |
|---|---|
| Number of cycloid teeth | 49 |
| Number of pin teeth | 50 |
| Radius of pin /mm | 0.975 |
| Eccentricity /mm | 0.462 |
| Radius of pin position circle /mm | 29.6 |
| Name | Case1 | Case2 | Case3 |
|---|---|---|---|
| /mm | 0.05 | 0.03 | 0.02 |
| /mm | 0.005 | 0.005 | 0.005 |
| /mm | 0.02 | 0.015 | 0.01 |
| /° | 0.252 | 0.3 | 0.2 |
| /° | 0.666 | 0.666 | 0.666 |
| /° | 1.515 | 1.756 | 1.245 |
| Density | Poisson Ratio | Elastic Modulus |
|---|---|---|
| 7800 kg/m3 | 0.3 | 2.1 × 1011 N/m2 |
| VISPM Groups | Group 1 | Group 2 | Group 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cases | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 | Case 8 | Case 9 |
| /mm | 0.04 | 0.03 | 0.02 | 0.03 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 |
| /mm | 0.005 | 0.005 | 0.005 | 0.005 | 0.01 | 0.015 | 0.005 | 0.005 | 0.005 |
| /mm | 0.01 | 0.01 | 0.01 | 0.005 | 0.01 | 0.015 | 0.01 | 0.01 | 0.01 |
| /° | 0.252 | 0.252 | 0.252 | 0.252 | 0.252 | 0.252 | 0.328 | 0.428 | 0.528 |
| /° | 0.666 | 0.666 | 0.666 | 0.666 | 0.666 | 0.666 | 0.726 | 0.826 | 0.926 |
| /° | 1.515 | 1.515 | 1.515 | 1.515 | 1.515 | 1.515 | 1.756 | 1.856 | 1.956 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Qian, Z.; Xu, Y.; Huang, J. Meshing Characteristic Analysis of CBR Reducer Considering Tooth Modification and Manufacturing Error. Machines 2024, 12, 915. https://doi.org/10.3390/machines12120915
Sun X, Qian Z, Xu Y, Huang J. Meshing Characteristic Analysis of CBR Reducer Considering Tooth Modification and Manufacturing Error. Machines. 2024; 12(12):915. https://doi.org/10.3390/machines12120915
Chicago/Turabian StyleSun, Xiaoxiao, Zhihao Qian, Yaochen Xu, and Jiacai Huang. 2024. "Meshing Characteristic Analysis of CBR Reducer Considering Tooth Modification and Manufacturing Error" Machines 12, no. 12: 915. https://doi.org/10.3390/machines12120915
APA StyleSun, X., Qian, Z., Xu, Y., & Huang, J. (2024). Meshing Characteristic Analysis of CBR Reducer Considering Tooth Modification and Manufacturing Error. Machines, 12(12), 915. https://doi.org/10.3390/machines12120915






