A Novel Method for Identifying Tool–Holder Interface Dynamics Based on Receptance Coupling

Abstract

The structural dynamics of a machine tool play a significant role in chatter occurrence, which significantly deteriorates the metal-cutting performance. The receptance coupling substructure analysis (RCSA) is known for eliminating the experimental dependency on repetitive impact hammer testing. However, the identified contact parameters between the holder and tool, which are necessary for RCSA, usually lose accuracy in predicting tool point dynamics when applied to other tool clamping lengths or to combinations with other tools. To this end, a new method based on conventional impact hammer testing and RCSA technique to identify these parameters is proposed. Two descriptions of the proposed method are presented for different tool combinations and different clamping lengths, respectively. This new method eliminates the need for specialized experimental setups. The predicted tool point dynamics, using the identified contact parameters from the proposed method, show deviations below 3% with one exception, indicating that the identifications are accurate for various clamping lengths. The new approach yields significant advancements in the predicted tool point dynamics and stability boundaries compared to a traditional identification method reported in the literature.

1. Introduction

Chatter is a significant issue in machining that impacts both the part quality and production efficiency [1,2]. To mitigate chatter during manufacturing, stability lobe diagrams (SLDs) are utilized to assess milling stability, aiming at identifying the boundaries between stable and unstable cutting depths in relation to spindle speed [3]. Although SLDs are valuable for stability analysis, their practical adoption in industry is limited by the high demands for precise measurements and sophisticated modeling to accurately implement the approach. Therefore, further research to enhance the chatter stability analysis must be carried out to address this issue.

Tool–workpiece interaction is essential in selecting an appropriate cutting strategy, as it directly affects the quality, shape, and dimensional accuracy of the machined surface. Varga et al. [4] developed a method for assessing the effective diameter of a copying cutter during the machining of complex surfaces. Their findings emphasized the significant impact of variations in the tool’s effective diameter, along with the area and volume, on the accuracy of the resulting shapes. Then, Varga et al. [5] investigated the influence of tool inclination by evaluating surface roughness and topography, and identified the best and unfavorable results of tool inclination for surface quality, giving constructive suggestions for planning the cutting process. Except for these tool–workpiece interactions, chatter is another critical factor that has to be considered when selecting an appropriate cutting strategy. To address this issue, the milling stability modeling has been widely studied in both analytical [6,7] and numerical forms [8]. Karandikar et al. [9] designed a Bayesian learning approach for identifying stability boundaries and optimal milling parameters. Their results showed that the method operates efficiently and robustly with a limited number of tests/data points. Song et al. [10] developed a method for predicting milling stability with higher efficiency and accuracy. Their results indicate that accounting for vibration velocity enhances both the efficiency and accuracy over traditional approaches. The primary factors affecting stability are the tooltip dynamics, characterized by frequency response functions (FRF), and the cutting force coefficients. While progress of chatter stability analysis has been achieved, accurately identifying the tooltip FRF remains a challenge that limits the effectiveness of chatter stability prediction.

The tooltip FRF is typically obtained through impact hammer testing, which employs Experimental Modal Analysis (EMA) to calculate the FRF of the tool point by measuring the impact force and the structural response [1]. However, it is common to use various tools and holders on a machine, requiring the tool point FRF to be measured for each tool–holder combination. This process must be repeated for every setup, which is time-consuming, increases machine downtime, and raises production costs. An alternative approach is the model-based approach [11,12], but modeling the entire machine tool structure, including the tool and holder, is challenging. This is mainly due to the lack of certain critical information, such as bearing locations, and the difficulty in determining the contact characteristics of the numerous joints within the machine tool structure.

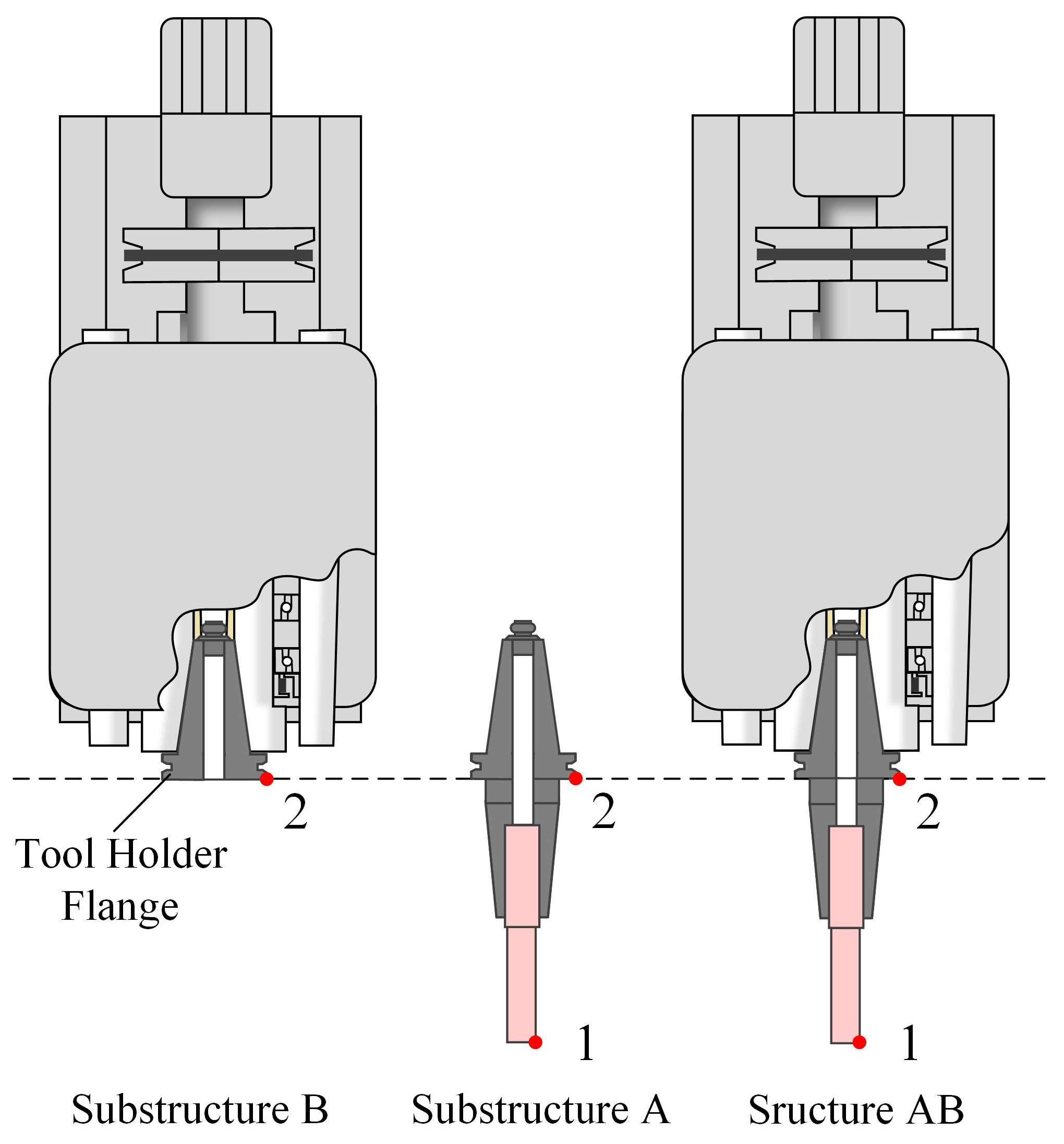
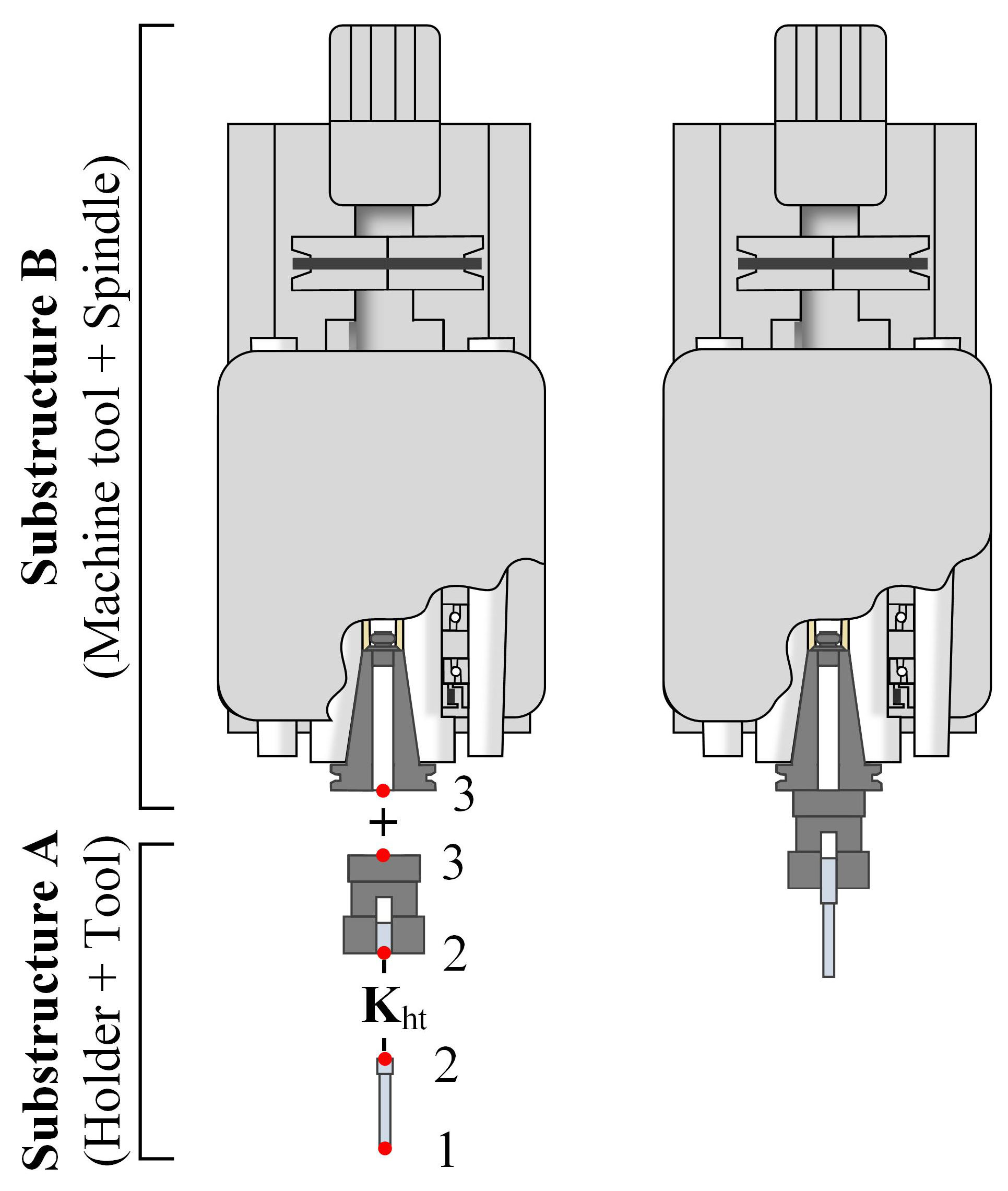
Receptance coupling (RC) or receptance coupling substructure analysis (RCSA) is an effective mathematical technique for predicting assembly dynamics, combining experimental dynamic measurements of the machine tool substructure with the analytically derived dynamics of the tool–holder assembly. Schmitz and Donalson [13] first introduced RCSA to the field of machining and, since then, it has gained widespread adoption among researchers for various applications in machine tool dynamics [14,15,16]. A major difficulty in implementing the RCSA method arises from the complexities of the joint interfaces between the spindle, holder, and tool. A widely adopted approach, proposed by Schmitz et al. [13,17], represents the tool–holder contact as a lumped spring–damper system, specifically at the location where the tool extends from the holder. The tool–holder interface is characterized by stiffness and damping coefficients, which are determined by manually matching the calculated tooltip FRF with the experimental measurements. They found that the dynamic response of the tooltip can be predicted by an appropriate contact model. Park et al. [18] presented an improved method for identifying the parameters of the lumped contact model for the tool–holder joint, considering both translational and rotational degrees of freedom. They verified that the rotational degree of freedom at the spindle played a significant role in tool point dynamics. Ertürk et al. [19] were the first to model the spindle–holder–tool system by combining Timoshenko beam theory with the lumped contact model. Their analysis revealed that the rotational contact parameters at both interfaces are less critical than the translational ones. Since then, many researchers [20,21,22] have made significant efforts to improve the identification of the lumped contact model for the tool–holder interface. More recently, Matthias et al. [23] found that while the first mode of a system can be well-fitted using different parameter sets from various identification methods, these parameters are not transferable to other tool clamping lengths or combinations with other tools, indicating they do not represent the true interface parameters. They suggested a new method for determining the real contact dynamics, which involves measuring the dynamics of the holder–tool assembly at free–free end conditions and identifying the contact parameters through a fitting algorithm. Yu et al. [24] investigated joint stiffness in the tool holder system using a practical approach that unified the system and its supports as constraints, reducing complexity. Their findings demonstrated the method’s effectiveness in simplifying modeling while ensuring engineering accuracy.

In contrast to the single lumped contact model between the tool and holder, a more realistic but more intricate approach incorporates a multi-point elastic coupling between the components, often referred to as the distributed joint interface. Namazi et al. [25] modeled the connection between the tapered surface of spindle and tool holder by uniformly distributed springs in orthogonal directions, whose parameters are identified using a least-squares curve-fitting algorithm. The method was experimentally validated and shown to facilitate wear analysis by removing discrete contact springs. Schmitz et al. [26] proposed a multi-point receptance coupling substructure analysis (RCSA) technique, involving coupling the portion of the tool within the holder to the clamping section of the holder at several equally spaced points along the insertion length. This study concluded that a second-order relationship effectively describes the dependence of stiffness on tool blank diameter. Kiran [27] modeled the holder–tool contact as a flexible component, and the results showed that the proposed identification procedure achieved excellent agreement between predictions and measurements, confirming the model’s efficiency. Recently, Akbari et al. [28] proposed techniques to obtain the real connection parameters with higher efficiency, combining simple sound measurement of tool–holder assembly under free–free end conditions with the distributed joint interface, and also presented an identification method for the model parameters. Despite their improved accuracy in predicting assembled dynamics, disturbed contact models are more complex and computationally intensive, leading to time-consuming calculations.

As seen in the above studies, although the lumped contact model simplifies the modeling and calculation effort significantly, the identified contact parameter values are valid only for that particular assembly of tool–holder, and are not transferable to other tool clamping lengths or to combinations with other tools. While some research has focused on identifying the true contact parameters, these methods often require specialized experimental setups, which are not commonly available in industrial environments.

This paper proposes a novel method to identify the contact parameters between the holder and tool based on the RCSA approach and conventional impact hammer testing. Two descriptions of the proposed method are provided, one for different tools and the other for varying clamping lengths. The novelties of this paper can be summarized in the following three points:

• The proposed method can identify transferable contact dynamics, enabling the extrapolation of the results to other tool lengths or tool clamping lengths. This is achieved through conventional impact hammer testing at the tooltip on a machine tool, eliminating the need for repeated hammer tests and specialized testing setups.
• Improved initial assumptions of the contact parameters are given based on physical laws and existing experimental observations. This facilitates the identification of the true contact dynamics, rather than a solution confined to a specific tool configuration.
• Two descriptions of the proposed method are developed based on the improved initial assumptions and receptance coupling, making it applicable to different tool lengths or tool clamping lengths, thus broadening the method’s range of application.

It has been demonstrated that these assumptions are reasonable, and enhance the accuracy of contact parameter identification. Further, based on the new method, the identified results can be transferred to other clamping lengths or combinations with other tools, which significantly improve the prediction accuracy in both tooltip dynamics and milling stability. Therefore, this study provides an industrial-friendly method for obtaining the tool–holder interface parameters, eliminating the need for repeated hammer tests and specialized testing setups.

2. Materials and Methods

2.1. Materials

This study aims to identify the contact dynamics at the interface between the tool and the collet chuck holder. It has been demonstrated in numerous studies that this coupling is generally considered an elastic coupling. The proposed contact dynamics identification method is experimentally evaluated on a 3-axis Fadal VMC 2216 vertical machining center. This machining center has a CAT 40 spindle taper. The parameters of the target tool and holder for the identifications are given in

Table 1. Characteristics of the collet chuck holder–tool combination.

	Parameter	Value
Holder	Model	LYNDEX NIKKEN-C4007-0032-3.13
	Type	ER32 Collet chuck
Tool	Model	Kyocera SGS 33125 E1S
	Type	Solid carbide endmill
	Total length	4 inches
	Diameter	5/16 inch (7.94 mm)
	Nb. Flutes	4
	Helix angle	30°
	Collet chuck clamping torque	100 ft/lbs (135.58 Nm)

.

The tool and holder were divided into cylindrical segments that were modeled as Timoshenko beam elements, and they were elastically coupled with a connection matrix at the holder tip, as illustrated in Figure 1.

This study proposed a new method based on conventional impact hammer tests at the tooltip on a machining center. The experimental setup for the impact hammer tests is shown in Figure 2. The FRFs at the tooltip were measured by an ICP 086E80 automatic hammer and Polytec CLV-2534 laser vibrometer.

At the very beginning of the tool–holder contact dynamics identification, it is necessary to determine the structural dynamics of the holder-spindle interface, which represents the dynamics of both the spindle and the taper shank portion of the holder. The spindle with CAT 40 interface was identified according to the method proposed by Namazi et al. [25], using a shrink-fit-type holder of model CV40TT20M400, because the tool–holder connection in the shrink-fit can be modeled as a rigid connection, eliminating the need to identify contact parameters at this interface. The tool and holder were modeled in a similar way, as illustrated in Figure 3.

Impact hammer tests are also necessary for obtaining the structural dynamics of the holder-spindle interface. The used measurement arrangement for this identification is depicted in Figure 4. Since the tool diameter for the shrink-fit holder is large, a DYTRAN 5800B4 conventional hammer and DYTRAN 3225F5 accelerometer are employed to measure the tooltip FRF.

The accuracy of the identified contact parameters is further validated by the predicted chatter stability in milling, and their influence on the predicted stability is also investigated. To achieve this goal, multiple chatter stability tests were conducted. The experimental setup for the chatter stability tests is shown in Figure 5. The tool–holder combination shown in Figure 1 was used for cutting Aluminum 7050-T7451. The cutting forces were measured using a Kistler 9257B multicomponent dynamometer.

The cutting force coefficients for the analytical model of chatter were taken as $K_{tc}=790$ MPa and $K_{rc}=230$ MPa, which are obtained in experiments with the average calibration method [1]. The feed rate was kept at 0.003 inch/tooth (equals 0.0762 mm/tooth) with a feed in Y direction. In total three cutting cases (a–d) are conducted as listed in

Table 2. Cutting cases and corresponding process parameters.

Case	Clamping Length (mm)	Radial Immersion (%)	${\mathit{a}}_{\mathit{p}}$ (mm)
a	25	70	0.03, 0.06, 0.09, 0.12, 0.15
b	30	95	0.02, 0.04, 0.06, 0.08, 0.1
c	35	70	0.03, 0.065, 0.1, 0.135, 0.17
d	40	95	0.03, 0.05, 0.07, 0.09, 0.11

.

2.2. Theory of Receptance Coupling

In this section, the theory of receptance coupling substructure analysis (RCSA) is succinctly reviewed, drawing from the previous literature [1,29]. Based on the nature of the connection between two substructures, there exist two fundamental types of couplings: rigid coupling and elastic coupling. According to different desired locations of the assembly response and force conditions of the assembly, different RCSA descriptions can be derived based on the RCSA theory. The receptance matrix for the assembled system C shown in Figure 6, which is formed by rigid coupling of substructure A and substructure B, is presented as

$$\left[C_{11}\right]=\left[A_{11}\right]-\left[A_{12}\right]{(\left[A_{22}\right]+\left[B_{11}\right])}^{-1}\left[A_{21}\right],$$

(1)

where each acceptance matrix includes the point and transfer acceptance functions of the component end points. For example, the point acceptance matrix of point $A1$ in substructure A is written by

$$\left[A_{11}\right]=\left[\begin{array}{cc}{H}_{A1A1}& L_{A1A1}\\ N_{A1A1}& P_{A1A1}\end{array}\right],$$

(2)

where letters H, L, N, and $P$ denote the receptance functions that relate the linear and angular displacements to the forces and the moments applied at these points. In Equation (5), they are defined as follows:

$$\begin{array}{cc}{X}_{A1}=H_{A1A1}{F}_{A1},& X_{A1}=L_{A1A1}{M}_{A1}\\ {\theta }_{A1}=N_{A1A1}{F}_{A1},& {\theta }_{A1}=P_{A1A1}{M}_{A1}\end{array}$$

(3)

Another case of receptance coupling considering the stiffness and damping between such connections for the assembly shown in Figure 7 can be expressed as follows:

$$\left[C_{11}\right]=\left[A_{11}\right]-\left[A_{12}\right]{(\left[A_{22}\right]+\left[B_{11}\right]+{\left[K\right]}^{-1})}^{-1}\left[A_{21}\right],$$

(4)

where $\left[K\right]$ represents the complex stiffness matrix, and can be written as

$$\left[K\right]=\left[\begin{array}{cc}{k}_{xf}+i\omega c_{xf}& 0\\ 0& k_{\theta M}+i\omega c_{\theta M}\end{array}\right],$$

(5)

where $k_{xf}$ and $c_{xf}$ denote the translational stiffness and damping between two substructures, while $k_{\theta M}$ and $c_{\theta M}$ denote the rotational stiffness and damping, respectively.

2.3. Identification of Structural Dynamics at the Spindle–Holder Interface

The structural dynamics at the spindle–holder interface determine the chatter stability of the machining process, and need to be identified. An approach proposed by Namazi et al. [25] to identify the rotational and translational dynamics of the spindle up to the tool holder flange is applied in this study, where the holder flange is standard and remains unchanged as shown in Figure 8. This approach is advantageous, because it bypasses the complicated task of identifying elastic coupling parameters at the spindle–holder taper joint and takes spindle rotational dynamics into account, resulting in more precise FRF predictions.

In this method, the structural dynamics at the spindle–holder interface are obtained by solving a set of nonlinear equations derived from the receptance coupling technique discussed in Section 2.2, presented here in a simplified form as follows:

$$f_i(\left\{x\right\},\left\{a\right\},\left\{b\right\})=0,i=1\mathrm{to}4$$

(6)

where

$$\left\{x\right\}=\{H_{B2B2},L_{B2B2},N_{B2B2},P_{B2B2}\}$$

(7)

$$\left\{a\right\}=\{H_{11},H_{12},H_{22}\}$$

(8)

$$\left\{b\right\}=\{A_{11},A_{12},A_{22}\}$$

(9)

The vector $\left\{x\right\}$ contains four unknown receptances of the assembly at point 2 that need to be solved. The terms in $\left\{a\right\}$ are obtained by three impact hammer tests. The FRFs of the free–free substructure A are contained in $\left\{b\right\}$, and calculated using the Timoshenko beam modeling [30]. Note that a shrink-fit-type holder is recommended for this process, because the tool–tool holder connection in the shrink-fit can be assumed to be rigid, eliminating the need to identify the elastic coupling parameters at this connection. More details on the identification method of structural dynamics at the spindle–holder interface are given in Ref. [25].

2.4. Identification of Contact Dynamics at the Holder–Tool Interface

As stated in Section 2.3, the holder flange is standard and remains unchanged. Therefore, for a new tool–holder combination of interest, only substructure A, the stick out of the tool–holder, is calculated analytically using Timoshenko beam theory. Based on the RCSA approach, different sections of the holder and tool are coupled rigidly and receptance matrix for the holder $\left[H\right]$ and tool $\left[T\right]$ for the free–free case are obtained. In the end, the holder receptances are coupled with the tool receptances elastically, as shown in Figure 9.

Next, the tool point FRF of the new holder–tool assembly is measured. To identify the real interface parameters at the tool–holder connection, Matthias et al. [23] and Akbari et al. [28] proposed techniques that require measuring the tool–holder assembly under free–free end conditions. However, these methods are challenging to implement in practice due to the need for specialized experimental setups. This paper proposes a new industry-friendly method that only requires standard impact hammer tests, where the holder–tool assembly is clamped to the machining center and the tool point FRF is measured directly. Here are two approaches to identify the elastic contact parameters.

Method Description I. Differently to the existing methods in the literature, which typically measure the dynamics of only one specific setup, this study uses two or more tools with equal shank diameters, but varying total lengths, fixed to the machining center with constant clamping lengths. The end point dynamics of these different setups are then measured. The elastic contact parameters for these different tools with the same tool holder are equal. According to the elastic coupling procedure given in Equation (4), the receptance matrix at the tooltip can be given as

$${\left[{\mathrm{SHT}}_{11}\right]}_j={\left[T_{11}\right]}_j-{\left[T_{12}\right]}_j{({\left[T_{22}\right]}_j+\left[{\mathrm{SH}}_{22}\right]+{\left[K_{ht}\right]}^{-1})}^{-1}{\left[T_{21}\right]}_j,j=1\mathrm{to}{N}_t$$

(10)

where j is the number of the tool, and the receptance matrix at the holder tip $\left[{\mathrm{SH}}_{22}\right]$ and complex stiffness matrix $\left[K_{ht}\right]$ between the tool and holder are kept constant for different tools. Then, a set of these elastic coupling equations can be obtained. These equations can be used to obtain an accurate set of contact parameters for a certain clamping length and tool diameter.

Method Description II. In practical situations, it may not be feasible to prepare multiple tools with different total lengths but the same diameter; often, only one tool is available. In such cases, an alternative method is employed: the tool is clamped to the machining center using two or more different clamping lengths, and standard impact hammer tests are conducted under these varying clamping conditions. Also, it is possible to model each linear displacement–force tooltip measurement by a single equation.

Here, some assumptions are considered. First, it can be assumed that damping parameters at the connection remain constant for different clamping conditions and can be identified by existing methods in the literature [13,17]. According to [23], the magnitude of damping varies with different clamping conditions. Since the damping is sufficiently low as to not impact the modeling of the spindle–holder–tool assembly, it can be neglected in further research on contact dynamics.

In addition to the contact damping behavior, we assume that, for a small-diameter end mill, both the translational and rotational contact stiffness increase linearly and slowly with the clamping length. Matthias et al. [23] demonstrated that, for a tool with a small diameter (no larger than 12.7 mm), different clamping lengths have a low effect on translational and rotational stiffness, which remains nearly constant. They provided a two-spring model for the clamping interface, as shown in Figure 10. The total stiffness can be calculated with the following equation:

$$K_{ser}={\displaystyle \frac{k_1{k}_2}{k_1+k_2}}$$

(11)

They indicated that the outer surface is bigger, which suggests that the stiffness $k_1$ in this area should be lower. Consequently, a change in $k_2$ has a lower influence on the total stiffness.

During the investigation, it was found that the assumption of constant contact stiffness across different clamping lengths is too strict for identifying the real contact dynamics. Thus, it is necessary to consider a more adaptable assumption for further investigation. Generally, as the clamping length increases, the contact area is the main factor affecting the contact stiffness between the holder and tool, leading to reduced contact deformation. This results in an increase in contact stiffness. However, it is important to note that this relationship is only an approximation of actual behavior, as the pressure distribution may change during modifying the clamping length.

Therefore, the contact stiffness can be assumed to increase linearly with the clamping length, subject to the following constraints:

$$\left\{\begin{array}{cc}{K}_{xf}\left(l_2\right)-K_{xf}\left(l_1\right)\le Q_1{K}_{xf}\left(l_1\right),\hfill & \mathrm{for}\mathrm{any}{l}_2>l_1\hfill \\ K_{\theta M}\left(l_2\right)-K_{\theta M}\left(l_1\right)\le Q_2{K}_{\theta M}\left(l_1\right),\hfill & \mathrm{for}\mathrm{any}{l}_2>l_1\hfill \end{array}\right.$$

(12)

where $l_1$ and $l_2$ represent two different clamping lengths in the feasible range, which is typically defined by the tool and collet manufacturer’s manual. The scaling factors $Q_1$ and $Q_2$ for the tool–holder connection are set empirically at 50% in this study. This scaling factor can be determined through experience, and it has been found by the authors that only a very loose restriction is needed for the identification to converge to the real solution. It should be noted that measurements of more than two clamping lengths can be induced for the identifications by expanding Equation (12).

Based on the above assumptions, the elastic coupling equations for the tooltip FRF can be expressed as

$${\left[{\mathrm{SHT}}_{11}\right]}_k={\left[T_{11}\right]}_k-{\left[T_{12}\right]}_k{({\left[T_{22}\right]}_k+{\left[{\mathrm{SH}}_{22}\right]}_k+{\left[K_{ht}\right]}_k^{-1})}^{-1}{\left[T_{21}\right]}_k,k=1\mathrm{to}{N}_c$$

(13)

where k denotes the number of the clamping length. All receptance matrices vary with different clamping lengths and can be calculated by Timoshenko beam theory. The complex stiffness matrix $\left[K_{ht}\right]$ between the tool and holder changes with the clamping length with respect to the proposed assumptions.

Equations (10) and (13) represent the tooltip FRF $\left[{\mathrm{SHT}}_{11}\right]$ analytically in terms of unknown contact parameters at the holder–tool interface. Therefore, the fitting algorithm can be employed to compare the measured and calculated $\left[{\mathrm{SHT}}_{11}\right]$ values, minimizing the absolute percentage difference between them. This algorithm fine-tunes the unknown contact stiffness parameters to reduce the deviation between the FRFs within a specified amplitude range.

Therefore, the unknown contact stiffness parameters are used to minimize the deviation of both FRFs in a fixed range around the amplitudes. As cases of different total lengths or clamping lengths are induced in the identification, the proposed method can provide the real contact parameters for different clamping lengths without measurements under free–free end conditions. Note that for Method Description II, since the stiffness parameters change approximately linearly, the contact parameters for any clamping length can be derived based on these identified results. Thus, the identified results by the presented method are transferable to other tool clamping lengths or combinations with other tools. An overview of the approach is shown in Figure 11.

3. Results

3.1. Experimental Validations for Identification of Contact Dynamics

To verify the method, first, contact parameters for two different clamping lengths are identified using the proposed method. The tooltip FRFs are then calculated and compared with the measurements to demonstrate the effectiveness of the identified contact parameters.

Based on the established model of the shrink-fit holder and tool combination, as illustrated in Figure 3, and measurements, as shown in Figure 4 in Section 2.1, the identified FRF at the holder–spindle interface in both x and y directions are shown in Figure 12.

Then, identified spindle dynamics are used to predict end point FRFs for the collet chuck holder and tool combination. Tool and holder parameters used in identification are given in Table 1 in Section 2.1. The model of the collet-type holder and tool combination is constructed as shown in Figure 2.

The contact dynamics in this study are derived from the measured tool point FRFs of the holder–tool assembly, with two different clamping lengths on the machining center. In contrast to the proposed method, existing approaches often rely on measured tool point FRFs under a single clamping length condition, as shown in the literature [13,17]. Since the damping magnitude is sufficiently small and fluctuates, it does not significantly impact the modeling of the spindle–holder–tool assembly, allowing it to be disregarded in the identification of contact dynamics [23]. The translational and rotational damping are taken as 10 Ns/m and 5 × 10⁻⁴ Nms/rad, respectively. In order to validate the proposed approach for identifications of contact dynamics, first, the holder–tool assembly was clamped by two clamping length conditions to the machining center, and the tool point FRFs were measured, as shown in Figure 2. Subsequently, the tooltip FRF was derived by combining the analytically computed holder–tool receptance matrices with the experimentally measured spindle receptances. Additionally, a comparison of various identification methods was conducted, employing different contact parameters to model the elastic interaction between the holder and tool dynamics, as shown in

Table 3. Different parameter sets for complex stiffness matrices of holder–tool connection.

	Clamping Length (mm)	${\mathit{k}}_{\mathit{xf}}$ (N/m)	${\mathit{k}}_{\mathit{\theta }\mathit{m}}$ (Nm/rad)
Method from the literature−set 1	25	1.86 × 106	1.53 × 105
Method from the literature−set 2	40	2.93 × 106	9.29 × 105
New approach	25	1.79 × 106	4.53 × 105
	30	2.13 × 106	5.28 × 105
	35	2.47 × 106	6.02 × 105
	40	2.81 × 106	6.76 × 105

.

Among the contact parameter sets given in Table 3, the literature sets 1 and 2 were obtained by a widely adopted approach proposed by Schmitz et al. [13,17], using measurements taken under single clamping lengths of 25 mm and 40 mm, respectively. According to the assumptions in the literature [31], the identified parameters under one clamping length can be approximately transferred to other clamping length conditions. On contrary, the four remaining parameter sets were obtained by the proposed method, based on measurements taken under two different clamping lengths of 25 mm and 40 mm. Predicted tool point FRFs for these two clamping conditions using different contact parameters with the measured tool point FRF in X and Y directions are given in Figure 13 and Figure 14, respectively. Note that measurements were only conducted in the X direction to identify the contact parameters and the prediction of tool point FRFs would be made in both X and Y directions.

As shown in Figure 13 and Figure 14, frequencies show a good match for each FRF in both X and Y directions for clamping lengths of 25 mm and 40 mm, with magnitude differences being acceptable in most cases for each set. In the case with a clamping length of 40 mm, the frequencies show a good match for each FRF; however, the magnitude differences in the X direction are relatively large, as shown in Figure 13b. This could be due to the close modes occurring at the tool point, which is more obvious in Y direction in Figure 14b, making precise predictions of the tool point FRF difficult. Thus, it can be assumed that both the method in the literature and the proposed method provide good results for the spindle–holder–tool assembly. However, problems become apparent if the parameters obtained by different techniques are used for various tool lengths or clamping lengths [23], which will be detailed in the next subsection.

3.2. Experimental Validations of Knowledge Transferability in Prediction of Tooltip Dynamics with Different Clamping Lengths

In this section, the knowledge transferability of identification results of contact dynamics in the prediction of tooltip dynamics with different clamping lengths is analyzed.

Note that, under the same clamping condition, the contact dynamics should be able to be transferred to various outer tool lengths. Furthermore, for a specific tool, the contact dynamics can be approximately transferred to various clamping lengths [31]. In other words, the influence of various clamping lengths is limited. This was experimentally validated by Matthias et al. [23]. A reason for this is that the stiffness at the collet–holder surface is smaller; thus, a change in stiffness at the tool–holder interface has a lower influence on the total stiffness.

However, problems appear when the contact dynamics from different approaches are used to predict the tool point dynamics. According to the results of Matthias et al. [23], contact parameters from multiple methods can not provide accurate predictions for the first mode in cases with the same clamping conditions but different outer tool lengths.

Therefore, a specific system can possibly be modeled by different parameter sets, which do not represent the real interface parameters. But only one set can be used to calculate the model for different tool overhang lengths or clamping lengths. Furthermore, the errors in spindle identification might be compensated by contact parameters, if the spindle–holder–tool assembly is used to identify these parameters.

The contact dynamics in Table 3 were applied to a tool with different clamping lengths. The predicted tool point FRFs in X and Y directions are shown in Figure 15 and Figure 16, respectively. The predicted natural frequencies are shown in Figure 17. Only frequencies of tool point FRFs from the proposed method show a good match for each FRF, as listed in

Table 4. Test errors of proposed approach for various clamping lengths.

Clamping Length (mm)	Type	${\mathit{\omega }}_{\mathbf{n},\mathit{x}}$ (Hz)	${\mathit{\omega }}_{\mathbf{n},\mathit{y}}$ (Hz)
25	Measured	1287	1284
	Predicted	1284	1291
	Error (%)	0.26	0.54
30	Measured	1425	1411
	Predicted	1456	1431
	Error (%)	2.15	1.40
35	Measured	1604	1552
	Predicted	1631	1611
	Error (%)	1.71	3.78
40	Measured	1770	1829
	Predicted	1773	1800
	Error (%)	0.17	1.58

. The parameters from set 1, identified solely from the measurement at a clamping length of 25 mm, yield significant errors in both frequencies and magnitudes when applied to a clamping length of 40 mm. Similarly, the predicted frequencies and magnitudes of the FRF under a clamping length of 25 mm exhibit significant errors when using contact parameters derived from the measurement taken at a clamping length of 40 mm. The prediction errors in frequencies from these two sets are, respectively, listed in

Table 5. Test errors of method in the literature (parameter set 1, identified from single clamping length of 25 mm) for various clamping lengths.

Clamping Length (mm)	Type	${\mathit{\omega }}_{\mathbf{n},\mathit{x}}$ (Hz)	${\mathit{\omega }}_{\mathbf{n},\mathit{y}}$ (Hz)
25	Measured	1287	1284
	Predicted	1284	1283
	Error (%)	0.26	0.09
30	Measured	1425	1411
	Predicted	1386	1358
	Error (%)	2.76	3.77
35	Measured	1604	1552
	Predicted	1466	1431
	Error (%)	8.58	7.82
40	Measured	1770	1829
	Predicted	1544	1526
	Error (%)	12.77	16.56

and

Table 6. Test errors of method in the literature (parameter set 2, identified from single clamping length of 40 mm) for various clamping lengths.

Clamping Length (mm)	Type	${\mathit{\omega }}_{\mathbf{n},\mathit{x}}$ (Hz)	${\mathit{\omega }}_{\mathbf{n},\mathit{y}}$ (Hz)
25	Measured	1287	1284
	Predicted	1466	1437
	Error (%)	13.87	11.90
30	Measured	1425	1411
	Predicted	1562	1531
	Error (%)	9.59	8.49
35	Measured	1604	1552
	Predicted	1678	1636
	Error (%)	4.64	5.39
40	Measured	1770	1829
	Predicted	1773	1800
	Error (%)	0.17	1.58

.

As the test errors of the three sets of identification results in Table 3 (including the results of the proposed method, and those of the method in the literature using single clamping lengths of 25 mm and 40 mm, respectively) have been obtained and listed in Table 4, Table 5, and Table 6, respectively, all of these test error data for the three sets are summarized in

Table 7. Test errors of three sets of results from different methods.

Clamping Length (mm)	Predicted Term	Proposed Method	Method in Literature−Set 1	Method in Literature−Set 2
25	${\omega }_{\mathrm{n},x}$	0.26	0.26	13.87
	${\omega }_{\mathrm{n},y}$	0.54	0.09	11.90
30	${\omega }_{\mathrm{n},x}$	2.15	2.76	9.59
	${\omega }_{\mathrm{n},y}$	1.40	3.77	8.49
35	${\omega }_{\mathrm{n},x}$	1.71	8.58	4.64
	${\omega }_{\mathrm{n},y}$	3.78	7.82	5.39
40	${\omega }_{\mathrm{n},x}$	0.17	12.77	0.17
	${\omega }_{\mathrm{n},y}$	1.58	16.56	1.58

for comparison.

Therefore, only the identified parameters from the proposed approach provide accurate predictions for all clamping lengths. Neither parameter set 1 nor set 2 produces the expected behavior across the different clamping lengths, except for the length used for identification. In addition, prediction errors in frequencies of these two sets are large enough to produce an error for the stability. As a consequence, contact parameter sets 1 and 3 lose their applicability for different tool clamping lengths.

The identified contact parameters from different optimization techniques are displayed in Figure 18. While the identified translational stiffness is comparable in Figure 18a, the identified rotational stiffness in parameter sets 1 and 2 differs significantly, even by an order of magnitude, as can be seen in Figure 18b, which contradicts the expected physical behavior. This indicates that the system of a specific clamping length can be modeled with different parameter sets, but not all of them represent the real interface parameters. The proposed new approach is capable of identifying the real contact parameters between the tool and holder.

3.3. Experimental Validations in Prediction of Stability Lobe Diagrams

As stated earlier, the machine tool dynamics characterized by tooltip FRF are a key input to the chatter stability model. Due to inaccuracies in incorporated dynamics into stability models, the stable pockets may shift, potentially causing severe chatter and subsequent adverse effects. This section studies the prediction accuracy of stability boundaries calculated by the contact dynamics that are identified from different optimization techniques. The experimental setup for the chatter stability tests is shown in Figure 5. The tool–holder combination shown in Figure 1 was used for milling operations.

The cutting force coefficients for the analytical model were taken as $K_{tc}=790$ MPa and $K_{rc}=230$ MPa, which are obtained in experiments with the average calibration method [1]. In total, four cutting cases (a–d) are conducted as listed in Table 2, corresponding to the stability diagrams in Figure 19a–d, respectively. The predicted FRFs in Figure 15 and Figure 16 are used for calculating the stability boundaries. At the end, the stability boundaries are calculated through a semi-discrete numerical method (SDM) by Insperger and Stépán [32]. As can be seen in Figure 19, the identified tool point dynamics from measurements under two clamping lengths using the proposed approach can provide the stability boundaries that are the closest to those calculated from the measured dynamics at each respective clamping length. The errors in predicted tool point FRF from the new approach might originate from the inaccurate identification of the spindle dynamics.

The test errors of the stability prediction by measured FRFs in X and Y directions are listed in

Table 8. Test errors of the stability prediction by measured FRFs in X and Y directions.

	Case a	Case b	Case c	Case d
Error (%)	24	21.3	20	26.67

. The test errors range from 20% to 26.67%. This is due to variations in the cutting coefficients and tooltip dynamics during operations, which caused the predicted stability lobes diagram (SLD) to deviate from the actual one.

In this study, we focus on predicting the tooltip dynamics under idle state. Therefore, the deviations between the predicted SLD from three sets of results in Table 3 by different methods and the predictions based on measured FRFs in the X and Y directions are interesting and significant. These deviations can depict the influence of the inaccuracy of the contact dynamics on the final chatter stability. These deviations are evaluated by the ratio of the points with inconsistent predictions to the total number of points, rather than the actual prediction accuracy evaluated with the experimental results. They are summarized in

Table 9. Deviations between the stability predictions from three sets of results in Table 3 by different methods and the predictions based on measured FRFs in the X and Y directions.

(Unit of Deviations:%)	Case a	Case b	Case c	Case d
New approach	6.67	12	10.67	26.67
Method from the literature−set 1	5.33	21.3	49.30	58.67
Method from the literature−set 2	68	50.67	26.67	26.67

. It can be seen that the stability boundaries by the proposed method achieve the closest alignment with the ones predicted from the measured tooltip dynamics in both the X and Y directions, with deviations below 12% in all but one case. In contrast, the deviations of traditional identification methods are significantly larger, reaching up to 68%. The deviation of the new approach in case d may be due to the presence of closely spaced modes in the tool point dynamics when the clamping length is 40 mm, which poses challenges for the proposed method in accurately identifying the contact dynamics.

4. Discussion

In the Results section, the tool–holder contact parameters are identified by different techniques. Then, these contact parameters are first used to predict the tool point dynamics under the clamping conditions from which those parameters are obtained. In essence, all identification techniques are curve-fitting approaches, so that the tool point FRF used for identification can be accurately predicted using the identified contact parameters.

As noted in [23], the real contact parameters should be able to predict tool point FRF when only the overhang length or total length of the tool is changed. Additionally, for a specific tool, the contact dynamics can also be approximately applied to various clamping lengths [31]. In other words, the influence of various clamping lengths on tool–holder contact dynamics is limited, which was experimentally validated by Matthias et al. [23]. Based on these conclusions, when the parameters obtained from different techniques are used to approximately predict the tool point FRFs under various clamping lengths, the results are expected to be close to the measured FRFs for each clamping length. However, only the proposed approach achieves predictions with acceptable accuracy. This conclusion is further validated by the predicted stability boundaries of chatter.

The reason for this outcome, as explained in [23], is that although the tool point FRFs can be accurately fitted, the identified contact parameters at the tool–holder interface may be unreliable due to the presence of multiple parameter sets that can achieve equally good fits to the FRFs. Matthias et al. [23] and Akbari et al. [28] proposed identification techniques that can identify the real contact parameters at the tool–holder connection. Both of the methods are based on the measurements under the free–free end condition with additional experimental devices, which are usually not available in the industrial environment. This paper proposes an approach that relies on measurements of only standard impact hammer testing under two clamping or overhang lengths. Assumptions that restrict the contact parameters for different clamping lengths are given based on the known physical findings. The results of both predicted tool point FRF using the identified parameters from this new approach and the stability boundaries with this FRF verify the efficiency of the proposed method. Therefore, the assumptions established in this study are proved to be reasonable.

The proposed approach can efficiently provide the approximate tool point FRF under different clamping lengths or overhang lengths with acceptable accuracy. It should be emphasized that it is an approximated identification method, so uncertainties are present in the identified results. One potential source of uncertainty lies in the identification errors of the spindle dynamics. Additionally, as a consequence of the flaw of the RCSA technique, the proposed method could have lower identification accuracy if close modes exist in the end point dynamics.

5. Conclusions

An efficient method for identifying the contact parameters at the tool–holder connection is proposed. The method aims to identify the real contact dynamics that can be applied to different clamping lengths or overhang lengths based on standard impact hammer testing. New assumptions that restrict the contact parameters are constructed based on known physical findings. The proposed approach is verified by a comparison with a published identification method for predicting tool point dynamics under various clamping lengths. Stability chatter tests were also performed to further validate the accuracy of the identified tool point dynamics. The following conclusions can be drawn:

• Compared to the previous method that uses impact hammer testing under a single clamping length, the proposed method can identify the real tool–holder contact parameters that can be applied to different clamping lengths or overhang lengths. The identifications use measurements of standard impact hammer testing, reducing the requirement for specialized experimental setups compared to recent methodologies.
• The identified contact parameters by the present approach can accurately predict the natural frequencies of dominant modes at the tooltip in both X and Y directions. The predicted tool point dynamics, using the identified contact parameters from the proposed method, show deviations below 3% with one exception, indicating that the identifications are accurate for various clamping lengths. In contrast, although using the results from the traditional method that uses measurement under a single clamping length can achieve high accuracy, but the deviations for other clamping lengths increase to even 16.56%, which would evidently influence the accuracy of chatter stability analysis.
• The identified contact parameters by the proposed method can achieve high accuracy of the chatter stability in milling under different clamping and cutting conditions. Using the stability boundaries predicted from the measured tooltip dynamics in both the X and Y directions as a benchmark, the proposed method achieves the closest alignment with the benchmark, with deviations below 12% in all but one case. In contrast, the deviations of traditional identification methods are significantly larger, reaching up to 68%.

This study proposes and validates an approximate relationship between contact dynamics and clamping length under the condition that the tool diameter is not excessively large. The assumption holds because the holder–collet contact surface is larger than the collet–tool contact surface, limiting the influence of clamping length variations. However, further investigation in the future should be conducted, as this assumption could be refined through the Additionally, the approximate relationship between contact dynamics and clamping lengths could potentially be transferred from one tool–holder combination to others using transfer learning approaches, thereby further reducing the need for impact hammer tests.