A Review of Physics-Based, Data-Driven, and Hybrid Models for Tool Wear Monitoring

Abstract

Tool wear is an inevitable phenomenon in the machining process. By monitoring the wear state of a tool, the machining system can give early warning and make advance decisions, which effectively ensures improved machining quality and production efficiency. In the past two decades, scholars have conducted extensive research on tool wear monitoring (TWM) and obtained a series of remarkable research achievements. However, physics-based models have difficulty predicting tool wear accurately. Meanwhile, the diversity of actual machining environments further limits the application of physical models. Data-driven models can establish the deep mapping relationship between signals and tool wear, but they only fit trained data well. They still have difficulty adapting to complex machining conditions. In this paper, physics-based and data-driven TWM models are first reviewed in detail, including the factors that affect tool wear, typical data-based models, and methods for extracting and selecting features. Then, tracking research hotspots, emerging physics–data fusion models are systematically summarized.

1. Introduction

In intelligent manufacturing, critical components used in aviation, energy, high-end equipment, new energy vehicles, and other fields are often made from materials that are difficult to process. These materials have characteristics such as high hardness, high strength, and high wear resistance values, which necessitate more precise and efficient metal-cutting techniques [1,2]. In the machining process, metal cutting is accomplished through the close cooperation of a tool and a machine [3,4]. As one of the most active and variable factors, cutting tools are prone to wear or damage during the material removal process [5,6,7]. According to statistics, about 20% of unplanned downtime and economic losses can be attributed to tool failures [8,9]. The costs of tools and changing tools account for 3–12% of the total machining cost [10]. Meanwhile, the performance of the tool directly affects the quality and production efficiency of the workpiece [11]. If not replaced in time, it can easily lead to reduced processing efficiency and workpiece surface quality, as well as the compromised stability of the machine tool. Therefore, the research and application of TWM are necessary and have attracted the attention of various industrialized countries [12,13].

Figure 1 shows the number of papers published in recent years for TWM. In addition, the ‘National Strategy for Key and Emerging Technologies’ issued by the United States, the ‘New European Industrial Strategy’ proposed by the European Union, and the ‘Made in China 2025’ proposed by China indicate that the manufacturing industry is developing towards digitalization, intelligence, sustainability, and customization [14,15,16,17], which require more accurate and stable TWM techniques.

In machining processes, TWM, tool RUL, and tool wear are key elements for tool management and process optimization. Among them, tool wear is the material wear that occurs gradually due to friction, temperature, and other factors in the machining process. Tool wear can lead to the passivation or fracture of the cutting edge, which directly affects the machining performance of the tool. TWM can monitor tool wear in the machining process in real time through sensor technology and ML or DL methods, thereby identifying and quantifying the degree of tool wear. RUL refers to the expected life of a tool to work effectively in its current wear state. By analyzing the wear degree, machining conditions, and historical wear data, a prediction can be made to determine whether the tool needs to be replaced. There is a close relationship between tool wear, TWM, and RUL. Tool wear describes the process of progressive tool failure. TWM provides important support for RUL prediction in real time. RUL prediction ensures the best tool change time based on a wear trend analysis. This collaborative approach reduces the cost of tool management, improves the accuracy of machining, and ensures the reliability of the production process.

In industry, TWM plays a crucial role. By monitoring the tool status in real time, the excessive wear or breakage of the tool can be detected promptly. Operators can optimize the production process according to the outputs of the TWM system, thereby improving the overall production efficiency. Meanwhile, through effective TWM technology, operators can adjust the machining parameters to extend the tool’s life and reduce the frequency of tool replacements, which consequently minimizes material waste and lowers equipment maintenance costs. In addition, monitoring the tool status ensures stability and consistency during machining, guaranteeing the quality of the workpiece. In the context of industrial big data, with the help of IoT technology, TWM can easily produce a data linkage effect when used with other system monitoring, such as production environment monitoring, machine-tool condition monitoring, processing center equipment monitoring, and energy consumption monitoring. Through the cooperation of these monitoring methods, the entire production chain can be comprehensively controlled and optimized, thereby improving the efficiency, quality, and stability of processing. In addition, TWM can provide the necessary basis and a reference for the chatter stability, milling force modeling, and machining dynamics in machining.

This paper mainly concerns academic research and provides some guidance for industrial applications to save costs and increase economic benefits. The wear of tools is a complex issue that requires considering various factors, such as the tool wear mechanisms, wear forms, and machining conditions. Figure 2 shows research topics in TWM, drawn using VOSviewer software1.16.20.

This paper mainly reviews the progressive wear of tools. Based on the large number of retrieved studies in the literature, TWM can be divided into physics-based, data-driven, and physics–data fusion models. Figure 3 shows the modeling process and method of these models. Physics-based models usually utilize prior knowledge to explore the relationship between tool wear and physical quantities, offering excellent interpretability and stability [18]. Cutting tools have been extensively studied over the past few decades, including tool wear mechanisms [19,20], tool wear laws [21,22], and tool life models [23]. These studies are comprehensive and in enough depth; however, the study of physics-based models is still a complex subject. Firstly, tool wear is a non-stationary, nonlinear process [24], showing various wear forms at different stages. Secondly, tool wear mechanisms do not occur in isolation but often exhibit multi-mechanism coupling [25]. Finally, the wear rate of a tool varies with different workpiece materials and tool combinations. These reasons make it difficult to establish general physics-based models. At the same time, actual machining conditions are influenced by many factors, such as personalized differences between tools and workpieces, random events, and environmental interference. These factors further limit the application scenarios and prediction accuracy of physics-based models.

With the development of modern sensors and artificial intelligence (AI), data-driven models establish the depth mapping relationship between signals and wear during the machining process and are usually more accurate [26]. Data-driven TWM technology can be divided into direct and indirect methods [27]. In general, direct methods are more accurate than indirect methods, as direct methods can effectively avoid measurement errors caused by repeated installation and removal [28,29,30]. However, direct methods are easily affected by cutting fluid, lighting conditions, and chips [31], requiring the setting of corresponding working conditions to mitigate these influences. Additionally, the machine needs to be stopped to take measurements in direct methods [32], and computational resources are required for processing. In contrast, indirect methods offer better economic practicability [33]. They complete TWM by collecting sensor signals such as cutting force [34,35], AE [36,37], vibration, and so on. While data-driven models can produce more accurate results, most models establish the mapping relationship by learning signal data [38,39], which lack good interpretability and physical consistency.

Considering that both have their own drawbacks, more and more researchers are combining traditional physics-based modeling with data-driven models to take full advantage of both, which is called physics-guided ML or physics-informed ML [40,41,42]. In the context of industrial big data, the importance of fusion models is increasingly being recognized. Firstly, hybrid models can utilize the powerful fitting ability of data-driven models to dynamically predict a tool’s state, thereby enhancing model robustness. Meanwhile, the integration of physical knowledge improves their generalization, which can output accurate results even in the face of actual complex machining conditions in a workshop. Secondly, in actual machining environments, it is difficult to obtain large-scale data to complete training. A tool wear law or model can provide reliable prior knowledge, which solves this problem to a certain extent. Meanwhile, this method can effectively prevent the overfitting of data-driven models. Thirdly, hybrid models not only focus on the current state of a tool, but also realize the full lifecycle data monitoring of the tool by incorporating physical knowledge. This advantage can help operators optimize machining parameters and extend tool life, providing economic benefits to enterprises.

Common physical and data fusion methods include physics-guided loss functions, structural designs embedding physical information, and physics-guided stochastic processes. In addition, in order to provide more concise and clearly guided approaches to building fusion models, this paper summarizes coupling strategies from the perspective of model decision making, which can be roughly divided into the following: using the outputs of a physical model as the inputs of a data model; integrating the outputs of a physical model and a data model; and improving a physical model with the outputs of a data model. Although physical and data fusion models have made some progress in tool wear prediction, there are still some shortcomings in the current TWM literature, as follows:

(1) Many studies only focus on the monitoring technology of a single sensor, lacking the complementary information and synergy provided by multi-source sensors;

(2) Many studies focus on specific processing types or processing environments, lacking wide applications in different industrial scenarios;

(3) Traditional data-driven models lack physical consistency and interpretability. Although some studies have attempted to combine physical models with data-driven methods to provide a clearer explanation, there is a lack of systematic and deep fusion methods.

This paper presents a comprehensive review of TWM-related theories and methods through an extensive literature search and analysis. The main contributions of this paper are as follows.

(1) In terms of data acquisition, this paper introduces the common sensors in TWM, including installation locations, advantages, and disadvantages and then summarizes and discusses multi-source sensor technology to provide necessary guidance;

(2) This paper summarizes the machine learning and deep learning algorithms used in the data model. Aiming at the shortcomings of common algorithms, some solutions are introduced to ensure that the algorithm has better levels of adaptability and robustness to adapt to complex processing conditions and different industrial scenarios;

(3) This paper tracks research hotspots and discusses and analyzes the physical and data fusion model in depth. It includes the physical information about a tool that is easy to fuse about a tool that facilitates fusion and the method of physical and data fusion. At the same time, the coupling strategy of the output results of the two is explored from the perspective of decision making, which is helpful to realize more accurate tool condition monitoring and performance improvements in the context of industrial big data.

The structure of this review is shown in Figure 4. Section 2 summarizes the physics-based TWM models, including the tool wear mechanism, factors affecting tool wear, and residual life research based on mechanism analyses. This section details tool wear from a physical point of view. Other monitoring factors are considered in the third and fourth sections, including surface topography monitoring of tool wear by direct methods, sensor signals during machining by indirect methods, and the joint monitoring of algorithms and tool wear. Specifically, Section 3 describes the steps of data-driven TWM, including signal acquisition and preprocessing, feature extraction and selection methods, and making decision systems. Section 4 outlines the physical information that can be easily coupled with the data-driven model, explores the coupling method in depth, and discusses the fusion strategies of the fusion model from the perspective of decision making. Section 5 analyzes the challenges faced by TWM and looks forward to future research directions. Finally, Section 6 concludes the paper.

2. Physics-Based TWM

By taking indicators that characterize the tool state as input, the physics-based model constructs an empirical model that incorporates actual machining or workpiece parameters [43]. It should be noted that the model must conform to the actual tool wear curve. Under single and stable working conditions, the physics-based model can explain the wear variables with a clear causal analysis mechanism and produce good results.

2.1. Tool Wear Mechanism

During metal machining, tool failure can occur in three different ways: an overall fracture, plastic deformation, and gradual wear. The first two are failure uncommon failures; TWM usually focuses on the third failure form [44]. Tool wear is a complex dynamic process of thermo-mechanical coupling [45], generated by the contact and relative sliding between the tool, workpiece, and chips [46]. Common tool wear forms include abrasive wear caused by hard particles scraping the surface of the tool [47], adhesive wear caused by material adhesion and tearing on the contact interface [48], chemical wear caused by the chemical reaction between a tool and workpiece material at a high temperature [49], oxidation wear caused by the oxidation of the tool surface at a high temperature [50], diffusion wear caused by the diffusion of elements in the tool material under a high temperature and chemical action [51], and so on [52,53].

At a low cutting speed, adhesive wear and abrasive wear are dominant. However, at high cutting speeds, the proportion of diffusion wear, chemical wear, and oxidation wear increases [54,55,56]. With the influence of these factors over a long time, the wear forms of tools mainly include flank wear, chipping, notch wear, flaking, and so on, as demonstrated in Figure 5.

In 1980, Suh [58] conducted a more prospective exploration of the wear mechanism and a brief evaluation of tool materials in terms of wear resistance, toughness, plastic deformation resistance, and the wear rate control mechanism. In addition to this, Oyane et al. [59], Soderberg and Hogmark [60], Sakuma and Seto [61], and Venkatesh et al. [62] also explored the tool wear mechanism. These studies provide a solid foundation for more complex tool wear mechanisms. At the same time, benefiting from the research on tool wear mechanisms, a series of better tool materials have been designed to delay tool wear. With the further study of tool wear mechanisms, researchers found that there are many wear mechanisms in metal cutting. In 2011, through experiments on machining Inconel718, Hao et al. [63] concluded that lamellar wear debris that had formed on and fallen off the tool surface was the main cause of tool wear in a low-speed cutting process. However, at a high cutting speed, tool wear is facilitated by element diffusion and oxidation reactions between the tool and workpiece. In 2022, through the study of turning nickel-based alloy GH4169, Liang et al. [64] found that serious abrasive wear, oxidation wear, and diffusion wear occurred in the whole wear stage of the tool. The degree of the oxidation reaction on the flank wear was particularly obvious, and the oxidation reaction on the rake face was relatively severe. With the development of modern sensors, researchers have used microscopy techniques to understand the microscopic manifestations of different wear mechanisms. In 2019, during the machining of Ti-6Al-4V alloy using a Ti (C₇N₃)-based ceramic micro-milling tool, Wang et al. [65] found that the main cutting edge was adhesive wear and microchipping at a feed rate of 1 μm/flute, which was high. In 2021, Lindvall et al. [66] determined that the main wear mechanism was temperature-driven diffusion wear through the experiment of the high-speed finish of an α + β titanium alloy Ti6Al4V with uncoated cemented carbide in a high-pressure directional coolant. Meanwhile, the adhesive wear occurred because of the interaction between the workpiece and tool material. The wear forms included a combination of flank wear and rake cratering.

Despite the various forms of tool wear, flank wear is the most common type. Meanwhile, the value of flank wear is easy to measure. Therefore, the value of flank wear is mainly used as an indicator to measure the tool wear degree [67]. According to the cutting laws derived from numerous cutting experiments and production practices, the relationship between typical tool wear and time is shown in Figure 6. The curve indicates that tool wear can be divided into three stages: initial wear, steady wear, and accelerated wear. In the third stage, the cutting force significantly increases and the cutting temperature rises rapidly, leading to an increased wear rate and easier tool failure. Thus, this stage needs to be accurately identified in TWM. The tool wear mechanism is very complex. However, it can provide a deeper understanding of the wear process, which is important for physics-based models. Therefore, the tool wear mechanism and different coupling forms still deserve further study, especially for new emerging difficult materials and tools.

2.2. Factors Affecting Tool Wear

Tool wear is a complex, nonlinear, and dynamic process. This is because it is not only related to the mechanism of the tool, but also related to the actual machining conditions. For example, increasing the cutting speed can shorten the machining time. However, excessively high speeds will increase the cutting temperature, thereby accelerating tool wear and reducing tool life. Similarly, increasing the feed rate can enhance the machining efficiency and material removal rate, but can also increase tool wear, especially in cutting hard workpieces.

Table 1. Impact of machining parameters and workpiece characteristics on tool wear types.

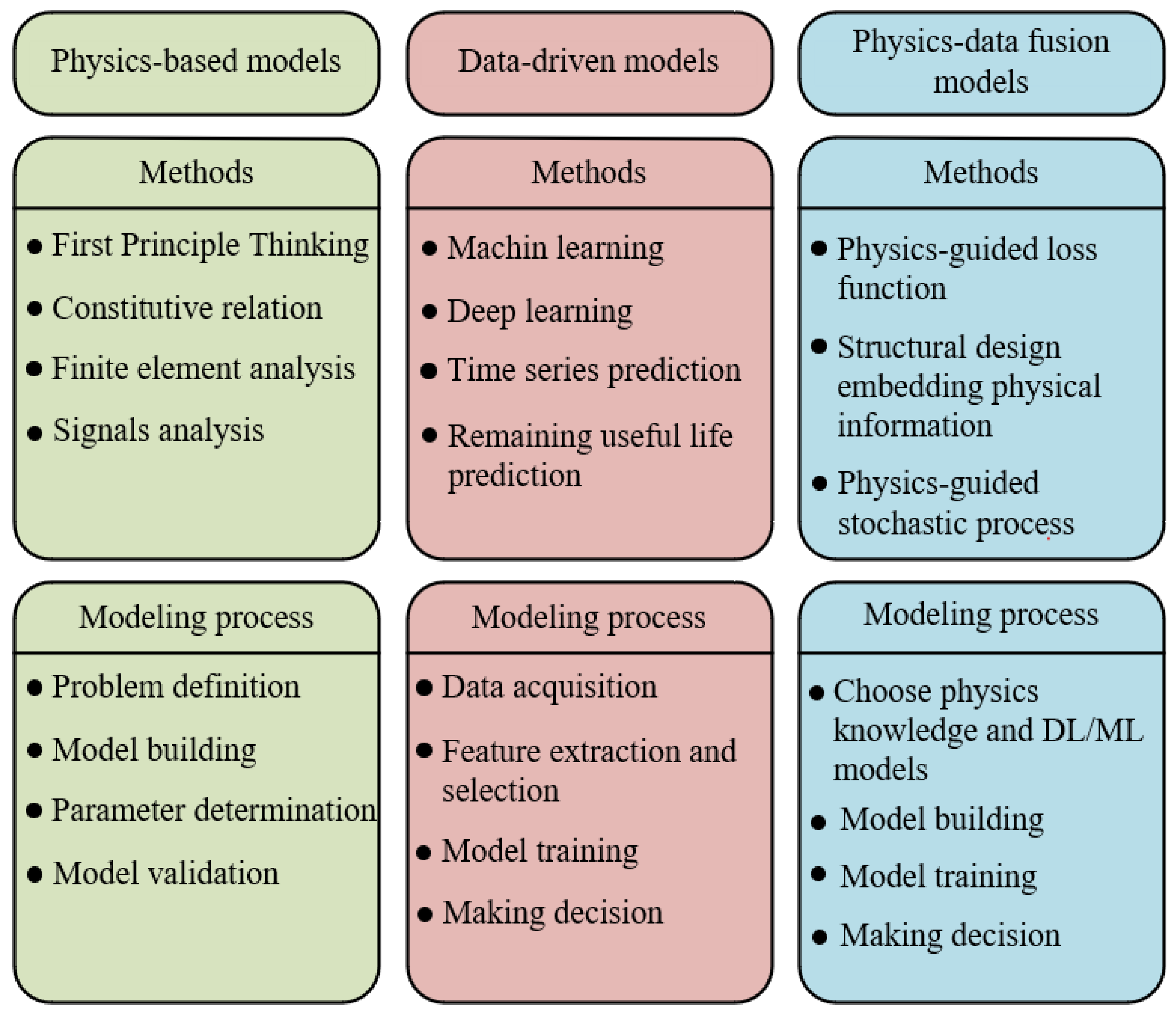
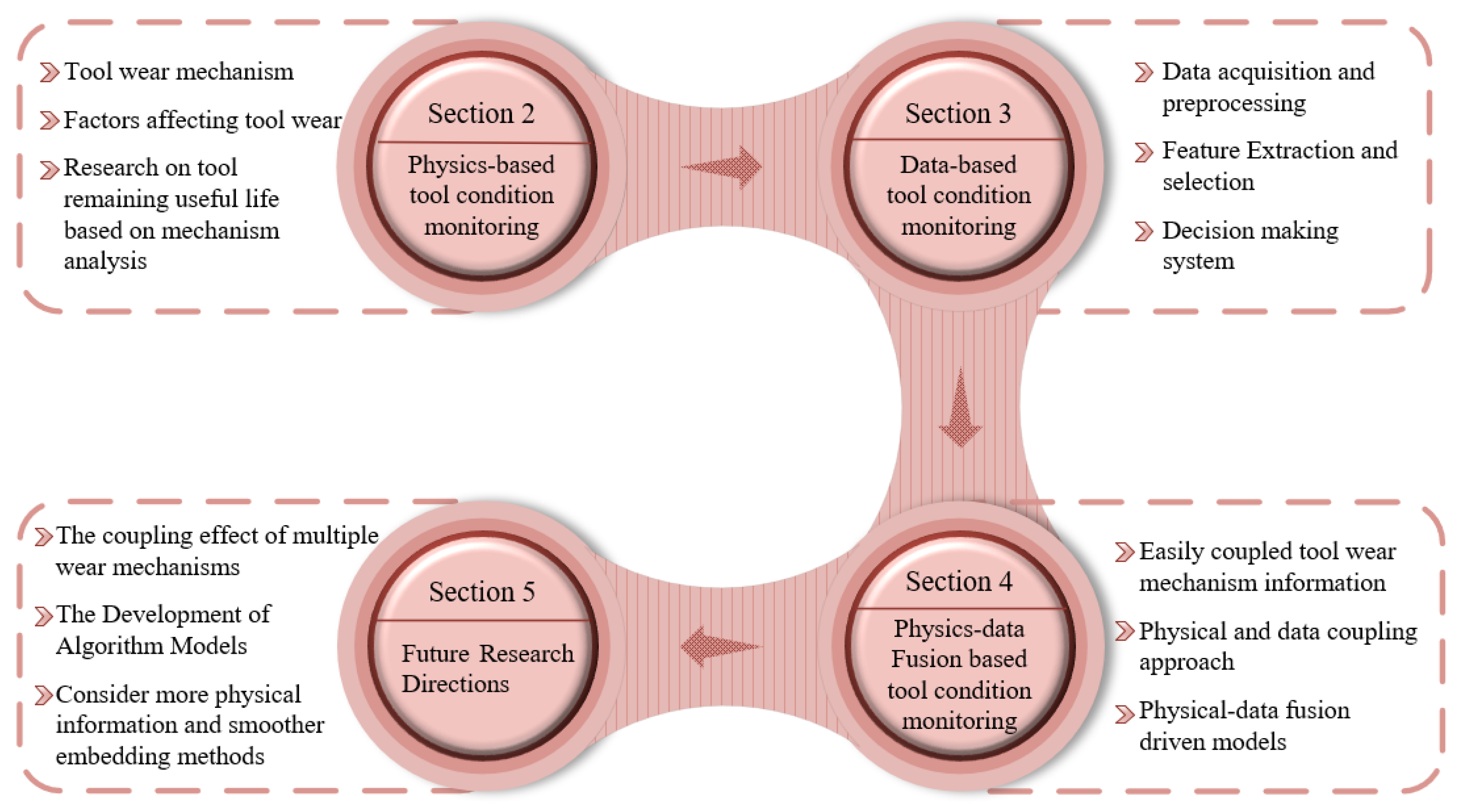
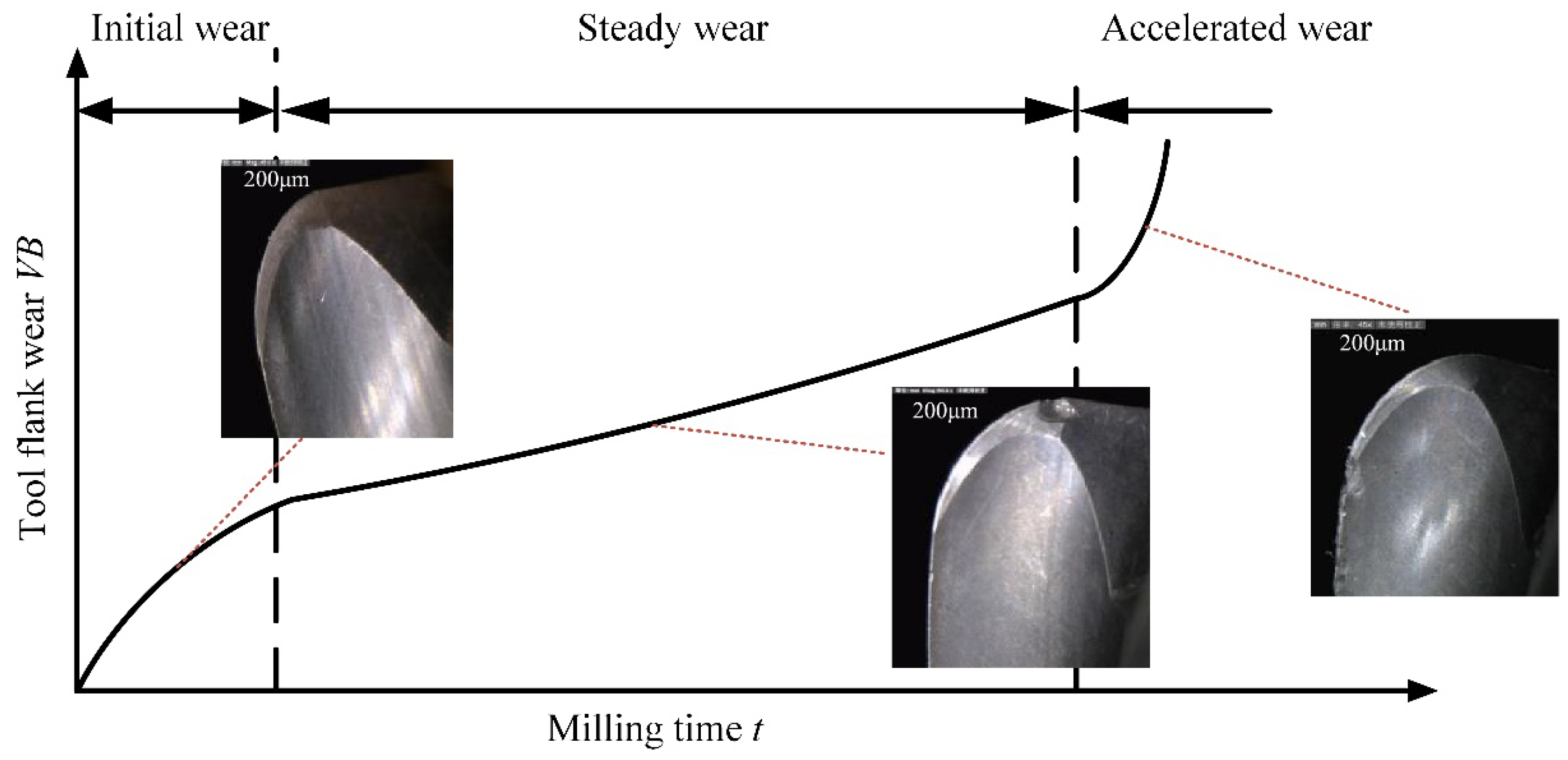
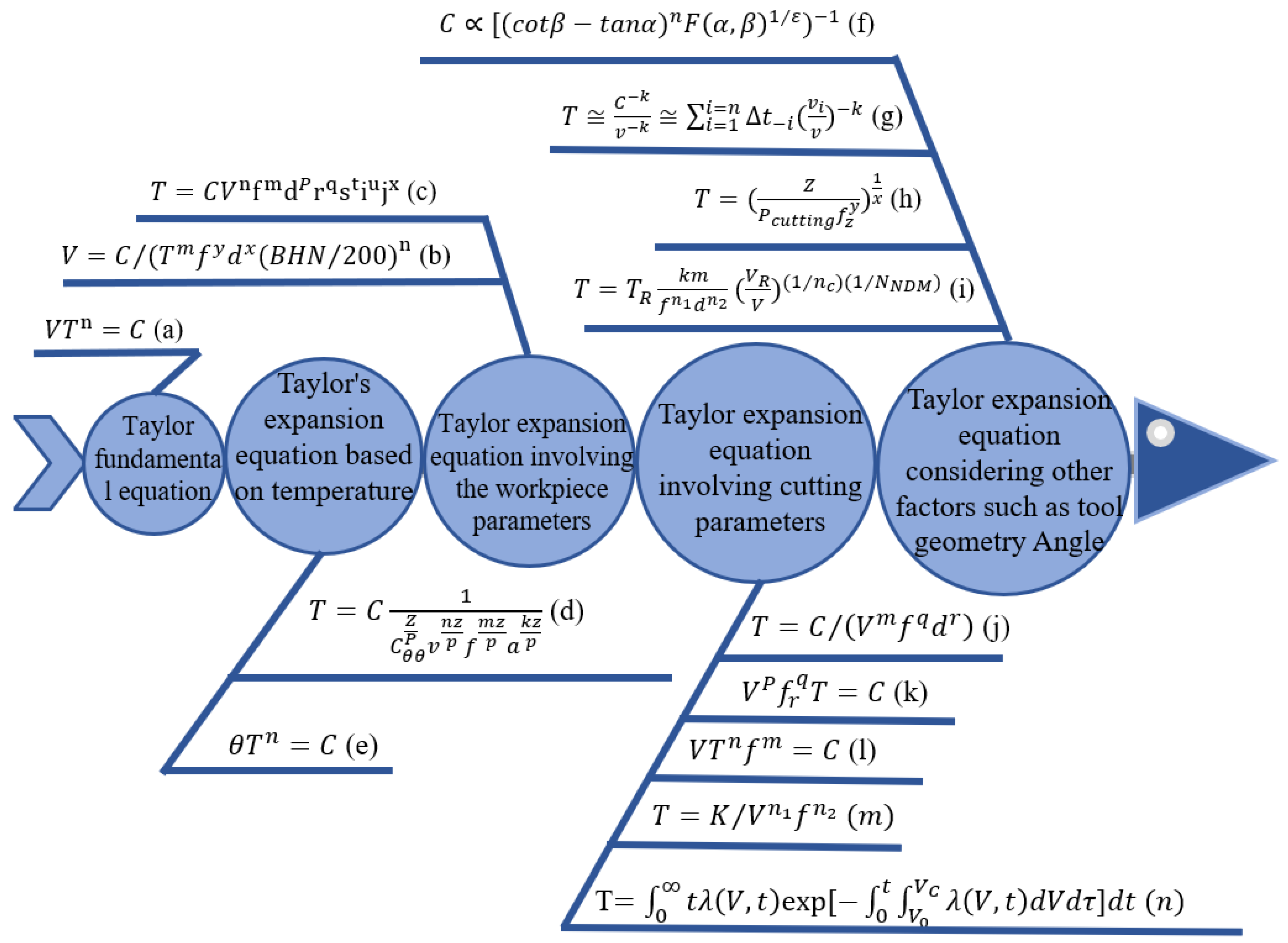
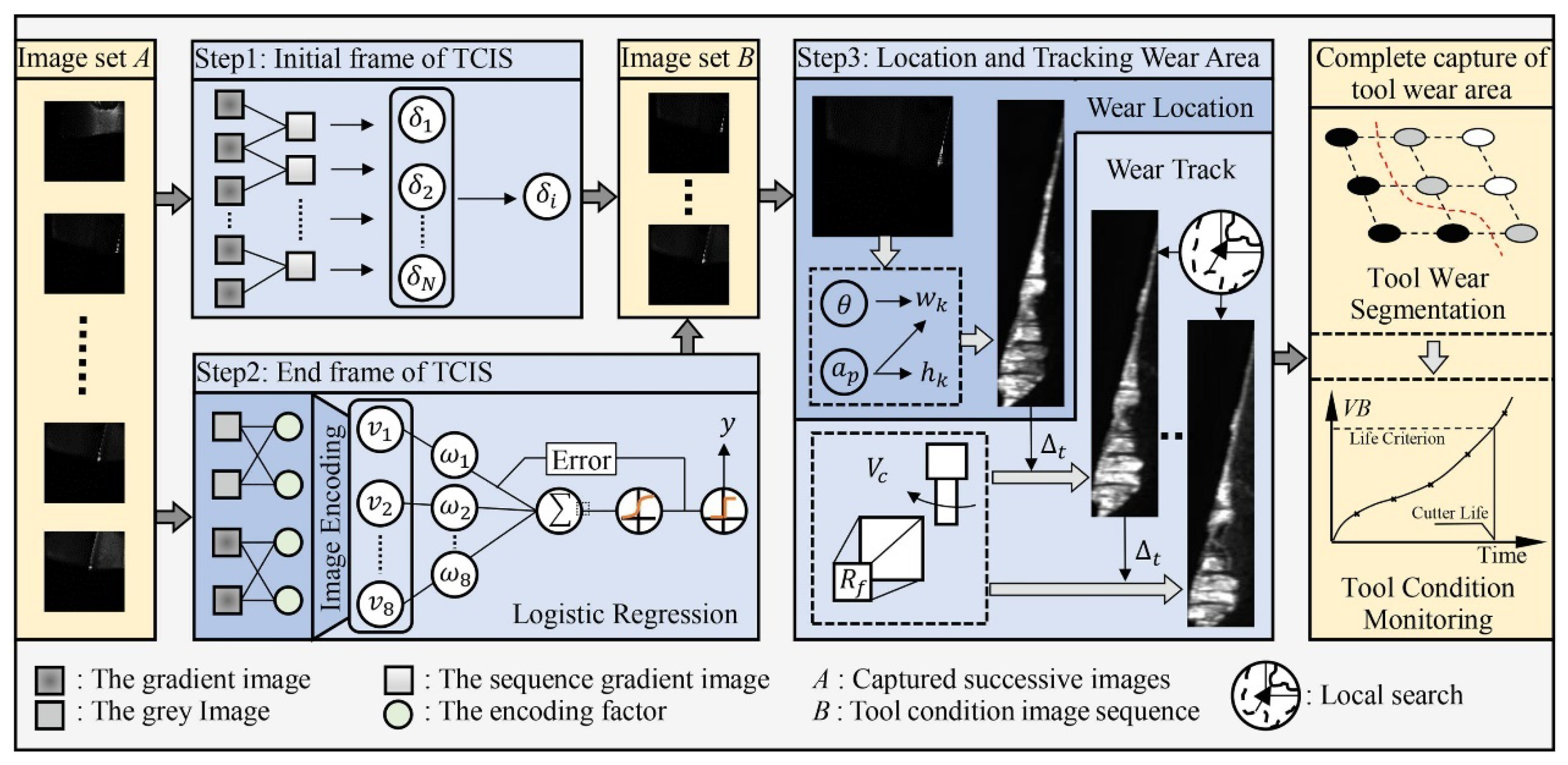
Influence Factor	Parameters	Effect on Tool Wear	Tool Wear Types
			Mechanical Wear	Thermal Wear
Machining parameter	Cutting speed	Higher speed increases cutting force and heat	Increase	Increase
	Feed rate	Higher rate increases tool load, causing wear	Increase	NA
	Cutting depth	Deeper cuts increase contact area and load	Increase	Increase
	Spindle speed	Higher spindle speed generates more heat	Increase	Increase
Workpiece material	Hardness	Harder materials cause abrasive wear	Increase	NA
	Toughness	Tougher materials resist cutting, causing wear	Increase	NA
	Thermal conductivity	Low conductivity retains heat at tool interface	NA	Increase
	Wear resistance	High-resistance materials reduce wear rate	Decrease	Decrease

shows the common factors affecting tool wear, which can be mainly divided into machining parameters and workpiece materials. In addition, there are other factors that influence the rate of tool wear, such as the coolant, as well as cooling and cutting methods. Factors affecting tool wear have been researched in depth, including single-factor analyses and multi-factor interactions. This section discusses the major factors of TWM.

2.2.1. Machining Parameters

In the process of metal cutting, adopting different machining parameters will have varying impacts on tool wear. The factors that significantly influence tool wear include the cutting speed, depth of cuts, and feed rate. Earlier studies found that a higher cutting speed leads to faster tool wear, which is the earliest verified effect of machining parameters on tool life. In an experiment machining high-strength steel with three types of alumina-based ceramic tools, Li and Low [69] discussed the influence of cutting parameters on cutting performance by combining different cutting speeds, feed rates, and cutting depths in 1994. In addition, Tipnis and Joseph [70] also conducted a similar study, which provides some guidance for slowing tool wear during machining. Furthermore, these studies influenced subsequent research. As experimental equipment improved, researchers began to examine other machining parameters, such as the feed rate and depth of cuts, and found that these parameters also significantly affected tool wear rates. For example, the higher the feed rate, the more severe the tool wear, especially in the processing of hard materials. In 2021, to study the characteristics of flank wear, Kuntoglu and Saglam [71] designed an experiment based on Taguchi’s L₂₇ orthogonal array during the turning of AISI 5140 steel. Figure 7a shows VB in different cutting conditions. In another study by the authors [72], VB developments can be seen in more diverse cutting conditions (see Figure 7b).

Figure 6 is a typical example. With more in-depth research, researchers have gradually realized the interrelation of processing parameters. At the same time, with the help of advanced measurement techniques, researchers have explored the impact of multivariate parameter combinations on wear. Given a determined cutting speed, VB is typically proportional to the depth of cuts. This is because a larger chip interface exacerbates chip removal. Meanwhile, the results in Figure 6 indicate that an excessive increase in the maximum depth of cuts or cutting speed significantly increases VB. In tool wear experiments machining titanium superalloy Ti-5553 via cryogenic machining with liquid nitrogen, Liu et al. [73] analyzed the tool mechanism using different cutting parameters. The results show that a built-up layer and a built-up edge always exist when the cutting speed is 90 m/min and the cutting depth is 0.5 mm. However, cater wear can be observed throughout the experiment for feed rate values when the cut a_p = 1.0 mm and 1.5 mm. Meanwhile, notch wear and chip flow occur when the cutting speed is 60 m/min and the cutting depth is one mm, but these two wear forms never appear under other cutting conditions. Similarly, Li et al. [74] investigated the wear behavior in the turning of AISI 321 austenitic stainless steel using a coated carbide tool. Experimental results showed that the feed rate has the greatest influence on tool wear. Meanwhile, they concluded that the material removal amount can be used as the primary evaluation parameter to select the appropriate cutting parameters in the turning process of stainless steel.

Adjusting machining parameters is an important method to delay tool wear. In in-depth studies of the relationship between machining parameters and tool wear, some researchers have also proposed models or methods based on this relationship [75,76,77]. Furthermore, these models are often used to select the best combination of machining parameters.

2.2.2. Tool Coatings

Techniques such as chemical vapor deposition (CVD), physical vapor deposition (PVD), electroplating, and thermal spraying to apply coatings on the surface of cutting tools are other common methods to reduce tool wear. Different coating methods have different mechanisms to delay tool wear. In a vacuum environment, the PVD coating method adheres the coating material to a tool’s surface by vaporization or arc evaporation. The PVD coating method can be carried out at relatively low temperatures, allowing high-hardness coatings to be deposited without damaging the properties of the substrate [78,79]. This coating method has the advantages of a high hardness value and a low coefficient of friction and is suitable for precision machining and high-speed applications. The CVD coating method relies on high-temperature chemical reactions to form dense compound coatings [80,81], such as TiC, TiN, and AI₂O₃. In order to enhance the wear resistance and oxidation resistance of the tool, the thermal spraying method forms a coating by heating metals, ceramics, or other materials and spraying them to the surface of the tool [82], which is usually suitable for large or high-load machining environments. The principle of ion implantation is to implant nitrogen or carbon plasma into the surface of the tool to enhance the material properties [83,84]. This method can increase the surface hardness and wear resistance values but only leads to a limited improvement in performance under high temperatures, making it suitable for applications with low-temperature or high-dimensional accuracy requirements. The electroplating coating method uses an electrochemical reaction to deposit metal on the tool surface to form a coating [85], which has the characteristics of a uniform thickness and strong adhesion. It is worth noting that this method mainly enhances the corrosion resistance and adhesion resistance of the tool, and the hardness is usually less than that of PVD or PCD.

To summarize, the PVD and ion implantation methods are designed to delay wear by increasing hardness and reducing friction. CVD relies on its high-temperature oxidation-resistant layer to provide resistance to thermal wear. Thermal spraying reduces wear by creating a physical protective layer. Electroplated coatings reduce wear by inhibiting the material adhesion.

It is worth noting that the effectiveness and impact of each coating method on reducing tool wear depend on properties such as the coating thickness, hardness, heat resistance, and adhesion [86]. However, in general, the PVD and PCD coating methods are generally more effective in delaying wear, and the coating methods of thermal spraying and ion implantation are in the middle. In comparison, the electroplating method has less of an effect on delaying tool wear, mainly because it focuses on corrosion resistance and anti-adhesion properties but lacks hardness and heat resistance compared to PVD and CVD.

Research on the influence of tool coating on wear has evolved from the exploration of basic coating materials to in-depth applications of multi-layer composite coatings. In the 1990s, researchers first tried to add hard coatings to the surface of tools, with the purpose of improving their wear resistance [87]. In the 1990s, many researchers conducted in-depth research on composite coating technology. As an example, Leyendecker et al. [88] used crystalline diamond composite coatings to replace conventional PCD technology. They also conducted a life test. The results show that the diamond composite coating tool performs well. In addition, Foxrabinovich [89] explored the relationship between complex tool coatings and the main wear mechanisms. At the same time, they concluded that the optimization of the coating structure can be achieved by changing the process parameters. Sokovic [90], Lee et al. [91], and Prengel et al. [92] for further investigations. From the perspective of processing technology, the service life of a tool is greatly improved, and it provides a certain basis for future research on tool coating. In 2020, Hao et al. [93] compared the cutting edge optical images of an H DLC-coated tool and an uncoated tool under the same machining conditions (see Figure 8). Meanwhile, through the machining process of Al-Si alloys, they conclude that the Cr/W-DLC/DLC composite-coated tool’s life is the longest, and the uncoated tool’s life is the shortest. This study demonstrates the advantages of DLC-coated tools over uncoated tools. On this basis, Khan et al. [94], Cakir et al. [95], Valleti et al. [96], and McMaster et al. [97] expanded DLC-coated tools further, including their wear mechanism, wear behavior, and influencing factors. These studies have played a role in promoting the application of DLC coatings. Since the 21st century, the research on tool coating has focused on the microstructure optimization of nano-coatings and coating materials. Researchers have further improved the wear resistance of tool coatings under high-temperature conditions through nano-level coating design and multi-layer composite technology. Some researchers have studied other coated tools to achieve better results. In 2020, Chenrayan et al. [98] coated carbon nanotubes (CNTs) on high-speed steel tools using the plasma-enhanced chemical vapor deposition method. Additionally, the authors compared the machining performance of DLC, CNT, and TiAlN. The results showed that the tool life with CNT coating increased by 96.3% and 26.8% compared to that of the TiAlN and DLC-coated tools, respectively. In 2023, Li et al. [99] demonstrated the advantage of a TiAlN-coated tool compared with an uncoated edge-strengthened tool and diamond-coated tools.

2.2.3. Cooling and Lubrication Methods

Cooling is an essential part of metal cutting, as it can effectively reduce the heat generated by the contact friction between the tool and the workpiece. Different cooling and lubrication methods can produce varying effects in machining environments.

The influence of cooling and lubrication methods on tool wear has been researched in depth from basic coolant applications to applications with trace lubrication and without a coolant. At the beginning of the 20th century, traditional water-based coolants were used to cool tool surfaces with the aim of reducing machining temperatures and preventing tool softening and wear. This method prolongs the tool life to a certain extent and is the earliest cooling method used to control tool wear. In the 21st century, with the progress of machining technology, MQL has gradually shown a better lubrication effect. In 2023, Rakesh and Chakradhar [100] investigated the impact of multiple sustainable machining techniques on tool wear in an experiment machining an Inconel 625 superalloy (see Figure 9). Meanwhile, an experiment on turning performance characteristics proved that low-temperature cutting had the largest reduction in tool face wear compared with dry cutting, MQL, and nMQL. In order to enhance the tribological performance of lead-free brass in high-speed microturning, Das et al. [101] adopted cutting oil MQL, LN2, and hybrid low-temperature cooling technology to carry out processing experiments. They concluded that the hybrid low-temperature cooling strategy was significantly better in terms of steady-state performance, surface quality, burr formation, and tool wear. They concluded that the hybrid low temperature technology performs better than the other two in improving steady-state performance and surface quality, suppressing burr formation and tool wear. In recent years, liquid nitrogen cooling technology has provided a better way to delay tool wear. In 2020, by analyzing the relationship between the liquid nitrogen flow rate, cutting force, and surface roughness, Meng et al. [102] utilized SEM image analysis technique to obtain microscopic images of tool wear under different cooling techniques. Meanwhile, they found that low-temperature liquid nitrogen cooling produces better results compared with cutting fluid cooling, increasing tool life by 25%. Junankar et al. [103] and Jerold and Kumar [104] obtained similar results, which show that cryogenic liquid nitrogen cooling-assisted cutting can effectively reduce the cutting temperature and tool wear compared with conventional methods.

2.2.4. Workpiece Materials

Different workpiece materials have different effects on tool wear forms, especially when tools with varying materials and coatings are used. Lin et al. [105] pointed out that variations in the relevant dimensions, the surface topography, and the element content of the tool can be used to express the degree of tool wear. Furthermore, Marousi et al. [106] stated that wear can be evaluated using SEM, EDS, and XEDS. For example, in order to investigate the performance of cemented carbide as a tool material, Lindvall et al. [66] used SEM, transmission electron microscopy, XEDS, and selected area electron diffraction to explore basic tool wear mechanisms. They concluded that diffusive wear is the dominant wear mechanism driven by temperature. Brinksmeier and Gläbe [107] conducted experiments on cutting ferrous materials using alumina ceramic tools, coated carbide tools, ion-modified diamond tools, and single-crystal diamond tools. The results show that the degree of wear of different tools is not the same. An alumina ceramic tool showed the highest degree of wear. At the same time, they also concluded that TiC and TiN coatings of diamond tools have the potential to eliminate chemical wear, but there is abrasive wear. Liu et al. [108] used two different cemented carbide tools for the turning of iron-based superalloy GH2132. The observation results of SEM and EDS show that the main wear mechanisms of the cemented carbide tool are adhesive wear and abrasive wear. The main wear mechanisms of the coated cemented carbide tool are adhesive wear and oxidation wear. Based on the above, even if the workpiece material is the same, different tool coatings will produce different wear mechanisms.

Tool wear can also be evaluated by the element content. For example, Wang et al. [109] concluded that the oxygen content at the back end of the tool is high, which indicates that oxidative wear occurs during ultra-high speed micro-drilling multi-layered PCB using a Ti(C₇N₃)-based cermet micro-drill. Wang et al. [110] used the same analytical method to evaluate tool wear when milling CFRP/steel. The results show that the oxygen atom content is 5.51% and oxidation wear also occurs.

In addition, some researchers use the variation in tool diameter to indicate the degree of tool wear. Saha et al. [111] established the relationship between the variation in tool edge features and the corresponding outer diameter and derived wear expressions for different wear scenarios. The experiment results of the sustainable MQL-assisted micro-milling of Ti–6Al–4V using TiAlN-coated WC/6Co micro-mills show that this method can effectively characterize the tool wear degree. Wang et al. [112] adopt a similar method to characterize the degree of tool wear when drilling CFRP. Experimental results show that the method is effective.

2.2.5. Others

In addition, the material of the cutting tool, the geometric angle of the cutting tool, changes in gas pressure, and machining methods can also affect tool wear. For the material of the cutting tool, in 2003, Vander et al. [113] concluded that the wear rate of soft tool materials can vary by two orders of magnitude depending on the type of zinc layer used. The relative performance of tool materials is closely related to the hardness of the workpiece. Some researchers have explored the relationship between the geometric angle of the cutting tool and wear. In 2022, Zhang et al. [114] designed drilling experiments on Cf/SiC ceramic matrix composites with different machining parameters. The results show that PCD tool wear is minimal when the point angle is 140° and the clearance angle is 20° (see Figure 10). Moreover, using low-speed and low-feed parameters can effectively reduce tool wear. In 2023, Amigo et al. [115] determined that reducing the angle of the side edge of the tool avoided grooving wear, which improved the tool life in turning experiments.

For changes in gas pressure, as early as 1978, Thornton and Wilks [116] studied the relationship between different pressure conditions and tool wear. At a cutting speed of 11 m/s, reducing the pressure from 760 torr to 0.1 torr decreased the wear rate by 50%. However, during turning at a speed of 0.16 m/s, reducing the pressure from 760 torr to 0.1 torr actually increased the level of wear. Liu et al. [117] investigated the wear mechanisms of (Ti, Al, and Zr) N-coated Si₃N₄ tools under different pressure conditions. Experimental results indicated that the primary wear mechanism for these tools was adhesive wear. The hardness and adhesion strength of the coating increased with rising pressure, reaching a peak at 2.5 Pa, and then decreased as the pressure continued to increase.

In addition, tool wear can also be delayed through different machining techniques. For example, Guan et al. [118] conducted experiments on the TC27 alloy using two types of tools for both electro-pulse-assisted turning (EPT) and conventional turning. The results showed that EPT improved the cutting performance of TC27 and enhanced the surface finish of the workpiece. This cutting method also reduced friction in the sticking and sliding zones, thus slowing down tool wear. Moreover, it effectively prevented the formation of a built-up edge (BUE) on the tool’s rake face. Zhao et al. [119] used both conventional dry turning and electro plastic-assisted dry turning on a tungsten alloy. Experimental results indicated that the electro plastic-assisted dry turning effectively reduced tool wear, though BUE formation was still observed at the tool tip. Li et al. [120] combined micro-textured tools with Fe₃O₄ nanofluid coolant for turning 316 stainless steel under an electromagnetic field. The results showed that this machining method rapidly dissipated the high amount of heat generated between the tool, chips, and workpiece, thereby reducing tool wear under the combined effects of Lorentz force, electroosmotic force, and pressure.

As a complex coupled phenomenon caused by many factors, tool wear still requires further exploration. Therefore, it is necessary to establish an empirical model that can accurately predict tool wear.

Based on the above, machining parameters are the primary factors affecting tool wear. Firstly, machining parameters directly influence the interaction mode between tools and workpieces. For example, higher cutting speeds lead to increased heat, which increases plastic deformation and thermal wear. The cutting depth and feed rate affect the load on the tool, thereby affecting tool wear. Secondly, tool coatings can improve the surface performance of the tool, but the effect of delaying tool wear still depends on the setting of the machining parameters. For example, a sudden increase in temperature may cause some coatings to fail quickly. By selecting appropriate processing parameters, tool coatings can be more effective. In addition, machining parameters also affect the effectiveness of cooling and lubrication methods. A high cutting speed may cause the coolant to penetrate into the cutting zone quickly, reducing its cooling effect. And a change in feed rate and cutting depth will also affect the flow and distribution of cooling and lubrication. Therefore, even if the cooling and lubrication methods are appropriate, the effect still depends on the reasonable selection of the machining parameters.

For industrial factories, it is important to implement reasonable strategies to delay tool wear and prolong tool life. Firstly, based on the material of the workpiece and tool, the appropriate machining parameters are selected to achieve a balance between the machining efficiency and tool life. Secondly, the use of high-performance tool materials and coatings can also further delay tool wear. In addition, TWM and a feedback control system should be established to ensure that the tool works under the best conditions, thereby reducing unnecessary wear. In addition, this strategy enables not only the real-time monitoring of the tool’s condition but also obtains the full life cycle data of the tool, which can help the factories make better plans to delay tool wear.

2.3. Research on Tool RUL Based on Physics Analysis

Tool wear is a complex multi-factor coupling process. According to the tool degradation mechanism during machining, a general tool wear model can be established by combining simplified relationships with machining parameters. Some researchers have conducted a lot of studies. Although each physics-based model considers different factors, they demonstrate good practicability within specific ranges.

Classical Tool Life Models

The most common tool wear model is the Taylor formula. It has become a common method for evaluating tool life since Taylor proposed it in 1906 [121]. Literature searches reveal that there are many variants based on the Taylor formula. These can be broadly classified into two types: generalizations of the Taylor formula itself and the Taylor formula for specific conditions. Figure 11 illustrates the generalization form of the Taylor formula considering different influencing factors. It can be seen that with further studies on tool life, the factors considered in the Taylor formula are becoming increasingly practical.

On the other hand, the Taylor expansion formula for specific machining conditions is shown in

Table 2. Taylor expansion formula for specific machining conditions.

Tool Material	Workpiece	Types of Machining Operation	Equation	Reference
High-speed steel	NERCs	Milling	$\mathrm{T}={10}^{3.171}{\mathrm{V}}^{-1.060}{\mathrm{f}}^{-0.685}{\mathrm{SC}}^{-0.695}{\mathrm{AR}}^{0.066}{\mathrm{R}}^2=0.948$	[135]
Uncoated tungsten carbide	Brass	Drilling	$\mathrm{T}={\displaystyle \frac{282.8264}{{\mathrm{S}}^{0.1007}{\mathrm{f}}^{0.7234}}}$	[136]
Carbide micro-mill	UNS S32205 duplex Stainless steel	Cutting	$\mathrm{v}·{\mathrm{T}}^{0.26}=$ 23.31	[137]
Special cemented carbide of WTVC8	HT250 gray cast iron	Cutting	$\mathrm{T}={\displaystyle \frac{1670.1236}{{\mathrm{v}}^{1.1531}{\mathrm{f}}^{0.456}{\mathrm{d}}^{0.5589}}}$	[138]
Carbide inserts	Tools steels	Milling	$\mathrm{V}\cdot {\mathrm{T}}^{0.35}=413$	[139]
Carbide tool	MS309 steel	Turning	${\mathrm{V}}^{3.39}{\mathrm{f}}_{\mathrm{r}}^{2.63}\mathrm{T}=9.83\times {10}^7$	[140]
Alloyed carbide tool	Titanium alloy Ti–6242S	Milling	${\mathrm{Tv}}^{3.3}\times {\mathrm{f}}_{\mathrm{z}}^{2.97}\times {\mathrm{a}}_{\mathfrak{a}}^{2.80}=1.56\times {10}^6$	[141]
Polycrystalline cubic boron nitrides (PCBNs)	100Cr6 steel	Turning	${\mathrm{VT}}^{0.285}{\mathrm{d}}^{0.112}{\mathrm{f}}^{0.335}{\left({\displaystyle \frac{\mathrm{H}}{{\mathrm{H}}_0}}\right)}^{1.07}=172$	[142]
Coated carbide	Cast iron	Turning	$\mathrm{Vc}·{\mathrm{T}}_1^{0.81}=5011.87$	[143]

. According to the table, its specific index term will also change when different tools, workpiece materials, and machining methods are used.

Research on physics-based TWM models is extensive. In addition to the Taylor formula, some researchers have modeled tool wear from other perspectives. In 1953, Archard [144] established an empirical formula including the wear rate and load and analyzed the causes of wear. In 2008, Lee et al. [145] proposed a comprehensive tool life model considering the influence of changes in workpieces’ mechanical properties. In 2003, Choudhury et al. [146] proposed a method to estimate tool wear by utilizing the relationship between flank wear and the average tangential cutting force coefficient. Additionally, they established a model that combined experimental data to explore the relationship between tool wear and cutting parameters. In 2004, Shao et al. [147] established a cutting power model for tool wear under variable cutting conditions. Meanwhile, they proposed a tool wear threshold update monitoring strategy whose effectiveness was proven with different cutting experiments. These studies build tool life models from different sides. They not only lay the foundation for the optimization of the machining process, but also provide a reference basis for follow-up tool life research. With sensor data, these lifetime models can be extended to adapt to more complex machining scenarios.

Table 3. The advantages and disadvantages of classical tool life models.

Classical Tool Life Models	Factors	Advantages	Disadvantages
${\mathrm{vT}}^{\mathrm{n}}=\mathrm{C}$	$\mathrm{v}$; $\mathrm{T}$; $\mathrm{n}$; $\mathrm{C}$	Simple and practical. Convenient for experimental verification. Speedy.	Lack of accuracy. Limited application scope. Lack of multi-factor consideration.
${\mathrm{v}}^{\mathrm{n}}{\mathrm{T}}^{\mathrm{m}}{\mathrm{f}}^{\mathrm{p}}{\mathrm{d}}^{\mathrm{q}}=\mathrm{C}$	$\mathrm{v}$; $\mathrm{T}$; $\mathrm{m}$; $\mathrm{f}$; $\mathrm{p}$; $\mathrm{d}$; $\mathrm{q}$; $\mathrm{C}$;	Multi-parameter consideration. More adaptable.	High complexity. High cost of experimentation.
$\mathrm{W}=\mathrm{k}{\displaystyle \frac{\mathrm{FL}}{\mathrm{H}}}$	$\mathrm{W}$; $\mathrm{k}$; $\mathrm{F}$; $\mathrm{L}$; $\mathrm{H}$	Good theoretical support. Wide range of applications. Simple in form.	Ignores environmental factors. Material variation is not considered. Not applicable to all wear mechanisms.
$\mathrm{T}={\displaystyle \frac{\mathrm{C}}{{\mathrm{V}}^{\mathrm{n}}\cdot \left({\mathrm{f}}^{\mathrm{p}}\right)\cdot \left({\mathrm{d}}^{\mathrm{q}}\right)\cdot {(\mathrm{M})}^{\mathrm{r}}}}$	$\mathrm{T}$; $\mathrm{C}$; $\mathrm{v}$; $\mathrm{n}$; $\mathrm{f}$; $\mathrm{p}$; $\mathrm{d}$; $\mathrm{q}$; $\mathrm{M}$; $\mathrm{r}$	Multi-parameter consideration. Considers material properties. High flexibility.	High computational complexity. Ignores other important factors. Nonlinear factors are not considered.
$\mathrm{VB}=\mathrm{C}\cdot {\mathrm{V}}^{\mathrm{n}}\cdot {\mathrm{f}}^{\mathrm{p}}\cdot {\mathrm{d}}^{\mathrm{q}}\cdot {\mathrm{F}}^{\mathrm{r}}$	$\mathrm{VB}$; $\mathrm{C}$; $\mathrm{v}$; $\mathrm{n}$; $\mathrm{f}$; $\mathrm{p}$; $\mathrm{d}$; $\mathrm{q}$; $\mathrm{F}$; $\mathrm{r}$	Introduces the cutting force factor. Clear physical meaning. Strong adaptability for complex working environments.	Limitations of exponential assumption. Lack of dynamic considerations. Empirical parameters lack generalizability.

compares the advantages and disadvantages of the classical tool life equations. As shown, as more factors are considered, the model becomes more accurate, but it introduces many problems, such as complex calculations, difficult parameters to determine, and a lack of generalization. It is still difficult to establish a general tool life model by experimental methods.

Although physics-based tool wear models can achieve good results under specific machining conditions, it is still difficult to achieve accurate predictions of tool wear. This is because the existing models only consider a few dominant factors and do not establish the coupling relationship between multiple variables. Additionally, most physics-based models are based on stationary assumptions, only applicable to constant operating conditions. However, actual machining conditions consider not only the diversity of tools, workpieces, and cutting parameters, but also the dynamic changes in physical parameters. The above limitations restrict the further application of physical models.

3. Data-Driven TWM

In the context of industrial big data, the development of AI provides a new pathway for TWM technology. Data-driven TWM is the process of obtaining machining data from a large number of milling, turning, and other machining processes and using these data to establish a deep mapping relationship between signals and the tool wear state. In the case of sufficient data, it becomes easier to fit the complex functional relationship between the two [148]. Compared to physics-based models, the monitoring results are generally more accurate. The development of data-based TWM technology has gone through stages from simple signal analyses to multivariate data fusion. In the 1970s, early TWM mainly relied on vibration signal analyses. The researchers found that by monitoring the frequency of and amplitude changes in the vibration signal, the tool wear state could be initially judged, which laid the foundation for the data-driven monitoring method. Now, data-driven TWM can be roughly divided into three parts: signal acquisition and preprocessing, feature extraction and selection, and model decision making, as shown in Figure 12.

3.1. Signal Acquisition and Preprocessing

Tool wear data are crucial for the accuracy of decision-making systems in issuing early warnings. The higher the quality of the data obtained, the more accurate the output results will be [154]. Tool wear data are usually obtained by direct or indirect methods. While there is no clear boundary between the two, a guideline with broad reference significance is provided in Ref. [155]. Direct methods collect data from the response of the tool to the formation of chips. Indirect methods collect data from the response outside the actual cutting interface.

3.1.1. Direct Methods

There is no mechanical interaction between the measurement system and the cutting interface in direct methods, so the system stiffness will not be affected, and the measurement results are accurate. The first step of direct methods is image acquisition. The most commonly used visual sensors are CCD [149,156] and CMOS [157,158,159,160,161]. The advantages of the former are that it has a higher level of sensitivity and better imaging quality. The latter has the advantages of a high acquisition rate and low cost. But stray points can appear easily in the process of CMOS, which is more likely to affect the image quality. In addition, an infrared thermal imager [162,163,164] can also monitor the tool wear condition. For common machining processes, such as milling and turning, the visual sensors are often placed directly in front of the milling tool at a fixed distance, as shown in Figure 13. Furthermore, better results can be achieved by flexibly building the platform. Dai et al. [165] designed a three-dimensional motion platform equipped with an imaging device, which can better detect and capture focused images within the predetermined machining intervals.

In the process of image acquisition, the selection of lens and illumination conditions is important for imaging quality. A telecentric lens has the advantages of a high resolution, ultra-low aberration, an ultra-wide depth of field, and a unique parallel light design. Therefore, it is more suitable for precision monitoring [167,168]. In addition, using a fixed focal length [169,170,171] and a macro zoom lens [172] can also capture images of tool wear. Aiming at solving the problem of insufficient and uneven illumination in the process of the image acquisition of tool wear using machine vision, a ring-shaped cold light source is generally placed around the lens to supplement the illumination. Li and An [173] provided a better way to study TWM based on image segmentation and a texture analysis. They used two ring-shaped light sources. One is placed in the tool retraction position, and the other is set directly above the workpiece, which can better capture tool wear images.

AI-Based Preprocessing Models in Direct Methods

After obtaining the image data, these images need to be preprocessed to improve their quality through specific methods like illumination homogenization, improving the contrast, and reducing noise [174]. In 2016, Szydlowski et al. [175] proposed an extended depth of field image reconstruction method based on wavelet transform, and used variable light intensity to detect regions with different reflection characteristics to evaluate tool wear. In 2017, similarly, Zhu and Yu [176] proposed a region growing algorithm based on a morphological component analysis, which can effectively extract the wear area of a tool image. In 2020, You et al. [177] designed a high-resolution TWM system under wind field-of-view and high resolution. In this system, the authors used homomorphic filtering to enhance the wear edge and histogram contrast to locate the tool wear area. This system also considers the difficulties of noise, fuzzy boundaries, and dislocation in collecting tool wear images.

Although direct methods have the advantage of accurate measurement results, they also produce a large amount of data, which require powerful algorithms and more computing resources for processing. Moreover, in actual machining conditions, there will be unavoidable phenomena, such as the splashing of coolant droplets, light diffusion, and swarf, which will lead to the low resolution and poor contrast of the imaging system.

3.1.2. Indirect Methods

Indirect methods collect signals from the external response of the cutting process. Their accuracy is often not as high as that of direct methods, but this lower accuracy is typically compensated for by multi-source sensor fusion technology [26]. Figure 14 shows common sensor installation locations in TWM, including dynamometers, acceleration sensors, and AE sensors.

The dynamometer is usually placed close to the bottom of the cutting tool to sensitively monitor the change in cutting force. Because it has extremely high levels of reliability and sensitivity and the capability to provide more comprehensive data by simultaneously measuring forces in different directions, the dynamometer has become the most frequently used sensor in TWM [181]. However, the installation process requires changing the original structure of the machine tool, which easily affects the rigidity of the system. Vibration signals are a direct reflection of cutting force oscillation in the cutting process [182], providing abundant information. Therefore, these signals are also one of the important sources in TWM. Vibration signals are usually monitored using acceleration sensors, which are placed as close as possible to the tool to reduce the damping effect caused by the inertia of the machine tool. In addition, three-component accelerometers can measure three perpendicular signals simultaneously to more sensitively detect outliers, but their cost will be further increased.

AE sensors monitor the transient stress waves propagated during the machining process. The frequency of these transient stress waves (usually greater than 50 KHz) is much higher than the characteristic frequency caused by the cutting itself [183]. Therefore, AE sensors can capture more details related to tool wear status [184]. The installation position of AE sensors is similar to that of acceleration sensors, which are placed as close as possible to the cutting interface. However, AE sensors are susceptible to external noise. Meanwhile, because AE sensors use a high acquisition rate, they require higher computational costs for processing [185]. In addition, motor current signals contain rich machining information, and they can be effectively utilized for TWM through signal demodulation and various signal analysis methods [186,187,188,189]. In TWM, in addition to the above methods, temperature, chip characteristics, and other factors can also provide key information for tool monitoring. The monitoring and analysis of these factors are able to significantly improve the accuracy of the assessment. For example, cutting tools generate a lot of heat during machining, especially at high cutting speeds. In this case, monitoring the temperature of the tool and the workpiece can detect the wear state of the tool indirectly, usually using thermocouples for measurement [190,191,192]. Chip characteristics such as chip shape, color, and size can also be used as indicators to identify tools’ condition. Overheated tools can cause chips to turn blue or darken. A tool with severe wear will produce irregular chips. These variations provide an intuitive way to judge tool wear. Through the combination of temperature and chip characteristics with traditional sensor data, such as vibration signals and AE signals, multi-feature and multi-dimensional tool wear assessment methods can be established to obtain more accurate prediction results.

In recent years, ORS and wireless sensor tool holders have provided another way to obtain signals. In 2021, Li et al. [193] obtained vibration signals by mounting ORS on a workpiece and built a multi-degree-of-freedom system consisting of a spindle, chuck, and workpiece. Next, the finite element model method was used to obtain its multimodal natural frequency, which establishes the basis for the relationship between tool wear and frequency. Subsequently, the authors conducted further research, and the results showed that the two frequency bands of 350–550 HZ and 600–900 HZ are more sensitive to TWM, especially the lateral vibration of 350–550 HZ. In another study by the authors [194], a three-axis vibration wireless ORS was developed. The design of the novel fixture ensures that it can sense axial, lateral, and rotational vibrations. Meanwhile, this ORS is innovatively mounted on the cutter arbor and rotates synchronously with the spindle. Compared with traditional accelerometers installed in common locations, ORS shows superior signal acquisition capabilities in terms of its sensitivity level and signal-to-noise ratio. Through the analysis of the time–domain signals, six characteristic parameters were identified that could be used for online monitoring, but the authors suggested the use of RMS and absolute mean values, as they are more in line with the dynamics of the wear process. The purpose of wireless sensing tool holders is to shorten the physical gap between the sensor and cutting process to obtain higher-quality vibration signals. For example, in order to avoid the poor signal quality and noise interference caused by traditional accelerometer installation methods, Zhou et al. [195] developed an integrated wireless vibration sensing tool holder system in 2020. Specifically, they made a small modification of a commonly used commercial tool holder and integrated the required electronics, batteries, and sensors into a resin housing. In another study by the authors [179], they evaluated the wireless vibration sensing tool holder system in more detail. A singularity analysis was used to quantify the small amplitude variation of the signal waveform to correlate different tool wear states. The results of milling and pulse experiments showed that the tool holder had good properties, such as a high sensitivity, a high efficiency, and an excellent dynamic performance. In 2020, Ostasevicius et al. [196] proposed a sensor node consisting of cone-shaped tool holder for mounting shank-type rotating tools. It is worth noting that the wireless data processing and transmission system is embedded inside the tools. Differently from the above studies, the authors used a self-powered system. Specifically, an axially polarized piezoelectric transducer is embedded in the tool holder, and the power supply is completed by increasing the voltage through an increase in torsional vibration caused by tool wear during the machining process. Meanwhile, the change in the tool state is monitored via the capacitor charging time.

Table 4. Comparison of different sensor-based indirect methods.

Sensors Types	Advantages	Disadvantage	Application Scenarios
Dynamometer	High sensitivity High reliability	Affects rigidity of system Complex installation	High-precision monitoring Complex wear pattern recognition
Accelerometer	Flexible installation Adapts to different frequency ranges	Can easily be affected by machine vibration Low sensitivity	High-speed cutting machining Low-load machining
AE sensor	Rapid response capability High sensitivity	Susceptible to noise interference Complex signal processing	Non-uniform machining process Hard material machining
Current sensor	Low installation cost Simple data processing	Low accuracy Susceptible to other factors	Stable machining environment Constant load machining
Temperature sensor	Sensitive to thermal wear Non-intrusive measurements	Can easily be affected by coolant Lag of monitoring	Dry or MQL machining condition Continuous machining
On-rotor sensing system	Less noise interference Comprehensive measurement of multiple data types	Complex installation and maintenance High complexity of data processing	Complex machining conditions High-precision machining
Wireless sensors tool holder	Real-time data transmission No cable interference	Signal delay High design and maintenance costs	Multi-axis machining Coolant machining conditions

shows a comparison of different sensor-based indirect methods. However, tool wear is a dynamic and non-stationary process; it is usually impossible to accurately monitor the tool state only by relying on single sensor. To address this problem, some researchers have used multiple types of sensors and different fusion strategies to monitor tool condition in recent years. For example, by collecting vibration, current, and AE signals during the machining process, Wang et al. [197] proposed an MSCAN prediction framework. In the proposed MSCAN, they effectively fuse the input multi-sensor information by constructing self-attention modules. Wang et al. [198] proposed a DTAE architecture (see Figure 15). This structure enables the model to focus more on wear-related features in the feature extraction stage, thus improving the accuracy of TCM. In 2019, based on AE and vibration signals, Ma et al. [199] proposed a tool health assessment method by establishing a DCRBM structure for data fusion. In this method, a coupled restricted Boltzmann machine is used to extract common features from vibration and AE signals, and DCRBM is responsible for extracting high-level features of multisensory signals. In the end, they mapped the vibration and AE signals to a feature space to predict the tool wear state. In 2022, Li et al. [200] proposed a method to accurately characterize tool wear changes from data of different dimensions and long-term time series. In this method, a dense convolutional network, long short-term memory networks, and a statistical analysis are used to extract spatial, temporal, and statistical features, respectively. Subsequently, they used a KPCA to construct the fusion features based on extracted features to eliminate redundant information.

Although sensor fusion technologies have been proven to be feasible from multiple perspectives [201,202,203,204], the combination of reliability, non-intrusiveness, cost, and performance must be considered in TWM. Too many sensors will have a greater impact on the mechanical system, but also cause data processing difficulties and signal interference problems [205]. The number of sensors in multi-sensor fusion technology is generally two to three [33]. AE sensors are a good choice, because they have a lower correlation with other signals and can provide sufficient complementary information.

AI-Based Preprocessing Models in Indirect Methods

Similar to direct methods, indirect methods also require preprocessing to ensure high-quality data are obtained. In 2022, Zhang et al. [206] proposed a hybrid model combining a residual structure and bi-directional LSTM network. In this model, tool wear characteristics and sensor signals are used to extract more abstract features for sequence learning. In 2023, Wei et al. [207] proposed the UKF CycleGAN model to remove noise in the signal (see Figure 16). In this model, a Kalman filter is used to avoid the limitation of initial noise distribution, and the CycleGAN structure is used to train a general denoising model. Based on a stacked multi-layer denoising autoencoder and multi-core GPR, Song et al. [208] established a TWM model, achieving a higher prediction accuracy, in 2023. Specifically, the construction of the Multi-kernel GPR addressed the drawback of original GPR, which can capture non-homogeneous data structures from multiple data sources or different data types. The indirect method can obtain abundant signals to characterize tool wear. However, the indirect method also causes difficulties in data processing. In addition, the obtained sensor data represent only the process signals of tool wear, which is an indirect characterization of tool wear. Achieving more accurate TWM still requires further research and exploration.

3.2. Feature Extraction and Selection

TWM is easily disturbed by machining conditions, mechanical vibration, and other factors in the actual machining process, leading to a large amount of redundant information in the collected signals. The purpose of feature extraction and selection is to obtain feature parameters from signals closely related to tool wear. Feature extraction technology in TWM ranges from the manual selection of basic features to the automatic learning of multi-dimensional deep features. Back in the 1970s, feature extraction mainly relied on simple time and frequency domain features, such as the mean, variance, and frequency peaks of the signal [209]. Researchers found that these basic features can reflect the trend of tool wear to a certain extent and provide data support for early TWM. According to the different signals obtained from the direct and indirect methods, feature extraction and selection methods can be divided into the following two types.

3.2.1. Digital Image

By converting a color picture of the tool wear zone into gray images, the gray information in the image can be used to extract features, including the mean gray, gray-level intensity histogram, and gray gradient distribution. At the same time, the texture information of the extracted image is also able to characterize the subtle structure of the tool surface. The commonly used methods include LBP in TWM. GLCM extracts the texture features of an image by calculating the co-occurrence frequency of pixel gray values at a certain distance and direction. LBP extracts texture information by comparing the gray value of a pixel with the gray values of its neighboring pixels.

In 2020, Qin et al. [30] extracted the target region using an OTSU threshold segmentation algorithm based on edge information. In addition, the image selection utilized the centroid, the orientation of the lowest-inertia moment axis, and the area of the target area. In 2022, You et al. [210] proposed an adaptive online monitoring method for milling cutter status (see Figure 17). In the proposed method, a tool condition image sequence is established in continuous images to express and enhance tool wear characteristics from multiple angles. The authors reported that the average measurement accuracy for flank wear was up to 97.02% and 94.71% in two experiments.

3.2.2. Physical Signals

After obtaining the preprocessed signal data, feature extraction is needed to extract and select the feature parameters closely related to the tool state. Time domain, frequency domain, and time–frequency domain analyses can significantly reduce the dimension of data and provide more accurate input for subsequent decision-making systems [211]. Figure 18 illustrates a typical application of feature extraction and selection in a TWM framework.

Specifically, through a time series analysis, time domain analysis directly extracts the statistical characteristics of time domain signals from the time dimension. Time domain signal analysis is the first method used, including the extraction of the average time, variance, and other statistical features to judge the tool wear state. Although these research studies are not in enough depth, they provide a good foundation for modern time domain analysis. Time domain analysis mainly includes AR [213], the AR moving average process [214], phase space reconstruction [215], and the autoregressive moving average model [216]. In addition, SSA does not need to assume the model structure, which is suitable for the analysis of nonlinear and non-stationary signals [217]. SSA has a very wide range of applications in TWM [218,219]. In the 1990s, with the development of spectrum analysis technology, researchers began to pay attention to the extraction of frequency domain features. Based on the frequency structure and harmonic components of the signals, the frequency domain analysis extracts the frequency domain features related to the tool state from the frequency perspective of the signals [220]. The fast Fourier transform is usually used to convert the acquired signals from the time domain to the frequency domain [221,222,223]. Subsequently, a further analysis was carried out on the converted frequency domain signals. Compared with the time domain analysis, the frequency domain analysis can selectively enhance or attenuate components of specific frequencies by filtering them, thus highlighting the stage of severe tool wear.

Time domain and frequency domain analyses can only provide feature information from a single point of view. Relying on these two analysis methods alone is insufficient for accurately characterizing the tool state [224]. A time–frequency domain analysis provides the distribution information of signals in both the time domain and the frequency domain simultaneously, which indicates the change in the information in the frequency domain with time [225]. In the 2000s, time–frequency analysis techniques were introduced to TWM. The analysis and extraction methods of time–frequency domain features mainly include EMD and WT. EMD was first proposed by Huang et al. [226]. It is an adaptive signal processing method for nonlinear and non-stationary signals. EMD does not depend on the predefined basis function and decomposes directly according to the characteristics of the signals. In recent years, EMD has been widely employed in TWM [227,228,229]. However, the classical EMD has some limitations, such as mode-mixing, noise sensitivity, and a high level of computational complexity [230]. In order to overcome these limitations, in 2011, Wu et al. [231] presented a new ensemble empirical mode decomposition (EEMD) method. In this method, white noise is added to the signals, and its average is taken as the final true result, which improves the stability of the decomposition. Furthermore, it has also been applied to TWM [232]. In 2018, Barbosh et al. [233] proposed multivariate empirical mode decomposition. They used an independent component analysis combined with multivariate empirical mode decomposition to reduce the mode-mixing in the resulting modal response. Similarly, the principle of WT is to decompose non-stationary signals into different frequency bands. And sensitive signals are selected in the time domain or frequency domain for feature extraction. Differently from EMD, WT needs to select wavelet basis functions. The application of CWT is very extensive [234,235,236,237], including rolling element bearing fault diagnosis [238], gearbox fault diagnosis [239], and others. CWT can provide continuous scale information. However, there is a lot of redundant information after processing, and the calculation is very slow. In order to further improve the accuracy, DWT [240,241] and WPD [242,243] are introduced into TWM [244]. In the machining process of a workpiece made of steel alloy 42CrMo4 using a face milling cutter, Madhusudana et al. [245] used different feature extraction techniques (DWT, statistical methods, and EMD) to process the obtained sound signals. The experimental results show that DWT is better than the statistical and EMD methods.

In the machining process, chips are an indirect characterization of tool wear. Different tool wear states produce varying chip colors and morphological information. A chip morphology analysis provides another way to extract tool wear characteristics [246]. Extracted chip shape characteristics include chip color [247], chip width [248], chip thickness [249], and chip surface curvature [250].

Subsequently, these characteristics were input into the decision system to make predictions. For example, Bhuiyan et al. [251] obtained the chip morphology under different machining conditions through several dry turning tests, as shown in Figure 19, and measured the corresponding tool flank wear values. Meanwhile, they measured and analyzed the response of different chip formation processes. The experimental results show that the tool state can be predicted. After acquiring and processing chip images, Pagani et al. [252] extracted different indicators from RGB and HSV image channels. Subsequently, a neural network was used to classify the chips. The authors reported that sensitivity analysis confirms the hue value H is the most sensitive image channel used to guide the network. In 2020, Chen et al. [253] established a relationship between the chip color and the Taylor tool life model. Although some studies [247,249,254] have proven the feasibility of using DL methods to indirectly understand tool wear from chip color features, this feasibility is limited to stable production processes. In the actual machining environment, light, coolant and other factors will affect the chip morphology analysis.

In recent years, with the development of machine learning and deep learning technology, feature extraction has been gradually automated. Deep learning models such as CNN can automatically learn complex high-dimensional features from a large amount of sensor data, which are no longer limited to the manually defined feature space [255,256].

3.3. Data-Driven TWM Decision-Making System

After feature extraction and selection, the data-driven TWM decision-making system needs to establish the mapping relationship between these features and tool wear, which is usually achieved through efficient training. The research process of the TWM decision system starts from a simple threshold judgment in the early stage and gradually develops to a multi-level intelligent decision. As early as the 1970s, TWM and decision systems were mainly based on manually set threshold judgments, and the tool wear state was determined by monitoring simple characteristic signal values, such as vibration or temperature exceeding a preset threshold. Tool wear is usually represented by three indicators: the wear state [256,257,258], VB value [259,260,261], and RUL of the tool [262,263,264]. The trained decision system outputs these indicators to predict the tool condition in actual machining conditions. Different from physics-based TWM, the training and predicting steps usually rely on AI technology. AI does not require a complex process analysis; it only relies on the input and output of the system to establish equivalent models. The introduction of AI technology has greatly improved the reliability, simplicity, and accuracy of decision-making systems. In TWM, AI technologies can be divided into ML and DL;

Table 5. Comparison of ML and DL methods.

Comparison Metric	Machine Learning (ML)	Deep Learning (DL)
Data requirement	Small	Large
Feature engineering	Yes	No
Model complexity	Low	High
Training time	Short	Long
Overfitting risk	Low	High
Response speed	Fast	Slow
Application scenarios	Small data sets	Multi-sensor complex data
Adaptation	Low	High
Parameters complexity	Low	High
Computing resource	Low	High

shows the comparison of ML and DL methods based on different metrics.

3.3.1. ML

ML models need to be trained effectively to accurately predict tool wear. During this process, a large number of images or obtained signal data are firstly labeled. Subsequently, ML models establish the relationship between highly correlated features of tool wear and the labels to judge the tool state. There are many ML algorithms used in TWM, such as decision tree [265,266,267], SVM [268,269,270], RF [271,272,273], and HMM [274,275] algorithms. At the beginning of the 21st century, linear regressions and decision trees were applied to TWM [276,277]. At the same time, simple neural networks also show some potential. This method lays a foundation for the use of more advanced and complex models. Since 2000, SVMs have been widely used in TWM with more complex algorithms [278,279]. These methods provide some value for subsequent research. At the same time, it provides some guidance for actual production, which can optimize the machining process, delay tool wear, and provide greater economic benefits. Although these ML models enhance the accuracy of TWM to some extent, they have some shortcomings. For example, SVM requires a long training time when dealing with large-scale data, and there are some difficulties in parameter tuning [280,281,282]. Decision trees are sensitive to hyperparameters, and a tree structure that is too complex will reduce the generalization ability of the model [26]. HMMs have flexible modeling capabilities and can handle many types of sequence data, including discrete and continuous sequences. However, in the face of unbalanced data and different machining conditions, the generalization ability and robustness of HMMs are low. Meanwhile, HMMs are sensitive to the initial parameter settings, which are not flexible enough to deal with continuous states [283].

In recent years, researchers have adopted various strategies to improve models and overcome these shortcomings. In 2017, Yu et al. [284] proposed a particular probabilistic approach to estimate tool wear (see Figure 20). In this approach, they use the wear rate as hidden states and construct multiple HMMs in a weighted manner. The experimental results show that the performance of the proposed method is better than that of the traditional HMM. In 2021, Gomes et al. [201] utilized recursive feature elimination to select the input parameters in the SVM model to improve the classification accuracy of the model. Lin et al. [285] and Salgado [218] applied the LS-SVM to estimate the tool state. Compared with SVM, LS-SVM is more efficient in processing large-scale data sets. This is because selecting the parameters of regularization and the kernel function is simpler, which makes the model tuning process more efficient. Similarly, Zhu and Liu [286] used the hidden semi-Markov model to model the tool wear process. The advantage is that it can better characterize complex non-stationary physical processes, which is suitable for TWM. In 2021, as shown in Figure 21, Li et al. [260] established an Adaboost decision tree ensemble model to identify the tool wear state and combined it with a stacked bidirectional long short-term memory DL network to achieve a comprehensive assessment of the tool state.

In addition, some researchers have applied ML algorithms with better performance and better robustness to further increase the accuracy of TWM, such as self-organizing maps [221,287,288], relevance vector machines [289], fuzzy logic [290], and adaptive neuro-fuzzy inference [291,292,293].

3.3.2. Deep Learning

Compared with traditional ML, DL does not require steps such as feature extraction and selection [27]. It uses the hierarchical structure in the model to complete these steps, which is more suitable for unlabeled data. Specifically, some techniques in the hierarchical structure of DL are able to deal with unlabeled data, such as self-supervised learning [294], unsupervised learning [152,295], and semi-supervised learning [296]. These techniques further improve the degree of the automation of DL. Common unsupervised learning methods include a cluster analysis, dimensionality reduction, and anomaly detection. The principle of cluster analysis is to cluster the unlabeled sensor data and divide the data into different groups, which represent different wear states. For example, based on the Davies–Bouldin index and an agglomerative hierarchical clustering analysis, Fan et al. [297] proposed an evolutionary cluster analysis method to summarize tool wear laws. On this basis, a tool wear model with a strong fitting ability was established to evaluate the tool wear state. Experimental results showed that the proposed model achieved a high level of accuracy.

The use of unsupervised methods such as PCA or autoencoders can reduce the data dimension and extract the key features that best represent tool wear, thereby enhancing the ability of the model to detect the wear state. This approach is particularly suitable for sensor data with high dimensions, allowing the model to focus on wear-related features. Unsupervised learning can detect abnormal wear or failure by identifying anomalies in the data. In recent years, some researchers have used semi-supervised learning methods combined with pseudo-label methods to further improve the generalization ability of models. For example, by incorporating the law of tool wear, Niu et al. [298] proposed a DL model with limited data. Specifically, a pseudo-labeled sample mechanism based on the confidence level and tool wear law was designed to maintain their accuracy and diversity. At the same time, the improved generative adversarial network is used to generate minority class samples to maintain the data class balance.

Meanwhile, DL captures the intrinsic structure and representation of data by gradually combining low-level features with higher-level abstract features. This characteristic makes DL perform better than traditional ML methods in dealing with complex data. Especially given the gradual increase in the scale of the TWM data set, the advantages of DL are obvious [299,300].

Common DL models used in TWM include CNNs, RNNs, LSTM networks, and residual networks. A CNN includes three basic layer types: a convolutional layer, pooling layer, and fully connected layer. Some researchers have adopted different strategies to improve CNNs for TWM. For example, Ross et al. [301] and Zhou et al. [302] applied AlexNet to classify tool wear states. This network has a deeper architecture than the classical CNN, which can extract more complex features. Zhang et al. [303] trained ResNet using a mixture of information from multi-dimensional cutting force data. Under variable working conditions, a small amount of mixed information can also be used for fine tuning. In addition, DenseNet [304,305,306,307], VGG [308,309], and EfficientNet [310] are also employed in TWM.

Differently from CNNs, RNNs can capture the time dependence and order relationship in a sequence. However, when dealing with long sequences, RNNs will face the problem of gradient disappearance or gradient explosion, making the model unable to effectively learn long-term dependencies. To address these challenges, its variants are usually used in TWM. For example, LSTM effectively solves the problem of gradient disappearance by introducing memory units and gate mechanisms to control the flow of information. The GRU simplifies the structure of LSTM and makes the calculation more efficient.

In addition, it can also be solved by combining it with other algorithms. In 2022, Guo et al. [311] proposed a pyramid LSTM autoencoder to monitor tool wear, in which periodic scales and fluctuations are concerned separately. High-speed milling experiments show that the proposed model is more stable, faster, and more accurate than the classical LSTM. As shown in Figure 22, Qin et al. [312] proposed a Siamese SLSTM to enhance the differentiation of TCM data by transforming the original data distribution, achieving more accurate predictions for TWM.

In 2023, Wang et al. [312] proposed a multi-feature adaptive superposition function and feature enhancement algorithm, in which a stacked bidirectional GRU model is used to sense the real-time tool state. Duan et al. [244] proposed an MFB-DCNN for TWM (see Figure 23). In this network, the signal samples are amplified and processed, and the wavelet coefficients of different frequency bands are obtained by three-layer WPD. In recent years, new neural network architectures are being employed increasingly, such as graph neural networks [215,313], self-attention mechanisms [314,315,316], and deep belief networks [317,318].

The data-driven TWM and decision systems have gradually evolved from a simple threshold judgment to a complex intelligent prediction system, constantly improving the monitoring accuracy and real-time performance of tool wear state. These technological advances provide strong support for real-time monitoring and automated decision making in smart manufacturing [319,320]. However, in actual machining conditions, more influencing factors often need to be considered. Even well-trained models still have difficulty achieving good results in practice. Meanwhile, data-driven TWM only establishes a mapping relationship by learning data, which lacks good interpretability and physical consistency. In addition, ML and DL models require a large number of data samples for training. However, it is difficult to obtain huge data in actual machining [321,322], so the generalization of the models is further limited.

In addition, more accurate TWM can be achieved by the integrated method. The first thing that should be considered is multi-model fusion. For example, neural networks are suitable for dealing with complex nonlinear data, while SVMs have accurate classification results. The advantages of the two models can be fused by integrating the algorithms. Secondly, hierarchical integration can also produce good results by dividing the data model into different levels, such as the processing layer, feature extraction layer, and decision layer. Each layer is responsible for its own part. For example, the preprocessing layer improves data quality through techniques such as denoising. The feature extraction layer extracts the features strongly related to tool wear through WPD and an attention mechanism. The decision layer is responsible for establishing the mapping relationships that lead to a comprehensive tool condition assessment. In addition, as a new method, an adaptive ensemble can select the appropriate algorithm model or adaptively update the model parameters in real time to ensure efficient monitoring under different working conditions. These methods avoid the limitations of a single technique for specific operating conditions to improve the robustness and accuracy of the monitoring system.

4. Physics–Data Fusion TWM

Physics-based models cannot accurately characterize the tool wear state. This is because they often only consider a few variables and lack consideration of multi-factor coupling. Moreover, the diversity of cutting conditions and the dynamic changes in physical parameters further limit their application scenarios and prediction accuracy. Data-driven models can capture complex time–space relationships, but they only fit well for trained data. In the face of unknown or variable machining conditions, it is still difficult to obtain good results. In addition, AI technologies used in data-based models are essentially ‘black box’ models, and their outputs lack a physically consistent explanation. Considering the shortcomings of both, some researchers have begun to explore the combination of physical models and data-based models to benefit from their complementary advantages.

In fact, the integration of scientific knowledge (physical models, professional theories, and laws of physics) with data-based models has achieved a lot of results in many fields, such as climate science [323,324,325], quantum chemistry [326,327], biological science [328,329,330], and hydrology [331,332]. In engineering, the use of physical knowledge to guide data-driven models is also considered to be a promising direction. Cheng et al. [333] proposed an adaptive fault attention residual network (AFARN) for bearing fault diagnosis, in which physical knowledge was incorporated into the process of domain shift alignment. Brian et al. [334] developed a hybrid implementation method of a Gaussian process regression, in which the physics-based prior model is constructed by the finite element method. For the real-time prediction of the critical mass of large components, Chen et al. [335] proposed a framework based on a data-driven physical model (see Figure 24). In this framework, the physical model takes into account the main causes of the residual base thickness error formation. Meanwhile, KPAC and a kernel support vector regression are incorporated with the physical model to achieve a better prediction accuracy.

Physical and data fusion methods have been proven to have the advantages of both data-based and physical-based models. In TWM, the benefits of these fusion methods can be summarized in two points: (1) By incorporating the physical information about tool wear, the data model is constrained to a low-dimensional space that conforms to the physical principle. Even if the training samples used are limited to a few machining conditions, the model can still have good generalizability. (2) The integration of domain knowledge and machining information enhances the interpretability of the model, resulting in outputs that are more in line with physical principles. The construction of the physical and data fusion model can be divided into the following sections. Firstly, extract physical information that is easy to couple with the data model from classical research on tool wear. This physics information includes simple wear laws and wear models. Then, different fusion methods are used to integrate physical information into the data model, such as physics-guided loss functions, structure designs embedding physical information, and physics-guided stochastic processes. In addition, considering that the output forms of the physical model and the data model are different, this paper further summarizes the fusion strategies of the two models from a decision-making perspective. The physical and data fusion models are divided into three types from a holistic perspective: using the outputs of a physical model as the inputs of a data model; integrating the outputs of a physical model and a data model; and improving a physical model using the outputs of a data model. These strategies are discussed in detail.

4.1. Physical Information

Over the past three decades, extensive research has been conducted on tool wear, including its causes, forms, and the relationship between machining parameters and wear. These studies provide a sufficient theoretical basis for physical–data fusion models. For example, Wang et al. [336] concluded that the wear forms of a tool are mainly abrasive wear and adhesive wear from the milling process of Ni-based superalloy GH4169 using TiAlN carbide coating blades. Similar results were reported by Kaplan et al. [337]. The authors concluded that tool wear is usually the result of a combination of chemical wear, abrasive wear, and adhesive wear mechanisms. However, through an experiment on binder-free cubic boron nitride in the machining of titanium alloy Ti6Al4V, Wang et al. [338] found that abrasive wear is not the main mechanism of BCBN tools, although various asperities and traces can be observed due to the abrasive wear mechanism on the flank surface at the initial stage of cutting. These studies are sufficiently detailed and comprehensive, but usually rely on the combination with specific workpieces and tools to produce conclusions. Once the combination is replaced, the wear mechanism and the rate of tool wear will also change.

Therefore, the above research does not provide good reference values for TWM, especially for predicting unknown working conditions. The wear laws coupled with the data-based model should be simple and easy to integrate. For example, as shown in Figure 25a, the feed rate accelerates flank wear by positively affecting the average chip thickness. Increasing the cutting speed will raise the temperature at the contact interface between the tool and the workpiece, reducing the hardness of the tool and further accelerating wear (see Figure 25b).

Some researchers have embedded these simple physical laws to achieve the fusion of physics and data. For example, Hao et al. [340] embedded hard and soft physical constraints in a transformer to predict milling tool wear in high-precision machining (see Figure 26). This hard physical constraint is achieved by setting the predicted value of the wear constant to be greater than zero, which means that the tool wear value is always positive. This method uses the specific rules of the algorithm to meet general cutting guidelines, making it suitable for variable working conditions. By assuming the tool wear is progressive, Li et al. [341] proposed a method for predicting the RUL of a tool under variable working conditions. In this method, the authors utilized the covariance matrix of the Gaussian model to constrain the predicted values at adjacent moments to a linear relationship, which provides a basis for subsequent wear process modeling.

Based on simple tool wear laws, some researchers have established the models that relate tool wear to physical quantities. These models cannot accurately describe instantaneous machining process changes. However, these models are a simplification of the real wear law, which can be introduced into the physics–data fusion models as a priori knowledge.

Table 6. The physical and data models used in physics–data fusion models for TWM.

Data Model	Physics Equation	Reference	Year of Publication
Texture digital twin	${\mathsf{\Delta }\mathrm{r}}_{\mathrm{s}}=\mathsf{\lambda }\cdot \mathrm{t}+\mathsf{\sigma }\cdot \mathcal{B}\left(\mathrm{t}\right)$	[342]	2024
Particle filter Support vector regression Autoregressive	${\displaystyle \frac{\mathrm{d}\mathsf{\theta }}{\mathrm{dt}}}={\displaystyle \frac{\mathrm{G}}{\mathrm{H}}}{\mathrm{N}}^{\mathrm{m}}{\mathrm{V}}_{\mathrm{c}}$	[343]	2015
Bi-directional GRU	$\mathsf{\Delta }\mathsf{\theta }={\mathrm{C}}_1{\mathrm{N}}^{{\mathrm{C}}_2}$	[344]	2020
Logistic classification	$\log \left(\mathrm{T}\right)=-{\displaystyle \frac{1}{\mathrm{n}}}\log \left(\mathrm{V}\right)+{\displaystyle \frac{\log \left(\mathrm{C}\right)}{\mathrm{n}}}$	[345]	2021
ANN	${\mathrm{F}}_{\mathrm{r}}^{\prime }={\mathsf{\sigma }\mathrm{a}}_{\mathrm{p}}\mathrm{VB}$	[346]	2022
Meta-learning	${\displaystyle \frac{\mathrm{d}\mathsf{\theta }}{\mathrm{dt}}}={\mathrm{CN}}^{\mathrm{m}}$	[347]	2022
Decision tree Neural network	$\mathrm{F}={\mathrm{K}}_{\mathrm{s}}\mathrm{A}={\mathrm{K}}_{\mathrm{s}}{\mathrm{a}}_{\mathrm{p}}\mathrm{h}$	[348]	2022
K-NN	${\mathrm{F}}_{\mathrm{t}}={\mathrm{K}}_{\mathrm{t}}{\mathrm{a}}_{\mathrm{p}}\mathrm{h}+{\mathsf{\mu }\mathrm{HWa}}_{\mathrm{p}}$	[349]	2022
ANFIS	$\mathrm{x}\left({\mathrm{t}}_{\mathrm{c}}\right)={\mathrm{t}}_{\mathrm{c}}\exp \left(\mathrm{A}+{\mathrm{Bt}}_{\mathrm{c}}+{\mathrm{Ct}}_{\mathrm{c}}^2\right)$	[350]	2019
ARIMA Wavelet neural network	${\mathrm{w}}_{\mathrm{t}}={\mathrm{w}}_{\mathrm{Et}}+{\mathrm{w}}_{\mathrm{Lt}}$ $\left\{\begin{array}{l}{\mathrm{w}}_{\mathrm{Et}}^{\prime }={\displaystyle \frac{{\mathrm{a}}_1}{\mathrm{t}+{\mathrm{b}}_1}}+{\mathrm{c}}_1\\ {\mathrm{w}}_{\mathrm{Lt}}^{″}={\mathrm{a}}_2\mathrm{t}+{\mathrm{b}}_2\end{array}\right.$	[351]	2022
Gaussian Process	${\mathsf{\nu }\mathrm{T}}^{\mathrm{n}}{\mathrm{f}}^{\mathrm{m}}=\mathrm{C}$	[352]	2023
TrAdaBoost.R2	${\mathrm{VB}}_1\left(\mathrm{t}\right)={\mathrm{K}}_1\mathrm{P}\left(\mathrm{t}\right)+{\mathrm{b}}_1$	[353]	2023
Particle filter	${\mathrm{x}}_{\mathrm{k}}={\mathrm{x}}_{\mathrm{k}-1}+\mathsf{\mu }\left({\mathrm{x}}_{\mathrm{k}-1},{\mathrm{t}}_{\mathrm{k}-1},\mathsf{\theta }\right){\mathsf{\Delta }\mathrm{t}}_{\mathrm{k}}+{\mathsf{\omega }}_{\mathrm{k}-1}$	[354]	2023
Stacked sparsity autoencoder	$\mathrm{w}\left(\mathrm{t}\right)=\mathrm{Aln}\left(\mathrm{Bt}+1\right)+{\mathrm{Ct}}^3$	[355]	2023

shows the physical and data models used in physics–data fusion models for TWM.

From Table 6, it can be seen that the most commonly used model is still the Taylor equation. It describes the relationship between tool life and cutting speed. Furthermore, the Taylor correction formula is also used in physics–data fusion models. It takes into account the feed speed and cutting time of the tool. Therefore, the tool wear state can be characterized more accurately. Sipos’s formula based on cutting speed can quickly estimate the tool wear rate at different cutting speeds, making it valuable for physics–data fusion models. In 2019, Zhu and Zhang [356] proposed a general explicit tool wear model with adjustable coefficients for high-speed ball-nose end milling. In this model, tool life is divided into three wear zones, and the flank wear was determined by interpreting and elaborating the intrinsic amplitudes and growth frequencies of earlier and later milling stages. Meanwhile, the relationship between milling forces and tool flank wear is determined according to the data measured by a dynamometer. On this basis, further extensions and generalizations were carried out by Zhang et al. [357]. A general tool wear model with fitting coefficients is established by using logarithmic and cubic polynomials to fit the front and back segments of the wear curve. In 2021, Pan et al. [358] proposed a TWM method using a physical model and acceleration signal. The feature fusion model and statistical method were used to study the rules of the tool from brand new to complete breakage. In 2023, Zhang et al. [359] theoretically developed a physical model of milling forces considering tool runout and wear. Combined with this model, a real-time tool wear estimation method is proposed, which was based on the seven-channel specific cutting force coefficient of the milling force, spindle box vibration, and driving current.

As a prior knowledge introduced into physics–data fusion models, physical models should have the advantages of simplicity and a high reliability. Although complex models can contain more comprehensive information, their parameters are difficult to obtain, making the next step challenging. Therefore, how to achieve a balance between the two is still a challenge.

4.2. Physics–Data Fusion Methods for TWM

In TWM, researchers have employed various methods to fuse physical knowledge and data-based models, which can be roughly divided into three categories: the physics-guided loss function method, structural design embedding physical information method, and physics-guided stochastic process method. Specifically, the physics-guided loss function takes the tool wear law as a constraint condition. After the data-based model prediction is completed, the output results are forced to consider the law to reduce unreasonable predictions. A structural design embedding physical information directly integrates physical knowledge into the architecture. This method fully considers the tool wear law in the process of model training and prediction and addresses the lack of interpretability of traditional data models. Meanwhile, this clear model structure helps to better understand the fusion method of physical information and the data model. And the physics-guided stochastic process provides a more flexible way to integrate physical knowledge into a data model. This method takes full advantage of the ability of the data model to deal with non-linearity. By being combined with the physical model, it can more comprehensively consider the physical information and provide more robust prediction results.

4.2.1. Physics-Guided Loss Function

The traditional loss function evaluates the gap between the real value and the predicted value. On this basis, the physics-guided loss function adds penalties for violating physical information, ensuring that the model takes physical laws into account in the process of training and prediction. Specifically, when the model prediction results do not conform to the laws of physics, the physical loss term will become larger, increasing the total loss. Subsequently, the optimization algorithm used in the training process of the model will continuously adjust the model parameters, so that the output results ensure physical consistency. The physics-guided loss function can be expressed as follows:

$$\mathrm{Loss}={\mathrm{Loss}}_{\mathrm{TRN}}\left({\mathrm{Y}}_{\mathrm{true}},{\mathrm{Y}}_{\mathrm{pred}}\right)+\mathsf{\lambda }\mathrm{R}\left(\mathrm{W}\right)+{\mathsf{\gamma }\mathrm{Loss}}_{\mathrm{PHY}}\left({\mathrm{Y}}_{\mathrm{pred}}\right)$$

(1)

where ${\mathrm{Loss}}_{\mathrm{TRN}}$ is the gap between the true label ${\mathrm{Y}}_{\mathrm{true}}$ and the predicted labels ${\mathrm{Y}}_{\mathrm{pred}}$, and $\mathsf{\lambda }$ is a hyperparameter of the loss weight of the control model complexity $\mathrm{R}\left(\mathrm{w}\right)$. The first two terms are the standard loss of data-based models. ${\mathrm{Loss}}_{\mathrm{PHY}}$ is used to guarantee physical consistency, which is weighted by hyperparameter $\mathsf{\gamma }$.

The physics-guided loss function is usually used for evaluating physical inconsistency and guiding optimization direction [360]. For example, Wang et al. [344] proposed a physics-guided loss function, which can quantitatively evaluate physical inconsistencies. The derivation process of the function can be seen in Figure 27. Wang et al. [361] used a monotonic loss function to reflect the monotonicity and trend of the tool wear process, which can explicitly describe the degradation information. Although the physics-guided loss function can improve the physical consistency of fusion models, it also has some shortcomings. For example, in the process of model optimization, data loss and physical loss need to be considered comprehensively. When an inappropriate weight coefficient is selected, the performance of the model will be greatly reduced. Meanwhile, the introduction of the physical loss term will increase the computational complexity, especially for complex machining conditions.

4.2.2. Structural Design Embedding Physical Information

The physics-guided loss function fuses physical information and a data model with the aim of limiting the model search space [362]. However, the ML or DL models structures employed remain a ‘black box’. The physical information of tools is not directly incorporated into these models. Therefore, it is necessary to establish a clear paradigm for physics–data fusion from the perspective of structural design. Embedding intermediate physical variables in the data models provides such a way [42], which is directly related to the wear law, and the training is more intuitive. At the same time, this method does not involve the weight adjustment of the physical loss term, and the training process is more efficient.

Due to the high degree of freedom and complexity of the ML or DL model structure, the position and form of embedding physical information are highly flexible. One method is to assign physical meaning to some neurons in the neural network. For example, in the lake temperature modeling process, Daw et al. [363] added novel physics-informed connections to capture physics information about lake temperature, acquiring physical consistency results. Similarly, Liu et al. [342] integrated prior texture knowledge about a tool’s condition into an adversarial model to enhance its convergence speed. Meanwhile, the lightweight converter architecture and global covariance pooling are designed to enhance its physical representation ability, which makes the model more interpretable. Yan et al. [364] established CAHSMM under time-varying operation conditions (see Figure 28). In this model, the Taylor equation is used to determine the state transition probabilities, which are strongly dependent on the cutting parameters and duration time. Another method is to fix one or more weights as parameters with physical information during training. Zhu et al. [365] proposed an attention-based feature extraction method. Different from the classical attention mechanism, physical information such as milling parameters is introduced into the attention unit and perceptron, guiding feature extraction by affecting the weight of the feature group.

4.2.3. Physics-Guided Stochastic Processes

A stochastic process is a process that changes randomly with time, which understands and predicts the dynamic behavior of complex systems by defining a set of random variables and their statistical properties. The applications of stochastic processes are extensively broad, including Gaussian processes, Wiener processes, and Poisson processes. In TWM, some researchers have utilized a Gaussian process or Wiener process to embed physical information and establish a physical–data coupling model. As shown in Figure 29, Qiang et al. [353] proposed a PITL framework for variable conditions to predict tool wear. A physics-guided recursive Gaussian regression is used as a base learner, which improves the generalization ability of the model. Ma et al. [354] established the relationship between data and physical models from the perspective of probability. This relationship uses the Bayesian framework to fuse the feature information with a prior model, which can adaptively identify the wear state. Zhu et al. [366] used a general tool wear model to constrain the mean function of the Gaussian process, making the Gaussian process regression more in line with the actual tool wear state.

Different from the Gaussian process, the Wiener process is usually used to establish a tool degradation model and output the prediction results in conjunction with the data model. For example, Sun et al. [367] established a tool state degradation model based on the Wiener process to predict the RUL of the tool. The authors report that the model based on the Wiener process model can characterize the tool degradation process well. However, tool wear is a multi-stage process, and different wear stages have different characteristics. It is difficult to accurately characterize the tool degradation information by using single-stage process modeling. Therefore, it is necessary to establish a Wiener process that characterizes different stages. In another study by the authors [368], the nonlinear Wiener process is used to establish the tool wear model. Meanwhile, they also derived the probability density function of the RUL to quantify the uncertainty. Similarly, based on the Wiener process, Li et al. [369] established a three-stage tool RUL prediction model considering the evolution of different wear stages and multi-layer uncertainty (see Figure 30). Furthermore, the weight optimization particle filter algorithm under the Bayesian framework is used to update the model parameters. The experimental results show that this method not only improves its accuracy, but also has a good generalization ability and level of robustness under different working conditions.

Similarly, Zhang et al. [370] established a nonlinear multi-stage Wiener process to describe the tool degradation process. The tool wear stage is judged by the output of the data model. Meanwhile, a maximum likelihood estimation and the Bayesian method are used to estimate and update the parameters. In addition, residual learning can also be used in physics–data fusion models in TWM. The principle of residual learning is to learn the deviation of the physical model relative to the actual value and use this deviation to correct the prediction based on the physical model. A major limitation is that it is not able to introduce strong and weak constraints of physics information [371].

4.3. Fusion Strategies for Making Decisions

In the previous subsection, the specific fusion methods of physics-based models and data-based models were introduced in detail. However, it is worth noting that the output forms of physical models and data models are not the same. For example, Sipos’s formulation, as the common physics-based model, outputs the tool life through the model parameters determined by experiments. In contrast, data models typically represent tool wear by mapping the relationship between signals and wear states. The prediction results of the two cannot be directly fused. Therefore, it is necessary to summarize the fusion strategies of the physical model and data model from the perspective of model decision making. By searching the literature, the fusion strategies can be divided into three types as follows. One strategy is to input the data model using the physical model output. The second strategy is to combine the outputs of the physical and data models for predictions. The third strategy is to use the output of the data model to improve the accuracy of the physical model.

4.3.1. Outputs of Physical Model as Inputs of Data-Driven Model

Taking the output of the physical model as the input of the data-based model is the most direct approach in TWM. The principle of this strategy is to regard the output of the physical model as features and to input these features into a data-based model for predictions. This strategy has several obvious advantages. Firstly, the output of the physical model conforms to the prior knowledge of tool wear, which alleviates the problem of insufficient wear data to a certain extent. Secondly, the original sensor data are often high-dimensional and complex. This strategy is equivalent to simplifying the input of the data-based model. This strategy not only reduces the input of computing resources, but also effectively reduces the risk of model overfitting.

For example, by introducing empirical equation parameters, Li et al. [347] proposed a data-driven modeling strategy based on physical information (see Figure 31), which can be used for TWM under variable wear rates. At the same time, the piecewise fitting method not only solves the difficulty of empirical equation parameter estimation, but also improves the interpretability and superiority of this modeling method. Liu et al. [372] proposed a regularization-based sensor modelling and model frequency analysis method for TWM. In this method, the physical information of the underlying machining process is used in the modeling process to complete the design of the model regularization parameters.

However, this strategy requires the further processing of the physical model’s output in order to adapt the input form of the data models, which increases the difficulty of model construction and parameter estimation. Therefore, it is necessary to propose another alternative strategy to avoid tedious processing steps. Specifically, it uses the wear law or physical model to generate labeled information and combines labeled information with the features extracted from the traditional data model. Wang and Shen [373] proposed the Auxiliary Input-enhanced Siamese Neural Network (AISNN) framework (see Figure 32b) and compared it to a traditional CNN and AISNN (see Figure 32). It can be seen that Siamese structures are incorporated into the CNN to distinguish feature differences. At the same time, the auxiliary input provides a feature that strongly depends on tool wear, which enables the model to learn general wear laws. Yuan et al. [355] proposed a physics-assisted online learning tool wear prediction method. In the pretraining stage, to more effectively train the monitoring model, the training set is constituted by the features extracted by the stacked sparse autoencoder and the physically generated labels. In the stage of online monitoring, pseudo labels and real-time signals are used to calibrate the model, which improves the generalizability of the model. Gao et al. [374] propose a similar approach. The physical information and the local features of the sensor signals are used as input to construct a hybrid physical data-driven model. At the same time, the Bayesian fusion mechanism is used to realize the fusion of physical information and data information. The experimental results show that the prediction error is significantly reduced compared with individual methods.

4.3.2. Integrating Outputs of Physical Model and Data-Driven Model

Physics-based models cannot provide accurate prediction results. Data-driven models may output results that do not conform to physical laws. Combining the prediction results of physical models and data models can reduce the prediction error of a single model and provide a more robust output. Hanachi et al. [350] proposed a hybrid data-driven physics-based model fusion framework for TWM. In this framework, the prediction results of Sipos’s model and the prediction results of an adaptive neuro-fuzzy inference system are combined in a stepwise manner, thus reducing the uncertainty of the physical model and the data model. The experiment results demonstrate that the fusion framework outperforms the individual models.

In addition, some researchers proposed another strategy to achieve more accurate predictions, in which the prediction results of the physics-based model and the prediction results of the data-based model are constructed as features. Subsequently, these features are input to another higher-level model to realize more accurate predictions. For example, Wang et al. [344] proposed a physics-guided neural network model for TWM. In this model, information in both the physical and data domains is extracted and mapped to the target space. Then, a regression analysis is used to fuse the prediction results of the two to obtain the final prediction results. Huang et al. [375] proposed a similar method. In this method, the physical model is expressed by the mathematical equation of tool degradation, and the data-driven model is predicted by a multi-layer perceptron. Finally, the particle filter algorithm is used to realize the accurate prediction of the tool state by fusing the results of the models. The experimental results show that the prediction error of the hybrid model is lower and the accuracy is higher than that of the single model. In order to deal with the rapid tool wear in the edge correction process of carbon fiber-reinforced polyethylene construction, Jin et al. [346] used trimming kinematics to train the working condition parameters as the characteristic parameters in the artificial neural network model and combined it with the physics-based kinematics model for predictions.

The combined prediction results of physical models and data models have higher levels of adaptability and flexibility. However, due to the need to deal with two different types of output results, the physical and data models require more complex fusion and processing algorithms, which increases the complexity of the system to a certain extent. At the same time, the parameters of the two models need to be optimized. This increases the difficulty of adjusting the parameters.

4.3.3. Improving Physical Model by the Outputs of Data-Driven Model

Although the physical model is accurate enough under complex conditions, it can provide a theoretical reference. Meanwhile, the physical model has high levels of interpretability and versatility. Some researchers use ML or DL techniques to establish relationships between tool wear and complex sensor signals. Subsequently, these relationships are applied to update parameters of physical models, thereby capturing more intricate process information.

Zhang et al. [376] proposed a general digital twin model update framework and selected a tool wear model as the object. The update steps are shown in Figure 33. Specifically, they use the back BPN to establish the relationship between tool wear and various sensor data. After training, the BPN outputs for flank wear are used to realize the iteration of tool wear values. In order to realize the long-term prediction of online TWM, Wang et al. [343] proposed a recursive Bayesian inference method based on particle filtering. In this method, a support vector regression and automatic regression analysis are used to predict future tool wear values, and the model parameters are updated by the particle filter framework. Li et al. [377] used a similar method, but the sliding window and particle filter algorithm were used to iteratively update the parameters of the tool wear model (see Figure 34). A support vector regression is used to establish the mapping relationship between sensor signals and tool wear. To predict the RUL of tools in various industrial scenarios, Jain et al. [378] proposed an adaptive, hybrid stochastic degradation model to mathematically represent the tool degradation process. In this model, real-time degradation signal features from sensors, degradation rate features from historical data, future operational profile changes, and jerks due to dynamic transitions are jointly considered. Additionally, the physical evolution of tool dynamic profiles is modeled to enhance the model’s generalization ability for different scenarios.

Physics-based models are the basis of physical–data fusion methods. Physics-based models can provide long-term predictions of tool wear and can provide a reasonable range for the data model to ensure that the outputs conform to the tool wear law. In addition, the parameters in the physical model usually need to be determined by machining experiments, which are beneficial to further explore the relationship between tool wear and machining conditions, such as the cutting speed and feed rate. Therefore, the physical model can guide the methods based on physical data. However, due to the complexity of tool wear, these models often have difficulty accurately describing the process information of tool wear. The data-based method can supplement the physical model by analyzing the sensor data. The integration of the two not only improves the accuracy of the model, but also enhances the physical interpretation. Meanwhile, in the actual machining process, it is often difficult to obtain data sets due to the influence of many factors. Physical models can provide reasonable prior knowledge and achieve good results even in cases of insufficient data. In addition, data models can dynamically update the parameters of fusion models, enabling them to adapt to various machining conditions.

Some integration methods can also improve fusion models’ performance. For example, it is possible to gradually combine the outputs of physical and data-driven models through multi-level fusion, which can provide more robust results. In addition, after the fusion model is established, the fusion mechanism is controlled by adding feedback. Specifically, the output of the data model is fed back into the physical model for correction, which ensures the real-time adaptability of the monitoring system to changes in the actual working condition.

5. Trends and Future Challenges

TWM covers multi-disciplinary knowledge, including mechanical engineering, artificial intelligence, and big data. An effective TWM system should possess autonomous decision-making capabilities, allowing it to proactively alert operators to replace tools before significant wear or breakage occurs. However, the application of TWM faces limitations due to the complex dynamic characteristics of tool wear and the variety of machining conditions. Therefore, further research is necessary, which is mainly described in the following aspects, as shown in Figure 35.

(1) It is important to establish a more general and accurate physical model to characterize the tool state. Researchers should focus on the non-stationarity of tool wear and study the main forms of wear at various stages. Meanwhile, different wear mechanisms and coupling effects should be considered in the modeling process. In addition, the use of advanced sensor data can obtain richer characterization information and provide more process information for physical modeling.

(2) Data-based models still focus on establishing the mapping relationship between data and tool wear. To enhance data quality, the use of more advanced denoising and fusion algorithms is crucial. Additionally, selecting fewer and more relevant features can improve the performance of model decision making, achieving more accurate results. In the decision-making process, using more advanced algorithms can improve the generalizability and scalability of the model, thereby increasing the robustness of TWM under unknown conditions. In addition, ensemble methods can be used to achieve more accurate prediction results. By integrating different data-driven methods, models can exploit the advantages of various algorithms to achieve more stable, accurate, and reliable monitoring results. These integrated methods have significant synergistic effects under various working conditions, and the complementarity between different models makes the whole system more flexible to deal with complex industrial processing environments, thereby improving the overall quality and effect of TWM.

(3) The fusion of physics and data models is an effective method to enhance the interpretability and generalization ability of TWM. However, the current research only applies some simple cutting laws and physical models, and there is a lot of physical information that is not taken into account. For the combination of physical information and ML algorithms, a smoother embedding method can further improve the physical consistency of the model. Similar to data-based TWM models, one trend of fusion models that deserves further investigation is ensemble methods. Physical and data fusion models can be highly collaborative through different integration methods. The physical model provides a reliable foundation and physical consistency, while the data model provides dynamic flexibility and adaptability. Their complementarity makes the whole monitoring system highly robust and accurate, which can adapt to complex industrial processing conditions and improve the quality of tool wear predictions. Meanwhile, under actual machining conditions, cutting parameters, workpiece shape, and material need to be considered in the construction of the model, which is a key step in extending the physical–data fusion model to the actual environment.

In addition, in practical machining environments, these models need to be adopted reasonably according to different scenarios. The physical model outputs tool life depending on machining parameters and material properties, which has high levels of interpretability and reliability. Therefore, they are suitable for scenarios in which the cutting process has clear physical laws. It is worth noting that the processed material is required to have fixed and consistent properties such as strength and stiffness. At the same time, the cutting parameters remain stable, such as cutting speed, feed rate, and cutting depth. Furthermore, the physical model is also suitable for scenarios in which there is a lack of tool wear data. In this case, the physical model relies on an explicit causal analysis mechanism, which can provide reasonable prior knowledge for TWM.

Compared with physical models, data-driven models usually use ML or DL techniques to establish the relationship between signals and tool wear. These techniques have powerful nonlinear fitting capabilities. Therefore, data-driven models are suitable for the machining processing of multivariate, multiple-interaction effects. In addition, for scenarios in which the physical laws may not be fully understood, data-driven models can build TWM models through existing measurement data to provide more accurate prediction results.

Physical and data fusion models are often suitable for emerging or uncommon machining processes. In this case, the physical model is difficult to build precisely, but physics knowledge about tool wear still provides a reasonable reference range. Data-driven models can use experimental data to continuously improve the accuracy of the output. Hybrid models can make full use of the advantages of both and provide more robust prediction results. In addition, hybrid models are suitable for complex cutting processes. They are able to comprehensively consider processing parameters, material properties, and sensor data. The tool wear knowledge is used to guide the model construction, and the data-driven model is used to modify the model, thereby predicting the tool state more accurately. Especially with the popularity of the IoT, hybrid models can be coupled with other systems to provide a more comprehensive system evaluation, thereby making more scientific production decisions and optimization strategies.

6. Conclusions

TWM is crucial for machining processes. It maximizes the RUL of tools, thereby reducing the safety risks and economic losses caused by tool failure. This paper comprehensively reviews the research progress of TWM and systematically summarizes the development of physics-based, data-based, and physics–data fusion models. The main conclusions drawn from this study are as follows:

(1) The physics-based TWM model offers excellent interpretability, which can achieve good results in specific scenarios. Common physical models include Sipos’s formula, the Taylor formula, and its variants. However, due to numerous factors influencing tool wear, these models face significant complexity. The existing physical models have difficulty establishing accurate relationships between multiple variables, leading to great uncertainty in the predictions of the models. Relying solely on physical models to achieve accurate TWM remains challenging.

(2) Data-driven TWM technology mainly involves three steps: data acquisition and preprocessing, feature extraction and selection, and decision making. In signal acquisition, indirect methods are still the main method used by researchers, often employing multi-source sensors to provide complementary information. The existing extraction methods mainly include the time domain, frequency domain, and time–frequency domain feature extraction methods in the feature extraction and selection stage. The decision-making system of the tool state are often built through ML or DL techniques. As DL technology does not require steps such as feature extraction or selection, its range of applications is broader, particularly in the context of the growing scale of tool data sets. However, it also brings some difficulties to the selection of model parameters. The purpose of data-based TWM is still to improve the prediction accuracy of the model under unknown operating conditions.

(3) The physics–data fusion model combines the advantages of physics-based models and data-based models. Incorporating physical prior knowledge into data-based models can address the disadvantage of ML or DL, which, to a certain extent, do not have interpretability. Various strategies have been explored for different levels of fusion, including physics-guided loss functions, structural designs including physical information, and physics-guided stochastic processes. Among these methods, the Gaussian process regression and Wiener process have been widely studied to express physical information, further facilitating the coupling of physical information and data models.