Abstract
To investigate four-point contact ball slewing bearings, a bearing support bolt-integrated model was created with HyperMesh and ANSYS software, and its accuracy was theoretically confirmed. This study examines how the rolling element number Z, contact angle α, bolt number N, bolt pre-tightening force coefficient P, and radial load-overturning moment angle θ affect the comprehensive performance of four-point contact ball slewing bearings and connecting bolts. The study found that increasing Z, α, N, P, and θ reduces overall bearing, ring, rolling element, and contact load deformations. The maximum deformation and stress of bolts rise with P but decrease with Z, α, N, and θ. The degree of influence of each parameter on the deformation of the inner and outer rings, the deformation of the rolling element, and the contact load of the rolling body from large to small is ranked as follows: α, N, Z, θ, and P; the degree of influence on bolt deformation and bolt stress distribution uniformity from large to small is ranked as follows: N, α, Z, θ, and P; the degree of influence on the overall deformation of the bearing from large to small is ranked as follows: N, θ, α, Z and P; the degree of impact on the maximum stress of the bolt from large to small is ranked as follows: P, N, Z, α, θ. To improve the overall performance of a four-point contact ball slewing bearing, increase α, N, Z, and θ.
1. Introduction
Slewing bearings play a vital role in heavy-duty mechanical transmission systems. They can withstand axial loads, radial loads, and overturning moments simultaneously. They are widely used in lifting equipment, metallurgical machinery, and aerospace technology. In recent years, many scholars have used the finite element method to study the comprehensive performance of slewing bearings [1].
In recent years, scholars have established finite element models of bearings, including rolling elements and rings, to study bearing performance. He et al. [2] established a finite element model of a slewing bearing and acquired the contact stresses between balls and raceways for analyzing fatigue life, and the accuracy of simulation results was verified by experiments. Porziani et al. [3] replaced the rolling element array with a toroid-shaped element when establishing a finite element model of a four-point contact slewing bearing.
Not only did this approach simplify the computational burden, but it also obtained highly accurate simulation results. He et al. [4] established a finite element model of a single-row ball slewing bearing and investigated the effect of mesh size on the finite element analysis of the load capacity of the bearing, and the accuracy and efficiency were demonstrated in this study. Martín et al. [5] established a finite element model of a crossed roller wire race bearing and investigated the effect of geometric dimensions on the bearing load capacity under an axial load. Martín et al. [6] introduced a simplified sub-model to simulate complex contact among rolling elements, wires, and raceways, with a high consistency between the simplified and original results. Skyba et al. [7] established a finite element model of a slewing bearing and analyzed bearing stiffness, and the results were consistent with the theory.
Due to much contact between the rolling elements and the bearing rings, computation has become quite complicated. To address this problem, Matthis et al. [8] replaced the ball–raceway contact with nonlinear spring elements when establishing a finite element model of double-row four-point contact ball bearings, and experiments proved that the method is correct. He [9] and Liu et al. [10] replaced the ball–raceway contact with nonlinear spring elements when establishing a finite element model of a four-point contact slewing bearing, and the results were consistent with the theory. He et al. [11] replaced the ball–raceway contact with nonlinear spring elements when establishing a finite element model of slewing bearings, and the results were consistent with the theory. Martín et al. [12] proposed a method for establishing a finite element model of crossed roller wire race bearings, using CONBIN39 in ANSYS to replace the contact between the wire and both the rolling elements and the raceway. Li et al. [13] replaced rolling elements with spring units when establishing a finite element model of double-row different-diameter ball slewing bearings, and the results showed that reducing the radius coefficient of the raceway and increasing the diameter of the rolling elements and the contact angle can improve the load capacity. Deng et al. [14] replaced the contact between the rolling elements and the raceways with non-linear springs when establishing a finite element model of a slewing bearing. The obtained results, including the load distribution, ring stress, and contact stress, were consistent with the theory. Li et al. [15] calculated the internal stress distribution of the bearing rings using the mixed finite element model with both solid and spring elements of the slewing bearing assembly. The results were consistent with the engineering practice for slewing bearings. He [16] and Wang et al. [17] replaced rolling elements with nonlinear springs when establishing a finite element model of three-row roller slewing bearings, and the results were consistent with the theory. Chen et al. [18] established four finite element models of slewing bearings with different structures and replaced the contact between the rolling elements and the raceways with spring units; additionally, they studied the effects of the bolt number, bolt pre-tightening force, and other factors on the performance of slewing bearings. Smolnicki et al. [19,20] considered that the contact between the rolling elements and raceways should be replaced with nonlinear springs when researching slewing bearings, and the results had good accuracy.
The use of spring units has greatly improved the efficiency of calculation. Furthermore, several researchers have replaced other units to study the complex contact between rolling elements and raceways. Heras et al. [21] used a cage-like structure composed of beam units to simulate the contact between rolling elements and raceways when establishing a finite element model of a slewing bearing, and the results were consistent with the theory. Duval et al. [22] replaced the contact between rolling elements and raceways with beam units when establishing a finite element model of a slewing bearing and performed fatigue analysis on the bearing, and the results were consistent with the theory. Kunc et al. [23] used bar units to simulate the contact between rolling elements and raceways in their finite element model of a slewing bearing. The results indicate that the method is correct. Alain et al. [24] proposed that a rolling element should be replaced with two nonlinear spring units and eight rigid bar units, and the method can simulate the changes in the contact load and contact angle of rolling elements. Chen et al. [25] replaced a rolling element with eight rigid bar units and two nonlinear spring units when establishing a finite element model of slewing bearings. Kania et al. [26] replaced the rolling elements and the connecting bolts with bar units and beam units when establishing a finite element model of a three-row cylindrical roller slewing bearing and obtained the load distribution of the rolling elements.
However, the majority of current researchers examining slewing bearings are primarily concerned with the performance of the rolling elements, paying little attention to the performance of the bolt. They also exclude the bolts while modeling, just including the inner and outer rings, as well as the rolling portions. Only a few academics, including Kania and Chen, have created finite element models using bolts. Instead of evaluating the bolts’ comprehensive performance, they model them for more accurate results.
The inner and outer rings, as well as the upper and lower supports, are connected by bolts, so it is also necessary to establish an integrated model of slewing bearings that includes the rings, the rolling elements, and the bolts for studying their performance.
Furthermore, the majority of the papers investigate the effect of conventional load parameters such as the radial load, axial load, and overturning moment, with few studies on structural parameters such as the number of rolling elements and bolts, as well as load parameters such as the contact angle, bolt preload, and the angle between radial load and overturning moment.
Therefore, in this paper, the QU2500.50 single-row four-point contact ball slewing bearing is taken as the research object. The bearing support bolt-integrated finite element model is established by HyperMesh 2021 and ANSYS 2022 R1, and its accuracy is theoretically verified. Then, the effects of the rolling element number, contact angle, bolt number, bolt pre-tightening force coefficient, and the angle between the radial load and overturning moment on the comprehensive performance of the bearings and the connecting bolts are investigated, respectively.
2. Finite Element Model
2.1. Basic Structural Parameters of the Slewing Bearing
The structure of the QU2500.50 four-point contact ball slewing bearing is illustrated in Figure 1, comprising inner and outer rings as well as upper and lower supports. The main structural parameters are presented in Table 1. The rings are composed of 42CrMo, with a modulus of elasticity of 210 GPa and a Poisson’s ratio of 0.3. The upper and lower supports are constructed from 45 steel, exhibiting a modulus of elasticity of 209 GPa and a Poisson’s ratio of 0.3. The bolt material is 40Cr, featuring a modulus of elasticity of 206 GPa and a Poisson’s ratio of 0.3. Fa represents the axial load, Fr represents the radial load, and M represents the overturning moment.
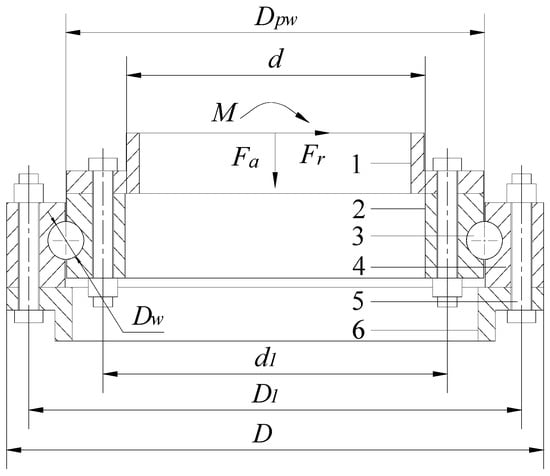
Figure 1.
Four-point contact ball slewing bearing structure sketch. 1–Upper support; 2–inner ring; 3–rolling element; 4–outer ring; 5–bolt; 6–lower support.

Table 1.
Main structural parameters of slewing bearings.
A 3D model of a four-point contact ball slewing bearing is constructed by Solidworks, as represented in Figure 2.
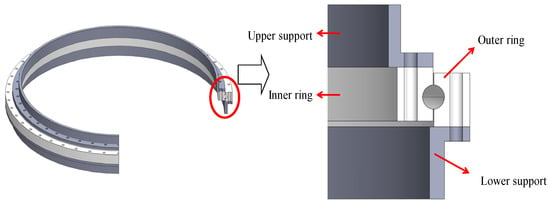
Figure 2.
3D model of a four-point contact ball slewing bearing.
2.2. Simplified Processing of the Finite Element Model
Mesh generation for slewing bearings results in numerous units due to their large structural dimensions and the large number of rolling elements. Moreover, the large number of nonlinear contacts between rolling elements and raceways, as well as the contacts between bolts and supports, not only prolong computational time but also lead to difficulties in achieving convergence of the results. To address this issue, a simplification of the nonlinear contact between rolling elements and raceways is proposed.
Modeling with ANSYS and HyperMesh, the supports and rings are meshed by SOLILD185 units. The inner and outer ring bolts are represented by BEAM188 cells, while each rolling element is modeled with two nonlinear spring units (COMBIN39) and eight rigid bar units (MPC184). This method simplifies the nonlinear contacts between rolling elements and raceways and reduces calculation time, and it also enables the nonlinear spring unit (COMBIN39) to output the contact load between the rolling elements and the raceways. The mesh size is critical to the accuracy of the simulation results. For the accuracy of the simulation results, a finite element model with the same mesh size as the one He [4] used is established. At the same time, the tolerances of lubrication and components are neglected [17,18]. The simplified finite element model is illustrated in Figure 3.
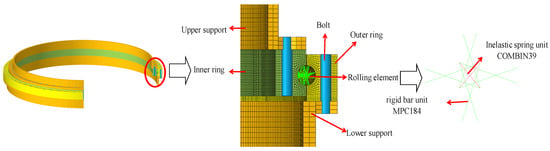
Figure 3.
Integral finite element model of a four-point contact ball slewing bearing.
The lower support is fully fixed by the lower-end face. There are frictional contacts with a friction coefficient of 0.2 [27] between the upper support and the inner ring, as well as between the lower support and the outer ring. The contact geometry we used in ANSYS is based on Hertzian contact theory. The rotational freedom of the non-linear spring units (COMBIN39) is limited to avoid circumferential movement. Preloads are applied to bolts on the inner and outer rings. A central node is established on the upper-end face of the upper support, and all nodes on this face are coupled to the node. External loads are applied to the central node. The loads and constraints are shown in Figure 4.
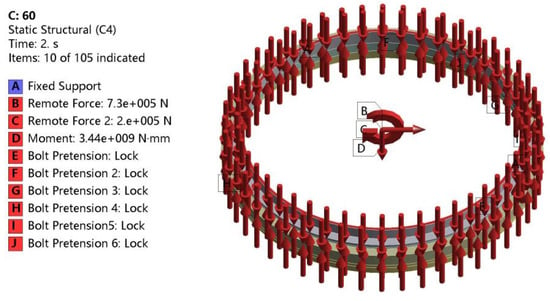
Figure 4.
Bearing constraints and load sketch.
According to the Hertzian contact theory, the nonlinear spring stiffness in the rolling element and the relationship between the deformation (δ) and the load (Q) are expressed by Equation (1).
Here, δ is the spring deformation; Q is the contact load; Σρi and Σρo represent the curvature sum functions of the inner and outer rings, respectively; δi* and δo* represent the dimensionless contact parameters, respectively; μI and μII represent the Poisson’s ratio of the rolling element and the inner and outer rings, respectively; EI and EII represent the elastic modulus of the rolling elements and the inner and outer rings, respectively. At the same time, the plastic deformation of the model is ignored [1]. The model is simulated to obtain the deformation and stress of the bearings and bolts.
The deformation cloud atlas of the slewing bearing, the rings, and the rolling elements and bolts, as well as the stress cloud atlas of the bolts, are shown in Figure 5, where the number of rolling elements is 60. The unit of the deformation of the rolling elements and the inner ring bolts is mm, and the unit of bolt stress is MPa. From Figure 5a,b, the maximum deformation of the bearing is on the upper support, and the maximum deformation of the rings is on the inner ring. From Figure 5c, the maximum deformation of the rolling elements is located at a position angle of 180°. From Figure 5d, the deformation of the inner ring bolts is significantly greater than that of the outer ring bolts. From Figure 5e, the stress of the inner ring bolts is larger than that of the outer ring bolts, and the maximum and minimum stresses appear on the inner ring bolt at 202.5°. At the same time, bolts are subjected to shear, tension, and bending moments. For instance, the bolt BEAM188 unit at the maximum stress is subjected to the forces and moments shown in Table 2.
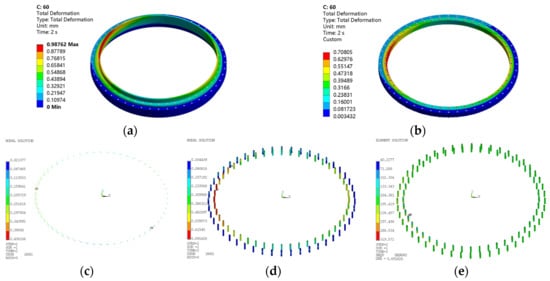
Figure 5.
Static simulation cloud atlas of a slewing bearing: (a) Overall deformation of slewing bearing; (b) Deformation of inner and outer rings; (c) Rolling element deformation; (d) Bolt deformation; (e) Bolt stress.

Table 2.
Forces and bending moments in BEAM188 units where the maximum stresses are located.
2.3. Validation of the Simulation Model
To prove the accuracy of the nonlinear contact between the rolling elements and the raceway, we use the empirical formula of maximum contact loads to verify the finite element model of different numbers of rolling elements. The empirical formula for the maximum contact load (Qmax) is presented in Equation (2):
where Z is the number of rolling elements; α is the contact angle; and H, I, and J are correction factors.
When the diameter of the rolling element and the pitch circle are known, we can calculate the number of rolling elements using Equation (3):
where Kz = 1.01 + 1.9/Dw.
The rolling element number Z ≤ 149.88 can be obtained by taking the parameters in Table 1 into the formula. Therefore, in subsequent studies, the rolling element number should not exceed 149. The maximum contact load is calculated by Equation (2) when the number of rolling elements is 60, 80, 100, 120, or 140. The results are illustrated in Figure 6.
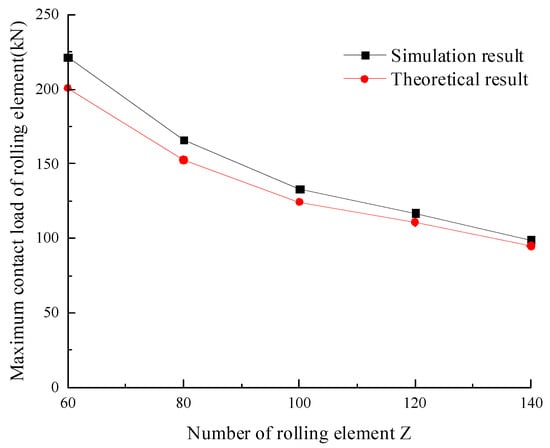
Figure 6.
Simulation and theoretical results of the maximum contact load on the rolling element.
In HyperMesh, the finite element model of slewing bearings is established with the number of rolling elements being 60, 80, 100, 120, or 140. The model is imported into ANSYS, and the same load and constraint conditions as those in the theoretical calculation are imported. The rolling element contact loads are defined, as presented in Figure 7. Q1 is the contact load between the inner ring upper raceway and the outer ring lower raceway; Q2 is the contact load between the inner ring lower raceway and the outer ring upper raceway.
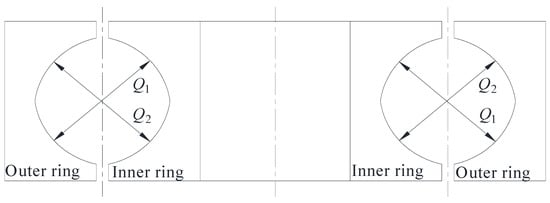
Figure 7.
Definition of rolling element contact loads.
The simulation results for the maximum contact load of the rolling element when the number of rolling elements is different are presented in Figure 6. From the diagram, it can be seen that with the increase in the rolling element number, the simulation results and theoretical results of the maximum contact load gradually decrease. Additionally, the error between the two is always less than 10%. The accuracy of the simplified rolling element in the integrated model is verified.
To verify the accuracy of the simplified BEAM188 model, firstly, Solidworks is used to create a 3D model of the bolt, as shown in Figure 8a. At the same time, the finite element model of the slewing bearing with different numbers of rolling elements is established. The maximum stress curve of the BEAM188 element with different numbers of rolling elements is obtained by static simulation, as shown in Figure 9. Then, the 3D model is imported into ANSYS, where the contact plane between the bolt and the support is set as a fixed constraint. The force and moment on the BEAM188 unit are extracted from the APDL of the ANSYS and applied to the surface of the stud, and then the maximum stress is obtained by static simulation.
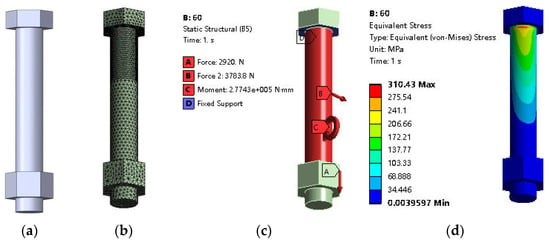
Figure 8.
3D model of solid bolt and simulation cloud atlas: (a) 3D model; (b) Mesh generation; (c) Load and constraint; (d) Stress cloud atlas.
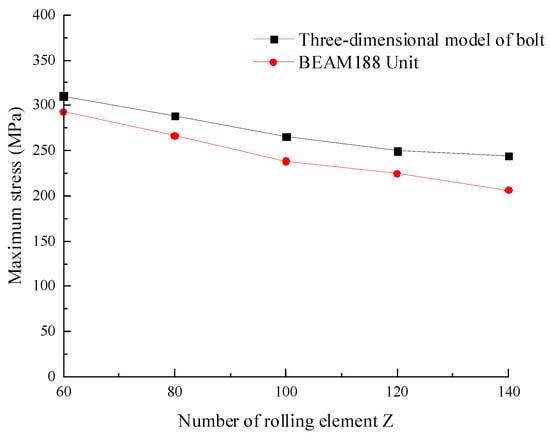
Figure 9.
Maximum stress curves of the 3D model of the bolt and BEAM188 unit with different rolling element numbers.
The mesh division, boundary conditions, and stress cloud atlas of the bolt when the number of rolling elements is 60 are shown in Figure 8. The maximum stress curves of the bolt 3D model with different numbers of rolling elements are shown in Figure 9.
As shown in Figure 9, the maximum stress of the bolt 3D model and the BEAM188 unit decrease gradually with the increases in the rolling element number. The maximum stress error is always less than 7%, which proves the accuracy of the BEAM188 simplified element in the integrated model.
3. Influence of Each Parameter on the Performance of Bearings and Bolts
3.1. Influence of the Rolling Element Number Z
The maximum deformation curves of slewing bearings, inner and outer rings, rolling elements, and bolts with different numbers of rolling elements (Z) are shown in Figure 10. From the diagram, it can be seen that as Z increases, the maximum deformation of the slewing bearing, inner and outer rings, rolling elements, and bolts gradually decreases. When Z increases from 60 to 140, the maximum deformation of the upper support decreases from 0.988 mm to 0.692 mm, the maximum deformation of the inner ring decreases from 0.708 mm to 0.453 mm, the maximum deformation of the rolling elements decreases from 0.436 mm to 0.287 mm, and the maximum deformation of the bolts decreases from 0.692 mm to 0.464 mm, representing decreases of 29.96%, 36.02%, 34.17%, and 32.95%, respectively.
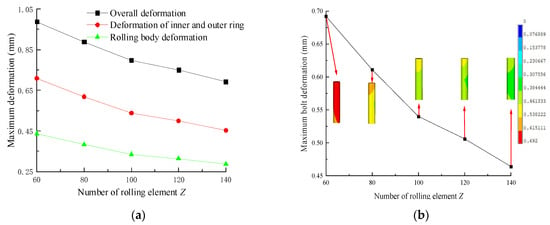
Figure 10.
Maximum deformation curves with different Z values: (a) Maximum deformation curves of bearing, rings, and rolling elements; (b) Maximum deformation curve of bolts.
The contact load distribution curves of the rolling element and the maximum contact load curve of the rolling element with different Z values are shown in Figure 11. From the diagram, it can be seen that the load distribution with different Z values is a cosine curve, and the contact load reaches the maximum when the position angle of the rolling element is 180°. The maximum contact load of the rolling element decreases gradually with the increase in Z. When Z increases from 60 to 140, the maximum contact load of the rolling element gradually decreases from 185.63 kN to 99.1 kN, with a decrease of 46.63%. When Z increases from 60 to 100, the contact load decreases sharply, while when Z increases from 100 to 140, the contact load decreases slowly.
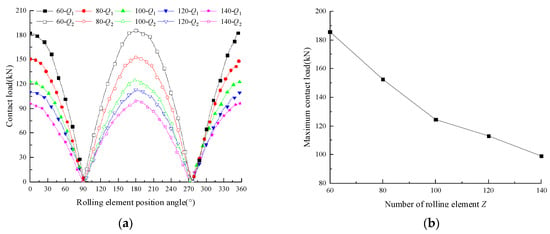
Figure 11.
Contact load curves with different Z: (a) Rolling element contact load distribution curves; (b) Rolling element maximum contact load curve.
The maximum and minimum stress curves of the bolts at different Z values and the stress range curve of the bolts are shown in Figure 12. From the diagram, it can be seen that with an increase in Z, the maximum stress of the bolt and the range of bolt stress decrease gradually, while the minimum stress of the bolt increases gradually, and they are linearly related to Z. When Z increases from 60 to 140, the maximum stress of the bolt decreases gradually from 319.57 MPa to 254.82 MPa, a decrease of 20.26%; the minimum stress increases gradually from 40.23 MPa to 104.02 MPa; and the bolt stress range decreases gradually from 279.34 MPa to 150.8 MPa, a decrease of 46.02%. These findings indicate that increasing Z is beneficial for improving the uniformity of bolt stress distributions.
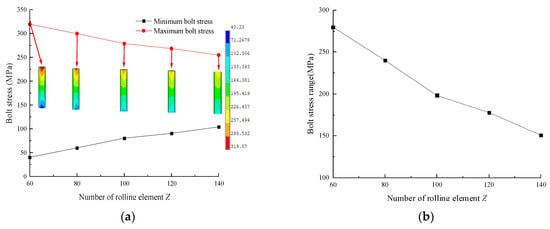
Figure 12.
Bolt stress curves with different Z values: (a) Maximum and minimum bolt stress curves; (b) Stress range curve.
The reason why the bearing deformation, inner and outer ring deformation, rolling element deformation, rolling element contact load, maximum stress and minimum stress of bolts, and bolt stress range change with Z is because the increase in contact area between the rolling element and the raceway increases under the same external load conditions. The external load is borne by more rolling elements, so the load borne by each rolling element and bolt decreases. This causes the deformation of the slewing bearing, inner and outer rings, rolling elements, and bolts, and the contact load of the bolts and the maximum stress of the bolts are also reduced. Therefore, in the case of meeting the structural size, selecting a higher value of Z is beneficial for improving the bearing capacity of the slewing bearing and bolts.
3.2. Influence of Contact Angle α
The maximum deformation curves of slewing bearings, inner and outer rings, rolling elements, and bolts with different values of contact angle α are shown in Figure 13. From the diagram, it can be seen that as α increases, the maximum deformation of the slewing bearing, inner and outer rings, rolling elements, and bolts gradually decreases. When α increases from 25° to 65°, the maximum deformation of the upper support decreases from 1.028 mm to 0.631 mm, the maximum deformation of the inner ring decreases from 0.819 mm to 0.391 mm, the maximum deformation of the rolling elements decreases from 0.605 mm to 0.264 mm, and the maximum deformation of the bolts decreases from 0.811 mm to 0.413 mm, representing decreases of 38.62%, 52.26%, 56.36%, and 49.08%, respectively.
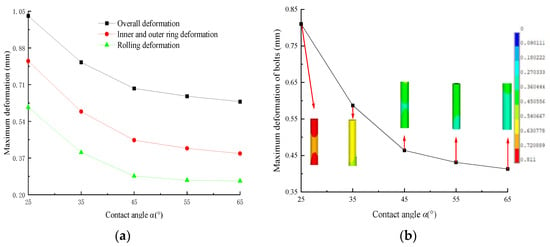
Figure 13.
Maximum deformation curves with different α values: (a) Maximum deformation curves of bearings, rings, and rolling elements; (b) Maximum deformation curve of bolts.
The contact load distribution curves of the rolling element and the maximum contact load curve of the rolling element with different α values are shown in Figure 14. From the diagram, it can be seen that the load distribution with different α values is a cosine curve, and the contact load reaches the maximum when the position angle of the rolling element is 180°. The maximum contact load of the rolling element decreases gradually with the increase in α. When α increases from 25° to 65°, the maximum contact load of the rolling element gradually decreases from 303.3 kN to 87.4 kN, a decrease of 71.20%. When α increases from 25° to 45°, the contact load decreases sharply, while when α increases from 45° to 65°, the contact load decreases slowly.
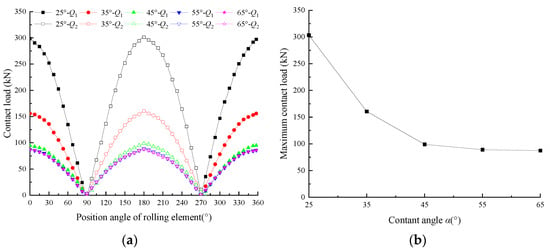
Figure 14.
Contact load curve with different α values: (a) Rolling element contact load distribution curves; (b) Rolling element maximum contact load curves.
The maximum and minimum stress curves of the bolts and the stress range curve of bolts with different α values are shown in Figure 15. From the diagram, it can be seen that with the increase in α, the maximum stress of the bolt and the range of bolt stress decrease gradually, while the minimum stress of the bolt increases gradually, and they are linearly related to α. When α increases from 25° to 65°, the maximum stress of the bolt decreases gradually from 299.5 MPa to 240.32 MPa, a decrease of 19.76%; the minimum stress increases gradually from 60.41 MPa to 118.2 MPa; and the bolt stress range decreases gradually from 239.09 MPa to 122.12 MPa, a decrease of 48.92%. These findings indicate that increasing α is beneficial for improving the uniformity of the bolt stress distribution.
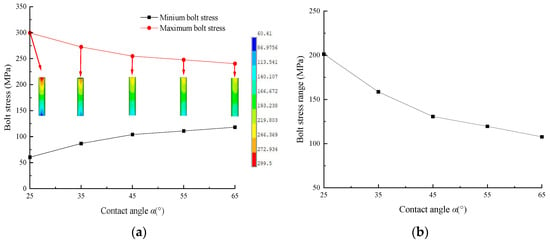
Figure 15.
Bolt stress curves with different α values: (a) Maximum and minimum bolt stress curves; (b) Stress range curve.
The reason why the bearing deformation, inner and outer ring deformation, rolling element deformation, rolling element contact load, maximum stress and minimum stress of bolts, and bolt stress range change with α is because under the same external load conditions, as α increases, the axial bearing capacity of the bearing increases, so that the load on the rolling element gradually decreases, and then the deformation decreases. However, too-large α values cause the contact elliptical surface to exceed the edge of the raceway and the force on the raceway to increase sharply, resulting in the edge collapsing. Therefore, selecting the appropriate α value according to the load conditions of the slewing bearing is beneficial for improving the bearing capacity of the slewing bearing and bolts.
3.3. Influence of the Bolt Number N
The maximum deformation curves of slewing bearings, inner and outer rings, rolling elements, and bolts with different values of the bolt number, N, are shown in Figure 16. From the diagram, it can be seen that as N increases, the maximum deformation of the slewing bearing, inner and outer rings, rolling elements, and bolts gradually decreases. When N increases from 24 to 72, the maximum deformation of the upper support decreases from 1.195 mm to 0.535 mm, the maximum deformation of the inner ring decreases from 0.764 mm to 0.382 mm, the maximum deformation of the rolling elements decreases from 0.570 mm to 0.249 mm, and the maximum deformation of the bolts decreases from 0.906 mm to 0.393 mm, representing decreases of 55.23%, 50%, 56.32%, and 56.32%, respectively.
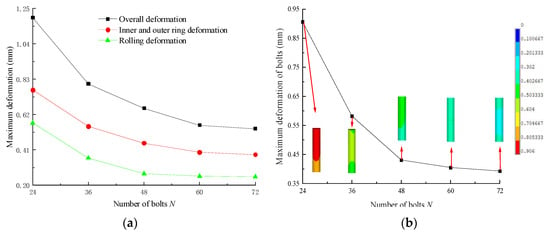
Figure 16.
Maximum deformation curves with different N values: (a) Maximum deformation curves of bearing, rings, and rolling elements; (b) Maximum deformation curve of bolts.
The contact load distribution curves of the rolling element and the maximum contact load curve of the rolling element with different N values are shown in Figure 17. From the diagram, it can be seen that the load distribution at different N values is a cosine curve, and the contact load reaches the maximum when the position angle of the rolling element is 180°. The maximum contact load of the rolling element decreases gradually with the increase in N. When N increases from 24 to 72, the maximum contact load of the rolling element gradually decreases from 277.1 kN to 80.2 kN, a decrease of 71.03%. When N increases from 24 to 48, the contact load decreases sharply, while when N increases from 48 to 70, the contact load decreases slowly.
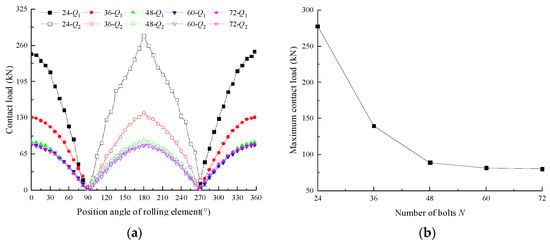
Figure 17.
Rolling element contact load curve with different N values: (a) Rolling element contact load distribution curves; (b) Rolling element maximum contact load curve.
The maximum and minimum stress curves of the bolts and the stress range curve of bolts with different N values are shown in Figure 18. From the diagram, it can be seen that with the increase in N, the maximum stress of the bolt and the range of bolt stress decrease gradually, while the minimum stress of the bolt increases gradually, and they are linearly related to N. When N increases from 24 to 72, the maximum stress of the bolt decreases gradually from 599.1 MPa to 195.28 MPa, a decrease of 67.40%; the minimum stress increases gradually from 0.65 MPa to 153.48 MPa; and the bolt stress range decreases gradually from 598.46 MPa to 41.8 MPa, a decrease of 93.02%. These findings indicate that increasing N is beneficial for improving the uniformity of the bolt stress distribution.
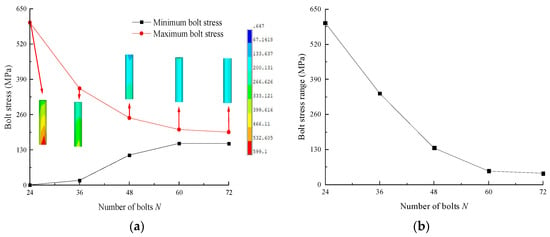
Figure 18.
Bolt stress curves with different N values: (a) Maximum and minimum bolt stress curves; (b) Stress range curve.
The reason why the bearing deformation, inner and outer ring deformation, rolling element deformation, rolling element contact load, maximum stress and minimum stress of bolts, and bolt stress range change with N is because, under the same external load conditions, as N increases, the external load is borne by more bolts, so the load on the rolling element and the single bolt decreases, and finally the deformation decreases. However, with the increase in N, the circumferential wall thickness of the inner and outer rings of the bearing are reduced, which leads to the decrease in the bearing capacity of the inner and outer rings of the bearing. Therefore, under the condition of meeting the structural size, selecting a higher N value is beneficial for improving the bearing capacity of slewing bearings and bolts.
3.4. Influence of Pre-Tightening Force Coefficient P
The maximum deformation curves of slewing bearings, inner and outer rings, rolling elements, and bolts with different pre-tightening force coefficients (P) are shown in Figure 19. From the diagram, it can be seen that as P increases, the maximum deformation of the slewing bearing, inner and outer rings, rolling elements, and bolts gradually decreases. When P increases from 0.4 to 0.8, the maximum deformation of the upper support decreases from 0.530 mm to 0.522 mm, the maximum deformation of the inner ring decreases from 0.385 mm to 0.374 mm, the maximum deformation of the rolling elements decreases from 0.266 mm to 0.251 mm, and the maximum deformation of the bolts decreases from 0.399 mm to 0.477 mm, representing decreases of 1.51%, 2.86%, 5.86%, and 19.55%, respectively.
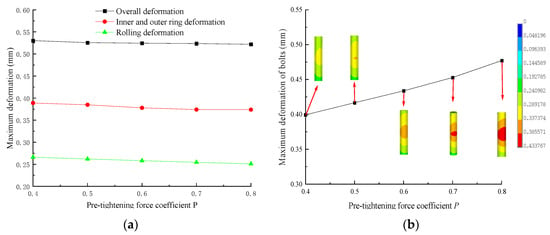
Figure 19.
Maximum deformation curves with different P values: (a) Maximum deformation curves of bearings, rings, and rolling elements; (b) Maximum deformation curve of bolts.
The contact load distribution curves of the rolling element and the maximum contact load curve of the rolling element with different P values are shown in Figure 20. From the diagram, it can be seen that the load distribution at different P values is a cosine curve, and the contact load reaches the maximum when the position angle of the rolling element is 37.5°. With the increase in P, the maximum contact load of the rolling element decreases, but the contact load distribution curve is close, indicating that the change has little effect on the contact load of the rolling element. When P increases from 0.4 to 0.8, the maximum contact load of the rolling element gradually decreases from 88.5 kN to 81 kN, a decrease of 8.42%.
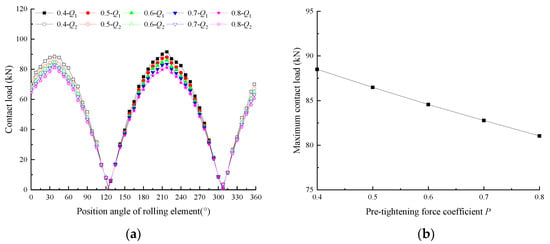
Figure 20.
Rolling element contact load curves with different P values: (a) Rolling element contact load distribution curves; (b) Rolling element maximum contact load curve.
The maximum and minimum stress curves of the bolts and the stress range curve of bolts with different P values are shown in Figure 21. From the diagram, it can be seen that with the increase in P, the maximum stress of the bolt and the range of bolt stress decrease gradually, while the minimum stress of the bolt increases gradually, and they are linearly related to P. When P increases from 0.4 to 0.8, the maximum stress of the bolt increases gradually from 217.03 MPa to 413.79 MPa, an increase of 90.66%; the minimum stress increases gradually from 176.72 MPa to 372.48 MPa; and the bolt stress range decreases gradually from 40.31 MPa to 41.31 MPa, a decrease of 2.48%. These findings indicate that increasing P has little effect on the uniformity of the bolt stress distribution.
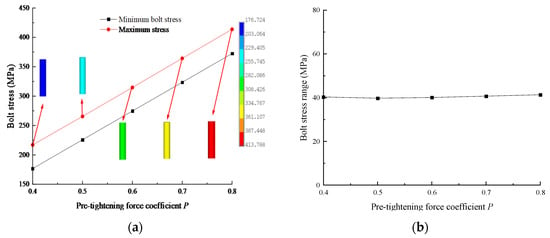
Figure 21.
Bolt stress curves with different P values: (a) Maximum and minimum bolt stress curves; (b) Stress range curve.
The reason why the bearing deformation, inner and outer ring deformation, rolling element deformation, rolling element contact load, maximum stress and minimum stress of bolts, and bolt stress range change with P is because, under the same external load conditions, as P increases, the deformation and stress of the bolt increase, and the connections between the inner and outer rings and the support become closer and closer, resulting in a decrease in the deformation and stress of the inner and outer rings and the rolling element. Therefore, increasing P will reduce the deformation of the slewing bearing, and the load and deformation of the rolling element will also decrease. Thus, under the condition of satisfying the yield strength of the bolt, selecting the appropriate P value is beneficial for improving the bearing capacity of the slewing bearing and the bolt.
3.5. Influence of Radial Load-Overturning Moment Angle θ
The maximum deformation curves of slewing bearings, inner and outer rings, rolling elements, and bolts with different radial loads and overturning moment angles (θ) are shown in Figure 22. From the diagram, it can be seen that as θ increases, the maximum deformation of the slewing bearing, inner and outer rings, rolling elements, and bolts gradually decreases. When θ increases from 0° to 180°, the maximum deformation of the upper support decreases from 1.070 mm to 0.580 mm, the maximum deformation of the inner ring decreases from 0.663 mm to 0.575 mm, the maximum deformation of the rolling elements decreases from 0.364 mm to 0.296 mm, and the maximum deformation of the bolts decreases from 0.685 mm to 0.505 mm, representing decreases of 45.79%, 13.27%, 18.27%, and 18.5%, respectively.
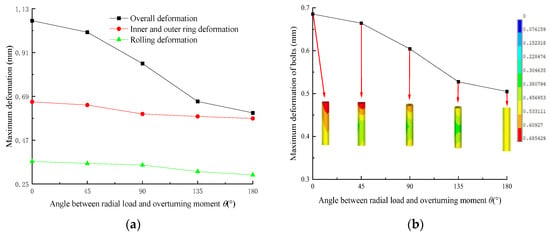
Figure 22.
Maximum deformation curves with different θ values: (a) Maximum deformation curves of bearings, rings and rolling elements; (b) Maximum deformation curve of bolts.
The contact load distribution curves of the rolling element and the maximum contact load curve of the rolling element with different θ values are shown in Figure 23. From the diagram, it can be seen that the load distribution at different θ values is a cosine curve, and the contact load reaches the maximum when the position angle of the rolling element is 142.5°. The maximum contact load of the rolling element decreases gradually with the increase in θ. When θ increases from 0° to 180°, the maximum contact load of the rolling element gradually decreases from 141.4 kN to 103.6 kN, a decrease of 26.74%.
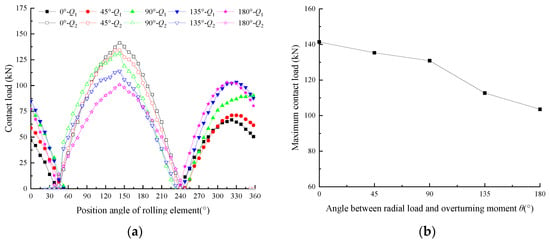
Figure 23.
Contact load curves with different θ values: (a) Rolling element contact load distribution curves; (b) Rolling element maximum contact curve.
The maximum and minimum stress curves of the bolts and the stress range curve of bolts with different θ values are shown in Figure 24. From the diagram, it can be seen that with the increase in θ, the maximum stress of the bolt and the range of bolt stress decrease gradually, while the minimum stress of the bolt increases gradually, and they are linearly related to θ. When θ increases from 0° to 180°, the maximum stress of the bolt decreases gradually from 240.05 MPa to 204.37 MPa, a decrease of 14.86%; the minimum stress increases gradually from 122.46 MPa to 137.85 MPa; and the bolt stress range decreases gradually from 117.59 MPa to 66.52 MPa, a decrease of 43.43%. These findings indicate that increasing θ can improve the uniformity of the bolt stress distribution.
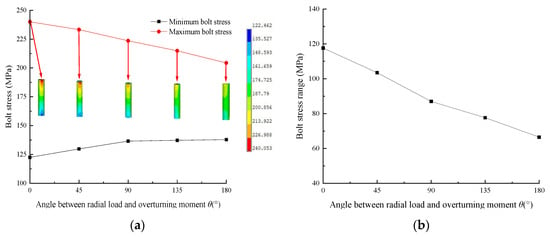
Figure 24.
Bolt stress curve with different θ values: (a) Maximum and minimum bolt stress curves; (b) Stress range curve.
The reason why the bearing deformation, inner and outer ring deformation, rolling element deformation, rolling element contact load, maximum stress and minimum stress of bolts, and bolt stress range change with θ is because, under the same external load conditions, when the radial load acts on the upper-end face of the upper support, an overturning moment is generated at the same time. When θ is 0°, this moment is superimposed with the overturning moment. With the increase in the angle, this moment is offset with the overturning moment, and the offset degree reaches the maximum when the angle reaches 180°. Therefore, with the increase in θ, the load on the rolling element and the bolt gradually decrease, and finally, the deformation of the rolling element and the deformation and stress of the bolt also decrease. Thus, situations where the value of θ is quite small should be avoided, which is beneficial for improving the bearing capacity of slewing bearings and bolts.
3.6. Analysis of the Influence Degree of Each Factor
The influence degrees of different influencing factors, determined through the above analysis, is shown in Figure 25. With increases in Z, α, N, P, and θ, as can be seen from Figure 25a, the maximum deformation of the bearing decreases by 29.96%, 38.62%, 55.23%, 1.51%, and 45.79% respectively; the degree of influence, ranked from large to small, is N, θ, α, Z, and P. It can be seen from Figure 25b that the maximum deformation of the inner and outer rings decreases by 36.02%, 52.26%, 50%, 2.86%, and 13.27%, respectively; the degree of influence, ranked from large to small, is α, N, Z, θ, and P. It can be seen from Figure 25c that the maximum deformation of the rolling body decreases by 34.17%, 56.36%, 56.32%, 5.63%, and 18.68%, respectively; the degree of influence, ranked from large to small, is α, N, Z, θ, and P. It can be seen from Figure 25d that the maximum contact load of the rolling element decreases by 46.63%, 71.20%, 71.03%, 8.42%, and 26.74%, respectively; the degree of influence, ranked from large to small, is α, N, Z, θ, and P. It can be seen from Figure 25e that the maximum deformation of the bolt decreases by 32.95%, 49.08%, 56.62%, 19.55%, and 23.07%, respectively; the degree of influence, ranked from large to small, is N, α, Z, θ, and P. It can be seen from Figure 25f that the maximum stress of the bolt decreases by 20.26%, 19.76%, 67.40%, 90.66%, and 14.86%, respectively; the degree of influence, ranked from large to small, is P, N, Z, α, θ. It can be seen from Figure 25g that the bolt stress range decreases by 46.02%, 48.92%, 93.02%, 2.48%, and 43.43%, respectively; the degree of influence, ranked from large to small, is N, α, Z, θ, P. From the above, it can be seen that increasing α, N, Z, and θ can reduce the deformation, and increasing α, N, Z, and θ can reduce the contact load. Increasing P, N, Z, and α can reduce the maximum stress of bolts. Increasing N, α, Z, and θ can increase the uniformity of bolt stress distribution. Considered comprehensively, the comprehensive performance of bearings and bolts can be improved by increasing α, N, Z, and θ.
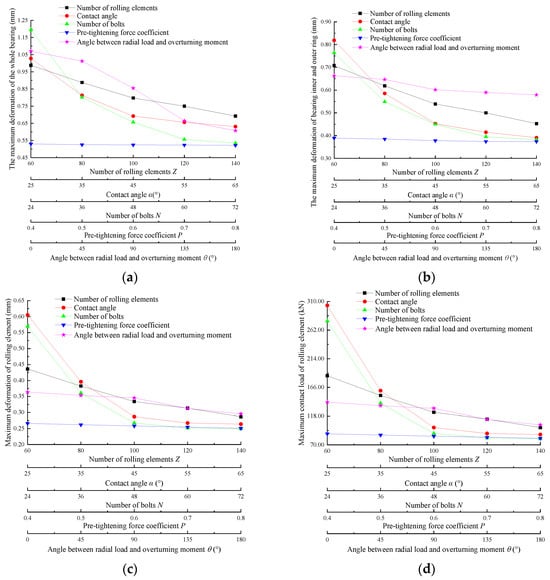
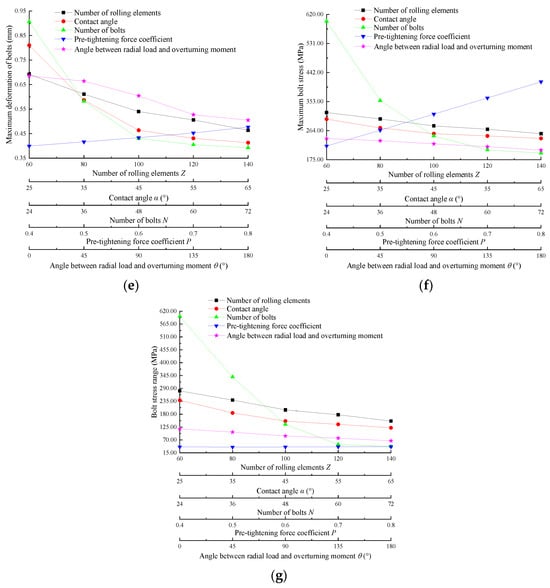
Figure 25.
The influence degree curve of (a) The maximum deformation of the whole bearing, (b) The maximum deformation of bearing inner and outer ring, (c) Maximum deformation of rolling element, (d) Maximum contact load of rolling element, (e) Maximum deformation of bolts, (f) Maximum bolt stress, (g) Bolt stress range.
4. Conclusions
- The simulation results for the maximum contact load of the rolling element were compared with the theoretical results, and the errors were all less than 10%, which verifies the accuracy of the simplified element of the rolling element in the integrated model. The error between the maximum stress of the three-dimensional model of the bolt and the maximum stress of the BEAM188 element was always less than 7%, so the BEAM188 bolt simplified element in the integrated model can be used for static simulation.
- With the increase in Z, α, N, and θ, the deformation of the rings, the deformation and contact load of the rolling element, the deformation and stress of the bolt decrease, and the uniformity of the bolt stress distribution increases. With the increase in P, the deformation of the inner and outer rings of the bearing, the deformation of the rolling element, and the contact load decrease, and the deformation and stress of the bolt increase.
- Among the parameters, the most influential factor on the bolt deformation, bolt stress, and stress distribution uniformity is N. The most influential factor on the ring deformation, rolling element deformation, and rolling element contact load is α. The most influential factor on the bolt stress is P.
- Under the condition of satisfying the structural size of the slewing bearing, increasing α, N, Z, and θ is beneficial for improving the comprehensive performance of the slewing bearing and the connecting bolt.
Author Contributions
Conceptualization, X.L. and Z.H.; methodology, Z.H.; software, X.L.; validation, Z.H., X.L. and Z.S.; formal analysis, Z.H.; investigation, Z.S.; resources, Z.H.; data curation, Z.S.; writing—original draft preparation, Z.S.; writing—review and editing, Z.S.; visualization, Z.S.; supervision, D.Q.; project administration, X.X.; funding acquisition, J.S. and J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Henan Provincial Science and Technology Research and Development Joint Fund (Industrial), grant number 225101610004, the Major Science and Technology Projects in Henan Province, grant number 221100220100, the Key Research and Development Project of Henan Province, grant number 221111220600, Science and Technology Project of Henan Provincial Department of Transportation, grant number 2023-1-2.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
Authors Jingbo Wen and Xinghui Xie are employed by Luoyang LYC bearing company, and Jinggan Shao is employed by Henan Jiaoyuan Engineering Technology company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Correction Statement
This article has been republished with a minor correction to the readability of figures 13, 14, 15, 22, 23, 24, and 25. This change does not affect the scientific content of the article.
References
- Wang, S.; Du, J.; Li, C.; Xia, S.; Jiang, S.; Sun, J. Crack propagation analysis of slewing bearings in wind turbines applying a modified sub-model technology. Eng. Fail. Anal. 2023, 153, 107556. [Google Scholar] [CrossRef]
- He, P.; Hong, R.; Wang, H.; Lu, C. Fatigue life analysis of slewing bearings in wind turbines. Int. J. Fatigue 2018, 111, 233–242. [Google Scholar] [CrossRef]
- Porziani, S.; Biancolini, M.E.; Brutti, C. Analysis of Wind Turbine Pitch 4-Point Contact Bearing. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1275, 012034. [Google Scholar] [CrossRef]
- He, P.; Qian, Q.; Wang, Y.; Liu, H.; Guo, E.; Wang, H. Influence of finite element mesh size on the carrying capacity analysis of single-row ball slewing bearing. Adv. Mech. Eng. 2021, 13, 16878140211009030. [Google Scholar] [CrossRef]
- Martín, I.; Heras, I.; Aguirrebeitia, J.; Macareno, L.M. Influence of the geometrical design on ball and crossed roller wire race bearing behavior under axial load. Tribol. Int. 2021, 156, 106817. [Google Scholar] [CrossRef]
- Martín Lorenzo, I.; Heras Miguel, I.; Coria Martínez, I.; Abasolo Bilbao, M.; Aguirrebeitia Celaya, J. Structural modeling of crossed roller wire race bearings: Analytical submodel for the roller-wire-ring set. Tribol. Int. 2020, 151, 106420. [Google Scholar] [CrossRef]
- Skyba, R.; Hrček, S.; Smetanka, L.; Majchrák, M. Stiffness analysis of slewing bearings. IOP Conf. Ser. Mater. Sci. Eng. 2018, 393, 012060. [Google Scholar] [CrossRef]
- Matthis, G.; Florian, S.; Matthias, S. Validation of a finite-element model of a wind turbine blade bearing. Finite Elem. Anal. Des. 2023, 221, 103957. [Google Scholar]
- He, P.; Wang, Y.; Liu, H.; Guo, E.; Wang, H. Optimization design of structural parameters of single-row four-point contact ball slewing bearing. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 479–496. [Google Scholar] [CrossRef]
- Liu, R.; Wang, H.; Pang, B.T.; Gao, X.H.; Zong, H.Y. Load Distribution Calculation of a four-Point-Contact Slewing Bearing and its Experimental Verification. Exp. Tech. 2018, 42, 243–252. [Google Scholar] [CrossRef]
- He, P.; Wang, Y.; Liu, H.; Guo, E.; Wang, H. Influence of the elastic and elastic-plastic material parameters on the mechanical properties of slewing bearings. Adv. Mech. Eng. 2021, 13, 1687814021992151. [Google Scholar] [CrossRef]
- Martin, I.; Aguirrebeitia, J.; Heras, I.; Abasolo, M. Efficient Finite Element modelling of crossed roller wire race slewing bearings. Tribol. Int. 2021, 161, 107098. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Mao, F. Calculation method for the static carrying curve of double-row different-diameter ball slewing bearings. Sci. Prog. 2023, 106, 368504231180026. [Google Scholar] [CrossRef]
- Deng, B.; Liu, Y.; Guo, Y.; Tang, S.; Su, W.; Lei, Z.; Wang, P. Integral finite element analysis of slewing bearing with flexible rings. IOP Conf. Ser. Mater. Sci. Eng. 2018, 322, 042011. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, D. Strength check of a three-row roller slewing bearing based on a mixed finite element model. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 3393–3400. [Google Scholar] [CrossRef]
- He, P.; Liu, R.; Hong, R.; Wang, H.; Yang, G.; Lu, C. Hardened raceway calculation analysis of a three-row roller slewing bearing. Int. J. Mech. Sci. 2018, 137, 133–144. [Google Scholar] [CrossRef]
- Wang, H.; He, P.; Pang, B.; Gao, X. A new computational model of large three-row roller slewing bearings using nonlinear springs. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 3831–3839. [Google Scholar] [CrossRef]
- Chen, G.; Wang, C.; Xiao, Z. Effects of supporting structure and bolt connection on the fatigue life and carrying capacity of a slewing bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 766–782. [Google Scholar] [CrossRef]
- Smolnicki, T.; Rusiński, E. Superelement-Based Modeling of Load Distribution in Large-Size Slewing Bearings. J. Mech. Des. 2007, 129, 459–463. [Google Scholar] [CrossRef]
- Smolnicki, T.; Derlukiewicz, D.; Stańco, M. Evaluation of load distribution in the superstructure rotation joint of single-bucket caterpillar excavators. Autom. Constr. 2007, 17, 218–223. [Google Scholar] [CrossRef]
- Heras, I.; Aguirrebeitia, J.; Abasolo, M.; Coria, I. An engineering approach for the estimation of slewing bearing stiffness in wind turbine generators. Wind Energy 2019, 22, 376–391. [Google Scholar] [CrossRef]
- Duval, R.; Bennebach, M.; Blasiak, J.; Guelbi, A. Modeling fatigue behavior of slewing rings in crane structures. Identification of influencing parameters on local stresses and fatigue damage calculations. Procedia Eng. 2018, 213, 323–334. [Google Scholar] [CrossRef]
- Kunc, R.; Prebil, I. Numerical determination of carrying capacity of large rolling bearings. J. Mater. Process. Tech 2004, 155–156, 1696–1703. [Google Scholar] [CrossRef]
- Alain, D.; Zouhair, C.; Antoine, G. 3D Simplified Finite Elements Analysis of Load and Contact Angle in a Slewing Ball Bearing. J. Mech. Des. 2008, 130, 082601. [Google Scholar]
- Chen, G.; Wen, J. Load Performance of Large-Scale Rolling Bearings with Supporting Structure in Wind Turbines. J. Tribol. 2012, 134, 041105-1–041105-9. [Google Scholar] [CrossRef]
- Kania, L.; Krynke, M.; Mazanek, E. A catalogue capacity of slewing bearings. Mech. Mach. Theory 2012, 58, 29–45. [Google Scholar] [CrossRef]
- Tian, J.; Bai, R.; Xu, B. Analysis on Factors Influencing Strength of Pitch Bearing Ring and Bolt. Bearing 2020, 3, 34–38. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).