Proposed Multi-ST Model for Collaborating Multiple Robots in Dynamic Environments

Abstract

Coverage path planning describes the process of finding an effective path robots can take to traverse a defined dynamic operating environment where there are static (fixed) and dynamic (mobile) obstacles that must be located and avoided in coverage path planning. However, most coverage path planning methods are limited in their ability to effectively manage the coordination of multiple robots operating in concert. In this paper, we propose a novel coverage path planning model (termed Multi-ST) which utilizes the spiral-spanning tree coverage algorithm with intelligent reasoning and knowledge-based methods to achieve optimal coverage, obstacle avoidance, and robot coordination. In experimental testing, we have evaluated the proposed model with a comparative analysis of alternative current approaches under the same conditions. The reported results show that the proposed model enables the avoidance of static and moving obstacles by multiple robots operating in concert in a dynamic operating environment. Moreover, the results demonstrate that the proposed model outperforms existing coverage path planning methods in terms of coverage quality, robustness, scalability, and efficiency. In this paper, the assumptions, limitations, and constraints applicable to this study are set out along with related challenges, open research questions, and proposed directions for future research. We posit that our proposed approach can provide an effective basis upon which multiple robots can operate in concert in a range of ‘real-world’ domains and systems where coverage path planning and the avoidance of static and dynamic obstacles encountered in completing tasks is a systemic requirement.

1. Introduction

Research has investigated the management of autonomous robots with studies addressing both single and multiple robot operation. Robots are required to navigate a specified operating space (hereafter termed: the defined operating environment (DOE)) where there are static (fixed) and dynamic (moving) obstacles. Such navigation requires the identification of an efficient path the robot will follow to complete the set task where the path will be defined using Coverage Path Planning (CPP) [1,2,3,4]. When considering dynamic obstacles where multiple mobile robots operate in concert (defined as arranging something by mutual agreement or coordination), the robots are, in effect, dynamic obstacles and CPP must accommodate all static and dynamic obstacles in ‘real-time’.

Robots can take many manifestations which include robots operating at ground level [using two-dimensional CPP] to unmanned aerial vehicles (UAV) [using three-dimensional CPP] where the goal is to optimize the operation of multiple UAVs while avoiding collisions [5,6]. We defer a discussion on related research to Section 2. In this study we are interested in the operation of multiple mobile robots operating in concert, the goal being to autonomously optimize the paths taken by the mobile robots within a DOE to achieve a pre-defined task [2] while implementing the avoidance of static and dynamic obstacles [4].

In this paper, we present our proposed Multi-ST model which combines intelligent robot reasoning with knowledge-based reasoning techniques to realize effective and flexible CPP in dynamic unknown environments. The Multi-ST model uses the Spiral Spanning Tree Coverage (SSTC) algorithm to enable a robot (or multiple robots operating in concert) to autonomously implement path planning decisions. The proposed model applies knowledge inference with the SSTC algorithm to enable optimal CPP with effective obstacle avoidance. In our research we have divided the CPP algorithms into two approaches using the spanning tree algorithm (STA) [7,8]: (i) offline, and (ii) online. We introduce these methods in Section 3.2 with the proposed Multi-ST model introduced in Section 4.

In experimental testing, we have evaluated the Multi-ST model in a simulation case study which implements physical robots in a cleaning task in a DOE including a comparative analysis of alternative current approaches under the same conditions. The results are reflected in performance metrics which include the coverage percentage, path length, and execution time. The reported results demonstrate the effectiveness of the Multi-ST model and its capability to implement the avoidance of static and moving obstacles by multiple robots operating in concert in a DOE. Moreover, the comparative analysis shows that our Multi-ST model outperforms existing models in coverage quality, robustness, and scalability.

Our contribution builds on earlier published studies where CPP with linguistic and semantic methods have been employed. Our contribution may be summarized as follows:

•

The Multi-ST model enables single and collaborating multiple robots to achieve optimal CPP while implementing avoidance of both static and dynamic obstacles. Novel obstacle avoidance is implemented using a rule-based approach with updating of the rules in the knowledge base (KB) to optimize CPP.

•

The proposal set out in this paper provides an effective basis upon which the complex problems resulting from CPP by multiple collaborating mobile robots can be solved (or at least mitigated). Where multiple robots operate in concert in a DOE, each robot can exchange the coverage and obstacle information with other collaborating robots.

•

Multiple robots operating in a DOE can complete a defined task more effectively than is the case for a single robot which provides: (a) operational advantages in diverse domains and systems, and (b) significant savings in terms of time with improved effectiveness when employed in the exploration and coverage of unknown environments.

The limitations of this study are set out along with related challenges, open research questions, and proposed directions for future research. We posit that our proposed approach can provide an effective basis upon which multiple robots can operate in concert in a range of ‘real-world’ domains and systems where CPP and the avoidance of static and dynamic obstacles encountered in completing tasks is a systemic requirement.

The remainder of this paper is as follows: related research isconsidered in Section 2. An overview of robot sensor design and development is set out in Section 3.1. Preliminaries are introduced in Section 3 where algorithm design is considered. The proposed Multi-ST model is set out in Section 4 with the processing by robots discussed in Section 5.2. Testing and evaluation is described in Section 6 with the results provided in Section 7. Section 8 provides a discussion with consideration of open research questions and directions for future research. The paper closes with concluding observations in Section 9.

2. Related Research

This paper is not a systematic survey of the field as the literature contains a large volume of published studies investigating CPP in heterogeneous domains as discussed in [1,2,9] where a multiplicity of published studies proposing methods to address CPP are introduced. For a survey on multi-robot CPP for model reconstruction and mapping see [10] with an overview of formulations and solution procedures for the multiple traveling salesman problem provided in [11]. Choset in [2] provides a survey of recent results related to CPP and “coverage for robotics”. Galceran and Carreras in [1] address CPP with a survey of the “most successful” CPP methods with a focus on the achievements made in the past decade. Galceran and Carreras consider CPP methods with the field of CPP for successful works. Significant examples of studies related to CPP that are relevant to the research which forms the focus of this paper are considered in this section.

CPP algorithms that rely on the SSTC algorithm and/or CPP problem constraints can be classified into two basic approaches: (i) complete coverage algorithms, and (ii) optimal coverage algorithms. In summary: complete coverage algorithms cover the entire DOE. In some studies, the algorithm is required to optimize the DOE including consideration of factors and conditions such as power and the maximum elapsed time. When the work area is large, complete coverage in CPP cannot be guaranteed; this is a limitation not shared by the optimal coverage algorithms.

The online sensor-based CPP is addressed by Gabriely et al. using an SSTC algorithm to implement CPP using the Spiral-STC in [8]. The algorithm has been implemented for a single robot operating alone with reported results claiming to realize a “guaranteed return-time bound”. For multi-robot operations, Hazon and Kaminka [12] propose the multi-robot SSTC algorithm termed MSTC where improvement in coverage time is achieved by backtracking optimization. However, the results for the MSTC algorithm are dependent on parameters to compute the edge cost in covering and spanning graphs. Agmon et al. have introduced an SSTC algorithm with two phases [7]: (i) a polynomial-time tree-construction algorithm for offline coverage, and (ii) an online coverage of a finite terrain based on a spanning-tree.

The multi-robot forest coverage (MFC) algorithm is a polynomial-time multi-robot coverage algorithm based on an algorithm introduced by Even et al. in [13]. The MFC algorithm is proposed in [14] where the approach utilizes multiple minimal spanning trees to cover the terrain generated by the min-max tree cover algorithm. In practical situations, there are many physical constraints that must be considered and addressed in CPP and analysis of these approaches identifies weaknesses in that they fail to consider constraints implicit in robot operation.

Zheng et al. in [15] consider CPP and the MFC algorithm providing simulation results that demonstrate that coverage times for the MFC method have been tested in scenarios of alternative multi-robot coverage algorithms. Zheng et al. show that solving several versions of multi-robot coverage problems with minimal coverage time is an NP-hard problem [16,17] and argue that this provides motivation for designing polynomial-time constant-factor approximation algorithms. Even et al. [13] consider constant factor approximation algorithms for covering the nodes of graphs using trees (rooted or unrooted) and argue that such problems are related to location routing and the traveling salesman problem [16]. In considering NP hard problems Cheeseman et al. in [18] consider “where the really hard problems are”. Additional discussion on random graphs can be found in [19,20,21] with a guide to the theory of NP-completeness as it relates to computers and intractability provided in [22]. We consider NP hard problems as they relate to this study CPP in Section 8.

CPP algorithms incorporating constraint satisfaction have been addressed in recently published studies. For example in [7,12,13,14] [introduced previously in this section] CPP for a single robot is addressed with consideration of the measurement of robot energy limitation. Zheng et al. in [23] present a study where CPP relates to multi-robot forest coverage where the DOE can be covered more effectively and efficiently using multi-robot operation. Zheng et al. observe that coverage times are “at most eight times larger than optimal” and their reported experimental results show that the proposed method performs “significantly better than existing multi-robot coverage algorithms”. Pengzhan Chen et al. have investigated CPP using deep reinforcement learning to target a destination for dynamic obstacle avoidance [24]. Studies have applied a multi-strategy particle swarm approach using exponential noise in order to solve low altitude penetration in secure space [25].

An interesting study in [26] proposes a new method for the path planning of the robotic arm mounted on the free-floating unmanned spacecraft where the path of the arm is described in the joint space by a spline function and the coordinates of spline knots form the vector of decision variables. The proposed model generates a collision-free path of the arm that “results in the desired position and orientation of the gripper and the desired attitude of the spacecraft”. The reported results show that the path obtained using the proposed model is shorter and smoother than the bi-directional Rapidly-exploring Random Trees (RRT) algorithm and the RRT path.

Complete CPP algorithms are represented in the decomposition strategies in both static and dynamic environments [1], a decomposition strategy being defined as sub-regions or cells that use space using simple trapezoidal or triangular shapes [27]. As noted in [28] a “Morse function” can be utilized for CPP in dynamic environments. For sensor-based robot systems, there is a range of graph-based methods [29] including 3D data [30,31], and landmarks [32] in CPP, with grid-based decomposition as proposed in [2,33]. Sipahioglu et al. in [34] propose a novel algorithm for sensor-based [robot] coverage of narrow environments by considering the energy capacities of the robots. In the model proposed in [34], path planning was “modeled by a Generalized Voronoi diagram-based graph to guarantee complete sensor-based coverage”.

A number of algorithms can be used to ‘section’ a DOE based on a grid strategy including the ‘energy-aware’ algorithm neural networks [35,36], and spanning trees [8]. The studies reduce the complexity required in terms of computational overhead incurred in determining a coverage path with the majority of CPP algorithms being based on the grid decomposition strategy. In related works, robot path planning is used to apply geometric models [37]. CPP for a mobile robot has been achieved by visiting a map in a dynamic environment [38], for example, selected map locations have been determined in [39] with CPP in DOE without obstacles being addressed in [9].

Huang et al. in [40] have investigated multi-robot coverage path planning (MCPP) algorithms to solve the CPP problem of robots in specific areas including outdoor environments, different landscapes, and emergency search and rescue tasks. The inherent complexities are noted along with a method to address such complexities. In summary, Huang et al. describe the “visual fields” of the robots by constructing hierarchical and topological relationships among the cells in the same and different layers. Reported results claim that the CPP achieved is an “efficient MCPP algorithm”.

Research has investigated intelligent robot CPP with a view to energy saving for both single and multiple robots in uncertain environments [41,42,43,44]. Hameed in [41] considers intelligent CPP for agricultural robots and autonomous machines in a 3D Terrain. Shnaps and Rimon in [42] address the online coverage of unknown planar environments by a battery-powered autonomous mobile robot operating with a limited energy capacity battery is considered. CPP in situations where energy constraint is the significant feature is discussed by Wei and Isler in [43,44] where energy-efficient CPP for general terrain by an autonomous vehicle is addressed. Applied energy-constrained multi-robot sensor network systems are designed to minimize energy cost which is a solution for aggregating multiple robots [34,40].

In a related study, Tang et al. in [45] note that for large-scale tasks, effective coverage with CPP can benefit greatly from the use of multiple robots operating in concert. Tang et al. introduce the $M^{\ast }$ algorithm for multi-robot coverage path planning (mCPP) based on spiral spanning tree coverage (Spiral-STC) which includes physical constraints such as “terrain traversability and material load capacity”. In a comparative analysis with the state-of-the-art in mCPP for regular grid maps and ‘real-field-terrains’ in simulation environments, the reported results support the conclusion that the $M^{\ast }$ method outperforms current existing SSTC-based mCPP methods. However, this algorithm cannot guarantee to find the optimal solution and importantly has not been verified and validated in experimental testing using actual physical robots.

In a paper entitled “On optimal coverage of a tree with multiple robots” Aldana-Galván et al. in [46] study the algorithmic problem of optimally covering a tree with k mobile robots where the tree is known to all robots. The goal here is to assign a walk to each robot in such a way that the union of these walks covers the whole tree. The study considers a variant in which the robots must rendezvous periodically at the same vertex in a certain number of moves and it is shown that for the two cost functions the problem formulation is different. For the “cover time minimization problem” the problem is shown to be NP-hard when k is part of the input irrespective of the requirement for periodic rendezvous. Aldana-Galván et al. posit that “the cover length minimization problem can be solved in polynomial time when periodic rendezvous are not required, and it is NP-hard otherwise”.

The $A^{\ast }$ algorithm is an approach to CPP employed in [47,48]. The $A^{\ast }$ algorithm has been used to control autonomous mobile robots as shown in [49,50]. The Spanning Tree Coverage (STC) algorithm has been used in CPP [8] with knowledge reasoning applied in [4,51] where it is argued that robot CPP and the STC algorithm with knowledge reasoning represents the optimal approach for decision-making for single robot operation. While the methods identified have shown significant experimental results there are limitations when implemented in dynamic environments where coordinated multiple mobile robots operating with optimal CPP are the preferred solution to realize the designated task.

Some advanced techniques such as knowledge graphs (KG) and fuzzy knowledge graphs (FKG) with reasoning can be applied to the decision-making of robots for healthcare domains [52,53,54,55]. In [52] a “novel Q-learning-based FKG-Pairs approach for extreme cases in decision making” is presented with the conclusion drawn that the FKG-Pairs approach is considered one of the best models to solve classification problems based on “uncertain and amplitude input datasets” as it can infer and find the output labels of new samples that are not in the fuzzy rule base. Further work in this area is presented in [54] where a novel fuzzy KG pairs approach to decision making is proposed.

In [55] a proposed deep learning model integrated with a KG to enable the monitoring of human behavior in forest protection situations is shown. Pham et al. in [55] address the modeling of the relationship between human behavior and forest protection using a deep learning model integrated with a KG. A deep learning technique has been investigated as it relates to the use of a robot(s) in forest fire rescues [11]. Applied optimal coverage using a deep learning model integrated with a KG for monitoring human behavior in forest protection has demonstrated the capability to solve complex problems in decision making [56] and applied smart autonomous robots in forests can enhance the performance of robots using ChatGPT in finding the road under uncertain environments [57,58,59].

Other techniques, including reasoning and the crowd-drawing effect, can be applied in ‘real-world’ applications of single and multiple robots in multiple decision making [3,60]. There is an interesting correlation between the discussion in [60] and the social force model [61], crowd dynamics, and the selection of an available route(s) during evacuation in emergency situations [62]. A robot(s) with a priori knowledge of the architectural layout of an area may be a useful guide.

From this brief review of relevant related research, we may conclude that CPP has been shown to be successful in many domains using a range of methods and algorithms. In this paper, we present our proposed Multi-ST model which combines robot reasoning with knowledge reasoning techniques using the SSTC algorithm. The proposed model is designed to enable optimal CPP while avoiding both static and dynamic obstacles and experimental results show that the proposed approach enables the avoidance of obstacles by multiple robots operating in a dynamic DOE with improvements in CPP and efficiency.

3. Preliminaries

In Section 2 we have identified a number of significant relevant CPP methods and algorithms. In this section we briefly consider networked robot systems (NRS) and provide an overview of spanning Trees (ST) (see Section 3.2), the online Spiral STC algorithm (see Section 3.3), and the full spiral-STC algorithm in (see Section 3.4). The proposed Multi-ST model is introduced in Section 4.

3.1. Networked Robot Systems

Prior to considering our proposed Multi-ST model, we provide a brief overview of sensors and related technologies as they relate to this study, such technologies are generally termed NRS. In this study, it is assumed that robots are equipped with networked onboard sensors designed to provide the data required to enable the detection of all obstacles, boundaries, and directions of travel. Moreover, the sensors will allow robot(s) to identify and scan the surrounding mega-cells and also in the current mega-cell.

Sensor technologies represent a large and complex topic and a detailed consideration is beyond the scope of this paper; however, readers interested in advances in robotics and related sensor technologies may consider the research documented in [63,64,65,66,67,68] where NRS and advances in sensor technologies are addressed.

Kala et al. in [63] consider emerging methods and their application in modeling, identification and robot control with the “multi-heterogeneous sensor data fusion method via convolutional neural network for fault diagnosis of wheeled mobile robot” operation addressed in [64]. The “3D self-deployment of jumping robot sensor nodes for improving network performance in obstacle dense environment” is addressed by Zhang et al. in [65].

Network Robot Systems (NRS) are introduced with related definitions in [66] “as is understood in Europe, USA and Japan”. Moreover, it describes some of the NRS projects in Europe and Japan and presents a summary of the papers published in a special issue on the topic. Sanfeliu et al. in [67] extend previous research in a study investigating “decentralized sensor fusion for ubiquitous networking robotics in urban areas”. The paper considers the architecture for the environment and sensors that have been built for the European Ubiquitous Networking Robotics in Urban Sites project.

Borenstein et al. in [68] have studied sensors and related techniques for the positioning of mobile robots. Seven categories for positioning systems are identified: (1) Odometry, (2) Inertial Navigation, (3) Magnetic Compasses, (4) Active Beacons, (5) Global Positioning Systems, (6) Landmark Navigation, and (7) Model Matching. However, given the multiplicity of “ingenious approaches”, Borenstein et al. caveat that “for reasons of brevity, not all could be cited in this article”.

There are seminal research studies where advanced sensor design has been realised; see for example the work of Sheila Nirenberg et al. and colleagues in [69,70]. The research had a focus on human vision with research addressing the “classification of Retinal Ganglion Cells” [69]; results from numerous studies have shown that such cells exhibit an array of responses to visual stimuli resulting in the notion that “these cells can be sorted into distinct physiological classes, such as linear versus non-linear or on versus off”. In [70] Retinal Ganglion Cells have been shown to “act largely as independent encoders” and “correlated firing among neurons is widespread in the visual system”. Nirenberg et al. have, in subsequent research, applied their research into human vision to robotic sensor systems with robots having vision sensors that can enable autonomous robot control. This work has interesting potential applications for robot control given the developments in artificial intelligence (AI) and machine vision as discussed in [71,72].

The design of autonomous robotic systems must address the required hardware and software systems where such systems will incorporate the hardware [and software functionality] in the form of sensors, actuators, and communication [between robots] where multiple robots operating in concert is clearly required. The operating system of a robot requires a variety of sensors including vision, sound, location, and an accelerometer. Moreover, depending on the operating environment (e.g., an external location) robots may need cloud-based systems, GPS, and possibly the Internet-of-Things (IoT) connectivity.

3.2. Spanning Trees

Considered in terms of graph theory, an ST T for an undirected graph G is a sub-graph that is a tree that includes all of the vertices of G. A graph G may have several STs but a graph that is not connected will not contain an ST. If all of the edges of graph G are also edges of a ST T of G, then graph G is an identical tree to ST T.

A deterministic ST algorithm is introduced by Pettie and Ramachandran in [73] where it is established that the algorithmic complexity of the minimum ST problem is equal to its decision-tree complexity. The ST algorithm introduced by Pettie and Ramachandran aims to identify an ST for a graph with n vertices and m edges that runs in time $\left\{O\left(T^{\ast }\left(m,n\right)\right)\right\}$ where $T^{\ast }$ is the minimum number of edge-weight comparisons needed to determine the solution. In operation, when viewed from the perspective of this study, the ST is implemented using two methods: (i) offline and (ii) online:

off-line ST: 

Provides a priori knowledge of the DOE to the robot(s) relating to static and dynamic obstacles. The algorithm finds an optimal path in linear time $O\left(n\right)$ [73] where n is the number of cells in the DOE. Pettie and Ramachandran note that “…although our time bound is optimal, the exact function describing it is not known at present…”, for a detailed discussion on the topic see [73].

on-line ST: 

Provides no a priori knowledge of the dynamic DOE where the location of static obstacles will be a priori known. This method addresses the related mathematics using information such as the location of static [generally known] and/or dynamic [generally unknown] obstacles. Dynamic obstacles will include cooperating with multiple robots operating in concert in the same DOE. Using the knowledge database, the online method can manage both static and dynamic obstacles. In the online ST algorithm, the robot incrementally constructs a spanning tree for a grid representing the DOE. The process is as follows:

Step 1 

The path of the robot is formed from the mega-cell containing the initial position of the robot to an empty neighbor mega-cell in a counter-clockwise direction.

Step 2 

During the construction of the spanning tree, the robot subdivides every cell it encounters into four identical sub-cells of $\left[2\times 2\right]$ size.

Step 3 

Following step 2, the robot follows a sub-cell path that circumnavigates the incrementally constructed spanning tree until the defined operational environment is covered.

Step 4 

The robot then returns to the initial (starting) position in the opposite direction, avoiding traversing any cell previously traversed twice (because the mega-cell size is of $\left[2\times 2\right]$ size).

The ST algorithm is based on the following:

Assumption: the size of mega-cell is $\left[2\times 2\right]$ where the smaller cell size is $\left[1\right]$.

Input: for the robot’s initial position cell there is no a priori knowledge of the DOE.

Recursive ST $\left(w,x\right)$ function: where $\left(x\right)$ is a cell containing the starting robot position         and $\left(w\right)$ is the parent cell.

Initial ST $\left(null,s\right)$ function: where $\left(s\right)$ is the starting cell.

The algorithmic process is as follows:

1 Mark the current cell $\left(x\right)$ as an old cell

2 Scan the neighboring cell of $\left(x\right)$ in counter-clockwise order         While (x has free neighboring cell):                    Cell $\left(y\right)$ is free                    Construct a spanning tree edge from $\left(xtoy\right)$                    Move to a sub-cell of $\left(y\right)$ as described below                    Execute function STC $\left(w,x\right)$         End While

3 If the current cell is not the initial cell $\left(x\#s\right)$ return to the parent-cell

4 Terminate function STC $\left(w,x\right)$

The path-finding procedure of the algorithm is not complex and the relative simplicity of the process is a result of a robot recognizing mega-cells with no obstacles. When assessing adjacent mega-cells, the robot prioritizes them in a counter-clockwise sequence (i.e., up, left, down, and finally right. For scenarios where no mega-cell is identified, the robot chooses to revert to a parent cell. The construction process for the STA edge is modeled in Figure 1.

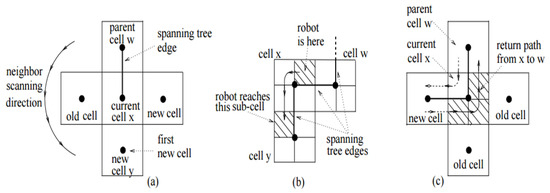
Figure 1. A model showing the path-finding procedure of the STA; (a) counterclockwise scanning of four neighbors. (b) a move from x to a new cell y. (c) a return from x to a parent cell w.

3.3. The Online Spiral Spanning Tree Algorithm

The ST algorithm has been shown to provide an effective basis upon which CPP can be achieved in unknown environments. However, it is not without limitations as it may not be capable of covering the whole of the DOE due to the potential for unidentified obstacles. This limitation has spurred the development of the online spiral spanning tree (OSST) algorithm which is an extension of the ST algorithm with the goal of ensuring complete coverage of the DOE.

In the CPP process path-finding introduces increased complexity and complication as a robot may try to traverse a mega-cell containing obstacles. Consequently, the assumption that a robot traverses the right side of spanning tree edges is not universally accurate. In certain instances, as depicted in Figure 2, robots must navigate in varying directions to guarantee complete coverage. When a robot encounters such a situation, as illustrated in Figure 2, it must pass through the edge of the spanning tree, as modeled in Figure 3.

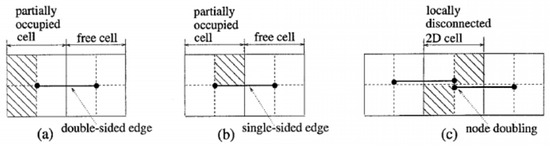
Figure 2. Special side-edges in STC consisting of (a) double-sided edge; (b) single-side edge; (c) node doubling.

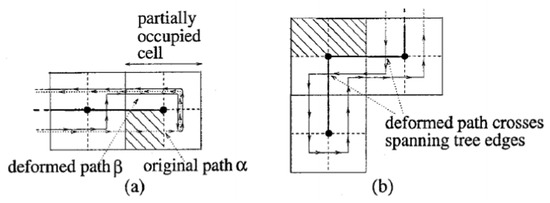
Figure 3. The approach to manage (i.e., avoid) special obstacles consisting of (a) partially occupied cell; (b) deformed path crosses spanning tree edges.

3.4. The Full Spiral Spanning Tree Algorithm

Here, we introduce the algorithmic process for the full spiral spanning tree (FSST) Algorithm:

Initialization: Call ST $\left(Null,S\right)$ where $\left(S\right)$ S is the starting cell

FSST $\left(p,c\right)$

1 Mark the current cell $\left(x\right)$ as an old cell

2 Scan the neighbor cell of $\left(c\right)$ in counter-clockwise order.         While ($\left(c\right)$ has new obstacles-free neighbor):                If ($\left(n\right)$ find obstacle):                     If there is a cell available return $\left(n\right)$                     Else continue to scan other neighbors                     If $\left(n\right)$ is suitable                          Construct a spanning tree edge from $\left(cton\right)$                          Move to cell $\left(n\right)$                          Call recursive STC-full $\left(c,n\right)$         End While

3 If the current cell is not the initial cell, return to the parent cell

4 Terminate FSST $\left(p,c\right)$

The pseudo-code is as follows:

FSST() {             current.setStatus $=$ false;             if (not scan neighbor cell) {                       neighbor $=$ findNewNeighbor(current);             } else {                        robotWork $\left(x,y\right)$;             } }

4. The Proposed Multi-ST Model

In Section 3 we have provided an overview of a number of significant relevant CPP methods and algorithms including the ST algorithm (see Section 3.2), and the FSST algorithm (see Section 3.4). In this section we introduce our proposed Multi-ST Model to collaborate multiple robots in a dynamic DOE as shown in Figure 4.

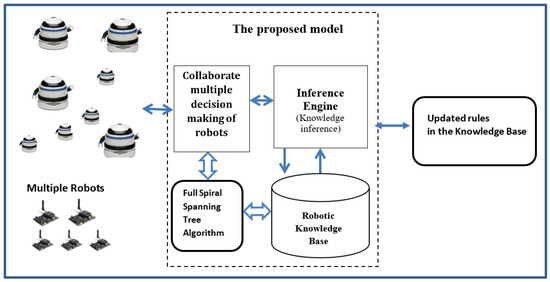
Figure 4. The proposed Multi-ST Model.

The proposed model consists of seven steps as follows: Step 1, identify multiple objectives for collaborative multiple decision-making in support multiple robots; Steps 2–3, consider an objective function as updated decision variables by dealing with multiple decision-making of Robots; Step 4, consider constraints in multiple decision-making for aggregation of multiple robots’ tasks; Step 5, a primary objective of the FSST algorithm is to ensure that each robot constructs a distinct spanning tree during the navigation of the DOE; Step 6, consider rule and update its weight to the Robotic Knowledge Base (KB); Step 7, find the appropriate rules considered by experts and applied these rules’ weights in the KB. In the processing steps, multiple robot operations can result in reductions in the time taken to cover the DOE given the parallel robot processing implemented in the FSST algorithm. In robot simulations in the experiments, the robot applies existing rules with good behaviors in the Inference Engine for coverage path planning.

4.1. Conceptual Terms and Definitions

We can formulate a conceptual term and definition as follows:

• Let CR be an objective function designed to minimize the optimal paths in priority selection of coverage robots in decision-making when dealing with multiple robots;
• Let $\left(D_j\left(Y\right)\right)$ be presented as a linguistic value in the variables and these linguistic values in the fuzzy weights $\left[0,1\right]$;
• Assume that a collaboration of multiple decision-making robots is present in domain S;
• Let E be the decision makers’ input for the proposed Multi-ST Model in domain S;
• Let $R{B}^S=\{R{B}_1^S,R{B}_2^S,\dots ,R{B}_m^S\}$ be a set of Robots S, where m is the number of Robots.
• Let the quantified semantics work in the mapping of $\left(CR\right)$, presented in linguistic values for $\left(w_j\right)$ fall in the range [0,1].
• Calculate an objective function value for $\left(D_j\left(Y\right)\right)$ in domain S;

4.2. Collaborate Multiple Decision Making of Robots

The proposed algorithm is described as follows:

Step 1:

Implement collaborative multiple decision-making to support multiple robots. The proposed model identified multiple objectives for the optimal paths in the priority selection of coverage robots as shown in Equation (1):

$$CR={\displaystyle \frac{Min}{x}}\sum w_j.D_j\left(Y\right)$$

(1)

where the constraints are as follows:

• ${\sum }_k{Y}_{ik}=1\forall i\in N$
• ${\sum }_{i\in P_{j}U{Q}_i}{x}_{i1}\ge 1$
• $x_{ik}=\{{\displaystyle \frac{1,IfoptioniisdecidedaRobottovisit\left(k\right)}{0,other}}$

Step 2:

Consider an objective function by dealing with multiple decision-making of Robots;

Step 3:

The decision variables $\left(Y_{ij}\right)$ can be considered objectives in the multiple criteria decision-making of robots.

Step 4:

Consider constraints in multiple decision-making for the aggregation of multiple robots’ tasks $\left(P_i^S\right)$ where $\left(\left(P_i^S\cap Q_j^S\right)=\left(\theta ,\forall i,j\in \{1,2,\cdots r\}\right)\right)$.

Step 5:

Identify all paths identified in monitoring multiple robots using the FSST algorithm.

Step 6:

Consider the rule and update its weight to the Knowledge Base for each node of $\left(V_i^S\right)$ visited, consider Rule $\left(j\right)$ represented by $\left(R_j\right)$ and apply $\left(V_i^S\right)$ as follows. In fuzzy rule-based reasoning, the fuzzy rules are generally expressed for two input variables and one output as a decision variable, as given by Equation (2):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{R}^i:\mathrm{if} x_1 \mathrm{is} Condition{A}_{i1} \mathrm{and} x_2 \mathrm{is} A_{i2} \mathrm{then} y \mathrm{is} V_i\hfill \\ ⋮\hfill \\ R^n: \mathrm{if} x_1 \mathrm{is} Condition{A}_{n1} \mathrm{and} x_2 \mathrm{is} A_{n2} \mathrm{then} y \mathrm{is} V_n\hfill \end{array}\right.\end{array}$$

(2)

where $x_1$ and $x_2$ represent input-quantitative variables ($x_1\in X_1,x_2\in X_2$) to a fuzzy system and y represents the output-decision variable ($y\in Y$). $A_{i1}$, $A_{i2}$ and $B_i$ are fuzzy subsets of $X_1$, $X_2$ and Y, respectively. When the non-fuzzy input data “$x_1$ is $x_1^{\ast }$ and $x_2$ is $x_2^{\ast }$” are given, the matched context degree $\left(w_j\right)$ is calculated by the weight $\left(w_j\right)$: representative of $\left(V_i^S\right)$ and $\left(w_j\right)$.

Step 7:

Find the appropriate rules considered by decision-makers and apply these weights and rules in the KB. $IF$ upon checking the KB, the rule currently being considered exists in the KB, $THEN$ action the considered rule $ELSE$ a new rule matched in the proposed model that can be added to the KB.

5. Experimental Results

In this section we present a multi-robot CPP case study in Section 5.1 with robot processing in CPP addressed in Section 5.2 and an analysis of the Multi-ST model implemented with the KB in Section 5.3.

5.1. Case Study of Multi-Robot Coverage Model

In operation, mobile robots must be capable of working independently and/or collaboratively within the DOE. However, mobile robots operating in concert present several potential issues, including:

• Effective collaboration: consider two mobile robots A and B. For robot A robot B is a potential dynamic obstacle and vice versa. Avoiding each other while completing the designated tasks requires managed collaboration.
• Division of the operating environment: how can robots cooperate in concert to assist with another robot’s errors while working to complete the designated task.

The design of the Multi-ST (MSTC) algorithm is predicated on the following assumptions related to the coverage of the DOE which is decomposed into cells that are used by a robot(s) to navigate the DOE (introduced in Section 3.2):

• A robot can move continuously among two sub-cells without obstacles in a vertical or horizontal direction.
• There will be an initial position for each robot and the robot terminates its run at the initial starting point.
• A complete coverage path is applied through a robot that has scanned the entire work area of a dynamic environment.
• The robot’s coordination works in each cell to avoid blocking another collaborating robot.

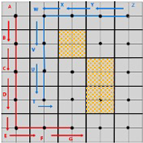
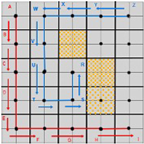
The implementation process is as shown below; the stepwise process implemented in the OMST algorithm is modeled in Figure 5 where the steps are as follows:

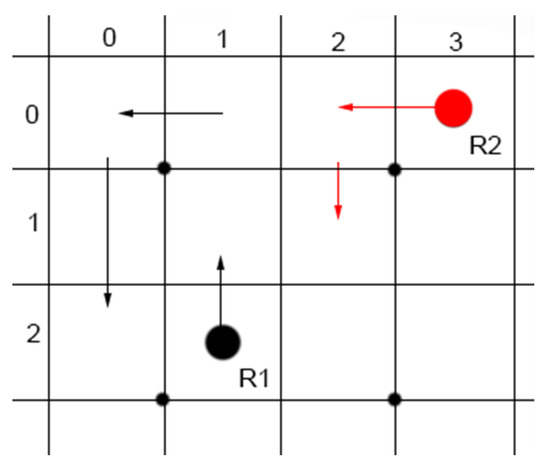
Figure 5. The stepwise process implemented in the OMST algorithm. Shown is a scenario where two robots share visited cell information.

1 

Robot $R_1$ moves to cell $\left[1,1\right]$ and Robot $R_2$ moves to cell $\left[0,2\right]$

2 

In step 1 mega-cell $\left[0,0\right]$ is marked as an old cell previously entered into the visited array for robot $R_1$ and this is repeated for the mega-cell $\left[2,0\right]$ for the robot $R_2$

3 

In step 2 while searching for new adjacent cells, robot $R_2$ failed to locate or identify new cells above or on the left because they belonged to the spanning tree of robot $R_1$. Therefore, robot $R_2$ moves to the cell below which was mega-cell $\left[2,2\right]$

4 

Robot $R_1$ failed to locate a new cell, and therefore, would return to the previous cell at step 3

5 

The FSST algorithm terminates when the whole of the DOE has been covered and the robot, e.g., robot $R_1$, has returned to its original initializing cell

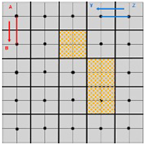
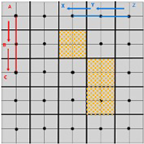
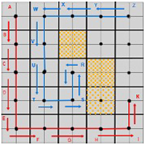
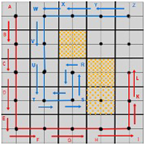
As shown in Figure 6 the STC algorithm prioritizes a robot visit to a cell not previously visited followed by a cell that is reachable from an obstacle with the parent cell being given the lowest priority. For instance, when robot $R_2$ visits cell $\left[1,1\right]$, its mega-cell is marked as an old mega-cell; however, robot $R_2$ would still enter this mega-cell as it is reachable, despite the under mega-cell of $R_2$ being unreachable. This scenario results in a high probability of collision between two robots when they enter the same mega-cell.

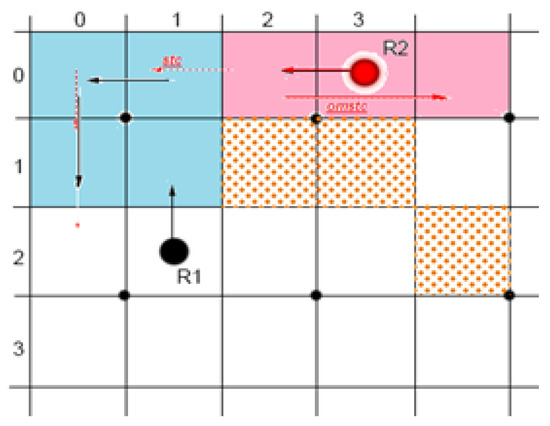
Figure 6. Two robots operating in the FSST algorithm where robot $R_1$ operates in the blue cells with robot $R_2$ operating in the red cells. The three hatched cells represent cells containing obstacles.

To address this potential collision scenario, the proposed solution to this issue is the FSST algorithm which has been conceived to ensure that a robot locates all unvisited cells before returning to its parent cell. In the scenario modeled in Figure 6, when the mega-cell containing cell $\left[0,0\right]$ is marked as an old cell by robot $R_1$, robot $R_2$ is not allowed to enter cell $\left[0,0\right]$ because that mega-cell has been added to the visited array. Consequently, robot $R_2$ would return to its previous cell.

The primary objective of the FSST algorithm is to ensure that each robot constructs a distinct spanning tree during the navigation of the DOE. Moreover, multiple robot operations can result in reductions in the time taken to cover the DOE given the parallel robot processing implemented in the FSST algorithm.

5.2. Robot Processing in Coverage Path Planning Collaborations

Each robot runs its own algorithm to create its own convex hull during the exploration process. The process adopted to traverse a DOE may be summarized as follows:

• The initial position of the robot is given as input to the algorithm and the output is the convex hull of that robot. The robot can scan neighboring cells clockwise (up-left-down-right) starting from its parent and create the convex hull clockwise.
• Following the scanning of the neighboring cells, the unvisited cells will be marked as visited. The robot moves to the right side of the convex hull and eventually reaches the position of the starting sub-cell. It is assumed that in practice the robot is capable of leaving traces in the sub-cells it covers.
• To track the traces created in the terrain we use a visited array so that robots can determine whether that sub-cell has been covered or not. It is also assumed that there is a detection device in the actual robot capable of checking the traces of sub-cells in the current cell and its four neighbors immediately. It is assumed that we will use a stack to store information about nodes after each robot visit. The steps and the state of the stack are represented as follows:
  • Push the current node onto the stack, find the first neighboring node $\left(n\right)$ counter-clockwise from the current node.
  • If node $\left(n\right)$ is not empty the robot moves from the current node to node $\left(n\right)$. Mark the current node as the pre-node of node $\left(n\right)$. Mark node $\left(n\right)$ as visited.
  • If node $\left(n\right)$ is empty pop the current node from the stack.
  • The robot moves from the current node to the node at the top of the stack. Mark the pre-node of the node at the top of the stack as the current node.
  • Repeat the process until the stack is empty.

The convex hull forms a closed curve that visits all sub-cells exactly once. The combination of areas covered by the convex hulls generated by different robots constitutes the entire DOE; therefore, choosing the starting positions for the robots will greatly affect the creation of each robot’s convex hull as well as the overall optimal working time of the collaborating robots. Collision is also a common issue for multiple robots; however, in this algorithm, as each robot builds its own separate convex hulls, there will be no convex hulls overlapping with each other or with other robots, thus avoiding collisions with other robots in the same working area. Table 1 shows in tabulated form a description of the steps and the related state(s) of the stack(s).

Table 1. Description of steps and state of the stack.

Stack R1	Stack R2
A (Initial node of Robot 1)	Z (Initial node of Robot 2)
A-B	Z-Y
A-B-C	Z-Y-X
…	…	…
A-B-C-D-E-F-G	Z-Y-X-W-V-U-T
Push I	Push R	…
A-B-C-D-E-F-G-H-I	Z-Y-X-W-V-U-T-S-R
Push K	Pop R	…
A-B-C-D-E-F-G-H-I-K	Z-Y-X-W-V-U-T-S
Push L	Pop S	…
A-B-C-D-E-F-G-H-I-K-L	Z-Y-X-W-V-U-T
…	…	…
A-B-C-D-E-F-G-H-I	Pop Z
…	null	…
Pop A	null
null		…
Finish

In summary, the algorithm ensures that the convex hulls generated are separate for each robot. Moreover, a key motivating factor for using multiple robots is the ability to reduce coverage time by parallel processing and to this end the proposed algorithm is implemented in parallel by each robot to ensure optimal efficiency.

5.3. Analysis of the Multi-ST with the Knowledge Base

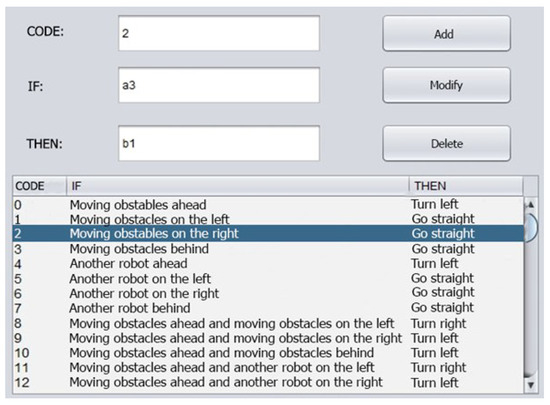
A major drawback of the ST algorithm is that it fails to accommodate and handle dynamic obstacles in the DOE. For example, in a scenario where a robot encounters a dynamic obstacle [within its current cell] it will stop all motion until the obstacle leaves the cell, this causes delays and inefficiencies in the robot’s coverage and the defined task. To address this limitation, our proposed Multi-ST model applies the robot KB to enable the avoidance of obstacles, make subsequent action decisions, and enhance the performance and robustness of CPP in uncertain environments. When using the KB robots can locate and apply an appropriate rule from the KB. All the steps can be repeated until the robot completes the coverage of the DOE and its actions in multiple decision-making objectives. The events and rules that apply are in Table 2 and Table 3.

Table 2. Robot navigation event rules and event codes.

Robot Event Rules and Event Code
Event Code	Rule Name	Event Code	Rule Name
a1	Mobile obstacle ahead	a10	Wall on the left
a2	Mobile obstacle on the left	a11	Wall on the right
a3	Mobile obstacle on the right	a12	Wall behind
a4	Mobile obstacle behind	b1	Go ahead
a5	Another robot ahead	b2	Turn left
a6	Another robot on the left	b3	Turn right
a7	Another robot on the right	b4	Backward
a8	Another robot behind	b5	Stand
a9	Wall ahead

Table 3. Examples of defined rules in the knowledge-base. The rules are essentially event-condition-action rules [74]. For the rules shown in this table, the assumption $\left(IF\right)$ represents a condition which results in an action that, in turn, triggers a particular rule (code), e.g., for code 1: $IF\left(a1\right)$ $THEN\left(b2\right)$.

Defined Rules in the Knowledge-Base
Code	IF	THEN	Code	IF	THEN
1	a1	b2	44	a1&&a7&&a8	b2
2	a2	b1	45	a2&&a3&&a4	b1
3	a3	b1	46	a2&&a3&&a5	b4
4	a4	b1	47	a2&&a3&&a8	b1
5	a5	b2	48	a2&&a4&&a5	b3
6	a6	b1	49	a2&&a4&&a7	b1
7	a7	b1	50	a2&&a5&&a7	b4
8	a8	b1	51	a2&&a5&&a8	b3
9	a1&&a2	b3	52	a2&&a7&&a8	b1
10	a1&&a3	b2	53	a3&&a4&&a5	b2
11	a1&&a4	b2	54	a3&&a4&&a6	b1
12	a1&&a6	b3	55	a3&&a5&&a6	b4
13	a1&&a7	b2	56	a3&&a5&&a8	b2
14	a1&&a8	b2	57	a3&&a6&&a8	b1
15	a1&&a8	b1	58	a4&&a5&&a6	b3
16	a2&&a4	b1	59	a4&&a5&&a7	b2
17	a2&&a5	b3	60	a4&&a6&&a7	b1
18	a2&&a7	b1	61	a5&&a6&&a7	b4
19	a2&&a8	b1	62	a5&&a6&&a8	b3
20	a3&&a4	b1	63	a6&&a7&&a8	b1
21	a3&&a5	b2	64	a1&&a2&&a3&&a4	b5
22	a3&&a6	b1	65	a1&&a2&&a3&&a8	b5
23	a3&&a8	b1	66	a1&&a2&&a7&&a4	b5
24	a4&&a5	b2	67	a1&&a2&&a7&&a8	b5
25	a4&&a6	b1	68	a1&&a6&&a3&&a4	b5
26	a4&&a7	b1	69	a1&&a6&&a3&&a8	b5
27	a5&&a6	b3	70	a5&&a2&&a3&&a4	b5
28	a5&&a7	b2	71	a5&&a2&&a3&&a8	b5
29	a5&&a8	b2	72	a9	b2
30	a6&&a7	b1	73	a10	b1
31	a6&&a8	b1	74	a11	b1
32	a7&&a8	b1	75	a12	b1
33	a1&&a2&&a3	b4	76	a1&&a10	b3
34	a1&&a2&&a4	b3	77	a1&&a11	b2
35	a1&&a2&&a7	b4	78	a1&&a12	b2
36	a1&&a2&&a8	b3	79	a2&&a9	b3
37	a1&&a3&&a4	b2	80	a2&&a11	b1
38	a1&&a3&&a6	b4	81	a2&&a12	b1
39	a1&&a3&&a8	b2	82	a3&&a9	b2
40	a1&&a4&&a6	b3	83	a3&&a10	b1
41	a1&&a4&&a7	b2	84	a3&&a12	b1
42	a1&&a6&&a7	b4	....	....	....
43	a1&&a6&&a8	b3

6. Experimental Testing and Evaluation

In this section, we describe the system requirements with an analysis of the basic elements of the system and an evaluation demonstration. The results are considered in Section 7. Section 8 provides a discussion with open research questions addressed in Section 8.

6.1. The System Requirements

The system to implement the evaluation of the proposed approach was created to realize the following criteria:

• The DOE and the operating system must provide the user with a system that enables easy robot manipulation and operation with data entry and options to easily change the input data being important factors in the design of the system.
• In operation, basic information related to the robot(s) operation will be shown in a status bar to aid efficient user monitoring, follow-up, and robot management.
• On termination of a system run, the data extracted will be automatically saved in an Excel spreadsheet file for analysis. The input KB data will be included using the Excel spreadsheet file.

6.2. The Basic Elements of the Operating System

The design of the proposed system requires a number of primary entities and Java classes:

• MegaCell: is a class that contains attributes of position $\left(x,y\right)$, the parent cell, and state (old or not).
• CellPane: is the cell that the robot passes through in each move where CellPane is equal to 1/4 of MegaCell. The primary task of this class is to hold state properties to know whether the cell has obstructions, properties to display the dirt (the evaluation uses a cleaning robot), and the robot’s direction on a map.
• Robot: is the most important class. The class holds the attributes for the initializing location, current cell location, working time, number of moves, the visited cell array, the parent-cell array, etc.
• Server: is a class that holds general information about the whole DOE map and includes data such as the list of all running robots, the list of cells, whether the cell status is old or not, and the list of static and dynamic obstructions, etc.
• MainGui: is the construction layer on the DOE map interface for robots. It contains menus along with component interfaces of the modes.
• Logger class: is responsible for reading and writing data to Excel files, classes related to KB system governance, and classes containing CPP properties on the dirty level of the floor, etc.

6.3. Evaluation Demonstration

In this section, we provide selected representative screenshots showing the screen output. Figure 7 shows the home screen of the system from which a user can select the modes that correspond to the STC (offline and online) algorithm, the STC-full algorithm, and the Multi-ST model optimized for the robot group.To evaluate the proposal, experimental testing has been conducted in a DOE comprised of a 24 × 24 cell grid with four robots as shown in Figure 8. Figure 8 illustrates the environment initialization following the entry of data for (i) the number of robots, and (ii) the DOE size. Figure 9 shows the result of the Multi-ST model with four robots and five random-shaped obstructions. The ST(s) generated by four robots are depicted in Figure 10 and the knowledge-based screen shown in Figure 11 shows robots as tested in the proposed model with multiple robots in the case studies.

Figure 7. The home screen of the system from which a user can select the modes corresponding to the offline and online algorithm.

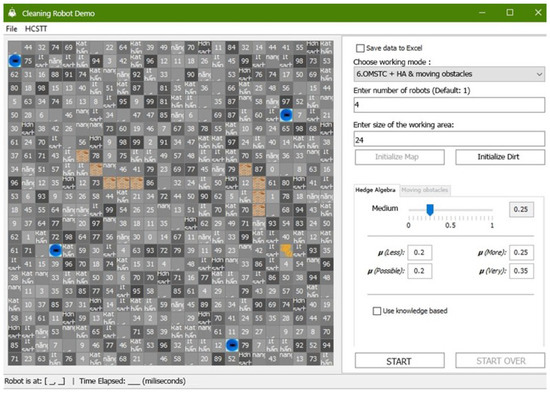
Figure 8. The DOE comprised a 24 × 24 cell grid with four robots.

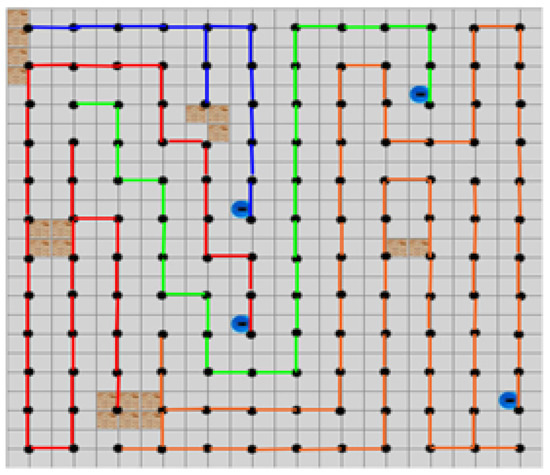
Figure 9. The result for the Multi-ST model with four robots and five random shaped obstructions.

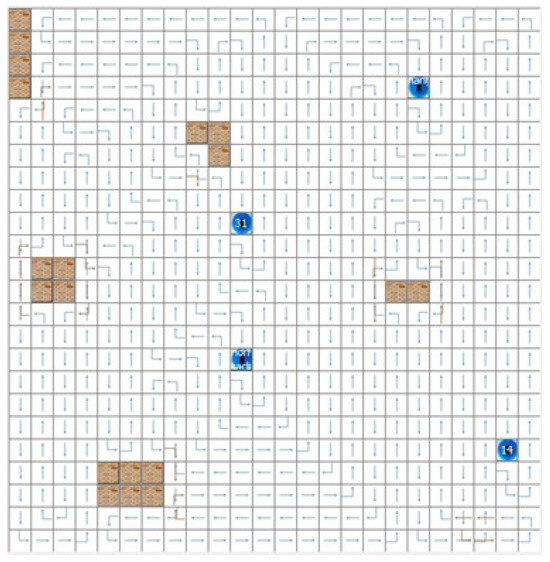
Figure 10. The figure shows the spanning trees generated by four robots.

Figure 11. The knowledge-base screen illustrating the rule-based system (see Table 2 and Table 3).

The results obtained in running the Multi-ST model on a 24 × 24 grid DOE are stored in Table 4 which shows the initial positions of the robots, the number of cells traversed, and the related moves. We may observe from Table 4 that:

Table 4. The results set out the number of cells traversed in the DOE with related starting positions.

Terrain Type	Starting Positions of Robot #
	1	2	3	4	1	2	3	4
Type	(0,0)	(23,23)	(23,0)	(0,23)	(11,11)	(11,12)	(12,11)	(12,12)
Obstacle Free	148	150	150	134	45	85	211	241
Indoor With Obstacles	145	131	142	161	70	72	199	233

• In the first case: robots were placed in the corner of the map or placed evenly; however, the DOE for each robot is the same.
• In the second case: when two robots are adjacently placed, it resulted in a bad case where one robot prevented the development of other robots resulting in uneven coverage (or) a different number of cells covered by the robots. Moreover, in this case, when the robots are placed in cells close to each other, it is easy to lead to a bad case where the robots will limit the growth of the ST for the other robot(s) resulting in the number of cells covered by each robots displaying significant unevenness and disparity.

7. Results and Analysis

An analysis for the Multi-ST model has computed the number of steps required to complete CPP for the set task based on the assumption that the runtime is equal to the number of steps × 100 (milliseconds). The results are presented in tabular form in Table 5 from which we can observe that the difference is not highly significant. Moreover, it can be seen that the use of multiple robots will reduce the maximum time required to cover the DOE. However, if the average duration of the group is used, there is a significant improvement over the single robot case. The results support the conclusion that multiple robots operating in concert improve the effectiveness in completing the defined task.

Table 5. A table showing: the number of robots, the time taken for different starting positions in milli-seconds, the average time taken, and the maximum time taken.

Number of Cells Covered by Each Robot in the Same Terrain with Different Starting Positions
Robots	Time						Average	Maximum
1	57,600	-	-	-	-	-	57,600	57,600
2	29300	28800	-	-	-	-	29,050	29,300
2*	28,900	28,900	-	-	-	-	28,900	28,900
3	4500	29,700	25,500	-	-	-	19,900	29,700
3*	20,000	18,800	18,800	-	-	-	19,200	20,000
4	4500	8500	21,100	24,100	-	-	14,550	24,100
4*	15,600	13,900	13,900	14,900	-	-	14,575	15,600
5	18,200	4800	10,200	16,200	9000	-	11,800	18,200
5*	2900	14,100	13,100	14,000	14,100	-	13,880	14,100
6	4500	4500	19,400	4400	15,800	9800	9734	19,400
6*	11,800	8800	15,000	7600	8200	7200	8567	15,000
7	-	-	-	-	-	-	8586	18,000
8	-	-	-	-	-	-	7688	14,100
9	-	-	-	-	-	-	6867	13,500
10	-	-	-	-	-	-	6180	9900
11	-	-	-	-	-	-	5664	9200
12	-	-	-	-	-	-	5083	8500

From Table 5 we can see that there is a time difference when using the same number of robots with different initial starting positions; this demonstrates that the runtime depends heavily on the original positions of the robots. The best case (marked (*)—see Table 5) is where the initial robot starting positions are roughly equidistant. This is because the robots will have nearly equal areas and the working time will be spread evenly among each robot. As a result, it generally reduces the maximum time required to work rather than in conventional cases. In the worst-case scenario, where the robots start at adjacent cells, the runtime of each robot shows a large time difference between the shortest and longest run times.

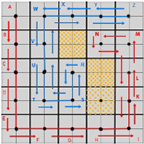
Locating robots too close together at initialization collaborates with the other robots’ ST; the minimum spacing must be where robots are located in non-adjacent cells. The result of locating robots too close together will be that there are robots that will operate only in a small area for a short period of time while there are robots that will have to operate in a very wide area for long periods of time. These results show the minimized working time of the whole group of robots in collaborations for coverage planning; a typical example is shown in Figure 9 where the movement of the red robot is moved by the collaborating robots that create green and blue ST.

The chart displayed in Figure 12 shows the results where multiple robots are operating in a DOE consisting of a 50 × 50 cell grid, the coverage rate $\left(C\right)$ as a % of the DOE covered by robots is calculated by Equation (3) where $\left(A_1\right)$ is the number of steps that have been moved, $\left(A_2\right)$ is the repeat number of steps, and $\left(A\right)$ is the total area of both DOE (the map) and does not count the fixed obstructions.

$$C={\displaystyle \frac{A_1-A_2}{A}}$$

(3)

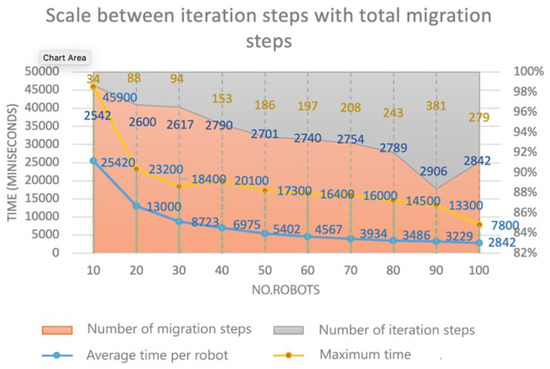
Figure 12. The results for multiple robots are operating on a DOE consisting of a 50 × 50 cell grid.

Based on the results reported in Table 5 we can conclude that the total number of moves is dependent on the repeat number of steps because as the number of iterations increases, the corresponding number of moves also increases. Therefore, the numeric elements of Equation (3) will roughly correspond with (i) the area of the entire DOE (map) that the robot can reach, or (ii) the % of the map covered will always be ∼$100\%$.

7.1. Analysis

Following a run of the Multi-ST model on a DOE consisting of a 24 × 24 grid, the influence of choosing the starting positions for each robot on the number of cells the robots will cover or the number of steps they will take can be observed as shown in Table 6. The results may be summarized as follows:

Table 6. The influence of the starting position on the number of cells covered in different environments.

	Starting Position of the Robot
	1	2	3	4	1	2	3	4
Position	(0,0)	(23,23)	(23,0)	(0,23)	(11,11)	(11,12)	(12,11)	(12,12)
Environment without obstacles	148	150	150	134	45	85	211	241
Environment with obstacles	145	131	142	161	70	72	199	233

• In the first case, when the robots are placed at the corners of the map or placed at equal distances from each other, the working area of each robot is approximately the same.
• However, in the second case, when the robots are placed in adjacent cells, it can lead to a worst-case scenario where the robots will restrict the growth of each other’s convex hulls, resulting in an uneven and significantly different number of cells covered by each robot.

Table 6 illustrates the impact of starting positions on the number of cells covered by robots in DOE with and without obstacles. When robots are placed at the corners of the map (Positions: (0,0), (23,23), (23,0), and (0,23)) they cover a relatively balanced number of cells, both in obstacle-free and obstacle-filled environments. In a clear environment, the robots cover 148, 150, 150, and 134 cells, respectively, while in an environment with obstacles, they cover 145, 131, 142, and 161 cells.

Conversely, when robots start from adjacent central cells (Positions: (11,11), (11,12), (12,11), and (12,12)), there is a significant disparity in coverage. In an environment without obstacles, they cover 45, 85, 211, and 241 cells, respectively, and in an obstacle-laden environment, they cover 70, 72, 199, and 233 cells. This disparity indicates inefficiencies and overlaps in coverage. Overall, the table demonstrates that starting robots at the corners leads to more balanced and efficient coverage while starting them from adjacent central cells results in significant inefficiencies, especially in environments with obstacles.

To analyze the number of steps required to complete the coverage task, the running time will be assumed as the product of [the number of steps the robot has to take × 100 (ms)].

As depicted in the results from Table 7, the proposed model has been performed in a variety of (four and 10) static obstacles. Iteration rate is calculated by the scale for the number of iterations (repeat steps) which is divided by the number of movement steps for robots visited. Experimental results in simulations show that the iteration rate is in the range between 0.48 and 7.42. It is indicated that the impact of obstacles on cell overlap is acceptable.

Table 7. The impact of obstacles on cell overlap.

	4 Obstacles			10 Obstacles
Number of Robots	Number of Movement Steps	Number of Iterations	Iteration Rate	Number of Movement Steps	Number of Iterations	Iteration Rate
1	2508	12	0.48	2523	32	1.26
2	2510	12	0.48	2524	32	1.27
3	2515	16	0.64	2529	36	1.42
5	2521	18	0.71	2532	40	1.58
10	2517	14	0.56	2549	52	2.04
20	2545	24	0.94	2580	72	2.79
30	2572	25	0.97	2617	98	3.74
50	2620	36	1.37	2734	203	7.42

Figure 13 shows the relationship between the number of robots and the total execution time in a simple environment and how the number of robots affects the time required to cover the entire DOE (map). As the number of robots increases, the coordination of tasks leads to a reduction in the maximum time needed for full coverage. For example, with one robot, the task completion time is significantly higher compared to using multiple robots. Specifically, the time required decreases from 500 units with one robot to 350 units with two robots, with a further reduction to 250 units with four robots. The figure also indicates that the average time for the entire team to complete the task decreases noticeably with more robots working simultaneously, highlighting the efficiency gains from using multiple robots.

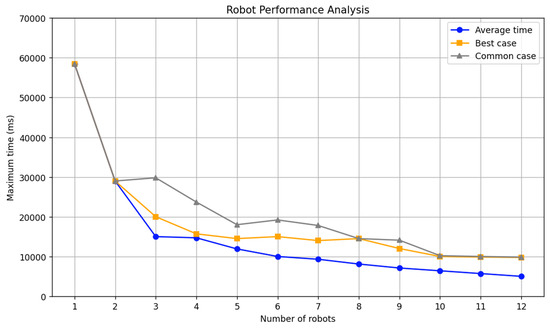
Figure 13. The result for the product of [the number of steps the robot has to take × 100 (ms)].

Additionally, Figure 13 reveals variations in time based on the initial positions of the robots. The best cases (marked (*), see Table 5) occur when robots start from positions that are almost equally spaced apart, resulting in nearly equal working areas and evenly distributed working times. This leads to shorter maximum working times compared to typical cases. For instance, the best-case scenarios show a reduction in maximum time to 200 units with optimal spacing of four robots. Moreover, in addition to finding solutions to optimize working time, reducing the number of iterations is also important for optimizing the Multi-ST model. Table 7 describes the simulation results on a 50 × 50 grid with different numbers of obstacles.

In contrast, the worst cases arise when robots start from adjacent or neighboring cells, causing significant differences between the minimum and maximum working times. This is due to the interference in the development of one robot’s convex hull by another, leading to some robots working in small areas for short periods while others cover large areas for extended periods. An exemplary case is depicted in Figure 14 which shows the red convex hull constrained by the green and black robots, illustrating how close starting positions can hinder efficient coverage and extend the overall working time, sometimes up to 400 units.

Figure 14. An exemplary case where the red convex hull is constrained by the green and black robots.

Table 7 sets out in a tabular format how varying the number of robots and the number of obstacles affects the iteration count. When the number of robots is increased from 1 to 4 in a constant DOE the number of iterations rises slightly; for instance, with one robot, the iteration count is 1000, whereas with four robots it increases to 1100. The iteration rate also shows a small increase, from 0.10 iterations per unit of time with one robot to 0.11 with four robots. However, when the number of obstacles is increased, while keeping the number of robots constant, the iteration rate increases significantly.

For example, with four robots and no obstacles, the iteration count is 1100 and the iteration rate is 0.11. When the number of obstacles is increased to 10, the iteration count rises to 1500, and the iteration rate jumps to 0.15. This substantial increase is due to the added complexity of navigating around obstacles, which requires the robots to traverse the edges of the convex hull more frequently. Therefore, the presence of complex obstacles necessitates more iterations, demonstrating that while the multi-robot algorithm does not drastically reduce overall performance, its efficiency is constrained by the same limitations as the original single-robot algorithm. The % of the area covered by the robots is calculated in Equation (4) which computes the number of repeated steps and the complexity of the DOE.

$$\begin{array}{c}\mathrm{coverage}\mathrm{rate}(\%)={\displaystyle \frac{A1-A2}{A}}\times 100\%\end{array}$$

(4)

where $\left(A1\right)$ is the number of steps, $\left(A2\right)$ is the repeat number of steps, and $\left(A\right)$ is the total area of the entire DOE (map) excluding fixed obstacles.

From Table 7 we can conclude that the total number of steps varies dependent on the repeat number of steps. When the repeat number of steps increases, the corresponding number of steps also increases. Therefore, the numerator of Equation (4) will be approximately equal to the denominator which is the area of the entire DOE (map) that the robot can reach (or) the coverage ratio of the Multi-ST model will always approximate to 100%.

7.1.1. Experimental Testing Results

Here, we set out the results of experimental resting runs based on a a large number of robots on a large DOE (cell map) where grids of 50 × 50, 80 × 80, and 100 × 100 cells are implemented. Figure 15 charts the results for a 50 × 50 cell map with Figure 16 charting the results for an 80 × 80 cell map, and Figure 17 charting the results for a 100 × 100 cell map. The results demonstrate the performance of the Multi-ST model with varying numbers of robots.

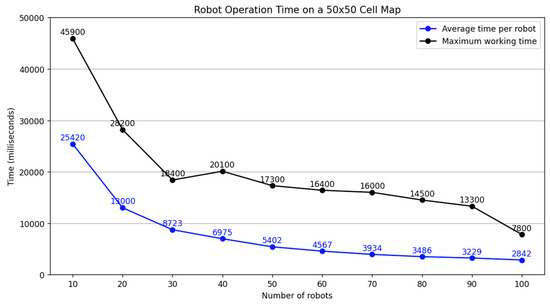
Figure 15. Operating times for robot operation on a 50 × 50 cell map.

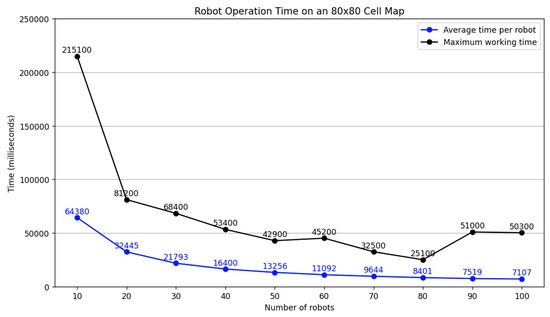
Figure 16. Operating times for robot operation on a 80 × 80 cell map.

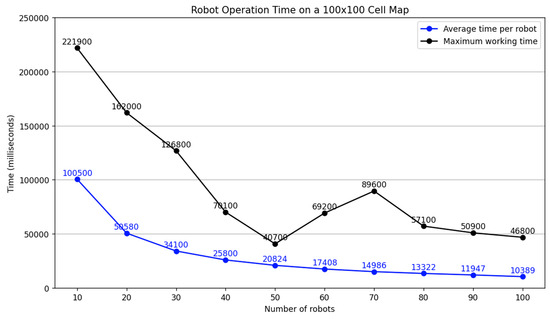
Figure 17. Operating time of the robot on a 100 × 100 cell map.

This analysis focuses on the impact of the number of robots and obstacles on the algorithm’s efficiency. The primary metrics relate to the relationship between the number of robots on the X axis and the time in milliseconds on the Y axis. From Figure 15, Figure 16 and Figure 17 we can see the average time per robot and the maximum working time.

Figure 15 shows the relationship between the number of robots and the total execution time in a simple environment. With one robot, the execution time is 500 units. As the number of robots increases, the execution time decreases, reaching 350 units with two robots, 275 units with three robots, and 200 units with four robots. This trend demonstrates that additional robots can significantly reduce the overall execution time.

Figure 16 depicts a similar trend in a moderately complex environment. Here, the execution time with one robot is 700 units. Increasing the number of robots to two reduces the time to 480 units, to 350 units with three robots, and to 260 units with four robots. The data highlight that even in more complex environments, increasing the number of robots results in considerable time savings.

Figure 17 illustrates the execution time in a highly complex environment with numerous obstacles. Initially, with one robot, the execution time is 1000 units. Adding a second robot reduces this time to 750 units, three robots bring it down to 560 units, and four robots further reduce it to 400 units. This figure emphasizes that the benefits of using multiple robots are even more pronounced in challenging environments.

From the experimental results with a large number of robots, it can be seen that if the number of robots is too high in a given area, it is necessary to place fewer robots; otherwise, the division of work areas will not be uniform due to the limitation of the development of convex hulls among the robots. Conversely, when placing a small number of robots in a relatively large area, the overall working time of the robots will be much longer. Therefore,

• It can be seen that using multiple robots is only effective when the number of robots in the area is sufficient to evenly divide the working areas, resulting in the most optimal time and number of iterations.
• From this analysis, we may conclude that for CPP, multiple-robot operation is more effective than is the case for single-robot operation and, from the analyzed results, choosing multiple robots is generally more effective than using a single robot.
• However, in reality, more robots do not always mean more efficiency. It is essential to consider using the required number of robots and the financial cost.
• Moreover, optimizing the number of robots and the choice of starting positions in the best cases will help save costs and reduce the number of iterations along with optimizing robot working time.

7.1.2. The Impact of the Knowledge Base

We have in Section 7.1.1 set out an analysis of the experimental testing results. However, a central feature of the Multi-ST model is the use of the KB. An illustration of the impact of applying the KB to the robots. Table 8 sets out the results obtained from a run on a 50 × 50 cell area.

Table 8. Effects of applying the KB to the algorithm.

	Not Applying KB			Applying KB
Number of Robots	Number of Movement Steps	Number of Iterations	Operating Time (s)	Number of Movement Steps	Number of Iterations	Operating Time (s)
1	2503	3	362,442	2523	32	103,512
2	2502	2	299,027	2524	32	53,212
5	2504	4	238,810	2532	40	34545
10	2516	16	144,395	2549	52	32,634
20	2536	20	108,630	2531	25	31,108
50	2668	56	87,961	2653	135	28,402

Table 8 shows the results from the application of the KB where the number of steps and iterations have increased slightly. However, if we consider the working time data, the use of the KB significantly reduces the overall working time of the robot team. We may summarise the reasons for these results as follows:

• The reason for the reduction in the working time is the initial limitation of the ST algorithm.
• Applying the KB helps to maximize the working time of the robots in dynamic DOE even though it may require the robots to increase movement, leading to unwanted overlapping areas. However, the overlapping area can be acceptable as it is insignificant compared to the total shared DOE.

The analysis of the results shows that multiple robot operations can improve the effectiveness of task completion when compared to the use of a single robot. However, when multiple robots operate in concert, there will be additional issues in collaboration reflected in reduced effectiveness in simultaneous task completion as discussed in Section 8.1. Therefore, we may conclude that it is necessary to incorporate the use of the optimal number of robots and their initial starting positions in the best cases. Optimizing the number of robots will reduce the number of iterations, optimize robot working time, and reduce financial factors.

8. Discussion

There are numerous examples of research investigating CPP in uncertain environments with studies addressing the avoidance of static and dynamic obstacles by both single robots operating alone and multiple robots operating in concert. The objective of CPP algorithms is to optimize robot coverage in a DOE and complete pre-defined tasks. Related research has been addressed in Section 2 where studies addressing CPP and related topics have been considered. Published studies addressing CPP solutions have shown their potential to realize effective CPP and have achieved varying degrees of success; however, many studies report limited success and many studies fail to effectively address dynamic obstacles.

In this paper, we have introduced our proposed Multi-ST model designed to address (or at least mitigate) the limitations identified in the CPP-related research considered in this study. The proposed model has been evaluated in experimental testing and has demonstrated the capability to realize effective collaborative working by multiple robots operating in concert in a DOE while avoiding both static and dynamic obstacles. We have introduced the technologies utilized in the design and development of our proposed model along with the related algorithmic and robot processing. The aim of this study is to enable multiple robots to operate in concert effectively by leaving traces on the DOE covered by the traversing robots.

In introducing the proposed model we have considered the basic assumptions upon which the implementation is predicated. To evaluate the proposed model, we have carried out experimental testing as set out in Section 6. Our results show that the proposed approach enables effective multiple-robot operations where robots operate in concert based on intelligent decision support systems. Moreover, we have demonstrated the capability of robots to achieve the avoidance of static and dynamic obstacles. A moving robot is in practice a dynamic obstacle viewed from the perspective of other robots and this induces significant complexities in managing CPP.

Any system designed to manage multiple-robot operations requires a platform to manage and control the robots and enable optimal autonomous decision-making by the robots to achieve multiple defined tasks. The proposed model has demonstrated high levels of robustness, effectiveness, and efficiency with the capability to manage effectively multiple robots operating in concert to complete defined shared tasks. The time taken to complete the coverage of a DOE is reduced as shown in our evaluation and experimental testing.

To evaluate the proposed model we have carried out experimental testing as set out in Section 6. Our results show that the proposed approach enables effective multiple-robot operations where robots operate in concert based on intelligent decision support systems. Reported experimental results demonstrate the following benefits in a software system designed to manage multiple-robot operations in ‘real-time’ with the shortest working time. The study presented in this paper has demonstrated a number of significant benefits:

• The capability for robots to achieve avoidance of static and dynamic obstacles in ‘real-time’. A moving robot is in practice a dynamic (moving) obstacle for other robots and this induced significant complexities in managing CPP. While our proposed approach displays good performance, identifying the optimal (best) solution in terms of time and traversing efficiency is arguably not possible.
• The robustness of the designed system algorithm in terms of effectiveness and efficiency along with the capability to manage effectively multiple robots operating in concert to complete defined shared tasks.
• Using individual rules for each robot with updating of the provided basis upon which improvements in the efficiency of CPP can be achieved. Moreover, minimizing duplication and repetition in areas covered in the DOE improves task efficiency. Rules considered for each robot can form the basis for intelligent data processing for collaborating robots based on common rules stored in the KB which is continually updated.
• The time taken to complete the coverage of a DOE is reduced as shown in our evaluation and experimental testing.
• The rule-based approach implemented in our proposed model allows robots with individual rules that are defined to enable optimal autonomous decision-making by the robots to achieve multiple tasks.
• The evaluation demonstration (see Section 6.3) has provided a basis upon which online and offline implementation may be realized.

While there are clear benefits derived from our proposed approach, there are also limitations and constraints that we have identified in this study:

• We have identified that locating robots too close together at initialization will lead to a robot blocking the development of other robots ST. As indicated in Figure 6, the minimum spacing must be where multiple robots are located in at least adjacent cells. Moreover, autonomous optimal rule definition and updating is a limitation of the proposed method.
• The CPP problem in a dynamic DOE for multiple robots operating in concert represents a challenge when considered in terms of NP-completeness, we briefly introduce research addressing NP-completeness and NP-hard problems in Section 2. For a discussion on the topic see [75,76]. As discussed in this paper, multi-robot operation represents an NP-hard problem where solutions are hard to find but easy to verify and are solved by a non-deterministic Machine in polynomial time.
• There are significant complexities inherent in managing CPP in a dynamic DOE where such complexities represent an NP Hard problem as discussed in Section 2. It is clear that the paths in CPP will change dynamically in ‘real-time’ and, while identifying an optimal static path is possible in a non-dynamic DOE, the identification of optimal paths in a dynamic DOE is not a realistic proposition. This limitation is shared with the Traveling Salesman Problem (TSP) as discussed in [11] and Bouzid et al. in [6] where CPP is addressed as it relates to UAV (i.e., drones) in a 3D DOE.
• The rule-based approach implemented in our proposed method requires robot-specific rules which are defined to enable the optimization of the rules based on rule frequency and robot experiences in the identification of the optimal path(s) in CPP. The design and optimization of autonomous rules currently represent an identified limitation.

In summary, the proposed method combines robot reasoning with knowledge reasoning techniques where the processing of robot data is enhanced by the application of knowledge inference. The combination of robot reasoning and knowledge inference provides an effective basis upon which good solutions for CPP can be realized while achieving static and dynamic obstacle avoidance. Moreover, we argue that the method proposed in this paper will generalize to a broad and diverse range of domains and systems.

8.1. Open Research Questions

In this paper, we have considered the advantages of our proposed approach along with the limitations and constraints. There remain open research questions (ORQ) which we have identified in the course of this research.

The limitations and constraints noted in this paper are clearly manageable with further ongoing research. However, we have identified a potential issue where two robots sharing locations in a DOE may encounter problems in completing a defined task (similar to cases where memory management in computer operating systems may lock a computer due to two processes requiring a single resource [77]).

Such a problem requires ‘task scheduling’ which features in [78] where robot scheduling is in flexible manufacturing systems; however, as with other studies, the development of a scheduling system in a real implementation environment with related practical factors is identified as future work. Task scheduling is not currently considered in the proposed approach to CPP as presented in this study. This problem may be realized in, for example, a use-case where two robots (i.e., robots A and B) are tasked with ‘picking’ a product (i.e., the same product) from the same location(in a warehouse DOE) at the same time. In such a use case, there is a requirement for task scheduling to be added to, and incorporated into, the Multi-ST model.

The provision of effective task scheduling of multiple robots operating in concert remains an ORQ; however, the rules-based approach adopted in our proposed model provides a potential solution that will form the basis for future research into decision-making under uncertain-complex environments for autonomous collaborating multiple robots.

8.2. Practical Managerial Significance

In this paper, we have demonstrated the potential utility of the proposed model along with limitations, constraints, and ORQ. Considering the proposed model from a practical managerial perspective (PMS) and practical application perspective, in ‘real-world’ conditions using appropriate robot configurations, for example, an online retailer warehouse), we argue that our proposed approach provides a basis upon which a system can be designed where multiple robots operate in concert. This will enable enhanced levels of automation with improved efficiency, reduced cost, and improved reliability.

9. Concluding Observations

In this study, we have introduced our proposed Multi-ST model which has been conceived and developed to enable effective control and management of multiple robots while achieving efficient CPP. We have provided an evaluation with a simulation and related results which have demonstrated the effectiveness of the proposed approach with a case study where physical robots are engaged in a cleaning task in a DOE. The proposed Multi-ST model has been shown to be effective in a dynamic DOE. In conclusion, multiple robot operations can cover path planning applied by using the FSST algorithm in the DOE given by the collaborative decision-making of robot processing implemented. Experimental results show that robots apply existing rules with good behavior in inference engines for optimal coverage path planning. The Multi-ST model enables single and collaborating multiple robots to achieve optimal CPP while implementing avoidance of both static and dynamic obstacles. Obstacle avoidance is implemented using a rule-based approach with updating rules in the knowledge base (KB) to optimize coverage path planning in collaborative decision-making robots.

In summary, our evaluation supports the conclusion that our proposed model provides for the ability to implement autonomous multiple robot operation in a dynamic DOE efficiently. We posit that our proposed approach can provide an effective generalizable basis upon which multiple robots can operate in concert in a range of ‘real-world’ domains and systems where CPP in a dynamic DOE forms a systemic requirement.

However, there remain a number of limitations and perceived ORQ which represent directions for future research as considered in Section 8.1. To apply the effective task scheduling of multiple robots operating in concert remains in future work, the rules-based approach adopted in our proposed model provides a potential solution that will form the basis for future research into decision-making under uncertain-complex environments for autonomous collaborating multiple robots.