Prediction and Analysis of Borosilicate Glass Surface Deformation Induced by Flame Jet
Abstract
1. Introduction
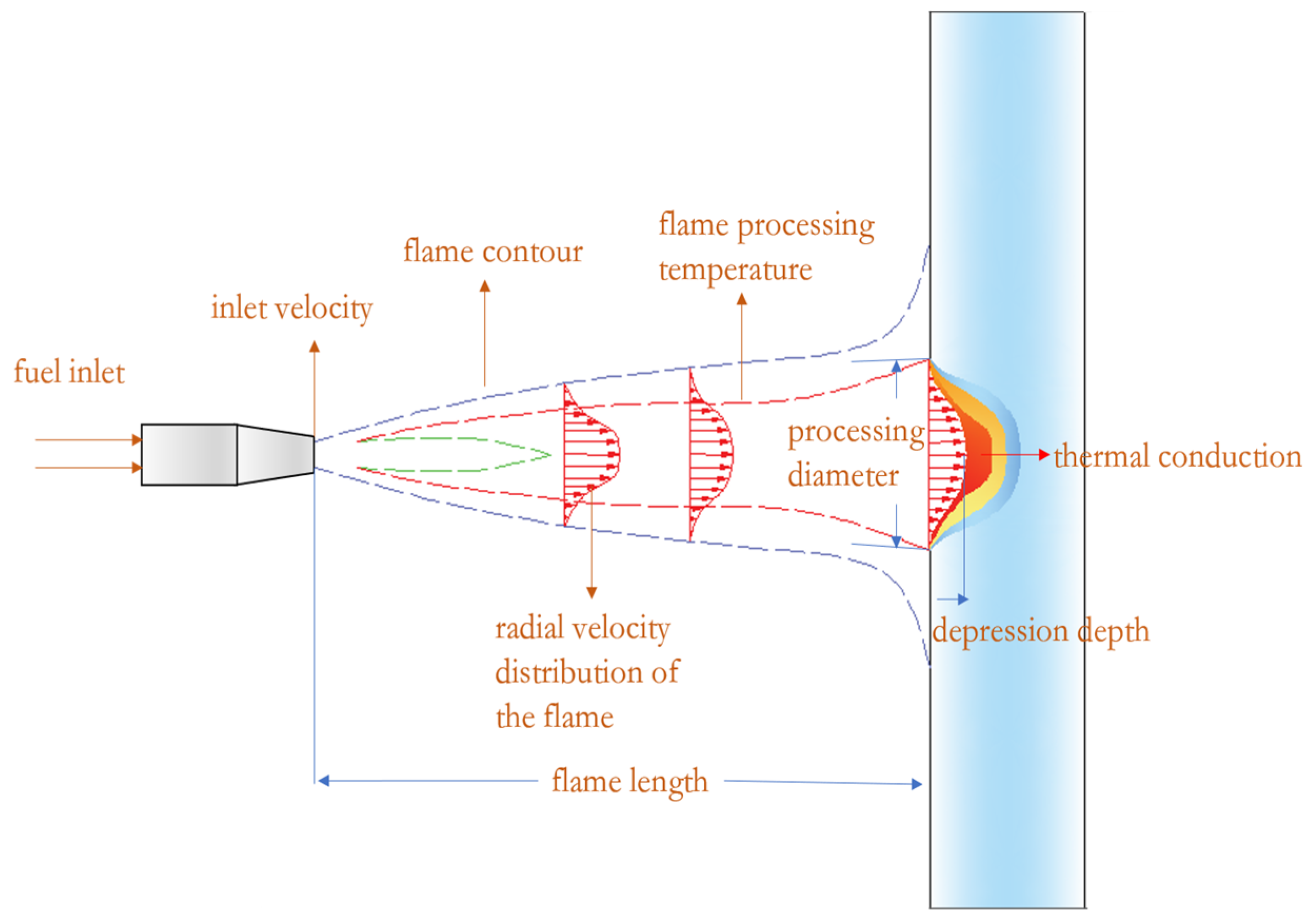
2. Modeling and Analysis
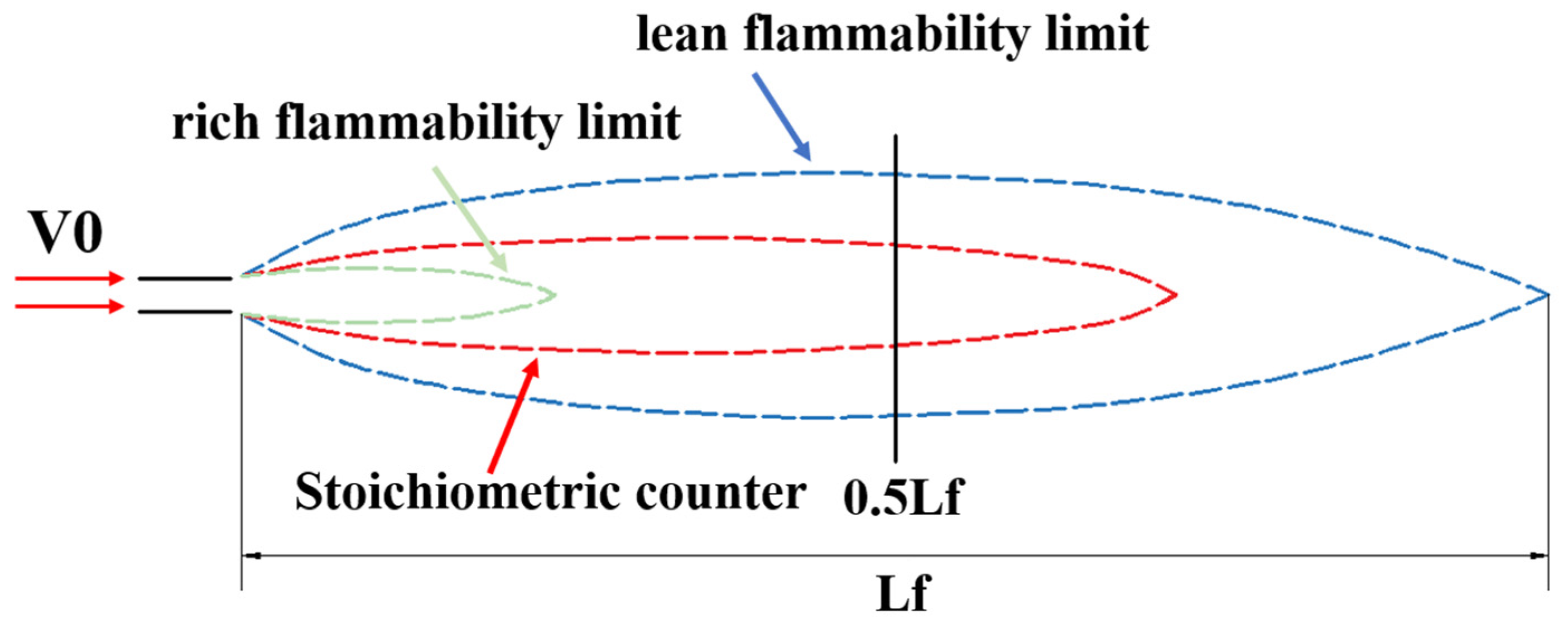
2.1. Determination of the Self-Shape Morphology of Flames
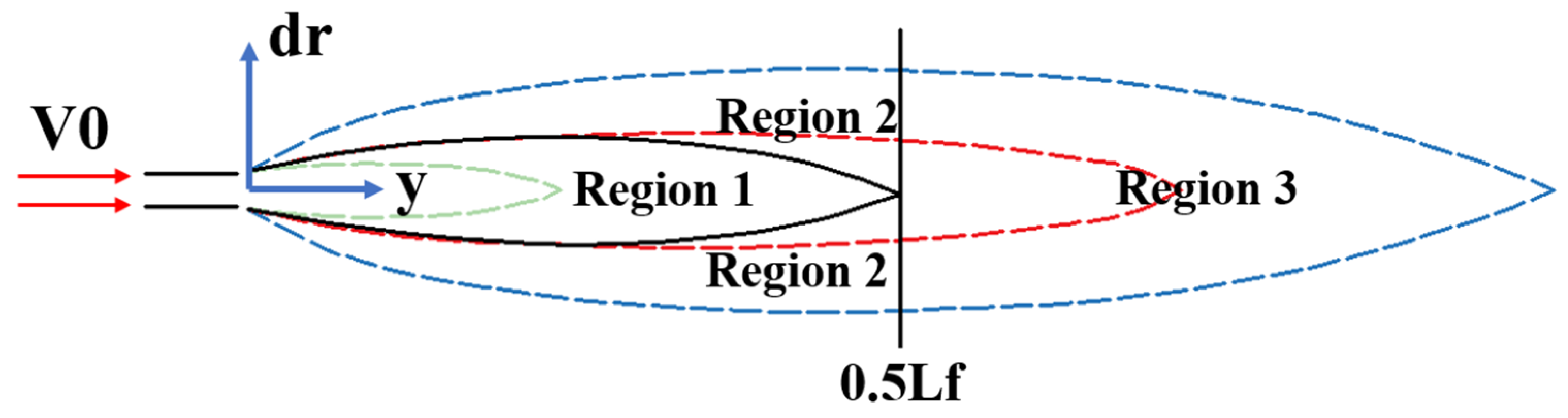
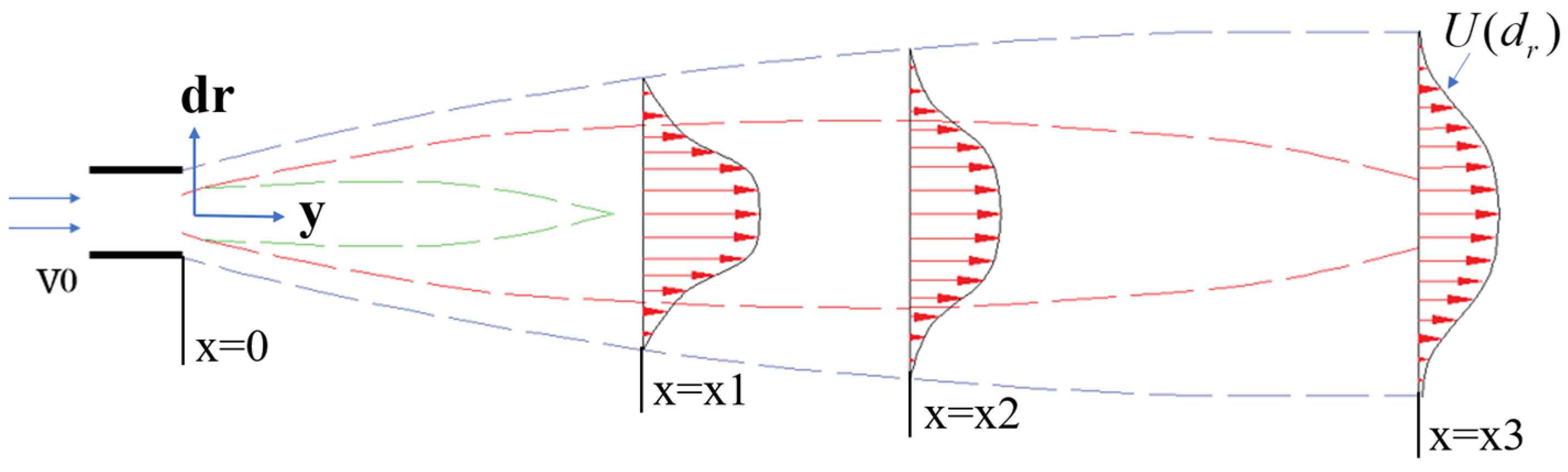
2.2. Determination of the Machining Scope
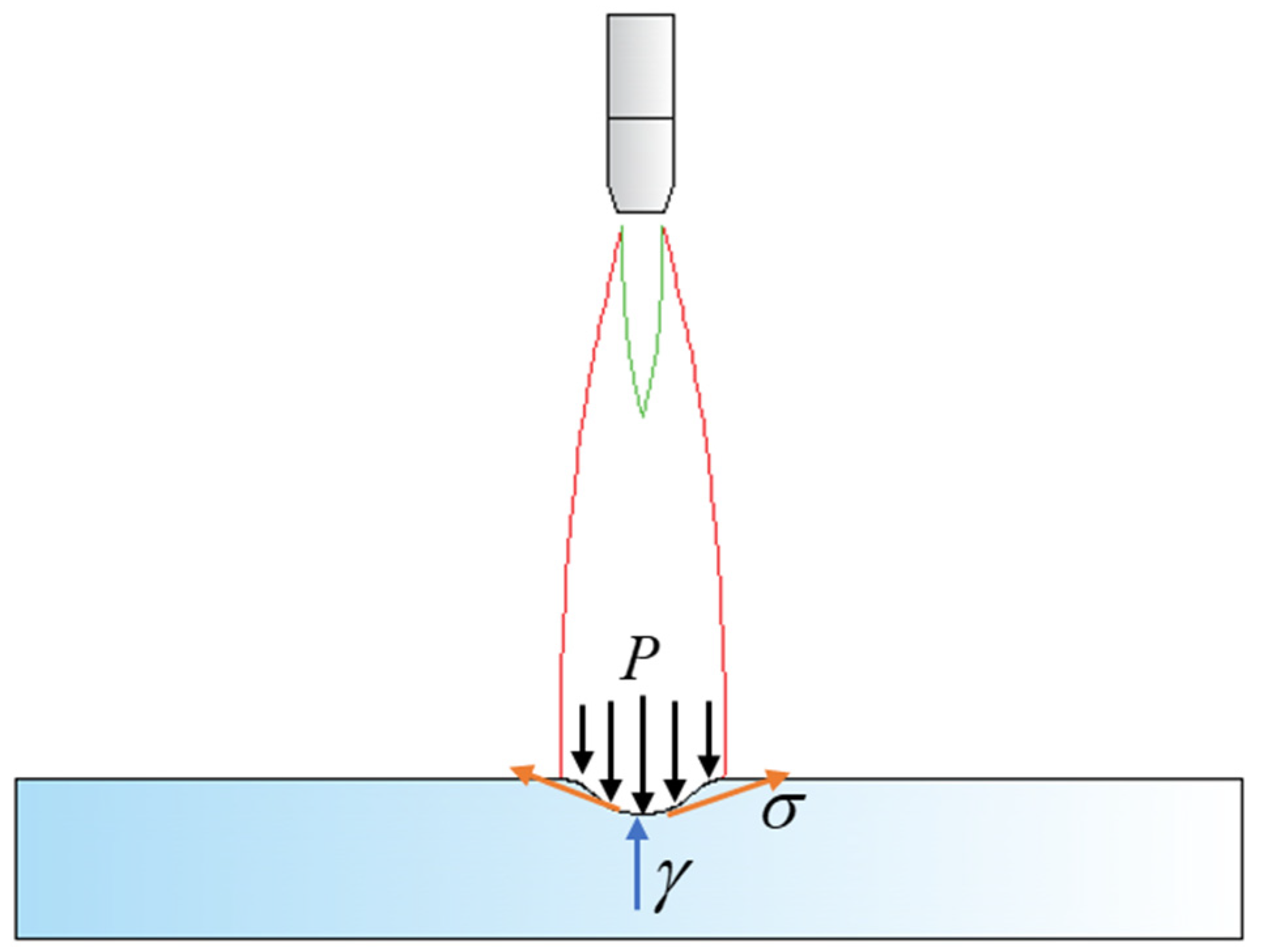
2.3. Establishment of the Theoretical Model
3. Numerical Methodology
3.1. Selection of Simulation Parameters
3.2. Establishment of the Simulation Models
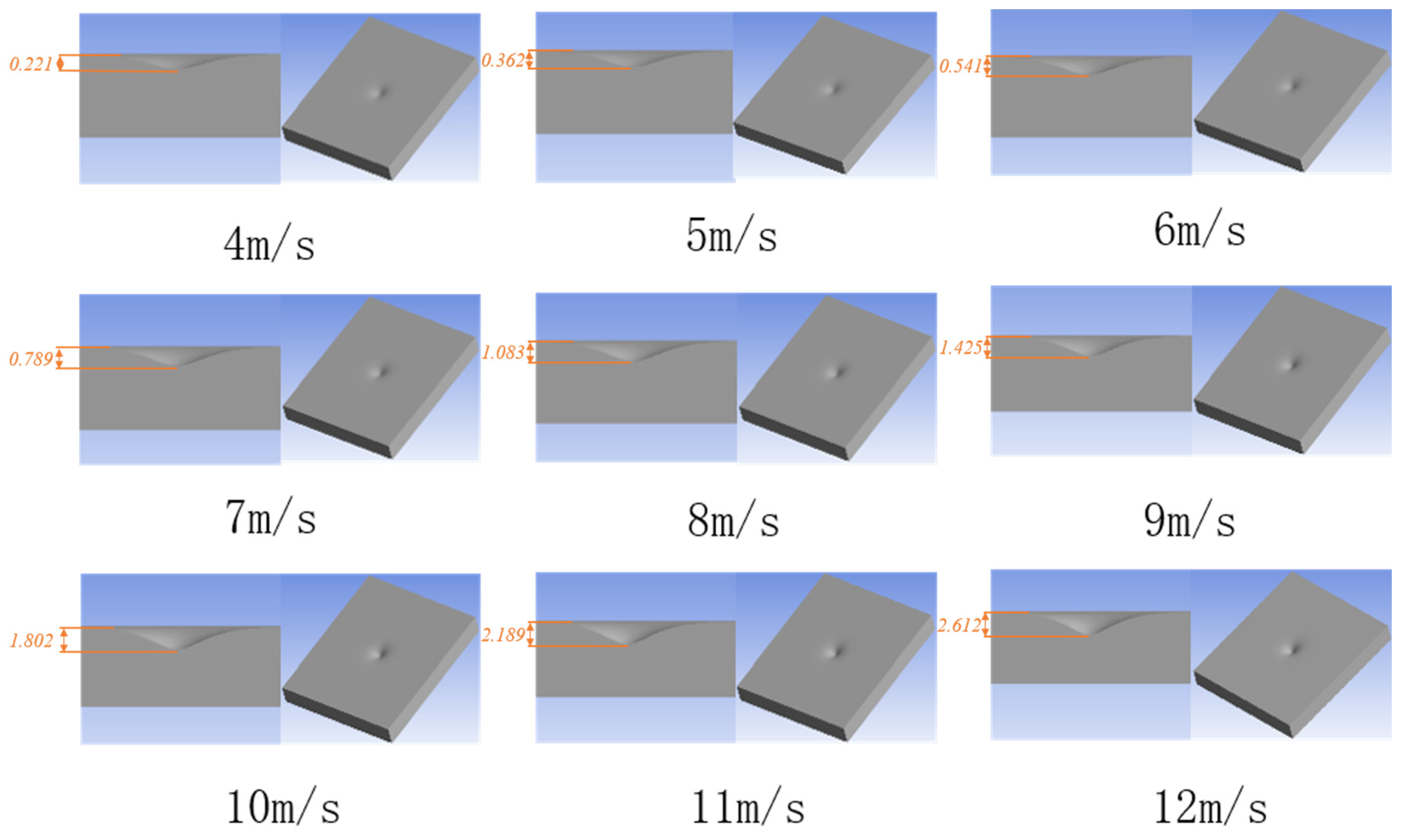
3.3. Analysis of the Simulation Results
4. Experiment
4.1. Experimental Setup
4.2. Measurement Methods for Experimental Results
5. Discussion
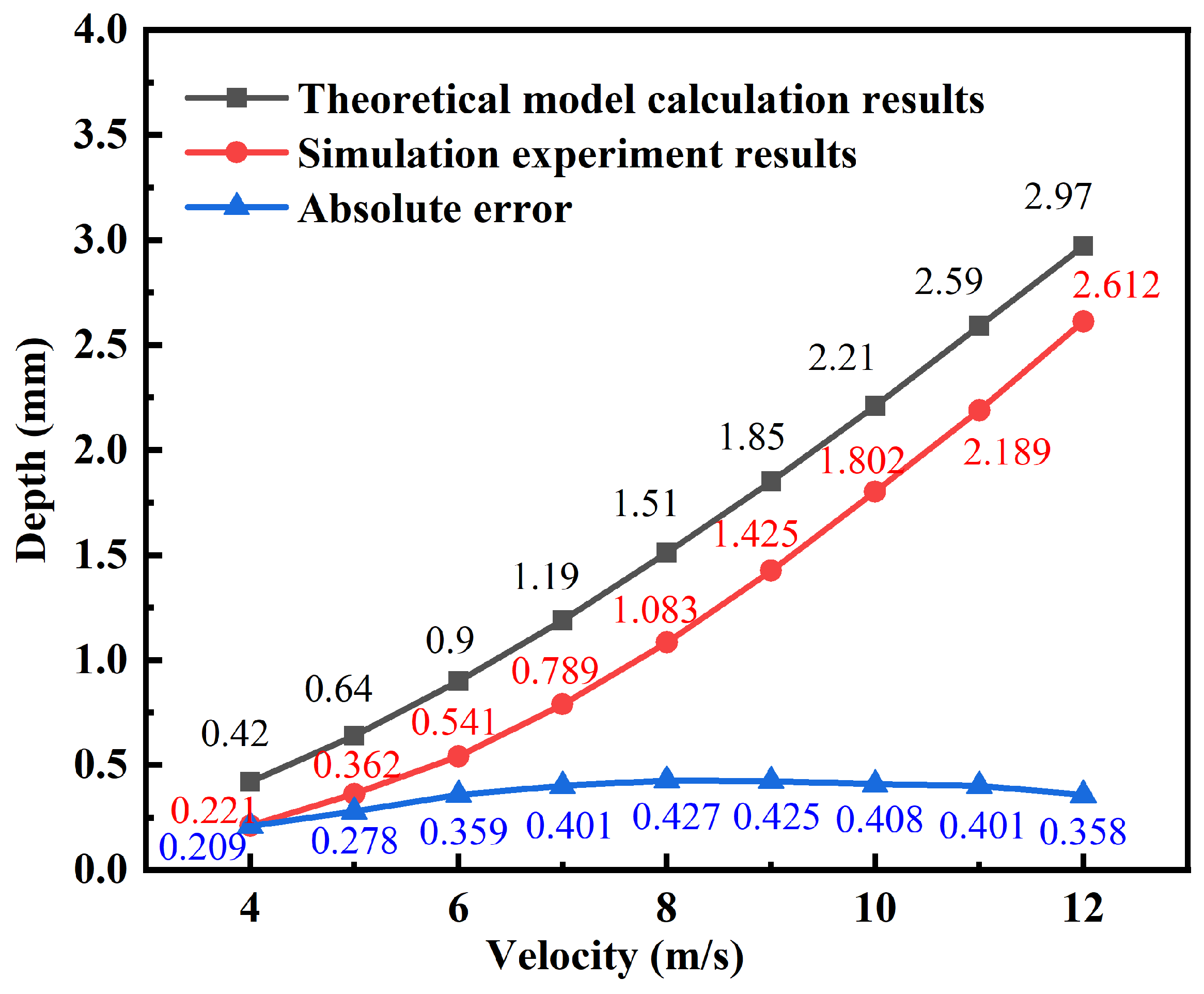
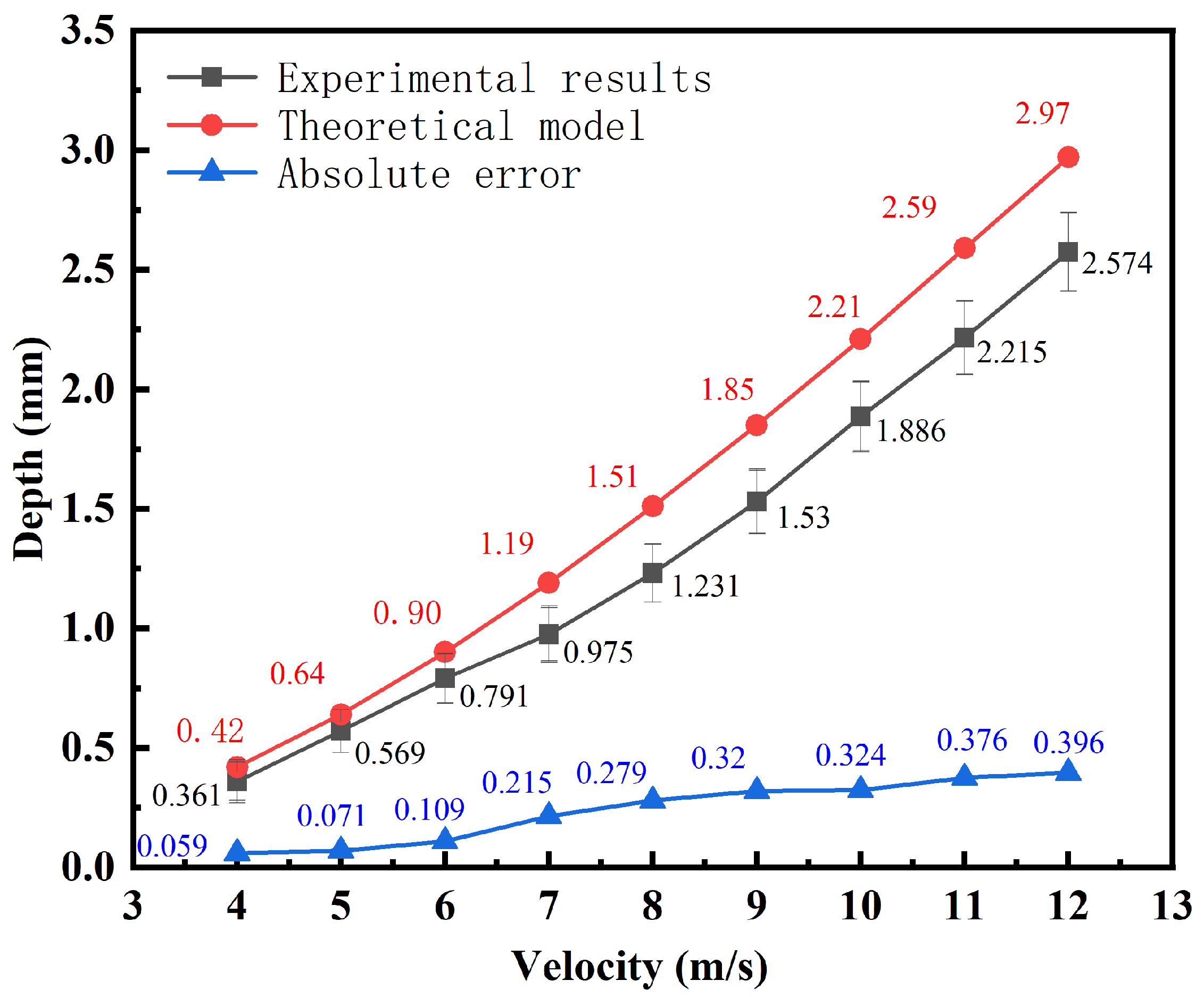
5.1. Discussion of Experimental Results
5.2. Improved Model for Incorporating Surface Tension
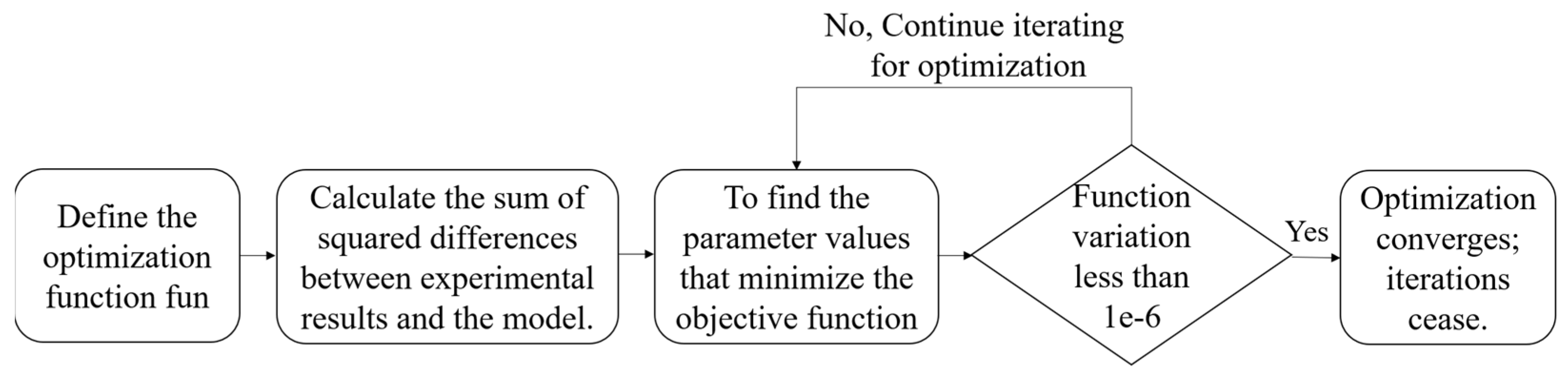
5.3. Optimization of the Theoretical Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Pan, J.; Zhang, Z.; Wu, H.; Yao, N.; Cai, D.; Xu, Y.; Zhang, J.; Sun, G.; Wang, L.; et al. Ultrasensitive skin-like wearable optical sensors based on glass micro/nanofibers. Opto-Electron. Adv. 2020, 3, 190022-1–190022-7. [Google Scholar] [CrossRef]
- Sa, B. Ferromagnetic Glass-Coated Micro-and Nanowires for Medical Application. Biomed. J. Sci. Tech. Res. 2021, 32, 25413–25417. [Google Scholar]
- Al-Buriahi, M.S.; Alzahrani, J.S.; Alrowaili, Z.A.; Olarinoye, I.; Sriwunkum, C. Recycling of waste cathode-ray tube glasses as building materials for shielding structures in medical and nuclear facilities. Constr. Build. Mater. 2023, 376, 131029. [Google Scholar] [CrossRef]
- Wang, S.; Kong, L.; Wang, C.; Cheung, C.F. Ultra-precision manufacturing of microlens arrays using an optimum machining process chain. Opt. Express 2023, 31, 2234–2247. [Google Scholar] [CrossRef]
- Liu, Y.; Tong, H.; Li, Y.; Chen, J. The effect of tool wear on the damaged layer thickness and tool wear rate in ultra-precision turning of quartz glass. J. Micromech. Microeng. 2023, 33, 095012. [Google Scholar] [CrossRef]
- Liu, Y.; Tong, H.; Liu, G.; Li, Y.; Tan, Q. Cutting model considering damage layer thickness for ultra-precision turning of quartz glass. The Int. J. Adv. Manuf. Technol. 2023, 126, 4087–4100. [Google Scholar] [CrossRef]
- Stamopoulos, A.; Di, I.; Di, G. Simulation of the thermoforming process of glass fiber–reinforced polymeric components: Investigation of the combined effect of the crosshead speed and material temperature. The Int. J. Adv. Manuf. Technol. 2021, 117, 2987–3009. [Google Scholar] [CrossRef]
- Bush, S.; Torres, F. Morphological characterisation of long glass fibre composites for the thermoforming process. Int. Polym. Process. 2022, 15, 208–214. [Google Scholar] [CrossRef]
- Gao, W.; Liu, N.; Jiao, Y.; Xie, X.; Zhang, L. Flame trajectory of a non-vertical turbulent buoyant jet flame. Appl. Energy Combust. Sci. 2021, 7, 100039. [Google Scholar] [CrossRef]
- Shmakov, A.; Kozlov, V.; Litvinenko, Y.; Pavlenko, A. Specific features of the flame structure of a pre-mixed hydrogen-oxygen mixture exhausting into air. Int. J. Hydrogen Energy 2024, 74, 121–127. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, J.; Wang, B.; Chang, L.; Palacios, A. Experimental study on trajectory flame length and axial temperature distribution of inclined turbulent jet flames. Fire Saf. J. 2022, 131, 103623. [Google Scholar] [CrossRef]
- Ba, Q.X.; Zhao, Z.Y.; Zhang, Y.P.; Liu, Y.; Christopher, D.M.; Ge, P.; Li, X. Modeling of cryogenic compressed hydrogen jet flames. Int. J. Hydrogen Energy 2024, 51, 917–927. [Google Scholar] [CrossRef]
- Li, F.; Pan, J.; Zhang, C.; Quaye, E.K.; Shao, X. Structure and combustion characteristics of methane/air premixed flame under the action of wall. Energy Eng. J. Assoc. Energy Eng. 2021, 118, 1135–1154. [Google Scholar] [CrossRef]
- Gong, L.; Han, Y.F.; Zheng, X.Q.; Wang, H.; Mo, T.; Yao, Y.; Zhang, Y. Effect of distance of vertical barrier wall and release temperature on the hydrogen jet flame width and temperature distribution induced by impingement of ignited release of cryogenic hydrogen. Combust. Flame 2024, 259, 113133. [Google Scholar] [CrossRef]
- Schuhler, E.; Lecordier, B.; Yon, J.; Godard, G.; Coppalle, A. Experimental investigation of a low Reynolds number flame jet impinging flat plates. Int. J. Heat Mass Transf. 2020, 156, 119856. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, H.; Lv, J.; Liu, X.; Zhang, F.; Jiang, S.; Ma, L.; Wang, C.; Ni, J.; Peng, G. Adhesive-free bonding fiber optic Fabry–Perot pressure sensor based on oxy-hydrogen flame welding and spiral tube. Opt. Commun. 2020, 476, 126307. [Google Scholar] [CrossRef]
- Jokiaho, T.; Santa-Aho, S.; Peura, P.; Vippola, M. Cracking and failure characteristics of flame cut thick steel plates. Metall. Mater. Trans. A 2020, 51, 1744–1754. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Li, C.; Li, S.; Han, X.; Jiang, H. Mechanism study on the influence of combustion models and spray gun geometric parameters on high-velocity oxygen-fuel (HVOF) thermal spraying. J. Manuf. Process. 2023, 98, 173–185. [Google Scholar] [CrossRef]
- Cremers MF, G.; Remie, M.J.; Schreel, K.; De Goey, L.P. Heat transfer mechanisms of laminar flames of hydrogen + oxygen. Combust. Flame 2004, 139, 39–51. [Google Scholar] [CrossRef]
- Tang, J.; Zhang, Y.; Li, X.; Wang, Q.; Zhou, P.; Zhang, L.; He, Q.; Deng, H. Conformal polishing of a glass microlens array through oxyhydrogen flame-induced viscoelasticity flow at nano/microscale. J. Mater. Process. Technol. 2024, 328, 118420. [Google Scholar] [CrossRef]
- Houf, W.; Schefer, R. Analytical and experimental investigation of small-scale unintended releases of hydrogen. Int. J. Hydrogen Energy 2008, 33, 1435–1444. [Google Scholar] [CrossRef]
- Kang, Y.; Lu, T.; Lu, X.; Gou, X.; Huang, X.; Peng, S.; Ji, X.; Zhou, Y.; Song, Y. On predicting the length, width, and volume of the jet diffusion flame. Appl. Therm. Eng. 2016, 94, 799–812. [Google Scholar] [CrossRef]
- Mogi, T.; Horiguchi, S. Experimental study on the hazards of high-pressure hydrogen jet diffusion flames. Loss Prev. Proc. 2008, 22, 45–51. [Google Scholar] [CrossRef]
- Wang, C.; Ding, L.; Wan, H.X.; Ji, J.; Huang, Y. Experimental study of flame morphology and size model of a horizontal jet flame impinging a wall. Process Saf. Environ. Prot. 2021, 147, 1009–1017. [Google Scholar] [CrossRef]
- Veser, A.; Kuznetsov, M.; Fast, G.; Friedrich, A.; Kotchourko, N.; Stern, G.; Schwall, M.; Breitung, W. The structure and flame propagation regimes in turbulent hydrogen jets. Int. J. Hydrogen Energy 2011, 36, 2351–2359. [Google Scholar] [CrossRef]
- Fu, W.; Jiang, W.; Zhang, X. Calculation model of the concave mirror depth in gas jet forming of the mirror blank. Int. J. Adv. Manuf. Technol. 2023, 125, 1679–1687. [Google Scholar] [CrossRef]
- Banks, R.; Chandrasekhara, D. Experimental investigation of the penetration of a high-velocity gas jet through a liquid surface. J. Fluid Mech. 1963, 15, 13–34. [Google Scholar] [CrossRef]
- Bellucci, D.; Cannillo, V.; Sola, A. Coefficient of thermal expansion of bioactive glasses: Available literature data and analytical equation estimates. Ceram. Int. 2011, 37, 2963–2972. [Google Scholar] [CrossRef]
- Karasu, B.; Demirel, İ.; Aydın, S.; Dalkıran, M.; Lik, B. Past and present approaches to borosilicate glasses. El-Cezeri 2020, 7, 940–969. [Google Scholar]




| Parameter | Numerical Value |
|---|---|
| Inlet gas velocity (m/s) | 4, 5, 6, 7, 8, 9, 10, 11, 12 |
| nozzle height (Distance between flame spray gun nozzle and glass surface) (mm) | 20 |
| experimental glass thickness (mm) | 5 |
| flame gun nozzle diameter (mm) | 0.5 |
| Softening temperature | 800 °C |
| linear expansion coefficient | 3.3 × 10−6 K−1 |
| density | 2.23 t m−3 |
| Specific heat | 0.9 J g−1 K−1 |
| Thermal conductivity | 1.2 W m−1 K−1 |
| SiO2 | 81% |
| Bi2O3 | 13% |
| Na2O | 4% |
| Al2O3 | 2% |
| Velocity (m/s) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Improved model (mm) | 0.405 | 0.62 | 0.85 | 1.10 | 1.40 | 1.70 | 2.05 | 2.44 | 2.79 |
| Experiment data (mm) | 0.361 | 0.569 | 0.791 | 0.975 | 1.231 | 1.53 | 1.886 | 2.215 | 2.574 |
| Velocity (m/s) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Theoretical model (mm) | 0.059 | 0.071 | 0.109 | 0.215 | 0.279 | 0.32 | 0.324 | 0.376 | 0.369 |
| Improved model (mm) | 0.045 | 0.051 | 0.791 | 0.975 | 1.231 | 1.53 | 1.886 | 2.215 | 2.574 |
| Velocity (m/s) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Iteratively optimized model (mm) | 0.38 | 0.58 | 0.80 | 1.00 | 1.30 | 1.60 | 1.90 | 2.28 | 2.61 |
| Experiment data (mm) | 0.361 | 0.569 | 0.791 | 0.975 | 1.231 | 1.53 | 1.886 | 2.215 | 2.574 |
| Velocity (m/s) | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Theoretical model (mm) | 0.059 | 0.071 | 0.109 | 0.215 | 0.279 | 0.32 | 0.324 | 0.376 | 0.369 |
| Improved model (mm) | 0.045 | 0.051 | 0.059 | 0.125 | 0.169 | 0.17 | 0.164 | 0.225 | 0.216 |
| Iteratively optimized model (mm) | 0.019 | 0.11 | 0.009 | 0.025 | 0.069 | 0.07 | 0.014 | 0.065 | 0.036 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhai, Y.; Zhang, X.; Qi, X.; Fu, W. Prediction and Analysis of Borosilicate Glass Surface Deformation Induced by Flame Jet. Machines 2024, 12, 765. https://doi.org/10.3390/machines12110765
Wang B, Zhai Y, Zhang X, Qi X, Fu W. Prediction and Analysis of Borosilicate Glass Surface Deformation Induced by Flame Jet. Machines. 2024; 12(11):765. https://doi.org/10.3390/machines12110765
Chicago/Turabian StyleWang, Biling, Yutang Zhai, Xinming Zhang, Xinxin Qi, and Weijie Fu. 2024. "Prediction and Analysis of Borosilicate Glass Surface Deformation Induced by Flame Jet" Machines 12, no. 11: 765. https://doi.org/10.3390/machines12110765
APA StyleWang, B., Zhai, Y., Zhang, X., Qi, X., & Fu, W. (2024). Prediction and Analysis of Borosilicate Glass Surface Deformation Induced by Flame Jet. Machines, 12(11), 765. https://doi.org/10.3390/machines12110765






