Multi-Agent Reinforcement Learning for Extended Flexible Job Shop Scheduling
Abstract
:1. Introduction
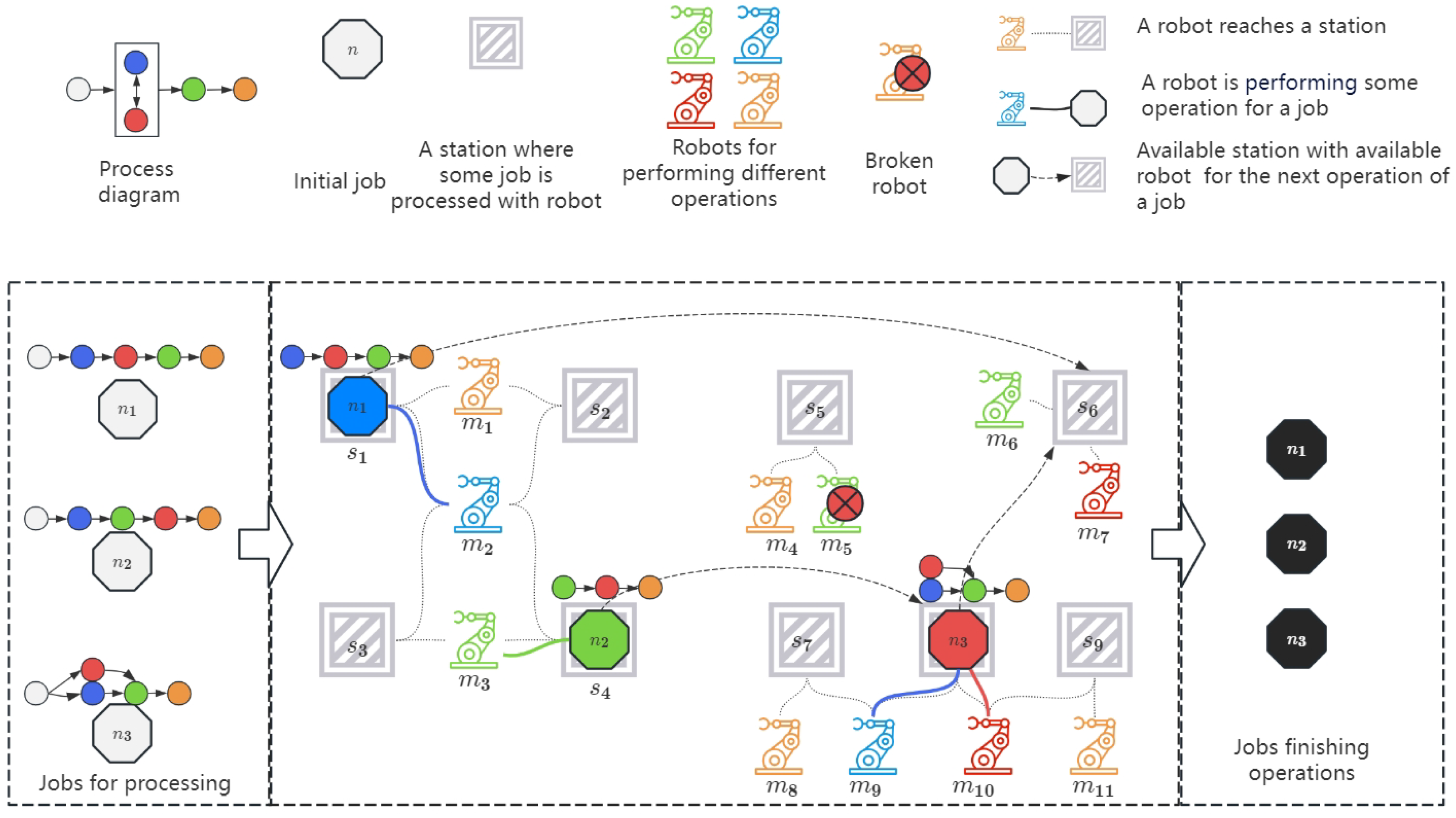
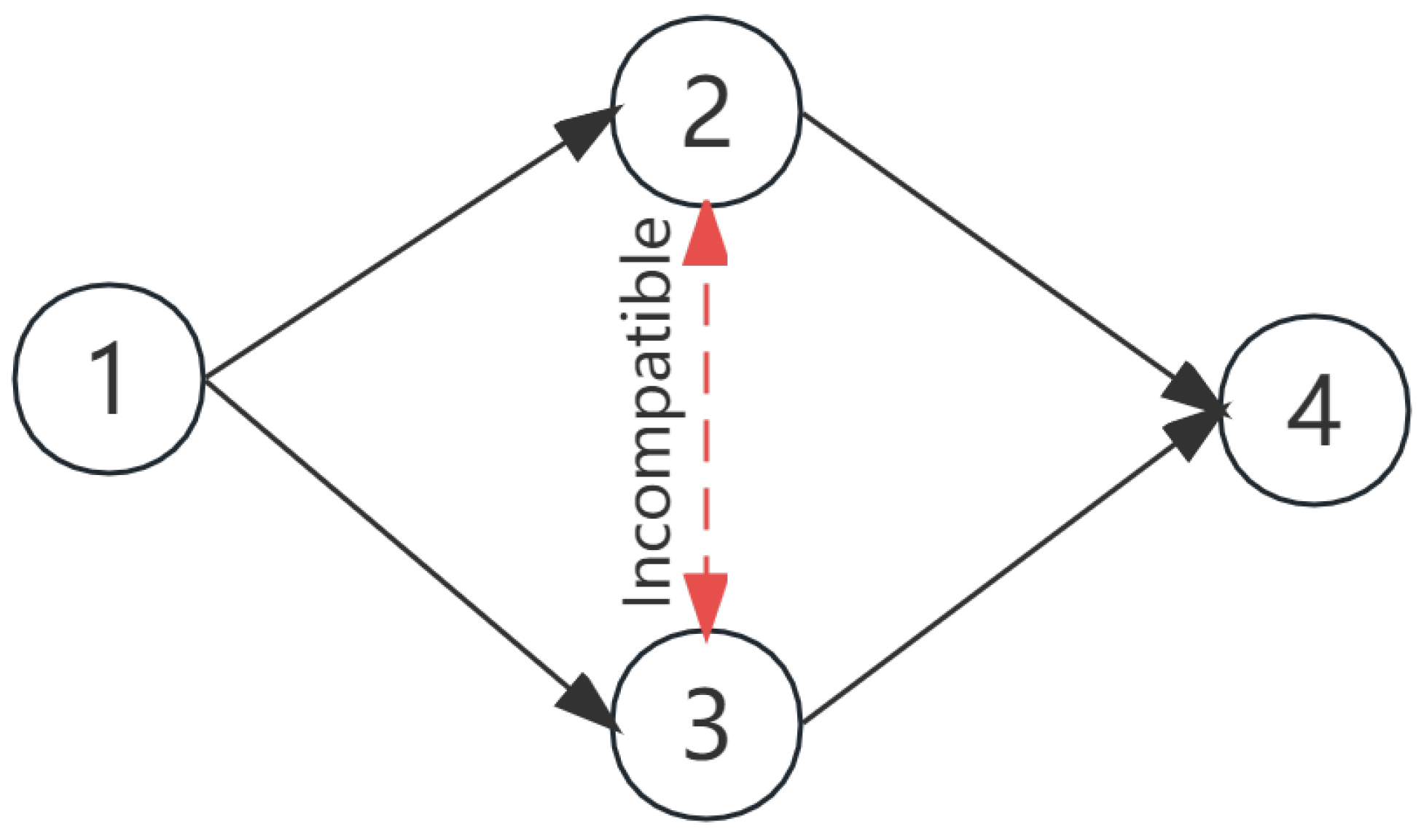
- Dual flexibity. FJSP-DT considers both technology and path flexibility. As shown in Figure 1, the blue operation may be processed before the red operation, or vice versa, which results in technology flexibility. The same operations can be processed by different robots, e.g., the orange operation can be processed by Robot or Robot , hence leading to path flexibility.
- Varied transportation time. One job needs to be processed through multiple stations, and the transportation time between operations varies depending on the distance between stations.
- Cooperative gaming and uncertain environment. Multiple jobs coordinate their operations to achieve shorter makespan employing preempt resources, such as robots, stations, etc. The environment also suffers from uncertain factors, e.g., robot failures.
- Generalization. The scheduling algorithm should be adaptable to changing conditions, such as altered operation sequences, modified stations, robot distributions, or varying job quantities.
- Real-time. Due to the uncertainty of the environment, the scheduler needs to respond in real time (in seconds) to robot failures and make real-time scheduling.
- Accuracy. Significant operational risks may arise in the application scenario corresponding to FJSP-DT. In automobile assembly scheduling, poor coordination between operations may lead to collisions. Therefore, the algorithm needs to ensure operational safety.
- Curse of dimensionality. The solution space expands as the number of agents and resources (such as robots, and stations) increases, resulting in a computational dilemma. Here, M, S, and T are used to represent the sets of robots, stations, and time respectively. N and O represent the sets of agents and operations respectively. The solution space of FJSP-DT is which causes an explosion in combinations.
- The FJSP-DT abstracted from real and complex scenarios is proposed. As far as our literature review is concerned, the problem is new and needs to be fully investigated. The FJSP-DT is modeled as a decentralized partially observable Markov decision process in that an agent may only observe the information around it in real applications. Then, the MARL-based method can be applied to achieve high adaptability and real-time decisions.
- We build an adaptive and stable multi-agent learning framework by combining a graph convolutional network (GCN) and the actor–critic structure. GCN extracts embedding graph’s structural features and represents system states in non-Euclidean space, thereby degrading dimension curses and adapting to various scheduling environments. The actor–critic structure can update the network parameters in a single step without running an episode, making it faster than the policy gradient algorithm.
- A double Q-value mixing algorithm (DQMIX) under the above framework is proposed to address the challenge of fast convergence and high adaptability. The algorithm combines an unrestricted optimal network with a monotonic mixing network to improve exploration and exploitation capabilities. It also integrates mechanistic constraints into data-based learning, mitigating the curse of dimensionality by eliminating invalid actions. In addition, the reward function is designed as a function of reduction in makespan estimation to mitigate the learning challenges caused by sparse feedback.
2. Related Works
- Single-Agent Reinforcement Learning (SARL): The algorithm only contains one agent that makes all the decisions for a control system.
- Multi-Agent Reinforcement Learning (MARL): The algorithm comprises multiple agents that interact with the environment through their respective policies.
2.1. SARL for Scheduling
2.1.1. SARL with Value Iteration
2.1.2. SARL with Policy Iteration
2.2. MARL for Scheduling
- Distributed Training Paradigm (DTP): In the distributed Paradigm, agents learn independently of other agents and do not rely on explicit information exchange.
- Centralized Training Paradigm (CTP): The centralized paradigm allows agents to exchange additional information during training, which is then abandoned during tests. Agents receive only the locally observable information and independently determine actions according to their policies during execution.
2.2.1. MARL with DTP
2.2.2. MARL with CTP
3. Problem Description and Model Formulation
3.1. Problem Description
- All jobs are available after release dates.
- A robot can only process one job at a time.
- Each operation can only be processed on one robot at a time.
- Each operation cannot be interrupted during processing.
- There is no buffer in the station, and each station can only accommodate one job at a time.
3.2. Dec-POMDP Framework
- is the set of agents;
- is a set of states denoting all joint states possible by the multi-agents;
- is the set of joint actions, where denotes the set of actions for agent i;
- is the transition probability function;
- is the reward function, mapping states and joint actions to real numbers;
- is the set of joint observations, where is the set of observations available to agent i;
- is the observation probability function;
- is a discount factor.
3.3. State and Observations
3.3.1. State
3.3.2. Observations
3.4. Actions
3.5. Reward
4. Algorithm
4.1. Algorithm Overview
- We utilize a learning algorithm to satisfy the real-time and adaptive requirements of FJSP-DT scheduling. The scheduling procedure of FJSP-DT is modeled as a Dec-POMDP model, and a real-time scheduling policy that can adapt to an uncertain environment is obtained through reinforcement learning.
- Regarding accuracy, we propose double critic networks to assist agent training, enhancing the stability and quality of learning. In addition, a MASK layer is added in the DQMIX output, which outputs a set of feasible actions based on the current state and conflicted relationships, ensuring that the output actions are accurate.
- The MARL architecture is adopted to reduce the dimensionality of action space. Each job agent only needs to choose actions based on their own observations, and each agent model only needs to output a dimensional vector instead of dimensional vectors. The GCN network layer is designed to compress the number of input parameters from to , which further alleviates the dimensionality curse.
- Firstly, an environment instance is generated according to FJSP-DT.
- Secondly, starting at time , each agent chooses an action based on its own observation and its own policy. The actions of all agents form the joint action vector .
- Thirdly, according to the processing state and scheduling action at time t, the environment updates the processing state and observations at time . The environment outputs a reward r according to the reward function, and stores the tuple as a POMDP instance in the experience memory.
- Next, the agents continue to interact with the environment until all jobs’ tasks are completed, or the makespan exceeds .
- Finally, when the scheduling ends, a complete POMDP chain is formed, and the environment gives the final reward r.
4.2. Agent Network
4.3. Critic Network
4.3.1. Motivation of Proposing Double Critic Networks
- The non-negative monotonicity of the mixing value function should be kept when the optimal policy has been recovered, consistent with the goal pursued in cooperative games. Each agent’s marginal return with the optimal policy is non-negative, i.e.,
- To overcome the limitations of when the optimal policy has not yet been recovered, a joint action-value function is introduced. is a function of state s, action–observation history and joint action a. It reduces the dependencies on agents’ utilities.
4.3.2. Mixing Network
4.3.3. Optimal Network
4.4. Loss Function
| Algorithm 1 DQMIX Algorithm. |
|
5. Case Study
5.1. Case Description and Algorithm Settings
5.1.1. Case Description
5.1.2. Experimental Settings
5.2. Solution Quality
5.3. Computation Time
5.4. Convergence
5.5. Scalability
5.6. Generalization
5.6.1. Generalization to Robot Breakdowns
5.6.2. Generalization to Varied Quantity of Jobs
5.6.3. Generalization to Changes in Operations
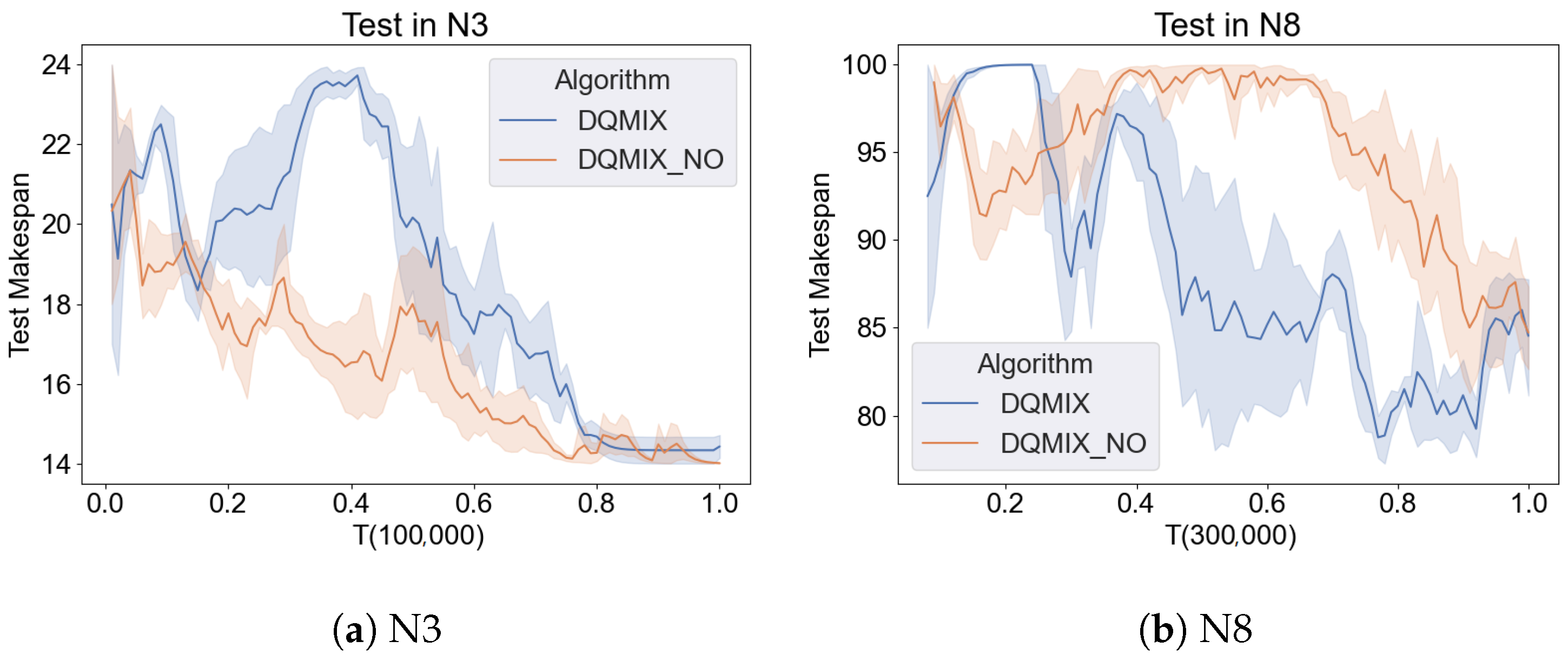
5.7. GCN Effectiveness Verification
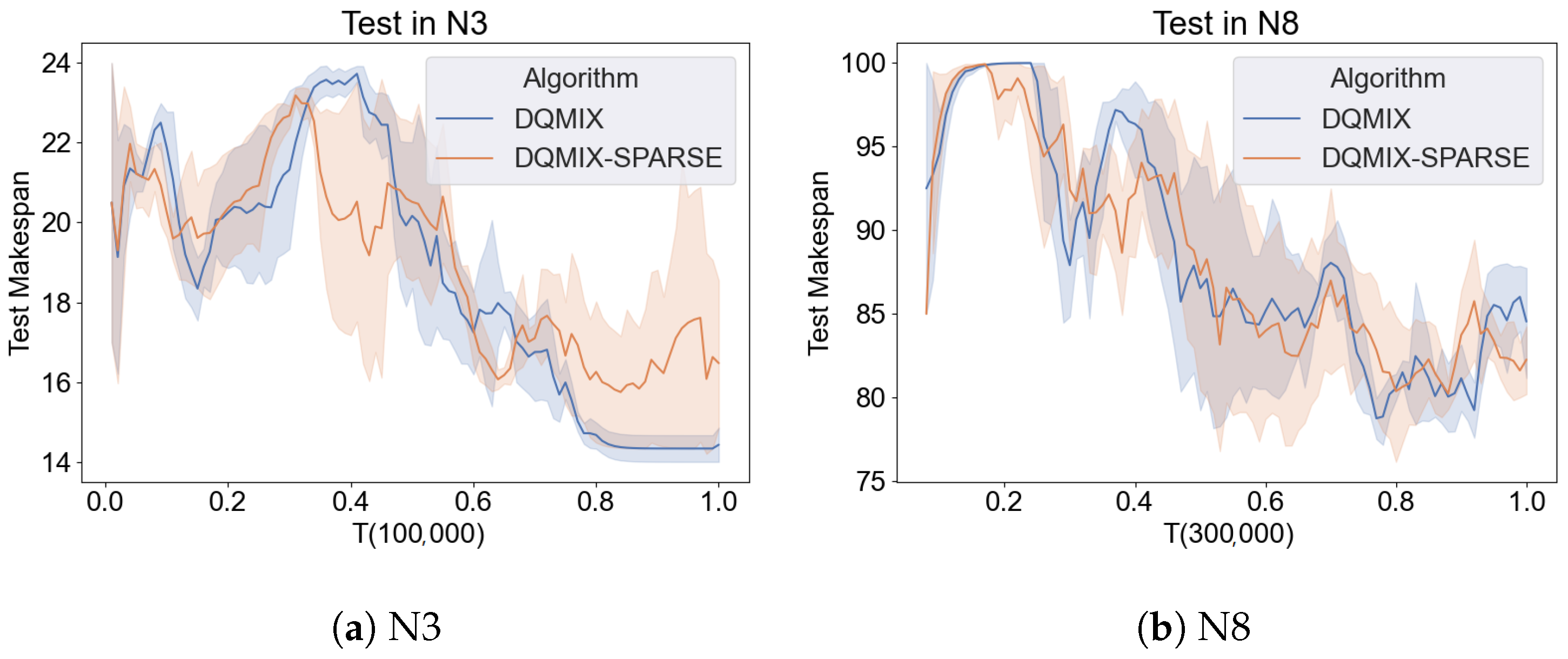
5.8. Ablation on Reward Function
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chaudhry, I.A.; Khan, A.A. A research survey: Review of flexible job shop scheduling techniques. Int. Trans. Oper. Res. 2016, 23, 551–591. [Google Scholar] [CrossRef]
- Xiong, H.; Shi, S.; Ren, D.; Hu, J. A survey of job shop scheduling problem: The types and models. Comput. Oper. Res. 2022, 142, 105731. [Google Scholar] [CrossRef]
- Luo, Q.; Deng, Q.; Xie, G.; Gong, G. A Pareto-based two-stage evolutionary algorithm for flexible job shop scheduling problem with worker cooperation flexibility. Robot. Comput.-Integr. Manuf. 2023, 82, 102534. [Google Scholar] [CrossRef]
- Wei, Z.; Liao, W.; Zhang, L. Hybrid energy-efficient scheduling measures for flexible job-shop problem with variable machining speeds. Expert Syst. Appl. 2022, 197, 116785. [Google Scholar] [CrossRef]
- Li, Y.; Gu, W.; Yuan, M.; Tang, Y. Real-time data-driven dynamic scheduling for flexible job shop with insufficient transportation resources using hybrid deep Q network. Robot. Comput.-Integr. Manuf. 2022, 74, 102283. [Google Scholar] [CrossRef]
- Du, Y.; Li, J.Q.; Chen, X.L.; Duan, P.Y.; Pan, Q.K. Knowledge-based reinforcement learning and estimation of distribution algorithm for flexible job shop scheduling problem. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 1036–1050. [Google Scholar] [CrossRef]
- Burggräf, P.; Wagner, J.; Saßmannshausen, T.; Ohrndorf, D.; Subramani, K. Multi-agent-based deep reinforcement learning for dynamic flexible job shop scheduling. Procedia CIRP 2022, 112, 57–62. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, H.; Tang, D.; Zhou, T.; Gui, Y. Dynamic job shop scheduling based on deep reinforcement learning for multi-agent manufacturing systems. Robot. Comput.-Integr. Manuf. 2022, 78, 102412. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Lin, T.; Zhao, C.; Wang, K.; Chen, Z. Solving job scheduling problems in a resource preemption environment with multi-agent reinforcement learning. Robot. Comput.-Integr. Manuf. 2022, 77, 102324. [Google Scholar] [CrossRef]
- Jing, X.; Yao, X.; Liu, M.; Zhou, J. Multi-agent reinforcement learning based on graph convolutional network for flexible job shop scheduling. J. Intell. Manuf. 2022, 1–19. [Google Scholar] [CrossRef]
- Ku, W.Y.; Beck, J.C. Mixed integer programming models for job shop scheduling: A computational analysis. Comput. Oper. Res. 2016, 73, 165–173. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Tian, Y.; Si, L.; Zhang, X.; Cheng, R.; He, C.; Tan, K.C.; Jin, Y. Evolutionary large-scale multi-objective optimization: A survey. ACM Comput. Surv. 2021, 54, 174. [Google Scholar] [CrossRef]
- Afshin, O.; Davood, H. A review of cooperative multi-agent deep reinforcement learning. Appl. Intell. 2023, 53, 13677–13722. [Google Scholar]
- Lihu, A.; Holban, S. Top five most promising algorithms in scheduling. In Proceedings of the 2009 5th International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 28–29 May 2009; pp. 397–404. [Google Scholar]
- Wang, X.; Zhang, L.; Ren, L.; Xie, K.; Wang, K.; Ye, F.; Chen, Z. Brief review on applying reinforcement learning to job shop scheduling problems. J. Syst. Simul. 2021, 33, 2782. [Google Scholar]
- Liu, Y.K.; Zhang, X.S.; Zhang, L.; Tao, F.; Wang, L.H. A multi-agent architecture for scheduling in platform-based smart manufacturing systems. Front. Inf. Technol. Electron. Eng. 2019, 20, 1465–1492. [Google Scholar] [CrossRef]
- Zhang, W.; Dietterich, T.G. A reinforcement learning approach to job-shop scheduling. In Proceedings of the IJCAI, Citeseer, Montreal, QU, Canada, 20–25 August 1995; Volume 95, pp. 1114–1120. [Google Scholar]
- Aydin, M.E.; Öztemel, E. Dynamic job-shop scheduling using reinforcement learning agents. Robot. Auton. Syst. 2000, 33, 169–178. [Google Scholar] [CrossRef]
- Waschneck, B.; Reichstaller, A.; Belzner, L.; Altenmüller, T.; Bauernhansl, T.; Knapp, A.; Kyek, A. Optimization of global production scheduling with deep reinforcement learning. Procedia CIRP 2018, 72, 1264–1269. [Google Scholar] [CrossRef]
- Luo, S. Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning. Appl. Soft Comput. 2020, 91, 106208. [Google Scholar] [CrossRef]
- Lang, S.; Behrendt, F.; Lanzerath, N.; Reggelin, T.; Müller, M. Integration of deep reinforcement learning and discrete-event simulation for real-time scheduling of a flexible job shop production. In Proceedings of the 2020 Winter Simulation Conference (WSC), Orlando, FL, USA, 14–18 December 2020; pp. 3057–3068. [Google Scholar]
- Gu, Y.; Chen, M.; Wang, L. A self-learning discrete salp swarm algorithm based on deep reinforcement learning for dynamic job shop scheduling problem. Appl. Intell. 2023, 53, 18925–18958. [Google Scholar] [CrossRef]
- Wang, L.; Hu, X.; Wang, Y.; Xu, S.; Ma, S.; Yang, K.; Liu, Z.; Wang, W. Dynamic job-shop scheduling in smart manufacturing using deep reinforcement learning. Comput. Netw. 2021, 190, 107969. [Google Scholar] [CrossRef]
- Gronauer, S.; Diepold, K. Multi-agent deep reinforcement learning: A survey. Artif. Intell. Rev. 2022, 55, 895–943. [Google Scholar] [CrossRef]
- Chandak, Y.; Theocharous, G.; Kostas, J.; Jordan, S.; Thomas, P. Learning action representations for reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 941–950. [Google Scholar]
- Liu, Y.; Li, Z.; Jiang, Z.; He, Y. Prospects for multi-agent collaboration and gaming: Challenge, technology, and application. Front. Inf. Technol. Electron. Eng. 2022, 23, 1002–1009. [Google Scholar] [CrossRef]
- Aissani, N.; Trentesaux, D.; Beldjilali, B. Multi-agent reinforcement learning for adaptive scheduling: Application to multi-site company. IFAC Proc. Vol. 2009, 42, 1102–1107. [Google Scholar] [CrossRef]
- Martínez Jiménez, Y.; Coto Palacio, J.; Nowé, A. Multi-agent reinforcement learning tool for job shop scheduling problems. In Proceedings of the International Conference on Optimization and Learning, Cadiz, Spain, 17–19 February 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–12. [Google Scholar]
- Hameed, M.S.A.; Schwung, A. Reinforcement learning on job shop scheduling problems using graph networks. arXiv 2020, arXiv:2009.03836. [Google Scholar]
- Zhou, T.; Tang, D.; Zhu, H.; Zhang, Z. Multi-agent reinforcement learning for online scheduling in smart factories. Robot. Comput.-Integr. Manuf. 2021, 72, 102202. [Google Scholar] [CrossRef]
- Popper, J.; Motsch, W.; David, A.; Petzsche, T.; Ruskowski, M. Utilizing multi-agent deep reinforcement learning for flexible job shop scheduling under sustainable viewpoints. In Proceedings of the 2021 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, 7–8 October 2021; pp. 1–6. [Google Scholar]
- Wang, S.; Li, J.; Luo, Y. Smart scheduling for flexible and hybrid production with multi-agent deep reinforcement learning. In Proceedings of the 2021 IEEE 2nd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 17–19 December 2021; Volume 2, pp. 288–294. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Zhang, C.; Song, W.; Cao, Z.; Zhang, J.; Tan, P.S.; Chi, X. Learning to dispatch for job shop scheduling via deep reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 1621–1632. [Google Scholar]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. QMIX: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 4295–4304. [Google Scholar]
- Son, K.; Kim, D.; Kang, W.J.; Hostallero, D.E.; Yi, Y. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 5887–5896. [Google Scholar]
- Mahajan, A.; Rashid, T.; Samvelyan, M.; Whiteson, S. MAVEN: Multi-agent variational exploration. Adv. Neural Inf. Process. Syst. 2019, 32, 7611–7622. [Google Scholar]
- Rashid, T.; Farquhar, G.; Peng, B.; Whiteson, S. Weighted QMIX: Expanding monotonic value function factorisation for deep multi-agent reinforcement learning. Adv. Neural Inf. Process. Syst. 2020, 33, 10199–10210. [Google Scholar]
- Son, K.; Ahn, S.; Reyes, R.D.; Shin, J.; Yi, Y. QTRAN++: Improved value transformation for cooperative multi-agent reinforcement learning. arXiv 2020, arXiv:2006.12010. [Google Scholar]
- Ha, D.; Dai, A.M.; Le, Q.V. HyperNetworks. In Proceedings of the 5th International Conference on Learning Representations, ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Li, X.; Gao, L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int. J. Prod. Econ. 2016, 174, 93–110. [Google Scholar] [CrossRef]
- Li, X.; Gao, L.; Pan, Q.; Wan, L.; Chao, K.M. An effective hybrid genetic algorithm and variable neighborhood search for integrated process planning and scheduling in a packaging machine workshop. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 49, 1933–1945. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Gao, L.; Li, Y. A modified genetic algorithm with new encoding and decoding methods for integrated process planning and scheduling problem. IEEE Trans. Cybern. 2020, 51, 4429–4438. [Google Scholar] [CrossRef]


| Type | Number 1 |
|---|---|
| Classical JSP | 68 |
| Dynamic JSP | 48 |
| JSP considering the machine availability | 52 |
| Flexible JSP with alternative machines (FJSP) | 225 |
| JSP with alternative routings | 32 |
| JSP considering batches | 39 |
| JSP considering setup times | 69 |
| JSP considering transportation time | 1 |
| JSP with nondeterministic or non-constant processing time | 32 |
| Distributed JSP (DSJSP) | 25 |
| JSP with dual-resource constraints (DRJSP) | 30 |
| JSP considering energy and pro-environment | 132 |
| JSP with a prior job | 5 |
| JSP with dependent jobs | 2 |
| JSP with no-wait constraint for operations on the same job | 18 |
| JSP with blocking constraint for capacities of buffer | 8 |
| JSP with reentrancy | 9 |
| JSP with preemption | 2 |
| JSP considering overtime work | 2 |
| JSP with limited buffer capacity | 2 |
| JSP considering outsourcing (subcontracting) | 6 |
| JSP considering robot or automated guided vehicle (AGV) | 28 |
| FJSP with worker cooperation flexibility | 1 |
| FJSP with technology and path flexibility (FJSP-DT) | - |
| Symbol | Definition |
|---|---|
| N | A set of jobs, . |
| The ith job in the set N. | |
| O | A set of all jobs’ operations, . |
| S | A set of all stations for processing, . |
| The kth station in the set S. | |
| M | A set of robots, . |
| The kth robot in the set M. | |
| A set of operations for job , . | |
| The jth operation of job . | |
| A set of robots that can support operation , . | |
| The kth robot that can support operation . | |
| A set of robots that the station can cover. | |
| The kth robot that the station can cover. | |
| A set of stations that the robot can reach. | |
| The lth station that the robot can reach. |
| Action | Description |
|---|---|
| Specifying a station and a robot are available for the agent to perform the next operation. | |
| Performing the transportation action. If the current station cannot support the next operation, the agent must move. | |
| Staying on processing. The agent must not be interrupted to carry out other things. | |
| Taking a wait action. The agent performs nothing. | |
| Representing stop. At this point, the agent has completed all operations. |
| Case | Number of Jobs | Number of Operations | Number of Stations | Number of Robots | LB | |
|---|---|---|---|---|---|---|
| N3 | 3 | 12 | 5 | 5 | 18 | 13 |
| N6 | 6 | 41 | 22 | 35 | 90 | 54 |
| N8 | 8 | 55 | 22 | 35 | 100 | 58 |
| N12 | 12 | 83 | 22 | 35 | 120 | 66 |
| Operation | Alternative Robots (Processing Time) |
|---|---|
| 1 | M1(1), M4(1) |
| 2 | M3(5), M4(5), M5(5) |
| 3 | M1(4), M2(4) |
| 4 | M2(1), M3(1), M5(1) |
| Robot | Available Stations |
|---|---|
| M1 | S1, S4, S5 |
| M2 | S2 |
| M3 | S2, S3, S5 |
| M4 | S4 |
| M5 | S2, S3, S5 |
| Station | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| S1 | 0 | 1 | 1 | 2 | 2 |
| S2 | 1 | 0 | 1 | 1 | 2 |
| S3 | 1 | 1 | 0 | 1 | 1 |
| S4 | 2 | 1 | 1 | 0 | 1 |
| S5 | 2 | 2 | 1 | 1 | 0 |
| Network | Parameters |
|---|---|
| GCN | One layer, with the hidden dimension of 512 |
| RNN | Two layers, with the hidden dimension of 512 in each layer. |
| Mixing Network | Two layers, with the hidden dimension of 512 in each layer. |
| Optimal Network | Three layers, with the hidden dimension of 512 in each layer. |
| Case | DQMIX | hGATS | hGAVNS | MGA | CWQMIX | QTRAN | MILP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BEST | MEAN | BEST | MEAN | BEST | MEAN | BEST | MEAN | BEST | MEAN | BEST | MEAN | ||
| N3 | 14 | 14 | 13 | 13 | 13 | 13 | 13 | 14.0 | 14.0 | 17.1 | 14.0 | 16.2 | 13 |
| N6 | 63 | 64.5 | 61 | 63.6 | 61 | 62 | 62 | 63.3 | 68.0 | 83.6 | 72.0 | 84.6 | - |
| N8 | 68 | 70.3 | 71 | 71.6 | 67 | 68 | 70 | 71 | 73 | 75.7 | 76 | 78.7 | - |
| N12 | 81 | 84.7 | 85 | 85.6 | 85 | 85.6 | 83 | 84 | 81 | 85.7 | 82 | 89.7 | - |
| Case | DQMIX | hGATS | hGAVNS | MGA | CWQMIX | QTRAN | MILP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BEST | MEAN | BEST | MEAN | BEST | MEAN | BEST | MEAN | BEST | MEAN | BEST | MEAN | ||
| N3 | 7.7% | 7.7% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 7.7% | 31.5% | 7.7% | 24.5% | 13 |
| N6 | 3.3% | 5.7% | 0.0% | 4.3% | 0.0% | 1.6% | 1.6% | 3.8% | 11.5% | 37.0% | 18.0% | 38.7% | 61 |
| N8 | 1.5% | 4.9% | 6.0% | 6.9% | 0.0% | 1.5% | 4.5% | 6.0% | 9.0% | 13.0% | 13.4% | 17.5% | 67 |
| N12 | 0.0% | 4.6% | 4.9% | 5.7% | 4.9% | 5.7% | 2.5% | 3.7% | 0.0% | 8.8% | 1.2% | 10.7% | 81 |
| Model | Training Duration | Execution Duration |
|---|---|---|
| DQMIX | 5.0 h 47.08 min | 4.59 s |
| hGATS | 47.77 min | 47.77 min |
| hGAVNS | 51.58 min | 51.58 min |
| MGA | 32.86 min | 32.86 min |
| Items | DQMIX | CWQMIX | QTRAN |
|---|---|---|---|
| StaticMakespan 1 | 69 | 73 | 76 |
| Number of instances 2 | 150 | 150 | 150 |
| Makespan mean 3 | 73.0 | 78.5 | 79.3 |
| Makespan variance | 6.0 | 3.7 | 3.6 |
| 5.7% | 7.5% | 4.4% | |
| 5.7% | 10.2% | 7.2% | |
| Success rate | 99.3% | 100% | 98.7% |
| Cases | Number of Jobs | DQMIX | CWQMIX | QTRAN |
|---|---|---|---|---|
| N4 | 4 | 68 | 65 | 81 |
| N5 | 5 | 68 | 66 | 79 |
| N6 | 6 | 70 | 68 | 81 |
| N7 | 7 | 71 | 79 | 76 |
| N8 | 8 | 81 | 79 | 83 |
| Mean | - | 71.6 | 71.4 | 80 |
| Variance | - | 29.3 | 49.3 | 7 |
| Case | DQMIX | CWQMIX | QTRAN |
|---|---|---|---|
| 1 | 77 | 73 | 74 |
| 2 | 89 | 73 | 72 |
| 3 | 71 | 72 | 88 |
| 4 | 79 | 72 | 74 |
| 5 | 68 | 69 | 69 |
| 6 | 75 | 100 | 72 |
| 7 | 66 | 100 | 72 |
| 8 | 69 | 66 | 78 |
| 9 | 68 | 67 | 71 |
| 10 | 67 | 100 | 72 |
| Mean | 72.9 | 79.2 | 74.2 |
| Success rate | 100% | 70% | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, S.; Xiong, G.; Yang, J.; Shen, Z.; Tamir, T.S.; Tao, Z.; Han, Y.; Wang, F.-Y. Multi-Agent Reinforcement Learning for Extended Flexible Job Shop Scheduling. Machines 2024, 12, 8. https://doi.org/10.3390/machines12010008
Peng S, Xiong G, Yang J, Shen Z, Tamir TS, Tao Z, Han Y, Wang F-Y. Multi-Agent Reinforcement Learning for Extended Flexible Job Shop Scheduling. Machines. 2024; 12(1):8. https://doi.org/10.3390/machines12010008
Chicago/Turabian StylePeng, Shaoming, Gang Xiong, Jing Yang, Zhen Shen, Tariku Sinshaw Tamir, Zhikun Tao, Yunjun Han, and Fei-Yue Wang. 2024. "Multi-Agent Reinforcement Learning for Extended Flexible Job Shop Scheduling" Machines 12, no. 1: 8. https://doi.org/10.3390/machines12010008
APA StylePeng, S., Xiong, G., Yang, J., Shen, Z., Tamir, T. S., Tao, Z., Han, Y., & Wang, F.-Y. (2024). Multi-Agent Reinforcement Learning for Extended Flexible Job Shop Scheduling. Machines, 12(1), 8. https://doi.org/10.3390/machines12010008







