Abstract
This paper introduces a two-stage intelligent fault diagnosis model for rolling element bearings (REBs) aimed at overcoming the challenge of limited real-world vibration training data. In this study, bearing characteristic frequencies (BCFs) extracted from a novel hybrid method combining cepstrum pre-whitening (CPW) and high-pass filtering developed by the authors’ group are used as input features, and a two-stage approach is taken to develop an intelligent REB fault detect and diagnosis model. In the first stage, various machine learning (ML) methods, including support vector machine (SVM), multinomial logistic regressions (MLR), and artificial neural networks (ANN), are evaluated to identify faulty bearings from healthy ones. The best-performing ML model is selected for this stage. In the second stage, a similar evaluation is conducted to find the most suitable ML technique for bearing fault classification. The model is trained and validated using vibration data from an EU Clean Sky2 I2BS project (An EU Clean Sky 2 project ‘Integrated Intelligent Bearing Systems’ collaborated between Schaeffler Technologies and the University of Southampton. Safran Aero Engines was the topic manager for this project) and tested on datasets from Case Western Reserve University (CWRU) and the US Society for Machinery Failure Prevention Technology (MFPT). The results show that the two-stage model, using an SVM with a polynomial kernel function in Stage-1 and an ANN with one hidden layer and 0.05 dropout rate in Stage-2, can successfully detect bearing conditions in both test datasets and perform better than the results in literature without the requirement of further training. Compared with a single-stage model, the two-stage model also shows improved performance.
1. Introduction
Rolling element bearings (REBs) are essential components in various types of rotating machinery. To ensure their reliability, it is crucial to comprehend the diverse factors contributing to bearing failure. These factors encompass incorrect design, faulty installation, brinelling, corrosion, lubrication issues, fatigue, wear, and plastic deformation. Effective maintenance and reliability hinge upon a comprehensive understanding of these elements. Moreover, operational parameters, including friction torque, radial internal clearance, and slippage, play pivotal roles in bearing performance [1,2,3]. This study focuses on developing an intelligent diagnostic algorithm specifically aimed at detecting failures due to fatigue. Fatigue failure is characterized by material removal and impulsive signals in the vibration pattern [4]. Fault diagnosis involves the detection and description of faulty components, such as identifying a faulty bearing in a machine and detecting its faulty element. The complexity and the large number of components used in modern machines make it a challenge to identify machine faults from vibration data. It thus requires specialized skills and experience to diagnose them. Furthermore, it requires a broad knowledge of the machine’s structure and working condition, with a general understanding of diagnosis, and expert engineers to know the details of the system. However, expert engineers are usually lacked, either busy with other tasks or unavailable at all for a specific component in real situations [5]. Therefore, several techniques were developed to automate diagnosis procedures and health state predictions, e.g., either by physics/math-based models or by ML-based approaches (data-driven). The model-based approaches use the physics or math models to detect any available fault in bearings. However, the development of these models is limited due to the complex structure, noisy environment, and multiple working conditions. In contrast, the data-driven approaches have gained popularity because they are model-free (primarily relying on learning) and do not require full prior physical knowledge. They can hence be easily implemented, and are able to identify and classify machine health states effectively, while also reducing the role of human labour in diagnosing machine faults [6,7]. However, data-driven techniques have been commonly developed for fault diagnosis under the assumption that the training and testing data come from the same source [8].
Over the recent few decades, researchers have implemented different ML techniques for fault diagnosis. These techniques aim to map the information available in input features to the corresponding machine health states using labelled training data and, as a final step, the test dataset is then used to evaluate the final fit of the model to the training dataset [9]. There are three main phases in development of the ML-based models, including classical machine learning techniques, deep learning algorithms, and transfer learning techniques [10]. The classical machine learning algorithms, such as decision trees, support vector machines, and k-nearest neighbours, are based on statistical and mathematical principles. They require handcrafted feature extraction, with domain experts to identify the most important features from the raw data that are relevant to the problem at hand. These features are then fed into the machine learning algorithms to learn to classify new data based on the extracted features and their labels. This category of ML techniques is highly dependent on the extracted features and adequate samples, so they may be inapplicable when one is unable to capture complex patterns in the data [11].
Deep learning, on the other hand, is a subset of machine learning methods that use multiple layers to learn from the data. Deep learning algorithms can in general automatically extract features from the raw data, so that they can handle more complex and diverse features in datasets. Multi-layer perceptron (MLP), convolutional neural networks (CNNs), and recurrent neural networks (RNNs) are popular deep learning types of neural networks used for bearing fault diagnosis. MLPs are generally powerful models that can learn complex non-linear relationships between the input and output data. CNNs can learn to recognize patterns in time–frequency spectrograms of vibration signals, while RNNs can learn to capture temporal dependencies between consecutive vibration measurements. However, deep learning algorithms require large amounts of labelled data and significant computational resources to train, but they can achieve high accuracy in many applications [12].
In the context of bearing fault diagnosis, transfer learning helps to improve the accuracy of deep learning models by initializing the weights of the neural network with pre-trained weights on similar vibration signal datasets. This initialization can help the model learn faster and achieve higher accuracy with less labelled data. Transfer learning is also used to fine-tune the pre-trained model on the target dataset by adjusting the weights in the final layers of the model [13]. One of the main limitations is the lack of pre-trained models for a target task. When the target dataset includes specific bearing types or health states that are not available in the pre-trained dataset, the pre-trained model may not be able to capture the relevant features and patterns in the data [14]. Therefore, the similarity between the pre-trained dataset and the target dataset is an important requirement for accurate diagnosis by transfer learning. If the pre-trained dataset is significantly different from the target dataset in terms of the data distribution, signal characteristics, or health states, the performance of the model on the target data may not be acceptable, and fine-tuning of the model requires a large amount of labelled data. In this case, the transfer learning approach may not be an effective method, and it is necessary to collect a new dataset or use other machine learning techniques [15]. Another limitation of transfer learning is that the pre-trained model may contain biases or limitations that affect its performance on the target dataset. For example, if the pre-trained model was trained on a dataset that is biased towards specific bearing types or operating conditions, it may not be able to generalize well to new or unseen data. In the context of bearing fault diagnosis, a significant challenge is therefore the assumption on the prior knowledge about the target domain’s label set. This needs a predefined understanding of all possible fault types, and hence potentially limits the model’s adaptability to real-world industrial scenarios where unforeseen faults may occur during the diagnostic process. It is thus crucial to carefully evaluate the performance of the model on the target dataset and be aware of any potential biases and limitations of the pre-trained model [16].
Due to the limitations mentioned above, the existing ML-based models have not been widely applied in industry especially due to their low generalizability, i.e., they require extensive training datasets to cover all operating conditions and health states of a typical bearing. Vibration signals from different machines contain different information owing to their different dynamic structures. Therefore, extracted features typically have different levels of machine health states. A solution to this problem is to identify features that accurately reflect machine health states without depending on machine type or operating conditions [17]. In this study, we propose to use bearing characteristic frequencies (BCFs) (BCFs include ball pass frequency outer race (BPFO), ball pass frequency inner race (BPFI), ball spin frequency (BSF), and fundamental train frequency (FTF)), which are highlighted in vibration signals in case of a fault occurring on any of the REB components, i.e., outer ring (OR), inner ring (IR), and balls or rollers, as the inputs for ML models. The high-frequency resonance technique (HFRT), also known as envelope analysis, is one of the most widely used techniques in the detection of BCFs [18]. The successful use of HFRT involves the step of selecting an appropriate band-pass filter around a resonance frequency [19]. However, the resonance frequency changes with machine type and their operating condition affects the band-pass filter selection, making HFRT a challenging method in accurately detecting BCFs without human intervention. To overcome this issue, a novel hybrid method, combining the cepstrum pre-whitening (CPW) and high-pass filtering developed by the authors of this study, which has been proven to be more effective [20], is applied to automatically extract BCFs as ML model inputs in this study.
Among the ML-based models developed for bearing fault diagnosis, artificial neural networks (ANNs) and support vector machines (SVMs) are the widely-used methods due to their capability [21]. Also unlike ANNs, which can lead to local rather than global solutions, SVMs have a global optimum and do not need a large number of samples to train [22]. However, for more complex problems, an optimised ANN is more accurate and powerful for classification tasks [12]. In addition, multinomial logistic regression (MLR) has been utilized in bearing fault diagnosis [23], which involves the generation of probability distributions for input features and calculation of maximum likelihood functions to identify the most appropriate fitting model [24]. Pandya et al. performed a comparative study between MLR, SVM, and ANN and concluded that an MLR model has achieved the highest accuracy for REB fault diagnosis [25].
Different from the commonly used “one-stage” methods, i.e., classifying healthy as well as a few bearing faults in one go, a two-stage approach is taken in this study, where the classification of faulty bearings from healthy ones is conducted in the first stage, followed by classifying bearing fault types (e.g., outer ring, inner ring, and ball fault) in the second. Several ML techniques, including SVM with different kernel functions, MLR, and ANN were studied to find the best model for both stages. The generalizability of the model is evaluated by using bearing vibration data from one source, i.e., the experiment tests conducted in the EU Clean Sky2 I2BS project [26] during training and evaluation, and using the CWRU [27] and MFPT [28] datasets for testing. In contrast to the existing ML-based models employed for bearing fault diagnosis, the methodology presented in this study aims at refraining from utilizing data for model training in model testing, i.e., using datasets originate from distinct sources and operating conditions for the model training and testing, thus develop an ML-based bearing fault diagnosis with high generalisability that can detect differentiate fault patterns across diverse scenarios.
Details of this study are presented in the following sections. Section 2 presents the methodology, including an overview of the model architecture, feature extraction, dataset description, and a summary of the applied ML techniques in this study. In Section 3, the training and testing results are discussed. Also, a comparison between the two-stage model and a single-stage model is given. Finally, conclusions from this study are drawn in Section 4. Moreover, an abbreviation list is provided in the Abbreviations section.
2. Methodology
The methodology of this study is illustrated in a flow chart in Figure 1, where a two-stage approach is taken for bearing health monitoring. Stage-1 focuses on classifying between healthy and faulty bearings. To achieve this objective, training data are split into two classes, i.e., faulty (including all faulty bearing samples) and healthy data. The vibration samples are then processed using the hybrid method [20] to extract the amplitudes of their BCFs, their harmonics, and sidebands, forming a 33-feature vector as the inputs to model training (details are given in Section 2.2). The input vectors are then fed into three selected ML models, including SVM, MLR, and ANN (details are given in Section 2.3) to train the models. The model (ML1) that achieved the highest training accuracy is thus chosen for Stage-1 classification. Stage-2 focuses on fault type classification. The ‘faulty data’ are then fed into the three model types in this stage to find the best performing model (ML2) for bearing fault classification, i.e., identifying OR, IR, and ball faults.
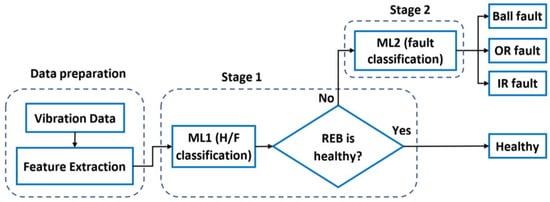
Figure 1.
A flow chart of the two-stage approach in developing a generalised intelligent model for bearing fault diagnosis.
The two models (ML1 and ML2) are then tested with vibration data from two other sources to evaluate their accuracy and generalisability. During the testing phase, a similar data preparation procedure is followed to extract the features for model inputs. To test ML1, all data are inputted into the model to detect healthy and faulty bearings. Then, only the data samples that were identified as faulty are used to test ML2 for bearing fault classification.
2.1. Datasets for Training and Testing in Model Development
To develop a generalised ML model, where a model developed based on datasets from one source (or more sources) can be used to monitor bearing conditions from a different machine, we have used datasets from the I2BS subscale bearing testing [26] to train and evaluate models, and the successful model is tested on datasets from two other sources, including the CWRU [27] and MFPT [28] in the public domain to check the model’s generalisability. Details of the bearings, including their sizes and test conditions, used in the three datasets as shown in Table 1, where PD, Z, and are the pitch diameter, number of the balls or rollers, and the sampling rate of the collected vibration samples, respectively. The defect sizes or information are also provided in this table. It clearly shows that the three datasets completely different.

Table 1.
Details of the three databases used in this study, including the bearing dimensions and their cooperating conditions, bearing defect information, and vibration data sampling rates.
The number of data samples in each category is shown in Table 2, including four classes of bearing health states, i.e., healthy, or with an OR, IR fault, or a ball fault. For the I2BS healthy bearing data, a combination of baseline test data, where healthy bearings were tested during the experiment, and synthesised data (see details in Appendix A) are used due to the relatively small number of baseline data available.

Table 2.
Number of samples in each health state from the three datasets for ML training.
2.2. Feature Extraction Process
Envelope spectra of vibration signals are produced using a novel hybrid method, which has shown to be effective in extracting BCFs from machines even operated in highly noisy environments [20]. Then, the BCFs, their harmonics, and sidebands are identified as model input features using an automated computer process developed in this study (more details are given below). In total, 33 BCF related features (listed below) are selected as inputs to ML models for bearing health monitoring in this study, including three harmonics of each BCF as well as two pairs of sidebands for each of the harmonics of the BPFI and BSF as listed below:
- BCFs and their harmonics (9 features):
- ▪
- .
- ▪
- .
- ▪
- .
- Sidebands for BPFIs and BSFs (24 features):
- ▪
- .
- ▪
- .
- ▪
- .
- ▪
- .
- ▪
- .
- ▪
- .
where (i = 1, 2, 3) represents 1st, 2nd, and 3rd harmonic of the ; for , six harmonics are used instead of three and the summation of 1st and 2nd forms the first BSF feature, 3rd and 4th the second, and 5th and 6th the third. For the sidebands, each pair contains the left (l) and right (r) sideband, and the first on the left is and so on. For the sidebands, similar summations are calculated as for the harmonics described above. The 33 features [23] are illustrated in Figure 2.
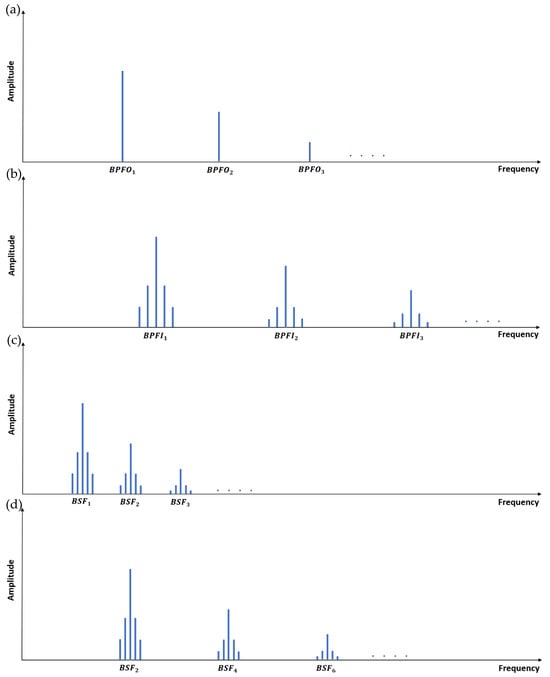
Figure 2.
Illustrations of the 33 features of BCFs, their harmonics, and sidebands. (a) OR fault (BPFO and its harmonics), (b) IR fault (BPFI, its harmonics and sidebands), (c) ball fault with both even and odd harmonics and sidebands, and (d) ball fault with even harmonics only and sidebands.
During the selection of BCF amplitudes, it is important to be aware there is typically a difference between theoretical BCF values and the actual frequencies in experimental data due to uncontrollable slippage in rolling element bearings and minor fluctuations in shaft rotation speed during machine operation. Therefore, the first harmonic of each actual BCF is selected based on the maximum value within the order band of the theoretical BCF value, defined as (1 ± 4%) × BCF. This 4% range is empirically chosen based on practical experience. Once the first harmonic is chosen, the amplitudes of the second and third harmonics are established by multiplying the selected order of the first BCF by 2 and 3, respectively, and their associated amplitudes are identified within a ±2% margin. This will create 9 harmonics as input features for model development, which are illustrated in Figure 2 for each fault type.
For BSFs, due to the possibility of having either even harmonics only or both even and odd harmonics [29], up to six orders of its harmonics are used to produce three features equivalent to the BPFO and BPFI harmonics by combining two of the adjacent BSF harmonics, e.g., is the summation of the first and second harmonics. Similarly, the corresponding sidebands (SBs) from each of the two BSF harmonics are combined to produce two pairs of sidebands for each of the three BSF combined harmonics.
2.3. ML Techniques Used in This Study
Three different ML techniques, including SVM, MLR, and ANN, are studied by programming them in MATLAB for both stages. The mathematical concepts of these ML technique are summarized as follows.
2.3.1. SVM
SVMs are based on the Structural Risk Minimization (SRM) principle in statistical learning theory which has an outstanding classification performance. SRM aims to maximize the margin between different classes. For a dataset with samples and labels of , a hyperplane —as shown in Equation (1)—is expected to find the maximum margin between the two categories. Moreover, the kernel function for finding the maximum margin between clusters is typically designed prior to the training procedure and it can be a linear, polynomial, radial basis function (RBF), or customised function [30]. During the training process in this study, the performance of three kernels, including linear, polynomial, and RBF, is examined in order to achieve the optimum model.
2.3.2. ANN
ANN is an intelligent technique based on a number of simple processors or neurons as activation functions in hidden layers and the output layer which could have different structures. Moreover, an ANN could be extended to a deep neural network (DNN) by adding more hidden layers to explore the useful functional relationship between raw signal data and health states [31]. To select the optimum structure, ANNs with different hyperparameters and training parameters are examined in this study. The learning rate, number of maximum epochs, and type of neurons are selected empirically during training, while the optimum number of the hidden layers and dropout rate are obtained during the optimisation process.
2.3.3. MLR
A logistic regression (LR) model is employed to estimate the likelihood of an event transpiring through the application of logistic curve modelling [32,33]. In this approach, the probability (p) of a binary outcome event is associated with a group of explanatory variables, as expressed by Equation (2):
For multi-class classification, the model estimates the likelihood of an event based on input features () and associated coefficients (). In a scenario with n variables and k categories or classes, logits are generated using one category as the reference level. This reference, designated as the base level ( class in this instance), is arbitrarily chosen, as there is no inherent order among the categories. To understand the relationship between the probability of an observation belonging to the category relative to the base (kth) category, the multi-class MLR model is expressed through Equation (3).
In contrast to SVMs and ANNs, this technique does not require any kernel function selection or hyperparameter optimisation. Furthermore, the coefficients corresponding to the input features are optimized through a maximum likelihood function process during training.
All three types of ML methods are investigated in both of the two stages and the best performing method in each stage is selected for the final model.
3. Results
Following the model development procedure shown in Figure 1, the training results for the two stages are shown first, followed by the test results in this section. The results from comparing a two-stage with a single-stage approach are then presented.
3.1. Model Training Results
3.1.1. Stage-1 Model (ML1): Classification of Healthy from Faulty Bearings
There are 283 healthy bearing samples and 937 faulty ones in the I2BS dataset (see Table 2) that are used to train three types of ML models, i.e., SVM, ANN, and MLR. For the SVM, three types of kernel functions, i.e., linear, polynomial, and radial basis function (RBF) kernels), were explored.
The training results from the first stage are summarised in the confusion matrices in Figure 3 for all five techniques. All the models with optimised architectures have achieved high capabilities of classifying the healthy from the faulty bearings at over 97.2% accuracy. To obtain the optimised ANN model, a range of hyperparameters and configurations were trained by varying the number of hidden layers (HL) and dropout rate (DR); the ANN with 1 hidden layer (HL) and 0 dropout rate (DR) has shown to be the best ANN for this problem (details of the optimisation procedure and results are attached in Appendix B). It uses the ReLu activation function for the hidden layer neuron. An initial learning rate of 0.2 with a drop rate of 0.9 after 30 epochs was considered empirically for the ANN.
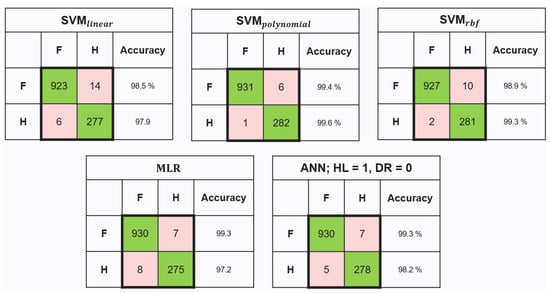
Figure 3.
Confusion matrices of training results of ML techniques for the first stage of the proposed model (healthy vs. faulty bearing classification).
Comparing the accuracies of the five techniques, the SVM model with a polynomial kernel function has the highest accuracy with an accuracy of 99.6% and 99.4% for healthy and faulty classification, respectively. Hence, this model was selected for the Stage-1 model (ML1) for healthy and faulty bearing classification.
3.1.2. Stage-2 Model (ML2): Classification of Bearing Faults
During the second stage, the vibration samples corresponding to the three types of faults (i.e., OR, IR, and ball) in the I2BS datasets are used to train the selected ML techniques. Interestingly, all five techniques have achieved 100% classification accuracy for all three types of faults (see Figure 4). Again, details of the ANN optimisation results are presented in Appendix C. In this case, the ANN with HL-1 and DR 0.05 was selected as the Stage-2 model (ML2) for bearing fault classification.
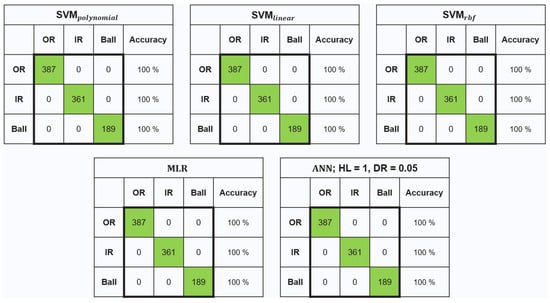
Figure 4.
Confusion matrices of training results of ML techniques for fault classification.
3.2. Model Test Results
In order to assess the generalisability of the diagnosis model, the successfully trained models for the two stages are tested with two completely different datasets from CRWU and MFPT. The results from these tests are shown in the following sections.
3.2.1. Test the Two-Stage Model with the CWRU Dataset
CWRU dataset has been widely used in ML-based model development. It is also one of the most challenging experimental case studies for bearing fault diagnosis [34]. In 2015, In a comprehensive study, Randall et al. [35] showed that due to rig-related defects, it is not possible to diagnose all of the bearing faults (labelled by the experimentalists) in the vibration samples. They have thus placed the vibration samples into three main categories based on their analysis: as diagnosable, partial diagnosable, and not diagnosable. The percentage of each category is shown in Table 3.

Table 3.
Percentages of diagnosable, partial diagnosable, and not diagnosable vibration samples in the CWRU dataset [35].
As shown in Table 2, there are 276 vibration samples in the CWRU that were used to test the two-stage model after feature extraction. The test results from the first-stage model ML1 (SVMpolynomial) and second-stage model ML2 (ANN with HL-1 and DR 0.05) are shown in Figure 5. In the first-stage model, all 8 healthy samples are classified accurately, which would effectively avoid false alarms in real applications. However, only 77.2% of the faulty data are classified accurately, which means over 28% of the faulty data would have missed the alarm in real applications.
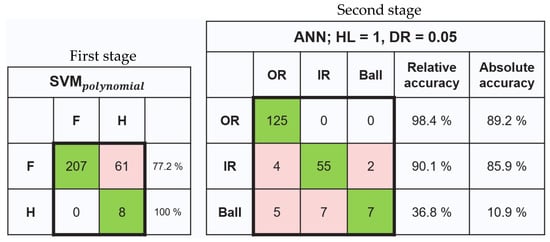
Figure 5.
Two-stage model confusion matrices for CWRU data testing.
The 207 samples classified as faulty bearings during the first-stage model are then fed into the second-stage model. The results from the ANN are shown in Figure 5 as it has a better accuracy in this stage than the other ML techniques (see details summarized in Appendix D).
Two types of accuracies are presented in Figure 5 for the second-stage model, i.e., relative accuracy and absolute accuracy. The relative accuracy is the percentage of samples accurately classified in the total number of the relevant class used in the second-stage model, while the absolute accuracy is the percentage of accurately classified samples in the total number of samples of this fault mentioned in Table 2. For example, . In other words, the relative accuracy shows the accuracy of the second-stage ML technique, and the absolute accuracy indicates the proposed model accuracy.
As it is shown in Figure 5, the two-stage model trained with the I2BS subscale dataset can identify all the healthy data, and the accuracy of classifying the OR and IR faults are 89.2% and 85.9%, respectively. The accuracy for ball fault classification is 10.9%, which is comparable to that achieved by [35]. Hence, the two-stage model has significantly improved the prediction of OR and IR faults and the overall faulty conditions, e.g., 29.7% (or 19 samples out of 64 samples) of the ball fault samples are classified as faulty classes containing OR, IR, and ball fault.
To summarise, the model has achieved an accuracy of 88.61% when considering vibration samples related to healthy bearings, bearings with outer race (OR) faults, and bearings with inner race (IR) faults. The overall accuracy for all samples is 70.59%, and was primarily influenced by lower accuracies in ball fault samples. In comparison to an investigation conducted by Guo et al. [13], they used vibration samples from CWRU corresponding to 2 HP power and a shaft speed of 1750 rpm in their development of a transfer learning model and achieved an average accuracy of 86.6% via emphasizing domain adaptation and distribution discrepancy metrics during the fine-tuning process. The method from this study has shown significant advantage in the development of a generalised machine learning model for bearing fault diagnosis.
3.2.2. Test the Two-Stage Model with the MFPT Dataset
The confusion matrices of the test results are presented in Figure 6. It can be seen that all data in the MFPT dataset were accurately classified with 100% accuracy in both stages.
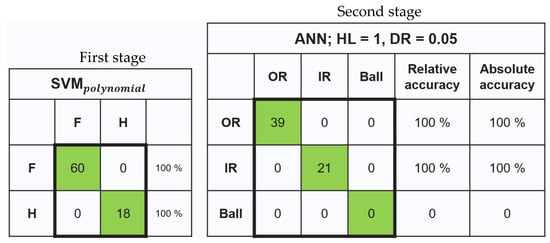
Figure 6.
Two-stage model confusion matrix for MFPT data testing.
3.3. Compare the Two-Stage Model with a Single-Stage Model
A thorough comparison between the two-stage model and the single-stage one was conducted. The single-stage model employs a single ML technique to classify all four conditions: healthy, over-rolled (OR), inner race fault (IR), and ball fault. To ensure a comprehensive evaluation, five different ML techniques (SVMpolynomial, SVMlinear, SVMrbf, MLR, and ANN) were applied to the single-stage model, employing the same training procedure for consistency. The training and testing results revealed that the highest accuracy among the various techniques was exhibited by a single hidden layer ANN without a dropout rate. Detailed comparative results are provided in Appendix E. When subjected to testing with the CWRU dataset, the outcomes are summarized in Figure 7.
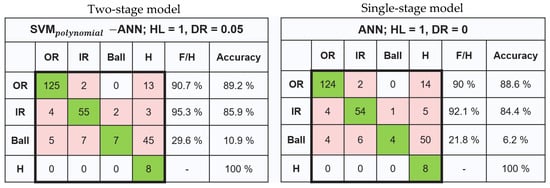
Figure 7.
Comparison of single-stage and two-stage model test results with the CWRU dataset.
Notably, like the two-stage model depicted in Figure 5, the exceptional accuracy (100%) in identifying healthy cases was demonstrated by the single-stage ANN model. However, for the remaining three categories, the accuracies lower than those achieved by the two-stage model were yielded by the single-stage model. This distinction is particularly highlighted in the case of ball fault detection. Upon closer examination, it was observed that 29.7% of the ball fault samples were categorized as faulty classes (albeit not specifically as ball fault) by the two-stage model. In contrast, only 21.8% of these samples were classified into faulty classes by the single-stage model. This discrepancy raises interesting considerations of the trade-offs between the two approaches.
4. Conclusions
A generalised two-stage intelligent fault diagnosis model for REBs was developed in this research. The first stage focuses on classification of the faulty bearings from healthy ones (detection) and the second on identifying the bearing fault type. Three ML model types, including SVM, MLR, and ANN, were evaluated to achieve the optimum architecture for each of the two stages. Training of the models has used the I2BS dataset while testing has used two datasets from the public domains CWRU and MFPT. The effectiveness of this model was assessed by using diverse datasets obtained from machines, including different type of REBs, deep groove rolling bearings, and three-point angular contact bearings.
The training results have shown that the SVM with a polynomial kernel function and an ANN with a single hidden layer and a 5% dropout rate have achieved the highest accuracies for the first and second stages, respectively. The two-stage model was then tested by the CWRU and MFPT datasets. Despite the challenges in the CWRU dataset, e.g., a large amount of data is not diagnosable, the two-stage model achieved better classification accuracies in three of the health states (healthy and fault in the outer ring and in the inner ring). When tested with the MFPT dataset, a 100% accuracy was achieved for all available conditions. Compared with a single-stage ML model, the two-stage model showed higher accuracies in fault classification.
The generalized modelling approach, developed with several experimental datasets from our study, has shown to be promising in effectively detecting bearing conditions for other datasets from completely different machines without re-training. This will potentially solve the problems related to the lack of available training datasets in industries for future bearing condition monitoring. The two-stage model developed in this study is a promising tool for use in real-world applications. The ongoing research being conducted should aim to improve the accuracy of the current model and to assess its performance on more complex machinery rather than being limited to the scope of shaft and bearing configurations. Meanwhile, we are working to incorporate the detection of other common faults in the drivetrain, including rotary faults such as unbalance, misalignment, and looseness in rotary components. The aim of this enhancement is to broaden the applicability of the two-stage model, making it more suitable for complex industrial scenarios.
Author Contributions
Conceptualization, A.K., Z.L. and L.W.; methodology, A.K.; software, A.K.; validation, A.K.; formal analysis, A.K.; investigation, A.K.; resources, A.K.; writing—original draft preparation, A.K.; writing—review and editing, A.K., Z.L., P.M., H.P. and L.W.; visualization, A.K.; supervision, Z.L., P.M., H.P. and L.W.; project administration, L.W.; funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Schaeffler Technologies, University of Southampton, and the framework of Clean Sky 2 Joint Undertaking through the 82 European Union Horizon 2020 Research and Innovation Programme under Grant I2BS: 717174.
Data Availability Statement
Data are contained within this article.
Conflicts of Interest
Author Patrick Mirring was employed by the company Schaeffler Technologies AG & Co. KG. Author Honor Powrie was employed by the company GE Aerospace. The remaining authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
Abbreviations
The following table provides a comprehensive list of abbreviations used throughout this paper for quick reference and clarity. List of all abbreviations used in this paper.
| ANN | Artificial neural network |
| BCF | Bearing characteristic frequency |
| BPFI | Ball pass frequency inner race |
| BPFO | Ball pass frequency outer race |
| BSF | Ball spin frequency |
| CNN | Convolutional neural networks |
| CPW | Cepstrum pre-whitening |
| CWRU | Case Western Reserve University |
| DNN | Deep neural network |
| DR | Dropout rate |
| HFRT | High-frequency resonance technique |
| HL | Hidden layers |
| IR | Inner ring |
| LR | Logistic regression |
| MFPT | Machinery Failure Prevention Technology |
| MLP | Multi-layer perceptron |
| MLR | Multinomial logistic regressions |
| ML | Machine learning |
| OR | Outer ring |
| RBF | Radial basis function |
| REB | Rolling element bearing |
| RNN | Recurrent neural networks |
| SB | Side band |
| SVM | Support vector machine |
Appendix A. I2BS Healthy Bearing Data Synthesis Process
There are 937 faulty but only 94 healthy bearing datasets from baseline tests in the I2BS project. To overcome the issues related to the incompatible input data sizes in healthy and faulty categories for ML model training, healthy bearing data are ‘synthesised’ in the method described below, generating sufficient healthy bearing data.
Faulty bearing data from two tests with different bearing faults, e.g., one test with BPFO and the other with BPFI, are ‘combined’ by taking the features related to BPFI and BSF from the former and those related to BPFO from the latter in order to form a 33-feature input vector of a ‘healthy bearing’. By verifying the combinations of the faulty bearing test data, 189 healthy bearing samples were synthesised for the investigation.
Appendix B. Optimization Results of the ANN for the First Stage of the Fault Diagnosis
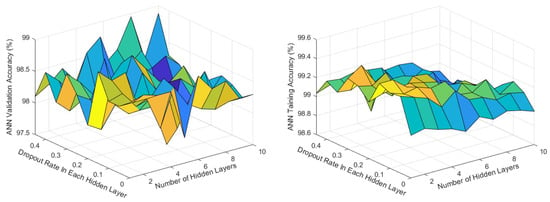
Figure A1.
First stage training and validation results of several ANN configurations during the optimization.
Appendix C. Optimization Results of the ANN for the Second Stage of the Fault Diagnosis
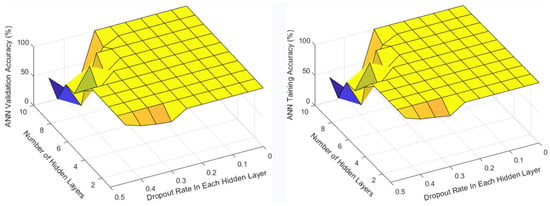
Figure A2.
Second stage training and validation results of several ANN configurations during the optimization.
Appendix D. The Test Results of the SVMs and MLR in the Second Stage
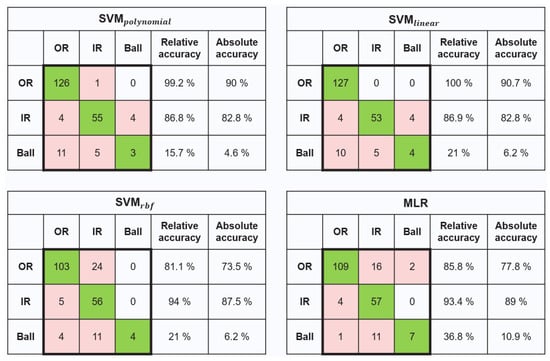
Figure A3.
Confusion matrices of the second stage results using SVMs and MLR techniques.
Appendix E. Optimization Results of the ANN for the Single-Stage Model
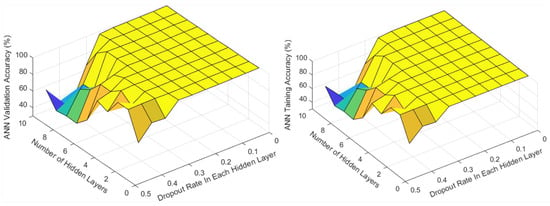
Figure A4.
Training and validation results of several ANN configurations during the optimization for the single-stage model.
References
- Ambrożkiewicz, B.; Syta, A.; Georgiadis, A.; Gassner, A.; Litak, G.; Meier, N. Intelligent Diagnostics of Radial Internal Clearance in Ball Bearings with Machine Learning Methods. Sensors 2023, 23, 5875. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Song, M.; Ma, X.; Guo, N.; Xue, Y. Research on H7006C Angular Contact Ball Bearing Slipping Behavior under Operating Conditions. Lubricants 2023, 11, 298. [Google Scholar] [CrossRef]
- Wu, C.; Yang, K.; Ni, J.; Lu, S.; Yao, L.; Li, X. Investigations for Vibration and Friction Torque Behaviors of Thrust Ball Bearing with Self-Driven Textured Guiding Surface. Friction 2023, 11, 894–910. [Google Scholar] [CrossRef]
- Toma, R.N.; Gao, Y.; Piltan, F.; Im, K.; Shon, D.; Yoon, T.H.; Yoo, D.S.; Kim, J.M. Classification Framework of the Bearing Faults of an Induction Motor Using Wavelet Scattering Transform-Based Features. Sensors 2022, Vol. 22, Page 8958 2022, 22, 8958. [Google Scholar] [CrossRef]
- Guo, C.; Li, L.; Hu, Y.; Yan, J. A Deep Learning Based Fault Diagnosis Method with Hyperparameter Optimization by Using Parallel Computing. IEEE Access 2020, 8, 131248–131256. [Google Scholar] [CrossRef]
- Alshorman, O.; Irfan, M.; Saad, N.; Zhen, D.; Haider, N.; Glowacz, A.; Alshorman, A. A Review of Artificial Intelligence Methods for Condition Monitoring and Fault Diagnosis of Rolling Element Bearings for Induction Motor. Shock Vib. 2020, 2020, 8843759. [Google Scholar] [CrossRef]
- Singh, V.; Gangsar, P.; Porwal, R.; Atulkar, A. Artificial Intelligence Application in Fault Diagnostics of Rotating Industrial Machines: A State-of-the-Art Review. J. Intell. Manuf. 2023, 34, 931–960. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.Q. Multi-Layer Domain Adaptation Method for Rolling Bearing Fault Diagnosis. Signal Processing 2019, 157, 180–197. [Google Scholar] [CrossRef]
- ALTobi, M.A.S.; Bevan, G.; Wallace, P.; Harrison, D.; Ramachandran, K.P. Fault Diagnosis of a Centrifugal Pump Using MLP-GABP and SVM with CWT. Eng. Sci. Technol. Int. J. 2019, 22, 854–861. [Google Scholar] [CrossRef]
- Hasan, M.J.; Kim, J.M. Bearing Fault Diagnosis under Variable Rotational Speeds Using Stockwell Transform-Based Vibration Imaging and Transfer Learning. Appl. Sci. 2018, 8, 2357. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial Intelligence for Fault Diagnosis of Rotating Machinery: A Review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnosticsx—A Comprehensive Review. IEEE Access 2020, 8, 29857–29881. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep Convolutional Transfer Learning Network: A New Method for Intelligent Fault Diagnosis of Machines with Unlabeled Data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An Intelligent Fault Diagnosis Approach Based on Transfer Learning from Laboratory Bearings to Locomotive Bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Zhang, A.; Li, C.; Qiu, L. A Novel Bearing Fault Diagnosis Method Based on Few-Shot Transfer Learning across Different Datasets. Entropy 2022, 24, 1295. [Google Scholar] [CrossRef]
- Mao, W.; Ding, L.; Tian, S.; Liang, X. Online Detection for Bearing Incipient Fault Based on Deep Transfer Learning. Meas. J. Int. Meas. Confed. 2020, 152, 107278. [Google Scholar] [CrossRef]
- Singh, J.; Azamfar, M.; Li, F.; Lee, J. A Systematic Review of Machine Learning Algorithms for Prognostics and Health Management of Rolling Element Bearings: Fundamentals, Concepts and Applications. Meas. Sci. Technol. 2021, 32, 012001. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, Y. Envelope Analysis Scheme for Multi-Faults Vibration of Gearbox Based on Self-Adaptive Noise Cancellation. In Proceedings of the 2018 Prognostics and System Health Management Conference, Chongqing, China, 26–28 October 2018; pp. 1188–1193. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and Improved Frequency Band Entropy in Bearing Fault Feature Extraction. ISA Trans. 2019, 88, 170–185. [Google Scholar] [CrossRef]
- Kiakojouri, A.; Lu, Z.; Mirring, P.; Powrie, H.; Wang, L. A Novel Hybrid Technique Combining Improved Cepstrum Pre-Whitening and High-Pass Filtering for Effective Bearing Fault Diagnosis Using Vibration Data. Sensors 2023, 23, 9048. [Google Scholar] [CrossRef]
- Mathur, A.; Kumar, P.; Harsha, S.P. Ranked Feature-Based Data-Driven Bearing Fault Diagnosis Using Support Vector Machine and Artificial Neural Network. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2023, 237, 1602–1619. [Google Scholar] [CrossRef]
- Yan, M.; Wang, X.; Wang, B.; Chang, M.; Muhammad, I. Bearing Remaining Useful Life Prediction Using Support Vector Machine and Hybrid Degradation Tracking Model. ISA Trans. 2020, 98, 471–482. [Google Scholar] [CrossRef] [PubMed]
- Kiakojouri, A.; Lu, Z.; Mirring, P.; Powrie, H.; Wang, L. A Generalised Machine Learning Model Based on Multinomial Logistic Regression and Frequency Features for Rolling Bearing Fault Classification. Insight—Non-Destr. Test. Cond. Monit. 2022, 64, 447–452. [Google Scholar] [CrossRef]
- Abdelrhman, A.M.; Ying, L.; Ali, Y.H.; Ahmad, I.; Georgantopoulou, C.G.; Nor, F.M.; Kurniawan, D. Diagnosis Model for Bearing Faults in Rotating Machinery by Using Vibration Signals and Binary Logistic Regression. AIP Conf. Proc. 2020, 2262, 030014. [Google Scholar]
- Parmar, U.; Pandya, D.H. Comparison of the Supervised Machine Learning Techniques Using WPT for the Fault Diagnosis of Cylindrical Roller Bearing. Int. J. Eng. Sci. Technol. 2021, 13, 50–56. [Google Scholar] [CrossRef]
- Bashir, I.; Zaghari, B.; Harvey, T.J.; Weddell, A.S.; White, N.M.; Wang, L. Design and Testing of a Sensing System for Aero-Engine Smart Bearings. Proceedings 2019, 2, 1005. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center. 2009. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 6 January 2022).
- Fault Data Sets—Society For Machinery Failure Prevention Technology. Available online: https://www.mfpt.org/fault-data-sets/ (accessed on 12 April 2022).
- Randall, R.B.; Antoni, J. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Gao, X.; Wei, H.; Li, T.; Yang, G. A Rolling Bearing Fault Diagnosis Method Based on LSSVM. Adv. Mech. Eng. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Hamadache, M.; Jung, J.H.; Park, J.; Youn, B.D. A Comprehensive Review of Artificial Intelligence-Based Approaches for Rolling Element Bearing PHM: Shallow and Deep Learning. JMST Adv. 2019, 1, 125–151. [Google Scholar] [CrossRef]
- Ahmed, H.O.A.; Nandi, A.K.; Delpha, C.; Ahmed, H.O.A.; Nandi, A.K. Intrinsic Dimension Estimation-Based Feature Selection and Multinomial Logistic Regression for Classification of Bearing Faults Using Compressively Sampled Vibration Signals. Entropy 2022, 24, 511. [Google Scholar] [CrossRef]
- Gao, S.; Yu, Y.; Zhang, Y. Reliability Assessment and Prediction of Rolling Bearings Based on Hybrid Noise Reduction and BOA-MKRVM. Eng. Appl. Artif. Intell. 2022, 116, 105391. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset with Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).