An Optimization Method of Flexible Manufacturing System Reliability Allocation Based on Two Dimension-Reduction Strategies
Abstract
:1. Introduction
2. Model Basis
3. Overall Reliability-Allocation Optimization Method Based on RWTS
3.1. Constraint Functions Considering Reliability and Cost
3.2. Reliability-Weight Double-Threshold Qualification Strategy
3.3. Overall Reliability-Allocation Optimization Model
3.4. Overall Optimization Algorithm Based on PSO
| Algorithm 1: Overall Optimization Algorithm Based on RWTS |
|
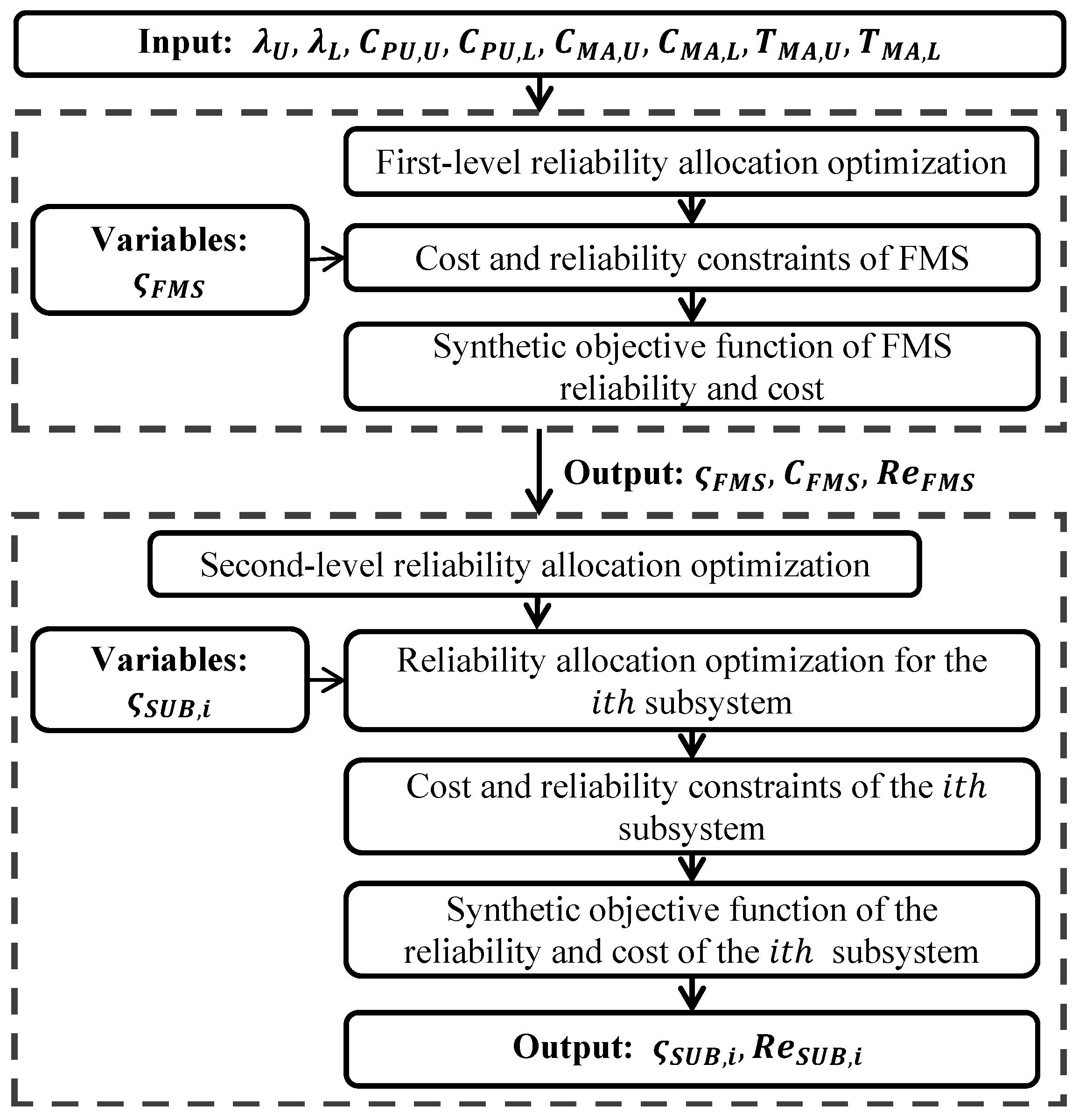
4. Reliability-Allocation Optimization Based on BLOS
4.1. Bi-Level Reliability-Allocation Optimization Models
4.2. Bi-Level Optimization Algorithm Based on PSO
| Algorithm 2: Optimization Algorithm Based on BLOS |
|
5. Application Case to a Box-Part Finishing FMS
5.1. Settings of the Application Case
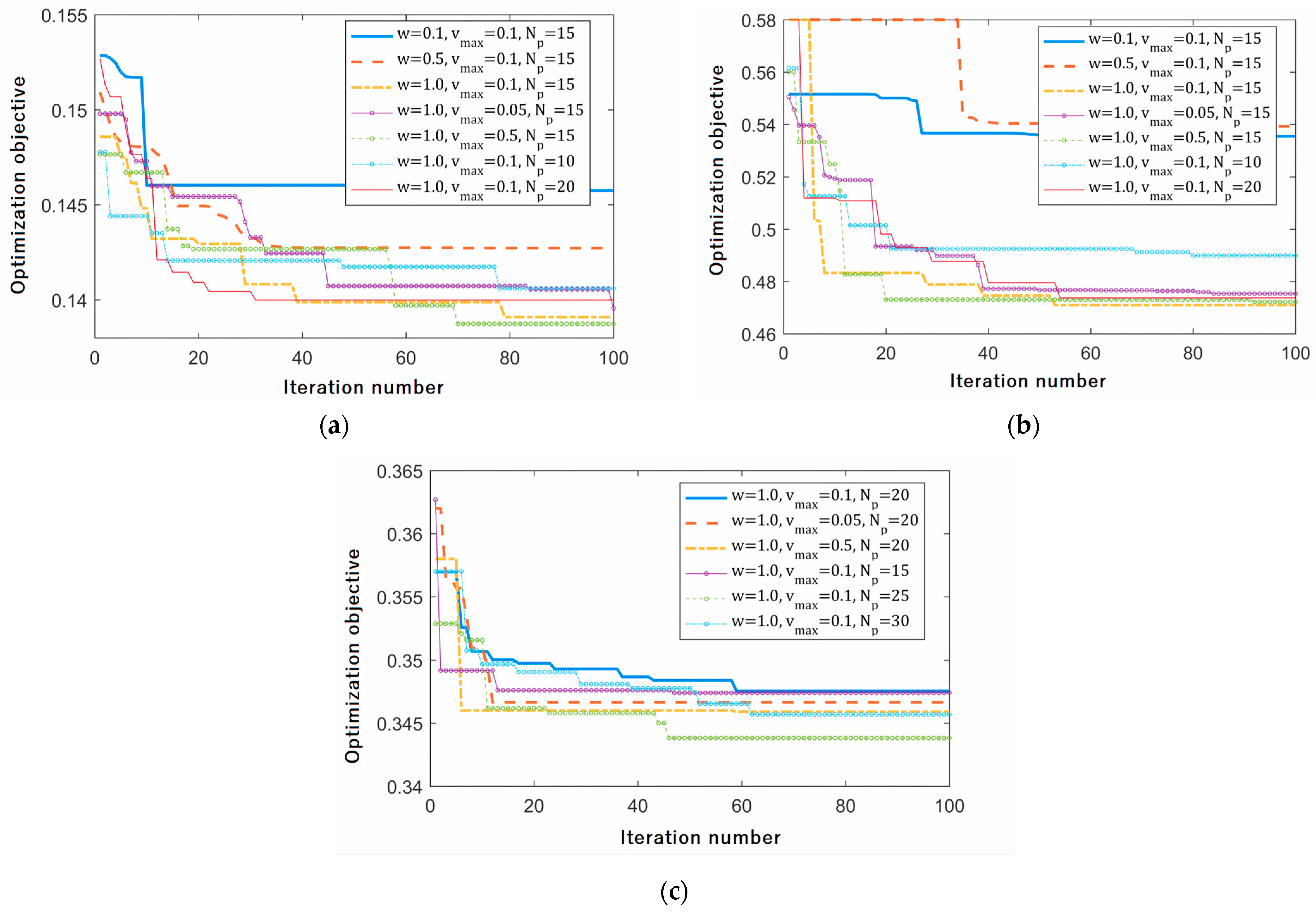
5.2. Validation of the RWTS-Based Algorithm
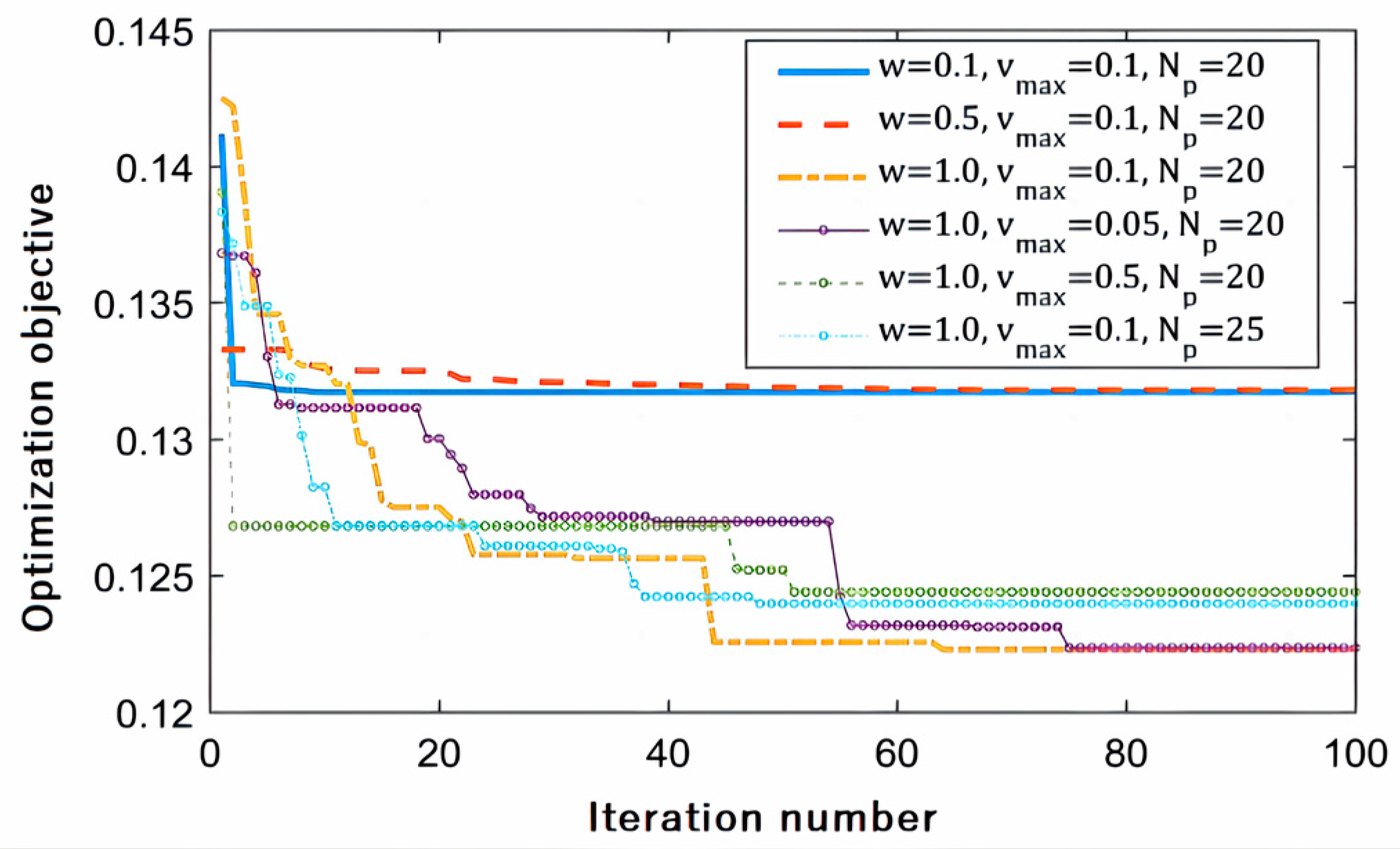
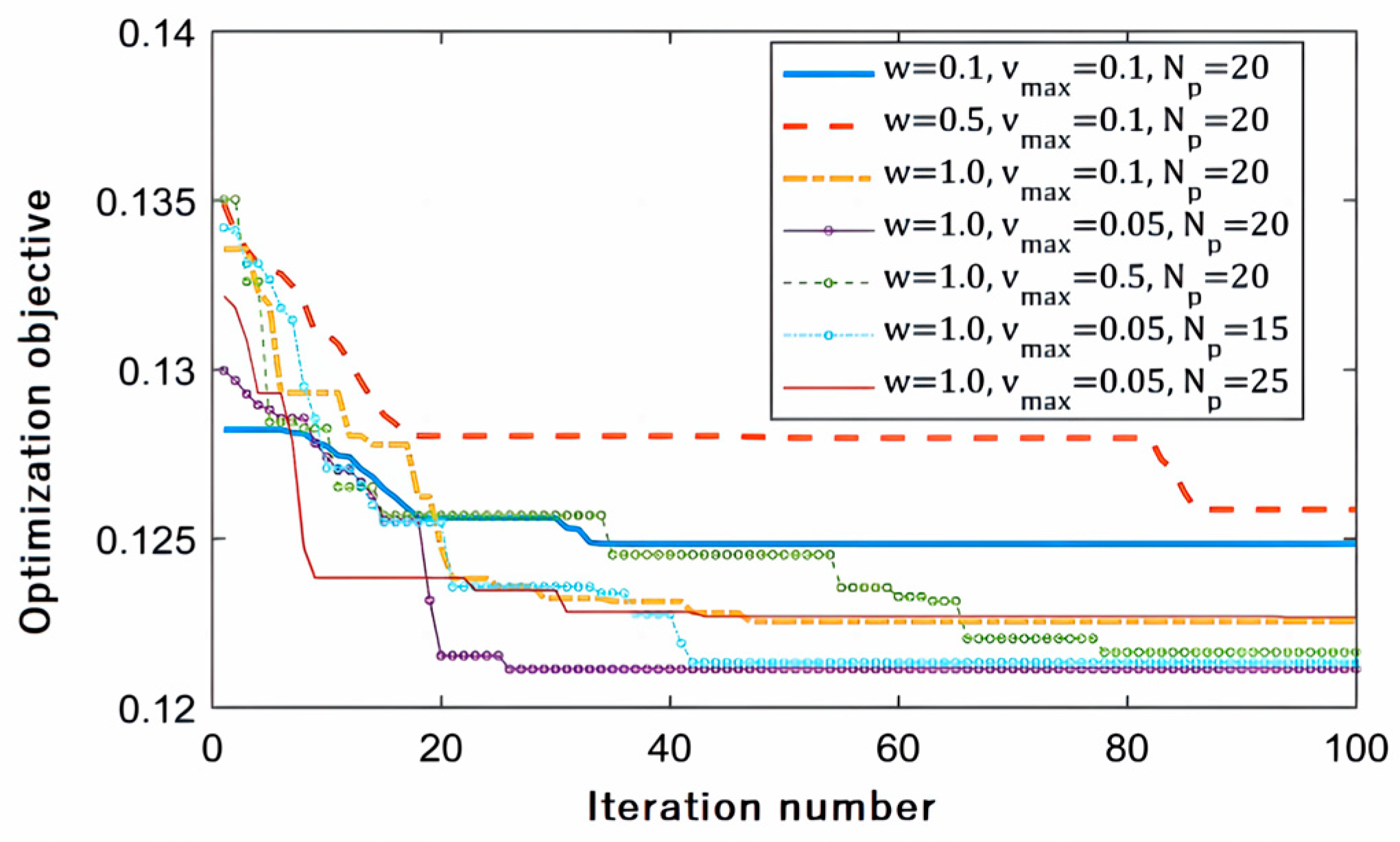
5.3. Validation of the BLOS-Based Algorithm
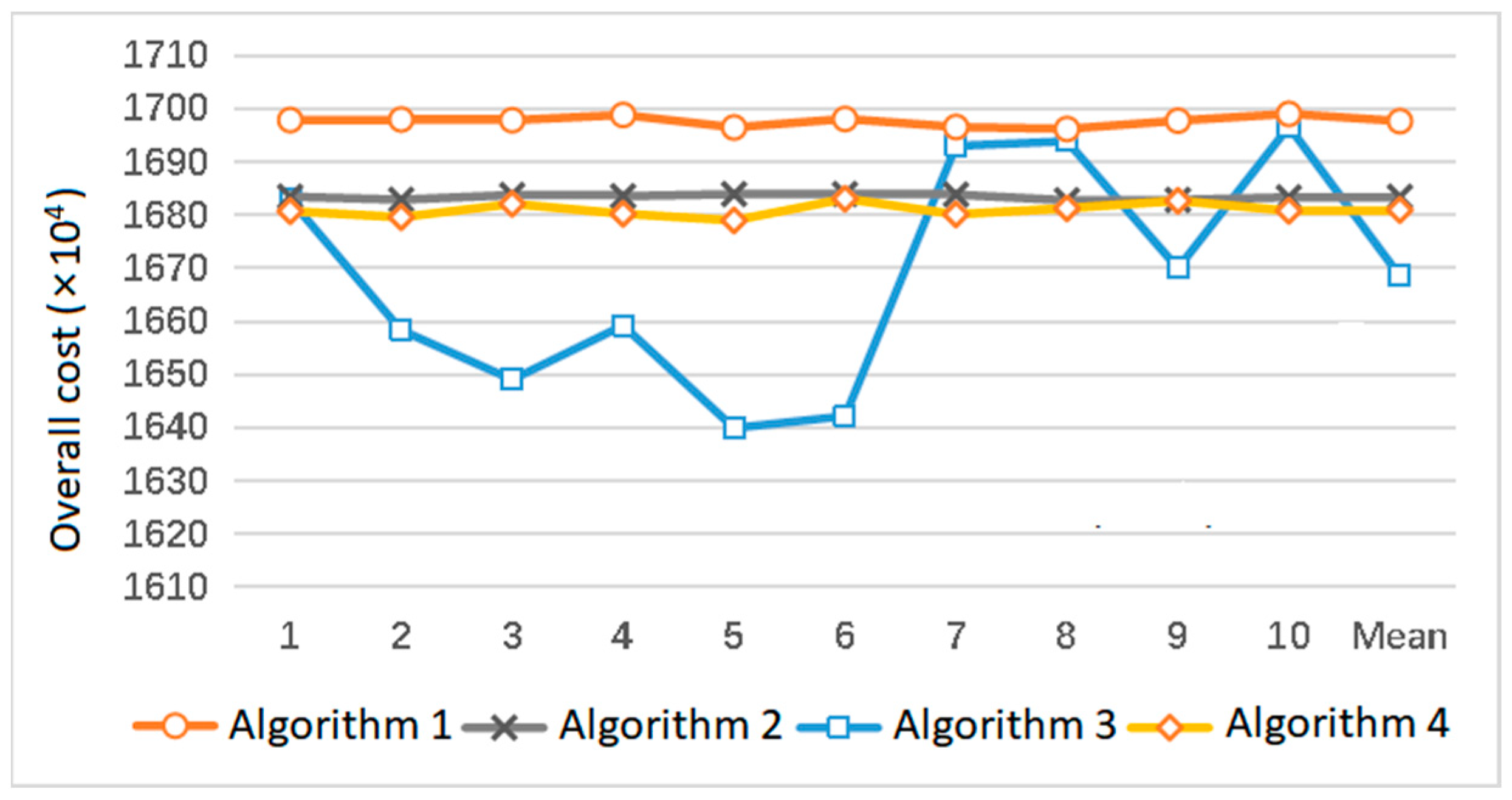
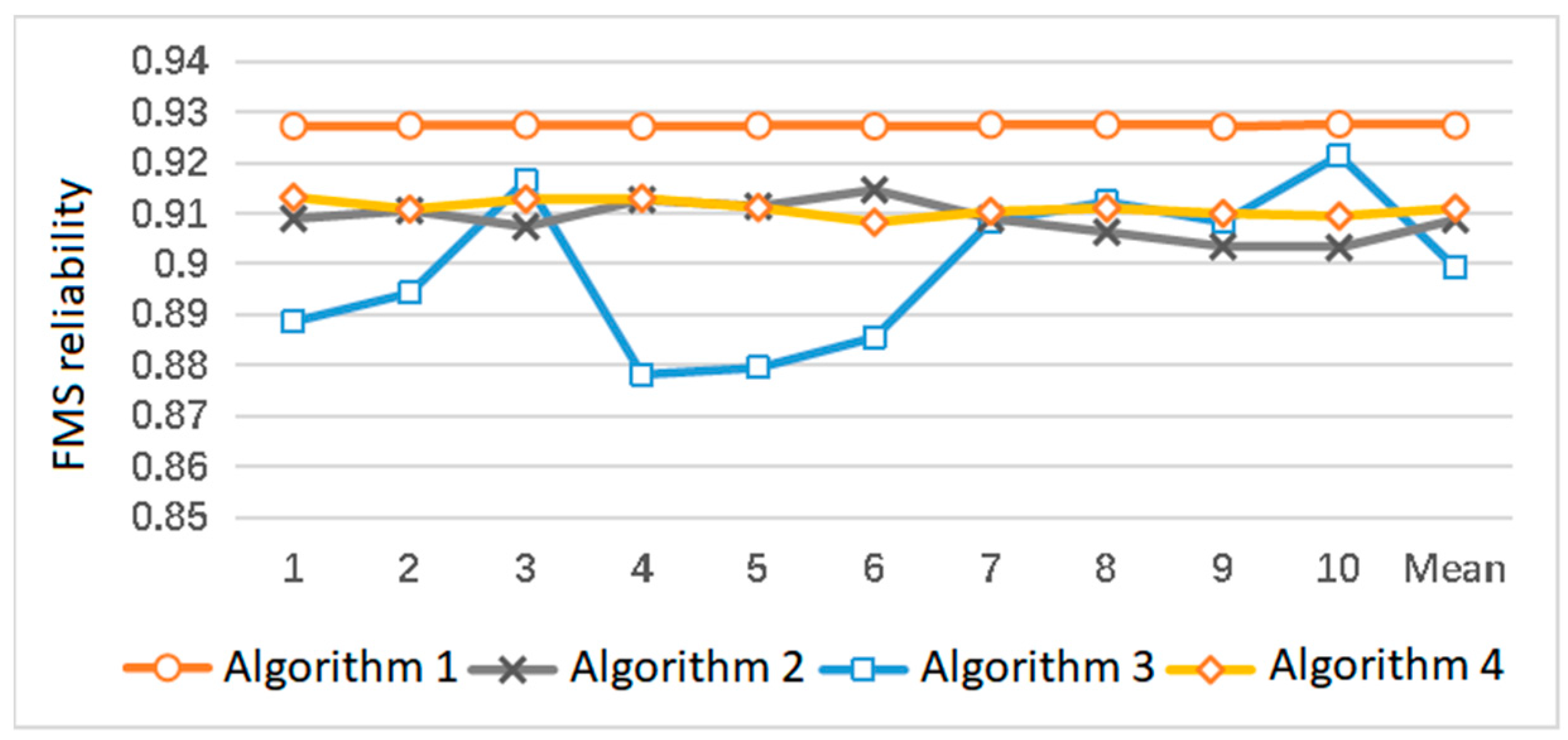
5.4. Overall Comparison of Four Algorithms
6. Conclusions and Future Works
6.1. Conclusions
6.2. Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Ran, Y.; Zhang, G.; Shao, Y. Optimal allocation of product reliability using novel multi-population particle swarm optimization algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 4565–4576. [Google Scholar] [CrossRef]
- Zhou, C. Research on Evaluation, Prediction and Distribution of Reliability Index of Industrial Robot. Ph.D. Thesis, Hebei University of Technology, Tianjing, China, 2022. [Google Scholar]
- Liang, K.W. Reliability Engineering; National Defense Industry Press: Arlington, VA, USA, 2014. [Google Scholar]
- You, M.Y.; Zheng, J.C. A multi-source information based generalized proportional combination approach to reliability allocation of electronic systems. Electron. Prod. Reliab. Environ. Test. 2011, 29, 15–21. [Google Scholar]
- Shi, C.; Chen, Y. Basic reliability distribution of a new ship steering control system based on scoring method. Ship Electron. Eng. 2021, 41, 115–118. [Google Scholar]
- Wu, J.; Yang, Y.; Wang, Z. Research on the reliability allocation method of micro-robot based on combined weight. Manuf. Autom. 2022, 44, 93–97. [Google Scholar]
- Du, Y.; Wu, G.; Tang, Y.; Cao, H.; Liu, S. Reliability Allocation Method for Remanufactured Machine Tools Based on Fuzzy Evaluation Importance and Failure Influence. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 1617–1628. [Google Scholar] [CrossRef]
- Abbas, S.; Hassan, Z. Use of ARINC Approach method to evaluate the reliability assignment for mixed system. J. Phys. Conf. Ser. 2021, 1999, 012102. [Google Scholar] [CrossRef]
- Qian, Y.; Jiang, C.; Su, L. Research of Reliability Allocation Based on Gray Theory. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1043, 022006. [Google Scholar] [CrossRef]
- Neha; Verma, V.; Tandon, A.; Aggarwal, A.G. Software reliability allocation incorporating Pythagorean fuzzy theory and AHP. Int. J. Ind. Syst. Eng. 2021, 38, 19–34. [Google Scholar] [CrossRef]
- Feng, Y.K.; Chen, X.W.; Li, H.B.; Hu, N.; Ge, Z.J. Object-oriented programming design of dynamic planning method of reliability allocation. Electron. Prod. Reliab. Environ. Test. 2019, 37 (Suppl. S1), 106–112. [Google Scholar]
- You, M.N.; Luo, R.X. Study on reliability of supply chain collaborative product development based on dynamic planning. Logist. Technol. 2017, 36, 158–161. [Google Scholar]
- Zeng, L.; Zhu, Z.D.; Zhang, F.; Dai, M.; Yang, J. Redundancy reliability optimization of electro-hydraulic control system of ball screw actuators based on dynamic programming method. J. Xuzhou Inst. Technol. (Nat. Sci. Ed.) 2018, 33, 6–13. [Google Scholar]
- Wu, X.Y. Importance Based Reliability Allocation Modelling and Algorithm for Phased Mission System. Master’s Thesis, National University of Defense Technology, Changsha, China, 2018. [Google Scholar]
- Arezki, M.M.; Abdellah, S. System reliability-redundancy allocation by the multiobjective plant propagation algorithm. Int. J. Qual. Reliab. Manag. 2022, 39, 902–909. [Google Scholar]
- Kang, R.; Liu, H.R.; Zhang, Q.Y.; Yu, L.; Zhai, G.F. Function oriented belief reliability design and optimization of new torsion spring electrical connectors. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48, 1745–1756. [Google Scholar]
- Pei, Y.; Liu, Z.; Xu, J.; Qi, B.; Cheng, Q. Grouping Preventive Maintenance Strategy of Flexible Manufacturing Systems and Its Optimization Based on Reliability and Cost. Machines 2023, 11, 74. [Google Scholar] [CrossRef]
- Sun, J.S. Research on Evaluation Index System for Patents Stratification in Universities. Master’s Thesis, Dalian University of Technology, Dalian, China, 2017. [Google Scholar]
- Xu, J.J.; Liu, Z.F.; Zhao, Y.S.; Pei, Y.; Cheng, Q. A path optimization technique with obstacle avoidance for an 8-dof robot in bolt looseness detection task. Int. J. Precis. Eng. Manuf. 2019, 20, 717–735. [Google Scholar] [CrossRef]
- Kim, H.J.; Kang, H.J.; Kim, M.K. Data-Driven Bidding Strategy for DER Aggregator Based on Gated Recurrent Unit-Enhanced Learning Particle Swarm Optimization. IEEE Access 2021, 9, 66420–66435. [Google Scholar] [CrossRef]




| WL | SSL | EL |
|---|---|---|
| — | ||
| — | ||
| — | ||
| — | ||
| Elements | () | Elements | |||
|---|---|---|---|---|---|
| HUMAN | MM | MM_MS | |||
| UCS | MM_CS | ||||
| SLCS-LS | PC | PC_MS | |||
| SLCS-MS | PC_CS | ||||
| LR (ULR) | LR(ULR)_MS | MT | MT_MS | ||
| LR(ULR)_CS | MT_CS | ||||
| LC | LC_MS | ME | ME_MS | ||
| LC_CS | ME_CS | ||||
| Buffer zone | - | - | |||
| Elements | (RMB) | (RMB) | (RMB) | (min) | (min) | (min) |
|---|---|---|---|---|---|---|
| HUMAN | 24,000 | 30,000 | 0 | 0 | 0 | 0 |
| UCS | 80,000 | 100,000 | 800 | 1000 | 150 | 180 |
| SLCS-LS | 50,000 | 100,000 | 500 | 1000 | 100 | 120 |
| SLCS-MS | 300,000 | 500,000 | 3000 | 5000 | 500 | 600 |
| XX_CS | 30,000 | 50,000 | 300 | 500 | 60 | 80 |
| LR(ULR)_MS | 200,000 | 300,000 | 2000 | 3000 | 400 | 500 |
| LC_MS | 50,000 | 100,000 | 500 | 1000 | 150 | 200 |
| MM_MS | 300,000 | 500,000 | 3000 | 5000 | 250 | 300 |
| PC_MS | 150,000 | 200,000 | 1500 | 2000 | 200 | 240 |
| MT_MS | 1,500,000 | 2,000,000 | 15,000 | 20,000 | 800 | 1000 |
| ME-MS | 350,000 | 500,000 | 3500 | 5000 | 300 | 400 |
| Parameters | Results with RWTS | Results without RWTS | |||
|---|---|---|---|---|---|
| Initial Value | Optimal Value | Initial Value | Optimal Value | ||
| 0.9269 | 0.8895 | 0.2733 | 0.1857 | 0.7038 | |
| 0.2720 | 0.9803 | 0.8366 | 1 | −0.0197 | |
| 0.3944 | 1 | 0.4308 | 0.9818 | 0.0182 | |
| 0.2441 | 0.0175 | 0.9103 | 0.5574 | −0.5399 | |
| 0.7398 | 0.6632 | 0.2192 | 0.5552 | 0.108 | |
| 0.9129 | 0.9967 | 0.8647 | 0.9444 | 0.0523 | |
| 0.0376 | 0.9313 | 0.0209 | 0.7206 | 0.2107 | |
| 0.2785 | 0.3640 | 0.4521 | 0.2233 | 0.1407 | |
| 0.8502 | 0.9038 | 0.2053 | 1 | −0.0962 | |
| 0.0360 | 0.2898 | 0.2816 | 0.3044 | −0.0146 | |
| 0.6596 | 0 | 0.9923 | 0.3833 | −0.3833 | |
| 0.5080 | 0 | 0.1007 | 0.4412 | −0.4412 | |
| 0.6302 | 0 | 0.6885 | 0.1045 | −0.1045 | |
| 0.5732 | 0.8339 | 0.0490 | 0.5615 | 0.2724 | |
| 0.0772 | 0 | 0.1057 | 0.7115 | −0.7115 | |
| 0.5490 | 0 | 0.8155 | 0.4152 | −0.4152 | |
| 0.8014 | 0 | 0.7269 | 0.7352 | −0.7352 | |
| 0.5060 | 0.8849 | 0.1489 | 0.7004 | 0.1845 | |
| 0.2029 | 0 | 0.0490 | 0.9433 | −0.9433 | |
| 0.5765 | 0 | 0.5939 | 0.0288 | −0.0288 | |
| 0.6953 | 0 | 0.0701 | 0.6211 | −0.6211 | |
| () | 1694.8 | 1699.1 | 1617.2 | 1696.7 | 0.14% |
| 0.8916 | 0.9277 | 0.8567 | 0.9215 | 0.67% | |
| 0.1389 | 0.1211 | 0.1525 | 0.1223 | −0.98% | |
| Convergence time(s) | 31.5057 (After 26 iterations) | 68.7121 (After 65 iterations) | 54.15% | ||
| First-Level Optimization | Second-Level Optimizations | ||||
|---|---|---|---|---|---|
| Parameters | Initial Value | Optimal Value | Parameters | Initial Value | Optimal Value |
| 0.6708 | 0.3632 | 0.7557 | 0.5222 | ||
| 0.8794 | 1 | 0.6616 | 1 | ||
| 0.4111 | 1 | 0.9971 | 1 | ||
| 0.4707 | 1 | 0.1987 | 0.0190 | ||
| 0.9795 | 0.8114 | 0.5339 | 0 | ||
| 0.1238 | 0.2692 | () | 105.3 | 87.9 | |
| () | 1627.2 | 1696.5 | 0.9325 | 0.9345 | |
| 0.8577 | 0.8921 | 0.5600 | 0.4722 | ||
| 0.1525 | 0.1387 | Convergence time(s) | 3.2501 (After 20 iterations) | ||
| 107.6 | 0.1907 | 0.2627 | |||
| 0.9324 | 0.1526 | 0.1327 | |||
| 358.7 | 0.3604 | 0.3086 | |||
| 0.6411 | 0.0221 | 0.2575 | |||
| Convergence time(s) | 9.4294 (After 69 iterations) | 0.2758 | 0.2640 | ||
| -- | -- | 0.3681 | 0.0688 | ||
| -- | -- | 0.1529 | 0.4675 | ||
| -- | -- | 0.0923 | 0.2179 | ||
| -- | -- | 0.3038 | 0.6188 | ||
| -- | -- | 0.4679 | 0.0705 | ||
| -- | -- | 0.1330 | 0 | ||
| -- | -- | 0.0605 | 0 | ||
| -- | -- | 353.9 | 357.6 | ||
| -- | -- | 0.6482 | 0.6700 | ||
| -- | -- | 0.3528 | 0.3438 | ||
| -- | -- | Convergence time(s) | 10.8344 (After 46 iterations) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Tao, L.; Pei, Y.; Liu, Z.; Yan, Q.; Cheng, Q. An Optimization Method of Flexible Manufacturing System Reliability Allocation Based on Two Dimension-Reduction Strategies. Machines 2024, 12, 24. https://doi.org/10.3390/machines12010024
Xu J, Tao L, Pei Y, Liu Z, Yan Q, Cheng Q. An Optimization Method of Flexible Manufacturing System Reliability Allocation Based on Two Dimension-Reduction Strategies. Machines. 2024; 12(1):24. https://doi.org/10.3390/machines12010024
Chicago/Turabian StyleXu, Jingjing, Long Tao, Yanhu Pei, Zhifeng Liu, Qiaobin Yan, and Qiang Cheng. 2024. "An Optimization Method of Flexible Manufacturing System Reliability Allocation Based on Two Dimension-Reduction Strategies" Machines 12, no. 1: 24. https://doi.org/10.3390/machines12010024
APA StyleXu, J., Tao, L., Pei, Y., Liu, Z., Yan, Q., & Cheng, Q. (2024). An Optimization Method of Flexible Manufacturing System Reliability Allocation Based on Two Dimension-Reduction Strategies. Machines, 12(1), 24. https://doi.org/10.3390/machines12010024






