Advancements in 3D-Printed Novel Nylon-6: A Taguchi Method for Surface Quality Sustainability and Mechanical Properties

Abstract

This research aims to establish the ideal settings for Nylon-6 (PA6) three-dimensional printing utilizing the fused filament production process and examine the resultant surface roughness. ANOVA, S/N ratio, and modeling are explained, along with their application in identifying the ideal values for surface roughness, sustainability, and mechanical properties. Average-surface roughness (Ra), root-mean-squared surface roughness (Rq), print time (PT), print energy (PE), and tensile testing (T) were explored as response parameters to identify the impact of PA6 parameters (layer thickness, extrusion temperature, print speed, and infill density). Tests of validity demonstrated a significant decline in Ra, Rq, PE, PT, and T for the ideal values of the developed product of 10.58 µm and 13.3 µm, 23 min, 0.13 kWh, and 42.7 Mpa, respectively. Ra, Rq, PT, PE, and T have all been optimized using Taguchi techniques as a preliminary step towards application in future research and prototypes.

1. Introduction

The method of joining materials successively layer by layer to construct an object is known as “additive manufacturing” (AM) [1]. Layers are added to create the material component [2]. Sheet lamination, binder jetting, directed energy deposition, and selective laser milling are the most popular AM processes [3,4,5]. Around 1988, Crump [6] registered a patent on the three-dimensional printing (3DP) fused filament fabrication (FFF) method, and the schematic of the FFF 3D Printer is depicted in Figure 1.

For example, 3D printers served as portable factories, aiding in rapid manufacturing during the emergency response to the COVID-19 pandemic [8]. Medical implants, orthodontics, aviation, refrigeration, and automotive products are some of the many areas of engineering and industry that have benefited from technological advancements [9]. FFF and PolyJet dental models are accurate and precise and manufactured using additive manufacturing [10]. Biological, building applications, medicinal [11,12,13], jewelry industries, lightweight heating components [14,15,16], and designs for investment artifacts are examples of where FFF 3DP has been put to use [17]. FFF finds extensive usage in enhancing the characteristics of a wide range of materials. These include bolstering tensile strength [18], optimizing car components [19], creating prototypes for research purposes [20], conducting microstructural investigations [21,22,23], and even contributing to the global effort against the COVID-19 pandemic [8,24]. However, compared to other AM techniques, the surface quality of components produced by FFF is inferior. The poor surface finish on finished products is an inevitable drawback of the FFF process because of the heating and cooling cycles required. Surface and dimensional flaws caused by the FFF process seem to be major roadblocks to using FFF components in quick tooling and casting. The FFF processing parameters used and the part configuration determine the fabricated component’s surface quality.

Numerous scientists have endeavored to improve the surface quality of parts produced by FFF. As indicated by [25], high building orientations and thinner slices reduce surface roughness. Based on surface morphological roughness and the production time of the component, a model was built for choosing standard part alignment. Surface roughness was shown to be significantly influenced by layer thickness (LT), surface angles, cross-sectional raster form, and overlap interval by Ahn et al. [26]. The contour widths and LT were shown to be essential criteria for the surface roughness, as reported by Bakar et al. [25]. According to Nancharaiah et al. [27], raster width affects manufactured components’ quality. Surface roughness was enhanced by slightly increasing print speed (S) and LT, as reported by Stephen Oluwashola Akande. However, the raster width, if any, was not indicated [28]. Lower LT values at 100% infill density (IN) significantly affect surface roughness, as discovered by Nuez et al. [29]. PA6 polymer components, when subjected to the same processing conditions as polylactic acid (PLA), were shown to have a greater surface roughness than other materials [30]. Thinner deposited layers are associated with better part surfaces, as stated by Perez et al. [31]. According to studies [32], authors recommend exercising extreme caution while selecting the extrusion temperature (ET) and the bed temperature, as the former might cause layers to separate from the latter and the latter to get damaged. The nozzle might become clogged at a low ET, and the material could get wrapped up at a high one. Surface roughness was shown to be affected by ET, S, and LT in a study by Gao et al. [33]. Researchers Vyavahare et al. [34] observed that surface roughness was affected by ET, depositing speed, and LT.

Regarding developing AM process parameters, Taguchi optimization has emerged as one of the most effective optimization strategies. Computer numerical control (CNC) procedures [35,36], laser cutting [37], investment casting [38,39], the electrical discharge machining (EDM) process [40], drilling [41], other machining [42,43,44], etc. are just a few examples of the many systems that researchers have found success optimizing using the Taguchi technique. The authors suggested the Taguchi approach to quickly and systematically enhance the quality, efficiency, and cost-effectiveness of operations [45,46]. Taguchi analysis was performed by the authors [14] to look into the best way to optimize the FFF 3DP process parameters. Taguchi and gray relational analysis were employed by Srivastava et al. to examine and improve the FFF process parameters, and the results were quite promising [47]. The FFF processing parameters were investigated by Vyavahare et al., who then utilized a regression model to investigate the resulting data and improve the model [34].

After reviewing the relevant literature, the parameter settings that may change the surface quality or mechanical characteristics were chosen. The authors made an effort to account for most of the variables. Print rate and raster width are chosen as independent variables to further characterize the influence on surface roughness [48]. According to the research [27,49], LT is the most essential factor in smoothing out surfaces. The building pattern significantly impacts surface roughness, good surface finish, and mechanical characteristics [50].

While companies strive to produce lightweight goods, doing so sometimes comes at the expense of strength and mechanical qualities. Selecting the best IN allows maximum strength with little material use [51]. According to [52], further research on the impact of ET on surface roughness is required. The authors have used this metric for this exact reason. The quality of a 3D-printed component is most affected by the bed temperature, as stated in [32].

There is much research on optimizing surface roughness using a variety of methods. Nonetheless, little is known about the printing and optimization of Nylon-6 (PA6) material, and (iii) little effort is made to assess the influence of additional process factors. This research aims to answer the following questions: (i). To investigate the impact of FFF parameters on the average surface roughness (Ra), mean squared surface roughness of PA6 (Rq), print time (PT), print energy (PE), and tensile testing (T), the authors tested the effects of varying the LT, ET, S, and IN. (ii). Taguchi and S/N ratio confirmation study on FFF 3DP parameters (iii). In order to learn about the parametric impact of regression, a regression model must be developed.

2. Materials and Methods

2.1. Materials

The experiment was conducted utilizing a PA6 material-equipped creality 10S Pro printer with a diameter of 1.75 mm. The “kexelled” company supplied the PA6 materials with the specifications listed in

Table 1. Experimental materials specifications (credit: Kexelled).

TYPE	Diameter	S mm/sec	ET °C	Bed Temperature °C	Tensile Strength MPa	Flexural Strength MPa
PA6	1.75 mm	40–80	240–280 °C	80–100 °C	40	85

.

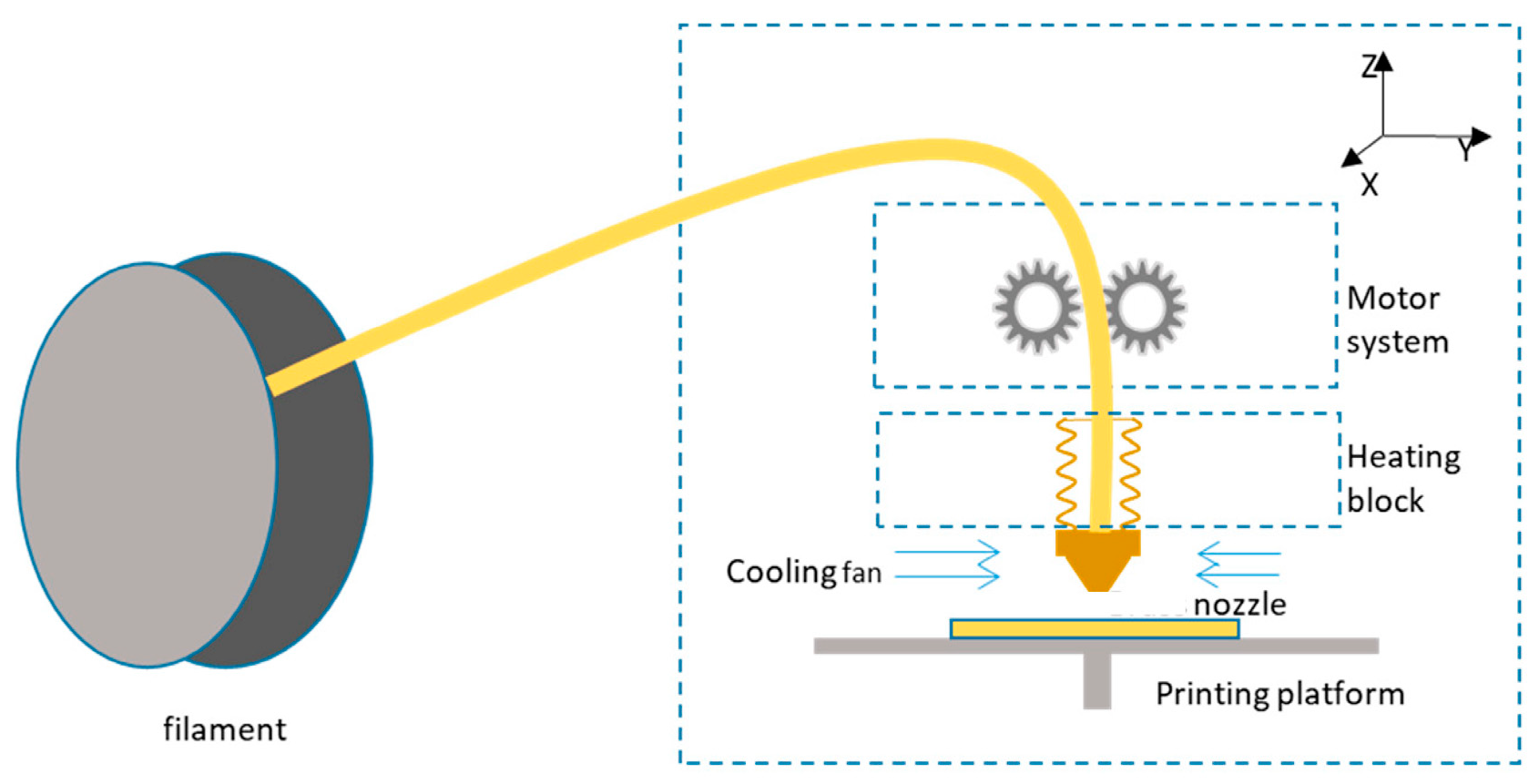
2.2. Methods

The PA6 material was chosen based on its compatibility with the Creality 10S Pro printer and its characteristics demonstrated in previous research [53]. The fabrication of test samples followed the specifications of the D638 type IV specimen, represented in Figure 2a,b. Figure 2a illustrates the tensile (T) testing setup, while Figure 2b presents detailed information about the Ra/Rq measurements taken at three distinct locations on the sample, and Figure 2c shows the Ra tester.

Following experimental design finalization, the STL format was imported into the slicer. Necessary adjustments were made before dispatching the file for 3D printing. The parameter range for FFF 3DP, pertaining to the PA6 polymer employed in this study, is outlined in

Table 2. Parameters for an FFF 3DP print of a PA6 polymer sample.

Parameter	Unit	Symbol	Level 1	Level2	Level3
LT	mm	LT	0.12	0.2	0.3
S	mm/s	S	40	55	70
ET	°C	ET	240	255	270
IN	%	IN	10	50	90

.

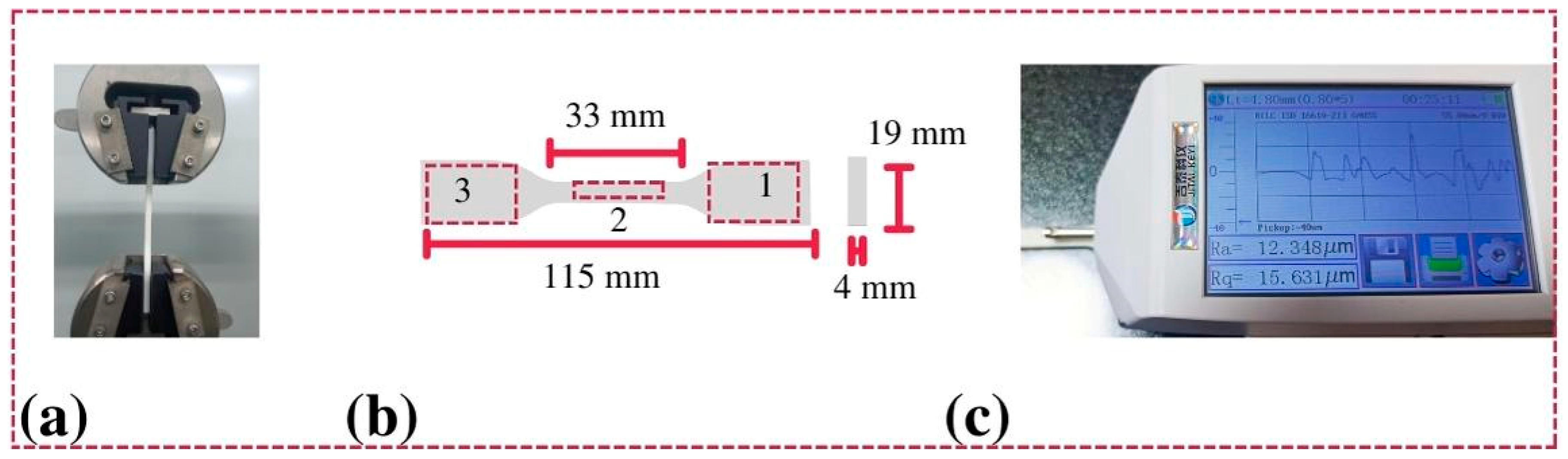
Measurement Procedure

For T testing, the GTM 2500 device, outfitted with a 5 KN payload, was utilized (refer to Figure 2a). This evaluation was performed at a steady crosshead speed of 5 mm/min, diligently following the ISO 527:1997 standard. The entire assessment was conducted in a controlled environment of 25 °C, employing a crosshead speed of 5 mm/s. Using a profilometer from the company ‘JITAI KEYI,’ model JD520, the value of the fabricated part’s surface roughness was determined as depicted in Figure 2c; this value was described using Equation (1) as the arithmetic mean of the actual values of all deviances in the surface profile along the centerline. Using Equation (2) [54], we determined the Rq by measuring the deviation of height from the mean line along the length. Analytical measurements were made using a sample length (Lw) = 4.8 mm in accordance with the ISO 16610-211 standard [55].

$$Ra=\frac{1}{Lw}{\int }_0^{Lw}\left|Z\left(\mathrm{y}\right)\right|d\mathrm{y}$$

(1)

$$Rq={\left[\frac{1}{Lw}{\int }_0^{Lt}{\left(Z\left(\mathrm{y}\right)\right)}^{2}d\mathrm{y}\right]}^{\frac{1}{2}}$$

(2)

Lw is the sample’s length while Z(y) is the coordinate of the curves used to create the profile.

Following the surface measurements, the samples underwent SEM analysis using an SEM 4000 machine. This analysis provided a visual examination of the sample’s microstructure and surface characteristics. To streamline experimentation efforts in relation to PA6, the implementation of L9 orthogonal array techniques has been adopted, aimed at optimizing both time and cost considerations [32,56]. Thereafter, results were meticulously analyzed using the Taguchi method, leading to the formulation of a rigorous statistical model to validate the study’s outcomes. The printed PA6 sample structures are exhibited in Figure 3. Three representative samples were printed for each test iteration, three measurements were undertaken for T testing, and nine measurements were undertaken for Ra/Rq, and the results were averaged to ensure precision.

3. Results and Discussions

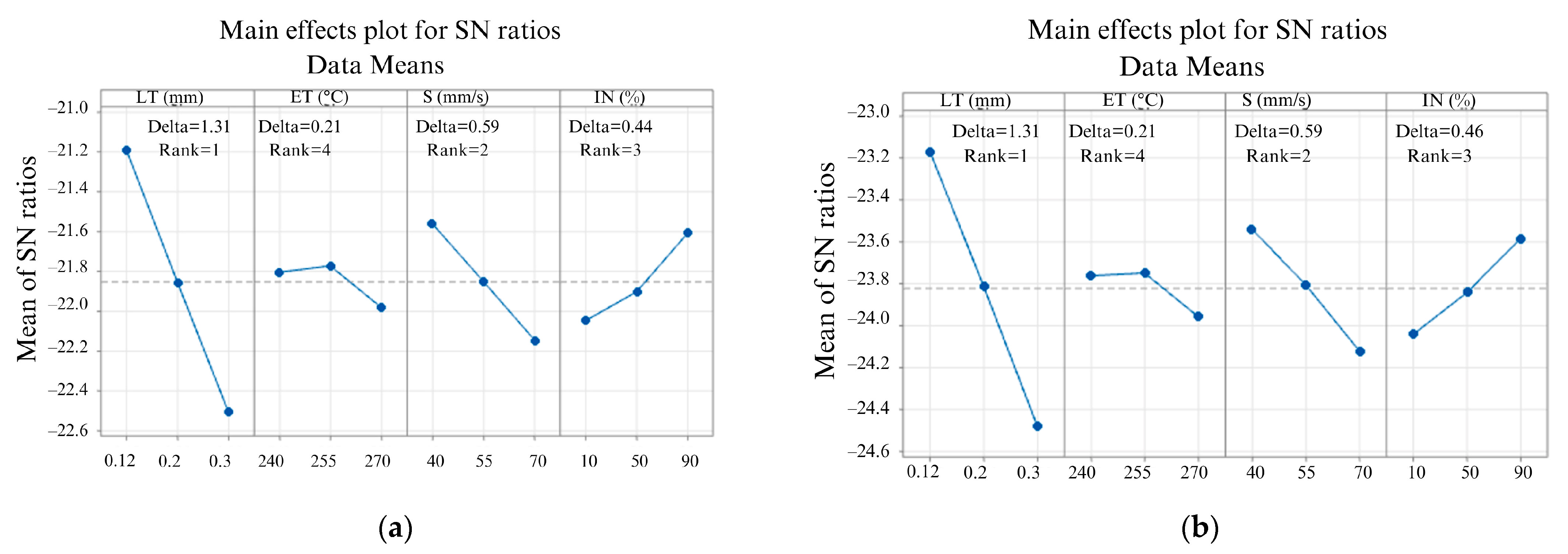
3.1. Taguchi Process

The A-loss function used by Genichi Taguchi [57] is the disparity and desired values translated into the signal-to-noise ratio. The ratio of means to standard deviation is denoted by the S/N ratio. This research reveals that surface quality is enhanced by decreasing Ra, Rq, PT, and PE [58]. The findings of the S/N ratio are presented in

Table 3. Design and outcomes of experiments with PA6 polymer.

LT (mm)	ET (°C)	S (mm/s)	IN (%)	T (MPa)	Ra (μm)	Rq (μm)	PT (min)	PE (kWh)
0.12	240	40	10	26.42	11.28	14.20	58	0.338
0.12	255	55	50	33.54	11.43	14.29	59	0.344
0.12	270	70	90	42.66	11.71	14.74	61	0.356
0.20	240	55	90	37.9	11.97	14.96	45	0.263
0.20	255	70	10	27.41	12.98	16.33	29	0.169
0.20	270	40	50	32.74	12.22	15.28	49	0.286
0.30	240	70	50	27.39	13.81	17.26	26	0.152
0.30	255	40	90	34.72	12.43	15.64	39	0.228
0.30	270	55	10	22.2	13.85	17.41	26	0.152

. Minitab 21.3 was used to conduct the Taguchi analysis.

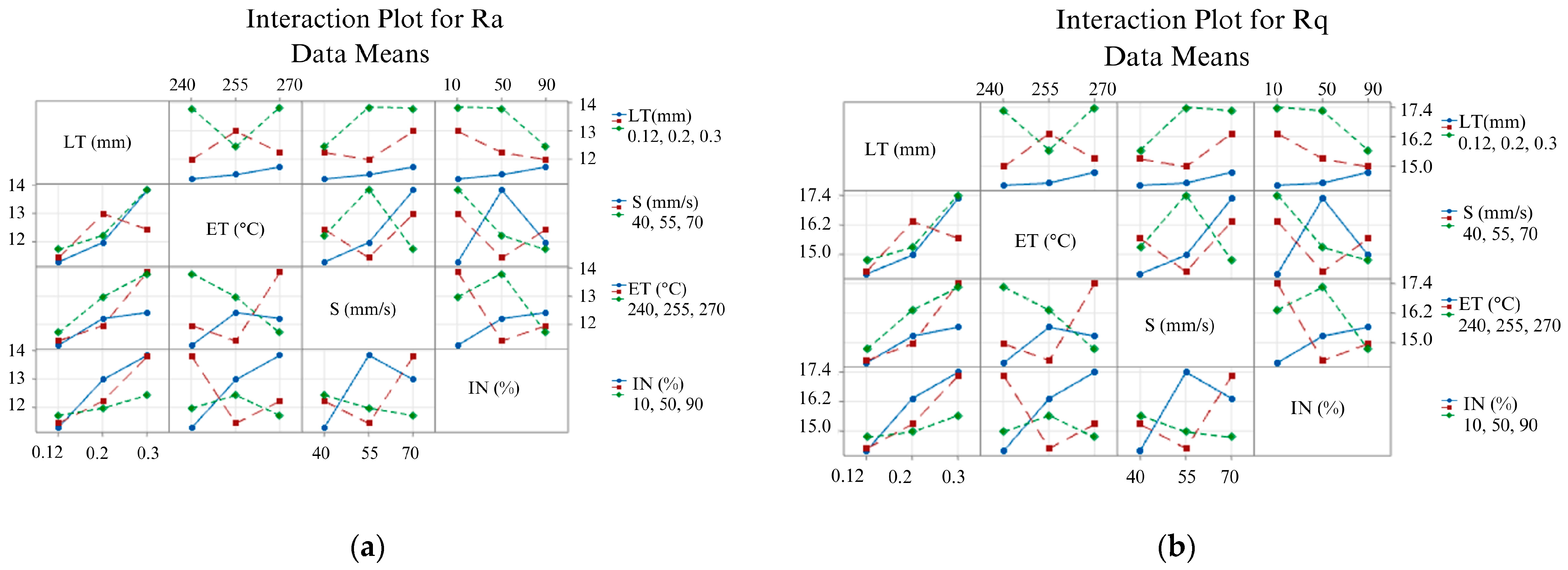
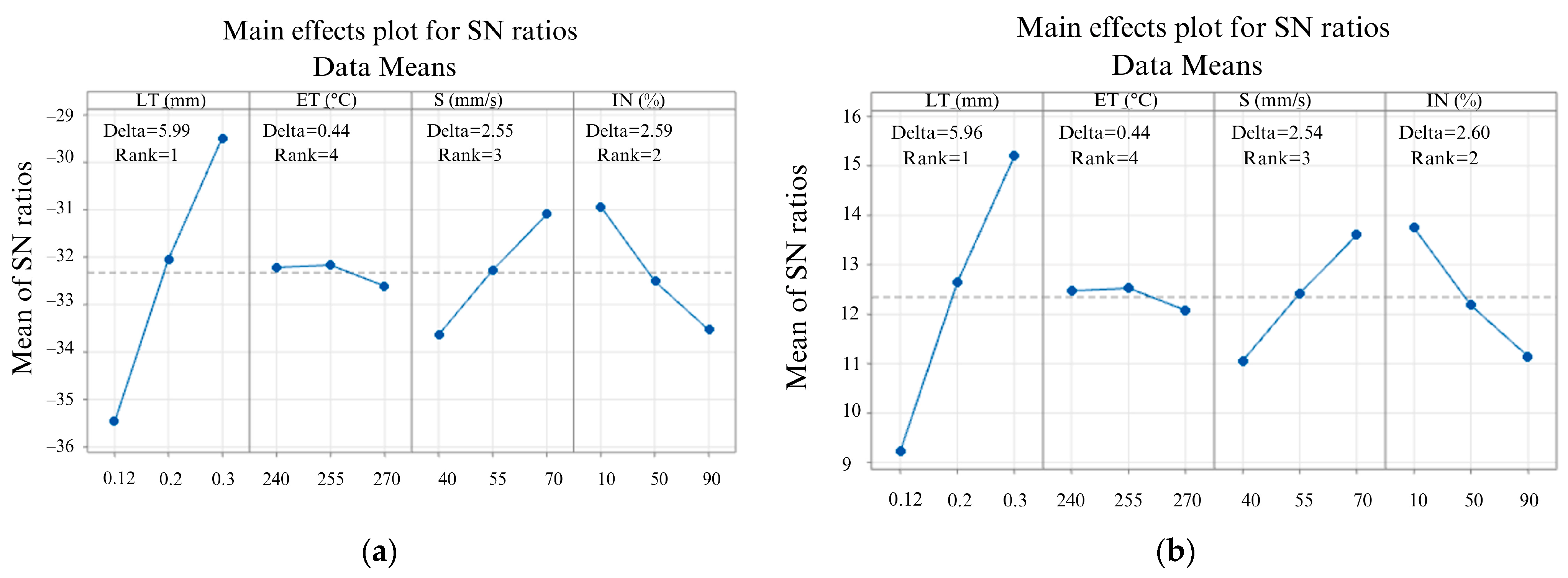
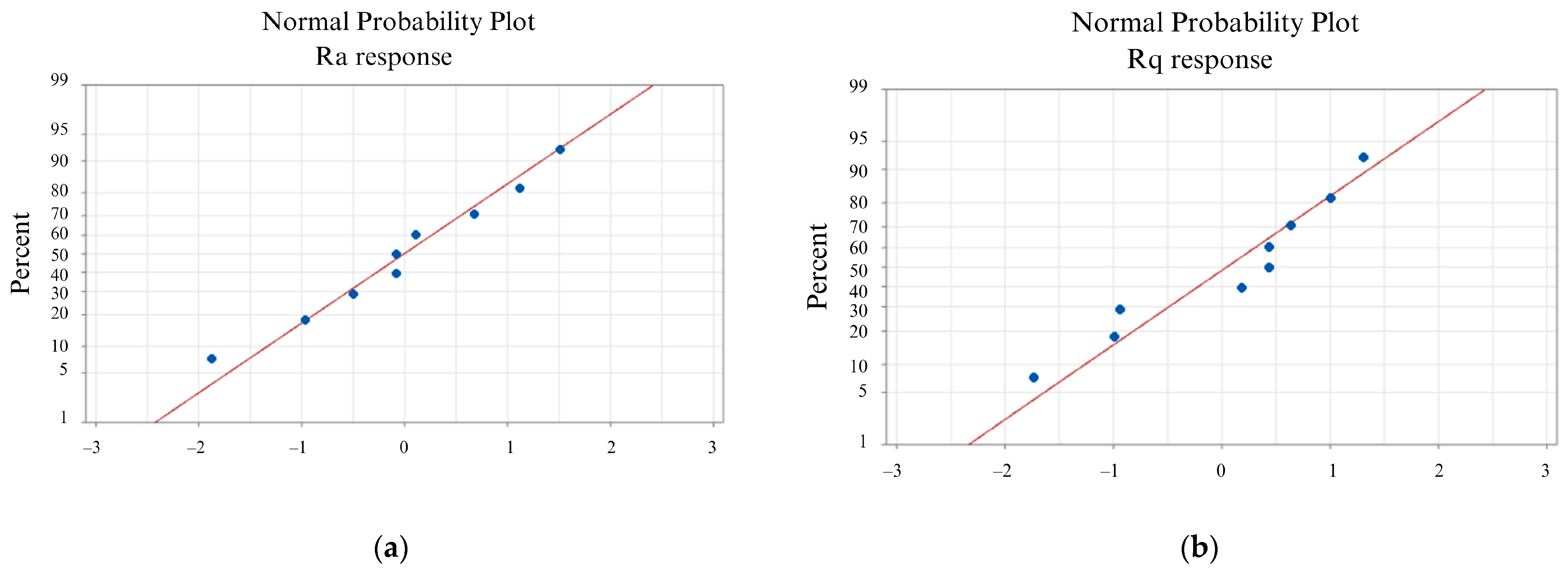
3.2. Effects of the 3D Printing Parameters on Ra and Rq

Due to its tendency to shrink, heat up, and harden during printing, PA-6 is rarely used [33]. Attempting to print PA-6 with a Creality CR10 S 3D Printer by varying eight parameters (starting line thickness, ID, raster breadth, bed temperature, build patterns, ET, S, and LT) proved unsuccessful. To print with the Creality CR10 S Pro, experimentation was conducted with the LT, S, ET, and IN settings. A print temperature of 235 degrees Celsius was tried, but the print tangled and failed to adhere to the bed surface. For PA-6, the temperature was set within a range of 240 °C to 270 °C. Printing at 0.08 mm and 0.1 mm LT was unfeasible, leading to the adoption of 0.12 mm and 0.3 mm, respectively. Print speeds between 40 and 80 mm per second were tested, aligning with the manufacturer-recommended minimum and maximum parametric values for the material. However, a maximum print speed of 70 mm/s was ultimately achieved with this material. The speed levels were established as 40mm/s for level 1, 55 mm/s for level 2, and 70 mm/s for level 3. As IN significantly affects PT and PE, this parameter was explored by setting values ranging from 10% to 90%. In the open-air printer, which had a minor effect on Ra and Rq due to rapid air flow causing flaws in layers, the sample was printed.

The influence of the FFF settings on Ra (Figure 4a) and Rq (Figure 4b) is shown. On the open-air printer, we printed the sample. Since the stair effect was constrained and the specimen was smooth, a reduction in “LT” resulted in a notable fall in Ra and Rq.

Also, the delta values of 1.89 and 2.36 for Ra and Rq place them in position 1 as the most crucial parameters for enhancing the Ra and Rq polymers. By lowering “S” from 70 mm/s to 40 mm/s, the values of Ra and Rq were drastically reduced. The result was a refined finish. With a delta output of 0.86, the “S” parameter placed second, demonstrating the significance of “S” in determining print quality. Increasing ET melted the material and made it lie flat and smooth before it was wrapped, resulting in a lower Ra and Rq. With a delta of 0.3, the “ET” parameter is placed fourth; at 90% IN, Ra and Rq dropped, whereas at 10% IN, a rougher surface was noticed due to the space within the structure acting as valleys. With a delta of 0.67, the “IN” parameter is placed third. The results are consistent with the broader literature [33,59,60,61].

The effect of the interaction on Ra and Rq was analyzed using parametric interactions. Figure 5a,b depict an interaction plot showing strong interactions between all factors. High levels of “ET” melt the material, low levels of “LT” provide thinner lines, and low levels of “S” create a decreased staircase effect, all of which contribute greatly to lowering Ra and Rq [62].

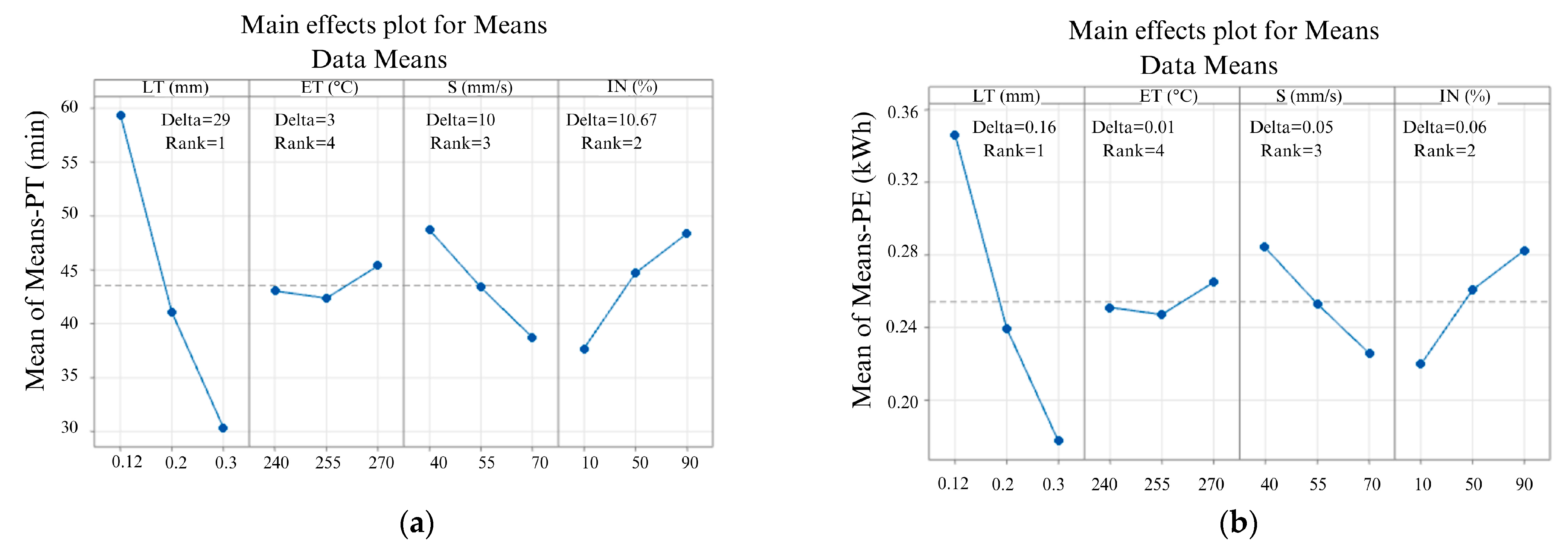
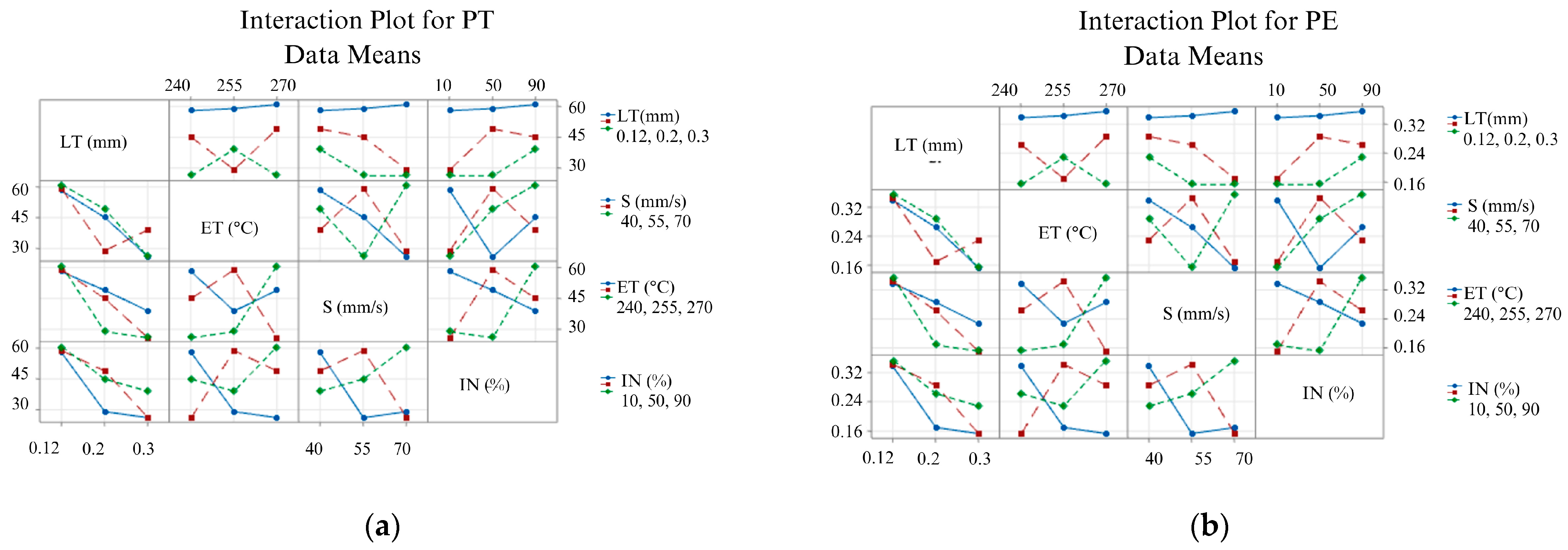
3.3. Effects of the FFF Parameters on Print Time and Energy

Decreasing the layer thickness will increase the amount of layer required to build the object, thus increasing the print time. Thinner layers may require more precise movements and finer details, increasing energy consumption. Delta values of 29 and 0.16 for PT and PE, respectively, place it in the first place as the most crucial parameter for enhancing the PT and PE of the polymer. A higher S reduces the time taken for each layer, thereby decreasing the overall print time. High-S often requires higher energy consumption due to increased motor movements and extrusion rates. Delta values of 10 and 0.05 for PT and PE, respectively, place it in third place as the most important parameter for enhancing the PT and PE of polymers. Higher ETs can reduce the viscosity of the filament, allowing it to flow more easily and thus potentially reducing print time. Increasing the ET may require more energy to heat the nozzle and maintain the desired temperature, resulting in higher energy consumption. Delta values of 3 and 0.01 for PT and PE, respectively, place it in fourth place as the most important parameter for enhancing the PT and PE of the polymer [63]. Higher INs require more time to print because they involve more filament deposition. Increased IN generally leads to higher energy consumption as more filament is required to fill the object’s internal structure. Delta values of 10.67 and 0.0.06 for PT and PE, respectively, place it in second place as the most important parameter for enhancing the PT and PE of polymers.

The impact of the FFF settings on PT and PE is shown in Figure 6a,b, respectively. The outdoor printer was used to print the sample. As the “LT” was lowered, PT and PE dropped noticeably due to the lack of a staircase effect and the uniformity of the surface.

The effect of the interaction on PT and PE was analyzed using parametric interactions. Figure 7a,b depict an interaction plot showing strong interactions between all factors. High “ET” melt the material, the highest levels of “LT” provide thicker lines, and high levels of “S” decrease the total PT of printing, all of which contribute greatly to lowering PT and PE [62].

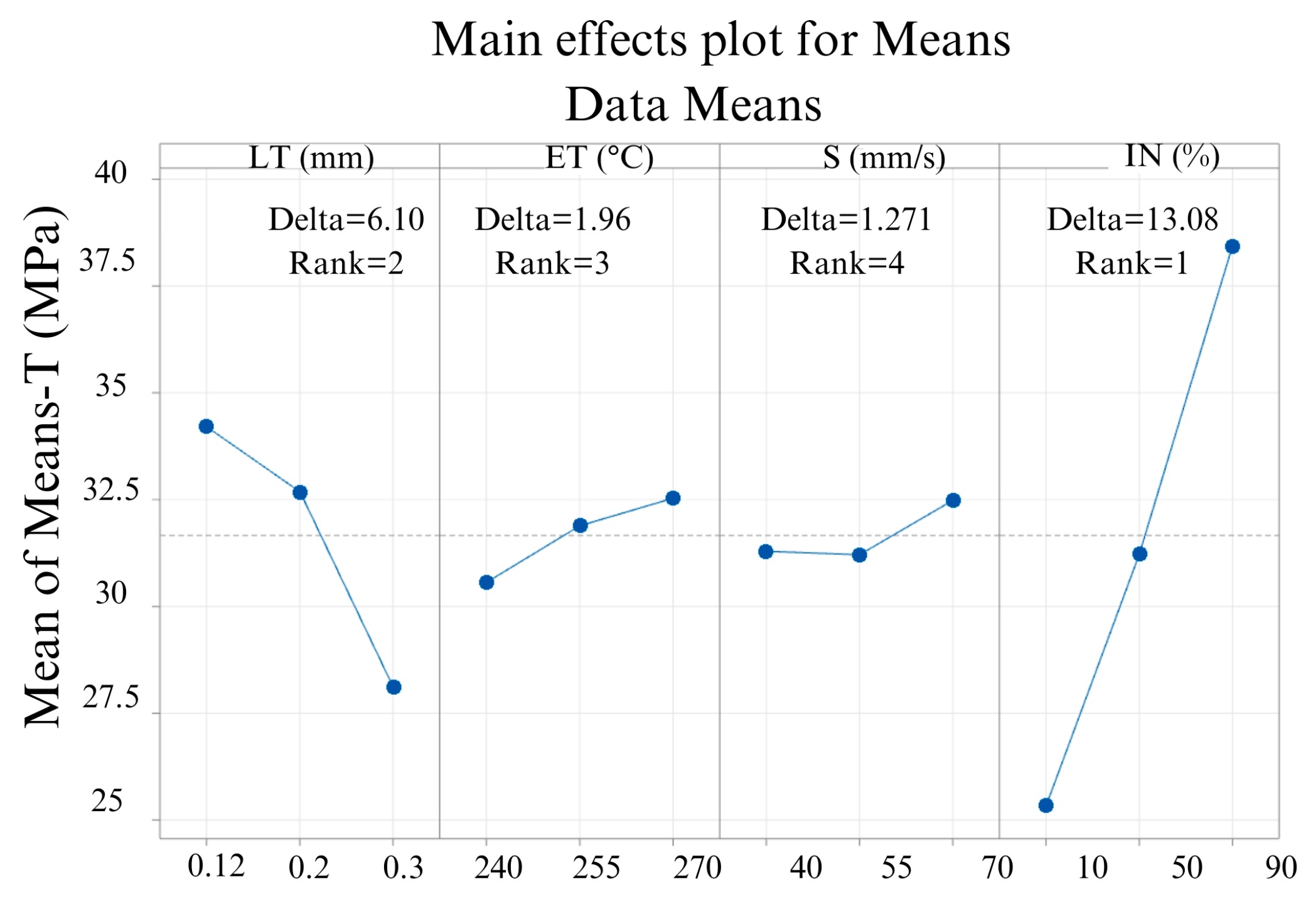
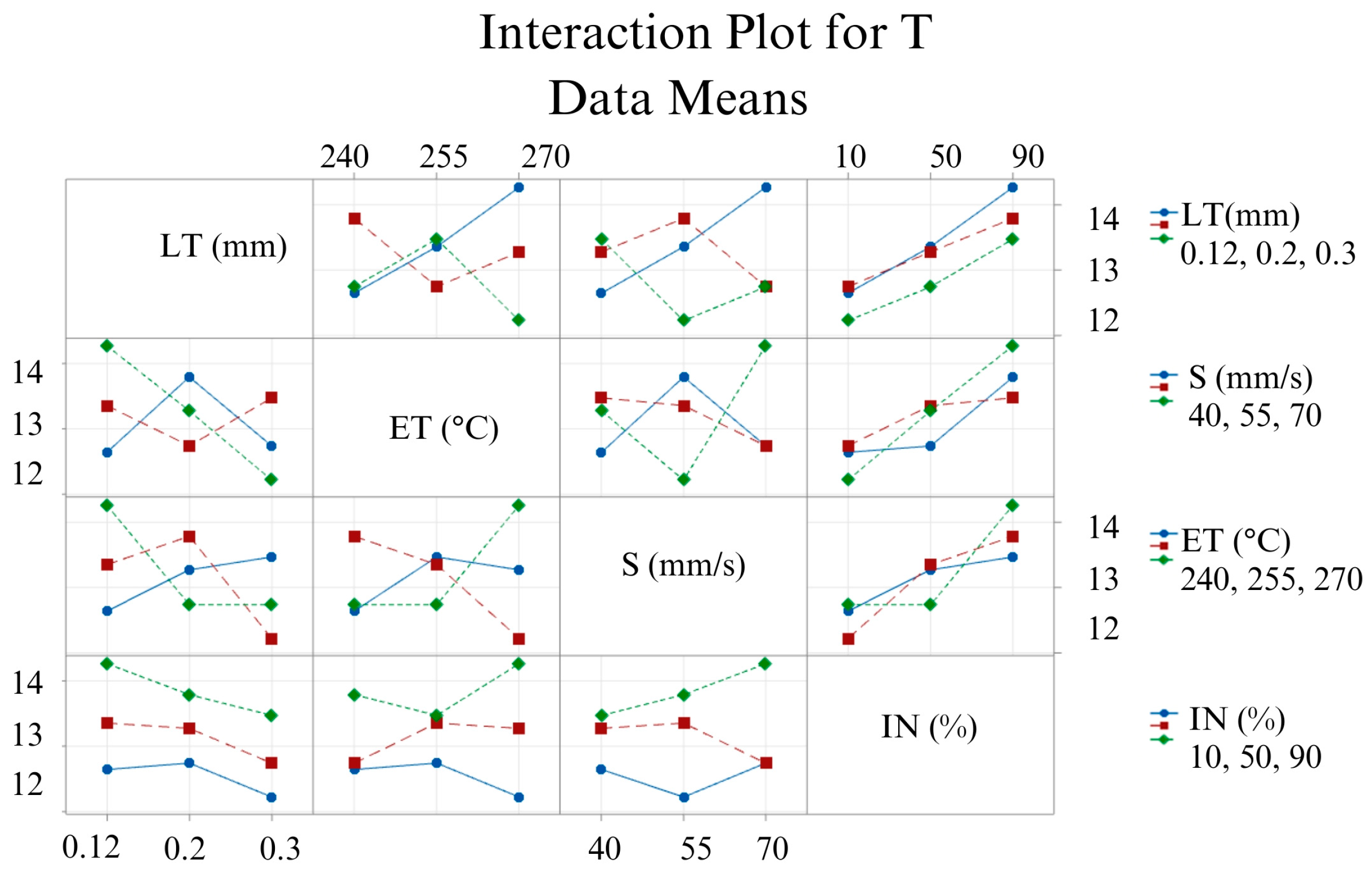
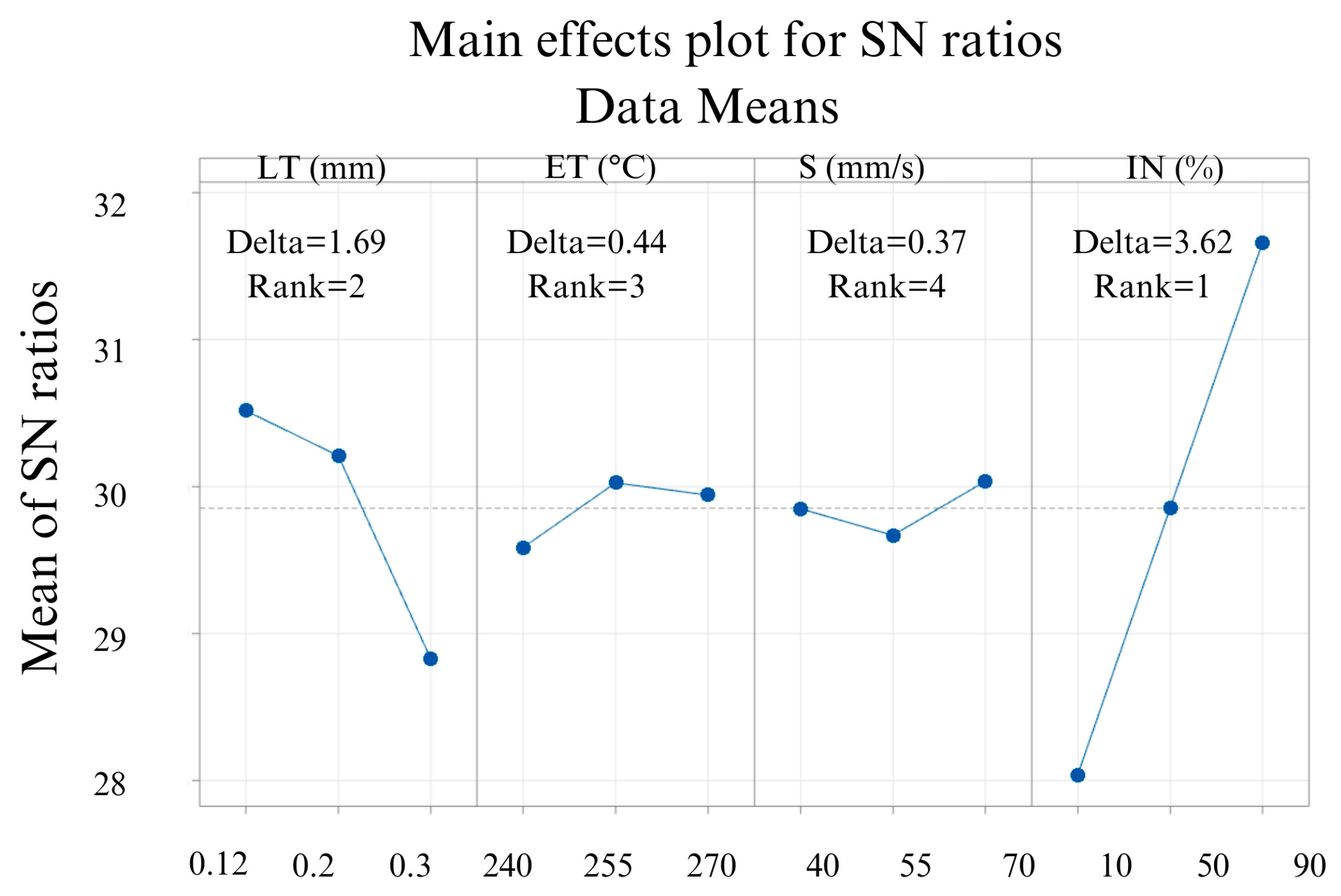
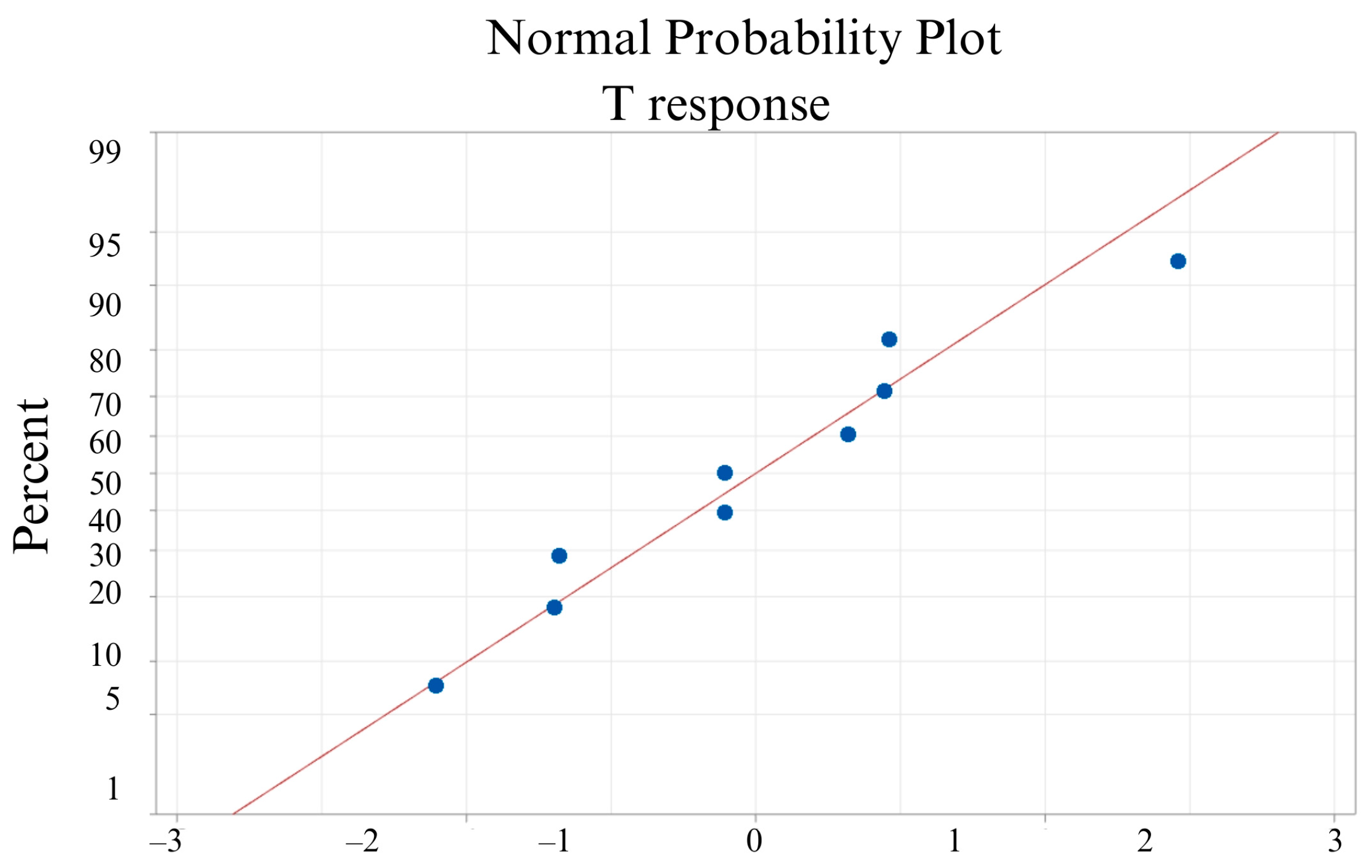
3.4. Effects of the 3D Printing Parameters on Tensile Strength (T)

The influence of the FFF settings on T, as shown in Figure 8, is evident. A reduction in “LT” led to a notable improvement in tensile strength, indicating the specimen’s enhanced mechanical properties when the layer thickness was reduced.

According to the delta values from the response table, “IN” is the most influential parameter, with a delta of 13.08, indicating its pivotal role in enhancing tensile strength. Adjusting “S” from 70 mm/s to 40 mm/s resulted in an appreciable increase in T, highlighting the material’s better mechanical response at slower print speeds—the delta value of 1.27 ranks “S” fourth in terms of its impact on tensile strength. An increase in ET ensures a more uniform melt of the material, leading to better layer adhesion and thereby improving T. With a delta value of 1.96, the “ET” parameter ranks third in influencing tensile strength. “LT”, with a delta value of 6.10, follows next. When “IN” was set at 90%, a surge in tensile strength was observed, possibly due to better material consolidation and reduced internal voids. At a mere 10% IN, the structure’s internal voids might have adversely impacted tensile strength. With its significant delta value of 13.08, the “IN” parameter is the most influential. These observations align well with findings from the broader literature [64,65].

Further, the interplay of these parameters and their collective impact on T were studied through parametric interactions. Figure 9 reveals strong interactions between all factors. Elevated “ET” values ensure optimal material melt, reduced “LT” values lead to finer printed lines, and slower “S” values minimize rapid cooling and ensure better layer fusion, collectively enhancing tensile strength T [62].

3.5. Optimal Parameters for Ra, Rq, PT, PE, and T Selection

Table A1. Mean response table of S/N ratio for Ra of PA6 polymer.

Level	LT (mm)	S (mm/s)	ET (°C)	IN
1	−21.19	−21.80	−21.56	−22.05
2	−21.86	−21.77	−21.85	−21.90
3	−22.51	−21.98	−22.15	−21.61
Delta	1.31	0.21	0.59	0.44
Rank	1	4	2	3

,

Table A2. Mean response table of S/N ratio for Rq of PA6 polymer.

Level	LT (mm)	S (mm/s)	ET (°C)	IN
1	−23.17	−23.76	−23.54	−24.04
2	−23.81	−23.75	−23.81	−23.84
3	−24.48	−23.96	−24.12	−23.58
Delta	1.31	0.21	0.59	0.46
Rank	1	4	2	3

,

Table A3. Mean response table of S/N ratio for PT of PA6 polymer.

Level	LT (mm)	S (mm/s)	ET (°C)	IN
1	−35.46	−32.21	−33.63	−30.94
2	−32.04	−32.16	−32.26	−32.51
3	−29.47	−32.60	−31.08	−33.53
Delta	5.99	0.44	2.55	2.59
Rank	1	4	3	2

,

Table A4. Mean response table of S/N ratio for PE of PA6 polymer.

Level	LT (mm)	S (mm/s)	ET (°C)	IN
1	9.220	12.462	11.045	13.742
2	12.639	12.517	12.411	12.168
3	15.189	12.069	13.592	11.138
Delta	5.969	0.449	2.547	2.605
Rank	1	4	3	2

and

Table A5. Mean response table of S/N ratio for T of PA6 polymer.

Level	LT (mm)	S (mm/s)	ET (°C)	IN
1	30.52	29.59	29.85	28.04
2	30.21	30.03	29.67	29.85
3	28.83	29.94	30.04	31.66
Delta	1.69	0.44	0.37	3.62
Rank	2	3	4	1

display the attained Ra, Rq, PT, PE, and T S/N response values. Graphs of the mean S/N ratio for PA6 were calculated in Minitab and are shown in Figure 10a,b. If the S/N ratio is high, the gap between the expected and actual values is minimal. From Figure 10a,b, we can deduce that the “LT” setting at 0.12 mm, the “ET” setting at 255 °C, the “S” setting at 40 mm/s, and the “IN” setting at 90% all yield the greatest mean S/N ratio for Ra and Rq. Therefore, Table A1 and Table A2 include bolded values for the anticipated ideal FFF parameters (LT = 0.12 mm, ET = 255 °C, S = 40 mm/s, IN = 1, and E = 90 percent) for obtaining the low Ra and Rq through the Taguchi approach. “LT-S1 ET-S2 S-S1 IN-S3” was the anticipated best combination for Ra and Rq. The significance of each parameter is illustrated by the S/N ratio obtained: for Ra and Rq influencing “LT,” the ratio is 1.31 (rank 1) and 1.31 (rank 1); for “ET,” it is 0.21 (rank 4) and 0.21 (rank 4); for “S”, it is 0.59 (rank 2) and 0.59 (rank 2); and for “IN,” it is 0.44 (rank 3) and 0.46 (rank 3).

From Figure 11a,b, we can deduce that the “LT” setting at 0.3 mm, the “ET” setting at 255 °C, the “S” setting at 70 mm/s, and the “IN” setting at 10% all yield the highest mean S/N ratio for PT and PE. Therefore, Table A3 and Table A4 include bolded values for the anticipated ideal FFF parameters (LT = 0.3 mm, ET = 255 °C, S = 70 mm/s, and IN = 10) for obtaining low PT and PE through the Taguchi approach. “LT-S3 ET-S2 S-S3 IN-S1” was the anticipated best combination for PT and PE. The significance of each parameter is illustrated by the S/N ratio obtained: for PT and PE influencing “LT,” the delta is 5.99 (rank 1) and 5.96 (rank 1); for “ET,” it is 0.44 (rank 4) and 0.44 (rank 4); for “S”, it is 2.55 (rank 3) and 2.55 (rank 3); and for “IN,” it is 2.59 (rank 2) and 2.60 (rank 2).

From Figure 12, we can deduce that the “LT” setting at Level 1, the “ET” setting at Level 2, the “S” setting at Level 3, and the “IN” setting at Level 3 all yield the highest mean S/N ratio for T. Therefore,

Table A8. The Validation test outcomes for T of PA6 polymer.

	Preliminary Parameters		Optimum Parameters
	Predicted	Experimented	Predicted	Experiment
Level	LT-S2 ET-S2 S-S2 IN-S2	LT-S2 ET-S2 S-S2 IN-S2	LT-S1 ET-S2 S-S3 IN-S3	LT-S1 ET-S2 S-S3 IN-S3
T (MPa)		32.2		42.7
S/N ratio (dB) for T (MPa)	30.25	30.34	32.68	32.69
S/N ratio (dB) improvement for T (MPa)	2.35
% increment in T	32.6

includes bolded values for the anticipated ideal FFF parameters (LT at Level 1, ET at Level 3, S at Level 3, and IN at Level 3) for obtaining high T through the Taguchi approach. “LT-S1 ET-S2 S-S3 IN-S3” was the anticipated best combination for T. The significance of each parameter is illustrated by the S/N ratio obtained: for T influencing “LT,” the delta is 1.69 (rank 2); for “ET,” it is 0.44 (rank 3); for “S,” it is 0.37 (rank 4); and for “IN,” it is 3.62 (rank 1).

3.6. Validation Test

It is necessary to conduct confirmation experiments to verify Taguchi’s projected ideal circumstances. Equation (3) [66] was used to calculate the projected S/N ratio (${\epsilon }_{predicted}$) and estimate and assess the responses under predicted ideal Ra conditions.

$${\epsilon }_{predicted}={\epsilon }_l+{\displaystyle \sum _{i=0}^x}{\epsilon }_0-{\epsilon }_M$$

(3)

${\epsilon }_M$ = Total mean S/N ratio

${\epsilon }_0$ = Mean S/N ratio at an optimal level

x = input number of FFF parameters

Table A6. The Validation test outcomes for Ra and Rq of PA6 polymer.

	Preliminary Parameters		Optimum Parameters
	Predicted	Experimented	Predicted	Experiment
Level	LT-S2 ET-S2 S-S2 IN-S2	LT-S2 ET-S2 S-S2 IN-S2	LT-S1 ET-S2 S-S1 IN-S3	LT-S1 ET-S2 S-S1 IN-S3
Ra (um)		12.35		10.58
Rq (um)		15.51		13.30
S/N ratio (dB) (Ra (um))	−21.82	−21.61	−20.57	−20.62
S/N ratio (dB) (Rq (um))	−23.74	−23.81	−22.57	−22.63
S/N ratio (dB) improvement for Ra (um)	1.25dB
S/N ratio (dB) improvement for Rq (um)	1.27dB
Percentage Reduction in Ra	14.35
% Reduction in Rq	14.25

for Ra and Rq,

Table A7. The Validation test outcomes for PT and PE of PA6 polymer.

	Preliminary Parameters		Optimum Parameters
	Predicted	Experimented	Predicted	Experiment
Level	LT-S2 ET-S2 S-S2 IN-S2	LT-S2 ET-S2 S-S2 IN-S2	LT-S3 ET-S2 S-S3 IN-S1	LT-S3 ET-S2 S-S3 IN-S1
PT (min)		40		23
PE (kWh)		0.234		0.13
S/N ratio (dB) for PT (min)	−31.99	−31.90	−26.67	−28.80
S/N ratio (dB) for PE (kWh)	12.68	12.70	17.99	−16.9
S/N ratio (dB) improvement for PT	5.32
S/N ratio (dB) improvement for PE	5.31
% Reduction in PT	42.5
% Reduction in PE	44.4

for PT and PE, and Table A8 for T detail the outcomes of confirmation experiments conducted at the optimal printing parameters predicted by Taguchi. When the optimal printing conditions are applied, the roughness performance attributes improve. The predicted and optimal printing settings for both polymers have similar S/N ratios, as shown in Table A6, Table A7 and Table A8. S/N ratios for Ra, Rq, PT, PE, and T were improved by 1.25 dB, 1.27 dB, 5.32 dB, 5.31 dB, and 2.35 dB, respectively, at the optimal FFF printing condition compared to initial parameter values. The verification studies show that the optimal printing conditions predicted by Taguchi yield superior results than the preliminary parameter settings. Ra, Rq, PT, and PE decreased by 14.35% and 14.25%, 44.50%, 44.40%, and 32.6%, respectively, when comparing the baseline parameter to Taguchi’s predicted ideal printing settings.

SEM TM4000 machine was used with initial settings and with Taguchi’s optimal settings are shown in Figure 13a,b. Figure 13a has a more rough surface and bulges, while Figure 13b has better surface quality.

4. ANOVA for Ra, Rq, PT and PE

The ANOVA identifies the most important FFF tuning knob to optimize performance.

Table 4. ANOVA for Ra of PA6 polymer.

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	p-Value
Regression	4	7.20193	98.44%	7.20193	1.80048	63.20	0.001
LT	1	5.34805	73.10%	5.34805	5.34805	187.72	0.000
ET	1	0.08640	1.18%	0.08640	0.08640	3.03	0.157
S	1	1.10082	15.05%	1.10082	1.10082	38.64	0.003
IN	1	0.66667	9.11%	0.66667	0.66667	23.40	0.008
Error	4	0.11396	1.56%	0.11396	0.02849
Total	8	7.31589	100.00%

,

Table 5. ANOVA Table for the Rq of PA6 polymer.

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	p-Value
Regression	4	11.3691	98.99%	11.3691	2.84226	98.43	0.000
LT	1	8.3550	72.75%	8.3550	8.35502	289.34	0.000
ET	1	0.1700	1.48%	0.1700	0.17002	5.89	0.072
S	1	1.7174	14.95%	1.7174	1.71735	59.47	0.002
IN	1	1.1267	9.81%	1.1267	1.12667	39.02	0.003
Error	4	0.1155	1.01%	0.1155	0.02888
Total	8	11.4846	100.00%

,

Table 6. ANOVA Table for the PT polymer.

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	p-Value
Regression	4	1560.68	95.62%	1560.68	390.17	21.82	0.006
LT	1	1231.85	75.47%	1231.85	1231.85	68.88	0.001
ET	1	8.17	0.50%	8.17	8.17	0.46	0.536
S	1	150.00	9.19%	150.00	150.00	8.39	0.044
IN	1	170.67	10.46%	170.67	170.67	9.54	0.037
Error	4	71.54	4.38%	71.54	17.89
Total	8	1632.22	100.00%

,

Table 7. ANOVA table for the PE polymer.

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	p-Value
Regression	4	0.052943	95.61%	0.052943	0.013236	21.78	0.006
LT	1	0.041668	75.25%	0.041668	0.041668	68.58	0.001
ET	1	0.000280	0.51%	0.000280	0.000280	0.46	0.534
S	1	0.005104	9.22%	0.005104	0.005104	8.40	0.044
IN	1	0.005891	10.64%	0.005891	0.005891	9.70	0.036
Error	4	0.002430	4.39%	0.002430	0.000608
Total	8	0.055374	100.00%

and

Table 8. ANOVA for T of PA6 polymer.

Source	DF	Seq SS	Contribution	Adj SS	Adj MS	F-Value	p-Value
Regression	4	322.409	98.52%	322.409	80.602	66.65	0.001
LT	1	57.731	17.64%	57.731	57.731	47.74	0.002
ET	1	5.782	1.77%	5.782	5.782	4.78	0.094
S	1	2.136	0.65%	2.136	2.136	1.77	0.255
IN	1	256.76	78.46%	256.76	256.76	212.31	0
Error	4	4.837	1.48%	4.837	1.209
Total	8	327.246	100.00%

display the results of the ANOVA tests conducted on Ra, Rq, and PT, PE, and T. Table 4 reveals that “LT,” followed by “S,” “IN,” and “ET,” has the biggest impact on Ra. In descending order, the effects of LT, ET, S, and IN on Ra were 73.10%, 1.18%, 15.10%, and 9.11%.

Table 5 reveals that “LT,” followed by “S,” “IN,” and “ET,” has the biggest impact on Rq. In descending order, the effects of LT, ET, S, and IN on Ra were 72.75%, 1.48%, 14.95%, and 9.81%, respectively.

Table 6 reveals that “LT,” followed by “IN”, “S”, and “ET”, has the biggest impact on PT. In descending order, the effects of LT, ET, S, and IN on Ra were 75.47%, 0.5%, 9.19%, and 10.46%, respectively.

Table 7 reveals that “LT,” followed by “IN”, “S”, and “ET”, has the biggest impact on PE. In descending order, the effects of LT, ET, S, and IN on Ra were 75.25%, 0.51%, 9.22%, and 10.64%, respectively.

Table 8 reveals that “LT,” followed by “S”, “IN”, and “ET”, has the biggest impact on T. In descending order, the effects of LT, ET, S, and IN on Ra were 17.64%, 1.77%, 0.65%, and 78.46%, respectively.

5. Mathematical Modeling

Minitab 21.3 was used to conduct a regression analysis, which allowed for the development of forecasting analytics for the variables Ra, Rq, PT, and PE as a function of “LT,” “ET”, “S”, and “IN”. None of the responses have had any adjustments made to them. The regression analysis yielded the prediction Equations (4) and (5) for Ra, Rq, PT, PE, and T.

$$\mathrm{R}\mathrm{a}=7.05+10.469\mathrm{L}\mathrm{T}+0.00800\mathrm{E}\mathrm{T}+0.02856\mathrm{S}-0.00833\mathrm{I}\mathrm{N}$$

(4)

$$\mathrm{R}\mathrm{q}=8.58+13.085\mathrm{L}\mathrm{T}+0.011223\mathrm{E}\mathrm{T}+0.03567\mathrm{S}-0.01083\mathrm{I}\mathrm{N}$$

(5)

$$\mathrm{PT}=68.2-158.9\mathrm{LT}+0.078\mathrm{ET}-0.333\mathrm{S}+0.1333\mathrm{IN}$$

(6)

$$\mathrm{PE}=0.397-0.924\mathrm{LT}+0.000456\mathrm{ET}-0.001944\mathrm{S}+0.000783\mathrm{IN}$$

(7)

T = 11.72 − 34.39 LT + 0.0654 ET + 0.0398 S + 0.1635 IN

(8)

The determination coefficient, R², was used to test the efficacy of the developed models [67]. A value close to one indicates high congruence between the dependent and independent variables [68]. If the updated data’s coefficient of determination (R2) is 94%, then the data was evaluated with 94% variability. The Ra and Rq mathematical models developed in this work obtained impressively high R2 values of 97.44 and 98.99, respectively. R² values of 95.62, 95.61, and 97.04 for the derived PT, PE, and T mathematical models are quite good. The predicted model’s coefficients were evaluated for significance using the residual graphs [69]. Significant coefficients and a straight residual graph indicate that the model’s residual errors are normally distributed [70]. Ra and Rq normal probability plots are displayed in Figure 14; the proximity of the Ra and Rq residuals to the straight line indicates the significance of the developed model coefficient models.

PT and PE normal probability plots are displayed in Figure 15. In contrast, Figure 16 for T. The proximity of the PT, PE, and T residuals to the straight line indicates the significance of the developed model coefficient models.

The built models were put through a series of conformance tests presented in

Table 9. Mathematical model developed for confirmation.

Run	Experimented					Predicted					Difference
	Ra	Rq	PT	PE	T	Ra	Rq-	PT	PE	T	Ra	Rq	PT	PE	T
2	11.43	14.29	59	0.344	33.54	11.50	14.43	57.33	0.334	34.64	−0.07	−0.14	+1.67	−0.01	+1.1
4	11.97	14.96	45	0.263	37.90	11.89	14.88	48.78	0.285	37.45	−0.08	−0.08	+3.78	−0.02	+0.4
6	12.22	15.28	49	0.286	32.74	12.03	15.11	50.78	0.296	32.27	−0.19	−0.17	+1.78	−0.01	+0.46
8	12.43	15.64	39	0.228	34.72	12.62	15.82	39.06	0.228	34.39	−0.19	−0.18	+0.06	0.00	+0.32

. The tests’ outcomes were casually chosen from the design of L9. The verification results showed that, within the given parameter range, the expected values from the model and the experimental data were in close agreement.

6. Conclusions and Future Directions

The following are the findings of the investigation:

• The optimal settings for 3D printing of Nylon-6 (PA6) using fused filament fabrication (FFF) were determined through a comprehensive study that analyzed the average surface roughness (Ra), root mean squared surface roughness (Rq), print time (PT), print energy (PE), and tensile strength (T).
• Through the application of Taguchi analysis via the S/N ratio, significant reductions in Ra, Rq, PT, and PE were achieved. The optimal values obtained were Ra of 10.58 µm, Rq of 13.3 µm, PT of 23 min, PE of 0.13 kWh, and T of 42.7 MPa.
• An analysis of variance (ANOVA) was utilized to understand the influence of the aforementioned parameters on surface roughness, print time, and print energy.
• Modeling based on the investigational results was also developed, which is expected to facilitate predicting the best printing conditions without the necessity for time-consuming trial tests.
• The study lays the foundation for future research and the practical implementation of these optimized parameters in the 3D printing of PA6 using FFF, promising surface finishes, and sustainability improvements.

Future Recommendations

• More PA6 parameters need to be studied, and then those values can be used to create useful industrial models.
• Determine PA-6’s mechanical characteristics by subjecting it to flexural testing.
• Reduce the surface’s roughness by employing various optimization strategies, such as the response surface methodology.